Band 4 – Page 26

Analyse how the 'Frequency' component of the FITT principle must be modified throughout a training year for an elite 800m runner. In your answer, refer to periodisation and physiological considerations. (8 marks)

--- 20 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Base/general preparation phase:

Aerobic training frequency: 4-5 sessions weekly to develop aerobic capacity essential for the 800 m
Anaerobic training frequency: Limited to 1-2 sessions weekly to establish foundation
The 800 m runner requires higher aerobic training frequency initially as the event demands approximately 60% aerobic energy contribution
Recovery between aerobic sessions can be shorter (24 hours) allowing higher frequency than anaerobic sessions

Specific preparation phase:

Aerobic training frequency: Reduces to 2-3 sessions weekly but maintains aerobic capacity
Anaerobic glycolytic training frequency: Increases to 2-3 sessions weekly targeting race-specific energy system
ATP-PCr system training: 1-2 sessions weekly for speed development
Balanced frequency between energy systems reflects the mixed aerobic-anaerobic nature of the 800 m event

Competition phase:

Race-specific training frequency: 2 high-quality sessions weekly combining aerobic and anaerobic demands
Maintenance aerobic sessions: 1-2 weekly at moderate intensity
Pure speed/ATP-PCr sessions: 1 weekly to maintain neuromuscular power
Overall reduction in frequency but increased specificity and quality

Energy system recovery requirements:

ATP-PCr system: Recovers within hours but neuromuscular fatigue requires 36-48 hours between high-intensity sessions
Glycolytic system: Requires 48-72 hours for enzyme restoration and lactate clearance, limiting frequency to 2-3 times weekly
Aerobic system: Can be trained more frequently (daily if necessary) with appropriate intensity modulation
800 m training frequency must balance all three energy systems’ recovery requirements

Adaptation considerations:

Anaerobic adaptations occur more rapidly than aerobic adaptations, requiring frequency adjustments
Early season higher aerobic frequency develops capillary density and mitochondrial content
Mid-season increased anaerobic frequency develops lactate tolerance and clearance capacity
Frequency must be adjusted based on individual adaptation rates to each energy system

Periodised frequency model:

Microcycle design: Hard anaerobic sessions separated by 48-72 hours with aerobic work between
Mesocycle pattern: 3 weeks of progressive frequency followed by 1 week reduced frequency (e.g., 3:1 loading pattern)
Seasonal fluctuation: Highest total frequency during base phase, most anaerobic-focused frequency mid-season, reduced but specific frequency during competition
Tapering: 30-50% reduction in frequency 7-14 days before major competition while maintaining intensity

Show Worked Solution

Sample Answer

Base/general preparation phase:

Aerobic training frequency: 4-5 sessions weekly to develop aerobic capacity essential for the 800 m
Anaerobic training frequency: Limited to 1-2 sessions weekly to establish foundation
The 800 m runner requires higher aerobic training frequency initially as the event demands approximately 60% aerobic energy contribution
Recovery between aerobic sessions can be shorter (24 hours) allowing higher frequency than anaerobic sessions

Specific preparation phase:

Aerobic training frequency: Reduces to 2-3 sessions weekly but maintains aerobic capacity
Anaerobic glycolytic training frequency: Increases to 2-3 sessions weekly targeting race-specific energy system
ATP-PCr system training: 1-2 sessions weekly for speed development
Balanced frequency between energy systems reflects the mixed aerobic-anaerobic nature of the 800 m event

Competition phase:

Race-specific training frequency: 2 high-quality sessions weekly combining aerobic and anaerobic demands
Maintenance aerobic sessions: 1-2 weekly at moderate intensity
Pure speed/ATP-PCr sessions: 1 weekly to maintain neuromuscular power
Overall reduction in frequency but increased specificity and quality

Energy system recovery requirements:

ATP-PCr system: Recovers within hours but neuromuscular fatigue requires 36-48 hours between high-intensity sessions
Glycolytic system: Requires 48-72 hours for enzyme restoration and lactate clearance, limiting frequency to 2-3 times weekly
Aerobic system: Can be trained more frequently (daily if necessary) with appropriate intensity modulation
800 m training frequency must balance all three energy systems’ recovery requirements

Adaptation considerations:

Anaerobic adaptations occur more rapidly than aerobic adaptations, requiring frequency adjustments
Early season higher aerobic frequency develops capillary density and mitochondrial content
Mid-season increased anaerobic frequency develops lactate tolerance and clearance capacity
Frequency must be adjusted based on individual adaptation rates to each energy system

Periodised frequency model:

Microcycle design: Hard anaerobic sessions separated by 48-72 hours with aerobic work between
Mesocycle pattern: 3 weeks of progressive frequency followed by 1 week reduced frequency (e.g., 3:1 loading pattern)
Seasonal fluctuation: Highest total frequency during base phase, most anaerobic-focused frequency mid-season, reduced but specific frequency during competition
Tapering: 30-50% reduction in frequency 7-14 days before major competition while maintaining intensity

HMS, BM EQ-Bank 305

Explain how the 'Type' component of the FITT principle should be applied when designing an anaerobic training program for a basketball player. Provide examples of specific training methods. (5 marks)

--- 15 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Court-based sprint drills develop basketball-specific anaerobic power through suicide runs, baseline-to-baseline sprints, and defensive slide patterns.
These movements are effective because they replicate game demands of 5-15 second high-intensity bursts.
This ensures direct transfer to match performance during fast breaks and defensive plays.
Plyometric exercises build explosive power essential for rebounding and shot-blocking.
Box jumps (40-60cm), depth jumps, and lateral bounds develop vertical and horizontal power.
Medicine ball chest passes and overhead throws enhance upper body explosiveness which improves passing and shooting power.
Resistance training using moderate loads for 3-8 repetitions develops strength for basketball movements.
Squats and deadlifts build lower body power for jumping, while bench press and rows develop contact strength for post play.
This type of training is necessary because basketball requires both explosive movements and physical contact.
Circuit training combines basketball skills with anaerobic conditioning to create sport-specific fitness.
Stations alternate between dribbling sprints, defensive slides, jump shots, and agility ladder work.
30 seconds maximum effort with 60-90 seconds recovery replicates game work-to-rest patterns.
This training method is effective because it maintains skill development while building anaerobic fitness for basketball’s repeated high-intensity demands.

Show Worked Solution

Sample Answer

Court-based sprint drills develop basketball-specific anaerobic power through suicide runs, baseline-to-baseline sprints, and defensive slide patterns.
These movements are effective because they replicate game demands of 5-15 second high-intensity bursts.
This ensures direct transfer to match performance during fast breaks and defensive plays.
Plyometric exercises build explosive power essential for rebounding and shot-blocking.
Box jumps (40-60cm), depth jumps, and lateral bounds develop vertical and horizontal power.
Medicine ball chest passes and overhead throws enhance upper body explosiveness which improves passing and shooting power.
Resistance training using moderate loads for 3-8 repetitions develops strength for basketball movements.
Squats and deadlifts build lower body power for jumping, while bench press and rows develop contact strength for post play.
This type of training is necessary because basketball requires both explosive movements and physical contact.
Circuit training combines basketball skills with anaerobic conditioning to create sport-specific fitness.
Stations alternate between dribbling sprints, defensive slides, jump shots, and agility ladder work.
30 seconds maximum effort with 60-90 seconds recovery replicates game work-to-rest patterns.
This training method is effective because it maintains skill development while building anaerobic fitness for basketball’s repeated high-intensity demands.

HMS, BM EQ-Bank 304

Compare the 'Time' component of the FITT principle for glycolytic and aerobic training methods. In your answer, explain how the 'Time' factors affect physiological responses. (5 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Similarities:

Both training methods require specific time durations to target their respective energy systems effectively.
Both need sufficient time to create training stimulus and promote fitness improvements.
Both require planned recovery periods, though at different intervals.

Differences:

Glycolytic training uses short work intervals of 30-90 seconds targeting the lactic acid system.
Aerobic training involves continuous activity lasting 20-60+ minutes at moderate intensity.
Glycolytic sessions total 15-30 minutes of high-intensity work due to accumulated fatigue.
Aerobic sessions extend much longer without excessive fatigue because of steady-state exercise.
Glycolytic training requires work-to-rest ratios of 1:2-3 to allow partial lactate clearance.
Aerobic training needs no rest intervals as steady-state exercise allows ongoing oxygen delivery.

Physiological responses from time differences:

Shorter glycolytic intervals create metabolic stress, which improves lactate buffering capacity.
This leads to enhanced glycolytic enzyme activity and better lactate removal.
Longer aerobic duration stimulates cardiovascular responses resulting in improved oxygen delivery.
Extended moderate intensity causes enhanced fat utilisation efficiency.
These distinct responses reflect each energy system’s role in different performance demands.

Show Worked Solution

Sample Answer

Similarities:

Both training methods require specific time durations to target their respective energy systems effectively.
Both need sufficient time to create training stimulus and promote fitness improvements.
Both require planned recovery periods, though at different intervals.

Differences:

Glycolytic training uses short work intervals of 30-90 seconds targeting the lactic acid system.
Aerobic training involves continuous activity lasting 20-60+ minutes at moderate intensity.
Glycolytic sessions total 15-30 minutes of high-intensity work due to accumulated fatigue.
Aerobic sessions extend much longer without excessive fatigue because of steady-state exercise.
Glycolytic training requires work-to-rest ratios of 1:2-3 to allow partial lactate clearance.
Aerobic training needs no rest intervals as steady-state exercise allows ongoing oxygen delivery.

Physiological responses from time differences:

Shorter glycolytic intervals create metabolic stress, which improves lactate buffering capacity.
This leads to enhanced glycolytic enzyme activity and better lactate removal.
Longer aerobic duration stimulates cardiovascular responses resulting in improved oxygen delivery.
Extended moderate intensity causes enhanced fat utilisation efficiency.
These distinct responses reflect each energy system’s role in different performance demands.

HMS, BM EQ-Bank 303

Explain why the 'Frequency' component of the FITT principle needs to be modified when an athlete moves from pre-season to in-season training. Use a specific sport to support your answer. (4 marks)

--- 12 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer – Chosen sport – Netball

Pre-season allows higher training frequency because no competitive matches exist to create additional stress.
Athletes can train 5-6 times weekly as recovery time is dedicated solely to training demands.
Example: A netball player completes 5 training sessions weekly during pre-season preparation.
In-season frequency must be reduced due to the physical and mental demands of regular competition.
This reduction is necessary because match play provides high-intensity stimulus requiring recovery time.
Training frequency drops to 2-3 sessions weekly to prevent accumulated fatigue affecting performance.
Match demands create significant physiological stress which limits available recovery time for additional training.
Therefore in-season training focuses on maintaining fitness rather than building new improvements.
Example: The same netball player reduces to 2 light training sessions between weekend matches.
This modification ensures optimal performance on match day while preventing overtraining and injury risk.

Show Worked Solution

Sample Answer

Pre-season allows higher training frequency because no competitive matches exist to create additional stress.
Athletes can train 5-6 times weekly as recovery time is dedicated solely to training demands.
Example: A netball player completes 5 training sessions weekly during pre-season preparation.
In-season frequency must be reduced due to the physical and mental demands of regular competition.
This reduction is necessary because match play provides high-intensity stimulus requiring recovery time.
Training frequency drops to 2-3 sessions weekly to prevent accumulated fatigue affecting performance.
Match demands create significant physiological stress which limits available recovery time for additional training.
Therefore in-season training focuses on maintaining fitness rather than building new improvements.
Example: The same netball player reduces to 2 light training sessions between weekend matches.
This modification ensures optimal performance on match day while preventing overtraining and injury risk.

HMS, BM EQ-Bank 299 MC

Which of the following BEST represents the appropriate training frequency for an athlete developing a high-intensity anaerobic training program?

5-6 days per week with minimal rest days
2-3 days per week with rest days between sessions
7 days per week with reduced intensity every third day
4-5 days per week with continuous low-intensity activity on rest days

Show Answers Only

\(B\)

Show Worked Solution

B is correct: 2-3 days weekly with rest days ensures adequate recovery.

Other Options:

A is incorrect: Excessive frequency lacks sufficient recovery time.
C is incorrect: No full rest days essential for anaerobic recovery.
D is incorrect: Too frequent; active recovery should be properly structured.

HMS, BM EQ-Bank 297

Compare and contrast how the FITT principle would be applied to aerobic training for a recreational marathon runner and a competitive volleyball player.

Justify your response with reference to the specific requirements of each activity. (12 marks)

--- 28 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Frequency

Marathon runner:

4-6 sessions per week focusing on building aerobic endurance with adequate recovery between longer runs

Volleyball player:

3-4 aerobic sessions per week supplemented with sport-specific and strength training sessions due to the multi-faceted nature of volleyball

Justification:

Marathon runners require higher running volume to develop specific endurance adaptations
Volleyball players need to balance aerobic conditioning with explosive power and technical skill development

Intensity

Marathon runner:

Primarily 65-75% MHR for long runs with 1-2 weekly sessions at 80-85% MHR for tempo runs and threshold training

Volleyball player:

Higher intensity intervals (85-95% MHR) to simulate the intermittent nature of volleyball, with shorter recovery periods

Justification:

Marathon running requires sustained aerobic capacity over hours
Volleyball demands repeated high-intensity efforts with short recovery periods during rallies and between points

Time

Marathon runner:

Varied durations from 30 minutes (recovery runs) to 180+ minutes (long runs) with a progressive increase in the long run duration

Volleyball player:

Shorter sessions (20-45 minutes) of aerobic training often incorporated into practice sessions

Justification:

Marathon training requires specific adaptation to prolonged effort
Volleyball requires integration of aerobic fitness within the context of game situations

Type

Marathon runner:

Primarily continuous running with variations in pace, terrain, and elevation to build specific endurance

Volleyball player:

Court-based interval training, shuttle runs, simulated game situations with continuous movement

Justification:

Marathon training must be sport-specific (primarily running)
Volleyball aerobic training should incorporate movement patterns specific to the sport (lateral movements, jumping, quick direction changes)

Additional considerations

Marathon runner:

Progressive overload applied primarily through increasing weekly kilometres
Periodisation to peak for a specific race date
Recovery strategies to prevent overuse injuries from repetitive impact

Volleyball player

Integration of aerobic training with technical and tactical aspects
Focus on anaerobic power development alongside aerobic capacity
Emphasis on sport-specific movement patterns that translate to game performance

FITT principle

Must be adapted to the energy system demands of each sport

Marathon running

Primarily aerobic development

Volleyball

Requires both aerobic and anaerobic power for optimal performance

Show Worked Solution

Sample Answer

Frequency

Marathon runner:

4-6 sessions per week focusing on building aerobic endurance with adequate recovery between longer runs

Volleyball player:

3-4 aerobic sessions per week supplemented with sport-specific and strength training sessions due to the multi-faceted nature of volleyball

Justification:

Marathon runners require higher running volume to develop specific endurance adaptations
Volleyball players need to balance aerobic conditioning with explosive power and technical skill development

Intensity

Marathon runner:

Primarily 65-75% MHR for long runs with 1-2 weekly sessions at 80-85% MHR for tempo runs and threshold training

Volleyball player:

Higher intensity intervals (85-95% MHR) to simulate the intermittent nature of volleyball, with shorter recovery periods

Justification:

Marathon running requires sustained aerobic capacity over hours
Volleyball demands repeated high-intensity efforts with short recovery periods during rallies and between points

Time

Marathon runner:

Varied durations from 30 minutes (recovery runs) to 180+ minutes (long runs) with a progressive increase in the long run duration

Volleyball player:

Shorter sessions (20-45 minutes) of aerobic training often incorporated into practice sessions

Justification:

Marathon training requires specific adaptation to prolonged effort
Volleyball requires integration of aerobic fitness within the context of game situations

Type

Marathon runner:

Primarily continuous running with variations in pace, terrain, and elevation to build specific endurance

Volleyball player:

Court-based interval training, shuttle runs, simulated game situations with continuous movement

Justification:

Marathon training must be sport-specific (primarily running)
Volleyball aerobic training should incorporate movement patterns specific to the sport (lateral movements, jumping, quick direction changes)

Additional considerations

Marathon runner:

Progressive overload applied primarily through increasing weekly kilometres
Periodisation to peak for a specific race date
Recovery strategies to prevent overuse injuries from repetitive impact

Volleyball player

Integration of aerobic training with technical and tactical aspects
Focus on anaerobic power development alongside aerobic capacity
Emphasis on sport-specific movement patterns that translate to game performance

FITT principle

Must be adapted to the energy system demands of each sport

Marathon running

Primarily aerobic development

Volleyball

Requires both aerobic and anaerobic power for optimal performance

HMS, BM EQ-Bank 296

Design an aerobic training program for a 16-year-old cross-country runner using the FITT principle. Evaluate how your application of each component addresses the specific needs of a cross-country athlete. (12 marks)

--- 28 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Frequency

4-5 sessions per week specifically designed for cross-country performance

Rationale:

Provides sufficient training stimulus while allowing recovery time for a developing athlete, balancing school commitments with training demands

Evaluation:

Frequency optimises adaptation without risking overtraining
Particularly important for adolescent runners whose recovery capacity may vary during growth phases

Intensity

3 sessions at 65-75% MHR (aerobic base development)
1-2 sessions at 80-85% MHR (threshold training)
1 session incorporating hills or terrain similar to race courses

Rationale:

Cross-country requires a strong aerobic base with the ability to maintain pace over varying terrain and handle race surges

Evaluation:

Intensity distribution effectively develops both aerobic capacity and lactate threshold necessary for cross-country performance
Also considers the developmental stage of a 16-year-old athlete

Time

3 medium sessions (40-45 minutes)
1 longer session (60-70 minutes)
1 shorter, higher-intensity session (30-35 minutes)

Rationale:

Matches typical cross-country race durations plus additional time to develop required endurance

Evaluation:

Time distribution appropriately prepares the athlete for race distances
Provides sufficient variety to maintain motivation
Addresses different physiological demands of cross-country racing

Type

Long steady runs on varied terrain
Tempo runs at race pace
Fartlek training with surges similar to racing tactics
One session on actual cross-country courses when possible

Rationale:

Specificity to cross-country demands including varied terrain, pace changes, and tactical considerations

Evaluation:

Variety of training types effectively addresses the multifaceted nature of cross-country racing
Maintains engagement for a young athlete

Overall program evaluation

Strengths:

Comprehensive development of aerobic systems specific to cross-country demands with appropriate variety for a developing athlete

Limitations:

May need adjustment based on individual growth patterns, previous training history, and specific physiological characteristics

Program success:

Monitored through performance in time trials, race results, and subjective feedback regarding fatigue and recovery

Show Worked Solution

Sample Answer

Frequency

4-5 sessions per week specifically designed for cross-country performance

Rationale:

Provides sufficient training stimulus while allowing recovery time for a developing athlete, balancing school commitments with training demands

Evaluation:

Frequency optimises adaptation without risking overtraining
Particularly important for adolescent runners whose recovery capacity may vary during growth phases

Intensity

3 sessions at 65-75% MHR (aerobic base development)
1-2 sessions at 80-85% MHR (threshold training)
1 session incorporating hills or terrain similar to race courses

Rationale:

Cross-country requires a strong aerobic base with the ability to maintain pace over varying terrain and handle race surges

Evaluation:

Intensity distribution effectively develops both aerobic capacity and lactate threshold necessary for cross-country performance
Also considers the developmental stage of a 16-year-old athlete

Time

3 medium sessions (40-45 minutes)
1 longer session (60-70 minutes)
1 shorter, higher-intensity session (30-35 minutes)

Rationale:

Matches typical cross-country race durations plus additional time to develop required endurance

Evaluation:

Time distribution appropriately prepares the athlete for race distances
Provides sufficient variety to maintain motivation
Addresses different physiological demands of cross-country racing

Type

Long steady runs on varied terrain
Tempo runs at race pace
Fartlek training with surges similar to racing tactics
One session on actual cross-country courses when possible

Rationale:

Specificity to cross-country demands including varied terrain, pace changes, and tactical considerations

Evaluation:

Variety of training types effectively addresses the multifaceted nature of cross-country racing
Maintains engagement for a young athlete

Overall program evaluation

Strengths:

Comprehensive development of aerobic systems specific to cross-country demands with appropriate variety for a developing athlete

Limitations:

May need adjustment based on individual growth patterns, previous training history, and specific physiological characteristics

Program success:

Monitored through performance in time trials, race results, and subjective feedback regarding fatigue and recovery

HMS, BM EQ-Bank 295

Analyse how the FITT principle would be applied differently for aerobic training in swimming compared to running. Provide examples to support your answer. (8 marks)

--- 24 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Overview Statement:

Swimming and running require different FITT applications due to their distinct environmental and biomechanical demands.
Key relationships exist between impact stress and frequency, body position and intensity measurement, plus equipment constraints affecting type variety.

Component Relationship 1:

Impact stress levels directly influence frequency capabilities between these activities.
Swimming enables 5-6 weekly sessions because water buoyancy reduces joint stress, while running limits training to 3-4 sessions due to high impact forces.
Water supports body weight, preventing overuse injuries that commonly affect runners.
This relationship means swimmers can accumulate greater weekly training volume without injury risk.

Component Relationship 2:

Environmental factors connect to intensity measurement accuracy and session duration.
Horizontal body position in water causes heart rates to run 10-15 beats lower than land-based activities.
This forces swimmers to rely on perceived exertion or pace times rather than heart rate monitoring.
Additionally, water resistance increases energy expenditure, resulting in shorter session durations (45-60 minutes) compared to running (60-90 minutes) for equivalent training stimulus.

Implications and Synthesis:

These component relationships demonstrate how environmental constraints shape FITT application.
Swimming’s supportive environment allows higher frequency but restricts type variety to stroke variations.
Running’s impact stress limits frequency but provides diverse terrain options.
The significance is that effective aerobic programs must adapt FITT components to match each activity’s unique biomechanical and environmental demands.

Show Worked Solution

Sample Answer

Overview Statement:

Swimming and running require different FITT applications due to their distinct environmental and biomechanical demands.
Key relationships exist between impact stress and frequency, body position and intensity measurement, plus equipment constraints affecting type variety.

Component Relationship 1:

Impact stress levels directly influence frequency capabilities between these activities.
Swimming enables 5-6 weekly sessions because water buoyancy reduces joint stress, while running limits training to 3-4 sessions due to high impact forces.
Water supports body weight, preventing overuse injuries that commonly affect runners.
This relationship means swimmers can accumulate greater weekly training volume without injury risk.

Component Relationship 2:

Environmental factors connect to intensity measurement accuracy and session duration.
Horizontal body position in water causes heart rates to run 10-15 beats lower than land-based activities.
This forces swimmers to rely on perceived exertion or pace times rather than heart rate monitoring.
Additionally, water resistance increases energy expenditure, resulting in shorter session durations (45-60 minutes) compared to running (60-90 minutes) for equivalent training stimulus.

Implications and Synthesis:

These component relationships demonstrate how environmental constraints shape FITT application.
Swimming’s supportive environment allows higher frequency but restricts type variety to stroke variations.
Running’s impact stress limits frequency but provides diverse terrain options.
The significance is that effective aerobic programs must adapt FITT components to match each activity’s unique biomechanical and environmental demands.

HMS, BM EQ-Bank 294

Describe how you would modify each component of the FITT principle throughout an 8-week aerobic training program for a recreational soccer player. Use examples to support your answer. (6 marks)

--- 12 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Frequency

Weeks 1-2: Start with 3 sessions weekly to establish routine without overtraining.
Weeks 3-6: Increase to 4 sessions as as fitness base develops.
Weeks 7-8: Maintain 4-5 sessions, ensuring recovery before matches.

Intensity

Weeks 1-2: 60-70% MHR builds aerobic base safely.
Weeks 3-4: Progress to 70-75% MHR as conditioning improves.
Weeks 5-6: Include intervals at 75-80% MHR developing lactate threshold.
Weeks 7-8: Incorporate match-intensity periods at 80-85% MHR.

Time

Weeks 1-2: 30-minute sessions prevent excessive fatigue.
Weeks 3-4: Extend to 40 minutes building endurance capacity.
Weeks 5-6: 45-50 minutes with varied intensities.
Weeks 7-8: 60 minutes matching game duration requirements.

Type

Weeks 1-2: Continuous jogging establishing base fitness.
Weeks 3-4: Add fartlek training introducing speed variations.
Weeks 5-6: Include ball work maintaining 70%+ MHR through dribbling circuits.
Weeks 7-8: Small-sided games (4v4) combining fitness with tactical practice.

Progressive overload:

Systematic increases occur across all training variables.
Each phase builds upon previous weeks’ foundation.
Soccer-specific elements increase throughout the program duration.

Show Worked Solution

Sample Answer

Frequency

Weeks 1-2: Start with 3 sessions weekly to establish routine without overtraining.
Weeks 3-6: Increase to 4 sessions as as fitness base develops.
Weeks 7-8: Maintain 4-5 sessions, ensuring recovery before matches.

Intensity

Weeks 1-2: 60-70% MHR builds aerobic base safely.
Weeks 3-4: Progress to 70-75% MHR as conditioning improves.
Weeks 5-6: Include intervals at 75-80% MHR developing lactate threshold.
Weeks 7-8: Incorporate match-intensity periods at 80-85% MHR.

Time

Weeks 1-2: 30-minute sessions prevent excessive fatigue.
Weeks 3-4: Extend to 40 minutes building endurance capacity.
Weeks 5-6: 45-50 minutes with varied intensities.
Weeks 7-8: 60 minutes matching game duration requirements.

Type

Weeks 1-2: Continuous jogging establishing base fitness.
Weeks 3-4: Add fartlek training introducing speed variations.
Weeks 5-6: Include ball work maintaining 70%+ MHR through dribbling circuits.
Weeks 7-8: Small-sided games (4v4) combining fitness with tactical practice.

Progressive overload:

Systematic increases occur across all training variables.
Each phase builds upon previous weeks’ foundation.
Soccer-specific elements increase throughout the program duration.

Vectors, SPEC2 2024 VCAA 18 MC

The point of intersection of the line \(\underset{\sim}{ r }=\underset{\sim}{ i }+\underset{\sim}{ j }-2 \underset{\sim}{ k }+t(-2 \underset{\sim}{ i }+\underset{\sim}{ j }+3 \underset{\sim}{ k })\), where \(t \in R\) and the plane \(3 x-2 y+4 z=5\) is

\((-5,-1,2)\)
\((-1,2,1)\)
\((3,4,1)\)
\((-5,4,7)\)

Show Answers Only

\(D\)

Show Worked Solution

\(\text{Find \(t\) such that \(\underset{\sim}{r}\) is a point on the plane.}\)

\(\text{Plane equation} \ \ 3x-2 y+4z=5\)

\(\text{Substitute} \ \ x=1-2t, \ y=1+t, \ z=-2+3t\)

\(\text{Solve for} \ t:\)

\(3(1-2 t)-2(1+t)+4(-2+3 t)=5\)

\(t=3\)

\(\text{Substitute \(t=3\) into \(\underset{\sim}{r}\):}\)

\(\underset{\sim}{r}(3)\)	\(=(1-6,1+3,-2+9)\)
	\(=(-5, 4, 7)\)

\(\Rightarrow D\)

Vectors, SPEC2 2024 VCAA 17 MC

Consider the following parallel lines.

\(L_1:\ {\underset{\sim}{r}}_1=\underset{\sim}{ i }+3 \underset{\sim}{ j }+\underset{\sim}{k}+s(\underset{\sim}{ i }+\underset{\sim}{ j }+\underset{\sim}{ k })\) and \(L_2:\ {\underset{\sim}{r}}_2=-2 \underset{\sim}{ i }+\underset{\sim}{ j }+3 \underset{\sim}{k}+t(\underset{\sim}{ i }+\underset{\sim}{ j }+\underset{\sim}{k })\) where \(s, t \in R\).

The shortest distance between \(L_1\) and \(L_2\) is

\(3\)
\(\sqrt{14}\)
\(\sqrt{17}\)
\(14\)

Show Answers Only

\(B\)

Show Worked Solution

\({\underset{\sim}{r}}_1=\underset{\sim}{a}+s \underset{\sim}{d}, \quad{\underset{\sim}{r}}_2=\underset{\sim}{b}+t \underset{\sim}{d}\)

\(\underset{\sim}{a}-\underset{\sim}{b}=\left(\begin{array}{c}1 \\ 3 \\ 1\end{array}\right)-\left(\begin{array}{c}-2 \\ 1 \\ 3\end{array}\right)=\left(\begin{array}{c}3 \\ 2 \\ -2\end{array}\right)\)

\(d=\left(\begin{array}{l}1 \\ 1 \\ 1\end{array}\right) \Rightarrow \abs{d}=\sqrt{3}\)

Mean mark 58%.

\(\text{Shortest distance}\)	\(=\abs{\hat{\underset{\sim}{d}} \times \left(\underset{\sim}{a}-\underset{\sim}{b}\right)}\)
	\(=\abs{\dfrac{1}{\sqrt{3}}\left(\underset{\sim}{i}+\underset{\sim}{j}+\underset{\sim}{k}\right) \times \left(3 \underset{\sim}{i}+2\underset{\sim}{j}-2 \underset{\sim}{k}\right)}\)
	\(=\abs{\dfrac{1}{\sqrt{3}}\left(-4\underset{\sim}{i}+5\underset{\sim}{j}-\underset{\sim}{k}\right)}\)
	\(=\sqrt{14}\)

\(\Rightarrow B\)

HMS, BM EQ-Bank 292

Compare how the 'Frequency' and 'Type' components of the FITT principle would be applied in designing anaerobic training programs for a tennis player versus a competitive 100 metre swimmer. (6 marks)

--- 18 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Similarities:

Both sports require careful scheduling around skill practice sessions.
Both limit anaerobic sessions to 2-3 times weekly to prevent overtraining.
Both utilise interval training with work periods under 60 seconds targeting anaerobic systems.
Both incorporate resistance training to develop power for sport-specific movements.
Both require 48-72 hour recovery periods between high-intensity anaerobic sessions.

Differences:

Tennis players can manage 2-3 weekly sessions due to high impact stress from jumping and lunging.
100m swimmers can handle 3 sessions as water-based training reduces joint stress, allowing quicker recovery.
Tennis training emphasises multi-directional movements through court sprints, lunging patterns and plyometric jumps.
100m swimming focuses on linear sprint power through 25-50m sprint sets and explosive starts.
Tennis sessions include agility ladders and reaction drills for sudden direction changes and net play.
100m swimmers use resistance equipment like parachutes and paddles for stroke-specific power development.
Tennis “type” component addresses explosive racquet swing power and rapid court coverage.
100m swimming “type” component develops propulsive force and streamlined body position for maximum speed.

Show Worked Solution

Sample Answer

Similarities:

Both sports require careful scheduling around skill practice sessions.
Both limit anaerobic sessions to 2-3 times weekly to prevent overtraining.
Both utilise interval training with work periods under 60 seconds targeting anaerobic systems.
Both incorporate resistance training to develop power for sport-specific movements.
Both require 48-72 hour recovery periods between high-intensity anaerobic sessions.

Differences:

Tennis players can manage 2-3 weekly sessions due to high impact stress from jumping and lunging.
100m swimmers can handle 3 sessions as water-based training reduces joint stress, allowing quicker recovery.
Tennis training emphasises multi-directional movements through court sprints, lunging patterns and plyometric jumps.
100m swimming focuses on linear sprint power through 25-50m sprint sets and explosive starts.
Tennis sessions include agility ladders and reaction drills for sudden direction changes and net play.
100m swimmers use resistance equipment like parachutes and paddles for stroke-specific power development.
Tennis “type” component addresses explosive racquet swing power and rapid court coverage.
100m swimming “type” component develops propulsive force and streamlined body position for maximum speed.

Statistics, SPEC2 2024 VCAA 19 MC

When conducting a hypothesis test, a type \(\text{II}\) error occurs when

a null hypothesis is not rejected when the alternative hypothesis is true.
a null hypothesis is rejected when it is true.
a null hypothesis is rejected when the alternative hypothesis is true.
a null hypothesis is not rejected when it is doubtful.

Show Answers Only

\(A\)

Show Worked Solution

\(\text{Pr(Type II error)} =\ \text{Pr(\(H_0\) is not rejected | \(H_1\) is true)}\)

\(\Rightarrow A\)

HMS, BM EQ-Bank 291

Explain how you would modify the FITT principle when designing an anaerobic training program for a boxer preparing for a championship fight. (6 marks)

--- 18 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Frequency:

Would increase gradually from 3 sessions per week during early preparation to 4-5 specialised anaerobic sessions weekly during the specific preparation phase, allowing for adequate recovery while building capacity.

Intensity:

Would follow a progressive pattern, starting with moderate bursts (70-80% effort) during general preparation and increasing to high-intensity intervals (85-95%) that simulate the energy demands of three-minute rounds with one-minute recovery.

Time parameters:

Would mirror the sport’s demands with work intervals of 10-20 seconds for power punching combinations, 30-60 seconds for sustained output during exchanges, and rest periods that gradually decrease from 1:4 to 1:2 work-to-rest ratio as fight preparation advances.

Type of training:

Would include sport-specific movements such as heavy bag work, pad drills, and shadow boxing performed at anaerobic intensities, supplemented with resistance exercises like medicine ball throws and plyometric push-ups for power development.

Progression:

During the final two weeks before the fight, intensity would remain high while volume decreases to ensure the boxer remains fresh yet maintains anaerobic power and capacity.

Throughout Training:

Boxing-specific metrics like punch output, punch force, and heart rate recovery would be used to monitor adaptations and ensure the FITT variables are optimised.

Show Worked Solution

Sample Answer

Frequency:

Would increase gradually from 3 sessions per week during early preparation to 4-5 specialised anaerobic sessions weekly during the specific preparation phase, allowing for adequate recovery while building capacity.

Intensity:

Would follow a progressive pattern, starting with moderate bursts (70-80% effort) during general preparation and increasing to high-intensity intervals (85-95%) that simulate the energy demands of three-minute rounds with one-minute recovery.

Time parameters:

Would mirror the sport’s demands with work intervals of 10-20 seconds for power punching combinations, 30-60 seconds for sustained output during exchanges, and rest periods that gradually decrease from 1:4 to 1:2 work-to-rest ratio as fight preparation advances.

Type of training:

Would include sport-specific movements such as heavy bag work, pad drills, and shadow boxing performed at anaerobic intensities, supplemented with resistance exercises like medicine ball throws and plyometric push-ups for power development.

Progression:

During the final two weeks before the fight, intensity would remain high while volume decreases to ensure the boxer remains fresh yet maintains anaerobic power and capacity.

Throughout Training:

Boxing-specific metrics like punch output, punch force, and heart rate recovery would be used to monitor adaptations and ensure the FITT variables are optimised.

HMS, BM EQ-Bank 290 MC

A sports scientist is designing an anaerobic training program for an Olympic weightlifter based on the FITT principle. Which of the following combinations would be most appropriate?

Frequency: daily training; Intensity: RPE 5-6; Time: 45-minute continuous sessions; Type: high-repetition Olympic lifts
Frequency: 4-5 sessions per week; Intensity: RPE 8-9; Time: sets of 1-5 repetitions with 3-5 minute rest periods; Type: Olympic lifts and strength exercises
Frequency: 2 sessions per week; Intensity: RPE 7; Time: 30-second maximum effort circuits; Type: machine-based resistance training
Frequency: 6 sessions per week; Intensity: RPE 6-7; Time: 20-repetition sets with 1-minute rest periods; Type: bodyweight exercises

Show Answers Only

\(B\)

Show Worked Solution

B is correct: Optimal frequency, high intensity, low reps with long rest for power development.

Other Options:

A is incorrect: Daily training excessive; low intensity/high reps for endurance not power.
C is incorrect: Insufficient frequency; machines lack Olympic lift technique requirements.
D is incorrect: Low intensity/high reps develop endurance not explosive power.

HMS, BM EQ-Bank 286

Analyse how the different components of the FITT principle could be manipulated to create an anaerobic training program for a 400 metre runner. (8 marks)

--- 28 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Overview Statement:

The FITT principle components must be carefully manipulated for 400m running due to the event’s unique anaerobic demands.
Key relationships exist between frequency and recovery needs, intensity and energy system targeting, plus time intervals affecting training effectiveness.

Component Relationship 1:

Frequency directly influences recovery and training quality in anaerobic programs.
400m runners require 2-3 sessions weekly because high-intensity training creates significant muscle fatigue requiring 48-72 hours recovery.
This relationship means more frequent sessions would compromise training quality and increase injury risk.
Training frequency connects to intensity levels – as workout intensity increases, frequency must decrease to allow adequate recovery between sessions.

Component Relationship 2:

Time and intensity work together to target specific energy systems crucial for 400m performance.
Work intervals of 30-90 seconds at 85-95% MHR enable glycolytic system development while shorter 10-30 second intervals at maximum effort target the ATP-PCr system.
Rest periods interact with work duration – longer work intervals require extended recovery (1:3 ratios) to prevent excessive fatigue accumulation.
This combination allows runners to develop both speed and lactate tolerance essential for 400m racing.

Implications and Synthesis:

These component relationships demonstrate how FITT manipulation shapes training effectiveness for 400m performance.
Frequency limitations force coaches to maximise session quality through careful intensity and time selection.
The significance is that successful 400m training depends on balancing high-intensity demands with adequate recovery while targeting both anaerobic energy systems through varied interval durations.

Show Worked Solution

Sample Answer

Overview Statement:

The FITT principle components must be carefully manipulated for 400m running due to the event’s unique anaerobic demands.
Key relationships exist between frequency and recovery needs, intensity and energy system targeting, plus time intervals affecting training effectiveness.

Component Relationship 1:

Frequency directly influences recovery and training quality in anaerobic programs.
400m runners require 2-3 sessions weekly because high-intensity training creates significant muscle fatigue requiring 48-72 hours recovery.
This relationship means more frequent sessions would compromise training quality and increase injury risk.
Training frequency connects to intensity levels – as workout intensity increases, frequency must decrease to allow adequate recovery between sessions.

Component Relationship 2:

Time and intensity work together to target specific energy systems crucial for 400m performance.
Work intervals of 30-90 seconds at 85-95% MHR enable glycolytic system development while shorter 10-30 second intervals at maximum effort target the ATP-PCr system.
Rest periods interact with work duration – longer work intervals require extended recovery (1:3 ratios) to prevent excessive fatigue accumulation.
This combination allows runners to develop both speed and lactate tolerance essential for 400m racing.

Implications and Synthesis:

These component relationships demonstrate how FITT manipulation shapes training effectiveness for 400m performance.
Frequency limitations force coaches to maximise session quality through careful intensity and time selection.
The significance is that successful 400m training depends on balancing high-intensity demands with adequate recovery while targeting both anaerobic energy systems through varied interval durations.

HMS, BM EQ-Bank 285

Compare and contrast how the FITT principle would be implemented for a basketball player focusing on anaerobic training versus aerobic training. (8 marks)

--- 18 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Similarities

Both training types require structured frequency of 3-4 sessions weekly, preventing overtraining while ensuring fitness improvements.
Both utilise progressive overload through systematic FITT manipulation.
Both incorporate basketball-specific movements maintaining skill transfer during conditioning.
Both require careful planning to balance training with skill practice sessions.
Both use heart rate monitoring and recovery tracking to ensure appropriate training loads.

Differences:

Anaerobic training requires 48-72 hour recovery between sessions due to high muscle fatigue.
Aerobic sessions allow consecutive days as lower intensity permits faster recovery, enabling 4-5 weekly sessions.
Anaerobic training demands 85-100% maximum effort targeting explosive power development.
Aerobic training maintains 65-80% MHR, allowing sustained energy production for endurance building.
Anaerobic sessions involve 10-60 second work intervals with extended rest periods, totalling 20-30 minutes high-intensity work.
Aerobic training requires continuous 30-60 minute sessions developing cardiovascular endurance for game demands.
Anaerobic training emphasises explosive movements like sprint drills, jumping exercises, and defensive slides.
Aerobic training utilises continuous running, cycling, or sustained basketball drills maintaining moderate intensity.

Application significance:

Basketball’s stop-start nature requires both energy systems working effectively.
Anaerobic training develops explosive plays, fast breaks, and jumping ability.
Aerobic training enables recovery between high-intensity efforts and maintains performance throughout games.
Successful programs combine both training types based on season timing and player needs.

Show Worked Solution

Sample Answer

Similarities

Both training types require structured frequency of 3-4 sessions weekly, preventing overtraining while ensuring fitness improvements.
Both utilise progressive overload through systematic FITT manipulation.
Both incorporate basketball-specific movements maintaining skill transfer during conditioning.
Both require careful planning to balance training with skill practice sessions.
Both use heart rate monitoring and recovery tracking to ensure appropriate training loads.

Differences:

Anaerobic training requires 48-72 hour recovery between sessions due to high muscle fatigue.
Aerobic sessions allow consecutive days as lower intensity permits faster recovery, enabling 4-5 weekly sessions.
Anaerobic training demands 85-100% maximum effort targeting explosive power development.
Aerobic training maintains 65-80% MHR, allowing sustained energy production for endurance building.
Anaerobic sessions involve 10-60 second work intervals with extended rest periods, totalling 20-30 minutes high-intensity work.
Aerobic training requires continuous 30-60 minute sessions developing cardiovascular endurance for game demands.
Anaerobic training emphasises explosive movements like sprint drills, jumping exercises, and defensive slides.
Aerobic training utilises continuous running, cycling, or sustained basketball drills maintaining moderate intensity.

Application significance:

Basketball’s stop-start nature requires both energy systems working effectively.
Anaerobic training develops explosive plays, fast breaks, and jumping ability.
Aerobic training enables recovery between high-intensity efforts and maintains performance throughout games.
Successful programs combine both training types based on season timing and player needs.

HMS, BM EQ-Bank 284

Explain how the Time and Intensity components of the FITT principle would be implemented for a sprinter competing in a 100 m event. (5 marks)

--- 15 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Time:

Work intervals must be 5-15 seconds to match the 100m race duration and target the ATP-PCr system.
Recovery periods require 2-5 minutes between efforts, which creates work-to-rest ratios of 1:10-20..
This extended recovery allows complete phosphate replenishment essential for maintaining sprint quality..

Intensity:

Training must occur at 90-100% maximum velocity to recruit fast-twitch muscle fibres.
This develops neuromuscular patterns specific to sprinting.
Sub-maximal efforts fail to stimulate the improvements required for elite speed development.

Relationship:

Short time periods enable maximum intensity maintenance throughout each repetition.
Attempting longer durations forces intensity reduction as the glycolytic system activates.
This compromises sprint-specific improvements.

Progressive application:

Early season uses slightly longer intervals (10-15 seconds) at 90-95% intensity because this builds capacity.
Competition phase shifts to race-specific times (9-11 seconds) at 100% intensity.
This progression develops speed endurance before pure speed, preventing injury while optimising 100m performance.

Show Worked Solution

Sample Answer

Time:

Work intervals must be 5-15 seconds to match the 100m race duration and target the ATP-PCr system.
Recovery periods require 2-5 minutes between efforts, which creates work-to-rest ratios of 1:10-20..
This extended recovery allows complete phosphate replenishment essential for maintaining sprint quality..

Intensity:

Training must occur at 90-100% maximum velocity to recruit fast-twitch muscle fibres.
This develops neuromuscular patterns specific to sprinting.
Sub-maximal efforts fail to stimulate the improvements required for elite speed development.

Relationship:

Short time periods enable maximum intensity maintenance throughout each repetition.
Attempting longer durations forces intensity reduction as the glycolytic system activates.
This compromises sprint-specific improvements.

Progressive application:

Early season uses slightly longer intervals (10-15 seconds) at 90-95% intensity because this builds capacity.
Competition phase shifts to race-specific times (9-11 seconds) at 100% intensity.
This progression develops speed endurance before pure speed, preventing injury while optimising 100m performance.

HMS, BM EQ-Bank 278

Analyse how the "type" component of the FITT principle can be manipulated to improve aerobic capacity in team sport athletes. (8 marks)

--- 24 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Overview Statement:

The “type” component interacts with other FITT elements to create sport-specific aerobic development that enhances transfer to team sport performance.

Sample Answer – Any 3 – 4 of the following in depth

Small-sided games:

Small-sided games (3v3 to 6v6) maintain high heart rates (70-85% MHR) while developing sport-specific movement patterns. This creates high transfer to competition while maintaining athlete motivation compared to traditional aerobic training.

Sport-specific interval training:

Intervals replicate movement patterns and work-to-rest ratios of specific sports. Basketball players perform court-length sprints and defensive slides rather than generic running. This enhances transfer of aerobic development to game performance.

Circuit training:

Circuits combine aerobic exercises with sport-specific skills to develop aerobic capacity while maintaining technical proficiency. Coaches manipulate work periods and exercise selection to create appropriate stimulus while reinforcing skill development.

Cross-training:

Different aerobic activities (cycling, swimming, rowing) provide effective stimulus while reducing strain from repeated sport-specific movements. This is particularly valuable during heavy competition periods or for injured athletes.

Fartlek training:

Variable-intensity training with sport-specific movements allows athletes to develop aerobic capacity that mimics the unpredictable nature of team sports. Sessions can be structured or unstructured depending on training phase needs.

Environmental manipulation:

Changing environments (sand, hills, water) increases training stimulus while maintaining sport-specific movement patterns. Beach volleyball players performing footwork drills in sand increases intensity while enhancing sport-specific benefits.

High-intensity aerobic intervals:

High-intensity intervals (85-95% MHR) develop both aerobic power and lactate buffering capacity. These must be carefully designed to match sport demands and recovery capacities.

Implications:

Effective “type” manipulation integrates multiple training methods throughout structured programs, with emphasis shifting from general aerobic development to sport-specific training as competition approaches.

Show Worked Solution

Overview Statement:

The “type” component interacts with other FITT elements to create sport-specific aerobic development that enhances transfer to team sport performance.

Sample Answer – Any 3 – 4 of the following in depth

Small-sided games:

Small-sided games (3v3 to 6v6) maintain high heart rates (70-85% MHR) while developing sport-specific movement patterns. This creates high transfer to competition while maintaining athlete motivation compared to traditional aerobic training.

Sport-specific interval training:

Intervals replicate movement patterns and work-to-rest ratios of specific sports. Basketball players perform court-length sprints and defensive slides rather than generic running. This enhances transfer of aerobic development to game performance.

Circuit training:

Circuits combine aerobic exercises with sport-specific skills to develop aerobic capacity while maintaining technical proficiency. Coaches manipulate work periods and exercise selection to create appropriate stimulus while reinforcing skill development.

Cross-training:

Different aerobic activities (cycling, swimming, rowing) provide effective stimulus while reducing strain from repeated sport-specific movements. This is particularly valuable during heavy competition periods or for injured athletes.

Fartlek training:

Variable-intensity training with sport-specific movements allows athletes to develop aerobic capacity that mimics the unpredictable nature of team sports. Sessions can be structured or unstructured depending on training phase needs.

Environmental manipulation:

Changing environments (sand, hills, water) increases training stimulus while maintaining sport-specific movement patterns. Beach volleyball players performing footwork drills in sand increases intensity while enhancing sport-specific benefits.

High-intensity aerobic intervals:

High-intensity intervals (85-95% MHR) develop both aerobic power and lactate buffering capacity. These must be carefully designed to match sport demands and recovery capacities.

Implications:

Effective “type” manipulation integrates multiple training methods throughout structured programs, with emphasis shifting from general aerobic development to sport-specific training as competition approaches.

HMS, BM EQ-Bank 281 MC

A basketball player is designing an anaerobic training program based on the FITT principle. Which of the following represents the most appropriate application of the principle for this athlete?

Training 5-6 days per week at 40-50% of maximum heart rate for 60 minutes of continuous jogging
Training 3-4 days per week at 80-90% of maximum heart rate for 20-30 seconds with 60-90 second rest periods
Training 2 days per week at 60-70% of maximum heart rate for 45 minutes of cycling
Training 1 day per week at 95-100% of maximum heart rate for 3 minutes of continuous sprinting

Show Answers Only

\(B\)

Show Worked Solution

B is correct: Appropriate frequency, high intensity, short intervals with adequate rest for anaerobic training.

Other Options:

A is incorrect: Low intensity continuous training develops aerobic not anaerobic capacity.
C is incorrect: Low frequency/intensity; continuous cycling targets aerobic systems.
D is incorrect: Once weekly insufficient; 3-minute sprints not sustainable.

PHYSICS, M1 EQ-Bank 18

The velocity-time graph of a particle moving along an east-west line with velocity \(v\) m s\(^{-1}\) at time \(t\) seconds, starting from a fixed origin \(O\), is shown below. The graph comprises two straight line segments.

The initial velocity of the particle is 40 m s\(^{-1}\) to the east.

How far, in metres, is the particle to the east of \(O\), 150 seconds later? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

\(500\ \text{m}\)

Show Worked Solution

\(\text{Distance travelled East = area under graph and above the}\ x\text{-axis.}\)

\(\text{Linear velocity graph cuts \(x\)-axis at}\ \ x=66 \dfrac{2}{3}\)

\(\text{Distance (east)}\ = \dfrac{1}{2} \times 66 \dfrac{2}{3} \times 40 = \dfrac{4000}{3}\ \text{m} \)

\(\text{Distance travelled West = area above graph and below the}\ x\text{-axis.}\)

\(\text{Distance (west)}\ = \dfrac{1}{2} \times 83 \dfrac{1}{3} \times 20 = \dfrac{2500}{3}\ \text{m} \)

\(\text{Net distance east (at 150 sec)}\ = \dfrac{4000}{3}-\dfrac{2500}{3}=500\ \text{m}\)

Calculus, SPEC2 2024 VCAA 11 MC

The initial velocity of the particle is 40 m s\(^{-1}\) to the east.

How far, in metres, is the particle to the east of \(O\), 150 seconds later?

\(450\)
\(500\)
\(1000\)
\(\dfrac{6500}{3}\)

Show Answers Only

\(B\)

Show Worked Solution

\(\text{Distance travelled East = area under graph and above the}\ x\text{-axis.}\)

\(\text{Gradient of line = }-0.6 \ \ \Rightarrow\ \ \text{Cuts axis at}\ \ x=66 \dfrac{2}{3}\)

\(\text{Distance (east)}\ = \dfrac{1}{2} \times 66 \dfrac{2}{3} \times 40 = \dfrac{4000}{3}\ \text{m} \)

\(\text{Distance travelled West = area above graph and below the}\ x\text{-axis.}\)

\(\text{Distance (west)}\ = \dfrac{1}{2} \times 83 \dfrac{1}{3} \times 20 = \dfrac{2500}{3}\ \text{m} \)

\(\text{Net distance east (at 150 sec)}\ = \dfrac{4000}{3}-\dfrac{2500}{3}=500\ \text{m}\)

\(\Rightarrow B\)

Mean mark 58%.

Calculus, SPEC2 2024 VCAA 10 MC

The curve defined by the parametric equations

\(x=5 t, \ y=12 t\), for \(0 \leq t \leq k\)

is rotated about the \(y\)-axis to form a surface of revolution.

The area of this surface is

\(65 \ k^2 \pi\)
\(130 \ k^2 \pi\)
\(156 \ k^2 \pi\)
\(825 \ k^2 \pi\)

Show Answers Only

\(A\)

Show Worked Solution

\(\text{S.A}\)	\(=2 \pi \displaystyle \int_0^k x \, \sqrt{\left(\frac{d x}{d t}\right)^2+\left(\frac{d y}{d t}\right)^2} \, dt\)
	\(=2 \pi \displaystyle \int_0^k 5t \, \sqrt{5^2+12^2} \, dt\)
	\(=130 \pi \displaystyle \int_0^k t \, dt\)
	\(=65 \pi \left[t^2\right] _0^k\)
	\(=65 \ k^2 \pi\)

\(\Rightarrow A\)

Calculus, SPEC2 2024 VCAA 8 MC

Consider the differential equation \(\dfrac{dy}{dx}=x y^2\) where \(y_0=y(0)=1\).

When Euler's method is applied using a step size of \(h\), where \(h>0, \ y_3=1.126528\)

The value of \(h\) is

\(0.01\)
\(0.02\)
\(0.20\)
\(0.36\)

Show Answers Only

\(C\)

Show Worked Solution

\(x_{n+1}\)	\(=x_{n}+h\)	\(y_{n+1}\)	\(=y_n+hx_ny_{n}^2\)
\(x_{0}\)	\(=0,\)	\(y_0\)	\(=1\)
\(x_{1}\)	\(=h,\)	\(y_1\)	\(=1+h\cdot 0 \cdot 1^2=1 \)
\(x_{2}\)	\(=2h,\)	\(y_2\)	\(=1+h\cdot h \cdot 1^2=1+h^2 \)
\(x_{3}\)	\(=3h,\)	\(y_3\)	\(=1+h^2+h \cdot 2h \cdot (1+h^2)^2 \)
			\(=1+h^2+2h^2(1+2h^2+h^4)\)
			\(=1+3h^2+4h^4+2h^6\)

\(\text{Solve:}\ \ 1+3h^2+4h^4+2h^6=1.126528\ \ \text{for}\ \ h>0\)

\(h=0.2 \ \text{(by CAS)}\)

\(\Rightarrow C\)

Calculus, EXT1 C3 2024 SPEC2 7 MC

A solution to the differential equation

\(\dfrac{d y}{d x}=e^{x-y}(\cos (x-y)-\cos (x+y))\) can be found using

\(\displaystyle \int e^y \cos (y) d y=2 \int e^x \cos (x) d x\)
\(\displaystyle\int \frac{e^y}{\sin (y)} d y=2 \int e^{-x} \sin (x) d x\)
\(\displaystyle\int \frac{e^y}{\sin (y)} d y=2 \int e^x \sin (x) d x\)
\(\displaystyle\int e^{-y} \sin (y) d y=2 \int \frac{e^x}{\cos (x)} d x\)

Show Answers Only

\(C\)

Show Worked Solution

\(\cos(x-y)-\cos(x+y)\)

\(=[\cos(x)\cos(y)+\sin(x)\sin(y)]-[\cos(x)\cos(y)-\sin(x)\sin(y)]\)

\(=2\sin(x)\sin(y)\)

\(\dfrac{d y}{d x}\)	\(=e^{x-y}(\cos (x-y)-\cos (x+y))\)
	\(=e^{x-y} \times 2\sin(x)\sin(y)\)
	\(=2e^{x}\sin(x) \left(\dfrac{\sin(y)}{e^{y}}\right) \)

\(\displaystyle \int \dfrac{e^{y}}{\sin(y)}\,dy=\displaystyle \int 2e^{x}\sin(x)\,dx\)

\(\Rightarrow C\)

Calculus, SPEC2 2024 VCAA 7 MC

A solution to the differential equation

\(\dfrac{d y}{d x}=e^{x-y}(\cos (x-y)-\cos (x+y))\) can be found using

\(\displaystyle \int e^y \cos (y) d y=2 \int e^x \cos (x) d x\)
\(\displaystyle\int \frac{e^y}{\sin (y)} d y=2 \int e^{-x} \sin (x) d x\)
\(\displaystyle\int \frac{e^y}{\sin (y)} d y=2 \int e^x \sin (x) d x\)
\(\displaystyle\int e^{-y} \sin (y) d y=2 \int \frac{e^x}{\cos (x)} d x\)

Show Answers Only

\(C\)

Show Worked Solution

\(\cos(x-y)-\cos(x+y)\)

\(=[\cos(x)\cos(y)+\sin(x)\sin(y)]-[\cos(x)\cos(y)-\sin(x)\sin(y)]\)

\(=2\sin(x)\sin(y)\)

\(\dfrac{d y}{d x}\)	\(=e^{x-y}(\cos (x-y)-\cos (x+y))\)
	\(=e^{x-y} \times 2\sin(x)\sin(y)\)
	\(=2e^{x}\sin(x) \left(\dfrac{\sin(y)}{e^{y}}\right) \)

\(\displaystyle \int \dfrac{e^{y}}{\sin(y)}\,dy=\displaystyle \int 2e^{x}\sin(x)\,dx\)

\(\Rightarrow C\)

HMS, BM EQ-Bank 279

Evaluate the effectiveness of different aerobic training methods for developing a marathon runner's conditioning program based on the FITT principle. (12 marks)

--- 28 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Evaluation Statement:

Different aerobic training methods show varying effectiveness for marathon preparation, with aerobic interval training proving highly effective overall.
Key criteria include race specificity, fitness improvements achieved, and injury risk considerations.

Race Specificity:

Long slow distance training (LSD) partially fulfils marathon demands through base endurance development at 60-70% MHR.
While strong in building aerobic foundation, it fails to achieve race-pace preparation.
Aerobic interval training at 75-85% MHR proves superior for developing marathon-specific pace, with endurance improvements directly transferring to race performance.
Although effective for aerobic fitness development, high-intensity interval training shows limitations in marathon application due to excessive intensity.

Fitness Improvements:

Evidence supporting LSD includes enhanced endurance capacity and fat burning through prolonged efforts.
Aerobic interval training proves highly effective in developing fatigue resistance critical for sustained pace.
The overall evaluation demonstrates aerobic interval training’s superiority in race-specific fitness development.
High-intensity interval training, while inadequate for primary marathon preparation, contributes valuable running efficiency improvements when used sparingly.

Injury Prevention:

LSD’s effectiveness lies in allowing high training volume with minimal physical stress on the body.
Aerobic interval training adequately fulfils safety requirements when limited to appropriate frequency.
The evidence indicates that excessive high-intensity work proves insufficient for safe marathon preparation.
Weighing these factors shows LSD’s critical role in injury-free endurance development

Final Evaluation:

The strengths outweigh the weaknesses because integrated programming maximises benefits while minimising risks.
While strong in different areas, no single method proves comprehensive.
The most effective approach combines 70% LSD, 20-25% aerobic intervals, and 5-10% high-intensity intervals.
Although effective for base fitness development, LSD alone proves less suitable for performance improvement without aerobic interval training’s race-specific training benefits.

Show Worked Solution

Sample Answer

Evaluation Statement:

Different aerobic training methods show varying effectiveness for marathon preparation, with aerobic interval training proving highly effective overall.
Key criteria include race specificity, fitness improvements achieved, and injury risk considerations.

Race Specificity:

Long slow distance training (LSD) partially fulfils marathon demands through base endurance development at 60-70% MHR.
While strong in building aerobic foundation, it fails to achieve race-pace preparation.
Aerobic interval training at 75-85% MHR proves superior for developing marathon-specific pace, with endurance improvements directly transferring to race performance.
Although effective for aerobic fitness development, high-intensity interval training shows limitations in marathon application due to excessive intensity.

Fitness Improvements:

Evidence supporting LSD includes enhanced endurance capacity and fat burning through prolonged efforts.
Aerobic interval training proves highly effective in developing fatigue resistance critical for sustained pace.
The overall evaluation demonstrates aerobic interval training’s superiority in race-specific fitness development.
High-intensity interval training, while inadequate for primary marathon preparation, contributes valuable running efficiency improvements when used sparingly.

Injury Prevention:

LSD’s effectiveness lies in allowing high training volume with minimal physical stress on the body.
Aerobic interval training adequately fulfils safety requirements when limited to appropriate frequency.
The evidence indicates that excessive high-intensity work proves insufficient for safe marathon preparation.
Weighing these factors shows LSD’s critical role in injury-free endurance development

Final Evaluation:

The strengths outweigh the weaknesses because integrated programming maximises benefits while minimising risks.
While strong in different areas, no single method proves comprehensive.
The most effective approach combines 70% LSD, 20-25% aerobic intervals, and 5-10% high-intensity intervals.
Although effective for base fitness development, LSD alone proves less suitable for performance improvement without aerobic interval training’s race-specific training benefits.

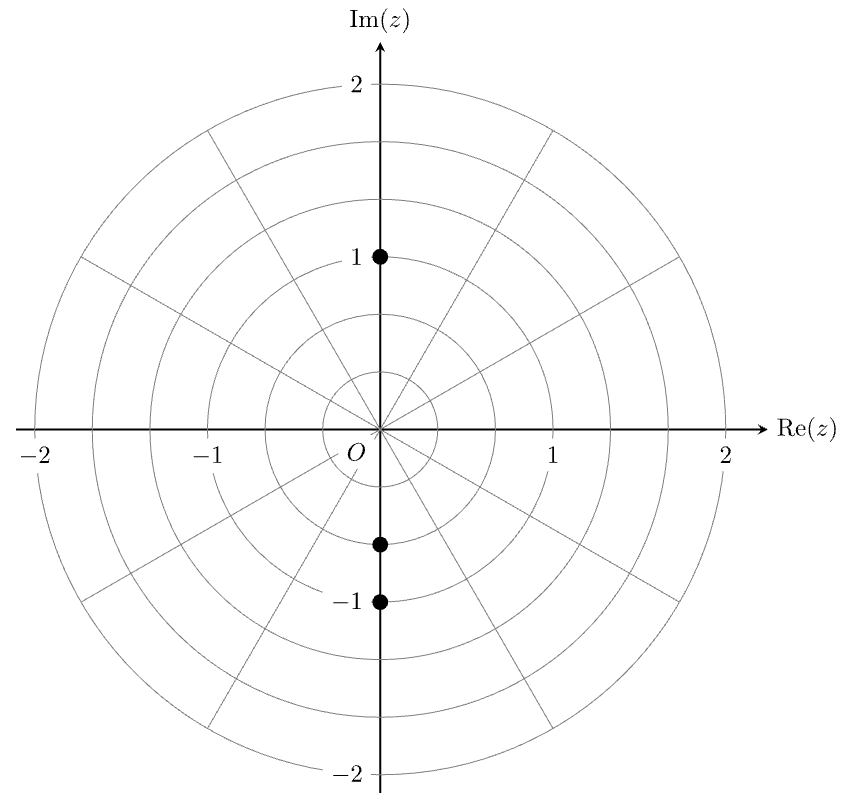
Complex Numbers, EXT2 N1 2024 VCAA 5 MC

If the point \(z=1+\sqrt{3} i\) is represented on an Argand diagram, the point representing \(-\bar{z}\) can be located by

reflecting the point representing \(z\) in the real axis.
rotating the point representing \(z\) anticlockwise about the origin by 90\(^{\circ}\).
reflecting the point representing \(z\) in the imaginary axis.
rotating the point representing \(z\) clockwise about the origin by 90\(^{\circ}\).

Show Answers Only

\(C\)

Show Worked Solution

\(z=1+\sqrt{3}i\ \ \Rightarrow\ \ \bar{z} = 1-\sqrt{3}i\)

\(-\bar{z} = -1+\sqrt{3}i\)

\(\therefore \text{It is a reflection of}\ z\ \text{in the imaginary axis.}\)

\(\Rightarrow C\)

HMS, BM EQ-Bank 275 MC

Which heart rate zone should a hockey player target during the aerobic development phase of their training program based on the FITT principle?

50-60% of maximum heart rate
65-75% of maximum heart rate
80-90% of maximum heart rate
90-100% of maximum heart rate

Show Answers Only

\(B\)

Show Worked Solution

B is correct: 65-75% MHR is moderate intensity for aerobic development.

Other Options:

A is incorrect: Too low for aerobic development; recovery intensity only.
C is incorrect: High intensity targets anaerobic not aerobic capacity.
D is incorrect: Maximum intensity for anaerobic training, not aerobic.

Complex Numbers, SPEC2 2024 VCAA 5 MC

If the point \(z=1+\sqrt{3} i\) is represented on an Argand diagram, the point representing \(-\bar{z}\) can be located by

reflecting the point representing \(z\) in the real axis.
rotating the point representing \(z\) anticlockwise about the origin by 90\(^{\circ}\).
reflecting the point representing \(z\) in the imaginary axis.
rotating the point representing \(z\) clockwise about the origin by 90\(^{\circ}\).

Show Answers Only

\(C\)

Show Worked Solution

\(z=1+\sqrt{3}i\ \ \Rightarrow\ \ \bar{z} = 1-\sqrt{3}i\)

\(-\bar{z} = -1+\sqrt{3}i\)

\(\therefore \text{It is a reflection of}\ z\ \text{in the imaginary axis.}\)

\(\Rightarrow C\)

Calculus, SPEC2 2024 VCAA 3 MC

The graph of \(f(x)=\dfrac{x-h}{(x+1)(x-4)}\), where \(h \in R\), will have no turning points when

\( h<-1\) and \(h>4\)
\(-4<h<1\)
\(-1 \leq h \leq 4\)
\(-4 \leq h \leq 1\)

Show Answers Only

\(C\)

Show Worked Solution

\(f(x)=\dfrac{x-h}{(x+1)(x-4)}\)

\(\text{Solve}\ \ f^{-1}(x)=0\ \ \text{(by CAS)}\)

\(x=h\pm \sqrt{h^2-3h-4}\)

\(\text{No turning points occur if}\ \ h^2-3h-4=(h-4)(h+1)<0\)

\(-1 \lt h \lt 4\)

\(\text{If}\ \ h=-1\ \ \text{or}\ \ 4, f(x)\ \text{is linear (no TPs)}\)

\(\therefore -1 \leq h \leq 4\)

\(\Rightarrow C\)

Proof, EXT2 P1 2024 SPEC2 1 MC

Consider the statement

'for any integers \(m\) and \(n\), if \(m+n \geq 9\) then \(m \geq 5\) or \(n \geq 5\) '.

The contrapositive of this statement is

if \(m<5\) or \(n<5\), then \(m+n<9\)
if \(m \geq 5\) or \(n \geq 5\), then \(m+n \geq 9\)
if \(m<5\) and \(n<5\), then \(m+n<9\)
if \(m \leq 5\) and \(n \leq 5\), then \(m+n \leq 9\)

Show Answers Only

\(C\)

Show Worked Solution

\(\text{Statement: If}\ \ m+n \geq 9\ \ \Rightarrow\ \ m \geq 5\ \ \text{or}\ \ n \geq 5\)

\(\text{Contrapositive statement:}\)

\(\text{If}\ \ m \ngeq 5\ \ \text{or}\ \ n \ngeq 5\ \ \Rightarrow\ \ \ m+n \ngeq 9\)

\(\text{i.e., if}\ \ m \lt 5\ \ \text{and}\ \ n \lt 5\ \ \Rightarrow\ \ \ m+n \lt 9\)

\(\Rightarrow C\)

Proof, SPEC2 2024 VCAA 1 MC

Consider the statement

'for any integers \(m\) and \(n\), if \(m+n \geq 9\) then \(m \geq 5\) or \(n \geq 5\) '.

The contrapositive of this statement is

if \(m<5\) or \(n<5\), then \(m+n<9\)
if \(m \geq 5\) or \(n \geq 5\), then \(m+n \geq 9\)
if \(m<5\) and \(n<5\), then \(m+n<9\)
if \(m \leq 5\) and \(n \leq 5\), then \(m+n \leq 9\)

Show Answers Only

\(C\)

Show Worked Solution

\(\text{Statement: If}\ \ m+n \geq 9\ \ \Rightarrow\ \ m \geq 5\ \ \text{or}\ \ n \geq 5\)

\(\text{Contrapositive statement:}\)

\(\text{If}\ \ m \ngeq 5\ \ \text{or}\ \ n \ngeq 5\ \ \Rightarrow\ \ \ m+n \ngeq 9\)

\(\text{i.e., if}\ \ m \lt 5\ \ \text{and}\ \ n \lt 5\ \ \Rightarrow\ \ \ m+n \lt 9\)

\(\Rightarrow C\)

Calculus, SPEC1 2024 VCAA 9

A car is travelling along a straight, flat road. The velocity, \(v\) km h\(^{-1}\), of the car and its position, \(x\) kilometres, are measured from the position on the road where \(x=0\).

The velocity \(v\) and the position \(x\) of the car are related by \(v^2=1600+\dfrac{672}{\pi} \arccos \left(\dfrac{x}{20}\right)\), where \(-15 \leq x \leq 15\) and \(v \geq 0\).

A speed detection device is positioned to detect the speed of a car as it passes the position \(x=0\). The speed limit on the road is 40 km h\(^{-1}\).

The speed detection device will be activated if the car is travelling at 10% or more above the speed limit.

Determine, with evidence, whether the speed detection device will be activated. (1 mark)

--- 5 WORK AREA LINES (style=lined) ---
Find the acceleration of the car, in km h\(^{-2}\), when \(x=12\).
Give your answer in the form \(\dfrac{k}{\pi}\), where \(k \in Z\). (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(v=44\)

\(\text{Since \(44 \geqslant 40+10 \%\), device will be activated}\)

b. \(a=\dfrac{-21}{\pi}\)

Show Worked Solution

a. \(\text{Find \(v\) when \(x=0\):}\)

\(v^2(0)\)	\(=1600+\dfrac{672}{\pi} \arccos \left(\dfrac{0}{20}\right)\)
	\(=1600+\dfrac{672}{\pi} \times\dfrac{\pi}{2}\)
	\(=1936\)
	\(=44^2\)
\(v\)	\(=44\)

\(\text{Since \(44 \geqslant 40+10 \%\), device will be activated}\)

♦♦ Mean mark (a) 32%.

b. \(\text{Using} \ \ a=\dfrac{d}{dx}\left(\dfrac{1}{2} v^2\right):\)

\(a\)	\(=\dfrac{d}{dx}\left(800+\dfrac{336}{\pi} \cos ^{-1}\left(\dfrac{x}{20}\right)\right)\)
	\(=\dfrac{336}{\pi} \cdot \dfrac{1}{20} \cdot \dfrac{-1}{\sqrt{1-\frac{x^2}{400}}}\)

\(\text{Find \(a\) when \(x=12\):}\)

\(\begin{aligned} a & =\frac{336}{\pi} \cdot \frac{1}{20} \cdot \frac{-1}{\sqrt{1-\frac{144}{400}}} \\
& =\frac{84}{5 \pi} \cdot \frac{-1}{\sqrt{\frac{16}{25}}} \\
& =\frac{84}{5 \pi} \cdot\frac{-5}{4} \\
& \\
& =\frac{-21}{\pi}
\end{aligned}\)

Calculus, SPEC1 2024 VCAA 8

Consider the relation \(x^2 y^2+x y=2\), where \(x, y \in R\).

Using implicit differentiation, show that \(\dfrac{d y}{d x}=-\dfrac{y}{x}\) given that \(2 x y \neq-1\). (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find all points on the graph of \(x^2 y^2+x y=2\) where the slope of the tangent is equal to \(-1\). (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(\text{See worked solutions}\)

b. \((1, 1), (-1,-1)\)

Show Worked Solution

a. \(x^2 y^2+x y=2\)

\(2 x y^2+2 x^2 y \cdot \dfrac{d y}{d x}+y+x \cdot \dfrac{d y}{d x}=0\)

\(\dfrac{d y}{d x} \cdot 2 x^2 y+\dfrac{d y}{d x} \cdot x\)	\(=-2 x y^2-y\)
\(\dfrac{dy}{dx}\left(2 x^2 y+x\right)\)	\(=-2 x y^2-y\)
\(\dfrac{d y}{d x}\)	\(=\dfrac{-2 x y^2-y}{2 x^2 y+x}\)
	\(=\dfrac{-y(2xy+1)}{x(2xy+1)}\)
	\(=\dfrac{-y}{x}(2xy+1 \neq 0)\)

b. \(\dfrac{dy}{dx}=-1 \ \ \text{when}\ \ y=x:\)

\(\text{Substitute} \ \ y=x \ \ \text{into} \ \ x^2 y^2+x y=2\)

\(x^4+x^2\)	\(=2\)
\(x^4+x^2-2\)	\(=0\)
\(\left(x^2+2\right)\left(x^2-1\right)\)	\(=0\)
\(x\)	\(=\pm 1\)

\(\therefore \text{ Points on graph where \(m=-1\) are} \ (1, 1), (-1,-1)\)

♦ Mean mark (b) 47%.

Calculus, SPEC1 2024 VCAA 7

Solve the differential equation \(x+2 y \sqrt{x^2+1} \dfrac{dy}{dx}=0\), expressing \(y\) as a function of \(x\), given that \(y(0)=-2\). (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

\(y=-\sqrt{5-\sqrt{x^2+1}}\)

Show Worked Solution

\(x+2 y \sqrt{x^2+1} \cdot \dfrac{d y}{d x}=0\)

	\(2y \cdot \dfrac{d y}{d x}\)	\(=\dfrac{-x}{\sqrt{x^2+1}}\)
	\(2y\, dy\)	\(=\dfrac{-x}{\sqrt{x^2+1}}\,dx\)
	\(\displaystyle{\int} 2 y\,d y\)	\(=\displaystyle \int \dfrac{-x}{\sqrt{x^2+1}}\,d x\)
	\(y^2\)	\(=-\sqrt{x^2+1}+c\)

Mean mark 55%.

\(\text{Since} \ \ y(0)=-2 \ \Rightarrow \ \ (-2)^2=-\sqrt{1}+c \ \Rightarrow \ \ c=5\)

	\(y\)	\(=\pm \sqrt{5-\sqrt{x^2+1}}\)
		\(=-\sqrt{5-\sqrt{x^2+1}} \quad(\text{given} \ y(0)=-2)\)

Calculus, SPEC1 2024 VCAA 5

The curve with equation \(y=\sqrt{k-\dfrac{1}{x^2}}\), for \(1 \leq x \leq \dfrac{k}{2}\) where \(k>2\), is rotated about the \(x\)-axis to form a solid of revolution that has volume \(\dfrac{7 \pi}{2}\) units\(^3\).

Show that \(k\) satisfies the equation \(k^3-2 k^2-9 k+4=0\). (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

	\(V\)	\(=\pi \displaystyle{\int}_1^{\frac{k}{2}}\left(k-\dfrac{1}{x^2}\right) dx\)
	\(\dfrac{7 \pi}{2}\)	\(=\pi\left[kx+\dfrac{1}{x}\right]_1^{\frac{k}{2}}\)
	\(7\)	\(=2\left[\left(\dfrac{k^2}{2}+\dfrac{2}{k}\right)-(k+1)\right]\)
	\(7\)	\(=k^2+\dfrac{4}{k}-2 k-2\)
	\(7k\)	\(=k^3+4-2 k^2-2 k\)
	\(0\)	\(=k^3-2k^2-9k+4\)

Show Worked Solution

\(y=\sqrt{k-\dfrac{1}{x^2}}\)

	\(V\)	\(=\pi \displaystyle{\int}_1^{\frac{k}{2}}\left(k-\dfrac{1}{x^2}\right) dx\)
	\(\dfrac{7 \pi}{2}\)	\(=\pi\left[kx+\dfrac{1}{x}\right]_1^{\frac{k}{2}}\)
	\(7\)	\(=2\left[\left(\dfrac{k^2}{2}+\dfrac{2}{k}\right)-(k+1)\right]\)
	\(7\)	\(=k^2+\dfrac{4}{k}-2 k-2\)
	\(7k\)	\(=k^3+4-2 k^2-2 k\)
	\(0\)	\(=k^3-2k^2-9k+4\)

Vectors, SPEC1 2024 VCAA 4

Consider the vectors \(\underset{\sim}{ a }=3 \underset{\sim}{ j }+3 \underset{\sim}{ k }, \ \underset{\sim}{ b }=2 \underset{\sim}{ i }-\underset{\sim}{ j }-2 \underset{\sim}{ k }\) and \(\underset{\sim}{ c }=n \underset{\sim}{ i }+2 \underset{\sim}{ j }+\underset{\sim}{ k }\), where \(n \in Z\).

Find the angle between \(\underset{\sim}{ a }\) and \(\underset{\sim}{ b }\). (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find all possible values of \(n\) such that the dot product of \(\underset{\sim}{ a }\) and \(\underset{\sim}{ c }\) is equal to the magnitude of the cross product of \(\underset{\sim}{ a }\) and \(\underset{\sim}{c}\). (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(\theta=\dfrac{3 \pi}{4}\left(\text{or} \ 135^{\circ}\right)\)

b. \(n= \pm 2\)

Show Worked Solution

a. \(\underset{\sim}{a}=\left(\begin{array}{l}0 \\ 3 \\ 3\end{array}\right) \Rightarrow \abs{\underset{\sim}{a}}=\sqrt{18}=3 \sqrt{2}\)

\(\underset{\sim}{b}=\left(\begin{array}{c}2 \\ -1 \\ -2\end{array}\right) \Rightarrow\abs{\underset{\sim}{b}}=\sqrt{9}=3\)

\(\underset{\sim}{c}=\left(\begin{array}{l}n \\ 2 \\ 1\end{array}\right) \Rightarrow \abs{\underset{\sim}{c}}=\sqrt{n^2+5}\)

\(\cos \theta=\dfrac{\underset{\sim}{a} \cdot \underset{\sim}{b}}{\abs{\underset{\sim}{a}} \cdot \abs{\underset{\sim}{b}}}=\dfrac{-3-6}{3 \sqrt{2} \times 3}=-\dfrac{1}{\sqrt{2}}\)

\(\therefore \theta=\cos ^{-1}\left(-\dfrac{1}{\sqrt{2}}\right)=\dfrac{3 \pi}{4}\left(\text{or} \ 135^{\circ}\right)\)

b. \(\underset{\sim}{a} \times \underset{\sim}{c}=\left|\begin{array}{ccc}\underset{\sim}{i} & \underset{\sim}{j} & \underset{\sim}{k} \\ 0 & 3 & 3 \\ n & 2 & 1\end{array}\right|=-3\underset{\sim}{i}+3 n\underset{\sim}{j}-3 n \underset{\sim}{k}\)

\(\abs{\underset{\sim}{a} \times \underset{\sim}{c}}=\sqrt{9+9n^2+9n^2}=\sqrt{18 n^2+9}\)

\(\underset{\sim}{a} \cdot \underset{\sim}{c}=0 \times n + 3 \times 2 + 3 \times 1=9\)

\(\text{Find \(n\) given:}\)

	\(\sqrt{18 n^2+9}\)	\(=9\)
	\(18 n^2+9\)	\(=81\)
	\(n^2\)	\(=4\)
	\(n\)	\(= \pm 2\)

HMS, BM EQ-Bank 273

Design a 6-week aerobic training program for a netball center court player using the FITT principle and explain how you would progress the program to ensure continuous improvement. (12 marks)

--- 30 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Program overview based on FITT principle:

Frequency: 3-4 sessions per week (gradually increasing)
Intensity: 65-85% MHR (progressively increasing)
Time: 20-45 minutes per session (gradually increasing)
Type: Combination of continuous training, fartlek, interval training and sport-specific conditioning

Week 1-2: Foundation Phase:

Frequency: 3 sessions per week
Intensity: 65-75% MHR (moderate)
Time: 20-30 minutes per session
Type: Continuous training (2 sessions) and basic fartlek (1 session)
Progression rationale: Establishes baseline aerobic fitness and prepares body for higher intensity work to follow

Week 3-4: Development Phase:

Frequency: 3-4 sessions per week (adding 4th session in week 4)
Intensity: 70-80% MHR (moderate-high)
Time: 30-40 minutes per session
Type: Continuous training (1 session), fartlek (1 session), basic interval training (1-2 sessions)
Progression rationale: Introduces higher intensity work to improve lactate threshold while maintaining aerobic base

Week 5-6: Specificity Phase:

Frequency: 4 sessions per week
Intensity: 75-85% MHR (high)
Time: 30-45 minutes per session
Type: Advanced interval training (2 sessions), netball-specific conditioning circuits (1 session), fartlek with court-specific movements (1 session)
Progression rationale: Incorporates sport-specific movement patterns while maintaining intensity to transfer fitness gains to netball performance

Weekly progression details:

Week 1: 3 x 20-min continuous runs at 65-70% MHR
Week 2: 2 x 25-min continuous runs at 70% MHR, 1 x basic fartlek (30 min total with 5 x 2-min efforts at 75% MHR)
Week 3: 1 x 30-min continuous run at 70-75% MHR, 1 x fartlek (30 min with 6 x 2-min efforts at 75-80% MHR), 1 x interval training (6 x 3-min at 75-80% MHR with 2-min recovery)
Week 4: 1 x 35-min continuous run at 70-75% MHR, 1 x fartlek (35 min with 7 x 2-min efforts at 75-80% MHR), 2 x interval training (8 x 3-min at 75-80% MHR with 2-min recovery)
Week 5: 1 x 40-min fartlek with court movements (8 x 2-min at 80% MHR), 2 x advanced intervals (8 x 4-min at 80-85% MHR with 2-min recovery), 1 x netball conditioning circuit (40 min total)
Week 6: 1 x 45-min fartlek with court movements (10 x 2-min at 80-85% MHR), 2 x advanced intervals (10 x 4-min at 80-85% MHR with 90-sec recovery), 1 x advanced netball conditioning circuit (45 min total)

Adaptation monitoring and progression criteria:

Heart rate recovery monitored between intervals – when recovery improves by 10+ BPM, increase intensity
RPE (Rating of Perceived Exertion) collected after each session – when RPE decreases below 7/10 for same workout, increase duration or intensity
30-15 Intermittent Fitness Test conducted pre-program and after week 3 to assess aerobic adaptation
Adjustments made based on individual response rates rather than strictly following predetermined progression

Recovery considerations:

At least 24 hours between aerobic sessions
Higher intensity sessions followed by either rest day or lower intensity session
Hydration and nutrition protocols provided to optimize recovery between sessions

Integration with overall netball training:

Aerobic sessions scheduled to avoid interference with skill training
Higher intensity sessions not scheduled before or after games
Coordination with strength training to prevent excessive fatigue

Show Worked Solution

Sample Answer

Program overview based on FITT principle:

Frequency: 3-4 sessions per week (gradually increasing)
Intensity: 65-85% MHR (progressively increasing)
Time: 20-45 minutes per session (gradually increasing)
Type: Combination of continuous training, fartlek, interval training and sport-specific conditioning

Week 1-2: Foundation Phase:

Frequency: 3 sessions per week
Intensity: 65-75% MHR (moderate)
Time: 20-30 minutes per session
Type: Continuous training (2 sessions) and basic fartlek (1 session)
Progression rationale: Establishes baseline aerobic fitness and prepares body for higher intensity work to follow

Week 3-4: Development Phase:

Frequency: 3-4 sessions per week (adding 4th session in week 4)
Intensity: 70-80% MHR (moderate-high)
Time: 30-40 minutes per session
Type: Continuous training (1 session), fartlek (1 session), basic interval training (1-2 sessions)
Progression rationale: Introduces higher intensity work to improve lactate threshold while maintaining aerobic base

Week 5-6: Specificity Phase:

Frequency: 4 sessions per week
Intensity: 75-85% MHR (high)
Time: 30-45 minutes per session
Type: Advanced interval training (2 sessions), netball-specific conditioning circuits (1 session), fartlek with court-specific movements (1 session)
Progression rationale: Incorporates sport-specific movement patterns while maintaining intensity to transfer fitness gains to netball performance

Weekly progression details:

Week 1: 3 x 20-min continuous runs at 65-70% MHR
Week 2: 2 x 25-min continuous runs at 70% MHR, 1 x basic fartlek (30 min total with 5 x 2-min efforts at 75% MHR)
Week 3: 1 x 30-min continuous run at 70-75% MHR, 1 x fartlek (30 min with 6 x 2-min efforts at 75-80% MHR), 1 x interval training (6 x 3-min at 75-80% MHR with 2-min recovery)
Week 4: 1 x 35-min continuous run at 70-75% MHR, 1 x fartlek (35 min with 7 x 2-min efforts at 75-80% MHR), 2 x interval training (8 x 3-min at 75-80% MHR with 2-min recovery)
Week 5: 1 x 40-min fartlek with court movements (8 x 2-min at 80% MHR), 2 x advanced intervals (8 x 4-min at 80-85% MHR with 2-min recovery), 1 x netball conditioning circuit (40 min total)
Week 6: 1 x 45-min fartlek with court movements (10 x 2-min at 80-85% MHR), 2 x advanced intervals (10 x 4-min at 80-85% MHR with 90-sec recovery), 1 x advanced netball conditioning circuit (45 min total)

Adaptation monitoring and progression criteria:

Heart rate recovery monitored between intervals – when recovery improves by 10+ BPM, increase intensity
RPE (Rating of Perceived Exertion) collected after each session – when RPE decreases below 7/10 for same workout, increase duration or intensity
30-15 Intermittent Fitness Test conducted pre-program and after week 3 to assess aerobic adaptation
Adjustments made based on individual response rates rather than strictly following predetermined progression

Recovery considerations:

At least 24 hours between aerobic sessions
Higher intensity sessions followed by either rest day or lower intensity session
Hydration and nutrition protocols provided to optimize recovery between sessions

Integration with overall netball training:

Aerobic sessions scheduled to avoid interference with skill training
Higher intensity sessions not scheduled before or after games
Coordination with strength training to prevent excessive fatigue

HMS, BM EQ-Bank 270

Explain how you would apply the FITT principle when designing an aerobic training program for an adolescent soccer player focusing on pre-season conditioning. (5 marks)

--- 15 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Begin with 3 sessions weekly in early pre-season, then increasing to 4 sessions as fitness improves because this allows recovery while building aerobic base essential for soccer’s continuous running demands.
Start intensity at 65-70% MHR for first 2-3 weeks to establish base fitness, then progress to 70-80% MHR as conditioning improves because gradual increases prevent overload in developing athletes.
Monitor intensity through heart rate zones because this ensures consistent training stimulus while accommodating adolescent growth variations that can affect training responses.
Begin with 20-30 minute sessions, progressively increasing to 35-45 minutes because longer durations develop the aerobic capacity needed for 90-minute match demands.
Vary between continuous running, fartlek training and soccer-specific drills with the ball because this maintains engagement while building aerobic foundation required for match fitness.
Include small-sided games (3v3, 4v4) as these maintain skill development while providing aerobic stimulus specific to soccer movement patterns.
Progressive overload occurs by increasing duration first, then frequency, finally intensity because this gradual progression prevents overtraining in adolescent athletes whose bodies are still developing.

Show Worked Solution

Sample Answer

Begin with 3 sessions weekly in early pre-season, then increasing to 4 sessions as fitness improves because this allows recovery while building aerobic base essential for soccer’s continuous running demands.
Start intensity at 65-70% MHR for first 2-3 weeks to establish base fitness, then progress to 70-80% MHR as conditioning improves because gradual increases prevent overload in developing athletes.
Monitor intensity through heart rate zones because this ensures consistent training stimulus while accommodating adolescent growth variations that can affect training responses.
Begin with 20-30 minute sessions, progressively increasing to 35-45 minutes because longer durations develop the aerobic capacity needed for 90-minute match demands.
Vary between continuous running, fartlek training and soccer-specific drills with the ball because this maintains engagement while building aerobic foundation required for match fitness.
Include small-sided games (3v3, 4v4) as these maintain skill development while providing aerobic stimulus specific to soccer movement patterns.
Progressive overload occurs by increasing duration first, then frequency, finally intensity because this gradual progression prevents overtraining in adolescent athletes whose bodies are still developing.

HMS, BM EQ-Bank 269

Explain how you would design an anaerobic training program based on the FITT principle for a 400 m track athlete. (5 marks)

--- 15 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Frequency:

3 anaerobic-specific sessions per week with at least 48 hours between high-intensity sessions to allow for adequate recovery of the neuromuscular system and replenishment of muscle glycogen.
Two additional sessions focusing on technique and lower-intensity work.

Intensity:

High to very high intensity (85-95% of maximum effort) to develop the anaerobic glycolytic system that predominates in 400 m events.
Heart rate typically reaches 90-100% of maximum during work intervals with incomplete recovery between repetitions.

Time:

Work intervals of 30-60 seconds (simulating race pace and duration), with total high-intensity work time of 10-15 minutes per session.
Rest intervals begin at 1:3 work-to-rest ratio (e.g., 45-second run, 135-second recovery) and progress to 1:2 as fitness improves.

Type:

Track-based interval training using distances of 200-500 m at race-specific pace, complemented by hill sprints and tempo intervals to develop lactate tolerance specific to 400m racing demands.

Progression:

The program would progress over 8-12 weeks by manipulating the work-to-rest ratio and increasing the total volume, while maintaining the specific intensity required for 400 m performance.

Show Worked Solution

Sample Answer

Frequency:

3 anaerobic-specific sessions per week with at least 48 hours between high-intensity sessions to allow for adequate recovery of the neuromuscular system and replenishment of muscle glycogen.
Two additional sessions focusing on technique and lower-intensity work.

Intensity:

High to very high intensity (85-95% of maximum effort) to develop the anaerobic glycolytic system that predominates in 400 m events.
Heart rate typically reaches 90-100% of maximum during work intervals with incomplete recovery between repetitions.

Time:

Work intervals of 30-60 seconds (simulating race pace and duration), with total high-intensity work time of 10-15 minutes per session.
Rest intervals begin at 1:3 work-to-rest ratio (e.g., 45-second run, 135-second recovery) and progress to 1:2 as fitness improves.

Type:

Track-based interval training using distances of 200-500 m at race-specific pace, complemented by hill sprints and tempo intervals to develop lactate tolerance specific to 400m racing demands.

Progess:

The program would progress over 8-12 weeks by manipulating the work-to-rest ratio and increasing the total volume, while maintaining the specific intensity required for 400 m performance.

HMS, BM EQ-Bank 265 MC

A rugby player is designing a 6-week pre-season anaerobic training program based on the FITT principle. Which progression of the 'Time' component is most appropriate?

Weeks 1-2: 15-20 minutes; Weeks 3-4: 20-25 minutes; Weeks 5-6: 25-30 minutes
Weeks 1-2: 60 minutes; Weeks 3-4: 75 minutes; Weeks 5-6: 90 minutes
Weeks 1-6: Consistent 45-minute sessions throughout
Weeks 1-2: 30 minutes; Weeks 3-4: 20 minutes; Weeks 5-6: 10 minutes

Show Answers Only

\(A\)

Show Worked Solution

A is correct: For anaerobic training, starting with 15-20 minutes and progressively increasing to 25-30 minutes is appropriate for building capacity while maintaining quality.

Other Options:

B is incorrect: Sessions lasting 60-90 minutes would be too long for high-intensity anaerobic work and would shift to aerobic development.
C is incorrect: No progression in session duration contradicts the principle of progressive overload needed for adaptation.
D is incorrect: Reducing session duration over time would likely lead to detraining rather than improved anaerobic capacity.

HMS, BM EQ-Bank 264 MC

A tennis player wants to improve court-specific endurance. Which application of the 'Type' component of the FITT principle would be most effective?

Weight training focusing on maximum strength with 2-minute rest periods
Long slow distance running on a treadmill for 45 minutes continuously
Swimming laps to develop general cardiovascular fitness
Court-based interval training with movement patterns specific to tennis

Show Answers Only

\(D\)

Show Worked Solution

D is correct: Court-based intervals match tennis movement patterns for best results.

Other Options:

A is incorrect: Develops strength not endurance; lacks tennis movements.
B is incorrect: Forward-only motion; lacks tennis multi-directional patterns.
C is incorrect: Different muscles/movements than tennis; limited relevance.

HMS, BM EQ-Bank 261

Analyse the differences between High Intensity Interval Training (HIIT) and Sprint Interval Training (SIT), and explain how each could be effectively incorporated into a training program for track cyclists. Provide specific examples to support your response. (8 marks)

--- 20 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Work intervals and MHR

HIIT typically involves work intervals of 1-4 minutes at submaximal intensity (85-95% MHR)
SIT uses shorter work intervals (10-30 seconds) performed at supramaximal or all-out effort (100%+ MHR)

Recovery

HIIT employs shorter recovery periods with work-to-rest ratios typically between 1:1 and 2:1
SIT requires longer recovery periods with work-to-rest ratios of 1:3 to 1:6 to allow for ATP-PC system replenishment

Power and endurance

HIIT’s ability to develop sustainable power and endurance is beneficial for track cyclists competing in endurance events like the 4000 m individual pursuit where maintaining high power for 4-5 minutes is essential.
Research shows HIIT sessions can significantly improve a cyclist’s ability to maintain high power outputs for extended durations, which directly translates to faster times in middle-distance track events.

Explosive power and acceleration

SIT predominantly develops explosive power and acceleration – essential qualities for sprint events like the 200 m flying sprint where maximum velocity in minimum time is the goal.

Middle distance events

HIIT could be implemented as 5×3-minute intervals at 90-95% maximum heart rate with 2-minute active recovery periods to simulate middle distance track events.

Sprint events

SIT featuring 6-8×30-second maximal efforts against high resistance with 3-4 minute complete recovery periods, could be used to develop the explosive power needed for sprint events.

Periodisation

Sprint specialists might use an 80:20 ratio of SIT to HIIT during competition preparation, while endurance track cyclists would employ the reverse ratio.

Choosing the correct method

Both methods should be implemented with careful consideration of total training load
- track cyclists typically require 48-72 hours recovery between high-intensity sessions to prevent fatigue accumulation.
Contemporary elite track cycling programs demonstrate effective integration of both methods.
- Olympic track cyclists perform 2-3 weekly HIIT sessions during general preparation phases to build endurance capacity, then transition to 2-3 weekly SIT sessions during specific preparation, while maintaining one HIIT session for endurance maintenance.

Show Worked Solution

Sample Answer

Work intervals and MHR

HIIT typically involves work intervals of 1-4 minutes at submaximal intensity (85-95% MHR)
SIT uses shorter work intervals (10-30 seconds) performed at supramaximal or all-out effort (100%+ MHR)

Recovery

HIIT employs shorter recovery periods with work-to-rest ratios typically between 1:1 and 2:1
SIT requires longer recovery periods with work-to-rest ratios of 1:3 to 1:6 to allow for ATP-PC system replenishment

Sustainable power and endurance

HIIT’s ability to develop sustainable power and endurance is beneficial for track cyclists competing in endurance events like the 4000 m individual pursuit where maintaining high power for 4-5 minutes is essential.
Research shows HIIT sessions can significantly improve a cyclist’s ability to maintain high power outputs for extended durations, which directly translates to faster times in middle-distance track events.

Explosive power and acceleration

SIT predominantly develops explosive power and acceleration – essential qualities for sprint events like the 200 m flying sprint where maximum velocity in minimum time is the goal.

Middle distance events

HIIT could be implemented as 5×3-minute intervals at 90-95% maximum heart rate with 2-minute active recovery periods to simulate middle distance track events.

Sprint events

SIT featuring 6-8×30-second maximal efforts against high resistance with 3-4 minute complete recovery periods, could be used to develop the explosive power needed for sprint events.

Periodisation

Sprint specialists might use an 80:20 ratio of SIT to HIIT during competition preparation, while endurance track cyclists would employ the reverse ratio.

Choosing the correct method

Both methods should be implemented with careful consideration of total training load
- track cyclists typically require 48-72 hours recovery between high-intensity sessions to prevent fatigue accumulation.
Contemporary elite track cycling programs demonstrate effective integration of both methods
- Olympic track cyclists perform 2-3 weekly HIIT sessions during general preparation phases to build endurance capacity, then transition to 2-3 weekly SIT sessions during specific preparation, while maintaining one HIIT session for endurance maintenance.

HMS, BM EQ-Bank 259 MC

A swimming coach is planning a training program for the team's sprinters. The coach wants to target anaerobic capacity through interval training. Which of the following training protocols would be most suitable for this purpose?

6 sets of 30-second maximal effort sprints with 4-minute complete rest periods
4 sets of 5-minute intervals at 85% maximum heart rate with 3-minute active recovery periods
30 minutes of continuous swimming at 70% maximum heart rate
10 sets of 1-minute intervals at 80% maximum heart rate with 1-minute active recovery periods

Show Answers Only

\(A\)

Show Worked Solution

A is correct: This describes a Sprint Interval Training (SIT) protocol with all-out maximal efforts and longer rest periods to allow for full ATP-PCr system recovery, making it ideal for developing anaerobic capacity in sprinters.

Other Options:

B is incorrect: HIIT protocol that would develop aerobic power rather than anaerobic capacity.
C is incorrect: Continuous aerobic training, not interval training.
D is incorrect: HIIT protocol with work-to-rest ratio that predominantly develops aerobic capacity and lactate threshold rather than anaerobic sprint capacity.

PHYSICS, M1 EQ-Bank 13

A motorboat was travelling 15 m/s relative to the water, heading due east according to its navigation system.

The boat then experiences a river current flowing south at 5 m/s relative to the shore. Using a vector diagram, determine the boat's resultant velocity relative to the shore. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

15.8 ms\(^{-1}\) at S72\(^{\circ}\)E.

Show Worked Solution

Using vector addition as shown in the diagram above:

\(R=\sqrt{15^2+5^2} = 15.8\ \text{ms}^{-1}\)

\(\tan \theta\)	\(=\dfrac{5}{15}\)
\(\theta\)	\(=\tan^{-1}\left(\dfrac{5}{15}\right)=18.4^{\circ}\)

The resultant velocity is 15.8 ms\(^{-1}\) at S72\(^{\circ}\)E.

Calculus, SPEC1 2024 VCAA 3

Let \(f: R \backslash\{-1\} \rightarrow R, f(x)=\dfrac{(x-1)^2}{(x+1)^2}\)

The rule \(f(x)\) can be written in the form \(f(x)=A+\dfrac{B}{x+1}+\dfrac{C}{(x+1)^2}\), where \(A, B, C \in Z\).

Show that \(A=1, B=-4\) and \(C=4\). (1 mark)

--- 5 WORK AREA LINES (style=lined) ---
The graph of \(f\) has one turning point.
Find the coordinates of this turning point. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Sketch the graph of \(y=f(x)\) on the set of axes below. Label the asymptotes with their equations and the axial intercepts with their coordinates. (3 marks)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(\text{See worked solutions.}\)

b. \(\text{Turning point at}\ (1,0)\)

Show Worked Solution

a.	\(\dfrac{(x-1)^2}{(x+1)^2}\)	\(=\dfrac{x^2-2x+1}{x^2+2x+1}\)
		\(=\dfrac{x^2+2x+1}{x^2+2x+1}-\dfrac{4x}{x^2+2x+1}\)
		\(=1-\dfrac{4(x+1)}{(x+1)^2}+\dfrac{4}{(x+1)^2}\)
		\(=1-\dfrac{4}{(x+1)}+\dfrac{4}{(x+1)^2}\)

b. \(f^{′}(x)=\dfrac{4}{(x+1)^2}-\dfrac{8}{(x+1)^3}\)

\(\text{SP’s when}\ \ f^{′}(x)=0:\)

\(\dfrac{4}{(x+1)^2}\)	\(=\dfrac{8}{(x+1)^3}\)
\(4(x+1)\)	\(=8\)
\(x\)	\(=1\)

\(f(1)=0\)

\(\therefore \text{Turning point at}\ (1,0)\)

c. \(\text{Vertical asymptote at}\ \ x=-1\)

\(f(0)=\dfrac{(-1)^2}{(1)^2}=1\ \ \Rightarrow \ \ y\text{-intercept at}\ (0,1)\)

\(\text{As}\ x\rightarrow \infty, \ 1-\dfrac{4}{(x+1)}+\dfrac{4}{(x+1)^2} \rightarrow 1^{-} \)

\(\text{As}\ x\rightarrow -\infty, \ 1-\dfrac{4}{(x+1)}+\dfrac{4}{(x+1)^2} \rightarrow 1^{+} \)

\(\text{Horizontal asymptote at}\ \ y=1 \)

♦♦ Mean mark (c) 31%.

HMS, BM EQ-Bank 257 MC

A water polo team is implementing High Intensity Interval Training (HIIT) in their in-season program. Which of the following best represents an appropriate HIIT session for these players?

40 minutes of steady lap swimming at 70% of maximum heart rate
5 sets of 3-minute high-intensity swimming efforts at 90% of maximum heart rate with 2 minutes active recovery between sets
8 sets of 20-second maximal swimming sprints with 5 seconds passive recovery between sets
90 minutes of low-intensity technique drills focusing on passing skills

Show Answers Only

\(B\)

Show Worked Solution

Consider Option B:

HIIT involves alternating between high-intensity exercise intervals and recovery periods.
The 3-minute efforts at 90% MHR with adequate recovery periods between sets is an appropriate HIIT structure for water polo players.

Other Options:

A is incorrect: This describes continuous aerobic training, not HIIT.
C is incorrect: This describes sprint interval training (SIT) with insufficient recovery, which differs from HIIT and would be too intense for water polo players.
D is incorrect: This describes skill-based training, not a HIIT session.

\(\Rightarrow B\)

PHYSICS, M1 EQ-Bank 12

An aircraft flies with a constant velocity of 95 ms\(^{-1}\) North. During the flight, a the plane experiences 2 different cross winds.

Determine the resultant velocity of the plane as seen from the ground when it experiences a wind blowing 40 ms\(^{-1}\) to the west. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Later in the flight when the plane is again travelling 95 ms\(^{-1}\) North, calculate its resultant velocity as seen from the ground when it experiences a cross wind of 50 ms\(^{-1}\) blowing towards a bearing of 150°T. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(103.1\ \text{ms}^{-1}\) at \(337^{\circ}\ \text{T}\)

b. \(57.4\ \text{ms}^{-1}\) at \(026^{\circ}\ \text{T}\)

Show Worked Solution

Using vector addition:

\(R=\sqrt{40^2+95^2} = 103.1\ \text{ms}^{-1}\)

\(\tan \theta\)	\(=\dfrac{40}{95}\)
\(\theta\)	\(=\tan^{-1}\left(\dfrac{40}{95}\right)=23^{\circ}\)

Resultant velocity \(=103.1\ \text{ms}^{-1}\ \text{at}\ 337^{\circ}\ \text{T}\)

Using the cosine rule:

\(c=\sqrt{50^2+95^2-2 \times 50 \times 95 \times \cos 30} = 57.4261\ \text{ms}^{-1}\)

Determine the angle (using sine rule):

\(\dfrac{\sin \theta}{50}\)	\(=\dfrac{\sin 30}{R}\)
\(\sin \theta\)	\(=\dfrac{50 \times \sin 30}{57.4261}\)
\(\theta\)	\(=\sin^{-1}\left(\dfrac{50 \times \sin 30}{57.4261}\right)=25.8^{\circ}\)

Resultant velocity on the plane \(=57.4\ \text{ms}^{-1}\ \text{at}\ 26^{\circ}\ \text{T}\)

Complex Numbers, SPEC1 2024 VCAA 1

Consider the function with rule \(f(z)=3 z^3+2 i z^2+3 z+2 i\), where \(z \in C\).

Verify that \(3 z+2 i\) is a factor of \(f(z)\). (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Hence or otherwise, solve the equation \(f(z)=0\).
Give your answers in Cartesian form. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Plot the solutions of \(f(z)=0\) on the Argand diagram below. (1 mark)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(\text{Method 1}\)

\(f(z)=3 z^3+2 i z^2+3 z+2 i = (3z+2i)(z^2+1)\)

\(\text{Method 2}\)

\(f\left( -\dfrac{2i}{3} \right)=\dfrac{8}{9}-\dfrac{8}{9}-2i+2i=0\)

\(\text{By factor theorem:}\)

\(z+ \dfrac{2}{3} i\ \ \text{is a factor of}\ f(z) \)

\(\text{Hence,}\ 3\left( z+\dfrac{2i}{3} \right) = 3z+2i\ \ \text{is a factor.}\)

b. \(f(z)= (3z+2i)(z^2+1)\)

\(z=-\dfrac{2i}{3} , z= \pm i\)

Show Worked Solution

a. \(\text{Method 1}\)

\(f(z)=3 z^3+2 i z^2+3 z+2 i = (3z+2i)(z^2+1)\)

\(\text{Method 2}\)

\(f\left( -\dfrac{2i}{3} \right)=\dfrac{8}{9}-\dfrac{8}{9}-2i+2i=0\)

\(\text{By factor theorem:}\)

\(z+ \dfrac{2}{3} i\ \ \text{is a factor of}\ f(z) \)

\(\text{Hence,}\ 3\left( z+\dfrac{2i}{3} \right) = 3z+2i\ \ \text{is a factor.}\)

b. \(f(z)= (3z+2i)(z^2+1)\)

\(z=-\dfrac{2i}{3} , z= \pm i\)

♦ Mean mark (c) 49%.

Statistics, 2ADV S3 2024 MET2 14*

A function, \(h(x)\), is defined as

\(h(x)=\left\{
\begin{array} {c}
\rule{0pt}{2.5ex} \ \ \ \ \ \dfrac{x}{6}+k \rule[-1ex]{0pt}{0pt} & -3 \leq x<0 \\
\rule{0pt}{2.5ex} \ \ -\dfrac{x}{2}+k \rule[-1ex]{0pt}{0pt} & 0 \leq x \leq 1 \\
\rule{0pt}{2.5ex} 0 \rule[-1ex]{0pt}{0pt} & \text { elsewhere } \\
\end{array}\right.\)

and \(k\) is a constant.

Find the value of \(k\) such that \(h(x)\) is a probability density function. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

\(k=\dfrac{1}{2}\)

Show Worked Solution

\(h(x)\ \text{is a PDF if}\ \ \displaystyle \int_{-3}^1 h(x)=1\)

\(\displaystyle \int_{-3}^1 h(x)\)	\(=\displaystyle \int_{-3}^0 \dfrac{x}{6}+k\,dx +\int_0^1 -\dfrac{x}{2}+k\,dx\)
\(1\)	\(=\left[\dfrac{x^2}{12}+kx\right] _{-3}^0 +\left[-\dfrac{x^2}{4}+kx\right] _0^1\)
\(1\)	\(=0-\left(\dfrac{9}{12}-3k\right)+\left(-\dfrac{1}{4}+k\right)-0\)
\(1\)	\(=4k-1\)
\(k\)	\(=\dfrac{1}{2}\)

HMS, BM EQ-Bank 256

Analyse the benefits and limitations of implementing either continuous aerobic training or High Intensity Interval Training (HIIT) as the primary training method for a cricket team during pre-season. (8 marks)

--- 20 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Continuous aerobic training benefits

Develops the aerobic capacity needed to maintain concentration and physical performance throughout a day’s play, particularly for fast bowlers and fielders who perform repeated efforts.
Establishes cardiovascular efficiency through adaptations including increased stroke volume and capillary density, enhancing oxygen delivery and facilitating quicker recovery between bowling spells or batting sessions.

Limitations

Insufficient development of the explosive power required for critical cricket actions like fast bowling, throwing from the boundary, or explosive batting strokes.
Lacks specificity for cricket’s intermittent nature, potentially leaving players underprepared for the varied intensity demands of competition across different formats (T20, ODI, Test).

HIIT benefits

Closer simulation of cricket’s intermittent intensity profile, particularly for shorter formats where high-intensity efforts are interspersed with recovery periods.
Simultaneously develops aerobic and anaerobic energy systems, improving players’ ability to perform repeated high-intensity efforts like consecutive boundaries when batting or maintaining bowling speed in later spells.
Improves lactate threshold and recovery between high-intensity efforts, crucial for maintaining performance quality in the closing stages of matches.

Limitations

Insufficient development of the extended aerobic foundation needed for longer format matches (Test cricket) if used exclusively.
Higher intensity creates greater neuromuscular and joint stress, potentially increasing injury risk for fast bowlers whose actions already place significant stress on the body.

Optimal pre-season approach

Periodising both methods – beginning with a greater emphasis on continuous aerobic training (70:30 ratio) to establish a foundation, then progressively shifting toward more cricket-specific HIIT sessions (30:70 ratio) as competition approaches.

Show Worked Solution

Sample Answer

Continuous aerobic training benefits

Develops the aerobic capacity needed to maintain concentration and physical performance throughout a day’s play, particularly for fast bowlers and fielders who perform repeated efforts.
Establishes cardiovascular efficiency through adaptations including increased stroke volume and capillary density, enhancing oxygen delivery and facilitating quicker recovery between bowling spells or batting sessions.

Limitations

Insufficient development of the explosive power required for critical cricket actions like fast bowling, throwing from the boundary, or explosive batting strokes.
Lacks specificity for cricket’s intermittent nature, potentially leaving players underprepared for the varied intensity demands of competition across different formats (T20, ODI, Test).

HIIT benefits

Closer simulation of cricket’s intermittent intensity profile, particularly for shorter formats where high-intensity efforts are interspersed with recovery periods.
Simultaneously develops aerobic and anaerobic energy systems, improving players’ ability to perform repeated high-intensity efforts like consecutive boundaries when batting or maintaining bowling speed in later spells.
Improves lactate threshold and recovery between high-intensity efforts, crucial for maintaining performance quality in the closing stages of matches.

Limitations

Insufficient development of the extended aerobic foundation needed for longer format matches (Test cricket) if used exclusively.
Higher intensity creates greater neuromuscular and joint stress, potentially increasing injury risk for fast bowlers whose actions already place significant stress on the body.

Optimal pre-season approach

Periodising both methods – beginning with a greater emphasis on continuous aerobic training (70:30 ratio) to establish a foundation, then progressively shifting toward more cricket-specific HIIT sessions (30:70 ratio) as competition approaches.

HMS, BM EQ-Bank 255

Compare how continuous aerobic training and High Intensity Interval Training (HIIT) would be applied differently for a triathlete versus a baseball pitcher. Provide specific examples from each sport. (6 marks)

--- 18 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Similarities:

Both athletes use continuous and HIIT training in their programs
Both need cardiovascular fitness for overall health
Both use training to support sport performance
Both adjust training based on competition schedules

Differences:

Training volume:
- Triathlete: 2-4 hour continuous sessions at 70-80% MHR
- Pitcher: 20-30 minute sessions for recovery only
Training emphasis:
- Triathlete: 80% continuous aerobic, 20% HIIT
- Pitcher: 20% continuous, 80% anaerobic intervals
HIIT application:
- Triathlete: Race-pace intervals (10 x 400m swim at 85-90% MHR)
- Pitcher: Pitch-specific bursts (10-second throws, 30-60 second rest)
Purpose of continuous training:
- Triathlete: Builds endurance for 2+ hour events
- Pitcher: Aids recovery between games
Recovery methods:
- Triathlete: Low-intensity continuous work at 60-70% MHR
- Pitcher: Complete rest to avoid fatigue

Show Worked Solution

Sample Answer

Similarities:

Both athletes use continuous and HIIT training in their programs
Both need cardiovascular fitness for overall health
Both use training to support sport performance
Both adjust training based on competition schedules

Differences:

Training volume:
- Triathlete: 2-4 hour continuous sessions at 70-80% MHR
- Pitcher: 20-30 minute sessions for recovery only
Training emphasis:
- Triathlete: 80% continuous aerobic, 20% HIIT
- Pitcher: 20% continuous, 80% anaerobic intervals
HIIT application:
- Triathlete: Race-pace intervals (10 x 400m swim at 85-90% MHR)
- Pitcher: Pitch-specific bursts (10-second throws, 30-60 second rest)
Purpose of continuous training:
- Triathlete: Builds endurance for 2+ hour events
- Pitcher: Aids recovery between games
Recovery methods:
- Triathlete: Low-intensity continuous work at 60-70% MHR
- Pitcher: Complete rest to avoid fatigue

HMS, BM EQ-Bank 254

Olympic kayaking includes 200 and 500 metre sprint events, of 35 seconds to 2 minute duration, requiring explosive power and anaerobic capacity. Distance events such as the 1000 metre lasting 3-4 minutes, demand sustained aerobic endurance.

Explain how continuous aerobic training and High Intensity Interval Training (HIIT) result in different physiological adaptations and performance outcomes for an Olympic kayaker. (5 marks)

--- 16 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Continuous training at 65-75% MHR develops endurance for 1000m events. This occurs because sustained paddling strengthens the heart and improves oxygen delivery to working muscles. Kayakers maintain steady speed for 3-4 minutes without excessive fatigue. As a result, they excel in distance events requiring consistent pace.
HIIT alternating 85-95% MHR efforts with recovery builds explosive power. The reason is high-intensity intervals train muscles for maximum force production. Sprint kayakers develop ability to paddle explosively for 35 seconds to 2 minutes. Consequently, they achieve faster starts and maintain speed throughout 200m and 500m races.
Each method creates different body responses. Continuous training improves heart efficiency and oxygen use during extended efforts. HIIT develops the ability to work hard despite lactic acid build-up. Therefore, each method prepares kayakers for their specific race demands.
Sprint kayakers emphasise 70% HIIT with 30% continuous work. Distance paddlers reverse this ratio. Hence, training programs match each event’s unique energy requirements.

Show Worked Solution

Sample Answer

Continuous training at 65-75% MHR develops endurance for 1000m events. This occurs because sustained paddling strengthens the heart and improves oxygen delivery to working muscles. Kayakers maintain steady speed for 3-4 minutes without excessive fatigue. As a result, they excel in distance events requiring consistent pace.
HIIT alternating 85-95% MHR efforts with recovery builds explosive power. The reason is high-intensity intervals train muscles for maximum force production. Sprint kayakers develop ability to paddle explosively for 35 seconds to 2 minutes. Consequently, they achieve faster starts and maintain speed throughout 200m and 500m races.
Each method creates different body responses. Continuous training improves heart efficiency and oxygen use during extended efforts. HIIT develops the ability to work hard despite lactic acid build-up. Therefore, each method prepares kayakers for their specific race demands.
Sprint kayakers emphasise 70% HIIT with 30% continuous work. Distance paddlers reverse this ratio. Hence, training programs match each event’s unique energy requirements.

HMS, BM EQ-Bank 253

Explain how continuous aerobic training and High Intensity Interval Training (HIIT) result in different physiological adaptations and performance outcomes for an 800 metre runner. (5 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

Sample Answer

Continuous aerobic training for 800 m runner

Enhances cardiovascular endurance through adaptations such as increased stroke volume, cardiac output and mitochondrial density, supporting sustained effort throughout the race.
Develops aerobic energy system efficiency, allowing greater oxygen utilisation during the race, particularly in the first 400-500m when aerobic contribution is significant.

HIIT

Builds the runner’s anaerobic capacity and lactate threshold through higher intensity efforts, crucial for maintaining speed in the final 300m when lactic acid accumulates.
Strengthens lactate tolerance and clearance during high-intensity efforts, essential for 800m performance where the lactic acid system is heavily taxed.

Combined effects

Provides optimal training specificity for 800 m, which requires both aerobic foundation (approximately 60%) and anaerobic capacity (approximately 40%) for elite performance.

Show Worked Solution

Sample Answer

Continuous aerobic training for 800 m runner

Enhances cardiovascular endurance through adaptations such as increased stroke volume, cardiac output and mitochondrial density, supporting sustained effort throughout the race.
Develops aerobic energy system efficiency, allowing greater oxygen utilisation during the race, particularly in the first 400-500m when aerobic contribution is significant.

HIIT

Builds the runner’s anaerobic capacity and lactate threshold through higher intensity efforts, crucial for maintaining speed in the final 300m when lactic acid accumulates.
Strengthens lactate tolerance and clearance during high-intensity efforts, essential for 800m performance where the lactic acid system is heavily taxed.

Combined effects

Provides optimal training specificity for 800 m, which requires both aerobic foundation (approximately 60%) and anaerobic capacity (approximately 40%) for elite performance.

PHYSICS, M1 EQ-Bank 17

A car is traveling east at 25 m/s relative to the ground. At the same time, a truck moving in the same direction overtakes the car at 35 m/s relative to the ground, while a motorcycle approaches the car from the opposite direction at 20 m/s.

What is the velocity of the truck relative to the car? (2 marks)

--- 3 WORK AREA LINES (style=lined) ---

What is the velocity of the motorcycle relative to the truck? (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(10\ \text{ms}^{-1}\ \text{East}\)

b. \(55\ \text{ms}^{-1}\ \text{West}

Show Worked Solution

a.	\(v_{\text{T rel C}}\)	\(=v_{\text{T}}-v_{\text{C}}\)
		\(=35-25\)
		\(=10\ \text{ms}^{-1}\ \text{East}\)

b. Let East be defined as the positive direction for velocity.

\(v_{\text{M rel T}}\)	\(=v_{\text{M}}-v_{\text{T}}\)
	\(=-20-35\)
	\(=-55\ \text{ms}^{-1}\)
	\(=55\ \text{ms}^{-1}\ \text{West}\)

Statistics, 2ADV S1 2024 MET2 7*

A fair six-sided die is repeatedly rolled. What is the minimum number of rolls required so that the probability of rolling a six at least once is greater than 0.95? (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

\(17\)

Show Worked Solution

\(P\text{(not rolling a 6)}\ = P(\bar6) = \dfrac{5}{6}\)

\(P(\bar6, \bar6) = \dfrac{5}{6} \times \dfrac{5}{6} \)

\(\text{Find}\ n\ \text{such that:}\)

\(\Big( \dfrac{5}{6}\Big)^n\)	\(\lt 0.05\)
\(n \times \ln{\Big( \dfrac{5}{6}}\Big)\)	\(\lt \ln{(0.05)}\)
\(n\)	\(\gt \dfrac{\ln{0.05}}{\ln{(\frac{5}{6})}}\)
	\(\gt 16.43…\)

\(\text{Minimum rolls = 17}\)

COMMENT: Note dividing by a negative number reverses < sign.

Calculus, 2ADV C3 2024 MET2 18*

A trapezium has the following dimensions.

Show that the total area of the trapezium is given by
\(A=2x\sqrt{100-x^2}\) (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
Find the value of \(x\) which maximises the area of the trapezium below. (3 marks)

--- 9 WORK AREA LINES (style=lined) ---

Show Answers Only

i. \(\text{See worked solutions}\)

ii. \(x=5\sqrt{2}\)

Show Worked Solution

i. \(A=\dfrac{h}{2}(a+b)\)

\(\text{By Pythagoras:}\ \ h=\sqrt{100-x^2}\)

\(A=\dfrac{\sqrt{100-x^2}}{2} \times (x + 3x) = 2x\sqrt{100-x^2}\)

ii.	\(\dfrac{dA}{dx}\)	\(=2\sqrt{(100-x^2}-\dfrac{2x^2}{\sqrt{100-x^2}}\)
		\(=\dfrac{2(100-x^2)-2x^2}{\sqrt{100-x^2}}\)
		\(=\dfrac{4(50-x^2)}{\sqrt{100-x^2}}\)

\(\text{Max/Min occurs when}\ \dfrac{dA}{dx}=0:\)

\(\dfrac{4(50-x^2)}{\sqrt{100-x^2}}\)	\(=0\quad(x \neq 10)\)
\(50-x^2\)	\(=0\)
(\(\sqrt{50}-x)(\sqrt{50}+x)\)	\(=0\)
\(\therefore\ x\)	\(=\sqrt{50}=5\sqrt{2}\quad (0<x<10)\)

\(\text{Check gradient for max using table:}\)

\(x\)	\(7\)	\(\sqrt{50}\)	\(7.2\)
\(A^{\prime}\)	\(0.56\)	\(0\)	\(-1.06\)
\(\text{Gradient}\)	\(+\)	\(0\)	\(-\)

\(\therefore\ x=5\sqrt{2}\ \text{maximises the area}\)

PHYSICS, M1 EQ-Bank 16

A soccer ball is kicked straight upward from a field at t = 0 seconds with an initial velocity.

It arrives at the exact height it was kicked from at t = 5 seconds and is caught.

Using the graph provided, plot the ball’s velocity versus time over the course of its flight. Assume that upward is positive and ignore the effects of air resistance. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

The velocity of the ball will decrease at a constant rate as the ball is under a constant acceleration due to gravity.

b.i	\(V\)	\(=\pi \displaystyle \int_1^6 x^2 \ dy\)
		\(=\pi \displaystyle\int_1^6 \frac{1-y+\sqrt{y^2+2y-3}}{2} \, dy \ \ \text{(by CAS)}\)

\(x^2-1\)	\(= \pm \sqrt{b+1}\)
\(x\)	\(=\pm \sqrt{1 \pm \sqrt{b+1}}\)

\(b+1 >\)	\(0\)	\(\text{and}\)	\(\sqrt{b+1}<1\)
\(b >\)	\( -1\)		\(b<0\)