SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Networks, STD1 N1 2025 HSC 14

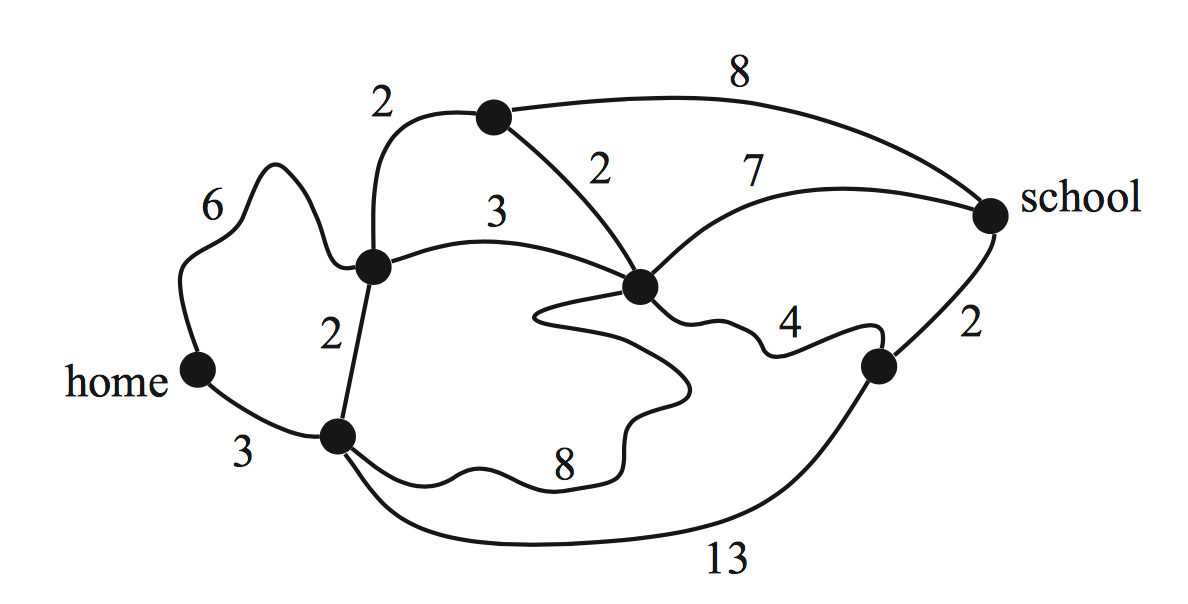
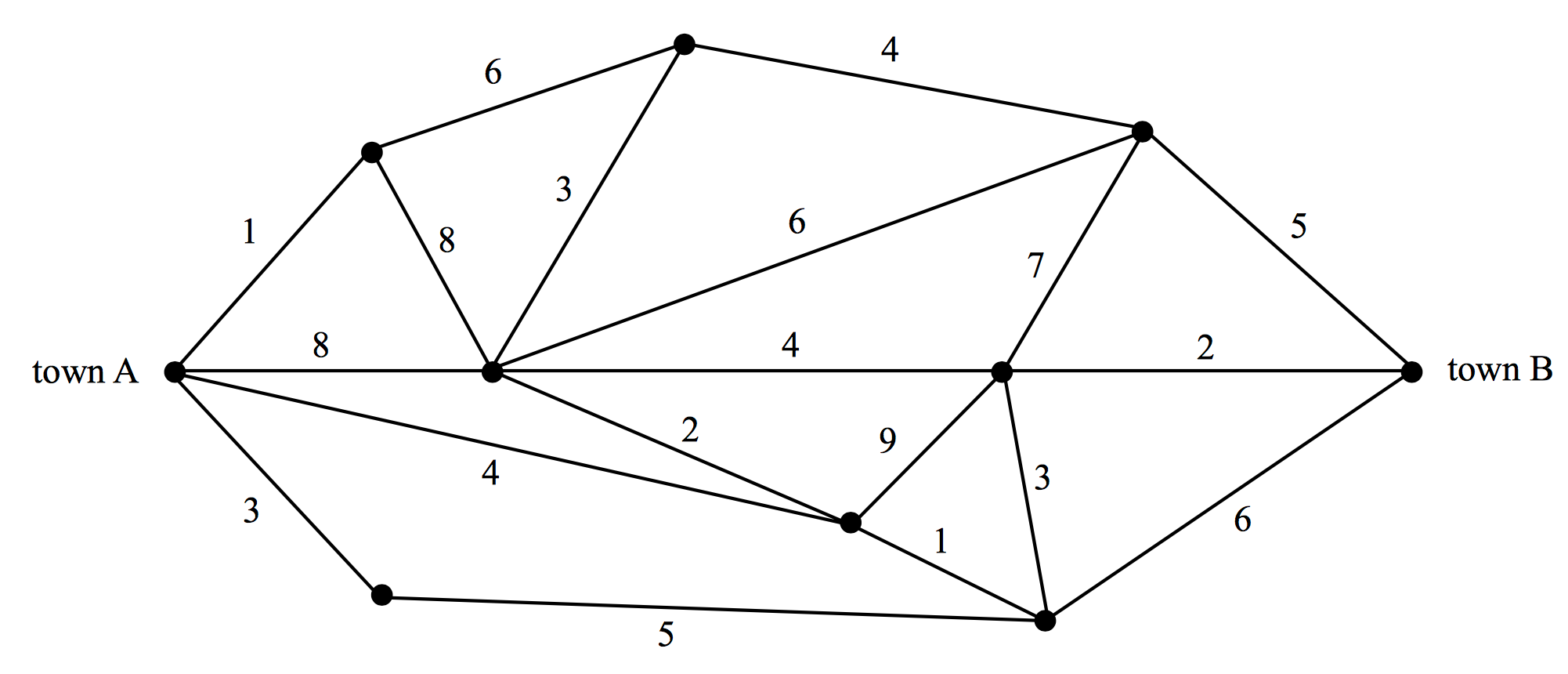
The time, in minutes, it takes to travel by road between six towns is recorded and shown in the network diagram below.
 

  1. In this network the shortest path corresponds to the minimum travel time.
  2. What is the minimum travel time between towns \(A\) and \(F\), and what is the corresponding path?   (2 marks)

New roads are built to connect a town \(G\) to towns \(A\) and \(D\). The table gives the times it takes to travel by the new roads.

\begin{array} {|c|c|c|}
\hline
\rule{0pt}{2.5ex} \textit{Town} \rule[-1ex]{0pt}{0pt} & \textit{Time} \text{(minutes)}  \rule[-1ex]{0pt}{0pt} & \textit{Town} \\
\hline
\rule{0pt}{2.5ex} A \rule[-1ex]{0pt}{0pt} & 8 \rule[-1ex]{0pt}{0pt} & G \\
\hline
\rule{0pt}{2.5ex} G \rule[-1ex]{0pt}{0pt} & 22 \rule[-1ex]{0pt}{0pt} & D \\
\hline
\end{array}

  1. Add the new roads and times to the network diagram below.   (2 marks)
     
      

     

  2. Explain whether the path in part (a) is still the shortest path from \(A\) to \(F\) after the new roads are added.   (1 mark)

Show Answers Only

a.    \(\text{Minimum travel time}\ = 15+20+10+5+8=58\ \text{minutes}\)

\(\text{Path: }A → B → C → D → E → F\)
 

b.    \(\text{New roads}\ A  → G\ \text{and }G → D \)
 

c.    \(\text{Using the new roads }A → G\ \text{and }G → D:\)

\(\text{Minimum travel time}\ =8+22+5+8=43\ \text{minutes.}\)

\(\text{Therefore the original path is no longer the shortest path.}\)

Show Worked Solution

a.    \(\text{Minimum travel time}\ = 15+20+10+5+8=58\ \text{minutes}\)

\(\text{Path: }A → B → C → D → E → F\)
 

b.    \(\text{New roads}\ A  → G\ \text{and }G → D \)
 

c.    \(\text{Using the new roads }A → G\ \text{and }G → D:\)

\(\text{Minimum travel time}\ =8+22+5+8=43\ \text{minutes.}\)

\(\text{Therefore the original path is no longer the shortest path.}\)

Networks, STD1 N1 2024 HSC 15

A network of towns and the distances between them in kilometres is shown.
 

  1. What is the shortest path from \(T\) to \(H\) ?   (2 marks)

  2. A truck driver needs to travel from \(Y\) to \(G\) but knows that the road from \(C\) to \(G\) is closed.
  3. What is the length of the shortest path the truck driver can take from \(Y\) to \(G\) after the road closure?  (2 marks)

Show Answers Only

a.   \(TYWH\)

b.  \(\text{Length of shortest path}\ (YWHMG) = 89 \text{km}\)

Show Worked Solution

a.    \(TYH=30+38=68, \quad TYWH=30+15+20=65\)

\(\therefore \text{ Shortest Path is}\ TYWH.\)
 

b.    \(Y W C M G=15+25+25+25=90\)

\(YWHMG=15+20+29+25=89\)

\(\Rightarrow \ \text{All other paths are longer.}\)

\(\therefore\text{ Length of shortest path = 89 km}\)

Networks, STD1 N1 2023 HSC 18

A network of running tracks connects the points \(A, B, C, D, E, F, G, H\), as shown. The number on each edge represents the time, in minutes, that a typical runner should take to run along each track.
 

 

  1. Which path could a typical runner take to run from point \(A\) to point \(D\) in the shortest time?  (2 marks)

  2. A spanning tree of the network above is shown.
     

  1. Is it a minimum spanning tree? Give a reason for your answer.  (2 marks)

Show Answers Only

a.    \(ABFGD\)

b.    \(\text{See worked solutions}\)

Show Worked Solution

a.    \(\text{Using Djikstra’s Algorithm:}\)
 

\(\text{Shortest route}\) \(=ABFGD\)  
  \(=3+1+5+5\)  
  \(=14\)  

 
b.   \(\text{Total time of given spanning tree}\)

\(=3+11+1+2+4+5+5\)

\(=31\)
 

\(\text{Consider the MST below:}\)
 

\(\text{Total time (MST)}= 3+1+2+4+5+5+9=29\)

\(\therefore \text{ Given tree is NOT a MST.}\)

♦♦ Mean mark (b) 21%.

Networks, STD2 N2 2019 HSC 30

The network diagram shows the tracks connecting 8 picnic sites in a nature park. The vertices `A` to `H` represents the picnic sites. The weights on the edges represent the distance along the tracks between the picnic sites, in kilometres.
 


 

  1. Each picnic site needs to provide drinking water. The main water source is at site `A`.

     

    Draw a minimum spanning tree and calculate the minimum length of water pipes required to supply water to all the sites if the water pipes can only be laid along the tracks.  (2 marks)

  2. One day, the track between `C` and `H` is closed. State the vertices that identify the shortest path from `C` to `E` that avoids the closed track.  (1 mark)

Show Answers Only
  1. `text(25 km)`
  2. `CGHE`
Show Worked Solution

a.   `text(One strategy – using Prim’s algorithm:)`

`text(Starting at)\ A`

`text(1st edge -)\ AB,\ \ text(2nd edge -)\ BC`

`text(3rd edge -)\ CH,\ \ text(4th edge -)\ HG`

`text(5th edge -)\ GF,\ \ text(6th edge -)\ HD`

`text(7th edge -)\ DE\ text(or)\ HE`
 

`text(Maximum length = 4 + 5 + 3 + 2 + 1 + 5 + 5 = 25 km)`

 

b.   `text(Shortest Path is)\ CGHE`

Networks, STD2 N2 2011 FUR2 1

Aden, Bredon, Carrie, Dunlop, Enwin and Farnham are six towns.

The network shows the road connections and distances between these towns in kilometres.

 

  1. In kilometers, what is the shortest distance between Farnham and Carrie?  (1 mark)

  2. How many different ways are there to travel from Farnham to Carrie without passing through any town more than once?  (1 mark)

Show Answers Only
  1. `200\ text(km)`
  2. `6`
Show Worked Solution

a.   `text{Farnham to Carrie (shortest)}`

`= 60 + 140`

`= 200\ text(km)`

 

b.   `text(Different paths are)`

`FDC, FEDC, FEBC,`

`FEABC, FDEBC,`

`FDEABC`

 
`:. 6\ text(different ways)`

Networks, STD2 N2 SM-Bank 10

Consider the network pictured below. 
 

Find the length of the shortest path from A to E.  (2 marks)

Show Answers Only

`10`

Show Worked Solution

`text(One strategy – Using Dijkstra’s algorithm:)`
 

 
`text{The shortest path A – B – I – E has a distance (weight)}`

`text(of 10.)`

Networks, STD2 N2 SM-Bank 13

An estate has large open parklands that contain seven large trees.

The trees are denoted as vertices A to G on the network diagram below.

Walking paths link the trees as shown.

The numbers on the edges represent the lengths of the paths in metres.
 

NETWORKS, FUR2 2007 VCAA 2

 
Jamie is standing at A and Michelle is standing at D.

Write down the shortest route that Jamie can take and the distance travelled to meet Michelle at D.  (1 mark) 

Show Answers Only

`text(Shortest path is)\ AFCD`

`text(Shortest distance is 500 metres.)`

Show Worked Solution

`text(One strategy – using Dijkstra’s algorithm:)`
 

 
`text(Shortest path is)\ AFCD`

`text(Shortest distance)` `= 200 + 150 + 150`
  `= 500\ text(metres)`

Networks, STD2 N2 SM-Bank 6

 
Describe the shortest path between A and J in the network above and its weight.  (2 marks)

Show Answers Only

`text(Shortest path is:)`

`text(A – B – E – F – J)`

`text(Weight of shortest path is 15.)`

Show Worked Solution

`text(One Strategy: Using Dijkstra’s algorithm)`
 


 

 `text(Shortest path is:)`

`text(A – B – E – F – J)`

`:.\ text(Weight of shortest path)`

`= 4 + 5 + 4 + 2`

`= 15`

Networks, STD2 N2 SM-Bank 5

A network of roads is pictured below, with the distances of each road represented, in kilometres, on each edge.
 

  
A driver wants to travel from A to H in the shortest distance possible.

Describe the possible paths she can take, and the total distance she must travel.  (2 marks)

Show Answers Only

`text(Shortest distance paths:)`

`text(A – E – H   or   A – F – G – H)`

`text(Shortest distance is 11 km.)`

Show Worked Solution

`text(One Strategy: Dijkstra’s algorithm)`
  


 
`text(Shortest distance paths:)`

`text(A – E – H   or   A – F – G – H)`

`text(Shortest distance is 11 km.)`

Networks, STD2 N2 2011 FUR2 1

Aden, Bredon, Carrie, Dunlop, Enwin and Farnham are six towns.

The network shows the road connections and distances between these towns in kilometres.
 

  1. In kilometres, what is the shortest distance between Farnham and Carrie?  (1 mark)

  2. How many different ways are there to travel from Farnham to Carrie without passing through any town more than once?  (1 mark)

An engineer plans to inspect all of the roads in this network.

He will start at Dunlop and inspect each road only once.

  1. At which town will the inspection finish?  (1 mark)

Show Answers Only
  1. `200\ text(km)`
  2. `6`
  3. `text(Bredon)`
Show Worked Solution

a.   `text{Farnham to Carrie (shortest)}`

`= 60 + 140`

`= 200\ text(km)`

 

b.   `text(Different paths are)`

`FDC, FEDC, FEBC, FEABC, FDEBC, FDEABC`

`:. 6\ text(different ways)`

 

c.   `text(A possible path is)\ DFEABCDEB\ text(and will finish)`

`text{at Bredon – the only other odd-degree vertex.}`

`text{(Note that solving this can be done quickly by applying the}`

`text{concept underlying the Konigsberg Bridge problem.)}`

Networks, STD2 N2 2010 FUR2 2

The diagram below shows a network of tracks (represented by edges) between checkpoints (represented by vertices) in a short-distance running course. The numbers on the edges indicate the time, in minutes, a team would take to run along each track.

 

Network, FUR2 2011 VCAA 2_1
 

A challenge requires teams to run from checkpoint `X` to checkpoint `Y` using these tracks.

What would be the shortest possible time for a team to run from checkpoint `X` to checkpoint `Y`? Mark the shortest route on the diagram below. (2 marks)

 
  Network, FUR2 2011 VCAA 2_2

 
Show Answers Only

`11\ text(minutes)`

Show Worked Solution

`text(Using Djikstra’s Algorithm:)`
 


 

`text(Shortest distance)\ \ X\ \ text(to)\ \ Y`

`=4 + 3 + 4`

`= 11\ text(minutes)`

Networks, STD2 N2 2017 FUR2 1

Bus routes connect six towns.

The towns are Northend (`N`), Opera (`O`), Palmer (`P`), Quigley (`Q`), Rosebush (`R`) and Seatown (`S`).

The graph below gives the cost, in dollars, of bus travel along these routes.

Bai lives in Northend (`N`) and he will travel by bus to take a holiday in Seatown (`S`).
 


 

  1. Bai considers travelling by bus along the route Northend (`N`) – Opera (`O`) – Seatown (`S`).
    How much would Bai have to pay?  (1 mark)

  2. If Bai takes the cheapest route from Northend (`N`) to Seatown (`S`), which other town(s) will he pass through?  (1 mark)

Show Answers Only
  1. `$120`
  2. `text(Quigley and Rosebush.)`
Show Worked Solution
a.    `text(C)text(ost)` `= 15 + 105`
    `= $120`

 

b.   `text(Using Djikstra’s algorithm:)`

`text(Fastest route is:)\ \ NQRS.` 

`:.\ text(Other towns are Quigley and Rosebush.)`

Networks, STD2 N2 2013 FUR2 1

The vertices in the network diagram below show the entrance to a wildlife park and six picnic areas in the park: `P1`, `P2`, `P3`, `P4`, `P5` and `P6`.

The numbers on the edges represent the lengths, in metres, of the roads joining these locations.

 


 

  1. In this graph, what is the degree of the vertex at the entrance to the wildlife park?  (1 mark)

  2. What is the shortest distance, in metres, from the entrance to picnic area `P3`?  (1 mark)

Show Answers Only
  1. `3`
  2. `1000\ text(m)`
Show Worked Solution

a.   `3`

b.  `text(Using Djikstra’s algorithm:)`
 


 

`text( Shortest distance)`

`= E – P1 – P3`

`= 600 + 400`

`= 1000\ text(m)`

Networks, STD2 N2 2014 FUR1 3 MC

The diagram below shows the network of roads that Stephanie can use to travel between home and school.

The numbers on the roads show the time, in minutes, that it takes her to ride a bicycle along each road.

Using this network of roads, the shortest time that it will take Stephanie to ride her bicycle from home to school is 

A.  `12\ text(minutes)`

B.  `13\ text(minutes)`

C.  `14\ text(minutes)`

D.  `15\ text(minutes)`

Show Answers Only

`C`

Show Worked Solution

`text(Using Djikstra’s algorithm:)`

`text(Shortest time riding)`

`=3+2+3+4+2`

`=14\ text(minutes)`

 
`=> C`

Networks, STD2 N2 2007 FUR1 4 MC

The following network shows the distances, in kilometres, along a series of roads that connect town `A` to town `B.`
 

 
The shortest distance, in kilometres, to travel from town `A` to town `B` is

A.     `9`

B.   `10`

C.   `11`

D.   `12`

Show Answers Only

`B`

Show Worked Solution

`text(Using Djikstra’s algorithm:)`

 
`text(Shortest path)`

`= 4 + 1 + 3 + 2`

`= 10`
 

`=>  B`

Networks, STD2 N2 2009 FUR1 2 MC

The network shows the distances, in kilometres, along roads that connect the cities of Austin and Boyle.
 

networks-fur1-2009-vcaa-2-mc

 
The shortest distance, in kilometres, from Austin to Boyle is

A.     `7`

B.     `8`

C.     `9`

D.   `10`

Show Answers Only

`B`

Show Worked Solution

`text(The shortest distance)`

`=2+4+1+1`

`=8`

`=>  B`