The diagram shows a network with weighted edges. --- 0 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- a. b. \(\text{Yes.}\) \(\text{→ The edge}\ FC\ \text{on the MST above could be replaced by the edge}\ BC\) \(\text{to create a second MST (with equivalent weight = 24)}\) a. \(\text{→ The edge}\ FC\ \text{on the MST above could be replaced by the edge}\ BC\) \(\text{to create a second MST (with equivalent weight = 24)}\)
b. \(\text{Yes.}\)
Networks, STD1 N1 2023 HSC 18
A network of running tracks connects the points \(A, B, C, D, E, F, G, H\), as shown. The number on each edge represents the time, in minutes, that a typical runner should take to run along each track. --- 4 WORK AREA LINES (style=lined) --- --- 4 WORK AREA LINES (style=lined) ---
a. \(\text{Using Djikstra’s Algorithm:}\) \(=3+11+1+2+4+5+5\) \(=31\) \(\text{Consider the MST below:}\) \(\text{Total time (MST)}= 3+1+2+4+5+5+9=29\) \(\therefore \text{ Given tree is NOT a MST.}\)
Show Worked Solution
\(\text{Shortest route}\)
\(=ABFGD\)
\(=3+1+5+5\)
\(=14\)
b. \(\text{Total time of given spanning tree}\)
♦♦ Mean mark (b) 21%.
Networks, STD1 N1 2022 HSC 20
The table below shows the distances, in kilometres, between a number of towns.
- Using the vertices given, draw a weighted network diagram to represent the information shown in the table. (2 marks)
- A tourist wishes to visit each town.
- Draw the minimum spanning tree which will allow for this AND determine its length. (3 marks)
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
-
-
- `1015\ text{km}`
Show Worked Solution
a.
b. `text{Using Prim’s algorithm (starting at}\ Y):`
`text{1st edge:}\ YC`
`text{2nd edge:}\ CB`
`text{3rd edge:}\ SB`
`text{4th edge:}\ YM`
`text{Length of minimum spanning tree}`
`=275 + 150+60+530`
`=1015\ text{km}`
Networks, STD1 N1 2021 HSC 17
The network diagram shows the travel times in minutes along roads connecting a number of different towns.
- Draw a minimum spanning tree for this network and determine its length. (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
- How long does it take to travel from Queentown to Underwood using the fastest route? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solution
a. `text{Using Prim’s algorithm (starting at}\ W):`
♦ Mean mark part (a) 40%.
`text(1st edge:)\ \ WM`
`text(2nd edge:)\ \ WP`
`text(3rd/4th edges:)\ \ MU\ text(and)\ \ WF`
`text(5th edge:)\ \ MK`
`text(6th edge:)\ \ KQ`
`text(7th edge:)\ \ PC`
`text{Length of minimum spanning tree} \ = 160`
| b. | `text{Fastest route}\ (Q\ text(to)\ U)` | `= 45 + 20` |
| `= 65 \ text{minutes}` |
Networks, STD2 N2 2019 HSC 30
The network diagram shows the tracks connecting 8 picnic sites in a nature park. The vertices `A` to `H` represents the picnic sites. The weights on the edges represent the distance along the tracks between the picnic sites, in kilometres.
- Each picnic site needs to provide drinking water. The main water source is at site `A`.
Draw a minimum spanning tree and calculate the minimum length of water pipes required to supply water to all the sites if the water pipes can only be laid along the tracks. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
- One day, the track between `C` and `H` is closed. State the vertices that identify the shortest path from `C` to `E` that avoids the closed track. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Show Worked Solution
a. `text(One strategy – using Prim’s algorithm:)`
`text(Starting at)\ A`
`text(1st edge -)\ AB,\ \ text(2nd edge -)\ BC`
`text(3rd edge -)\ CH,\ \ text(4th edge -)\ HG`
`text(5th edge -)\ GF,\ \ text(6th edge -)\ HD`
`text(7th edge -)\ DE\ text(or)\ HE`
`text(Maximum length = 4 + 5 + 3 + 2 + 1 + 5 + 5 = 25 km)`
b. `text(Shortest Path is)\ CGHE`
Networks, STD2 N2 SM-Bank 8
Highlight the minimal spanning tree of this network on the diagram above, or in a separate diagram. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
Show Worked Solution
`text(One Strategy – Using Prim’s algorithm:)`
`text(6 vertices → 5 edges on spanning tree)`
`text(Starting at vertex A)`
`text(Edge 1: AC)`
`text(Edge 2: AD)`
`text{Edge 3: ED (reject CD which creates a cycle)}`
`text(Edge 4: EF)`
`text(Edge 5: BF)`
Networks, STD2 N2 SM-Bank 4
Complete the minimal spanning tree of the network above on the diagram below. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
Show Worked Solution
`text(One Strategy: Using Prim’s algorithm)`
`text(6 vertices → need 5 edges.)`
`text{Starting at vertex A (any vertex can be chosen)}`
`text(1st Edge: AB)`
`text{2nd Edge: AC (BF also possible)}`
`text(3rd Edge: CD)`
`text(4th Edge: BF)`
`text(5th Edge: AS)`
Networks, STD2 N2 SM-Bank 3
The diagram below is a connected network.
Complete the diagram below to show the minimal spanning tree of this network. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
`text(or)`
Show Worked Solution
`text(One Strategy – Kruskul’s algorithm)`
`text(There are 6 vertices, so we need 5 edges.)`
`text{Edge 1: BC (least weight) – could have chosen ED}`
`text{Edge 2: DE (next least weight)}`
`text{Edge 3: AF (could have been CD)}`
`text(Edge 4: CD)`
`text{Edge 5: CF or EF (reject CE as it creates a cycle)}`
`text(or)`
Networks, STD2 N2 SM-Bank 2
A school is designing a computer network between five key areas within the school.
The cost of connecting the rooms is shown in the diagram below.
- Complete the spanning tree below that creates the school's network at a minimum cost. (1 mark)
- What is the minimum cost of the network? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Show Answers Only
-
- `$1500`
Show Worked Solution
i. `text(One Strategy: Using Prim’s Algorithm)`
`text(Starting vertex – Staff Room)`
`text(1st edge: Staff Room – Library)`
`text(2nd edge: Library – School Office)`
`text(3rd edge: Staff Room – IT Staff)`
`text(4th edge: Library – Computer Room)`
| ii. | `text(Minimum Cost)` | `= 300 + 300 + 400 + 500` |
| `= $1500` |
Networks, STD2 N2 SM-Bank 14
Water will be pumped from a dam to eight locations on a farm.
The pump and the eight locations (including the house) are shown as vertices in the network diagram below.
The numbers on the edges joining the vertices give the shortest distances, in metres, between locations.
- How many vertices on the network diagram have an odd degree? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
The total length of all edges in the network is 1180 metres.
The total length of pipe that supplies water from the pump to the eight locations on the farm is a minimum.
This minimum length of pipe is laid along some of the edges in the network.
- On the diagram below, draw the minimum length of pipe that is needed to supply water to all locations on the farm. (2 marks)
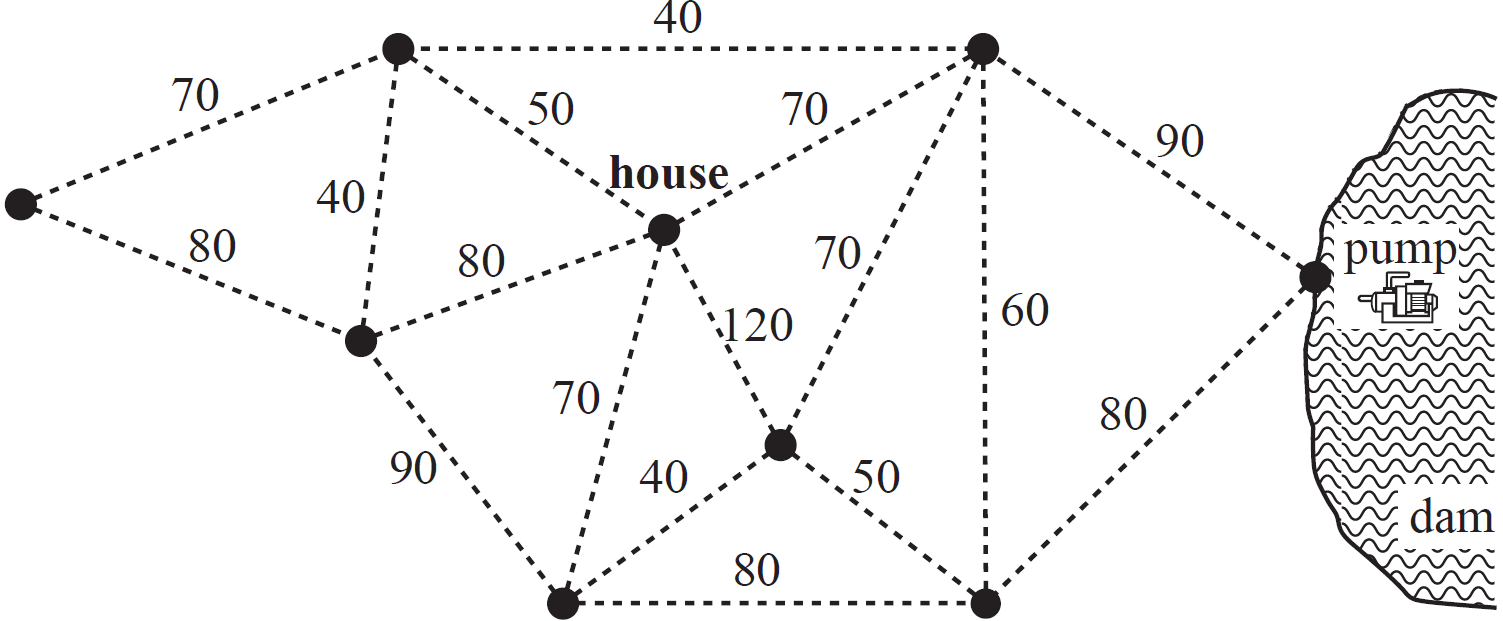
- What is the mathematical term that is used to describe this minimum length of pipe? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Show Answers Only
- `2`
- `1250\ text(m)`
- `text(Minimum spanning tree)`
Show Worked Solution
i. `2\ text{(the house and the top right vertex)}`
MARKER’S COMMENT: Many students, surprisingly, had problems with part (i).
ii. `text(One Strategy – Using Prim’s algorithm:)`
`text(Starting at the house)`
`text(1st edge: 50)`
`text{2nd edge: 40 (either)}`
`text(3rd edge: 40)`
`text(4th edge: 60 etc…)`
iii. `text(Minimum spanning tree)`
Networks, STD2 N2 2007 FUR2 1
A new housing estate is being developed.
There are five houses under construction in one location.
These houses are numbered as points 1 to 5 below.
The builders require the five houses to be connected by electrical cables to enable the workers to have a supply of power on each site.
- What is the minimum number of edges needed to connect the five houses? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- On the diagram above, draw a connected graph with this number of edges. (1 mark)
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
- `4`
-
Show Worked Solution
a. `text(Minimum number of edges = 4)`
b. `text(One of many possibilities,)`
Networks, STD2 N2 2017 FUR2 3a
While on holiday, four friends visit a theme park where there are nine rides.
On the graph below, the positions of the rides are indicated by the vertices.
The numbers on the edges represent the distances, in metres, between rides.
Electrical cables are required to power the rides.
These cables will form a connected graph.
The shortest total length of cable will be used.
- Give a mathematical term to describe a graph that represents these cables. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Draw in the graph that represents these cables on the diagram below. (1 mark)
--- 0 WORK AREA LINES (style=lined) ---
Show Answers Only
a. `text{Minimum spanning tree}`
b.
Show Worked Solution
a. `text{Minimum spanning tree.}`
b. `text(Using Kruskal’s Algorithm)`
`text(Edge 1: 50)`
`text(Edges 2–3: 100)`
`text{Edge 4: 150 (ignore the 150 edge that creates a circuit)}`
`text{Edges 5–6: 200 (ignore the 200 edge that creates a circuit)} `
`text(Edge 7: 300)`
`text(Edge 8: 400)`
Networks, STD2 N2 2015 FUR2 1
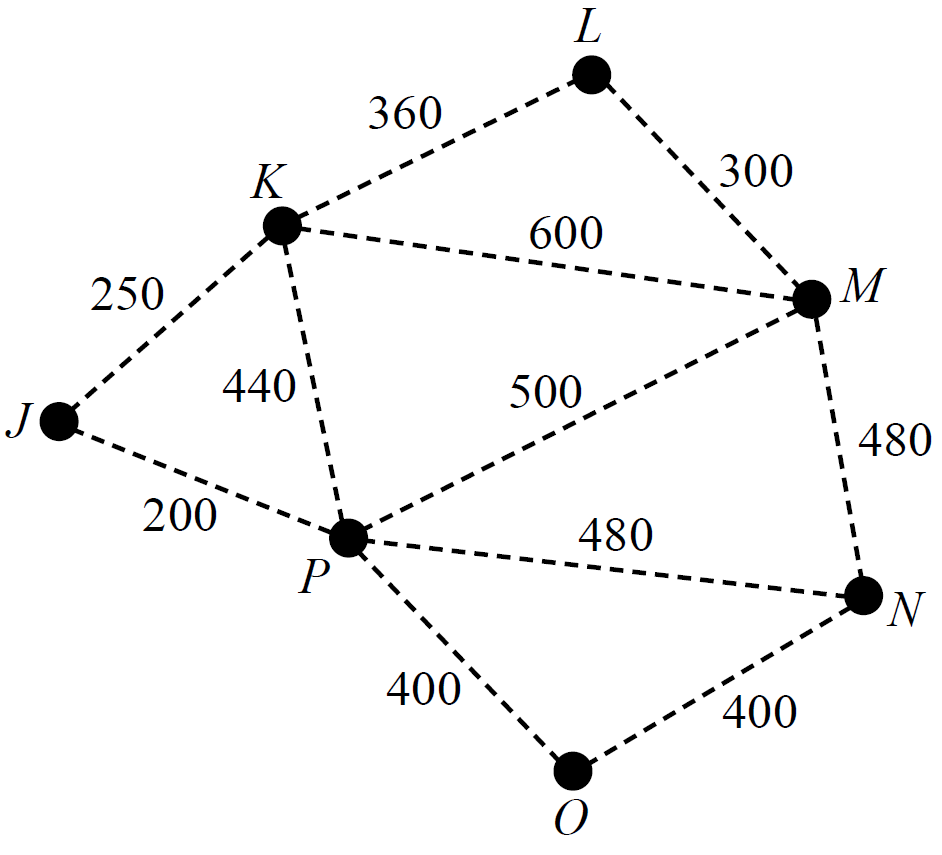
A factory requires seven computer servers to communicate with each other through a connected network of cables.
The servers, `J`, `K`, `L`, `M`, `N`, `O` and `P`, are shown as vertices on the graph below.
The edges on the graph represent the cables that could connect adjacent computer servers.
The numbers on the edges show the cost, in dollars, of installing each cable.
- What is the cost, in dollars, of installing the cable between server `L` and server `M`? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- What is the cheapest cost, in dollars, of installing cables between server `K` and server `N`? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- The computer servers will be able to communicate with all the other servers as long as each server is connected by cable to at least one other server.
- The cheapest installation that will join the seven computer servers by cable in a connected network follows a minimum spanning tree.
- The factory’s manager has decided that only six connected computer servers will be needed, rather than seven.
How much would be saved in installation costs if the factory removed computer server `P` from its minimum spanning tree network?
A copy of the graph above is provided below to assist with your working. (1 mark)
--- 0 WORK AREA LINES (style=lined) ---
- The cheapest installation that will join the seven computer servers by cable in a connected network follows a minimum spanning tree.
Show Answers Only
- `$300`
- `$920`
- `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`
-
- `$120`
-
Show Worked Solution
a. `$300`
b. `text(Minimum cost of)\ K\ text(to)\ N`
`= 440 + 480`
`= $920`
MARKER’S COMMENT: Many students had difficulty finding the minimum spanning tree, often incorrectly excluding `PO` or `KL`.
c.i. `text(Using Prim’s Algorithm:)`
`text(Starting at Vertex)\ L`
`text{1st Edge: L → M (300)}`
`text{2nd Edge: L → K (360)}`
`text{3rd Edge: K → J (250)}`
`text{4th Edge: J → P (200) etc…}`
c.ii. `text(Disconnect)\ J – P\ text(and)\ O – P`
`text(Savings) = 200 + 400 = $600`
`text(Add in)\ M – N`
`text(C)text(ost) = $480`
| `:.\ text(Net savings)` | `= 600 – 480` |
| `= $120` |
Networks, STD2 N2 2011 FUR2 2
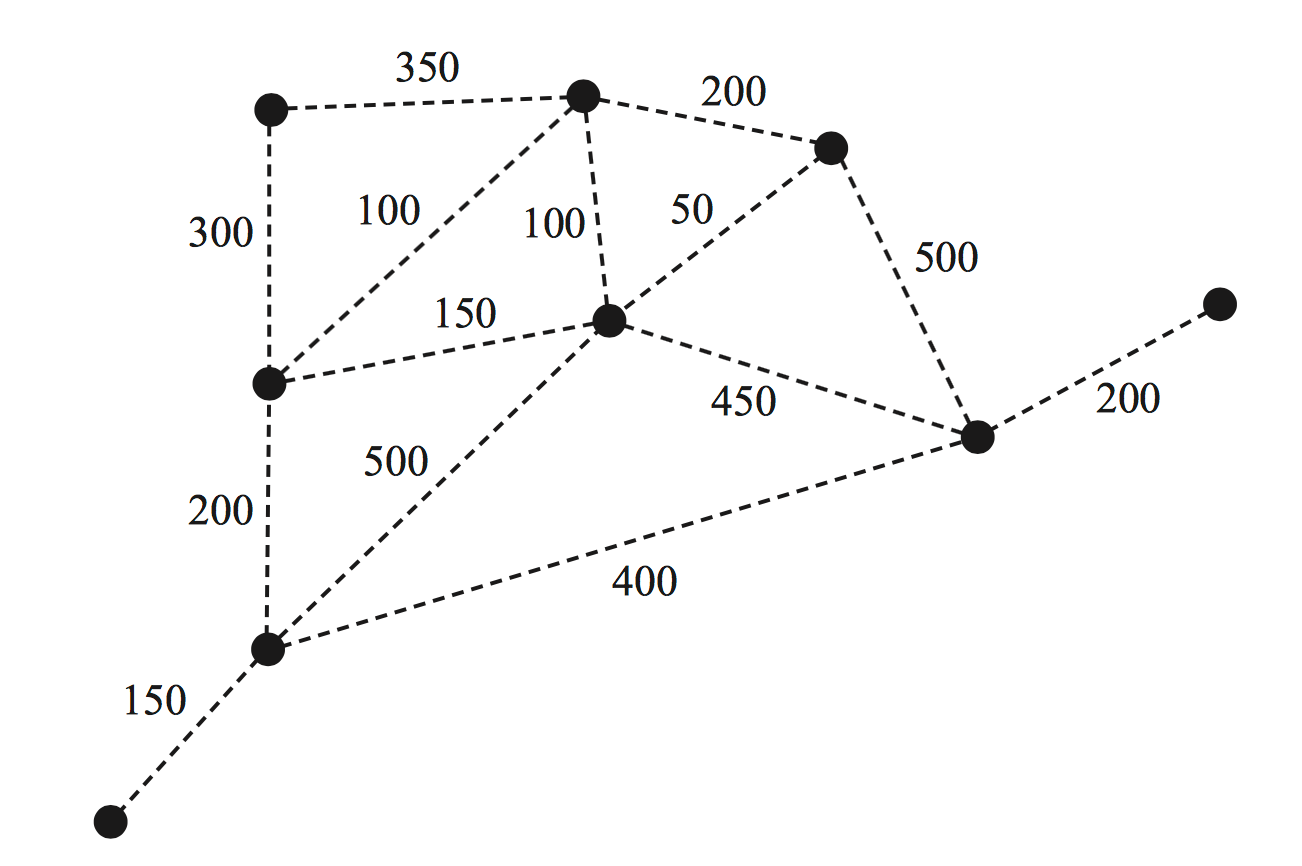
At the Farnham showgrounds, eleven locations require access to water. These locations are represented by vertices on the network diagram shown below. The dashed lines on the network diagram represent possible water pipe connections between adjacent locations. The numbers on the dashed lines show the minimum length of pipe required to connect these locations in metres.
All locations are to be connected using the smallest total length of water pipe possible.
- On the diagram, show where these water pipes will be placed. (1 mark)
- Calculate the total length, in metres, of water pipe that is required. ( 1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Show Answers Only
-
- `510\ text(metres)`
Show Worked Solution
a. `text(Using Prim’s Algorithm)`
`text(Starting at bottom right vertex)`
`text{1st Edge: 50}`
`text{2nd Edge: 40`
`text(3rd Edge: 50)`
`text(4th Edge: 40 etc…)`
b. `text(Total length of water pipe)`
`= 50+40+50+40+50+60+40+60+60+60`
`= 510\ text(metres)`
Networks, STD2 N2 2008 FUR2 1
James, Dante, Tahlia and Chanel are four children playing a game.
In this children’s game, seven posts are placed in the ground.
The network below shows distances, in metres, between the seven posts.
The aim of the game is to connect the posts with ribbon using the shortest length of ribbon.
This will be a minimal spanning tree.
- Draw in a minimal spanning tree for this network on the diagram below. (1 mark)
- Determine the length, in metres, of this minimal spanning tree. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- How many different minimal spanning trees can be drawn for this network? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Show Worked Solution
a. `text(Using Kruskal’s Algorithm)`
`text{Edges 1-3: 2}`
`text{Edges 4-5: 3 (2 edges with weight 3 create a circuit and are ignored)`
`text(Edge 6: 4)`
`text(or)`
b. `text(Length of minimal spanning tree)`
`= 2+2+2+3+3+4`
`= 16\ text(metres)`
c. `2`