SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, SPEC2-NHT 2019 VCAA 8 MC

The total area enclosed between the `x`-axis and the graph of `f(x) = |x^3| - x^2 - |x|` is closest to

  1.  −2.015
  2.  −1.008
  3.     1.008
  4.     2.015
  5.     2.824
Show Answers Only

`D`

Show Worked Solution

`text(Graph)\ \ f(x) = |x^3| – x^2 – |x|\ \ \ (text(by CAS))`

`text(Intersection occurs at:)`

`x = 0, ±((1 + sqrt5)/2)`

`=>\ text(Function is even)`

`:.\ text(Area)` `= −2int_0^(1 + sqrt5) f(x)\ dx\ \ (text(area is below axis))`
  `= 2.015`

 
`=>\ D`

Calculus, SPEC1-NHT 2019 VCAA 9

  1.   Show that  `tan((5pi)/(12)) = sqrt3 + 2`.   (2 marks)
  2.  
     
         
     
    Hence, find the area bounded by the graph of  `f(x) = (2)/(x^2 - 4x + 8)`  shown above, the `x`-axis and the lines  `x = 0`  and  `x = 2 sqrt3 +6`.   (4 marks)
Show Answers Only
  1. `text(Proof (See Worked Solution))`
  2. `(2pi)/(3)`
Show Worked Solution

a.    `text(Method 1:)`

`tan \ (5pi)/(12)` `= tan ((pi)/(4) + (pi)/(6))`
  `= (tan \ (pi)/(4) + tan\ (pi)/(6))/(1 – tan \ (pi)/(4) · tan \ (pi)/(6))`
  `= (1 + (1)/(sqrt3))/(1 – (1)/(sqrt3))`
  `= (sqrt3+1)/(sqrt3-1) xx (sqrt3+1)/(sqrt3+1)`
  `= (3+ 2 sqrt3 + 1)/(3 – 1)`
  `= sqrt3 +2`

  
`text(Method 2:)`

`tan \ (5pi)/(6)` `= (2tan \ (5pi)/(12))/(1 – tan^2 \ (5pi)/(12))`
`- 1/sqrt3` `=(2tan \ (5pi)/(12))/(1 – tan^2 \ (5pi)/(12))`
`-2 sqrt3 tan \ (5pi)/(12)` `= 1 – tan^2 \ (5pi)/(12)`

 

`tan^2 \ (5pi)/(12) – 2 sqrt(3) tan \ (5pi)/(12) – 1 = 0`

`tan \ (5pi)/(12)` `= (2 sqrt3 ± sqrt(12 + 4))/(2)`
  `= sqrt3 + 2 \ \ \ (tan theta > 0)`

 

b.   `text(Area)` `= int_0 ^(2 sqrt3 + 6) \ (2)/(x^2 – 4x + 8)\ dx`
  `= int_0 ^(2 sqrt3 + 6) \ (2)/((x -2)^2 + 2^2)`
  `= [tan^-1 ((x – 2)/(2))]_0 ^(2 sqrt3 + 6)`
  `= tan^-1 (sqrt3 + 2) – tan^-1 (-1)`
  `= (5pi)/(12) – (-(pi)/(4))`
  `= (2pi)/(3)`

Calculus, MET2 2019 VCAA 1

Let  `f: R -> R,\ \ f(x) = x^2e^(-x^2)`.

  1. Find `f^{\prime}(x)`.  (1 mark)
  2. i.  State the nature of the stationary point on the graph of  `f`  at the origin.  (1 mark)
  3. ii.  Find the maximum value of the function  `f`  and the values of  `x`  for which the maximum occurs.  (2 marks)
  4. iii. Find the values of  `d in R`  for which  `f(x) + d`  is always negative.  (1 mark)
  5. i.  Find the equation of the tangent to the graph of  `f`  at  `x = –1`.  (1 mark)
  6. ii. Find the area enclosed by the graph of  `f`  and the tangent to the graph of  `f`  at  `x = –1`, correct to four decimal places.  (2 marks)
  7. Let  `M(m, n)`  be a point on the graph of  `f`, where  `m in [0, 1]`.

     

    Find the minimum distance between  `M`  and the point  `(0, e)`, and the value of  `m`  for which this occurs, correct to three decimal places.  (3 marks)

Show Answers Only
  1. `2x e^(-x^2)(1 – x^2)`
  2. i.  `text(Local minimum)`
  3. ii. `f(x)_max= 1/e\ \ text(when) \ x = -1 and 1`
  4. iii. `d<1/e`
  5. i.  `y = 1/e` 
  6. ii. `0.3568\ text{(to 4 d.p.)}`
  7. `D_(min) = 2.511\ \ text(when)\ \ m ~~ 0.783`
Show Worked Solution
a.    `f^{\prime}(x)` `= x^2 ⋅ -2x ⋅ e^(-x^2) + e^(-x^2) ⋅ 2x`
    `= 2x e^(-x^2) (1 – x^2)`

​

b.i.    `f ^{″}(0) = 2 > 0\ \ \ text{(by CAS)}`
  `:.\ text(Local minimum)`

 

b.ii.    `text(SP’s occur when)\ \ x = –1, 0, 1`
  `f(x)_max = 1/e\ \ text(when)\ \ x = –1  and  1`

 

b.iii.    `f(x)_max + d` `< 0`
  `d` `< 1/e`

 

c.i.    `text(At)\ \ x = –1, \ f(x)\ text(has a max turning point).`
  `:.\ text(T)text(angent:)\ \ y = 1/e`

 

c.ii.    `text(Area)` `= int_(_1)^1 1/e – x^2e^(-x^2) dx`
    `~~ 0.3568\ text{(to 4 d.p.)}`

 

d.   `text(When)\ x = m,\ \ n = m^2 e^(-m^2)`

`text(Find distance between)\ \ M(m, m^2 e^(-m^2)) and P(0, e):`

`D = sqrt((m – 0)^2 + (m^2 e^(-m^2) – e)^2)`

`=>\ text(MIN distance when)\ \ (dD)/(dm) = 0`

`D_(min) = 2.511\ \ text(when)\ \ m ~~ 0.783\ \ \ text{(by CAS)}`

Calculus, SPEC1 2011 VCAA 3

  1. Show that  `f(x) = (2x^2 + 3)/(x^2 + 1)`  can be written in the form  `f(x) = 2 + 1/(x^2 + 1).`  (1 mark)
  2. Sketch the graph of the relation  `y = (2x^2 + 3)/(x^2 + 1)`  on the axes below.

     

    Label any asymptotes with their equations and label any intercepts with the axes, writing them as coordinates.  (3 marks)

     

     
    VCAA 2011 spec 3b
     

  3. Find the area enclosed by the graph of the relation  `y = (2x^2 + 3)/(x^2 + 1)`, the `x`-axis, and the lines  `x = -1`  and  `x = 1.`  (3 marks)
Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. “
    VCAA 2011 spec 3bi
  3. `4 + pi/2`
Show Worked Solution
a.    `f(x)` `= (2x^2 + 3)/(x^2 + 1)`
    `= (2(x^2 + 1) + 1)/(x^2 + 1)`
    `= 2 + 1/(x^2 + 1)`

 

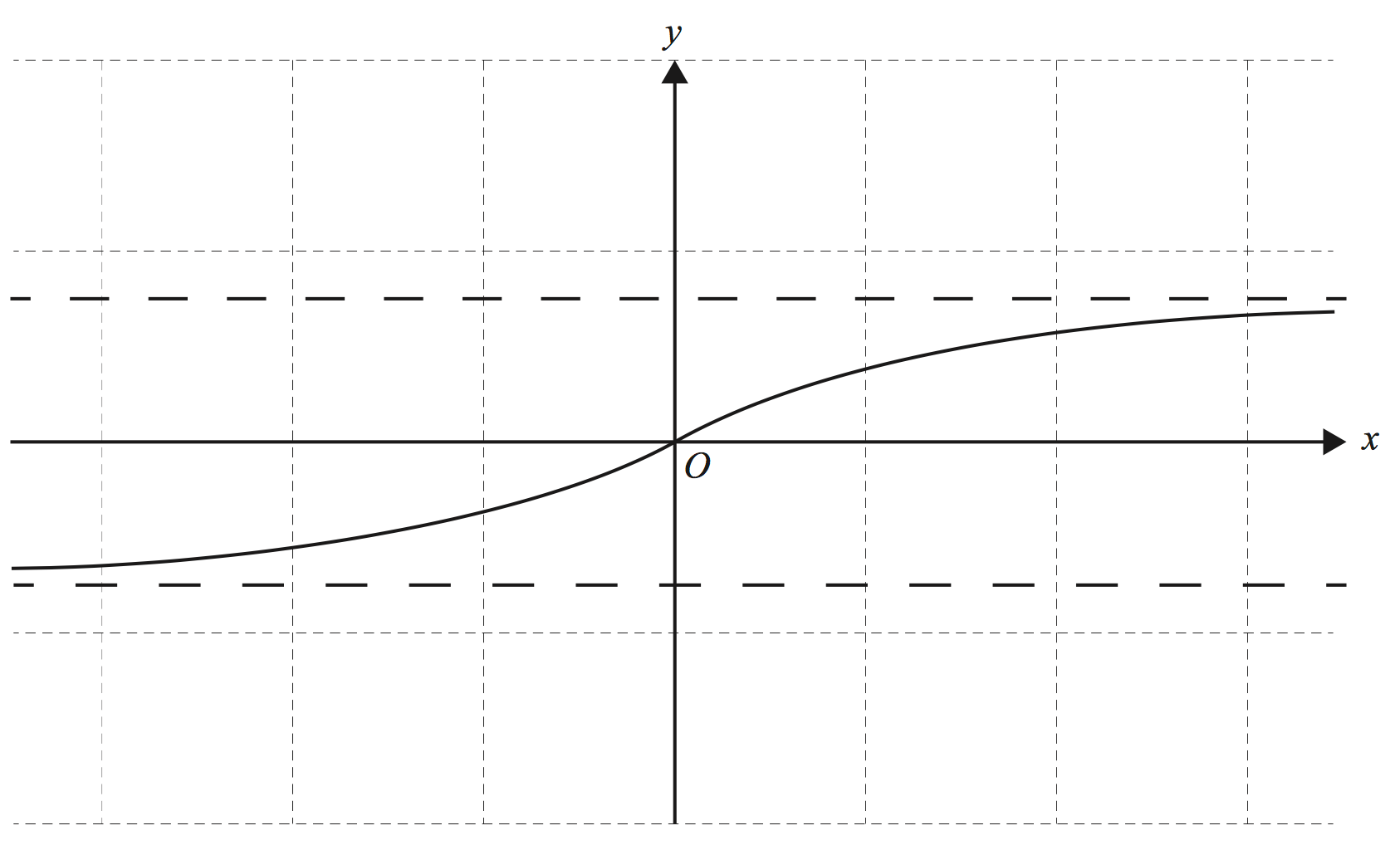
b.   `underset (x→oo) (lim y) = 2`

`text(S)text(ince)\ \ x^2>0\ \ text(for all)\ x,`

`=> f(x)_text(max)\ \ text(occurs when)\ \ x=0\ \ text(at)\ \ (0,3)`
 

VCAA 2011 spec 3bi

 

c.   `f(x)\ \ text(is an even function.)`

`:.\ text(Area)` `= 2 int_0^1 2 + 1/(x^2 + 1)\ dx`  
  `= 2[2x + tan^(−1)(x)]_0^1`  
  `=2[(2+pi/4) – 0]`  
  `= 4 + pi/2`  

Calculus, SPEC1 2012 VCAA 7

Consider the curve with equation  `y = (x - 1) sqrt (2 - x),\ \ 1 <= x <= 2.`

Calculate the area of the region enclosed by the curve and the `x`-axis.  (3 marks)

Show Answers Only

`4/15`

Show Worked Solution

`x – 1 >= 0\ \ text(for)\ \ \ 1 <= x <= 2`

`sqrt(2 – x) >= 0\ \ text(for)\ \ \ 1 <= x <= 2`

`:. (x – 1) sqrt(2 – x) >=0\ \ text(for)\ \ \ 1 <= x <= 2`
 

`text(Let)\ \ u=2-x\ \ =>\ \ x=2-u`

`(du)/dx = -1\ \ =>\ \ dx = -du`

`text(When)\ \ x=2,\ \ u=0`

`text(When)\ \ x=1,\ \ u=1`
 

`A` `= int_1^2 (x – 1) sqrt(2 – x)\ dx`
  `= int_1^0 -(2 – u -1) u^(1/2)\ du`
  `= int_1^0 (u-1) u^(1/2)\ du`
  `= int_1^0 u^(3/2) – u^(1/2)\ du`
  `= [2/5u^(5/2)-2/3 u^(3/2)]_1^0`
  `= [0-(2/5-2/3)]`
  `= -((6-10))/15`
  `= 4/15`

Calculus, SPEC2 2017 VCAA 3

A brooch is designed using inverse circular functions to make the shape shown in the diagram below.
 


 

The edges of the brooch in the first quadrant are described by the piecewise function
 

`f(x){(3text(arcsin)(x/2)text(,), 0 <= x <= sqrt2),(3text(arccos)(x/2)text(,), sqrt2 < x <= 2):}`
 

  1. Write down the coordinates of the corner point of the brooch in the first quadrant.  (1 mark)
  2. Specify the piecewise function that describes the edges in the third quadrant.  (1 mark)
  3. Given that each unit in the diagram represents one centimetre, find the area of the brooch.

     

    Give your answer in square centimetres, correct to one decimal place.  (3 marks)

  4. Find the acute angle between the edges of the brooch at the origin. Give your answer in degrees, correct to one decimal place.  (3 marks)
  5. The perimeter of the brooch has a border of gold.
    Show that the length of the gold border needed is given by a definite integral of the form  `int_0^2 (sqrt(a + b/(4 - x^2)))dx`, where  `a, b ∈ R`. Find the values of `a` and `b`.  (2 marks)
Show Answers Only
  1. `(sqrt2,(3pi)/4)`
  2. `text(See Worked Solutions)`
  3. `9.9\ text(cm²)`
  4. `67.4°`
  5. `a = 16, b = 144`
Show Worked Solution

a.   `text(Corner point occurs when)\ \ x=sqrt2.`

`y=3 sin^(-1) (sqrt2/2) = (3pi)/4`

`:.\ text(Coordinates are:)\ \ (sqrt2, (3pi)/4)`
 

b.    `text(Reflect in the)\ xtext(-axis and then the)\ ytext(-axis:)`

♦ Mean mark 49%.

`g(x){(-3text(arccos)(- x/2)text(,), -2 <= x < -sqrt2),(-3text(arcsin)(- x/2)text(,), -sqrt2 <= x <= 0):}`

 

c.    `A` `= 4 xx (int_0^sqrt2 3sin^(−1)(x/2)dx + int_sqrt2^2 3cos^(−1)(x/2)dx)`
    `~~ 9.9\ text(cm²)`

 

d.   `text(Find the gradient of graph at)\ \ x=0:`

`f′(0) = 3/2`

`alpha = tan^(−1)(3/2) = 56.31…°`

`beta = pi/2 – tan^(−1)(1.5) = 33.69°`


 
`:.\ text(Acute angle between the edges)`

`=2 xx 33.69`

`=67.4°`
  

e.  `f′(x)\ {(3/sqrt(4-x^2)text(,), 0<= x <= sqrt2),((-3)/sqrt(4-x^2)text(,), sqrt2 < x <= 2):}`
 

`:.\ text(Length of border)`

♦♦ Mean mark 27%.

`= 4 int_0^sqrt2 sqrt(1 + (3/sqrt(4 – x^2))^2)\ dx + 4 int_sqrt2^2 sqrt(1 + ((-3)/sqrt(4 – x^2))^2)\ dx`

`= 4 int_0^2 sqrt(1 + (3/sqrt(4 – x^2))^2)\ dx`

`= int_0^2 sqrt(16 + 144/(4 – x^2)\ dx`

  
`:. a=16, \ b=144`

Calculus, SPEC1 2015 VCAA 8

  1.  Show that  `int tan (2x)\ dx = 1/2 log_e |\ sec (2x)\ | + c.`  (2 marks)
  2.  The graph of  `f(x) = 1/2 arctan (x)`  is shown below
     
         
     
  3. i.  Write down the equations of the asymptotes.  (1 mark)
  4. ii. On the axes above, sketch the graph of  `f^-1`, labelling any asymptotes with their equations.  (1 mark)
  5.  Find  `f(sqrt 3).`  (1 mark)
  6.  Find the area enclosed by the graph of  `f`, the `x`-axis and the line  `x = sqrt 3.`   (2 marks)
Show Answers Only

a.   `text(Proof)\ \ text{(See Worked Solutions)}`

b. (i)   `y = -pi/4,\ \ y = pi/4`
  (ii)  

c.   `pi/6`

d.   `(sqrt 3 pi)/6 – log_e sqrt 2`

Show Worked Solution

a.   `text(Let)\ \ u = cos(2x)`

`(du)/(dx) = -2 sin (2x)\ \ =>\ \ -1/2 xx du = sin (2x)\ dx`

`int tan (2x)\ dx` `= int (sin(2x))/(cos(2x))\ dx`
  `= -1/2 int 1/u\ du`
  `= -1/2 log_e |\ u\ | + c`
  `= -1/2 log_e |\ cos (2x)\ | + c`
  `= 1/2 log_e |\ sec (2x)\ | + c`

 

b.i.  `text(Range:)\ \ tan^(-1)(x) in (- pi/2,pi/2)`

`=>1/2 tan^(-1)(x) in (- pi/4, pi/4)`

`:.\ text(Asymptotes:)\ \ y = -pi/4,\ \ y = pi/4`

 

b.ii.

 

c.   `f(sqrt 3)` `= 1/2 tan^(-1) (sqrt 3)`
    `= 1/2 xx pi/3`
    `= pi/6`

 

d.    `y` `= 1/2tan^(−1)(x)`
  `2y` `= tan^(−1)(x)`
  `x` `= tan(2y)`

 

 

♦ Mean mark part (d) 49%.

`text(Area)` `=\ text(Area of rectangle – Area between graph and y-axis)`
  `= sqrt3 xx pi/6 – int_0^(pi/6) tan(2y)\ dy`
  `= (sqrt3 pi)/6 -1/2[ln\ | sec(2y) |]_0^(pi/6)`
  `= (sqrt3 pi)/6 – 1/2[ ln(sec(pi/3)) – ln(sec 0)]`
  `= (sqrt3 pi)/6 – 1/2 (ln2 -ln1)`
  `= (sqrt3 pi)/6 – 1/2 ln2`

Calculus, SPEC1 2014 VCAA 7

Consider  `f(x) = 3x arctan (2x)`.

  1.  Write down the range of  `f`.  (1 mark)
  2.  Show that  `f prime(x) = 3 arctan (2x) + (6x)/(1 + 4x^2)`.  (1 mark)
  3.  Hence evaluate the area enclosed by the graph of  `g(x) = arctan (2x)`, the `x`-axis and the lines  `x = 1/2`  and  `x = sqrt 3/2`.  (3 marks)
Show Answers Only
  1. `f(x) in [0, oo)`
  2. `text(Proof)\ text{(See Worked Solutions)}`
  3. `(pi sqrt 3)/6 – pi/8 – 1/4 ln2`
Show Worked Solution

a.  `f(x) = 3x arctan (2x)`

`f(0) = 0`

♦♦♦ Mean mark 4%.

`text(When)\ \ x < 0, \ \ 3x<0,\ \ text(and)\ \ y = tan^(-1) (2x) < 0`

`text(When)\ \ x>0,\ \ 3x>0,\ \ text(and)\ \ y = tan^(-1) (2x) > 0`
 


 
 `:. f(x) in [0, oo)`

 

b.  `u = 3x, qquad v = tan^(-1)(2x)`

`u prime = 3, qquad v prime = 2/(1 + 4x^2)`

`:. f prime (x)` `= 3(arctan (2x)) + (2/(1 + 4x^2))(3x)`
  `= 3 arctan (2x) + (6x)/(1 + 4x^2)`

 

c.    `A` `= int_(1/2)^(sqrt 3/2) arctan (2x)\ dx`
    `= 1/3 int_(1/2)^(sqrt 3/2) 3arctan (2x)\ dx`
    `=1/3 int_(1/2)^(sqrt 3/2) (3 arctan (2x) + (6x)/(1 + 4x^2) – (6x)/(1 + 4x^2))\ dx`
    `= 1/3 int_(1/2)^(sqrt 3/2) 3 arctan (2x) + (6x)/(1 + 4x^2) dx – int_(1/2)^(sqrt 3/2) (2x)/(1 + 4x^2)\ dx`
    `= 1/3 [3x arctan (2x)]_(1/2)^(sqrt 3/2) – 1/4 int_(1/2)^(sqrt 3/2) (8x)/(1 + 4x^2)\ dx`
    `= [sqrt 3/2 arctan (sqrt 3) – 1/2 arctan (1)] – 1/4[ln (1 + 4x^2)]_(1/2)^(sqrt 3/2)`
    `= sqrt 3/2 (pi/3) – 1/2 (pi/4) – 1/4 [ln (1 + 4(3/4)) – ln(1 + 4 (1/4)]`
    `= (pi sqrt 3)/6 – pi/8 – 1/4 (ln4 – ln 2)`
    `= (pi sqrt 3)/6 – pi/8 – 1/4 ln2`