- For positive real numbers \(a\) and \(b\), prove that \(\dfrac{a+b}{2} \geq \sqrt{a b}\). (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- Hence, or otherwise, show that \(\dfrac{2 n+1}{2 n+2}<\dfrac{\sqrt{2 n+1}}{\sqrt{2 n+3}}\) for any integer \(n \geq 0\). (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Proof, EXT2 P1 2023 HSC 12b
Prove that for all real numbers \(x\) and \(y\), where \(x^2+y^2 \neq 0\),
\(\dfrac{(x+y)^2}{x^2+y^2} \leq 2 \text {. }\) (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
Proof, EXT2 P1 2022 HSC 12a
For real numbers `a,b >= 0` prove that `(a+b)/(2) >= sqrt(ab)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Proof, EXT2 P1 2020 HSC 13c
- By considering the right-angled triangle below, or otherwise, prove that
`frac{a + b}{2} ≥ sqrt(ab)`, where `a > b ≥ 0`. (2 marks)
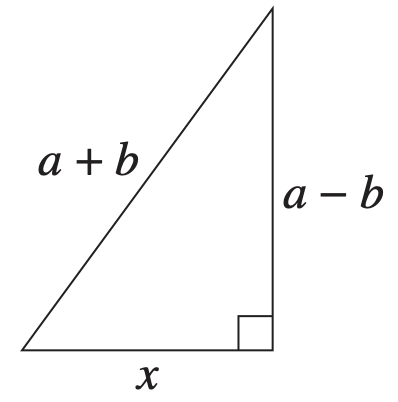
--- 5 WORK AREA LINES (style=lined) ---
- Prove that `p^2 + 4q^2 ≥ 4 pq`. (1 marks)
--- 4 WORK AREA LINES (style=lined) ---
Proof, EXT2 P1 SM-Bank 6
If `x, y, z ∈ R` and `x ≠ y ≠ z`, then
- Prove `x^2 + y^2 + z^2 > yz + zx + xy` (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- If `x + y + z = 1`, show `yz+zx+xy<1/3` (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
Proof, EXT2 P1 2018 HSC 9 MC
It is given that `a`, `b` are real and `p`, `q` are purely imaginary.
Which pair of inequalities must always be true?
- `a^2p^2 + b^2q^2 <= 2abpq,qquada^2b^2 + p^2q^2 <= 2abpq`
- `a^2p^2 + b^2q^2 <= 2abpq,qquada^2b^2 + p^2q^2 >= 2abpq`
- `a^2p^2 + b^2q^2 >= 2abpq,qquada^2b^2 + p^2q^2 <= 2abpq`
- `a^2p^2 + b^2q^2 >= 2abpq,qquada^2b^2 + p^2q^2 >= 2abpq`
Proof, EXT2 P1 2017 HSC 13a
Show that `(r + s)/2 >= sqrt (rs)` for `r >= 0` and `s >= 0`. (1 mark)
Proof, EXT2 P1 2016 HSC 14c
Show that `x sqrt x + 1 >= x + sqrt x,` for `x >= 0.` (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
Proof, EXT2 P1 2015 HSC 15c
For positive real numbers `x` and `y`, `sqrt (xy) <= (x + y)/2`. (Do NOT prove this.)
- Prove `sqrt (xy) <= sqrt ((x^2 + y^2)/2)`, for positive real numbers `x` and `y.` (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- Prove `root4(abcd) <= sqrt ((a^2 + b^2 + c^2 + d^2)/4)`, for positive real numbers `a, b, c` and `d.` (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
Proof, EXT2 P1 2012 HSC 15a
- Prove that `sqrt(ab) ≤ (a + b)/2`, where `a ≥ 0` and `b ≥ 0`. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- If `1 ≤ x ≤ y`, show that `x(y − x + 1) ≥ y`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- Let `n` and `j` be positive integers with `1 ≤ j ≤ n`.
Prove that `sqrtn ≤ sqrt(j(n − j + 1)) ≤ (n + 1)/2.` (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- For integers `n ≥ 1`, prove that
`(sqrtn)^n ≤ n! ≤ ((n + 1)/2)^n`. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---