SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Data Analysis, GEN2 2024 VCAA 3

The Olympic gold medal-winning height for the women's high jump, \(\textit{Wgold}\), is often lower than the best height achieved in other international women's high jump competitions in that same year.

The table below lists the Olympic year, \(\textit{year}\), the gold medal-winning height, \(\textit{Wgold}\), in metres, and the best height achieved in all international women's high jump competitions in that same year, \(\textit{Wbest}\), in metres, for each Olympic year from 1972 to 2020.

A scatterplot of \(\textit{Wbest}\) versus \(\textit{Wgold}\) for this data is also provided.
  

year 1972 1976 1980 1984 1988 1992 1996 2000 2004 2008 2012 2016 2020

Wgold
(m)

 1.92 1.93 1.97 2.02 2.03 2.02 2.05 2.01 2.06 2.05 2.05 1.97 2.04

Wbest
(m)

 1.94 1.96 1.98 2.07 2.07 2.05 2.05 2.02 2.06 2.06 2.05 2.01 2.05

 

When a least squares line is fitted to the scatterplot, the equation is found to be:

\(Wbest =0.300+0.860 \times Wgold\)

The correlation coefficient is 0.9318

  1. Name the response variable in this equation.   (1 mark)

  2. Draw the least squares line on the scatterplot above.  (1 mark)

  3. Determine the value of the coefficient of determination as a percentage.  (1 mark)
  4. Round your answer to one decimal place.
  5. Describe the association between \(\textit{Wbest}\) and \(\textit{Wgold}\) in terms of strength and direction.  (1 mark)

\begin{array}{|l|l|}
\hline
\rule{0pt}{2.5ex}\text { strength } \rule[-1ex]{0pt}{0pt} & \quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\
\hline
\rule{0pt}{2.5ex}\text { direction } \rule[-1ex]{0pt}{0pt} & \\
\hline
\end{array}

  1. Referring to the equation of the least squares line, interpret the value of the slope in terms of the variables \(\textit{Wbest}\) and \(\textit{Wgold}\).  (1 mark)

  2. In 1984, the \(\textit{Wbest}\) value was 2.07 m for a \(\textit{Wgold}\) value of 2.02 m .
  3. Show that when this least squares line is fitted to the scatterplot, the residual value for this point is 0.0328.  (2 marks)

  4. The residual plot obtained when the least squares line was fitted to the data is shown below. The residual value from part f is missing from the residual plot.
     

    1. Complete the residual plot by adding the residual value from part f, drawn as a cross ( X ), to the residual plot above.   (1 mark)

    2. In part b, a least squares line was fitted to the scatterplot. Does the residual plot from part g justify this? Briefly explain your answer.  (1 mark)

  1. In 1964, the gold medal-winning height, \(\textit{Wgold}\), was 1.90m . When the least squares line is used to predict \(\textit{Wbest}\), it is found to be 1.934 m .
  2. Explain why this prediction is not likely to be reliable.  (1 mark)

Show Answers Only

a.    \(Wbest\)

b.    

c.    \(86.8\%\)

d.    \(\text{Strong, positive}\)

e.    \(Wbest\ \text{will increase, on average by 0.86 metres for every metre of increase in}\ Wgold.\)

f.      \(Wbest\) \(=0.300 +0.86\times 2.02\)
    \(=2.0372\)

\(\therefore\ \text{Residual}\ =2.07-2.0372=0.0328\)

g.i.

g.ii.  \(\text{Yes, it is justified as there is no clear pattern, linear or otherwise.}\)

h.    \(\text{This prediction is outside the data range (1972 – 2020 → extrapolation)}\)

\(\text{and therefore cannot be relied upon.}\)

Show Worked Solution

a.    \(Wbest\)

b.    \(\text{Using points:}\ (1.90, 1.934)\ \text{and}\ (2.00, 2.02)\)

c.    \(r=0.9318\)

\(r^2=0.9318^2=0.8682\dots\)

\(\therefore\ \text{Coefficient of determination} \approx 86.8\%\)

d.    \(\text{Strong, positive}\)

e.    \(Wbest\ \text{will increase, on average by 0.86 metres for every metre of increase in}\ Wgold.\)   

f.      \(Wbest\) \(=0.300 +0.86\times 2.02\)
    \(=2.0372\)

\(\therefore\ \text{Residual}\ =2.07-2.0372=0.0328\)

g.i.

g.ii.  \(\text{Yes, it is justified as there is no clear pattern, linear or otherwise.}\)

h.    \(\text{This prediction is outside the data range (1972 – 2020 → extrapolation)}\)

\(\text{and therefore cannot be relied upon.}\)

Data Analysis, GEN1 2024 VCAA 9-10 MC

The least squares equation for the relationship between the average number of male athletes per competing nation, \(males\), and the number of the Summer Olympic Games, \(number\), is

\(males =67.5-1.27 \times number\)

Part A

The summary statistics for the variables number and males are shown in the table below.
 

The value of Pearson's correlation coefficient, \(r\), rounded to three decimal places, is closest to

  1. \(-0.569\)
  2. \(-0.394\)
  3. \(0.394\)
  4. \(0.569\)

Part B

At which Summer Olympic Games will the predicted average number of \(males\) be closest to 25.6 ?

  1. 31st
  2. 32nd
  3. 33rd
  4. 34th
Show Answers Only

Part A

\(A\)

Part B

\(C\)

Show Worked Solution

Part A

\(b\) \(=r\dfrac{s_y}{s_x}\)
\(-1.27\) \(=r\times\dfrac{19}{8.51}\)
\(\therefore\ r\) \(=\dfrac{-1.27\times 8.51}{19}\)
  \(=-0.5688\dots\)

\(\Rightarrow A\)

  
Part B

\(males\) \(=67.5-1.27\times number\)
\(25.6\) \(=67.5-1.27\times number\)
\(number\) \(=\dfrac{67.5-25.6}{1.27}\)
  \(=32.992\dots\)
  \(\approx 33\)

\(\Rightarrow C\)

Data Analysis, GEN2 2023 VCAA 3

The scatterplot below plots the average monthly ice cream consumption, in litres/person, against average monthly temperature, in °C. The data for the graph was recorded in the Northern Hemisphere.
 

When a least squares line is fitted to the scatterplot, the equation is found to be:

consumption = 0.1404 + 0.0024 × temperature

The coefficient of determination is 0.7212

  1. Draw the least squares line on the scatterplot graph above.  (1 mark)

  2. Determine the value of the correlation coefficient \(r\).
  3. Round your answer to three decimal places.  (1 mark)

  4. Describe the association between average monthly ice cream consumption and average monthly temperature in terms of strength, direction and form.  (1 mark)

    \begin{array} {|l|c|}
    \hline
    \rule{0pt}{2.5ex} \textbf{strength} \rule[-1ex]{0pt}{0pt} & \quad \quad \quad \quad \quad \quad \quad \quad \\
    \hline
    \rule{0pt}{2.5ex} \textbf{direction} \rule[-1ex]{0pt}{0pt} & \\
    \hline
    \rule{0pt}{2.5ex} \textbf{form} \rule[-1ex]{0pt}{0pt} & \\
    \hline
    \end{array}

  5. Referring to the equation of the least squares line, interpret the value of the intercept in terms of the variables consumption and temperature.  (1 mark)

  6. Use the equation of the least squares line to predict the average monthly ice cream consumption, in litres per person, when the monthly average temperature is –6°C.  (1 mark)

  7. Write down whether this prediction is an interpolation or an extrapolation.  (1 mark)

Show Answers Only

a.    
         

b.    \(r = \sqrt{0.7212} = 0.849\ \text{(3 d.p.)}\)

c.   

\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \textbf{strength} \rule[-1ex]{0pt}{0pt} & \text{strong} \\
\hline
\rule{0pt}{2.5ex} \textbf{direction} \rule[-1ex]{0pt}{0pt} & \text{positive} \\
\hline
\rule{0pt}{2.5ex} \textbf{form} \rule[-1ex]{0pt}{0pt} & \text{linear} \\
\hline
\end{array}

 
d.    \(\text{At 0°C, the predicted average consumption is:}\)

\(\textit{consumption} = 0.1404 + 0.002 \times 0 = 0.1404\ \text{L/person}\)

 
e.    \(\text{Find consumption} (c)\ \text{when temperature} (t) = -6:\)

\(c=0.1404 + 0.002 \times -6 = 0.1284\ \text{L/person} \)

 
f.     \(\text{Extrapolation (even though the axes extend to –6°C, the data set} \)

\(\text{range finishes with a lower limit around –4.5°C.)}\)

Show Worked Solution

a.    
         

b.    \(r = \sqrt{0.7212} = 0.849\ \text{(3 d.p.)}\)

c.   

\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \textbf{strength} \rule[-1ex]{0pt}{0pt} & \text{strong} \\
\hline
\rule{0pt}{2.5ex} \textbf{direction} \rule[-1ex]{0pt}{0pt} & \text{positive} \\
\hline
\rule{0pt}{2.5ex} \textbf{form} \rule[-1ex]{0pt}{0pt} & \text{linear} \\
\hline
\end{array}

 
d.    \(\text{At 0°C, the predicted average consumption is:}\)

\(\textit{consumption} = 0.1404 + 0.002 \times 0 = 0.1404\ \text{L/person}\)

 
e.    \(\text{Find consumption} (c)\ \text{when temperature} (t) = -6:\)

\(c=0.1404 + 0.002 \times -6 = 0.1284\ \text{L/person} \)

 
f.     \(\text{Extrapolation (even though the axes extend to –6°C, the data set} \)

\(\text{range finishes with a lower limit around –4.5°C.)}\)

Data Analysis, GEN1 2022 VCAA 12-14 MC

The scatterplot below displays the body length, in centimetres, of 17 crocodiles, plotted against their head length, in centimetres. A least squares line has been fitted to the scatterplot. The explanatory variable is head length.
 

Question 12

The equation of the least squares line is closest to

  1. head length = –40 + 7 × body length
  2. body length = –40 + 7 × head length
  3. head length = 168 + 7 × body length
  4. body length = 168 – 40 × head length
  5. body length = 7 + 168 × head length

 
Question 13

The median head length of the 17 crocodiles, in centimetres, is closest to

  1. 49
  2. 51
  3. 54
  4. 300
  5. 345

 
Question 14

The correlation coefficient \(r\) is equal to 0.963

The percentage of variation in body length that is not explained by the variation in head length is closest to

  1. 0.9%
  2. 3.7%
  3. 7.3%
  4. 92.7%
  5. 96.3%
Show Answers Only

\(\text{Question 12}:\ B\)

\(\text{Question 13}:\ B\)

\(\text{Question 12}:\ C\)

Show Worked Solution

\(\text{Question 12}\)

\(\text{Gradient}\ = \dfrac{550-170}{85-30}=6.9\ \ \text{(eliminate D and E)}\)

\(\text{Head length is the explanatory variable  (eliminate A and C)}\)

\(\Rightarrow  B\)

 
\(\text{Question 13}\)

\(\text{Median score}\ =\dfrac{17+1}{2} = 9\text{th score}\)

\(\text{Median head length = 51 cm}\)

\(\Rightarrow B\)


♦ Mean mark (Q13) 51%.

 
\(\text{Question 14}\)

\(\text{Percentage explained by variation in head length}\)

\(r^2 = 0.963^2 = 0.9273 \approx 92.7\% \)

\(\text{Percentage not explained by variation in head length}\)

\(100-92.7 \approx 7.3\%\) 

\(\Rightarrow C\)


♦ Mean mark (Q14) 48%.

Data Analysis, GEN1 2023 VCAA 10 MC

A study of Year 10 students shows that there is a negative association between the scores of topic tests and the time spent on social media. The coefficient of determination is 0.72

From this information it can be concluded that

  1. a decreased time spent on social media is associated with an increased topic test score.
  2. less time spent on social media causes an increase in topic test performance.
  3. an increased time spent on social media is associated with an increased topic test score.
  4. too much time spent on social media causes a reduction in topic test performance.
  5. a decreased time spent on social media is associated with a decreased topic test score.
Show Answers Only

\(A\)

Show Worked Solution

\(\text{Negative association:}\)

  • \(\text{does not mean causality (eliminate B and D).}\)
  • \(\text{Option A: if time spent on social media ↓, topic test scores ↑}\ \checkmark \)
  • \(\text{Option C: if time spent on social media ↑, topic test scores ↓}\ \cross \)
  • \(\text{Option E: if time spent on social media ↓, topic test scores ↓}\ \cross \)

\(\Rightarrow A\)

CORE, FUR2 2021 VCAA 3

The time series plot below shows the winning time, in seconds, for the women's 100 m freestyle swim plotted against year, for each year that the Olympic Games were held during the period 1956 to 2016.

A least squares line has been fitted to the plot to model the decreasing trend in the winning time over this period.
 

The equation of the least squares line is

winning time = 357.1 – 0.1515 × year

The coefficient of determination is 0.8794

  1. Name the explanatory variable in this time series plot.  (1 mark)
  2. Determine the value of the correlation coefficient (`r`).
  3. Round your answer to three decimal places.  (1 mark)
  4. Write down the average decrease in winning time, in seconds per year, during the period 1956 to 2016.  (1 mark)
  5. The predicted winning time for the women's 100 m freestyle in 2000 was 54.10 seconds.
  6. The actual winning time for the women's 100 m freestyle in 2000 was 53.83 seconds.
  7. Determine the residual value in seconds.  (1 mark)
  8. The following equation can be used to predict the winning time for the women's 100 m freestyle in the future.
  9.      winning time =  357.1 – 0.1515 × year
  10.  i. Show that the predicted winning time for the women's 100 m freestyle in 2032 is 49.252 seconds.  (1 mark)
  11. ii. What assumption is being made when this equation is used to predict the winning time for the women's 100 m freestyle in 2032?   (1 mark)
Show Answers Only
  1. `text{year}`
  2. `- 0.938`
  3. `0.1515 \ text{seconds}`
  4. `-0.27`
  5.  i. `49.252 \ text{seconds}`
  6. ii. `text{The same trend continues when the graph is extended beyond 2016.}`
Show Worked Solution

a.      `text{year}`
 

b. `r^2` `= 0.8794 \ text{(given)}`
  `r` `= ± sqrt{0.8794}`
    `= ± 0.938 \ text{(to 3 d.p.)}`

 
`text{By inspection of graph, correlation is negative}`

`:. \ r = -0.938`
 

c.    `text{Average decrease in winning time = 0.1515 seconds}`

`text{(this is given by the slope of the line.)}`
 

d.    `text{Residual Value}` `= text{actual} – text{predicted}`
    `= 53.83 – 54.10`
    `= -0.27`

 

e.i.      `text{winning time (2032)}` `= 357.1 – 0.1515 xx 2032`
      `=49.252 \ text{seconds}`

 

e.ii.  `text{The assumption is that the graph is accurate when it is extended}`

  `text{beyond 2016 (i.e decreasing trend continues).}`

CORE, FUR2 2021 VCAA 2

The two running events in the heptathlon are the 200 m run and the 800 m run. The times taken by the athletes in these two events, times200 and time800, are linearly related.

When a least squares line is fitted to the data, the equation of this line is found to be

                      time800 = 0.03931 + 5.2756 × time200

  1. Round the values for the intercept and the slope to three significant figures. Write your answers in the boxes provided.   (1 mark)
     

    time800=  
     
    		   +  
     
    		   × time200
  2. The mean and the standard deviation for each variable, time200 and time800, are shown in the table below.
     

     
    The equation of the least squares line is
     
            time800 = 0.03931 + 5.2756 × time200 
     
    Use this information to calculate the coefficient of determination as a percentage.

    Round your answer to the nearest percentage.  (2 marks)

Show Answers Only
  1. `text{See Worked Solutions}`
  2. `38text{%}`
Show Worked Solution

a.    `text{time800} = 0.0393 + 5.28 xx text{time200}`

b.    `b = r xx s_y/s_x`
 

`text{Solve for} \ r:`

`5.2756` `= r xx 8.2910/0.96956`
`r` `= 0.6169 …`
`r^2` `= (0.6169 …)^2`
  `= 0.3806 …`
  `= 38text{% (nearest %)}`

CORE, FUR2 2020 VCAA 5

The scatterplot below shows body density, in kilograms per litre, plotted against waist measurement, in centimetres, for 250 men.
 


 

When a least squares line is fitted to the scatterplot, the equation of this line is

body density = 1.195 – 0.001512 × waist measurement

  1. Draw the graph of this least squares line on the scatterplot above.  (1 mark)

(Answer on the scatterplot above.)

  1. Use the equation of this least squares line to predict the body density of a man whose waist measurement is 65 cm.

     

    Round your answer to two decimal places.  (1 mark)

  2. When using the equation of this least squares line to make the prediction in part b., are you extrapolating or interpolating?  (1 mark)
  3. Interpret the slope of this least squares line in terms of a man’s body density and waist measurement.  (1 mark)
  4. In this study, the body density of the man with a waist measurement of 122 cm was 0.995 kg/litre.

     

    Show that, when this least squares line is fitted to the scatterplot, the residual, rounded to two decimal places, is –0.02  (1 mark)

  5. The coefficient of determination for this data is 0.6783

     

    Write down the value of the correlation coefficient `r`.

     

    Round your answer to three decimal places.  (1 mark)

  6. The residual plot associated with fitting a least squares line to this data is shown below.
     

     

       
     

     

    Does this residual plot support the assumption of linearity that was made when fitting this line to this data? Briefly explain your answer.  (1 mark)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `1.10\ text(kg/litre)`
  3. `text(extrapolating)`
  4. `text(See Worked Solutions)`
  5. `-0.02`
  6. `-0.824`
  7. `text(See Worked Solutions)`
Show Worked Solution

a.   `text(LSRL passes through)\ (60, 1.1043) and (130, 0.998)`

♦ Mean mark part a. 41%.

b.   `text(body density)` `= 1.195 – 0.001512 xx 65`
    `= 1.09672`
    `= 1.10\ text{kg/litre (to 2 d.p.)}`
♦ Mean mark part c. 38%.
c.   `text(A waist of 65 cm is outside the)`
  `text(range of the existing data set.)`

 
`:.\ text(Extrapolating)`

 

♦ Mean mark part d. 44%.
d.   `text(Body density decreases by 0.001512 kg/litre)`
  `text(for each increase in waist size of 1 cm.)`

 

e.   `text{Body density (predicted)}`

`= 1.195 – 0.001512 xx 122`

`~~ 1.0105\ text(kg/litre)`
 

`text(Residual)` `= text(Actual – predicted)`
  `~~ 0.995 – 1.0105`
  `~~ -0.0155`
  `~~ -0.02\ text{(to 2 d.p.)}`

 

♦♦ Mean mark part f. 25%.

f.   `r` `= -sqrt(0.6783)`
    `= – 0.8235…`
    `= -0.824\ text{(to 3 d.p.)}`

 

g.  `text(The residual plot has no pattern and is)`

`text(centred around zero.)`

`:.\ text(It supports the assumption of linearity)`

`text(of the LSRL.)`

CORE, FUR2 2020 VCAA 4

The age, in years, body density, in kilograms per litre, and weight, in kilograms, of a sample of 12 men aged 23 to 25 years are shown in the table below.
 

          Age       
(years)

        Body density        
(kg/litre)

        Weight        
(kg)
  23 1.07 70.1
  23 1.07 90.4
  23 1.08 73.2
  23 1.08 85.0
  24 1.03 84.3
  24 1.05 95.6
  24 1.07 71.7
  24 1.06 95.0
  25 1.07 80.2
  25 1.09 87.4
  25 1.02 94.9
  25 1.09 65.3

 

  1. For these 12 men, determine
  2.  i. their median age, in years  (1 mark)
  3. ii. the mean of their body density, in kilograms per litre.  (1 mark)
  4. A least squares line is to be fitted to the data with the aim of predicting body density from weight.
  5.  i. Name the explanatory variable for this least squares line.  (1 mark)
  6. ii. Determine the slope of this least squares line.
  7.     Round your answer to three significant figures.  (1 mark)
  8. What percentage of the variation in body density can be explained by the variation in weight?
  9. Round your answer to the nearest percentage.  (1 mark)
Show Answers Only
  1.  i. `24`
  2. ii. `1.065\ text(kg/litre)`
  3. i. `text(Weight)`
  4. ii. `text(Slope) = -0.00112\ text{(by CAS)}`
  5. `29 text(%)`
Show Worked Solution
a.i.   `n = 12`  
  `text(Median)` `= (text{6th + 7th})/2`
    `= (24 + 24)/2`
    `= 24`

 

a.ii.   `text(Mean)` `= (∑\ text{body density})/12`
    `= 1.065\ text(kg/litre)`

 

b.i.   `text(Weight)`

♦ Mean mark b.ii. 29%.
MARKER’S COMMENT: Most students did not round correctly.

b.ii.   `text(Slope) = -0.00112\ text{(by CAS)}`

 

c.   `r` `= -0.53847\ text{(by CAS)}`
  `r^2` `= 0.289…`

 
`:. 29 text(%)`

CORE, FUR2-NHT 2019 VCAA 4

The scatterplot below plots the variable life span, in years, against the variable sleep time, in hours, for a sample of 19 types of mammals.
 


 

On the assumption that the association between sleep time and life span is linear, a least squares line is fitted to this data with sleep time as the explanatory variable.

The equation of this least squares line is

life span = 42.1 – 1.90 × sleep time

The coefficient of determination is 0.416

  1. Draw the graph of the least squares line on the scatterplot above.  (1 mark)
  2. Describe the linear association between life span and sleep time in terms of strength and direction.  (2 marks)
  3. Interpret the slope of the least squares line in terms of life span and sleep time.  (2 marks)
  4. Interpret the coefficient of determination in terms of life span and sleep time.  (1 mark)
  5. The life of the mammal with a sleep time of 12 hours is 39.2 years.

     

    Show that, when the least squares line is used to predict the life span of this mammal, the residual is 19.9 years.  (2 marks)

Show Answers Only
  1.  

  2. `text(Strength is moderate.)`

     

    `text(Direction is negative.)`

  3. `text(The gradient of –1.9 means that life span decreases by)` 

     

    `text(1.9 years for each additional hour of sleep time.)`

  4. `text(41.6% of the variation in life span can be explained by the)`

     

    `text(variation in sleep time.)`

  5. `text(Proof(See Worked Solution))`
Show Worked Solution

a.    `text{Graph endpoints (0, 42.1) and (18, 7.9)}`
 


 

b.   `text(Strength is moderate.)`

`text(Direction is negative.)`
 

c.    `text(The gradient of –1.9 means that life span decreases by)`

`text(1.9 years for each additional hour of sleep time.)`

 

d.    `text(41.6% of the variation in life span can be explained by the )`

`text(variation in sleep time.)`
 

e.    `text(Predicted value)` `= 42.1 – 1.9 xx 12`
  `= 19.3 \ text(years)`

 

`text(Residual)` `= text(actual) – text(predicted)`
  `= 39.2 – 19.3`
  `= 19.9 \ text(years)`

CORE, FUR2-NHT 2019 VCAA 3

The life span, in years, and gestation period, in days, for 19 types of mammals are displayed in the table below.
 

 

  1. A least squares line that enables life span to be predicted from gestation period is fitted to this data.  (1 mark)

     

    Name the explanatory variable in the equation of this least squares line.

  2. Determine the equation of the least squares line in terms of the variables life span and gestation period.

     

    Write your answers in the appropriate boxes provided below.

     

    Round the numbers representing the intercept and slope to three significant figures.  (2 marks)
      
        =    +    ×   
     

  3. Write the value of the correlation rounded to three decimal places.   (1 mark)
     
         `r =`  
Show Answers Only
  1. `text(gestation period)`
  2. `text(life span) = 7.58 + 0.101 xx \ text(gestation period)`
  3. `0.904`
Show Worked Solution

a.    `text(gestation period)`
 

b.    `text(Input data points into CAS:)`

`text(life span) = 7.58 + 0.101 xx \ text(gestation period)`
 

c.    `r = 0.904 \ text{(by CAS)}`

CORE, FUR1-NHT 2019 VCAA 13 MC

The association between amount of protein consumed (in grams/day) and family income (in dollars) is best displayed using

  1. a scatterplot.
  2. a time series plot.
  3. parallel boxplots.
  4. back-to-back stem plots.
  5. a two-way frequency table.
Show Answers Only

`A`

Show Worked Solution

`text(Both variables are numerical and continuous.)`

`:.\ text(A scatterplot is best.)`

`=>\ A`

CORE, FUR1-NHT 2019 VCAA 12 MC

Which one of the following statements could be true when written as part of the results of a statistical investigation?

  1. The correlation coefficient between height (in centimetres) and foot length (in centimetres) was found to be  `r = 1.24`
  2. The correlation coefficient between height (below average, average, above average) and arm span (in centimetres) was found to be  `r = 0.64`
  3. The correlation coefficient between blood pressure (low, normal, high) and age (under 25, 25–49, over 50) was found to be  `r = 0.74`
  4. The correlation coefficient between the height of students of the same age (in centimetres) and the money they spent on snack food (in dollars) was found to be  `r = 0.22`
  5. The correlation coefficient between height of wheat (in centimetres) and grain yield (in tonnes) was found to be  `r = –0.40`  and the coefficient of determination was found to be  `r^2 = –0.16`
Show Answers Only

`D`

Show Worked Solution

`text(Consider each option,)`

`A: \ r <= 1\ (text(incorrect))`

`B: \ text(height categories are ordinal) :. r\ text(not applicable)`

`C: \ text(both variables are ordinal) :. r\ text(not applicable)`

`D: \ text(possibly true)`

`E: \ text(Coefficient of determination cannot be negative (incorrect))`

`=>\ D`

CORE, FUR2 2019 VCAA 5

The scatterplot below shows the atmospheric pressure, in hectopascals (hPa), at 3 pm (pressure 3 pm) plotted against the atmospheric pressure, in hectopascals, at 9 am (pressure 9 am) for 23 days in November 2017 at a particular weather station.
 


 

A least squares line has been fitted to the scatterplot as shown.

The equation of this line is

pressure 3 pm = 111.4 + 0.8894 × pressure 9 am

  1. Interpret the slope of this least squares line in terms of the atmospheric pressure at this weather station at 9 am and at 3 pm.  (1 mark)
  2. Use the equation of the least squares line to predict the atmospheric pressure at 3 pm when the atmospheric pressure at 9 am is 1025 hPa.

     

    Round your answer to the nearest whole number.  (1 mark)

  3. Is the prediction made in part b. an example of extrapolation or interpolation?  (1 mark)
  4. Determine the residual when the atmospheric pressure at 9 am is 1013 hPa.

     

    Round your answer to the nearest whole number.  (1 mark)

  5. The mean and the standard deviation of pressure 9 am and pressure 3 pm for these 23 days are shown in Table 4 below.
     


 

    1. Use the equation of the least squares line and the information in Table 4 to show that the correlation coefficient for this data, rounded to three decimal places, is  `r` = 0.966  (1 mark)
    2. What percentage of the variation in pressure 3 pm is explained by the variation in pressure 9 am?

       

      Round your answer to one decimal place.  (1 mark)

  1. The residual plot associated with the least squares line is shown below.
     


 

    1. The residual plot above can be used to test one of the assumptions about the nature of the association between the atmospheric pressure at 3 pm and the atmospheric pressure at 9 am.

       

      What is this assumption?  (1 mark)

    2. The residual plot above does not support this assumption.

       

      Explain why.  (1 mark)

Show Answers Only
  1. `text(An increase in 1hPa of pressure at 9 am is associated)`
    `text(with an increase of 0.8894 hPa of pressure at 3 pm.)`
  2. `1023\ text(hPa)`
  3. `text(Interpolation)`
  4. `3\ text(hPa)`
    1. `0.966`
    2. `93.3%`
    1. `text(The assumption is that a linear relationship)`
      `text(exists between the pressure at 9 am and the)`
      `text(pressure at 3 pm.)`
    2. `text(The residual plot does not appear to be random.)`
Show Worked Solution

a.    `text(An increase in 1hPa of pressure at 9 am is associated)`

`text(with an increase of 0.8894 hPa of pressure at 3 pm.)`

 

b.   `text(pressure 3 pm)` `= 111.4 + 0.8894 xx 1025`
    `= 1023\ text(hPa)`

 

c.  `text{Interpolation (1025 is within the given data range)}`

 

d.   `text(Residual)` `= text(actual) – text(predicted)`
    `= 1015 – (111.4 + 0.8894 xx 1013)`
    `= 1015 – 1012.36`
    `= 2.63…`
    `~~ 3\ text(hPa)`

 

e.i.   `r= b (s_x)/(s_y)`

    `= 0.8894 xx 4.5477/4.1884`
    `= 0.96569…`
    `= 0.966`

 

e.ii.   `r` `= 0.966`
  `r^2` `= 0.9331`
    `= 93.3%`

 

f.i.   `text(The assumption is that a linear relationship)`
 

`text(exists between the pressure at 9 am and the)`

`text(pressure at 3 pm.)`

 

f.ii.  `text(The residual plot does not appear to be random.)`

CORE, FUR2 2019 VCAA 4

The relative humidity (%) at 9 am and 3 pm on 14 days in November 2017 is shown in Table 3 below.
 

A least squares line is to be fitted to the data with the aim of predicting the relative humidity at 3 pm (humidity 3 pm) from the relative humidity at 9 am (humidity 9 am).

  1. Name the explanatory variable.  (1 mark)
  2. Determine the values of the intercept and the slope of this least squares line.

     

    Round both values to three significant figures and write them in the appropriate boxes provided.

humidity 3 pm = 
 
   +  
 
   × humidity 9 am  (1 mark)

 

  1. Determine the value of the correlation coefficient for this data set.

     

    Round your answer to three decimal places.  (1 mark)

Show Answers Only
  1. `text(humidity 9 am)`
  2. `text(humidity 3 pm) = -1.26 + 0.765 xx text(humidity 9 am)`
  3. `r = 0.871`
Show Worked Solution

a.  `text(humidity 9 am)`
 

b.  `text(Input all data points into CAS:)`

`text(humidity 3 pm) = -1.26 + 0.765 xx text(humidity 9 am)`
 

c.    `r = 0.871\ \ text{(3 d.p.)}`

CORE, FUR1 2019 VCAA 9-10 MC

A least squares line is used to model the relationship between the monthly average temperature and latitude recorded at seven different weather stations. The equation of the least squares line is found to be
 

`quad text(average temperature) = 42.9842 - 0.877447 xx text(latitude)`

 
Part 1

When the numbers in this equation are correctly rounded to three significant figures, the equation will be

  1. `text(average temperature) = 42.984 - 0.877 xx text(latitude)`
  2. `text(average temperature) = 42.984 - 0.878 xx text(latitude)`
  3. `text(average temperature) = 43.0 - 0.878 xx text(latitude)`
  4. `text(average temperature) = 42.9 - 0.878 xx text(latitude)`
  5. `text(average temperature) = 43.0 - 0.877 xx text(latitude)`

 
Part 2

The coefficient of determination was calculated to be 0.893743

The value of the correlation coefficient, rounded to three decimal places, is

  1. − 0.945
  2. − 0.898
  3.  0.806
  4.  0.898
  5.  0.945
Show Answers Only

`text(Part 1:)\ E`

`text(Part 2:)\ A`

Show Worked Solution

`text(Part 1)`

`42.9842 \ => \ 43.0\ text{(3 sig)}`

`0.877447 \ => \ 0.877\ text{(3 sig)}`

`=>  E`
 

`text(Part 2)`

`text(Correlation coefficient)`

`= -sqrt(0.893743)`

`= -0.945`

`=>  A`

CORE, FUR2 2018 VCAA 2

The congestion level in a city can be recorded as the percentage increase in travel time due to traffic congestion in peak periods (compared to non-peak periods).

This is called the percentage congestion level.

The percentage congestion levels for the morning and evening peak periods for 19 large cities are plotted on the scatterplot below.
 


 

  1. Determine the median percentage congestion level for the morning peak period and the evening peak period.

     

    Write your answers in the appropriate boxes provided below.  (2 marks)

Median percentage congestion level for morning peak period
%
Median percentage congestion level for evening peak period
%

 
A least squares line is to be fitted to the data with the aim of predicting evening congestion level from morning congestion level.

The equation of this line is.

evening congestion level = 8.48 + 0.922 × morning congestion level
 

  1. Name the response variable in this equation.  (1 mark)
  2. Use the equation of the least squares line to predict the evening congestion level when the morning congestion level is 60%.  (1 mark)
  3. Determine the residual value when the equation of the least squares line is used to predict the evening congestion level when the morning congestion level is 47%.

     

    Round your answer to one decimal place?  (2 marks)

  4. The value of the correlation coefficient `r` is 0.92

     

    What percentage of the variation in the evening congestion level can be explained by the variation in the morning congestion level?

     

    Round your answer to the nearest whole number.  (1 mark)

Show Answers Only
  1. `52 text(%);\ 56 text(%)`
  2. `text(evening congestion level)`
  3. `63.8 text(%)`
  4. `-1.8 text{% (to 1 d.p.)}`
  5. `85 text(%)`
Show Worked Solution

a.   `19\ text(data points of morning peak)`

Mean mark 56%.
COMMENT: This question was surprisingly poorly answered. Review carefully!

`text(Median is 10th data point moving left to right.)`

`:.\ text{Median (morning peak) = 52%}`

 

`text(Median of evening peak is 10th data point)`

`text(moving bottom to top.)`

`:.\ text{Median (afternoon peak) = 56%}`
 

b.   `text(Response variable is evening congestion level.)`
 

c.    `text(evening congestion level)` `= 8.48 + 0.922 xx 60`
    `= 63.8 text(%)`

 
d.  `text(When morning level = 47%, Actual = 50%)`

Mean mark part (d) 53%.
COMMENT: Many students had problems at a number of stages in this part.

`text(Residual)` `=\ text(Actual evening congestion − predicted)`
  `= 50 – (8.48 + 0.922 xx 47)`
  `= -1.814`
  `= -1.8 text{% (to 1 d.p.)}`

 

e.    `r` `= 0.92`
  `r^2` `= 0.8464`
    `= 85 text{% (nearest whole)}`

 
`:. 85 text(% of the variations is explained.)`

CORE, FUR1 2018 VCAA 14 MC

A least squares line is fitted to a set of bivariate data.

Another least squares line is fitted with response and explanatory variables reversed.

Which one of the following statistics will not change in value?

  1. the residual values
  2. the predicted values
  3. the correlation coefficient `r`
  4. the slope of the least squares line
  5. the intercept of the least squares line
Show Answers Only

`C`

Show Worked Solution

`text(If the variables are reversed, the equation changes.)`

♦ Mean mark 42%.

`:.\ text(Differences will occur in:)`

`text(- slope)`

`text(- intercept)`

`text(- predicted and residual values)`
 

`text(The correlation co-efficient will remain unchanged however,)`

`text(as the scattering of the points around the line of best fit is)`

`text{the same (i.e. scattering of}\ x\ text(values relative to)\ y\ text(values)`

`text(is the same as)\ y\ text(values relative to)\ x).`

`=> C`

CORE, FUR1 2018 VCAA 7-9 MC

The scatterplot below displays the resting pulse rate, in beats per minute, and the time spent exercising, in hours per week, of 16 students. A least squares line has been fitted to the data.
 

 
Part 1

Using this least squares line to model the association between resting pulse rate and time spent exercising, the residual for the student who spent four hours per week exercising is closest to

  1. –2.0 beats per minute.
  2. –1.0 beats per minute.
  3. –0.3 beats per minute.
  4.   1.0 beats per minute.
  5.   2.0 beats per minute.

 
Part 2

The equation of this least squares line is closest to

  1. resting pulse rate = 67.2 – 0.91 × time spent exercising
  2. resting pulse rate = 67.2 – 1.10 × time spent exercising
  3. resting pulse rate = 68.3 – 0.91 × time spent exercising
  4. resting pulse rate = 68.3 – 1.10 × time spent exercising
  5. resting pulse rate = 67.2 + 1.10 × time spent exercising

 
Part 3

The coefficient of determination is 0.8339

The correlation coefficient `r` is closest to

  1. –0.913
  2. –0.834
  3. –0.695
  4.   0.834
  5.   0.913
Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ D`

`text(Part 3:)\ A`

Show Worked Solution

`text(Part 1)`

`text(Predicted rate = 64 bpm)`

`:.\ text(Residual)` `=\ text(actual − predicted)`
  `= 63 – 64`
  `= −1.0\ text(bpm)`

`=> B`

 

`text(Part 2)`

♦ Mean mark 46%.

`text(By elimination:)`

`ytext(-intecept) != 67.2\ text(since the)\ xtext(-axis starts)`

`text(at)\ \ x = 1\ \ (text(not)\ \ x = 0)`

`:.\ text(Eliminate)\ A, B\ text(and)\ E.`
 

`text(Consider the gradient.)`

`text(For each horizontal run of 1 unit, the line)`

`text(decreases vertically more than 1 unit.)`

`:.\ text(Eliminate)\ C.`

`=> D`

 

`text(Part 3)`

♦ Mean mark 45%.

`text(The correlation is clearly negative.)`

`:. r` `= −sqrt(0.8339)`
  `= −0.913`

`=>A`

CORE, FUR2 2017 VCAA 3

The number of male moths caught in a trap set in a forest and the egg density (eggs per square metre) in the forest are shown in the table below.
 


 

  1. Determine the equation of the least squares line that can be used to predict the egg density in the forest from the number of male moths caught in the trap.

     

    Write the values of the intercept and slope of this least squares line in the appropriate boxes provided below.

     

    Round your answers to one decimal place.  (2 marks)

     
     

         

  2. The number of female moths caught in a trap set in a forest and the egg density (eggs per square metre) in the forest can also be examined.

     

    A scatterplot of the data is shown below.
     


     
    The equation of the least squares line is

     

                  egg density = 191 + 31.3 × number of female moths
     

    1. Draw the graph of this least squares line on the scatterplot (provided above).  (1 mark)
    2. Interpret the slope of the regression line in terms of the variables egg density and number of female moths caught in the trap.  (1 mark)
    3. The egg density is 1500 when the number of female moths caught is 55.

       

      Determine the residual value if the least squares line is used to predict the egg density for this number of female moths.  (1 mark)

    4. The correlation coefficient is  `r = 0.862`

       

      Determine the percentage of the variation in egg density in the forest explained by the variation in the number of female moths caught in the trap.

       

      Round your answer to one decimal place.  (1 mark)

Show Answers Only
  1. `text(egg density)\ = −46.8 + 18.9 xx text(number of male moths)`
  2.    
  3. `text(Egg density per square metre increases)`
     `text(by 31.3 eggs for every extra female moth)`
     `text(caught in the trap.)`
  4. `−412.5`
  5. `text(74.3%)`
Show Worked Solution

a.   `text(By calculator)`

`text(egg density)\ = −46.8 + 18.9 xx text(number of male moths)`

 

b.i.   `text(Calculating extreme points on graph.)`

♦♦ Mean mark 26%.
MARKER’S COMMENT: Not well answered! Many students did not realise the graph started at 10 on the `x`-axis and many did not use a ruler!

`x = 10, y = 191 + 31.3 xx 10 = 504`

`x = 60, y = 191 + 31.3 xx 60 = 2069`

 

♦ Mean mark 39%.
MARKER’S COMMENT: Students must clearly refer to the increase in egg density for every one-unit increase in female moths.

b.ii.   `text(Egg density per square metre increases)`

 `text(by 31.3 eggs for every extra female moth)`

 `text(caught in the trap.)`

 

b.iii.   `text(Predicted egg density)`

♦ Mean mark 48%.

`= 191 + 31.3 xx 55`

`= 1912.5`

`:.\ text(Residual value)` `= 1500 – 1912.5`
  `= −412.5`

 

b.iv.   `r = 0.862`

♦ Mean mark 47%.

`r^2 = 0.862^2 = 0.7430… = 74.3text{%  (1 d.p.)}`

`:.\ text(74.3% is explained.)`

CORE, FUR1 2017 VCAA 12 MC

Data collected over a period of 10 years indicated a strong, positive association between the number of stray cats and the number of stray dogs reported each year (`r = 0.87`) in a large, regional city.

A positive association was also found between the population of the city and both the number of stray cats (`r = 0.61`) and the number of stray dogs (`r = 0.72`).

During the time that the data was collected, the population of the city grew from 34 564 to 51 055.

From this information, we can conclude that

  1. if cat owners paid more attention to keeping dogs off their property, the number of stray cats reported would decrease.
  2. the association between the number of stray cats and stray dogs reported cannot be causal because only a correlation of +1 or –1 shows causal relationships.
  3. there is no logical explanation for the association between the number of stray cats and stray dogs reported in the city so it must be a chance occurrence.
  4. because larger populations tend to have both a larger number of stray cats and stray dogs, the association between the number of stray cats and the number of stray dogs can be explained by a common response to a third variable, which is the increasing population size of the city.
  5. more stray cats were reported because people are no longer as careful about keeping their cats properly contained on their property as they were in the past.
Show Answers Only

`D`

Show Worked Solution

`text(Because larger populations tend to have both a larger)`

`text(number of stray cats and stray dogs, the association)`

`text(between the number of stray cats and the number of stray)`

`text(dogs can be explained by a common response to a third)`

`text(variable, which is the increasing population size of the city.)`

`=> D`

CORE, FUR2 2016 VCAA 3

The data in the table below shows a sample of actual temperatures and apparent temperatures recorded at a weather station. A scatterplot of the data is also shown.

The data will be used to investigate the association between the variables apparent temperature and actual temperature.
 


 

  1. Use the scatterplot to describe the association between apparent temperature and actual temperature in terms of strength, direction and form.  (1 mark)
    1. Determine the equation of the least squares line that can be used to predict the apparent temperature from the actual temperature.

       

      Write the values of the intercept and slope of this least squares line in the appropriate boxes provided below.

       

      Round your answers to two significant figures.  (3 marks)
       

           apparent temperature `=`    
       
      		 `+`  
       
      		 `xx`   actual temperature

       

    2. Interpret the intercept of the least squares line in terms of the variables apparent temperature and actual temperature.  (1 mark)
  1. The coefficient of determination for the association between the variables apparent temperature and actual temperature is 0.97

     

    Interpret the coefficient of determination in terms of these variables.  (1 mark)

  2. The residual plot obtained when the least squares line was fitted to the data is shown below.
     
     

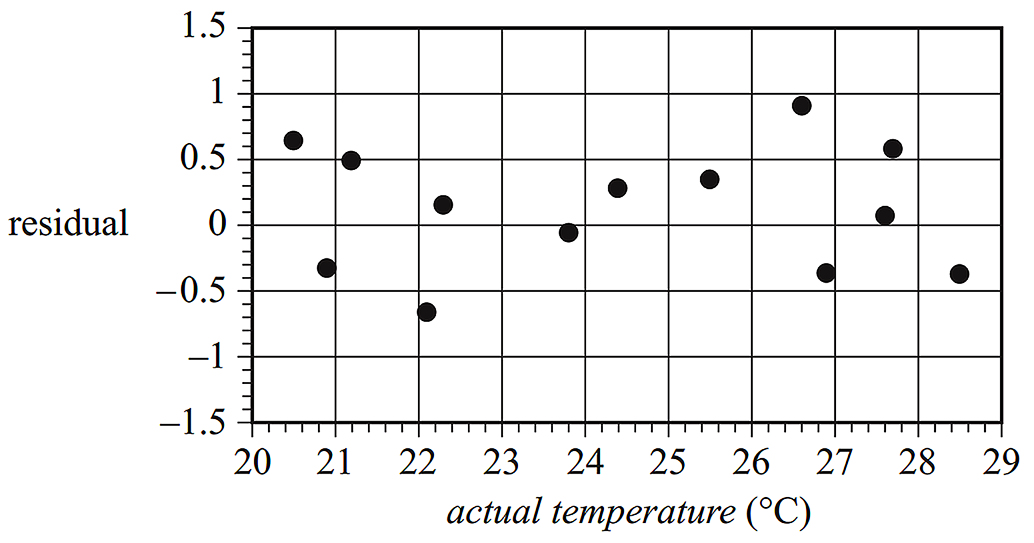
    1. A residual plot can be used to test an assumption about the nature of the association between two numerical variables.

       

      What is this assumption?  (1 mark)

    2.  Does the residual plot above support this assumption? Explain your answer.  (1 mark)
Show Answers Only
  1. `text(Strong, positive and linear)`
    1. `text(apparent temperature) = -1.7 xx 0.94 xx text(actual temperature)`
    2. `text(See Worked Solutions)`
  3. `text(See Worked Solutions)`
    1. `text(See Worked Solutions)`
    2. `text(See Worked Solutions)`
Show Worked Solution

a.   `text(Strong, positive and linear)`

 

b.i.    `text(By calculator,)`
  `text(apparent temperature) = -1.7 xx 0.94 xx text(actual temperature)`

 

♦♦ Mean mark of part (b)(ii) – 28%.
MARKER’S COMMENT: “the predicted apparent temp is -1.7°C” also gained a mark.
b.ii.    `text(When actual temperature is 0°C, on average,)`
 

`text(the apparent temperature is)\ − 1.7^@\text(C.)`

 

♦ Mean mark 49%.
IMPORTANT: Any mention of causality loses a mark!
c.    `text(97% of the variation in the apparent temperature)`
 

`text(can be explained by the variation in the)`

`text(actual temperature.)`

 

d.i.    `text(There is a linear relationship)`
  `text(between the two variables.)`
♦ Mean mark of both parts of (d) was 46%.
MARKER’S COMMENT: Students should refer to randomness or a lack of pattern explicitly here.

 

d.ii.    `text(The random pattern supports)`
  `text(the assumption.)`

 

CORE, FUR1 2016 VCAA 11-12 MC

The table below gives the Human Development Index (HDI) and the mean number of children per woman (children) for 14 countries in 2007.

A scatterplot of the data is also shown. 
 

 

Part 1

The scatterplot is non-linear.

A log transformation applied to the variable children can be used to linearise the scatterplot.

With HDI as the explanatory variable, the equation of the least squares line fitted to the linearised data is closest to

  1. log(children) = 1.1 – 0.0095 × HDI
  2. children = 1.1 – 0.0095 × log(HDI)
  3. log(children) = 8.0 – 0.77 × HDI
  4. children = 8.0 – 0.77 × log(HDI)
  5. log(children) = 21 – 10 × HDI

 

Part 2

There is a strong positive association between a country’s Human Development Index and its carbon dioxide emissions.

From this information, it can be concluded that

  1. increasing a country’s carbon dioxide emissions will increase the Human Development Index of the country.
  2. decreasing a country’s carbon dioxide emissions will increase the Human Development Index of the country.
  3. this association must be a chance occurrence and can be safely ignored.
  4. countries that have higher human development indices tend to have higher levels of carbon dioxide emissions.
  5. countries that have higher human development indices tend to have lower levels of carbon dioxide emissions.
Show Answers Only

`text(Part 1:)\ A`

`text(Part 2:)\ D`

Show Worked Solution

`text(Part 1)`

`=>A`

 

`text(Part 2)`

`text(A strong positive association does not mean)`

`text(an increase in one variable causes an increase)`

`text(in the other.)`

`=> D`

CORE, FUR1 2016 VCAA 9-10 MC

The scatterplot below shows life expectancy in years (life expectancy) plotted against the Human Development Index (HDI) for a large number of countries in 2011.

A least squares line has been fitted to the data and the resulting residual plot is also shown.
 

The equation of this least squares line is

life expectancy = 43.0 + 0.422 × HDI

The coefficient of determination is  `r^2` = 0.875
 

Part 1

Given the information above, which one of the following statements is not true?

  1. The value of the correlation coefficient is close to 0.94
  2. 12.5% of the variation in life expectancy is not explained by the variation in the Human Development Index.
  3. On average, life expectancy increases by 43.0 years for each 10-point increase in the Human Development Index.
  4. Ignoring any outliers, the association between life expectancy and the Human Development Index can be described as strong, positive and linear.
  5. Using the least squares line to predict the life expectancy in a country with a Human Development Index of 75 is an example of interpolation.

 

Part 2

In 2011, life expectancy in Australia was 81.8 years and the Human Development Index was 92.9

When the least squares line is used to predict life expectancy in Australia, the residual is closest to

  1. `–0.6`
  2. `–0.4`
  3.    `0.4`
  4.  `11.1`
  5.  `42.6`
Show Answers Only

`text(Part 1:)\ C`

`text(Part 1:)\ B`

Show Worked Solution

`text(Part 1)`

`text(Consider option)\ C,`

`text(If HDI increases by 10,)`

`text(Increase in life expectancy)`

`= 0.422 xx 10`

`= 4.22\ text(years)`

`!= 43\ text(years)`

`=> C`

 

`text(Part 2)`

`text(Predicted life expectancy)`

`= 43.0 + 0.422 xx 92.90`

`= 82.20…`

`:.\ text(Residual)` `= 81.8 – 82.20…`
  `= −0.40…`

`=> B`

CORE, FUR2 2006 VCAA 2

The heights (in cm) and ages (in months) of a random sample of 15 boys have been plotted in the scatterplot below. The least squares regression line has been fitted to the data.
 


   
The equation of the least squares regression line is 

`text(height = 75.4 + 0.53 × age)`

The correlation coefficient is  `r= 0.7541`

  1. Complete the following sentence.

     

    On average, the height of a boy increases by _______ cm for each one-month increase in age.  (1 mark)

    1. Evaluate the coefficient of determination.

       

      Write your answer, as a percentage, correct to one decimal place.  (1 mark)

    2. Interpret the coefficient of determination in terms of the variables height and age.  (1 mark)


Show Answers Only
  1. `0.53`
    1. `text(56.9%)`
    2. `text{The coefficient of determination 0.569 (56.9%) represents}`

       

      `text{the proportion (percentage) of the variability in height with age}`

       

      `text(that is explained by the least squares regression line.)`

Show Worked Solution

a.   `0.53`

♦ Average mean mark for all parts 44%.
MARKER’S COMMENT: Q.bi caused problems with common errors of not converting to %, or rounding as a decimal before converting and answering 60%.

 

b.i.    `r^2` `= 0.7541^2`
    `= 0.5686…`
    `= 56.9text(%)`
MARKER’S COMMENT: Any reference to causation in Q.bii was marked incorrect.

 

b.ii.  `text{56.9% of the variation in height is}`

`text{explained by the variation in age.}`

 

CORE, FUR2 2007 VCAA 3

The table below displays the mean surface temperature (in °C) and the mean duration of warm spell (in days) in Australia for 13 years selected at random from the period 1960 to 2005.
 

CORE, FUR2 2007 VCAA 31
 

This data set has been used to construct the scatterplot below. The scatterplot is incomplete.

  1. Complete the scatterplot below by plotting the bold data values given in the table above. Mark the point with a cross (×).  (1 mark)

          

     

  2. Mean surface temperature is the explanatory variable.

     

    1. Determine the equation of the least squares regression line for this set of data. Write the equation in terms of the variables mean duration of warm spell and mean surface temperature. Write the value of the coefficients correct to one decimal place.  (2 marks)

    2. Plot the least squares regression line on Scatterplot 1.  (1 mark)

The residual plot below was constructed to test the assumption of linearity for the relationship between the variables mean duration of warm spell and the mean surface temperature.

CORE, FUR2 2007 VCAA 33

  1. Explain why this residual plot supports the assumption of linearity for this relationship.  (1 mark)

  2. Write down the percentage of variation in the mean duration of a warm spell that is explained by the variation in mean surface temperature. Write your answer correct to the nearest per cent.  (1 mark)

  3. Describe the relationship between the mean duration of a warm spell and the mean surface temperature in terms of strength, direction and form.  (2 marks)

Show Answers Only
  1.  
    CORE, FUR2 2007 VCAA 3 Answer

    1. `text{See part b.ii. below.}`
    2. `text(Mean duration of warm spell)`
      `= -776.9 + 60.3 xx text(mean surface temperature)`
  2. `text(Linearity is supported because there is no)`
    `text(pattern to the residual data.)`
  3. `83text(%)`
  4. `text(Strong, positive, and linear.)`
Show Worked Solution
a.    CORE, FUR2 2007 VCAA 3 Answer

 

b.i.   `text(Mean duration of warm spell)`

`= -776.9 + 60.3 xx text(mean surface temperature)`

 

MARKER’S COMMENT: A consistent error in these type of questions is taking 2 points that are too close together!

b.ii.   `text(Taking extreme points on the above graph,)`

  `text(When)\ \ x = 13.2, \ y = -776.9 + 60.3 xx 13.2 = 19.06`

`:.\ text(Passes through)\ \ A (13.2, 19.06)`

  `text(When)\ x = 13.8, y = -776.9 + 60.3 xx 13.8 = 55.24`

`:.\ text(Passes through)\ \ B (13.8, 55.24)`

`text(*See the regression line plotted above.)`

 

c.   `text(Linearity is supported because there is no)`

`text(pattern to the residual data.)`
 

d.   `text(By Calculator,)`

`r^2 = 0.828… = 83text{%  (nearest %)}`
 

e.   `text(Strong, positive, and linear.)`

CORE, FUR2 2009 VCAA 3

The scatterplot below shows the rainfall (in mm) and the percentage of clear days for each month of 2008. 
 

An equation of the least squares regression line for this data set is

rainfall = 131 – 2.68 × percentage of clear days

  1. Draw this line on the scatterplot.  (1 mark)
  2. Use the equation of the least squares regression line to predict the rainfall for a month with 35% of clear days. Write your answer in mm correct to one decimal place.  (1 mark)
  3. The coefficient of determination for this data set is 0.8081.

     

    1. Interpret the coefficient of determination in terms of the variables rainfall and percentage of clear days.  (1 mark)
    2. Determine the value of Pearson’s product moment correlation coefficient. Write your answer correct to three decimal places.  (2 marks)
Show Answers Only
  1.  
    CORE, FUR2 2009 VCAA 3 Answer
  2. `37.2\ text(mm)`
    1. `text(The coefficient means that 80.81% of the)`
      `text(variation in the rainfall can be explained by)`
      `text(the variation in the percentage of clear days.)`
    2. `-0.899`
Show Worked Solution
a.    CORE, FUR2 2009 VCAA 3 Answer

 

b.    `text(Rainfall)` `= 131 – 2.68 xx 35`
    `= 37.2\ text(mm)`
MARKER’S COMMENT: Any answers that suggested causation with terms like “is due to” etc.., did not receive a mark.

 

c.i.   `text(The coefficient means that 80.81% of the)`

  `text(variation in the rainfall can be explained by)`

  `text(the variation in the percentage of clear days.)`

 

MARKER’S COMMENT: Many students failed to include the negative sign as indicated by the negative slope of the graph.
c.ii.    `r` `= -sqrt(0.8081)`
    `= -0.8989…`
    `=-0.899\ \ text{(to 3 d.p.)}`

CORE, FUR2 2011 VCAA 2

Table 1 shows information about a particular country. It shows the percentage of women by age at first marriage, for the years 1986, 1996 and 2006.
 

CORE, FUR2 2011 VCAA 2
 

  1. Of the women who first married in 1986, what percentage were aged 20 to 29 years inclusive?  (1 mark)
  2. Does the information in Table 1 support the opinion that, for the years 1986, 1996 and 2006, the age of women at first marriage was associated with years of marriage?

     

    Justify your answer by quoting appropriate percentages. It is sufficient to consider one age group only when justifying your answer.  (2 marks) 

Show Answers Only
  1. `text(65.5%)`
  2. `text(Yes. See Worked solutions.)`
Show Worked Solution

a.   `text(Percentage aged 20 – 29 who married in 1986)`

`=42.1 + 23.4`

`= 65.5 text(%)`
 

b.   `text(Yes.)`

`text(Considering the 25 – 29 age group, the)`

`text{percentage of women increased from 23.4%}`

`text{(1986), to 31.7% (1996), to 34.5% (2006).}`

CORE, FUR2 2012 VCAA 2

The maximum temperature and the minimum temperature at this weather station on each of the 30 days in November 2011 are displayed in the scatterplot below.
 

CORE, FUR2 2012 VCAA 2

The correlation coefficient for this data set is  `r = 0.630`. 

The equation of the least squares regression line for this data set is

maximum temperature = `13 + 0.67` × minimum temperature

  1. Draw this least squares regression line on the scatterplot above.  (1 mark)
  2. Interpret the vertical intercept of the least squares regression line in terms of maximum temperature and minimum temperature.  (1 mark)
  3. Describe the relationship between the maximum temperature and the minimum temperature in terms of strength and direction.  (1 mark)
  4. Interpret the slope of the least squares regression line in terms of maximum temperature and minimum temperature.  (1 mark)
  5. Determine the percentage of variation in the maximum temperature that may be explained by the variation in the minimum temperature.

     

    Write your answer, correct to the nearest percentage.  (1 mark)

On the day that the minimum temperature was 11.1 °C, the actual maximum temperature was 12.2 °C.

  1. Determine the residual value for this day if the least squares regression line is used to predict the maximum temperature.

     

    Write your answer, correct to the nearest degree.  (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(On average, when the minimum temperature is)`
    `text(0 °C, the maximum temperature is 13 °C)`
  3. `text(Moderate and positive.)`
  4. `text(On average, it is predicted that the maximum)`
    `text(temperature increases by 0.67 °C for every 1 °C)`
    `text(increase in the minimum temperature.)`
  5. `40text(%)`
  6. `-8^@text(C)`
Show Worked Solution

a.   `text(The two widest points in this data range are,)`

`text{(0, 13) and (20, 26.4).}`

 CORE, FUR2 2012 VCAA 2 Answer 

b.   `text(On average, when the minimum temperature is)`

`text(0 °C, the maximum temperature is 13 °C.)`

 

♦ Parts (i) to (vi) have an average mean mark of 41%.

c.   `text(Given)\ r = 0.630,`

`text(Strength: moderate)`

`text(Direction: positive)`

 

d.   `text(On average, it is predicted that \the maximum)`

 `text(temperature increases by 0.67 °C for every 1 °C)`

 `text(increase in the minimum temperature.)`

 

e.    `r^2` `= 0.630^2`
    `=0.3969`
    `=40text{%  (nearest %)}`

 

f.   `text(When the minimum temperature was)\ 11.1 text(°C),`

MARKER’S COMMENT: Students had particular difficulty with this part, with many using the incorrect calculation of  12.2 – 11.1 = 1.1.
`text(Predicted Value)` `= 13 + 0.67 xx 11.1`
  `=20.437…`
`:.\ text(Residual)` `= 12.2 − 20.437…`
  `= – 8.237…`
  `= – 8\ text{°C (nearest degree)}`

CORE, FUR2 2014 VCAA 4

The scatterplot below shows the population density, in people per square kilometre, and the area, in square kilometres, of 38 inner suburbs of the same city.
 

Core, FUR2 2015 VCAA 41

For this scatterplot, `r^2 = 0.141`

  1. Describe the association between the variables population density and area for these suburbs in terms of strength, direction and form.  (1 mark)
  2. The mean and standard deviation of the variables population density and area for these 38 inner suburbs are shown in the table below.
     
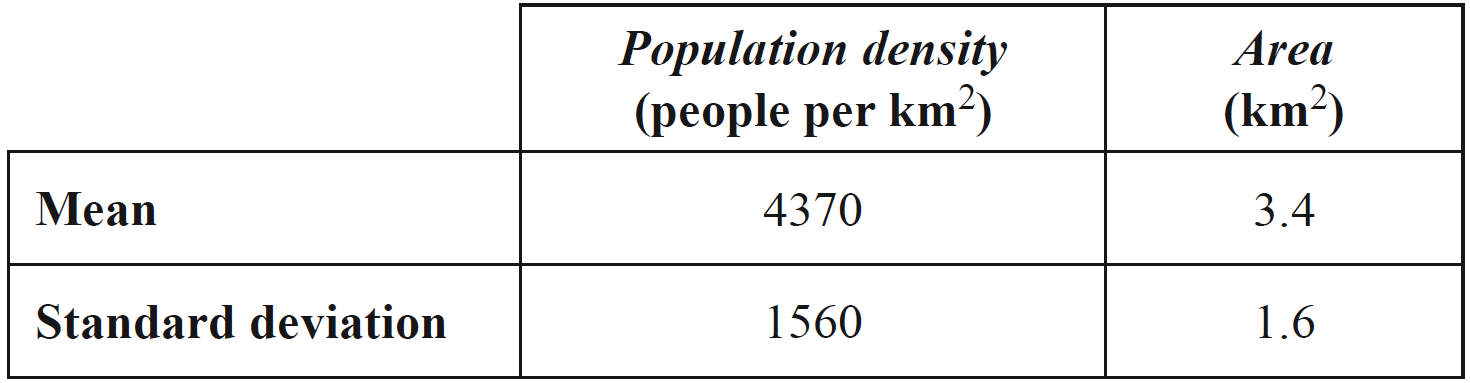
    Core, FUR2 2015 VCAA 42
     

    1. One of these suburbs has a population density of 3082 people per square kilometre.

       

      Determine the standard `z`-score of this suburb’s population density.

       

      Write your answer, correct to one decimal place.  (1 mark)

Assume the areas of these inner suburbs are approximately normally distributed.

  1. How many of these 38 suburbs are expected to have an area that is two standard deviations or more above the mean?

     

    Write your answer, correct to the nearest whole number.  (1 mark)

  2. How many of these 38 inner suburbs actually have an area that is two standard deviations or more above the mean?  (1 mark)
Show Answers Only
  1. `text(The association is weak, negative and linear.)`
    1. `− 0.8`
    2. `1`
    3. `2`
Show Worked Solution
♦♦ Mean mark 30%.
MARKER’S COMMENT: The most common error was to describe the association as positive.
a.    `r` `= −sqrt(0.141)`
    `= −0.3755`

 
`:.\ text(The association is weak, negative and linear.)`

 

b.i    `z` `=(x-bar x)/s`
    `= (3082 − 4370)/1560`
    `= − 0.82…`
    `= – 0.8\ \ text{(to 1 d.p.)}`

 

b.ii.   `2.5text(%) xx 38 =0.95=1\ text{(nearest whole)}`

 

b.iii.   `text{Area size (2 std deviation above mean)}`

♦♦ Very few students answered this part correctly.

`= 3.4 + 2 xx 1.6`

`=6.6\ text(km²)`

 

`:.\ text{From the graph, 2 inner suburbs have an area}`

`text(2 standard deviations above the mean.)`

CORE, FUR2 2014 VCAA 2

The scatterplot below shows the population and area (in square kilometres) of a sample of inner suburbs of a large city.
 

Core, FUR2 2015 VCAA 2

The equation of the least squares regression line for the data in the scatterplot is

population = 5330 + 2680 × area

  1. Write down the response variable.  (1 mark)
  2. Draw the least squares regression line on the scatterplot above.

(Answer on the scatterplot above.)  (1 mark)

  1. Interpret the slope of this least squares regression line in terms of the variables area and population.  (2 marks)
  2. Wiston is an inner suburb. It has an area of 4 km² and a population of 6690.

     

    The correlation coefficient, `r`, is equal to 0.668

    1. Calculate the residual when the least squares regression line is used to predict the population of Wiston from its area.  (1 mark)
    2. What percentage of the variation in the population of the suburbs is explained by the variaton in area.

       

      Write your answer, correct to one decimal place.  (1 mark)

Show Answers Only
  1. `text(Population.)`
  2.  
          Core, FUR2 2015 VCAA 2 Answer
  3. `text(Population increases by 2680 people, on average,)`
    `text(for each additional 1 km² in area.)`
    1. ` −9360`
    2. `text(44.6%)`
Show Worked Solution

a.   `text(Population.)`

 

♦ Mean mark 36%.
MARKER’S COMMENT: Use the equation to draw the line and use points at the extremities.
b.   

Core, FUR2 2015 VCAA 2 Answer

 

c.   `text(Population increases by 2680 people, on average,)`

♦ Mean mark 41% (part (iii)).

`text(for each additional 1 km² in area.)`

 

d.i.   `text(The population predicted by the equation)`

`= 5330 + 2680× 4`

`= 16\ 050`

`:.\ text(Residual)` `= 6690 −16\ 050`
  `= − 9360`

 

♦ Part (iv) in total had a mean mark 42%.
d.ii.    `r` `= 0.668^2`
  `r^2` `= 0.4462…`
    `= 44.6 text{%  (to 1 d.p.)}`

 

`:.\ text(44.6% of the variation in the population is explained)`

`text(by variation in the area.)`

CORE, FUR2 2015 VCAA 4

The table below shows male life expectancy (male) and female life expectancy (female) for a number of countries in 2013. The scatterplot has been constructed from this data.
 

Core, FUR2 2015 VCAA 4 
 

  1. Use the scatterplot to describe the association between male life expectancy and female life expectancy in terms of strength, direction and form.  (1 mark)
  2. Determine the equation of a least squares regression line that can be used to predict male life expectancy from female life expectancy for the year 2013.

     

    Complete the equation for the least squares regression line below by writing the intercept and slope in the space provided.

     

    Write these values correct to two decimal places.  (1 mark)

male = ______________ + ______________ ×  female

Show Answers Only
  1. `text(Strong, positive and linear.)`
  2. `text(male) = 9.69 + 0.81 xx text(female)`
Show Worked Solution

a.   `text(Strong, positive and linear.)`

♦ Mean mark 49%.
MARKER’S COMMENT: Common errors included using the 1st column as the independent (`x`) variable and poor rounding.

 

b.   `text(By calculator,)`

`text(male) = 9.69 + 0.81 xx text(female)`

CORE, FUR2 2015 VCAA 3

The scatterplot below plots male life expectancy (male) against female life expectancy (female) in 1950 for a number of countries. A least squares regression line has been fitted to the scatterplot as shown.
 


 

The slope of this least squares regression line is 0.88

  1. Interpret the slope in terms of the variables male life expectancy and female life expectancy.  (1 mark)

The equation of this least squares regression line is

male = 3.6 + 0.88 × female

  1. In a particular country in 1950, female life expectancy was 35 years.

     

    Use the equation to predict male life expectancy for that country.  (1 mark)

  2. The coefficient of determination is 0.95

     

    Interpret the coefficient of determination in terms of male life expectancy and female life expectancy.  (1 mark)

Show Answers Only
  1. `text(A slope of 0.88 means that for each year that a)`
    `text(female lives longer in a particular country, a male)`
    `text(in that country, on average, will tend to live 0.88)`
    `text(of a year longer.)`
  2. `34.4\ text(years)`
  3. `text(This figure means that 95% of the variability in)`
    `text(the male life expectancy can be explained by the)`
    `text(variation in female life expectancy.)`
Show Worked Solution

a.   `text(A slope of 0.88 means that for each year)`

♦ Mean mark 40%.
MARKER’S COMMENT: Many students did not describe the slope, despite being specifically asked about it!

`text(that a female lives longer in a particular)`

`text(country, a male in that country, on average,)`

`text(will tend to live 0.88 of a year longer.)`

 

b.   `text(Male life expectancy)`

`=3.6 + 0.88 xx 35`

`=34.4\ text(years)`

 

c.   `text(This figure means that 95% of the variability)`

MARKER’S COMMENT: A common error: use of `r^2 = 90.25 text(%)` as the basis of the interpretation.

`text(in the male life expectancy can be explained)`

`text(by the variation in female life expectancy.)`

 

CORE, FUR1 2007 VCAA 7-8 MC

The lengths and diameters (in mm) of a sample of jellyfish selected were recorded and displayed in the scatterplot below. The least squares regression line for this data is shown.

The equation of the least squares regression line is

length = 3.5 + 0.87 × diameter

The correlation coefficient is  `r = 0.9034`
 

Part 1

Written as a percentage, the coefficient of determination is closest to

  1. `0.816 text(%)`
  2. `0.903text(%)`
  3. `81.6text(%)`
  4. `90.3text(%)`
  5. `95.0text(%)`

 

Part 2

From the equation of the least squares regression line, it can be concluded that for these jellyfish, on average

  1. there is a 3.5 mm increase in diameter for each 1 mm increase in length.
  2. there is a 3.5 mm increase in length for each 1 mm increase in diameter.
  3. there is a 0.87 mm increase in diameter for each 1 mm increase in length.
  4. there is a 0.87 mm increase in length for each 1 mm increase in diameter.
  5. there is a 4.37 mm increase in diameter for each 1 mm increase in length.
Show Answers Only

`text (Part 1:)\ C`

`text (Part 2:)\ D`

Show Worked Solution

`text (Part 1)`

`r^2` `=0.9034^2`
  `=0.8161…`

 
`rArr C`
 

`text(Part 2)`

`text(Length)\ =3.5 + 0.87 xx text(diameter)`

`text(Gradient)\ = 0.87`

`text(i.e. the length increases 0.87 mm for each 1 mm)`

`text(increase in diameter.)`

`rArr D`

CORE, FUR1 2011 VCAA 11 MC

For a group of 15-year-old students who regularly played computer games, the correlation between the time spent playing computer games and fitness level was found to be  `r = -0.56.`

On the basis of this information it can be concluded that

  1. 56% of these students were not very fit.
  2. these students would become fitter if they if they spent less time playing computer games.
  3. these students would become fitter if they if they spent more time playing computer games.
  4. the students in the group who spent a short amount of time playing computer games tended to be fitter.
  5. the students in the group who spent a large amount of time playing computer games tended to be fitter.
Show Answers Only

`D`

Show Worked Solution

`text(Negative correlation means that as time spent playing)`

`text(computer games decreases, fitness levels tend to increase.)`

`text(Note that)\ B\ text(is incorrect because it assumes one causes the)`

`text(other.)`

`=> D`

CORE, FUR1 2011 VCAA 6-8 MC

When blood pressure is measured, both the systolic (or maximum) pressure and the diastolic (or minimum) pressure are recorded.

Table 1 displays the blood pressure readings, in mmHg, that result from fifteen successive measurements of the same person's blood pressure.
 

core 2011 VCAA 6-8

Part 1

Correct to one decimal place, the mean and standard deviation of this person's systolic blood pressure measurements are respectively

A.   `124.9 and 4.4`

B.   `125.0 and 5.8`

C.   `125.0 and 6.0`

D.   `125.9 and 5.8`

E.   `125.9 and 6.0`

 

Part 2

Using systolic blood pressure (systolic) as the response variable, and diastolic blood pressure (diastolic) as the explanatory variable, a least squares regression line is fitted to the data in Table 1.

The equation of the least squares regression line is closest to

A.   `text(systolic) = 70.3 + 0.790 xx text(diastolic)`

B.   `text(diastolic) = 70.3 + 0.790 xx text(systolic)`

C.   `text(systolic) = 29.3 + 0.330 xx text(diastolic)`

D.   `text(diastolic) = 0.330 + 29.3 xx text(systolic)`

E.   `text(systolic) = 0.790 + 70.3 xx text(diastolic)`

 

Part 3

From the fifteen blood pressure measurements for this person, it can be concluded that the percentage of the variation in systolic blood pressure that is explained by the variation in diastolic blood pressure is closest to

A.   `25.8text(%)`

B.   `50.8text(%)`

C.   `55.4text(%)`

D.   `71.9text(%)`

E.   `79.0text(%)`

Show Answers Only

`text(Part 1:)\ E`

`text(Part 2:)\ A`

`text(Part 3:)\ A`

Show Worked Solution

`text(Part 1)`

`text{By calculator (using sample standard deviation)}`

`text{the results are: }`

`text(Mean = 125.9, std dev = 6.0)`

`=>E`

 

`text(Part 2)`

`text{By calculator (making sure diastolic values are}`

`text{the explanatory or}\ x text{-variable), the regression line}`

`text(can be expressed as follows,)`

`text(systolic) = 70.3 + 0.790 xx text(diastolic)`

`=>A`

 

`text(Part 3)`

`text{By calculator, the regression line (above) should}`

`text(have found) \ \ r^2 = 0.258,\ text(which means that)`

`text(25.8% of the variation in systolic pressure can be)`

`text(explained by variation in diastolic pressure.)`

`=>A`

CORE, FUR1 2008 VCAA 10 MC

A large study of Year 12 students shows that there is a negative association between the time spent doing homework each week and the time spent watching television. The correlation coefficient is `r = – 0.6`.

From this information it can be concluded that

  1. the time spent doing homework is 60% lower than the time spent watching television.  
  2. 36% of students spend more time watching television than doing homework.  
  3. the slope of the least squares regression line is 0.6.
  4. if a student spends less time watching television, they will do more homework.
  5. an increased time spent watching television is associated with a decreased time doing homework.
Show Answers Only

`E`

Show Worked Solution

`text(A negative correlation means that the greater the time)`

`text(spent watching television is associated with the less)`

`text(time spent doing homework.)`

`D\ text(assumes one causes the other and is therefore incorrect.)`

`=>E`

CORE, FUR1 2010 VCAA 7-9 MC

The height (in cm) and foot length (in cm) for each of eight Year 12 students were recorded and displayed in the scatterplot below.
A least squares regression line has been fitted to the data as shown.
 

Part 1

By inspection, the value of the product-moment correlation coefficient `(r)` for this data is closest to

  1. `0.98`
  2. `0.78`
  3. `0.23`
  4. `– 0.44`
  5. `– 0.67`

 

Part 2

The explanatory variable is foot length.

The equation of the least squares regression line is closest to

  1. height = –110 + 0.78 × foot length.
  2. height = 141 + 1.3 × foot length.
  3. height = 167 + 1.3 × foot length.
  4. height = 167 + 0.67 × foot length.
  5. foot length = 167 + 1.3 × height.

 

Part 3

The plot of the residuals against foot length is closest to

CORE, FUR1 2010 VCAA 7-9 MCab

CORE, FUR1 2010 VCAA 7-9 MCcd

CORE, FUR1 2010 VCAA 7-9 MCe

Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ B`

`text(Part 3:)\ B`

Show Worked Solution

`text(Part 1)`

`text(The correlation is positive and strong.)`

`text(Eliminate)\ C, D\ text(and)\ E.`

`r= 0.98\  text(is too strong. Eliminate)\ A.`

`=> B`

 

`text(Part 2)`

♦♦ Mean mark 35%.
STRATEGY: An alternate but less efficient strategy could be to find 2 points and calculate the gradient and then use the point gradient formula.

`text(The intercept with the height axis)\ (ytext{-axis)}`

`text{is below 167 because that is the height when}`

`text{foot length = 20 cm.}`

`text(Eliminate)\ C, D\ text(and)\ E.`

`text(The gradient is approximately 1.3, by observing)`

`text(the increase in height values when the foot)`

`text(length increases from 20 to 22 cm.)`

`=>  B`

 

`text(Part 3)`

`text(First residual is positive. Eliminate)\ A, D, E.`

`text(The next 3 residuals are negative. Eliminate)\ C`

`=>  B`

CORE, FUR1 2012 VCAA 7 MC

The table below shows the percentage of students in two age groups (15–19 years and 20–24 years) who regularly use the internet at one or more of three locations.

  • at home
  • at an educational institution
  • at work 

     

For the students surveyed, which one of the following statements, by itself, supports the contention that the location of internet use is associated with the age group of the internet user?

  1. 85% of students aged 15–19 years used the internet at an educational institution.
  2. 95% of students aged 15–19 years used the internet at home, but only 38% of 15–19 year olds used it at work.
  3. 95% of students aged 15–19 years used the internet at home and 18% of 20–24 year olds used the internet at an educational institution.
  4. The percentage of students who used the internet at an educational institution decreased from 85% for those aged 15–19 years to 18% for those aged 20–24 years.
  5. The percentage of students who used the internet at home was 95% for those aged 15–19 years and 95% for those aged 20–24 years. 
Show Answers Only

`D`

Show Worked Solution

`text (The contention requires that the two age groups are)`

`text(compared at the same location.)`

`:.\ text(Eliminates A, B, and C.)`
 

`text (Considering E,)`

`text(the usage at home is THE SAME for both groups)`

`text(and therefore age group doesn’t matter.)`
 

`text (Considering D,)`

`text(the same location is used and the usage differs)`

`text(between groups.)`

`rArr D`

CORE, FUR1 2009 VCAA 9-10 MC

The table below lists the average life span (in years) and average sleeping time (in hours/day) of 12 animal species.
 


 

Part 1

Using sleeping time as the independent variable, a least squares regression line is fitted to the data.

The equation of the least squares regression line is closest to

A.   life span = 38.9 – 2.36 × sleeping time.

B.   life span = 11.7 – 0.185 × sleeping time.

C.   life span = – 0.185 – 11.7 × sleeping time.

D.   sleeping time = 11.7 – 0.185 × life span.

E.   sleeping time = 38.9 – 2.36 × life span.

 

Part 2

The value of Pearson’s product-moment correlation coefficient for life span and sleeping time is closest to

A.  `–0.6603`

B.  `–0.4360`

C.  `–0.1901`

D.   `0.4360`

E.   `0.6603` 

Show Answers Only

`text(Part 1:)\ A`

`text(Part 2:)\ A`

Show Worked Solution

`text(Part 1)`

♦ Mean mark 49%.
MARKERS’ COMMENT: Almost a quarter of students incorrectly assumed the independent variable was in the first column!

`text{By calculator (with “life span” as the}`

`text{dependent variable), the equation is:}`

`text(life span = 38.9 – 2.36 × sleeping time.)`

`=>A`

 

`text(Part 2)`

`text (By calculator)`

`=>A`

CORE, FUR1 2013 VCAA 8 MC

The table below shows the hourly rate of pay earned by 10 employees in a company in 1990 and in 2010.
 

CORE, FUR1 2013 VCAA 8 MC
 

The value of the correlation coefficient, `r`, for this set of data is closest to

A.   `0.74`  

B.   `0.86`  

C.   `0.92`

D.   `0.93`

E.   `0.96`

Show Answers Only

`E`

Show Worked Solution

`text(By calculator)`

`r=0.962…`

`=> E`

CORE, FUR1 2013 VCAA 7 MC

For a city, the correlation coefficient between

  • population density and distance from the centre of the city is `r` = – 0.563
  • house size and distance from the centre of the city is `r` = 0.357.

Given this information, which one of the following statements is true?

  1. Around 31.7% of the variation observed in house size in the city can be explained by the variation in distance from the centre of the city.
  2. Population density tends to increase as the distance from the centre of the city increases.
  3. House sizes tend to be larger as the distance from the centre of the city decreases.
  4. The slope of a least squares regression line relating population density to distance from the centre of the city is positive.
  5. Population density is more strongly associated with distance from the centre of the city than is house size.
Show Answers Only

`E`

Show Worked Solution

`text(Population density)`

♦ Mean mark 49%.

`r^2=(-0.563)^2=0.3169…~~31.7%`

`text(House size)`

`r^2=(0.357)^2 = 0.1274…~~12.7%`

 

`text(In A, 12.7% of the variability is explained. Not true.)`

`text(In B,)\ r = –0.563. text(The negative correlation means population)`

`text(density increases as distance decreases. Not true.)`

`text(In C, statement assumes a negative correlation which is not the case)`

`text(given)\ r = 0.357.\ \ text(Not true.)`

`text(In D, negative correlation would have a negatively slope. Not true.)`

`text{In E, true since}\ \ | \ r^2\  |\ \ text{for house size is greater.}`

`=>\ E`