A pin-jointed truss is shown. Member \(AB\) has been determined to be 250 N in compression. Complete the table. You must use the method specified to solve each component. (6 marks) --- 0 WORK AREA LINES (style=lined) --- \begin{array} {|l|l|} \begin{array} {|l|l|} \begin{array} {|l|l|} External reaction at \(E\) (Mathematical method): Internal reaction of \(CF\) (Method of sections): \( \Sigma \text{F}_\text{V} \uparrow^{+}=0=\left(\sin \, 60^{\circ} \times \text{CF}\right)-75+58.33 \) Internal reaction of \(BG\) (Graphical): External reaction at \(E\) (Mathematical method): Internal reaction of \(CF\) (Method of sections): \( \Sigma \text{F}_\text{V} \uparrow^{+}=0=\left(\sin \, 60^{\circ} \times \text{CF}\right)-75+58.33 \) Internal reaction of \(BG\) (Graphical):
\hline
\rule{0pt}{2.5ex} \quad \textit{Determine}\quad & \quad \textit{Method to} \quad & \quad \quad \quad \quad \quad \quad \quad \quad\textit{Working} \quad \quad \quad \quad \quad \quad \quad \quad\\
\textit{} \rule[-1ex]{0pt}{0pt} & \quad \quad \ \ \ \textit{use} & \textit{}\\
\hline
\rule{0pt}{2.5ex} \text{External} & \text{Mathematical} & \\
\text{reaction at \(E\)} \rule[-1ex]{0pt}{0pt} & \text{} &\\
\\ \\ \\ \\ \\ \\ \\ \\
\text{} & \text{} & \text{........................... N} \\
\text{} & \text{} & \text{Direction: ...........................} \\
\hline
\end{array}
\hline
\rule{0pt}{2.5ex} \quad \textit{Determine}\quad & \quad \textit{Method to} \quad & \quad \quad \quad \quad \quad \quad \quad \quad\textit{Working} \quad \quad \quad \quad \quad \quad \quad \quad\\
\textit{} \rule[-1ex]{0pt}{0pt} & \quad \quad \ \ \ \textit{use} & \\
\hline
\rule{0pt}{2.5ex} \text{Internal} & \text{Methods of} & \\
\text{reaction of} & \text{section} &\\
\text{member of \(CF\)} & &\\
\\ \\ \\ \\ \\ \\ \\ \\
\text{} & \text{} & \text{........................... N} \\
\text{} & \text{} & \text{Nature of force (T or C): ...........................} \\
\hline
\end{array}
\hline
\rule{0pt}{2.5ex} \quad \textit{Determine}\quad & \quad \textit{Method to} \quad & \quad \quad \quad \quad \quad \quad \quad \quad\textit{Working} \quad \quad \quad \quad \quad \quad \quad \quad\\
\textit{} \rule[-1ex]{0pt}{0pt} & \quad \quad \ \ \ \textit{use} & \\
\hline
\rule{0pt}{2.5ex} \text{Internal} & \text{Graphical} & \\
\text{reaction of} & &\\
\text{member \(BG\)} & &\\
\\ \\ \\ \\ \\ \\ \\ \\
\text{} & \text{} & \text{........................... N} \\
\text{} & \text{} & \text{Nature of force (T or C): ...........................} \\
\hline
\end{array}
\( \Sigma \text{M}_\text{A}\Large{⤸} ^{\small{+}}\)
\(=0=(200 \times 2)+(75 \times 10)-(129.9 \times 3.46)-\left(\text{R}_\text{E} \times 12\right) \)
\(0\)
\(=400+750-450-\text{R}_\text{E} \times 12 \)
\(\text{R}_\text{E}\)
\(=\dfrac{700}{12} = 58.33\ \text{N} \uparrow \)
\(-\sin \, 60^{\circ} \times \text{CF} \)
\(=-75+58.33 \)
\(\text{CF}\)
\(=\dfrac{16.67}{\sin \, 60^{\circ}} \)
\(=19.25\ \text{N (T)} \)
\( \Sigma \text{M}_\text{A}\large{⤸} ^{\small{+}}\)
\(=0=(200 \times 2)+(75 \times 10)-(129.9 \times 3.46)-\left(\text{R}_\text{E} \times 12\right) \)
\(0\)
\(=400+750-450-\text{R}_\text{E} \times 12 \)
\(\text{R}_\text{E}\)
\(=\dfrac{700}{12} = 58.33\ \text{N} \uparrow \)
\(-\sin \, 60^{\circ} \times \text{CF} \)
\(=-75+58.33 \)
\(\text{CF}\)
\(=\dfrac{16.67}{\sin \, 60^{\circ}} \)
\(=19.25\ \text{N (T)} \)
ENGINEERING, CS 2023 HSC 19 MC
A loaded truss is shown.
Which of the following is the redundant member?
- \(AB\)
- \(BD\)
- \(BE\)
- \(CD\)
ENGINEERING, CS 2023 HSC 26c
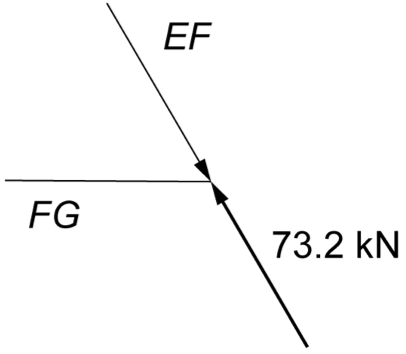
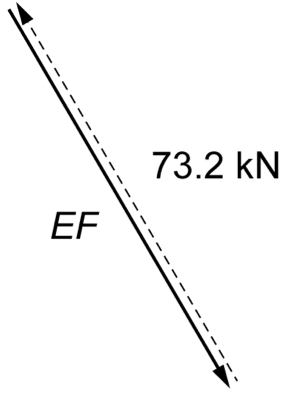
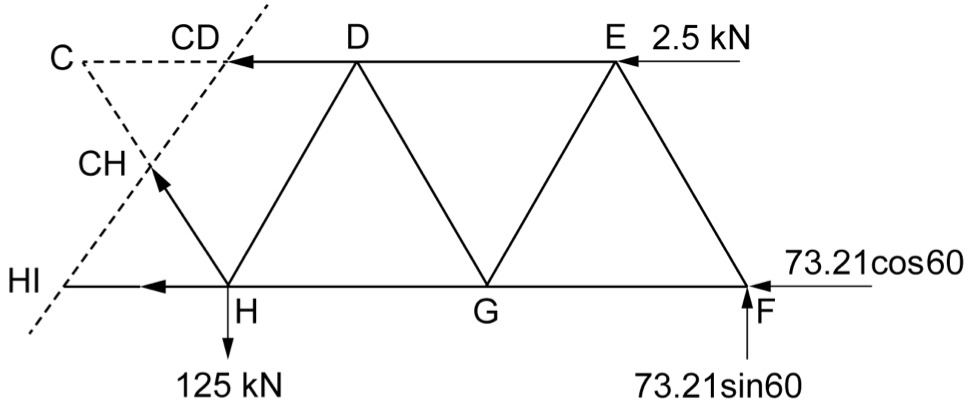
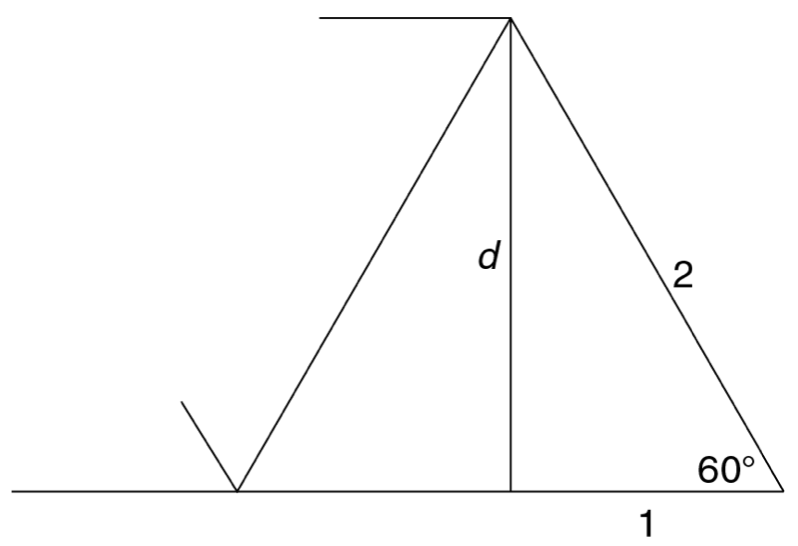
A truss is loaded as shown.
Showing working, complete the table. (6 marks)
\begin{array} {|l|c|c|}
\hline
\rule{0pt}{2.5ex} \rule[-1ex]{0pt}{0pt} & \textit{Magnitude} & \textit{Nature of force}\\ & \text{(kN)} & \text{(T or C)} \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ EF \rule[-1ex]{0pt}{0pt} & & \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ CH \rule[-1ex]{0pt}{0pt} & & \\
\hline
\end{array}
\hline
\rule{0pt}{2.5ex} \rule[-1ex]{0pt}{0pt} & \textit{Magnitude} & \textit{Nature of force}\\ & \text{(kN)} & \text{(T or C)} \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ EF \rule[-1ex]{0pt}{0pt} & & \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ CH \rule[-1ex]{0pt}{0pt} & & \\
\hline
\end{array}
Show Worked Solution
\begin{array} {|l|c|c|}
\hline
\rule{0pt}{2.5ex} \rule[-1ex]{0pt}{0pt} & \textit{Magnitude} & \textit{Nature of force}\\ & \text{(kN)} & \text{(T or C)} \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ EF \rule[-1ex]{0pt}{0pt} & 73.2\ \text{kN} & \text{Compression} \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ CH \rule[-1ex]{0pt}{0pt} & 71.138\ \text{kN} & \text{Tension} \\
\hline
\end{array}
\(\text{Consider member}\ EF:\)
→ \(\text{Force diagram closes with two collinear forces}\)
→ \(FG\ \text{is a zero force member}\)
→ \(EF = 73.2\ \text{kN (compression)} \)
♦♦♦ Mean mark 36%.
\(\text{Consider member}\ CH:\)
| \(+ \uparrow \Sigma F_{V}\) | \(=0\) | |
| \(0\) | \(=-125 + 73.2 \times \sin\,60^{\circ} + CH \times \sin\,60^{\circ}\) | |
| \(CH \times \sin\,60^{\circ}\) | \(=61.607\) | |
| \(CH\) | \(= \dfrac{61.607}{\sin\,60^{\circ}} \) | |
| \(=71.138\ \text{kN (tension)} \) |
ENGINEERING, CS 2023 HSC 22b
The diagram shows a child with a mass of 45 kg hanging 2 metres from the left end of a structure, and an adult with a mass of 85 kg hanging 1 metre from the right end. \begin{array} {ll}
\text{R}_\text{L} = \text{............................... N} & \text{Direction ...............................} \\
& \\
\text{R}_\text{R} = \text{............................... N} & \text{Direction ...............................} \end{array}
i. \( \text{R}_{\text{L}}=860\ \text{N} \uparrow \) \( \text{R}_{\text{L}}= 440\ \text{N} \uparrow \) Show Answers Only
ii. 
i. \( \stackrel {\curvearrowright} {\sum{ \text{M}}{^{+}_\text{L}}}: \) \( \sum \text{F}_\text{V} \uparrow:\) Show Worked Solution
\(0\)
\(=(2 \times 450)+(4 \times 850)-(\text{R}_\text{R} \times 5) \)
\(5 \times \text{R}_\text{R}\)
\(=900 + 3400\)
\(\text{R}_\text{R}\)
\(=860\ \text{N} \uparrow \)
\(0\)
\(= -450-850+860+\text{R}_\text{L} \)
\( \text{R}_{\text{L}}\)
\(= 440\ \text{N} \uparrow \)
ii.
ENGINEERING, CS 2016 HSC 26b
What are redundant truss members? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
ENGINEERING, CS 2016 HSC 26a
A simplified diagram of a pin jointed truss of a hammerhead crane is shown. It is lifting a load of 54 kN.
- Calculate the reactions at supports `A` and `B`. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
- Determine the magnitude and nature of the force in member `M`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
i.
`text{R}_(BH)-27=0`
`text{R}_(BH)=27`
`text{From the diagram,}\ \ text{R}_(BH)=27\ text{kN →}`
| +\({\circlearrowleft}\)`sumM_B` | `=0` | |
| `0` | `=27xx2+54xx5-75xx1-R_Axx1` | |
| `R_A` | `=54+270-75` | |
| `=249\ text{kN ↑}` | ||
| + ↑`sumF_V` | `=0` | |
| `0` | `=249-75-54+R_B` | |
| `R_B` | `=129-249` | |
| `=-120\ text{kN}` | ||
| `=120\ text{kN ↓}` |
`R_A=249\ text{kN @ 0° ↑}`
`text{Reaction at}\ B:`
Reaction at `A` = 249 kN acting vertically, up
Reaction at `B` = 123 kN @ 12.7° acting down and to the right.
Mean mark (i) 52%.
ii. `theta = tan^(-1)(20/40)=26.6°`
| `F` | `=sqrt(108^2+54^2)` | |
| `=sqrt(14\ 580)` | ||
| `=120.747…` |
Force in `M` = 121 kN (Compression)
♦ Mean mark (ii) 49%.
ENGINEERING, CS 2018 HSC 18 MC
The force `F` is moved from joint `W` to joint `X`, as shown.
Which row of the table correctly describes the changes in the internal force in member `XY` and the reaction force at `W` as a result of force `F` moving from `W` to `X` ?
ENGINEERING, CS 2017 HSC 25a
A pin-jointed truss designed to support a roadside sign is shown.
- Determine the magnitude and direction of the reactions at `A` and `B`. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
- Determine the magnitude and nature of the force in member `C`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Explain why concrete would be a suitable material to support the roadside sign around point `D`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
\[\textbf{i}. \ \ \ce{->[\ce{+}]} \sum M_A = 0 \]
`3xx1.5-20 xx3+R_(B)xx1.5=0`
`4.5-60+1.5R_(B)=0`
| `1.5R_(B)` | `=55.5` | |
| `R_(B)` | `=(55.5)/(1.5)` | |
| `=37\ text{N} larr` |
Mean mark 56%.
`uarr sumF_(V)=0`
`R_(AV)=20\ text{kN} +uarr`
\[\ce{->[\ce{+}]} \sum F_H = 0 \]
`R_(AH)=37+3=40\ text{kN} rarr^(+)`
| `R_A` | `=sqrt(20^(2)+40^(2))` | |
| `=sqrt2000` | ||
| `=44.7\ text{kN}` |
| `tan\ theta` | `=(R_(AV))/(R_(AH))` | |
| `=20/40` | ||
| `=0.5` | ||
| `:.theta` | `=26.6^(@)` |
\[\textbf{ii}. \]
`text{Taking moments about X:}`
\({+ \circlearrowleft} \Sigma M_X = 0\)
| `0` | `=-1.5 xxF_(C)+1.5 xx20-1.5 xx3` | |
| `0` | `=-F_(C)+20-3` | |
| `F_(C)` | `=17\ text{kN (compression)}` |
♦♦ Mean mark (ii) 38%.
iii. Suitability of concrete
→ Easily poured and formed around the sign.
→ Relatively quick to cure.
→ Weather resistant.
→ Hardens and sets with high strength and hardness.
♦ Mean mark (iii) 52%.
ENGINEERING, CS 2019 HSC 22c
The diagram shows some dimensions and forces associated with a telecommunications tower.
By considering any necessary reaction, calculate the magnitude of the forces in members `M` and `N`. State the nature of each force. Ignore the weight of the tower. (6 marks)
--- 12 WORK AREA LINES (style=lined) ---
Show Worked Solution
Forces at Joint `A`
Horizontal forces `=0`
`:.` To calculate vertical force at `A ` → use moments.
♦♦ Mean mark 36%.
| \({\circlearrowright}\)`+SigmaM_C` | `=0` | |
| `0` | `=-(12xx4)+(R_Axx12)-(10xx7)-(3xx18)` | |
| `12R_A` | `=48+70+54` | |
| `R_A` | `=172/12` | |
| `=14.33\ text{kN}↑` |
Forces in Member `N` → method of joints at `A`
→ No horizontal forces
→ Member `AC` redundant and carrying no load
→ `F_(up) = F_(down)`
`:.` Member `AB` in compression (the force acting down on joint `A` from member `AB` is 14.33 kN)
`:.` Force in N = 14.33 kN (compression)
Using Method of Sections → take moments about Joint `H`
Find the perpendicular distance `d`
| `BH^2` | `=18^2+6^2` | |
| `BH` | `=sqrt{360}` | |
| `sin\ 40.6º` | `=d/(sqrt{360})` | |
| `d` | `=sqrt{360}xx sin\ 40.6º` | |
| `d` | `=12.348\ text{m}` |
| \({\circlearrowright}\)`+SigmaM_H` | `=0` |
| `0` | `=+(12xx2)+(Mxx12.348)-(7xx4)` |
| `12.348M` | `=-24+28` |
| `M` | `=4/12.348` |
| `M` | `=0.324\ text{kN (tension)}` |
| `:.\ ` | `M` | `=0.324\ text{kN (tension)}` |
| `N` | `=14.33\ text{kN (compression)}` |
ENGINEERING, CS 2022 HSC 26a
- The diagram shows a tower crane being used in the construction of a building.
- Determine the number of 100 kg concrete blocks required to place the boom arm in equilibrium. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Under a different set of conditions, a wind force is applied, as shown in the diagram.
- Determine the magnitude and nature of the internal reaction in member A. (6 marks)
--- 12 WORK AREA LINES (style=lined) ---
Show Worked Solution
i. Let the total weight of the concrete blocks `= x`
| `50x` | `=9.23xx65` | |
| `50x` | `=600` | |
| `x` | `=600/50` | |
| `=12\ text{kN ↓}` | ||
| `=12\ 000\ text{N ↓}` | ||
| `m` | `=1200\ text{kg}` |
∴ 12 × 100 kg concrete blocks are needed for the counterweight.
♦ Mean mark (i) 46%.
ii. Magnitude and nature of internal reaction
| \( \circlearrowright+\Sigma M_R \) | `=0` | |
| `0` | `=-(6xx5.5)+(R_Lxx1)+(10xx6)-(10.4xx7)` | |
| `R_L` | `=45.8\ text{kN}↑` |
Taking the horizontal section shown:
| \( \circlearrowright + \Sigma M_P \) | \(= 0\) | |
| `0` | `=(Axx1)+(45.8xx1)-(10.4xx2)` | |
| `A` | `=-25\ text{kN}` |
∴ `A=25\ text{kN in compression}`
♦ Mean mark (ii) 43%.
ENGINEERING, CS 2020 HSC 25c
A cycle bridge has been constructed using a Warren girder truss loaded as shown. The diagram is drawn to scale.
By considering necessary loads and reactions, calculate the magnitude and nature of the force in member `C`. (6 marks)
--- 12 WORK AREA LINES (style=lined) ---
Show Worked Solution
Let the length of a member be 2 units
| `sin60°` | `=d/2` | |
| `d` | `=2 xx sin60°` | |
| `=1.732\ text{units}` |
| \({+ \circlearrowleft \Sigma M_B}\) | `=0` | |
| `0` | `=(3000xx1.732)+(20\ 000xx4)+(-R_Axx6)+(1200xx8)` | |
| `0` | `=5196+80\ 000-6R_A+9600` | |
| `6R_A` | `=94\ 796` | |
| `R_A` | `=15\ 799.33` | |
| `=15.80\ text{kN} ↑` |
| `sin60°` | `= y/C` | |
| `y` | `= C\ sin60°` | |
| `+↑ SigmaF_Y` | `= – \ 1200 + 15\ 799.33 – 20\ 000 – C\ sin60°` | |
| `0` | `= – \ 5400.667 – C\ sin60°` | |
| `C\ sin60°` | `= – \ 5401` | |
| `C` | `= – \ 5401/(sin60°)` | |
| `= – \ 6236.54` |
∴ Assumed direction was incorrect and reaction in `C` is away from the joint.
∴ `C` = 6.24 kN in tension
♦ Mean mark 48%.
ENGINEERING, CS 2021 HSC 25b
A truss is fixed to a wall at `A` and `B` as shown. Ignore the mass of the truss.
- Determine the horizontal reaction at `A`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Determine, using method of joints, the internal reaction in member `AC`. Indicate the nature of the force in the member. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
- Determine, using method of sections, the internal reaction in member `CE`. Indicate the nature of the force. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Show Worked Solution
i. Horizontal reaction at `A`
| \(\circlearrowright \Sigma \text{M}_\text{B}\) | \(= 0\) | |
| `0` | `= -(A_H xx 4\ text{m}) + (1500\ text{N} xx 10\ text{m})` | |
| `A_H` | `= 3750\ text{N}` | |
| `= 3.75\ text{kN ←}` |
ii. Method of joints at A
| →Σ`F_H` | `=0` | |
| `0` | `= -3750+AC xx sin(51.34°)` | |
| `AC` | `=3750/sin(51.34°)` | |
| `=4802\ text{N}` |
♦♦ Mean mark (ii) 41%.
iii. Method of Sections
| \(\circlearrowright \Sigma \text{M}_\text{B}\) | \(=0\) |
|
`0` |
`= (1500 xx 10)-(CE xx 5)` | |
| `CE` | `=(15\ 000)/5` | |
| `=3000\ text{N}` | ||
| `=3\ text{kN (tension)}` |
♦♦♦ Mean mark (iii) 30%.
ENGINEERING, CS 2021 HSC 7 MC
The diagram shows a section of a pin jointed truss in equilibrium. The force in Member 1 is 200 kN in compression.
Which row of the table identifies the magnitude and nature of the forces in Member 2 and Member 3?
