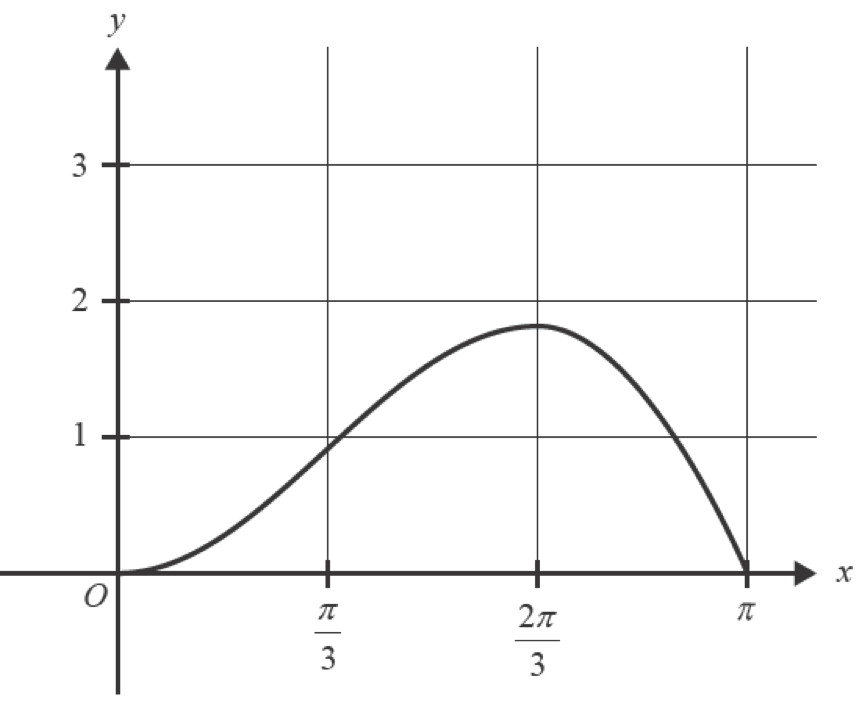
Part of the graph of \(f:[-\pi, \pi] \rightarrow R, f(x)=x \sin (x)\) is shown below. --- 8 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 0 WORK AREA LINES (style=lined) --- a. \(\dfrac{\sqrt{3}\pi^2}{6}\) bi. \(x\cos(x)+\sin(x)\) bii. \(\left[-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{3},\ 1\right]\) biii. \(\text{In the interval }\left[\dfrac{\pi}{2}, \dfrac{2\pi}{3}\right],\ f^{\prime}(x)\ \text{changes from positive to negative.}\) \(f^{\prime}(x)=0\ \text{at some point in the interval.}\) \(\therefore\ \text{A stationary point must exist in the given range.}\) b.ii. \(\text{Gradient in given range gradually decreases.}\) \(\text{Range of}\ f^{\prime}(x)\ \text{will be defined by the endpoints.}\) \(f^{\prime}(x)=0\ \text{at some point in the interval.}\) \(\therefore\ \text{A stationary point must exist in the given range.}\) \(f^{\prime}(-\pi)=-\pi\cos(-\pi)+\sin(-\pi)=\pi\) \(\therefore\ \text{Endpoints are }\ (-\pi,\ \pi)\ \text{and}\ (\pi,\ -\pi).\)
a.
\(A\)
\(=\dfrac{\pi}{3}\times\dfrac{1}{2}\left(f(0)+2f\left(\dfrac{\pi}{3}\right)+2f\left(\dfrac{2\pi}{3}\right)+f(\pi)\right)\)
\(=\dfrac{\pi}{6}\left(0+2\times \dfrac{\pi}{3}\sin\left(\dfrac{\pi}{3}\right)+2\times \dfrac{2\pi}{3}\sin\left(\dfrac{2\pi}{3}\right)+\pi\sin({\pi})\right)\)
\(=\dfrac{\pi}{6}\left(2\times \dfrac{\pi}{3}\times\dfrac{\sqrt{3}}{2}+2\times\dfrac{2\pi}{3}\times \dfrac{\sqrt{3}}{2}+0\right)\)
\(=\dfrac{\pi}{6}\left(\dfrac{2\pi\sqrt{3}}{6}+\dfrac{4\pi\sqrt{3}}{6}\right)\)
\(=\dfrac{\pi}{6}\times \dfrac{6\pi\sqrt{3}}{6}\)
\(=\dfrac{\sqrt{3}\pi^2}{6}\)
bi.
\(f(x)\)
\(=x\sin(x)\)
\(f^{\prime}(x)\)
\(=x\cos(x)+\sin(x)\)
\(f^{\prime}\left(\dfrac{\pi}{2}\right)\)
\(=1\)
\(f^{\prime}\left(\dfrac{2\pi}{3}\right)\)
\(=\dfrac{2\pi}{3}\left(\dfrac{-1}{2}+\dfrac{\sqrt{3}}{2}\right)=-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{3}\)
\(\therefore\ \text{Range of }\ f^{\prime} (x)\ \text{is}\quad\left[-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{3},\ 1\right]\)
♦♦♦ Mean mark (b.iii.) 12%.
biii. \(\text{In the interval }\left[\dfrac{\pi}{2}, \dfrac{2\pi}{3}\right],\ f^{\prime}(x)\ \text{changes from positive to negative.}\)
c. \(f^{\prime}(\pi)=\pi\cos(\pi)+\sin(\pi)=-\pi\)
Calculus, MET1 2023 VCAA SM-Bank 5
Let \(f: R \rightarrow R\), where \(f(x)=2-x^2\).
- Calculate the average rate of change of \(f\) between \(x=-1\) and \(x=1\). (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Calculate the average value of \(f\) between \(x=-1\) and \(x=1\). (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Four trapeziums of equal width are used to approximate the area between the functions \(f(x)=2-x^2\) and the \(x\)-axis from \(x=-1\) to \(x=1\).
- The heights of the left and right edges of each trapezium are the values of \(y=f(x)\), as shown in the graph below.
- Find the total area of the four trapeziums. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Calculus, MET2 EQ-Bank 2
Jac and Jill have built a ramp for their toy car. They will release the car at the top of the ramp and the car will jump off the end of the ramp. The cross-section of the ramp is modelled by the function \(f\), where \(f(x)= \begin{cases}\displaystyle \ 40 & 0 \leq x<5 \\ \dfrac{1}{800}\left(x^3-75 x^2+675 x+30\ 375\right) & 5 \leq x \leq 55\end{cases}\) \(f(x)\) is both smooth and continuous at \(x=5\). The graph of \(y=f(x)\) is shown below, where \(x\) is the horizontal distance from the start of the ramp and \(y\) is the height of the ramp. All lengths are in centimetres. --- 2 WORK AREA LINES (style=lined) --- --- 1 WORK AREA LINES (style=lined) --- --- 1 WORK AREA LINES (style=lined) --- --- 1 WORK AREA LINES (style=lined) --- Jac and Jill decide to use two trapezoidal supports, each of width \(10 cm\). The first support has its left edge placed at \(x=5\) and the second support has its left edge placed at \(x=15\). Their cross-sections are shown in the graph below. --- 5 WORK AREA LINES (style=lined) --- --- 4 WORK AREA LINES (style=lined) --- --- 6 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) ---
a. \(\text{Using CAS: Define f(x) then}\) \(\text{OR}\quad f^{\prime}(x)= \begin{cases}\displaystyle \ 0 & 0 < x<5 \\ \dfrac{1}{800}\left(3x^2-150 x+675 \right) & 5 \leq x < 55\end{cases}\) b.i \(\text{Using CAS: Find }f^”(x)\ \text{then solve }=0\) \(\therefore\ \text{Point of inflection at }(25, 20)\) b.ii \(\text{Gradient function strictly increasing for }x\in [25, 55]\) b.iii \(\text{Gradient function strictly decreasing for }x\in [5, 25]\) c. \(\text{Using CAS:}\)
\(\therefore\ \text{The sloped edges of the trapeziums would be above }f(x)\) \(\text{making the trapezium rule approximation greater than the}\) \(\text{actual area.}\) e.i \(f(55)=\dfrac{35}{4}\ \text{(Using CAS)}\) \(\text{and }f(55)=g(55)\rightarrow g(55)=\dfrac{35}{4}\) \(\text{and }g'(55)=f'(55)\) \(\rightarrow\ f'(55)=\dfrac{1}{800}(3\times 55^2-150\times 55+675)=\dfrac{15}{8}\) \(\rightarrow\ -\dfrac{55}{8}+b=\dfrac{15}{8}\) \(\therefore b=\dfrac{35}{4}\quad (2)\) \(\text{Sub (2) into (1)}\) \(c=\dfrac{3165}{16}-55\times\dfrac{35}{4}\) \(c=-\dfrac{4535}{16}\) \(\therefore\ b=\dfrac{35}{4}\ \text{or}\ 8.75 , c=-\dfrac{4535}{16}\ \text{or}\ -283.4375\) e.ii \(\text{Using CAS: Solve }g(x)=0|x>55\) \(\text{Horizontal distance}=\sqrt{365}+70-55=34.104\dots\approx 34.10\ \text{cm (2 d.p.)}\)
Show Worked Solution
\(\text{Area}\)
\(=\dfrac{h}{2}\Big(f(5)+2f(15)+f(25)\Big)\)
\(=\dfrac{10}{2}\Big(40+2\times 33.75+20\Big)=637.5\)
\(\therefore\ \text{Estimate : Exact}\)
\(=637.5:650\)
\(=\dfrac{637.5}{650}\times 100\)
\(=98.0769\%\approx 98.1\%\)
d. \(\text{In the interval }x\in [25, q]\text{ the curve is concave up.}\)
\(\therefore -\dfrac{1}{16}\times 55^2+55b+c\)
\(=\dfrac{35}{4}\)
\(c\)
\(=\dfrac{35}{4}+\dfrac{3025}{16}-55b\)
\(c\)
\(=\dfrac{3165}{16}-55b\quad (1)\)
\(g'(x)=-\dfrac{x}{8}+b\)
Calculus, MET2 2023 VCE SM-Bank 5 MC
The algorithm below, described in pseudocode, estimates the value of a definite integral using the trapezium rule.
Consider the algorithm implemented with the following inputs.
The value of the variable sum after one iteration of the while loop would be closest to
- 1.281
- 1.289
- 1.463
- 1.617
- 2.136
Calculus, MET2 2023 VCE SM-Bank 3 MC
The area between the curve \(\displaystyle y=\frac{1}{27}(x-3)^2(x+3)^2+1\) and the \(x\)-axis on the interval \(x \in[0,4]\) has been approximated using the trapezium rule, as shown in the graph below.
Using the trapezium rule, the approximate area calculated is equal to
- \(\displaystyle \frac{1}{2}\left(4+\frac{91}{27}+\frac{52}{27}+1+\frac{76}{27}\right)\)
- \(\displaystyle \frac{1}{2}\left(4+\frac{182}{27}+\frac{104}{27}+2+\frac{76}{27}\right)\)
- \(\displaystyle \frac{1}{2}\left(8+\frac{182}{27}+\frac{104}{27}+2+\frac{152}{27}\right)\)
- \(\displaystyle \frac{1}{2}\left(\frac{182}{27}+\frac{104}{27}+2+\frac{76}{27}\right)\)
- \(\displaystyle \frac{1}{2}\left(8+\frac{182}{27}+\frac{104}{27}+2\right)\)
Calculus, MET2 2023 VCE SM-Bank 2 MC
Newton's method is being used to approximate the non-zero \(x\)-intercept of the function with the equation \(f(x)=\dfrac{x^3}{5}-\sqrt{x}\). An initial estimate of \(x_0=1\) is used.
Which one of the following gives the first estimate that would correctly approximate the intercept to three decimal places?
- \(x_6\)
- \(x_7\)
- \(x_8\)
- \(x_9\)
- The intercept cannot be correctly approximated using Newton's method.
Show Worked Solution
| \(f(x)\) | \(=\dfrac{x^3}{5}-\sqrt{x}\) |
| \(f'(x)\) | \(=\dfrac{3x^2}{5}-\dfrac{1}{2\sqrt{x}}\) |
\(\text{For Newton’s Method: }\)
| \(x_o\) | \(=1\) |
| \(x_{n+1}\) | \(=x_n-\dfrac{f(x_n)}{f'(x_n)}\) |
\(\text{Check using CAS:}\)
\begin{array} {|c|c|}
\hline
\ \ \ n\ \ \ & x_n \\
\hline
\ 0 \ & 1\\
\hline
\ 1 \ & 1-\dfrac{\dfrac{1^3}{5}-\sqrt{1}}{\dfrac{3\times 1^2}{5}-\dfrac{1}{2\sqrt{1}}}=9\\
\hline
\ 2 \ & 9-\dfrac{\dfrac{9^3}{5}-\sqrt{9}}{\dfrac{3\times 9^2}{5}-\dfrac{1}{2\sqrt{9}}}\approx 6.05\\
\hline
\ 3 \ & 6.05-\dfrac{\dfrac{6.05^3}{5}-\sqrt{6.05}}{\dfrac{3\times 6.05^2}{5}-\dfrac{1}{2\sqrt{6.05}}}\approx 4.13\\
\hline
\ 4 \ & 4.13-\dfrac{\dfrac{4.13^3}{5}-\sqrt{4.13}}{\dfrac{3\times 4.13^2}{5}-\dfrac{1}{2\sqrt{4.13}}}\approx 2.92\\
\hline
\ 5 \ & 2.92-\dfrac{\dfrac{2.92^3}{5}-\sqrt{2.92}}{\dfrac{3\times 2.92^2}{5}-\dfrac{1}{2\sqrt{2.92}}}\approx 2.24\\
\hline
\ 6 \ & 2.24-\dfrac{\dfrac{2.24^3}{5}-\sqrt{2.24}}{\dfrac{3\times 2.24^2}{5}-\dfrac{1}{2\sqrt{2.24}}}\approx 1.96\\
\hline
\ 7 \ & 1.96-\dfrac{\dfrac{1.96^3}{5}-\sqrt{1.96}}{\dfrac{3\times 1.96^2}{5}-\dfrac{1}{2\sqrt{1.96}}}\approx 1.906\\
\hline
\ 8 \ & 1.906-\dfrac{\dfrac{1.906^3}{5}-\sqrt{1.906}}{\dfrac{3\times 1.906^2}{5}-\dfrac{1}{2\sqrt{1.906}}}\approx 1.90366\\
\hline
\end{array}
\(\Rightarrow C\)
Calculus, MET2 2023 VCAA 13 MC
The following algorithm applies Newton's method using a For loop with 3 iterations.
The Return value of the function \(\text{newton}\ (x^3\ \ +\ \ 3x\ \ -\ \ 3,\ \ 3x^2\ \ +\ \ 3,\ \ 1)\) is closest to
- \(083333\)
- \(0.81785\)
- \(0.81773\)
- \(1\)
- \(3\)
Calculus, MET1 2023 VCAA 4
The graph of \(y=x+\dfrac{1}{x}\) is shown over part of its domain.
Use two trapeziums of equal width to approximate the area between the curve, the \(x\)-axis and the lines \(x=1\) and \(x=3\). (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Calculus, 2ADV C4 2022 HSC 29
- The diagram shows the graph of `y=2^{-x}`. Also shown on the diagram are the first 5 of an infinite number of rectangular strips of width 1 unit and height `y=2^{-x}` for non-negative integer values of `x`. For example, the second rectangle shown has width 1 and height `(1)/(2)`.
- The sum of the areas of the rectangles forms a geometric series.
- Show that the limiting sum of this series is 2. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Show that `int_(0)^(4)2^(-x)\ dx=(15)/(16 ln 2)`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- Use parts (a) and (b) to show that `e^(15) < 2^(32)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Calculus, 2ADV C4 2022 HSC 13
Use two applications of the trapezoidal rule to find an approximate value of `int_(0)^(2)sqrt(1+x^(2))\ dx`. Give your answer correct to 2 decimal places. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Calculus, 2ADV C4 2020 HSC 20
Kenzo is driving his car along a road while his friend records the velocity of the car, `v(t)`, in km/h every minute over a 5-minute period. The table gives the velocity `v(t)` at time `t` hours.
The distance covered by the car over the 5-minute period is given by
`int_0^(5/60) v(t)\ dt`.
Use the trapezoidal rule and the velocity at each of the six time values to find the approximate distance in kilometres the car has travelled in the 5-minute period. Give your answer correct to one decimal place. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Show Worked Solution
| `int_0^(5/60) v(t)\ dt` | `~~ 1/2 xx 1/60 [60 + 2(55 + 65 + 68 + 70) + 67]` |
| `~~ 1/120 (643)` | |
| `~~ 5.358…` | |
| `~~ 5.4\ text(km)` |
2ADV C4 Snapshot: Trapezoidal Rule
HISTORICAL CONTRIBUTION
- C4 Integration has contributed a substantial 14.0% to new syllabus Advanced exams since it was introduced in 2020.
- This topic has been split into four sub-topics for analysis purposes: 1-Integrals (3.2%), 2-Areas Under Curves (5.8%), 3-Trapezoidal Rule (2.2%) and 4-Other Integration Examples (2.8%).
- This analysis looks at Trapezoidal Rule.
HSC ANALYSIS - What to expect and common pitfalls
- Trapezoidal Rule (2.2%) is the surviving area approximation method in the new Advanced course, with Simpson's Rule no longer examinable.
- Trapezoidal Rule has been examined in 3 of the last 4 new syllabus exams (most recently in 2024), including two separate questions in 2022 (review 2022 Adv 29 - a cracking question).
- Note that while the standard formula and calculations are generally well answered, the follow up questions have produced sub-50% mean marks 4 times in the last decade.
- Where possible, past Simpson Rule approximation questions have been rewritten as Trapezoidal Rule questions to help address the problem areas identified above.
Calculus, 2ADV C4 2019 HSC 16b
A particle moves in a straight line, starting at the origin. Its velocity, `v\ text(ms)^(_1)`, is given by `v = e^(cos t) - 1`, where `t` is in seconds.
The diagram shows the graph of the velocity against time.
Using the Trapezoidal Rule with three function values, estimate the position of the particle when it first comes to rest. Give your answer correct to two decimal places. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Calculus, 2ADV C4 2014* HSC 16a
Use the Trapezoidal rule with five function values to show that
`int_(- pi/3)^(pi/3) sec x\ dx ~~ pi/6 (3 + 4/sqrt3)`. (3 marks)
--- 7 WORK AREA LINES (style=lined) ---
Show Worked Solution
♦ Mean mark below 50%. BE CAREFUL!
| `A` | `~~ h/2 [y_0 + 2(y_1 + y_2 + y_3) + y_5]` |
| `~~ pi/12 [2 + 2(2/sqrt3 + 1 + 2/sqrt3) + 2]` | |
| `~~ pi/12 [6 + 8/sqrt3]` | |
| `~~ pi/6 (3 + 4/sqrt3)\ text(u² … as required)` |
Calculus, 2ADV C4 2013* HSC 15a
The diagram shows the front of a tent supported by three vertical poles. The poles are 1.2 m apart. The height of each outer pole is 1.5 m, and the height of the middle pole is 1.8 m. The roof hangs between the poles.
The front of the tent has area `A\ text(m²)`.
- Use the trapezoidal rule to estimate `A`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Does the Trapezoidal rule give a higher or lower estimate of the actual area? Justify your answer. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. | `A` | `~~ h/2 [y_0 + 2y_1 + y_2]` |
| `~~ 1.2/2 [1.5 + (2 xx 1.8) + 1.5]` | ||
| `~~ 0.6 [6.6]` | ||
| `~~ 3.96\ text(m²)` |
| ii. |  |
`text(S)text(ince the tent roof is concave up, the)`
`text(Trapezoidal rule uses straight lines and)`
`text(will estimate a higher area.)`
Calculus, 2ADV C4 2004* HSC 10a
- Use the Trapezoidal rule with 3 function values to find an approximation to the area under the curve `y = 1/x` between `x = a ` and `x = 3a`, where `a` is positive. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Using the result in part (i), show that `ln 3 ≑ 7/6`. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. |  |
| `A` | `~~ a/2[1/a + 2(1/(2a)) + 1/(3a)]` |
| `~~ a/2(7/(3a))` | |
| `~~ 7/6` |
ii. `text{Area under the curve}\ \ y=1/x`
`= int_a^(3a) 1/x\ dx`
`= [ln x]_(\ a)^(3a)`
`= ln 3a − ln a`
`= ln\ (3a)/a`
`= ln 3`
`text{Trapezoidal rule in part (i) found the approximate}`
`text(value of the same area.)`
`:. ln 3 ≑ 7/6.`
Calculus, 2ADV C4 2018* HSC 15c
The shaded region is enclosed by the curve `y = x^3 - 7x` and the line `y = 2x`, as shown in the diagram. The line `y = 2x` meets the curve `y = x^3 - 7x` at `O(0, 0)` and `A(3, 6)`. Do NOT prove this.
- Use integration to find the area of the shaded region. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Use the Trapezoidal rule and four function values to approximate the area of the shaded region. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
The point `P` is chosen on the curve `y = x^3 − 7x` so that the tangent at `P` is parallel to the line `y = 2x` and the `x`-coordinate of `P` is positive
- Show that the coordinates of `P` are `(sqrt 3, -4 sqrt 3)`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- Using the perpendicular distance formula `|ax_1 + by_1 + c|/sqrt(a^2 + b^2)`, find the area of `Delta OAP`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. | `text(Area)` | `= int_0^3 2x – (x^3 – 7x)\ dx` |
| `= int_0^3 9x – x^3\ dx` | ||
| `= [9/2 x^2 – 1/4 x^4]_0^3` | ||
| `= [(9/2 xx 3^2 – 1/4 xx 3^4) – 0]` | ||
| `= 81/2 – 81/4` | ||
| `= 81/4\ text(units²)` |
ii. `f(x) = 9x – x^3`
| `text(Area)` | `~~ 1/2[0 + 2(8 + 10) + 0]` |
| `~~ 1/2(36)` | |
| `~~ 18\ text(u²)` |
iii. `y = x^3 – 7x`
`(dy)/(dx) = 3x^2 – 7`
`text(Find)\ \ x\ \ text(such that)\ \ (dy)/(dx) = 2`
| `3x^2 – 7` | `= 2` |
| `3x^2` | `= 9` |
| `x^2` | `= 3` |
| `x` | `= sqrt 3 qquad (x > 0)` |
| `y` | `= (sqrt 3)^3 – 7 sqrt 3` |
| `= 3 sqrt 3 – 7 sqrt 3` | |
| `= -4 sqrt 3` |
`:. P\ \ text(has coordinates)\ (sqrt 3, -4 sqrt 3)`
| iv. |  |
| `text(dist)\ OA` | `= sqrt((3 – 0)^2 + (6 – 0)^2)` |
| `= sqrt 45` | |
| `= 3 sqrt 5` |
`text(Find)\ _|_\ text(distance of)\ \ P\ \ text(from)\ \ OA`
`P(sqrt 3, -4 sqrt 3),\ \ 2x – y=0`
| `_|_\ text(dist)` | `= |(2 sqrt 3 + 4 sqrt 3)/sqrt (3 + 2)|` |
| `= (6 sqrt 3)/sqrt 5` | |
| `:.\ text(Area)` | `= 1/2 xx 3 sqrt 5 xx (6 sqrt 3)/sqrt 5` |
| `= 9 sqrt 3\ text(units²)` |
Calculus, 2ADV C4 2017* HSC 14b
- Find the exact value of `int_0^(pi/3) cos x\ dx`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Using the Trapezoidal rule with three function values, find an approximation to the integral `int_0^(pi/3) cos x\ dx,` leaving your answer in terms of `pi` and `sqrt 3`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Using parts (i) and (ii), show that `pi ~~ (12 sqrt 3)/(3 + 2 sqrt 3)`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. | `int_0^(pi/3) cos x\ dx` | `= [sin x]_0^(pi/3)` |
| `= sin\ pi/3-0` | ||
| `= sqrt 3/2` |
| ii. |  |
\begin{array} {|l|c|c|c|}\hline
x & \ \ \ 0\ \ \ & \ \ \ \dfrac{\pi}{6}\ \ \ & \ \ \ \dfrac{\pi}{3}\ \ \ \\ \hline
\text{height} & 1 & \dfrac{\sqrt{3}}{2} & \dfrac{1}{2} \\ \hline
\text{weight} & 1 & 2 & 1 \\ \hline \end{array}
| `int_0^(pi/3) cos x\ dx` | `~~ 1/2 xx pi/6[1 + 2(sqrt3/2) + 1/2]` |
| `~~ pi/12((3 + 2sqrt3)/2)` | |
| `~~ ((3+2sqrt3)pi)/24` |
♦ Mean mark part (iii) 49%.
| (iii) | `((3+2sqrt3)pi)/24` | `~~ sqrt3/2` |
| `:. pi` | `~~ (24sqrt3)/(2(3+2sqrt3))` | |
| `~~ (12sqrt3)/(3 + 2sqrt3)` |
Calculus, 2ADV C4 2011* HSC 5c
The table gives the speed `v` of a jogger at time `t` in minutes over a 20-minute period. The speed `v` is measured in metres per minute, in intervals of 5 minutes.
\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \ \ \ t\ \ \ \rule[-1ex]{0pt}{0pt} & \ \ \ 0\ \ \ &\ \ \ 5\ \ \ &\ \ \ 10\ \ \ &\ \ \ 15\ \ \ &\ \ \ 20\ \ \ \\
\hline
\rule{0pt}{2.5ex} \ \ \ v\ \ \ \rule[-1ex]{0pt}{0pt} & 173 & 81 & 127 & 195 & 168 \\
\hline
\end{array}
The distance covered by the jogger over the 20-minute period is given by `int_0^20 v\ dt`.
Use the Trapezoidal rule and the speed at each of the five time values to find the approximate distance the jogger covers in the 20-minute period. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Calculus, 2ADV C4 2006* HSC 10a
Use the Trapezoidal rule with three function values to find an approximation to the value of
`int_0.5^1.5 (log_e x )^3\ dx`.
Give your answer correct to three decimal places. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Show Worked Solution
`text(Let)\ \ f(x) = (log_e x )^3`
| `int_0.5^1.5(log_e x)^3 dx` | `~~ 0.5/2[−0.3330… + 2(0) + 0.0666…]` |
| `~~ 0.25(−0.2663…)` | |
| `~~ −0.06659…` | |
| `~~ −0.067\ \ \ text{(to 3 d.p.)}` |
Calculus, 2ADV C4 2005* HSC 6a
Five values of the function `f(x)` are shown in the table.
Use the Trapezoidal rule with the five values given in the table to estimate
`int_0^20 f(x)\ dx`. (3 marks)
Show Worked Solution
| `:. int_0^20 f(x)\ dx` | `~~ 5/2[15 + 2(25 + 22 + 18) + 10]` |
| `~~ 5/2(155)` | |
| `~~ 387.5` |
Calculus, 2ADV C4 2012* HSC 12d
At a certain location a river is 12 metres wide. At this location the depth of the river, in metres, has been measured at 3 metre intervals. The cross-section is shown below.
- Use the Trapezoidal rule with the five depth measurements to calculate the approximate area of the cross-section. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
- The river flows at 0.4 metres per second.
- Calculate the approximate volume of water flowing through the cross-section in 10 seconds. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. |  |
| `A` | `~~ 3/2[0.5 + 2(2.3 + 2.9 + 3.8) + 2.1]` |
| `~~ 3/2(20.6)` | |
| `~~ 30.9\ text(m²)` |
♦ Mean mark 49%.
| ii. `text(Distance water flows)` | `= 0.4 xx 10` |
| `= 4 \ text(metres)` |
| `text(Volume flow in 10 seconds)` | `~~ 4 xx 30.9` |
| `~~ 123.6 text(m³)` |
Calculus, 2ADV C4 2016* HSC 14a
The diagram shows the cross-section of a tunnel and a proposed enlargement.
The heights, in metres, of the existing section at 1 metre intervals are shown in Table `A.`
The heights, in metres, of the proposed enlargement are shown in Table `B.`
Use the Trapezoidal rule with the measurements given to calculate the approximate increase in area. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Show Worked Solution
`text(Consider the shaded area distances:)`
| `A` | `~~ 1/2[0 + 2(0.4 + 0.5 + 0.4) + 0]` |
| `~~ 1/2(2.6)` | |
| `~~ 1.3\ text(m²)` |
Calculus, 2ADV C4 2015 HSC 5 MC
Using the trapezoidal rule with 4 subintervals, which expression gives the approximate area under the curve `y = xe^x` between `x = 1` and `x = 3`?
- `1/4(e^1 + 6e^1.5 + 4e^2 + 10e^2.5 + 3e^3)`
- `1/4(e^1 + 3e^1.5 + 4e^2 + 5e^2.5 + 3e^3)`
- `1/2(e^1 + 6e^1.5 + 4e^2 + 10e^2.5 + 3e^3)`
- `1/2(e^1 + 3e^1.5 + 4e^2 + 5e^2.5 + 3e^3)`
Show Worked Solution
`y = xe^x`
| `A` | `~~ h/2[y_0 + 2y_1 + 2y_2 + 2y_3 + y_4]` |
| `~~ 1/4[e^1 + 3e^1.5 + 4e^2 + 5e^2.5 + 3e^3]` |
`=> B`
Calculus, 2ADV C4 2010 HSC 3b
- Sketch the curve `y=lnx`. (1 mark)
--- 6 WORK AREA LINES (style=lined) ---
- Use the trapezoidal rule with 3 function values to find an approximation to `int_1^3 lnx\ dx` (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- State whether the approximation found in part (ii) is greater than or less than the exact value of `int_1^3 lnx\ dx`. Justify your answer. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solutions
| i. |  |
MARKER’S COMMENT: Many students failed to illustrate important features in their graph such as the concavity, `x`-axis intercept and `y`-axis asymptote (this can be explicitly stated or made graphically clear).
| ii. `text(Area)` | `~~h/2[f(1)+2xxf(2)+f(3)]` |
| `~~1/2[0+2ln2+ln3]` | |
| `~~1/2[ln(2^2 xx3)]` | |
| `~~1/2ln12` | |
| `~~1.24\ \ text(u²)` `text{(to 2 d.p.)}` |
| iii. |  |
♦♦♦ Mean mark 12%.
MARKER’S COMMENT: Best responses commented on concavity and that the trapezia lay beneath the curve. Diagrams featured in the best responses.
MARKER’S COMMENT: Best responses commented on concavity and that the trapezia lay beneath the curve. Diagrams featured in the best responses.
`text(The approximation is less because the sides)`
`text{of the trapezia lie below the concave down}`
`text{curve (see diagram).}`