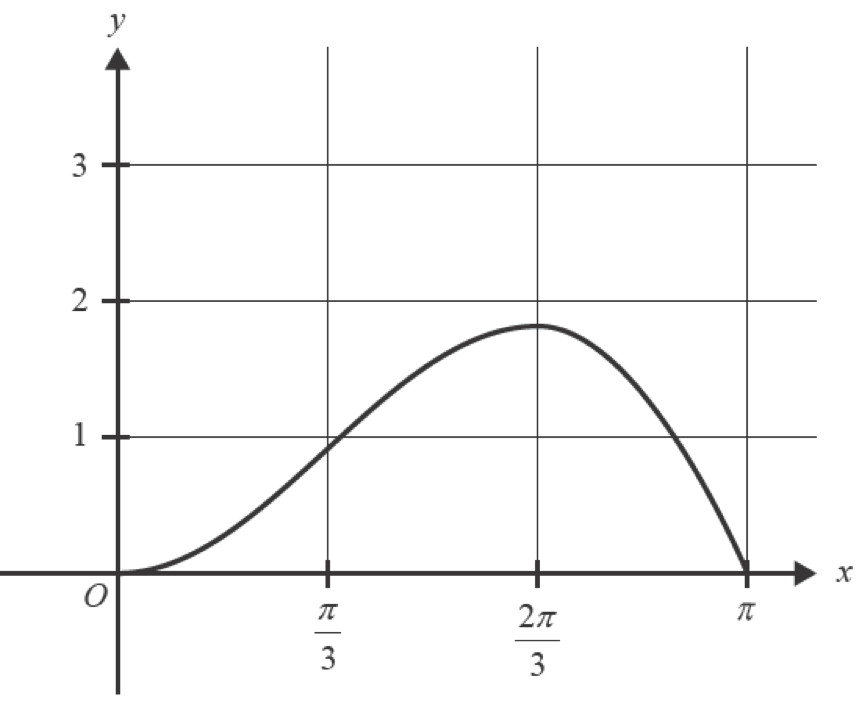
Part of the graph of \(f:[-\pi, \pi] \rightarrow R, f(x)=x \sin (x)\) is shown below. --- 8 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 0 WORK AREA LINES (style=lined) --- a. \(\dfrac{\sqrt{3}\pi^2}{6}\) bi. \(x\cos(x)+\sin(x)\) bii. \(\left[-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{3},\ 1\right]\) biii. \(\text{In the interval }\left[\dfrac{\pi}{2}, \dfrac{2\pi}{3}\right],\ f^{\prime}(x)\ \text{changes from positive to negative.}\) \(f^{\prime}(x)=0\ \text{at some point in the interval.}\) \(\therefore\ \text{A stationary point must exist in the given range.}\) b.ii. \(\text{Gradient in given range gradually decreases.}\) \(\text{Range of}\ f^{\prime}(x)\ \text{will be defined by the endpoints.}\) \(f^{\prime}(x)=0\ \text{at some point in the interval.}\) \(\therefore\ \text{A stationary point must exist in the given range.}\) \(f^{\prime}(-\pi)=-\pi\cos(-\pi)+\sin(-\pi)=\pi\) \(\therefore\ \text{Endpoints are }\ (-\pi,\ \pi)\ \text{and}\ (\pi,\ -\pi).\)
a.
\(A\)
\(=\dfrac{\pi}{3}\times\dfrac{1}{2}\left(f(0)+2f\left(\dfrac{\pi}{3}\right)+2f\left(\dfrac{2\pi}{3}\right)+f(\pi)\right)\)
\(=\dfrac{\pi}{6}\left(0+2\times \dfrac{\pi}{3}\sin\left(\dfrac{\pi}{3}\right)+2\times \dfrac{2\pi}{3}\sin\left(\dfrac{2\pi}{3}\right)+\pi\sin({\pi})\right)\)
\(=\dfrac{\pi}{6}\left(2\times \dfrac{\pi}{3}\times\dfrac{\sqrt{3}}{2}+2\times\dfrac{2\pi}{3}\times \dfrac{\sqrt{3}}{2}+0\right)\)
\(=\dfrac{\pi}{6}\left(\dfrac{2\pi\sqrt{3}}{6}+\dfrac{4\pi\sqrt{3}}{6}\right)\)
\(=\dfrac{\pi}{6}\times \dfrac{6\pi\sqrt{3}}{6}\)
\(=\dfrac{\sqrt{3}\pi^2}{6}\)
bi.
\(f(x)\)
\(=x\sin(x)\)
\(f^{\prime}(x)\)
\(=x\cos(x)+\sin(x)\)
\(f^{\prime}\left(\dfrac{\pi}{2}\right)\)
\(=1\)
\(f^{\prime}\left(\dfrac{2\pi}{3}\right)\)
\(=\dfrac{2\pi}{3}\left(\dfrac{-1}{2}+\dfrac{\sqrt{3}}{2}\right)=-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{3}\)
\(\therefore\ \text{Range of }\ f^{\prime} (x)\ \text{is}\quad\left[-\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{3},\ 1\right]\)
♦♦♦ Mean mark (b.iii.) 12%.
biii. \(\text{In the interval }\left[\dfrac{\pi}{2}, \dfrac{2\pi}{3}\right],\ f^{\prime}(x)\ \text{changes from positive to negative.}\)
c. \(f^{\prime}(\pi)=\pi\cos(\pi)+\sin(\pi)=-\pi\)
Calculus, MET1 2023 VCAA 4
The graph of \(y=x+\dfrac{1}{x}\) is shown over part of its domain.
Use two trapeziums of equal width to approximate the area between the curve, the \(x\)-axis and the lines \(x=1\) and \(x=3\). (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Calculus, 2ADV C4 2022 HSC 13
Use two applications of the trapezoidal rule to find an approximate value of `int_(0)^(2)sqrt(1+x^(2))\ dx`. Give your answer correct to 2 decimal places. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Calculus, 2ADV C4 2019 HSC 16b
A particle moves in a straight line, starting at the origin. Its velocity, `v\ text(ms)^(_1)`, is given by `v = e^(cos t) - 1`, where `t` is in seconds.
The diagram shows the graph of the velocity against time.
Using the Trapezoidal Rule with three function values, estimate the position of the particle when it first comes to rest. Give your answer correct to two decimal places. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Calculus, 2ADV C4 2014* HSC 16a
Use the Trapezoidal rule with five function values to show that
`int_(- pi/3)^(pi/3) sec x\ dx ~~ pi/6 (3 + 4/sqrt3)`. (3 marks)
--- 7 WORK AREA LINES (style=lined) ---
Show Worked Solution
♦ Mean mark below 50%. BE CAREFUL!
| `A` | `~~ h/2 [y_0 + 2(y_1 + y_2 + y_3) + y_5]` |
| `~~ pi/12 [2 + 2(2/sqrt3 + 1 + 2/sqrt3) + 2]` | |
| `~~ pi/12 [6 + 8/sqrt3]` | |
| `~~ pi/6 (3 + 4/sqrt3)\ text(u² … as required)` |
Calculus, 2ADV C4 2013* HSC 15a
The diagram shows the front of a tent supported by three vertical poles. The poles are 1.2 m apart. The height of each outer pole is 1.5 m, and the height of the middle pole is 1.8 m. The roof hangs between the poles.
The front of the tent has area `A\ text(m²)`.
- Use the trapezoidal rule to estimate `A`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Does the Trapezoidal rule give a higher or lower estimate of the actual area? Justify your answer. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. | `A` | `~~ h/2 [y_0 + 2y_1 + y_2]` |
| `~~ 1.2/2 [1.5 + (2 xx 1.8) + 1.5]` | ||
| `~~ 0.6 [6.6]` | ||
| `~~ 3.96\ text(m²)` |
| ii. |  |
`text(S)text(ince the tent roof is concave up, the)`
`text(Trapezoidal rule uses straight lines and)`
`text(will estimate a higher area.)`
Calculus, 2ADV C4 2004* HSC 10a
- Use the Trapezoidal rule with 3 function values to find an approximation to the area under the curve `y = 1/x` between `x = a ` and `x = 3a`, where `a` is positive. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Using the result in part (i), show that `ln 3 ≑ 7/6`. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. |  |
| `A` | `~~ a/2[1/a + 2(1/(2a)) + 1/(3a)]` |
| `~~ a/2(7/(3a))` | |
| `~~ 7/6` |
ii. `text{Area under the curve}\ \ y=1/x`
`= int_a^(3a) 1/x\ dx`
`= [ln x]_(\ a)^(3a)`
`= ln 3a − ln a`
`= ln\ (3a)/a`
`= ln 3`
`text{Trapezoidal rule in part (i) found the approximate}`
`text(value of the same area.)`
`:. ln 3 ≑ 7/6.`
Calculus, 2ADV C4 2018* HSC 15c
The shaded region is enclosed by the curve `y = x^3 - 7x` and the line `y = 2x`, as shown in the diagram. The line `y = 2x` meets the curve `y = x^3 - 7x` at `O(0, 0)` and `A(3, 6)`. Do NOT prove this.
- Use integration to find the area of the shaded region. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Use the Trapezoidal rule and four function values to approximate the area of the shaded region. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
The point `P` is chosen on the curve `y = x^3 − 7x` so that the tangent at `P` is parallel to the line `y = 2x` and the `x`-coordinate of `P` is positive
- Show that the coordinates of `P` are `(sqrt 3, -4 sqrt 3)`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- Using the perpendicular distance formula `|ax_1 + by_1 + c|/sqrt(a^2 + b^2)`, find the area of `Delta OAP`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. | `text(Area)` | `= int_0^3 2x – (x^3 – 7x)\ dx` |
| `= int_0^3 9x – x^3\ dx` | ||
| `= [9/2 x^2 – 1/4 x^4]_0^3` | ||
| `= [(9/2 xx 3^2 – 1/4 xx 3^4) – 0]` | ||
| `= 81/2 – 81/4` | ||
| `= 81/4\ text(units²)` |
ii. `f(x) = 9x – x^3`
| `text(Area)` | `~~ 1/2[0 + 2(8 + 10) + 0]` |
| `~~ 1/2(36)` | |
| `~~ 18\ text(u²)` |
iii. `y = x^3 – 7x`
`(dy)/(dx) = 3x^2 – 7`
`text(Find)\ \ x\ \ text(such that)\ \ (dy)/(dx) = 2`
| `3x^2 – 7` | `= 2` |
| `3x^2` | `= 9` |
| `x^2` | `= 3` |
| `x` | `= sqrt 3 qquad (x > 0)` |
| `y` | `= (sqrt 3)^3 – 7 sqrt 3` |
| `= 3 sqrt 3 – 7 sqrt 3` | |
| `= -4 sqrt 3` |
`:. P\ \ text(has coordinates)\ (sqrt 3, -4 sqrt 3)`
| iv. |  |
| `text(dist)\ OA` | `= sqrt((3 – 0)^2 + (6 – 0)^2)` |
| `= sqrt 45` | |
| `= 3 sqrt 5` |
`text(Find)\ _|_\ text(distance of)\ \ P\ \ text(from)\ \ OA`
`P(sqrt 3, -4 sqrt 3),\ \ 2x – y=0`
| `_|_\ text(dist)` | `= |(2 sqrt 3 + 4 sqrt 3)/sqrt (3 + 2)|` |
| `= (6 sqrt 3)/sqrt 5` | |
| `:.\ text(Area)` | `= 1/2 xx 3 sqrt 5 xx (6 sqrt 3)/sqrt 5` |
| `= 9 sqrt 3\ text(units²)` |
Calculus, 2ADV C4 2017* HSC 14b
- Find the exact value of `int_0^(pi/3) cos x\ dx`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Using the Trapezoidal rule with three function values, find an approximation to the integral `int_0^(pi/3) cos x\ dx,` leaving your answer in terms of `pi` and `sqrt 3`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Using parts (i) and (ii), show that `pi ~~ (12 sqrt 3)/(3 + 2 sqrt 3)`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. | `int_0^(pi/3) cos x\ dx` | `= [sin x]_0^(pi/3)` |
| `= sin\ pi/3-0` | ||
| `= sqrt 3/2` |
| ii. |  |
\begin{array} {|l|c|c|c|}\hline
x & \ \ \ 0\ \ \ & \ \ \ \dfrac{\pi}{6}\ \ \ & \ \ \ \dfrac{\pi}{3}\ \ \ \\ \hline
\text{height} & 1 & \dfrac{\sqrt{3}}{2} & \dfrac{1}{2} \\ \hline
\text{weight} & 1 & 2 & 1 \\ \hline \end{array}
| `int_0^(pi/3) cos x\ dx` | `~~ 1/2 xx pi/6[1 + 2(sqrt3/2) + 1/2]` |
| `~~ pi/12((3 + 2sqrt3)/2)` | |
| `~~ ((3+2sqrt3)pi)/24` |
♦ Mean mark part (iii) 49%.
| (iii) | `((3+2sqrt3)pi)/24` | `~~ sqrt3/2` |
| `:. pi` | `~~ (24sqrt3)/(2(3+2sqrt3))` | |
| `~~ (12sqrt3)/(3 + 2sqrt3)` |
Calculus, 2ADV C4 2006* HSC 10a
Use the Trapezoidal rule with three function values to find an approximation to the value of
`int_0.5^1.5 (log_e x )^3\ dx`.
Give your answer correct to three decimal places. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Show Worked Solution
`text(Let)\ \ f(x) = (log_e x )^3`
| `int_0.5^1.5(log_e x)^3 dx` | `~~ 0.5/2[−0.3330… + 2(0) + 0.0666…]` |
| `~~ 0.25(−0.2663…)` | |
| `~~ −0.06659…` | |
| `~~ −0.067\ \ \ text{(to 3 d.p.)}` |
Calculus, 2ADV C4 2012* HSC 12d
At a certain location a river is 12 metres wide. At this location the depth of the river, in metres, has been measured at 3 metre intervals. The cross-section is shown below.
- Use the Trapezoidal rule with the five depth measurements to calculate the approximate area of the cross-section. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
- The river flows at 0.4 metres per second.
- Calculate the approximate volume of water flowing through the cross-section in 10 seconds. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solution
| i. |  |
| `A` | `~~ 3/2[0.5 + 2(2.3 + 2.9 + 3.8) + 2.1]` |
| `~~ 3/2(20.6)` | |
| `~~ 30.9\ text(m²)` |
♦ Mean mark 49%.
| ii. `text(Distance water flows)` | `= 0.4 xx 10` |
| `= 4 \ text(metres)` |
| `text(Volume flow in 10 seconds)` | `~~ 4 xx 30.9` |
| `~~ 123.6 text(m³)` |
Calculus, 2ADV C4 2015 HSC 5 MC
Using the trapezoidal rule with 4 subintervals, which expression gives the approximate area under the curve `y = xe^x` between `x = 1` and `x = 3`?
- `1/4(e^1 + 6e^1.5 + 4e^2 + 10e^2.5 + 3e^3)`
- `1/4(e^1 + 3e^1.5 + 4e^2 + 5e^2.5 + 3e^3)`
- `1/2(e^1 + 6e^1.5 + 4e^2 + 10e^2.5 + 3e^3)`
- `1/2(e^1 + 3e^1.5 + 4e^2 + 5e^2.5 + 3e^3)`
Show Worked Solution
`y = xe^x`
| `A` | `~~ h/2[y_0 + 2y_1 + 2y_2 + 2y_3 + y_4]` |
| `~~ 1/4[e^1 + 3e^1.5 + 4e^2 + 5e^2.5 + 3e^3]` |
`=> B`
Calculus, 2ADV C4 2010 HSC 3b
- Sketch the curve `y=lnx`. (1 mark)
--- 6 WORK AREA LINES (style=lined) ---
- Use the trapezoidal rule with 3 function values to find an approximation to `int_1^3 lnx\ dx` (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- State whether the approximation found in part (ii) is greater than or less than the exact value of `int_1^3 lnx\ dx`. Justify your answer. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solutions
| i. |  |
MARKER’S COMMENT: Many students failed to illustrate important features in their graph such as the concavity, `x`-axis intercept and `y`-axis asymptote (this can be explicitly stated or made graphically clear).
| ii. `text(Area)` | `~~h/2[f(1)+2xxf(2)+f(3)]` |
| `~~1/2[0+2ln2+ln3]` | |
| `~~1/2[ln(2^2 xx3)]` | |
| `~~1/2ln12` | |
| `~~1.24\ \ text(u²)` `text{(to 2 d.p.)}` |
| iii. |  |
♦♦♦ Mean mark 12%.
MARKER’S COMMENT: Best responses commented on concavity and that the trapezia lay beneath the curve. Diagrams featured in the best responses.
MARKER’S COMMENT: Best responses commented on concavity and that the trapezia lay beneath the curve. Diagrams featured in the best responses.
`text(The approximation is less because the sides)`
`text{of the trapezia lie below the concave down}`
`text{curve (see diagram).}`