SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Functions, MET1 2021 VCAA 9

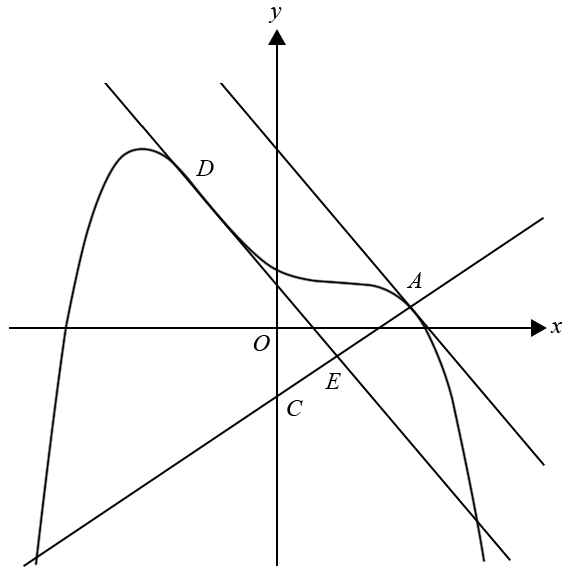
Consider the unit circle  `x^2 + y^2 = 1`  and the tangent to the circle at the point `P`, shown in the diagram below.
  

  1. Show that the equation of the line that passes through the points `A` and `P` is given by  `y = -x/sqrt3 + 2/sqrt3`.   (2 marks)

Let  `T : R^2 -> R^2, T ([(x),(y)]) = [(1, 0),(0, q)][(x),(y)]`,  where  `q ∈ R text{\}{0}`, and let the graph of the function `h` be the transformation of the line that passes through the points `A` and `P` under `T`.

    1. Find the values of `q` for which the graph of `h` intersects with the unit circle at least once.   (1 mark)

    2. Let the graph of `h` intersect the unit circle twice.
    3. Find the values of `q` for which the coordinates of the points of intersection have only positive values.   (1 mark)

  2. For  `0 < q <= 1`, let  `P^{′}` be the point of intersection of the graph of `h` with the unit circle, where  `P^{′}` is always the point of intersection that is closest to `A`, as shown in the diagram below.
     
         

Let `g` be the function that gives the area of triangle `OAP^{′}` in terms of `theta`.

    1. Define the function `g`.   (2 marks)

    2. Determine the maximum possible area of triangle `OAP^{′}`.   (2 marks)

Show Answers Only
  1. `text(See Worked Solution)`
  2.  i. `q in [–1,1]text{\}{0}`
  3. ii. `q in (sqrt3/2, 1)`
  4. i. `g(theta) = sin theta,\ \ theta in (0, pi/3]`
  5. ii. `sqrt3/2\ text(u²)`
Show Worked Solution

a.   `text(In)\ ΔOAP, text(by Pythagoras:)`

♦♦♦ Mean mark part (a) 18%.

`AP=sqrt(2^2-1^2) = sqrt3`

`tan ∠OAP = 1/sqrt3`

`=> m_(AP) =-1/sqrt3`

`text{Find equation of line}\ \ m=-1/sqrt3\ \ text{through (2, 0):}`

`y-0` `=- 1/sqrt3 (x-2)`  
`y` `=- x/sqrt3 + 2/sqrt3\ \ text{… as required}`  

 

♦♦♦ Mean mark part (b)(i) 6%.
bi.  `text{Transformation matrix → dilates line by a factor of}\ q\ text{from}\ xtext{-axis}`

`:. h(x)\ text{intersects circle for}\ \ q in [–1,1]text{\}{0}`

 

b.ii. `text(Positive coordinates → line can only intersect circle in top right quadrant.)`

 `text(Line)\ AP\ text{can move down until it cuts the circle at (0, 1)`

♦♦♦ Mean mark part (b)(ii) 4%.

`=>\ text(S)text(ince)\ AP\ text(cuts)\ ytext{-axis at}\ 2/sqrt3,`

`q=sqrt3/2\ \ text{dilates}\ AP\ text{where it cuts at (0, 1)`

`:. q in (sqrt3/2, 1)`
 

c.i.   `text(If)\ \ q=1, \ P^{′} = P and theta=pi/3`

♦♦♦ Mean mark part (c)(i) 10%.
`g(theta)` `=1/2 xx 1 xx 2 xx sin theta`  
  `=sin theta, \ \ theta in (0, pi/3]`  

 
c.ii.  `text{S}text{ince}\ \ g(theta) = sin theta\ \ text(for)\ \ theta in (0, pi/3],`

♦♦♦ Mean mark part (c)(ii) 12%.

`text(Maximum)\ g(theta)\ text(occurs when)\ \ theta = pi/3`

`:.g(theta)_text(max)=sin (pi/3)=sqrt3/2\ \ text(u²)`

Calculus, MET2 2017 VCAA 1

Let  `f : R → R,\  f (x) = x^3-5x`. Part of the graph of `f` is shown below.
 

  1. Find the coordinates of the turning points.   (2 marks)

  2. `A(−1, f (−1))`  and  `B(1, f (1))`  are two points on the graph of `f`.

     

    1. Find the equation of the straight line through `A` and `B`.   (2 marks)

    2. Find the distance `AB`.   (1 mark)

Let  `g : R → R, \ g(x) = x^3-kx, \ k ∈ R^+`.

  1. Let  `C(–1, g(−1))` and `D(1, g(1))` be two points on the graph of `g`.

     

    1. Find the distance `CD` in terms of `k`.   (2 marks)

    2. Find the values of `k` such that the distance `CD` is equal to  `k + 1`.   (1 mark)

  2. The diagram below shows part of the graphs of `g` and  `y = x`. These graphs intersect at the points with the coordinates `(0, 0)` and `(a, a)`.
  3.  
       
  4.  
    1. Find the value of `a` in terms of `k`.   (1 mark)

    2. Find the area of the shaded region in terms of `k`.   (2 marks)

Show Answers Only
  1. `(- sqrt15/3,(10sqrt15)/9)\ text(and)\ (sqrt15/3,-(10sqrt15)/9)`
    1. `y =-4x`
    2. `2sqrt17`
    1. `2sqrt(k^2-2k + 2)`
    2. `k = 1quadtext(or)quadk = 7/3`
    1. `sqrt(k + 1)`
    2. `((k + 1)^2)/4\ text(units)²`
Show Worked Solution
a.   
`text(Solve)\ \ f^{^{′}}(x)` `= 0\ \ text(for)\ x:`
`x` `= ± sqrt15/3`

 
`f(sqrt15/3) = -(10sqrt15)/9`

`f(−sqrt15/3) = (10sqrt15)/9`

`:.\ text(Turning points:)`

`(- sqrt15/3,(10sqrt15)/9)\ text(and)\ (sqrt15/3,-(10sqrt15)/9)`
 

b.i.   `A(-1,4),\ \ B(1,–4)`

`m_(AB) = (4-(−4))/(−1-(1)) = −4`

`text(Equation of)\ AB, m=-4, text(through)\ \ (-1,4):`

` y-4` `= −4(x-(−1))`
`:. y` `= −4x`

 

MARKER’S COMMENT: Students skilled in the use of technology will be much more efficient and minimise errors here.
b.ii.    `d_(text(AB))` `=sqrt((x_2-x_1)^2+(f(x_2)-f(x_1))^2)`
    `= sqrt((1- (- 1))^2 + (f(1)-f(−1))^2)`
    `= 2sqrt17`

 

c.i.    `d_(text(CD))` `=sqrt((x_2-x_1)^2+(g(x_2)-g(x_1))^2)`
    `=sqrt((1-(-1))^2+(g(1)-g(-1))^2)`
    `= 2sqrt(k^2-2k + 2)`

 

c.ii.   `text(Solve:)quad2sqrt(k^2-2k + 2) = k + 1quadtext(for)quadk > 0`

`:. k = 1quadtext(or)quadk = 7/3`
 

d.i.   `text(Solve:)quada^3-ka = a\ \ \ text(for)quad a,\ \ (a > 0)`

`:. a = sqrt(k + 1)`
 

d.ii.    `text(Area)` `= int_0^(sqrt(k + 1))(x-g(x))\ dx`
    `= ((k + 1)^2)/4\ text(units)²`

Calculus, MET2 2016 VCAA 2

Consider the function  `f(x) = -1/3 (x + 2) (x-1)^2.`

  1.  i. Given that  `g^{′}(x) = f (x) and g (0) = 1`,
  2.      show that  `g(x) = -x^4/12 + x^2/2-(2x)/3 + 1`.   (1 mark)

  3. ii. Find the values of `x` for which the graph of  `y = g(x)`  has a stationary point.   (1 mark)

The diagram below shows part of the graph of  `y = g(x)`, the tangent to the graph at  `x = 2`  and a straight line drawn perpendicular to the tangent to the graph at  `x = 2`. The equation of the tangent at the point `A` with coordinates  `(2, g(2))`  is  `y = 3-(4x)/3`.

The tangent cuts the `y`-axis at `B`. The line perpendicular to the tangent cuts the `y`-axis at `C`.
 


 

  1.   i. Find the coordinates of `B`.   (1 mark)

  2.  ii. Find the equation of the line that passes through `A` and `C` and, hence, find the coordinates of `C`.   (2 marks)

  3. iii. Find the area of triangle `ABC`.   (2 marks)

  4. The tangent at `D` is parallel to the tangent at `A`. It intersects the line passing through `A` and `C` at `E`.

     


     
     i. Find the coordinates of `D`.   (2 marks)

  5. ii. Find the length of `AE`.   (3 marks)

Show Answers Only
  1.  i. `text(Proof)\ \ text{(See worked solutions)}`
  2. ii. `x = -2, 1`
  3.   i. `(0, 3)`
  4. ii. `y = 3/4 x-7/6`
  5.      `(0, -7/6)`
  6. iii. `25/6\ text(u²)`
  7. `(-1, 25/12)`
  8. `27/20\ text(u)`
Show Worked Solution
a.i.    `g(x)` `= int f(x)\ dx`
    `=-1/3 int (x + 2) (x-1)^2\ dx`
    `=-1/3int(x^3-3x+2)\ dx`
  `:.g(x)` `= -x^4/12 + x^2/2-(2x)/3 + c`

 
`text(S)text(ince)\ \ g(0) = 1,`

`1` `= 0 + 0-0 + c`
`:. c` `= 1`

  
`:. g(x) = -x^4/12 + x^2/2-(2x)/3 + 1\ \ …\ text(as required)`
 

a.ii.   `text(Stationary point when:)`

`g^{′}(x) = f(x) = 0`

`-1/3(x + 2) (x-1)^2=0`

`:. x = -2, 1`
 

b.i.   

`B\ text(is the)\ y text(-intercept of)\ \ y = 3-4/3 x`

`:. B (0, 3)`
 

b.ii.   `m_text(norm) = 3/4, \ text(passes through)\ \ A(2, 1/3)`

   `text(Equation of normal:)`

`y-1/3` `=3/4(x-2)`
`y` `=3/4 x-7/6`
   

`:. C (0, -7/6)`
 

b.iii.   `text(Area)` `= 1/2 xx text(base) xx text(height)`
    `= 1/2 xx (3 + 7/6) xx 2`
    `= 25/6\ text(u²)`

 

♦ Mean mark part (c)(i) 43%.
MARKER’S COMMENT: Many students gave an incorrect `y`-value here. Be careful!
c.i.    `text(Solve)\ \ \ g^{′}(x)` `= -4/3\ \ text(for)\ \ x < 0`
  `=> x` `= -1`
  `g(-1)` `=-1/12+1/2+2/3+1`
    `=25/12`

  
`:. D (−1, 25/12)`
 

c.ii.   `text(T) text(angent line at)\ \ D:`

`y-25/12` `=-4/3(x+1)`
`y` `=-4/3x + 3/4`

 
`DE\ \ text(intersects)\ \ AE\ text(at)\ E:`

♦♦ Mean mark 32%.
`-4/3 x + 3/4` `= 3/4 x-7/6`
`25/12 x` `= 23/12`
`x` `=23/25`

 
`:. E (23/25, -143/300)`
 

`:. AE` `= sqrt((2-23/25)^2 + (1/3-(-143/300))^2)`
  `= 27/20\ text(units)`