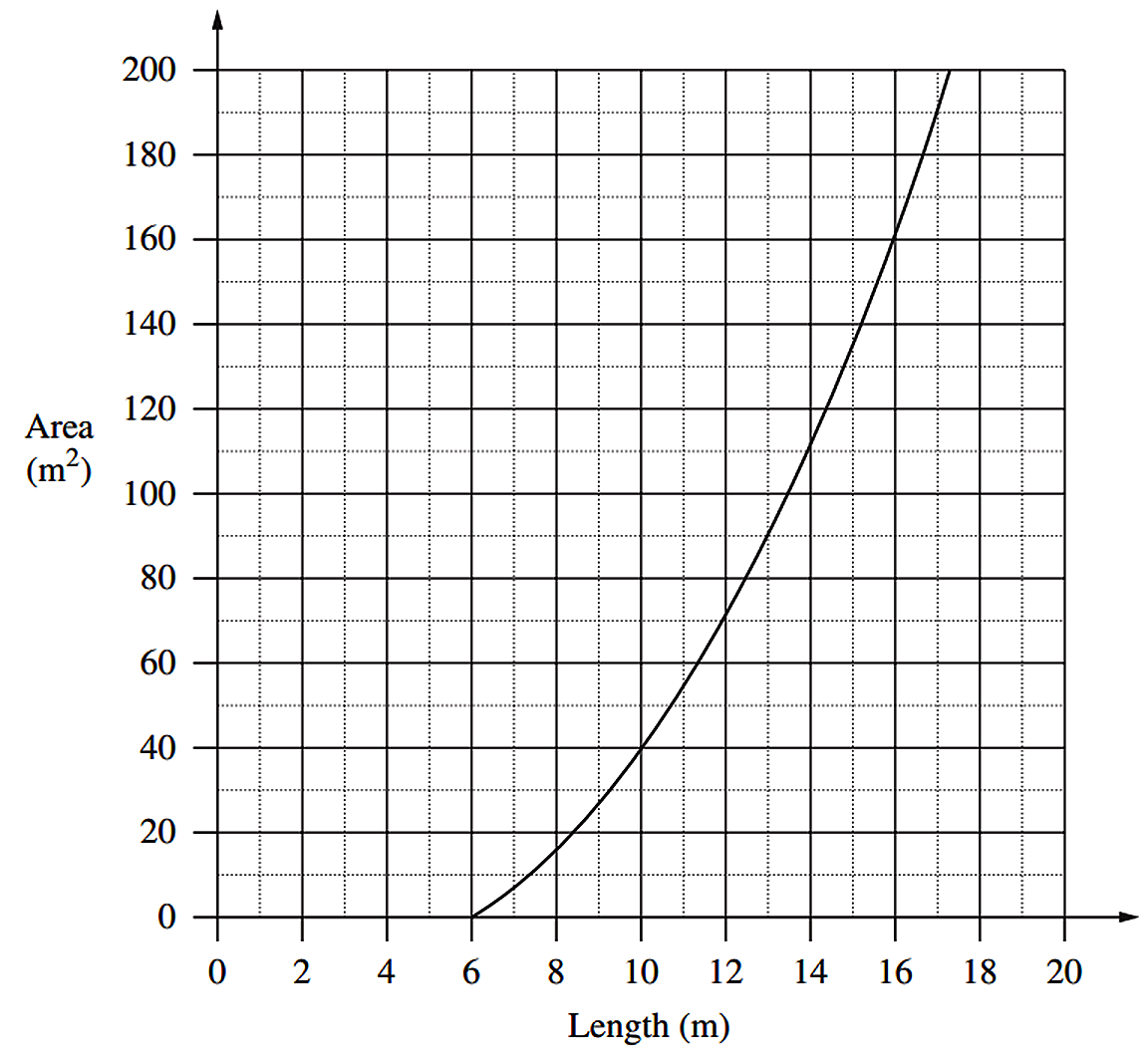
A golf club hires an entire course for a charity event at a total cost of `$40\ 000`. The cost will be shared equally among the players, so that `C` (in dollars) is the cost per player when `n` players attend.
- Complete the table below by filling in the three missing values. (1 mark)
\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\text{Number of players} (n) \rule[-1ex]{0pt}{0pt} & \ 50\ & \ 100 \ & 200 \ & 250 \ & 400\ & 500 \ \\
\hline
\rule{0pt}{2.5ex}\text{Cost per person} (C)\rule[-1ex]{0pt}{0pt} & & & & 160 & 100\ & 80 \ \\
\hline
\end{array} - Using the values from the table, draw the graph showing the relationship between `n` and `C`. (2 marks)
- What equation represents the relationship between `n` and `C`? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Give ONE limitation of this equation in relation to this context. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Is it possible for the cost per person to be $94? Support your answer with appropriate calculations. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---