The diagram shows a triangle `ABC` where `AC` = 25 cm, `BC` = 16 cm, `angle BAC` = 28° and angle `ABC` is obtuse.
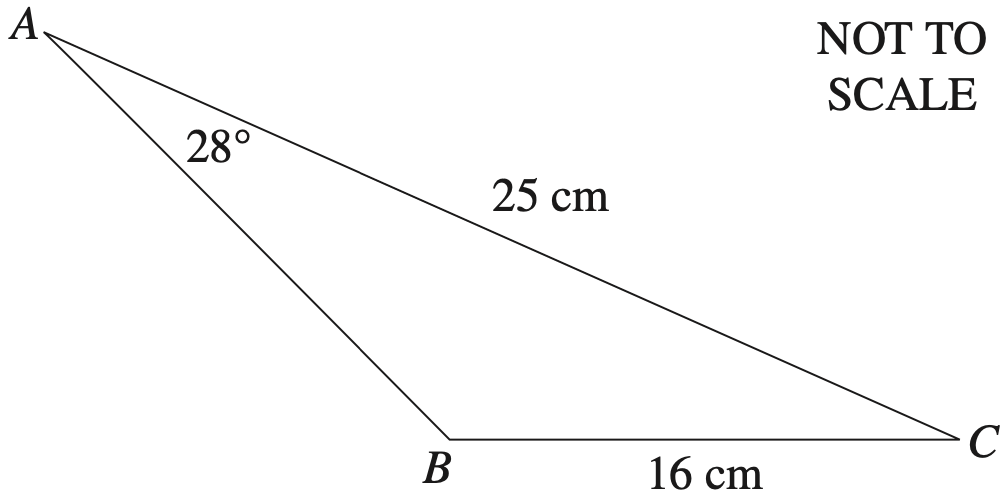
Find the size of the obtuse angle `ABC` correct to the nearest degree. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Measurement, STD2 M6 2021 HSC 37
The diagram shows a triangle `ABC` where `AC` = 25 cm, `BC` = 16 cm, `angle BAC` = 28° and angle `ABC` is obtuse.
Find the size of the obtuse angle `ABC` correct to the nearest degree. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Statistics, 2ADV S3 2021 HSC 22
A random variable is normally distributed with mean 0 and standard deviation 1. The table gives the probability that this random variable lies between 0 and `z` for different values of `z`.
The probability values given in the table for different values of `z` are represented by the shaded area in the following diagram.
- Using the table, find the probability that a value from a random variable that is normally distributed with a mean of 0 and standard deviation 1 lies between 0.1 and 0.5. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Birth weights are normally distributed with a mean of 3300 grams and a standard deviation of 570 grams. By first calculating a `z`-score, find how many babies, out of 1000 born, are expected to have a birth weight greater than 3528 grams. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Functions, 2ADV F1 2021 HSC 11
Solve `x+(x-1)/2 = 9`. (2 marks)
Probability, 2ADV S1 2021 HSC 6 MC
There are 8 chocolates in a box. Three have peppermint centres (P) and five have caramel centres (C).
Kim randomly chooses a chocolate from the box and eats it. Sam then randomly chooses and eats one of the remaining chocolates.
A partially completed probability tree is shown.
What is the probability that Kim and Sam choose chocolates with different centres?
- `\frac{15}{64}`
- `\frac{15}{56}`
- `\frac{15}{32}`
- `\frac{15}{28}`
Show Worked Solution
| `Ptext{(different centres)}` | `= P text{(PC)} + P text{(CP)}` |
| `=\frac{3}{8} · \frac{5}{7} + \frac{5}{8} · \frac{3}{7}` | |
| `= \frac{15}{56} + \frac{15}{56}` | |
| `= \frac{15}{28}` |
`=> D`
Probability, STD2 S2 2021 HSC 11 MC
There are 8 chocolates in a box. Three have peppermint centres (P) and five have caramel centres (C).
Kim randomly chooses a chocolate from the box and eats it. Sam then randomly chooses and eats one of the remaining chocolates.
A partially completed probability tree is shown.
What is the probability that Kim and Sam choose chocolates with different centres?
- `\frac{15}{64}`
- `\frac{15}{56}`
- `\frac{15}{32}`
- `\frac{15}{28}`
Show Worked Solution
♦♦ Mean mark 35%.
| `Ptext{(different centres)}` | `= P text{(PC)} + P text{(CP)}` |
| `=\frac{3}{8} · \frac{5}{7} + \frac{5}{8} · \frac{3}{7}` | |
| `= \frac{15}{56} + \frac{15}{56}` | |
| `= \frac{15}{28}` |
`=> D`
L&E, 2ADV E1 2021 HSC 5 MC
Which of the following best represents the graph of `y = 10 (0.8)^x`?
Algebra, STD2 A4 2021 HSC 10 MC
Which of the following best represents the graph of `y = 10 (0.8)^x`?
Statistics, 2ADV S2 2021 HSC 4 MC
The number of downloads of a song on each of twenty consecutive days is shown in the following graph.
Which of the following graphs best shows the cumulative number of downloads up to and including each day?
Statistics, STD2 S1 2021 HSC 7 MC
The number of downloads of a song on each of twenty consecutive days is shown in the following graph.
Which of the following graphs best shows the cumulative number of downloads up to and including each day?
Algebra, STD2 A1 2021 HSC 29
Solve `x+(x-1)/2 = 9` (2 marks)
Statistics, STD2 S4 2020 HSC 36
A cricket is an insect. The male cricket produces a chirping sound.
A scientist wants to explore the relationship between the temperature in degrees Celsius and the number of cricket chirps heard in a 15-second time interval.
Once a day for 20 days, the scientist collects data. Based on the 20 data points, the scientist provides the information below.
- A box-plot of the temperature data is shown.
- The mean temperature in the dataset is 0.525°C below the median temperature in the dataset.
- A total of 684 chirps was counted when collecting the 20 data points.
The scientist fits a least-squares regression line using the data `(x, y)`, where `x` is the temperature in degrees Celsius and `y` is the number of chirps heard in a 15-second time interval. The equation of this line is
`y = −10.6063 + bx`,
where `b` is the slope of the regression line.
The least-squares regression line passes through the point `(barx, bary)`, where `barx` is the sample mean of the temperature data and `bary` is the sample mean of the chirp data.
Calculate the number of chirps expected in a 15-second interval when the temperature is 19° Celsius. Give your answer correct to the nearest whole number. (5 marks)
Measurement, STD2 M6 2020 HSC 32
The diagram shows a regular decagon (ten-sided shape with all sides equal and all interior angles equal). The decagon has centre `O`.
The perimeter of the shape is 80 cm.
By considering triangle `OAB`, calculate the area of the ten-sided shape. Give your answer in square centimetres correct to one decimal place. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
Show Worked Solution
`angle AOB = 360/10 = 36^@`
♦♦ Mean mark 33%.
`AB = 80/10 = 8\ text(cm)`
`DeltaAOB\ text(is made up of 2 identical right-angled triangles)`
| `tan 18^@` | `= 4/x` |
| `x` | `= 4/(tan 18^@)` |
| `:.\ text(Area of decagon)` | `= 20 xx 1/2 xx 4/(tan 18^@) xx 4` |
| `= 492.429…` | |
| `= 492.4\ text(cm² (to 1 d.p.))` |
Measurement, STD2 M6 2020 HSC 31
Mr Ali, Ms Brown and a group of students were camping at the site located at `P`. Mr Ali walked with some of the students on a bearing of 035° for 7 km to location `A`. Ms Brown, with the rest of the students, walked on a bearing of 100° for 9 km to location `B`.
- Show that the angle `APB` is 65°. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Find the distance `AB`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Find the bearing of Ms Brown's group from Mr Ali's group. Give your answer correct to the nearest degree. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Show Worked Solution
| a. | `angle APB` | `= 100 – 35` |
| `= 65^@` |
b. `text(Using cosine rule:)`
Mean mark 53%.
| `AB^2` | `= AP^2 + PB^2 – 2 xx AP xx PB cos 65^@` |
| `= 49 + 81 – 2 xx 7 xx 9 cos 65^@` | |
| `= 76.750…` | |
| `:.AB` | `= 8.760…` |
| `= 8.76\ text{km (to 2 d.p.)}` |
c.
`anglePAC = 35^@\ (text(alternate))`
♦♦ Mean mark 22%.
`text(Using cosine rule, find)\ anglePAB:`
| `cos anglePAB` | `= (7^2 + 8.76 – 9^2)/(2 xx 7 xx 8.76)` | |
| `= 0.3647…` | ||
| `:. angle PAB` | `= 68.61…^@` | |
| `= 69^@\ \ (text(nearest degree))` |
`:. text(Bearing of)\ B\ text(from)\ A\ (theta)`
`= 180 – (69 – 35)`
`= 146^@`
Functions, 2ADV F1 2020 HSC 11
There are two tanks on a property, Tank `A` and Tank `B`. Initially, Tank `A` holds 1000 litres of water and Tank B is empty.
- Tank `A` begins to lose water at a constant rate of 20 litres per minute. The volume of water in Tank `A` is modelled by `V = 1000 - 20t` where `V` is the volume in litres and `t` is the time in minutes from when the tank begins to lose water. (1 mark)
On the grid below, draw the graph of this model and label it as Tank `A`.
- Tank `B` remains empty until `t=15` when water is added to it at a constant rate of 30 litres per minute.
By drawing a line on the grid (above), or otherwise, find the value of `t` when the two tanks contain the same volume of water. (2 marks)
- Using the graphs drawn, or otherwise, find the value of `t` (where `t > 0`) when the total volume of water in the two tanks is 1000 litres. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Answers Only
- `text{T} text{ank} \ A \ text{will pass trough (0, 1000) and (50, 0)}`
- `29 \ text{minutes}`
- `45 \ text{minutes}`
Show Worked Solution
a. `text{T} text{ank} \ A \ text{will pass trough (0, 1000) and (50, 0)}`
b. `text{T} text{ank} \ B \ text{will pass through (15, 0) and (45, 900)}`
`text{By inspection, the two graphs intersect at} \ \ t = 29 \ text{minutes}`
c. `text{Strategy 1}`
`text{By inspection of the graph, consider} \ \ t = 45`
`text{T} text{ank A} = 100 \ text{L} , \ text{T} text{ank B} =900 \ text{L} `
`:.\ text(Total volume = 1000 L when t = 45)`
`text{Strategy 2}`
| `text{Total Volume}` | `=text{T} text{ank A} + text{T} text{ank B}` |
| `1000` | `= 1000 – 20t + (t – 15) xx 30` |
| `1000` | `= 1000 – 20t + 30t – 450 ` |
| `10t` | `= 450` |
| `t` | `= 45 \ text{minutes}` |
Algebra, STD2 A4 2020 HSC 24
There are two tanks on a property, Tank A and Tank B. Initially, Tank A holds 1000 litres of water and Tank B is empty.
- Tank A begins to lose water at a constant rate of 20 litres per minute.
The volume of water in Tank A is modelled by `V = 1000 - 20t` where `V` is the volume in litres and `t` is the time in minutes from when the tank begins to lose water.
On the grid below, draw the graph of this model and label it as Tank A. (1 mark)
- Tank B remains empty until `t=15` when water is added to it at a constant rate of 30 litres per minute.
By drawing a line on the grid (above), or otherwise, find the value of `t` when the two tanks contain the same volume of water. (2 marks)
--- 2 WORK AREA LINES (style=lined) ---
- Using the graphs drawn, or otherwise, find the value of `t` (where `t > 0`) when the total volume of water in the two tanks is 1000 litres. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Show Answers Only
- `text{T} text{ank} \ A \ text{will pass trough (0, 1000) and (50, 0)}`
- `29 \ text{minutes}`
- `45 \ text{minutes}`
Show Worked Solution
a. `text{T} text{ank} \ A \ text{will pass trough (0, 1000) and (50, 0)}`
b. `text{T} text{ank} \ B \ text{will pass through (15, 0) and (45, 900)}`
`text{By inspection, the two graphs intersect at} \ \ t = 29 \ text{minutes}`
c. `text{Strategy 1}`
♦♦ Mean mark part (c) 22%.
`text{By inspection of the graph, consider} \ \ t = 45`
`text{T} text{ank A} = 100 \ text{L} , \ text{T} text{ank B} =900 \ text{L} `
`:.\ text(Total volume = 1000 L when t = 45)`
`text{Strategy 2}`
| `text{Total Volume}` | `=text{T} text{ank A} + text{T} text{ank B}` |
| `1000` | `= 1000 – 20t + (t – 15) xx 30` |
| `1000` | `= 1000 – 20t + 30t – 450 ` |
| `10t` | `= 450` |
| `t` | `= 45 \ text{minutes}` |
Statistics, 2ADV S2 2020 HSC 27
A cricket is an insect. The male cricket produces a chirping sound.
A scientist wants to explore the relationship between the temperature in degrees Celsius and the number of cricket chirps heard in a 15-second time interval.
Once a day for 20 days, the scientist collects data. Based on the 20 data points, the scientist provides the information below.
- A box-plot of the temperature data is shown.
- The mean temperature in the dataset is 0.525°C below the median temperature in the dataset.
- A total of 684 chirps was counted when collecting the 20 data points.
The scientist fits a least-squares regression line using the data `(x, y)`, where `x` is the temperature in degrees Celsius and `y` is the number of chirps heard in a 15-second time interval. The equation of this line is
`y = −10.6063 + bx`,
where `b` is the slope of the regression,
The least-squares regression line passes through the point `(barx, bary)`, where `barx` is the sample mean of the temperature data and `bary` is the sample mean of the chirp data.
Calculate the number of chirps expected in a 15-second interval when the temperature is 19° Celsius. Give your answer correct to the nearest whole number. (5 marks)
Trigonometry, 2ADV T1 2020 HSC 22
The diagram shows a regular decagon (ten-sided shape with all sides equal and all interior angles equal). The decagon has centre `O`.
The perimeter of the shape is 80 cm.
By considering triangle `OAB`, calculate the area of the ten-sided shape. Give your answer in square centimetres correct to one decimal place. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
Show Worked Solution
`angle AOB = 360/10 = 36^@`
`AB = 80/10 = 8\ text(cm)`
`DeltaAOB\ text(is made up of 2 identical right-angled triangles)`
| `tan 18^@` | `= 4/x` |
| `x` | `= 4/(tan 18^@)` |
| `:.\ text(Area of decagon)` | `= 20 xx 1/2 xx 4/(tan 18^@) xx 4` |
| `= 492.429…` | |
| `= 492.4\ text(cm² (to 1 d.p.))` |
Financial Maths, STD2 F5 2020 HSC 34
Tina inherits $60 000 and invests it in an account earning interest at a rate of 0.5% per month. Each month, immediately after the interest has been paid, Tina withdraws $800.
The amount in the account immediately after the `n`th withdrawal can be determined using the recurrence relation
`A_n = A_(n - 1)(1.005) - 800`,
where `n = 1, 2, 3, …` and `A_0 = 60\ 000`
- Use the recurrence relation to find the amount of money in the account immediately after the third withdrawal. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Calculate the amount of interest earned in the first three months. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Trigonometry, 2ADV T1 2020 HSC 15
Mr Ali, Ms Brown and a group of students were camping at the site located at `P`. Mr Ali walked with some of the students on a bearing of 035° for 7 km to location `A`. Ms Brown, with the rest of the students, walked on a bearing of 100° for 9 km to location `B`.
- Show that the angle `APB` is 65°. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Find the distance `AB`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- Find the bearing of Ms Brown's group from Mr Ali's group. Give your answer correct to the nearest degree. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Show Worked Solution
| a. | `angle APB` | `= 100-35` |
| `= 65^@` |
b. `text(Using cosine rule:)`
| `AB^2` | `= AP^2 + PB^2-2 xx AP xx PB cos 65^@` |
| `= 49 + 81-2 xx 7 xx 9 cos 65^@` | |
| `= 76.750…` | |
| `:.AB` | `= 8.760…` |
| `= 8.76\ text{km (to 2 d.p.)}` |
c.
`anglePAC = 35^@\ (text(alternate))`
`text(Using cosine rule, find)\ anglePAB:`
| `cos anglePAB` | `= (7^2 + 8.76-9^2)/(2 xx 7 xx 8.76)` | |
| `= 0.3647…` | ||
| `:. angle PAB` | `= 68.61…^@` | |
| `= 69^@\ \ (text(nearest degree))` |
`:. text(Bearing of)\ B\ text(from)\ A\ (theta)`
`= 180-(69-35)`
`= 146^@`
Statistics, 2ADV S3 2020 HSC 3 MC
John recently did a class test in each of three subjects. The class scores on each test were normally distributed.
The table shows the subjects and John's scores as well as the mean and standard deviation of the class scores on each test.
Relative to the rest of class, which row of the table below shows John's strongest subject and his weakest subject?
Statistics, STD2 S5 2020 HSC 8 MC
John recently did a class test in each of three subjects. The class scores on each test were normally distributed.
The table shows the subjects and John's scores as well as the mean and standard deviation of the class scores on each test.
Relative to the rest of class, which row of the table below shows John's strongest subject and his weakest subject?