SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Conics, EXT2 2018 HSC 02 MC

What are the equations of the asymptotes of the hyperbola  `9x^2 - 4y^2 = 36`?

  1. `y = +- 9/4x`
  2. `y = +- 2/3x`
  3. `y = +- 3/2x`
  4. `y = +- 4/9x`
Show Answers Only

`text(C)`

Show Worked Solution
`9x^2 – 4y^2` `= 36`
`(x^2)/4 – (y^2)/9` `= 1`

 
`:.\ text(Asymptotes are:)\ \ y = +- 3/2x`

`=>\ text(C)`

Financial Maths, 2ADV M1 2018 HSC 14d

An artist posted a song online. Each day there were  `2^n + n`  downloads, where `n` is the number of days after the song was posted.

  1. Find the number of downloads on each of the first 3 days after the song was posted.  (1 mark)

  2. What is the total number of times the song was downloaded in the first 20 days after it was posted?  (2 marks)

Show Answers Only
  1. `text(Day 1) : 3`
    `text(Day 2) : 6`
    `text(Day 3) : 11`

  2. `2\ 097\ 360`
Show Worked Solution

i.   `text(Day 1:)\ \ 2^1 + 1 = 3`

`text(Day 2:)\ \ 2^2 + 2 = 6`

`text(Day 3:)\ \ 2^3 + 3 = 11`

 

ii.  `text{Total downloads (20 days)}`

♦ Mean mark 38%.

`= 2^1 + 1 + 2^2 + 2 + … + 2^20 + 20`

`= underbrace(2^1 + 2^2 + … + 2^20)_{text(GP),\ a = 2,\ r=2} + underbrace(1 + 2 + … + 20)_{text(AP),\ a = 1,\ d = 1}`

`= (2(2^20 – 1))/(2 – 1) + 20/2(1 + 20)`

`= 2\ 097\ 150 + 210`

`= 2\ 097\ 360`

Calculus, EXT1* C1 2018 HSC 13c

The population of a country grew exponentially between 1910 and 2010. This population can be modelled by the equation  `P(t) = 92e^(kt)`, where  `P(t)`  is the population of the country in millions, `t` is the time in years after 1910 and `k` is a positive constant. The population of the country in 1960 was 184 million.

  1. Show that the value of `k` is 0.0139, correct to 4 decimal places.  (2 marks)

  2. Assuming that this model continues to be valid after 2010, estimate the population of the country in 2020 to the nearest million.  (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `424\ text{million  (nearest million)}`
Show Worked Solution

i.   `P(t) = 92 e^(kt)`

`text(Find)\ \ k\ \ text(given)\ \ t = 50\ \ text(when)\ \ P = 184`

`184` `= 92 e^(50k)`
`e^(50 k)` `= 2`
`50k` `= ln 2`
`k` `= 1/50 xx ln 2`
  `= 0.01386…`
  `= 0.0139\ \ text{(to 4 d.p.)}`

 

ii.  `text(In 2020),\ t = 110`

`:.\ text(Estimated population)`

`= 92 e^(110 xx 0.0139)`

`= 92 e^1.529`

`= 424.44…`

`= 424\ text{million  (nearest million)}`

Calculus, 2ADV C3 2018 HSC 13a

Consider the curve  `y = 6x^2 - x^3`.

  1. Find the stationary points and determine their nature.  (3 marks)

  2. Given that the point  (2,16)  lies on the curve, show that it is a point of inflection.  (2 marks)

  3. Sketch the curve, showing the stationary points, the point of inflection and the `x` and `y` intercepts.  (2 marks)

Show Answers Only
  1. `text(MIN at)\ (0, 0);\ text(MAX at)\ (4, 32)`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(See Worked Solutions)`
Show Worked Solution

i.    `y = 6x^2 – x^3`

`(dy)/(dx) = 12x – 3x^2`

`(d^2y)/(dx^2) = 12 – 6x`
 

`text(S.P.s occur when)\ \ (dy)/(dx) = 0`

`12x – 3x^2 = 0`

`3x(4 – x) = 0`

`x = 0 or 4`
 

`text(When)\ \ x = 0,\ (d^2y)/(dx^2) > 0`

`:.\ text(MIN at)\ (0, 0)`
 

`text(When)\ \ x = 4,\ (d^2y)/(dx^2) < 0`

`:.\ text(MAX at)\ (4, 32)`

 

ii.  `text(P.I. occur when)\ \ (d^2y)/(dx^2) = 0,`

`12 – 6x` `= 0`
`x` `= 2`

 
`text(When)\ \ x = 2,\ y = 16`

 
`text(S)text(ince the concavity changes)`

`=>\ text(P.I. occurs at)\ \ (2, 16)`

 

iii.  

Calculus, 2ADV C1 2018 HSC 12d

The displacement of a particle moving along the `x`-axis is given by

`x = t^3/3 - 2t^2 + 3t,`

where `x` is the displacement from the origin in metres and `t` is the time in seconds, for `t >= 0`.

  1. What is the initial velocity of the particle?  (1 mark)

  2. At which times is the particle stationary?  (2 marks)

  3. Find the position of the particle when the acceleration is zero.  (2 marks)

Show Answers Only
  1. `3\ text(ms)^(-1)`
  2. `t = 1 or 3\ text(seconds)`
  3. `2/3\ text(m)`
Show Worked Solution

i.    `x = t^3/3 – 2t^2 + 3t`

`v = (dx)/(dt) = t^2 – 4t + 3`
 

`text(Find)\ \ v\ \ text(when)\ \ t = 0:`

`v` `= 0 – 0 + 3`
  `= 3\ text(ms)^(-1)`

 

ii.  `text(Particle is stationary when)\ \ v = 0`

`t^2 – 4t + 3 = 0`

`(t – 3) (t – 1) = 0`

`t = 1 or 3\ text(seconds)`
 

iii.  `a = (dv)/(dt) = 2t – 4`
 

`text(Find)\ \ t\ \ text(when)\ \ a = 0`

`2t – 4` `= 0`
`t` `= 2`
`x(2)` `= 2^3/3 – 2(2^2) + 3(2)`
  `= 8/3 – 8 + 6`
  `= 2/3`

Trigonometry, 2ADV T1 2018 HSC 12a

A ship travels from Port A on a bearing of 050° for 320 km to Port B. It then travels on a bearing of 120° for 190 km to Port C.
 


 

  1. What is the size of  `/_ ABC`?  (1 mark)

  2. What is the distance from Port A to Port C ? Answer to the nearest 10 kilometres.  (2 marks)

Show Answers Only
  1. `110^@`
  2. `420\ text(km)`
Show Worked Solution
i.  

`text(Let)\ \ D\ \ text(be south of)\ \ B`

`/_ ABD = 50^@ qquad text{(alternate angles)}`

`/_DBC = 60^@ qquad text{(180° in straight line)}`

`:. /_ ABC` `= 50 + 60`
  `= 110^@`

 

ii.  `text(Using the cosine rule:)`

`AC^2` `= AB^2 + BC^2 – 2 *AB*BC* cos /_ ABC`
  `= 320^2 + 190^2 – 2 xx 320 xx 190 xx cos 110^@`
  `= 180\ 089.64…`
`:. AC` `= 424.36…`
  `= 420\ text{km (nearest 10 km)}`

Calculus, 2ADV C2 2018 HSC 11g

Differentiate  `e^x/(x + 1)`.  (2 marks)

Show Answers Only

`(xe^x)/(x + 1)^2`

Show Worked Solution

`y = e^x/(x + 1)`

`text(Differentiate using quotient rule:)`

`u = e^x` `v = x + 1`
`u prime = e^x` `v prime = 1`
   
`(dy)/(dx)` `= (u prime v – u v prime)/v^2`
  `= (e^x(x + 1) – e^x ⋅ 1)/(x + 1)^2`
  `= (x e^x)/(x + 1)^2`

Financial Maths, 2ADV M1 2018 HSC 11d

In an arithmetic series, the third term is 8 and the twentieth term is 59.

  1. Find the common difference.  (1 mark)

  2. Find the 50th term.  (2 marks)

Show Answers Only
  1. `d = 3`
  2. `149`
Show Worked Solution
i.   `a + 2d` `= 8 qquad text{… (1)}`
  `a + 19d` `= 59 qquad text{… (2)}`

 
`text(Substract)\ \ (2) – (1)`

`17d` `= 51`
`:. d` `= 3`

 

ii.  `text(Find)\ \ T_50`

`text(Substitute)\ \ d = 3\ \ text{into (1)}`

`=> a = 12`

`T_n` `=a+(n-1)d`
`:. T_50` `= 2 + 49 xx 3`
  `= 149`

Functions, 2ADV F1 2018 HSC 11a

Rationalise the denominator of  `3/(3 + sqrt 2)`.  (2 marks)

Show Answers Only

`(3 (3 – sqrt 2))/7`

Show Worked Solution
`3/(3 + sqrt 2) xx (3 – sqrt 2)/(3 – sqrt 2)` `= (3(3 – sqrt 2))/(3^2 – (sqrt 2)^2)`
  `= (3(3 – sqrt2))/7`

Measurement, STD2 M1 2018 HSC 28a

A field is bordered on one side by a straight road and on the other side by a river, as shown. Measurements are taken perpendicular to the road every 7.5 metres along the road.
 

 
Use four applications of the Trapeziodal rule to find an approximation to the area of the field. Answer to the nearest square metre.  (3 marks)

Show Answers Only

`242\ text{m²  (nearest m²)}`

Show Worked Solution

`text(Strategy 1)`

`A` `~~ 7.5/2(8.8 + 7.1) + 7.5/2(7.1 + 9.8) + 7.5/2(9.8 + 8.5) + 7.5/2(8.5 + 4.9)`
  `~~ 241.875`
  `~~ 242\ text{m²  (nearest m²)}`

 

`text(Strategy 2)`

`A` `~~ 7.5/2(8.8 + 2 xx 7.1 + 2 xx 9.8 + 2 xx 8.5 + 4.9)`
  `~~ 242\ text(m²)`

Calculus, 2ADV C2 2018 HSC 5 MC

What is the derivative of  `sin(ln x),` where  `x > 0`?

  1. `cos (1/x)`
  2. `cos (ln x)`
  3. `cos ((ln x)/x)`
  4. `(cos (ln x))/x`
Show Answers Only

`D`

Show Worked Solution
`y` `= sin (ln x)`
`(dy)/(dx)` `= cos (ln x) xx d/(dx) (ln x)`
  `= cos (ln x) xx 1/x`
  `= (cos (ln x))/x`

 `=>  D`

Statistics, STD2 S5 2018 HSC 27e

Joanna sits a Physics test and a Biology test.

  1. Joanna’s mark in the Physics test is 70. The mean mark for this test is 58 and the standard deviation is 8.

     

    Calculate the `z`-score for Joanna’s mark in this test.  (1 mark)

  2. In the Biology test, the mean mark is 64 and the standard deviation is 10.

     

    Joanna’s `z`-score is the same in both the Physics test and the Biology test.

     

    What is her mark in the Biology test?  (2 marks)

Show Answers Only
  1. `1.5`
  2. `79`
Show Worked Solution

i.   `x = 70, \ mu = 58, \ sigma = 8`

`:. ztext(-score)` `= (x – mu)/sigma`
  `= (70 – 58)/8`
  `= 1.5`

 

ii.    `1.5` `= (x – 64)/10`
  `x – 64` `= 15`
  `:. x` `= 79`

Algebra, STD2 A4 2018 HSC 27d

The graph displays the cost (`$c`) charged by two companies for the hire of a minibus for `x` hours.
 


  

Both companies charge $360 for the hire of a minibus for 3 hours.

  1. What is the hourly rate charged by Company A?  (1 mark)

  2. Company B charges an initial booking fee of $75.

     

    Write a formula, in the form of  `c = mx + b`, for the cost of hiring a minibus from Company B for `x` hours.  (2 marks)

  3. A minibus is hired for 5 hours from Company B.

     

    Calculate how much cheaper this is than hiring from Company A.  (2 marks)

Show Answers Only
  1. `$120`
  2. `c = 95x + 75`
  3. `$50`
Show Worked Solution
i.    `text(Hourly rate)\ (A)` `= 360 ÷ 3`
    `= $120`

 

ii.   `m = text(hourly rate)`

`text(Find)\ m,\ text(given)\ c = 360,\ text(when)\ \ x = 3\ \ text(and)\ \ b = 75`

`360` `= m xx 3 + 75`
`3m` `= 285`
`m` `= 95`

 
`:. c = 95x + 75`
 

iii.    `text(C)text(ost)\ (A)` `= 120 xx 5 = $600`
  `text(C)text(ost)\ (B)` `= 95 xx 5 + 75 = $550`

 
`:.\ text(Company)\ B’text(s hiring cost is $50 cheaper.)`

Financial Maths, STD2 F4 2018 HSC 26h

A car is purchased for $23 900.

The value of the car is depreciated by 11.5% each year using the declining-balance method.

What is the value of the car after three years?  (2 marks)

Show Answers Only

`$16\ 566\ \ (text(nearest dollar))`

Show Worked Solution
`S` `= V_0(1-r)^n`
  `= 23\ 900(1-0.115)^3`
  `= 23\ 900(0.885)^3`
  `= 16\ 566.383…`
  `= $16\ 566\ \ (text(nearest dollar))`

Algebra, STD2 A1 2018 HSC 26b

Clark’s formula, given below, is used to determine the dosage of medicine for children.
 

`text(Dosage) = (text(weight in kg × adult dosage))/70`

 
For a particular medicine, the adult dosage is 325 mg and the correct dosage for a specific child is 90 mg.

How much does the child weigh, to the nearest kg?  (2 marks)

Show Answers Only

`19\ text(kg)`

Show Worked Solution

`90 = (text(weight) xx 325)/70`

`:.\ text(weight)` `= (70 xx 90)/325`
  `= 19.38…`
  `= 19\ text(kg  (nearest kg))`

Functions, 2ADV F1 2018 HSC 3 MC

What is the `x`-intercept of the line  `x + 3y + 6 = 0`?

  1. `(-6, 0)`
  2. `(6, 0)`
  3. `(0, -2)`
  4. `(0, 2)`
Show Answers Only

`A`

Show Worked Solution

`x text(-intercept occurs when)\ y = 0:`

`x + 0 + 6` `= 0`
`x` `= -6`

 
`:. x text{-intercept is}\  (-6, 0)`

`=>  A`

Probability, STD2 S2 2018 HSC 9 MC

An experiment has three distinct outcomes, A, B and C.

Outcome A occurs 50% of the time. Outcome B occurs 23% of the time.

What is the expected number of times outcome C would occur if the experiment is conducted 500 times?

  1. 115
  2. 135
  3. 250
  4. 365
Show Answers Only

`text(B)`

Show Worked Solution

`text(Expectation of outcome)\ C`

`= 1 – 0.5 – 0.23`

`= 0.27`
 

`:.\ text(Expected times)\ C\ text(occurs)`

`= 0.27 xx 500`

`= 135`

`=>\ text(B)`

Algebra, STD2 A2 2018 HSC 5 MC

The driving distance from Alex's home to his work is 20 km. He drives to and from work five times each week. His car uses fuel at the rate of 8 L/100 km.

How much fuel does he use driving to and from work each week?

  1.  16 L
  2.  20 L
  3.  25 L
  4.  40 L
Show Answers Only

`text(A)`

Show Worked Solution

`text(Total distance travelled each week)`

`= 5 xx 2 xx 20`

`= 200\ text(km)`
 

`:.\ text(Total fuel used)`

`= 200/100 xx 8\ text(L)`

`= 16\ text(L)`

`=>\ text(A)`

Statistics, STD2 S1 2018 HSC 1 MC

A set of scores has the following five-number summary.

lower extreme = 2
lower quartile = 5
median = 6
upper quartile = 8
upper extreme = 9

What is the range?

  1. 2
  2. 3
  3. 6
  4. 7
Show Answers Only

`text(D)`

Show Worked Solution
`text(Range)` `=\ text(upper extreme − lower extreme)`
  `= 9 – 2`
  `= 7`

`=>\ text(D)`

Plane Geometry, EXT1 2018 HSC 14c

In triangle `ABC, BC` is perpendicular to `AC`. Side `BC` has length `a`, side `AC` has length `b` and side `AB` has length `c`. A quadrant of a circle of radius `x`, centered at `C`, is constructed. The arc meets side `BC` at `E`. It touches the side `AB` at `D`, and meets side `AC` at `F`. The interval `CD` is perpendicular to `AB`.
 


 

  1. Show that `Delta ABC` and `Delta ACD` are similar.  (1 mark)
  2. Show that
     
    `qquad x = (ab)/c`.  (1 mark)
     

  3. From `F`, a line perpendicular to `AC` is drawn to meet `AB` at `G`, forming the right-angled triangle `GFA`. A new quadrant is constructed in triangle `GFA` touching side `AB` at `H`. The process is then repeated indefinitely.
     

                
     

  4. Show that the limiting sum of the areas of all the quadrants is
     
    `qquad (pi ab^2)/(4(2c - a)).`  (4 marks)
     

  5. Hence, or otherwise, show that
     
    `qquad pi/2 < (2c - a)/b`.  (1 mark)

 

 

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
  4. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution

(i)   `text(In)\ triangle ABC,`

`/_BCA = 90^@\ \ \ (BC _|_ AC)`
 

`/_ BCA = /_ ADC\ \ text{(right-angles)}`

`/_ BAC = /_ DAC\ \ text{(common)}`
 

`:. Delta ABC\ text(|||)\ Delta ACD\ \ text{(equiangular)}`

 

(ii) `(CD)/(BC)` `= (AC)/(AB)` `text{(corresponding sides of}`
   `text{similar triangles)}`
  `x/a` `= b/c`  
  `:. x` `= (ab)/c`  


(iii)  `text(Area of)\ Q_1 = 1/4 pi x^2`

♦♦♦ Mean mark part (iii) 19%.

`text(Area of)\ Q_2 => text(find)\ x_1`

 

`text(Consider)\ Delta ACD and Delta AFH`

`/_ADC = /_AHF\ \ text{(right angles)}`

`/_ CAD = /_FAH\ \ text{(common)}`

`:. Delta ACD\ text(|||)\ Delta AFH\ \ text{(equiangular)}`

 

`(FH)/(CD)` `= (AF)/(AC)` `text{(corresponding sides}`
`text{of similar triangles)}`
`x_1/x` `= (AC – CF)/(AC)`  
  `= (b – x)/b`  
  `= (b – (ab)/c)/b` `text{(using part (ii))}`
  `= (cb – ab)/(bc)`  
  `= (c – a)/c`  
`:. x_1` `= x((c – a)/c)`  

 

`=> x_2\ text(will be shorter again by the same ratio)`

`x_2` `= x_1 ((c – a)/c)`
  `= x((c – a)/c)^2`
  `vdots`
`x_n` `= x((c – a)/c)^n`

 

`text(Limiting sum of quadrant areas)`

`= Q_1 + Q_2 + … + Q_n`

`= 1/4 pi x^2 + 1/4 {:pi x_1:}^ 2 + … + 1/4 {:pi x_n:}^2`

`= 1/4 pi x^2 + 1/4 pi x^2 ((c – a)/c)^2 + … + 1/4 pi x^2 ((c – a)/c)^(2n)`

`= 1/4 pi x^2 underbrace{[1 + ((c – a)/c)^2 + … + ((c – a)/c)^(2n)]}_{text(GP with)\ a = 1, \ r = ((c-a)/c)^2`

`= 1/4 pi x^2 [1/(1 – ((c-a)/c)^2)]`

`= 1/4 pi ((ab)/c)^2 (c^2/(c^2 – (c – a)^2))`

`= pi/4 xx (a^2 b^2)/(c^2 – c^2 + 2ac – a^2)`

`= pi/4 xx (a^2 b^2)/(a(2c – a))`

`= (pi ab^2)/(4(2c – a))\ \ \ text(… as required)`

 

(iv)  `text(S)text{ince the limiting sum all the quadrants (from part (iii))}`

♦♦ Mean mark part (iv) 21%.

`text(is less than the area of)\ \ Delta ABC:`

`(pi ab^2)/(4(2c – a))` `< (ab)/2`
`(pi b)/(4(2c – a))` `< 1/2`
`pi/4` `< (2c – a)/(2b)`
`pi/2` `< (2c – a)/b\ \ \ text(… as required)`

Proof, EXT1 P1 2018 HSC 13a

Prove by mathematical induction that, for  `n >= 1,`

`2-6 + 18-54 + … + 2 (-3)^(n-1) = (1-(-3)^n)/2.`  (3 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

`text(If)\ \ n = 1,`

`text(LHS)` `= 2 (-3)^0 = 2`
`text(RHS)` `= (1-(-3)^1)/2 = 2`

`:.\ text(True for)\ n = 1`
 

`text(Assume true for)\ n = k`

`2-6 + 18-54 + … + 2 (-3)^(k-1) = (1-(-3)^k)`
 

`text(Prove true for)\ \ n = k + 1`

`text(i.e.)\ \ 2-6 + … + 2 (-3)^(k-1) + 2 (-3)^k = (1-(-3)^(k + 1))/2`

`text(LHS)` `= underbrace{2-6 + … + 2(-3)^(k-1)}_text(Sum of GP, r = –3) + 2 (-3)^k`
  `= (2(1-(-3)^k))/(1+3) + 2 (-3)^k`
  `= (1-(-3)^k + 4 (-3)^k)/2`
  `= (1 + 3(-3)^k)/2`
  `= (1-(-3)(-3)^k)/2`
  `= (1-(-3)^(k + 1))/2`
  `=\ text(RHS)`

 
`=>\ text(True for)\ \ n=k+1`

`:.\ text(S)text(ince true for)\ \ n=1, text(by PMI, true for integral)\ n >= 1.`

Mechanics, EXT2* M1 2018 HSC 13c

An object is projected from the origin with an initial velocity of  `V` at an angle  `theta`  to the horizontal. The equations of motion of the object are

`x(t)` `= Vt cos theta`
`y(t)` `= Vt sin theta - (g t^2)/2.`  (Do NOT prove this.)

 

  1. Show that when the object is projected at an angle  `theta`, the horizontal range is

     

         `V^2/g sin 2 theta`  (2 marks)

  2. Show that when the object is projected at an angle  `pi/2 - theta`, the horizontal range is also 

     

         `V^2/g sin 2 theta`.  (1 mark)

  3. The object is projected with initial velocity `V` to reach a horizontal distance `d`, which is less than the maximum possible horizontal range. There are two angles at which the object can be projected in order to travel that horizontal distance before landing.

     

    Let these angles be `alpha`  and  `beta`, where  `beta = pi/2 - alpha.`

     

    Let  `h_alpha`  be the maximum height reached by the object when projected at the angle `alpha` to the horizontal.

     

    Let  `h_beta`  be the maximum height reached by the object when projected at the angle `beta` to the horizontal.
     
         
     
    Show that the average of the two heights, `(h_alpha + h_beta)/2`, depends only on `V` and `g`.  (3 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution

i.    `text(Horizontal range occurs when)\ \ y = 0`

`Vt sin theta – (g t^2)/2` `= 0`
`V sin theta – (g t)/2` `= 0`
`t` `= (2V sin theta)/g`

 
`text(Find)\ \ x\ \ text(when)\ \ t=(2V sin theta)/g :`

`x` `= Vt cos theta`
  `= V((2V sin theta)/g) cos theta`
  `= (V^2 * 2sin theta cos theta)/g`
  `= V^2/g sin 2 theta\ \ \ text(.. as required)`

 

ii.  `text(Find)\ \ x\ \ text(when)\ \ theta = (pi/2 – theta):`

`x` `= V^2/g sin 2 (pi/2 – theta)`
  `= V^2/g underbrace {sin (pi – 2 theta)}_{text(Using)\ \ sin (pi-theta) = sin theta}`
  `= V^2/g sin 2 theta\ \ \ text(.. as required)`

 

iii.  `text(Highest point → half way through the flight.)`

`=> h_alpha\ \ text(occurs when)\ \ t=(V sin alpha)/g\ \ text{(by symmetry)}`
  

`:. h_alpha` `= V((V sin alpha)/g) sin alpha – g/2 ((V sin alpha)/g)^2`
  `= (V^2 sin^2 alpha)/g – g/2 ((V^2 sin^2 alpha)/g^2)`
  `= (V^2 sin^2 alpha)/g – (V^2 sin^2 alpha)/(2g)`
  `= (V^2 sin^2 alpha)/(2g)`

 

`text(Similarly,)\ \ h_beta = (V^2 sin^2 beta)/(2g)`

♦ Mean mark 44%.
 

`:. (h_alpha + h_beta)/2` `= 1/2 ((V^2 sin^2 alpha)/(2g) + (V^2 sin^2 beta)/(2g))`
  `= V^2/(4g) (sin^2 alpha + underbrace{sin^2 beta}_{text(Using)\ \ beta= pi/2 -alpha})`
  `= V^2/(4g) (sin^2 alpha + sin^2(pi/2 – alpha)) `
  `= V^2/(4g) (sin^2 alpha + cos^2 alpha)`
  `= V^2/(4g)`

 
`:. text(The average height depends only on)\ V\ text(or)\ g.`

Calculus, EXT1 C2 2018 HSC 12c

Let  `f(x) = sin^(-1) x + cos^(-1) x`.

  1. Show that  `f^{′}(x) = 0`  (1 mark)

  2. Hence, or otherwise, prove
     
    `qquad sin^(-1) x + cos^(-1) x = pi/2`.  (1 mark)

  3. Hence, sketch
     
    `qquad f(x) = sin^(-1) x + cos^(-1) x`.  (1 mark)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(See Worked Solutions)`
Show Worked Solution

i.    `f^{′}(x) = 1/sqrt(1-x^2) + (-1/sqrt (1-x^2)) = 0`

 

ii.  `text(S)text(ince)\ \ f^{′}(x) = 0\ \ => f(x)\ \ text(is a constant.)`

♦ Mean mark (ii) 37%.

`text(Substituting)\ \ x=1\ \ text{into the equation  (any value works)}`

  `sin^(-1) 1 + cos^(-1) 1` `= pi/2 + 0`
    `= pi/2\ \ text(… as required)`

 

iii.  `text(Domain restrictions require:)\ \ -1<x<1`

♦ Mean mark (iii) 40%.

 

Calculus, EXT1 C1 2018 HSC 12b

A ferris wheel has a radius of 20 metres and is rotating at a rate of 1.5 radians per minute. The top of a carriage is `h` metres above the horizontal diameter of the ferris wheel. The angle of elevation of the top of the carriage from the centre of the ferris wheel is `theta`.
 


 

  1. Show that  `(dh)/(d theta) = 20 cos theta`.  (1 mark)

  2. At what speed is the top of the carriage rising when it is 15 metres higher than the horizontal diameter of the ferris wheel? Give your answer correct to one decimal place.  (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solution)}`
  2. `19.8\ text{metres per minute  (1 d.p)}`
Show Worked Solution

i.   `text(From the diagram,)`

`sin theta` `= h/20`
`h` `= 20 sin theta`
`:. (dh)/(d theta)` `= 20 cos theta`

 

ii.   `text(Find)\ \ (dh)/(dt)\ text(when)\ h = 15:`

`(dh)/(dt)` `= (dh)/(d theta) xx (d theta)/(dt)`
  `= (20 cos theta) xx 1.5`
  `= 30 cos theta`

 
`text(Find)\ cos theta\ \ text(when)\ h = 15`

`text(Using Pythagoras,)`

`cos theta` `=sqrt(20^2 – 15^2)/20`  
  `=sqrt7/4`  

 

`:. (dh)/(dt)` `= 30 cos theta`
  `= (15 sqrt 7)/2`
  `~~ 19.8\ text{metres per minute  (1 d.p)}`

Calculus, EXT1 C2 2018 HSC 11f

Evaluate  `int_-3^0 x/sqrt(1 - x) dx`, using the substitution  `u = 1 - x`.  (3 marks)

Show Answers Only

`- 8/3`

Show Worked Solution
`u` `= 1 – x\ \ => x=1-u`
`(du)/dx` `= -1`
`dx` `= -du`

 
`text(When)\ \ x=0, \ u=1`

`text(When)\ \ x=-3, \ u=4`
 
`int_-3^0 x/sqrt (1- x)\ dx`

  `= -int_4^1 (1 – u)/sqrt(u)\ du`
  `= – int_4^1 u^(- 1/2) – u^(1/2)\ du`
  `= – [2 u^(1/2) – 2/3 u^(3/2)]_4^1`
  `= -[(2-2/3) – (2 sqrt 4 – 2/3 (sqrt 4)^3)`
  `= -[4/3 – (4-16/3)]`
  `= -8/3`

Real Functions, EXT1 2018 HSC 11e

Consider the function  `f(x) = 1/(4x - 1)`.
 

  1. Find the domain of  `f(x)`.  (1 mark)
  2. For what values of  `x`  is  `f(x) < 1`?  (2 marks)
Show Answers Only
  1. `{text(all real)\ x,  x!=1/4}`
  2. `x > 1/2 or x < 1/4`
Show Worked Solution

(i)   `text(Domain is)\ {text(all real)\ x,  x!=1/4}`

 

(ii)   `1/(4x – 1)` `< 1`
  `(4x – 1)` `< (4 x – 1)^2`
  `(4x – 1)^2 – (4x – 1)` `> 0`
  `(4x – 1)[4x – 1- 1]` `> 0`
  `2 (4x – 1) (2x – 1)` `> 0`

 
`text(Sketching the parabola:)`

`x > 1/2 or x < 1/4.`

`text(From the graph,)`

`y > 1\ \ text(when)\ \ x < 1/4 or x > 1/2`

Trigonometry, EXT1 T3 2018 HSC 11c

Write  `sqrt 3 sin x + cos x`  in the form  `R sin (x + alpha)`  where  `R > 0`  and  `0 <= alpha <= pi/2.`  (2 marks)

Show Answers Only

`text(See Worked Solution)`

Show Worked Solution
`R sin (x + alpha)` `=sqrt 3 sin x + cos x`
`R sin x cos alpha + R cos x sin alpha` `=sqrt 3 sin x + cos x`

 
`text(Equating coefficients:)`

`=> R cos alpha` `= sqrt 3`  
`=> R sin alpha` `= 1`  

 

`R^2` `= (sqrt 3)^2 + 1^2=4`
`:.R` `= 2`

 

`=> 2sin alpha` `=1`
`sin alpha` `= 1/2`
`alpha` `= pi/6 qquad (0 <= alpha <= pi/2)`

 
`:. sqrt 3 sin x + cos x = 2 sin (x + pi/6).`

L&E, EXT1 2018 HSC 11b

Solve  `log_2 5 + log_2(x - 2) = 3.`  (2 marks)

Show Answers Only

`x=18/5`

Show Worked Solution
`log_2 (5) + log_2 (x – 2)` `= 3`
`log_2(5 (x – 2))` `= 3`
`5(x – 2)` `= 2^3`
`5x – 10` `= 8`
`5x` `= 18`
`x` `= 18/5`

 
`text(S)text(ince the domain requires)\ x>2,`

`x=18/5`

Functions, EXT1 F2 2018 HSC 11a

Consider the polynomial  `P(x) = x^3-2x^2-5x + 6`.

  1. Show that  `x = 1`  is a zero of  `P(x)`.  (1 mark)

  2. Find the other zeros.  (2 marks)

Show Answers Only
  1. `text(See Worked Solution)`
  2. `x = -2 and x = 3`
Show Worked Solution

i.   `P(1) = 1-2-5 + 6 = 0`

`:. x=1\ \ text(is a zero)`

 

ii.   `text{Using part (i)} \ => (x-1)\ text{is a factor of}\ P(x)`

`P(x) = (x-1)*Q(x)`
 

`text(By long division:)`

`P(x)` `= (x-1) (x^2-x-6)`
  `= (x-1) (x-3) (x + 2)`

 
`:.\ text(Other zeroes are:)`

`x = -2 and x = 3`

Linear Functions, EXT1 2018 HSC 2 MC

The acute angle between the lines  `y = 3x`  and  `y = 5x`  is  `theta.`

What is the value of  `tan theta?`

A.     `1/8`

B.     `1/7`

C.     `1/2`

D.     `4/7`

Show Answers Only

`A`

Show Worked Solution
`tan theta` `= |(m_1 – m_2)/(1 + m_1 m_2)|`
  `= |(5 – 3)/(1 + 5 xx 3)|`
  `= 1/8`

 

`⇒  A`

Polynomials, EXT1 2018 HSC 1 MC

The polynomial  `2x^3 + 6x^2 - 7x - 10`  has zeros  `alpha, beta and gamma.`

What is the value of  `alpha beta gamma (alpha + beta + gamma)?`

A.     `−60`

B.     `−15`

C.     `15`

D.     `60`

Show Answers Only

`B`

Show Worked Solution

`a = 2, \quad b = 6, \quad c = -7, \quad d = -10`

`alpha beta gamma` `= -d/a`
  `= -((-10))/2`
  `= 5`

 

`alpha + beta + gamma` `= -b/a`
  `= -6/2`
  `= -3`

 

`:. alpha beta gamma (alpha + beta + gamma) = -15`

`⇒  B`

Networks, STD2 N3 2013 FUR2 2

A project will be undertaken in the wildlife park. This project involves the 13 activities shown in the table below. The duration, in hours, and predecessor(s) of each activity are also included in the table.


NETWORKS, FUR2 2013 VCAA 21
 

Activity `G` is missing from the network diagram for this project, which is shown below.

 
NETWORKS, FUR2 2013 VCAA 22
 

  1. Complete the network diagram above by inserting activity `G`.  (1 mark)
  2. Determine the earliest starting time of activity `H`.  (1 mark)

  3. Given that activity `G` is not on the critical path

     

    1. write down the activities that are on the critical path in the order that they are completed  (1 mark)

    2. find the latest starting time for activity `D`.  (1 mark)

  4. Consider the following statement.

     

    ‘If the time to complete just one of the activities in this project is reduced by one hour, then the minimum time to complete the entire project will be reduced by one hour.’

    Explain the circumstances under which this statement will be true for this project.  (1 mark)

  5. Assume activity `F` is reduced by two hours.
    What will be the minimum completion time for the project?  (1 mark)

Show Answers Only

a.

networks-fur2-2013-vcaa-2-answer

b.  `7\ text(hours)`

c.i.  `AFIM`

c.ii. `14\ text(hours)`

d.  `text(The statement will only be true if the crashed activity)`
      `text(is on the critical path)\ \ A F I M.`

e.  `text(36 hours)`

Show Worked Solution
a.    networks-fur2-2013-vcaa-2-answer

 

b.  `text(Scanning forwards and backwards:)`

`text(EST for Activity)\ H`

`= 4 + 3`

`= 7\ text(hours)`
 

c.i.   `A F I M`

♦♦ Mean mark of parts (c)-(e) (combined) was 40%.
 

c.ii.  `text(LST of)\ G = 20 – 4 = 16\ text(hours)`

 `text(LST of)\ D = 16 – 2 = 14\ text(hours)`
 

d.   `text(The statement will only be true if the time reduced activity)`

MARKER’S COMMENT: Most students struggled with part (d).

`text(is on the critical path)\ \ A F I M.`
 

e.   `A F I M\ text(is 37 hours.)`

`text(If)\ F\ text(is reduced by 2 hours, the new critical)`

`text(path is)\ \ C E H G I M\ text{(36 hours)}`

`:.\ text(Minimum completion time = 36 hours)`

Networks, STD2 N3 2012 FUR2 2

Thirteen activities must be completed before the produce grown on a farm can be harvested. 

The directed network below shows these activities and their completion times in days.
 


 

  1. Determine the earliest starting time, in days, for activity `E`.  (1 mark)

  2. An activity with zero duration starts at the end of activity `B`.

     

    Explain why this activity is used on the network diagram.  (1 mark)

  3. Determine the earliest starting time, in days, for activity `H`.  (1 mark)

  4. In order, list the activities on the critical path.  (1 mark)

  5. Determine the latest starting time, in days, for activity `J`.  (1 mark)

Show Answers Only
  1. `12\ text(days)`
  2. `F\ text(has)\ B\ text(as a predecessor while)\ G\ text(and)\ H`
    `text(have)\ B\ text(and)\ C\ text(as predecessors.)`
    `text(S)text(ince there cannot be 2 activities called)\ B, text(a zero)`
    `text{duration activity is drawn as an extension of}\ B\ text(to)`
    `B\ text(show that it is also a predecessor of)\ G\ text(and)\ H.`
  3. `15\ text(days)`
  4. `ABHILM`
  5. `25\ text(days)`
Show Worked Solution
a.    `text(EST of)\ E` `= 10 + 2`
    `= 12\ text(days)`
♦ Mean mark of all parts (combined) 47%.

 

b.   `F\ text(has)\ B\ text(as a predecessor while)\ G\ text(and)\ H`

`text(have)\ B\ text(and)\ C\ text(as predecessors.)`

`text(S)text(ince there cannot be 2 activities called)\ B, text(a zero)`

`text{duration activity is drawn as an extension of}\ B\ text(to)`

`text(show that it is also a predecessor of)\ G\ text(and)\ H.`
 

♦♦ “Few students” were able to correctly deal with the zero duration activity in part (c).

c.  `text(Scanning forwards:)`
 

  
`text(EST for)\ H = 15\ text(days)`
 

d.   `text(The critical path is)\ \ ABHILM`
 


 

e.   `text(The shortest time to complete all the activities)`

MARKER’S COMMENT: A correct calculation based on an incorrect critical path in part (d) gained a consequential mark here. Show your working!.

`= 10 + 5 + 4 + 3  + 4 + 2`

`= 28\ text(days)`
 

`:.\ text(LST of)\ J` `= 28 − 3`
  `= 25\ text(days)`

Networks, STD2 N3 2006 FUR1 5 MC

For a particular project there are ten activities that must be completed.

These activities and their immediate predecessors are given in the following table.
 

networks-fur1-2006-vcaa-5-mc

 
A directed graph that could represent this project is

 

A.
B.
C.
D.
Show Answers Only

`D`

Show Worked Solution

`text(Consider the information in the table:)`

`text(D and E are prerequisites to F → eliminate B)`

`text(G is a prerequisite to I → eliminate A and C)`

`=>\ text(Option D reflects the information in the table:)`
 

`rArr D`

Networks, STD2 N2 SM-Bank 13

An estate has large open parklands that contain seven large trees.

The trees are denoted as vertices A to G on the network diagram below.

Walking paths link the trees as shown.

The numbers on the edges represent the lengths of the paths in metres.
 

NETWORKS, FUR2 2007 VCAA 2

 
Jamie is standing at A and Michelle is standing at D.

Write down the shortest route that Jamie can take and the distance travelled to meet Michelle at D.  (1 mark) 

Show Answers Only

`text(Shortest path is)\ AFCD`

`text(Shortest distance is 500 metres.)`

Show Worked Solution

`text(One strategy – using Dijkstra’s algorithm:)`
 

 
`text(Shortest path is)\ AFCD`

`text(Shortest distance)` `= 200 + 150 + 150`
  `= 500\ text(metres)`

Networks, STD2 N3 2006 FUR1 2 MC

The following directed graph represents a series of one-way streets with intersections numbered as nodes 1 to 8.
 

networks-fur1-2006-vcaa-2-mc-1

 
All intersections can be reached from

A.   intersection 4

B.   intersection 5

C.   intersection 6

D.   intersection 8 

Show Answers Only

`B`

Show Worked Solution

`text(The two edges connected to vertex 5 both flow away from the)`

`text(vertex. Therefore, vertex 5 cannot be reached in this network)`

`text(starting from any other vertex, eliminating options A, C and D.)` 

`rArr B`

Networks, STD2 N2 SM-Bank 2

A school is designing a computer network between five key areas within the school.

The cost of connecting the rooms is shown in the diagram below.
  


 

  1. Complete the spanning tree below that creates the school's network at a minimum cost.  (1 mark)

      

         
     
     

  2. What is the minimum cost of the network?  (1 mark)

Show Answers Only
  1.  
         
     
  2. `$1500`
Show Worked Solution

a.   `text(One Strategy: Using Prim’s Algorithm)`

`text(Starting vertex – Staff Room)`

`text(1st edge: Staff Room – Library)`

`text(2nd edge: Library – School Office)`

`text(3rd edge: Staff Room – IT Staff)`

`text(4th edge: Library – Computer Room)`
  

 

b.    `text(Minimum Cost)` `= 300 + 300 + 400 + 500`
    `= $1500`

Networks, STD2 N2 SM-Bank 1 MC

This diagram shows the possible paths (in km) for laying gas pipes between various locations.
 

 
Gas is to be supplied from one location. Any one of the locations can be the source of the supply.

What is the minimum total length of the pipes required to provide gas to all the locations?

A. 32 km
B. 34 km
C. 36 km
D. 38 km
Show Answers Only

`B`

Show Worked Solution

`text(Using Kruskal’s Algorithm:)`
 

 
`text(1st edge: Parkview – Summerville)\ (5)`

`text(2nd edge: Summerville – Newville)\ (8)`

`text(3rd edge: Beachview – Summerville)\ (10)`

`text(4th edge: Old Town – Newville)\ (11)`

 
`:.\ text(Minimum length of pipes.)`

`= 5 + 8 + 10 + 11`

`= 34`
 

`=> B`

Networks, STD2 N2 SM-Bank 14

Water will be pumped from a dam to eight locations on a farm.

The pump and the eight locations (including the house) are shown as vertices in the network diagram below.

The numbers on the edges joining the vertices give the shortest distances, in metres, between locations.
 

NETWORKS, FUR2 2012 VCAA 1

 

  1. How many vertices on the network diagram have an odd degree?  (1 mark)

     

    The total length of all edges in the network is 1180 metres.

     

    The total length of pipe that supplies water from the pump to the eight locations on the farm is a minimum.

     

    This minimum length of pipe is laid along some of the edges in the network.

  2. On the diagram below, draw the minimum length of pipe that is needed to supply water to all locations on the farm.  (2 marks)
     
     
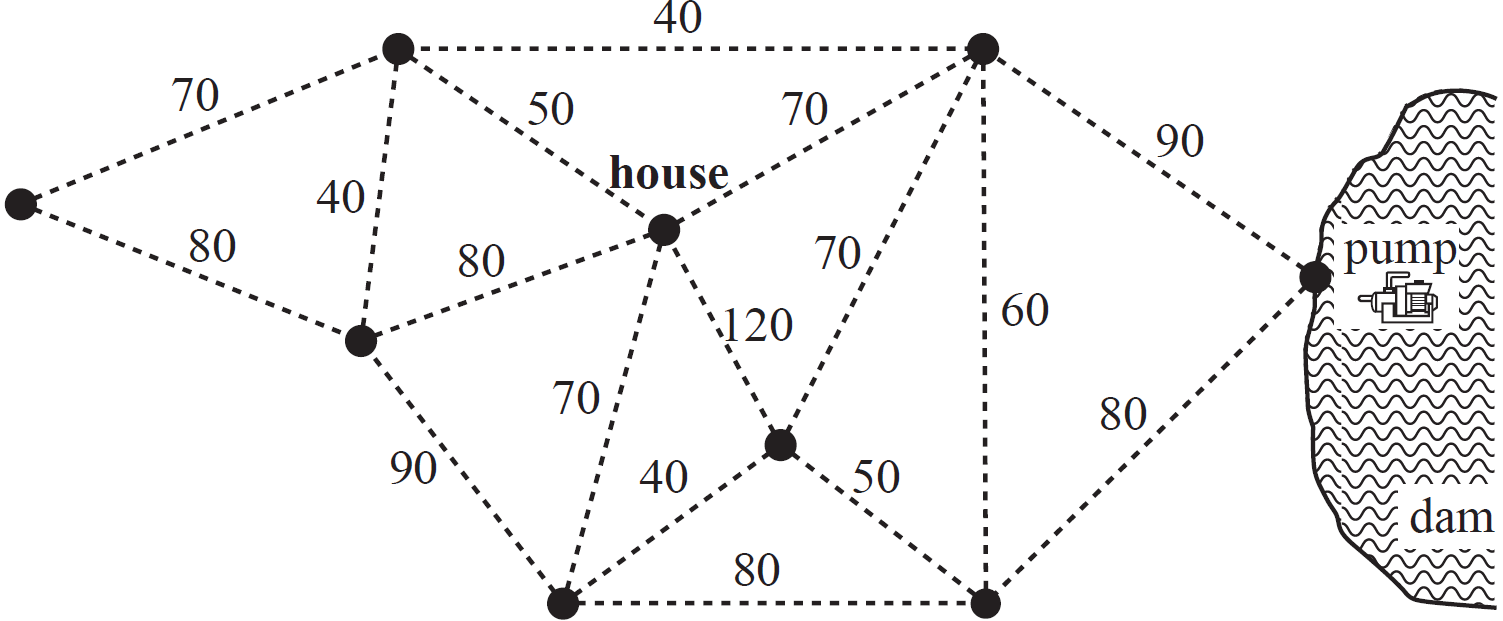
    NETWORKS, FUR2 2012 VCAA 1

  3. What is the mathematical term that is used to describe this minimum length of pipe?  (1 mark)

Show Answers Only
  1. `2`
  2. `1250\ text(m)`
     
    NETWORKS, FUR2 2012 VCAA 1 Answer

  3. `text(Minimum spanning tree)`
Show Worked Solution

a.   `2\ text{(the house and the top right vertex)}`

MARKER’S COMMENT: Many students, surprisingly, had problems with part (i).
 

b.   `text(One Strategy – Using Prim’s algorithm:)`

`text(Starting at the house)`

`text(1st edge: 50)`

`text{2nd edge: 40 (either)}`

`text(3rd edge: 40)`

`text(4th edge: 60  etc…)`
 

NETWORKS, FUR2 2012 VCAA 1 Answer


c.    `text(Minimum spanning tree)`

Networks, FUR2 2015 VCE 2

The factory supplies groceries to stores in five towns, `Q`, `R`, `S`, `T` and `U`, represented by vertices on the graph below.

 

Networks, FUR2 2015 VCAA 2

The edges of the graph represent roads that connect the towns and the factory.

The numbers on the edges indicate the distance, in kilometres, along the roads.

Vehicles may only travel along the road between towns `S` and `Q` in the direction of the arrow due to temporary roadworks.

Each day, a van must deliver groceries from the factory to the five towns.

The first delivery must be to town `T`, after which the van will continue on to the other four towns before returning to the factory.

Describe the order in which these deliveries would follow to achieve the shortest possible circuit and the length, in kilometres, of the circuit.  (2 marks)

Show Answers Only

`text(Route: factory)\ −T − S −Q − R − S −U − text(factory)`

`text(Shortest circuit)\ = 162\ text(km)`

Show Worked Solution

`text(Route: factory)\ −T − S −Q − R − S −U − text(factory)`

`text(Distance)`

`= 44 + 38 + 12 + 8 + 38 + 22`

`= 162\ text(km)`

Networks, STD2 N2 2011 FUR2 1

Aden, Bredon, Carrie, Dunlop, Enwin and Farnham are six towns.

The network shows the road connections and distances between these towns in kilometres.
 

  1. In kilometres, what is the shortest distance between Farnham and Carrie?  (1 mark)

  2. How many different ways are there to travel from Farnham to Carrie without passing through any town more than once?  (1 mark)

An engineer plans to inspect all of the roads in this network.

He will start at Dunlop and inspect each road only once.

  1. At which town will the inspection finish?  (1 mark)

Show Answers Only
  1. `200\ text(km)`
  2. `6`
  3. `text(Bredon)`
Show Worked Solution

a.   `text{Farnham to Carrie (shortest)}`

`= 60 + 140`

`= 200\ text(km)`

 

b.   `text(Different paths are)`

`FDC, FEDC, FEBC, FEABC, FDEBC, FDEABC`

`:. 6\ text(different ways)`

 

c.   `text(A possible path is)\ DFEABCDEB\ text(and will finish)`

`text{at Bredon – the only other odd-degree vertex.}`

`text{(Note that solving this can be done quickly by applying the}`

`text{concept underlying the Konigsberg Bridge problem.)}`

Networks, STD2 N2 2010 FUR2 2

The diagram below shows a network of tracks (represented by edges) between checkpoints (represented by vertices) in a short-distance running course. The numbers on the edges indicate the time, in minutes, a team would take to run along each track.

 

Network, FUR2 2011 VCAA 2_1
 

A challenge requires teams to run from checkpoint `X` to checkpoint `Y` using these tracks.

What would be the shortest possible time for a team to run from checkpoint `X` to checkpoint `Y`? Mark the shortest route on the diagram below. (2 marks)

 
  Network, FUR2 2011 VCAA 2_2

 
Show Answers Only

`11\ text(minutes)`

Show Worked Solution

`text(Using Djikstra’s Algorithm:)`
 


 

`text(Shortest distance)\ \ X\ \ text(to)\ \ Y`

`=4 + 3 + 4`

`= 11\ text(minutes)`

Networks, STD2 N3 2009 FUR2 2

One of the landmarks in a city is a hedge maze. The maze contains eight statues. The statues are labelled `F` to `M` on the following directed graph. Walkers within the maze are only allowed to move in the directions of the arrows.
 

NETWORKS, FUR2 2009 VCAA 2
 

  1. Write down the two statues that a walker could not reach from statue `M`.  (1 mark)

  2. One way that statue `H` can be reached from statue `K` is along path `KFH`.

     

    List the three other ways that statue `H` can be reached from statue `K`.  (1 mark)

Show Answers Only
  1. `F and K`
  2. `KJH, KMJH, KFJH`
Show Worked Solution

a.   `F and K`

b.   `KJH, KMJH, KFJH`

Networks, STD2 N2 2017 FUR2 1

Bus routes connect six towns.

The towns are Northend (`N`), Opera (`O`), Palmer (`P`), Quigley (`Q`), Rosebush (`R`) and Seatown (`S`).

The graph below gives the cost, in dollars, of bus travel along these routes.

Bai lives in Northend (`N`) and he will travel by bus to take a holiday in Seatown (`S`).
 


 

  1. Bai considers travelling by bus along the route Northend (`N`) – Opera (`O`) – Seatown (`S`).
    How much would Bai have to pay?  (1 mark)

  2. If Bai takes the cheapest route from Northend (`N`) to Seatown (`S`), which other town(s) will he pass through?  (1 mark)

Show Answers Only
  1. `$120`
  2. `text(Quigley and Rosebush.)`
Show Worked Solution
a.    `text(C)text(ost)` `= 15 + 105`
    `= $120`

 

b.   `text(Using Djikstra’s algorithm:)`

`text(Fastest route is:)\ \ NQRS.` 

`:.\ text(Other towns are Quigley and Rosebush.)`

Networks, STD2 N2 2013 FUR2 1

The vertices in the network diagram below show the entrance to a wildlife park and six picnic areas in the park: `P1`, `P2`, `P3`, `P4`, `P5` and `P6`.

The numbers on the edges represent the lengths, in metres, of the roads joining these locations.

 


 

  1. In this graph, what is the degree of the vertex at the entrance to the wildlife park?  (1 mark)

  2. What is the shortest distance, in metres, from the entrance to picnic area `P3`?  (1 mark)

Show Answers Only
  1. `3`
  2. `1000\ text(m)`
Show Worked Solution

a.   `3`

b.  `text(Using Djikstra’s algorithm:)`
 


 

`text( Shortest distance)`

`= E – P1 – P3`

`= 600 + 400`

`= 1000\ text(m)`

Networks, FUR2 2012 VCE 1

Water will be pumped from a dam to eight locations on a farm.

The pump and the eight locations (including the house) are shown as vertices in the network diagram below.

The numbers on the edges joining the vertices give the shortest distances, in metres, between locations.
 

NETWORKS, FUR2 2012 VCAA 1
 

a.i.  Determine the shortest distance between the house and the pump.  (1 mark)

a.ii. How many vertices on the network diagram have an odd degree?  (1 mark)

The total length of pipe that supplies water from the pump to the eight locations on the farm is a minimum.

This minimum length of pipe is laid along some of the edges in the network.

b.i.  On the diagram below, draw the minimum length of pipe that is needed to supply water to all locations on the farm.  (1 mark)

 

   
  NETWORKS, FUR2 2012 VCAA 1
 

b.ii. What is the mathematical term that is used to describe this minimum length of pipe in part b.i.?  (1 mark)

Show Answers Only

a.i.  `160\ text(m)`

a.ii. `2`

b.i.  `1250\ text(m)`

NETWORKS, FUR2 2012 VCAA 1 Answer

b.ii. `text(Minimal spanning tree)`

Show Worked Solution

a.i.   `text(Shortest distance)`

`=70 + 90`

`= 160\ text(m)`

MARKER’S COMMENT: Many students, surprisingly, had problems with part (a)(ii).

 

a.ii.   `2\ text{(the house and the top right vertex)}`

 

b.i.    NETWORKS, FUR2 2012 VCAA 1 Answer

 

b.ii.   `text(Minimal spanning tree)`

Networks, STD2 N2 2015 FUR2 1

A factory requires seven computer servers to communicate with each other through a connected network of cables.

The servers, `J`, `K`, `L`, `M`, `N`, `O` and `P`, are shown as vertices on the graph below.
 

Networks, FUR2 2015 VCAA 11

 
The edges on the graph represent the cables that could connect adjacent computer servers.

The numbers on the edges show the cost, in dollars, of installing each cable.

  1. What is the cost, in dollars, of installing the cable between server `L` and server `M`?  (1 mark)

  2. What is the cheapest cost, in dollars, of installing cables between server `K` and server `N`?  (1 mark)

  3. The computer servers will be able to communicate with all the other servers as long as each server is connected by cable to at least one other server.

    1. The cheapest installation that will join the seven computer servers by cable in a connected network follows a minimum spanning tree.

       

      Draw the minimum spanning tree on the plan below.  (1 mark) 
       

      Networks, FUR2 2015 VCAA 12
       

    2. The factory’s manager has decided that only six connected computer servers will be needed, rather than seven.

       

      How much would be saved in installation costs if the factory removed computer server `P` from its minimum spanning tree network?

       

      A copy of the graph above is provided below to assist with your working.  (1 mark)

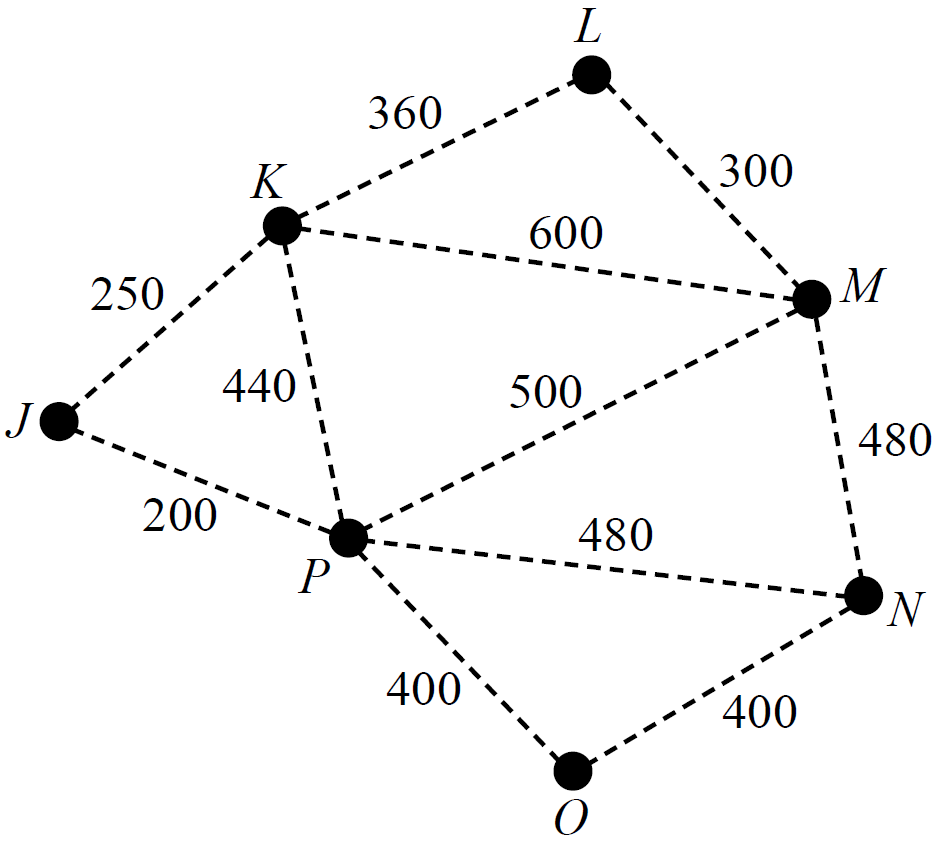
      Networks, FUR2 2015 VCAA 12

Show Answers Only
  1. `$300`
  2. `$920`
  3. `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`
    1.  
      Networks, FUR2 2015 VCAA 12 Answer
    2. `$120`
Show Worked Solution

a.   `$300`

 

b.   `text(Minimum cost of)\ K\ text(to)\ N`

`= 440 + 480`

`= $920`
 

MARKER’S COMMENT: Many students had difficulty finding the minimum spanning tree, often incorrectly excluding `PO` or `KL`.

c.i.  `text(Using Prim’s Algorithm:)`

`text(Starting at Vertex)\ L`

`text{1st Edge: L → M (300)}`

`text{2nd Edge: L → K (360)}`

`text{3rd Edge: K → J (250)}`

`text{4th Edge: J → P (200)  etc…}`
 

Networks, FUR2 2015 VCAA 12 Answer


c.ii.   `text(Disconnect)\ J – P\ text(and)\ O – P`

`text(Savings) = 200 + 400 = $600`

`text(Add in)\ M – N`

`text(C)text(ost) = $480`

`:.\ text(Net savings)` `= 600 – 480`
  `= $120`

Networks, STD2 N2 2011 FUR2 2

At the Farnham showgrounds, eleven locations require access to water. These locations are represented by vertices on the network diagram shown below. The dashed lines on the network diagram represent possible water pipe connections between adjacent locations. The numbers on the dashed lines show the minimum length of pipe required to connect these locations in metres.
 

NETWORKS, FUR2 2011 VCAA 2 

 
All locations are to be connected using the smallest total length of water pipe possible.

  1. On the diagram, show where these water pipes will be placed.  (1 mark)
  2. Calculate the total length, in metres, of water pipe that is required.  ( 1 mark) 
Show Answers Only
  1.  
    NETWORKS, FUR2 2011 VCAA 2 Answer
  2. `510\ text(metres)`
Show Worked Solution

a. `text(Using Prim’s Algorithm)`

`text(Starting at bottom right vertex)`

`text{1st Edge: 50}`

`text{2nd Edge: 40`

`text(3rd Edge: 50)`

`text(4th Edge: 40   etc…)`
 

NETWORKS, FUR2 2011 VCAA 2 Answer


b.   `text(Total length of water pipe)`

`= 50+40+50+40+50+60+40+60+60+60`

`= 510\ text(metres)`

Networks, STD2 N2 2008 FUR2 1

James, Dante, Tahlia and Chanel are four children playing a game.

In this children’s game, seven posts are placed in the ground.

The network below shows distances, in metres, between the seven posts.

The aim of the game is to connect the posts with ribbon using the shortest length of ribbon.

This will be a minimal spanning tree.

 

NETWORKS, FUR2 2008 VCAA 11

  1. Draw in a minimal spanning tree for this network on the diagram below.  (1 mark)


NETWORKS, FUR2 2008 VCAA 12

  1. Determine the length, in metres, of this minimal spanning tree.  (1 mark)

  2. How many different minimal spanning trees can be drawn for this network?  (1 mark)

Show Answers Only
  1.  

    `text(or)`
  2. `16\ text(metres)`
  3. `2`
Show Worked Solution

a.  `text(Using Kruskal’s Algorithm)`

`text{Edges 1-3: 2}`

`text{Edges 4-5: 3  (2 edges with weight 3 create a circuit and are ignored)`

`text(Edge 6: 4)` 
 

`text(or)`

 

b.   `text(Length of minimal spanning tree)`

`= 2+2+2+3+3+4`

`= 16\ text(metres)`
 

c.   `2`

Networks, STD2 N2 2014 FUR1 5 MC

 
Which one of the following is the minimal spanning tree for the weighted graph shown above?

vcaa-networks-fur1-2014-5ii

Show Answers Only

`A`

Show Worked Solution

`text(Using Prim’s algorithm:)`

`text(Starting at vertex)\ A,`

`text(1st edge:)\ A → J\ (6)`

`text(2nd edge:)\ A → B\ (8)`

`text(3rd edge:)\ B → C\ (9)`

`text(4th edge:)\ J → I\ (10)`

`text(3rd edge:)\ B → D\ (10)\ \ text(etc…)`

 
`=>  A`

Networks, STD2 N2 2013 FUR1 3 MC

 
The vertices of the graph above represent nine computers in a building. The computers are to be connected with optical fibre cables, which are represented by edges. The numbers on the edges show the costs, in hundreds of dollars, of linking these computers with optical fibre cables.

Based on the same set of vertices and edges, which one of the following graphs shows the cable layout (in bold) that would link all the computers with optical fibre cables for the minimum cost?
 

 

vcaa-networks-fur1-2013-3ii

Show Answers Only

`A`

Show Worked Solution

`text(Using Prim’s algorithm)`

`text(Starting at far left vertex,)`

`text{1st edge: 2}`

`text(2nd edge: 3)`

`text{3rd edge: 4}`

`text(4th edge: 3   etc…)`

`=>  A`