SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

CORE*, FUR2 2012 VCAA 1

A club purchased new equipment priced at $8360. A 15% deposit was paid.

  1. Calculate the deposit.   (1 mark)

    1. Determine the amount of money that the club still owes on the equipment after the deposit is paid.   (1 mark)
    2. The amount owing will be fully repaid in 12 installments of $650.
    3. Determine the total interest paid.   (1 mark)

Show Answers Only

  1. `$1254`
  2. i.  `$7106`
  3. ii. `$684`

Show Worked Solution

a.    `text(Deposit)` `= 15text(%) xx 8360`
    `= $1254`

 

b.i.    `text(Amount still owed)` `= 8360-1254`
    `= $7106`

 

b.ii.    `text(Total repayments)` `= 12 xx 650`
    `= $7800`

 
`:.\ text(Total interest paid)`

`= 7800-7106`

`= $694`

NETWORKS, FUR1 2006 VCAA 2 MC

The following directed graph represents a series of one-way streets with intersections numbered as nodes 1 to 8.
 

networks-fur1-2006-vcaa-2-mc-1
 

All intersections can be reached from

A.   intersection 4

B.   intersection 5

C.   intersection 6

D.   intersection 7

E.   intersection 8 

Show Answers Only

`B`

Show Worked Solution

`rArr B`

NETWORKS, FUR1 2007 VCAA 2 MC

A connected planar graph has 12 edges.

This graph could have

  1. 5 vertices and 6 faces.
  2. 5 vertices and 8 faces.
  3. 6 vertices and 8 faces.
  4. 6 vertices and 9 faces.
  5. 7 vertices and 9 faces.
Show Answers Only

`C`

Show Worked Solution

`text(Consider option C,)`

`v + f` `= e + 2`
`6 + 8` `= 12 + 2`
`14` `= 14`

 

 
`text(i.e. Euler’s formula holds.)`

`=>  C`

NETWORKS, FUR1 2011 VCAA 6 MC

A store manager is directly in charge of five department managers.

Each department manager is directly in charge of six sales people in their department.

This staffing structure could be represented graphically by

A.   a tree.

B.   a circuit.

C.   an Euler path.

D.   a Hamiltonian path.

E.   a complete graph.

Show Answers Only

`A`

Show Worked Solution

`=>  A`

NETWORKS, FUR1 2011 VCAA 5 MC

A network is represented by the following graph.
 

Which of the following graphs could not be used to represent the same network?

vcaa-networks-fur1-2011-5ii

vcaa-networks-fur1-2011-5iii

Show Answers Only

`E`

Show Worked Solution

`E\ text(has 2 vertices with degree 2, whereas all the)`

`text(vertices of the given network are degree 3.)`

`=>  E`

MATRICES*, FUR1 2013 VCAA 9 MC

Alana, Ben, Ebony, Daniel and Caleb are friends. Each friend has a different age.

The arrows in the graph below show the relative ages of some, but not all, of the friends. For example, the arrow in the graph from Alana to Caleb shows that Alana is older than Caleb.
  

 
Using the information in the graph, it can be deduced that the second-oldest person in this group of friends is

A.   Alana

B.   Ben

C.   Caleb

D.   Daniel

E.   Ebony

Show Answers Only

`B`

Show Worked Solution

`text(Completing the graph,)`

vcaa-networks-fur1-2013-9i

`:.\ text(Oldest to youngest is:)`

`text(Alana, Ben, Daniel, Caleb, Ebony.)`

`=>  B`

NETWORKS, FUR1 2013 VCAA 4 MC

Kate, Lexie, Mei and Nasim enter a competition as a team. In this competition, the team must complete four tasks, `W, X, Y\ text(and)\ Z`, as quickly as possible.

The table shows the time, in minutes, that each person would take to complete each of the four tasks.
 

     
 

If each team member is allocated one task only, the minimum time in which this team would complete the four tasks is

A.   `10\ text(minutes)`

B.   `12\ text(minutes)`

C.   `13\ text(minutes)`

D.   `14\ text(minutes)`

E.   `15\ text(minutes)`

Show Answers Only

`D`

Show Worked Solution

`text(The tasks should be allocated according to the table below:)`

vcaa-networks-fur1-2013-4i

 
`:.\ text(Minimum time)`

`= 5 + 3 + 4 + 2`

`= 14\ text(minutes)`

`=>  D`

NETWORKS, FUR1 2013 VCAA 3 MC


 

The vertices of the graph above represent nine computers in a building. The computers are to be connected with optical fibre cables, which are represented by edges. The numbers on the edges show the costs, in hundreds of dollars, of linking these computers with optical fibre cables.

Based on the same set of vertices and edges, which one of the following graphs shows the cable layout (in bold) that would link all the computers with optical fibre cables for the minimum cost?
 

 

vcaa-networks-fur1-2013-3ii

vcaa-networks-fur1-2013-3iii

Show Answers Only

`A`

Show Worked Solution

`=>  A`

MATRICES*, FUR2 2006 VCAA 2

The five musicians, George, Harriet, Ian, Josie and Keith, compete in a music trivia game.

Each musician competes once against every other musician.

In each game there is a winner and a loser.

The results are represented in the dominance matrix, Matrix 1, and also in the incomplete directed graph below.

On the directed graph an arrow from Harriet to George shows that Harriet won against George.
 

NETWORKS, FUR2 2006 VCAA 2

  1. Explain why the figures in bold in Matrix 1 are all zero.   (1 mark)

One of the edges on the directed graph is missing.

  1. Using the information in Matrix 1, draw in the missing edge on the directed graph above and clearly show its direction.   (1 mark)

The results of each trivia contest (one-step dominances) are summarised as follows.

networks-fur2-2006-vcaa-2_2 

In order to rank the musicians from first to last in the trivia contest, two-step (two-edge) dominances will be considered.

The following incomplete matrix, Matrix 2, shows two-step dominances.
 

`{:(qquadqquadqquadtext(Matrix 2)),(qquadqquad{:GquadHquadI\ quadJquad\ K:}),({:(G),(H),(I),(J),(K):}[(0,1,1,2,0),(1,0,1,1,1),(1,0,0,0,0),(0,0,1,0,1),(2,0,1,x,0)]):}`
 

  1. Explain the two-step dominance that George has over Ian.   (1 mark)

  2. Determine the value of the entry `x` in Matrix 2.   (1 mark)

  3. Taking into consideration both the one-step and two-step dominances, determine which musician was ranked first and which was ranked last in the trivia contest.   (2 marks)

Show Answers Only
  1. `text(A musicians does not compete against him/herself.)`
  2.  
    networks-fur2-2006-vcaa-2-anwer
  3. `text(Two step dominance occurs because George is dominant)`

     

    `text(over Keith who is in turn dominant over Ian.)`

  4. `2`
  5. `text{First is Keith (8), last is Ian (2)}`
Show Worked Solution

a.   `text(A musicians does not compete against him/herself.)`

 

b.   `text(Josie won against George.)`

 

networks-fur2-2006-vcaa-2-anwer

 

c.   `text(Two step dominance occurs because George is dominant)`

`text(over Keith who is in turn dominant over Ian.)`

 

d.   `text(Following the edges on network diagram:)`

`text(Keith over Harriet who beats Josie.)`

`text(Keith over Ian who beats Ian.)`

`:. x = 2`

 

e.    `D_1 + D_2 =` `[(0,1,2,2,1),(2,0,2,2,1),(1,0,0,1,0),(1,0,1,0,1),(2,1,2,3,0)]{:(G – 6),(H – 7),(I – 2),(J – 3),(K – 8):}`

 

`text{Summing the rows (above),}`

`:.\ text{First is Keith (8), last is Ian (2).}`

NETWORKS, FUR2 2006 VCAA 1

George, Harriet, Ian, Josie and Keith are a group of five musicians. 

They are forming a band where each musician will fill one position only. 

The following bipartite graph illustrates the positions that each is able to fill.

 

NETWORKS, FUR2 2006 VCAA 1
 

  1. Which musician must play the guitar?   (1 mark)

  2. Complete the table showing the positions that the following musicians must fill in the band.   (2 marks)

     

       
      NETWORKS, FUR2 2006 VCAA 11

Show Answers Only
  1. `text(George)`
  2.  
    networks-fur2-2006-vcaa-1-answer
Show Worked Solution

a.    `text(Harriet must play the drums, which means that)`

`text(George will play the guitar.)`

 

b.    networks-fur2-2006-vcaa-1-answer

NETWORKS, FUR2 2007 VCAA 2

The estate has large open parklands that contain seven large trees.

The trees are denoted as vertices `A` to `G` on the network diagram below.

Walking paths link the trees as shown.

The numbers on the edges represent the lengths of the paths in metres.
 

NETWORKS, FUR2 2007 VCAA 2

  1. Determine the sum of the degrees of the vertices of this network.   (1 mark)

  2. One day Jamie decides to go for a walk that will take him along each of the paths between the trees.

    He wishes to walk the minimum possible distance.


    i.     State a vertex at which Jamie could begin his walk?   (1 mark)

  3. ii. Determine the total distance, in metres, that Jamie will walk.   (1 mark)

Michelle is currently at `F`.

She wishes to follow a route that can be described as the shortest Hamiltonian circuit.

  1. Write down a route that Michelle can take.   (1 mark) 
Show Answers Only
  1. `24`
    1. `C\ text(or)\ G`
    2. `2800\ text(m)`

  3. `F-G-A-B-C-D-E-F,\ text(or)`
    `F-E-D-C-B-A-G-F`

Show Worked Solution

a.   `text(Sum of degrees of vertices)`

♦ Mean mark of all parts (combined) 44%.

`= 4 + 2 + 5 + 2 + 4 + 4 + 3`

`= 24`
  

b.i.   `C\ text(or)\ G`

`text(An Euler path is required and)`

`text(therefore the starting point is at)`

`text(a vertex with an odd degree.)`
  

b.ii.   `2800\ text(m)`

MARKER’S COMMENT: Many students incorrectly found the shortest Hamiltonian path.

c.    `F-G-A-B-C-D-E-F,\ text(or)`

`F-E-D-C-B-A-G-F`

NETWORKS, FUR2 2007 VCAA 1

A new housing estate is being developed.

There are five houses under construction in one location.

These houses are numbered as points 1 to 5 below.
 

NETWORKS, FUR2 2007 VCAA 1

  
The builders require the five houses to be connected by electrical cables to enable the workers to have a supply of power on each site.

  1. What is the minimum number of edges needed to connect the five houses?  (1 mark)

  2. On the diagram above, draw a connected graph with this number of edges.  (1 mark) 

Show Answers Only
  1. `4`
  2.  
    networks-fur2-2007-vcaa-1-answer
Show Worked Solution

a.   `text(Minimum number of edges = 4)`
 

b.   `text(One of many possibilities:)`

networks-fur2-2007-vcaa-1-answer

NETWORKS, FUR1 2014 VCAA 1 MC

The graph below shows the roads connecting four towns: Kelly, Lindon, Milton and Nate.


A bus starts at Kelly, travels through Nate and Lindon, then stops when it reaches Milton.

The mathematical term for this route is

A.  a loop.

B.  an Eulerian path.

C.  an Eulerian circuit.

D.  a Hamiltonian path.

E.  a Hamiltonian circuit.

Show Answers Only

`D`

Show Worked Solution

`text(A Hamiltonian path touches every vertex)`

`text(exactly once.)`

`=>D` 

NETWORKS, FUR1 2015 VCAA 7 MC

Four people, Abe, Bailey, Chris and Donna, are each to be allocated one of four tasks. Each person can complete each of the four tasks in a set time. These times, in minutes, are shown in the table below.
 

NETWORKS, FUR1 2015 VCAA 7 MC

 
If each person is allocated a different task, the minimum total time for these four people to complete these four tasks is

A.   260 minutes

B.   355 minutes

C.   360 minutes

D.   365 minutes

E.   375 minutes

Show Answers Only

`B`

Show Worked Solution

`text(Minimum total time)`

♦ Mean mark 43%.

`=80 +  90 + 125 + 60`

`= 355\ text(minutes)`

`=> B`

NETWORKS, FUR2 2013 VCAA 2

A project will be undertaken in the wildlife park. This project involves the 13 activities shown in the table below. The duration, in hours, and predecessor(s) of each activity are also included in the table.
 
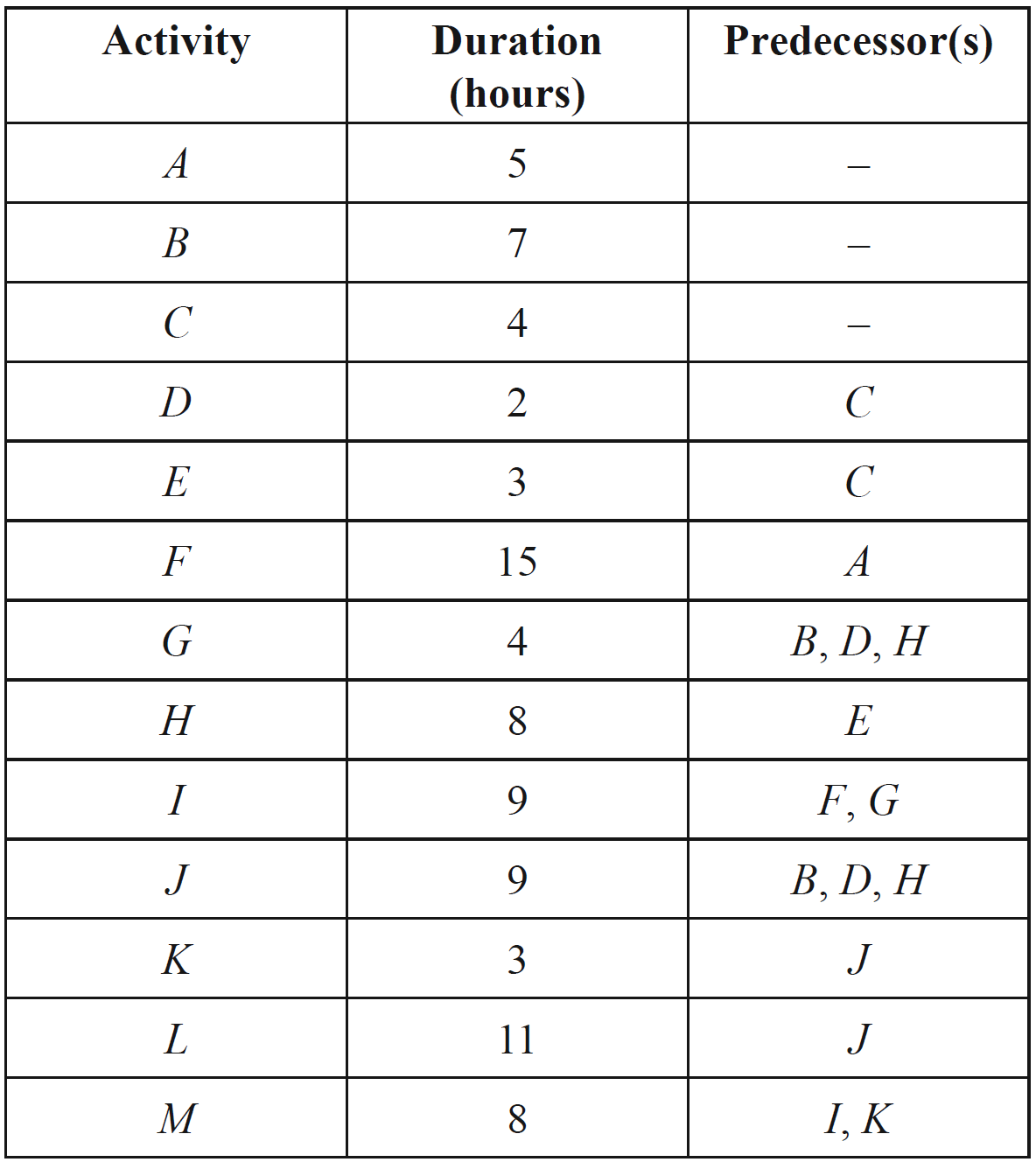
NETWORKS, FUR2 2013 VCAA 21
 

Activity `G` is missing from the network diagram for this project, which is shown below.

 
NETWORKS, FUR2 2013 VCAA 22
 

  1. Complete the network diagram above by inserting activity `G`.   (1 mark)

  2. Determine the earliest starting time of activity `H`.   (1 mark)

  3. Given that activity `G` is not on the critical path:
    i.     Write down the activities that are on the critical path in the order that they are completed.   (1 mark)

  4. ii. Find the latest starting time for activity `D`.   (1 mark)

  5. Consider the following statement.
     
    ‘If just one of the activities in this project is crashed by one hour, then the minimum time to complete the entire project will be reduced by one hour.’

    Explain the circumstances under which this statement will be true for this project.   (1 mark)

  6. Assume activity `F` is crashed by two hours.

    What will be the minimum completion time for the project?   (1 mark) 

Show Answers Only
  1.  
    networks-fur2-2013-vcaa-2-answer
  2. `7\ text(hours)`
  3. i. `A-F-I-M`
    ii. `14\ text(hours)`
  4. `text(The statement will only be true if the crashed activity)`
    `text(is on the critical path)\ \ A-F-I-M.`
  5. `text(36 hours)`
Show Worked Solution
a.    networks-fur2-2013-vcaa-2-answer

 

b.    `text(EST of)\ H` `= 4 + 3`
    `= 7\ text(hours)`

 

c.i.   `A-F-I-M`

♦♦ Mean mark of parts (c)-(e) (combined) was 40%.

 

c.ii.  networks-fur2-2013-vcaa-23-answer

`G\ text(precedes)\ I`

`:. text(LST of)\ G = 20-4 = 16\ text(hours)`

`:. text(LST of)\ D = 16-2 = 14\ text(hours)`

  
d.   `text(The statement will only be true if the crashed activity)`

MARKER’S COMMENT: Most students struggled with part (d).

`text(is on the critical path)\ \ A-F-I-M.`
  

e.   `A-F-I-M\ text(is 37 hours.)`

`text(If)\ F\ text(is crashed by 2 hours, the new)`

`text(new critical path is)`

`C-E-H-G-I-M\ text{(36 hours)}`

`:.\ text(Minimum completion time = 36 hours)`

NETWORKS, FUR2 2008 VCAA 1

James, Dante, Tahlia and Chanel are four children playing a game.

In this children’s game, seven posts are placed in the ground.

The network below shows distances, in metres, between the seven posts.

The aim of the game is to connect the posts with ribbon using the shortest length of ribbon.

This will be a minimal spanning tree.

 

NETWORKS, FUR2 2008 VCAA 11
 

  1. Draw in a minimal spanning tree for this network on the diagram below.   (1 mark)


NETWORKS, FUR2 2008 VCAA 12

  1. Determine the length, in metres, of this minimal spanning tree.   (1 mark)

  2. How many different minimal spanning trees can be drawn for this network?   (1 mark)

Show Answers Only
  1.  
    networks-fur2-2008-vcaa-1-answer1
    `text(or)`
    networks-fur2-2008-vcaa-1-answer2
  2. `16\ text(metres)`
  3. `2`
Show Worked Solution
a.    networks-fur2-2008-vcaa-1-answer1

`text(or)`

networks-fur2-2008-vcaa-1-answer2

 

b.   `text(Length of minimal spanning tree)`

`= 4 + 2 + 2 + 3 + 2 + 3`

`= 16\ text(metres)`
 

c.   `2`

NETWORKS, FUR2 2009 VCAA 3

The city of Robville contains eight landmarks denoted as vertices `N` to `U` on the network diagram below. The edges on this network represent the roads that link the eight landmarks.
 


  

  1. Write down the degree of vertex `U`.  (1 mark)

  2. Steven wants to visit each landmark, but drive along each road only once. He will begin his journey at landmark `N`.
    1. Michael was the best player in 2014 and he considered purchasing cricket equipment that was valued at $750.
    2. At which landmark must he finish his journey?   (1 mark)
    3. Regardless of which route Steven decides to take, how many of the landmarks (including those at the start and finish) will he see on exactly two occasions?   (1 mark)
  3. Cathy decides to visit each landmark only once.
    1. Suppose she starts at `S`, then visits `R` and finishes at `T`.
    2. Write down the order Cathy will visit the landmarks.   (1 mark)

    3. Suppose Cathy starts at `S`, then visits `R` but does not finish at `T`.
    4. List three different ways that she can visit the landmarks.   (1 mark)

Show Answers Only

  1. `4`
    1. `P\ text{(the other odd degree vertex)}`
    2. `5`
    1. `(SR)QPONU(T)`
    2. `text(Other paths are)`
      `(SR)QPUTNO`
      `(SR)QPONTU`
      `(SR)TUNOPQ`
      `(SR)UTNOPQ`
      `text{(only 3 paths required)}`

Show Worked Solution

a.   `4`

b.i.   `P\ text{(the other odd degree vertex)}`

b.ii.   `5 (N, T, R, P, U)`

c.i.   `(SR)QPONU(T)`

c.ii.   `text(Other paths are)`

`(SR)QPUTNO`

`(SR)QPONTU`

`(SR)TUNOPQ`

`(SR)UTNOPQ`

`text{(only 3 paths required)}`

NETWORKS, FUR2 2009 VCAA 2

One of the landmarks in the city is a hedge maze. The maze contains eight statues. The statues are labelled `F` to `M` on the following directed graph. Walkers within the maze are only allowed to move in the directions of the arrows.
 

NETWORKS, FUR2 2009 VCAA 2
 

  1. Write down the two statues that a walker could not reach from statue `M`.   (1 mark)

  2. One way that statue `H` can be reached from statue `K` is along path `KFH`.

     

    List the three other ways that statue `H` can be reached from statue `K`.   (1 mark)

Show Answers Only
  1. `F and K`
  2. `KJHqquadKMJHqquadKFJH`
Show Worked Solution

a.   `F and K`
  

b.   `KJHqquadKMJHqquadKFJH`

NETWORKS, FUR2 2010 VCAA 2

The diagram below shows a network of tracks (represented by edges) between checkpoints (represented by vertices) in a short-distance running course. The numbers on the edges indicate the time, in minutes, a team would take to run along each track.

 

Network, FUR2 2011 VCAA 2_1
 

Another challenge requires teams to run from checkpoint `X` to checkpoint `Y` using these tracks.

  1. What would be the shortest possible time for a team to run from checkpoint `X` to checkpoint `Y`?  (1 mark)

  2. Teams are required to follow a route from checkpoint `X` to checkpoint `Y` that passes through every checkpoint once only.

  3.  i. What mathematical term is used to describe such a route?   (1 mark)

  4. ii. On the network diagram below, draw in the route from checkpoint `X` to checkpoint `Y` that passes through every checkpoint once only.   (1 mark)

   
  Network, FUR2 2011 VCAA 2_2

Show Answers Only
  1. `11\ text(minutes)`
  2. i. `text(Hamiltonian path)`
    ii. 
    Network, FUR2 2011 VCAA 2 Answer
Show Worked Solution

a.   `4 + 3 + 4 = 11\ text(minutes)`
  

b.i.   `text(Hamiltonian path)`

 

b.ii.    Network, FUR2 2011 VCAA 2 Answer

NETWORKS, FUR2 2011 VCAA 2

At the Farnham showgrounds, eleven locations require access to water. These locations are represented by vertices on the network diagram shown below. The dashed lines on the network diagram represent possible water pipe connections between adjacent locations. The numbers on the dashed lines show the minimum length of pipe required to connect these locations in metres.
 

NETWORKS, FUR2 2011 VCAA 2 
 

All locations are to be connected using the smallest total length of water pipe possible.

  1. On the diagram, show where these water pipes will be placed.   (1 mark)

  2. Calculate the total length, in metres, of water pipe that is required.   ( 1 mark) 
Show Answers Only
  1.  
    NETWORKS, FUR2 2011 VCAA 2 Answer
  2. `510\ text(metres)`
Show Worked Solution
a.    NETWORKS, FUR2 2011 VCAA 2 Answer

 

b.   `text(Total length of water pipe)`

`= 60 + 60 + 40 + 60 + 50 + 40 + 60`

`+ 40 + 50 + 50`

`= 510\ text(metres)`

NETWORKS, FUR2 2011 VCAA 1

Aden, Bredon, Carrie, Dunlop, Enwin and Farnham are six towns.

The network shows the road connections and distances between these towns in kilometres.

 

  1. In kilometres, what is the shortest distance between Farnham and Carrie?   (1 mark)

  2. How many different ways are there to travel from Farnham to Carrie without passing through any town more than once?   (1 mark)

An engineer plans to inspect all of the roads in this network.

He will start at Dunlop and inspect each road only once.

  1. At which town will the inspection finish?   (1 mark)

Another engineer decides to start and finish her road inspection at Dunlop.

If an assistant inspects two of the roads, this engineer can inspect the remaining six roads and visit each of the other five towns only once.

  1. How many kilometres of road will the assistant need to inspect?   (1 mark)

Show Answers Only
  1. `200\ text(km)`
  2. `6`
  3. `text(Bredon)`
  4. `240\ text(km)`
Show Worked Solution

a.   `text{Farnham to Carrie (shortest)}`

`= 60 + 140`

`= 200\ text(km)`
  

b.   `text(Different paths are)`

`FDC, FEDC, FEBC,`

`FEABC, FDEBC,`

`FDEABC`

`:. 6\ text(different ways)`
  

c.   `text(A possible path is)\ DFEABCDEB\ text(and will finish)`

`text{at Bredon (the other odd-degree vertex).}`
  

d.   `text(If the engineer’s path is)`

`DFEABCD,`

`text(Distance assistant inspects)`

`= 110 + 130`

`= 240\ text(km)`

NETWORKS, FUR2 2013 VCAA 1

The vertices in the network diagram below show the entrance to a wildlife park and six picnic areas in the park: `P1`, `P2`, `P3`, `P4`, `P5` and `P6`.

The numbers on the edges represent the lengths, in metres, of the roads joining these locations.

 

 

  1. In this graph, what is the degree of the vertex at the entrance to the wildlife park?   (1 mark)

  2. What is the shortest distance, in metres, from the entrance to picnic area `P3`?   (1 mark)

  3. A park ranger starts at the entrance and drives along every road in the park once.
  4. i. At which picnic area will the park ranger finish?   (1 mark)

  5. ii. What mathematical term is used to describe the route the park ranger takes?   (1 mark)

  6. A park cleaner follows a route that starts at the entrance and passes through each picnic area once, ending at picnic area `P1`.

     

    Write down the order in which the park cleaner will visit the six picnic areas.   (1 mark)

Show Answers Only
  1. `3`
  2. `1000\ text(m)`
  3. i. `P4`
    ii. `text(Euler path)` 
  4. `E-P5-P4-P6-P3-P2-P1`
Show Worked Solution

a.   `3`
  

b.   `text( Shortest distance)`

`= E-P1-P3`

`= 600 + 400`

`= 1000\ text(m)`
  

c.i.   `text(A route could be)`

`E-P1-P2-P3-P4-P5`

`-E-P6-P1-P3-P6-P4`

`:.\ text(Finish at)\ P4\ \ text{(the other odd degree vertex)}`
  

c.ii.   `text(Euler path)`
  

d.   `E-P5-P4-P6-P3-P2-P1`

NETWORKS, FUR2 2014 VCAA 3

The diagram below shows a network of train lines between five towns: Attard, Bower, Clement, Derrin and Eden.

The numbers indicate the distances, in kilometres, that are travelled by train between connected towns.
 

Charlie followed an Eulerian path through this network of train lines.

  1. i. Write down the names of the towns at the start and at the end of Charlie’s path.   (1 mark)

    ii. What distance did he travel?   (1 mark)

Brianna will follow a Hamiltonian path from Bower to Attard.

  1. What is the shortest distance that she can travel?   (1 mark)

The train line between Derrin and Eden will be removed. If one other train line is removed from the network, Andrew would be able to follow an Eulerian circuit through the network of train lines.

  1. Which other train line should be removed?

     

    In the boxes below, write down the pair of towns that this train line connects.  (1 mark) 

     
    NETWORKS, FUR2 2014 VCAA 32

Show Answers Only
  1.  i.  `text(Bower, Eden)`
    ii.  `910\ text(km)`
  2. `270\ text(km)`
  3. `text(Bower and Derrin)`
Show Worked Solution

a.i.   `text(Bower, Eden or Eden, Bower)`
  

a.ii.   `text(Distance)\ \ BDABCDEACE`

`= 160 + 130 + 80 + 70 + 60 + 40 + 100 + 150 + 120`

`= 910\ text(km)`
  

b.   `text(Shortest Hamiltonian path is)\ BCDEA`

`text(Distance)` `= 70 + 60 + 40 + 100`
  `= 270\ text(km)`

  
c.   `text(Remove the line between Bower and Derrin.)`

NETWORKS, FUR2 2014 VCAA 2

Planning a train club open day involves four tasks.

Table 1 shows the number of hours that each club member would take to complete these tasks.
 

     NETWORKS, FUR2 2014 VCAA 21
 

The Hungarian algorithm will be used to allocate the tasks to club members so that the total time taken to complete the tasks is minimised.

The first step of the Hungarian algorithm is to subtract the smallest element in each row of Table 1 from each of the elements in that row.

The result of this step is shown in Table 2 below.

  1. Complete Table 2 by filling in the missing numbers for Andrew.   (1 mark)

     

     

    NETWORKS, FUR2 2014 VCAA 22
     

After completing Table 2, Andrew decided that an allocation of tasks to minimise the total time taken was not yet possible using the Hungarian algorithm.

  1. Explain why Andrew made this decision.   (1 mark)

Table 3 shows the final result of all steps of the Hungarian algorithm.
 

NETWORKS, FUR2 2014 VCAA 23

  1.  i. Which task should be allocated to Andrew?   (1 mark)

  2. ii. How many hours in total are used to plan for the open day?   (1 mark)

Show Answers Only
  1.  
    Networks, FUR2 2014 VCAA 2_2 answer
  2. `text(The minimum number of lines to cover all zeros)`
    `text(is less than four.)`
    1. `text(Equipment)`
    2. `36`
Show Worked Solution
a.    Networks, FUR2 2014 VCAA 2_2 answer

 

b.   `text(The minimum number of lines to cover all zeros)`

MARKER’S COMMENT: An answer of “there were not enough zeros” did not gain a mark.

`text(is less than four.)`
  

c.i.   `text(Equipment)`
  

c.ii.   `text(Total hours to plan)`

`= 8 +10 +10 + 8`

`= 36`

NETWORKS, FUR2 2015 VCAA 2

The factory supplies groceries to stores in five towns, `Q`, `R`, `S`, `T` and `U`, represented by vertices on the graph below.
 

Networks, FUR2 2015 VCAA 2
 

The edges of the graph represent roads that connect the towns and the factory.

The numbers on the edges indicate the distance, in kilometres, along the roads.

Vehicles may only travel along the road between towns `S` and `Q` in the direction of the arrow due to temporary roadworks.

Each day, a van must deliver groceries from the factory to the five towns.

The first delivery must be to town `T`, after which the van will continue on to the other four towns before returning to the factory.

  1. i. The shortest possible circuit from the factory for this delivery run, starting from town `T`, is not Hamiltonian.
     
    Complete the order in which these deliveries would follow this shortest possible circuit.   (1 mark)

     factory – `T` – ___________________________ – factory

  2. ii. With reference to the town names in your answer to part (a)(i), explain why this shortest circuit is not a Hamiltonian circuit.   (1 mark)

  3. Determine the length, in kilometres, of a delivery run that follows a Hamiltonian circuit from the factory to these stores if the first delivery is to town `T`.   (1 mark)

Show Answers Only

a.i.  `text(factory)\-T-S-Q-R-S-U-text(factory)`

aii.  `text(The van passes through town)\ S\ text(twice.)`

b.   `162\ text(km)`

Show Worked Solution

a.i.   `text(factory)\-T-S-Q-R-S-U- text(factory)`
  

a.ii.   `text(The van passes through town)\ S\ text(twice.)`
  

b.   `text(Hamiltonian circuit is)`

`text(factory)\-T-S-R-Q-U-text(factory)`

`= 44 + 38 + 12 + 8 + 38 + 22`

`= 162\ text(km)`

NETWORKS, FUR2 2015 VCAA 1

A factory requires seven computer servers to communicate with each other through a connected network of cables.

The servers, `J`, `K`, `L`, `M`, `N`, `O` and `P`, are shown as vertices on the graph below.
 

Networks, FUR2 2015 VCAA 11

 
The edges on the graph represent the cables that could connect adjacent computer servers.

The numbers on the edges show the cost, in dollars, of installing each cable.

  1. What is the cost, in dollars, of installing the cable between server `L` and server `M`?   (1 mark)

  2. What is the cheapest cost, in dollars, of installing cables between server `K` and server `N`?   (1 mark)

  3. An inspector checks the cables by walking along the length of each cable in one continuous path.
    To avoid walking along any of the cables more than once, at which vertex should the inspector start and where would the inspector finish?   (1 mark)

     

  4. The computer servers will be able to communicate with all the other servers as long as each server is connected by cable to at least one other server.
    i.     The cheapest installation that will join the seven computer servers by cable in a connected network follows a minimum spanning tree.

    Draw the minimum spanning tree on the plan below?   (1 mark)


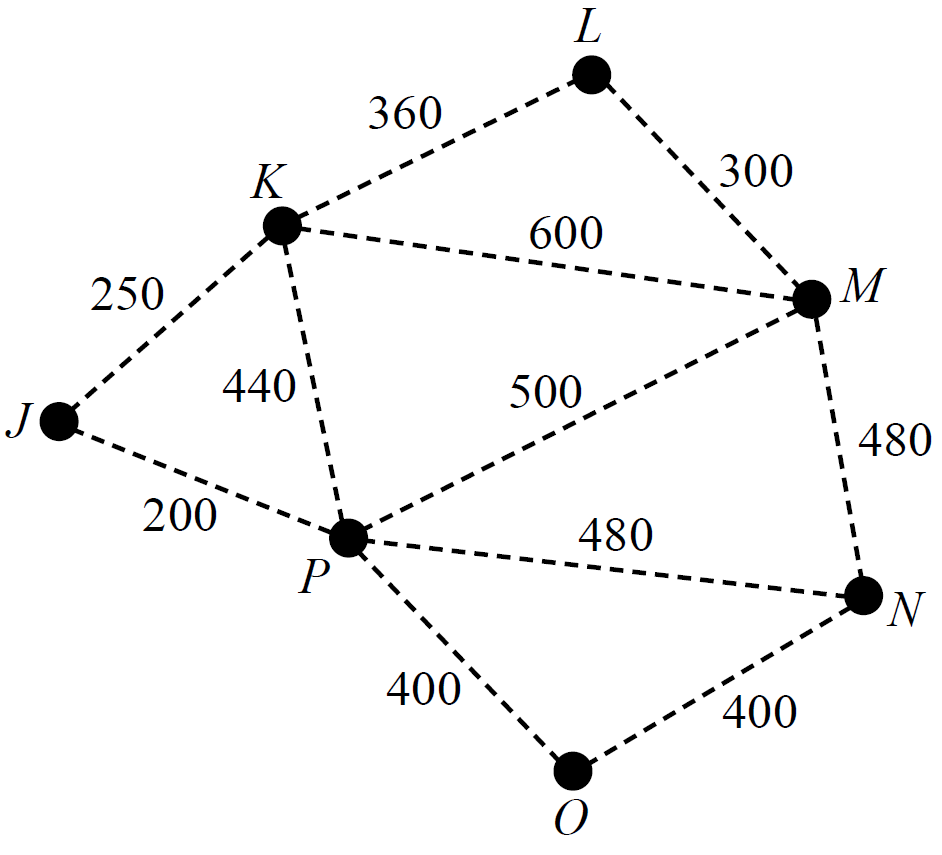
    Networks, FUR2 2015 VCAA 12
  5. ii. The factory’s manager has decided that only six connected computer servers will be needed, rather than seven. 

    How much would be saved in installation costs if the factory removed computer server `P` from its minimum spanning tree network?
    A copy of the graph above is provided below to assist with your working.   (1 mark)

    Networks, FUR2 2015 VCAA 12

Show Answers Only
  1. `$300`
  2. `$920`
  3. `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`
  4. i. 

 Networks, FUR2 2015 VCAA 12 Answer
d.ii.`$120`

Show Worked Solution

a.   `$300`
  

b.   `text(C)text(ost of)\ K\ text(to)\ N`

`= 440 + 480`

`= $920`
  

c.   `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`

MARKER’S COMMENT: Many students had difficulty finding the minimum spanning tree, often incorrectly excluding `PO` or `KL`.
d.i.    Networks, FUR2 2015 VCAA 12 Answer

 

d.ii.   `text(Disconnect)\ J – P\ text(and)\ O – P`

`text(Savings) = 200 + 400 = $600`

`text(Add in)\ M – N`

`text(C)text(ost) = $480`

`:.\ text(Net savings)` `= 600 – 480`
  `= $120`

MATRICES, FUR2 2006 VCAA 2

A new shopping centre called Shopper Heaven (`S`) is about to open. It will compete for customers with Eastown (`E`) and Noxland (`N`).

Market research suggests that each shopping centre will have a regular customer base but attract and lose customers on a weekly basis as follows.

80% of Shopper Heaven customers will return to Shopper Heaven next week
12% of Shopper Heaven customers will shop at Eastown next week
8% of Shopper Heaven customers will shop at Noxland next week

76% of Eastown customers will return to Eastown next week
9% of Eastown customers will shop at Shopper Heaven next week
15% of Eastown customers will shop at Noxland next week

85% of Noxland customers will return to Noxland next week
10% of Noxland customers will shop at Shopper Heaven next week
5% of Noxland customers will shop at Eastown next week

  1. Enter this information into transition matrix `T` as indicated below (express percentages as proportions, for example write 76% as 0.76).   (2 marks)

     

     
    `qquad{:(qquadqquadqquadtext(this week)),((qquadqquadqquad S,qquad E, quad N)),(T = [(qquadqquadqquadqquadqquadqquad),(),()]{:(S),(E),(N):}{:qquadtext(next week):}):}`
     

During the week that Shopper Heaven opened, it had 300 000 customers.

In the same week, Eastown had 120 000 customers and Noxland had 180 000 customers.

  1. Write this information in the form of a column matrix, `K_0`, as indicated below.   (1 mark)

     

     
    `qquadK_0 = [(quadqquadqquadqquadqquad),(),()]{:(S),(E),(N):}`
     

  2. Use `T` and `K_0` to write and evaluate a matrix product that determines the number of customers expected at each of the shopping centres during the following week.   (2 marks)

  3. Show by calculating at least two appropriate state matrices that, in the long term, the number of customers expected at each centre each week is given by the matrix   (2 marks)
  4. `qquadK = [(194\ 983),(150\ 513),(254\ 504)]`
Show Answers Only
  1.  
    `{:((qquadqquadqquad\ S,qquadE,qquadN)),(T = [(0.8,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)]{:(S),(E),(N):}):}`
  2.  
    `K_0 = [(300\ 000),(120\ 000),(180\ 000)]{:(S),(E),(N):}`
  3.  
    `TK_0 = [(268\ 800),(136\ 200),(195\ 000)]`
  4. `text(See Worked Solutions)`
Show Worked Solution
a.     `{:((qquadqquadqquad\ S,qquadE,qquadN)),(T = [(0.8,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)]{:(S),(E),(N):}):}`

 

b.     `K_0 = [(300\ 000),(120\ 000),(180\ 000)]{:(S),(E),(N):}`

 

c.   `text(Customers expected at each centre the next week,)`

`TK_0` `= [(0.80,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)][(300\ 000),(120\ 000),(180\ 000)]`
  `= [(268\ 800),(136\ 200),(195\ 000)]`

 

d.   `text(Consider)\ \ T^nK_0\ \ text(when)\ n\ text(large),`

`text(say)\ n=50, 51`

`T^50K_0` `= [(0.8,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)]^50[(300\ 000),(120\ 000),(180\ 000)]= [(194\ 983),(150\ 513),(254\ 504)]`

 

`T^51K_0` `= [(0.8,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)]^51[(300\ 000),(120\ 000),(180\ 000)]= [(194\ 983),(150\ 513),(254\ 504)]`
  ` = T^50K_0`

MATRICES, FUR2 2006 VCAA 1

A manufacturer sells three products, `A`, `B` and `C`, through outlets at two shopping centres, Eastown (`E`) and Noxland (`N`). 

The number of units of each product sold per month through each shop is given by the matrix `Q`, where

`{:((qquadqquadqquad\ A,qquadquadB,qquad\ C)),(Q=[(2500,3400,1890),(1765,4588,2456)]{:(E),(N):}):}`

  1. Write down the order of matrix `Q`.   (1 mark)

The matrix `P`, shown below, gives the selling price, in dollars, of products `A`, `B`, `C`.

`P = [(14.50),(21.60),(19.20)]{:(A),(B),(C):}`

  1.   i. Evaluate the matrix `M`, where `M = QP`.   (1 mark)

  2.  ii. What information does the elements of matrix `M` provide?   (1 mark)

  3. Explain why the matrix `PQ` is not defined.   (1 mark)

Show Answers Only
  1. `2 xx 3`
    1. `M = QP = [(135\ 320.5),(171\ 848.5)]`
    2. `text(The total of selling products)\ A, B,and C`
      `text(at each of Eastown and Noxland.)`
  3. `PQ\ text(is not defined because the number of)`
    `text(columns in)\ P !=\ text(the number of rows in)\ Q.`
Show Worked Solution

a.   `2 xx 3`
 

b.i.    `M` `= QP`
    `= [(2500,3400,1890),(1765,4588,2456)][(14.50),(21.60),(19.20)]`
    `= [(135\ 320.5),(171\ 848.5)]`

 
b.ii.  `text(The total revenue from selling products)\ A, B,`

   `text(and)\ C\ text(at each of Eastown and Noxland.)`
 

c.   `PQ\ text(is not defined because the number of)`

`text(columns in)\ P !=\ text(the number of rows in)\ Q.`

MATRICES, FUR2 2007 VCAA 2

To study the life-and-death cycle of an insect population, a number of insect eggs (`E`), juvenile insects (`J`) and adult insects (`A`) are placed in a closed environment.

The initial state of this population can be described by the column matrix

`S_0 = [(400),(200),(100),(0)]{:(E),(J),(A),(D):}`

A row has been included in the state matrix to allow for insects and eggs that die (`D`).

  1. What is the total number of insects in the population (including eggs) at the beginning of the study?   (1 mark)

In this population

    • eggs may die, or they may live and grow into juveniles
    • juveniles may die, or they may live and grow into adults
    • adults will live a period of time but they will eventually die.

In this population, the adult insects have been sterilised so that no new eggs are produced. In these circumstances, the life-and-death cycle of the insects can be modelled by the transition matrix
 

`{:(qquadqquadqquadqquadquadtext(this week)),((qquadqquadqquadE,quad\ J,quadA,\ D)),(T = [(0.4,0,0,0),(0.5,0.4,0,0),(0,0.5,0.8,0),(0.1,0.1,0.2,1)]{:(E),(J),(A),(D):}):}`
 

  1. What proportion of eggs turn into juveniles each week?   (1 mark)

    1. Evaluate the matrix product  `S_1 = TS_0`   (1 mark)

    2. Write down the number of live juveniles in the population after one week.   (1 mark)

    3. Determine the number of live juveniles in the population after four weeks. Write your answer correct to the nearest whole number.   (1 mark)

    4. After a number of weeks there will be no live eggs (less than one) left in the population.
    5. When does this first occur?   (1 mark)

    6. Write down the exact steady-state matrix for this population.  (1 mark)

  3. If the study is repeated with unsterilised adult insects, eggs will be laid and potentially grow into adults.
  4. Assuming 30% of adults lay eggs each week, the population matrix after one week, `S_1`, is now given by
  5. `qquad S_1 = TS_0 + BS_0`
  6. where   `B = [(0,0,0.3,0),(0,0,0,0),(0,0,0,0),(0,0,0,0)]`   and   `S_0 = [(400),(200),(100),(0)]{:(E),(J),(A),(D):}`
     

    1. Determine `S_1`  (1 mark)

    2. This pattern continues. The population matrix after `n` weeks, `S_n`, is given by
    3. `qquad qquad qquad S_n = TS_(n - 1) + BS_(n - 1)`
    4. Determine the number of live eggs in this insect population after two weeks.  (1 mark)

Show Answers Only
  1. `700`
  2. `50text(%)`
  3.  
    1. `[(160),(280),(180),(80)]{:(E),(J),(A),(D):}`
    2. `280`
    3. `56`
    4. `text(7th week)`
    5. `[(0),(0),(0),(700)]`
    1. `[(190),(280),(180),(80)]`
    2. `130`
Show Worked Solution

a.   `400 + 200 + 100 + 0 = 700`
 

b.   `50text(%)`
 

c.i.    `S_1` ` = TS_0`
    `= [(0.4,0,0,0),(0.5,0.4,0,0),(0,0.5,0.8,0),(0.1,0.1,0.2,1)][(400),(200),(100),(0)]`
    `= [(160),(280),(180),(80)]{:(E),(J),(A),(D):}`

 
c.ii.   `280`
 

c.iii.    `S_4` ` = T^4S_0`
    `= [(10.24),(56.32),(312.96),(320.48)]{:(E),(J),(A),(D):}\ \ \ text{(by graphics calculator)}`

 
`:. 56\ text(juveniles still alive after 4 weeks.)`
 

c.iv.  `text(Each week, only 40% of eggs remain.)`

`text(Find)\ \ n\ \ text(such that)`

`400 xx 0.4^n` `< 1`
`0.4^n` `<1/400`
`n` `> 6.5`

 
`:.\ text(After 7 weeks, no live eggs remain.)`

 

c.v.   `text(Consider)\ \ n\ \ text{large (say}\ \ n = 100 text{)},`

`[(0.4, 0, 0, 0), (0.5, 0.4, 0, 0), (0, 0.5, 0.8, 0), (0.1, 0.1, 0.2, 1)]^100 [(400), (200), (100), (0)] ~~ [(0), (0), (0), (700)]`

 

d.i.   `S_1` `= TS_0 + BS_0`
    `= [(160),(280),(180),(80)] + [(0,0,0.3,0),(0,0,0,0),(0,0,0,0),(0,0,0,0)][(400),(200),(100),(0)]= [(190),(280),(180),(80)]`

 

♦♦ Mean mark for part (d) was 30%.
d.ii.   `S_2` `= TS_1 + BS_1= [(130), (207), (284), (163)]`

 
`:.\ text(There are 130 live egss after 2 weeks.)`

MATRICES, FUR2 2007 VCAA 1

The table below displays the energy content and amounts of fat, carbohydrate and protein contained in a serve of four foods: bread, margarine, peanut butter and honey.
 

MATRICES, FUR2 2007 VCAA 1
 

  1. Write down a 2 x 3 matrix that displays the fat, carbohydrate and protein content (in columns) of bread and margarine.   (1 mark)

  2. `A` and `B` are two matrices defined as follows.
     
         `A = [(2,2,1,1)]`     `B = [(531),(41),(534),(212)]`

    1. Evaluate the matrix product  `AB`.   (1 mark)

    2. Determine the order of matrix product  `BA`.   (1 mark)

Matrix `A` displays the number of servings of the four foods: bread, margarine, peanut butter and honey, needed to make a peanut butter and honey sandwich.

Matrix `B` displays the energy content per serving of the four foods: bread, margarine, peanut butter and honey.

    1. Explain the information that the matrix product `AB` provides.   (1 mark)

  1. The number of serves of bread (`b`), margarine (`m`), peanut butter (`p`) and honey (`h`) that contain, in total, 53 grams of fat, 101.5 grams of carbohydrate, 28.5 grams of protein and 3568 kilojoules of energy can be determined by solving the matrix equation
      
         `[(1.2,6.7,10.7,0),(20.1,0.4,3.5,12.5),(4.2,0.6,4.6,0.1),(531,41,534,212)][(b),(m),(p),(h)] = [(53),(101.5),(28.5),(3568)]`
      
    Solve the matrix equation to find the values `b`, `m`, `p` and `h`.   (2 marks)

Show Answers Only
  1.  
    `[(1.2,20.1,4.2),(6.7,0.4,0.6)]`
    1. `[1890]`
    2. `underset (4 xx 1) B xx underset (1 xx 4) A = underset (4 xx 4) (BA)`
    3. `BA\ text(provides the total energy)`
      `text(content of the servings of these)`
      `text(four foods in one sandwich.)`
  3. `b = 4, m = 4, p = 2, h = 1`
Show Worked Solution
a.    `[(1.2,20.1,4.2),(6.7,0.4,0.6)]`

 

b.i.    `AB` `= [(2, 2, 1, 1)] [(531), (41), (534), (212)]`
    `= [1890]`

 

b.ii.   `underset (4 xx 1) B xx underset (1 xx 4) A = underset (4 xx 4) (BA)`

 

b.iii.   `BA\ text(provides the total energy content of the)`
 

`text(servings of these four foods in one sandwich.)`

 

c.    `[(b),(m),(p),(h)]` `= [(1.2,6.7,10.7,0),(20.1,0.4,3.5,12.5),(4.2,0.6,4.6,0.1),(531,41,534,212)]^(-1)[(53),(101.5),(28.5),(3568)]`
    `= [(4),(4),(2),(1)]\ \ \ text{(by graphics calculator)}`

 
`:. b = 4, m = 4, p = 2\ text(and)\ h = 1.`

NETWORKS, FUR2 2010 VCAA 1

The members of one team are Kristy (`K`), Lyn (`L`), Mike (`M`) and Neil (`N`). 

In one of the challenges, these four team members are only allowed to communicate directly with each other as indicated by the edges of the following network.
 

Network, FUR2 2011 VCAA 1
 

The adjacency matrix below also shows the allowed lines of communication.

`{:(quadKquadLquadMquadN),([(0,1,0,0),(1,0,1,0),(0,f,0,1),(0,g,1,0)]{:(K),(L),(M),(N):}):}`

 

  1. Explain the meaning of a zero in the adjacency matrix.   (1 mark)

  2. Write down the values of `f` and `g` in the adjacency matrix.   (1 mark)

Show Answers Only
  1. `text(No direct communication is allowed.)`
  2. `f = 1, g = 0`
Show Worked Solution

a.   `text(No direct communication is allowed.)`
  

b.   `f = 1, g = 0`

MATRICES, FUR2 2009 VCAA 3

In 2009, the school entered a Rock Eisteddfod competition.

When rehearsals commenced in February, all students were asked whether they thought the school would make the state finals. The students’ responses, ‘yes’, ‘no’ or ‘undecided’ are shown in the initial state matrix `S_0`.
 

`S_0 = [(160),(120),(220)]{:(text(yes)),(text(no)),(text(undecided)):}`
 

  1. How many students attend this school?   (1 mark)

Each week some students are expected to change their responses. The changes in their responses from one week to the next are modelled by the transition matrix `T` shown below.
 

`{:(qquadqquadqquadtext( response this week)),(qquadqquadquadtext( yes       no     undecided)),(T = [(0.85quad,0.35quad,0.60),(0.10quad,0.40quad,0.30),(0.05quad,0.25quad,0.10)]{:(text(yes)),(text(no)),(text(undecided)):}qquad{:(text(response)),(text(next week)):}):}`
 

The following diagram can also be used to display the information represented in the transition matrix `T`.

MATRICES, FUR2 2009 VCAA 3

    1. Complete the diagram above by writing the missing percentage in the shaded box.   (1 mark)

    2. Of the students who respond ‘yes’ one week, what percentage are expected to respond ‘undecided’ the next week when asked whether they think the school will make the state finals?   (1 mark)

    3. In total, how many students are not expected to have changed their response at the end of the first week?   (2 marks)

  2. Evaluate the product  `S_1 = TS_0`, where `S_1` is the state matrix at the end of the first week.   (1 mark)

  3. How many students are expected to respond ‘yes’ at the end of the third week when asked whether they think the school will make the state finals?   (1 mark)

Show Answers Only
  1. `500`
    1. `text(25%)`
    2. `text(5%)`
    3. `206`
  3. `S_1 = [(310),(130),(60)]`
  4. `361`
Show Worked Solution

a.   `text(Total students attending)`

`= 160 + 120 + 220`

`= 500`
 

b.i.   `text(25%)`
 

b.ii.   `text(5%)`
 

b.iii.   `text(Students not expected to change)`

`= 0.85 xx 160 + 0.4 xx 120 + 0.1 xx 220`

`= 206`
 

c.    `S_1` `=TS_0`
    `= [(0.85,0.35,0.60),(0.10,0.40,0.30),(0.05,0.25,0.10)][(160),(120),(220)]= [(310),(130),(60)]`

 

d.    `S_3` `= T^3 S_0` 
    `= [(0.85,0.35,0.60),(0.10,0.40,0.30),(0.05,0.25,0.10)]^3[(160),(120),(220)]= [(361),(91.1),(47.9)]` 

 
`:. 361\ text(students expected to respond “yes” at end of week 3.)`

MATRICES, FUR2 2009 VCAA 2

Tickets for the function are sold at the school office, the function hall and online.

Different prices are charged for students, teachers and parents.

Table 1 shows the number of tickets sold at each place and the total value of sales.

MATRICES, FUR2 2009 VCAA 21

For this function

    • student tickets cost  `$x`
    • teacher tickets cost  `$y`
    • parent tickets cost  `$z`.
  1. Use the information in Table 1 to complete the following matrix equation by inserting the missing values in the shaded boxes.   (1 mark)

     
         MATRICES, FUR2 2009 VCAA 22
     

  2. Use the matrix equation to find the cost of a teacher ticket to the school function.   (2 marks)

Show Answers Only
  1. `text(35 and 2)`
  2. `$32`
Show Worked Solution

a.   `text(35 and 2)`
 

MARKER’S COMMENT: Simply writing the column matrix in part (b) did not earn full marks. Students must extract the required data.
b.    `[(x),(y),(z)]` `= [(283,28,5),(35,4,2),(84,3,7)]^(-1)[(8712),(1143),(2609)]`
    `= [(27),(32),(35)]`

 

`:.\ text(C)text(ost of a teacher ticket = $32)`

MATRICES, FUR2 2009 VCAA 1

Three types of cheese, Cheddar (`C`), Gouda (`G`) and Blue (`B`), will be bought for a school function.

The cost matrix `P` lists the prices of these cheeses, in dollars, at two stores, Foodway and Safeworth.
 

`P = [(6.80, 5.30, 6.20),(7.30, 4.90, 6.15)]{:(text(Foodway)),(text(Safeworth)):}`
 

  1. What is the order of matrix `P`?   (1 mark)

The number of packets of each type of cheese needed is listed in the quantity matrix `Q`.
 

`Q = [(8),(11),(3)]{:(C),(G),(B):}`
 

    1. Evaluate the matrix  `W = PQ`.   (1 mark)
    2. At which store will the total cost of the cheese be lower?   (1 mark)

Show Answers Only

  1. `2 xx 3`
    1. `W = PQ = [(131.30),(130.75)]`
    2. `text(Safeworth)`

Show Worked Solution

a.   `2 xx 3`

 

b.i.    `W` `=PQ`
    `= [(6.80,5.30,6.20),(7.30,4.90,6.15)][(8),(11),(3)]`
    `= [(131.30),(130.75)]`

 

b.ii.   `text(Safeworth)`

MATRICES, FUR2 2010 VCAA 2

The 300 players in Oscar’s league are involved in a training program. In week one, 90 players are doing heavy training (`H`), 150 players are doing moderate training (`M`) and 60 players are doing light training (`L`). The state matrix, `S_1`, shows the number of players who are undertaking each type of training in the first week
 

`S_1 = [(90),(150),(60)]{:(H),(M),(L):}`
 

The percentage of players that remain in the same training program, or change their training program from week to week, is shown in the transition diagram below.
 

MATRICES, FUR2 2010 VCAA 2
 

  1. What information does the 20% in the diagram above provide?   (1 mark)

The information in the transition diagram above can also be written as the transition matrix `T`.
 

`{:(qquadqquadqquadquad\ text(this week)),((qquadqquadqquadH,quadM,\ L)),(T = [(0.5,0.1,0.1),(0.2,0.6,0.5),(0.3,0.3,0.4)]{:(H),(M),(L):}qquad{:text(next week):}):}`
 

  1. Determine how many players will be doing heavy training in week two.   (1 mark)

  2. Determine how many fewer players will be doing moderate training in week three than in week one.   (1 mark)

  3. Show that, after seven weeks, the number of players (correct to the nearest whole number) who are involved in each type of training will not change.   (1 mark) 
Show Answers Only
  1. `text(It means that 20% of the players doing heavy training one)`

     

    `text(week will switch to moderate training the next.)`

  2. `text(66 players)`
  3. `text(6 fewer players)`
  4. `text(See Worked Solutions)`
Show Worked Solution

a.   `text(It means that 20% of the players doing heavy)`

`text(training one week will switch to moderate)`

`text(training the next.)`

 

b.    `S_2` `= TS_1`
    `= [(0.5,0.1,0.1),(0.2,0.6,0.5),(0.3,0.3,0.4)][(90),(150),(60)]`
    `= [(66),(138),(96)]`

 

`:. 66\ text(players will be in hard training)`

`text(in week 2.)`

 

c.   `text(150 in moderate training in week 1.)`

`text(In week 3,)`

`S_3` `= T^2S_1`
  `= [(0.5,0.1,0.1),(0.2,0.6,0.5),(0.3,0.3,0.4)]^2[(90),(150),(60)]`
  `= [(56.4),(144),(99.6)]`

 

`:.\ text(The reduction in players training moderately)`

`= 150-144`

`= 6`

 

d.   `text(Need to show steady numbers for consecutive)`

`text(weeks 8 and week 9,)`

`S_8 = T^7S_1 = [(50),(150),(100)]`

`S_9 = T^8S_1 = [(50),(150),(100)]`

 

`:. S_8 = S_9`

`text{(i.e. player numbers don’t change after week 7.)}`

MATRICES, FUR2 2010 VCAA 1

In a game of basketball, a successful shot for goal scores one point, two points, or three points, depending on the position from which the shot is thrown.

`G`  is a column matrix that lists the number of points scored for each type of successful shot.

`G = [(1),(2),(3)]`

In one game, Oscar was successful with

    • 4 one-point shots for goal
    • 8 two-point shots for goal
    • 2 three-point shots for goal.
  1. Write a row matrix, `N`, that shows the number of each type of successful shot for goal that Oscar had in that game.   (1 mark)

  2. Matrix `P` is found by multiplying matrix `N` with matrix `G` so that  `P = N xx G`
  3. Evaluate matrix `P`.   (1 mark)

  4. In this context, what does the information in matrix `P` provide?   (1 mark)

Show Answers Only
  1. `N = [(4, 8, 2)]`
  2. `P = [26]`
  3. `text(The total points scored by Oscar in the game.)`
Show Worked Solution

a.   `N = [(4, 8, 2)]`
 

b.    `P` `= NG`
    `= [(4, 8, 2)][(1),(2),(3)]`
    `= [26]`

 
c.   `text(The total points scored by Oscar in the game.)`

NETWORKS, FUR2 2012 VCAA 2

Thirteen activities must be completed before the produce grown on a farm can be harvested. 

The directed network below shows these activities and their completion times in days.

 

NETWORKS, FUR2 2012 VCAA 2
  

  1. Determine the earliest starting time, in days, for activity `E`.   (1 mark)

  2. A dummy activity starts at the end of activity `B`.

     

    Explain why this dummy activity is used on the network diagram.   (1 mark)

  3. Determine the earliest starting time, in days, for activity `H`.   (1 mark)

  4. In order, list the activities on the critical path.   (1 mark)

  5. Determine the latest starting time, in days, for activity `J`.   (1 mark)

Show Answers Only
  1. `12\ text(days)`
  2. `F\ text(has)\ B\ text(as a predecessor while)\ G\ text(and)\ H`
    `text(have)\ B\ text(and)\ C\ text(as predecessors.)`
    `text(S)text(ince there cannot be 2 activities called)\ B,`
    `text{a dummy activity is drawn as an extension of}`
    `B\ text(to show that it is also a predecessor of)\ G\ text(and)`
    `H\ text{(with zero time).}`
  3. `15\ text(days)`
  4. `A-B-H-I-L-M`
  5. `25\ text(days)`
Show Worked Solution
a.    `text(EST of)\ E` `= 10 + 2`
    `= 12\ text(days)`
♦ Mean mark of all parts (combined) 47%.

 

b.   `F\ text(has)\ B\ text(as a predecessor while)\ G\ text(and)\ H`

`text(have)\ B\ text(and)\ C\ text(as predecessors.)`

`text(S)text(ince there cannot be 2 activities called)\ B,`

`text{a dummy activity is drawn as an extension of}`

`B\ text(to show that it is also a predecessor of)\ G\ text(and)`

`H\ text{(with zero time).}`

 

♦♦ Exact data unavailable but “few students” were able to correctly deal with the dummy activity in this question.
c.    `text(EST of)\ H` `= 10 + 5`
    `= 15\ text(days)`

 

d.   `text(The critical path is)`

`A-B-H-I-L-M`

 

e.   `text(The shortest time to complete all the activities)`

MARKER’S COMMENT: A correct calculation based on an incorrect critical path in part (d) gained a consequential mark here. Show your working!

`= 10 + 5 + 4 + 3  + 4 + 2`

`= 28\ text(days)`

 

`:.\ text(LST of)\ J` `= 28-3`
  `= 25\ text(days)`

NETWORKS, FUR2 2012 VCAA 1

Water will be pumped from a dam to eight locations on a farm.

The pump and the eight locations (including the house) are shown as vertices in the network diagram below.

The numbers on the edges joining the vertices give the shortest distances, in metres, between locations.
 

NETWORKS, FUR2 2012 VCAA 1
 

    1. Determine the shortest distance between the house and the pump.   (1 mark)

    2. How many vertices on the network diagram have an odd degree?   (1 mark)
    3. The total length of all edges in the network is 1180 metres.
    4. A journey starts and finishes at the house and travels along every edge in the network.
    5. Determine the shortest distance travelled.   (1 mark)

The total length of pipe that supplies water from the pump to the eight locations on the farm is a minimum.

This minimum length of pipe is laid along some of the edges in the network.

    1. On the diagram below, draw the minimum length of pipe that is needed to supply water to all locations on the farm.   (1 mark)

       

     NETWORKS, FUR2 2012 VCAA 1

    1. What is the mathematical term that is used to describe this minimum length of pipe in part i.?   (1 mark)

Show Answers Only

  1. i.  `160\ text(m)`
    ii.  `2`
    iii. `1250\ text(m)`
  2. i.
    NETWORKS, FUR2 2012 VCAA 1 Answer
    ii.     `text(Minimal spanning tree)`

Show Worked Solution

a.i.   `text(Shortest distance)`

`=70 + 90`

`= 160\ text(m)`

MARKER’S COMMENT: Many students, surprisingly, had problems with part (a)(ii).

  

a.ii.   `2\ text{(the house and the top right vertex)}`
 

a.iii.   `text{An Eulerian path is possible if it starts at}`

♦♦ “Very poorly answered”.
MARKER’S COMMENT: An Euler circuit is optimal but not possible here because of the two odd degree vertices.

   `text{the house (odd vertex) and ends at the top}`

   `text{right vertex (the other odd vertex). However,}`

   `text{70 metres must be added to return to the}`

   `text{house.}`

`:.\ text(Total distance)` `= 1180 + 70`
  `= 1250\ text(m)`

 

b.i.    NETWORKS, FUR2 2012 VCAA 1 Answer

 

b.ii.   `text(Minimal spanning tree)`

MATRICES, FUR2 2011 VCAA 2

To reduce the number of insects in a wetland, the wetland is sprayed with an insecticide.

The number of insects (`I`), birds (`B`), lizards (`L`) and frogs (`F`) in the wetland that has been sprayed with insecticide are displayed in the matrix `N` below.
 

`{:((qquadqquadqquadqquadI,qquadquad B,qquadL,\ qquadF)),(N = [(100\ 000, 400,1000,800)]):}`
 

Unfortunately, the insecticide, that is used to kill the insects can also kill birds, lizards and frogs. The proportion of insects, birds, lizards and frogs that have been killed by the insecticide are displayed in the matrix `D` below.
 

`{:(qquadqquadqquadquadquadtext(alive before spraying)),((qquadqquadqquadqquadI,qquad\ B,qquad\ L,qquad\ F)),(D = [(0.995,0,0,0),(0,0.05,0,0),(0,0,0.025,0),(0,0,0,0.30)]{:(I),(B),(L),(F):}{:qquadtext(dead after spraying):}):}`
 

  1. Evaluate the matrix product  `K = ND`.   (1 mark)

  2. Use the information in matrix `K` to determine the number of birds that have been killed by the insecticide.   (1 mark)

  3. Evaluate the matrix product  `M = KF`, where `F = [(0),(1),(1),(1)]`.   (1 mark)

  4. In the context of the problem, what information does matrix `M` contain?   (1 mark)

Show Answers Only
  1. `K = [(99\ 500,20,25,240)]`
  2. `20`
  3. `M = [285]`
  4. `M\ text(contains the combined number)`
    `text(of birds, lizards and frogs that died.)`
Show Worked Solution
a.    `K` `= ND`
    `= [(99\ 500,20,25,240)]`
MARKER’S COMMENT: In part (a), separating matrix elements by commas or dots is not correct notation.

 
b.   `text(Birds dead after spraying) = 20`
 

c.    `M` `= KF`
    `= [(99\ 500,20,25,240)][(0),(1),(1),(1)]`
    `= [0 + 20 + 25 + 240]`
    `= [285]`
     
MARKER’S COMMENT: The ability of many students to interpret the result of a matrix product was poor.

d.   `text(Matrix)\ M\ text(contains the combined number)`

`text(of birds, lizards and frogs that died.)`

 

MATRICES, FUR2 2011 VCAA 1

The diagram below shows the feeding paths for insects (`I`), birds (`B`) and lizards (`L`). The matrix `E` has been constructed to represent the information in this diagram. In matrix `E`, a 1 is read as "eat" and a  0  is read as "do not eat".
 

MATRICES, FUR2 2011 VCAA 11

  1. Referring to insects, birds or lizards
  2.  i. what does the 1 in column `B`, row `L`, of matrix `E` indicate?   (1 mark)

  3. ii. what does the row of zeros in matrix `E` indicate?   (1 mark)

The diagram below shows the feeding paths for insects (`I`), birds (`B`), lizards (`L`) and frogs (`F`).

The matrix `Z` has been set up to represent the information in this diagram.

Matrix `Z` has not been completed.
 

MATRICES, FUR2 2011 VCAA 12

  1. Complete the matrix `Z` above by writing in the seven missing elements.   (1 mark)

Show Answers Only

a.i.    `text(Birds eat lizards)`

a.ii.   `text(Insects, birds or lizards do not eat birds)`

b.
      `{:((qquadqquadquadI,B,L,F)),(Z = [(0,1,1,1),(0,0,0,0),(0,1,0,0),(0,1,1,0)]{:(I),(B),(L),(F):}):}`

Show Worked Solution

a.i.   `text(The 1 represents that birds eat lizards.)`
 

a.ii.   `text(It indicates that insects, birds or lizards DO NOT)`

   `text(eat birds.)`
 

b.    `{:((qquadqquadquadI,B,L,F)),(Z = [(0,1,1,1),(0,0,0,0),(0,1,0,0),(0,1,1,0)]{:(I),(B),(L),(F):}):}`

MATRICES, FUR2 2013 VCAA 2

10 000 trout eggs, 1000 baby trout and 800 adult trout are placed in a pond to establish a trout population.

In establishing this population

    • eggs (`E`) may die (`D`) or they may live and eventually become baby trout (`B`)
    • baby trout (`B`) may die (`D`) or they may live and eventually become adult trout (`A`)
    • adult trout (`A`) may die (`D`) or they may live for a period of time but will eventually die.

From year to year, this situation can be represented by the transition matrix `T`, where
 

`{:(qquadqquadqquadqquadqquadtext(this year)),((qquadqquadqquadE,quad\ B,quad\ A,\ D)),(T = [(0,0,0,0),(0.4,0,0,0),(0,0.25,0.5,0),(0.6,0.75,0.5,1)]):}{:(),(),(E),(B),(A),(D):}{:(),(),(qquadtext(next year)):}`
 

  1. Use the information in the transition matrix `T` to
    1. determine the number of eggs in this population that die in the first year.   (1 mark)

    2. complete the transition diagram below, showing the relevant percentages.   (2 marks)

       

          Matrices, FUR2 2013 VCAA 2_a

The initial state matrix for this trout population, `S_0`, can be written as
 

`S_0 = [(10\ 000),(1000),(800),(0)]{:(E),(B),(A),(D):}`
 

Let `S_n` represent the state matrix describing the trout population after `n` years.

  1. Using the rule  `S_n = T S_(n-1)`, determine each of the following.

     

    1. `S_1`   (1 mark)

    2. the number of adult trout predicted to be in the population after four years   (1 mark)

  2. The transition matrix `T` predicts that, in the long term, all of the eggs, baby trout and adult trout will die.
    1. How many years will it take for all of the adult trout to die (that is, when the number of adult trout in the population is first predicted to be less than one)?   (1 mark)

    2. What is the largest number of adult trout that is predicted to be in the pond in any one year?   (1 mark)

  3. Determine the number of eggs, baby trout and adult trout that, if added to or removed from the pond at the end of each year, will ensure that the number of eggs, baby trout and adult trout in the population remains constant from year to year.   (2 marks)

The rule  `S_n = T S_(n – 1)`  that was used to describe the development of the trout in this pond does not take into account new eggs added to the population when the adult trout begin to breed.

  1. To take breeding into account, assume that 50% of the adult trout lay 500 eggs each year.
  2. The matrix describing the population after one year, `S_1`, is now given by the new rule
  3. `S_1 = T S_0 + 500\ M\ S_0`
  4. where      `T=[(0,0,0,0),(0.40,0,0,0),(0,0.25,0.50,0),(0.60,0.75,0.50,1.0)], M=[(0,0,0.50,0),(0,0,0,0),(0,0,0,0),(0,0,0,0)]\ text(and)\ S_0=[(10\ 000),(1000),(800),(0)]`
    1. Use this new rule to determine `S_1`.   (1 mark)

  5. This pattern continues so that the matrix describing the population after `n` years, `S_n`, is given by the rule
  6.       `S_n = T\ S_(n-1) + 500\ M\ S_(n-1)`
     

    1. Use this rule to determine the number of eggs in the population after two years   (2 marks)

Show Answers Only

a.i.   `6000`

a.ii.  `text(See Worked Solutions)`

b.i.   `S_1= [(0),(4000),(650),(7150)]`

b.ii. `S_4= [(0),(0),(331.25),(11\ 468.75)]`

c.i.   `text{13 years}`

c.ii.  `1325`

d.    `text(Add 10 000 eggs, remove 3000 baby trout and add 150)`

`text(150 adult trout to keep the population constant.)`

e.i.   `S_1= [(200\ 000),(4000),(650),(7150)]`

e.ii.   `text(See Worked Solutions)`

Show Worked Solution

a.i.   `text(60% of eggs die in 1st year,)`

`:.\ text(Eggs that die in year 1)`

`= 0.60 xx 10\ 000`

`= 6000`
 

MARKER’S COMMENT: A 100% cycle drawn at `D` was a common omission. Do not draw loops and edges of 0%!
a.ii.   

Matrices-FUR2-2013-VCAA-2_a Answer
b.i.    `S_1` `= TS_0`
    `= [(0,0,0,0),(0.4,0,0,0),(0,0.25,0.5,0),(0.6,0.75,0.5,1)][(10\ 000),(1000),(800),(0)]= [(0),(4000),(650),(7150)]`

 

b.ii.    `S_4` `= T^4S_0`
    `= [(0,0,0,0),(0.4,0,0,0),(0,0.25,0.5,0),(0.6,0.75,0.5,1)]^4[(10\ 000),(1000),(800),(0)]= [(0),(0),(331.25),(11\ 468.75)]`

 

`:. 331\ text(trout is the predicted population after 4 years.)`

 

c.i.    `S_12 = T^12S_0 = [(0),(0),(1.29),(11\ 791)]`

`S_13 = T^13S_0 = [(0),(0),(0.65),(11\ 799)]`
 

`:.\ text{It will take 13 years (when the trout population drops below 1).}`
 

c.ii.    `S_1 = TS_0 = [(0),(4000),(650),(7150)]`

`text(After 1 year, 650 adult trout.)`

`text(Similarly,)`

`S_2 = T^2S_0 = [(0),(0),(1325),(10\ 475)]`

`S_3 = T^3S_0 = [(0),(0),(662.5),(11\ 137.5)]`

`S_4 = T^4S_0 = [(0),(0),(331),(11\ 469)]`
 

`:.\ text(Largest number of adult trout = 1325.)`
 

d.    `S_0-S_1 = [(10\ 000),(1000),(800),(0)]-[(0),(4000),(650),(7150)] = [(10\ 000),(−3000),(150),(−7150)]`

 

`:.\ text(Add 10 000 eggs, remove 3000 baby trout and add 150 adult)`

`text(trout to keep the population constant.)`

 

e.i.    `S_1` `= TS_0 + 500MS_0`
    `= [(0),(4000),(650),(7150)] + 500 xx [(0,0,0.5,0),(0,0,0,0),(0,0,0,0),(0,0,0,0)][(10\ 000),(1000),(800),(0)]`
    `= [(0),(4000),(650),(7150)] + 500[(400),(0),(0),(0)]`
    `= [(200\ 000),(4000),(650),(7150)]`

 

e.ii.    `S_2` `= TS_1 + 500MS_1`
   

`= [(0,0,0,0),(0.4,0,0,0),(0,0.25,0.5,0),(0.6,0.75,0.5,1)][(200\ 000),(4000),(650),(7150)]`

       `+ 500 xx [(0,0,0.5,0),(0,0,0,0),(0,0,0,0),(0,0,0,0)][(200\ 000),(4000),(650),(7150)]`
    `= [(162\ 500),(80\ 000),(1325),(130\ 475)]`

MATRICES, FUR2 2013 VCAA 1

Five trout-breeding ponds, `P`, `Q`, `R`, `X` and `V`, are connected by pipes, as shown in the diagram below.
 

Matrices, FUR2 2013 VCAA 1 

The matrix `W` is used to represent the information in this diagram.

`{:({:\ qquadqquadqquadPquadQquad\ Rquad\ Xquad\ V:}),(W = [(0,1,1,1,0), (1,0,0,1,0),(1,0,0,1,0),(1,1,1,0,1),(0,0,0,1,0)]):}{:(),(P),(Q),(R),(X),(V):}`

In matrix `W`

•  the 1 in column 1, row 2, for example, indicates that a pipe directly connects pond `P` and pond `Q`

•  the 0 in column 1, row 5, for example, indicates that pond `P` and pond `V` are not directly connected by a pipe.

  1. Find the sum of the elements in row 3 of matrix `W`.   (1 mark)

  2. In terms of the breeding ponds described, what does the sum of the elements in row 3 of matrix `W` represent?   (1 mark)

The pipes connecting pond `P` to pond `R` and pond `P` to pond `X` are removed.

Matrix `N` will be used to show this situation. However, it has missing elements.

  1. Complete matrix `N` below by filling in the missing elements in row 1 and column 1.   (1 mark)

        
             Matrices, FUR2 2013 VCAA 1_c

Show Answers Only
  1. `2`
  2. `text(The sum means that 2 other)`
    `text(ponds connect directly to pond)\ R.`
  3.  
    `{:({:qquadqquadqquadPquadQquadRquadXquadV:}),(N = [(0,1,0,0,0),(1,0,0,1,0),(0,0,0,1,0),(0,1,1,0,1),(0,0,0,1,0)]):}{:(),(P),(Q),(R),(X),(V):}`
Show Worked Solution

a.   `1+ 0 + 0 +1+ 0 = 2`
 

b.   `text(The sum means that 2 other ponds)`

`text(connect directly to pond)\ R.`
 

c.    `{:({:qquadqquadqquadPquadQquad\ Rquad\ Xquad\ V:}),(N = [(0,1,0,0,0),(1,0,0,1,0),(0,0,0,1,0),(0,1,1,0,1),(0,0,0,1,0)]):}{:(),(P),(Q),(R),(X),(V):}`

MATRICES, FUR1 2008 VCAA 5 MC

The determinant of  `[(3, 2), (6, x)]`  is equal to 9.

The value of `x` is

A.  `– 7`

B.  `– 4.5`

C.      `1`

D.      `4.5`

E.      `7`

Show Answers Only

`E`

Show Worked Solution
`text(det) [(3, 2), (6, x)]` `= 3x – 2 xx 6`
 `:. 9` `= 3x – 12`
 `3x` `= 21`
 `x` `= 7`

`=>   E`

MATRICES, FUR1 2009 VCAA 7-8 MC

In a country town, people only have the choice of doing their food shopping at a store called Marks (`M`) or at a newly opened store called Foodies (`F`).

In the first week that Foodies opened, only 300 of the town’s 800 shoppers did their food shopping at Marks. The remainder did their food shopping at Foodies.
 

Part 1

A state matrix `S_1` that can be used to represent this situation is
 

A.   `S_1 = [[300],[800]]{:(M),(F):}`

B.   `S_1 = [[500],[300]]{:(M),(F):}`

C.   `S_1 = [[800],[300]]{:(M),(F):}`

D.   `S_1 = [[300],[500]]{:(M),(F):}`

E.   `S_1 = [[800],[500]]{:(M),(F):}`

 

Part 2

A market researcher predicts that

    • of those who do their food shopping at Marks this week, 70% will shop at Marks next week and 30% will shop at Foodies
    • of those who do their food shopping at Foodies this week, 90% will shop at Foodies next week and 10% will shop at Marks.

A transition matrix that can be used to represent this situation is
 

MATRICES, FUR1 2009 VCAA 7-8 MC ab

MATRICES, FUR1 2009 VCAA 7-8 MC cd

MATRICES, FUR1 2009 VCAA 7-8 MC e

Show Answers Only

`text(Part 1:)\ D`

`text(Part 2:)\ B`

Show Worked Solution

`text(Part 1)`

`=>  D`

 

`text(Part 2)`

`text(Columns must add up to 1.0,)`

`:.\ text(Eliminate)\ C\ text(and)\ D.`
 

`text(The information that 90% of Foodies)`

`text(shoppers stay means that)\ \ e_(FF) = 0.90.`

`:.\ text(Eliminate)\ A\ text(and)\ E.`

`=> B`

MATRICES, FUR1 2009 VCAA 6 MC

`T` is a transition matrix, where
 

`{:(qquadqquadqquadquadtext(from)),({:qquadqquadqquad\ PqquadQ:}),(T = [(0.6,0.7),(0.4,0.3)]{:(P),(Q):}{:qquadtext(to):}):}`
 

An equivalent transition diagram, with proportions expressed as percentages, is
 

MATRICES, FUR1 2009 VCAA 6 MC ab 1

MATRICES, FUR1 2009 VCAA 6 MC cd 1

MATRICES, FUR1 2009 VCAA 6 MC e

 

Show Answers Only

`C`

Show Worked Solution

`text(The loop at)\ P\ text(is 60% and)\ Q\ text(is 30%.)`

`=>  C`

MATRICES, FUR1 2009 VCAA 4 MC

The matrix equation `[[4,2,8],[2,0,3],[0,3,−1]][[x],[y],[z]]=[[7],[2],[6]]` can be used to solve the system of simultaneous linear equations

 

A.    `4x + 2y + 8z = 7`
     `2x + 3y = 2`
     `3x - y = 6`

 

B.    `4x + 2y + 8z = 7`
     `2x + 3y = 2`
     `3y - z = 6`

 

C.    `4x + 2y + 8z = 7`
     `2y + 3z = 2`
     `3x - z = 6`

 

D.    `4x + 2y + 8z = 7`
     `2x + 3z = 2`
     `3y - z = 6`

 

E.    `4x + 2y + 8z = 7`
     `2x + 3z = 2`
     `3x - z = 6`

 

Show Answers Only

`D`

Show Worked Solution

`text(Expanding the matrix equation,)`

`4x + 2y + 8z = 7`

`2x + 3z = 2`

`3y – z = 6`

`=>  D`

MATRICES, FUR1 2009 VCAA 2 MC

The matrix `[[12,15,3],[−6,0,24]]` can also be written as
 

A.   `[12,15,3] + [−6,0,24]`

B.   `[[12],[−6]] + [[15],[0] ]+ [[3],[24]]`

C.   `[[3],[6]] [[4,5,1],[−1,0,4]]`

D.   `1/3 × [[4,5,1],[−2,0,8]]`

E.   `3 × [[4,5,1],[−2,0,8]]`

 

Show Answers Only

`E`

Show Worked Solution

`=>  E`

MATRICES, FUR1 2012 VCAA 5 MC

There are two fast-food shops in a country town: Big Burgers (B) and Fast Fries (F).

Every week, each family in the town will purchase takeaway food from one of these shops.

The transition diagram below shows the way families in the town change their preferences for fast food from one week to the next.
 

MATRICES, FUR1 2012 VCAA 5 MC 
 

A transition matrix that provides the same information as the transition diagram is

MATRICES, FUR1 2012 VCAA 5 MC ab

MATRICES, FUR1 2012 VCAA 5 MC cd

MATRICES, FUR1 2012 VCAA 5 MC e

Show Answers Only

`D`

Show Worked Solution

MATRICES, FUR1 2012 VCAA 5 MC Answer

`{:(qquadqquadqquadqquadquad\ text(from)),({:qquadqquadqquadqquad\ BqquadquadF:}),( :. T = [(0.8,0.3),(0.2,0.7)]{:(B),(F):}qquadtext(to)):}`

`rArr D`

MATRICES, FUR1 2012 VCAA 4 MC

The diagram below shows the tracks directly linking four camping sites `P, Q, R` and `S` in a national park.

The shortest time that it takes to walk between the camping sites (in minutes), along each of these tracks, is also shown.
 

MATRICES, FUR1 2012 VCAA 4 MC

 
A matrix that could be used to present the same information is

MATRICES, FUR1 2012 VCAA 4 MC ab

MATRICES, FUR1 2012 VCAA 4 MC cd

MATRICES, FUR1 2012 VCAA 4 MC e

Show Answers Only

`E`

Show Worked Solution

`text(Presenting the “same information” involves)`

`text(recording the exact walk times in the matrix.)`

`rArr E`

MATRICES, FUR1 2013 VCAA 5 MC

Five students, Richard (R), Brendon (B), Lee (L), Arif (A) and Karl (K), were asked whether they played each of the following sports, football (F), golf (G), soccer (S) or tennis (T). Their responses are displayed in the table below.
 

MATRICES, FUR1 2013 VCAA 5 MC
 

If 1 is used to indicate that the student plays a particular sport and 0 is used to indicate that the student does not play a particular sport, which one of the following matrices could be used to represent the information in the table?
 

MATRICES, FUR1 2013 VCAA 5 MC ab1

MATRICES, FUR1 2013 VCAA 5 MC cd1

MATRICES, FUR1 2013 VCAA 5 MC e

Show Answers Only

`C`

Show Worked Solution

`rArr C`

MATRICES, FUR1 2013 VCAA 2 MC

Matrix `A` has three rows and two columns.

Matrix `B` has four rows and three columns.

Matrix `C = B × A`  has 

A.   two rows and three columns.

B.   three rows and two columns.

C.   three rows and three columns.

D.   four rows and two columns.

E.   four rows and three columns.

Show Answers Only

`D`

Show Worked Solution
   `B` `xx`  `A` `=`   `C`
`4 xx 3`    `3 xx 2`     `4 xx 2`

`rArr D`

MATRICES, FUR1 2006 VCAA 4 MC

Three teams, Blue (`B`), Green (`G`) and Red (`R`), compete for three different sporting competitions.

The table shows the competition winners for the past three years.
 

MATRICES, FUR1 2006 VCAA 4 MC
 

A matrix that shows the total number of competitions won by each of the three teams in each of these three years could be
 

MATRICES, FUR1 2006 VCAA 4 MC ab

MATRICES, FUR1 2006 VCAA 4 MC cd

MATRICES, FUR1 2006 VCAA 4 MC e

Show Answers Only

`B`

Show Worked Solution

`rArr B`

MATRICES, FUR1 2006 VCAA 3 MC

Let  `A = [(1,0), (0,1)], B = [(2,1), (1,0)]`  and  `C = [(1,-1), (-1,1)]`

Then  `A^3 (B - C)`  equals

A.    `[(1,2),(2,−1)]` B.    `[(1,0),(0,−1)]`
       
C.    `[(3,6),(6,−3)]` D.    `[(3,0),(0,−3)]`
       
E.    `[(5,10),(10,−5)]`    

 

Show Answers Only

`A`

Show Worked Solution
`A^3(B – C)` `= [(1,0),(0,1)]^3([(2,1),(1,0)] – [(1,−1),(−1,1)])`
  `= [(1,0),(0,1)][(1,2),(2,−1)]`
  `= [(1,2),(2,−1)]` 

`rArr A`