SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Harder Ext1 Topics, EXT2 2017 HSC 14b

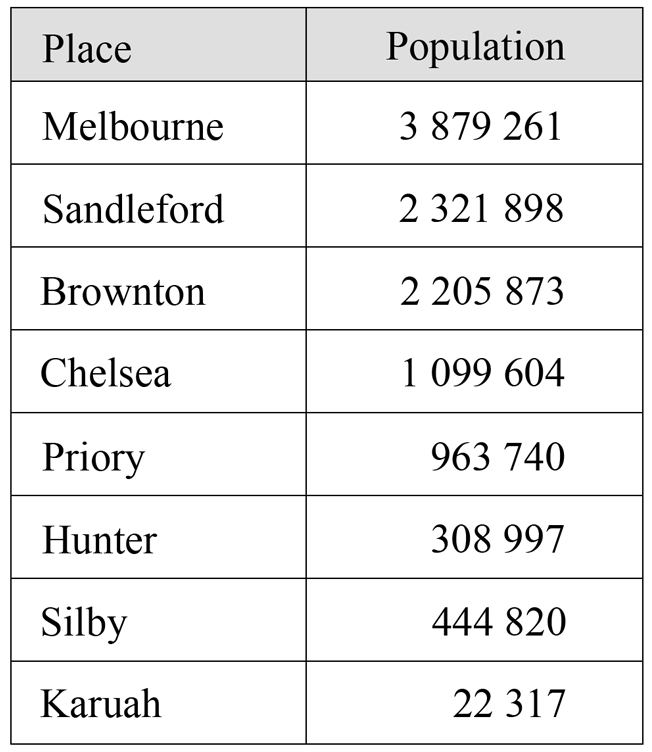
Two circles, `cc"C"_1` and `cc"C"_2`, intersect at the points `A` and `B`. Point `C` is chosen on the arc `AB` of `cc"C"_2` as shown in the diagram.

The line segment `AC` produced meets `cc"C"_1` at `D`.

The line segment `BC` produced meets `cc"C"_1` at `E`.

The line segment `EA` produced meets `cc"C"_2` at `F`.

The line segment `FC` produced meets the line segment `ED` at `G`.

Copy or trace the diagram into your writing booklet.

  1. State why `/_ EAD = /_ EBD`.  (1 mark)
  2. Show that `/_ EDA = /_ AFC`.  (1 mark)
  3. Hence, or otherwise, show that `B, C, G` and `D` are concyclic points.  (3 marks)
Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution

(i)  `text(Join)\ DB`

`/_ EAD = /_ EBD` `text{(angles at circumference}`
  `text(sitting on same arc)\ ED\ text(of)\ cc”C”_1 text{)}`

 

(ii)  `text(Join)\ AB`

`/_ EDA = /_ EBA` `text{(angles at circumference}`
  `text(sitting on same arc)\ EA\ text(of)\ cc”C”_1 text{)}`

 

`text(Consider arc)\ AC\ text(in)\ cc”C”_2`

`/_ EBA = /_ CBA = /_ AFC` `text{(angles at circumference}`
  `text(sitting on same arc)\ AC\ text(of)\ cc”C”_2 text{)}`

 

`:. /_ EDA = /_ AFC\ text(… as required.)`

 

(iii)   `text(Let)\ \ ` `/_ EDA = /_ AFC = theta\ \ text{(part (ii))}`
    `/_ EAD = /_ EBD = phi\ \ text{(part (i))}`

 

`text(Consider)\ Delta EAD:`

♦ Mean mark 47%.

`/_ AED = pi – theta – phi`

`text(Consider)\ Delta EGF:`

`/_ EGF` `= pi – (theta + pi – theta – phi)`
  `= phi`

 

`text(In)\ BCGD`

`text(External angle)\ EGF = phi`

`text(Interior opposite angle)\ EBD = phi`

`:. BCGD\ text(is a cyclic quadrilateral.)`

Algebra, STD2 A4 SM-Bank 4

Penny is a baker and makes meat pies every day.

The cost of making `p` pies, `$C`,  can be calculated using the equation

`C = 675 + 3.5 p`

Penny sells the pies for $5.75 each, and her income is calculated using the equation

`I = 5.75 p`

  1. On the graph, draw the graphs of  `C`  and  `I`.  (2 marks)

  2. On the graph, label the breakeven point and the loss zone.  (2 marks)

Show Answers Only

(i) and (ii)

Show Worked Solution
i.   

 

ii.  `text(Loss zone occurs when)\ C > I,\ text(which is shaded)`

`text(in the diagram above.)`

Complex Numbers, EXT2 N2 2017 HSC 13e

The points  `A, B, C`  and  `D`  on the Argand diagram represent the complex numbers  `a, b, c`  and  `d` respectively. The points form a square as shown on the diagram.
 


 

By using vectors, or otherwise, show that  `c = (1 + i) d - ia`.  (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

♦ Mean mark 49%.
`c – d` `= i (d – a)\ \ \ text{(rotation of}\ pi/2 text{)}`
`:. c ` `= d + id – ia`
  `= (1 + i) d – ia\ text(… as required.)`

Proof, EXT2 P1 2017 HSC 10 MC

Suppose  `f(x)`  is a differentiable function such that

`(f(a) + f(b))/2 >= f((a + b)/2)`, for all `a` and `b`.

Which statement is always true?

  1. `int_0^1 f(x)\ dx >= (f(0) + f(1))/2`
  2. `int_0^1 f(x)\ dx <= (f(0) + f(1))/2`
  3. `f′(1/2) >= 0`
  4. `f′(1/2) <= 0`
Show Answers Only

`B`

Show Worked Solution

`text(Representing the equation graphically)`

♦ Mean mark 41%.

`text{(one of many possibilities)}`

 

 

`f(x)\ text(is an increasing function between)`

`a\ text(and)\ b\ text(such that:)`

`(f(a) + f(b))/2 >= f((a + b)/2)`
 

`text(If)\ \ a = 0\ text(and)\ \ b = 1,`

`int_0^1 f(x)\ dx` `<=\ text(Area of trapezium)`
  `<= 1/2(1) (f(0) + f(1))`
  `<= (f(0) + f(1))/2`

`=> B`

Mechanics, EXT2 2017 HSC 9 MC

A particle is travelling on the circle with equation  `x^2 + y^2 = 16`.

It is given that  `(dx)/(dt) = y`.

Which statement about the motion of the particle is true?

  1. `(dy)/(dt) = x`  and the particle travels clockwise
  2. `(dy)/(dt) = x`  and the particle travels anticlockwise
  3. `(dy)/(dt) = −x`  and the particle travels clockwise
  4. `(dy)/(dt) = −x`  and the particle travels anticlockwise
Show Answers Only

`C`

Show Worked Solution
♦ Mean mark 46%.
`x^2 + y^2` `= 16`
`y^2` `= 16 – x^2`
`y` `= sqrt(16 – x^2)`
`(dy)/(dx)` `= 1/2 · (−2x)/(sqrt(16 – x^2)) = (−x)/(sqrt(16 – x^2))`
`(dy)/(dt)` `= (dy)/(dx) · (dx)/(dt)`
  `= (−x)/(sqrt16 – x^2) · sqrt(16 – x^2)\ \ \ (text(given)\ \ (dx)/(dt) = y)`
  `= −x`

 

`text{Test (1, 3) on circle:}`

`(dx)/(dt) = 3, (dy)/(dt) = −1`

`text(Interpretation:)\ y↓\ text(as)\ x↑\ text(in 1st quadrant)`

`:.\ text(Travelling in clockwise direction.)`

`=> C`

Conics, EXT2 2017 HSC 16b

The hyperbola with equation

`(x^2)/(a^2) - (y^2)/(b^2) = 1`

has eccentricity 2.

The distance from one of the foci to one of the vertices is 1.

What are the possible values of `a`?  (2 marks)

Show Answers Only

`1/3\ \ text(or)\ \ 1`

Show Worked Solution

`text(Focus)\ (F)\ text(co-ordinates:)\ (ae,0) = (2a,0)`

♦ Mean mark 45%.

`text(Consider vertex 1)\ (V_1):`

`V_1F = 2a + a` `= 1`
`a` `= 1/3`

 

`text(Consider vertex 2)\ (V_2):`

`V_2F = 2a – a` `= 1`
`a` `= 1`

 

`:.a=1/3\ \ text(or)\ \ 1`

Harder Ext1 Topics, EXT2 2017 HSC 16a

  Let  `alpha = costheta + i sintheta`, where  `0 < theta < 2pi`.

  1. Show that  `alpha^k + alpha^(−k) = 2 cos ktheta`, for any integer `k`.  (1 mark)
  3. Let  `C = alpha^(−n) + … + alpha^(−1) + 1 + alpha + … + alpha^n`, where `n` is a positive integer.
  4. By summing the series, prove that  

    `C = (alpha^n + alpha^(−n) - (a^(n + 1) + alpha^(−(n + 1))))/((1 - alpha)(1 - baralpha))`.  (3 marks)

  6. Deduce, from parts (i) and (ii), that`1 + 2(costheta + cos2theta + … + cosntheta) = (cosntheta - cos(n + 1)theta)/(1 - costheta)`.  (2 marks)

  7. Show that  
    `cos\ pi/n + cos\ (2pi)/n + …  + cos\ (npi)/n`  is independent of `n`.  (1 mark)

 

 

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(See Worked Solutions)`
  3. `text(See Worked Solutions)`
  4. `text(See Worked Solutions)`
Show Worked Solution

(i)   `alpha = costheta – isintheta`

`text(Using de Moivre:)`

`alpha^k` `= cos(ktheta) + isin(ktheta)`
`alpha^(−k)` `= cos(−ktheta) + isin(−ktheta)`
  `= cos(ktheta) – isin(ktheta)`
`:. alpha^k + alpha^(−k)` `= cos(ktheta) + isin(ktheta) + cos(ktheta) – isin(ktheta)`
  `= 2cos(ktheta)\ …\ \ text(as required.)`

 

(ii)   `C = alpha^(−n) + … + alpha^(−1) + 1 + alpha + … + alpha^n`

♦♦ Mean mark 34%.

`=> text(GP where)\ \ a = alpha^(−n), r = alpha`

`=> text(Number of terms) = 2n + 1`

`:. C` `= (a(1 – r^n))/(1 – r)`
  `= (alpha^(−n)(1 – alpha^(2n + 1)))/(1 – alpha)`
  `= (alpha^(−n)(1 – alpha^(2n + 1)))/(1 – alpha) xx (1 – baralpha)/(1 – baralpha)\ \ \ \ text{(where}\ baralpha = alpha^(−1) text{)}`
  `= ((alpha^(−n) – alpha^(n + 1))(1 – alpha^(−1)))/((1 – alpha)(1 – baralpha))`
  `= (alpha^(−n) – alpha^(−n – 1) – alpha^(n + 1) + alpha^n)/((1 – alpha)(1 – baralpha))`
  `= (alpha^n + alpha^(−n) – (alpha^(n + 1) + alpha^(−(n + 1))))/((1 – alpha)(1 – baralpha))\ …\ \ text(as required.)`
♦ Mean mark part (iii) 48%.

 

(iii)    `C` `= alpha^(−n) + a^(−n + 1) … + alpha^(−1) + 1 + alpha + … + alpha^n `
    `= 1 + (alpha + alpha^(−1)) + (alpha^2 + alpha^(−2)) + … + (alpha^n + alpha^(−n))`
    `= 1 + 2costheta + 2cos2theta + … + 2cosntheta\ \ \ \ (text{using part (i)})`
    `= 1 + 2(costheta + 2cos2theta + … + cosntheta)`

 

`text{Also, using part (ii)}`

`C` `= (alpha^n + alpha^(−n) – (alpha^(n + 1) + alpha^(−(n + 1))))/((1 – alpha)(1 – baralpha))`
  `= (2cosntheta – 2cos(n + 1)theta)/(1 – baralpha – alpha + 1)\ \ (text{part (i)})`
  `= (2cosntheta – 2cos(n + 1)theta)/(2 – (alpha + alpha^(−1)))`
  `= (2cosntheta – 2cos(n + 1)theta)/(2 – 2costheta)`
  `= (cosntheta – cos(n + 1)theta)/(1 – costheta)`

`:. 1 + 2(costheta, cos2theta + … + cosntheta) = (cosntheta – cos(n + 1)theta)/(1 – costheta)`

♦♦♦ Mean mark part (iv) 28%.

 

(iv)   `text{Rearrange the result from (iii):}`

`costheta + cos2theta + … + cosntheta = 1/2((cosntheta – cos(n + 1)theta)/(1 – costheta) – 1)`

`text(Let)\ \ theta = pi/n`

`:. cos\ pi/n + cos\ (2pi)/n + … + cos\ (npi)/n`

`= 1/2((cos((npi)/n) – cos(((n + 1)pi)/n))/(1 – cos(pi/n)) – 1)`
`= 1/2((cospi – cos(pi + pi/n))/(1 – cos(pi/n)) – 1)`
`= 1/2((−(1 – cos(pi/n)))/(1 – cos(pi/n)) – 1)`
`= 1/2 (−1 – 1)`
`= −1`

 

`=> text(which is independent of)\ n.`

CORE, FUR2 2017 VCAA 1

The number of eggs counted in a sample of 12 clusters of moth eggs is recorded in the table below.
     

  1. From the information given, determine
  2.  i. the range   (1 mark)

  3. ii. the percentage of clusters in this sample that contain more than 170 eggs.   (1 mark)

In a large population of moths, the number of eggs per cluster is approximately normally distributed with a mean of 165 eggs and a standard deviation of 25 eggs.

  1. Using the 68–95–99.7% rule, determine
  2.  i. the percentage of clusters expected to contain more than 140 eggs.   (1 mark)

  3. ii. the number of clusters expected to have less than 215 eggs in a sample of 1000 clusters.   (1 mark)

  4. The standardised number of eggs in one cluster is given by  `z = –2.4`
  5. Determine the actual number of eggs in this cluster.   (1 mark)

Show Answers Only

a.    `72`

b.i.  `25text(%)`

b.ii.  `-1`

c.  `105\ text(eggs)`

Show Worked Solution

a.i.  `text(Range)\ = 197-125= 72`

a.ii.  `text(3 clusters > 170 eggs)`

`:.\ text(Percentage)` `= 3/12 xx 100text(%)`
  `= 25text(%)`

 

b.i.    `ztext{-score (140)}` `= (140-165)/25`
    `= −1`

`:.\ text(Percentage over 140)`

`= 68 + 16`

`= 84text(%)`

 

b.ii.    `ztext{-score (215)}` `= (215-165)/25`
    `= 2`

 

`:.\ text(Percentage less than 215)`

`= 97.5text(%) xx 1000`

`= 975`

 

c.    `text(Using)\ \ \ z` `= (x-barx)/s`
  `−2.4` `= (x-165)/25`
  `x` `= (−2.4 xx 25) + 165`
    `= 105\ text(eggs)`

MATRICES, FUR1 2017 VCAA 6 MC

The table below shows information about two matrices, `A` and `B`.
 

 
The element in row `i` and column `j` of matrix `A` is `a_(ij)`.

The element in row `i` and column `j` of matrix `B` is `b_(ij)`.

The sum  `A + B`  is

A.

`[(5,7,9),(8,10,12),(11,13,15)]`

 

 B.

`[(5,8,11),(7,10,13),(9,12,15)]`

 
C.

`[(3,6,9),(3,6,9),(3,6,9)]`

 

 D.

`[(3,3,3),(6,6,6),(9,9,9)]`

 
E.

`[(3,6,3),(6,3,9),(3,9,3)]`

 

    
Show Answers Only

`D`

Show Worked Solution
`a_(ij) + b_(ij)` `= 2i + j + i – j`
  `= 3i`
`A + B` `= [(3xx1,3xx1,3xx1),(3xx2,3xx2,3xx2),(3xx3,3xx3,3xx3)]`
  `= [(3,3,3),(6,6,6),(9,9,9)]`

`=> D`

MATRICES, FUR1 2017 VCAA 5 MC

Four teams, `A`, `B`, `C` and `D`, competed in a round-robin competition where each team played each of the other teams once. There were no draws.

The results are shown in the matrix below.
 

`{:(),(),(text(winner)\ ):}{:(qquadqquadqquad\ text(loser)),(qquadqquadAquadBquadCquadD),({:(A),(B),(C),(D):}[(0,0,f,1),(1,0,0,0),(1,g,0,1),(0,1,0,h)]):}`
 

A 1 in the matrix shows that the team named in that row defeated the team named in that column.

For example, the 1 in row 2 shows that team `B` defeated team `A`.

In this matrix, the values of  `f`, `g` and `h` are

  1. `f = 0,qquadg = 1,qquadh = 0`
  2. `f = 0,qquadg = 1,qquadh = 1`
  3. `f = 1,qquadg = 0,qquadh = 0`
  4. `f = 1,qquadg = 1,qquadh = 0`
  5. `f = 1,qquadg = 1,qquadh = 1`
Show Answers Only

`A`

Show Worked Solution

`text(Consider column 1:)`

`C\ text(defeated)\ A => f = 0`

`text(Consider column 3:)`

`B\ text(lost to)\ C => g = 1`

`h = 0, text(s)text(ince team)\ D\ text(cannot play itself.)`

`=> A`

GRAPHS, FUR1 2017 VCAA 7 MC

Connor makes 200 meat pies to sell at his local market.

The cost, `$C`, of producing `n` pies can be determined from the rule below.

`C = 0.8n + 250`

Connor sells the first 150 pies at full price and sells the remaining 50 pies at half-price.

To break even, the full price of each pie must be closest to

  1. `$1.85`
  2. `$2.05`
  3. `$2.35`
  4. `$2.50`
  5. `$2.75`
Show Answers Only

`C`

Show Worked Solution
`text(Total cost)` `= 0.8 xx 200 + 250`
  `= $410`

 

`text(Let)\ \ x =\ text(full price)`

`text(Breakeven occurs when:)`

`150x + 50 xx 1/2x` `= 410`
`175x` `= 410`
`x` `= 410/175`
  `= $2.342…`

`=> C`

GRAPHS, FUR1 2017 VCAA 6 MC

The ticket office at a circus sells adult tickets and child tickets:

• The Payne family bought two adult tickets and three child tickets for $69.50
• The Tran family bought one adult ticket and five child tickets for $78.50
• The Saunders family bought three adult tickets and four child tickets.

What is the total amount spent by the Saunders family?

  1.   `$83.40`
  2.   `$87.50`
  3.   `$98.00`
  4. `$101.50`
  5. `$112.00`
Show Answers Only

`C`

Show Worked Solution

`text(Let)\ a\ text(= cost of 1 adult ticket)`

`text(Let)\ c\ text(= cost of 1 child ticket)`

`2a + 3c` `= 69.50\ \ …\ (1)`
`a + 5c` `= 78.50\ \ …\ (2)`

 

`text(Multiply)\ (2) xx 2`

`2a + 10c = 157.00\ \ …\ (3)`

 

`text(Subtract)\ (3) – (1)`

`7c` `= 87.50`
`c` `= $12.50`

 

`text(Substitute)\ \ c=$12.50\ \ text{into (2)}`

`a + 5 xx 12.50` `= 78.50`
`:. a` `= $16`

 

`:.\ text(Saunders family cost)`

`= 3 xx 16 + 4 xx 12.50`

`= $98`

`=> C`

GRAPHS, FUR1 2017 VCAA 5 MC

A childcare centre requires at least one teacher employed for every 15 children enrolled.

Let `x` be the number of teachers employed.

Let `y` be the number of children enrolled.

Which one of the following is the inequality that represents this situation?

  1. `y >= 15x`
  2. `y <= x/15`
  3. `y <= 15/x`
  4. `y <= 15x`
  5. `y >= x/15`
Show Answers Only

`D`

Show Worked Solution
`x` `>= y/15`
`:. y` `<= 15x`

`=> D`

NETWORKS, FUR1 2017 VCAA 7 MC

A graph with six vertices has no loops or multiple edges.

Which one of the following statements about this graph is not true?

  1. If the graph is a tree it has five edges.
  2. If the graph is complete it has 15 edges.
  3. If the graph has eight edges it may have an isolated vertex.
  4. If the graph is bipartite it will have a minimum of nine edges.
  5. If the graph has a cycle it will have a minimum of three edges.
Show Answers Only

`D`

Show Worked Solution

`text(Consider option)\ D:`

`text(It is easy to construct a bipartite graph in this)`

`text(example with less than nine edges.)`

`text(For example, the graph below is bipartite with)`

`text(6 vertices and 5 edges.)`
 

`=> D`

NETWORKS, FUR1 2017 VCAA 4-5 MC

The directed graph below shows the sequence of activities required to complete a project.

The time to complete each activity, in hours, is also shown.
 


 

Part 1

The earliest starting time, in hours, for activity `N` is

  1. 3
  2. 10
  3. 11
  4. 12
  5. 13

 

Part 2

To complete the project in minimum time, some activities cannot be delayed.

The number of activities that cannot be delayed is

  1. 2
  2. 3
  3. 4
  4. 5
  5. 6
Show Answers Only

`text(Part 1:)\ D`

`text(Part 1:)\ C`

Show Worked Solution

`text(Part 1)`

`text(EST of)\ N:\ CGJ`

`:.\ text(EST of)\ N` `= 4 + 3 +5`
  `= 12\ text(hours)`

`=> D`

 

`text(Part 2)`

`text(Critical path is:)\ CFHM`

`:. 4\ text(activities can’t be delayed.)`

`=> C`

NETWORKS, FUR1 2017 VCAA 3 MC

Consider the following graph.
 

 
The adjacency matrix for this graph, with some elements missing, is shown below.
 

 
This adjacency matrix contains 16 elements when complete.

Of the 12 missing elements

  1. eight are ‘1’ and four are ‘2’.
  2. four are ‘1’ and eight are ‘2’.
  3. six are ‘1’ and six are ‘2’.
  4. two are ‘0’, six are ‘1’ and four are ‘2’.
  5. four are ‘0’, four are ‘1’ and four are ‘2’.
Show Answers Only

`A`

Show Worked Solution

`text(Completing the adjacency matrix:)`
 

`=> A`

GEOMETRY, FUR1 2017 VCAA 6 MC

A hemispherical bowl of radius 10 cm is shown in the diagram below.

The bowl contains water with a maximum depth of 2 cm.

The radius of the surface of the water, in centimetres, is

  1.   `2`
  2.   `6`
  3.   `8`
  4.   `9`
  5. `10`
Show Answers Only

`B`

Show Worked Solution

`text(Using Pythagoras,)`

`r^2` `= 10^2 – 8^2`
  `= 36`
`:. r` `= 6\ text(cm)`

`=> B`

GEOMETRY, FUR1 2017 VCAA 5 MC

A segment is formed by an angle of 75° in a circle of radius 112 mm.

This segment is shown shaded in the diagram below.
 

Which one of the following calculations will give the area of the shaded segment?

  1. `pi xx 112^2 xx (75/360)`
  2. `pi xx 112^2 xx (285/360)`
  3. `pi xx 112^2 xx (75/360) - 1/2 xx 112^2 xx sin(75°)`
  4. `pi xx 112^2 xx (285/360) - 1/2 xx 112^2 xx sin(75°)`
  5. `pi xx 112^2 xx (75/180) - 1/2 xx 112^2 xx sin(75°)`
Show Answers Only

`C`

Show Worked Solution
`text(Area)` `=\ text(Area small sector − Area of triangle)`
  `= pi xx 112^2 xx 75/360 – 1/2 xx 112^2 xx sin(75°)`

`=> C`

Measurement, STD2 M1 2013 HSC 15a*

The diagram shows the front of a tent supported by three vertical poles. The poles are 1.2 m apart. The height of each outer pole is 1.5 m, and the height of the middle pole is 1.8 m. The roof hangs between the poles.

2013 15a

The front of the tent has area `A\ text(m²)`. 

  1. Use the trapezoidal rule to estimate `A`.    (2 marks)

  2. Explain whether the trapezoidal rule give a greater or smaller estimate of  `A`?  (1 mark)

Show Answers Only
  1. `3.96\ text(m²)`
  2. `text(The trapezoidal rule assumes a straight line between)`

     

    `text(all points and therefore would estimate a greater)`

     

    `text(area than the actual area of the tent front.)`

Show Worked Solution
i.    `A` `~~ h/2 [y_0 + 2y_1 + y_2]`
    `~~ 1.2/2 [1.5 + (2 xx 1.8) + 1.5]`
    `~~ 0.6 [6.6]`
    `~~ 3.96\ text(m²)`

 

ii.  `text(The trapezoidal rule assumes a straight line between)`

`text(all points and therefore would estimate a greater)`

`text(area than the actual area of the tent front.)`

Algebra, STD2 A2 SM-Bank 2

The weight of a steel beam, `w`, varies directly with its length, `ℓ`.

A 1200 mm steel beam weighs 144 kg.

Calculate the weight of a 750 mm steel beam.  (2 marks)

Show Answers Only

`90\ text(kg)`

Show Worked Solution

`w propto ℓ`

`w = kℓ`

`text(When)\ \ w = 144\ text(kg),\ \ ℓ = 1200\ text(mm)`

`144` `= k xx 1200`
`k` `= 144/1200`
  `= 3/25`

 

`text(When)\ \ ℓ = 750\ text(mm),`

`w` `= 3/25 xx 750`
  `= 90\ text(kg)`

Algebra, STD2 A1 SM-Bank 4

Doris is driving in a school zone at a speed of 35 kilometres per hour and needs to stop immediately to avoid an accident.

It takes her 1.25 seconds to react and her breaking distance is 5.3 metres.

Stopping distance can be calculated using the following formula
 

`text(stopping distance = {reaction time distance} + {braking distance})`
 

What is Doris' total stopping distance? Give your answer to 1 decimal place.  (2 marks)

Show Answers Only

`17.5\ text{metres  (to 1 d.p.)}`

Show Worked Solution
`35\ text(km/hr)` `= 35\ 000\ text(m/hr)`
  `= (35\ 000)/(60 xx 60)\ text(m/sec)`
  `= 9.722…\ text(m/sec)`

 

`:.\ text(Total stopping distance)`

`=\ text(Reaction time distance) + text(braking distance)`

`= 1.25 xx 9.722… +5.3`

`= 17.452…`

`= 17.5\ text{metres  (to 1 d.p.)}`

CORE, FUR1 2017 VCAA 23 MC

Four lines of an amortisation table for an annuity investment are shown below.

The interest rate for this investment remains constant, but the payment value may vary.
 

     
 

The balance of the investment after payment number 20 is $7500.

The value of payment number 20 is closest to

  1.   `$29`
  2. `$100`
  3. `$135`
  4. `$237`
  5. `$295`
Show Answers Only

`D`

Show Worked Solution

`text(Principal addition)`

`= 7500 – 7233.83`

`= $266.17`

 

`text(From the table,)`

`text{Interest applicable (expected) ≈ $29}`

`:.\ text(Payment)` `~~ 266.17 – 29`
  `~~ $237.17`

`=> D`

CORE, FUR1 2017 VCAA 22 MC

Consider the graph below.
 

 
This graph could show the value of

  1. a piano depreciating at a flat rate of 6% per annum.
  2. a car depreciating with a reducing balance rate of 6% per annum.
  3. a compound interest investment earning interest at the rate of 6% per annum.
  4. a perpetuity earning interest at the rate of 6% per annum.
  5. an annuity investment with additional payments of 6% of the initial investment amount per annum.
Show Answers Only

`B`

Show Worked Solution

`text(Consider the change in the)\ y text(-values:)`

`7000 xx 0.94` `= 6580`
`6580 xx 0.94` `= 6185.20`
`…\ \ text(and so on)`

 

`:.\ text(The asset is depreciating at 6% p. a. on a reducing)`

`text(balance basis.)`

`=> B`

CORE, FUR1 2017 VCAA 21 MC

A printer was purchased for $680.

After four years the printer has a value of $125.

On average, 1920 pages were printed every year during those four years.

The value of the printer was depreciated using a unit cost method of depreciation.

The depreciation in the value of the printer, per page printed, is closest to

  1.  3 cents.
  2.  4 cents.
  3.  5 cents.
  4.  6 cents.
  5.  7 cents.
Show Answers Only

`E`

Show Worked Solution

`text(Value lost each year)`

`= (680 – 125)/4`

`= $138.75`
 

`:.\ text(Depreciation per page)`

`= 138.75/1920`

`= 0.072…`

`~~ 7\ text(cents per page.)`

`=> E`

Algebra, STD2 A4 SM-Bank 3

Temperature can be measured in degrees Celsius (`C`) or degrees Fahrenheit (`F`).

The two temperature scales are related by the equation  `F = (9C)/5 + 32`.

  1. Calculate the temperature in degrees Fahrenheit when it is  −20 degrees Celsius.  (1 mark)

  2. The following two graphs are drawn on the axes below:
     
           `F = (9C)/5 + 32`  and  `F = C`
     

         

    Explain what happens at the point where the two graphs intersect.  (1 mark)

Show Answers Only
  1. `−4^@F`
  2. `text(The two graphs intersect at a temperature where)`

     

    `text(Celcius and Farenheit are the same.)`

Show Worked Solution
i.   `F` `= (9(−20))/5 + 32`
    `= −4^@F`

 

ii.   `text(The two graphs intersect at a temperature where)`

`text(Celcius and Farenheit are the same.)`

CORE, FUR1 2017 VCAA 16 MC

The seasonal index for the sales of cold drinks in a shop in January is 1.6

To correct the January sales of cold drinks for seasonality, the actual sales should be

  1. `text(reduced by 37.5%)`
  2. `text(reduced by 40%)`
  3. `text(reduced by 62.5%)`
  4. `text(increased by 60%)`
  5. `text(increased by 62.5%)`
Show Answers Only

`A`

Show Worked Solution

`text(Deseasonalised sales)`

`= text(Actual)/text(index)`

`= text(Actual) xx 1/1.6`

`=\ text(Actual × 62.5%)`

 

`:.\ text(Actual sales need to be reduced by 37.5%)`

`=> A`

CORE, FUR1 2017 VCAA 13-15 MC

The wind speed at a city location is measured throughout the day.

The time series plot below shows the daily maximum wind speed, in kilometres per hour, over a three-week period.
  

 

Part 1

The time series is best described as having

  1. seasonality only.
  2. irregular fluctuations only.
  3. seasonality with irregular fluctuations.
  4. a decreasing trend with irregular fluctuations.
  5. an increasing trend with irregular fluctuations.

 

Part 2

The seven-median smoothed maximum wind speed, in kilometres per hour, for day 4 is closest to

  1. `22`
  2. `26`
  3. `27`
  4. `30`
  5. `32`

 

Part 3

The table below shows the daily maximum wind speed, in kilometres per hour, for the days in week 2.

A four-point moving mean with centring is used to smooth the time series data above.

The smoothed maximum wind speed, in kilometres per hour, for day 11 is closest to

  1. `22`
  2. `24`
  3. `26`
  4. `28`
  5. `30`
Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ D`

`text(Part 3:)\ D`

Show Worked Solution

`text(Part 1)`

`text(The time series plot shows no obvious trend and)`

`text(is over too short a period to show seasonality.)`

`=> B`

 

`text(Part 2)`

`text(Consider the 7 values where day 4 is the middle)`

`text(data point.)`

`text(By inspection of the graph, the 4th highest point = 30.)`

`=> D`

 

`text(Part 3)`

`text(Mean for Day 9 – 12)`

`= (22 + 19 + 22 + 43)/4 = 26.5`

 

`text(Mean for Day 10 – 13)`

`= (19 + 22 + 43 + 37)/4 = 30.25`

 

`:. 4text(-point moving mean with centring)`

`= (26.5 + 30.25)/2`

`= 28.375`

`=> D`

`

CORE, FUR1 2017 VCAA 8-10 MC

The scatterplot below shows the wrist circumference and ankle circumference, both in centimetres, of 13 people. A least squares line has been fitted to the scatterplot with ankle circumference as the explanatory variable.
 

Part 1

The equation of the least squares line is closest to

  1. ankle = 10.2 + 0.342 × wrist
  2. wrist = 10.2 + 0.342 × ankle
  3. ankle = 17.4 + 0.342 × wrist
  4. wrist = 17.4 + 0.342 × ankle
  5. wrist = 17.4 + 0.731 × ankle

 

Part 2

When the least squares line on the scatterplot is used to predict the wrist circumference of the person with an ankle circumference of 24 cm, the residual will be closest to

  1. `–0.7`
  2. `–0.4`
  3. `–0.1`
  4.    `0.4`
  5.    `0.7`

 

Part 3

The residuals for this least squares line have a mean of 0.02 cm and a standard deviation of 0.4 cm.

The value of the residual for one of the data points is found to be  – 0.3 cm.

The standardised value of this residual is

  1. `–0.8`
  2. `–0.7`
  3. `–0.3`
  4.    `0.7`
  5.    `0.8`
Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ A`

`text(Part 3:)\ A`

Show Worked Solution

`text(Part 1)`

`ytext(-intercept = 10.2)`

`(text(note)\ xtext(-axis in graph begins at 21 cm))`

`:. text(wrist) = 10.2 + 0.342 xx text(ankle)`

`=> B`

 

`text(Part 2)`

`text(Predicted wrist)` `= 10.2 + 0.342 xx 24`
  `= 18.4`

 

`text(Residual)` `=\ text(actual − predicted)`
  `~~ 17.7 – 18.4`
  `~~ −0.7`

 
`=> A`

 
`text(Part 3)`

`barx = 0.02,qquad s_x = 0.4`

`text(If)\ \ x = −0.3,`

`z` `= (x – barx)/s_x`
  `= (−0.3 – 0.02)/0.4`
  `= −0.8`

 
`=> A`

CORE, FUR1 2017 VCAA 5-7 MC

A study was conducted to investigate the association between the number of moths caught in a moth trap (less than 250, 250–500, more than 500) and the trap type (sugar, scent, light). The results are summarised in the percentaged segmented bar chart below.
 

Part 1

There were 300 sugar traps.

The number of sugar traps that caught less than 250 moths is closest to

  1. 30
  2. 90
  3. 250
  4. 300
  5. 500

 
Part 2

The data displayed in the percentaged segmented bar chart supports the contention that there is an association between the number of moths caught in a moth trap and the trap type because

  1. most of the light traps contained less than 250 moths.
  2. 15% of the scent traps contained 500 or more moths.
  3. the percentage of sugar traps containing more than 500 moths is greater than the percentage of scent traps containing less than 500 moths.
  4. 20% of sugar traps contained more than 500 moths while 50% of light traps contained less than 250 moths.
  5. 20% of sugar traps contained more than 500 moths while 10% of light traps contained more than 500 moths.

 
Part 3

The variables number of moths (less than 250, 250–500, more than 500) and trap type (sugar, scent, light) are

  1. both nominal variables.
  2. both ordinal variables.
  3. a numerical variable and a categorical variable respectively.
  4. a nominal variable and an ordinal variable respectively.
  5. an ordinal variable and a nominal variable respectively.
Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ E`

`text(Part 3:)\ E`

Show Worked Solution

`text(Part 1)`

`text(Sugar traps that caught < 250)`

`= 30text(%) xx 300`

`= 90`

`=> B`

 

`text(Part 2)`

`text(An association should compare different)`

`text(trap types against the same value of)`

`text(number of moths caught.)`

`=> E`

 

`text(Part 3)`

`text{Number of moths (grouped) – ordinal variable}`

`text(Trap type – nominal variable)`

`=> E`

Calculus, EXT1 C1 2017 HSC 14c

The concentration of a drug in a body is  `F(t)`, where `t` is the time in hours after the drug is taken.

Initially the concentration of the drug is zero. The rate of change of concentration of the drug is given by   

`F^{′}(t) = 50e^(−0.5t)-0.4F(t)`.

  1. By differentiating the product  `F(t)e^(0.4t)` show that

     

    `qquadd/(dt)(F(t)e^(0.4t)) = 50e^(−0.1t)`.  (2 marks)

  2. Hence, or otherwise, show that  `F(t) = 500(e^(−0.4t)-e^(−0.5t))`.  (2 marks)

  3. The concentration of the drug increases to a maximum.

     

    For what value of `t` does this maximum occur?  (2 marks)

Show Answers Only
  1. `text(Show Worked Solutions)`
  2. `text(Show Worked Solutions)`
  3. `10 ln\ 5/4`
Show Worked Solution

i.  `text(Show)\ \ d/(dt)(F(t)e^(0.4t)) = 50e^(−0.1t)`

`F^{′}(t) = 50e^(−0.5t)-0.4F(t)\ …\ text{(1)  (given)}`

 
`text(Using product rule:)`

`d/(dt)(F(t)e^(0.4t))` `= F^{′}(t)e^(0.4t) + 0.4e^(0.4t)F(t)`
  `= e^(0.4t)(F^{′}(t) + 0.4F(t))`
  `= e^(0.4t) · 50e^(−0.5t)\ \ text{(using (1) above)}`
  `= 50e^(−0.1t)\ \ …\ text(as required)`

 

ii.   `text(Show)\ \ F(t) = 500(e^(−0.4t)-e^(−0.5t))`

♦♦ Mean mark 37%.
`F(t)e^(0.4t)` `= int 50e^(−0.1t)\ dt`
  `= 50/(−0.1) · e^(−0.1t) + c`
  `= −500 e^(−0.1t) + c`

 
`text(When)\ \ t = 0, \ F(t) = 0`

`0` `= −500 e^0 + c`
`c` `= 500`

 

`F(t)e^(0.4t)` `= 500-500e^(−0.1t)`
`:. F(t)` `= 500e^(−0.4t)-500e^(−0.5t)`
  `= 500 (e^(−0.4t)-e^(−0.5t))`

 

iii.    `F(t)` `= 500(e^(−0.4t)-e^(−0.5t))`
  `F^{′}(t)` `= 500(−0.4e^(-0.4t) + 0.5e^(−0.5t))`

 

`text(Find)\ t\ text(when)\ F^{′}(t) = 0 :`

♦♦ Mean mark 39%.
`0.4e^(−0.4t)` `= 0.5e^(−0.5t)`
`(e^(−0.4t))/(e^(−0.5t))` `= 0.5/0.4`
`e^(0.1t)` `= 5/4`
`0.1t` `= ln (5/4)`
`:. t_text(max)` `= 10 ln (5/4)`

Quadratic, EXT1 2017 HSC 14b

Let  `P(2p, p^2)`  be a point on the parabola  `x^2 = 4y`.

The tangent to the parabola at `P` meets the parabola  `x^2 = −4ay`, `a > 0`, at `Q` and `R`. Let `M` be the midpoint of `QR`.

  1. Show that the `x` coordinates of `R` and `Q` satisfy
  2. `qquadx^2 + 4apx - 4ap^2 = 0`.  (2 marks)

  3. Show that the coordination of `M` are  `(−2ap, −p^2(2a + 1))`.  (2 marks)
  4. Find the value of `a` so that the point `M` always lies on the parabola  `x^2 = −4y`.  (2 marks)

 

Show Answers Only
  1. `text(See Worked Solution)`
  2. `text(See Worked Solution)`
  3. `1 + sqrt2, a > 0`
Show Worked Solution

(i)   `x^2 = 4y,\ \ =>y = (x^2)/4`

`(dy)/(dx) = x/2`

`text(At)\ P(2p, p^2),`

`(dy)/(dx) = p`

`text(Equation of tangent:)`

`y = px – p^2`

 

`R and Q\ text(at intersection)`

`y` `= px – p^2\ …\ (1)`
`y` `= −(x^2)/(4a)\ …\ (2)`

 

`text(Subtract)\ (1) – (2)`

`px – p^2 + (x^2)/(4a)` `= 0`
`x^2 + 4apx – 4ap^2` `= 0\ …\ text(as required)`

 

(ii)   `x^2 + 4apx – 4ap^2 = 0`

♦♦ Mean mark 30%.
`x=` `\ (−4ap ± sqrt((4ap)^2 – 4 · 1 · (−4ap^2)))/2`
`=`  `\ (−4ap ± sqrt(16ap^2(a + 1)))/2`
`=`  `\ −2ap ± 2psqrt(a(a + 1))`

 

`=> xtext(-coordinate of)\ M\ text(is)\ −2ap.`

 

`M\ text(lies on tangent)\ \ y = px – p^2`

`:.y` `= p(−2ap) – p^2`
  `= −2ap^2 – p^2`
  `= −p^2(2a + 1)`

`:. M\ text(has coordinates)\ \ (−2ap, −p^2(2a + 1))`

 

(iii)   `text(If)\ M\ text(always lies on)\ \ x^2 = −4y`

♦♦ Mean mark 23%.
`(−2ap)^2` `= −4(−p^2(2a + 1))`
`4a^2p^2` `= 4p^2(2a + 1)`
`a^2` `= 2a + 1`
`a^2 – 2a – 1` `= 0`
`:. a` `= (+2 ± sqrt(4 + 4 · 1· 1))/2`
  `= 1 ± sqrt2`
  `= 1 + sqrt2, \ a > 0`

Mechanics, EXT2* M1 2017 HSC 13c

A golfer hits a golf ball with initial speed `V\ text(ms)^(−1)` at an angle `theta` to the horizontal. The golf ball is hit from one side of a lake and must have a horizontal range of 100 m or more to avoid landing in the lake.
 

     

Neglecting the effects of air resistance, the equations describing the motion of the ball are

`x = Vt costheta`

`y = Vt sintheta - 1/2 g t^2`,

where `t` is the time in seconds after the ball is hit and `g` is the acceleration due to gravity in `text(ms)^(−2)`. Do NOT prove these equations.

  1. Show that the horizontal range of the golf ball is
     
         `(V^2sin 2theta)/g` metres.  (2 marks)

  2. Show that if  `V^2 < 100 g`  then the horizontal range of the ball is less than 100 m.  (1 mark)

It is now given that  `V^2 = 200 g`  and that the horizontal range of the ball is 100 m or more.

  1. Show that  `pi/12 <= theta <= (5pi)/12`.  (2 marks)

  2. Find the greatest height the ball can achieve.  (2 marks)

Show Answers Only
  1. `text(See Worked Solution)`
  2. `text(See Worked Solution)`
  3. `text(See Worked Solution)`
  4. `25(2 – sqrt 3)\ text(metres)`
Show Worked Solution

i.   `text(Find)\ \ t\ \ text(when)\ \ y = 0:`

`1/2 g t^2` `= Vtsintheta`
`1/2 g t` `= Vsintheta`
`t` `= (2Vsintheta)/g`

 

`text(Horizontal range)\ (x)\ text(when)\ \ t = (2Vsintheta)/g :`

`x` `= V · (2Vsintheta)/g costheta`
  `= (V^2 2sintheta costheta)/g`
  `= (V^2sin2theta)/g\ … text(as required)`

 

ii.   `text(If)\ \ V^2 < 100 g`

♦ Mean mark 44%.
`x` `< (100 g sin2theta)/g`
`x` `< 100 sin2theta`

 

`text(S)text(ince)\ −1 <= 2theta <= 1,`

`x < 100\ text(metres)`

 

iii.   `V^2 = 200g,\ \ x >= 100`

`(200 g · sin2theta)/g` `>= 100`
`sin2theta` `>= 1/2`

`:. pi/6 <= 2theta <= (5pi)/6`

`:. pi/12 <= theta <= (5pi)/12\ …\ text(as required)`

 

iv.   `text(Max height occurs when)`

♦♦ Mean mark 35%.
`t` `= 1/2 xx text(time of flight)`
  `= (Vsintheta)/g`

 
`text(Find)\ \ y\ \ text(when)\ \ t = (Vsintheta)/g`

`y` `= V · (Vsintheta)/g · sintheta – 1/2 g ((Vsintheta)/g)^2`
  `= (V^2 sin^2theta)/g – 1/2 · (V^2 sin^2 theta)/g`
  `= (V^2 sin^2theta)/(2g)`

 

`text(Max height when)\ theta = (5pi)/12\ (text(steepest angle)), V^2 = 200 g\ (text(given))`

`y_text(max)` `= (200 g · sin^2 ((5pi)/12))/(2g)`
  `= 100 sin^2 ((5pi)/12)`
  `= 50(1 – cos((5pi)/6))`
  `= 50(1 + sqrt3/2)`
  `= 25(2 + sqrt 3)\ text(metres)`

Binomial, EXT1 2017 HSC 13b

Let `n` be a positive EVEN integer.

  1. Show that
  2. `(1 + x)^n + (1 - x)^n = 2[((n),(0)) + ((n),(2))x^2 + … + ((n),(n))x^n]`.  (2 marks)

  3. Hence show that
  4. `n[(1 + n)^(n - 1) - (1 - x)^(n - 1)] = 2[2((n),(2))x + 4((n),(4))x^3 + … + n((n),(n))x^(n - 1)]`.  (1 mark)

  5. Hence show that
  6. `((n),(2)) + 2((n),(4)) + 3((n),(6)) + … + n/2((n),(n)) = n2^(n - 3)`.  (2 marks)

 

 

Show Answers Only
  1. `text(See Worked Solution)`
  2. `text(See Worked Solution)`
  3. `text(See Worked Solution)`
Show Worked Solution

(i)   `text(Show)\ (1 + x)^n + (1 – x)^n = 2[\ ^nC_0 + \ ^nC_2x^2 + … + \ ^nC_nx^n]`

`text(Using binomial expansion)`

`(1 + x)^n + (1 – x)^n`

`= \ ^nC_0 + \ ^nC_1x + \ ^nC_2x^2 + … + \ ^nC_nx^n`

`+ \ ^nC_0 – \ ^nC_1x + \ ^nC_2x^2 + … + \ ^nC_nx^n`

`= 2[\ ^nC_0 + \ ^nC_2x^2 + \ ^nC_4x^4 + … + \ ^nC_nx^n]`

`…\ text(as required)`

 

(ii)   `text{Differentiate both sides of part (i):}`

`n(1 + x)^(n-1) – n(1 – x)^(n-1)`

`= 2[2\ ^nC_2x + 4\ ^nC_4x^3 + … + n \ ^nC_nx^(n – 1)]`

`n[(1 + x)^(n – 1) + (1 – x)^(n – 1)]`

`= 2[2\ ^nC_2x + 4\ ^nC_4x^3 + … + n \ ^nC_nx^(n – 1)]`

`…\ text(as required.)`

♦ Mean mark part (iii) 48%.

 

(iii)   `text(Let)\ \ x = 1\ \ text{in part (ii)}`

`n(2^(n – 1) + 0) = 2[2\ ^nC_2 + 4\ ^nC_4 + 6\ ^nC_6 + … + n\ ^nC_n]`

`text(Divide both sides by)\ 2^2:`

`(n2^(n – 1))/(2^2)` `= 2/(2^2)[2\ ^nC_2 + 4\ ^nC_4 + 6\ ^nC_6 + … + n\ ^nC_n]`
`n2^(n – 3)`

`= \ ^nC_2 + 2\ ^nC_4 + 3\ ^nC_6 + … + n/2\ ^nC_ n`

`…\ text(as required)`

Mechanics, EXT2* M1 2017 HSC 13a

A particle is moving along the `x`-axis in simple harmonic motion centred at the origin.

When  `x = 2`  the velocity of the particle is 4.

When  `x = 5`  the velocity of the particle is 3.

Find the period of the motion.  (3 marks)

Show Answers Only

`2sqrt3pi`

Show Worked Solution

`text(S)text(ince motion centred at origin,)`

♦ Mean mark 42%.
`{:d/(dx):}^(1/2 v^2)` `= −n^2x`
`1/2 v^2`  `= int −n^2x\ dx`
  `= −1/2n^2x^2 + c`
 `v^2` `= c-n^2x^2`

 

`text(When)\ v = 4, x = 2`

`16 = c-4n^2\ …\ (1)`

`text(When)\ v = 3, x = 5`

`9 = c-25n^2\ …\ (2)`

`text(Subtract)\ (1)-(2)`

`7` `= 21n^2`
`n^2` `= 1/3`
`n` `= 1/sqrt3`

 
`:.\ text(Period)= (2pi)/n= 2sqrt3 pi`

Plane Geometry, 2UA 2017 HSC 16c

In the triangle `ABC`, the point `M` is the mid-point of `BC`. The point `D` lies on `AB` and

`BD = DA + AC`.

The line that passes through the point `C` and is parallel to `MD` meets `BA` produced at `E`.

Copy or trace this diagram into your writing booklet.

  1. Prove that `Delta ACE` is isosceles.  (3 marks)
  2. The point `F` is chosen on `BC` so that `AF` is parallel to `DM`.
    `qquad` 
    Show that `AF` bisects `/_ BAC`.  (2 marks)

 

 

 

 

 

 

 

 

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution
(i)  

`text(Prove)\ Delta ACE\ text(is isosceles)`

♦♦♦ Mean mark 21%.

`text(S) text(ince)\ DM text(||) EC,`

`∠BDM = ∠BEC\ \ text{(corresponding angles)}`

`∠DBM\ \ text(is common)`

`:. Delta BDM\ text(|||)\ Delta BEC\ \ text{(AAA)}`

`text(Using ratios of similar)\ Delta text(s):`

`(BM)/(BD)` `= (BC)/(BE)`
`(BM)/(BC)` `= (BD)/(BE) = 1/2\ \ text{(}M\ text(is midpoint of)\ BC text{)}`

 

`=> D\ text(is the midpoint of)\ BE.`

`=> BD = DE`

`AE` `= DE – DA`
`AC` `= BD – DA\ text{(given)}`
  `= DE – DA`
`:.  AE` `= AC`

`:. Delta ACE\ text(is isosceles)`

 

(ii)  

`text(Show)\ AF\ text(bisects)\ /_ BAC`

♦♦ Mean mark 31%.

`/_ BAF = /_ AEC\ \ \ text{(corresponding angles)}`

`text{From part (i)}`

`/_ AEC` `= /_ ECA\ \ \ text{(}Delta AEC\ text{is isosceles)}`
`/_ FAC` `= /_ ECA\ \ \ text{(alternate angles)}`
`:. /_ BAF` `= /_ FAC`

`:. AF\ text(bisects)\  /_ BAC\ \ \ text(… as required)`

Financial Maths, 2ADV M1 2017 HSC 16b

A geometric series has first term  `a`  and limiting sum 2.

Find all possible values for  `a`.  (3 marks)

Show Answers Only

`0 < a < 4`

Show Worked Solution

`S_oo = a/(1 – r)`

♦ Mean mark 39%.

`text(If)\ \ S_oo = 2:`

`2` `= a/(1 – r)`
`2(1 – r)` `= a`
`1 – r` `= a/2`
`r` `= 1 – a/2`

 

`text(S)text(ince)\ \ |r| < 1,`

`|1 – a/2| < 1`

`1 – a/2` `< 1` `or qquad -(1 – a/2)` `< 1`
`a/2` `> 0` `a/2` `< 2`
`a` `> 0` `a` `< 4`

 

`:. 0 < a < 4`

Calculus, 2ADV C3 2017 HSC 16a

John’s home is at point `A` and his school is at point `B`. A straight river runs nearby.

The point on the river closest to `A` is point `C`, which is 5 km from `A`.

The point on the river closest to `B` is point `D`, which is 7 km from `B`.

The distance from `C` to `D` is 9 km.

To get some exercise, John cycles from home directly to point `E` on the river, `x` km from `C`, before cycling directly to school at `B`, as shown in the diagram.
 


  

The total distance John cycles from home to school is `L` km.

  1. Show that  `L = sqrt (x^2 + 25) + sqrt (49 + (9 - x)^2)`.   (1 mark)

  2. Show that if  `(dL)/(dx) = 0`, then  `sin alpha = sin beta`.   (3 marks)

  3. Find the value of `x` that makes  `sin alpha = sin beta`.   (2 marks)

  4. Explain why this value of `x` gives a minimum for `L`.   (1 mark)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `45/12`
  4. `text(See Worked Solutions)`
Show Worked Solution
i.  

`text(Using Pythagoras:)`

`L` `= AE + EB`
  `= sqrt (5^2 + x^2) + sqrt (7^2 + (9 – x)^2)`
  `= sqrt(25 + x^2) + sqrt (49 + (9 – x)^2)\ text(… as required)`

 

ii.  `text(From diagram):`

♦ Mean mark 41%.

`sin alpha = x/sqrt(25 + x^2) and sin beta = (9 – x)/sqrt(49 + (9 – x)^2)`

`L` `= sqrt(25 + x^2) + sqrt (49 + (9 – x)^2)`
`(dL)/(dx)` `= (2x)/sqrt(25 + x^2) – (2(9 – x))/sqrt(49 + (9 – x)^2)`

 

`text(If)\ \ (dL)/(dx) = 0,`

`=> (2x)/sqrt(25 + x^2)` `= (2(9 – x))/sqrt(49 + (9 – x)^2)`
`x/sqrt(25 + x^2)` `= (9 – x)/sqrt(49 + (9 – x)^2)`
`sin alpha` `= sin beta\ text(… as required)`

 

iii.  `text(If)\ sin alpha = sin beta,\ text(then)\ alpha = beta and`

♦♦ Mean mark 29%.

`Delta ACE\ text(|||)\ Delta BDE`

`text(Using corresponding sides of similar triangles:)`

`x/5` `= (9 – x)/7`
`7x` `= 45 – 5x`
`12x` `= 45`
`:. x` `= 45/12\ text(km)`
♦♦♦ Mean mark 9%.

 

iv.  

`text(If point)\ B\ text(is reflected across the)`

`text(river),\ AEB\ text(will be a straight line.)`

`text(If any other point is chosen,)\ AEB`

`text(would not be straight and the distance)`

`text(would be longer.)`

Calculus, EXT1* C1 2017 HSC 15c

Two particles move along the `x`-axis.

When  `t = 0`, particle `P_1` is at the origin and moving with velocity 3.

For  `t >= 0`, particle `P_1` has acceleration given by  `a_1 = 6t + e^(-t)`.

  1. Show that the velocity of particle `P_1` is given by  `v_1 = 3t^2 + 4-e^(-t)`  (2 marks)

When  `t = 0`, particle `P_2` is also at the origin.

For  `t >= 0`, particle `P_2` has velocity given by  `v_2 = 6t + 1-e^(-t)`.

  1. When do the two particles have the same velocity?  (2 marks)

  2. Show that the two particles do not meet for  `t > 0`.  (3 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `t = 1`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution
i.   `a_1` `= 6t + e^(-t)`
  `v_1` `= int a_1\ dt`
    `= int 6t + e^(-t)\ dt`
    `= 3t^2-e^(-t) + c`

 

`text(When)\ t = 0,\ v_1 = 3`

`3` `= 0-1 + c`
`c` `= 4`
`:. v_1` `= 3t^2 + 4-e^(-t) …\ text(as required)`

 

ii.  `v_2 = 6t + 1-e^(-t)`

`text(Find)\ \ t\ \ text(when)\ \ v_1 = v_2`

`3t^2 + 4-e^(-t)` `= 6t + 1-e^(-t)`
`3t^2-6t + 3` `= 0`
`t^2-2t + 1` `= 0`
`(t-1)^2` `= 0`
`:. t` `=1`

 

iii.   `x_1` `= int v_1\ dt`
    `= int 3t^2 + 4-e^(-t)\ dt`
    `= t^3 + 4t + e^(-t) + c`

 

`text(When)\ \ t = 0,\ \ x_1 = 0`

♦ Mean mark (iii) 39%.
`0` `= 0 + 0 + 1 + c`
`c` `= -1`
`:. x_1` `= t^3 + 4t + e^(-t)-1`

 

`x_2` `= int 6t + 1-e^(-t)\ dt`
  `= 3t^2 + t + e^(-t) + c`

 
`text(When)\ \ t = 0,\ \ x_2 = 0`

`0` `= 0 + 0 + 1 + c`
`c` `= -1`
`:. x_2` `= 3t^2 + t + e^(-t)-1`

 

`text(Find)\ \ t\ \ text(when)\ \ x_1 = x_2`

`t^3 + 4t + e^(-t)-1` `= 3t^2 + t + e^(-t)-1`
`t^3-3t^2 + 3t` `= 0`
`t(t^2-3t + 3)` `= 0`

 

`text(S)text(ince)\ \ Delta < 0\ \ text(for)\ \ t^2-3t + 3`

`=>\ text(No real solution)`

 

`:.\ text(The particles do not meet)`

`(x_1 != x_2)\ \ text(for)\ \ t > 0.`

Financial Maths, 2ADV M1 2017 HSC 15b

Anita opens a savings account. At the start of each month she deposits `$X` into the savings account. At the end of each month, after interest is added into the savings account, the bank withdraws $2500 from the savings account as a loan repayment. Let `M_n` be the amount in the savings account after the `n`th  withdrawal.

The savings account pays interest of 4.2% per annum compounded monthly.

  1. Show that after the second withdrawal the amount in the savings account is given by
    `qquad qquad M_2 = X(1.0035^2 + 1.0035) - 2500 (1.0035 + 1)`.  (2 marks)

  2. Find the value of  `X`  so that the amount in the savings account is $80 000 after the last withdrawal of the fourth year.  (3 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `$ 4019.42\ text{(nearest cent)}`
Show Worked Solution
i.   `M_1` `= X (1 + 4.2/(12 xx 100)) – 2500`
    `= X (1.0035) – 2500`
  `M_2` `= X (1.0035) + M_1 (1.0035) – 2500`
    `=X(1.0035)+(1.0035)[X(1.0035)-2500]-2500`
    `= X (1.0035) + X (1.0035^2) – 2500 (1.0035) – 2500`
    `= X (1.0035^2 + 1.0035) – 2500 (1.0035 + 1)`
♦ Mean mark part (ii) 48%.

 

ii.  

`M_3 = X (1.0035^3 + … + 1.0035) – 2500 (1.0035^2 + 1.0035 + 1)`

`vdots`

`M_n = X (1.0035^n + … + 1.0035) – 2500 (1.0035^(n – 1) + … + 1)`

`text(Find)\ X\ text(such that)\ \ M_n = 80\ 000\ \ text(when)\ n = 48`

`80\ 000 = X (1.0035^48 + …\ 1.0035) – 2500 (1.0035^47 + … + 1)`

`text(Using)\ S_n = (a(r^n – 1))/(r – 1)`

`80\ 000` `= X [(1.0035(1.0035^48 – 1))/(1.0035 – 1)] – 2500 [(1(1.0035^48 – 1))/(1.0035 – 1)]`
`80\ 000` `= X (52.351…) – 130\ 421.20…`
   
`:. X` `= (80\ 000 + 130\ 421.20…)/(52.351…)`
  `= $4019.42\ text{(nearest cent)}`

Calculus, 2ADV C4 2017 HSC 14b

  1. Find the exact value of
     
  2. `qquad int_0^(pi/3) cos x\ dx`.  (1 mark)

  3. Using Simpson’s rule with one application, find an approximation to the integral
  4.  
    `qquad int_0^(pi/3) cos x\ dx,`
     
  5. leaving your answer in terms of `pi` and `sqrt 3`.  (2 marks)
     

  6. Using parts (i) and (ii), show that
     
  7. `qquad pi ~~ (18 sqrt 3)/(3 + 4 sqrt 3)`.  (1 mark)

 

 

Show Answers Only
(i)   `sqrt 3/2`
(ii)   `((4 sqrt 3 + 3)pi)/36`
(iii)   `text{Proof (See Worked Solutions)}`
Show Worked Solution
(i)   `int_0^(pi/3) cos x\ dx` `= [sin x]_0^(pi/3)`
    `= sin\ pi/3 – 0`
    `= sqrt 3/2`

 

(ii)  
    `x`     `0`    `overset(pi) underset(6) _`     `overset(pi) underset(3) _`  
    `y`     `1`     `overset(sqrt 3) underset(2) _`     `overset(1) underset(2) _`  
      `y_0`     `y_1`     `y_2`  
`int_0^(pi/3) cos x\ dx` `~~ h/3 [y_0 + 4y_1 + y_2]`
  `~~ pi/6 ⋅ 1/3 [1 + 4 ⋅ sqrt 3/2 + 1/2]`
  `~~ pi/18 ((4 sqrt 3 + 3)/2)`
  `~~ ((4 sqrt 3 + 3) pi)/36`

 

(iii)  `text{Using parts (i) and (ii)}`

♦ Mean mark 49%.
`((4 sqrt 3 + 3) pi)/36` `~~ sqrt 3/2`
`:. pi` `~~ (36 sqrt 3)/(2(3 + 4 sqrt 3))`
  `~~ (18 sqrt 3)/(3 + 4 sqrt 3) … text( as required)`

Calculus, 2ADV C3 2017 HSC 9 MC

The graph of  `y = f^{′}(x)`  is shown.
 

The curve  `y = f (x)`  has a maximum value of 12.

What is the equation of the curve  `y = f (x)`?

  1. `y = x^2-4x + 12`
  2. `y = 4 + 4x-x^2`
  3. `y = 8 + 4x-x^2`
  4. `y = x^2-4x + 16`
Show Answers Only

`C`

Show Worked Solution

`text(Find the equation of)\ \ f^{′}(x):`

`m = -2,\ \ y text(-int) = 4`

`y = -2x + 4`

`f(x)` `= int -2x + 4\ dx`
  `= -x^2 + 4x + c`

 

`text(Maximum)\ \ f(x) = 12\ \ text(when)\ \ f^{′}(x) = 0:`

`-2x + 4` `= 0`
`x` `= 2`

 
`text(Substitute)\ \ x=2\ \ text(into)\ \ f(x):`

`:. 12` `= -2^2 + 4 ⋅ 2 + c`
`c` `= 8`

 

`:. f(x) = 8 + 4x-x^2`

`=>  C`

Algebra, 2UG 2017 HSC 30d

In an investigation, students used different numbers of identical small solar panels to power model cars. The cars were then tested and their speed measured in km/h. The results are summarised in the table.
 


 

The equation of the least-squares line of best fit, relating the speed and the number of solar panels, has been calculated to be
 

`y = 2.125x + 2.0375`
 

  1. What would be the speed of a car powered by 5 solar panels, based on this equation?  (1 mark)
  2. Calculate the correlation coefficient, `r`, between the number of solar panels and the speed of a car.  (2 marks)

 

Show Answers Only
  1. `12.6625\ text(km/h)`
  2. `0.85`
Show Worked Solution
(i)    `text(Speed)(y)` `= 2.125(5) + 2.0375`
    `= 12.6625\ text(km/h)`

 

(ii)   `text(Using the formula sheet:)`

♦♦ Mean mark 23%.
`text(gradient)` `= r xx (text(std dev)(y))/(text(std dev)(x))`
`2.125` `= r xx 2/0.8`
`:. r` `= (2.125 xx 0.8)/2`
  `= 0.85`

Measurement, STD2 M6 2017 HSC 30c

The diagram shows the location of three schools. School `A` is 5 km due north of school `B`, school `C` is 13 km from school `B` and `angleABC` is 135°.
 


 

  1. Calculate the shortest distance from school `A` to school `C`, to the nearest kilometre.  (2 marks)

  2. Determine the bearing of school `C` from school `A`, to the nearest degree.  (3 marks)

Show Answers Only
  1. `17\ text{km  (nearest km)}`
  2. `213^@`
Show Worked Solution

i.   `text(Using cosine rule:)`

`AC^2` `= AB^2 + BC^2 – 2 xx AB xx BC xx cos135^@`
  `= 5^2 + 13^2 – 2 xx 5 xx 13 xx cos135^@`
  `= 285.923…`
`:. AC` `= 16.909…`
  `= 17\ text{km  (nearest km)}`

 

ii.   

`text(Using sine rule, find)\ angleBAC:`

♦♦ Mean mark 31%.
`(sin angleBAC)/13` `= (sin 135^@)/17`
`sin angleBAC` `= (13 xx sin 135^@)/17`
  `= 0.5407…`
`angleBAC` `= 32.7^@`

 

`:. text(Bearing of)\ C\ text(from)\ A`

`= 180 + 32.7`

`= 212.7^@`

`= 213^@`

Statistics, STD2 S1 2017 HSC 30a

A set of data has a lower quartile (`Q_L`) of 10 and an upper quartile (`Q_U`) of 16.

What is the maximum possible range for this set of data if there are no outliers?  (2 marks)

Show Answers Only

`24`

Show Worked Solution

`IQR = 16 – 10 = 6`

♦♦ Mean mark 34%.

`text(If no outliers,)`

`text(Upper limit)` `= Q_U + 1.5 xx IQR`
  `= 16 + 1.5 xx 6`
  `= 25`
`text(Lower limit)` `= Q_L – 1.5 xx IQR`
  `= 10 – 1.5 xx 6`
  `= 1`

 

`:.\ text(Maximum range)` `= 25 – 1`
  `= 24`