SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Functions, MET2 2024 VCAA 1

Consider the function  \( f: R \rightarrow R, f(x)=(x+1)(x+a)(x-2)(x-2 a) \text { where } a \in R \text {. } \)

  1. State, in terms of \(a\) where required, the values of \(x\) for which \(f(x)=0\).  (1 mark
  1. Find the values of \(a\) for which the graph of \(y=f(x)\) has
      
     i. exactly three \(x\)-intercepts.   (2 marks)

    ii. exactly four \(x\)-intercepts.   (1 mark)

  1. Let \(g\) be the function \(g: R \rightarrow R, g(x)=(x+1)^2(x-2)^2\), which is the function \(f\) where \(a=1\).
      
      i. Find \(g^{\prime}(x)\)   (1 mark)

     ii. Find the coordinates of the local maximum of \(g\).   (1 mark)

    iii. Find the values of \(x\) for which \(g^{\prime}(x)>0\).   (1 mark)

     iv. Consider the two tangent lines to the graph of \(y=g(x)\) at the points where
    \(x=\dfrac{-\sqrt{3}+1}{2}\) and \(x=\dfrac{\sqrt{3}+1}{2}\). Determine the coordinates of the point of intersection of these two tangent lines.   (2 marks)

  1. Let \(g\) remain as the function \(g: R \rightarrow R, g(x)=(x+1)^2(x-2)^2\), which is the function \(f\) where \(a=1\).

    Let \(h\) be the function \(h: R \rightarrow R, h(x)=(x+1)(x-1)(x+2)(x-2)\), which is the function \(f\) where \(a=-1\).
      
     i. Using translations only, describe a sequence of transformations of \(h\), for which its image would have a local maximum at the same coordinates as that of \(g\).   (1 mark)

    ii. Using a dilation and translations, describe a different sequence of transformations of \(h\), for which its image would have both local minimums at the same coordinates as that of \(g\).   (2 marks)

Show Answers Only

a.    \(x=-1, x=a, x=2, x=2a\)

bi.  \(a=0, -2, -\dfrac{1}{2}\)

bii. \(R\ \backslash\left\{ -2, -\dfrac{1}{2}, 0, 1\right\}\)

ci.  \(g^{\prime}(x)=2(x-2)(x+1)(2x-1)\)

cii. \(\left(\dfrac{1}{2} , \dfrac{81}{16}\right)\)

ciii. \(x\in\left(-1, \dfrac{1}{2}\right)\cup (2, \infty)\)

civ. \(\left(\dfrac{1}{2}, \dfrac{27}{4}\right)\)

di.   \(\text{Translate }\dfrac{1}{2}\ \text{unit to the right and }\dfrac{81}{16}-4=\dfrac{17}{16}\ \text{units upwards.}\)

dii.  \(\text{Combination is a dilation of }h(x)\ \text{by a factor of}\ \dfrac{3}{\sqrt{10}}\ \text{followed by a }\)

\(\text{translation of }\dfrac{1}{2} \ \text{a unit to the right and an upwards translation of}\ \dfrac{9}{4} \ \text{units}\)

Show Worked Solution

a.    \(x=-1, x=a, x=2, x=2a\)

bi.  \(a=0, -2, -\dfrac{1}{2}\)

bii. \(\text{The solution must be all }R\ \text{except those that give 3 or less solutions.}\)

\(\therefore\ R\ \backslash\left\{ -2, -\dfrac{1}{2}, 0, 1\right\}\)

ci.    \(g^{\prime}(x)\) \(=2(2-x)(x+1)^2+(x-2)^22(x+1)\)
    \(=2(x-2)(x+1)(x+1+x+2)\)
    \(=2(x-2)(x+1)(2x-1)\)

  
cii.  \(\text{When  }g^{\prime}(x)=0, x=2, -1, \dfrac{1}{2}\)

\(\text{From graph local maximum occurs when }x=\dfrac{1}{2}\)

\(g\left(\dfrac{1}{2}\right)\) \(=\left(\dfrac{1}{2}+1\right)^2\left(\dfrac{1}{2}-2\right)^2\)
  \(=\dfrac{9}{4}\times \dfrac{9}{4}=\dfrac{81}{16}\)

  
\(\therefore\ \text{Local maximum at}\ \left(\dfrac{1}{2} , \dfrac{81}{16}\right)\)

ciii. \(\text{From graph}\ g^{\prime}(x)>0\ \text{when }x\in\left(-1, \dfrac{1}{2}\right)\cup (2, \infty)\)

civ.  \(\text{Use CAS to find tangent lines and solve to find intersection.}\)

\(\text{Point of intersection of tangent lines}\ \left(\dfrac{1}{2}, \dfrac{27}{4}\right)\)

di.  \(\text{Local maximum of }g(x)\ \rightarrow\left(\dfrac{1}{2}, \dfrac{81}{16}\right)\)

\(\text{From CAS local maximum of }h(x)\ \rightarrow \left(0, 4\right)\)

\(\therefore\ \text{Translate }\dfrac{1}{2}\ \text{unit to the right and }\dfrac{81}{16}-4=\dfrac{17}{16}\ \text{units upwards.}\)

dii. \(\text{Using CAS to solve }g^{\prime}(x)=0\ \text{and }h^{\prime}(x)=0\)

\(\text{Local Minimums for }g(x)\ \text{at }(-1, 0)\ \text{and }(2, 0)\ \text{which are 3 apart.}\)

\(\text{Local minimums for at }h(x)\ \text{at }\left(-\sqrt{\dfrac{5}{2}}, -\dfrac{9}{4}\right)\ \text{and }\left(\sqrt{\dfrac{5}{2}}, -\dfrac{9}{4}\right)\)

\(\therefore\ \text{Combination is a dilation of }h(x)\ \text{by a factor of}\ \dfrac{3}{\sqrt{10}}\ \text{followed by a }\)

\(\text{translation of }\dfrac{1}{2} \ \text{a unit to the right and an upwards translation of}\ \dfrac{9}{4} \ \text{units.}\)

 

Calculus, MET2 2022 VCAA 1

The diagram below shows part of the graph of `y=f(x)`, where `f(x)=\frac{x^2}{12}`.
 

  1. State the equation of the axis of symmetry of the graph of `f`.   (1 mark)

  2. State the derivative of `f` with respect to `x`.   (1 mark)

The tangent to `f` at point `M` has gradient `-2` .

  1. Find the equation of the tangent to `f` at point `M`.   (2 marks)

The diagram below shows part of the graph of `y=f(x)`, the tangent to `f` at point `M` and the line perpendicular to the tangent at point `M`.
 

 

  1.  i. Find the equation of the line perpendicular to the tangent passing through point `M`.   (1 mark)

  2. ii. The line perpendicular to the tangent at point `M` also cuts `f` at point `N`, as shown in the diagram above.
  3.     Find the area enclosed by this line and the curve `y=f(x)`.   (2 marks)

  4. Another parabola is defined by the rule `g(x)=\frac{x^2}{4 a^2}`, where `a>0`.
  5. A tangent to `g` and the line perpendicular to the tangent at `x=-b`, where `b>0`, are shown below.

  1. Find the value of `b`, in terms of `a`, such that the shaded area is a minimum.   (4 marks)

Show Answers Only

a.    `x=0`

b.    ` f^{\prime}(x)=1/6x`

c.    `x=-12`

di.    `y=1/2x + 18`

dii.   Area`= 375` units²

e.    `b = 2a^2`

Show Worked Solution

a.   Axis of symmetry:  `x=0`
  

b.    `f(x)`  `=\frac{x^2}{12}`  
  ` f^{\prime}(x)` `= 1/6x`  

  
c.   At `M` gradient `= -2`

`1/6x` `= -2`  
`x` `= -12`  

 
When  `x = -12`
 

`f(x) = (-12)^2/12 = 12`
 
Equation of tangent at `(-12 , 12)`:

`y-y_1` `=m(x-x_1)`  
`y-12` `= -2(x + 12)`  
`y` `= -2x-12`  


d.i   Gradient of tangent `= -2`

`:.`  gradient of normal `= 1/2` 

Equation at `M(- 12 , 12)`

`y -y_1` `=m(x-x_1)`  
`y-12` `= 1/2(x + 12)`  
`y` `=1/2x + 18`  


d.ii  Points of intersection of `f(x)` and normal are at  `M` and `N`.

So equate ` y = x^2/12` and  `y = 1/2x + 18` to find `N`

`x^2/12` `=1/2x + 18`  
`x^2-6x-216` `=0`  
`(x + 12)(x-18)` `=0`  

   
`:.\  x = -12` or `x = 18`

Area `= \int_{-12}^{18}\left(\frac{1}{2} x+18-\frac{x^2}{12}\right) d x`  
  `= [x^2/4 + 18x-x^3/36]_(-12)^18`  
  `= [18^2/4 +18^2-18^3/36] – [12^2/4 + 18 xx (-12)-(-12)^3/36]`  
  `= 375` units²  

 

e.   `g(x) = x^2/(4a^2)`   `a > 0`

At `x = -b`   `y = (-b)^2/(4a^2) = b^2/4a^2`

`g^{\prime}(x) = (2x)/(4a^2) = x/(2a^2)`

Gradient of tangent `= (-b)/(2a^2)`

Gradient of normal `= (2a^2)/b`

Equation of normal at `(- b , b^2/(4a^2))`

`y-y_1` `= m(x-x_1)`  
`y-b^2/(4a^2)` `= (2a^2)/b(x-(-b))`  
`y` `= (2a^2x)/b + 2a^2 + b^2/(4a^2)`  
`y` `= (2a^2x)/b +(8a^4 + b^2)/(4a^2)`  

 
Points of intersection of normal and parabola (Using CAS)

solve `((2a^2x)/b +(8a^4 + b^2)/(4a^2) = x^2/(4a^2),x)`

`x =-b`  or  `x = (8a^4+b^2)/b`

 
Calculate area using CAS

`A = \int_{-b}^{(8a^4+b^2)/b}\left(\frac{2a^2x}{b} +\frac{8a^4 + b^2}{4a^2}-frac{x^2}{4a^2} \right) dx`

`A = frac{64a^12 + 48a^8b^2 + 12a^4b^4 + b^6}{3a^2b^3}`
 
Using CAS Solve derivative of `A = 0`  with respect to `b` to find `b`

solve`(d/(db)(frac{64a^12 + 48a^8b^2 + 12a^4b^4 + b^6}{3a^2b^3})=0,b)`

 
`b =-2a^2`   and  `b = 2a^2`

Given `b > 0`

`b = 2a^2`


♦♦ Mean mark (e) 33%.
MARKER’S COMMENT: Common errors: Students found `\int_{-b}^{\frac{8 a^4+b^2}{b}}\left(y_n\right) d x` and failed to subtract `g(x)` or had incorrect terminals.

Calculus, MET2 2023 VCAA 1

Let \(f:R \rightarrow R, f(x)=x(x-2)(x+1)\). Part of the graph of \(f\) is shown below.

  1. State the coordinates of all axial intercepts of \(f\).   (1 mark)
  2. Find the coordinates of the stationary points of \(f\).   (2 marks)
    1. Let \(g:R\rightarrow R, g(x)=x-2\).
    2. Find the values of \(x\) for which \(f(x)=g(x)\).   (1 mark)
    1. Write down an expression using definite integrals that gives the area of the regions bound by \(f\) and \(g\).  (2 marks)
    2. Hence, find the total area of the regions bound by \(f\) and \(g\), correct to two decimal places.   (1 mark)
  1. Let \(h:R\rightarrow R, h(x)=(x-a)(x-b)^2\), where \(h(x)=f(x)+k\) and \(a, b, k \in R\).
  2. Find the possible values of \(a\) and \(b\).   (4 marks)
Show Answers Only

a.    \((-1, 0), (0, 0), (2, 0)\)

b.    \(\Bigg(\dfrac{1-\sqrt{7}}{3}, \dfrac{2(7\sqrt{7}-10}{27}\Bigg), \Bigg(\dfrac{1+\sqrt{7}}{3}, \dfrac{-2(7\sqrt{7}-10}{27}\Bigg)\)

c.i.  \(x=2,\ \text{or}\ x=\dfrac{-1\pm \sqrt{5}}{2}\)

c.ii. \(\text{Let }a=\dfrac{-1-\sqrt{5}}{2}\ \text{and }b=\dfrac{-1+\sqrt{5}}{2}\)

 \(\text{Then}\ A=\displaystyle\int_a^b (x-2)(x^2+x-1)\,dx+\displaystyle\int_b^2 -(x-2)(x^2+x-1)\,dx\)

c.iii. \(5.95\)

d.   \(\text{1st case }\rightarrow \ a=\dfrac{2\sqrt{7}+1}{3}, b=\dfrac{1-\sqrt{7}}{3}\)

\(\text{2nd case }\rightarrow \ a=\dfrac{-2\sqrt{7}+1}{3}, b=\dfrac{1+\sqrt{7}}{3}\)

Show Worked Solution

a.    \((-1, 0), (0, 0), (2, 0)\)
  

b.    \(\text{Using CAS solve for}\ x:\)

\(\dfrac{d}{dx}(x(x-2)(x+1))=0\)

\(\therefore\ x=\dfrac{1-\sqrt{7}}{3}\ \text{and }x=\dfrac{1+\sqrt{7}}{3}\)

\(\text{Substitute }x\ \text{values into }f(x)\ \text{using CAS to get}\ y\ \text{values}\)

\(\text{The stationary points of }f\ \text{are}:\)

\(\Bigg(\dfrac{1-\sqrt{7}}{3}, \dfrac{2(7\sqrt{7}-10}{27}\Bigg), \Bigg(\dfrac{1+\sqrt{7}}{3}, \dfrac{-2(7\sqrt{7}-10}{27}\Bigg)\)
  

ci    \(\text{Given }f(x)=g(x)\)

\(x(x-2)(x+1)\) \(=x-2\)
\(x(x-2)(x+1)(x-2)\) \(=0\)
\((x-2)(x(x+1)-1)\) \(=0\)
\((x-2)(x^2+x-1)\) \(=0\)

  
\(\therefore\ \text{Using CAS: } \)

\(x=2,\ \text{or}\ x=\dfrac{-1\pm \sqrt{5}}{2}\)

cii  \(\text{Area of bounded region:}\)

\(\text{Let }a=\dfrac{-1-\sqrt{5}}{2}\ \text{and }b=\dfrac{-1+\sqrt{5}}{2}\)

\(\text{Then}\ A=\displaystyle\int_a^b (x-2)(x^2+x-1)\,dx+\displaystyle\int_b^2 -(x-2)(x^2+x-1)\,dx\)
  

ciii  \(\text{Solve the integral in c.ii above using CAS:}\)
  \(\text{Total area}=5.946045..\approx 5.95\)

  

d.   \(\text{Method 1 – Equating coefficients}\)

\((x-a)(x-b)^2=x(x-2)(x+1)+k\)

\(x^3-2bx^2-ax^2+b^2x+2abx-ab^2=x^3-x^2-2x+k\)

\((x^3-(a+2b)x^2+(2ab+b^2)x-ab^2=x^3-x^2-2x+k\)

\(\therefore\ -(a+2b)=-1\ \to\ a=1-2b …(1)\)

\(2ab+b^2=-2\ \ …(2)\)

\(\text{Substitute (1) into (2) and solve for }b.\)

\(2b(1-2b)+b^2\) \(=-2\)
\(3b^2-2b-2\) \(=0\)
\(b\) \(=\dfrac{1\pm \sqrt{7}}{3}\)
\(\text{When }b\) \(=\dfrac{1+\sqrt{7}}{3}\)
\(a\) \(=1-2\Bigg(\dfrac{1+\sqrt{7}}{3}\Bigg)=\dfrac{-2\sqrt{7}+1}{3}\)
\(\text{When }b\) \(=\dfrac{1-\sqrt{7}}{3}\)
\(a\) \(=1-2\Bigg(\dfrac{1-\sqrt{7}}{3}\Bigg)=\dfrac{2\sqrt{7}+1}{3}\)

  

\(\text{Method 2 – Using transformations}\)

\(\text{The squared factor in }(x-a)(x-b)^2=x(x-2)(x+1)+k,\)

\(\text{shows that the turning point is on the }x\ \text{axis}.\)

\(\therefore\ \text{Lowering }f(x)\ \text{by }\dfrac{2(7\sqrt{7}-10)}{27}\ \text{and raising }f(x)\ \text{by }\dfrac{2(7\sqrt{7}+10)}{27}\)

\(\text{will give the 2 possible sets of values for }a\ \text{and}\ b.\)

\(\text{1st case – lowering using CAS solve }h(x) =0\ \rightarrow\ h(x)=f(x)-\dfrac{2(7\sqrt{7}-10)}{27}\)

\(\therefore\ x-\text{intercepts}\rightarrow \ a=\dfrac{2\sqrt{7}+1}{3}, b=\dfrac{1-\sqrt{7}}{3}\)

\(\text{2nd case – raising using CAS solve }h(x) =0\ \rightarrow\ h(x)=f(x)+\dfrac{2(7\sqrt{7}+10)}{27}\)

\(\therefore\ x-\text{intercepts}\rightarrow \ a=\dfrac{-2\sqrt{7}+1}{3}, b=\dfrac{1+\sqrt{7}}{3}\)

 

Calculus, MET2 2023 VCAA 14 MC

A polynomial has the equation  \(y=x(3x-1)(x+3)(x+1)\).

The number of tangents to this curve that pass through the positive \(x\)-intercept is

  1. 0
  2. 1
  3. 2
  4. 3
  5. 4
Show Answers Only

\(D\)

Show Worked Solution

\(\text{Positive}\ x\text{-intercept occurs at}\ \Big(\dfrac{1}{3}, 0\Big) \)

\(\text{Find tangent line at}\ \ x=a\ \text{(by CAS):}\)

\(y_{\text{tang}}=\Big(12a^3+33a^2+10a-3\Big)x-a^2\Big(9a^2+22a+5\Big)\)

\(\text{Solve}\ \ \ y_{\text{tang}}\Bigg(\dfrac{1}{3}\Bigg)=0\ \text{for }a:\)

\(a=\dfrac{-\sqrt{7}-4}{3},\ a=\dfrac{\sqrt{7}-4}{3}\text{ or}\ a=\dfrac{1}{3}\)

\(\therefore\ \text{3 solutions exist.}\)

\(\Rightarrow D\)

\(\text{NOTE: Graphical methods could also be used}\)


♦♦♦ Mean mark 29%.

Calculus, MET2 2020 VCAA 5

Let  `f: R to R, \ f(x)=x^{3}-x`.

Let  `g_{a}: R to R`  be the function representing the tangent to the graph of `f` at  `x=a`, where  `a in R`.

Let `(b, 0)` be the `x`-intercept of the graph of `g_{a}`.

  1. Show that  `b= {2a^{3}}/{3 a^{2}-1}`.   (3 marks)

  2. State the values of `a` for which `b` does not exist.    (1 mark)

  3. State the nature of the graph of `g_a` when `b` does not exist.   (1 mark)

  4. i.  State all values of `a` for which  `b=1.1`. Give your answer correct to four decimal places.   (1 mark)

  5. ii. The graph of `f` has an `x`-intercept at (1, 0).
  6.      State the values of  `a`  for which  `1 <= b <= 1.1`.
  7.      Give your answers correct to three decimal places.   (1 mark)

The coordinate `(b, 0)` is the horizontal axis intercept of `g_a`.

Let `g_b` be the function representing the tangent to the graph of `f` at  `x=b`, as shown in the graph below.
 
 
     
 

  1. Find the values of `a` for which the graphs of `g_a` and `g_b`, where `b` exists, are parallel and where  `b!=a`.   (3 marks)

Let  `p:R rarr R, \ p(x)=x^(3)+wx`, where  `w in R`.

  1. Show that  `p(-x)=-p(x)`  for all  `w in R`.   (1 mark)

A property of the graphs of `p` is that two distinct parallel tangents will always occur at `(t, p(t))` and `(-t,p(-t))` for all  `t!=0`.

  1. Find all values of `w` such that a tangent to the graph of `p` at `(t, p(t))`, for some  `t > 0`, will have an `x`-intercept at `(-t, 0)`.   (1 mark)

  2. Let  `T:R^(2)rarrR^(2),T([[x],[y]])=[[m,0],[0,n]][[x],[y]]+[[h],[k]]`, where  `m,n in R text(\{0})`  and  `h,k in R`.
     
    State any restrictions on the values of `m`, `n`, `h`, and `k`, given that the image of `p` under the transformation `T` always has the property that parallel tangents occur at  `x = -t`  and  `x = t`  for all  `t!=0`.   (1 mark)

Show Answers Only
  1. `text(See Worked Solutions.)`
  2. `a=+-sqrt3/3`
  3. `text(Horizontal line.)`
  4.  i. `a=-0.5052, 0.8084, 1.3468`
  5. ii. `a in (-0.505,-0.500]uu(0.808,1.347)`
  6. `a=+- sqrt5/5`
  7. `text(See Worked Solutions.)`
  8. `w=-5t^2`
  9. `h=0`
Show Worked Solution

a.   `f^{prime}(a) = 3a^2-1`

`g_a(x)\ \ text(has gradient)\ \ 3a^2-1\ \ text(and passes through)\ \ (a, a^3-a)`

`g_a(x)-(a^3-a)` `=(3a^2- 1)(x-a)`  
`g_a(x)` `=(3a^2-1)(x-a)+a^3-a`  

  
`x^{primeprime}-text(intercept occurs at)\ (b,0):`

`0=(3a^2-1)(b-a) + a^3-a`

`(3a^2-1)(b-a)` `=a-a^3`  
`3a^2b-3a^3-b+a` `=a-a^3`  
`b(3a^2-1)` `=a-a^3+3a^3-a`  
`:.b` `=(2a^3)/(3a^2-1)`  

 
b.   `b\ text{does not exist when:}`

♦ Mean mark part (b) 46%.

`(3a^2-1)=0`

`a=+-sqrt3/3`

♦♦ Mean mark part (c) 23%.
 

c.   `text{If}\ \ a=+-sqrt3/3,\ \ g_a^{prime}(x) = 0`

`=>\ text{the graph is a horizontal line (does not cross the}\ xtext{-axis).}`
 

d.i.  `text(Solve)\ {2a^{3}}/{3 a^{2}-1}=1.1\ text(for)\ a:`

`a=-0.5052\ text(or )\ =0.8084\ text(or)\ a=1.3468\ \ text{(to 4 d.p.)}`
  

d.ii.  `text(Solve)\ 1 <= (2a^(3))/(3a^(2)-1) < 1.1\ text(for)\ a:`

♦♦♦ Mean mark part (d)(ii) 13%.

`a in (-0.505,-0.500]uu(0.808,1.347)\ \ text{(to 3 d.p.)}`
 

e.   `f^{prime}(b) = 3b^2-1`

`g_b(x)\ \ text(has gradient)\ \ 3b^2-1\ \ text(and passes through)\ \ (b, b^3-b)`

`g_b(x)-(b^3-b)` `=(3b^2-1)(x-b)`  
`g_b(x)` `=(3b^2-1)(x-b)+b^3-b`  

 
`g_a(x)\ text{||}\ g_b(x)\ \ text{when}`

♦♦♦ Mean mark part (e) 13%.
`3a^2-1` `=3b^2-1`  
  `=3 cdot((2a^3)/(3a^2-1))-1`  

 
`=> a=+-1, +- sqrt5/5, 0`

`text(Test each solution so that)\ \ b!=a :`

`text(When)\ \ a=+-1, 0 \ => \ b=a`

`:. a=+- sqrt5/5`
 

f.    `p(-x)` `=(-x)^3-wx`
    `=-x^3-wx`
    `=-(x^3+wx)`
    `=-p(x)`

 
g.  `p^{prime}(t) = 3t^2+w`

♦♦♦ Mean mark part (g) 3%.

`p(t)\ \ text(has gradient)\ \ 3t^2+w\ \ text(and passes through)\ \ (t, t^3+wt)`

`p(t)-(t^3+wt)` `=(3t^2+w)(x-t)`  
`p(t)` `=(3t^2+w)(x-t) + t^3+wt`  

 
`text{If}\ p(t)\ text{passes through}\ \ (-t, 0):`

`0=(3t^2+w)(-2t) + t^3+wt`

`=>w=-5t^2\ \ (t>0)`
 

h.   `text{Property of parallel tangents is retained under transformation}`

♦♦♦ Mean mark part (h) 2%.

`text{if rotational symmetry remains (odd function).}`

`=>h=0`

`text(No further restrictions apply to)\ m, n\ \ text{or}\ \ k.`

Calculus, MET2 2021 VCAA 7 MC

The tangent to the graph of  `y = x^3 - ax^2 + 1`  at  `x = 1` passes through the origin.

The value of `a` is

  1. `1/2`
  2. `1`
  3. `3/2`
  4. `2`
  5. `5/2`
Show Answers Only

`B`

Show Worked Solution
`y` `= x^3 – ax^2 + 1`
`dy/dx` `= 3x^2 – 2ax`

 
`text{At} \ \ x = 1 \ => \  y = 2-a, \ dy/dx = 3-2a`
 

`text{T} text{angent passes through} \ (1,2-a) \ text{and} \ (0,0)`

`m_text{tang} = 2 – a`

`text{Equating gradients:}`

`3-2a` `= 2-a`
`:. a` `= 1`

 
`=> B`

Calculus, MET2 2019 VCAA 5

Let  `f: R -> R, \ f(x) = 1-x^3`. The tangent to the graph of `f` at  `x = a`, where  `0 < a < 1`, intersects the graph of `f` again at `P` and intersects the horizontal axis at `Q`. The shaded regions shown in the diagram below are bounded by the graph of `f`, its tangent at  `x = a`  and the horizontal axis.
 

  1. Find the equation of the tangent to the graph of `f` at  `x = a`, in terms of `a`.   (1 mark)

  2. Find the `x`-coordinate of `Q`, in terms of `a`.   (1 mark)

  3. Find the `x`-coordinate of `P`, in terms of `a`.   (2 marks)

Let  `A`  be the function that determines the total area of the shaded regions.

  1. Find the rule of `A`, in terms of `a`.   (3 marks)

  2. Find the value of `a` for which `A` is a minimum.   (2 marks)

Consider the regions bounded by the graph of `f^(-1)`, the tangent to the graph of `f^(-1)` at  `x = b`, where  `0 < b < 1`, and the vertical axis.

  1. Find the value of `b` for which the total area of these regions is a minimum.   (2 marks)

  2. Find the value of the acute angle between the tangent to the graph of `f` and the tangent to the graph of `f^(-1)` at  `x = 1`.   (1 mark)

Show Answers Only
  1. `y = 2a^3-3a^2x + 1`
  2. `(2a^3 + 1)/(3a^2)`
  3. `-2a`
  4. `(80a^6 + 8a^3-9a^2 + 2)/(12a^2)`
  5. `10^(-1/3)`
  6. `9/10`
  7. `tan^(-1)(1/3)`
Show Worked Solution

a.   `f(x) = 1-x^3,\ \ f^{\prime}(x) = -3x^2`

`m_text(tang) = -3a^2\ \ text(through)\ \ (a, 1-a^3)`

`y = 2a^3-3a^2x + 1`
 

b.   `text(Solve for)\ \x:`

`2a^3-3a^2x + 1 = 0`

`x = (2a^3 + 1)/(3a^2)`
 

c.   `text(Solve for)\ \ x:`

`2a^3-3a^2x + 1 = 1-x^3`

`x=-2a`

`:. x text(-coordinate of)\ P = -2a`
 

d.   `P(-2a, 8a^3 + 1),\ \ Q((2a^3 + 1)/(3a^2), 0)`

`A` `= text(Area of triangle)-int_(-2a)^1 f(x)\ dx`
  `= 1/2((2a^3 + 1)/(3a^2) + 2a)(8a^3 + 1)-int_(-2a)^1 1-x^3\ dx`
  `= (80a^6 + 8a^3-9a^2 + 2)/(12a^2)\ \ text{(by CAS)}`

 

e.   `text(Solve for)\ a: \ (dA)/(da) = 0\ \ text{(by CAS)}`

`a = 10^(-1/3)`
 

f.   `text(Consider)\ f(x):\ \ f(10^(-1/3)) = 9/10`

`A_text(min)\ text(for)\ \ f(x)\ \ text(occurs at)\ \ (10^(-1/3), 9/10)`

`=> A_text(min)\ text(for)\ \ f^(-1)(x)\ \ text(occurs when)\ \ x=9/10`

`:. b = 9/10`
 

g.   `f^{\prime} (1)  = -3`

`text(Gradient of)\ \  f^(-1)(x)\ \ text(at)\ \ x = 1\ \ text(is vertical line.)`

`tan theta` `= 1/3`
`theta` `= tan^(-1)(1/3)`
  `=18.4°\ \ text{(to 1 d.p.)}`

Calculus, MET2 2016 VCAA 2

Consider the function  `f(x) = -1/3 (x + 2) (x-1)^2.`

  1.  i. Given that  `g^{′}(x) = f (x) and g (0) = 1`,
  2.      show that  `g(x) = -x^4/12 + x^2/2-(2x)/3 + 1`.   (1 mark)

  3. ii. Find the values of `x` for which the graph of  `y = g(x)`  has a stationary point.   (1 mark)

The diagram below shows part of the graph of  `y = g(x)`, the tangent to the graph at  `x = 2`  and a straight line drawn perpendicular to the tangent to the graph at  `x = 2`. The equation of the tangent at the point `A` with coordinates  `(2, g(2))`  is  `y = 3-(4x)/3`.

The tangent cuts the `y`-axis at `B`. The line perpendicular to the tangent cuts the `y`-axis at `C`.
 


 

  1.   i. Find the coordinates of `B`.   (1 mark)

  2.  ii. Find the equation of the line that passes through `A` and `C` and, hence, find the coordinates of `C`.   (2 marks)

  3. iii. Find the area of triangle `ABC`.   (2 marks)

  4. The tangent at `D` is parallel to the tangent at `A`. It intersects the line passing through `A` and `C` at `E`.

     


     
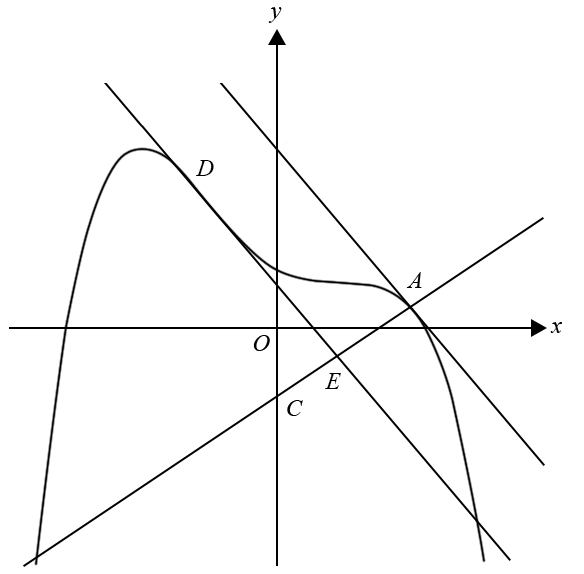
     i. Find the coordinates of `D`.   (2 marks)

  5. ii. Find the length of `AE`.   (3 marks)

Show Answers Only
  1.  i. `text(Proof)\ \ text{(See worked solutions)}`
  2. ii. `x = -2, 1`
  3.   i. `(0, 3)`
  4. ii. `y = 3/4 x-7/6`
  5.      `(0, -7/6)`
  6. iii. `25/6\ text(u²)`
  7. `(-1, 25/12)`
  8. `27/20\ text(u)`
Show Worked Solution
a.i.    `g(x)` `= int f(x)\ dx`
    `=-1/3 int (x + 2) (x-1)^2\ dx`
    `=-1/3int(x^3-3x+2)\ dx`
  `:.g(x)` `= -x^4/12 + x^2/2-(2x)/3 + c`

 
`text(S)text(ince)\ \ g(0) = 1,`

`1` `= 0 + 0-0 + c`
`:. c` `= 1`

  
`:. g(x) = -x^4/12 + x^2/2-(2x)/3 + 1\ \ …\ text(as required)`
 

a.ii.   `text(Stationary point when:)`

`g^{′}(x) = f(x) = 0`

`-1/3(x + 2) (x-1)^2=0`

`:. x = -2, 1`
 

b.i.   

`B\ text(is the)\ y text(-intercept of)\ \ y = 3-4/3 x`

`:. B (0, 3)`
 

b.ii.   `m_text(norm) = 3/4, \ text(passes through)\ \ A(2, 1/3)`

   `text(Equation of normal:)`

`y-1/3` `=3/4(x-2)`
`y` `=3/4 x-7/6`
   

`:. C (0, -7/6)`
 

b.iii.   `text(Area)` `= 1/2 xx text(base) xx text(height)`
    `= 1/2 xx (3 + 7/6) xx 2`
    `= 25/6\ text(u²)`

 

♦ Mean mark part (c)(i) 43%.
MARKER’S COMMENT: Many students gave an incorrect `y`-value here. Be careful!
c.i.    `text(Solve)\ \ \ g^{′}(x)` `= -4/3\ \ text(for)\ \ x < 0`
  `=> x` `= -1`
  `g(-1)` `=-1/12+1/2+2/3+1`
    `=25/12`

  
`:. D (−1, 25/12)`
 

c.ii.   `text(T) text(angent line at)\ \ D:`

`y-25/12` `=-4/3(x+1)`
`y` `=-4/3x + 3/4`

 
`DE\ \ text(intersects)\ \ AE\ text(at)\ E:`

♦♦ Mean mark 32%.
`-4/3 x + 3/4` `= 3/4 x-7/6`
`25/12 x` `= 23/12`
`x` `=23/25`

 
`:. E (23/25, -143/300)`
 

`:. AE` `= sqrt((2-23/25)^2 + (1/3-(-143/300))^2)`
  `= 27/20\ text(units)`

Calculus, MET2 2016 VCAA 10 MC

For the curve  `y = x^2 - 5`, the tangent to the curve will be parallel to the line connecting the positive x-intercept and the y-intercept when `x` is equal to

A.   `sqrt 5`

B.   `5`

C.   `−5`

D.   `sqrt 5/2`

E.   `1/sqrt 5`

Show Answers Only

`D`

Show Worked Solution

`text{Intercepts: (0, −5) and}\ (sqrt 5, 0)`

`text(Gradient between intercepts:)`

`m = (0 – (−5))/(sqrt 5 – 0) = 5/sqrt 5`

`text(Solve:)`

`f prime (x)` `= 5/sqrt 5`
`2x` `= 5/sqrt 5`
`:. x` `=5/(2sqrt5) xx sqrt5/sqrt5`
  `= sqrt 5/2`

 
`=>   D`

Calculus, MET2 2015 VCAA 1

Let  `f: R -> R,\ \ f(x) = 1/5 (x-2)^2 (5-x)`. The point  `P(1, 4/5)`  is on the graph of  `f`, as shown below.

The tangent at `P` cuts the y-axis at `S` and the x-axis at `Q.`

VCAA 2015 1ai

  1. Write down the derivative  `f^{prime} (x)` of `f (x)`.   (1 mark)

  2.  i. Find the equation of the tangent to the graph of  `f` at the point  `P(1, 4/5)`.   (1 mark)

    ii. Find the coordinates of points `Q` and `S`.   (2 marks)

  3. Find the distance `PS` and express it in the form  `sqrt b/c`, where `b` and `c` are positive integers.  (2 marks)

VCAA 2015 1di

  1. Find the area of the shaded region in the graph above.   (3 marks)

Show Answers Only
  1. `-3/5(x-4)(x-2)`
  2.  i.`y = -9/5x + 13/5`
    ii. `S (0, 13/5), \ \ Q (13/9, 0)`
  3. `sqrt 106/5`
  4. `108/5\ text(units²)`
Show Worked Solution
a.    `f(x)` `= 1/5 (x-2)^2 (5-x)`
  `f^{prime}(x)` `=1/5 xx 2(x-2)(5-x)-1/5 (x-2)^2`
    `= -3/5(x-4)(x-2)`

 

b.i.   `text(Solution 1)`

`y = -9/5x + 13/5qquad[text(CAS:tangentLine)\ (f(x),x,1)]`
  

`text(Solution 2)`

`m_text(tan) = -9/5,\ \ text(through)\ \ (1, 4/5)`

`y-4/5` `=-9/5 (x-1)`
`y` `=-9/5 x +13/5`

  
b.ii.   `text(At)\ S,\ \ x=0`

`y =-9/5 xx 0 + 13/5 = 13/5`

`:. S(0,13/5)`
  

`text(At)\ Q,\ \ y=0`

`0` `=-9/5x + 13/5`
`x` `=13/5 xx 5/9=13/9`

 
`:. Q(13/9,0)`
  

c.   `P(1, 4/5),\ \ S(0,13/5)`

`text(dist)\ PS` `=sqrt((x_2-x_1)^2 + (y_2-y_1)^2)`
  `= sqrt((1-0)^2 + (4/5-13/5)^2)`
  `= (sqrt106)/5`

 

d.   `text(Find intersection pts of)\ SQ\ text(and)\ f(x),`

MARKER’S COMMENT: Many students complicated their answer by splitting up the area.

`text{Solve (using technology):}`

`1/5 (x-2)^2 (5-x) =-9/5x + 13/5`

`x = 1,7`

`:.\ text(Area)` `= int_1^7(f(x)-(-9/5x + 13/5))dx`
  `= 108/5\ text(u²)`

Calculus, MET2 2013 VCAA 4

Part of the graph of a function `g: R -> R, \ g (x) = (16-x^2)/4` is shown below.

VCAA 2013 4a

  1. Points `B` and `C` are the positive `x`-intercept and `y`-intercept of the graph `g`, respectively, as shown in the diagram above. The tangent to the graph of `g` at the point `A` is parallel to the line segment `BC.`
    1. Find the equation of the tangent to the graph of `g` at the point `A.`   (2 marks)

    2. The shaded region shown in the diagram above is bounded by the graph of `g`, the tangent at the point `A`, and the `x`-axis and `y`-axis.
    3. Evaluate the area of this shaded region.   (3 marks)
  2. Let `Q` be a point on the graph of  `y = g(x)`.
  3. Find the positive value of the `x`-coordinate of `Q`, for which the distance `OQ` is a minimum and find the minimum distance.   (3 marks)

The tangent to the graph of `g` at a point `P` has a negative gradient and intersects the `y`-axis at point  `D(0, k)`, where  `5 <= k <= 8.`
 

VCAA 2013 4c
 

  1. Find the gradient of the tangent in terms of `k.`   (2 marks)

  2.   i. Find the rule `A(k)` for the function of `k` that gives the area of the shaded region.   (2 marks)

  3.  ii. Find the maximum area of the shaded region and the value of `k` for which this occurs.   (2 marks)

  4. iii. Find the minimum area of the shaded region and the value of `k` for which this occurs.  (2 marks)

Show Answers Only
    1. `A: y = 5-x`
    2. `text(See Worked Solutions)`
  2. `2sqrt3\ text(units when)\ x = 2sqrt2`
  3. `gprime(2sqrt(k-4)) =-sqrt(k-4)`
    1. `A(k) = (k^2)/(2sqrt(k-4))-32/3, k ∈ [5,8]`
    2. `A_text(max) = 16/3quadtext(when)quadk = 8`
    3. `A_text(min) = (64sqrt3)/9-32/3quadtext(when)quadk = 16/3`
Show Worked Solution

a.i.   `B(4,0), C(0,4), A(a,(16-a^2)/4)`

`m_(BC) = m_text(tan) = (4-0)/(0-4) = -1`

`g(x)` `= (16-x^2)/4`
`g^{prime}(x)` `=-x/2`

 
`text(S)text(ince)\ \ g^{prime}(a) = -1,`

`=>a = 2`

`text(T)text(angent passes through)\ \ (2,3),`

`y-3` `=-(x-2)`
`y` `=-x + 5`

 
`text(Alternatively, using technology:)`

`[text(CAS: tangent Line)]\ (g(x),x,2)`
 

a.ii.   `text(Solution 1)`

♦ Mean mark 37%.
MARKER’S COMMENT: A common incorrect answer:
`int_0^5((-x+5)-g(x))dx=35/12`.  Know why it’s wrong!

  `D(5,0), E(0,5)`

`text(Area)` `= DeltaEOD-int_0^4 g(x)\ dx`
  `= 1/2 xx 5 xx 5-32/3`
  `= 11/6\ text(u²)`

 
`text(Solution 2)`

`text(Area)` `= int_0^5 (-x+5)\ dx-int_0^4 g(x)\ dx`
  `= 11/6\ text(u²)`

 

b.   `Q(x, (16-x^2)/4), O(0,0)`

♦♦♦ Mean mark 20%.
`z` `= OQ`
  `= sqrt(x^2 + ((16-x^2)/4)^2), x > 0`

 
`text(Max or min when)\ \ (dz)/(dx)=0,`

`text(Solve:)\ (dz)/dx = 0quadtext(for)quadx > 0`

`=> x = 2sqrt2`

`=>z(2sqrt2) = 2sqrt3`

`:. text(Min distance of)\ \ 2sqrt3\ \ text(units when)\ \ x = 2sqrt2`
 

c.   `text(Let)\ \ P(p, (16-p^2)/4)`

♦♦♦ Mean mark 8%.

`m_text(tan)\ text(at)\ P =-p/2`

`m_(PD) = ((16-p^2)/4-k)/(p-0)`
 

`text(Equating gradients,)`

`text(Solve:)\ \ ((16-p^2)/4-k)/p=-p/2\ \ text(for)\ p,`

`=> p=2sqrt(k-4)`
 

 `:.\ text(Gradient of tangent:)`

`g^{prime}(2sqrt(k-4)) =-sqrt(k-4)`
 

d.i.   `text(Equation of tangent:)`

♦♦♦ Mean mark 8%.

`y = -sqrt(k-4)x + k`

`text(CAS: tangent Line)\ (g(x),x,2sqrt(k-4))`

`xtext(-int of tangent:)\ x = k/(sqrt(k-4))`
 

`:. A(k)` `= 1/2 xx (k/(sqrt(k-4))) xx k-int_0^4 g(x)\ dx`
  `= (k^2)/(2sqrt(k-4))-32/3, \ \ k ∈ [5,8]`

 

d.ii.   `text(Solve:)\ \ A(k)=0quadtext(for)quadk ∈ [5,8]`

♦♦♦ Mean mark 5%.

`=> k=16/3`

  `text(Sketch the graph of)\ \ A(k)\ \ text(for)\ \ 5<=k<=8`

 

 met2-2013-vcaa-sec4-answer

`:. A_text(max) = 16/3quadtext(when)quadk = 8`
 

d.iii.   `A_text(min)\ text(occurs at the turning point)\ (k=16/3).`

♦♦♦ Mean mark 3%.
 `A_text(min)` `=A(16/3)`
  `=(64sqrt3)/9-32/3`

Calculus, MET2 2015 VCAA 4 MC

Consider the tangent to the graph of  `y = x^2`  at the point  `(2, 4).`

Which of the following points lies on this tangent?

A.   `text{(1, −4)}`

B.   `(3, 8)`

C.   `text{(−2, 6)}`

D.   `(1, 8)`

E.   `text{(4, −4)}`

Show Answers Only

`B`

Show Worked Solution

`text(Find equation of tangent line)`

`text(at)\ x = 2:`

`y = 4x – 4qquadtext([CAS: tangentLine) (x^2,x,2)]`

`(3,8)\ \ text(is on)\ y = 4x – 4`

`=>   B`