smc-643-10-Single Box-Plots

Data Analysis, GEN2 2024 VCAA 2

The boxplot below displays the distribution of all gold medal-winning heights for the women's high jump, \(\textit{Wgold}\), in metres, for the 19 Olympic Games held from 1948 to 2020.

Describe the shape of this data distribution. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
For this boxplot, what is the smallest possible number of \(\textit{Wgold}\) heights lower than 1.85 m (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
i. Using the boxplot, show that the lower fence is 1.565 m and the upper fence is 2.325 m. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
ii. Referring to the boxplot, the lower fence and the upper fence, explain why no outliers exist. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

a. \(\text{Negatively skewed}\)

b. \(1\)

c.i. \(Q_1=1.85,\ Q_3=2.04,\ IQR=2.04-1.85=0.19\)

\(\text{Lower Fence}\)	\(=Q_1-1.5\times IQR\)
	\(=1.85-1.5\times 0.19\)
	\(=1.565\)

\(\text{Upper Fence}\)	\(=Q_1+1.5\times IQR\)
	\(=2.04+1.5\times 0.19\)
	\(=2.325\)

c.ii. \(\text{No values exist below the lower fence or above the upper fence.}\)

\(\therefore\ \text{No outliers exist.}\)

Show Worked Solution

a. \(\text{Negatively skewed}\)

b. \(25\%\ \text{of the games had heights}\ <1.85\ \text{m}\)

\(25\%\times 19= 4.75\rightarrow 4\ \text{games}\)

\(\therefore\ \text{The smallest number of games is 1}\)

c.i. \(Q_1=1.85,\ Q_3=2.04,\ IQR=2.04-1.85=0.19\)

\(\text{Lower Fence}\)	\(=Q_1-1.5\times IQR\)
	\(=1.85-1.5\times 0.19\)
	\(=1.565\)

\(\text{Upper Fence}\)	\(=Q_1+1.5\times IQR\)
	\(=2.04+1.5\times 0.19\)
	\(=2.325\)

c.ii. \(\text{No values exist below the lower fence or above the upper fence.}\)

\(\therefore\ \text{No outliers exist.}\)

Data Analysis, GEN2 2024 VCAA 1

Table 1 lists the Olympic year, \(\textit{year}\), and the gold medal-winning height for the men's high jump, \(\textit{Mgold}\), in metres, for each Olympic Games held from 1928 to 2020. No Olympic Games were held in 1940 or 1944, and the 2020 Olympic Games were held in 2021.

Table 1

\begin{array}{|c|c|}
\hline \quad \textit{year} \quad & \textit{Mgold}(m) \\
\hline 1928 & 1.94 \\
\hline 1932 & 1.97 \\
\hline 1936 & 2.03 \\
\hline 1948 & 1.98 \\
\hline 1952 & 2.04 \\
\hline 1956 & 2.12 \\
\hline 1960 & 2.16 \\
\hline 1964 & 2.18 \\
\hline 1968 & 2.24 \\
\hline 1972 & 2.23 \\
\hline 1976 & 2.25 \\
\hline 1980 & 2.36 \\
\hline 1984 & 2.35 \\
\hline 1988 & 2.38 \\
\hline 1992 & 2.34 \\
\hline 1996 & 2.39 \\
\hline 2000 & 2.35 \\
\hline 2004 & 2.36 \\
\hline 2008 & 2.36 \\
\hline 2012 & 2.33 \\
\hline 2016 & 2.38 \\
\hline 2020 & 2.37 \\
\hline
\end{array}

For the data in Table 1, determine:
1. the maximum \(\textit{Mgold}\) in metres (1 mark)
  
  --- 1 WORK AREA LINES (style=lined) ---
2. the percentage of \(\textit{Mgold}\) values greater than 2.25 m. (1 mark)
  
  --- 2 WORK AREA LINES (style=lined) ---
The mean of these \(\textit{Mgold}\) values is 2.23 m , and the standard deviation is 0.15 m .
Calculate the standardised \(z\)-score for the 2000 \(\textit{Mgold}\) of 2.35 m. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Construct a boxplot for the \(\textit{Mgold}\) data in Table 1 on the grid below. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

A least squares line can also be used to model the association between \(\textit{Mgold}\) and \(\textit{year}\).
Using the data from Table 1, determine the equation of the least squares line for this data set.
Use the template below to write your answer.
Round the values of the intercept and slope to three significant figures. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

The coefficient of determination is 0.857
Interpret the coefficient of determination in terms of \(\textit{Mgold}\) and \(\textit{year}\). (1 mark)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a.i. \(2.39\)

a.ii. \(50\%\)

b. \(0.8\)

e. \(\text{A coefficient of determination of 85.7% shows the variation in the}\ Mgold\)

\(\text{that is explained by the variation in the }year.\)

Show Worked Solution

a.i. \(2.39\)

a.ii. \(\dfrac{11}{22}=50\%\)

b.	\(z\)	\(=\dfrac{x-\overline x}{s_x}\)
		\(=\dfrac{2.35-2.23}{0.15}\)
		\(=0.8\)

c. \(Q_2=\dfrac{2.33+2.25}{2}=2.29\)

\(Q_1=2.12, \ Q_3=2.36\)

\(\text{Min}\ =1.94, \ \text{Max}\ =2.39\)

d. \(\text{Using CAS:}\)

e. \(\text{A coefficient of determination of 85.7% shows the variation in the}\ Mgold\)

\(\text{that is explained by the variation in the }year.\)

Data Analysis, GEN1 2024 VCAA 5 MC

The number of siblings of each member of a class of 24 students was recorded.

The results are displayed in the table below.

\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} \quad 2 \quad \rule[-1ex]{0pt}{0pt} & \quad 1 \quad & \quad 3 \quad & \quad 2 \quad & \quad 1 \quad & \quad 1 \quad & \quad 1 \quad & \quad 4 \quad & \quad 1 \quad & \quad 1 \quad & \quad 1 \quad & \quad 1 \quad \\
\hline
\rule{0pt}{2.5ex} 1 \rule[-1ex]{0pt}{0pt} & 2 & 1 & 2 & 2 & 1 & 3 & 4 & 2 & 2 & 3 & 1 \\
\hline
\end{array}

A boxplot was constructed to display the spread of the data.

Which one of the following statements about this boxplot is correct?

There are no outliers.
The value of the interquartile range (IQR) is 1.5
The value of the median is 1.5
All of the five-number summary values are whole numbers.

Show Answers Only

\(C\)

Show Worked Solution

\(Q_1=1,\ Q_2=1.5,\ Q_3=2\rightarrow\ \text{eliminate D}\)

\(IQR=2-1=1\rightarrow\ \text{eliminate B}\)

\(Q_3+1.5\times IQR=2+1.5\times 1\rightarrow 4\ \text{is an outlier}\rightarrow\ \text{eliminate A}\)

\(Q_2=1.5 \longrightarrow \text{Median }=1.5\rightarrow\ \text{C correct}\)

\(\Rightarrow C\)

CORE, FUR2 2021 VCAA 1

In the sport of heptathlon, athletes compete in seven events.

These events are the 100 m hurdles, high jump, shot-put, javelin, 200 m run, 800 m run and long jump.

Fifteen female athletes competed to qualify for the heptathlon at the Olympic Games.

Their results for three of the heptathlon events – high jump, shot-put and javelin – are shown in Table 1.

Write down the number of numerical variables in Table 1. (1 mark)
Complete Table 2 below by calculating the mean height jumped for the high jump, in metres, by the 15 athletes. Write your answer in the space provided in the table. (1 mark)
In shot-put, athletes throw a heavy spherical ball (a shot) as far as they can.
Athlete number six, Jamilia, threw the shot 14.50 m.
Calculate Jamilia's standardised score (`z`).
Round your answer to one decimal place. (1 mark)
In the qualifying competition, the heights jumped in the high jump are expected to be approximately normally distributed.
Chara's jump in this competition would give her a standardised score of `z = –1.0`
Use the 68–95–99.7% rule to calculate the percentage of athletes who would be expected to jump higher than Chara in the qualifying competition. (1 mark)
The boxplot below was constructed to show the distribution of high jump heights for all 15 athletes in the qualifying competition.

Explain why the boxplot has no whisker at its upper end. (1 mark)
For the javelin qualifying competition (refer to Table 1), another boxplot is used to display the distribution of athlete's results.
An athlete whose result is displayed as an outlier at the upper end of the plot is considered to be a potential medal winner in the event.
What is the minimum distance that an athlete needs to throw the javelin to be considered a potential medal winner? (2 marks)

Show Answers Only

`3`
`1.81`
`0.5 \ text{(to d.p.)}`
`84text(%)`
`text{See Worked Solutions}`
`46.89 \ text{m}`

Show Worked Solution

a. `3 \ text{High jump, shot-put and javelin}`

`text{Athlete number is not a numerical variable}`

b. `text{High jump mean}`

`= (1.76 + 1.79 + 1.83 + 1.82 + 1.87 + 1.73 + 1.68 + 1.82 +`

`1.83 + 1.87 + 1.87 + 1.80 + 1.83 + 1.87 + 1.78) ÷ 15`

`= 1.81`

c.	`z text{-score} (14.50)`	`= {14.50 – 13.74}/{1.43}`
		`= 0.531 …`
		`= 0.5 \ text{(to 1 d.p.)}`

d. `P (z text{-score} > -1 ) = 84text(%)`

e. `text{If the} \ Q_3 \ text{value is also the highest value in the data set,}`

`text{there is no whisker at the upper end of a boxplot.}`

f. `text{Javelin (ascending):}`

`38.12, 39.22, 40.62, 40.88, 41.22, 41.32, 42.33, 42.41, `

`42.51, 42.65, 42.75, 42.88, 45.64, 45.68, 46.53`

`Q_1 = 40.88 \ \ , \ Q_3 = 42.88 \ \ , \ \ IQR = 42.88 – 40.88 = 2`

`text{Upper Fence}`	`= Q_3 + 1.5 xx IQR`
	`= 42.88 + 1.5 xx 2`
	`= 45.88`

`:. \ text{Minimum distance = 45.89 m (longer than upper fence value)}`

CORE, FUR2 2020 VCAA 2

The neck size, in centimetres, of 250 men was recorded and displayed in the dot plot below.

Write down the modal neck size, in centimetres, for these 250 men. (1 mark)
Assume that this sample of 250 men has been drawn at random from a population of men whose neck size is normally distributed with a mean of 38 cm and a standard deviation of 2.3 cm.
i. How many of these 250 men are expected to have a neck size that is more than three standard deviations above or below the mean?
Round your answer to the nearest whole number. (1 mark)
ii. How many of these 250 men actually have a neck size that is more than three standard deviations above or below the mean? (1 mark)
The five-number summary for this sample of neck sizes, in centimetres, is given below.

`qquad`

Use the five-number summary to construct a boxplot, showing any outliers if appropriate, on the grid below. (2 marks)

Show Answers Only

`text(Mode) = 38\ text(cm)`
1. `1`
2. `1`
`text(See Worked Solutions)`

Show Worked Solution

a. `text(Mode) = 38\ text(cm)`

♦ Mean mark part b.i. 40%.

b.i.	`text(Expected number of men)`	`= (1 – 0.997) xx 250`
		`= 0.75`
		`= 1\ text{(nearest whole)}`

♦ Mean mark part b.ii. 42%.

b.ii.	`text(When)\ \ z = +- 3`
	`text(Neck size limits)`	`= 38 +- (2.3 xx 3)`
		`= 44.9 or 31.1`

`:.\ text(1 man has neck size outside 3 s.d.)`

c. `IQR = 39-36=3`

`text(Upper fence)`	`=Q_3 + 1.5 xx 3`
	`=39 + 4.5`
	`=43.5`

`text(Lower fence)`	`=Q_1 – 1.5 xx 3`
	`=36 – 4.5`
	`=31.5`

CORE, FUR1-NHT 2019 VCAA 4 MC

The boxplot and dot plot shown below both display the distribution of the gestation period, in weeks, for 117 baby girls.

The median gestation period, in weeks, of these baby girls is

38
38.5
39
39.5
40

Show Answers Only

`E`

Show Worked Solution

`text(Median =) (117 + 1)/2 = 54text(th datapoint)`

`:.\ text(Median = 40)`

`=>\ E`

CORE, FUR1-NHT 2019 VCAA 1-2 MC

The histogram and boxplot shown below both display the distribution of the birth weight, in grams, of 200 babies.

Part 1

The shape of the distribution of the babies’ birth weight is best described as

positively skewed with no outliers.
negatively skewed with no outliers.
approximately symmetric with no outliers.
positively skewed with outliers.
approximately symmetric with outliers.

Part 2

The number of babies with a birth weight between 3000 g and 3500 g is closest to

Show Answers Only

`text(Part 1:)\ E`
`text(Part 2:)\ D`

Show Worked Solution

`text(Part 1)`

`text(Approximately symmetric with outliers.)`

`=>\ E`

`text(Part 2)`

`text(Column representing 3000 – 3500g) ~~ 37text(%)`

`text(37%) xx 200 = 74\ text(babies)`

`=> D`

CORE, FUR2 2018 VCAA 1

The data in Table 1 relates to the impact of traffic congestion in 2016 on travel times in 23 cities in the United Kingdom (UK).

The four variables in this data set are:

city — name of city
congestion level — traffic congestion level (high, medium, low)
size — size of city (large, small)
increase in travel time — increase in travel time due to traffic congestion (minutes per day).

How many variables in this data set are categorical variables? (1 mark)
How many variables in this data set are ordinal variables (1 mark)
Name the large UK cities with a medium level of traffic congestion. (1 mark)
Use the data in Table 1 to complete the following two-way frequency table, Table 2. (2 marks)
What percentage of the small cities have a high level of traffic congestion? (1 mark)

Traffic congestion can lead to an increase in travel times in cities. The dot plot and boxplot below both show the increase in travel time due to traffic congestion, in minutes per day, for the 23 UK cities.

Describe the shape of the distribution of the increase in travel time for the 23 cities. (1 mark)
The data value 52 is below the upper fence and is not an outlier.

Determine the value of the upper fence. (1 mark)

Show Answers Only

`3\ text(city, congestion level, size)`
`2\ text(congestion level, size)`
`text(Newcastle-Sunderland and Liverpool)`
`text(See Worked Solutions)`
`25 text(%)`
`text(Positively skewed)`
`52.5`

Show Worked Solution

a. `3\ – text(city, congestion level, size)`

b. `2\ – text(congestion level, size)`

c. `text(Newcastle-Sunderland and Liverpool)`

e.	`text(Percentage)`	`= text(Number of small cities high congestion)/text(Number of small cities) xx 100`
		`= 4/16 xx 100`
		`= 25 text(%)`

f. `text(Positively skewed)`

g. `IQR = 39 – 30 = 9`

`text(Calculate the Upper Fence:)`

`Q_3 + 1.5 xx IQR`	`= 39 + 1.5 xx 9`
	`= 52.5`

CORE, FUR1 2017 VCAA 1-3 MC

The boxplot below shows the distribution of the forearm circumference, in centimetres, of 252 people.

Part 1

The percentage of these 252 people with a forearm circumference of less than 30 cm is closest to

`text(15%)`
`text(25%)`
`text(50%)`
`text(75%)`
`text(100%)`

Part 2

The five-number summary for the forearm circumference of these 252 people is closest to

`\ \ \ 21,\ 27.4,\ 28.7,\ 30,\ 34`
`\ \ \ 21,\ 27.4,\ 28.7,\ 30,\ 35.9`
`24.5,\ 27.4,\ 28.7,\ 30,\ 34`
`24.5,\ 27.4,\ 28.7,\ 30,\ 35.9`
`24.5,\ 27.4,\ 28.7,\ 30,\ 36`

Part 3

The table below shows the forearm circumference, in centimetres, of a sample of 10 people selected from this group of 252 people.

The mean, `barx`, and the standard deviation, `s_x`, of the forearm circumference for this sample of people are closest to

`barx = 1.58qquads_x = 27.8`
`barx = 1.66qquads_x = 27.8`
`barx = 27.8qquads_x = 1.58`
`barx = 27.8qquads_x = 1.66`
`barx = 27.8qquads_x = 2.30`

Show Answers Only

`text(Part 1:)\ D`

`text(Part 2:)\ B`

`text(Part 3:)\ D`

Show Worked Solution

`text(Part 1)`

`Q_3 = 30\ text(cm)`

`:. 75text(% have a circumference less than 30 cm.)`

`=> D`

`text(Part 2)`

`text(Outliers are relevant data points and form)`

`text(part of the five-number summary.)`

`=> B`

`text(Part 3)`

`text(By calculator,)`

`barx = 27.8,\ \ s_x = 1.66`

`=> D`

CORE, FUR2 2016 VCAA 2

A weather station records daily maximum temperatures

The five-number summary for the distribution of maximum temperatures for the month of February is displayed in the table below.

There are no outliers in this distribution.
1. Use the five-number summary above to construct a boxplot on the grid below. (1 mark)
2. What percentage of days had a maximum temperature of 21°C, or greater, in this particular February? (1 mark)
The boxplots below display the distribution of maximum daily temperature for the months of May and July.
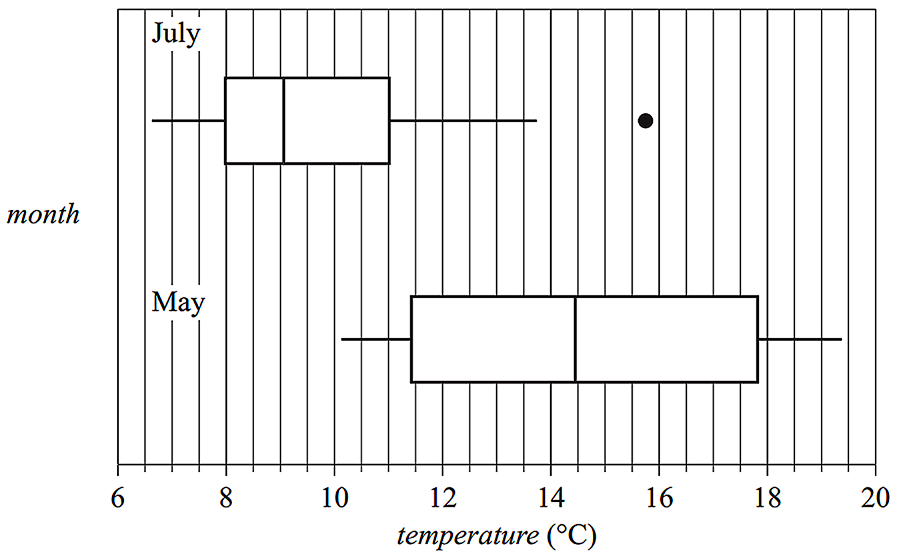
1. Describe the shapes of the distributions of daily temperature (including outliers) for July and for May. (1 mark)
2. Determine the value of the upper fence for the July boxplot. (1 mark)
3. Using the information from the boxplots, explain why the maximum daily temperature is associated with the month of the year. Quote the values of appropriate statistics in your response. (1 mark)

Show Answers Only

1. `text(See Worked Solutions)`
2. `75text(%)`
1. `text(July – Positively skewed with an outlier)`
  
  `text(May – Symmetrical with no outliers.)`
2. `15.5^@\text(C)`
3. `text(See Worked Solutions)`

Show Worked Solution

a.i.

a.ii. `text(75%)`

MARKER’S COMMENT: Incorrect May descriptors included “evenly or normally distributed”, “bell shaped” and “symmetrically skewed.”

b.i.	`text(July – Positively skewed with an outlier.)`
	`text(May – Symmetrical with no outliers.)`

b.ii.	`text(Upper fence)`	`= Q_3 + 1.5 xx IQR`
		`= 11 + 1.5 xx (11 – 8)`
		`= 11 + 4.5`
		`= 15.5^@\text(C)`

♦♦ Mean mark (b)(iii) – 30%.
COMMENT: Refer to the difference in medians. Just quoting the numbers was not enough to gain a mark here.

b.iii. `text{The median temperature in May (14.5°C)}`

`text(differs from the median temperature in July)`

`text{(just over 9°C). This difference is why the}`

`text(maximum daily temperature is associated)`

`text(with the month.)`

CORE, FUR1 2015 VCAA 8 MC

A dot plot for a set of data is shown below.

Which one of the following boxplots would best represent the dot plot above?

Show Answers Only

`C`

Show Worked Solution

`text(S)text(ince dot plots order data numerically,)`

♦ Mean mark 47%.

`text(Min value = 1001, Max value = 1004)`

`text(Median)`	`=1001\ \ text{(lies between the 12th and 13th}`
	`text{data points given 24 values.)`

`Q_1 = 1001\ \ \ text{(see dot plot above)}`

`Q_3 = (1002+1003)/2=1002.5\ \ \ text{(see dot plot above)}`

`text(Only C satisfies the median,)\ Q_1 and Q_3\ text(conditions.)`

`=> C`

CORE, FUR1 2009 VCAA 4-6 MC

The percentage histogram below shows the distribution of the fertility rates (in average births per woman) for 173 countries in 1975.

Part 1

In 1975, the percentage of these 173 countries with fertility rates of 4.5 or greater was closest to

A. `12text(%)`

B. `35text(%)`

C. `47text(%)`

D. `53text(%)`

E. `65text(%)`

Part 2

In 1975, for these 173 countries, fertility rates were most frequently

A. less than 2.5

B. between 1.5 and 2.5

C. between 2.5 and 4.5

D. between 6.5 and 7.5

E. greater than 7.5

Part 3

Which one of the boxplots below could best be used to represent the same fertility rate data as displayed in the percentage histogram?

Show Answers Only

`text(Part 1:)\ E`

`text(Part 2:)\ D`

`text(Part 3:)\ B`

Show Worked Solution

`text(Part 1)`

`text(Adding up the histogram bars from 4.5.)`

`%`	`= 12 + 19 + 28 + 5 + 1`
	`= 65text(%)`

`=> E`

`text(Part 2)`

`text(Fertility rates between 6.5 and 7.5 were 28%)`

`text(which is greater than any other range given.)`

`=> D`

`text(Part 3)`

♦ Mean mark 43%.
MARKERS’ COMMENT: A systemic approach where students calculated the median, `Q_1` and `Q_3` was most successful.

`text(The boxplots have the same range, therefore)`

`text(consider the values of)\ Q_1,\ Q_3\ text(and median.)`

`text(By elimination,)`

`Q_1\ text{estimate is slightly below 3.5 (the first 2}`

`text{bars add up to 29%), therefore not A, D or E.}`

`Q_3\ text(estimate is around 7. Eliminate C.)`

`=> B`

CORE, FUR1 2008 VCAA 1-4 MC

The box plot below shows the distribution of the time, in seconds, that 79 customers spent moving along a particular aisle in a large supermarket.

Part 1

The longest time, in seconds, spent moving along this aisle is closest to

A. `40`

B. `60`

C. `190`

D. `450`

E. `500`

Part 2

The shape of the distribution is best described as

A. symmetric.

B. negatively skewed.

C. negatively skewed with outliers.

D. positively skewed.

E. positively skewed with outliers.

Part 3

The number of customers who spent more than 90 seconds moving along this aisle is closest to

A. `7`

B. `20`

C. `26`

D. `75`

E. `79`

Part 4

From the box plot, it can be concluded that the median time spent moving along the supermarket aisle is

A. less than the mean time.

B. equal to the mean time.

C. greater than the mean time

D. half of the interquartile range.

E. one quarter of the range.

Show Answers Only

`text(Part 1:)\ D`

`text(Part 2:)\ E`

`text(Part 3:)\ B`

`text(Part 4:)\ A`

Show Worked Solution

`text(Part 1)`

`text(Longest time is represented by the farthest right)`

`text(data point.)`

`=>D`

`text(Part 2)`

`text(Positively skewed as the tail of the distribution can)`

`text(clearly be seen to extend to the right.)`

`text(The data also clearly shows outliers.)`

`=>E`

`text(Part 3)`

♦ Mean mark 43%.
MARKERS’ COMMENT: Note that the outliers are already accounted for in the boxplot.

`text(From the box plot,)`

`text(Q)_3=90\ text{s}\ \ text{(i.e. 25% spend over 90 s)}`

`:.\ text(Customers that spend over 90 s)`

`= 25text(%) xx 79`

`=19.75`

`=>B`

`text(Part 4)`

`text(The mean is greater than the median for positively)`

`text(skewed data.)`

`=>A`

CORE, FUR1 2014 VCAA 6 MC

The dot plot below shows the distribution of the time, in minutes, that 50 people spent waiting to get help from a call centre.

Which one of the following boxplots best represents the data?

Show Answers Only

`A`

Show Worked Solution

`text(There are 50 data points.)`

♦ Mean mark 37%.
MARKER’S COMMENT: A majority of students failed to calculate the outer fence where outliers begin, a step required to get the correct answer.

`Q_1 = 30,\ \ Q_3 = 50\ \ \text{(from dot plot)}`

`text(IQR)\ = 50-30 = 20`

`∴\ text(Outliers occur above)`

`Q3 + 1.5 xx IQR`	`=50 + (1.5 xx 20)`
	`=80\ text(minutes)`
`text(S)text(ince the dot plot has only 2 values above 80,)`

`=> A`

CORE, FUR1 2012 VCAA 5 MC

The temperature of a room is measured at hourly intervals throughout the day.

The most appropriate graph to show how the temperature changes from one hour to the next is a

A. boxplot.

B. stem plot.

C. histogram.

D. time series plot.

E. two-way frequency table.

Show Answers Only

`D`

Show Worked Solution

` text (A time series plot is best because the temperature)`

`text(is measured at regular time intervals.)`

`rArr D`

CORE, FUR1 2010 VCAA 1-3 MC

To test the temperature control on an oven, the control is set to 180°C and the oven is heated for 15 minutes.
The temperature of the oven is then measured. Three hundred ovens were tested in this way. Their temperatures were recorded and are displayed below using both a histogram and a boxplot.

Part 1

A total of 300 ovens were tested and their temperatures were recorded.

The number of these temperatures that lie between 179°C and 181°C is closest to

A. `40`

B. `50`

C. `70`

D. `110`

E. `150`

Part 2

The interquartile range for temperature is closest to

A. `1.3°text(C)`

B. `1.5°text(C)`

C. `2.0°text(C)`

D. `2.7°text(C)`

E. `4.0°text(C)`

Part 3

Using the 68–95–99.7% rule, the standard deviation for temperature is closest to

A. `1°text(C)`

B. `2°text(C)`

C. `3°text(C)`

D. `4°text(C)`

E. `6°text(C)`

Show Answers Only

`text(Part 1:)\ D`

`text(Part 2:)\ D`

`text(Part 3:)\ B`

Show Worked Solution

`text(Part 1)`

`text(22% of ovens had temperatures between 179 – 180°)`

`text{and 16% between 180 – 181° (from bar chart).}`

`:.\ text(Number of ovens between 179° and 181°)`
	`=\ text{(22% + 16%)} xx 300`
	`= 38text(%) xx 300`
	`= 114`

`=> D`

`text(Part 2)`

`text(IQR)`	`=\ text(Q3 – Q1)`
	`= 181.5- 179`
	`= 2.5text(%)`

`=> D`

`text(Part 3)`

♦ Mean mark 43%.

`text(The percentage of ovens between 179 – 181°)`

`=21 + 16 = 38text(%)`

`text(Taking another bar column either side, we have)`

`text{178 – 179° (13%) and 181–182° (15%).}`

`:.\ text(178 – 182° accounts for approximately 66% of all values.)`

`:.\ text(1 standard deviation is approximately 2°.)`

`=> B`