SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Trigonometry, 2ADV T1 2021 HSC 18

The diagram shows a triangle `ABC` where `AC` = 25 cm, `BC` = 16 cm, `angle BAC` = 28° and angle `ABC` is obtuse.
 


 

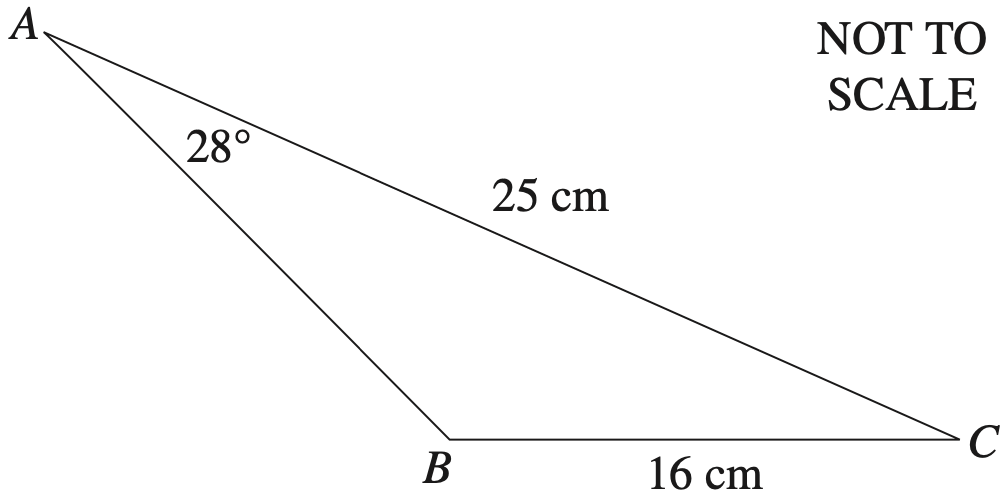
Find the size of the obtuse angle `ABC` correct to the nearest degree.  (3 marks)

Show Answers Only

`133°`

Show Worked Solution

`text(Using the sine rule:)`

`sin theta/25` `= (sin 28°)/16`
`sin theta` `= (25 xx sin 28°)/16`
`sin theta` `= 0.73355`
`theta` `= 47°`
 
 
`:. angleABC= 180-47= 133°`

Trigonometry, 2ADV T1 EQ-Bank 19

Determine all possible dimensions for triangle `ABC` given  `AB = 6.2\ text(cm)`, `angleABC = 35°`  and  `AC = 4.1`.

Give all dimensions correct to one decimal place.   (3 marks)

Show Answers Only

`text(7.1 cm, 6.2 cm, 4.1 cm or)`

`text(3.0 cm, 6.2 cm, 4.1 cm.)`

Show Worked Solution

`text(Using the sine rule:)`

`(sinangleACB)/6.2` `= (sin35^@)/4.1`
`sinangleACB` `= (6.2 xx sin35^@)/4.1= 0.8673…`
`angleACB` `= 60.15…^@\ text(or)\ 119.84…^@`

  
`text(If)\ \ angleACB = 60.15^@,`

`angleBAC = 180-(35 + 60.15) = 84.85^@`
 

`(BC)/(sin84.85^@)` `= 4.1/(sin35^@)`
`BC` `= (4.1 xx sin84.85^@)/(sin35^@)=7.11… = 7.1\ text(cm)`

 
`text(If)\ \ angleACB = 119.85^@,`

`angleBAC = 180-(35 + 119.85) = 25.15^@`
 

`(BC)/(sin25.15)` `= 4.1/(sin35^@)`
`BC` `= (4.1 xx sin25.15^@)/(sin35^@) = 3.03… = 3.0\ text(cm)`

 
`:.\ text(Possible dimensions are:)`

`text(7.1 cm, 6.2 cm, 4.1 cm or)`

`text(3.0 cm, 6.2 cm, 4.1 cm.)`

Trigonometry, 2ADV T1 2018 HSC 14a

In  `Delta KLM, KL`  has length 3, `LM` has length 6 and `/_KLM` is 60°. The point `N` is chosen on side `KM` so that `LN` bisects `/_KLM`. The length `LN` is `x`.
 


 

  1. Find the exact value of the area of `Delta KLM`.   (1 mark)

  2. Hence, or otherwise, find the exact value of `x`.   (2 marks)

Show Answers Only
  1. `(9 sqrt 3)/2`
  2. `2 sqrt 3`
Show Worked Solution

i.   `text(Using sine rule:)`

`text(Area)\ \ Delta KLM= 1/2 xx 3 xx 6 xx sin 60^@= (9 sqrt 3)/2\ \ text(u)^2`
 

ii.  `text(Area)\ \ Delta KLN + text(Area)\ \ Delta NLM = text(Area)\ \ Delta KLM`

`1/2 xx 3 xx x xx sin 30^@ + 1/2 xx x xx 6 xx sin 30^@ = (9 sqrt 3)/2`

♦ Mean mark 37%.

`3/4 x + 3/2 x` `= (9 sqrt 3)/2`
`9/4 x` `= (9 sqrt 3)/2`
`:. x` `= (9 sqrt 3)/2 xx 4/9`
  `= 2 sqrt 3`

Trigonometry, 2ADV T1 2006 HSC 1d

2006 1d

 
Find the value of `theta` in the diagram. Give your answer to the nearest degree.   (2 marks)

Show Answers Only

`18°`

Show Worked Solution

`text(Using the sine rule:)`

`sin theta / 5` `= (sin 33°)/9`
`sin theta` `= (5 xx sin 33°)/9= 0.30257…`
`:. theta` `= 17.612…`
  `= text{18°  (nearest degree)}`

Trigonometry, 2ADV T1 2013 HSC 14c

2013 14c

The right-angled triangle `ABC` has hypotenuse  `AB = 13`. The point `D` is on `AC` such that  `DC = 4`, `/_DBC = pi/6`  and  `/_ABD = x`.

Using the sine rule, or otherwise, find the exact value of `sin x`.   (3 marks)

Show Answers Only

 `(7sqrt3)/26 text(.)`

Show Worked Solution

`text(Find)\ \ /_ADB:`

`/_ADB= pi/6 + pi/2 \ \ \ text{(exterior angle of}\ Delta BDC text{)}= (2pi)/3`

`text(Find)\ AD:`

♦ Mean mark 36%.
STRATEGY TIP: The hint to use the sine rule indicates non-right angled trig is required (i.e. `Delta ABD`).
`tan (pi/6)` `= 4/(BC)`
`1/sqrt3` `=4/(BC)`
`BC` `=4 sqrt3`

 

`text(Using Pythagoras:)`

`AC^2 + BC^2` `= AB^2`
`AC^2 + (4sqrt3)^2` `= 13^2`
`AC^2` `= 16-48= 121`
`AC` `= 11`

 
`:.AD=AC-DC= 11-4=7`
 

`text(Using sine rule:)`

`(AB)/(sin /_BDA)` `= (AD)/(sinx)`
`13/(sin ((2pi)/3))` `=7/(sinx)`
`13 xx sinx` `= 7 xx sin ((2pi)/3)`
`sinx` `= 7/13 xx sin((2pi)/3)`
  `= 7/13 xx sqrt3/2`
  `= (7 sqrt3)/26`

 
`:.\ text(The exact value of)\ sinx = (7sqrt3)/26 text(.)`