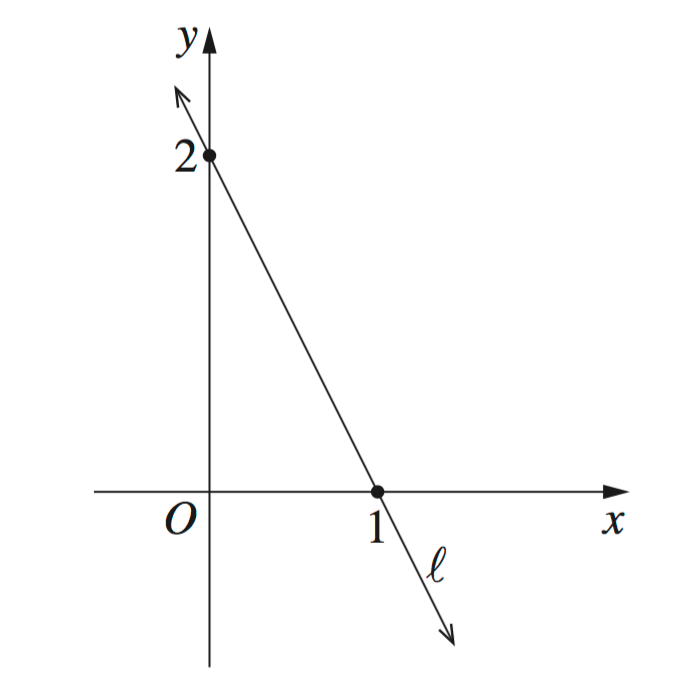SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Cartesian Plane, SMB-021

An equilateral triangle has vertices  `O(0,0)` and `A(8,0)` as shown in the diagram below.

Find `k` if the coordinates of the third vertex are `B(4,k)`.  (4 marks)

Show Answers Only

`text{Proof (See worked solutions)}`

Show Worked Solution

`ΔOAB\ text{is equilateral}\ \ =>\ \ OA=AB=OB=8`

`text{Let}\ C=(0,4)`

`text{Consider}\ ΔOCB:`

`OB^2` `=OC^2+CB^2`  
`64` `=16+CB^2`  
`CB^2` `=48`  
`CB` `=sqrt(48)`  
  `=4sqrt(2)`  

 
`B=(4,4sqrt(2))`

`:.k=4sqrt(2)`

Cartesian Plane, SMB-020

Prove the points `(1,-1), (-1,1)` and `(-sqrt3,-sqrt3)` are the vertices of a equilateral triangle.  (4 marks)

Show Answers Only

`text{Proof (See worked solutions)}`

Show Worked Solution

`text{Let points be:}\ A(1,-1), B(-1,1) and C(-sqrt3,-sqrt3)`

`text(Using the distance formula):`

`d_(AB)` `=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}`  
  `=sqrt{(1-(-1))^2+(-1-1)^2}`  
  `=sqrt8`  

 

`d_(BC)` `=sqrt{(-1-(-sqrt3))^2+(1-(-sqrt3))^2}`  
  `=sqrt{(-1+sqrt3)^2+(1+sqrt3)^2}`  
  `=sqrt(1-2sqrt3+3 +1+2sqrt3+3)`  
  `=sqrt8`  

 

`d_(AC)` `=sqrt{(1-(-sqrt3))^2+(-1-(-sqrt3))^2}`  
  `=sqrt{(1+sqrt3)^2+(-1+sqrt3)^2}`  
  `=sqrt(1+2sqrt3+3 +1-2sqrt3+3)`  
  `=sqrt8`  

 
`text{Since}\ AB=BC=AC`

`:. ΔABC\ text{is equilateral.}`

Cartesian Plane, SMB-019

A straight line passes through points `Q(3,-2)` and `R(-1,4)` .

Find the equation of `QR` and express in general form.  (3 marks)

Show Answers Only

`2y+3x-5=0`

Show Worked Solution

`text{Line goes through}\ (3,-2) and (-1,4).`

`text(Using the gradient formula):`

`m` `=(y_2-y_1)/(x_2-x_1)`  
  `=(-2-4)/(3-(-1))`  
  `=-3/2`  

 
`text{Find equation through}\ (3,-2), m=-3/2:`

`y-y_1` `=m(x-x_1)`  
`y-(-2)` `=-3/2(x-3)`  
`2(y+2)` `=-3(x-3)`  
`2y+4` `=-3x+9`  
`2y+3x-5` `=0`  

Cartesian Plane, SMB-018

A straight line passes through points `A(-2,-2)` and `B(1,5)` .

Find the equation of `AB` and express in form  `y=mx+c`.  (3 marks)

Show Answers Only

`y=7/3x+8/3`

Show Worked Solution

`text{Line goes through}\ (-2,-2) and (1,5).`

`text(Using the gradient formula):`

`m` `=(y_2-y_1)/(x_2-x_1)`  
  `=(5-(-2))/(1-(-2))`  
  `=7/3`  

 
`text{Find equation through}\ (1,5), m=7/3:`

`y-y_1` `=m(x-x_1)`  
`y-5` `=7/3(x-1)`  
`y-5` `=7/3x-7/3`  
`y` `=7/3x+8/3`  

Cartesian Plane, SMB-017

Albert drew a straight line through points `P` and `Q` as shown on the graph below.

Find the equation of Albert's line and express in general form.  (3 marks)

Show Answers Only

`3y-5x+2=0`

Show Worked Solution

`text{Line goes through}\ (-2,-4) and (1,1).`

`text(Using the gradient formula):`

`m` `=(y_2-y_1)/(x_2-x_1)`  
  `=(1-(-4))/(1-(-2))`  
  `=5/3`  

 
`text{Find equation through}\ (1,1), m=5/3:`

`y-y_1` `=m(x-x_1)`  
`y-1` `=5/3(x-1)`  
`3y-3` `=5x-5`  
`3y-5x+2` `=0`  

Cartesian Plane, SMB-016

Calculate the value(s) of `p` given that the points `(p,3)` and `(1,p)` are exactly 10 units apart.  (3 marks)

Show Answers Only

`p=9\ text{or}\ -5`

Show Worked Solution

`(p,3),\ \ (1,p)`

`text{Using the distance formula:}`

`d` `=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}`  
`10` `=sqrt{(p-1)^2+(3-p)^2}`  
`10` `=sqrt{p^2-2p+1+9-6p+p^2}`  
`10` `=sqrt{2p^2-8p+10}`  
`100` `=2p^2-8p+10`  
`0` `=2p^2-8p-90`  
`0` `=p^2-4p-45`  
`0` `=(p-9)(p+5)`  

 
`:.p=9\ text{or}\ -5`

Cartesian Plane, SMB-015

Calculate the distance between the points `(2,-3)` and `(-5,4)`.

Round your answer to the nearest tenth.  (2 marks)

Show Answers Only

`9.9\ text{units}`

Show Worked Solution

`(2,-3),\ \ (-5,4)`

`text{Using the distance formula:}`

`d` `=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}`  
  `=sqrt{(2-(-5))^2+(-3-4)^2}`  
  `=sqrt{49+49}`  
  `=sqrt{98}`  
  `=9.899…`  
  `=9.9\ text{units (nearest tenth)}`  

Cartesian Plane, SMB-014

Calculate the distance between the points `(6,-5)` and `(0,3)`.  (2 marks)

Show Answers Only

`10\ text{units}`

Show Worked Solution

`(6,-5),\ \ (0,3)`

`text{Using the distance formula:}`

`d` `=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}`  
  `=sqrt{(6-0)^2+(-5-3)^2}`  
  `=sqrt{36+64}`  
  `=sqrt{100}`  
  `=10\ text{units}`  

Cartesian Plane, SMB-013

Calculate the distance between the point `(-6,2)` and the origin.

Give your answer in exact form.  (2 marks)

Show Answers Only

`2sqrt{10}\ \ text{units}`

Show Worked Solution

`(-6,2),\ \ (0,0)`

`text{Using the distance formula:}`

`d` `=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}`  
  `=sqrt{(-6-0)^2+(2-0)^2}`  
  `=sqrt{36+4}`  
  `=sqrt{40}`  
  `=2sqrt{10}\ \ text{units}`  

Cartesian Plane, SMB-012

What is the equation of the line `l`?  (2 marks)
 

Show Answers Only

`y = -2x + 2`

Show Worked Solution

`l\ text{passes through (0, 2) and (1, 0)}`

`text(Gradient)` `= (y_2-y_1)/(x_2-x_1)`
  `= (0-2)/(1-0)`
  `= -2`

 
`y\ text(intercept = 2)`

`:.y = -2x + 2`

Cartesian Plane, SMB-011

Rambo drew a line as shown on the grid below.

What is the gradient of Rambo's line?  (3 marks)

Show Answers Only

`-7/5`

Show Worked Solution

`text{Line goes through}\ (-3,4) and (2,-3).`

`text(Using the gradient formula):`

`m` `=(y_2-y_1)/(x_2-x_1)`  
  `=(-3-4)/(2-(-3))`  
  `=-7/5`  

Cartesian Plane, SMB-010

The point  `C(-2,3)`  is the midpoint of the interval `AB`, where `B` has coordinates  `(-1,0).`

What are the coordinates of  `A`?  (3 marks)

Show Answers Only

`(-3,6)`

Show Worked Solution

`text(Using the midpoint formula):`

`(x_A + x_B)/2` `= x_C` `(y_A + y_B)/2` `= y_C`
`(x_A-1)/2` `= -2` `(y_A + 0)/2` `= 3`
`x_A` `= -3` `y_A` `= 6`

 
`:. A\ text(has coordinates)\ (-3,6).`

Cartesian Plane, SMB-007

On the Cartesian plane below, graph the equation  `y-1=-1/2x`.

Clearly label the coordinates of the intercepts with both the `x` and `y`-axes.  (2 marks)

Show Answers Only

Show Worked Solution

`y-1=-1/2x\ \ =>\ \ y=-1/2x+1`

`ytext{-intercept = 1,  gradient}\ = -1/2`

`xtext{-intercept occurs when}\ y=0:`

`0=-1/2x+1\ \ =>\ \ x=2`

Cartesian Plane, SMB-006

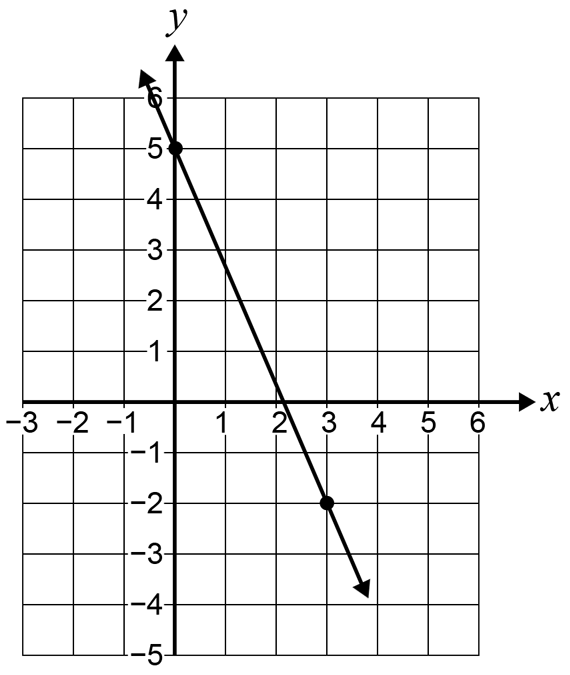
On the Cartesian plane below, graph the equation  `y=3x+2`.

Clearly label the coordinates of the intercepts with both the `x` and `y`-axes.  (2 marks)

Show Answers Only

Show Worked Solution

`ytext{-intercept = 2,  gradient = 3}`

`xtext{-intercept occurs when}\ y=0:`

`0=3x+2\ \ =>\ \ x=-2/3`
 

Cartesian Plane, SMB-005

On the Cartesian plane below, graph the equation  `y=2x-1`.

Clearly label the coordinates of all intercepts.  (2 marks)

Show Answers Only

Show Worked Solution

`ytext{-intercept = –1,  gradient = 2}`

`xtext{-intercept occurs when}\ y=0:`

`0=2x-1\ \ =>\ \ x=1/2`
 

Cartesian Plane, SMB-004 MC

The graph of   `y = 2x-3`  will be drawn on this grid.

Which two points will the straight line pass through?

  1. `C and D`
  2. `D and A`
  3. `B and D`
  4. `A and C`
Show Answers Only

`D`

Show Worked Solution

`text(Solution 1)`

`y = 2x-3\ text(passes through)\ (0, -3)`

`text(with a gradient of 2.)`

`:. A and C`
 

`text(Solution 2)`

`text{Substitute the coordinates of each point into the equation:}`

`A(-1, -5), \ B(1, -5), \ C(3, 3), \ D(-2, 1)`

`text(Only)\ A and C\ text(satisfy the equation) \ \ y = 2x-3.`

`=>D`

Cartesian Plane, SMB-003 MC

The coordinates of point `A` are `(7, 5)`.
 

`AB` is parallel to the `y`-axis.

If  `AB = 3, BC = 4 and AC = 5`, what are the coordinates of point `C`?

  1. `(3,2)`
  2. `(2,3)`
  3. `(1,5)`
  4. `(5,1)`
Show Answers Only

`A`

Show Worked Solution

`text(Coordinates of)\ C\ text(are):`

`(7-4, 5-3) = (3, 2)`

`=>A`

Cartesian Plane, SMB-002 MC

A Cartesian plane is shown.
 

Select the correct statement below.

  1. `O` is located where `x = 0` and `y < 0.`
  2. `P` is located where `x < 0` and `y < 0.`
  3. `Q` is located where `x = 0` and `y > 0.`
  4. `R` is located where `x < 0` and `y < 0.`
Show Answers Only

`D`

Show Worked Solution

`R\ text(occurs when)`

`x < 0 and y < 0`

`=>D`

Linear Relationships, SMB-001 MC

Leo drew a straight line through the points (0, 5) and (3, -2) as shown in the diagram below.
 


  

What is the gradient of the line that Leo drew?

  1. `7/3`
  2. `3/7`
  3. `-3/7`
  4. `-7/3`
Show Answers Only

`-7/3`

Show Worked Solution

`text{Line passes through (0, 5) and (3, – 2)}`

`text(Gradient)` `= (y_2-y_1)/(x_2-x_1)`
  `= (5-(-2))/(0-3)`
  `= -7/3`

Functions, 2ADV F1 2022 HSC 1 MC

Which of the following could be the graph of  `y= -2 x+2`?
 

Show Answers Only

`A`

Show Worked Solution

`text{By elimination:}`

`y text{-intercept = 2  →  Eliminate}\ B and C`

`text{Gradient is negative  → Eliminate}\ D`

`=>A`

Functions, 2ADV F1 2018 HSC 3 MC

What is the `x`-intercept of the line  `x + 3y + 6 = 0`?

  1. `(-6, 0)`
  2. `(6, 0)`
  3. `(0, -2)`
  4. `(0, 2)`
Show Answers Only

`A`

Show Worked Solution

`x text(-intercept occurs when)\ y = 0:`

`x + 0 + 6` `= 0`
`x` `= -6`

 
`:. x text{-intercept is}\  (-6, 0)`

`=>  A`

Linear Functions, 2UA 2018 HSC 2 MC

The point  `R(9, 5)`  is the midpoint of the interval  `PQ`, where `P` has coordinates  `(5, 3).`
 

What are the coordinates of  `Q`?

  1. `(4, 7)`
  2. `(7, 4)`
  3. `(13, 7)`
  4. `(14, 8)`
Show Answers Only

`C`

Show Worked Solution

`text(Using the midpoint formula):`

`(x_Q + x_P)/2` `= x_R` `(y_Q + y_P)/2` `= y_R`
`(x_Q + 5)/2` `= 9` `(y_Q + 3)/2` `= 5`
`x_Q` `= 13` `y_Q` `= 7`

 
`:. Q\ text(has coordinates)\ (13, 7).`

`=>  C`

Functions, 2ADV F1 2017 HSC 1 MC

What is the gradient of the line  `2x + 3y + 4 = 0`?

  1. `-2/3`
  2. `2/3`
  3. `-3/2`
  4. `3/2`
Show Answers Only

`A`

Show Worked Solution
`2x + 3y + 4` `= 0`
`3y` `= -2x-4`
`y` `= -2/3 x-4/3`
`:.\ text(Gradient)` `= -2/3`

 
`=>  A`

Algebra, STD2 A2 2016 HSC 14 MC

The graph shows a line which has an equation in the form  `y = mx + c`.
 

Which of the following statements is true?

  1. `m` is positive and `c` is negative
  2. `m` is negative and `c` is positive
  3. `m` and `c` are both positive
  4. `m` and `c` are both negative
Show Answers Only

`=> A`

Show Worked Solution

`m` is the gradient and the line slopes to the right so `m` is positive.

`c` is the `y`-intercept which is negative.

`:.\ m` is positive and `c` is negative.

`=> A`

Functions, 2ADV F1 2007 HSC 1f

Find the equation of the line that passes through the point `(1, 3)` and is perpendicular to  `2x + y + 4 = 0`.  (2 marks)

Show Answers Only

`x-2y + 7 = 0`

Show Worked Solution
`2x + y + 4` `= 0`
`y` `= -2x-4`

  
`=>\ text(Gradient) = -2`

`:. text(⊥ gradient) = 1/2\ \ \ (m_1 m_2=-1)`
 

`text(Equation of line)\ \ m = 1/2, \ text(through)\ (1, 3):`

`y-y_1` `= m (x-x_1)`
`y-3` `= 1/2 (x-1)`
`y` `= 1/2 x + 5/2`
`2y` `= x + 5`
`:. x-2y + 5` `= 0`

Algebra, STD2 A2 2004 HSC 2 MC

Susan drew a graph of the height of a plant.
  

What is the gradient of the line?

  1. `1`
  2. `5`
  3. `7.5`
  4. `10`
Show Answers Only

`B`

Show Worked Solution

`text(2 points on graph)\ \ (0, 10),\ (1, 15)`

`text(Gradient)` `= (y_2-y_1) / (x_2-x_1)`
  `= (15-10) / (1-0)`
  `= 5`

`=> B`

Linear Functions, 2UA 2008 HSC 2b

Let  `M`  be the midpoint of  `(-1, 4)`  and  `(5, 8)`.

Find the equation of the line through  `M`  with gradient  `-1/2`.   (2 marks)

Show Answers Only

`x + 2y-14 = 0`

Show Worked Solution

`(-1,4)\ \ \ (5,8)`

`M` `= ( (x_1 + x_2)/2, (y_1 + y_2)/2)`
  `= ( (-1 + 5)/2, (4 + 8)/2)`
  `= (2, 6)`

 

`text(Equation through)\ (2,6)\ text(with)\ m = -1/2`

`y-y_1` `= m (x-x_1)`
`y-6` `= -1/2 (x-2)`
`2y-12` `= -x + 2`
`x + 2y-14` `= 0`

Functions, 2ADV F1 2014 HSC 5 MC

Which equation represents the line perpendicular to  `2x-3y = 8`, passing through the point `(2, 0)`?

  1. `3x + 2y = 4`
  2. `3x + 2y = 6`
  3. `3x-2y = -4`
  4. `3x-2y = 6`
Show Answers Only

`B`

Show Worked Solution
`2x-3y` `= 8`
`3y` `= 2x-8`
`y` `= 2/3x-8/3`

 
`m= 2/3`

`:.\ m_text(perp)= -3/2\ \ \ (m_1 m_2=-1\text( for)_|_text{lines)}`

 
`text(Equation of line)\ \ m = -3/2\ \ text(through)\ \ (2,0):`

`y-y_1` `= m (x-x_1)`
`y-0` `= -3/2 (x-2)`
`y` `= -3/2x + 3`
`2y` `= -3x + 6`
`3x + 2y` `= 6`

 
`=>  B`

Algebra, STD2 A2 2014 HSC 7 MC

Which of the following is the graph of   `y = 2x-2`? 
  


  

Show Answers Only

`D`

Show Worked Solution
♦ Mean mark 46%

`y = 2x-2`

`text(From the equation:)`

`y\ text(intercept of)\ -2`

`=> text(Eliminate)\ B\ text(and)\ C`

 

`text(From the equation:)`

`text(Gradient)=2`

`=> text(Eliminate)\ A`

`=>  D`

Functions, 2ADV F1 2009 HSC 1a

Sketch the graph of  `y-2x = 3`, showing the intercepts on both axes.   (2 marks)

Show Answers Only

 

Show Worked Solution

`y-2x=3\ \ =>\ \ y=2x+3`

`ytext{-intercept}\ = 3`

`text{Find}\ x\ text{when}\ y=0:`

`0-2x=3\ \ =>\ \ x=-3/2`
 

Algebra, STD2 A2 2012 HSC 5 MC

The line  `l`  has intercepts  `p`  and  `q`,  where  `p`  and  `q`  are positive integers. 
  

What is the gradient of line  `l ` ? 

  1. `-p/q`  
  2. `-q/p`  
  3. `p/q`  
  4. `q/p`  
Show Answers Only

`A`

Show Worked Solution
 
♦ Mean mark 45%
`text(Gradient)` `= text(rise)/text(run)`
  `= -p/q`

`=>  A`