SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

NETWORKS, FUR1 2007 VCAA 4 MC

The following network shows the distances, in kilometres, along a series of roads that connect town `A` to town `B.`
 

 

 
The shortest distance, in kilometres, to travel from town `A` to town `B` is

A.     `9`

B.   `10`

C.   `11`

D.   `12`

E.   `13`

Show Answers Only

`B`

Show Worked Solution

`text(Shortest path)`

`= 4 + 1 + 3 + 2`

`= 10`

`=>  B`

NETWORKS, FUR1 2009 VCAA 7 MC

Four workers, Anna, Bill, Caitlin and David, are each to be assigned a different task.

The table below gives the time, in minutes, that each worker takes to complete each of the four tasks.
 

     networks-fur1-2009-vcaa-7-mc
 

The tasks are allocated so as to minimise the total time taken to complete the four tasks.

This total time, in minutes, is

A.   `21`

B.   `28`

C.   `31`

D.   `34`

E.   `38`

Show Answers Only

`C`

Show Worked Solution

networks-fur1-2009-vcaa-7-mc-answer 

 
`:.\ text(Minimum time)`

`= 7 + 5 + 15 + 4`

`= 31`

`=>  C`

NETWORKS, FUR1 2009 VCAA 5-6 MC

The network shows the activities that are needed to complete a particular project.

networks-fur1-2009-vcaa-5-6-mc

Part 1

The total number of activities that need to be completed before activity `L` may begin is

A.   `2`

B.   `4`

C.   `6`

D.   `7`

E.   `8`

 

Part 2

The duration of every activity is initially 5 hours. For an extra cost, the completion times of both activity `F` and activity `K` can be reduced to 3 hours each.

If this is done, the completion time for the project will be

A.   decreased by 2 hours.

B.   decreased by 3 hours.

C.   decreased by 4 hours.

D.   decreased by 6 hours.

E.   unchanged. 

Show Answers Only

`text(Part 1:)\ D`

`text(Part 1:)\ E`

Show Worked Solution

`text(Part 1)`

`A, B, C, D, E, H\ text(and)\ I\ text(must be)`

`text(completed before)\ L.`

`=>  D`

 

`text(Part 2)`

♦ Mean mark 45%.

`F\ text(and)\ K\ text(are not on any critical path and a)`

`text(reduction of 3 hours on either activity will not change)`

`text(the completion time for the project.)`

`=>E`

NETWORKS, FUR1 2011 VCAA 8 MC

The diagram shows the tasks that must be completed in a project.

Also shown are the completion times, in minutes, for each task.
 

 
The critical path for this project includes activities

A.   `B and I.`

B.   `C and H.`

C.   `D and E.`

D.   `F and K.`

E.   `G and J.`

Show Answers Only

`D`

Show Worked Solution

`text(The critical path is)\ \ ACFIK.`

`=>  D`

NETWORKS, FUR1 2011 VCAA 3-4 MC

The map of Australia shows the six states, the Northern Territory and the Australian Capital Territory (ACT).
 

In the network diagram below, each of the vertices `A` to `H` represents one of the states or territories shown on the map of Australia. The edges represent a border shared between two states or between a state and a territory.
 

 
Part 1

In the network diagram, the order of the vertex that represents the Australian Capital Territory (ACT) is

A.   `0`

B.   `1`

C.   `2`

D.   `3`

E.   `4`

 

Part 2

In the network diagram, Queensland is represented by

A.   vertex A.

B.   vertex B.

C.   vertex C.

D.   vertex D.

E.   vertex E.

Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ A`

Show Worked Solution

`text(Part 1)`

`text {ACT has 1 border (with NSW)}`

`:.\ text(Its vertex will be one degree.)`

`=>  B`

 

`text(Part 2)`

`text(NSW is Vertex)\ B`

`:.\ text(Queensland is vertex)\ A\ text(as it is)`

`text(connected to)\ B\ text(and has degree)`

`text{3  (}C\ text{is Victoria as it has degree 2)}`

`=>  A`

MATRICES*, FUR1 2011 VCAA 2 MC

The graph below shows the one-step dominances between four farm dogs, Kip, Lab, Max, and Nim.

In this graph, an arrow from Lab to Kip indicates that Lab has a one-step dominance over Kip.
 

 
From this graph, it can be concluded that Kip has a two-step dominance over

A.   Max only.

B.   Nim only.

C.   Lab and Nim only.

D.   all of the other three dogs.

E.   none of the other three dogs.

Show Answers Only

`C`

Show Worked Solution

`=>  C`

NETWORKS, FUR1 2012 VCAA 6 MC

networks-fur1-2012-vcaa-6-mc
 

In the digraph above, all vertices are reachable from every other vertex.

All vertices would still be reachable from every other vertex if we remove the edge in the direction from

A.  `Q` to `U`

B.  `R` to `S`

C.  `S` to `T`

D.  `T` to `R`

E.  `V` to `U`

Show Answers Only

`A`

Show Worked Solution

`rArr A`

NETWORKS, FUR1 2012 VCAA 4 MC

`{:({:qquadqquadPquadQquadRquadS:}),({:(P),(Q),(R),(S):}[(0,0,2,1),(0,0,1,1),(2,1,0,1),(1,1,1,0)]):}` 

 

The adjacency matrix above represents a planar graph with four vertices.

The number of faces (regions) on the planar graph is

A.   `1`

B.   `2`

C.   `3`

D.   `4`

E.   `5`

Show Answers Only

`D`

Show Worked Solution

`text(The graph can be represented)`
 

networks-fur1-2012-vcaa-4-mc-answer

`rArr D`

MATRICES*, FUR1 2013 VCAA 5 MC

Four people, Ash (A), Binh (B), Con (C) and Dan (D), competed in a table tennis tournament.

In this tournament, each competitor played each of the other competitors once.

The results of the tournament are summarised in the directed graph below.

Each arrow shows the winner of a game played in the tournament. For example, the arrow from `C` to `A` shows that Con defeated Ash.
 

 
In the tournament, each competitor was given a ranking that was determined by calculating the sum of their one-step and two-step dominances. The competitor with the highest sum is ranked number one (1). The competitor with the second-highest sum was ranked number two (2), and so on.

Using this method, the rankings of the competitors in this tournament were

A.   Dan (1), Ash (2), Con (3), Binh (4)

B.   Dan (1), Ash (2), Binh (3), Con (4)

C.   Con (1), Dan (2), Ash (3), Binh (4)

D.   Ash (1), Dan (2), Binh (3), Con (4)

E.   Ash (1), Dan (2), Con (3), Binh (4)

Show Answers Only

`E`

Show Worked Solution

`text(One step dominance matrix)`

`{: (quad qquad qquad qquad A quad B quad C quad D), (D_1 = [(0, 1, 0, 1), (0, 0, 1, 0), (1, 0, 0, 0), (0, 1, 1, 0)] {:(A), (B), (C), (D):}\ \ \ text{wins}):}`

 

`text(Two step dominance matrix)`

`{: (quad qquad qquad qquad A quad B quad C quad D), (D_2 = [(0, 1, 0, 2), (0, 0, 1, 0), (2, 0, 0, 0), (0, 1, 1, 0)] {:(A), (B), (C), (D):}\ \ \ text{wins}):}`

 

`D_1 + D_2 = [(0, 2, 0, 3), (0, 0, 2, 0), (3, 0, 0, 0), (0, 2, 2, 0)] {:(5), (2), (3), (4):}`

 

`text(Adding up rows, the ranking)`

`text{(highest to lowest) is:}`

`A, D, C, B`

`=>  E`

NETWORKS, FUR1 2013 VCAA 2 MC

The number of edges needed to make a complete graph with four vertices is

A.   `2`

B.   `3`

C.   `4`

D.   `5`

E.   `6`

Show Answers Only

`E`

Show Worked Solution

`text(Let)\ \ v=\ text(number of vertices)`

`text(Number of Edges)` `= (v(v – 1))/2`
  `= (4 xx 3)/2`
  `= 6`

 
`=>  E`

NETWORKS, FUR2 2006 VCAA 3

The five musicians are to record an album. This will involve nine activities.

The activities and their immediate predecessors are shown in the following table.

The duration of each activity is not yet known.
 

NETWORKS, FUR2 2006 VCAA 31
 

  1. Use the information in the table above to complete the network below by including activities `G`, `H` and `I`.  (2 marks)

     

NETWORKS, FUR2 2006 VCAA 32

There is only one critical path for this project.

  1. How many non-critical activities are there?   (1 mark)

The following table gives the earliest start times (EST) and latest start times (LST) for three of the activities only. All times are in hours.


Networks, FUR2 2006 VCAA 3_3

  1. Write down the critical path for this project.   (1 mark)

The minimum time required for this project to be completed is 19 hours.

  1. What is the duration of activity `I`?   (1 mark)

The duration of activity `C` is 3 hours.

  1. Determine the maximum combined duration of activities `F` and `H`.   (1 mark) 
Show Answers Only
  1.  
    networks-fur2-2006-vcaa-3-answer
  2. `5`
  3. `B-E- G-I`
  4. `text(7 hours)`
  5. `text(8 hours)`
Show Worked Solution
a.    networks-fur2-2006-vcaa-3-answer

 

b.   `text(Possible critical paths are,)`

`ADGI, BEGI\ text(or)\ CFHI`

`:.\ text(Non-critical activities)`

`= 9-4 = 5`

 

c.   `text(Critical activities have zero slack time.)`

♦ Mean mark of parts (c)-(e) (combined) was 36%.

`:. A\ text(and)\ C\ text(are non-critical.)`

`:. B-E-G-I\ \ text(is the critical path.)`

 

d.    `text(Duration of)\ \ I` `= 19-12`
    `= 7\ text(hours)`

 

e.   `text(Maximum time for)\ F\ text(and)\ H`

`=\ text(LST of)\ I-text(duration)\ C-text(slack time of)\ C`

`= 12-3-1`

`= 8\ text(hours)`

MATRICES*, FUR2 2006 VCAA 2

The five musicians, George, Harriet, Ian, Josie and Keith, compete in a music trivia game.

Each musician competes once against every other musician.

In each game there is a winner and a loser.

The results are represented in the dominance matrix, Matrix 1, and also in the incomplete directed graph below.

On the directed graph an arrow from Harriet to George shows that Harriet won against George.
 

NETWORKS, FUR2 2006 VCAA 2

  1. Explain why the figures in bold in Matrix 1 are all zero.   (1 mark)

One of the edges on the directed graph is missing.

  1. Using the information in Matrix 1, draw in the missing edge on the directed graph above and clearly show its direction.   (1 mark)

The results of each trivia contest (one-step dominances) are summarised as follows.

networks-fur2-2006-vcaa-2_2 

In order to rank the musicians from first to last in the trivia contest, two-step (two-edge) dominances will be considered.

The following incomplete matrix, Matrix 2, shows two-step dominances.
 

`{:(qquadqquadqquadtext(Matrix 2)),(qquadqquad{:GquadHquadI\ quadJquad\ K:}),({:(G),(H),(I),(J),(K):}[(0,1,1,2,0),(1,0,1,1,1),(1,0,0,0,0),(0,0,1,0,1),(2,0,1,x,0)]):}`
 

  1. Explain the two-step dominance that George has over Ian.   (1 mark)

  2. Determine the value of the entry `x` in Matrix 2.   (1 mark)

  3. Taking into consideration both the one-step and two-step dominances, determine which musician was ranked first and which was ranked last in the trivia contest.   (2 marks)

Show Answers Only
  1. `text(A musicians does not compete against him/herself.)`
  2.  
    networks-fur2-2006-vcaa-2-anwer
  3. `text(Two step dominance occurs because George is dominant)`

     

    `text(over Keith who is in turn dominant over Ian.)`

  4. `2`
  5. `text{First is Keith (8), last is Ian (2)}`
Show Worked Solution

a.   `text(A musicians does not compete against him/herself.)`

 

b.   `text(Josie won against George.)`

 

networks-fur2-2006-vcaa-2-anwer

 

c.   `text(Two step dominance occurs because George is dominant)`

`text(over Keith who is in turn dominant over Ian.)`

 

d.   `text(Following the edges on network diagram:)`

`text(Keith over Harriet who beats Josie.)`

`text(Keith over Ian who beats Ian.)`

`:. x = 2`

 

e.    `D_1 + D_2 =` `[(0,1,2,2,1),(2,0,2,2,1),(1,0,0,1,0),(1,0,1,0,1),(2,1,2,3,0)]{:(G – 6),(H – 7),(I – 2),(J – 3),(K – 8):}`

 

`text{Summing the rows (above),}`

`:.\ text{First is Keith (8), last is Ian (2).}`

NETWORKS, FUR2 2007 VCAA 4

A community centre is to be built on the new housing estate.

Nine activities have been identified for this building project.

The directed network below shows the activities and their completion times in weeks.
 

NETWORKS, FUR2 2007 VCAA 4
 

  1. Determine the minimum time, in weeks, to complete this project.   (1 mark)

  2. Determine the slack time, in weeks, for activity `D`.   (2 marks)

The builders of the community centre are able to speed up the project.

Some of the activities can be reduced in time at an additional cost.

The activities that can be reduced in time are `A`, `C`, `E`, `F` and `G`.

  1. Which of these activities, if reduced in time individually, would not result in an earlier completion of the project?   (1 mark)

The owner of the estate is prepared to pay the additional cost to achieve early completion.

The cost of reducing the time of each activity is $5000 per week.

The maximum reduction in time for each one of the five activities, `A`, `C`, `E`, `F`, `G`, is 2 weeks.

  1. Determine the minimum time, in weeks, for the project to be completed now that certain activities can be reduced in time.   (1 mark)

  2. Determine the minimum additional cost of completing the project in this reduced time.   (1 mark)

Show Answers Only
  1. `19\ text(weeks)`
  2. `5\ text(weeks)`
  3. `A, E, G`
  4. `text(15 weeks)`
  5. `$25\ 000`
Show Worked Solution

a.   `B-C-F-H-I\ \ text(is the critical path.)`

♦ Mean mark of all parts (combined) 40%.
`:.\ text(Minimum time)` `= 4 + 3 + 4 + 2 + 6`
  `= 19\ text(weeks)`

 

b.    `text(EST of)\ D` `= 4`
  `text(LST of)\ D` `= 9`
`:.\ text(Slack time of)\ D` `= 9-4`
  `= 5\ text(weeks)`

  
c.   `A, E,\ text(and)\ G\ text(are not currently on)`

`text(the critical path, therefore crashing)`

`text(them will not affect the completion)`

`text(time.)`
  

d.   `text(Reduce)\ C\ text(and)\ F\ text(by 2 weeks.)`

`text(However, a new critical path)`

`B-E-H-I\ text(takes 16 weeks.)`

`:.\ text(Also reduce)\ E\ text(by 1 week.)`

`:.\ text(Minimum time = 5 weeks)`

 

e.    `text(Additional cost)` `= 5 xx $5000`
    `= $25\ 000`

NETWORKS, FUR2 2007 VCAA 2

The estate has large open parklands that contain seven large trees.

The trees are denoted as vertices `A` to `G` on the network diagram below.

Walking paths link the trees as shown.

The numbers on the edges represent the lengths of the paths in metres.
 

NETWORKS, FUR2 2007 VCAA 2

  1. Determine the sum of the degrees of the vertices of this network.   (1 mark)

  2. One day Jamie decides to go for a walk that will take him along each of the paths between the trees.

    He wishes to walk the minimum possible distance.


    i.     State a vertex at which Jamie could begin his walk?   (1 mark)

  3. ii. Determine the total distance, in metres, that Jamie will walk.   (1 mark)

Michelle is currently at `F`.

She wishes to follow a route that can be described as the shortest Hamiltonian circuit.

  1. Write down a route that Michelle can take.   (1 mark) 
Show Answers Only
  1. `24`
    1. `C\ text(or)\ G`
    2. `2800\ text(m)`

  3. `F-G-A-B-C-D-E-F,\ text(or)`
    `F-E-D-C-B-A-G-F`

Show Worked Solution

a.   `text(Sum of degrees of vertices)`

♦ Mean mark of all parts (combined) 44%.

`= 4 + 2 + 5 + 2 + 4 + 4 + 3`

`= 24`
  

b.i.   `C\ text(or)\ G`

`text(An Euler path is required and)`

`text(therefore the starting point is at)`

`text(a vertex with an odd degree.)`
  

b.ii.   `2800\ text(m)`

MARKER’S COMMENT: Many students incorrectly found the shortest Hamiltonian path.

c.    `F-G-A-B-C-D-E-F,\ text(or)`

`F-E-D-C-B-A-G-F`

NETWORKS, FUR2 2007 VCAA 1

A new housing estate is being developed.

There are five houses under construction in one location.

These houses are numbered as points 1 to 5 below.
 

NETWORKS, FUR2 2007 VCAA 1

  
The builders require the five houses to be connected by electrical cables to enable the workers to have a supply of power on each site.

  1. What is the minimum number of edges needed to connect the five houses?  (1 mark)

  2. On the diagram above, draw a connected graph with this number of edges.  (1 mark) 

Show Answers Only
  1. `4`
  2.  
    networks-fur2-2007-vcaa-1-answer
Show Worked Solution

a.   `text(Minimum number of edges = 4)`
 

b.   `text(One of many possibilities:)`

networks-fur2-2007-vcaa-1-answer

NETWORKS, FUR1 2014 VCAA 6-7 MC

Consider the following four graphs.
 


 

Part 1

How many of these four graphs have an Eulerian circuit?

A.  `0`

B.  `1`

C.  `2`

D.  `3`

E.  `4`

 

Part 2

How many of these four graphs are planar?

A.  `0`

B.  `1`

C.  `2`

D.  `3`

E.  `4`

Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ E`

Show Worked Solution

`text(Part 1)`

`text(An Euler circuit cannot exist if any vertices)`

`text(have an odd degree.)`

`=>  B` 

♦♦♦ Mean mark part 2: 7%!
MARKER’S COMMENT: A majority of students chose option A, not understanding that a graph with intersecting edges can still be planar.

 

`text(Part 2)`

`=>  E`

 

MATRICES*, FUR1 2014 VCAA 4 MC

The directed graph below shows the results of a chess competition between five players: Alex, Ben, Cindi, Donna and Elise.
 

 
Each arrow indicates the winner of individual games. For example, the arrow from Alex to Donna indicates that Alex beat Donna in their game.

The sum of their one-step and two-step dominances is calculated to give each player a dominance score. The dominance scores are then used to rank the players.

The ranking of the players in this competition, from highest to lowest dominance score, is

A. Ben, Elise, Donna, Alex, Cindi

B. Ben, Elise, Cindi, Donna, Alex

C. Ben, Elise, Donna, Cindi, Alex

D. Elise, Ben, Donna, Alex, Cindi

E. Elise, Ben, Donna, Cindi, Alex

Show Answers Only

`A`

Show Worked Solution

`text(Let)\ \ D_1 = 1 text(-step dominance matrix)`

`{: (quad qquad qquad qquad A quad B\ quad C\ quad D\ quad E), (D_1 = [(0, 1, 1, 0, 1), (0, 0, 0, 1, 0), (0, 1, 0, 1, 1), (1, 0, 0, 0, 1), (0, 1, 0, 0, 0)] {:(A), (B), (C), (D), (E):}\ \ \ \ text(loses)):}`

 

`text(Let)\ \ D_2 = 2 text(-step dominance matrix)`

 `{: (quad qquad qquad qquad A quad B quad C quad D quad E), (D_1 = [(0, 2, 0, 2, 1), (1, 0, 0, 0, 1), (1, 1, 0, 1, 1), (0, 2, 1, 0, 1), (0, 0, 0, 1, 0)] {:(A), (B), (C), (D), (E):}):}`

 

`{: (D_1 + D_2 = [(0, 3, 1, 2, 2), (1, 0, 0, 1, 1), (1, 2, 0, 2, 2), (1, 2, 1, 0, 2), (0, 1, 0, 1, 0)]), (quad quad qquad qquad qquad qquad qquad 3\ \ \ 8\ \ \ 2\ \ \ \ 6\ \ \ \ 7):}`

 

`:.\ text(Summing the columns, the High-Low ranking)`

`text(is)\ BEDAC.`

`=>  A`

NETWORKS, FUR1 2014 VCAA 3 MC

The diagram below shows the network of roads that Stephanie can use to travel between home and school.
 

 
The numbers on the roads show the time, in minutes, that it takes her to ride a bicycle along each road.

Using this network of roads, the shortest time that it will take Stephanie to ride her bicycle from home to school is 

A.  `12\ text(minutes)`

B.  `13\ text(minutes)`

C.  `14\ text(minutes)`

D.  `15\ text(minutes)`

E.  `16\ text(minutes)`

Show Answers Only

`C`

Show Worked Solution

`text(Shortest time riding)`

`=3+2+3+4+2`

`=14\ text(minutes)`

`=> C`

NETWORKS, FUR1 2015 VCAA 9 MC

The table below shows, in minutes, the duration, the earliest starting time (EST) and the latest starting time (LST) of eight activities needed to complete a project.
 

NETWORKS, FUR1 2015 VCAA 9 MC

 
Which one of the following directed graphs shows the sequence of these activities?

NETWORKS, FUR1 2015 VCAA 9 MCabcde

Show Answers Only

`B`

Show Worked Solution

`=> B`

NETWORKS, FUR1 2015 VCAA 6 MC

The map below shows all road connections between five towns, `U`, `V`, `W`, `X` and `Y`.
 

NETWORKS, FUR1 2015 VCAA 6 MC1

 
A graph, shown below, was constructed to represent this map.


NETWORKS, FUR1 2015 VCAA 6 MC2

 
A mistake has been made in constructing this graph.

This mistake can be corrected by

A.   drawing another edge between `V` and `W`.

B.   drawing a loop at `W`.

C.   removing the loop at `V`.

D.   removing one edge between `U` and `V`.

E.   removing one edge between `X` and `V`.

Show Answers Only

`A`

Show Worked Solution

`=> A`

NETWORKS, FUR2 2013 VCAA 3

The rangers at the wildlife park restrict access to the walking tracks through areas where the animals breed.

The edges on the directed network diagram below represent one-way tracks through the breeding areas. The direction of travel on each track is shown by an arrow. The numbers on the edges indicate the maximum number of people who are permitted to walk along each track each day.
 

NETWORKS, FUR2 2013 VCAA 31
 

  1. Starting at `A`, how many people, in total, are permitted to walk to `D` each day?   (1 mark)

One day, all the available walking tracks will be used by students on a school excursion.

The students will start at `A` and walk in four separate groups to `D`.

Students must remain in the same groups throughout the walk.

  1. i. Group 1 will have 17 students. This is the maximum group size that can walk together from `A` to `D`.
    Write down the path that group 1 will take.  (1 mark)

  2. ii. Groups 2, 3 and 4 will each take different paths from `A` to `D`.
    Complete the six missing entries shaded in the table below.   (2 marks)

NETWORKS, FUR2 2013 VCAA 32

Show Answers Only
  1. `37`
    1. `A-B-E-C-D`
    2.  `text{One possible solution is:}`
       
      Networks, FUR2 2013 VCAA 3_2 Answer1
Show Worked Solution
a.    `text(Maximum flow)` `=\ text(minimum cut through)\ CD and ED`
    `= 24 + 13`
    `= 37`
♦ Mean mark of all parts (combined) was 41%.

 

`:.\ text(A maximum of 37 people can walk)`

`text(to)\ D\ text(from)\ A.`
  

b.i.   `A-B-E-C-D`
  

b.ii.   `text(One solution using the second possible largest)`

  `text(group of 11 students and two groups from the)`

  `text(remaining 9 students is:)`

Networks, FUR2 2013 VCAA 3_2 Answer1

NETWORKS, FUR2 2013 VCAA 2

A project will be undertaken in the wildlife park. This project involves the 13 activities shown in the table below. The duration, in hours, and predecessor(s) of each activity are also included in the table.
 
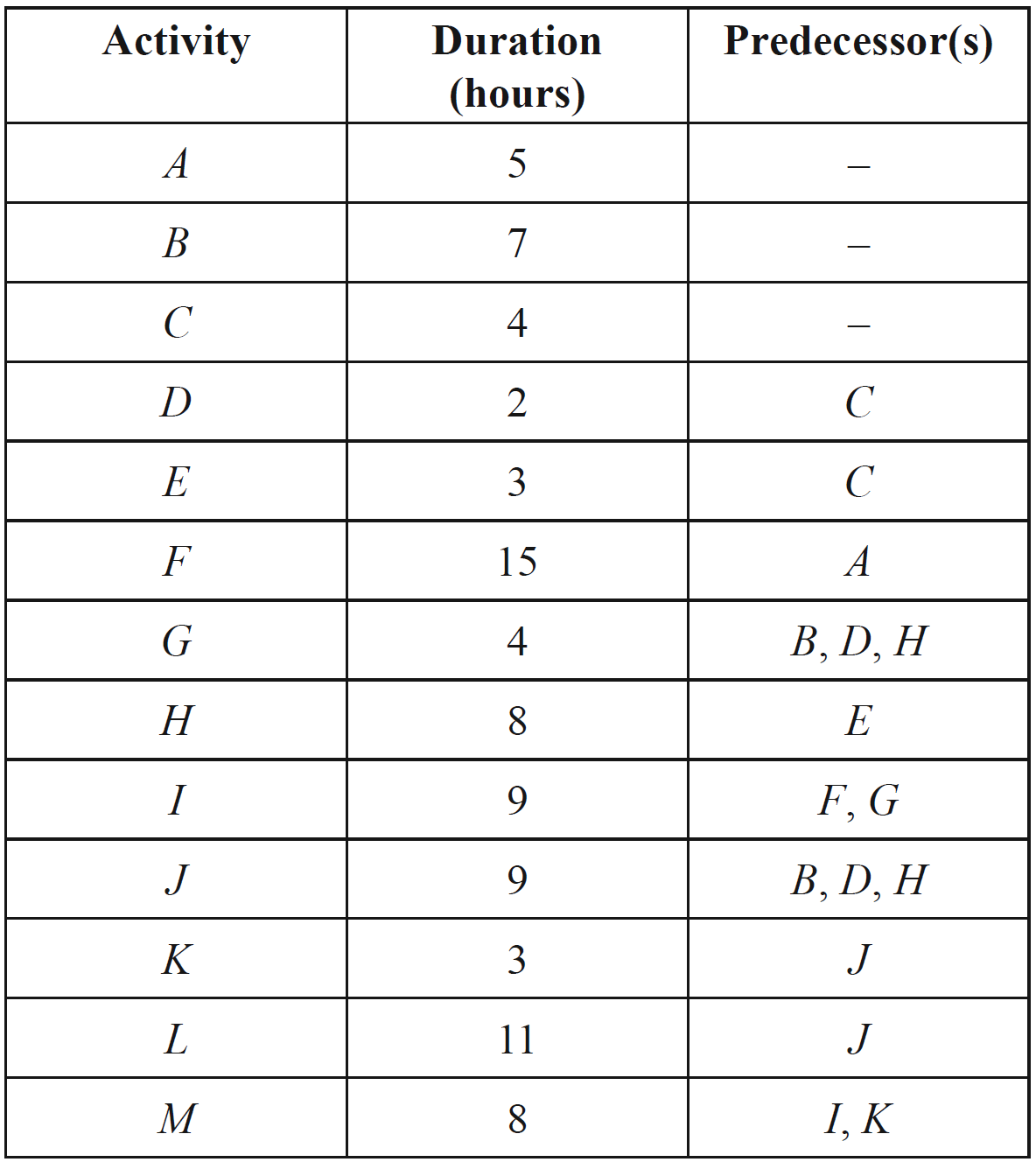
NETWORKS, FUR2 2013 VCAA 21
 

Activity `G` is missing from the network diagram for this project, which is shown below.

 
NETWORKS, FUR2 2013 VCAA 22
 

  1. Complete the network diagram above by inserting activity `G`.   (1 mark)

  2. Determine the earliest starting time of activity `H`.   (1 mark)

  3. Given that activity `G` is not on the critical path:
    i.     Write down the activities that are on the critical path in the order that they are completed.   (1 mark)

  4. ii. Find the latest starting time for activity `D`.   (1 mark)

  5. Consider the following statement.
     
    ‘If just one of the activities in this project is crashed by one hour, then the minimum time to complete the entire project will be reduced by one hour.’

    Explain the circumstances under which this statement will be true for this project.   (1 mark)

  6. Assume activity `F` is crashed by two hours.

    What will be the minimum completion time for the project?   (1 mark) 

Show Answers Only
  1.  
    networks-fur2-2013-vcaa-2-answer
  2. `7\ text(hours)`
  3. i. `A-F-I-M`
    ii. `14\ text(hours)`
  4. `text(The statement will only be true if the crashed activity)`
    `text(is on the critical path)\ \ A-F-I-M.`
  5. `text(36 hours)`
Show Worked Solution
a.    networks-fur2-2013-vcaa-2-answer

 

b.    `text(EST of)\ H` `= 4 + 3`
    `= 7\ text(hours)`

 

c.i.   `A-F-I-M`

♦♦ Mean mark of parts (c)-(e) (combined) was 40%.

 

c.ii.  networks-fur2-2013-vcaa-23-answer

`G\ text(precedes)\ I`

`:. text(LST of)\ G = 20-4 = 16\ text(hours)`

`:. text(LST of)\ D = 16-2 = 14\ text(hours)`

  
d.   `text(The statement will only be true if the crashed activity)`

MARKER’S COMMENT: Most students struggled with part (d).

`text(is on the critical path)\ \ A-F-I-M.`
  

e.   `A-F-I-M\ text(is 37 hours.)`

`text(If)\ F\ text(is crashed by 2 hours, the new)`

`text(new critical path is)`

`C-E-H-G-I-M\ text{(36 hours)}`

`:.\ text(Minimum completion time = 36 hours)`

MATRICES*, FUR2 2008 VCAA 4

The children are taken to the zoo where they observe the behaviour of five young male lion cubs. The lion cubs are named Arnold, Barnaby, Cedric, Darcy and Edgar. A dominance hierarchy has emerged within this group of lion cubs. In the directed graph below, the directions of the arrows show which lions are dominant over others.
 

NETWORKS, FUR2 2008 VCAA 41
 

  1. Name the two pairs of lion cubs who have equal totals of one-step dominances.   (2 marks)

  2. Over which lion does Cedric have both a one-step dominance and a two-step dominance?   (1 mark)

In determining the final order of dominance, the number of one-step dominances and two-step dominances are added together.

  1. Complete the table below for the final order of dominance.   (1 mark)


    NETWORKS, FUR2 2008 VCAA 42

Over time, the pattern of dominance changes until each lion cub has a one-step dominance over two other lion cubs.

  1. Determine the total number of two-step dominances for this group of five lion cubs.   (1 mark)

Show Answers Only
  1. `text{Arnold and Edgar (1 each)}`
    `text{Barnaby and Cedric (2 each)}`
  2. `text(Edgar)`
  3.  
    networks-fur2-2008-vcaa-4-answer1
  4. `20`
Show Worked Solution

a.   `text(One step dominances:)`

`text{Arnold and Edgar (1 each)}`

`text{Barnaby and Cedric (2 each)}`
 

b.   `text(Edgar)`
 

c.    networks-fur2-2008-vcaa-4-answer

networks-fur2-2008-vcaa-4-answer1

 

d.   `text(Each lion has a one step dominance over 2 others.)`

`=>\ text(Each lion must have a two step)`

`text(dominance over 2 × 2 = 4 lions)`

 

`:.\ text(Total 2 step dominances in group)`

`= 5 xx 4`

`= 20`

NETWORKS, FUR2 2008 VCAA 3

Each of four children is to be driven by his or her parents to one of four different concerts. The following table shows the distance that each car would have to travel, in kilometres, to each of the four concerts. 

   NETWORKS, FUR2 2008 VCAA 31
  

The concerts will be allocated so as to minimise the total distance that must be travelled to take the children to the concerts. The hungarian algorithm is to be used to find this minimum value.

  1. Step 1 of the hungarian algorithm is to subtract the minimum entry in each row from each element in the row. Complete step 1 for Tahlia by writing the missing values in the table below.   (1 mark)

     

NETWORKS, FUR2 2008 VCAA 32
 

After further steps of the hungarian algorithm have been applied, the table is as follows.
 
  NETWORKS, FUR2 2008 VCAA 33

It is now possible to allocate each child to a concert.

  1. Explain why this table shows that Tahlia should attend Concert 2.   (1 mark)

  2. Determine the concerts that could be attended by James, Dante and Chanel to minimise the total distance travelled. Write your answers in the table below.   (1 mark)

     


    NETWORKS, FUR2 2008 VCAA 34

  3. Determine the minimum total distance, in kilometres, travelled by the four cars.   (1 mark)

Show Answers Only
  1.  
    networks-fur2-2008-vcaa-3-answer
  2. `text(She is the only child with a zero in the)`
    `text(column for Concert 2.)`
  3.  
    networks-fur2-2008-vcaa-3-answer1
  4. `56\ text(km)`
Show Worked Solution
a.    networks-fur2-2008-vcaa-3-answer

  
b.   `text(She is the only child with a zero in the)`

`text(column for Concert 2.)`
  

c.   `text(A possibility:)`

networks-fur2-2008-vcaa-3-answer1

`text{(*3, 1, 4, 2  was also accepted.)}`
  

d.   `text(Minimum total distance)`

`= 18 + 15 + 13 + 10`

`= 56\ text(km)`

NETWORKS, FUR2 2008 VCAA 2

Four children, James, Dante, Tahlia and Chanel each live in a different town. 

The following is a map of the roads that link the four towns, `A`, `B`, `C` and `D`.
 

NETWORKS, FUR2 2008 VCAA 21
 

  1. How many different ways may a vehicle travel from town `A` to town `D` without travelling along any road more than once?   (1 mark)

James’ father has begun to draw a network diagram that represents all the routes between the four towns on the map. This is shown below.


NETWORKS, FUR2 2008 VCAA 22
 

In this network, vertices represent towns and edges represent routes between tow

  1. i. One more edge needs to be added to complete this network. Draw in this edge clearly on the diagram above.   (1 mark)

  2. ii. With reference to the network diagram, explain why a motorist at `A` could not drive each of these routes once only and arrive back at `A`.   (1 mark)

Show Answers Only
  1. `7`
  2. i.  

networks-fur2-2008-vcaa-2-answer

b.ii.  `text(See worked solution)`

Show Worked Solution

a.   `text(Let the two unnamed intersections be)\ T_1\ text{(top) and}\ T_2.`

`text(The possible paths are:)`

♦♦ Exact data unavailable but “few students” answered this question correctly.

`ACD, ACT_2BD, ACT_2T_1BD, AT_1T_2CD,`

`AT_1T_2BD, AT_1BD, AT_1,BT_2CD.`

`:. 7\ text(different ways from)\ A\ text(to)\ D.`

 

b.i.    networks-fur2-2008-vcaa-2-answer

 

b.ii.   `text(Driving each route once and arriving back at)`

MARKER’S COMMENT: Be specific! Note that “an Eulerian circuit requires all vertices of an even degree” did not gain a mark here.

   `A\ text(requires an Eulerian circuit where all)`

   `text(vertices must be an even degree.)`

   `text(The vertices at)\ C\ text(and)\ B\ text(are odd.)`

   `:.\ text(No Eulerian circuit exists.)`

NETWORKS, FUR2 2008 VCAA 1

James, Dante, Tahlia and Chanel are four children playing a game.

In this children’s game, seven posts are placed in the ground.

The network below shows distances, in metres, between the seven posts.

The aim of the game is to connect the posts with ribbon using the shortest length of ribbon.

This will be a minimal spanning tree.

 

NETWORKS, FUR2 2008 VCAA 11
 

  1. Draw in a minimal spanning tree for this network on the diagram below.   (1 mark)


NETWORKS, FUR2 2008 VCAA 12

  1. Determine the length, in metres, of this minimal spanning tree.   (1 mark)

  2. How many different minimal spanning trees can be drawn for this network?   (1 mark)

Show Answers Only
  1.  
    networks-fur2-2008-vcaa-1-answer1
    `text(or)`
    networks-fur2-2008-vcaa-1-answer2
  2. `16\ text(metres)`
  3. `2`
Show Worked Solution
a.    networks-fur2-2008-vcaa-1-answer1

`text(or)`

networks-fur2-2008-vcaa-1-answer2

 

b.   `text(Length of minimal spanning tree)`

`= 4 + 2 + 2 + 3 + 2 + 3`

`= 16\ text(metres)`
 

c.   `2`

NETWORKS, FUR2 2009 VCAA 4

A walkway is to be built across the lake.

Eleven activities must be completed for this building project.

The directed network below shows the activities and their completion times in weeks.
 

NETWORKS, FUR2 2009 VCAA 4
 

  1. What is the earliest start time for activity `E`?   (1 mark)

  2. Write down the critical path for this project.   (1 mark)

  3. The project supervisor correctly writes down the float time for each activity that can be delayed and makes a list of these times.

     

    Determine the longest float time, in weeks, on the supervisor’s list.   (1 mark)

A twelfth activity, `L`, with duration three weeks, is to be added without altering the critical path.

Activity `L` has an earliest start time of four weeks and a latest start time of five weeks.

 

NETWORKS, FUR2 2009 VCAA 4

  1. Draw in activity `L` on the network diagram above.   (1 mark)

  2. Activity `L` starts, but then takes four weeks longer than originally planned.

     

    Determine the total overall time, in weeks, for the completion of this building project.   (1 mark)

Show Answers Only
  1. `7`
  2. `BDFGIK`
  3. `H\ text(or)\ J\ text(can be delayed for)`
    `text(a maximum of 3 weeks.)`
  4.  
    NETWORKS, FUR2 2009 VCAA 4 Answer
  5. `text(25 weeks)`
Show Worked Solution

a.   `7\ text(weeks)`

♦ Mean mark of all parts (combined): 44%.
  

b.   `BDFGIK`
  

c.   `H\ text(or)\ J\ text(can be delayed for a maximum)`

`text(of 3 weeks.)`
  

d.    NETWORKS, FUR2 2009 VCAA 4 Answer

  
e.   `text(The new critical path is)\ BLEGIK.`

`L\ text(now takes 7 weeks.)`

`:.\ text(Time for completion)`

`= 4 + 7 + 1 + 5 + 2 + 6`

`= 25\ text(weeks)`

NETWORKS, FUR2 2009 VCAA 3

The city of Robville contains eight landmarks denoted as vertices `N` to `U` on the network diagram below. The edges on this network represent the roads that link the eight landmarks.
 


  

  1. Write down the degree of vertex `U`.  (1 mark)

  2. Steven wants to visit each landmark, but drive along each road only once. He will begin his journey at landmark `N`.
    1. Michael was the best player in 2014 and he considered purchasing cricket equipment that was valued at $750.
    2. At which landmark must he finish his journey?   (1 mark)
    3. Regardless of which route Steven decides to take, how many of the landmarks (including those at the start and finish) will he see on exactly two occasions?   (1 mark)
  3. Cathy decides to visit each landmark only once.
    1. Suppose she starts at `S`, then visits `R` and finishes at `T`.
    2. Write down the order Cathy will visit the landmarks.   (1 mark)

    3. Suppose Cathy starts at `S`, then visits `R` but does not finish at `T`.
    4. List three different ways that she can visit the landmarks.   (1 mark)

Show Answers Only

  1. `4`
    1. `P\ text{(the other odd degree vertex)}`
    2. `5`
    1. `(SR)QPONU(T)`
    2. `text(Other paths are)`
      `(SR)QPUTNO`
      `(SR)QPONTU`
      `(SR)TUNOPQ`
      `(SR)UTNOPQ`
      `text{(only 3 paths required)}`

Show Worked Solution

a.   `4`

b.i.   `P\ text{(the other odd degree vertex)}`

b.ii.   `5 (N, T, R, P, U)`

c.i.   `(SR)QPONU(T)`

c.ii.   `text(Other paths are)`

`(SR)QPUTNO`

`(SR)QPONTU`

`(SR)TUNOPQ`

`(SR)UTNOPQ`

`text{(only 3 paths required)}`

NETWORKS, FUR2 2009 VCAA 1

The city of Robville is divided into five suburbs labelled as `A` to `E` on the map below. 

A lake which is situated in the city is shaded on the map.

 

NETWORKS, FUR2 2009 VCAA 11

An adjacency matrix is constructed to represent the number of land borders between suburbs.

`{:({:qquadqquadAquadBquadCquadDquadE:}),({:(A),(B),(C),(D),(E):}[(0,1,1,1,0),(1,0,1,2,0),(1,1,0,0,0),(1,2,0,0,0),(0,0,0,0,0)]):}`

 

  1. Explain why all values in the final row and final column are zero.   (1 mark)

In the network diagram below, vertices represent suburbs and edges represent land borders between suburbs. 

The diagram has been started but is not finished.

 

Networks, FUR2 2009 VCAA 1_1
 

  1. The network diagram is missing one edge and one vertex. 

     

    On the diagram

  2.  i. draw the missing edge.   (1 mark)

  3. ii. draw and label the missing vertex.   (1 mark)

Show Answers Only
  1. `E\ text(has no land borders with other suburbs.)`
  2. i. & ii.
    Networks, FUR2 2009 VCAA 1 Answer
Show Worked Solution

a.   `E\ text(has no land borders with other suburbs.)`

 

b.i. & ii.    Networks, FUR2 2009 VCAA 1 Answer

NETWORKS, FUR2 2010 VCAA 4

In the final challenge, each of four teams has to complete a construction project that involves activities `A` to `I`.
 

NETWORKS, FUR2 2010 VCAA 4
 

Table 1 shows the earliest start time (EST), latest start time (LST) and duration, in minutes, for each activity. 

The immediate predecessor is also shown. The earliest start time for activity `F` is missing.

  1. What is the least number of activities that must be completed before activity `F` can commence?   (1 mark)

  2. What is the earliest start time for activity `F`?   (1 mark)

  3. Write down all the activities that must be completed before activity `G` can commence.   (1 mark)

  4. What is the float time, in minutes, for activity `G`?   (1 mark)

  5. What is the shortest time, in minutes, in which this construction project can be completed?   (1 mark)

  6. Write down the critical path for this network.   (1 mark)

Show Answers Only
  1. `2`
  2. `9\ text(minutes)`
  3. `A\ text(and)\ C`
  4. `4\ text(minutes)`
  5. `16\ text(minutes)`
  6. `A-B-D-H`
Show Worked Solution

a.   `2`
  

b.    `text(EST for)\ F` `= 5 + 4`
    `= 9\ text(minutes)`

  
c.   `A\ text(and)\ C`
  

d.    `text(Float time for)\ G` `= 13-9`
    `= 4\ text(minutes)`

 

e.   `text(Shortest construction time)`

`= 5 + 6 + 2 + 3`

`= 16\ text(minutes)`

 

f.   `A-B-D-H`

NETWORKS, FUR2 2010 VCAA 3

The following network diagram shows the distances, in kilometres, along the roads that connect six intersections `A`, `B`, `C`, `D`, `E` and `F`.
 

  1. If a cyclist started at intersection `B` and cycled along every road in this network once only, at which intersection would she finish?  (1 mark)

  2. The next challenge involves cycling along every road in this network at least once.

     

    Teams have to start and finish at intersection `A`.

     

    The blue team does this and cycles the shortest possible total distance.

     

    i. Apart from intersection `A`, through which intersections does the blue team pass more than once?   (1 mark)

  3. ii. How many kilometres does the blue team cycle?   (1 mark)

  4. The red team does not follow the rules and cycles along a bush path that connects two of the intersections.

     

    This route allows the red team to ride along every road only once.

     

    Which two intersections does the bush path connect?   (1 mark)

Show Answers Only
  1. `D`
    1. `B, D\ text(and)\ F`
    2. `32\ text(km)`
  3. `B\ text(and)\ D`
Show Worked Solution

a.   `D`
  

b.i.   `text(Consider the path)`

`AFDEFBCDFBA`

`:.\ text(Passes through)\ B, D,\ text(and)\ F\ text(more)`

`text(than once.)`
  

b.ii.   `text{Total distance (Blue)}`

`= 6 + 3 + 3 + 4 + 2 + 4 + 2 + 3 + 2 + 3`

`= 32\ text(km)`
  

c.   `text(An Euler circuit can only exist when the)`

`text(degree of all vertices is even.)`

`:.\ text(The bush track joins)\ B\ text(and)\ D.`

NETWORKS, FUR2 2011 VCAA 4

Stormwater enters a network of pipes at either Dunlop North (Source 1) or Dunlop South (Source 2) and flows into the ocean at either Outlet 1 or Outlet 2.

On the network diagram below, the pipes are represented by straight lines with arrows that indicate the direction of the flow of water. Water cannot flow through a pipe in the opposite direction.

The numbers next to the arrows represent the maximum rate, in kilolitres per minute, at which stormwater can flow through each pipe.

 

NETWORKS, FUR2 2011 VCAA 4_1
 

  1. Complete the following sentence for this network of pipes by writing either the number 1 or 2 in each box.  (1 mark)

NETWORKS, FUR2 2011 VCAA 4_2

  1. Determine the maximum rate, in kilolitres per minute, that water can flow from these pipes into the ocean at Outlet 1 and Outlet 2.  (2 marks)

A length of pipe, show in bold on the network diagram below, has been damaged and will be replaced with a larger pipe.

 

NETWORKS, FUR2 2011 VCAA 4_3
 

  1. The new pipe must enable the greatest possible rate of flow of stormwater into the ocean from Outlet 2.
  2. What minimum rate of flow through the pipe, in kilolitres per minute, will achieve this?  (1 mark)

Show Answers Only

  1. `text(Storm water from Source 2 cannot reach Outlet 1)`
  2. `text(Outlet 1: 700 kL/min)`
    `text(Outlet 2: 700 kL/min)`
  3. `text(300 kL per min)`

Show Worked Solution

a.   `text(Storm water from Source 2 cannot reach Outlet 1)`

♦ Mean mark of all parts (combined) was 35%.

 

b.    NETWORKS, FUR2 2011 VCAA 4 Answer

 
`text(The minimum cut includes the 200 kL/min pipe from Source 1.)`

`:.\ text(Maximum rates are)`

`text(Outlet 1: 700 kL/min)`

`text(Outlet 2: 700 kL/min)`

 

c.   `text(The next smallest cut in the lower pipe system is 800.)`

`:.\ text(The minimum flow through the new pipe that will achieve)`

`text(this is 300 kL/min.)`

NETWORKS, FUR2 2011 VCAA 3

A section of the Farnham showgrounds has flooded due to a broken water pipe. The public will be stopped from entering the flooded area until repairs are made and the area has been cleaned up.

The table below shows the nine activities that need to be completed in order to repair the water pipe. Also shown are some of the durations, Earliest Start Times (EST) and the immediate predecessors for the activities.
 

NETWORKS, FUR2 2011 VCAA 3 

  1. What is the duration of activity `B`?   (1 mark)

  2. What is the Earliest Start Time (EST) for activity `D`?   (1 mark)

  3. Once the water has been turned off (Activity `B`), which of the activities `C` to `I` could be delayed without affecting the shortest time to complete all activities?   (1 mark)

It is more complicated to replace the broken water pipe (Activity `E`) than expected. It will now take four hours to complete instead of two hours.

  1. Determine the shortest time in which activities `A` to `I` can now be completed.   (1 mark)

Turning on the water to the showgrounds (Activity `H`) will also take more time than originally expected. It will now take five hours to complete instead of one hour.

  1. With the increased duration of Activity `H` and Activity `E`, determine the shortest time in which activities `A` to `I` can be completed.   (1 mark)

Show Answers Only
  1. `text(2 hours)`
  2. `text(3 hours)`
  3. `text(Activities)\ F and H`
  4. `13\ text(hours)`
  5. `14\ text(hours)`
Show Worked Solution
a.    `text(Duration of)\ B` `= text(EST of)\ C`
    `= 2\ text(hours)`
♦ Mean mark of all parts (combined) was 42%.

  
b.   `text(EST of)\ C = 3\ text(hours)`

  
c.   `text(Activities)\ F and H`

MARKER’S COMMENT: Many students incorrectly included `G` in this answer (note that `G` is not on the critical path).

  
d.   `text(Shortest time)\ (A\ text(to)\ I)`

`= 2 + 1 + 1 + 4 + 4 + 1`

`= 13\ text(hours)`
  

e.   `text(New shortest time)`

`= 2 + 1 + 1 + 4 + 5 + 1`

`= 14\ text(hours)`

NETWORKS, FUR2 2011 VCAA 2

At the Farnham showgrounds, eleven locations require access to water. These locations are represented by vertices on the network diagram shown below. The dashed lines on the network diagram represent possible water pipe connections between adjacent locations. The numbers on the dashed lines show the minimum length of pipe required to connect these locations in metres.
 

NETWORKS, FUR2 2011 VCAA 2 
 

All locations are to be connected using the smallest total length of water pipe possible.

  1. On the diagram, show where these water pipes will be placed.   (1 mark)

  2. Calculate the total length, in metres, of water pipe that is required.   ( 1 mark) 
Show Answers Only
  1.  
    NETWORKS, FUR2 2011 VCAA 2 Answer
  2. `510\ text(metres)`
Show Worked Solution
a.    NETWORKS, FUR2 2011 VCAA 2 Answer

 

b.   `text(Total length of water pipe)`

`= 60 + 60 + 40 + 60 + 50 + 40 + 60`

`+ 40 + 50 + 50`

`= 510\ text(metres)`

NETWORKS, FUR2 2011 VCAA 1

Aden, Bredon, Carrie, Dunlop, Enwin and Farnham are six towns.

The network shows the road connections and distances between these towns in kilometres.

 

  1. In kilometres, what is the shortest distance between Farnham and Carrie?   (1 mark)

  2. How many different ways are there to travel from Farnham to Carrie without passing through any town more than once?   (1 mark)

An engineer plans to inspect all of the roads in this network.

He will start at Dunlop and inspect each road only once.

  1. At which town will the inspection finish?   (1 mark)

Another engineer decides to start and finish her road inspection at Dunlop.

If an assistant inspects two of the roads, this engineer can inspect the remaining six roads and visit each of the other five towns only once.

  1. How many kilometres of road will the assistant need to inspect?   (1 mark)

Show Answers Only
  1. `200\ text(km)`
  2. `6`
  3. `text(Bredon)`
  4. `240\ text(km)`
Show Worked Solution

a.   `text{Farnham to Carrie (shortest)}`

`= 60 + 140`

`= 200\ text(km)`
  

b.   `text(Different paths are)`

`FDC, FEDC, FEBC,`

`FEABC, FDEBC,`

`FDEABC`

`:. 6\ text(different ways)`
  

c.   `text(A possible path is)\ DFEABCDEB\ text(and will finish)`

`text{at Bredon (the other odd-degree vertex).}`
  

d.   `text(If the engineer’s path is)`

`DFEABCD,`

`text(Distance assistant inspects)`

`= 110 + 130`

`= 240\ text(km)`

Calculus, MET1 2006 VCAA 11

Part of the graph of the function  `f: R-> R, f(x) = -x^2 + ax + 12`  is shown below. If the shaded area is 45 square units, find the values of `a, m` and `n` where `m` and `n` are the `x`-axis intercepts of the graph of `y = f(x).`  (5 marks)

vcaa-2006-meth-11a

Show Answers Only

`m = 6;\ \ \ n = – 2`

Show Worked Solution

`text(Shaded Area) = 45`

`45` `= int_0^3 (– x^2 + ax + 12)\ dx`
`45` `= [– 1/3x^3 + 1/2 ax^2 + 12x]_0^3`
`45` `= – 9 + 9/2a + 36`
`9/2 a` `= 18`
`:. a` `= 36/9`
  `= 4`

 

`f(x) = – x^2 + 4x + 12`

`text(Factorise to find)\ x text(-intercepts:)`

`- (x^2 – 4x – 12)` `=0`
`(x – 6) (x + 2)` `=0`

 

`:. m = 6, and n = – 2`

NETWORKS, FUR2 2014 VCAA 4

To restore a vintage train, 13 activities need to be completed.

The network below shows these 13 activities and their completion times in hours.
 

NETWORKS, FUR2 2014 VCAA 4
 

  1. Determine the earliest starting time of activity `F`.   (1 mark)

The minimum time in which all 13 activities can be completed is 21 hours.

  1. What is the latest starting time of activity `L`?   (1 mark)

  2. What is the float time of activity `J`?   (1 mark)

Just before they started restoring the train, the members of the club needed to add another activity, `X`, to the project.

Activity `X` will take seven hours to complete.

Activity `X` has no predecessors, but must be completed before activity `G` starts.

  1. What is the latest starting time of activity `X` if it is not to increase the minimum completion time of the project?   (1 mark)

Activity `A` can be crashed by up to four hours at an additional cost of $90 per our.

This may reduce the minimum completion time for the project, including activity `X`.

  1. Determine the least cost of crashing activity `A` to give the greatest reduction in the minimum completion time of the project.   (1 mark)

Show Answers Only
  1. `text(7 hours)`
  2. `text(18 hours)`
  3. `text(2 hours)`
  4. `text(4 hours)`
  5. `$270`
Show Worked Solution

a.   `5 + 2 = 7\ text(hours)`

♦ Mean mark for all parts (combined) was 42%.

  
b.   `text(Latest starting time of)\ L`

`= text(Length of critical path – duration of)\ L`

`= 21-3`

`= 18\ text(hours)`
  

c.   `text(Float time of)\ J`

`=\ text(LST-EST)`

`= 13-11`

`= 2\ text(hours)`
  

d.   `X\ text(precedes)\ G`

`text(EST of)\ G = 11`

`:. text(LST of)\ X = 11`
  

`text(EST)\ text(of)\ X`

`= text(LST of)\ X-text(duration of)\ X`

`= 11-7`

`= 4\ text(hours)`
  

e.   `text(Longer paths are)`

`A-C-G-K = 21\ text{hours (critical path)}`

`A-D-E-H-K = 20\ text(hours)`

`A-D-F-J-M = 19\ text(hours)`

`A-D-E-I-M = 18\ text(hours)`

`B-E-H- K = 18\ text(hours)`

`B-F-J-M = 17\ text(hours)`

 

`:.\ text(Reduce)\ \ A-C-G-K\ \ text(by 3 hours to get)`

`text{to 18 hours (equals}\ \ B-E-H-K)`
 

`:.\ text(Least cost)` `= 3 xx 90`
  `= $270`

NETWORKS, FUR2 2014 VCAA 3

The diagram below shows a network of train lines between five towns: Attard, Bower, Clement, Derrin and Eden.

The numbers indicate the distances, in kilometres, that are travelled by train between connected towns.
 

Charlie followed an Eulerian path through this network of train lines.

  1. i. Write down the names of the towns at the start and at the end of Charlie’s path.   (1 mark)

    ii. What distance did he travel?   (1 mark)

Brianna will follow a Hamiltonian path from Bower to Attard.

  1. What is the shortest distance that she can travel?   (1 mark)

The train line between Derrin and Eden will be removed. If one other train line is removed from the network, Andrew would be able to follow an Eulerian circuit through the network of train lines.

  1. Which other train line should be removed?

     

    In the boxes below, write down the pair of towns that this train line connects.  (1 mark) 

     
    NETWORKS, FUR2 2014 VCAA 32

Show Answers Only
  1.  i.  `text(Bower, Eden)`
    ii.  `910\ text(km)`
  2. `270\ text(km)`
  3. `text(Bower and Derrin)`
Show Worked Solution

a.i.   `text(Bower, Eden or Eden, Bower)`
  

a.ii.   `text(Distance)\ \ BDABCDEACE`

`= 160 + 130 + 80 + 70 + 60 + 40 + 100 + 150 + 120`

`= 910\ text(km)`
  

b.   `text(Shortest Hamiltonian path is)\ BCDEA`

`text(Distance)` `= 70 + 60 + 40 + 100`
  `= 270\ text(km)`

  
c.   `text(Remove the line between Bower and Derrin.)`

NETWORKS, FUR2 2014 VCAA 2

Planning a train club open day involves four tasks.

Table 1 shows the number of hours that each club member would take to complete these tasks.
 

     NETWORKS, FUR2 2014 VCAA 21
 

The Hungarian algorithm will be used to allocate the tasks to club members so that the total time taken to complete the tasks is minimised.

The first step of the Hungarian algorithm is to subtract the smallest element in each row of Table 1 from each of the elements in that row.

The result of this step is shown in Table 2 below.

  1. Complete Table 2 by filling in the missing numbers for Andrew.   (1 mark)

     

     

    NETWORKS, FUR2 2014 VCAA 22
     

After completing Table 2, Andrew decided that an allocation of tasks to minimise the total time taken was not yet possible using the Hungarian algorithm.

  1. Explain why Andrew made this decision.   (1 mark)

Table 3 shows the final result of all steps of the Hungarian algorithm.
 

NETWORKS, FUR2 2014 VCAA 23

  1.  i. Which task should be allocated to Andrew?   (1 mark)

  2. ii. How many hours in total are used to plan for the open day?   (1 mark)

Show Answers Only
  1.  
    Networks, FUR2 2014 VCAA 2_2 answer
  2. `text(The minimum number of lines to cover all zeros)`
    `text(is less than four.)`
    1. `text(Equipment)`
    2. `36`
Show Worked Solution
a.    Networks, FUR2 2014 VCAA 2_2 answer

 

b.   `text(The minimum number of lines to cover all zeros)`

MARKER’S COMMENT: An answer of “there were not enough zeros” did not gain a mark.

`text(is less than four.)`
  

c.i.   `text(Equipment)`
  

c.ii.   `text(Total hours to plan)`

`= 8 +10 +10 + 8`

`= 36`

NETWORKS, FUR2 2015 VCAA 3

Nine activities are needed to prepare a daily delivery of groceries from the factory to the towns.

The duration, in minutes, earliest starting time (EST) and immediate predecessors for these activities are shown in the table below.
 

   Networks, FUR2 2015 VCAA 31
 

The directed network that shows these activities is shown below.
 

 Networks, FUR2 2015 VCAA 32
 

All nine of these activities can be completed in a minimum time of 26 minutes.

  1. What is the EST of activity `D`?   (1 mark)

  2. What is the latest starting time (LST) of activity `D`?   (1 mark)

  3. Given that the EST of activity `I` is 22 minutes, what is the duration of activity `H`?   (1 mark)

  4. Write down, in order, the activities on the critical path.   (1 mark)

  5. Activities `C` and `D` can only be completed by either Cassie or Donna.

     

    One Monday, Donna is sick and both activities `C` and `D` must be completed by Cassie. Cassie must complete one of these activities before starting the other.

     

    What is the least effect of this on the usual minimum preparation time for the delivery of groceries from the factory to the five towns?   (1 mark)

  6. Every Friday, a special delivery to the five towns includes fresh seafood. This causes a slight change to activity `G`, which then cannot start until activity `F` has been completed.
      
    i.     Michael was the best player in 2014 and he considered purchasing cricket equipment that was valued at $750.
    On the directed graph below, show this change without duplicating any activity?   (1 mark)


    Networks, FUR2 2015 VCAA 32
     
  7. ii. What effect does the inclusion of seafood on Fridays have on the usual minimum preparation time for deliveries from the factory to the five towns?   (1 mark)

Show Answers Only
  1. `text(3 minutes)`
  2. `text(4 minutes)`
  3. `text(3 minutes)`
  4. `A-C-F-H-I`
  5. `text(The critical path is increased by)`
    `text(7 minutes to 33 minutes.)`
  6. i. 
    Networks, FUR2 2015 VCAA 3 Answer
    ii. `text(The critical path is increased by)`
         `text(2 minutes to 28 minutes.)`

Show Worked Solution

a.   `text(3 minutes)`
 

b.   `text(4 minutes)`
 

c.   `text(3 minutes)`
 

d.   `A-C-F-H-I`
 

e.   `text(The critical path is increased by 7 minutes)`

`text(to 33 minutes.)`

 

f.i.    Networks, FUR2 2015 VCAA 3 Answer

 

f.ii.   `text(The critical path is increased by 2 minutes)`

`text(to 28 minutes.)`

NETWORKS, FUR2 2015 VCAA 2

The factory supplies groceries to stores in five towns, `Q`, `R`, `S`, `T` and `U`, represented by vertices on the graph below.
 

Networks, FUR2 2015 VCAA 2
 

The edges of the graph represent roads that connect the towns and the factory.

The numbers on the edges indicate the distance, in kilometres, along the roads.

Vehicles may only travel along the road between towns `S` and `Q` in the direction of the arrow due to temporary roadworks.

Each day, a van must deliver groceries from the factory to the five towns.

The first delivery must be to town `T`, after which the van will continue on to the other four towns before returning to the factory.

  1. i. The shortest possible circuit from the factory for this delivery run, starting from town `T`, is not Hamiltonian.
     
    Complete the order in which these deliveries would follow this shortest possible circuit.   (1 mark)

     factory – `T` – ___________________________ – factory

  2. ii. With reference to the town names in your answer to part (a)(i), explain why this shortest circuit is not a Hamiltonian circuit.   (1 mark)

  3. Determine the length, in kilometres, of a delivery run that follows a Hamiltonian circuit from the factory to these stores if the first delivery is to town `T`.   (1 mark)

Show Answers Only

a.i.  `text(factory)\-T-S-Q-R-S-U-text(factory)`

aii.  `text(The van passes through town)\ S\ text(twice.)`

b.   `162\ text(km)`

Show Worked Solution

a.i.   `text(factory)\-T-S-Q-R-S-U- text(factory)`
  

a.ii.   `text(The van passes through town)\ S\ text(twice.)`
  

b.   `text(Hamiltonian circuit is)`

`text(factory)\-T-S-R-Q-U-text(factory)`

`= 44 + 38 + 12 + 8 + 38 + 22`

`= 162\ text(km)`

NETWORKS, FUR2 2015 VCAA 1

A factory requires seven computer servers to communicate with each other through a connected network of cables.

The servers, `J`, `K`, `L`, `M`, `N`, `O` and `P`, are shown as vertices on the graph below.
 

Networks, FUR2 2015 VCAA 11

 
The edges on the graph represent the cables that could connect adjacent computer servers.

The numbers on the edges show the cost, in dollars, of installing each cable.

  1. What is the cost, in dollars, of installing the cable between server `L` and server `M`?   (1 mark)

  2. What is the cheapest cost, in dollars, of installing cables between server `K` and server `N`?   (1 mark)

  3. An inspector checks the cables by walking along the length of each cable in one continuous path.
    To avoid walking along any of the cables more than once, at which vertex should the inspector start and where would the inspector finish?   (1 mark)

     

  4. The computer servers will be able to communicate with all the other servers as long as each server is connected by cable to at least one other server.
    i.     The cheapest installation that will join the seven computer servers by cable in a connected network follows a minimum spanning tree.

    Draw the minimum spanning tree on the plan below?   (1 mark)


    Networks, FUR2 2015 VCAA 12
  5. ii. The factory’s manager has decided that only six connected computer servers will be needed, rather than seven. 

    How much would be saved in installation costs if the factory removed computer server `P` from its minimum spanning tree network?
    A copy of the graph above is provided below to assist with your working.   (1 mark)

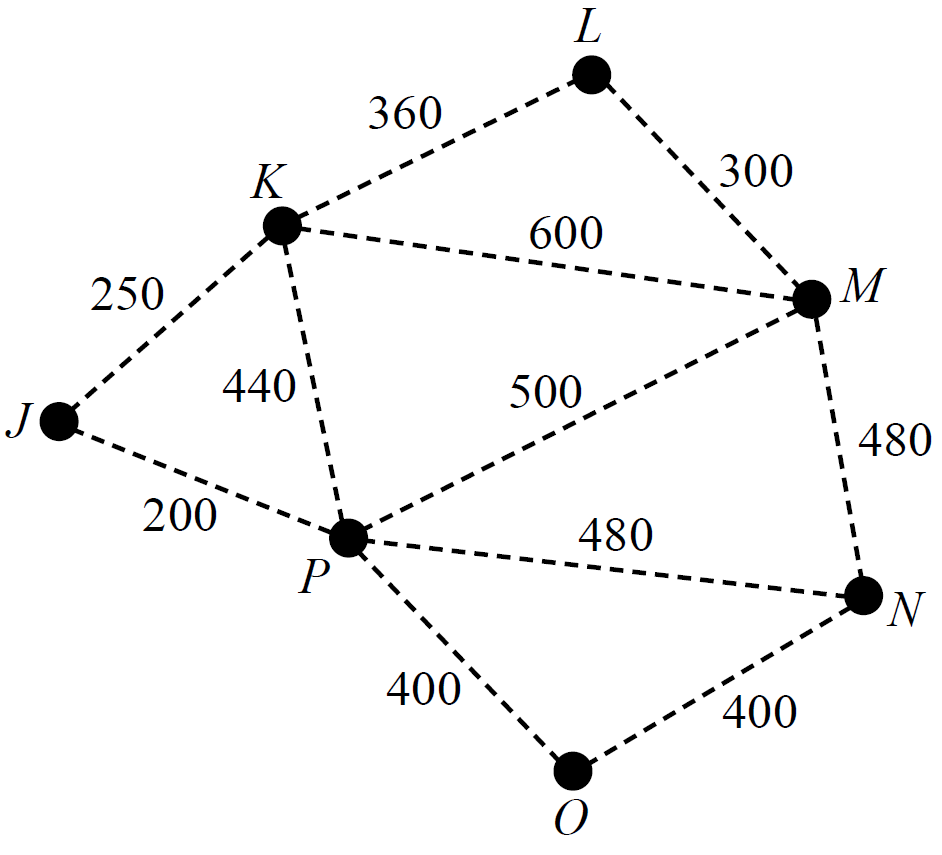
    Networks, FUR2 2015 VCAA 12

Show Answers Only
  1. `$300`
  2. `$920`
  3. `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`
  4. i. 

 Networks, FUR2 2015 VCAA 12 Answer
d.ii.`$120`

Show Worked Solution

a.   `$300`
  

b.   `text(C)text(ost of)\ K\ text(to)\ N`

`= 440 + 480`

`= $920`
  

c.   `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`

MARKER’S COMMENT: Many students had difficulty finding the minimum spanning tree, often incorrectly excluding `PO` or `KL`.
d.i.    Networks, FUR2 2015 VCAA 12 Answer

 

d.ii.   `text(Disconnect)\ J – P\ text(and)\ O – P`

`text(Savings) = 200 + 400 = $600`

`text(Add in)\ M – N`

`text(C)text(ost) = $480`

`:.\ text(Net savings)` `= 600 – 480`
  `= $120`

MATRICES, FUR2 2006 VCAA 3

Market researchers claim that the ideal number of bookshops (`x`), sports shoe shops (`y`) and music stores (`z`) for a shopping centre can be determined by solving the equations

`2x + y + z = 12`

`x-y+z=1`

`2y-z=6`

  1. Write the equations in matrix form using the following template.   (1 mark)

     

     
    `qquad[(qquadqquadqquadqquadqquad),(),()][(qquadquad),(qquadquad),(qquadquad)] = [(qquadquad),(qquadquad),(qquadquad)]`
     

     

  2. Do the equations have a unique solution? Provide an explanation to justify your response.   (1 mark)

  3. Write down an inverse matrix that can be used to solve these equations.   (1 mark)

  4. Solve the equations and hence write down the estimated ideal number of bookshops, sports shoe shops and music stores for a shopping centre.   (1 mark)

Show Answers Only
  1.  
    `[(2,1,1),(1,-1,1),(0,2,-1)][(x),(y),(z)] = [(12),(1),(6)]`
  2.  `text(Yes. See worked solutions.)`
  3.  
    `[(2,1,1),(1,-1,1),(0,2,-1)]^(-1) = [(-1,3,2),(1,-2,-1),(2,-4,-3)]`
  4. `text(3 bookshops, 4 sports shoe shops, 2 music stores.)`
Show Worked Solution
a.    `[(2,1,1),(1,-1,1),(0,2,-1)][(x),(y),(z)] = [(12),(1),(6)]`
♦ Mean mark 35% for all parts (combined).

 

b.    `text(det)\ [(2,1,1),(1,-1,1),(0,2,-1)] = 1 != 0`

 
`:.\ text(A unique solution exists.)`

 

c.   `text(By CAS,)`

`[(2,1,1),(1,-1,1),(0,2,-1)]^(-1) = [(-1,3,2),(1,-2,-1),(2,-4,-3)]`

 

d.  `[(x),(y),(z)]= [(-1,3,2),(1,-2,-1),(2,-4,-3)][(12),(1),(6)]= [(3),(4),(2)]`

`:.\ text(Estimated ideal numbers are:)`

`text(3 bookshops)`

`text(4 shoe shops)`

`text(2 music stores)`

MATRICES, FUR2 2006 VCAA 2

A new shopping centre called Shopper Heaven (`S`) is about to open. It will compete for customers with Eastown (`E`) and Noxland (`N`).

Market research suggests that each shopping centre will have a regular customer base but attract and lose customers on a weekly basis as follows.

80% of Shopper Heaven customers will return to Shopper Heaven next week
12% of Shopper Heaven customers will shop at Eastown next week
8% of Shopper Heaven customers will shop at Noxland next week

76% of Eastown customers will return to Eastown next week
9% of Eastown customers will shop at Shopper Heaven next week
15% of Eastown customers will shop at Noxland next week

85% of Noxland customers will return to Noxland next week
10% of Noxland customers will shop at Shopper Heaven next week
5% of Noxland customers will shop at Eastown next week

  1. Enter this information into transition matrix `T` as indicated below (express percentages as proportions, for example write 76% as 0.76).   (2 marks)

     

     
    `qquad{:(qquadqquadqquadtext(this week)),((qquadqquadqquad S,qquad E, quad N)),(T = [(qquadqquadqquadqquadqquadqquad),(),()]{:(S),(E),(N):}{:qquadtext(next week):}):}`
     

During the week that Shopper Heaven opened, it had 300 000 customers.

In the same week, Eastown had 120 000 customers and Noxland had 180 000 customers.

  1. Write this information in the form of a column matrix, `K_0`, as indicated below.   (1 mark)

     

     
    `qquadK_0 = [(quadqquadqquadqquadqquad),(),()]{:(S),(E),(N):}`
     

  2. Use `T` and `K_0` to write and evaluate a matrix product that determines the number of customers expected at each of the shopping centres during the following week.   (2 marks)

  3. Show by calculating at least two appropriate state matrices that, in the long term, the number of customers expected at each centre each week is given by the matrix   (2 marks)
  4. `qquadK = [(194\ 983),(150\ 513),(254\ 504)]`
Show Answers Only
  1.  
    `{:((qquadqquadqquad\ S,qquadE,qquadN)),(T = [(0.8,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)]{:(S),(E),(N):}):}`
  2.  
    `K_0 = [(300\ 000),(120\ 000),(180\ 000)]{:(S),(E),(N):}`
  3.  
    `TK_0 = [(268\ 800),(136\ 200),(195\ 000)]`
  4. `text(See Worked Solutions)`
Show Worked Solution
a.     `{:((qquadqquadqquad\ S,qquadE,qquadN)),(T = [(0.8,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)]{:(S),(E),(N):}):}`

 

b.     `K_0 = [(300\ 000),(120\ 000),(180\ 000)]{:(S),(E),(N):}`

 

c.   `text(Customers expected at each centre the next week,)`

`TK_0` `= [(0.80,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)][(300\ 000),(120\ 000),(180\ 000)]`
  `= [(268\ 800),(136\ 200),(195\ 000)]`

 

d.   `text(Consider)\ \ T^nK_0\ \ text(when)\ n\ text(large),`

`text(say)\ n=50, 51`

`T^50K_0` `= [(0.8,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)]^50[(300\ 000),(120\ 000),(180\ 000)]= [(194\ 983),(150\ 513),(254\ 504)]`

 

`T^51K_0` `= [(0.8,0.09,0.10),(0.12,0.76,0.05),(0.08,0.15,0.85)]^51[(300\ 000),(120\ 000),(180\ 000)]= [(194\ 983),(150\ 513),(254\ 504)]`
  ` = T^50K_0`

MATRICES, FUR2 2006 VCAA 1

A manufacturer sells three products, `A`, `B` and `C`, through outlets at two shopping centres, Eastown (`E`) and Noxland (`N`). 

The number of units of each product sold per month through each shop is given by the matrix `Q`, where

`{:((qquadqquadqquad\ A,qquadquadB,qquad\ C)),(Q=[(2500,3400,1890),(1765,4588,2456)]{:(E),(N):}):}`

  1. Write down the order of matrix `Q`.   (1 mark)

The matrix `P`, shown below, gives the selling price, in dollars, of products `A`, `B`, `C`.

`P = [(14.50),(21.60),(19.20)]{:(A),(B),(C):}`

  1.   i. Evaluate the matrix `M`, where `M = QP`.   (1 mark)

  2.  ii. What information does the elements of matrix `M` provide?   (1 mark)

  3. Explain why the matrix `PQ` is not defined.   (1 mark)

Show Answers Only
  1. `2 xx 3`
    1. `M = QP = [(135\ 320.5),(171\ 848.5)]`
    2. `text(The total of selling products)\ A, B,and C`
      `text(at each of Eastown and Noxland.)`
  3. `PQ\ text(is not defined because the number of)`
    `text(columns in)\ P !=\ text(the number of rows in)\ Q.`
Show Worked Solution

a.   `2 xx 3`
 

b.i.    `M` `= QP`
    `= [(2500,3400,1890),(1765,4588,2456)][(14.50),(21.60),(19.20)]`
    `= [(135\ 320.5),(171\ 848.5)]`

 
b.ii.  `text(The total revenue from selling products)\ A, B,`

   `text(and)\ C\ text(at each of Eastown and Noxland.)`
 

c.   `PQ\ text(is not defined because the number of)`

`text(columns in)\ P !=\ text(the number of rows in)\ Q.`

MATRICES, FUR2 2007 VCAA 2

To study the life-and-death cycle of an insect population, a number of insect eggs (`E`), juvenile insects (`J`) and adult insects (`A`) are placed in a closed environment.

The initial state of this population can be described by the column matrix

`S_0 = [(400),(200),(100),(0)]{:(E),(J),(A),(D):}`

A row has been included in the state matrix to allow for insects and eggs that die (`D`).

  1. What is the total number of insects in the population (including eggs) at the beginning of the study?   (1 mark)

In this population

    • eggs may die, or they may live and grow into juveniles
    • juveniles may die, or they may live and grow into adults
    • adults will live a period of time but they will eventually die.

In this population, the adult insects have been sterilised so that no new eggs are produced. In these circumstances, the life-and-death cycle of the insects can be modelled by the transition matrix
 

`{:(qquadqquadqquadqquadquadtext(this week)),((qquadqquadqquadE,quad\ J,quadA,\ D)),(T = [(0.4,0,0,0),(0.5,0.4,0,0),(0,0.5,0.8,0),(0.1,0.1,0.2,1)]{:(E),(J),(A),(D):}):}`
 

  1. What proportion of eggs turn into juveniles each week?   (1 mark)

    1. Evaluate the matrix product  `S_1 = TS_0`   (1 mark)

    2. Write down the number of live juveniles in the population after one week.   (1 mark)

    3. Determine the number of live juveniles in the population after four weeks. Write your answer correct to the nearest whole number.   (1 mark)

    4. After a number of weeks there will be no live eggs (less than one) left in the population.
    5. When does this first occur?   (1 mark)

    6. Write down the exact steady-state matrix for this population.  (1 mark)

  3. If the study is repeated with unsterilised adult insects, eggs will be laid and potentially grow into adults.
  4. Assuming 30% of adults lay eggs each week, the population matrix after one week, `S_1`, is now given by
  5. `qquad S_1 = TS_0 + BS_0`
  6. where   `B = [(0,0,0.3,0),(0,0,0,0),(0,0,0,0),(0,0,0,0)]`   and   `S_0 = [(400),(200),(100),(0)]{:(E),(J),(A),(D):}`
     

    1. Determine `S_1`  (1 mark)

    2. This pattern continues. The population matrix after `n` weeks, `S_n`, is given by
    3. `qquad qquad qquad S_n = TS_(n - 1) + BS_(n - 1)`
    4. Determine the number of live eggs in this insect population after two weeks.  (1 mark)

Show Answers Only
  1. `700`
  2. `50text(%)`
  3.  
    1. `[(160),(280),(180),(80)]{:(E),(J),(A),(D):}`
    2. `280`
    3. `56`
    4. `text(7th week)`
    5. `[(0),(0),(0),(700)]`
    1. `[(190),(280),(180),(80)]`
    2. `130`
Show Worked Solution

a.   `400 + 200 + 100 + 0 = 700`
 

b.   `50text(%)`
 

c.i.    `S_1` ` = TS_0`
    `= [(0.4,0,0,0),(0.5,0.4,0,0),(0,0.5,0.8,0),(0.1,0.1,0.2,1)][(400),(200),(100),(0)]`
    `= [(160),(280),(180),(80)]{:(E),(J),(A),(D):}`

 
c.ii.   `280`
 

c.iii.    `S_4` ` = T^4S_0`
    `= [(10.24),(56.32),(312.96),(320.48)]{:(E),(J),(A),(D):}\ \ \ text{(by graphics calculator)}`

 
`:. 56\ text(juveniles still alive after 4 weeks.)`
 

c.iv.  `text(Each week, only 40% of eggs remain.)`

`text(Find)\ \ n\ \ text(such that)`

`400 xx 0.4^n` `< 1`
`0.4^n` `<1/400`
`n` `> 6.5`

 
`:.\ text(After 7 weeks, no live eggs remain.)`

 

c.v.   `text(Consider)\ \ n\ \ text{large (say}\ \ n = 100 text{)},`

`[(0.4, 0, 0, 0), (0.5, 0.4, 0, 0), (0, 0.5, 0.8, 0), (0.1, 0.1, 0.2, 1)]^100 [(400), (200), (100), (0)] ~~ [(0), (0), (0), (700)]`

 

d.i.   `S_1` `= TS_0 + BS_0`
    `= [(160),(280),(180),(80)] + [(0,0,0.3,0),(0,0,0,0),(0,0,0,0),(0,0,0,0)][(400),(200),(100),(0)]= [(190),(280),(180),(80)]`

 

♦♦ Mean mark for part (d) was 30%.
d.ii.   `S_2` `= TS_1 + BS_1= [(130), (207), (284), (163)]`

 
`:.\ text(There are 130 live egss after 2 weeks.)`

MATRICES, FUR2 2007 VCAA 1

The table below displays the energy content and amounts of fat, carbohydrate and protein contained in a serve of four foods: bread, margarine, peanut butter and honey.
 

MATRICES, FUR2 2007 VCAA 1
 

  1. Write down a 2 x 3 matrix that displays the fat, carbohydrate and protein content (in columns) of bread and margarine.   (1 mark)

  2. `A` and `B` are two matrices defined as follows.
     
         `A = [(2,2,1,1)]`     `B = [(531),(41),(534),(212)]`

    1. Evaluate the matrix product  `AB`.   (1 mark)

    2. Determine the order of matrix product  `BA`.   (1 mark)

Matrix `A` displays the number of servings of the four foods: bread, margarine, peanut butter and honey, needed to make a peanut butter and honey sandwich.

Matrix `B` displays the energy content per serving of the four foods: bread, margarine, peanut butter and honey.

    1. Explain the information that the matrix product `AB` provides.   (1 mark)

  1. The number of serves of bread (`b`), margarine (`m`), peanut butter (`p`) and honey (`h`) that contain, in total, 53 grams of fat, 101.5 grams of carbohydrate, 28.5 grams of protein and 3568 kilojoules of energy can be determined by solving the matrix equation
      
         `[(1.2,6.7,10.7,0),(20.1,0.4,3.5,12.5),(4.2,0.6,4.6,0.1),(531,41,534,212)][(b),(m),(p),(h)] = [(53),(101.5),(28.5),(3568)]`
      
    Solve the matrix equation to find the values `b`, `m`, `p` and `h`.   (2 marks)

Show Answers Only
  1.  
    `[(1.2,20.1,4.2),(6.7,0.4,0.6)]`
    1. `[1890]`
    2. `underset (4 xx 1) B xx underset (1 xx 4) A = underset (4 xx 4) (BA)`
    3. `BA\ text(provides the total energy)`
      `text(content of the servings of these)`
      `text(four foods in one sandwich.)`
  3. `b = 4, m = 4, p = 2, h = 1`
Show Worked Solution
a.    `[(1.2,20.1,4.2),(6.7,0.4,0.6)]`

 

b.i.    `AB` `= [(2, 2, 1, 1)] [(531), (41), (534), (212)]`
    `= [1890]`

 

b.ii.   `underset (4 xx 1) B xx underset (1 xx 4) A = underset (4 xx 4) (BA)`

 

b.iii.   `BA\ text(provides the total energy content of the)`
 

`text(servings of these four foods in one sandwich.)`

 

c.    `[(b),(m),(p),(h)]` `= [(1.2,6.7,10.7,0),(20.1,0.4,3.5,12.5),(4.2,0.6,4.6,0.1),(531,41,534,212)]^(-1)[(53),(101.5),(28.5),(3568)]`
    `= [(4),(4),(2),(1)]\ \ \ text{(by graphics calculator)}`

 
`:. b = 4, m = 4, p = 2\ text(and)\ h = 1.`

MATRICES, FUR2 2009 VCAA 4

A series of extra rehearsals commenced in April. Each week participants could choose extra dancing rehearsals or extra singing rehearsals.

A matrix equation used to determine the number of students expected to attend these extra rehearsals is given by

`L_(n + 1) = [(0.85,0.25),(0.15,0.75)] xx L_n-[(5),(7)]`

where `L_n` is the column matrix that lists the number of students attending in week `n`.

The attendance matrix for the first week of extra rehearsals is given by

`L_1 = [(95),(97)]{:(text(dancing)),(text(singing)):}`

  1. Calculate the number of students who are expected to attend the extra singing rehearsals in week 3.   (1 mark)

  2. Of the students who attended extra rehearsals in week 3, how many are not expected to return for any extra rehearsals in week 4?   (1 mark)

Show Answers Only
  1. `text(68 students)`
  2. `12`
Show Worked Solution

a.   `text(Using matrix equation,)`

`L_2` `= T xx L_1-[(5),(7)]`
  `= [(0.85,0.25),(0.15,0.75)][(95),(97)]-[(5),(7)]= [(100),(80)]`
`L_3` `= [(0.85,0.25),(0.15,0.75)][(100),(80)]-[(5),(7)]= [(100),(68)]`

 
`:.\ text(68 students are expected to attend singing in week 3.)`
 

b.    `L_4` `= [(0.85,0.25),(0.15,0.75)][(100),(68)]-[(5),(7)]= [(97),(59)]`

 
`:.\ text(Students expected not to return)`

`= (100 + 68)-(97 + 59)`

`= 12`

MATRICES, FUR2 2009 VCAA 3

In 2009, the school entered a Rock Eisteddfod competition.

When rehearsals commenced in February, all students were asked whether they thought the school would make the state finals. The students’ responses, ‘yes’, ‘no’ or ‘undecided’ are shown in the initial state matrix `S_0`.
 

`S_0 = [(160),(120),(220)]{:(text(yes)),(text(no)),(text(undecided)):}`
 

  1. How many students attend this school?   (1 mark)

Each week some students are expected to change their responses. The changes in their responses from one week to the next are modelled by the transition matrix `T` shown below.
 

`{:(qquadqquadqquadtext( response this week)),(qquadqquadquadtext( yes       no     undecided)),(T = [(0.85quad,0.35quad,0.60),(0.10quad,0.40quad,0.30),(0.05quad,0.25quad,0.10)]{:(text(yes)),(text(no)),(text(undecided)):}qquad{:(text(response)),(text(next week)):}):}`
 

The following diagram can also be used to display the information represented in the transition matrix `T`.

MATRICES, FUR2 2009 VCAA 3

    1. Complete the diagram above by writing the missing percentage in the shaded box.   (1 mark)

    2. Of the students who respond ‘yes’ one week, what percentage are expected to respond ‘undecided’ the next week when asked whether they think the school will make the state finals?   (1 mark)

    3. In total, how many students are not expected to have changed their response at the end of the first week?   (2 marks)

  2. Evaluate the product  `S_1 = TS_0`, where `S_1` is the state matrix at the end of the first week.   (1 mark)

  3. How many students are expected to respond ‘yes’ at the end of the third week when asked whether they think the school will make the state finals?   (1 mark)

Show Answers Only
  1. `500`
    1. `text(25%)`
    2. `text(5%)`
    3. `206`
  3. `S_1 = [(310),(130),(60)]`
  4. `361`
Show Worked Solution

a.   `text(Total students attending)`

`= 160 + 120 + 220`

`= 500`
 

b.i.   `text(25%)`
 

b.ii.   `text(5%)`
 

b.iii.   `text(Students not expected to change)`

`= 0.85 xx 160 + 0.4 xx 120 + 0.1 xx 220`

`= 206`
 

c.    `S_1` `=TS_0`
    `= [(0.85,0.35,0.60),(0.10,0.40,0.30),(0.05,0.25,0.10)][(160),(120),(220)]= [(310),(130),(60)]`

 

d.    `S_3` `= T^3 S_0` 
    `= [(0.85,0.35,0.60),(0.10,0.40,0.30),(0.05,0.25,0.10)]^3[(160),(120),(220)]= [(361),(91.1),(47.9)]` 

 
`:. 361\ text(students expected to respond “yes” at end of week 3.)`

MATRICES, FUR2 2009 VCAA 2

Tickets for the function are sold at the school office, the function hall and online.

Different prices are charged for students, teachers and parents.

Table 1 shows the number of tickets sold at each place and the total value of sales.

MATRICES, FUR2 2009 VCAA 21

For this function

    • student tickets cost  `$x`
    • teacher tickets cost  `$y`
    • parent tickets cost  `$z`.
  1. Use the information in Table 1 to complete the following matrix equation by inserting the missing values in the shaded boxes.   (1 mark)

     
         MATRICES, FUR2 2009 VCAA 22
     

  2. Use the matrix equation to find the cost of a teacher ticket to the school function.   (2 marks)

Show Answers Only
  1. `text(35 and 2)`
  2. `$32`
Show Worked Solution

a.   `text(35 and 2)`
 

MARKER’S COMMENT: Simply writing the column matrix in part (b) did not earn full marks. Students must extract the required data.
b.    `[(x),(y),(z)]` `= [(283,28,5),(35,4,2),(84,3,7)]^(-1)[(8712),(1143),(2609)]`
    `= [(27),(32),(35)]`

 

`:.\ text(C)text(ost of a teacher ticket = $32)`

MATRICES, FUR2 2010 VCAA 4

The Dinosaurs (`D`) and the Scorpions (`S`) are two basketball teams that play in different leagues in the same city.

The matrix `A_1` is the attendance matrix for the first game. This matrix shows the number of people who attended the first Dinosaur game and the number of people who attended the first Scorpion game.
 

`A_1 = [(2000),(1000)]{:(D),(S):}`
 

The number of people expected to attend the second game for each team can be determined using the matrix equation

`A_2 = GA_1`

where `G` is the matrix     `{:(qquadqquadqquadtext(this game)),((qquadqquadqquadD,qquad\ S)),(G = [(1.2,-0.3),(0.2,0.7)]{:(D),(S):}qquad{:text(next game):}):}`

    1. Determine `A_2`, the attendance matrix for the second game.   (1 mark)

    2. Every person who attends either the second Dinosaur game or the second Scorpion game will be given a free cap. How many caps, in total, are expected to be given away?   (1 mark)

Assume that the attendance matrices for successive games can be determined as follows.

`A_3 = GA_2`

`A_4 = GA_3`

and so on such that `A_(n + 1) = GA_n`

  1. Determine the attendance matrix (with the elements written correct to the nearest whole number) for game 10.   (1 mark)

  2. Describe the way in which the number of people attending the Dinosaurs’ games is expected to change over the next 80 or so games.   (1 mark)

The attendance at the first Dinosaur game was 2000 people and the attendance at the first Scorpion game was 1000 people.

Suppose, instead, that 2000 people attend the first Dinosaur game, and 1800 people attend the first Scorpion game.

  1. Describe the way in which the number of people attending the Dinosaurs’ games is expected to change over the next 80 or so games.   (1 mark)

Show Answers Only
    1.  
      `A_2 = [(2100),(1100)]`
    2. `3200\ text(people)`
  2.  
    `A_10 = [(2613),(1613)]`
  3. `text(Attendance at the Dinosaur’s games increases gradually)`

     

    `text(to 3000, at which level it remains steady.)`

  4. `text(Attendence at the Dinosaur’s games decreases)`

     

    `text(gradually to 600, where it remains steady.)`

Show Worked Solution
a.i.    `A_2` `= GA_1`
    `= [(1.2,-0.3),(0.2,0.7)][(2000),(1000)]`
    `= [(2100),(1100)]`

 

a.ii.   `text(Total attending second games)`

`= 2100 + 1100`

`= 3200\ text(people)`
 

b.    `A_10` `= GA_9`
    `= G^9A_1`
    `= [(1.2,-0.3),(0.2,0.7)]^9[(2000),(1000)]`
    `= [(2613),(1613)]`

 

c.    `A_80` `= G^79A_1= [(3000),(2000)]`
`A_81` `= G^80A_1= [(3000),(2000)]`

 
`:.\ text{Attendance at the Dinosaur’s games increases gradually to 3000,}`

`text{at which level it remains steady.}`
 

d.   `text(Using the new initial attendences,)`

`A_80 = [(1.2,-0.3),(0.2,0.7)]^79[(2000),(1800)] = [(600),(400)]`

`A_81 = [(1.2,-0.3),(0.2,0.7)]^80[(2000),(1800)] = [(600),(400)]`
 

`:.\ text{Attendence at the Dinosaur’s games decreases gradually to 600,}`

`text{where it remains steady.}`

MATRICES, FUR2 2010 VCAA 3

The basketball coach has written three linear equations which can be used to predict the number of points, `p`, rebounds, `r`, and assists, `a`, that Oscar will have in his next game.

The equations are    `p + r + a` `= 33`
`2p - r + 3a` `= 40`
`p + 2r + a` `= 43`
  1. These equations can be written equivalently in matrix form.
  2. Complete the missing information below.   (1 mark)

 
`[(qquadqquad),(qquadqquad),(qquadqquad)][(p),(r),(a)] = [(33),(40),(43)]`
 

This matrix equation can be solved in the following way.

 
`[(p),(r),(a)] = [(7,-1,-4),(-1,0,1),(x,1,3)][(33),(40),(43)]`
 

  1. Determine the value of `x` shown in the matrix equation above.   (1 mark)

  2. How many rebounds is Oscar predicted to have in his next game?   (1 mark)

Show Answers Only
  1.  
    `[(1,1,1),(2,-1,3),(1,2,1)][(p),(r),(a)] = [(33),(40),(43)]`
  2. `-5`
  3. `10`
Show Worked Solution
a.    `[(1,1,1),(2,-1,3),(1,2,1)][(p),(r),(a)] = [(33),(40),(43)]`

 

b.    `[(7,-1,-4),(-1,0,1),(x,1,3)]` `=[(1,1,1),(2,-1,3),(1,2,1)]^(-1)`
    `= [(7,-1,-4),(-1,0,1),(-5,1,3)]`

 

`:.x = -5`

 

c.    `[(p),(r),(a)]` `= [(7,-1,-4),(-1,0,1),(-5,1,3)][(33),(40),(43)]`
    `= [(19),(10),(4)]`

 

 

`:.\ text(Oscar is predicted to have 10 rebounds in the next game.)`

MATRICES, FUR2 2010 VCAA 2

The 300 players in Oscar’s league are involved in a training program. In week one, 90 players are doing heavy training (`H`), 150 players are doing moderate training (`M`) and 60 players are doing light training (`L`). The state matrix, `S_1`, shows the number of players who are undertaking each type of training in the first week
 

`S_1 = [(90),(150),(60)]{:(H),(M),(L):}`
 

The percentage of players that remain in the same training program, or change their training program from week to week, is shown in the transition diagram below.
 

MATRICES, FUR2 2010 VCAA 2
 

  1. What information does the 20% in the diagram above provide?   (1 mark)

The information in the transition diagram above can also be written as the transition matrix `T`.
 

`{:(qquadqquadqquadquad\ text(this week)),((qquadqquadqquadH,quadM,\ L)),(T = [(0.5,0.1,0.1),(0.2,0.6,0.5),(0.3,0.3,0.4)]{:(H),(M),(L):}qquad{:text(next week):}):}`
 

  1. Determine how many players will be doing heavy training in week two.   (1 mark)

  2. Determine how many fewer players will be doing moderate training in week three than in week one.   (1 mark)

  3. Show that, after seven weeks, the number of players (correct to the nearest whole number) who are involved in each type of training will not change.   (1 mark) 
Show Answers Only
  1. `text(It means that 20% of the players doing heavy training one)`

     

    `text(week will switch to moderate training the next.)`

  2. `text(66 players)`
  3. `text(6 fewer players)`
  4. `text(See Worked Solutions)`
Show Worked Solution

a.   `text(It means that 20% of the players doing heavy)`

`text(training one week will switch to moderate)`

`text(training the next.)`

 

b.    `S_2` `= TS_1`
    `= [(0.5,0.1,0.1),(0.2,0.6,0.5),(0.3,0.3,0.4)][(90),(150),(60)]`
    `= [(66),(138),(96)]`

 

`:. 66\ text(players will be in hard training)`

`text(in week 2.)`

 

c.   `text(150 in moderate training in week 1.)`

`text(In week 3,)`

`S_3` `= T^2S_1`
  `= [(0.5,0.1,0.1),(0.2,0.6,0.5),(0.3,0.3,0.4)]^2[(90),(150),(60)]`
  `= [(56.4),(144),(99.6)]`

 

`:.\ text(The reduction in players training moderately)`

`= 150-144`

`= 6`

 

d.   `text(Need to show steady numbers for consecutive)`

`text(weeks 8 and week 9,)`

`S_8 = T^7S_1 = [(50),(150),(100)]`

`S_9 = T^8S_1 = [(50),(150),(100)]`

 

`:. S_8 = S_9`

`text{(i.e. player numbers don’t change after week 7.)}`

MATRICES, FUR2 2010 VCAA 1

In a game of basketball, a successful shot for goal scores one point, two points, or three points, depending on the position from which the shot is thrown.

`G`  is a column matrix that lists the number of points scored for each type of successful shot.

`G = [(1),(2),(3)]`

In one game, Oscar was successful with

    • 4 one-point shots for goal
    • 8 two-point shots for goal
    • 2 three-point shots for goal.
  1. Write a row matrix, `N`, that shows the number of each type of successful shot for goal that Oscar had in that game.   (1 mark)

  2. Matrix `P` is found by multiplying matrix `N` with matrix `G` so that  `P = N xx G`
  3. Evaluate matrix `P`.   (1 mark)

  4. In this context, what does the information in matrix `P` provide?   (1 mark)

Show Answers Only
  1. `N = [(4, 8, 2)]`
  2. `P = [26]`
  3. `text(The total points scored by Oscar in the game.)`
Show Worked Solution

a.   `N = [(4, 8, 2)]`
 

b.    `P` `= NG`
    `= [(4, 8, 2)][(1),(2),(3)]`
    `= [26]`

 
c.   `text(The total points scored by Oscar in the game.)`