Band 5 – Page 30

CHEMISTRY, M6 2015 VCE 22 MC

What is the pH of a 0.0500 M solution of barium hydroxide, $\ce{Ba(OH)2}$?

1.00
1.30
12.7
13.0

Show Answers Only

$D$

Show Worked Solution

$\ce{Ba(OH)2(aq) \rightarrow Ba^{2+}(aq) + 2OH-(aq)} $

$\ce{[OH-] = 2 \times [Ba(OH)2] = 2 \times 0.0500 = 0.100 M} $

$\ce{[H3O+]} = \dfrac{10^{-14}}{\ce{[OH-]}} = \dfrac{10^{-14}}{0.100} = 10^{-13}\ \text{M} $

$\text{pH}\ = -\log_{10} 10^{-13} = 13$

$\Rightarrow D$

♦ Mean mark 49%.

CHEMISTRY, M6 2015 VCE 8

Hydrogen sulfide, in solution, is a diprotic acid and ionises in two stages.

$\ce{H2S(aq) + H2O(l)\rightleftharpoons HS-(aq) + H3O+(aq)}$ $\quad K_{a1} = 9.6 × 10^{–8} \text{ M}$

$\ce{HS–(aq) + H2O(l)\rightleftharpoons S^{2-}(aq) + H3O+(aq)}$ $\quad K_{a2} = 1.3 × 10^{–14} \text{ M}$

A student made two assumptions when estimating the pH of a $0.01 \text{ M}$ solution of $\ce{H2S}$:

Assumption 1: The pH can be estimated by considering only the first ionisation reaction.

Assumption 2: The concentration of $\ce{H2S}$ at equilibrium is approximately equal to $0.01 \text{ M}$.

Explain why these two assumptions are justified. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Use the two assumptions given above to calculate the pH of a 0.01 M solution of $\ce{H2S}$. (3 marks)

--- 5 WORK AREA LINES (style=lined) ---
Some solid sodium hydrogen sulfide, $\ce{NaHS}$, is added to a 0.01 M solution of $\ce{H2S}$.
Predict the effect of this addition on the pH of the hydrogen sulfide solution. Justify your prediction. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. 1st assumption:

$K_{a2}$ is significantly smaller than the first ionisation $\ce{(K_{a1})}$, making its impact on the $\ce{[H3O+]}$ / pH level negligible.

2nd assumption:

$K_{a1}$ is very small, making the extent of the ionisation of $\ce{H2S}$ very small and hence a minimal change in $\ce{[H2S]}$ results.

b. $\text{pH}\ = -\log{10}(3.1 \times 10^{-5}) = 4.5 $

c. Adding $\ce{NaHS}$:

Increases the $\ce{[HS-]}$.
This increase causes the 1st ionisation equilibrium back to the left.
This left shift in the equilibrium decreases the $\ce{[H3O+]}$ and the pH will therefore increase.

Show Worked Solution

a. 1st assumption:

$K_{a2}$ is significantly smaller than the first ionisation $\ce{(K_{a1})}$, making its impact on the $\ce{[H3O+]}$ / pH level negligible.

2nd assumption:

$K_{a1}$ is very small, making the extent of the ionisation of $\ce{H2S}$ very small and hence a minimal change in $\ce{[H2S]}$ results.

♦♦ Mean mark (a) 27%.

b.	$K_{a1}$	$=\dfrac{\ce{[HS-][H3O+]}}{\ce{[H2S]}} $
	$9.6 \times 10^{-8}$	$=\dfrac{\ce{[H3O+]^2}}{0.01}$
	$\ce{[H3O+]^2}$	$=0.01 \times 9.6 \times 10^{-8} $
	$\ce{[H3O+]}$	$=\sqrt{9.6 \times 10^{-10}}=3.1 \times 10^{-5}\ \text{M} $
	$\text{pH}$	$= -\log{10}(3.1 \times 10^{-5}) = 4.5 $

c. Adding $\ce{NaHS}$:

Increases the $\ce{[HS-]}$.
This increase causes the 1st ionisation equilibrium back to the left.
This left shift in the equilibrium decreases the $\ce{[H3O+]}$ and the pH will therefore increase.

♦♦ Mean mark (c) 35%.

CHEMISTRY, M6 2015 VCE 23 MC

The following table shows the value of the ionisation constant of pure water at various temperatures and at a constant pressure.

$\text{Temperature (°C)}$	$0$	$25$	$50$	$75$	$100$
$K_W$	$ 1.1 \times 10^{-15}$	$ 1.0 \times 10^{-14}$	$ 5.5 \times 10^{-14}$	$ 2.0 \times 10^{-13}$	$ 5.6 \times 10^{-13}$

Given this data, which one of the following statements about pure water is correct?

The $\ce{[OH–]}$ will decrease with increasing temperature.
The $\ce{[H3O+]}$ will increase with increasing temperature.
Its pH will increase with increasing temperature.
Its pH will always be exactly 7 at any temperature.

Show Answers Only

$B$

Show Worked Solution

$\ce{2H2O(l) \rightleftharpoons H3O+(aq) + OH-(aq)} $

Table shows that $K_W$ increases as temperature increases.
Ionisation equation shifts right as temperature increases, causing an increase in $\ce{[H3O+]}$ and $\ce{[OH-]}$ (eliminate A).
pH decreases as $\ce{[H3O+]}$ and temperature increase (eliminate C).
pH of water = 7 at 25°C only (eliminate D).

$\Rightarrow B$

♦ Mean mark 55%.

PHYSICS, M1 EQ-Bank 1

A physics student comes across a river which runs north to south and has a current of 3 ms$^{-1}$ running south.

The student starts on the west side of the river at point A and paddles a kayak at 5 ms$^{-1}$ directly across the river to finish at point B.

Calculate the angle which he must position the boat to travel in a straight line across the river. (2 mark)

--- 5 WORK AREA LINES (style=blank) ---
If the river is 100 metres wide, determine the time it takes for the student to cross the river. (2 mark)

--- 4 WORK AREA LINES (style=blank) ---

Show Answers Only

a. $36.9^{\circ}$

b. $\text{25 seconds}$

Show Worked Solution

$\sin \theta$	$=\dfrac{3}{5}$
$\theta$	$=\sin^{-1}\Big(\dfrac{3}{5}\Big)=36.9^{\circ}$

The student must turn 36.9$^{\circ}$ into the current as shown on the diagram.

b. Using Pythagoras:

$v=\sqrt{5^2-3^2}=4\ \text{ms}^{-1}$

$t=\dfrac{d}{s}=\dfrac{100}{4}=25\ \text{s}$

$\therefore$ It will take the student 25 seconds to travel from A to B.

PHYSICS, M1 EQ-Bank 7

Below is a description of the motion of a runner. The motion can be divided into three stages.

Stage 1: Runner travels 120 metres south taking 20 seconds.

Stage 2: Runner turns west and travels at 5 ms$^{-1}$ for half a minute.

Stage 3: Runner travels directly back to their starting position.

Determine the distance that the runner ran during Stage 2 of their journey. (1 mark)

--- 2 WORK AREA LINES (style=blank) ---
Find the displacement of the start point from the runner Stage 2 is completed. (3 marks)

--- 6 WORK AREA LINES (style=blank) ---

Show Answers Only

a. $\text{150 m}$

b. $\text{192.1 m, N51.3°E.}$

Show Worked Solution

a. $d=v \times t=5 \times 30=150\ \text{m}$

b. Stage 1 and Stage 2 displacement diagram:

Using Pythagoras:

$d=\sqrt{150^2 + 120^2}=\sqrt{36900}=192.1\ \text{m}$

$\tan\,\theta$	$=\dfrac{120}{150} $
$\theta$	$=\tan^{-1}\Big(\dfrac{120}{150}\Big)=38.7^{\circ}$

$\therefore$ Displacement of the start point from the runner is 192.1 m, N51.3°E.

Data Analysis, GEN1 2022 VCAA 1-3 MC

The histogram below displays the distribution of skull width, in millimetres, for 46 female possums.

Question 1

The shape of the distribution is best described as

negatively skewed.
approximately symmetric.
negatively skewed with a possible outlier.
positively skewed with a possible outlier.
approximately symmetric with a possible outlier.

Question 2

The percentage of the 46 possums with a skull width of less than 55 mm is closest to

Question 3

The third quartile $(Q_3)$ for this distribution, in millimetres, could be

55.8
56.2
56.9
57.7
58.3

Show Answers Only

$\text{Question 1:} \ C$

$\text{Question 2:} \ B$

$\text{Question 3:} \ D$

Show Worked Solution

$\text{Question 1}$

The distribution’s centre is in the 56–57 group and if the possible outlier is disregarded, the tail of the distribution is spread more to the left → i.e. negatively skewed with possible outlier.

$\Rightarrow C$

♦♦ Mean mark (Q1) 36%.
COMMENT: 54% of students chose $E$. The graph distribution however, shows that more than 50% of the data is to the left of the median.

$\text{Question 2}$

$\text{Percentage}$	$= \dfrac{1+1+2+1+2+5}{46} \times 100$
	$=\dfrac{12}{46} \times 100$
	$=26.086…$%

$\Rightarrow B$

$\text{Question 3}$

$ Q_3\ =0.75 \times 46 = 34.5 $

The 34.5th score lies between 57 and 58, therefore, 57.7.

$\Rightarrow D$

PHYSICS, M1 EQ-Bank 7

A plane is travelling at 315 ms$^{-1}$ north when it passes through a dense cloud and slows down to a velocity of 265 ms$^{-1}$ for safety precautions.

The plane did not change direction and travelled 2.5 km while it was slowing down.

Using north as the positive direction for all calculations, determine:

the change in velocity of the plane. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
the plane's acceleration. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
the time over which the plane slowed down. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $\text{50 ms}^{-1}\ \text{south}$

b. $\text{5.8 ms}^{-2}\ \text{south}$

c. $\text{8.62 s}$

Show Worked Solution

a.	$\Delta v$	$=v-u$
		$=265-315$
		$=-50\ \text{ms}^{-1}$
		$=50\ \text{ms}^{-1}\ \text{south}$

b. Using $v^2=u^2 +2as$ (time is not given):

$a$	$=\dfrac{v^2-u^2}{2s}$
	$=\dfrac{(265)^2-(315)^2}{2 \times 2500}$
	$=-5.8\ \text{ms}^{-2}$
	$=5.8\ \text{ms}^{-2}$ to the south.

c. Using $v=u+at$:

$t$	$=\dfrac{v-u}{a}$
	$=\dfrac{265-315}{-5.8}$
	$=8.62\ \text{s}$

PHYSICS, M1 EQ-Bank 5

Plane A is flying due north at 300 kmh$^{-1}$ when it measures the velocity of plane B flying due south to be 750 kmh$^{-1}$.

Calculate the velocity of plane B as measured by the pilots on plane B? (3 marks)

--- 6 WORK AREA LINES (style=blank) ---

Show Answers Only

$\text{ 450 kmh}^{-1}\ \text{south.} $

Show Worked Solution

Let north be the positive direction and south be the negative direction.

$v_{\text{B rel A}}$	$=v_{\text{B}}-\ v_{\text{A}}$
$-750$	$=v_B-300$
$v_B$	$=-450$
	$=450\ \text{kmh}^{-1}\ \text{south} $

PHYSICS, M1 EQ-Bank 3

A hot-air balloon is travelling at a constant upwards velocity of 15 ms$^{-1}$.

A passenger on the hot-air balloon decides to time how long it takes a pen to hit the ground when dropped from a height of 50 m.

Ignoring air resistance, determine how long it will take the pen to hit the ground. (4 marks)

Show Answers Only

$5.07\ \text{s}$

Show Worked Solution

$s= 50, \ a=9.8, \ u=-15$

Downwards $\Rightarrow$ positive direction

$s$	$=ut+\dfrac{1}{2}at^2$
$50$	$=-15t + \dfrac{1}{2} \times 9.8 \times t^2$
$0$	$=4.9t^2-15t-50$
$t$	$=\dfrac{15\pm \sqrt{225-4 \times 9.8 \times -50}}{2 \times 4.9}$
	$=5.07, -2.01$

Time for the pen to fall = 5.07 seconds $ (t \gt 0) $.

Networks, STD2 N3 SM-Bank 24

The network below shows the one-way paths between the entrance, $A$, and the exit, $H$, of a children's maze.

The vertices represent the intersections of the one-way paths.

The number on each edge is the maximum number of children who are allowed to travel along that path per minute.

The minimum cut of the network is drawn, showing the maximum flow capacity of the maze is 23 children per minute.

One path in the maze is to be changed.

Determine the changes in the maximum flow capacity of the network in each of the following changes

the capacity of flow along the edge $GH$ is increased to 16. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
the capacity of flow along the edge $C E$ is increased to 12. (2 marks)

--- 2 WORK AREA LINES (style=lined) ---
the direction of flow along the edge $G F$ is reversed. (2 marks)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

i. $GH ↑ 16,\ \text{minimum cut = 27}$

$\text{Change: increases by 4}$

ii. $CE ↑ 12,\ \text{minimum cut = 24}$

$\text{Change: increases by 1}$

iii. $GF\ \text{is reversed, minimum cut = 30 (close to exit H)}$

$\text{Change: increases by 7}$

Show Worked Solution

i. $GH ↑ 16,\ \text{minimum cut = 27}$

$\text{Change: increases by 4}$

ii. $CE ↑ 12,\ \text{minimum cut = 24}$

$\text{Change: increases by 1}$

iii. $GF\ \text{is reversed, minimum cut = 30 (close to exit H)}$

$\text{Change: increases by 7}$

Networks, STD2 N3 SM-Bank 22

The network below shows the one-way paths between the entrance, $A$, and the exit, $H$, of a children's maze.

The vertices represent the intersections of the one-way paths.

The number on each edge is the maximum number of children who are allowed to travel along that path per minute.

Cuts on this network are used to consider the possible flow of children through the maze.

Determine the capacity of the minimum cut of this network. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Minimum cut = 23} $

Show Worked Solution

$\text{Minimum cut}\ = 12+4+7 = 23$

Networks, GEN1 2023 VCAA 39-40 MC

The network below shows the one-way paths between the entrance, $A$, and the exit, $H$, of a children's maze.

The vertices represent the intersections of the one-way paths.

The number on each edge is the maximum number of children who are allowed to travel along that path per minute.

Question 39

Cuts on this network are used to consider the possible flow of children through the maze. The capacity of the minimum cut would be

Question 40

One path in the maze is to be changed.

Which one of these five changes would lead to the largest increase in flow from entrance to exit?

increasing the capacity of flow along the edge $C E$ to 12
increasing the capacity of flow along the edge $FH$ to 14
increasing the capacity of flow along the edge $GH$ to 16
reversing the direction of flow along the edge $C F$
reversing the direction of flow along the edge $G F$

Show Answers Only

$\text{Question 39:}\ B $

$\text{Question 40:}\ E $

Show Worked Solution

$\text{Question 39} $

$\text{Minimum cut}\ = 12+4+7 = 23$

$\Rightarrow B$

$\text{Question 40}$

$CE ↑ 12,\ \text{minimum cut = 24}$

$FH ↑ 14,\ \text{minimum cut = 23}$

$GH ↑ 16,\ \text{minimum cut = 27}$

$CF\ \text{is reversed, minimum cut = 29}$

$GF\ \text{is reversed, minimum cut = 30 (close to exit H)}$

$\Rightarrow E$

Networks, GEN1 2023 VCAA 37 MC

The adjacency matrix below represents a planar graph with five vertices.

\begin{aligned}
& \ \ \ J\ \ \ K\ \ \ L\ \ M\ \ N \\
& {\left[\begin{array}{lllll}
0 & 1 & 0 & 1 & 1 \\
1 & 0 & 2 & 1 & 1 \\
0 & 2 & 0 & 1 & 1 \\
1 & 1 & 1 & 0 & 1 \\
1 & 1 & 1 & 1 & 0
\end{array}\right] \begin{array}{l}
J \\
K \\
L \\
M \\
N
\end{array}} \\
\end{aligned}

The number of faces on the planar graph is

Show Answers Only

$B$

Show Worked Solution

$\text{Sketch network:}$

$\Rightarrow B$

Networks, GEN1 2023 VCAA 36 MC

Four employees, Anthea, Bob, Cho and Dario, are each assigned a different duty by their manager.

The time taken for each employee to complete duties 1,2,3 and 4, in minutes, is shown in the table below

\begin{array} {|l|c|c|c|c|}
\hline \rule{0pt}{2.5ex} \text{} \rule[-1ex]{0pt}{0pt} & \text{Duty 1} & \text{Duty 2} & \text{Duty 3} & \text{Duty 4} \\
\hline \rule{0pt}{2.5ex} \text{Anthea} \rule[-1ex]{0pt}{0pt} & \text{8} & \text{7} & \text{7} & \text{8}\\
\hline \rule{0pt}{2.5ex} \text{Bob} \rule[-1ex]{0pt}{0pt} & \text{10} & \text{8} & \text{10} & \text{9}\\
\hline \rule{0pt}{2.5ex} \text{Cho} \rule[-1ex]{0pt}{0pt} & \text{8} & \text{9} & \text{7} & \text{10}\\
\hline \rule{0pt}{2.5ex} \text{Dario} \rule[-1ex]{0pt}{0pt} & \text{7} & \text{7} & \text{8} & \text{9}\\
\hline
\end{array}

The manager allocates the duties so as to minimise the total time taken to complete the four duties.

The minimum total time taken to complete the four duties, in minutes, is

Show Answers Only

$B$

Show Worked Solution

$\text{By CAS:}$

\begin{array} {|l|c|c|c|c|}
\hline \rule{0pt}{2.5ex} \text{} \rule[-1ex]{0pt}{0pt} & \text{Duty 1} & \text{Duty 2} & \text{Duty 3} & \text{Duty 4} \\
\hline \rule{0pt}{2.5ex} \text{Anthea} \rule[-1ex]{0pt}{0pt} & \text{8} & \textbf{[7]} & \text{7} & \text{8}\\
\hline \rule{0pt}{2.5ex} \text{Bob} \rule[-1ex]{0pt}{0pt} & \text{10} & \text{8} & \text{10} & \textbf{[9]}\\
\hline \rule{0pt}{2.5ex} \text{Cho} \rule[-1ex]{0pt}{0pt} & \text{8} & \text{9} & \textbf{[7]} & \text{10}\\
\hline \rule{0pt}{2.5ex} \text{Dario} \rule[-1ex]{0pt}{0pt} & \text{7} & \textbf{[7]} & \text{8} & \text{9}\\
\hline
\end{array}

$\text{Minimum time}\ = 7+9+7+7 = 30\ \text{mins} $

$\Rightarrow B$

Matrices, GEN1 2023 VCAA 32 MC

For one particular week in a school year, students at Phyllis Island Primary School can spend their lunch break at the playground $(P)$, basketball courts $(B)$, oval $(O)$ or the library $(L)$.

Students stay at the same location for the entire lunch break.

The transition diagram below shows the proportion of students who change location from one day to the next.

The transition diagram is incomplete.

On the Monday, 150 students spent their lunch break at the playground, 50 students spent it at the basketball courts, 220 students spent it at the oval, and 40 students spent it in the library.

Of the students expected to spend their lunch break on the oval on the Wednesday, the percentage of these students who also spent their lunch break on the oval on Tuesday is closest to

Show Answers Only

$C$

Show Worked Solution

$\text{Transition matrix}\ (T): $

\begin{aligned}
& \quad \quad \quad \ \ \ \ \textit{today} \\
& \quad \ \ \ \ P \ \ \ \ \ B \ \ \ \ \ \ O \ \ \ \ \ \ L \ \ \\
\ \ \textit{next day}\ \ \ & \begin{array}{l}
P \\
B \\
O \\
L
\end{array}\begin{bmatrix}
0.2 & 0.4 & 0.3 & 0.4 \\
0.3 & 0.3 & 0.3 & 0.2 \\
0.4 & 0.2 & 0.3 & 0.1 \\
0.1 & 0.1 & 0.1 & 0.3
\end{bmatrix}
\begin{bmatrix}
150 \\
50 \\
220 \\
40
\end{bmatrix}
= \begin{bmatrix}
132 \\
134 \\
140 \\
54 \\
\end{bmatrix}
\end{aligned}

$T \times \begin{bmatrix}
132 \\
134 \\
140 \\
54
\end{bmatrix}
= \begin{bmatrix}
143.6 \\
132.6 \\
127 \\
56.8
\end{bmatrix}$

$\text{Students at oval Tue and Wed}\ = 0.3 \times 140 = 42$

$\text{Percentage}\ = \dfrac{42}{127} = 0.3307 \approx 33\% $

$\Rightarrow C$

Matrices, GEN1 2023 VCAA 31 MC

A species of bird has a life span of three years.

The females in this species do not reproduce in their first year but produce an average of four female offspring in their second year, and three in their third year.

The Leslie matrix, $L$, below is used to model the female population distribution of this species of bird.

$L=\begin{bmatrix}
0 & 4 & 3\\
0.2 & 0 & 0\\
0 & 0.4 & 0
\end{bmatrix}$

The element in the second row, first column states that on average 20% of this population will

be female.
never reproduce.
survive into their second year.
produce offspring in their first year.
live for the entire lifespan of three years.

Show Answers Only

$C$

Show Worked Solution

$\text{Second and third rows represent survival rates from one year to the next.} $

$e_{21}\ \text{indicates an average of 20% survive into their second year.}$

$\Rightarrow C$

Matrices, GEN1 2023 VCAA 30 MC

How many of the following statements are true?

All square matrices have an inverse.
The inverse of a matrix could be the same as the transpose of that matrix.
If the determinant of a matrix is equal to zero, then the inverse does not exist.
It is possible to take the inverse of an identity matrix.

Show Answers Only

$D$

Show Worked Solution

$\text{All square matrices have an inverse → not true}$

$\text{The inverse of a matrix could be the same as the transpose of that matrix → true}$

$\text{If the determinant of a matrix is equal to zero, then the inverse does not exist → true}$

$\text{It is possible to take the inverse of an identity matrix → true}$

$\Rightarrow D$

Proof, EXT2 P1 2023 HSC 16b

Prove that $x>\ln x$, for $x>0$. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
Using part (i), or otherwise, prove that for all positive integers $n$,

$ e^{n^2+n}>(n !)^2 .$ (3 marks)

--- 11 WORK AREA LINES (style=lined) ---

Show Answers Only

i. $\text{See Worked Solutions}$

ii. $\text{See Worked Solutions}$

Show Worked Solution

i. $\text{Prove}\ \ x > \ln x\ \ \text{for} \ \ x>0: $

$\Rightarrow \ \text{Show}\ \ f(x) = x-\ln x > 0 $

$\text{SP’s occur when}\ \ f^{′}(x) = 1-\dfrac{1}{x} = 0$

$\text{SP at}\ (1,1) $

$f^{″} = x^{-2}>0,\ \ \forall x>0 $

$\text{SP at (1, 1) is a global minimum for}\ x>0 $

$\Rightarrow f(x) \geq 1 > 0 $

$\therefore x > \ln x\ \ \text{for} \ \ x>0 $

♦ Mean mark (i) 39%.

ii. $x > \ln x\ \ \text{for} \ \ x>0 \ \ \Rightarrow \ \ e^x > x\ \ \text{(by definition)} $

$\text{Choose any positive integer}\ n: $

$e^n$	$>n $
$e^{n-1}$	$>n-1 $
$\ \ \vdots $
$e^2$	$>2$
$e^1$	$>1$

$\text{Multiply each side of the equations above:}$

$e^n \times e^{n-1} \times \cdots \times e^{1} $	$>n(n-1)(n-2) \cdots (2)(1) $
$e^{n+(n-1)+(n-2)+ \cdots + 2+1}$	$>n!$
$e^{\frac{n(n+1)}{2}} $	$>n!\ \ (\text{using AP formula}\ \ S_n=\frac{n}{2}(a+l) ) $
$e^{\frac{n(n+1)}{2} \times 2}$	$>(n!)^2$
$e^{n^2+n}$	$>(n!)^2\ \ …\ \text{as required}$

♦♦ Mean mark (ii) 28%.

CHEMISTRY, M3 EQ-Bank 7

Complete the table below, describing the reactivity characteristics of the three metals listed. (3 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

\begin{array} {|l|l|l|l|}
\hline
\ \ \ \ \textbf{Metal} \ & \ \ \ \ \textbf{Reactivity with} \ \ \ \ &\ \ \ \ \textbf{Reactivity with}\ \ \ \ & \ \ \ \ \textbf{Reactivity with}\ \ \ \ \ \ \\ & \ \ \ \ \ \ \ \ \ \ \ \textbf{water} & \ \ \ \ \ \ \ \ \textbf{dilute acid} & \ \ \ \ \ \ \ \ \textbf{oxygen}\\
\hline
& \text{Violent reaction that} & \text{Highly exothermic,} & \text{Burns rapidly to form} \\ \text{Potassium (K)} & \text{ignites hydrogen gas} & \text{ignition of the hydrogen} & \text{oxide which combusts}\\ & \text{produced.} & \text{produced.} & \text{spontaneously in air.} \\
\hline
& \text{Reacts slower with no} & \text{Bubbles slowly to} & \text{Burns when heated with} \\ \text{Zinc (Zn)} & \text{combustion (can be sped} & \text{moderately with no} & \text{oxygen, forming a less} \\ & \text{up using steam).} & \text{ignition.} & \text{reactive oxide layer (may}\\ & & & \text{further react with water).} \\
\hline
& & & \text{Slowly reacts, producing} \\ \text{Copper (Cu)} & \text{No reaction.} & \text{No reaction.} & \text{highly stable oxide layer} \\ & & & \text{that prevents further} \\ & & & \text{oxidation.} \\
\hline
\end{array}

Show Worked Solution

CHEMISTRY, M3 EQ-Bank 6

Metals such as Lead, Copper, Mercury and Silver do not react with dilute acids but will react with the same acids at higher concentration levels.

Explain why this occurs with reference to first ionisation energy. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

First ionsiation energy refers to the energy required to remove a valence electron from a metal.
Metals react in their ionised state and the less energy that is required to reach this state, the more reactive the metal.
Lead, Copper, Mercury and Silver require more energy to remove their outer valence electrons and consequently are only reactive in the presence of stronger oxidising agents.
Concentrated acids have more oxidising ability than their dilute counterparts and can react with these metals.

Show Worked Solution

First ionsiation energy refers to the energy required to remove a valence electron from a metal.
Metals react in their ionised state and the less energy that is required to reach this state, the more reactive the metal.
Lead, Copper, Mercury and Silver require more energy to remove their outer valence electrons and consequently are only reactive in the presence of stronger oxidising agents.
Concentrated acids have more oxidising ability than their dilute counterparts and can react with these metals.

CHEMISTRY, M3 EQ-Bank 1 MC

In a laboratory, students reacted aluminium with water to produce an oxide and hydrogen gas.

Which of the following equations correctly represents this reaction.

$\ce{Al(s) + H2O(g) \rightarrow AlO(s) + H2(g)}$
$\ce{2Al(s) + 3H2O(l) \rightarrow Al2O3(s) + H2(l)}$
$\ce{Al(s) + 3H2O(g) \rightarrow AlO3(s) + H2(l)}$
$\ce{2Al(s) + 3H2O(g) \rightarrow Al2O3(s) + H2(g)}$

Show Answers Only

$D$

Show Worked Solution

Aluminium is not reactive enough to form an oxide with liquid water over a short period. For this to occur additional energy needs to be input (eliminate B).
This can however be achieved by reacting the aluminium with steam, which has more energy than water.
Option D provides the only balanced equation of the remaining options.

$\Rightarrow D$

CHEMISTRY, M3 EQ-Bank 9

Two moles of butane $\ce{C3H8(g)}$ were reacted with 224 grams of oxygen $\ce{O2(g)}$.

Write the balanced equation for this reaction. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Determine the mass, in grams, of $\ce{CO2(g)}$ produced by this reaction. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $\ce{2C3H8(g) + 7O2(g)\ \rightarrow 2C(s) + 2CO(g) + 2CO2(g) + 8H2O(l)}$

b. $\ce{m(CO2) = 88.02\ \text{g}}$

Show Worked Solution

a. Complete combustion equation:

$\ce{C3H8(g) + 5O2(g)\ \rightarrow 3CO2(g) + 4H2O(l)} $

Two moles of butane require 10 moles of oxygen to fully combust.
$\ce{n(O2) = \dfrac {m}{MM}= \dfrac {224}{32} = 7}$
Oxygen is limiting reagent and butane will undergo incomplete combustion according to the following balanced equation:
$\ce{2C3H8(g) + 7O2(g)\ \rightarrow 2C(s) + 2CO(g) + 2CO2(g) + 8H2O(l)}$

b. Using the equation in part (i), 2 moles of $\ce{CO2}$ will be produced

$\ce{m(CO2) = n \times MM = 2 \times 44.01 = 88.02\ \text{g}}$

Recursion, GEN1 2023 VCAA 24 MC

The following recurrence relation models the value, $P_n$, of a perpetuity after $n$ time periods.

$P_0=a, \quad P_{n+1}=R P_n-d$

The value of $R$ can be found by calculating

$a+d$
$\dfrac{a+d}{a}$
$\dfrac{a+d}{d}$
$1+\dfrac{a+d}{a}$
$1+\dfrac{a+d}{d}$

Show Answers Only

$B$

Show Worked Solution

$P_0=a, \quad P_{n+1}=R P_n-d$

$P_1=R P_0-d$

$\text{Since}\ \ P_0=P_1\ \ \text{(perpetuities retain same value)} $

$a$	$=Ra-d$
$Ra$	$=a+d$
$R$	$=\dfrac{a+d}{a} $

$\Rightarrow B$

Recursion, GEN1 2023 VCAA 22 MC

Timmy took out a reducing balance loan of $500 000, with interest calculated monthly.

The balance of the loan, in dollars, after $n$ months, $T_n$, can be modelled by the recurrence relation

$T_0=500\ 000, \quad T_{n+1}=1.00325 T_n-2611.65$

A final repayment that will fully repay the loan to the nearest cent is

$2605.65
$2609.18
$2611.65
$2614.12
$2615.81

Show Answers Only

$D$

Show Worked Solution

$r \text{(annual)}\ = 12 \times 0.00325 = 3.9\% $

$\text{Find}\ N \ \text{when}\ FV=0\ \text{(by TVM solver)}:$

$N$	$= ?$
$I(\%)$	$= 3.9$
$PV$	$= -500\ 000$
$PMT$	$= 2611.65$
$FV$	$= 0$
$\text{P/Y}$	$=\ \text{C/Y}\ = 12$

$N=300.00094…$

$\text{Find}\ FV \ \text{when}\ N=300\ \text{(by TVM solver)}:$

$N$	$= 300$
$I(\%)$	$= 3.9$
$PV$	$= -500\ 000$
$PMT$	$= 2611.65$
$FV$	$= ?$
$\text{P/Y}$	$=\ \text{C/Y}\ = 12$

$FV=-2.466$

$\text{Final payment}\ = 2611.65+2.47 = $2614.12$

$\Rightarrow D$

Financial Maths, GEN1 2023 VCAA 20-21 MC

For taxation purposes, Audrey depreciates the value of her $3000 computer over a four-year period. At the end of the four years, the value of the computer is $600.

Question 20

If Audrey uses flat rate depreciation, the depreciation rate, per annum is

Question 21

If Audrey uses reducing balance depreciation, the depreciation rate, per annum is closest to

Show Answers Only

$\text{Question 20:}\ C$

$\text{Question 21:}\ E$

Show Worked Solution

$\text{Question 20}$

$\text{Depreciation value}\ = 3000-600=$2400 $

$\text{Depreciation value (per year)}\ = \dfrac{2400}{4} =$600 $

$\text{Depreciation rate}\ = \dfrac{600}{3000} \times 100 =20\% $

$\Rightarrow C$

$\text{Question 21}$

$A = $600, \ P= $3000,\ n=4$

$A$	$=PR^n$
$600$	$=3000 \times R^4$
$R^4$	$=\dfrac{600}{3000} $
$R$	$=\sqrt[4]{0.2} $
	$=0.668…$

$\text{Depreciation rate}\ =1-0.668… = 0.331… \approx 33\% $

$\Rightarrow E$

Data Analysis, GEN1 2023 VCAA 16 MC

The number of visitors each month to a zoo is seasonal.

To correct the number of visitors in January for seasonality, the actual number of visitors, to the nearest percent, is increased by 35%.

The seasonal index for that month is closest to

0.61
0.65
0.69
0.74
0.77

Show Answers Only

$D$

Show Worked Solution

$\text{Seasonal index}$	$=\ \dfrac{\text{actual}}{\text{deseasonalised}} $
	$=\ \dfrac{\text{actual}}{1.35 \times \text{actual}} $
	$=0.741$

$\Rightarrow D$

Data Analysis, GEN1 2023 VCAA 15 MC

The number of visitors to a public library each day for 10 consecutive days was recorded.

These results are shown in the table below.

\begin{array} {|l|c|c|c|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} \textbf{Day number} \rule[-1ex]{0pt}{0pt} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
\hline
\rule{0pt}{2.5ex} \textbf{Number of visitors} \rule[-1ex]{0pt}{0pt} & 337 & 317 & 313 & 335 & 322 & 335 & 322 & 338 & 302 & 349 \\
\hline
\end{array}

The eight-mean smoothed number of visitors with centring for day number 6 is

Show Answers Only

$C$

Show Worked Solution

$\text{8 Mean average (days 2 – 9):}$

$(317+313+335+322+335+322+338+302)\ ÷\ 8 = 323 $

$\text{8 Mean average (days 3 – 10):}$

$(313+335+322+335+322+338+302+349)\ ÷\ 8 = 327 $

$\text{Centred value}\ = \dfrac{323+327}{2} = 325$

$\Rightarrow C$

Data Analysis, GEN1 2023 VCAA 13-14 MC

The following graph shows a selection of winning times, in seconds, for the women's 800 m track event from various athletic events worldwide. The graph shows one winning time for each calendar year from 2000 to 2022.

Question 13

The time series is smoothed using seven-median smoothing.

The smoothed value for the winning time in 2006, in seconds, is closest to

116.0
116.4
116.8
117.2
117.6

Question 14

The median winning time, in seconds, for all the calendar years from 2000 to 2022 is closest to

116.8
117.2
117.6
118.0
118.3

Show Answers Only

$\text{Question 13:}\ C$

$\text{Question 14:}\ B$

Show Worked Solution

$\text{Question 13}$

$\text{Consider the 2006 data point and 3 data points either side.}$

$\text{Median value (of 7 data points) = 116.8}$

$\Rightarrow C$

$\text{Question 14}$

$\text{23 data points between 2000 – 2022.}$

$\text{Median value = 12th data point (in order) = 117.2}$

$\Rightarrow B$

Data Analysis, GEN1 2023 VCAA 9 MC

A least squares line can be used to model the birth rate (children per 1000 population) in a country from the average daily food energy intake (megajoules) in that country.

When a least squares line is fitted to data from a selection of countries it is found that:

- for a country with an average daily food energy intake of 8.53 megajoules, the birth rate will be 32.2 children per 1000 population
- for a country with an average daily food energy intake of 14.9 megajoules, the birth rate will be 9.9 children per 1000 population.

The slope of this least squares line is closest to

$-4.7$
$-3.5$
$-0.29$
$2.7$
$25$

Show Answers Only

$B$

Show Worked Solution

$\text{Independent variable}\ (x)\ \text{= energy intake} $

$\text{Dependent variable}\ (y)\ \text{= birth rate} $

$\text{LSLR passes through (8.53, 32.2) and (14.9, 9.9) }$

$\text{Slope of LSRL}\ = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{32.2-9.9}{8.53-14.9} = -3.501 $

$\Rightarrow B$

Data Analysis, GEN1 2023 VCAA 7-8 MC

A teacher analysed the class marks of 15 students who sat two tests.

The test 1 mark and test 2 mark, all whole number values, are shown in the scatterplot below.

A least squares line has been fitted to the scatterplot.

Question 7

The equation of the least squares line is closest to

test 2 mark = – 6.83 + 1.55 × test 1 mark
test 2 mark = 15.05 + 0.645 × test 1 mark
test 2 mark = – 6.78 + 0.645 × test 1 mark
test 2 mark = 1.36 + 1.55 × test 1 mark
test 2 mark = 6.83 + 1.55 × test 1 mark

Question 8

The least squares line shows the predicted test 2 mark for each student based on their test 1 mark.

The number of students whose actual test 2 mark was within two marks of that predicted by the line is

Show Answers Only

$\text{Question 7:}\ A$

$\text{Question 8:}\ C$

Show Worked Solution

$\text{Question 7}$

$\text{By inspection, gradient is greater than 1 (eliminate B and C)}$

$\text{LSRL passes through (16, 18):}$

$\text{Option A:}\ -6.83 + 1.55 \times 16 = 18.0\ \checkmark $

$\Rightarrow A$

$\text{Question 8}$

$\text{5 values are within 1 grid height (measured vertically), or 2 marks,}$

$\text{from the LRSR.}$

$\Rightarrow C$

Data Analysis, GEN1 2023 VCAA 5 MC

The heights of a group of Year 8 students have a mean of $163.56 cm and a standard deviation of $8.14 cm.

One student's height has a standardised $z$-score of –0.85 .

This student's height, in centimetres, is closest to

155.4
156.6
162.7
170.5
171.7

Show Answers Only

$B$

Show Worked Solution

$\bar x = 163.56, \ s_x = 8.14$

$\text{Find}\ x\ \text{given}\ \ z=-0.85:$

$z$	$= \dfrac{x-\bar x}{s_x}$
$-0.85$	$=\dfrac{x-163.56}{8.14}$
$x-163.56$	$=8.14 \times -0.85$
$x$	$=163.56-6.919$
	$=156.641$

$\Rightarrow B$

PHYSICS, M2 EQ-Bank 3

In the system diagram below, a 5-kilogram mass and masses $A$ and $B$ are held by high tensile frictionless wire in static equilibrium.

Using a vector diagram, calculate the masses of both $A$ and $B$. (4 mark)

--- 8 WORK AREA LINES (style=blank) ---

Show Answers Only

$\text{Mass}_A =3.91\ \text{kg}$

$\text{Mass}_B =4.55\ \text{kg}$

Show Worked Solution

Using the sin rule both $F_B$ and $F_A$ can be calculated:

$\dfrac{F_A}{\sin 48^{\circ}}$	$=\dfrac{5 \times 9.8}{\sin 72^{\circ}}$
$F_A$	$=\dfrac{49\,\sin 48^{\circ}}{\sin 72^{\circ}}=38.3\ \text{N}$

$\text{Mass}_A =\dfrac{F}{a}=\dfrac{38.3}{9.8}=3.91\ \text{kg}$

$\dfrac{F_B}{\sin 60^{\circ}}$	$=\dfrac{49}{\sin 72^{\circ}}$
$F_B$	$=\dfrac{49\, \sin 60^{\circ}}{\sin 72^{\circ}}=44.6\ \text{N}$

$\text{Mass}_B =\dfrac{F}{a}=\dfrac{44.6}{9.8}=4.55\ \text{kg}$

PHYSICS, M4 EQ-Bank 5

Outline and explain the process by which ferromagnetic materials can become magnetised using a bar magnet. (3 marks)

--- 8 WORK AREA LINES (style=blank) ---

Show Answers Only

A ferromagnetic material contains many free electrons due to its metallic bonding.
Each electron has its own magnetic domain but due to the electrons spinning in opposite directions, the domains cancel each other out.
Using a bar magnet, stroke the ferromagnetic material in one direction.
This causes the electrons to spin in the same direction, hence all of their domains line up.
The cumulative effect of all the small magnetic domains creates a large magnetic field, turning the ferromagnetic material into a magnet.

Show Worked Solution

A ferromagnetic material contains many free electrons due to its metallic bonding.
Each electron has its own magnetic domain but due to the electrons spinning in opposite directions, the domains cancel each other out.
Using a bar magnet, stroke the ferromagnetic material in one direction.
This causes the electrons to spin in the same direction, hence all of their domains line up.
The cumulative effect of all the small magnetic domains creates a large magnetic field, turning the ferromagnetic material into a magnet.

PHYSICS, M4 EQ-Bank 4

A wire with a current of $I$ amps running through it was measured to have a magnetic field strength of 2 × 10$^{-3}$ T at a distance of $ r$ metres from the wire.

If the current through the wire is halved and the distance $r$ is increased to $3r$, find the new magnetic field strength measured. (2 marks)

--- 4 WORK AREA LINES (style=blank) ---

Show Answers Only

$3.33 \times 10^{-4}\ \text{T}$

Show Worked Solution

$B_{\text{initial}}= 2 \times 10^{-3} = \dfrac{\mu_0 \times I}{2\pi \times r}$

$\text{Find}\ B\ \text{when}\ I → \dfrac{I}{2},\ \text{and}\ r → 3r:$

$B_{\text{new}}$	$=\dfrac{\mu_0 \times \frac{I}{2}}{2\pi \times 3r}$
	$=\dfrac{1}{6} \times \dfrac{\mu_0 \times I}{2\pi \times r}$
	$=\dfrac{1}{6} \times 2 \times 10^{-3}$
	$=3.33 \times 10^{-4}\ \text{T}$

PHYSICS, M4 2023 VCE 3a

Two long, straight current-carrying wires, $\text{P}$ and $\text{Q}$, are parallel, as shown below. The current in the wires is the same in magnitude and opposite in direction.

The Top View diagram below shows the wires as viewed from above.

On the Top View diagram, sketch the magnetic field around the wires, showing the direction of the magnetic field. Use at least five field lines. (3 marks)

--- 0 WORK AREA LINES (style=blank) ---

Show Answers Only

Show Worked Solution

Use the right-hand grip rule to determine the directions of the magnetic fields surrounding the currents, remembering that an $X$ means “into the page” and the dot means “out of the page”.
As the distance from the wire increases the field strength decreases according to the inverse square law and therefore does not decrease at a linear rate (as seen in the diagram by the greater distances between field lines the further from the wires).

♦ Mean mark 48%.

PHYSICS, M4 2023 VCE 1

Some physics students are conducting an experiment investigating both electrostatic and gravitational forces. They suspend two equally charged balls, each of mass 4.0 g, from light, non-conducting strings suspended from a low ceiling.

The charged balls repel each other with the strings at an angle of 60°, as shown in Figure 1.

There are three forces acting on each ball:

- a tension force, $T$
- a gravitational force, $F_{g}$
- an electrostatic force, $F_{E}$.

On Figure 1, using the labels $T, F_{g}$ and $F_{E}$, draw each of the three forces acting on each of the charged balls. (3 marks)

--- 0 WORK AREA LINES (style=lined) ---
Show that the tension force, $T$, in each string is $4.5 \times 10^{-2} \text{ N}$. Use $g=9.8 \text{ N kg}^{-1}$.
Show your working. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Calculate the magnitude of the electrostatic force, $F_{ E }$. Show your working. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

b. System is in an equilibrium state:

The sum of the forces must add to zero as seen in the triangle below.

$F_g = 9.8 \times 4 \times 10^{-3} = 3.92 \times 10^{-2}\ \text{N}$

$\sin\,60^{\circ}$	$=\dfrac{3.92 \times 10^{-2}}{T}$
$T$	$=\dfrac{3.92 \times 10^{-2}}{\sin\,60^{\circ}}=4.5 \times 10^{-2}\ \text{N}$

c. Using the same triangle as part (b):

$\tan\,60^{\circ}$	$=\dfrac{3.92 \times 10^{-2}}{F_E}$
$F_E$	$=\dfrac{3.92 \times 10^{-2}}{\tan\,60^{\circ}}=2.3 \times 10^{-2}\ \text{N}$

Show Worked Solution

b. System is in an equilibrium state:

The sum of the forces must add to zero as seen in the triangle below.

$F_g = 9.8 \times 4 \times 10^{-3} = 3.92 \times 10^{-2}\ \text{N}$

$\sin\,60^{\circ}$	$=\dfrac{3.92 \times 10^{-2}}{T}$
$T$	$=\dfrac{3.92 \times 10^{-2}}{\sin\,60^{\circ}}=4.5 \times 10^{-2}\ \text{N}$

c. Using the same triangle as part (b):

$\tan\,60^{\circ}$	$=\dfrac{3.92 \times 10^{-2}}{F_E}$
$F_E$	$=\dfrac{3.92 \times 10^{-2}}{\tan\,60^{\circ}}=2.3 \times 10^{-2}\ \text{N}$

♦ Mean mark 41%.

PHYSICS, M3 2023 VCE 12

A ray of monochromatic light is incident on a triangular glass prism with a refractive index of 1.52 . The ray is perpendicular to the side $\text{AB}$ of the glass prism, as shown in the diagram below.

The ray of light travels through the glass prism before reaching side $\text{AC}$.

Calculate the critical angle for the glass prism at the glass-air interface. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Will the ray of light undergo total internal reflection at side $\text{AC}$ of the glass prism? Justify your answer. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. 41°

b. Total internal reflection:

The angle of incidence 45° is greater than the critical angle 41°.
Therefore, total internal reflection will occur on side $\text{AC}$.

Show Worked Solution

a.	$\sin \theta_c$	$=\dfrac{n_2}{n_1}$
	$\theta_c$	$=\sin^{-1}(\dfrac{n_2}{n_1})=\sin^{-1}(\dfrac{1.0}{1.52})=41^{\circ}$

b. Total internal reflection:

The angle of incidence 45° is greater than the critical angle 41°.
Therefore, total internal reflection will occur on side $\text{AC}$.

♦ Mean mark (b) 46%.

PHYSICS, M3 2023 VCE 11

A guitar string of length 0.75 m and fixed at both ends is plucked and a standing wave is produced. The envelope of the standing wave is shown in the diagram.

The speed of the wave along the string is 393 m s$ ^{-1}$.

What is the frequency of the wave? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Describe how the standing wave is produced on the string fixed at both ends. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

a. 262 Hz

b. Standing wave:

When waves encounter fixed ends, they reflect.
If the string’s length is a multiple of half the wavelength, the reflected wave combines with the original wave, resulting in interference that forms a standing wave pattern

Show Worked Solution

a. $f=\dfrac{v}{\lambda}=\dfrac{393}{1.5}=262\ \text{Hz}$

b. Standing wave:

When waves encounter fixed ends, they reflect.
If the string’s length is a multiple of half the wavelength, the reflected wave combines with the original wave, resulting in interference that forms a standing wave pattern

♦ Mean mark (b) 47%.

PHYSICS, M2 2023 VCE 8

Maia is at a skatepark. She stands on her skateboard as it rolls in a straight line down a gentle slope at a constant speed of 3.0 m s$^{-1}$, as shown in the figure below. The slope is 5° to the horizontal.

The combined mass of Maia and the skateboard is 65 kg.

The combined system of Maia and the skateboard is modelled as a small box with point $\text{M}$ at the centre of mass, as shown below.
Draw and label arrows to represent each of the forces acting on the system - that is, Maia and skateboard as they roll down the slope. (3 marks)

--- 0 WORK AREA LINES (style=lined) ---

Calculate the magnitude of the total frictional forces acting on Maia and the skateboard. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Near the bottom of the ramp, Maia takes hold of a large pole and comes to a complete rest while still standing on the skateboard. Maia and the skateboard now have no momentum or kinetic energy.

Explain what happened to both the momentum and the kinetic energy of Maia and the skateboard. No calculations are required. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

b. 55.5 N

c. Momentum:

Maia and the skateboards momentum was transferred into the pole and hence into the Earth. Due to the Earth’s very large mass, the effect on its velocity is negligible.

Kinetic energy:

The kinetic energy of Maia and the skateboard would have been transformed into heat energy between the contact of Maia and the pole and/or transferred into the work done by Maia’s muscles in slowing herself down.

Show Worked Solution

b. Total frictional forces:

Constant speed means that the force down the slope of the incline is equal to the sum of the frictional forces acting on Maia and the skateboard.

$F_{\text{down slope}}$	$=F_f$	$=mg\, \sin\, \theta$
		$=65 \times 9.8 \times \sin\,5^{\circ}$
		$=55.5\ \text{N}$

♦ Mean mark (b) 50%.

c. Momentum:

Maia and the skateboards momentum was transferred into the pole and hence into the Earth. Due to the Earth’s very large mass, the effect on its velocity is negligible.

Kinetic energy:

The kinetic energy of Maia and the skateboard would have been transformed into heat energy between the contact of Maia and the pole and/or transferred into the work done by Maia’s muscles in slowing herself down.

♦♦♦ Mean mark (c) 26%.

PHYSICS, M2 2023 VCE 4 MC

The diagram below shows the force versus time graph of the force on a tennis ball when it is hit by a tennis racquet. The tennis ball is stationary when the tennis racquet first comes into contact with the ball.

Which one of the following is closest to the impulse experienced by the tennis ball as it is hit by the tennis racquet?

$0.50 \text{ N s}$
$5.0 \text{ N s}$
$10 \text{ N s}$
$50 \text{ N s}$

Show Answers Only

$B$

Show Worked Solution

The impulse is equal to the area under the curve $(I=Ft)$.
By splitting the areas into whole number of squares, there are about 10 squares.
Each square is $50\ \text{N} \times 0.01\ \text{s}=0.5\ \text{N s}$
Hence the impulse experienced by the tennis ball $\approx 5.0\ \text{N s}$.

$\Rightarrow B$

♦ Mean mark 49%.

PHYSICS, M4 2023 VCE 2 MC

The diagram below shows two charges, $Q_1$ and $Q_2$, separated by a distance, $d$.

There is a force, $F$, acting between the two charges.

Which one of the following is closest to the magnitude of the force acting between the two charges if both $d$ and the charge on $Q_1$ are halved?

$\dfrac{F}{4}$
$F$
$2 F$
$4 F$

Show Answers Only

$C$

Show Worked Solution

$\text{Initially,}\ \ F=\dfrac{1}{4 \pi \varepsilon_0} \times \dfrac{Q_1Q_2}{d^2}$

$\text{After}\ \ Q_1\ \ \Rightarrow \ \ \dfrac{Q_1}{2}, \ \text{and}\ \ d\ \ \Rightarrow \ \ \dfrac{d}{2}:$

$F_{\text{new}}$	$=\dfrac{1}{4 \pi \varepsilon_0} \times \dfrac{\frac{Q_1}{2}Q_2}{(\frac{d}{2})^2}$
	$=\dfrac{1}{4 \pi \varepsilon_0} \times \dfrac{\frac{Q_1}{2}Q_2}{\frac{d^2}{4}}$
	$=\dfrac{1}{4 \pi \varepsilon_0} \times \dfrac{4Q_1Q_2}{2d^2}$
	$=\dfrac{1}{4 \pi \varepsilon_0} \times \dfrac{2Q_1Q_2}{d^2}$
	$=2F$

$\Rightarrow C$

♦ Mean mark 55%.

PHYSICS, M3 2017 VCE 16

Standing waves are formed on a string of length 4.0 m that is fixed at both ends. The speed of the waves is 240 m s$^{-1}$.

Calculate the wavelength of the lowest frequency resonance. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---
Calculate the frequency of the second-lowest frequency resonance. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---
Explain the physics of how standing waves are formed on the string. Include a diagram in your response. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

a. 30 Hz

b. 60 Hz

c. Standing waves:

Produced when a wave travels down a string and is reflected back on itself such that the superposition of the two waves produce an interference pattern to form a standing wave.
The two waves must be travelling in opposite directions with the same frequency, wavelength and amplitude.

Show Worked Solution

a. Lowest frequency resonance:

Occurs at the maximum wavelength. The maximum wavelength is 8 metres since the half wavelength is the length of the string (4m).
$f=\dfrac{v}{\lambda}=\dfrac{240}{8}=30\ \text{Hz}$

b. When $\lambda = 4: $

$f=\dfrac{v}{\lambda}=\dfrac{240}{4}=60\ \text{Hz}$

c. Standing waves:

Produced when a wave travels down a string and is reflected back on itself such that the superposition of the two waves produce an interference pattern to form a standing wave.
The two waves must be travelling in opposite directions with the same frequency, wavelength and amplitude.

♦ Mean mark (c) 43%.

CHEMISTRY, M4 EQ-Bank 36

The enthalpies of formation for a number of chemical reactions are as follows:

$\ce{C6H12O6(s)}$ $\Delta H^{\circ}_f = -1271\ \text{kJmol}^{-1}$

$\ce{C2H5OH(aq)}$ $\Delta H^{\circ}_f = -277.7\ \text{kJmol}^{-1}$

$\ce{CO2(g)}$ $\Delta H^{\circ}_f = -393.5\ \text{kJmol}^{-1}$

Calculate the enthalpy change for the fermentation of glucose (reaction below) using the enthalpies of formation above.

$\ce{C6H12O6(s) \rightarrow 2C2H5OH(aq) + 2CO2(g)}$ (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

$\Delta H^{\circ}_{\text{reaction}} = -71.4\ \text{kJmol}^{-1}$

Show Worked Solution

$\Sigma\ \text{Enthalpy (reactants)}\ = 1 \times -1271 = -1271\ \text{kJ}$

$\Sigma\ \text{Enthalpy (products)}\ = 2 \times -277.7 + 2 \times -393.5 = -1342.4\ \text{kJ}$

$\Delta H^{\circ}_{\text{reaction}}$	$= \Delta H^{\circ} (\text{products})-\Delta H^{\circ} (\text{reactants}) $
	$=-1342.4-(-1271)$
	$= -71.4\ \text{kJ mol}^{-1}$

BIOLOGY, M4 EQ-Bank 38

What fundamental change occurred with the Neolithic revolution? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Explain TWO consequences of the Neolithic revolution on human civilisation. (4 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

a. → The Neolithic revolution refers to the beginning of agriculture

→ It occurred about 10 000 years ago and includes the first instances of cultivating crops and domesticating animals.

b. Answers could include two of the following:

→ The Neolithic revolution heavily influenced the evolution of the human race, as well as the impacted ecosystems and related flora and fauna.

→ One immediate impact was an increase in human populations. The beginning of agriculture displaced a hunter gatherer lifestyle for many populations, providing an abundance of available food and leading to the first instances of villages and towns.

→ Another impact is soil erosion. The removal of deep-rooted vegetation for crops depleted the environment for many organisms and caused major disruption of the ecosystem. This process leads directly to deforestation which remains a major problem in modern agriculture.

Show Worked Solution

a. → The Neolithic revolution refers to the beginning of agriculture

→ It occurred about 10 000 years ago and includes the first instances of cultivating crops and domesticating animals.

b. Answers could include two of the following:

→ The Neolithic revolution heavily influenced the evolution of the human race, as well as the impacted ecosystems and related flora and fauna.

CHEMISTRY, M3 EQ-Bank 6

Three unknown metals are reacted with dilute $\ce{HCl(aq)}$ and the following observations are made:

\begin{array} {|c|l|}
\hline
\rule{0pt}{2.5ex} \textit{Metal} \rule[-1ex]{0pt}{0pt} & \ \ \ \ \ \ \textit{Observations} \\
\hline
\rule{0pt}{2.5ex} \text{A} \rule[-1ex]{0pt}{0pt} & \text{No observable reaction} \\
\hline
\rule{0pt}{2.5ex} \text{B} \rule[-1ex]{0pt}{0pt} & \text{Slow bubbling} \\
\hline
\rule{0pt}{2.5ex} \text{C} \rule[-1ex]{0pt}{0pt} & \text{Fast, abrupt bubbling} \\
\hline
\end{array}

You are told that the metals in question are Magnesium, Platinum and Zinc.

Explain which of the above metals correspond to $\text{A}$, $\text{B}$ and $\text{C}$, giving reasons for your answer. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Describe the type of reaction between $\ce{HCl}$ and metal $\ce{C}$. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Provide one balanced chemical equation between $\ce{HCl}$ and either metal $\text{B}$ or metal $\text{C}$. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Identifying metals $\text{A}$, $\text{B}$ and $\text{C}$:

The metals $\text{A}$, $\text{B}$ and $\text{C}$ differ by their relative reactivity.
Magnesium is the most reactive as it is an alkali earth metal (Metal $\text{C}$).
Zinc and Platinum are both less reactive than magnesium. Zinc however exists higher on the reactivity series of metals than Platinum which is the least reactive of the three metals.
Therefore, metal $\text{B}$ is zinc and metal $\text{A}$ is platinum.

b. A single displacement reaction.

c. Include one of the following:

$\ce{Mg(s) + 2HCl(aq) \rightarrow MgCl2(aq) + H2(g) }$

$\ce{Zn(s) + 2HCl(aq) \rightarrow ZnCl2(aq) + H2(g) }$

Show Worked Solution

a. Identifying metals $\text{A}$, $\text{B}$ and $\text{C}$:

The metals $\text{A}$, $\text{B}$ and $\text{C}$ differ by their relative reactivity.
Magnesium is the most reactive as it is an alkali earth metal (Metal $\text{C}$).
Zinc and Platinum are both less reactive than magnesium. Zinc however exists higher on the reactivity series of metals than Platinum which is the least reactive of the three metals.
Therefore, metal $\text{B}$ is zinc and metal $\text{A}$ is platinum.

b. A single displacement reaction.

c. Include one of the following:

$\ce{Mg(s) + 2HCl(aq) \rightarrow MgCl2(aq) + H2(g) }$

$\ce{Zn(s) + 2HCl(aq) \rightarrow ZnCl2(aq) + H2(g) }$

ENGINEERING, AE 2023 HSC 20 MC

A transition duct is shown.

What is the true angle of the line $1-a$ to the horizontal plane?

$69°$
$81°$
$90°$
$101°$

Show Answers Only

$ A $

Show Worked Solution

$ \Rightarrow A $

♦ Mean mark 41%.

BIOLOGY, M4 EQ-Bank 37

Climate change is altering the Earth’s habitats and ecosystems, putting many species at risk of global population reductions or extinction.

Justify this statement, giving real world examples of climate change. (5 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

Climate change is altering organisms environments across the globe, causing drastic population reductions and even extinctions of entire species.
One reason for sudden changes in populations is the increase in devastating and extreme weather events because of climate change. Storms, fires and extended droughts result in devastating death tolls in both plant and animal communities, eliminating individuals and drastically changing the gene pool.
Climate change also produces more incremental impacts on the environment. Steadily increasing temperatures and changes in precipitation patterns are two examples. Many organisms cannot adapt to these changes, causing depopulation and extinctions.
One example of a changing temperature on the environment is ocean acidification. Rising temperatures have a drastic effect coral health and its associated marine life. Acidification of the water also makes it difficult for many crustaceans to form hard shells.
The ecosystems themselves also play a large role in climate change, as plants act as a climate regulator due to their ability to store carbon. However, as climate change grows at an exponential rate, plants cannot adapt quickly enough and die out. This results in less carbon storage and a dangerous negative feedback loop.
It is therefore accurate to state that climate change alters ecosystems worldwide causing large population declines of species and eventually climate extinctions for some.

Show Worked Solution

Climate change is altering organisms environments across the globe, causing drastic population reductions and even extinctions of entire species.
One reason for sudden changes in populations is the increase in devastating and extreme weather events because of climate change. Storms, fires and extended droughts result in devastating death tolls in both plant and animal communities, eliminating individuals and drastically changing the gene pool.
Climate change also produces more incremental impacts on the environment. Steadily increasing temperatures and changes in precipitation patterns are two examples. Many organisms cannot adapt to these changes, causing depopulation and extinctions.
One example of a changing temperature on the environment is ocean acidification. Rising temperatures have a drastic effect coral health and its associated marine life. Acidification of the water also makes it difficult for many crustaceans to form hard shells.
The ecosystems themselves also play a large role in climate change, as plants act as a climate regulator due to their ability to store carbon. However, as climate change grows at an exponential rate, plants cannot adapt quickly enough and die out. This results in less carbon storage and a dangerous negative feedback loop.
It is therefore accurate to state that climate change alters ecosystems worldwide causing large population declines of species and eventually climate extinctions for some.

ENGINEERING, PPT 2023 HSC 12 MC

A rail switch lever is shown.

What is the calculated mechanical advantage when operating this rail switch lever?

3.7
6.3
14.7
16.0

Show Answers Only

$ D $

Show Worked Solution

$MA=\dfrac{d_{input}}{d_{output}} = \dfrac{1100+100}{75}=16.0$

$\Rightarrow D $

♦ Mean mark 51%.

ENGINEERING, AE 2023 HSC 6 MC

The landing gear on an aircraft uses a hydraulic braking system. A force of 60 N is applied at the master cylinder with a piston diameter of 12 mm.

What is the force at the brake calliper with a piston diameter of 42 mm ?

4.9 N
17.14 N
210 N
735 N

Show Answers Only

$ D $

Show Worked Solution

Pressure is the same in both master cylinder and brake calliper $\big(P = \frac{F}{A}\big) $
Convert units: $12\ \text{mm} = \dfrac{12}{1000} = 0.012\ \text{m, 42 mm}\ =\dfrac{42}{1000} = 0.042\ \text{m} $
Using $\dfrac{F_2}{A_2} = \dfrac{F_1}{A_1} $:
$F_2 = \dfrac{F_1 \times A_2}{A_1} = \dfrac{60 \times \ \pi \times 0.021^2}{\pi \times 0.006^2} = 735\ \text{N} $

$\Rightarrow D $

♦ Mean mark 45%.

ENGINEERING, PPT 2023 HSC 27b

A portion of a roller coaster wheel sub-assembly is shown.

An exploded pictorial of the wheel sub-assembly is shown.

Complete an assembled sectioned front view of the wheel sub-assembly at scale 1: 2. Apply AS 1100 drawing standards. Do NOT add dimensions. (6 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

♦ Mean mark 49%.

CHEMISTRY, M4 EQ-Bank 32

The enthalpies of reaction of a number of chemical reactions are as follows:

Reaction 1: $\ce{C2H2(g) + \frac{5}{2}O2(g) \rightarrow 2CO2(g) + H2O(l)}$ $\Delta H_1=-1299.5\ \text{kJ mol}^{-1}$

Reaction 2: $\ce{C(s) + O2(g) \rightarrow CO2(g)}$ $\Delta H_2=-393.5\ \text{kJ mol}^{-1}$

Reaction 3: $\ce{H2(g) + \frac{1}{2}O2(g) \rightarrow H2O(l)}$ $\Delta H_3=-285.8\ \text{kJ mol}^{-1}$

Calculate the enthalpy change for the reaction below, stating whether the reaction is exothermic or endothermic:

$\ce{2C(s) + H2(g) \rightarrow C2H2(g)}$ $\Delta H_4=?$ (4 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

$\Delta H_4=+226.7\ \text{kJ mol}^{-1}$

Show Worked Solution

Reverse equation 1 to make $\ce{C2H2(g)}$ a product (changes the sign of the enthalpy).
$\ce{2CO2(g) + H2O(l) \rightarrow C2H2(g) + \frac{5}{2}O2(g)}$ $-\Delta H_1=+1299.5\ \text{kJ mol}^{-1}$
Add a multiplier to Reaction 2 as this will allow the $\ce{CO2(g)}$ to cancel when applying Hess’s Law.
$\ce{2C(s) +2O2(g) \rightarrow 2CO2(g)}$ $2\Delta H_2=2 \times -393.5= -787\ \text{kJ mol}^{-1}$
Add the equations and their $\Delta H$ values and cancel any reactants and products.

$\cancel{ \ce{2CO2(g)}} + \cancel{ \ce{H2O(l)}}$	$ \rightarrow \ce{C2H2(g)} + \cancel{ \ce{\frac{5}{2}O2(g)}}$	$-\Delta H_1=+1299.5\ \text{kJ mol}^{-1}$
$\ce{2C(s)} +\cancel{\ce{2O2(g)}}$	$\rightarrow \cancel{ \ce{2CO2(g)}}$	$2\Delta H_2= -787\ \text{kJ mol}^{-1}$
$\ce{H2(g)} + \cancel{\ce{\frac{1}{2}O2(g)}}$	$\rightarrow \cancel{\ce{H2O(l)}}$	$\Delta H_3=-285.8\ \text{kJ mol}^{-1}$
$\ce{2C(s) + H2(g)}$	$\ce{\rightarrow C2H2(g)}$	$\Delta H_4=+226.7\ \text{kJ mol}^{-1}$

The reaction is endothermic.

BIOLOGY, M4 EQ-Bank 36

What is/are the producer(s) in this food web? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Identify ONE carnivore and ONE herbivore. (2 marks)

--- 2 WORK AREA LINES (style=lined) ---
If the grasshopper species became extinct, describe THREE changes that may occur. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Grass, carrots and grain.

b. Carnivore: Owl or fox

Herbivore: Bird

c. Extinction of the grasshopper effects:

Will result in a greater availability of the grass and grain they (previously) ate.
Subsequently, there will be less competition for food among the other species which also eat grass and grain. These species will thrive and an increase in the bird, mouse and rabbit populations would be expected.
The grasshoppers’ extinction will also cause its consumers, the bird and the owl, to have to find other food sources.
Population fluctuations of birds and owls would be expected as they adapt to new hunting or grazing habits to replace their lost food source.
The complexity of nature in such extinction events can be seen particularly on birds who benefit from more grain availability but lose grasshoppers as a direct food source.

Show Worked Solution

a. Grass, carrots and grain.

b. Carnivore: Owl or fox

Herbivore: Bird

c. Extinction of the grasshopper effects:

Will result in a greater availability of the grass and grain they (previously) ate.
Subsequently, there will be less competition for food among the other species which also eat grass and grain. These species will thrive and an increase in the bird, mouse and rabbit populations would be expected.
The grasshoppers’ extinction will also cause its consumers, the bird and the owl, to have to find other food sources.
Population fluctuations of birds and owls would be expected as they adapt to new hunting or grazing habits to replace their lost food source.
The complexity of nature in such extinction events can be seen particularly on birds who benefit from more grain availability but lose grasshoppers as a direct food source.

ENGINEERING, PPT 2023 HSC 1 MC

Which of the following is a recognised impact test?

Brinell
Erichsen
Notch
Punch

Show Answers Only

$ C$

Show Worked Solution

The recognised impact test among the options provided is option C, Notch.
The Brinell test measure material hardness, Erichsen test measures the properties of metals (including hardness and wear) while the punch test looks at material behaviour under stress.

$\Rightarrow C $

♦♦ Mean mark 33%.

ENGINEERING, CS 2023 HSC 2 MC

Why did steel replace cast iron in bridges built after 1850 ?

It is lighter in weight.
It is easier to produce.
It has greater tensile strength.
It has greater compressive strength.

Show Answers Only

$ C $

Show Worked Solution

Steel is stronger, more ductile, and has a higher tensile strength compared to cast iron, allowing for the construction of larger and more durable structures.
Cast iron generally has greater compressive strength than steel (eliminate D).

$\Rightarrow C $

♦ Mean mark 55%.

ENGINEERING, CS 2023 HSC 26c

A truss is loaded as shown.

Showing working, complete the table. (6 marks)

\begin{array} {|l|c|c|}
\hline
\rule{0pt}{2.5ex} \rule[-1ex]{0pt}{0pt} & \textit{Magnitude} & \textit{Nature of force}\\ & \text{(kN)} & \text{(T or C)} \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ EF \rule[-1ex]{0pt}{0pt} & & \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ CH \rule[-1ex]{0pt}{0pt} & & \\
\hline
\end{array}

Show Answers Only

\begin{array} {|l|c|c|}
\hline
\rule{0pt}{2.5ex} \rule[-1ex]{0pt}{0pt} & \textit{Magnitude} & \textit{Nature of force}\\ & \text{(kN)} & \text{(T or C)} \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ EF \rule[-1ex]{0pt}{0pt} & 73.2\ \text{kN} & \text{Compression} \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ CH \rule[-1ex]{0pt}{0pt} & 71.138\ \text{kN} & \text{Tension} \\
\hline
\end{array}

Show Worked Solution

\begin{array} {|l|c|c|}
\hline
\rule{0pt}{2.5ex} \rule[-1ex]{0pt}{0pt} & \textit{Magnitude} & \textit{Nature of force}\\ & \text{(kN)} & \text{(T or C)} \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ EF \rule[-1ex]{0pt}{0pt} & 73.2\ \text{kN} & \text{Compression} \\
\hline
\rule{0pt}{2.5ex} \text{Internal reaction of member}\ CH \rule[-1ex]{0pt}{0pt} & 71.138\ \text{kN} & \text{Tension} \\
\hline
\end{array}

$\text{Consider member}\ EF:$

$\text{Force diagram closes with two collinear forces}$
$FG\ \text{is a zero force member}$
$EF = 73.2\ \text{kN (compression)} $

♦♦♦ Mean mark 36%.

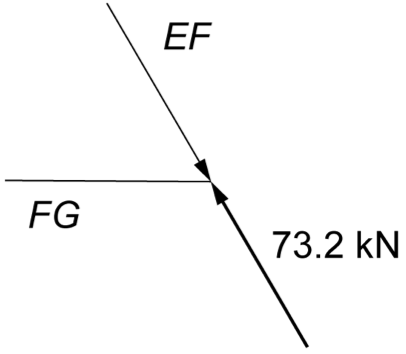
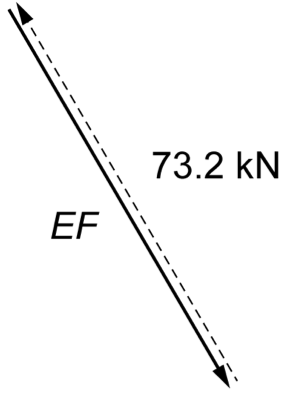
$\text{Consider member}\ CH:$

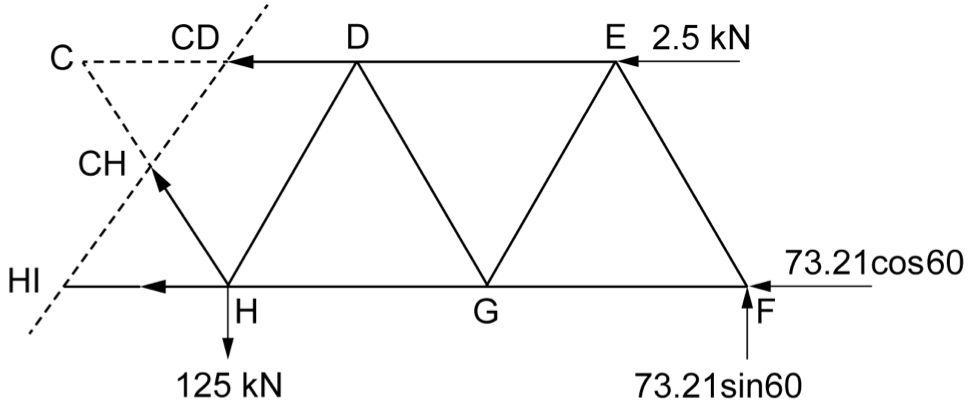
$+ \uparrow \Sigma F_{V}$	$=0$
$0$	$=-125 + 73.2 \times \sin\,60^{\circ} + CH \times \sin\,60^{\circ}$
$CH \times \sin\,60^{\circ}$	$=61.607$
$CH$	$= \dfrac{61.607}{\sin\,60^{\circ}} =71.138\ \text{kN (tension)} $

ENGINEERING, CS 2023 HSC 26a

A component of a roller coaster car bogie is to be punched out from a 10 mm thick rectangular plate of mild steel as shown.

Calculate the shear force of the punching die if the shear stress is 345 MPa. (3 marks)

Show Answers Only

$1630\ \text{kN} $

Show Worked Solution

$ \text{Using}\ \ \sigma_\text{s} = \dfrac{\text{F}}{\text{A}_\text{s}} $

$ \text {Perimeter}\ = (112 \times 2)+(15 \times 4) + (\pi \times 60) = 472.5 \ \text{mm}$

$ \text {Shear Area}\ ( \text{A}_\text{s}) = \text {perimeter of punch-out × thickness of plate} $

$ \text {Shear Area}\ ( \text{A}_\text{s})= 472.5 \times 10=4725 \ \text{mm}^2= 4725 \times 10^{-6}\ \text{m}^2$

$\text{Shear force}$	$=\ \text {shear stress } \times \text {shear area} $
	$= 345 \times 10^6 \ \text{Pa} \times 4725 \times 10^{-6}\ \text{m}^2$
	$=1\ 630\ 125\ \text{N}$
	$=1630\ \text{kN}$

♦ Mean mark 43%.

ENGINEERING, PPT 2023 HSC 25d

A uniform 8-metre ladder with a mass of 12 kg has been placed against a smooth wall.

Determine the minimum coefficient of static friction between the ground and the ladder. Assume there is no friction between the ladder and the wall. (4 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

$\mu = 0.287$

Show Worked Solution

Graphical solution:

$\phi = 16^{\circ}$

$\mu = \tan \phi = \tan 16^{\circ} = 0.287\ \text{(3 d.p.)}$

♦♦ Mean mark 31%.

Analytical solution:

$\cos 60^{\circ} = \dfrac{\text{d}_1}{4}\ \Rightarrow \ \text{d}_1 = 2\ \text{m} $

$\sin 60^{\circ} = \dfrac{\text{d}_2}{8}\ \Rightarrow \ \text{d}_2 = 6.928\ \text{m} $

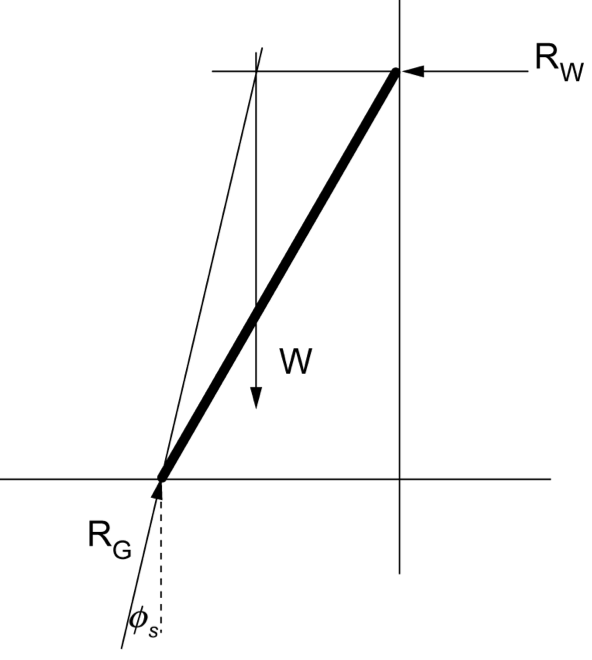
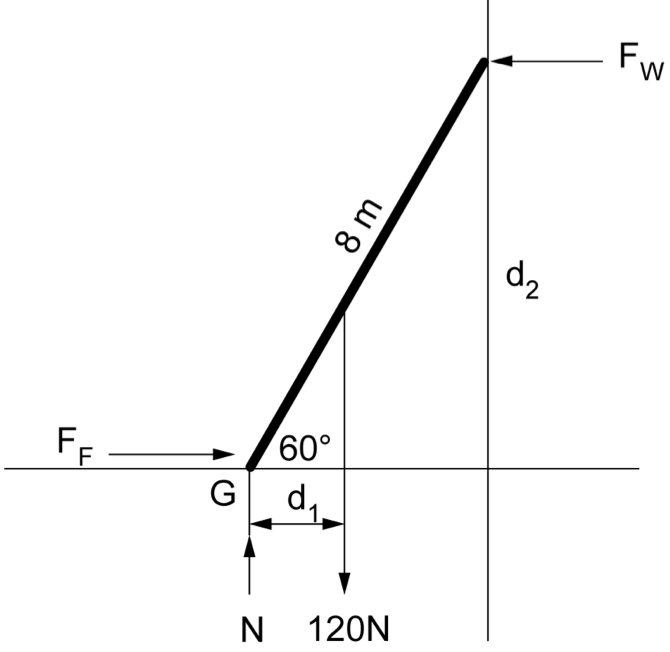
$ \Sigma \text{M}_{\text{G}} $	$=0$
$0$	$=(120 \times 2)-(\text{F}_{\text{W}} \times 6.928) $
$\text{F}_{\text{W}}$	$=\dfrac{240}{6.928}= 34.64\ \text{N}$

$\therefore \text{F}_{\text{F}} = 34.64 \text{ N}$

$\text{F}_{\text{g}}=mg=120\ \text{N}$

$\therefore \text{N} = 120 \text{N}\uparrow $

$\text{F}_{\text{F}}$	$= \mu \text{N}$
$\mu$	$= \dfrac{34.64}{120}=0.289\ \text{(3 d.p.)} $

ENGINEERING, TE 2023 HSC 25c

Outline how GPS satellites determine a position on the planet. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

Position is determined when a GPS satellites triangulate signals.
Triangulation depends on the accurate measurement of the time differences between signals traveling from satellites to GPS receivers.

Show Worked Solution

Position is determined when a GPS satellites triangulate signals.
Triangulation depends on the accurate measurement of the time differences between signals traveling from satellites to GPS receivers.

♦ Mean mark 44%.

ENGINEERING, TE 2023 HSC 25b

Explain the functions of a transistor in an electrical circuit. (3 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

One transistor function is to act as an amplifier. It magnifies a signal by allowing a current to flow from the emitter to the collector when a small current passes through the base.
A transistor can also operate as a switch. In this capacity, it allows current to flow or not, depending on whether certain conditions are satisfied.

Show Worked Solution

One transistor function is to act as an amplifier. It magnifies a signal by allowing a current to flow from the emitter to the collector when a small current passes through the base.
A transistor can also operate as a switch. In this capacity, it allows current to flow or not, depending on whether certain conditions are satisfied.

♦♦ Mean mark 36%.

ENGINEERING, AE 2023 HSC 25a

Describe the process of compression moulding when used to manufacture aircraft components. (3 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

The process of compression moulding of aircraft components requires a polymer to be fed into an open, heated mould cavity.
Once the polymer is soft, the mould is then closed and compressed.
Compression allows the material to fill the mould entirely. The charge cures within the heated mould.
When the piece is cured it is removed and the mould can be reused.

Show Worked Solution

The process of compression moulding of aircraft components requires a polymer to be fed into an open, heated mould cavity.
Once the polymer is soft, the mould is then closed and compressed.
Compression allows the material to fill the mould entirely. The charge cures within the heated mould.
When the piece is cured it is removed and the mould can be reused.

♦ Mean mark 50%.

b.	\(K_{a1}\)	\(=\dfrac{\ce{[HS-][H3O+]}}{\ce{[H2S]}} \)
	\(9.6 \times 10^{-8}\)	\(=\dfrac{\ce{[H3O+]^2}}{0.01}\)
	\(\ce{[H3O+]^2}\)	\(=0.01 \times 9.6 \times 10^{-8} \)
	\(\ce{[H3O+]}\)	\(=\sqrt{9.6 \times 10^{-10}}=3.1 \times 10^{-5}\ \text{M} \)
	\(\text{pH}\)	\(= -\log{10}(3.1 \times 10^{-5}) = 4.5 \)

\(\text{Temperature (°C)}\)	\(0\)	\(25\)	\(50\)	\(75\)	\(100\)
\(K_W\)	\( 1.1 \times 10^{-15}\)	\( 1.0 \times 10^{-14}\)	\( 5.5 \times 10^{-14}\)	\( 2.0 \times 10^{-13}\)	\( 5.6 \times 10^{-13}\)

\(\sin \theta\)	\(=\dfrac{3}{5}\)
\(\theta\)	\(=\sin^{-1}\Big(\dfrac{3}{5}\Big)=36.9^{\circ}\)

\(\tan\,\theta\)	\(=\dfrac{120}{150} \)
\(\theta\)	\(=\tan^{-1}\Big(\dfrac{120}{150}\Big)=38.7^{\circ}\)

\(\text{Percentage}\)	\(= \dfrac{1+1+2+1+2+5}{46} \times 100\)
	\(=\dfrac{12}{46} \times 100\)
	\(=26.086…\)%

a.	\(\Delta v\)	\(=v-u\)
		\(=265-315\)
		\(=-50\ \text{ms}^{-1}\)
		\(=50\ \text{ms}^{-1}\ \text{south}\)

\(a\)	\(=\dfrac{v^2-u^2}{2s}\)
	\(=\dfrac{(265)^2-(315)^2}{2 \times 2500}\)
	\(=-5.8\ \text{ms}^{-2}\)
	\(=5.8\ \text{ms}^{-2}\) to the south.

\(t\)	\(=\dfrac{v-u}{a}\)
	\(=\dfrac{265-315}{-5.8}\)
	\(=8.62\ \text{s}\)

\(v_{\text{B rel A}}\)	\(=v_{\text{B}}-\ v_{\text{A}}\)
\(-750\)	\(=v_B-300\)
\(v_B\)	\(=-450\)
	\(=450\ \text{kmh}^{-1}\ \text{south} \)