Band 5 – Page 76

CORE*, FUR1 2012 VCAA 3 MC

The transaction details for a savings account for the month of July 2012 are shown below.

Interest is calculated and paid monthly on the minimum monthly balance.

The annual rate of interest paid on this account is closest to

A. `3.5text(%)`

B. `4.3text(%)`

C. `4.7text(%)`

D. `4.9text(%)`

E. `5.2text(%)`

Show Answers Only

`E`

Show Worked Solution

`text(Interest) = 21.99`

♦ Mean mark 39%.

`text(Minimum balance) = 5101.82`

`text{Rate of interest (monthly)}`	`= 21.99 / 5101.82`
	`= 0.0043…`

`:.\ text(Yearly rate of interest)`

`= 0.0043… xx 12`

`= 0.0517…`

`= 5.17text(%)`

`=> E`

CORE*, FUR1 2013 VCAA 5 MC

$100 000 is invested in a perpetuity at an interest rate of 6% per annum.

After 10 quarterly payments have been made, the amount of money that remains invested in the perpetuity is

A. $15 000

B. $40 000

C. $85 000

D. $94 000

E. $100 000

Show Answers Only

`E`

Show Worked Solution

`text(A perpetuity, by definition, is designed to last)`

♦ Mean mark 38%.

`text(indefinitely which is done by only paying out)`

`text(the interest it receives.)`

`=> E`

GRAPHS, FUR1 2014 VCAA 2 MC

The vertical line that passes through the point `(3, 2)` has the equation

A. `x + y = 5`

B. `xy = 6`

C. `3y = 2x`

D. `y = 2`

E. `x = 3`

Show Answers Only

`E`

Show Worked Solution

♦ Mean mark 50%.
COMMENT: A 50% mean mark for this question flags that attention is required for this basic concept.

`=>E`

Xavier and Yvette share a job.
Yvette must work at least twice as many hours as Xavier.
They must work at least 40 hours each week, in total.
Xavier must work at least 10 hours each week.
Yvette can only work for a maximum of 30 hours each week.

Let `x` represent the number of hours that Xavier works each week.
Let `y` represent the number of hours that Yvette works each week.

In which one of the following graphs does the shaded area show the feasible region defined by these conditions?

Show Answers Only

`C`

Show Worked Solution

`text(Given Xavier and Yvette must work at least)`

♦ Mean mark 45%.

`text(40 hours, the feasible region MUST be above)`

`text(the line cutting both axes at 40.)`

`x + y >=40`

`:.\ text(Eliminate)\ A, B, and D.`

`text(S)text{ince Yvette (} y text{-axis) must work twice}`

`text(as long as Xavier, the feasible region is to the)`

`text(left of a gradient 2 line.)`

`y>=2x`

`:.\ text(Eliminate)\ E`

`text(Note that)\ C\ text(also satisfies)\ \ y<=30, and x>=10.`

`=> C`

CORE*, FUR1 2014 VCAA 6 MC

A loan of $1000 is to be repaid with six payments of $180 per month.

The effective annual rate of interest charged is closest to

A. 8.0%

B. 13.7%

C. 16.0%

D. 27.4%

E. 30.9%

Show Answers Only

`D`

Show Worked Solution

`text(Total interest paid)`

♦ Mean mark 36%.
MARKERS’ COMMENT: A 2-step process is required here that first calculates a flat rate of interest and then converts this to an effective rate.

`= text(total payments) – text(principal)`

`= 6 xx 180 – 1000`

`= 1080 – 1000`

`= 80`

`r_(flat)`	`= (text{interest paid} / text{loan × time in years}) × 100`
	`= (80 / {1000 xx 1/2}) xx 100`
	`= 16text(%)`

`:.\ text(Effective Interest)`	`= ({2n}/{n + 1}) xx r_f`
	`= ({2 xx 6} / {6 + 1}) xx 16`
	`= 27.42…text(% p.a.)`

`=> D`

GRAPHS, FUR1 2006 VCAA 9 MC

The four inequalities below were used to construct the feasible region for a linear programming problem.

`x >= 0`

`y >= 0`

`x + y <= 9`

`y <= 1/2 x`

A point that lies within this feasible region is

A. `(4, 4)`

B. `(5, 3)`

C. `(6, 2)`

D. `(6, 4)`

E. `(7, 3)`

Show Answers Only

`C`

Show Worked Solution

`text(Test the coordinates of each option to see which)`

`text(one satisfies all the given constraints.)`

`text(Consider)\ C,`

COMMENT: Students could draw a quick sketch of the feasible region to narrow down the possible choices and answer more efficiently.

`x>=0 and y>=0\ \ text(are satisfied.)`

`text(Substitute)\ (6, 2)\ text(into)\ \ x + y <= 9`

`6+2`	`<=9`
`8`	`<= 9\ \ \ text{(correct)}`

`text(Substitute)\ (6, 2)\ text(into)\ \ y <= 1/2x`

`2`	`<= 1/2 xx 6`
`2`	`<=3\ \ \ text{(correct)}`

`=> C`

GRAPHS, FUR1 2006 VCAA 6 MC

The point of intersection of two lines is `(2, – 2)`.

One of these two lines could be

A. `x - y = 0`

B. `2x + 2y = 8`

C. `2x + 2y = 0`

D. `2x - 2y = 4`

E. `2x - 2y = 0`

Show Answers Only

`C`

Show Worked Solution

`text{Test each option to see if (2, – 2) satisfies the}`

`text(equation and therefore lies on the line.)`

`text(Consider)\ C,`

`2x + 2y`	`=0`
`2(2) + 2(-2)`	`=0\ \ \ text{(True)}`

`=> C`

GRAPHS, FUR1 2006 VCAA 5 MC

Which one of the following statements about the line with equation `12x - 4y = 0` is not true?

A. the line passes through the origin

B. the line has a slope of 12

C. the line has the same slope as the line with the equation `12x - 4y = 12`

D. the point `(1, 3)` lies on the line

E. for this line, as `x` increases `y` increases

Show Answers Only

`B`

Show Worked Solution

`12x − 4y = 0`

♦ Mean mark 44%.

`text(Consider)\ A,`

`12(0) – 4(0) =0\ \ \ text{(True)}`

`text(Consider)\ B,`

`12x − 4y`	`= 0`
`4y`	`= 12x`
`y`	`= 3x`

`:.\ text{Gradient = 3 (Not true)}`

`text(Similarly,)\ C, D\ text(and)\ E\ text(can be shown to be true.)`

`=> B`

GRAPHS, FUR1 2006 VCAA 3-4 MC

A gas-powered camping lamp is lit and the gas is left on for six hours. During this time the lamp runs out of gas.

The graph shows how the mass, `M`, of the gas container (in grams) changes with time, `t` (in hours), over this period.

Part 1

Assume that the loss in weight of the gas container is due only to the gas being burnt.

From the graph it can be seen that the lamp runs out of gas after

A. `1.5\ text(hours.)`

B. `3\ text(hours.)`

C. `4.5\ text(hours.)`

D. `6\ text(hours.)`

E. `220\ text(hours.)`

Part 2

Which one of the following rules could be used to describe the graph above?

A. `M={(332.5 − 25t \ \ \ \ \ text( for ) \ \ \ \ \ \ 0 ≤ t ≤ 4.5),(220 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ text(for ) \ \ \ 4.5 < t ≤ 6) :}`

B. `M={(332.5 − 25t \ \ \ \ \ text( for ) \ \ \ \ \ \ 0 ≤ t ≤ 4.5),(220t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ text( for ) \ \ \ 4.5 < t ≤ 6) :}`

C. `M={(332.5 + 25t \ \ \ \ \ text( for ) \ \ \ \ \ \ 0 ≤ t ≤ 4.5),(220t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ text( for ) \ \ \ 4.5 < t ≤ 6) :}`

D. `M={(332.5 − 12.5t \ \ text( for ) \ \ \ \ \ \ 0 ≤ t ≤ 4.5),(220t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ text( for ) \ \ \ 4.5 < t ≤ 6) :}`

E. `M={(332.5 − 12.5t \ \ text( for ) \ \ \ \ \ \ 0 ≤ t ≤ 4.5),(220 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ text(for ) \ \ \ 4.5 < t ≤ 6) :}`

Show Answers Only

`text(Part 1:)\ C`

`text(Part 1:)\ A`

Show Worked Solution

`text(Part 1)`

`text(From the graph, the container stops losing mass)`

`text{at}\ (4.5, 220).`

`:.\ text(Gas runs out after 4.5 hrs.)`

`=> C`

`text(Part 2)`

♦ Mean mark 50%.

`text(Consider the period)\ \ 0 <= t <= 4.5,`

`text(Using)\ \ \ M = mt + b`

`b`	`= 332.5\ \ \ (y text{-intercept}), and`
`m`	`= (y_2 – y_1)/(x_2 – x_1)`
	`= (332.5 – 220)/(0 – 4.5)`
	`= 112.5/text(− 4.5)`
	`= -25`

`:. M= 332.5 − 25t`

`text(When)\ \ 4.5 <= t <= 6,`

`y = 220`

`=> A`

GRAPHS, FUR1 2008 VCAA 8 MC

A region is defined by the following inequalities

`y >= -4x + 10`

`y - x >= 1`

A point that lies within this region is

A. `(1, 3)`

B. `(2, 1)`

C. `(3, 2)`

D. `(4, 6)`

E. `(5, 1)`

Show Answers Only

`D`

Show Worked Solution

`text(Substituting the coordinates of each option)`

♦ Mean mark 46%.

`text(into the equations,)`

`y >= text(−4)x + 10\ \ \ …\ (1), and`

`y >= x+1\ \ \ …\ (2)`

`text(Consider)\ D,`

`D(4, 6):`	` \ \ 6 >= text(− 4)(4) + 10\ \ \ …\ (1)`
	` \ \ 6 >= text(− 6)\ \ \ text(Correct)`
	` \ \ 6≥ 4+1\ \ \ …\ (2)`
	` \ \ 6>= 5\ \ \ text(Correct)`

`text(Similarly,)\ A, B, C\ text(and)\ E\ text(can be shown to)`

`text(not satisfy both equations.)`

`=> D`

GRAPHS, FUR1 2008 VCAA 7 MC

The graph above shows the relationship between `y` and `x^2`.

The relationship between `y` and `x` is

A. `y = 4x`

B. `y = 1/4 x`

C. `y = 1/4 x^2`

D. `y = 16x^2`

E. `y = 1/16 x^2`

Show Answers Only

`C`

Show Worked Solution

`text(The gradient of the graph that shows)`

♦ Mean mark 50%.

`y\ text(versus)\ x^2=1/4`

`:. y=1/4 x^2`

`=>C`

GRAPHS, FUR1 2008 VCAA 5 MC

A mixture contains two liquids, `A` and `B`.

Liquid `A` costs $2 per litre and liquid `B` costs $3 per litre.

Let `x` be the volume (in litres) of liquid `A` purchased.
Let `y` be the volume (in litres) of liquid `B` purchased.

Which graph below shows all possible volumes of liquid `A` and liquid `B` that can be purchased for exactly $12?

Show Answers Only

`B`

Show Worked Solution

`text(Maximum volume of liquid)\ A`

♦ Mean mark 48%.

`= 12/2 = 6\ text(litres)`

`:.\ text(When)\ x = 6, \ \ y = 0`

`text(Maximum volume of liquid)\ B`

`= 12/3 = 4\ text(litres)`

`:.\ text(When)\ y = 4, \ \ x = 0`

`=> B`

Statistics, STD2 S5 SM-Bank 3 MC

The time, in hours, that each student spent sleeping on a school night was recorded for `1550` secondary-school students. The distribution of these times was found to be approximately normal with a mean of 7.4 hours and a standard deviation of 0.7 hours.

How many students would you expect to spend more than 8.1 hours sleeping on a school night?

You may assume for normally distributed data that:

- `text(68%)` of scores have `z`-scores between `–1` and `1`
- `text(95%)` of scores have `z`-scores between `–2` and `2`
- `text(99.7%)` of scores have `z`-scores between `–3` and `3`.

A. `16`

B. `248`

C. `1302`

D. `1510`

Show Answers Only

`B`

Show Worked Solution

`text (Need to find z-score of 8.1 hours)`

`text(z-score)`	`= (x-mu)/sigma`
	`= (8.1-7.4)/0.7`
	`= 1`

`text(68% students with –1 < z-score < 1)`

`:.\ text(16% have z-score > 1)`

`text(# Students)`	`= 16%×1550`
	`= 248`

`=>B`

GEOMETRY, FUR1 2008 VCAA 5 MC

For the triangle shown, the value of `sin x^@` is given by

A. `(sin 125.1^@)/2`

B. `(5^2 + 4^2 − 8^2)/(2 xx 5 xx 4)`

C. `2 xx sin 125.1^@`

D. `(5^2 + 8^2 − 4^2)/(2 xx 5 xx 8)`

E. `(5 xx sin 125.1^@)/8`

Show Answers Only

`A`

Show Worked Solution

`text(Using sine rule:)`

♦ Mean mark 41%.

`(sin x^@)/4`	`= (sin 125.1^@)/8`
`:. sin x^@`	`= (4 xx sin 125.1^@)/8`
	`= (sin 125.1^@)/2`

`=> A`

Measurement, 2UG 2007 HSC 28c

A piece of plaster has a uniform cross-section, which has been shaded, and has dimensions as shown.

Use two applications of Simpson’s rule to approximate the area of the cross-section. (3 marks)
The total surface area of the piece of plaster is `7480.8\ text(cm²)`.
Calculate the area of the curved surface as shown on the diagram. (2 marks)

Show Answers Only

`50.4\ text(cm²)`
`3500\ text(cm²)`

Show Worked Solution

(i)

`A`	`= h/3 [y_0 +4y_1 + y_2]\ text(… applied twice)`
	`= 3.6/3 (5 + 4 xx 4.6 + 3.7) + 3.6/3 (3.7 + 4 xx 2.8 + 0)`
	`= 32.52 + 17.88`
	`= 50.4\ text(cm²)`

(ii) `text(Total Area) = 7480.8\ text(cm²)`

`text(Area of Base)`	`= 14.4 xx 200`
	`= 2880\ text(cm²)`

`text(Area of End)`	`= 5 xx 200`
	`= 1000\ text(cm²)`

`text(Area of sides)`	`= 2 xx 50.4\ \ \ text{(from (i))}`
	`= 100.8\ text(cm²)`

`:.\ text(Area of curved surface)`

`= 7480.8 – (2880 + 1000 + 100.8)`

`= 3500\ text(cm²)`

Probability, 2UG 2007 HSC 28a

Two unbiased dice, `A` and `B`, with faces numbered `1`, `2`, `3`, `4`, `5` and `6` are rolled.

The numbers on the uppermost faces are noted. This table shows all the possible outcomes.

A game is played where the difference between the highest number showing and the lowest number showing on the uppermost faces is calculated.

What is the probability that the difference between the numbers showing on the uppermost faces of the two dice is one? (1 mark)
In the game, the following applies.
What is the financial expectation of the game? (3 marks)
If Jack pays `$1` to play the game, does he expect a gain or a loss, and how much will it be? (1 mark)

Show Answers Only

`5/18`
`$0.75`
`text(If Jack pays $1 to play, he should expect)`
`text(a loss of $0.25.)`

Show Worked Solution

(i) `text(# Outcomes with a difference of 1)`

`= 10`

`:.\ P text{(diff of 1)} = 10/36 = 5/18`

(ii) `P text{(no difference)} = 6/36 = 1/6`

`P text{(2, 3, 4 or 5)}`	`= 1 – [P(0) + P(1)]`
	`= 1 – [5/18 + 1/6]`
	`= 1 – 8/18`
	`= 5/9`

`:.\ text(Financial Expectation)`

`= (1/6 xx 3.50) – (5/18 xx 5) + (5/9 xx 2.80)`

`= $0.75`

(iii) `text(If Jack pays $1 to play, he should expect)`

`text(a loss of $0.25.)`

GEOMETRY, FUR1 2007 VCAA 9 MC

The points `M`, `N` and `P` form the vertices of a triangular course for a yacht race.

`MN = MP = 4\ text(km.)`

The bearing of `N` from `M` is 070°

The bearing of `P` from `M` is 180°

Three people perform different calculations to determine the length of `NP` in kilometres.

Graeme	`\ \ \ \ \ NP`	`= sqrt(16 + 16 − 2 xx 4 xx 4 xx cos110^@)`
Shelley	`NP`	`= 2 xx 4 xx cos 35^@`
Tran	`NP`	`= (4 xx sin110^@)/sin35^@`

The correct length of `NP` would be found by

A. Graeme only.

B. Tran only.

C. Graeme and Shelley only.

D. Graeme and Tran only.

E. Graeme, Shelley and Tran.

Show Answers Only

`E`

Show Worked Solution

`text(Using cosine rule in)\ \ Delta MNP:`

`NP = sqrt(4^2 + 4^2 − 2 xx 4 xx 4 xx cos110^@)`

`:.\ text(Graeme is correct)`

`text(Using sine rule in)\ \ Delta MNP:`

`(NP)/sin110^@`	`= 4/sin35^@`
`NP`	`= (4 xx sin110^@)/sin35^@`

`:.\ text(Tran is correct)`

`text(Let)\ \ Q\ text(be the midpoint of)\ NP`

`text(In)\ \ Delta PQM:`

`cos35^@`	`= x/4`
`x`	`= 4 xx cos35^@`
`NP`	`= 2 xx 4 xx cos35^@`

`:.\ text(Shelley is correct.)`

`=> E`

GEOMETRY, FUR1 2007 VCAA 7 MC

A closed cubic box of side length 36 cm is to contain a thin straight metal rod.

The maximum possible length of the rod is closest to

A. `36\ text(cm)`

B. `51\ text(cm)`

C. `62\ text(cm)`

D. `108\ text(cm)`

E. `216\ text(cm)`

Show Answers Only

`C`

Show Worked Solution

`text(The maximum length rod would go from)`

♦ Mean mark 46%.

`A\ text(to)\ G.`

`text(Using Pythagoras in)\ Delta ACD,`

`AC^2`	`= 36^2 + 36^2`
	`= 2592`
`:. AC`	`= 50.91…`

`text(Using Pythagoras in)\ Delta AGC,`

`AG^2`	`= AC^2 + GC^2`
	`= (50.91…)^2 + 36^2`
	`= 3888`
`:.AG`	`= 62.35…\ text(cm)`

`=> C`

GEOMETRY, FUR1 2008 VCAA 9 MC

Two hikers, Anton and Beth, walk in different directions from the same camp.

Beth walks for 12 km on a bearing of 135° to a picnic ground.

Anton walks for 6 km on a bearing of 045° to a lookout tower.

On what bearing (to the nearest degree) should Anton walk from the lookout tower to meet Beth at the picnic ground?

A. `063°`

B. `108°`

C. `153°`

D. `162°`

E. `180°`

Show Answers Only

`D`

Show Worked Solution

♦ Mean mark 38%.

`text(S)text(ince)\ T\ text(is on a bearing)\ 045^@\ text(from)\ O\ text(and)\ P`

`text(is on a bearing)\ 135^@,\ /_ TOP= 90^@`

`text(In)\ Delta TOP,`

`tan /_ OTP`	`= 12/6 = 2`
`:. /_ OTP`	`= 63.43…^@`

`text(Let)\ A\ text(be directly south of)\ T`

`/_ OTA`	`= 45^@\ text{(alternate)}`
`:.\ /_ATP`	`= 63.43… − 45`
	`= 18.43…^@`

`:.\ text(Bearing of)\ P\ text(from)\ T`

`= 180 − 18.43…`

`= 161.57…^@`

`=> D`

GEOMETRY, FUR1 2008 VCAA 6 MC

A tent with semicircular ends is in the shape of a prism. The diameter of the ends is 1.5 m. The tent is 2.5 m long.

The total surface area (in m²) of the tent, including the base, is closest to

A. `5.5`

B. `7.7`

C. `8.8`

D. `11.4`

E. `15.3`

Show Answers Only

`D`

Show Worked Solution

`text{S.A. (base)}`	`= 1.5 xx 2.5 = 3.75\ text(m²)`
`text{S.A. (ends)}`	`= 2 xx 1/2 pi r^2`
	`= 2 xx 1/2 xx pi xx 0.75^2`
	`= 1.76…\ text(m²)`

`text{S.A. (sides and roof)} = 2.5 xx l,\ \ text(where),`

♦ Mean mark 39%.
MARKER’S COMMENTS: Almost a third of students didn’t include the base of the tent in their calculations.

`l`	`=\ text(length of semicircle arc)`
	`= 1/2 xx pi xx\ text(diameter)`
	`= 1/2 xx pi xx 1.5`
	`= 2.356…\ text(m)`

`:.\ text{S.A. (sides and roof)}`

`=2.5 xx 2.356…`

`= 5.89…\ text(m²)`

`:.\ text(Total surface area)`

`= 3.75 + 1.76… + 5.89…`

`= 11.4…\ text(m²)`

`=> D`

Algebra, MET1 SM-Bank 28

Consider the simultaneous linear equations below.

`4x-2y = 18`

`3x + ky = 10`

where `k` is a real constant.

What are the values of `k` where no solutions exist? (3 marks)

--- 10 WORK AREA LINES (style=lined) ---
What values of `k` do the simultaneous equations have a unique solution? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`k=-3/2`
`k\ in R text(\) {-3/2}`

Show Worked Solution

a.	`4x-2y`	`=18`
	`y`	`=2x-9\ \ …\ (1)`

`=> m_1 = 2,\ \ c_1=-9`

`3x +ky`	`=10`
`y`	`=-3/k x +10/k\ \ …\ (2)`

`=> m_2 =-3/k,\ \ c_2=10/k`

`text(No solution if)\ \ m_1=m_2, and c_1!=c_2.`

`-3/k`	`=2`
`k`	`=- 3/2`

`text(When)\ \ k=-3/2, c_1!=c_2.`

`:.\ text(No solution when)\ \ k=-3/2.`

b. `text(A unique solution exists when)\ \ m_1 != m_2,`

`k in R\ text(\) {-3/2}`

Algebra, STD2 A2 2007 HSC 27b

A clubhouse uses four long-life light globes for five hours every night of the year. The purchase price of each light globe is $6.00 and they each cost `$d` per hour to run.

Write an equation for the total cost (`$c`) of purchasing and running these four light globes for one year in terms of `d`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Find the value of `d` (correct to three decimal places) if the total cost of running these four light globes for one year is $250. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
If the use of the light globes increases to ten hours per night every night of the year, does the total cost double? Justify your answer with appropriate calculations. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
The manufacturer’s specifications state that the expected life of the light globes is normally distributed with a standard deviation of 170 hours.

What is the mean life, in hours, of these light globes if 97.5% will last up to 5000 hours? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`$c = 24 + 7300d`
`0.031\ $ text(/hr)\ text{(3 d.p.)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(4660 hours.)`

Show Worked Solution

a. `text(Purchase price) = 4 xx 6 = $24`

`text(Running cost)`	`= text(# Hours) xx text(Cost per hour)`
	`= 4 xx 5 xx 365 xx d`
	`= 7300d`

`:.\ $c = 24 + 7300d`

b. `text(Given)\ \ $c = $250`

`250`	`= 24 + 7300d`
`7300d`	`= 226`
`d`	`= 226/7300`
	`= 0.03095…`
	`= 0.031\ $ text(/hr)\ text{(3 d.p.)}`

c. `text(If)\ d\ text(doubles to 0.062)\ \ $text(/hr)`

`$c`	`= 24 + 7300 xx 0.062`
	`= $476.60`

`text(S) text(ince $476.60 is less than)\ 2 xx $250\ ($500),`
`text(the total cost increases to less than double)`
`text(the original cost.)`

d. `sigma = 170`

`z\ text(-score of 5000 hours) = 2`

`z`	`= (x – mu)/sigma`
`2`	`= (5000 – mu)/170`
`340`	`= 5000 – mu`
`mu`	`= 4660`

`:.\ text(The mean life of these globes is 4660 hours.)`

Financial Maths, 2ADV M1 SM-Bank 13 MC

The first term of a geometric sequence is `a`, where `a < 0`.

The common ratio of this sequence, `r`, is such that `r < –1`.

Which one of the following graphs best shows the first `10` terms of this sequence?

Show Answers Only

`B`

Show Worked Solution

`text(Using elimination)`

`a < 0. text(Cannot be C.)`

`r < -1. text(Successive terms change sign and)`

`text(increase exponentially.)`

`text(Cannot be A, D.)`

`=> B`

Financial Maths, 2ADV M1 SM-Bank 12

There are 10 checkpoints in a 4500 metre orienteering course. Checkpoint 1 is the start and checkpoint 10 is the finish.

The distance between successive checkpoints increases by 50 metres as each checkpoint is passed.

Calculate the distance, in metres, between checkpoint 2 and checkpoint 3. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(350 m)`

Show Worked Solution

`text(9 intervals exist between 10 checkpoints)`

`=>\ text(9 distances form an AP)`

`text(Where ) d = 50`

`S_9 = 4500`

`S_n`	`= n/2[2a + (n − 1)d]`
`4500`	`= 9/2 [2a + (9 − 1) × 50]`
`4500`	`= 9/2[2a + 400]`
`9a`	`= 2700`
`a`	`= 300`

`text(Distance between checkpoint 1 and 2)`

`= a=300\ text(m)`

`:.\ text(Distance between checkpoint 2 and 3)`

`= a+d=350\ text(m)`

Financial Maths, 2ADV M1 SM-Bank 9 MC

The graph above shows consecutive terms of a sequence.

The sequence could be

geometric with common ratio r, where r < 0
geometric with common ratio r, where 0 < r < 1
geometric with common ratio r, where r > 1
arithmetic with common difference d, where d < 0

Show Answers Only

`B`

Show Worked Solution

`text (As)\ \ n\ \ text (increases,) \ \ t_n →0.`

`:.\ text (Series is a GP with a limiting sum,)`

`text(i.e.)\ \ |\ r\ | < 1.`

`text (Only one choice satisfies these conditions.)`

`rArr B`

Algebra, STD2 A4 2007 HSC 27a

A rectangular playing surface is to be constructed so that the length is 6 metres more than the width.

Give an example of a length and width that would be possible for this playing surface. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Write an equation for the area (`A`) of the playing surface in terms of its length (`l`). (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

A graph comparing the area of the playing surface to its length is shown.
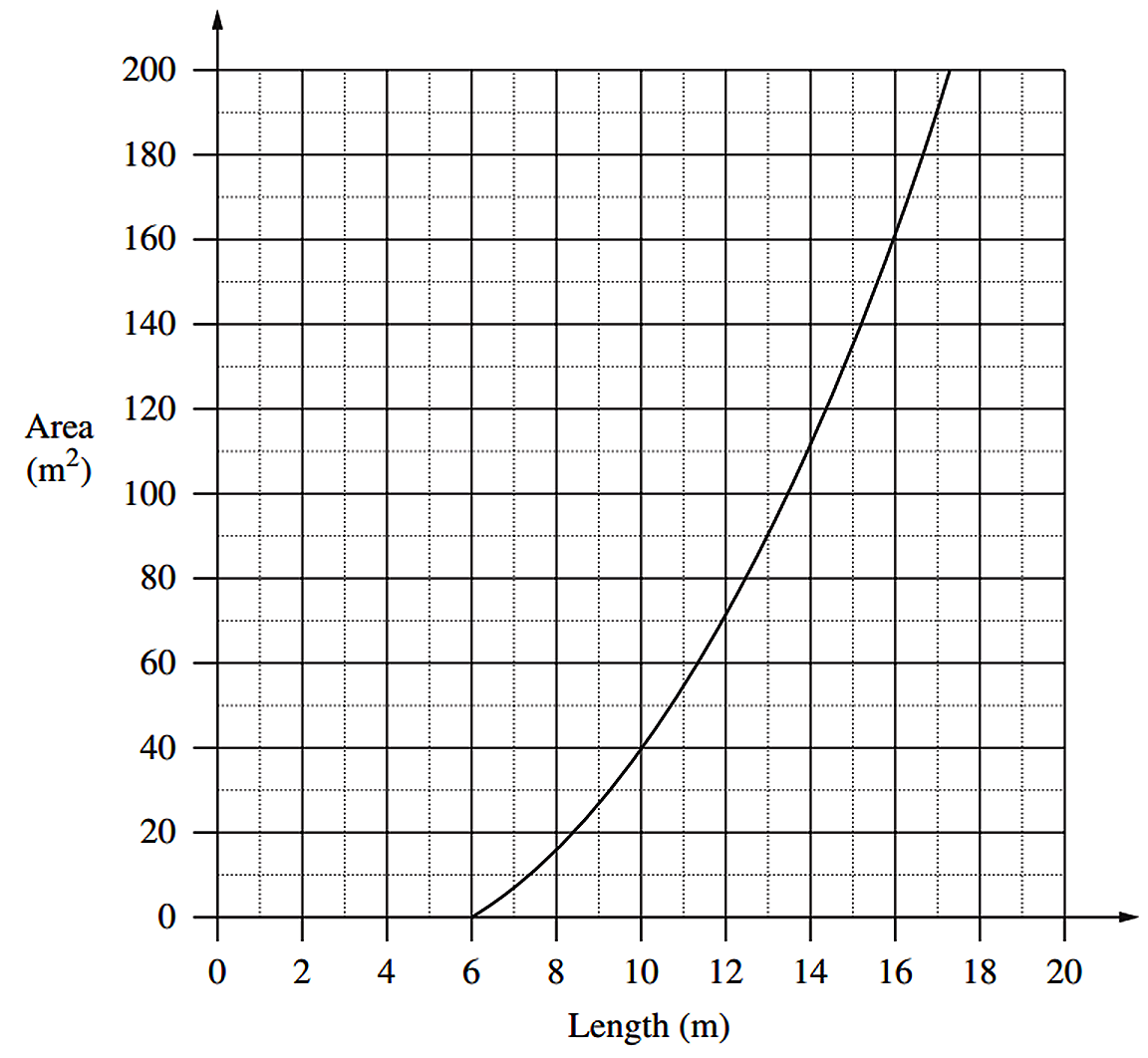
Why are lengths of 0 metres to 6 metres impossible? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
What would be the dimensions of the playing surface if it had an area of 135 m²? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Company `A` constructs playing surfaces.
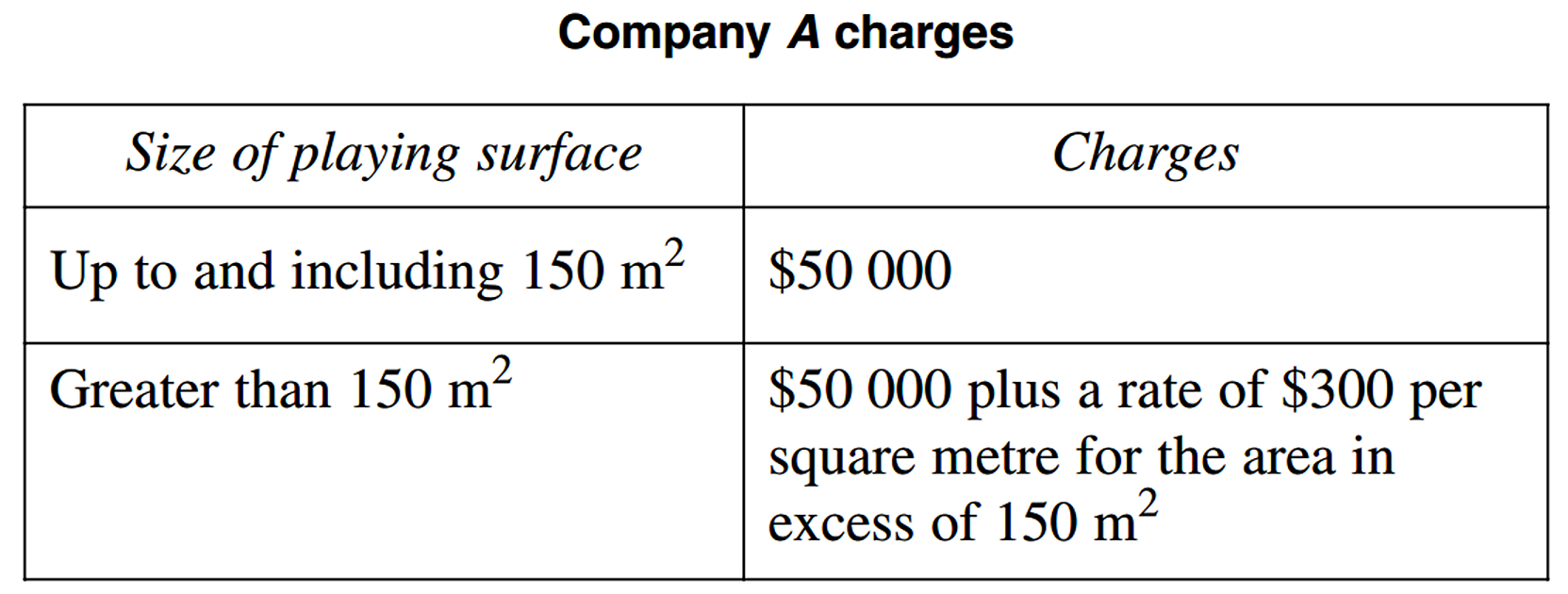
Draw a graph to represent the cost of using Company `A` to construct all playing surface sizes up to and including 200 m².

Use the horizontal axis to represent the area and the vertical axis to represent the cost. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
Company `B` charges a rate of $360 per square metre regardless of size.
Which company would charge less to construct a playing surface with an area of 135 m²

Justify your answer with suitable calculations. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(One possibility is a length of 10 m, and a width)`

`text{of 4 m (among many possibilities).}`
`A = l (l – 6)\ \ text(m²)`
`text(Given the length must be 6 m more than)`

`text(the width, it follows that the length)`

`text(must be greater than 6 m.)`
`text(15 m × 9 m)`
`text(Proof)\ \ text{(See worked solutions)}`

Show Worked Solution

i. `text(One possibility is a length of 10 m, and a width)`

`text{of 4 m (among many possibilities).}`

ii. `text(Length) = l\ text(m)`

`text(Width) = (l – 6)\ text(m)`

`:.\ A`

`= l (l – 6)`

iii. `text(Given the length must be 6m more than the width,)`

`text(it follows that the length must be greater than 6 m)`

`text(so that the width is positive.)`

iv. `text(From the graph, an area of 135 m² corresponds to)`

`text(a length of 15 m.)`

`:.\ text(The dimensions would be 15 m × 9 m.)`

vi. `text(Company)\ A\ text(cost) = $50\ 000`

`text(Company)\ B\ text(cost)`	`= 135 xx 360`
	`= $48\ 600`

`:.\ text(Company)\ B\ text(would charge $1400 less)`

`text(than Company)\ A.`

Financial Maths, STD2 F1 2007 HSC 26b

Myles is in his third year as an apprentice film editor.

Myles purchased film-editing equipment for $5000.

After 3 years it has depreciated to $3635 using the straight-line method.

Calculate the rate of depreciation per year as a percentage. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Myles earns $800 per week. Calculate his taxable income for this year if the only allowable deduction is the amount of depreciation of his film-editing equipment in the third year of use. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Use this tax table to calculate Myles’s tax payable. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(9.1%)`
`$41\ 145`
`$8443.50`

Show Worked Solution

a.	`S = V_0 – Dn`
	`S = $3635,\ \ \ V_0 = 5000,\ \ \ n = 3`

`3635`	`= 5000 – D xx 3`
`3D`	`= 1365`
`D`	`= $455`

`:.\ text(Rate of depreciation per year)`

`= 455/5000 xx 100`

`= 9.1 text(%)`

b.	`text(Income per year)`	`= 52 xx 800`
		`= $41\ 600`

`text(Taxable income)`	`=\ text(Income – Deductions)`
	`= 41\ 600 – 455`
	`= $41\ 145`

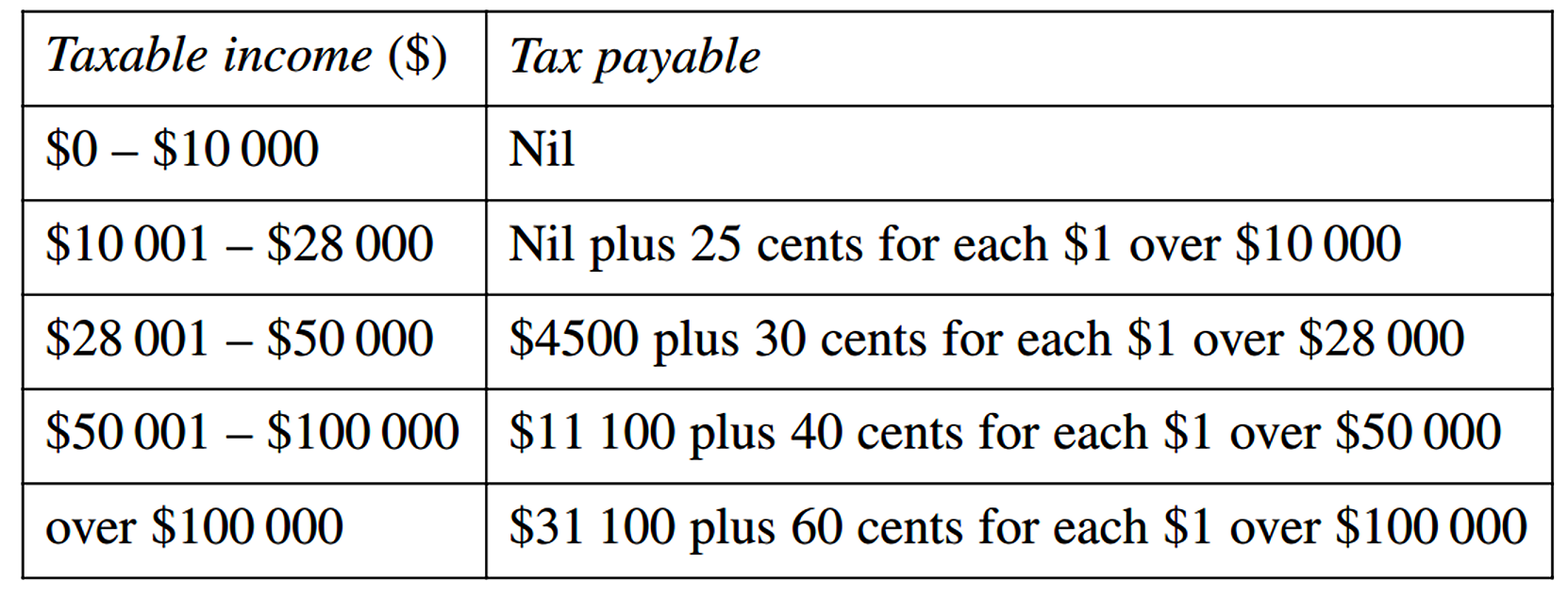
c.	`text(Tax payable)`	`= 4500 + 0.3(41\ 145 – 28\ 000)`
		`= 4500 + 3943.50`
		`= $8443.50`

Measurement, STD2 M6 2007 HSC 26a

The diagram shows information about the locations of towns `A`, `B` and `Q`.

It takes Elina 2 hours and 48 minutes to walk directly from Town `A` to Town `Q`.

Calculate her walking speed correct to the nearest km/h. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Elina decides, instead, to walk to Town `B` from Town `A` and then to Town `Q`.

Find the distance from Town `A` to Town `B`. Give your answer to the nearest km. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Calculate the bearing of Town `Q` from Town `B`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`5\ text(km/hr)\ text{(nearest km/hr)}`
`18\ text(km)\ text{(nearest km)}`
`236^@`

Show Worked Solution

i. `text(2 hrs 48 mins) = 168\ text(mins)`

`text(Speed)\ text{(} A\ text(to)\ Q text{)}`	`= 15/168`
	`= 0.0892…\ text(km/min)`

`text(Speed)\ text{(in km/hr)}`	`= 0.0892… xx 60`
	`= 5.357…\ text(km/hr)`
	`= 5\ text(km/hr)\ text{(nearest km/hr)}`

ii.

`text(Using cosine rule)`

`AB^2`	`= 15^2 + 10^2 – 2 xx 15 xx 10 xx cos 87^@`
	`= 309.299…`
`AB`	`= 17.586…`
	`= 18\ text(km)\ text{(nearest km)}`

`:.\ text(The distance from Town)\ A\ text(to Town)\ B\ text(is 18 km.)`

iii

`/_CAQ`	`= 31^@\ \ \ text{(} text(straight angle at)\ A text{)}`
`/_AQD`	`= 31^@\ \ \ text{(} text(alternate angle)\ AC\ text(\|\|)\ DQ text{)}`
`/_DQB`	`= 87 – 31 = 56^@`
`/_QBE`	`= 56^@\ \ \ text{(} text(alternate angle)\ DQ \ text(\|\|)\ BE text{)}`

`:.\ text(Bearing of)\ Q\ text(from)\ B`

`= 180 + 56`

`= 236^@`

GEOMETRY, FUR1 2013 VCAA 9 MC

A rectangular prism with a square base, `ABCD`, is shown above.

The diagonal of the prism, `AH`, is 8 cm.

The height of the prism, `HC`, is 4 cm.

The volume of this rectangular prism is

A. `64\ text(cm³)`

B. `96\ text(cm³)`

C. `128\ text(cm³)`

D. `192\ text(cm³)`

E. `256\ text(cm³)`

Show Answers Only

`B`

Show Worked Solution

`text(Using Pythagoras in)\ Delta AHC,`

♦ Mean mark 47%.

`AH^2`	`= HC^2 + AC^2`
`8^2`	`= 4^2 + AC^2`
`AC^2`	`= 48`
`:. AC`	`= 6.928…\ text(cm)`

`Delta ABC\ text(is a right-angled and isosceles.)`

`:. /_ CAB = /_ ACB = 45°`

`sin 45°`	`= (CB)/(6.298…)`
`CB`	`= 6.928… xx sin 45°`
	`= 4.898…\ text(cm)`

`:.\ text(Volume)`	`= (CB)^2 xx 4`
	`= (4.898…)^2 xx 4`
	`= 96\ text(cm³)`

`=> B`

GEOMETRY, FUR1 2013 VCAA 8 MC

There are four telecommunications towers in a city. The towers are called Grey Tower, Black Tower, Silver Tower and White Tower.

Grey Tower is 10 km due west of Black Tower.

Silver Tower is 10 km from Grey Tower on a bearing of 300°.

White Tower is 10 km due north of Silver Tower.

Correct to the nearest degree, the bearing of Black Tower from White Tower is

A. `051°`

B. `129°`

C. `141°`

D. `309°`

E. `321°`

Show Answers Only

`B`

Show Worked Solution

`text(S)text(ince bearing of Silver from Grey is 300°)`

♦ Mean mark 39%.

`/_ XGS = 60°, and /_SGO = 30°`

`text(In)\ Delta SGO,`

`sin 30°`	`= a/10`
`a`	`= 10 xx sin 30`
	`= 5`

`cos 30°`	`= b/10`
`b`	`= 10 xx cos 30`
	`= 8.66…`

`tan theta`	`= (OB)/(OW)`
	`= (10 + 8.66…)/(10 + 5)`
	`=1.244…`
`theta`	`= 51.2…°`

`:.\ text(Bearing of Black from White tower)`

`= 180 – 51.2…º`

`= 128.79…°`

`=> B`

GEOMETRY, FUR1 2013 VCAA 4 MC

A cafe sells two sizes of cupcakes with a similar shape.

The large cupcake is 6 cm wide at the base and the small cupcake is 4 cm wide at the base.

The price of a cupcake is proportional to its volume.

If the large cupcake costs $5.40, then the small cupcake will cost

A. `$1.60`

B. `$2.32`

C. `$2.40`

D. `$3.40`

E. `$3.60`

Show Answers Only

`A`

Show Worked Solution

`text(Linear scale factor of cupcake lengths)`

♦♦ Mean mark 22%.

`k = 4/6 = 2/3`

`text(Volume scale factor is)`

`k^3 = (2/3)^3=8/27`

`text(S)text(ince price is proportional to volume,)`

`text(Cost)_text(small)/text(Cost)_text(large)`	`=8/27`
`:. \ text(Cost)_text(small)`	`=(8 xx 5.40)/27`
	`=$1.60`

`=> A`

GEOMETRY, FUR1 2008 VCAA 2-3 MC

An orienteering course is triangular in shape and is marked by three points, `A`, `B` and `C`, as shown in the diagram below.

Part 1

In this course, the bearing of `B` from `A` is `050^@` and the bearing of `C` from `B` is `120^@`.

The bearing of `B` from `C` is

A. `060°`

B. `120°`

C. `240°`

D. `300°`

E. `310°`

Part 2

In this course, `B` is 7.0 km from `A`, ` C` is 8.0 km from `B` and `A` is 12.3 km from `C`.

The area (in km²) enclosed by this course is closest to

A. `21`

B. `24`

C. `25`

D. `26`

E. `28`

Show Answers Only

`text(Part 1:)\ D`

`text(Part 2:)\ D`

Show Worked Solution

`text(Part 1)`

`text(Let)\ D\ text(be directly North of)\ C`

`/_ BCD = 60^@\ \ \ `	`text{(cointerior, North South}` `\ \ text{lines are parallel)}`

`∴ text(Bearing of)\ B\ text(from)\ C`

♦ Mean mark (Part 1) 43%.
MARKER’S COMMENT: The low mean mark for this question flagged a fundamental lack of understanding in this area.

`= 360 − 60`

`= 300^@`

`=> D`

`text(Part 2)`

`text(Using cosine rule in)\ Delta ABC,`

`cos /_ BAC`	`= (7.0^2 + 12.3^2 − 8.0^2) / (2 xx 7.0 xx 12.3)`
	`= 0.7914…`
`/_ BAC`	`= 37.67…^@`

`text(Using sine rule,)`

`text(Area of)\ Delta ABC`	`= 1/2 xx 7.0 xx 12.3 xx sin 37.67…^@`
	`= 26.31…\ text(km²)`

`=> D`

Statistics, STD2 S5 2007 HSC 25d

The results of two class tests are normally distributed. The means and standard deviations of the tests are displayed in the table.

Stuart scored 63 in Test 1 and 62 in Test 2. He thinks that he has performed better in Test 1. Do you agree? Justify your answer using appropriate calculations. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
If 150 students sat for Test 2, how many students would you expect to have scored less than 64? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`126`

Show Worked Solution

i. `text(In Test 1,)\ \ mu = 60,\ sigma = 6.2`

`z text(-score)\ (63)`	`= (x – mu)/sigma`
	`= (63 – 60)/6.2`
	`= 0.483…`

`text(In Test 2,)\ \ mu = 58,\ sigma = 6.0`

`z text(-score)\ (62)`	`= (62 – 58)/6.0`
	`= 0.666…`

`text(S) text(ince Stuart’s)\ z\ text(-score is higher in Test 2,)`

`text(his performance relative to the class is better)`

`text(despite his mark being slightly lower.)`

ii. `text(In Test 2)`

`z text(-score)\ (64)`	`= (64 – 58)/6`
	`= 1`

`=> text(84% have)\ z text(-score) < 1`

`:.\ text(# Students expected below 64)`

`= text(84%) xx 150`

`= 126`

Probability, STD2 S2 2007 HSC 25c

In a stack of 10 DVDs, there are 5 rated PG, 3 rated G and 2 rated M.

A DVD is selected at random. What is the probability that it is rated M? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Grant chooses two DVDs at random from the stack. Copy or trace the tree diagram into your writing booklet.

Complete the tree diagram by writing the correct probability on each branch. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---
Calculate the probability that Grant chooses two DVDs with the same rating. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`1/5`
`14/45`

Show Worked Solution

i. `text(5 PG, 3 G, 2 M)`

`P text{(M)} = 2/10 = 1/5`

ii.

iii. `P text{(same rating)}`

`= P text{(PG, PG)} + P text{(G, G)} + P text{(M, M)}`

`= (1/2 xx 4/9) + (3/10 xx 2/9) + (1/5 xx 1/9)`

`= 2/9 + 1/15 + 1/45`

`= 14/45`

Measurement, STD2 M6 2007 HSC 25b

The angle of depression from `J` to `M` is 75°. The length of `JK` is 20 m and the length of `MK` is 18 m.

Copy or trace this diagram into your writing booklet and calculate the angle of elevation from `M` to `K`. Give your answer to the nearest degree. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`58^@`

Show Worked Solution

`/_AJL = 90^@`

`/_MJL = 90 – 75 = 15^@`

`text(Using sine rule in)\ Delta MJK`

`text(Let)\ /_JMK = x^@`

`20/sin x`	`= 18/sin15^@`
`18 sin x`	`= 20 xx sin 15^@`
`sin x`	`= (20 xx sin 15^@)/18 = 0.2875…`
`x`	`= 16.71…^@`

`/_JML = 75^@\ text{(} text(alternate angles,)\ ML \ text(\|\|) \ AJ text{)}`

`:.\ /_KML`	`= 75^@ – 16.71…`
	`= 58.287…^@`
	`= 58^@\ \ \ text{(nearest degree)}`

`:.\ text(Angle of Elevation from)\ M\ text(to)\ K\ text(is)\ 58^@.`

Statistics, STD2 S1 2007 HSC 24d

Barry constructed a back-to-back stem-and-leaf plot to compare the ages of his students.

Write a brief statement that compares the distribution of the ages of males and females from this set of data. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
What is the mode of this set of data? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Liam decided to use a grouped frequency distribution table to calculate the mean age of the students at Barry’s Ballroom Dancing Studio.

For the age group 30 - 39 years, what is the value of the product of the class centre and the frequency? (2 marks)

--- 3 WORK AREA LINES (style=lined) ---
Liam correctly calculated the mean from the grouped frequency distribution table to be 39.5.

Caitlyn correctly used the original data in the back-to-back stem-and-leaf plot and calculated the mean to be 38.2.

What is the reason for the difference in the two answers? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(More males attend than females and a higher proportion)`
`text(of those are younger males, with the distribution being)`
`text(positively skewed. Female attendees are generally older)`
`text(and have a negatively skewed distribution.)`
`text(Mode) = 64\ \ \ text{(4 times)}`
`172.5`
`text(The difference in the answers is due to the class)`
`text(centres used in group frequency tables distorting)`
`text(the mean value from the exact data.)`

Show Worked Solution

a.	`text(More males attend than females and a higher proportion)`
	`text(of those are younger males, with the distribution being)`
	`text(positively skewed. Female attendees are generally older)`
	`text(and have a negatively skewed distribution.)`

b.	`text(Mode) = 64\ \ \ text{(4 times)}`

c.	`text(Class centre)`	`= (30 + 39)/2`
		`= 34.5`
	`text(Frequency) = 5`

`:.\ text(Class centre) xx text(frequency)`

`= 34.5 xx 5`

`= 172.5`

d.	`text(The difference in the answers is due to the class)`
	`text(centres used in group frequency tables distorting)`
	`text(the mean value from the exact data.)`

Measurement, STD2 M7 2007 HSC 23c

A scientific study uses the ‘capture-recapture’ technique.

In the first stage of the study, 24 crocodiles were caught, tagged and released.

Later, in the second stage of the study, some crocodiles were captured from the same area. Eighteen of these were found to be tagged, which was 40% of the total captured during the second stage.

How many crocodiles were captured in total during the second stage of the study? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Calculate the estimate for the total population of crocodiles in this area. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(45 crocodiles)`
`text(60 crocodiles)`

Show Worked Solution

i.	`text(Let)\ C_1`	`=\ text(crocodiles captured in stage 1)`
	`C_2`	`=\ text(crocodiles captured in stage 2)`

`C_1`	`=\ text(40%)\ xx C_2`
`18`	`=\ text(40%)\ xx C_2`
`:.\ C_2`	`= 18/0.4 = 45\ text(crocodiles)`

COMMENT: Std2 sample exam questions from NESA included capture/recapture as examinable content within M7 Rates and Ratios.

ii.

`text(Capture) = 24/text(Population)`

`text(Recapture) = 18/45`

`24/text(Population)`	`= 18/45`
`:.\ text(Population)`	`= (24 xx 45)/18`
	`= 60`

GEOMETRY, FUR1 2012 VCAA 5 MC

The rectangle shown below is 54 cm high and 20 cm wide.

The rhombuses drawn inside the rectangle are all the same size and shape.

The size of the angle `theta`, in the shaded rhombus, is closest to

A. `34°`

B. `45°`

C. `56°`

D. `58°`

E. `67°`

Show Answers Only

`D`

Show Worked Solution

`text(Diagonals of shaded rhombus are,)`

`54/3 = 18\text (cm), and\ 20/2 = 10\ text(cm)`

`:.\ text (Rhombus is 4 right-angled triangles.)`

`theta`	`= 2x`
`tan x`	`= 5/9`
`x`	`= 29.054…°`
`:. theta`	`= 58.109…°`

`=> D`

GEOMETRY, FUR1 2009 VCAA 8 MC

A hose with a circular cross-section is 85 metres long.

The outside diameter of the hose is 29 millimetres. Its walls are 2 millimetres thick.

One litre of water occupies a volume of 1000 cm³.

When the hose is full with water, the volume it holds (in litres) is closest to

A. `4`

B. `42`

C. `49`

D. `56`

E. `167`

Show Answers Only

`B`

Show Worked Solution

♦ Mean mark 43%.
MARKER’S COMMENT: A significant number of students calculated the diameter as 27 mm!

`V`	`= pir^2h`
`h`	`= 85\ text(m (given))`
`r`	`= (29 − 4)/2`
	`= 12.5\ text(mm)`
	`= 0.0125\ text(m)`

`∴V`	`= pi × (0.0125)^2 × 85`
	`= 0.0417… \ text(m³)`
	`= 41.7… \ text(L)`

`=> B`

CORE*, FUR1 2009 VCAA 8 MC

A patient takes 15 milligrams of a prescribed drug at the start of each day.

Over the next 24 hours, 85% of the drug in his body is used. The remaining 15% stays in his body.

Let `D_n` be the number of milligrams of the drug in the patient’s body immediately after taking the drug at the start of the `n`th day.

A difference equation for determining `D_(n+1)`, the number of milligrams in the patient’s body immediately after taking the drug at the start of the `n+1`th day, is given by

A. `D_(n + 1) = 85 D_n + 15`	`D_1 = 15`
B. `D_(n + 1) = 0.85 D_n + 15`	`D_1 = 15`
C. `D_(n + 1)= 0.15 D_n + 15`	`D_1 = 15`
D. `D_(n + 1)= 0.15 D_n + 0.85`	`D_1 = 15`
E. `D_(n + 1)= 15 D_n + 85`	`D_1 = 15`

Show Answers Only

`C`

Show Worked Solution

`D_1=15`

♦♦ Mean mark 34%.

`text(85% of the drug is used up before the second dose.)`

`D_2`	`=0.15 D_1 + 15\ \ \ text{(drug left from 1st day + new dose)}`
`D_3`	`= 0.15 D_2 + 15\ \ \ text{(drug left from 2nd day + new dose)}`
	`vdots`
`D_(n+1)`	`=0.15 D_n+15`

`=> C`

CORE*, FUR1 2009 VCAA 6 MC

The `n`th term of a sequence is given by `t_n = 100 − 20n`, where `n = 1, 2, 3, 4\ . . .`

A difference equation that generates the same sequence is

A. `t_(n +1)= 100 - 20t_n`	`t_1 = 80`
B. `t_(n+1) = 100t_n - 20`	`t_1 = 1`
C. `t_(n+1) = 80t_n`	`t_1 = 80`
D. `t_(n+1) = 100 - t_n`	`t_1 = 20`
E. `t_(n+1) = t_n - 20`	`t_1 = 80`

Show Answers Only

`E`

Show Worked Solution

`text(By elimination,)`

♦♦ Mean mark 33%.
MARKERS’ COMMENT: Many students clearly did not reason their way through the solution by generating a few terms. This is an efficient and effective strategy.

`t_n`	`= 100 − 20_n text( for ) n = 1, 2, …`
`t_1`	`= 100 \ – 20 × 1`
	`= 80`

`∴\ text(Eliminate)\ B\ text(and)\ D`

`t_2`	`= 100 − 20 × 2`
	`= 60`

`∴\ text(Eliminate)\ A\ text(and)\ C`

`=> E`

PATTERNS, FUR1 2009 VCAA 5 MC

On Monday morning, Jim told six friends a secret. On Tuesday morning, those six friends each told the secret to six other friends who did not know it. The secret continued to spread in this way on Wednesday, Thursday and Friday mornings.

The total number of people (not counting Jim) who will know the secret on Friday afternoon is

A. `259`

B. `1296`

C. `1555`

D. `7776`

E. `9330`

Show Answers Only

`E`

Show Worked Solution

`text(Sequence is 6, 6 × 6, 6 × 6 × 6, …)`

♦♦ Mean mark 25%.
MARKERS’ COMMENT: Over 50% of students calculated the 5th term and not the sum of the first 5 terms!

`text(GP where)\ \ \ a`	`= 6, and`
`r`	`= 6 `

`S_n=`	`text(total number who know the secret)`
	`text(on the afternoon of day)\ n`

`text(On Friday,)\ \ n = 5`

`S_n`	`= (a (r^n − 1)) / (r −1)`
`:.S_5`	`= (6(6^5 −1)) / (6 −1)`
	`= 9330`

`=> E`

PATTERNS, FUR1 2011 VCAA 9 MC

A toy train track consists of a number of pieces of track which join together.

The shortest piece of the track is 15 centimetres long and each piece of track after the shortest is 2 centimetres longer than the previous piece.

The total length of the complete track is 7.35 metres.

The length of the longest piece of track, in centimetres, is

A. `21`

B. `47`

C. `49`

D. `55`

E. `57`

Show Answers Only

`D`

Show Worked Solution

`text(Sequence is 15, 17, 19 , . . .)`

`text(AP where)\ \ \ a`	`= 15, and`
`d`	`= 2`

`S_n`	`= n / 2 [ 2a + (n – 1) d ] = 735\ text(cm)`
`:. 735`	`= n / 2 [ 2 xx 15 + (n – 1) 2 ]`
	`= n / 2 [ 30 + 2n – 2 ]`
	`= n^2 + 14n`
`0`	`= n^2 + 14n – 735`

`text(Using the quadratic formula)`

`n`	`= {–14 +- sqrt (14^2 – 4. 1. (–735))} / (2 xx 1)`
	`= (–14 +-56) / 2`
	`= 21 \ \ \ \ (n > 0)`

`:.\ text(Longest piece of track)`	`= a + (n – 1) d`
	`= 15 + (21 – 1) 2`
	`= 55\ text(cm)`

`=> D`

PATTERNS, FUR1 2011 VCAA 8 MC

The first three terms of an arithmetic sequence are `1, 3, 5 . . .`

The sum of the first `n` terms of this sequence, `S_n`, is

A. `S_n = n^2`

B. `S_n = n^2 - n`

C. `S_n = 2n`

D. `S_n = 2n - 1`

E. `S_n = 2n + 1`

Show Answers Only

`A`

Show Worked Solution

`text(Sequence is 1, 3, 5 , . . .)`

♦ Mean mark 38%.

`text(AP where)\ \ \ a`	`= 1, and`
`d`	`= 3 – 1 = 2`

`S_n`	`= n / 2 [ 2a + (n – 1) d ]`
	`= n / 2 [ 2 xx 1 + (n – 1) 2 ]`
	`= n / 2 [ 2 + 2n – 2 ]`
	`= n^2`

`=> A`

PATTERNS, FUR1 2011 VCAA 6 MC

For which one of the following geometric sequences is an infinite sum not able to be determined?

A. `4, 2, 1, 1 / 2\ . . .`

B. `1, 2, 4, 8\ . . .`

C. `–4, 2, –1, 1 / 2\ . . .`

D. `1, 1 / 2, 1 / 4, 1 / 8\ . . .`

E. `–1, 1/2, –1 / 4, 1 / 8\ . . .`

Show Answers Only

`B`

Show Worked Solution

`text(An infinite sum can only be determined when)`

`|\ r\ | <= 1`

♦ Mean mark 50%.

`text(In A,)\ \ \ r = t_2 / t_1 = 1 / 2`

`text(In B,)\ \ \ r = 2 / 1 = 2`

`text(In C,)\ \ \ r = 2 / (–4) = – 1 / 2`

`text(In D,)\ \ \ r = 1 / 2`

`text(In E,)\ \ \ r = – 1 / 2`

`=> B`

CORE*, FUR1 2011 VCAA 5 MC

The difference equation

`t_(n+2) = t_(n+1) + t_n` where `t_1 = a` and `t_2 = 7`

generates a sequence with `t_5 = 27`.

The value of `a` is

A. 0

B. 1

C. 2

D. 3

E. 4

Show Answers Only

`D`

Show Worked Solution

`t_(n+2) = t_(n+1) + t_n\ \ text(where)\ \ t_1 = a\ \ text(and)\ \ t_2 = 7`

`text(Calculating this equation from)\ \ n = 1,`

`t_3 `	` = t_2 + t_1`
	` = 7 + a`
`t_4 `	` = t_3 + t_2`
	` = 7 + a + 7`
	` = 14 + a`
`t_5`	` = t_4 + t_3`
`:. 27 `	` = 14 + a + 7 + a`
`2a `	` = 6`
`a `	` = 3`

`=> D`

GEOMETRY, FUR1 2012 VCAA 6 MC

A cylinder of radius `R` and height `H` has volume `V.`

The volume of a cylinder with radius `3R` and height `3H` is

A. `3V`

B. `6V`

C. `9V`

D. `27V`

E. `81V`

Show Answers Only

`D`

Show Worked Solution

`V = pi xx R^2 xx H`

♦ Mean mark 47%.

`text(Let)\ V_1\ text(be the volume of the new cylinder where)`

`r= 3R quad text (and) quad h= 3H`

`V_1`	`= pi xx (3R)^2 xx (3H)`
	`= 27 xx (pi xx R^2 xx H)`
	`= 27V`

`rArr D`

Statistics, STD2 S1 2007 HSC 21 MC

This set of data is arranged in order from smallest to largest.

`5, \ 6, \ 11, \ x, \ 13, \ 18, \ 25`

The range is six less than twice the value of `x`.

Which one of the following is true?

The median is 12 and the interquartile range is 7.
The median is 12 and the interquartile range is 12.
The median is 13 and the interquartile range is 7.
The median is 13 and the interquartile range is 12.

Show Answers Only

`D`

Show Worked Solution

`5, 6, 11, x, 13, 18, 25`

`text(Range)`	`= 2x – 6`
`25 – 5`	`= 2x – 6`
`2x`	`= 26`
`x`	`= 13`
`:.\ text(Median)`	`= 13`

`Q_1 = 6\ \ \ \ \ Q_3 = 18`

`:.\ text(IQR) = 12`

`=> D`

Algebra, STD2 A1 2007 HSC 19 MC

Which of the following correctly expresses `T` as the subject of `B = 2pi (R + T/2)`?

`T = B/pi-2R`
`T = B/pi-R`
`T = 2R-B/pi`
`T = B/(4pi)-R/2`

Show Answers Only

`A`

Show Worked Solution

`B`	`= 2pi (R + T/2)`
`B/(2pi)`	`= R + T/2`
`T/2`	`= B/(2pi)-R`
`T`	`= B/pi-2R`

`=> A`

Statistics, STD2 S1 2007 HSC 17 MC

Ms Wigginson decided to survey a sample of 10% of the students at her school.

The school enrolment is shown in the table.

She surveyed the same number of students in each year group.

How would the numbers of students surveyed in Year 10 and Year 11 have changed if Ms Wigginson had chosen to use a stratified sample based on year groups?

Increased in both Year 10 and Year 11
Decreased in both Year 10 and Year 11
Increased in Year 10 and decreased in Year 11
Decreased in Year 10 and increased in Year 11

Show Answers Only

`C`

Show Worked Solution

`text(Total students surveyed)`

`= text(10%) xx 1200`

`= 120`

`text(Students surveyed per year group)`

`= 120/6`

`= 20`

`text(A stratified sample would have sampled 10%)`

`text(of each year group.)`

`text(In Year 10, 10%) xx 230 = 23`

`text(In Year 11, 10%) xx 150 = 15`

`:.\ text(More students sampled in Year 10 and)`

`text(less in Year 11.)`

`=> C`

Algebra, STD2 A4 2007 HSC 15 MC

If pressure (`p`) varies inversely with volume (`V`), which formula correctly expresses `p` in terms of `V` and `k`, where `k` is a constant?

`p = k/V`
`p = V/k`
`p = kV`
`p = k + V`

Show Answers Only

`A`

Show Worked Solution

`p prop 1/V`

`p = k/V`

`=> A`

GEOMETRY, FUR1 2014 VCAA 6-7 MC

A cross-country race is run on a triangular course. The points `A, B` and `C` mark the corners of the course, as shown below.

The distance from `A` to `B` is 2050 m.

The distance from `B` to `C` is 2250 m.

The distance from `A` to `C` is 1900 m.

The bearing of `B` from `A` is 140°.

Part 1

The bearing of `C` from `A` is closest to

A. `032°`

B. `069°`

C. `192°`

D. `198°`

E. `209°`

Part 2

The area within the triangular course `ABC`, in square metres, can be calculated by evaluating

A. `sqrt (3100 xx 1200 xx 1050 xx 850)`

B. `sqrt (3100 xx 2250 xx 2050 xx 1900)`

C. `sqrt (6200 xx 4300 xx 4150 xx 3950)`

D. `1/2 xx 2050 xx 2250 xx sin\ (140^@)`

E. `1/2 xx 2050 xx 2250 xx sin\ (40^@)`

Show Answers Only

`text(Part 1:)\ E`

`text(Part 2:)\ A`

Show Worked Solution

`text(Part 1)`

♦ Mean mark 43%.

`text(Using the cosine rule:)`

`cos ∠CAB`	`= ((AC)^2 + (AB)^2 – (CB)^2)/(2 xx AC xx AB)`
	`= (1900^2 + 2050^2 – 2250^2)/(2 xx 1900 xx 2050)`
	`= 0.3530…`
`/_ CAB`	`= 69.32…°`

`∴\ text(Bearing of C from A)`

`= 140 + 69.32…`

`= 209.32…°`

`=>E`

`text(Part 2)`

`text(Using Heron’s rule,)`

`text{Semi-perimeter (s)}`

`= (1900 + 2050 + 2250)/2`

`= 3100`

`∴ A`	`= sqrt{s (s-a)(s-b)(s-c)}`
	`= sqrt{3100 xx 1200 xx 1050 xx 850}`

`=> A`

CORE*, FUR1 2014 VCAA 9 MC

Sam takes a tablet containing 200 mg of medicine once every 24 hours.

Every 24 hours, 40% of the medicine leaves her body. The remaining 60% of the medicine stays in her body.

Let `D_n` be the number of milligrams of the medicine in Sam’s body immediately after she takes the `n`th tablet.

The difference equation that can be used to determine the number of milligrams of the medicine in Sam’s body immediately after she takes each tablet is shown below.

`D_(n + 1) = 0.60D_n + 200,\ \ \ \ \ \ D_1 = 200`

Which one of the following statements is not true?

A. The number of milligrams of the medicine in Sam’s body never exceeds 500.

B. Immediately after taking the third tablet, 392 mg of the medicine is in Sam’s body.

C. The number of milligrams of the medicine that leaves Sam’s body during any 24-hour period will always be less than 200.

D. The number of milligrams of the medicine that leaves Sam’s body during any 24-hour period is constant.

E. If Sam stopped taking the medicine after the fifth tablet, the amount of the medicine in her body would drop to below 200 mg after a further 48 hours.

Show Answers Only

`D`

Show Worked Solution

`text(Consider A:)`

♦ Mean mark 44%.

`text(Maximum medicine in body when)`

`D_(n+1)`	`= D_n`
`x`	`= 0.6x + 200`
`0.4x`	`= 200`
`x`	`=500,\ =>\ text(A true)`

`text(Consider B:)`

`D_1 = 200`

`D_2 = 0.6(200) + 200 = 320`

`D_3 = 0.6(320) + 200 = 392,\ =>\ text(B true)`

`text(Consider C:)`

`text{Max medicine never exceeds 500 mg (from A),}\ =>\ text(C true)`

`text(Consider D:)`

`text(Medicine leaving body is 40% of a changing number,)\ =>\ text(D not true)`

`text(Consider E:)`

`D_4 = 0.6(392) + 200 = 435.2`

`D_5 = 0.6(435.2) + 200 = 461.12`

`D_6 = 0.6(461.12) = 276.67`

`D_7 = 0.6(276.672) = 166.00,\ =>\ text(E true)`

`=>D`

PATTERNS, FUR1 2014 VCAA 8 MC

The first term of a geometric sequence is `a`, where `a < 0`.
The common ratio of this sequence, `r`, is such that `r < –1`.
Which one of the following graphs best shows the first 10 terms of this sequence?

Show Answers Only

`B`

Show Worked Solution

`text(By elimination)`

♦ Mean mark 40%.

`a < 0. text(Cannot be C.)`

`r < -1. text(Successive terms change sign and)`

`text(increase exponentially.)`

`text(Cannot be A, D, or E.)`

`=> B`

CORE, FUR1 2014 VCAA 13 MC

The time series plot below shows the hours of sunshine per day at a particular location for 16 consecutive days.

The three median method is used to fit a trend line to the data.

The slope of this trend line will be closest to

A. `–0.7`

B. `–0.2`

C. `0.0`

D. `0.2`

E. `0.7`

Show Answers Only

`C`

Show Worked Solution

`text(16 data points)`

♦ Mean mark 37%.

`text{Divide into 5, 6, 5 (3 groups)}`

`text(Median points for group)`

`text{Lower (3, 8)}`

`text{Upper (14, 8)}`

`text{Trend line from (3, 8) to (14, 8) is}`

`text(horizontal.)`

`∴\ text(Slope) = 0`

`=> C`

`text(Total after 3rd year)`	`= 3000(1.065)^3 \ \ \ \ \ (n =3)`
	`= $3623.848875…`
	`= $3623.85 \ \ (text(2 d.p.))`
`text(Total after 4th year)`	`= 3000(1.065)^4 \ \ \ \ \ (n = 4)`
	`= $3859.399…`
	`= $3859.40 \ \ (text(2 d.p.))`

`text(Using)\ \ I`	`= (PrT) / 100`
`1800`	`= (3000 xx r xx 5) / 100`
`r`	`= (1800 xx 100) / (3000 xx 5)`
	`= 12.0`

`text(Perpetuity)\ xx text(5.9%)`	`= 26\ 000`
`:.\ text(Perpetuity)`	`= (26\ 000) / text(5.9%)`
	`= 440\ 677.96…`

`text(Amount owing)`	`= 3500 – 500`
	`= 3000`

`text(Total repayment)`	`= 80 xx 5 xx 12`
	`= 4800`

`text(Interest paid)`	`= 4800 – 3000`
	`= 1800`

`text{Total payment ($) per year}`	`= 500 xx 52`
	`= 26\ 000`