SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Algebraic Techniques, SMB-066

Factorise the expression  `-12y^2+18y-6`  (2 marks)

Show Answers Only

`6(2y-1)(1-y)\ \ text(or)\ \ 6(1-2y)(y-1)`

Show Worked Solution

`-12y^2+18y-6=-6(2y^2-3y+1)`
 

`-6(2y^2-3y+1)=>\ \ ` `text{P}` `=2xx1=2`
  `text{S}` `=-3`
  `text{F}` `=-2,-1`

 

`-6(2y^2-3y+1)` `=(-6(2y-1)(2y-2))/2`
  `=-6(2y-1)(y-1)`
  `=6(2y-1)(1-y)\ \ text(or)\ \ 6(1-2y)(y-1)`

Algebraic Techniques, SMB-065

Fully factorise the expression  `6y^2+10y-4`  (2 marks)

Show Answers Only

`2(3y-1)(y+2)`

Show Worked Solution

`6y^2+10y-4=2(3y^2+5y-2)`
 

`2(3y^2+5y-2)=>\ \ ` `text{P}` `=3xx-2=-6`
  `text{S}` `=5`
  `text{F}` `=-1,6`

 

`2(3y^2+5y-2)` `=(2(3y-1)(3y+6))/3`
  `=2(3y-1)(y+2)`

Algebra, STD2 A4 2022 HSC 24

A student believes that the time it takes for an ice cube to melt (`M` minutes) varies inversely with the room temperature `(T^@ text{C})`. The student observes that at a room temperature of `15^@text{C}` it takes 12 minutes for an ice cube to melt.

  1. Find the equation relating `M` and `T`.   (2 marks)

  2. By first completing this table of values, graph the relationship between temperature and time from `T=5^@C` to `T=30^@ text{C}.`   (2 marks)

\begin{array} {|l|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ T\ \  \rule[-1ex]{0pt}{0pt} & \ \ \ 5\ \ \  & \ \ 15\ \ \  & \ \ \ 30\ \ \  \\
\hline
\rule{0pt}{2.5ex} \ \ M\ \ \rule[-1ex]{0pt}{0pt} & & & \\
\hline
\end{array}

 
           

Show Answers Only

a.  `M prop 1/T \ \ =>\ \ M=k/T`

  `12` `=k/15`
  `k` `=15 xx 12=180`

 
`:.M=180/T`

b.   

\begin{array} {|l|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ T\ \  \rule[-1ex]{0pt}{0pt} & \ \ \ 5\ \ \  & \ \ 15\ \ \  & \ \ 30\ \  \\
\hline
\rule{0pt}{2.5ex} \ \ M\ \ \rule[-1ex]{0pt}{0pt} & 36 & 12 & 6 \\
\hline
\end{array}

 

     

Show Worked Solution
a.    `M` `prop 1/T`
  `M` `=k/T`
  `12` `=k/15`
  `k` `=15 xx 12`
    `=180`

 
`:.M=180/T`


♦♦ Mean mark part (a) 29%.

b.   

\begin{array} {|l|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ T\ \  \rule[-1ex]{0pt}{0pt} & \ \ \ 5\ \ \  & \ \ 15\ \ \  & \ \ 30\ \  \\
\hline
\rule{0pt}{2.5ex} \ \ M\ \ \rule[-1ex]{0pt}{0pt} & 36 & 12 & 6 \\
\hline
\end{array}

 

     


♦ Mean mark 44%.

Measurement, STD2 M6 2022 HSC 26

The diagram shows two right-angled triangles, `ABC` and `ABD`,

where `AC=35 \ text{cm},BD=93 \ text{cm}, /_ACB=41^(@)` and `/_ADB=theta`.
 
     

Calculate the size of angle `theta`, to the nearest minute.  (4 marks)

Show Answers Only

`19^@6^{′}`

Show Worked Solution

`text{In}\ Delta ABC:`

`cos 41^@` `=35/(BC)`  
`BC` `=35/(cos 41^@)`  
  `=46.375…`  

 
`angle BCD = 180-41=139^@`
 

`text{Using sine rule in}\ Delta BCD:`

`sin theta/(46.375)` `=sin139^@/93`  
`sin theta` `=(sin 139^@ xx 46.375)/93`  
`:.theta` `=sin^(-1)((sin 139^@ xx 46.375)/93)`  
  `=19.09…`  
  `=19^@6^{′}\ \ text{(nearest minute)}`  

♦ Mean mark 50%.

Algebra, STD2 A2 2022 HSC 14 MC

Which of the following correctly expresses `x` as the subject of  `y=(ax-b)/(2)` ?

  1. `x=(2y+b)/(a)`
  2. `x=(y+b)/(2a)`
  3. `x=(2y)/(a)+b`
  4. `x=(y)/(2a)+b`
Show Answers Only

`A`

Show Worked Solution
`y` `=(ax-b)/(2)`  
`2y` `=ax-b`  
`ax` `=2y+b`  
`:.x` `=(2y+b)/a`  

 
`=>A`

Functions, 2ADV F2 2021 HSC 19

Without using calculus, sketch the graph of  `y = 2 + 1/(x + 4)`, showing the asymptotes and the `x` and `y` intercepts.  (3 marks)

Show Answers Only

Show Worked Solution

`text(Asymptotes:)\ x = -4`

`text(As)\ \ x -> ∞, y -> 2`

`ytext(-intercept occurs when)\ \ x = 0:`

`y = 2.25`

`xtext(-intercept occurs when)\ \ y = 0:`

`2 + 1/(x + 4) = 0 \ => \ x = -4.5`
 

Measurement, STD2 M6 2021 HSC 32

A right-angled triangle  `XYZ`  is cut out from a semicircle with centre `O`. The length of the diameter  `XZ`  is 16 cm and  `angle YXZ`  = 30°, as shown on the diagram.
 


 

  1. Find the length of  `XY`  in centimetres, correct to two decimal places.  (2 marks)

  2. Hence, find the area of the shaded region in square centimetres, correct to one decimal place.  (3 marks)

Show Answers Only
  1. `13.86 \ text{cm}`
  2. `45.1 \ text{cm}^2`
Show Worked Solution

 

a.    `cos 30^@` `=(XY)/16`
  `XY` `= 16 \ cos 30^@`
    `= 13.8564`
    `= 13.86 \ text{cm (2 d.p.)}`

 

b.    `text{Area of semi-circle}` `= 1/2 times pi r^2`
    `= 1/2 pi times 8^2`
    `= 100.531 \ text{cm}^2`

♦ Mean mark part (b) 36%.
`text{Area of} \ Δ XYZ` `= 1/2 ab\ sin C`  
  `= 1/2 xx 16 xx 13.856 xx sin 30^@`  
  `= 55.42 \ text{cm}^2`  

 

`:. \ text{Shaded Area}` `= 100.531-55.42`  
  `= 45.111`  
  `= 45.1 \ text{cm}^2 \ \ text{(1 d.p.)}`  

Functions, 2ADV F1 2020 HSC 24

The circle of  `x^2-6x + y^2 + 4y-3 = 0`  is reflected in the `x`-axis.

Sketch the reflected circle, showing the coordinates of the centre and the radius.  (3 marks)

Show Answers Only

Show Worked Solution
`x^2-6x + y^2 + 4y-3` `= 0`
`x^2-6x + 9 + y^2 + 4y + 4-16` `= 0`
`(x-3)^2 + (y + 2)^2` `= 16`

 
`=>\  text{Original circle has centre (3, − 2), radius = 4}`

`text(Reflect in)\ xtext(-axis):`

♦ Mean mark 48%.

`text{Centre (3, − 2) → (3, 2)}`
 

Algebra, STD2 A1 2019 HSC 11 MC

Which of the following correctly expresses `y` as the subject of the formula  `3x-4y-1 = 0`?

  1.  `y = 3/4 x-1`
  2.  `y = 3/4 x + 1`
  3.  `y = (3x-1)/4`
  4.  `y = (3x + 1)/4`
Show Answers Only

`C`

Show Worked Solution

♦ Mean mark 50%.

`3x-4y-1` `= 0`
`4y` `= 3x-1`
`:. y` `= (3x-1)/4`

 
`=> C`

Plane Geometry, 2UA 2018 HSC 13b

In `Delta ABC`, sides `AB` and `AC` have length 3, and `BC` has length 2. The point `D` is chosen on `AB` so that `DC` has length 2.
 

  1. Prove that `Delta ABC` and `Delta CBD` are similar.  (2 marks)

  2. Find the length `AD`.  (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `5/3`
Show Worked Solution

i.    `text(Prove)\ \ Delta ABC\ text(|||)\ Delta CBD`

`Delta ABC\ text{is isosceles:}`

`/_ ABC = /_ ACB qquad text{(angles opposite equal sides)}`

`Delta CBD\ text{is isosceles:}`

`/_ CBD = /_ CDB qquad text{(angles opposite equal sides)}`

 
`text{Since}\ \ /_ ABC =  /_ CBD`

`:. Delta ABC\ text(|||)\ Delta CDB qquad text{(equiangular)}`
 

ii.   `text(Using ratios of similar triangles)`

`(DB)/(CB)` `= (BC)/(AC)`
`{(3-AD)}/2` `= 2/3`
`3-AD` `= 4/3`
`:. AD` `= 5/3`

 

Plane Geometry, 2UA 2018 HSC 12c

The diagram shows the square `ABCD`. The point `E` is chosen on `BC` and the point `F` is chosen on `CD` so that  `EC = FC`.
 

  1. Prove that `Delta ADF` is congruent to `Delta ABE`.   (2 marks)

  2. The side length of the square is 14 cm and `EC` has length 4 cm. Find the area of  `AECF`.   (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `56\ text(cm)^2`
Show Worked Solution

i.    `AB = AD\ \ text{(sides of a square)}`

`DF = DC-CF`

`BE = BC-CE`

`text{Since}\ CE = CF\ \ text{(given), and}\ DC = BC\ \ text{(sides of a square)}`

`=> DF = BE`

`=> /_ ADF = /_ ABE = 90^@`

`:. Delta ADF \equiv Delta ABE\ \ text{(SAS)}`

 

ii.   `text(Area of)\ Delta ABE` `= 1/2 xx 14 xx 10`
    `= 70\ text(cm)^2`

 
`:.\ text(Area of)\ AECF`

`= text(Area of)\ ABCD-(2 xx 70)`

`= (14 xx 14)-140`

`= 56\ text(cm)^2`

Measurement, STD2 M6 2018 HSC 30c

The diagram shows two triangles.

Triangle `ABC` is right-angled, with  `AB = 13 text(cm)`  and  `/_ABC = 62°`.

In triangle  `ACD, \ AD = x\ text(cm)`  and  `/_DAC = 40°`. The area of triangle  `ACD`  is 30 cm².
 

 
What is the value of `x`, correct to one decimal place?  (3 marks)

Show Answers Only

`8.1\ text{cm  (1 d.p.)}`

Show Worked Solution

`text(Find)\ AC:`

♦ Mean mark 39%.

`sin62°` `= (AC)/13`
`AC` `= 13 xx sin62°`
  `= 11.478…`

 
`text(Using the sine rule in)\ DeltaACD :`

`text(Area)` `= 1/2 xx AC xx AD xx sin40°`
`30` `= 1/2 xx 11.478… xx x xx sin40°`
`:.x` `= (30 xx 2)/(11.478… xx sin40°)`
  `= 8.13…`
  `= 8.1\ text{cm  (1 d.p.)}`

Algebra, STD2 A1 2018 HSC 28b

Solve the equation  `(2x)/5 + 1 = (3x + 1)/2`, leaving your answer as a fraction.  (3 marks)

Show Answers Only

`5/11`

Show Worked Solution

♦ Mean mark 35%.

`underbrace{(2x)/5 + 1}_text(multiply x10)` `=underbrace{(3x + 1)/2}_text(multiply x10)`
`4x + 10` `= 15x + 5`
`11x` `= 5`
`x` `= 5/11`

Functions, 2ADV F1 2018 HSC 3 MC

What is the `x`-intercept of the line  `x + 3y + 6 = 0`?

  1. `(-6, 0)`
  2. `(6, 0)`
  3. `(0, -2)`
  4. `(0, 2)`
Show Answers Only

`A`

Show Worked Solution

`x text(-intercept occurs when)\ y = 0:`

`x + 0 + 6` `= 0`
`x` `= -6`

 
`:. x text{-intercept is}\  (-6, 0)`

`=>  A`

Linear Functions, 2UA 2018 HSC 2 MC

The point  `R(9, 5)`  is the midpoint of the interval  `PQ`, where `P` has coordinates  `(5, 3).`
 

What are the coordinates of  `Q`?

  1. `(4, 7)`
  2. `(7, 4)`
  3. `(13, 7)`
  4. `(14, 8)`
Show Answers Only

`C`

Show Worked Solution

`text(Using the midpoint formula):`

`(x_Q + x_P)/2` `= x_R` `(y_Q + y_P)/2` `= y_R`
`(x_Q + 5)/2` `= 9` `(y_Q + 3)/2` `= 5`
`x_Q` `= 13` `y_Q` `= 7`

 
`:. Q\ text(has coordinates)\ (13, 7).`

`=>  C`

Measurement, STD2 M6 2018 HSC 12 MC

The diagram shows a triangle with side lengths 8 m, 9 m and 10m.
 


 

What is the value of `theta`, marked on the diagram, to the nearest degree?

  1. 49°
  2. 51°
  3. 59°
  4. 72°
Show Answers Only

`text(D)`

Show Worked Solution

`text(Using the cosine rule:)`

`costheta` `= (8^2 + 9^2 – 10^2)/(2 xx 8 xx 9)`
  `= 0.3125`
`:.theta` `= cos^(−1)(0.3125)`
  `= 71.790…^@`

 
`=>D`

Plane Geometry, 2UA 2017 HSC 15a

The triangle `ABC` is isosceles with  `AB = AC`  and the size of `/_BAC` is `x^@`.

Points `D` and `E` are chosen so that `Delta ABC, Delta ACD` and `Delta ADE` are congruent, as shown in the diagram.
 

Find the value of `x` for which `AB` is parallel to `ED`, giving reasons.  (3 marks)

Show Answers Only

`x = 36`

Show Worked Solution

`text(All base angles) = 1/2(180-x)\ \ text{(Angle sum of}\ Delta text{)}`

`text(If)\ \ AB\ text(||)\ ED,`

`/_ BAD` `= /_ ADE\ \ \ text{(alternate angles)}`
`2x` `= 1/2 (180-x)`
`4x` `= 180-x`
`5x` `= 180`
`x` `= 36^{\circ}`

Functions, 2ADV F1 2017 HSC 2 MC

Which expression is equal to  `3x^2-x-2`?

  1. `(3x-1) (x + 2)`
  2. `(3x + 1) (x-2)`
  3. `(3x-2) (x + 1)`
  4. `(3x + 2) (x-1)`
Show Answers Only

`D`

Show Worked Solution

`3x^2-x-2= (3x + 2) (x-1)`

`=>  D`

Functions, 2ADV F1 2017 HSC 1 MC

What is the gradient of the line  `2x + 3y + 4 = 0`?

  1. `-2/3`
  2. `2/3`
  3. `-3/2`
  4. `3/2`
Show Answers Only

`A`

Show Worked Solution
`2x + 3y + 4` `= 0`
`3y` `= -2x-4`
`y` `= -2/3 x-4/3`
`:.\ text(Gradient)` `= -2/3`

 
`=>  A`

Algebra, STD2 A1 2016 HSC 24 MC

Which of the following correctly expresses `Q` as the subject of  `e = iR + Q/C`?

  1. `Q = Ce + CiR`
  2. `Q = Ce-CiR`
  3. `Q = (e + iR)/C`
  4. `Q = (e-iR)/C`
Show Answers Only

`=> B`

Show Worked Solution
`e` `= iR + Q/C`
`Q/C` `= e-iR`
`:. Q` `= C(e-iR)`
  `= Ce-CiR`

 
`=> B`

Measurement, STD2 M7 2016 HSC 16 MC

The width (`W`) of a river can be calculated using two similar triangles, as shown in the diagram.
  

What is the approximate width of the river?

  1. `17.8\ text(m)`
  2. `19.3\ text(m)`
  3. `23.2\ text(m)`
  4. `24.9\ text(m)`
Show Answers Only

`=> A`

Show Worked Solution

`text{Triangles are similar (equiangular)}`

`text(Using similar ratios:)`

`W/(7.1)` `= 20.3/8.1`
`:. W` `= (20.3 xx 7.1)/8.1`
  `= 17.79…`

 
`=> A`

Functions, 2ADV F1 2016 HSC 11a

Sketch the graph of  `(x-3)^2 + (y + 2)^2 = 4.`  (2 marks)

Show Answers Only

Show Worked Solution

`(x-3)^2 + (y + 2)^2 = 4\ \ text(is a circle),`

`text(centre)\ (3, -2),\ text(radius 2.)`
 

Functions, 2ADV F1 2007 HSC 1f

Find the equation of the line that passes through the point `(1, 3)` and is perpendicular to  `2x + y + 4 = 0`.  (2 marks)

Show Answers Only

`x-2y + 7 = 0`

Show Worked Solution
`2x + y + 4` `= 0`
`y` `= -2x-4`

  
`=>\ text(Gradient) = -2`

`:. text(⊥ gradient) = 1/2\ \ \ (m_1 m_2=-1)`
 

`text(Equation of line)\ \ m = 1/2, \ text(through)\ (1, 3):`

`y-y_1` `= m (x-x_1)`
`y-3` `= 1/2 (x-1)`
`y` `= 1/2 x + 5/2`
`2y` `= x + 5`
`:. x-2y + 5` `= 0`

Algebra, STD2 A1 2015 HSC 28d

The formula  `C = 5/9 (F-32)`  is used to convert temperatures between degrees Fahrenheit `(F)` and degrees Celsius `(C)`.

Convert 3°C to the equivalent temperature in Fahrenheit.   (2 marks)

Show Answers Only

`37.4\ text(degrees)\ F`

Show Worked Solution
`C` `= 5/9(F-32)`
`F-32` `= 9/5C`
`F`  `= 9/5C + 32`

 
`text(When)\ \ C = 3,`

`F` `= (9/5 xx 3) + 32`
  `= 37.4\ text(degrees)\ F`

Measurement, STD2 M7 2015 HSC 27a

At a particular time during the day, a tower of height 19.2 metres casts a shadow. At the same time, a person who is 1.65 metres tall casts a shadow 5 metres long.

  

What is the length of the shadow cast by the tower at that time?  (2 marks)

Show Answers Only

`58\ text{m}`

Show Worked Solution

`text(Both triangles have right angles and a common)`

`text(angle to the ground.)`

`:.\ text{Triangles are similar (equiangular)}`

 

`text(Let)\ x =\ text(length of tower shadow)`

`x/5` `= 19.2/1.65\ \ text{(corresponding sides of similar triangles)}`

 
`x` `= (5 xx 19.2)/1.65`  
  `= 58.1818…`  
  `= 58\ text{m  (nearest m)}`  

Algebra, STD2 A1 2015 HSC 24 MC

Consider the equation  `(2x)/3-4 = (5x)/2 + 1`.

Which of the following would be a correct step in solving this equation?

  1. `(2x)/3-3 = (5x)/2`
  2. `(2x)/3 = (5x)/2 + 5`
  3. `2x-4 = (15x)/2 + 3`
  4. `(4x)/6-8 = 5x + 2`
Show Answers Only

`B`

Show Worked Solution
`(2x)/3-4` `= (5x)/2 + 1`
`(2x)/3` `= (5x)/2 + 5`

 
`=>B`

Measurement, STD2 M6 2015 HSC 22 MC

The area of the triangle shown is 250 cm².
 


 

What is the value of `x`, correct to the nearest whole number?

  1. `11`
  2. `18`
  3. `22`
  4. `24`
Show Answers Only

`D`

Show Worked Solution

`text(Using)\ \ \ A = 1/2ab\ sin\ C`

♦ Mean mark 42%.
`250` `= 1/2 xx 30x\ sin\ 44^@`
`250` `= 15x\ sin\ 44 ^@`
`:.x` `= 250/(15\ sin\ 44^@)`
  `= 23.99…\ text(m)`

 
`=>D`

Plane Geometry, 2UA 2004 HSC 2b

In the diagram, `ABC`  is an isosceles triangle with  `AB = AC`  and  `/_BAC = 38^@`. The line `BC` is produced to `D`. 

Find the size of `/_ACD`. Give reasons for your answer.   (2 marks)

Show Answers Only

`109^@`

Show Worked Solution

Plane Geometry, 2UA 2004 HSC 2b Answer

`/_ABC` `= 1/2 (180-38)\ \ \ text{(base angle of isosceles}\ Delta ABC text{)}`
  `= 71^@`

 

`:.\ /_ACD` `= 71 + 38\ \ \ text{(exterior angle of}\ Delta ABC text{)}`
  `= 109^@`

Plane Geometry, 2UA 2005 HSC 5b

The diagram shows a parallelogram `ABCD` with `∠DAB = 120^@`. The side `DC` is produced to `E` so that `AD = BE`.

Prove that `ΔBCE` is equilateral.  (3 marks)

Show Answers Only

`text(See Worked Solutions)`

Show Worked Solution

`BC` `= AD\ text{(opposite sides of parallelogram}\ ABCD)`
`∠BCD` `= 120^@\ text{(opposite angles of parallelogram}\ ABCD)`
`∠BCE` `= 60^@\ (∠DCE\ text{is a straight angle)}`
`∠CEB` `= 60^@\ text{(base angles of isosceles}\ \Delta BCE)`
`∠CBE` `= 60^@\ text{(angle sum of}\ ΔBCE)`

 
`:.ΔBCE\ text(is equilateral)`

Functions, 2ADV F1 2005 HSC 1d

Express  `((2x-3))/2-((x-1))/5`  as a single fraction in its simplest form.  (2 marks)

Show Answers Only

`(8x-13)/10`

Show Worked Solution

`((2x-3))/2-((x-1))/5`

`= (5(2x-3)-2(x-1))/10`

`= (10x-15-2x + 2)/10`

`= (8x-13)/10`

Measurement, STD2 M6 2006 HSC 24b

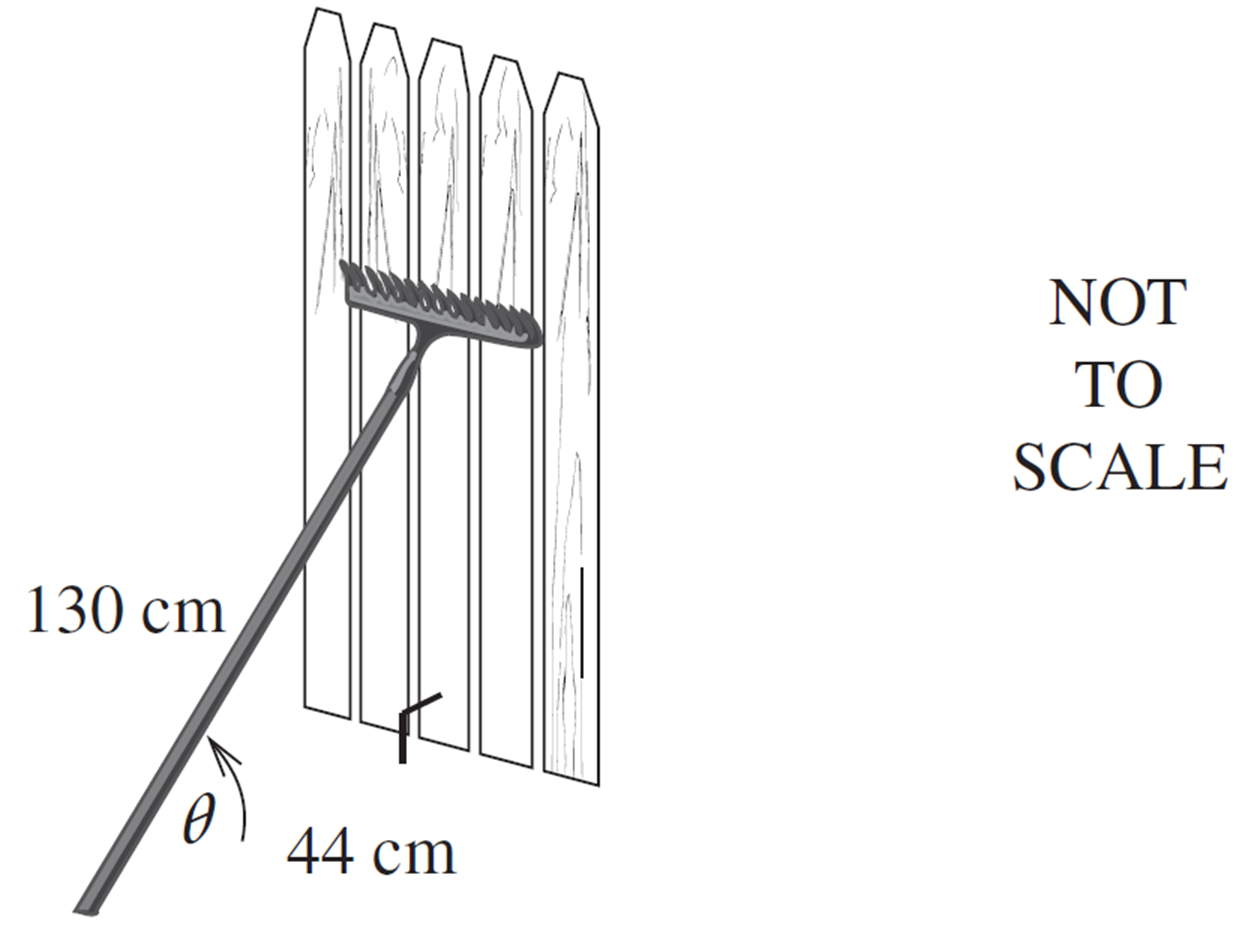
A 130 cm long garden rake leans against a fence. The end of the rake is 44 cm from the base of the fence.

  1. If the fence is vertical, find the value of `theta` to the nearest degree.  (2 marks)
      
          2UG-2006-24b-i

     

  2. The fence develops a lean and the rake is now at an angle of 53° to the ground. Calculate the new distance (`x` cm) from the base of the fence to the head of the rake. Give your answer to the nearest centimetre.  (2 marks)
     
          2UG-2006-24b-ii

Show Answers Only
  1. `text{70°  (nearest degree)}`
  2. `text{109 cm  (nearest cm)}`
Show Worked Solution
i.   

2UG-2006-24b1 Answer
`cos theta` `= 44/130`
  `= 70.216… ^@`
  `= 70^@\ \ \ text{(nearest degree)}`

 

ii.   

2UG-2006-24b2 Answer

`text(Using cosine rule)`

`x^2` `= 130^2 + 44^2-2 xx 130 xx 44 xx cos 53^@`
  `= 11\ 951.23…`
`x` `= 109.32…`
  `= 109\ text{cm  (nearest cm)}`

Algebra, STD2 A1 2005 HSC 24c

Make  `L`  the subject of the equation  `T = 2piL^2`.   (2 marks)

Show Answers Only

`± sqrt(T/(2pi))`

Show Worked Solution
`T` `= 2piL^2`
`L^2` `= T/(2pi)`
`:.L` `= ±sqrt(T/(2pi))`

Measurement, STD2 M6 2006 HSC 9 MC

What is the area of this triangle, to the nearest square metre?
 

 

  1. `text(152 m²)`
  2. `text(283 m²)`
  3. `text(328 m²)`
  4. `text(351 m²)`
Show Answers Only

`C`

Show Worked Solution

`text(Using the Sine rule)`

`A` `= 1/2 ab\ sin C`
  `= 1/2 xx 39 xx 47 xx sin 21^@`
  `=\ text(328.44… m²)`

 
`=>  C`

Functions, 2ADV F1 2004 HSC 1d

 Find integers  `a`  and  `b`  by showing working to expand and simplify 

`(3-sqrt2)^2 = a-b sqrt2`.  (2 marks)

Show Answers Only

`a = 11,\ b = 6`

Show Worked Solution
`(3-sqrt2)^2` `= 9-6 sqrt2 + (sqrt2)^2`
  `= 9-6 sqrt2 + 2`
  `= 11-6 sqrt2`
   
`:.\ a = 11, \ \ b = 6`

Functions, 2ADV F1 2004 HSC 1c

Solve   `(x-5)/3-(x+1)/4 = 5`.   (2 marks)

Show Answers Only

`83`

Show Worked Solution
`(x-5)/3-(x+1)/4` `= 5`
`12((x-5)/3)-12((x+1)/4)` `= 12 xx 5`
`4x-20-3x-3` `= 60`
`x-23` `= 60`
`:. x` `= 83`

Measurement, STD2 M6 2005 HSC 5 MC

Which formula should be used to calculate the distance between Toby and Frankie?

  1. `a/(sin A) = b/(sin B)`
  2. `c^2 = a^2 + b^2`
  3. `A = 1/2 ab\ sinC`
  4. `c^2 = a^2 + b^2 − 2ab\ cosC`
Show Answers Only

`A`

Show Worked Solution

`text(The triangle is not a right-angled triangle,)`

`:.\ text(Not)\ B`

`text(Given the information on the diagram provides)`

`text(2 angles and 1 side, the sine rule will work best.)`

`a/sinA = b/sinB`

`=> A`

Algebra, STD2 A1 2004 HSC 11 MC

If  `d = 6t^2`, what is a possible value of `t` when  `d = 2400`?

  1. `0.05`
  2. `20`
  3. `120`
  4. `400`
Show Answers Only

`B`

Show Worked Solution
`d` `= 6t^2`
`t^2` `= d/6`
`t` `= +- sqrt(d/6)`

 
`text(When)\ \ d = 2400:`

`t` `= +- sqrt(2400/6)`
  `= +- 20`

 
`=> B`

Measurement, STD2 M6 2004 HSC 9 MC

What is the area of the triangle to the nearest square metre?
 

 

  1. `text(102 m²)`
  2. `text(153 m²)`
  3. `text(172 m²)`
  4. `text(178 m²)`
Show Answers Only

`C`

Show Worked Solution

`text(Using sine rule,)`

`text(Area)` `= 1/2 ab sin C`
  `= 1/2 xx 30 xx 20 xx sin 35^@`
  `=172.072…\ text(m²)`

`=> C`

Algebra, STD2 A2 2004 HSC 2 MC

Susan drew a graph of the height of a plant.
  

What is the gradient of the line?

  1. `1`
  2. `5`
  3. `7.5`
  4. `10`
Show Answers Only

`B`

Show Worked Solution

`text(2 points on graph)\ \ (0, 10),\ (1, 15)`

`text(Gradient)` `= (y_2-y_1) / (x_2-x_1)`
  `= (15-10) / (1-0)`
  `= 5`

`=> B`