SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Data Analysis, GEN2 2024 NHT 1

Data was collected to investigate the behaviour of tides in Sydney Harbour.

There are usually two high tides and two low tides each day.

The variables in this study were:

  • Day: the day number in the sample
  • LLT: the height of the lowest low tide for that day (in metres)
  • HHT: the height of the highest high tide for that day (in metres)

Table 1 displays the data collected for a sample of 14 consecutive days in February 2021.

Table 1

\begin{array}{|c|c|c|}
\hline
 \rule{0pt}{2.5ex}\ \ \ \textit{Day}\ \ \ \rule[-1ex]{0pt}{0pt}& \textit{LLT (m)} & \textit{HHT (m)}\\
\hline \rule{0pt}{2.5ex}1 \rule[-1ex]{0pt}{0pt}& 0.43 & 1.65 \\
\hline \rule{0pt}{2.5ex}2 \rule[-1ex]{0pt}{0pt}& 0.49 & 1.55 \\
\hline \rule{0pt}{2.5ex}3 \rule[-1ex]{0pt}{0pt}& 0.55 & 1.44 \\
\hline \rule{0pt}{2.5ex}4 \rule[-1ex]{0pt}{0pt}& 0.61 & 1.42 \\
\hline \rule{0pt}{2.5ex}5 \rule[-1ex]{0pt}{0pt}& 0.68 & 1.42 \\
\hline \rule{0pt}{2.5ex}6 \rule[-1ex]{0pt}{0pt}& 0.73 & 1.42 \\
\hline \rule{0pt}{2.5ex}7 \rule[-1ex]{0pt}{0pt}& 0.72 & 1.42 \\
\hline \rule{0pt}{2.5ex}8 \rule[-1ex]{0pt}{0pt}& 0.65 & 1.47 \\
\hline \rule{0pt}{2.5ex}9 \rule[-1ex]{0pt}{0pt}& 0.57 & 1.55 \\
\hline \rule{0pt}{2.5ex}10 \rule[-1ex]{0pt}{0pt}& 0.48 & 1.64 \\
\hline \rule{0pt}{2.5ex}11 \rule[-1ex]{0pt}{0pt}& 0.39 & 1.74 \\
\hline \rule{0pt}{2.5ex}12 \rule[-1ex]{0pt}{0pt}& 0.30 & 1.83 \\
\hline \rule{0pt}{2.5ex}13 \rule[-1ex]{0pt}{0pt}& 0.25 & 1.90 \\
\hline \rule{0pt}{2.5ex}14 \rule[-1ex]{0pt}{0pt}& 0.22 & 1.92 \\
\hline
\end{array}

  1. For the \(H H T\) values in Table 1:
    1. Calculate the mean, in metres.
    2. Round your answer to one decimal place.   (1 mark)

    3. Calculate the standard deviation, in metres.
    4. Round your answer to three decimal places.    (1 mark)

  2. Use the \(HHT\) data from Table 1 to construct a boxplot on the grid below.    (2 marks)

     

  1. The five-number summary of the \(L L T\) data is shown in Table 2 below.
  2. Table 2

\begin{array}{|c|c|c|c|c|}
\hline \rule{0pt}{2.5ex}\textbf{Minimum} \rule[-1ex]{0pt}{0pt}& \ \ \textbf{Q1} \ \ & \textbf{Median} & \ \  \textbf{Q3} \ \ & \textbf{Maximum} \\
\hline \rule{0pt}{2.5ex}0.22 \rule[-1ex]{0pt}{0pt}& 0.39 & 0.52 & 0.65 & 0.73 \\
\hline
\end{array}

  1. Show that the minimum \(L L T\) value of 0.22 m is not an outlier.    (2 marks)

  2. A least squares line can be used to model the association between \(L L T\) and \(H H T\). In this model, \(H H T\) is the response variable.
  3. Use the data from Table 1 to determine the equation of this least squares line.
  4. Round the values of the intercept and slope to four significant figures.
  5. Write your answers in the boxes provided.    (2 marks)

Show Answers Only

a.i.   \(\text{Mean = 1.6}\)

a.ii.  \(\text{Std dev = 0.185}\)

b.   
               

c.   \(IQR (LLT) = 0.65-0.39=0.26\)

\(\text{Lower fence}\ =Q_1-1.5 \times IQR = 0.39-1.5 \times o.26=0\)

\(\text{Since 0.22 > 0, 0.22 is not an outlier.}\)

d.   \(HHT = 2.130 + (-1.054) \times LLT\)

Show Worked Solution

a.i.   \(\text{Mean = 1.6}\)

a.ii.  \(\text{Std dev = 0.185}\)
 

b.   \(\text{Order \(HHT\) data:}\)

\(1.42, 1.42, 1.42, [1.42], 1,44, 1.47, 1.55 | 1.55, 1.64, 1.65, [1.74],\)

\(1.83, 1.90, 1.92\)

\(\text{High = 1.92, Low = 1.42, \(Q_1=1.42, Q_3=1.74\), Median = 1.55}\)

 
c.   \(IQR (LLT) = 0.65-0.39=0.26\)

\(\text{Lower fence}\ =Q_1-1.5 \times IQR = 0.39-1.5 \times 0.26=0\)

\(\text{Since 0.22 > 0, 0.22 is not an outlier.}\)
 

d.   \(HHT\ \text{is the response \((y)\) variable.}\)

\(\text{By CAS:}\)

\(HHT = 2.130 + (-1.054) \times LLT\)

Data Analysis, GEN1 2024 NHT 9-10 MC

The scatterplot below shows the average annual income, in dollars, plotted against life expectancy, in years, for 42 countries in 2020.

A least squares line has been fitted to the scatterplot.

The coefficient of determination is 0.306.
 

Question 9

The equation of the least squares line is closest to

  1. income \(=-19\,000+345 \times\) life expectancy
  2. income \(=-19\,250+355 \times\) life expectancy
  3. income \(=-19\,500+365 \times\) life expectancy
  4. income \(=-19\,750+375 \times\) life expectancy
  5. income \(=-20\,000+385 \times\) life expectancy

 
Question 10

Which one of the following statements is true?

  1. The value of the correlation coefficient is 0.306
  2. There are more data points above the least squares line than below.
  3. 30.6% of the variation in annual income is not explained by the variation in life expectancy.
  4. The country with the longest life expectancy has a positive residual associated with it.
  5. Using the least squares line to predict the annual income of a country whose citizens have a life expectancy of 54 years is an example of extrapolation.
Show Answers Only

\(\text{Question 9:} \ D \)

\(\text{Question 10:} \ E \)

Show Worked Solution

\(\text{Question 9}\)

\(\text{Using points (58, 2000) and (74, 8000):}\)

\(m=\dfrac{8000-2000}{74-58}=375\)
 

\(\text{Find equation of line:}\)

\(y-y_1\) \(=m(x-x_1)\)  
\(y-2000\) \(=375(x-58) \)  
\(y\) \(=375x-19\,750\)  

 
\(\Rightarrow D\)
 

\(\text{Question 10}\)

\(\text{A life expectancy of  54 years is outside the dataset range}\ \Rightarrow \ \text{extrapolation}\)

\(\Rightarrow E\)

Data Analysis, GEN1 2024 NHT 8 MC

A class investigation considered 20 countries and any association between the birth rate, per 1000 people, and the life expectancy, in years.

Students were given the following table of summary statistics.
 

Scatterplots A, B, C, D and E show attempts by five students to fit the calculated least squares line to a scatterplot of the original data.

Which one of these attempts has been completed correctly?
 

Show Answers Only

\(A\)

Show Worked Solution

\(\text{Find the equation of the LSRL:}\)

\(b=r \times \dfrac{s_y}{s_x} = -0.752 \times \dfrac{4.70}{1.64} = -2.155…\)

\(a=\overline{y}-b\overline{x}=31.5-(-2.16) \times 61.7 = 164.772…\)

\(\text{Calculate key points using LSRL:}\)

\( (59,37.6), (65, 24.6) \)

\(\Rightarrow A\)

Data Analysis, GEN2 2024 VCAA 1

Table 1 lists the Olympic year, \(\textit{year}\), and the gold medal-winning height for the men's high jump, \(\textit{Mgold}\), in metres, for each Olympic Games held from 1928 to 2020. No Olympic Games were held in 1940 or 1944, and the 2020 Olympic Games were held in 2021.

Table 1

\begin{array}{|c|c|}
\hline \quad \textit{year} \quad & \textit{Mgold}\,\text{(m)} \\
\hline 1928 & 1.94 \\
\hline 1932 & 1.97 \\
\hline 1936 & 2.03 \\
\hline 1948 & 1.98 \\
\hline 1952 & 2.04 \\
\hline 1956 & 2.12 \\
\hline 1960 & 2.16 \\
\hline 1964 & 2.18 \\
\hline 1968 & 2.24 \\
\hline 1972 & 2.23 \\
\hline 1976 & 2.25 \\
\hline 1980 & 2.36 \\
\hline 1984 & 2.35 \\
\hline 1988 & 2.38 \\
\hline 1992 & 2.34 \\
\hline 1996 & 2.39 \\
\hline 2000 & 2.35 \\
\hline 2004 & 2.36 \\
\hline 2008 & 2.36 \\
\hline 2012 & 2.33 \\
\hline 2016 & 2.38 \\
\hline 2020 & 2.37 \\
\hline
\end{array}

  1. For the data in Table 1, determine:
  2.  i. the maximum \(\textit{Mgold}\) in metres   (1 mark)

  3. ii. the percentage of \(\textit{Mgold}\) values greater than 2.25 m.   (1 mark)

  4. The mean of these \(\textit{Mgold}\) values is 2.23 m, and the standard deviation is 0.15 m.
  5. Calculate the standardised \(z\)-score for the 2000 \(\textit{Mgold}\) of 2.35 m.   (1 mark)

  6. Construct a boxplot for the \(\textit{Mgold}\) data in Table 1 on the grid below.   (2 marks)

     

  1. A least squares line can also be used to model the association between \(\textit{Mgold}\) and \(\textit{year}\).
  2. Using the data from Table 1, determine the equation of the least squares line for this data set.
  3. Use the template below to write your answer.
  4. Round the values of the intercept and slope to three significant figures.   (2 marks)

     

  1. The coefficient of determination is 0.857
  2. Interpret the coefficient of determination in terms of \(\textit{Mgold}\) and \(\textit{year}\).   (1 mark)

Show Answers Only

a.i.   \(2.39\)

a.ii.  \(50\%\)

b.    \(0.8\)

c.     

d.   
    

e.    \(\text{A coefficient of determination of 85.7% shows the variation in}\)

\(\text{the}\ Mgold\ \text{that is explained by the variation in the }year.\)

Show Worked Solution

a.i.   \(2.39\)

a.ii.  \(\dfrac{11}{22}=50\%\)

b.     \(z\) \(=\dfrac{x-\overline x}{s_x}\)
    \(=\dfrac{2.35-2.23}{0.15}\)
    \(=0.8\)

  
c.    \(Q_2=\dfrac{2.33+2.25}{2}=2.29\)

\(Q_1=2.12, \ Q_3=2.36\)

\(\text{Min}\ =1.94, \ \text{Max}\ =2.39\)
  

d.   \(\text{Using CAS:}\)


  
 

Mean mark (d) 52%.
Mean mark (e) 52%.

e.    \(\text{A coefficient of determination of 85.7% shows the variation in}\)

\(\text{the}\ Mgold\ \text{that is explained by the variation in the }year.\)

Data Analysis, GEN1 2024 VCAA 8 MC

The scatterplot below displays the average number of female athletes per competing nation, females, against the number of the Summer Olympic Games, number, from the first Olympic Games, in 1896, to the 29th Olympic Games, held in 2021.

A least squares line has been fitted to the scatterplot.
 

The equation of the least squares line is closest to

  1. \(females =-4.87+1.02 \times number\)
  2. \( females =-3.39+0.91 \times number\)
  3. \(number =-3.39+0.91 \times females\)
  4. \(number =-0.91+3.39 \times females\)
Show Answers Only

\(B\)

Show Worked Solution

\(\text{LSRL is in the form}\ \ y=a+bx\ \rightarrow \ \ \text{Eliminate C and D}\)

\(\text{Using points}\ (29, 23)\ \text{and}\ (7, 3):\)

\(\text{Gradient}\ =\dfrac{23-3}{29-7}=\dfrac{10}{11} \approx 0.91\)

\(\Rightarrow B\)

Data Analysis, GEN1 2022 VCAA 12-14 MC

The scatterplot below displays the body length, in centimetres, of 17 crocodiles, plotted against their head length, in centimetres. A least squares line has been fitted to the scatterplot. The explanatory variable is head length.
 

Question 12

The equation of the least squares line is closest to

  1. head length = –40 + 7 × body length
  2. body length = –40 + 7 × head length
  3. head length = 168 + 7 × body length
  4. body length = 168 – 40 × head length
  5. body length = 7 + 168 × head length

 
Question 13

The median head length of the 17 crocodiles, in centimetres, is closest to

  1. 49
  2. 51
  3. 54
  4. 300
  5. 345

 
Question 14

The correlation coefficient \(r\) is equal to 0.963

The percentage of variation in body length that is not explained by the variation in head length is closest to

  1. 0.9%
  2. 3.7%
  3. 7.3%
  4. 92.7%
  5. 96.3%
Show Answers Only

\(\text{Question 12}:\ B\)

\(\text{Question 13}:\ B\)

\(\text{Question 12}:\ C\)

Show Worked Solution

\(\text{Question 12}\)

\(\text{Gradient}\ = \dfrac{550-170}{85-30}=6.9\ \ \text{(eliminate D and E)}\)

\(\text{Head length is the explanatory variable  (eliminate A and C)}\)

\(\Rightarrow  B\)

 
\(\text{Question 13}\)

\(\text{Median score}\ =\dfrac{17+1}{2} = 9\text{th score}\)

\(\text{Median head length = 51 cm}\)

\(\Rightarrow B\)


♦ Mean mark (Q13) 51%.

 
\(\text{Question 14}\)

\(\text{Percentage explained by variation in head length}\)

\(r^2 = 0.963^2 = 0.9273 \approx 92.7\% \)

\(\text{Percentage not explained by variation in head length}\)

\(100-92.7 \approx 7.3\%\) 

\(\Rightarrow C\)


♦ Mean mark (Q14) 48%.

Data Analysis, GEN2 2023 VCAA 1

Data was collected to investigate the use of electronic images to automate the sizing of oysters for sale. The variables in this study were:

    • ID: identity number of the oyster
    • weight: weight of the oyster in grams (g)
    • volume: volume of the oyster in cubic centimetres (cm³)
    • image size: oyster size determined from its electronic image (in megapixels)
    • size: oyster size when offered for sale: small, medium or large

The data collected for a sample of 15 oysters is displayed in the table.
 

  1. Write down the number of categorical variables in the table.   (1 mark)

  2. Determine, in grams:
    1. the mean weight of all the oysters in this sample.   (1 mark)

    2. the median weight of the large oysters in this sample.   (1 mark)
  3. When a least squares line is used to model the association between oyster weight and volume, the equation is: 

    1. \(\textit{volume} = 0.780 + 0.953 \times \textit{weight} \)
    1. Name the response variable in this equation.   (1 mark)

    2. Complete the following sentence by filling in the blank space provided.   (1 mark)

      This equation predicts that, on average, each 10 g increase in the weight of an oyster is associated with a ________________ cm³ increase in its volume.
  1. A least squares line can also be used to model the association between an oyster's volume, in cm³, and its electronic image size, in megapixels. In this model, image size is the explanatory variable.
  2. Using data from the table, determine the equation of this least squares line. Use the template below to write your answer. Round the values of the intercept and slope to four significant figures.   (2 marks)

  3. The number of megapixels needed to construct an accurate electronic image of an oyster is approximately normally distributed.
  4. Measurements made on recently harvested oysters showed that:
    • 97.5% of the electronic images contain less than 4.6 megapixels
    • 84% of the electronic images contain more than 4.3 megapixels.
  1. Use the 68-95-99.7% rule to determine, in megapixels, the mean and standard deviation of this normal distribution.   (2 marks)

Show Answers Only

a.    \(\text{Categorical variables = 2 (ID and size)}\)

b.i.  \(\text{Mean weight}\ = \dfrac{\text{sum of oyster weights}}{15} = \dfrac{171.3}{15} = 11.42 \)

b.ii.  \(\text{Median}\ = 11.4 \)

c.i.   \(\text{Volume}\)

c.ii.  \(\text{Increase}\ = 0.953 \times 10 = 9.53\ \text{cm}^{3} \)

d.    \(\text{Volume}\ = 0.002857 + 2.571 \times \text{image size} \)

e.    \(s_x = 0.1 \)

\(\bar x = 4.4\) 

Show Worked Solution

a.    \(\text{Categorical variables = 2 (ID and size)}\)
 

b.i.  \(\text{Mean weight}\ = \dfrac{\text{sum of oyster weights}}{15} = \dfrac{171.3}{15} = 11.42 \)
 

b.ii.  \(\text{15 data points}\ \ \Rightarrow \ \ \text{Median = 8th data point (in order)}\)

 \(\text{Median}\ = 11.4 \)
 

c.i.   \(\text{Volume}\)
 

c.ii.  \(\text{Increase}\ = 0.953 \times 10 = 9.53\ \text{cm}^{3} \)
 

d.    \(\text{Input the image size column values}\ (x)\ \text{and volume} \)

\(\text{values}\ (y)\ \text{into the calculator:}\)

\(\textit{Volume}\ = 0.002857 + 2.571 \times \textit{image size} \)
 

e.    \(z\text{-score (4.6)}\ = 2\ \ \Rightarrow \bar x + 2 \times s_x = 4.6\ …\ (1)\)

\(z\text{-score (4.3)}\ = -1\ \ \Rightarrow \bar x-s_x = 4.3\ …\ (2)\)

\( (1)-(2) \)

\(3 s_x = 0.3 \ \ \Rightarrow\ \ s_x = 0.1 \)

\(\bar x = 4.4\) 

Data Analysis, GEN1 2023 VCAA 9 MC

A least squares line can be used to model the birth rate (children per 1000 population) in a country from the average daily food energy intake (megajoules) in that country.

When a least squares line is fitted to data from a selection of countries it is found that:

    • for a country with an average daily food energy intake of 8.53 megajoules, the birth rate will be 32.2 children per 1000 population
    • for a country with an average daily food energy intake of 14.9 megajoules, the birth rate will be 9.9 children per 1000 population.

The slope of this least squares line is closest to

  1. \(-4.7\)
  2. \(-3.5\)
  3. \(-0.29\)
  4. \(2.7\)
  5. \(25\)
Show Answers Only

\(B\)

Show Worked Solution

\(\text{Independent variable}\ (x)\ \text{= energy intake} \)

\(\text{Dependent variable}\ (y)\ \text{= birth rate} \)

\(\text{LSLR passes through (8.53, 32.2) and (14.9, 9.9) }\)

\(\text{Slope of LSRL}\ = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{32.2-9.9}{8.53-14.9} = -3.501 \)

\(\Rightarrow B\)

CORE, FUR1 2021 VCAA 10 MC

Oscar walked for nine consecutive days. The time, in minutes, that Oscar spent walking on each day is shown in the table below.
 

At least squares line is fitted to the data.

The equation of this line predicts that on day 10 the time Oscar spends walking will be the same as the time he spent walking on

  1. day 3
  2. day 4
  3. day 6
  4. day 8
  5. day 9
Show Answers Only

`B`

Show Worked Solution

`text{By calculator (day number = explanatory or} \ x text{-variable), the regression line is}`

`text{time}` `= 44 -\ text{day number}`
`:.\ text{time (day 10)}` `= 44 – 10`
  `= 34 \ text{minutes}`

 
`:. \ text{Day 10 time prediction is same as day 4}`
 

`=> B`

CORE, FUR2 2020 VCAA 6

The table below shows the mean age, in years, and the mean height, in centimetres, of 648 women from seven different age groups.
 


 

  1. What was the difference, in centimetres, between the mean height of the women in their twenties and the mean height of the women in their eighties?  (1 mark)

A scatterplot displaying this data shows an association between the mean height and the mean age of these women. In an initial analysis of the data, a line is fitted to the data by eye, as shown.
 

 

  1. Describe this association in terms of strength and direction.  (1 mark)

  2. The line on the scatterplot passes through the points (20,168) and (85,157).

     

    Using these two points, determine the equation of this line. Write the values of the intercept and the slope in the appropriate boxes below.

     

    Round your answers to three significant figures.  (1 mark)

mean height = 
 
   +  
 
   × mean age

 

  1. In a further analysis of the data, a least squares line was fitted.

     

    The associated residual plot that was generated is shown below.

     
     

          

     

    The residual plot indicates that the association between the mean height and the mean age of women is non-linear.

     

    The data presented in the table in part a is repeated below. It can be linearised by applying an appropriate transformation to the variable mean age.

     

      

     

    Apply an appropriate transformation to the variable mean age to linearise the data. Fit a least squares line to the transformed data and write its equation below.

     

    Round the values of the intercept and the slope to four significant figures.  (2 marks)


Show Answers Only
  1. `10.4\ text(cm)`
  2. `text(Strong and negative)`
  3. `text(mean height) = 171 – 0.169 xx text(mean age)`
  4. `text(mean height) = 167.9 – 0.001621 xx text{(mean age)}^2`
Show Worked Solution
a.   `text(Difference)` `= 167.1 – 156.7`
    `= 10.4\ text(cm)`

 

Mean mark part b. 51%.

b.  `text(Strong and negative.)`

 

♦♦ Mean mark part c. 23%.

c.   `text(Slope) = (157 – 168)/(85 – 20) = -0.169`

`text(Equation of line)`

`y – 168` `= -0.1692 (x – 20)`
`y` `= -0.169x + 171`

 
`:.\ text(mean height) = 171 – 0.169 xx text(mean age)`

 

D.    `text(By CAS)`

`text(mean height) = 167.9 – 0.001621 xx text{(mean age)}^2`

CORE, FUR2 2020 VCAA 4

The age, in years, body density, in kilograms per litre, and weight, in kilograms, of a sample of 12 men aged 23 to 25 years are shown in the table below.
 

          Age       
(years)

        Body density        
(kg/litre)

        Weight        
(kg)
  23 1.07 70.1
  23 1.07 90.4
  23 1.08 73.2
  23 1.08 85.0
  24 1.03 84.3
  24 1.05 95.6
  24 1.07 71.7
  24 1.06 95.0
  25 1.07 80.2
  25 1.09 87.4
  25 1.02 94.9
  25 1.09 65.3
     
  1. For these 12 men, determine
  2.  i. their median age, in years.   (1 mark)

  3. ii. the mean of their body density, in kilograms per litre.   (1 mark)

  4. A least squares line is to be fitted to the data with the aim of predicting body density from weight.
  5.  i. Name the explanatory variable for this least squares line.   (1 mark)

  6. ii. Determine the slope of this least squares line.
  7.     Round your answer to three significant figures.   (1 mark)

  8. What percentage of the variation in body density can be explained by the variation in weight?
  9. Round your answer to the nearest percentage.   (1 mark)

Show Answers Only
  1.  i. `24`
  2. ii. `1.065\ text(kg/litre)`
  3. i. `text(Weight)`
  4. ii. `text(Slope) = -0.00112\ text{(by CAS)}`
  5. `29 text(%)`
Show Worked Solution
a.i.   `n = 12`  
  `text(Median)` `= (text{6th + 7th})/2`
    `= (24 + 24)/2`
    `= 24`

 

a.ii.   `text(Mean)` `= (∑\ text{body density})/12`
    `= 1.065\ text(kg/litre)`

 

b.i.   `text(Weight)`

♦ Mean mark b.ii. 29%.
MARKER’S COMMENT: Most students did not round correctly.

b.ii.   `text(Slope) = -0.00112\ text{(by CAS)}`

 

c.   `r` `= -0.53847\ text{(by CAS)}`
  `r^2` `= 0.289…`

 
`:. 29 text(%)`

Data Analysis, GEN2 2019 NHT 3

The life span, in years, and gestation period, in days, for 19 types of mammals are displayed in the table below.
 

  1. A least squares line that enables life span to be predicted from gestation period is fitted to this data.
  2. Name the explanatory variable in the equation of this least squares line.   (1 mark)

  3. Determine the equation of the least squares line in terms of the variables life span and gestation period.
  4. Round the numbers representing the intercept and slope to three significant figures.   (2 marks)

  5. Write the value of the correlation rounded to three decimal places.   (1 mark)

Show Answers Only
  1. `text(gestation period)`
  2. `text(life span) = 7.58 + 0.101 xx \ text(gestation period)`
  3. `0.904`
Show Worked Solution

a.    `text(gestation period)`
 

b.    `text(Input data points into CAS:)`

`text(life span) = 7.58 + 0.101 xx \ text(gestation period)`
 

c.    `r = 0.904 \ text{(by CAS)}`

CORE, FUR2 2019 VCAA 4

The relative humidity (%) at 9 am and 3 pm on 14 days in November 2017 is shown in Table 3 below.

A least squares line is to be fitted to the data with the aim of predicting the relative humidity at 3 pm (humidity 3 pm) from the relative humidity at 9 am (humidity 9 am).

  1. Name the explanatory variable.   (1 mark)

  2. Determine the values of the intercept and the slope of this least squares line.
  3. Round both values to three significant figures and write them in the appropriate boxes provided.   (1 mark)

humidity 3 pm = 
 
   +  
 
   × humidity 9 am  (1 mark)
  1. Determine the value of the correlation coefficient for this data set.
  2. Round your answer to three decimal places.   (1 mark)

Show Answers Only
  1. `text(humidity 9 am)`
  2. `text(humidity 3 pm) = -1.26 + 0.765 xx text(humidity 9 am)`
  3. `r = 0.871`
Show Worked Solution

a.  `text(humidity 9 am)`
 

b.  `text(Input all data points into CAS:)`

`text(humidity 3 pm) = -1.26 + 0.765 xx text(humidity 9 am)`
 

c.    `r = 0.871\ \ text{(3 d.p.)}`

CORE, FUR1 2019 VCAA 13-14 MC

The time, in minutes, that Liv ran each day was recorded for nine days.

These times are shown in the table below.
  


  

The time series plot below was generated from this data.
  

Part 1

Both three-median smoothing and five-median smoothing are being considered for this data.

Both of these methods result in the same smoothed value on day number

  1. 3
  2. 4
  3. 5
  4. 6
  5. 7

 
Part 2

A least squares line is to be fitted to the time series plot shown above.

The equation of this least squares line, with day number as the explanatory variable, is closest to

  1. day number = 23.8 + 2.29 × time
  2. day number = 28.5 + 1.77 × time
  3. time = 23.8 + 1.77 × day number
  4. time = 23.8 + 2.29 × day number
  5. time = 28.5 + 1.77 × day number
Show Answers Only

`text(Part 1:)\ E`

`text(Part 2:)\ E`

Show Worked Solution

`text(Part 1)`

`text{Add 3-median (dots) and 5-median (Δ) smoothing to the plot:}`
 

`=>  E`
 

`text(Part 2)`

`text(time) = 28.5 + 1.77 xx text(day number)\ \ \ text{(by CAS)}`

`=>  E`

CORE, FUR2 2018 VCAA 3

Table 3 shows the yearly average traffic congestion levels in two cities, Melbourne and Sydney, during the period 2008 to 2016. Also shown is a time series plot of the same data.

The time series plot for Melbourne is incomplete.

  1. Use the data in Table 3 to complete the time series plot above for Melbourne.   (1 mark)

  2. A least squares line is used to model the trend in the time series plot for Sydney. The equation is

       `text(congestion level = −2280 + 1.15 × year)`

  1.   i. Draw this least squares line on the time series plot.   (1 mark)

  2.  ii. Use the equation of the least squares line to determine the average rate of increase in percentage congestion level for the period 2008 to 2016 in Sydney.   (1 mark)

    iii. Use the least squares line to predict when the percentage congestion level in Sydney will be 43%.   (1 mark)

The yearly average traffic congestion level data for Melbourne is repeated in Table 4 below.

  1. When a least squares line is used to model the trend in the data for Melbourne, the intercept of this line is approximately –1514.75556
  2. Round this value to four significant figures.   (1 mark)

  3. Use the data in Table 4 to determine the equation of the least squares line that can be used to model the trend in the data for Melbourne. The variable year is the explanatory variable.
  4. Write the values of the intercept and the slope of this least squares line in the appropriate boxes provided below.
  5. Round both values to four significant figures.   (2 marks)

congestion level = 
 
  + 
 
  × year
  1. Since 2008, the equations of the least squares lines for Sydney and Melbourne have predicted that future traffic congestion levels in Sydney will always exceed future traffic congestion levels in Melbourne.

     

    Explain why, quoting the values of appropriate statistics.   (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
    1. `text(See Worked Solutions)`
    2. `1.15 text(%)`
    3. `2020`
  2. `-1515`
  3. `text(congestion level) = -1515 + 0.7667 xx text(year)`
  4. `text(See Worked Solutions)`
Show Worked Solution
a.   

 

b.i.   

 

b.ii.  `text(The least squares line is 1.15% higher each year.)`

♦ Mean mark (b)(ii) 36%.
COMMENT: Major problems caused by part (b)(ii). Review!

  ` :.\ text(Average rate of increase) = 1.15 text(%)`

 

b.iii.    `text(Find year when:)`
  `43` `= -2280 + 1.15 xx text(year)`
  `text(year)` `= 2323/1.15`
    `= 2020`

 

c.  `-1515`

 

d.   `text(congestion level) = -1515 + 0.7667 xx text(year)`

 

e.   `text(Melbourne congestion level in 2008)`

♦♦♦ Mean mark 18%.

`= -1515 + 0.7667 xx 2008`

`= 24.5 text(%)`

 
`text{In 2008 Sydney has higher congestion (29.2 > 24.5)}`

`text(After 2008, Sydney congestion grows at 1.15% per)`

`text(year and Melbourne grows at 0.7667% per year.)`

`:.\ text(Sydney predicted to always exceed Melbourne.)`

CORE, FUR1 2018 VCAA 7-9 MC

The scatterplot below displays the resting pulse rate, in beats per minute, and the time spent exercising, in hours per week, of 16 students. A least squares line has been fitted to the data.
 

 
Part 1

Using this least squares line to model the association between resting pulse rate and time spent exercising, the residual for the student who spent four hours per week exercising is closest to

  1. –2.0 beats per minute.
  2. –1.0 beats per minute.
  3. –0.3 beats per minute.
  4.   1.0 beats per minute.
  5.   2.0 beats per minute.

 
Part 2

The equation of this least squares line is closest to

  1. resting pulse rate = 67.2 – 0.91 × time spent exercising
  2. resting pulse rate = 67.2 – 1.10 × time spent exercising
  3. resting pulse rate = 68.3 – 0.91 × time spent exercising
  4. resting pulse rate = 68.3 – 1.10 × time spent exercising
  5. resting pulse rate = 67.2 + 1.10 × time spent exercising

 
Part 3

The coefficient of determination is 0.8339

The correlation coefficient `r` is closest to

  1. –0.913
  2. –0.834
  3. –0.695
  4.   0.834
  5.   0.913
Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ D`

`text(Part 3:)\ A`

Show Worked Solution

`text(Part 1)`

`text(Predicted rate = 64 bpm)`

`:.\ text(Residual)` `=\ text(actual − predicted)`
  `= 63 – 64`
  `= −1.0\ text(bpm)`

`=> B`

 

`text(Part 2)`

♦ Mean mark 46%.

`text(By elimination:)`

`ytext(-intecept) != 67.2\ text(since the)\ xtext(-axis starts)`

`text(at)\ \ x = 1\ \ (text(not)\ \ x = 0)`

`:.\ text(Eliminate)\ A, B\ text(and)\ E.`
 

`text(Consider the gradient.)`

`text(For each horizontal run of 1 unit, the line)`

`text(decreases vertically more than 1 unit.)`

`:.\ text(Eliminate)\ C.`

`=> D`

 

`text(Part 3)`

♦ Mean mark 45%.

`text(The correlation is clearly negative.)`

`:. r` `= −sqrt(0.8339)`
  `= −0.913`

`=>A`

CORE, FUR2 2017 VCAA 3

The number of male moths caught in a trap set in a forest and the egg density (eggs per square metre) in the forest are shown in the table below.
 

  1. Determine the equation of the least squares line that can be used to predict the egg density in the forest from the number of male moths caught in the trap.
  2. Write the values of the intercept and slope of this least squares line in the appropriate boxes provided below.
  3. Round your answers to one decimal place.  (2 marks)

     

         

  4. The number of female moths caught in a trap set in a forest and the egg density (eggs per square metre) in the forest can also be examined.

     

    A scatterplot of the data is shown below.
     


     
    The equation of the least squares line is

     

                  egg density = 191 + 31.3 × number of female moths

    1. Draw the graph of this least squares line on the scatterplot (provided above).   (1 mark)

    2. Interpret the slope of the regression line in terms of the variables egg density and number of female moths caught in the trap.   (1 mark)

    3. The egg density is 1500 when the number of female moths caught is 55.
    4. Determine the residual value if the least squares line is used to predict the egg density for this number of female moths.   (1 mark)
    5. The correlation coefficient is  `r = 0.862`
    6. Determine the percentage of the variation in egg density in the forest explained by the variation in the number of female moths caught in the trap.
    7. Round your answer to one decimal place.   (1 mark)
Show Answers Only

a.   `text(egg density)\ = −46.8 + 18.9 xx text(number of male moths)`

b.i.  

b.ii.  `text(Egg density per square metre increases)`

`text(by 31.3 eggs for every extra female moth)`

`text(caught in the trap.)`

b.iii.  `−412.5`

b.iv.  `text(74.3%)`

Show Worked Solution

a.   `text(By calculator)`

`text(egg density)\ = −46.8 + 18.9 xx text(number of male moths)`

 

b.i.   `text(Calculating extreme points on graph.)`

♦♦ Mean mark 26%.
MARKER’S COMMENT: Not well answered! Many students did not realise the graph started at 10 on the `x`-axis and many did not use a ruler!

`x = 10, y = 191 + 31.3 xx 10 = 504`

`x = 60, y = 191 + 31.3 xx 60 = 2069`

 

♦ Mean mark 39%.
MARKER’S COMMENT: Students must clearly refer to the increase in egg density for every one-unit increase in female moths.

b.ii.   `text(Egg density per square metre increases)`

 `text(by 31.3 eggs for every extra female moth)`

 `text(caught in the trap.)`

 

b.iii.   `text(Predicted egg density)`

♦ Mean mark 48%.

`= 191 + 31.3 xx 55`

`= 1912.5`

`:.\ text(Residual value)` `= 1500-1912.5`
  `= −412.5`

 

b.iv.   `r = 0.862`

♦ Mean mark 47%.

`r^2 = 0.862^2 = 0.7430… = 74.3text{%  (1 d.p.)}`

`:.\ text(74.3% is explained.)`

CORE, FUR1 2017 VCAA 8-10 MC

The scatterplot below shows the wrist circumference and ankle circumference, both in centimetres, of 13 people. A least squares line has been fitted to the scatterplot with ankle circumference as the explanatory variable.
 

Part 1

The equation of the least squares line is closest to

  1. ankle = 10.2 + 0.342 × wrist
  2. wrist = 10.2 + 0.342 × ankle
  3. ankle = 17.4 + 0.342 × wrist
  4. wrist = 17.4 + 0.342 × ankle
  5. wrist = 17.4 + 0.731 × ankle

 

Part 2

When the least squares line on the scatterplot is used to predict the wrist circumference of the person with an ankle circumference of 24 cm, the residual will be closest to

  1. `–0.7`
  2. `–0.4`
  3. `–0.1`
  4.    `0.4`
  5.    `0.7`

 

Part 3

The residuals for this least squares line have a mean of 0.02 cm and a standard deviation of 0.4 cm.

The value of the residual for one of the data points is found to be  – 0.3 cm.

The standardised value of this residual is

  1. `–0.8`
  2. `–0.7`
  3. `–0.3`
  4.    `0.7`
  5.    `0.8`
Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ A`

`text(Part 3:)\ A`

Show Worked Solution

`text(Part 1)`

`ytext(-intercept = 10.2)`

`(text(note)\ xtext(-axis in graph begins at 21 cm))`

`:. text(wrist) = 10.2 + 0.342 xx text(ankle)`

`=> B`

 

`text(Part 2)`

`text(Predicted wrist)` `= 10.2 + 0.342 xx 24`
  `= 18.4`

 

`text(Residual)` `=\ text(actual − predicted)`
  `~~ 17.7 – 18.4`
  `~~ −0.7`

 
`=> A`

 
`text(Part 3)`

`barx = 0.02,qquad s_x = 0.4`

`text(If)\ \ x = −0.3,`

`z` `= (x – barx)/s_x`
  `= (−0.3 – 0.02)/0.4`
  `= −0.8`

 
`=> A`

CORE, FUR2 2016 VCAA 3

The data in the table below shows a sample of actual temperatures and apparent temperatures recorded at a weather station. A scatterplot of the data is also shown.

The data will be used to investigate the association between the variables apparent temperature and actual temperature.
 

  1. Use the scatterplot to describe the association between apparent temperature and actual temperature in terms of strength, direction and form.   (1 mark)

  2.  i. Determine the equation of the least squares line that can be used to predict the apparent temperature from the actual temperature.
  3. Write the values of the intercept and slope of this least squares line in the appropriate boxes provided below.
  4. Round your answers to two significant figures.   (3 marks)
     apparent temperature `=`    
 
 `+`  
 
 `xx`   actual temperature
  1. ii. Interpret the intercept of the least squares line in terms of the variables apparent temperature and actual temperature.   (1 mark)

  2. The coefficient of determination for the association between the variables apparent temperature and actual temperature is 0.97
  3. Interpret the coefficient of determination in terms of these variables.   (1 mark)

  4. The residual plot obtained when the least squares line was fitted to the data is shown below.
     
     
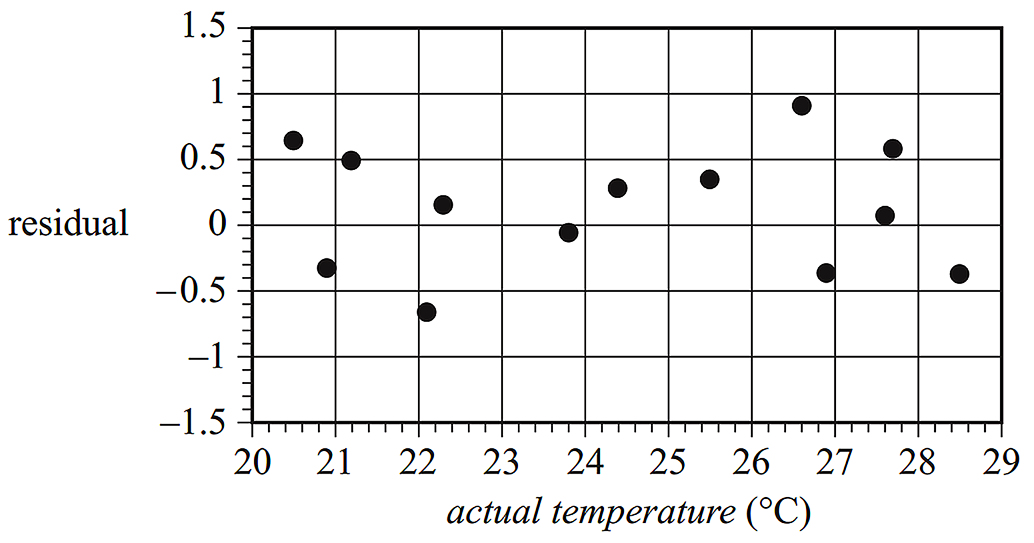
  5.  i. A residual plot can be used to test an assumption about the nature of the association between two numerical variables.
  6.     What is this assumption?   (1 mark)
  7. ii. Does the residual plot above support this assumption? Explain your answer.   (1 mark)
Show Answers Only

a.   `text(Strong, positive and linear)`

b.i.  `text(apparent temperature) = -1.7 xx 0.94 xx text(actual temperature)`

b.ii.  `text(When actual temperature is 0°C, on average,)`

`text(the apparent temperature is)\ − 1.7^@\text(C.)`

c.  `text(97% of the variation in the apparent temperature can be explained)`

`text(by the variation in the actual temperature.)`

d.i.  `text(There is a linear relationship between the two variables.)`

d.ii.  `text(The random pattern supports the assumption.)`

`text{(Students should refer to randomness or a lack of pattern}`

`text{explicitly here).}`

Show Worked Solution

a.   `text(Strong, positive and linear)`
 

b.i.   `text(By calculator:)`

`text(apparent temperature) = -1.7 xx 0.94 xx text(actual temperature)`
 

♦♦ Mean mark of part (b)(ii) – 28%.
MARKER’S COMMENT: “the predicted apparent temp is -1.7°C” also gained a mark.
b.ii.    `text(When actual temperature is 0°C, on average,)`
 

`text(the apparent temperature is)\ − 1.7^@\text(C.)`

 

♦ Mean mark 49%.
IMPORTANT: Any mention of causality loses a mark!

c.  `text(97% of the variation in the apparent temperature can be explained)`

`text(by the variation in the actual temperature.)`
  

d.i.  `text(There is a linear relationship between the two variables.)`

♦ Mean mark of both parts of (d) was 46%.

d.ii.  `text(The random pattern supports the assumption.)`

`text{(Students should refer to randomness or a lack of pattern}`

`text{explicitly here).}`

CORE, FUR2 2007 VCAA 3

The table below displays the mean surface temperature (in °C) and the mean duration of warm spell (in days) in Australia for 13 years selected at random from the period 1960 to 2005.
 

CORE, FUR2 2007 VCAA 31
 

This data set has been used to construct the scatterplot below. The scatterplot is incomplete.

  1. Complete the scatterplot below by plotting the bold data values given in the table above. Mark the point with a cross (×).  (1 mark)

          

     

  2. Mean surface temperature is the explanatory variable.

     

    1. Determine the equation of the least squares regression line for this set of data. Write the equation in terms of the variables mean duration of warm spell and mean surface temperature. Write the value of the coefficients correct to one decimal place.  (2 marks)

    2. Plot the least squares regression line on Scatterplot 1.  (1 mark)

The residual plot below was constructed to test the assumption of linearity for the relationship between the variables mean duration of warm spell and the mean surface temperature.

CORE, FUR2 2007 VCAA 33

  1. Explain why this residual plot supports the assumption of linearity for this relationship.  (1 mark)

  2. Write down the percentage of variation in the mean duration of a warm spell that is explained by the variation in mean surface temperature. Write your answer correct to the nearest per cent.  (1 mark)

  3. Describe the relationship between the mean duration of a warm spell and the mean surface temperature in terms of strength, direction and form.  (2 marks)

Show Answers Only
  1.  
    CORE, FUR2 2007 VCAA 3 Answer

    1. `text{See part b.ii. below.}`
    2. `text(Mean duration of warm spell)`
      `= -776.9 + 60.3 xx text(mean surface temperature)`
  2. `text(Linearity is supported because there is no)`
    `text(pattern to the residual data.)`
  3. `83text(%)`
  4. `text(Strong, positive, and linear.)`
Show Worked Solution
a.    CORE, FUR2 2007 VCAA 3 Answer

 

b.i.   `text(Mean duration of warm spell)`

`= -776.9 + 60.3 xx text(mean surface temperature)`

 

MARKER’S COMMENT: A consistent error in these type of questions is taking 2 points that are too close together!

b.ii.   `text(Taking extreme points on the above graph,)`

  `text(When)\ \ x = 13.2, \ y = -776.9 + 60.3 xx 13.2 = 19.06`

`:.\ text(Passes through)\ \ A (13.2, 19.06)`

  `text(When)\ x = 13.8, y = -776.9 + 60.3 xx 13.8 = 55.24`

`:.\ text(Passes through)\ \ B (13.8, 55.24)`

`text(*See the regression line plotted above.)`

 

c.   `text(Linearity is supported because there is no)`

`text(pattern to the residual data.)`
 

d.   `text(By Calculator,)`

`r^2 = 0.828… = 83text{%  (nearest %)}`
 

e.   `text(Strong, positive, and linear.)`

CORE, FUR2 2008 VCAA 4

The arm spans (in cm) and heights (in cm) for a group of 13 boys have been measured. The results are displayed in the table below.
 

CORE, FUR2 2008 VCAA 4 

The aim is to find a linear equation that allows arm span to be predicted from height.

  1. What will be the explanatory variable in the equation?   (1 mark)

  2. Assuming a linear association, determine the equation of the least squares regression line that enables arm span to be predicted from height. Write this equation in terms of the variables arm span and height. Give the coefficients correct to two decimal places.   (2 marks)

  3. Using the equation that you have determined in part b., interpret the slope of the least squares regression line in terms of the variables height and arm span.   (1 mark)

Show Answers Only
  1. `text(Height)`
  2. `text(Arm span)\ = 1.09 xx text(height) – 15.63`
  3. `text(On average, arm span increases by 1.09 cm)`

     

    `text(for each 1 cm increase in height.)`

Show Worked Solution

a.   `text(Height)`

♦ Mean mark sub 50% (exact data not available).
MARKER’S COMMENT: Many students did not understand the term co-efficients as it applies to the regression equation.

 

b.   `text(By calculator,)`

`text(Arm span)\ = 1.09 xx text(height) – 15.63`

 

c.   `text(On average, arm span increases by 1.09 cm)`

`text(for each 1 cm increase in height.)`

CORE, FUR2 2015 VCAA 4

The table below shows male life expectancy (male) and female life expectancy (female) for a number of countries in 2013. The scatterplot has been constructed from this data.
 

Core, FUR2 2015 VCAA 4

  1. Use the scatterplot to describe the association between male life expectancy and female life expectancy in terms of strength, direction and form.   (1 mark)

  2. Determine the equation of a least squares regression line that can be used to predict male life expectancy from female life expectancy for the year 2013.

     

    Complete the equation for the least squares regression line below by writing the intercept and slope in the space provided.

     

    Write these values correct to two decimal places.  (1 mark)

male = ______________ + ______________ ×  female

Show Answers Only
  1. `text(Strong, positive and linear.)`
  2. `text(male) = 9.69 + 0.81 xx text(female)`
Show Worked Solution

a.   `text(Strong, positive and linear.)`

♦ Mean mark 49%.
MARKER’S COMMENT: Common errors included using the 1st column as the independent (`x`) variable and poor rounding.

 

b.   `text(By calculator,)`

`text(male) = 9.69 + 0.81 xx text(female)`

CORE, FUR1 2015 VCAA 9 MC

A least squares regression line has been fitted to the scatterplot above to enable distance, in kilometres, to be predicted from time, in minutes.

The equation of this line is closest to

A.   distance `= 3.5 + 1.6 ×`time

B.   time `= 3.5 + 1.6 ×`distance

C.   distance `= 1.6 + 3.5 ×`time

D.   time `= 1.8 + 3.5 ×`distance

E.   distance `= 3.5 + 1.8 ×`time

Show Answers Only

`A`

Show Worked Solution

`text{Line passes through  (0, 3.5) and (50, 82)`

`:.\ text(Gradient) ` `=(y_2-y_1)/(x_2-x_1)`
  `~~(82 – 3.5)/(50 – 0)`
  `~~ 1.57`

`text(Distance is the dependent variable and the)`

`y text(-intercept is approximately 3.5.)`

`=> A`

CORE, FUR1 2014 VCAA 9 MC

The equation of a least squares regression line is used to predict the fuel consumption, in kilometres per litre of fuel, from a car’s weight, in kilograms.

This equation predicts that a car weighing 900 kg will travel 10.7 km per litre of fuel, while a car weighing 1700 kg will travel 6.7 km per litre of fuel.

The slope of this least squares regression line is closest to

A.   `–250`

B.   `–0.005`

C.   `–0.004`

D.   `0.005`

E.   `200`

Show Answers Only

`B`

Show Worked Solution

 

`text(Gradient)` `=(y_2-y_1)/(x_2 – x_1)`
  `=(6.7 – 10.7)/(1700 – 900)`
  `=- 4/800`
  `=-0.005`

 
`=>  B`

CORE, FUR1 2011 VCAA 6-8 MC

When blood pressure is measured, both the systolic (or maximum) pressure and the diastolic (or minimum) pressure are recorded.

Table 1 displays the blood pressure readings, in mmHg, that result from fifteen successive measurements of the same person's blood pressure.
 

core 2011 VCAA 6-8

Part 1

Correct to one decimal place, the mean and standard deviation of this person's systolic blood pressure measurements are respectively

A.   `124.9 and 4.4`

B.   `125.0 and 5.8`

C.   `125.0 and 6.0`

D.   `125.9 and 5.8`

E.   `125.9 and 6.0`

 

Part 2

Using systolic blood pressure (systolic) as the response variable, and diastolic blood pressure (diastolic) as the explanatory variable, a least squares regression line is fitted to the data in Table 1.

The equation of the least squares regression line is closest to

A.   `text(systolic) = 70.3 + 0.790 xx text(diastolic)`

B.   `text(diastolic) = 70.3 + 0.790 xx text(systolic)`

C.   `text(systolic) = 29.3 + 0.330 xx text(diastolic)`

D.   `text(diastolic) = 0.330 + 29.3 xx text(systolic)`

E.   `text(systolic) = 0.790 + 70.3 xx text(diastolic)`

 

Part 3

From the fifteen blood pressure measurements for this person, it can be concluded that the percentage of the variation in systolic blood pressure that is explained by the variation in diastolic blood pressure is closest to

A.   `25.8text(%)`

B.   `50.8text(%)`

C.   `55.4text(%)`

D.   `71.9text(%)`

E.   `79.0text(%)`

Show Answers Only

`text(Part 1:)\ E`

`text(Part 2:)\ A`

`text(Part 3:)\ A`

Show Worked Solution

`text(Part 1)`

`text{By calculator (using sample standard deviation)}`

`text{the results are: }`

`text(Mean = 125.9, std dev = 6.0)`

`=>E`

 

`text(Part 2)`

`text{By calculator (making sure diastolic values are}`

`text{the explanatory or}\ x text{-variable), the regression line}`

`text(can be expressed as follows,)`

`text(systolic) = 70.3 + 0.790 xx text(diastolic)`

`=>A`

 

`text(Part 3)`

`text{By calculator, the regression line (above) should}`

`text(have found) \ \ r^2 = 0.258,\ text(which means that)`

`text(25.8% of the variation in systolic pressure can be)`

`text(explained by variation in diastolic pressure.)`

`=>A`

CORE, FUR1 2010 VCAA 7-9 MC

The height (in cm) and foot length (in cm) for each of eight Year 12 students were recorded and displayed in the scatterplot below.
A least squares regression line has been fitted to the data as shown.
 

Part 1

By inspection, the value of the product-moment correlation coefficient `(r)` for this data is closest to

  1. `0.98`
  2. `0.78`
  3. `0.23`
  4. `– 0.44`
  5. `– 0.67`

 

Part 2

The explanatory variable is foot length.

The equation of the least squares regression line is closest to

  1. height = –110 + 0.78 × foot length.
  2. height = 141 + 1.3 × foot length.
  3. height = 167 + 1.3 × foot length.
  4. height = 167 + 0.67 × foot length.
  5. foot length = 167 + 1.3 × height.

 

Part 3

The plot of the residuals against foot length is closest to

CORE, FUR1 2010 VCAA 7-9 MCab

CORE, FUR1 2010 VCAA 7-9 MCcd

CORE, FUR1 2010 VCAA 7-9 MCe

Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ B`

`text(Part 3:)\ B`

Show Worked Solution

`text(Part 1)`

`text(The correlation is positive and strong.)`

`text(Eliminate)\ C, D\ text(and)\ E.`

`r= 0.98\  text(is too strong. Eliminate)\ A.`

`=> B`

 

`text(Part 2)`

♦♦ Mean mark 35%.
STRATEGY: An alternate but less efficient strategy could be to find 2 points and calculate the gradient and then use the point gradient formula.

`text(The intercept with the height axis)\ (ytext{-axis)}`

`text{is below 167 because that is the height when}`

`text{foot length = 20 cm.}`

`text(Eliminate)\ C, D\ text(and)\ E.`

`text(The gradient is approximately 1.3, by observing)`

`text(the increase in height values when the foot)`

`text(length increases from 20 to 22 cm.)`

`=>  B`

 

`text(Part 3)`

`text(First residual is positive. Eliminate)\ A, D, E.`

`text(The next 3 residuals are negative. Eliminate)\ C`

`=>  B`

CORE, FUR1 2012 VCAA 8 MC

The maximum wind speed and maximum temperature were recorded each day for a month. The data is displayed in the scatterplot below and a least squares regression line has been fitted. The response variable is temperature. The explanatory variable is wind speed.
 

 The equation of the least squares regression line is closest to

A.  `text(temperature) = 25.7 - 0.191 xx text(wind speed)`

B.  `text(wind speed) = 25.7 - 0.191 xx text(temperature)`

C.  `text(temperature) = 0.191 + 25.7 xx text(wind speed)`

D.  `text(wind speed) = 25.7 + 0.191 xx text(temperature)`

E.  `text(temperature) = 25.7 + 0.191 xx text(wind speed)`

Show Answers Only

`A`

Show Worked Solution

`text (Using the form)\ \ y = mx +b\ \ text(where)`

`y rArr text (temperature)`

`x rArr text (wind speed)`

`text (b = 25.7 (y intercept))`

 

`text (Gradient is negative because temperature decreases as)`

`text(wind speed increases.)`

`:.\ text (Equation must take the form of A.)`

`rArr A`

CORE, FUR1 2009 VCAA 9-10 MC

The table below lists the average life span (in years) and average sleeping time (in hours/day) of 12 animal species.
 


 

Part 1

Using sleeping time as the independent variable, a least squares regression line is fitted to the data.

The equation of the least squares regression line is closest to

A.   life span = 38.9 – 2.36 × sleeping time.

B.   life span = 11.7 – 0.185 × sleeping time.

C.   life span = – 0.185 – 11.7 × sleeping time.

D.   sleeping time = 11.7 – 0.185 × life span.

E.   sleeping time = 38.9 – 2.36 × life span.

 

Part 2

The value of Pearson’s product-moment correlation coefficient for life span and sleeping time is closest to

A.  `–0.6603`

B.  `–0.4360`

C.  `–0.1901`

D.   `0.4360`

E.   `0.6603` 

Show Answers Only

`text(Part 1:)\ A`

`text(Part 2:)\ A`

Show Worked Solution

`text(Part 1)`

♦ Mean mark 49%.
MARKERS’ COMMENT: Almost a quarter of students incorrectly assumed the independent variable was in the first column!

`text{By calculator (with “life span” as the}`

`text{dependent variable), the equation is:}`

`text(life span = 38.9 – 2.36 × sleeping time.)`

`=>A`

 

`text(Part 2)`

`text (By calculator)`

`=>A`