SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

HMS, BM EQ-Bank 87

Describe how the endocrine system's release of cortisol affects an athlete's movement efficiency during periods of prolonged stress.   (3 marks)

Show Answers Only

Sample Answer

  • Cortisol released by the adrenal glands increases blood glucose levels to provide energy for movement during stress.
  • Prolonged high cortisol levels can break down muscle protein for energy, potentially reducing movement efficiency and strength.
  • Extended periods of elevated cortisol can lead to fatigue and decreased performance as energy systems become depleted.
  • Chronic cortisol elevation also suppresses growth hormone, impairing muscle recovery and adaptation to training.
Show Worked Solution

Sample Answer

  • Cortisol released by the adrenal glands increases blood glucose levels to provide energy for movement during stress.
  • Prolonged high cortisol levels can break down muscle protein for energy, potentially reducing movement efficiency and strength.
  • Extended periods of elevated cortisol can lead to fatigue and decreased performance as energy systems become depleted.
  • Chronic cortisol elevation also suppresses growth hormone, impairing muscle recovery and adaptation to training.

HMS, BM EQ-Bank 86

Outline how the digestive system responds to acute stress during participation in a competitive sports event.  (3 marks)

Show Answers Only

Sample Answer

  • Slowed/stopped digestion: The digestive system slows down or stops digestion as blood is diverted to muscles and vital organs during the stress response.
  • Decreased saliva production: The mouth becomes dry as saliva production decreases, making it harder to digest food during competition.
  • Nausea/stomach discomfort: Stress hormones can cause nausea or “butterflies” in the stomach as the digestive system responds to the fight or flight response.
Show Worked Solution

Sample Answer

  • Slowed/stopped digestion: The digestive system slows down or stops digestion as blood is diverted to muscles and vital organs during the stress response.
  • Decreased saliva production: The mouth becomes dry as saliva production decreases, making it harder to digest food during competition.
  • Nausea/stomach discomfort: Stress hormones can cause nausea or “butterflies” in the stomach as the digestive system responds to the fight or flight response.

HMS, BM EQ-Bank 85 MC

Which statement best describes how protein intake affects the endocrine system's ability to support movement?

  1. The thyroid gland increases metabolism to break down protein for immediate energy
  2. The adrenal glands produce adrenaline to convert protein into glucose during exercise
  3. The pituitary gland releases growth hormone to store protein as fat for later use
  4. The pancreas releases insulin to help transport amino acids to muscles for repair
Show Answers Only

\(D\)

Show Worked Solution
  • D is correct: Insulin from the pancreas facilitates amino acid transport to muscles for repair and growth.

Other Options:

  • A is incorrect: Protein isn’t used for immediate energy; this is primarily carbohydrates’ role.
  • B is incorrect: Adrenaline mobilises glucose from glycogen, not from protein conversion.
  • C is incorrect: Growth hormone aids protein synthesis, not storage as fat.

HMS, BM EQ-Bank 76

Explain how growth hormone and cortisol interact during a high-intensity interval training session.  (5 marks)

Show Answers Only

Sample Answer

  • During HIIT, the pituitary gland releases growth hormone while the adrenal glands secrete cortisol.
  • This dual hormone release creates competing effects on protein metabolism in muscle tissue.
  • Growth hormone stimulates muscle protein synthesis for repair and growth, while cortisol breaks down muscle protein for energy.
  • Therefore, the endocrine system balances anabolic and catabolic processes during intense exercise.
      
  • Both hormones work together to maintain energy availability during high-intensity intervals.
  • Growth hormone promotes fat breakdown for fuel while cortisol increases glucose production through gluconeogenesis.
  • As a result, muscles receive both fatty acids and glucose to meet extreme energy demands.
  • The interaction demonstrates how multiple hormones coordinate to support intense movement.
      
  • Timing and balance of these hormones affects training outcomes.
  • Excessive cortisol can override growth hormone’s benefits if stress is prolonged.
  • Short HIIT sessions optimise growth hormone release while minimising excessive cortisol elevation.
  • Consequently, HIIT duration and recovery prove critical for positive adaptations.
Show Worked Solution

Sample Answer

  • During HIIT, the pituitary gland releases growth hormone while the adrenal glands secrete cortisol.
  • This dual hormone release creates competing effects on protein metabolism in muscle tissue.
  • Growth hormone stimulates muscle protein synthesis for repair and growth, while cortisol breaks down muscle protein for energy.
  • Therefore, the endocrine system balances anabolic and catabolic processes during intense exercise.
      
  • Both hormones work together to maintain energy availability during high-intensity intervals.
  • Growth hormone promotes fat breakdown for fuel while cortisol increases glucose production through gluconeogenesis.
  • As a result, muscles receive both fatty acids and glucose to meet extreme energy demands.
  • The interaction demonstrates how multiple hormones coordinate to support intense movement.
      
  • Timing and balance of these hormones affects training outcomes.
  • Excessive cortisol can override growth hormone’s benefits if stress is prolonged.
  • Short HIIT sessions optimise growth hormone release while minimising excessive cortisol elevation.
  • Consequently, HIIT duration and recovery prove critical for positive adaptations.

HMS, BM EQ-Bank 75

Describe the impact of exercise-induced thermal stress on digestive enzyme production.   (3 marks)

Show Answers Only

Sample Answer

Exercise-induced thermal stress affects digestive enzyme production by:

  • Reducing pancreatic secretion: Because blood flow diverts to working muscles, reduced secretion of digestive enzymes by the pancreas occurs.
  • Decreasing salivary amylase: Initial carbohydrate breakdown is less efficient due to decreased salivary amylase.
  • Impairing enzyme efficiency: Existing enzyme efficiency becomes impaired due to altered temperature conditions.
  • Slowing overall digestive processes: As the body prioritises cooling and muscle function overall digestive processes are slowed.

These changes can affect nutrient breakdown during and after exercise, potentially leading to digestive discomfort.

Show Worked Solution

Sample Answer

Exercise-induced thermal stress affects digestive enzyme production by:

  • Reducing pancreatic secretion: Because blood flow diverts to working muscles, reduced secretion of digestive enzymes by the pancreas occurs.
  • Decreasing salivary amylase: Initial carbohydrate breakdown is less efficient due to decreased salivary amylase.
  • Impairing enzyme efficiency: Existing enzyme efficiency becomes impaired due to altered temperature conditions.
  • Slowing overall digestive processes: As the body prioritises cooling and muscle function overall digestive processes are slowed.

These changes can affect nutrient breakdown during and after exercise, potentially leading to digestive discomfort.

HMS, BM EQ-Bank 70 MC

An archer notices their hands shaking before competition. This response is primarily caused by which hormone?

  1. Insulin
  2. Thyroxine
  3. Epinephrine
  4. Growth hormone
Show Answers Only

\(C\)

Show Worked Solution
  • C is correct: Epinephrine causes trembling during stress through sympathetic nervous system activation.

Other Options:

  • A is incorrect: Insulin lowers blood glucose, not involved in stress response.
  • B is incorrect: Thyroxine affects metabolism, not acute stress symptoms.
  • D is incorrect: Growth hormone aids tissue repair, not stress responses.

HMS, BM EQ-Bank 58 MC

During a 400 metre sprint, an athlete's oxygen demand increases. Which sequence correctly shows the pathway of oxygen from inhalation to the working muscles?

  1. Alveoli → Pulmonary vein → Left atrium → Left ventricle → Systemic circulation
  2. Alveoli → Pulmonary artery → Left atrium → Left ventricle → Systemic circulation
  3. Bronchi → Pulmonary vein → Right atrium → Right ventricle → Systemic circulation
  4. Bronchi → Pulmonary artery → Right atrium → Right ventricle → Systemic circulation
Show Answers Only

\(A\)

Show Worked Solution
  • A is correct: Oxygen diffuses into alveoli, enters pulmonary veins (oxygenated blood), flows to left atrium then left ventricle, enters systemic circulation to muscles.

Other Options:

  • B is incorrect: Pulmonary arteries carry deoxygenated blood
  • C is incorrect: Right side of heart receives deoxygenated blood; bronchi are airways not blood vessels
  • D is incorrect: combines multiple errors (wrong vessels and wrong heart side)

HMS, BM EQ-Bank 52 MC

A volleyball player performs a jump serve. Which respiratory system change enables efficient movement?

  1. Decreased gas exchange at the site of alveoli
  2. Reduced breathing rate during acceleration
  3. Increased pulmonary ventilation as muscles activate
  4. Slower respiratory rate with muscle contraction
Show Answers Only

\(C\)

Show Worked Solution

C is correct: Gaseous exchange increases in alveoli. This links increased ventilation with muscle activation for movement

Other options:

  • Other options incorrectly suggest decreases/reductions during activity

HMS, BM EQ-Bank 41

Outline how the principle of stability relates to safe movement in a standing position.  (3 marks)

Show Answers Only

Sample Answer

  • A wider base of support increases stability by creating a larger area for the body’s weight to be distributed.
  • This extended support base reduces the risk of falling when standing.
  • Keeping the centre of gravity low and within the base of support maintains balance.
  • Proper balance prevents dangerous tilting or loss of equilibrium.
  • Aligning body weight directly over the base ensures forces are distributed evenly through joints.
  • Even force distribution reduces strain on ankles, knees and hips during prolonged standing.
Show Worked Solution

Sample Answer

  • A wider base of support increases stability by creating a larger area for the body’s weight to be distributed.
  • This extended support base reduces the risk of falling when standing.
  • Keeping the centre of gravity low and within the base of support maintains balance.
  • Proper balance prevents dangerous tilting or loss of equilibrium.
  • Aligning body weight directly over the base ensures forces are distributed evenly through joints.
  • Even force distribution reduces strain on ankles, knees and hips during prolonged standing.

HMS, BM EQ-Bank 39 MC

In which movement does balance have the GREATEST impact on safe execution?

  1. Bench press
  2. Bicep curl
  3. Seated row
  4. Handstand
Show Answers Only

\(D\)

Show Worked Solution
  • D is correct: Handstand requires precise balance over center of gravity for safety

Other Options:

  • A is incorrect: Supported by bench, balance less critical
  • B is incorrect: Supported standing/seated position
  • C is incorrect: Fully supported seated position

HMS, BM EQ-Bank 38 MC

During a squat, which biomechanical principle is MOST important for maintaining safety? 

  1. Fluid mechanics
  2. Base of support
  3. Projectile motion
  4. Angular momentum
Show Answers Only

\(B\)

Show Worked Solution
  • B is correct: Wider base of support increases stability and prevents falling during squats.

Other Options:

  • A is incorrect: Fluid mechanics applies to movement through water/air, not squatting
  • C is incorrect: No projectile motion occurs in stationary squats
  • D is incorrect: Angular momentum is not the primary safety principle in squatting

HMS, BM EQ-Bank 34

Outline TWO structural characteristics of slow twitch muscle fibres.  (3 marks)

Show Answers Only

Answers could include TWO of the following:

Slow twitch fibres have:

  • Abundant mitochondria
    • They contain numerous mitochondria throughout the muscle fibre to support aerobic metabolism.
    • These organelles enable efficient ATP production through oxidative pathways, allowing sustained energy generation for prolonged endurance activities.
  • Rich blood supply:
    • Possess an extensive capillary network surrounding each fibre, providing continuous oxygen delivery for aerobic respiration.
    • This vascular density supports the high oxygen demands of endurance activities and contributes to their red appearance.
  • High myoglobin content:
    • Store significant amounts of myoglobin, an oxygen-binding protein within the muscle fibres.
    • This gives them their characteristic red colour and provides an oxygen reserve for sustained aerobic metabolism during prolonged activities.
  • Smaller diameter:
    • Slow twitch fibres have a smaller cross-sectional area compared to fast-twitch fibres.
    • While this limits maximum force production, the smaller size allows for more efficient oxygen diffusion throughout the fibre, enhancing endurance capacity.
Show Worked Solution

Answers could include TWO of the following:

Slow twitch fibres have:

  • Abundant mitochondria
    • They contain numerous mitochondria throughout the muscle fibre to support aerobic metabolism.
    • These organelles enable efficient ATP production through oxidative pathways, allowing sustained energy generation for prolonged endurance activities.
  • Rich blood supply:
    • Possess an extensive capillary network surrounding each fibre, providing continuous oxygen delivery for aerobic respiration.
    • This vascular density supports the high oxygen demands of endurance activities and contributes to their red appearance.
  • High myoglobin content:
    • Store significant amounts of myoglobin, an oxygen-binding protein within the muscle fibres.
    • This gives them their characteristic red colour and provides an oxygen reserve for sustained aerobic metabolism during prolonged activities.
  • Smaller diameter:
    • Slow twitch fibres have a smaller cross-sectional area compared to fast-twitch fibres.
    • While this limits maximum force production, the smaller size allows for more efficient oxygen diffusion throughout the fibre, enhancing endurance capacity.

HMS, BM EQ-Bank 29

Name THREE major muscles of the upper body and outline their primary functions.   (3 marks)

Show Answers Only

Sample Answer

Deltoid:

  • Located covering the shoulder joint, this muscle primarily abducts the arm (raises it laterally).
  • Also assists with flexion and extension depending on which portion contracts.

Pectoralis major:

  • Large chest muscle responsible for horizontal adduction of the arm (bringing arms together).
  • Also performs internal rotation and assists with arm flexion.

Latissimus dorsi:

  • Broad back muscle that extends, adducts and internally rotates the arm at the shoulder joint.
  • Essential for pulling movements.
Show Worked Solution

Sample Answer

Deltoid:

  • Located covering the shoulder joint, this muscle primarily abducts the arm (raises it laterally).
  • Also assists with flexion and extension depending on which portion contracts.

Pectoralis major:

  • Large chest muscle responsible for horizontal adduction of the arm (bringing arms together).
  • Also performs internal rotation and assists with arm flexion.

Latissimus dorsi:

  • Broad back muscle that extends, adducts and internally rotates the arm at the shoulder joint.
  • Essential for pulling movements.

HMS, BM EQ-Bank 27 MC

Which pair of muscles work together in an agonist-antagonist relationship?

  1. Deltoid and trapezius
  2. Biceps and gastrocnemius
  3. Triceps and biceps brachii
  4. Quadriceps and deltoid
Show Answers Only

\(C\)

Show Worked Solution
  • C is correct: Biceps and triceps are antagonists at the elbow – biceps flexes, triceps extends.

Other Options:

  • A is incorrect: Work in different regions, not antagonistic
  • B is incorrect: Work at different joints (elbow vs ankle)
  • D is incorrect: Work at different joints (knee vs shoulder)

HMS, BM EQ-Bank 23 MC

During a biceps curl, what occurs at the elbow joint?

  1. The biceps contracts concentrically as the primary agonist
  2. The triceps contracts concentrically as the primary agonist
  3. The biceps and triceps contract simultaneously
  4. The triceps relaxes while the biceps stabilises
Show Answers Only

\(A\)

Show Worked Solution
  • A is correct: The biceps contracts concentrically as the agonist, producing elbow flexion to lift the weight.

Other options:

  • B is incorrect: The triceps extends the elbow, not flexes it.
  • C is incorrect: Reciprocal inhibition prevents simultaneous contraction
  • D is incorrect: The biceps contracts, not stabilises

HMS, BM EQ-Bank 21

Outline the joint actions that occur at the knee and ankle when performing a squat.  (3 marks)

Show Answers Only

Sample Answer

Downward phase:

  • The knee joint undergoes flexion as the femur-tibia angle decreases.
  • Simultaneously, the ankle performs dorsiflexion with the foot tilting upward toward the shin.

Upward phase:

  • The knee extends, increasing the joint angle to straighten the leg.
  • The ankle undergoes plantarflexion to push through the foot.

Joint actions:

  • These coordinated joint actions enable controlled body lowering and raising throughout the squat movement.
Show Worked Solution

Sample Answer

Downward phase:

  • The knee joint undergoes flexion as the femur-tibia angle decreases.
  • Simultaneously, the ankle performs dorsiflexion with the foot tilting upward toward the shin.

Upward phase:

  • The knee extends, increasing the joint angle to straighten the leg.
  • The ankle undergoes plantarflexion to push through the foot.

Joint actions:

  • These coordinated joint actions enable controlled body lowering and raising throughout the squat movement.

HMS, BM EQ-Bank 15 MC

Which type of muscular contraction is occurring in the quadriceps when descending into a squat?

  1. Isometric contraction
  2. Eccentric contraction
  3. Concentric contraction
  4. Dynamic contraction
Show Answers Only

\(B\)

Show Worked Solution

B is correct: During descent, the quadriceps lengthen under tension to control movement – this is eccentric contraction.

\(\Rightarrow B\)

HMS, BM EQ-Bank 14 MC

Which row correctly identifies the action of performing a bicep curl? 

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex} \ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|l|l|l|}
\hline
\rule{0pt}{2.5ex}\textbf{Agonist Muscle}\rule[-1ex]{0pt}{0pt}& \textbf{Muscular Contraction}& \textbf{Joint Action} \\
\hline
\rule{0pt}{2.5ex}\text{Biceps brachii}\rule[-1ex]{0pt}{0pt}&\text{Isometric eccentric}&\text{Elbow extension}\\
\hline
\rule{0pt}{2.5ex}\text{Biceps brachii}\rule[-1ex]{0pt}{0pt}& \text{Isometric concentric}&\text{Elbow flexion}\\
\hline
\rule{0pt}{2.5ex}\text{Triceps brachii}\rule[-1ex]{0pt}{0pt}& \text{Isometric concentric}&\text{Elbow flexion} \\
\hline
\rule{0pt}{2.5ex}\text{Triceps brachii}\rule[-1ex]{0pt}{0pt}& \text{Isometric eccentric}&\text{Elbow extension} \\
\hline
\end{array}
\end{align*}

Show Answers Only

\(B\)

Show Worked Solution

B is correct: During the upward (concentric) phase of a bicep curl:

  • The biceps brachii is the agonist muscle.
  • It contracts concentrically (shortens) to generate force.
  • This produces elbow flexion to lift the weight.

\(\Rightarrow B\)

HMS, HIC 2022 HSC 3 MC

Which row in the table shows the current infant mortality and life expectancy trends in Australia?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex} \ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\quad\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\quad\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\quad\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\quad\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|c|c|}
\hline
\rule{0pt}{2.5ex}\textit{Infant Mortality}\rule[-1ex]{0pt}{0pt}& \textit{Life Expectancy} \\
\hline
\rule{0pt}{2.5ex}\text{Decreasing}\rule[-1ex]{0pt}{0pt}&\text{Increasing}\\
\hline
\rule{0pt}{2.5ex}\text{Decreasing}\rule[-1ex]{0pt}{0pt}& \text{Decreasing}\\
\hline
\rule{0pt}{2.5ex}\text{Increasing}\rule[-1ex]{0pt}{0pt}& \text{Stable} \\
\hline
\rule{0pt}{2.5ex}\text{Stable}\rule[-1ex]{0pt}{0pt}& \text{Increasing} \\
\hline
\end{array}
\end{align*}

 

Show Answers Only

\( A\)

Show Worked Solution

  • A is correct: Australia shows decreasing infant mortality rates and increasing life expectancy trends.

Other Options:

  • B is incorrect: Life expectancy continues to increase in Australia.
  • C is incorrect: Infant mortality is decreasing, not increasing.
  • D is incorrect: Infant mortality is decreasing, not stable.

HMS, BM EQ-Bank 2 MC

An Olympic weightlifter continues to train despite a minor injury because they are afraid of losing their sponsorship deals and disappointing their parents who have invested significant money in their career. This athlete's motivation is primarily:

  1. Negative and intrinsic
  2. Negative and extrinsic
  3. Positive and intrinsic
  4. Positive and extrinsic
Show Answers Only

\(B\)

Show Worked Solution

The athlete demonstrates:

    • Extrinsic motivation – driven by external factors: sponsorship deals and parental pressure 
    • Negative motivation – fear of loss and disappointment, rather than positive goal achievement

\(\Rightarrow B\)

HMS, BM EQ-Bank 1 MC

A swimmer trains consistently at 5 a.m. every morning, setting personal goals to improve their technique and times, with the aim of qualifying for the Olympic team. This athlete's motivation is primarily:

  1. Negative and extrinsic
  2. Positive and extrinsic
  3. Negative and intrinsic
  4. Positive and intrinsic
Show Answers Only

\(D\)

Show Worked Solution

The athlete demonstrates:

    • Intrinsic motivation – self-driven, personal goal setting, focus on self-improvement
    • Positive motivation – consistent commitment to training, constructive goal-setting approach

\(\Rightarrow D\)

PHYSICS, M5 2017 HSC 22a

A torque is applied to a nut, using a wrench, as shown.
 
   
 
Suggest TWO ways that the applied torque could be increased.   (2 marks)

Show Answers Only

The applied torque can be increased by:

  • Increasing the magnitude of the applied force.
  • Increasing the distance between the nut and the point of applied force.
Show Worked Solution

The applied torque can be increased by:

  • Increasing the magnitude of the applied force.
  • Increasing the distance between the nut and the point of applied force.

ENGINEERING, CS 2024 HSC 27a

A towbar hitch and shear pin is shown.

The hitch is exposed to various environmental conditions.

Outline a method to protect against corrosion.   (2 marks)

Show Answers Only

  • Applying protective finishes like paint or powder coating provides a barrier that shields the component from corrosive elements.
  • This resistance is a result of preventing the hitch from exposure to oxygen, moisture, and environmental contaminants.

Show Worked Solution

  • Applying protective finishes like paint or powder coating provides a barrier that shields the component from corrosive elements.
  • This resistance is a result of preventing the hitch from exposure to oxygen, moisture, and environmental contaminants.

ENGINEERING, TE 2024 HSC 26a

Outline ways in which satellite services have benefited people living and working in rural areas.   (2 marks)

Show Answers Only

  • Satellite technology enables communication in remote regions beyond traditional cellular coverage.
  • Because satellites operate independently of ground-based infrastructure, they can deliver services across vast territories without the distance limitations of cellular networks.

Other possible answers could refer to:

  • Portability
  • Relatively cost effective
  • Uses existing infrastructure

Show Worked Solution

  • Satellite technology enables communication in remote regions beyond traditional cellular coverage.
  • Because satellites operate independently of ground-based infrastructure, they can deliver services across vast territories without the distance limitations of cellular networks.

Other possible answers could refer to:

  • Portability
  • Relatively cost effective
  • Uses existing infrastructure

ENGINEERING, AE 2024 HSC 25a

Outline how 'Black Box' flight data recorders have led to improved aviation safety.   (2 marks)

Show Answers Only

  • Flight data analysis allows engineers to investigate the causes of flight incidents.
  • This enables them to identify necessary safety improvements and implement preventive measures based on their findings.

Show Worked Solution

  • Flight data analysis allows engineers to investigate the causes of flight incidents.
  • This enables them to identify necessary safety improvements and implement preventive measures based on their findings.

ENGINEERING, TE 2024 HSC 23c

An orthogonal drawing of a wi-fi router is shown.
 

Construct a freehand pictorial sketch of the wi-fi router as viewed in the direction of the arrow.   (3 marks)

\begin{array} {|l|}
\hline
\  \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\ \\
\ \\
\ \\
\ \\
\ \\
\ \\
\ \\
\ \\
\ \\
\ \\
\ \\
\ \\
\ \\
\hline
\end{array}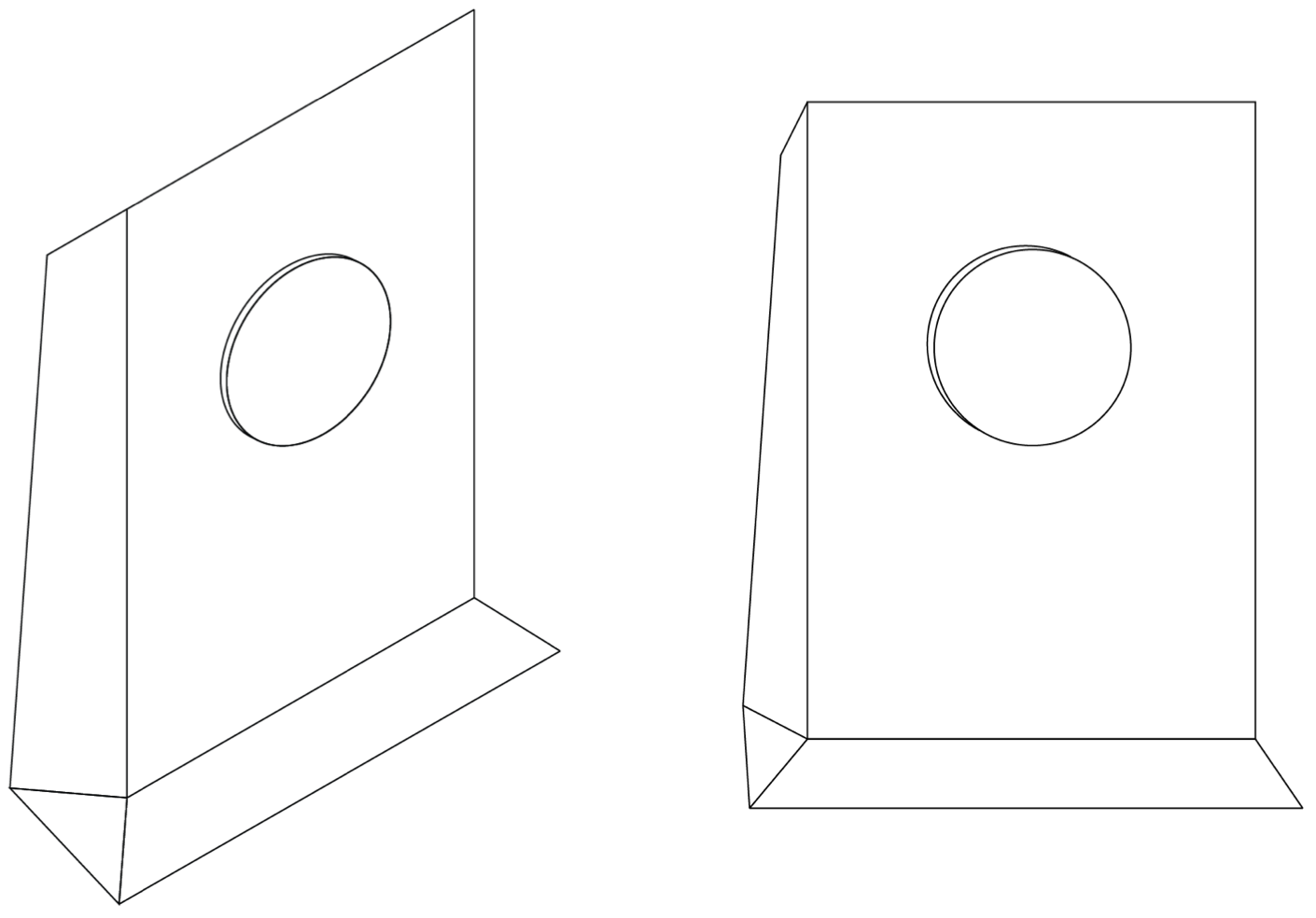

Show Answers Only

Answers could include:

  • Oblique view in the direction of the arrow
  • Perspective view in the direction of the arrow
  • Planometric view in the direction of the arrow.

Show Worked Solution

Answers could include:

  • Oblique view in the direction of the arrow
  • Perspective view in the direction of the arrow
  • Planometric view in the direction of the arrow.

ENGINEERING, TE 2024 HSC 23b

Telecommunications engineers face many work health and safety risks while carrying out their duties.

With reference to ONE issue, describe strategies that can be implemented to reduce the risk for the engineer.   (3 marks)

Show Answers Only

  • Telecommunications engineers work on satellite dishes and other structures at height.
  • To minimise the risk, they must ensure that they wear safety harnesses that prevent injuries from falling from heights.
  • The engineer should have completed relevant safety training before undertaking the task so that they are aware of the possible risks and how to avoid them. 

Other answers could include:

  • UV/EMR exposure during installation and maintenance of equipment; PPE training, warning signage and barriers.
  • Electrocution; training and safe work practices, work site inspections, SWMSs, emergency management plans/drills.
  • Operating equipment within guidance specifications.

Show Worked Solution

  • Telecommunications engineers work on satellite dishes and other structures at height.
  • To minimise the risk, they must ensure that they wear safety harnesses that prevent injuries from falling from heights.
  • The engineer should have completed relevant safety training before undertaking the task so that they are aware of the possible risks and how to avoid them. 

Other answers could include:

  • UV/EMR exposure during installation and maintenance of equipment; PPE training, warning signage and barriers.
  • Electrocution; training and safe work practices, work site inspections, SWMSs, emergency management plans/drills.
  • Operating equipment within guidance specifications.

ENGINEERING, AE 2024 HSC 22c

Discuss the use of computer-aided drawing (CAD) in aeronautical engineering.   (3 marks)

Show Answers Only
  • CAD enables precise geometrical modelling that can be translated into physical objects through methods like 3D printing and other more traditional manufacturing processes.
  • CAD can be used to analyse aircraft component performance under various conditions, including bending stress of airframes.
  • Simulation results refine CAD designs, ensuring compliance with safety and performance standards.
  • While CAD provides accurate specifications for computer-controlled machining, it has drawbacks – it requires significant investment in both training time to develop expertise and the substantial cost of implementing CAD systems.
Show Worked Solution
  • CAD enables precise geometrical modelling that can be translated into physical objects through methods like 3D printing and other more traditional manufacturing processes.
  • CAD can be used to analyse aircraft component performance under various conditions, including bending stress of airframes.
  • Simulation results refine CAD designs, ensuring compliance with safety and performance standards.
  • While CAD provides accurate specifications for computer-controlled machining, it has drawbacks – it requires significant investment in both training time to develop expertise and the substantial cost of implementing CAD systems.

ENGINEERING, AE 2024 HSC 22a

Outline the environmental responsibilities of an aeronautical engineer.   (2 marks)

Show Answers Only

Answers could include two of the following:

  • Engineers have a professional obligation to operate within environmental laws and regulations. 
  • Engineers should design and implement proper waste management protocols to minimise environmental harm.
  • Ensuring aircraft components are designed, tested and certified to meet environmental requirements, particularly regarding noise emission standards.

Show Worked Solution

Answers could include two of the following:

  • Engineers have a professional obligation to operate within environmental laws and regulations. 
  • Engineers should design and implement proper waste management protocols to minimise environmental harm.
  • Ensuring aircraft components are designed, tested and certified to meet environmental requirements, particularly regarding noise emission standards.

ENGINEERING, CS 2024 HSC 21a

Two piers from different eras, used to support civil structures, are shown.
 

Outline how innovations in engineering materials have improved the inservice properties of piers.   (2 marks)

Show Answers Only

Improvements in pier properties :

  • Concrete better than timber at resisting insect attack
  • Concrete less susceptible to environmental conditions.
  • Concrete properties include increased strength and durability
  • Less maintenance with concrete blocks

Show Worked Solution

Improvements in pier properties :

  • Concrete better than timber at resisting insect attack
  • Concrete less susceptible to environmental conditions.
  • Concrete properties include increased strength and durability
  • Less maintenance with concrete blocks

ENGINEERING, PPT 2024 HSC 19 MC

Which is the correct angle of repose for rock fill, used on a highway construction, that has a coefficient of friction of 0.84?

  1. 20°
  2. 30°
  3. 40°
  4. 50°
Show Answers Only

\(C\)

Show Worked Solution

\(\mu = 0.84\)

\(\tan \theta\) \(=0.84\)  
\(\theta\) \(= \tan^{-1} 0.84=40^{\circ}\)  

 
\(\Rightarrow C\)

ENGINEERING, TE 2024 HSC 13 MC

What is the primary function of GPS satellites?

  1. Receiving magnetic field data for accuracy of location
  2. Receiving signals from GPS devices to determine distance
  3. Transmitting signals that provide accurate timing and positioning data
  4. Transmitting weather system data to ground-based stations for tracking
Show Answers Only

\(C\)

Show Worked Solution
  • GPS satellites continuously broadcast precisely timed radio signals containing their exact orbital position data, which GPS receivers use to calculate their location through trilateration.

\(\Rightarrow C\)

PHYSICS, M6 2024 HSC 28

An electron gun fires a beam of electrons at 2.0 × 10\(^6\) m s\(^{-1}\) through a pair of parallel charged plates towards a screen that is 30 mm from the end of the plates as shown.

There is a uniform electric field between the plates of 1.5 × 10\(^4\) N C\(^{-1}\). The plates are 5.0 mm wide and 20 mm apart. The electron beam enters mid-way between the plates. \(X\) marks the spot on the screen where an undeflected beam would strike.

Ignore gravitational effects on the electron beam.
 

 

  1. Show that the acceleration of an electron between the parallel plates is 2.6 × 10\(^{15}\) m s\(^{-2}\).   (2 marks)

  2. Show that the vertical displacement of the electron beam at the end of the parallel plates is approximately 8.1 mm.   (2 marks)

  3. How far from point \(X\) will the electron beam strike the screen?   (3 marks)

Show Answers Only

a.   \(\text{Using}\ \ F=qE\ \ \text{and}\ \ F=ma:\)

  \(a=\dfrac{qE}{m} = \dfrac{1.5 \times 10^{4} \times 1.602 \times 10^{-19}}{9.109 \times 10^{-31}} = 2.6 \times 10^{15}\ \text{m s}^{-2} \)
 

b.  \(\text{Time of beam between the plates:}\)

\(\text{Horizontal velocity}\ (v)\ = 2 \times 10^{6}\ \text{m s}^{-1} \)

\(\text{Distance to screen}\ (s)\ = 5.0\ \text{mm}\ = \dfrac{5}{1000} = 0.005\ \text{m}\)

  \(t=\dfrac{s}{v} = \dfrac{0.005}{2 \times 10^{6}} = 2.5 \times 10^{-9}\ \text{s} \)
 

\(\text{Find vertical displacement at end of plates:}\)

  \(s=\dfrac{1}{2} at^{2} = 0.5 \times 2.6 \times 10^{15} \times (2.5 \times 10^{-9})^{2} = 0.008125\ \text{m}\ = 8.1\ \text{mm} \)
 

c.   \(\text{Find vertical velocity of beam when leaving the plates:}\)

  \(v=at=2.6 \times 10^{15} \times 2.5 \times 10^{-9} = 6.5 \times 10^{6}\ \text{m s}^{-1} \)
 

\(\text{Time for beam to hit screen:}\)

\(\text{Distance to screen}\ (s)\ = 30\ \text{mm}\ = \dfrac{30}{1000} = 0.03\ \text{m}\)

  \(t=\dfrac{s}{v} = \dfrac{0.03}{2 \times 10^{6}} = 1.5 \times 10^{-8}\ \text{s} \)
 

\(\text{Vertical displacement (from end of plates):}\)

  \(s=vt=6.5 \times 10^{6} \times 1.5 \times 10^{-8} = 0.0975\ \text{m} \)
 

\(\text{Distance from}\ X = 0.0081 + 0.0975 = 0.11\ \text{m} \)

Show Worked Solution

a.   \(\text{Using}\ \ F=qE\ \ \text{and}\ \ F=ma:\)

  \(a=\dfrac{qE}{m} = \dfrac{1.5 \times 10^{4} \times 1.602 \times 10^{-19}}{9.109 \times 10^{-31}} = 2.6 \times 10^{15}\ \text{m s}^{-2} \)
 

b.  \(\text{Time of beam between the plates:}\)

\(\text{Horizontal velocity}\ (v)\ = 2 \times 10^{6}\ \text{m s}^{-1} \)

\(\text{Distance to screen}\ (s)\ = 5.0\ \text{mm}\ = \dfrac{5}{1000} = 0.005\ \text{m}\)

  \(t=\dfrac{s}{v} = \dfrac{0.005}{2 \times 10^{6}} = 2.5 \times 10^{-9}\ \text{s} \)
 

\(\text{Find vertical displacement at end of plates:}\)

  \(s=\dfrac{1}{2} at^{2} = 0.5 \times 2.6 \times 10^{15} \times (2.5 \times 10^{-9})^{2} = 0.008125\ \text{m}\ = 8.1\ \text{mm} \)
 

c.   \(\text{Find vertical velocity of beam when leaving the plates:}\)

  \(v=at=2.6 \times 10^{15} \times 2.5 \times 10^{-9} = 6.5 \times 10^{6}\ \text{m s}^{-1} \)
 

\(\text{Time for beam to hit screen:}\)

\(\text{Distance to screen}\ (s)\ = 30\ \text{mm}\ = \dfrac{30}{1000} = 0.03\ \text{m}\)

  \(t=\dfrac{s}{v} = \dfrac{0.03}{2 \times 10^{6}} = 1.5 \times 10^{-8}\ \text{s} \)
 

\(\text{Vertical displacement (from end of plates):}\)

  \(s=vt=6.5 \times 10^{6} \times 1.5 \times 10^{-8} = 0.0975\ \text{m} \)
 

\(\text{Distance from}\ X = 0.0081 + 0.0975 = 0.11\ \text{m} \)

♦ Mean mark (c) 40%.

Calculus, MET2 2024 VCAA 3

The points shown on the chart below represent monthly online sales in Australia.

The variable \(y\) represents sales in millions of dollars.

The variable \(t\) represents the month when the sales were made, where \(t=1\) corresponds to January 2021, \(t=2\) corresponds to February 2021 and so on.

  1. A cubic polynomial \(p ;(0,12] \rightarrow R, p(t)=a t^3+b t^2+c t+d\) can be used to model monthly online sales in 2021.

    The graph of \(y=p(f)\) is shown as a dashed curve on the set of axes above.

    It has a local minimum at (2,2500) and a local maximum at (11,4400).

     i. Find, correct to two decimal places, the values of \(a, b, c\) and \(d\).   (3 mark)

    ii. Let \(q:(12,24] \rightarrow R, q(t)=p(t-h)+k\) be a cubic function obtained by translating \(p\), which can be used to model monthly online sales in 2022.

    Find the values of \(h\) and \(k\) such that the graph of \(y=q(t)\) has a local maximum at \((23,4750)\).   (2 marks)

  2. Another function \(f\) can be used to model monthly online sales, where
     
    \(f:(0,36] \rightarrow R, f(t)=3000+30 t+700 \cos \left(\dfrac{\pi t}{6}\right)+400 \cos \left(\dfrac{\pi t}{3}\right)\)

    Part of the graph of \(f\) is shown on the axes below.

    1. Complete the graph of \(f\) on the set of axes above until December 2023, that is, for \(t \in(24,36]\).Label the endpoint at \(t=36\) with its coordinates.   (2 marks)
    1. The function \(f\) predicts that every 12 months, monthly online sales increase by \(n\) million dollars.

      Find the value of \(n\).   (1 mark)

    1. Find the derivative \(f^{\prime}(t)\).   (1 mark)
    1. Hence, find the maximum instantaneous rate of change for the function \(f\), correct to the nearest million dollars per month, and the values of \(t\) in the interval \((0,36]\) when this maximum rate occurs, correct to one decimal place.   (2 marks)
Show Answers Only

ai.   \(a\approx -5.21, b\approx 101.65, c\approx -344.03, d\approx 2823.18\)

aii.  \(h=12, k=350\)

bi.  

bii.  \( n=360\)

biii. \(f^{\prime}(t)=30-\dfrac{350\pi}{3}\sin\left(\dfrac{\pi t}{6}\right)-\dfrac{400\pi}{3}\sin\left(\dfrac{\pi t}{3}\right)\)

biv. \(\text{Maximum rate occurs at }t=10.2, 22.2, 34.2\)

\(\text{Maximum rate}\ \approx 725\ \text{million/month}\)

Show Worked Solution
ai.   \(\text{Given}\ p(2)=2500, p(11)=4400, p^{\prime}(2)=0\ \text{and}\ p^{\prime}(11)=0\) 
  
\(p(t)=at^3+bt^2+ct+d\ \Rightarrow\ p^{\prime}(t)=3at^2+2bt+c\)
  
\(\text{Using CAS:}\)
    
\(\text{Solve}
\begin{cases}
8a+4b+2c+d=2500 \\
1331a+121b+11c+d=4400 \\
12a+4b+c=0  \\
363a+22b+c=0
\end{cases}\)
  

\(a\approx -5.21, b\approx 101.65, c\approx -344.03, d\approx 2823.18\)

aii. \(\text{Local maximim }p(t)\ \text{is}\ (11, 4400)\)

\(\therefore\ h\) \(=23-11=12\)
\(k\) \(=4750-4400=350\)

 

bi.   \(\text{Plotting points from CAS:}\)

\((24,4820), (26, 3930), (28, 3290), (30, 3600), (32, 3410), (34, 4170), (36, 5180)\)

bii.  \(\text{Using CAS: }\)

\(f(12)-f(0)\) \(=4460-4100=360\)
\(f(24)-f(12)\) \(=4820-4460=360\)
\(f(36)-f(24)\) \(=5180-4820=360\) 

\(\therefore\ n=360\)

biii.  \(f(t)\) \(=3000+30t+700\cos\left(\dfrac{\pi t}{6}\right)+400\cos\left(\dfrac{\pi t}{3}\right)\)
  \(f^{\prime}(t)\) \(=30-\dfrac{700\pi}{6}\sin\left(\dfrac{\pi t}{6}\right)-\dfrac{400\pi}{3}\sin\left(\dfrac{\pi t}{3}\right)\)
    \(=30-\dfrac{350\pi}{3}\sin\left(\dfrac{\pi t}{6}\right)-\dfrac{400\pi}{3}\sin\left(\dfrac{\pi t}{3}\right)\)

  
biv.  \(\text{Max instantaneous rate of change occurs when }f^{\prime\prime}(t)=0\)

\(\text{Maximum rate occurs at }t=10.2, 22.2, 34.2\)

\(\text{Maximum rate using CAS:}\)

\(f^{\prime}(10.2)=f^{\prime}(22.2)=f^{\prime}(34.2)=725.396\approx 725\ \text{million/month}\)

Calculus, MET2 2024 VCAA 2

A model for the temperature in a room, in degrees Celsius, is given by

\(f(t)=\left\{
\begin{array}{cc}12+30 t & \quad \quad 0 \leq t \leq \dfrac{1}{3} \\
22 & t>\dfrac{1}{3}
\end{array}\right.\)

where \(t\) represents time in hours after a heater is switched on.

  1. Express the derivative \(f^{\prime}(t)\) as a hybrid function.   (2 marks)
  1. Find the average rate of change in temperature predicted by the model between \(t=0\) and \(t=\dfrac{1}{2}\).
  2. Give your answer in degrees Celsius per hour.   (1 mark)
  1. Another model for the temperature in the room is given by \(g(t)=22-10 e^{-6 t}, t \geq 0\).
  2.  i. Find the derivative \(g^{\prime}(t)\).   (1 mark)
  3. ii. Find the value of \(t\) for which \(g^{\prime}(t)=10\).
  4.     Give your answer correct to three decimal places.   (1 mark)
  1. Find the time \(t \in(0,1)\) when the temperatures predicted by the models \(f\) and \(g\) are equal.
  2. Give your answer correct to two decimal places.   (1 mark)
  1. Find the time \(t \in(0,1)\) when the difference between the temperatures predicted by the two models is the greatest.
  2. Give your answer correct to two decimal places.   (1 mark)
  1. The amount of power, in kilowatts, used by the heater \(t\) hours after it is switched on, can be modelled by the continuous function \(p\), whose graph is shown below.

\(p(t)=\left\{
\begin{array}{cl}1.5 & 0 \leq t \leq 0.4 \\
0.3+A e^{-10 t} & t>0.4
\end{array}\right.\)

The amount of energy used by the heater, in kilowatt hours, can be estimated by evaluating the area between the graph of \(y=p(t)\) and the \(t\)-axis.
 

  1.   i. Given that \(p(t)\) is continuous for \(t \geq 0\), show that \(A=1.2 e^4\).   (1 mark)
  2.  ii. Find how long it takes, after the heater is switched on, until the heater has used 0.5 kilowatt hours of energy.
  3.     Give your answer in hours.   (1 mark)
  4. iii. Find how long it takes, after the heater is switched on, until the heater has used 1 kilowatt hour of energy.
  5.     Give your answer in hours, correct to two decimal places.   (2 marks)

Show Answers Only

a.    \(f^{\prime}(t)=\left\{
\begin{array}{cc}30  & \quad \quad 0 \leq t <\dfrac{1}{3} \\
0 & t>\dfrac{1}{3}
\end{array}\right.\)

b.    \(20^{\circ}\text{C/h}\)

ci.    \(g^{\prime}(t)=60e^{-6t}\)

cii.   \(0.299\ \text{(3 d.p.)}\)

d.    \(0.27\ \text{(2 d.p.)}\)

e.    \(0.12\ \text{(2 d.p.)}\)

fi.   \(\text{Because function is continuous}\)

\(0.3+Ae^{-10t}\) \(=1.5\)
\(Ae^{-10\times 0.4}\) \(=1.2\)
\(A\) \(=\dfrac{1.2}{e^{-10\times 0.4}}\)
  \(=1.2e^4\)

fii.  \(\dfrac{1}{3}\ \text{hours}\)

fiii. \(1.33\ \text{(2 d.p.)}\)

Show Worked Solution

a.    \(f^{\prime}(t)=\left\{
\begin{array}{cc}30  & \quad \quad 0 \leq t < \dfrac{1}{3} \\
0 & t>\dfrac{1}{3}
\end{array}\right.\)

b.    \(\text{When }\ t=0, f(t)=12\ \ \text{and when }\ t=\dfrac{1}{2}, f(t)=22\)

\(\therefore\ \text{Average rate of change}\) \(=\dfrac{22-12}{\frac{1}{2}}\)
  \(=20^{\circ}\text{C/h}\)

 

ci.    \(g(t)\) \(=22-10 e^{-6 t}\)
  \(g^{\prime}(t)\) \(=60e^{-6t},\ \ t\geq 0\)

 

cii.   \(60e^{-6t}\) \(=10\)
  \(-6t\,\ln{e}\) \(=\ln{\dfrac{1}{6}}\)
  \(t\) \(=\dfrac{\ln{\frac{1}{6}}}{-6}\)
      \(=0.2986…\approx 0.299\ \text{(3 d.p.)}\)

 

d.     \(\left\{
\begin{array}{cc}12+30 t & \ \  0 \leq t \leq \dfrac{1}{3} \\
22 & t>\dfrac{1}{3}
\end{array}\right.\)		 \(=22-10e^{-6t}\)

\(\text{Using CAS:}\)

\(\text{Temps equal when}\ t\approx 0.27\ \text{(2 d.p.)}\)

 

e.     \(\text{Difference }(D)\) \(=|g(t)-f(t)|\)
    \(=\left(22-10e^{-6t}\right)-(12+30t)\)
  \(\dfrac{dD}{dt}\) \(=60e^{-6t}-30\)

\(\text{Max time diff when}\ \dfrac{dD}{dt}=0\)

\(\therefore\ 60e^{-6t}-30\) \(=0\)
\(e^{-6t}\) \(=0.5\)
\(-6t\) \(=\ln{0.5}\)
\(t\) \(=0.1155\dots\)
  \(\approx 0.12\ \text{(2 d.p.)}\)

 

fi.   \(\text{Because function is continuous}\)

\(0.3+Ae^{-10t}\) \(=1.5\)
\(Ae^{-10\times 0.4}\) \(=1.2\)
\(A\) \(=\dfrac{1.2}{e^{-10\times 0.4}}\)
  \(=1.2e^4\)

  
fii.  \(\text{Using CAS:}\)

\(\text{Or, considering the graph, the area from 0 to 0.4 }=0.6\ \rightarrow t<0.4\)

\(\therefore\ \text{Solving}\ 1.5t=0.5\ \rightarrow\ t=\dfrac{1}{3}\)

\(\therefore\ \text{It takes }\dfrac{1}{3}\ \text{hours for heater to use 0.5  kilowatts.}\)
  

fiii. \(\text{Using CAS:}\)

\(1.5\times 4+\displaystyle\int_{0.4}^{t}0.3+1.2e^4.e^{-10t}dt\) \(=1\)
\(\Bigg[0.3t+0.12e^4.e^{-10t}\Bigg]_{0.4}^{t}\) \(=0.4\)
\(t\) \(=1.3333\dots\)
  \(\approx 1.33\ \text{(2 d.p.)}\)

 

Functions, MET2 2024 VCAA 1

Consider the function  \( f: R \rightarrow R, f(x)=(x+1)(x+a)(x-2)(x-2 a) \text { where } a \in R \text {. } \)

  1. State, in terms of \(a\) where required, the values of \(x\) for which \(f(x)=0\).  (1 mark
  1. Find the values of \(a\) for which the graph of \(y=f(x)\) has
      
     i. exactly three \(x\)-intercepts.   (2 marks)

    ii. exactly four \(x\)-intercepts.   (1 mark)

  1. Let \(g\) be the function \(g: R \rightarrow R, g(x)=(x+1)^2(x-2)^2\), which is the function \(f\) where \(a=1\).
      
      i. Find \(g^{\prime}(x)\)   (1 mark)

     ii. Find the coordinates of the local maximum of \(g\).   (1 mark)

    iii. Find the values of \(x\) for which \(g^{\prime}(x)>0\).   (1 mark)

     iv. Consider the two tangent lines to the graph of \(y=g(x)\) at the points where
    \(x=\dfrac{-\sqrt{3}+1}{2}\) and \(x=\dfrac{\sqrt{3}+1}{2}\). Determine the coordinates of the point of intersection of these two tangent lines.   (2 marks)

  1. Let \(g\) remain as the function \(g: R \rightarrow R, g(x)=(x+1)^2(x-2)^2\), which is the function \(f\) where \(a=1\).

    Let \(h\) be the function \(h: R \rightarrow R, h(x)=(x+1)(x-1)(x+2)(x-2)\), which is the function \(f\) where \(a=-1\).
      
     i. Using translations only, describe a sequence of transformations of \(h\), for which its image would have a local maximum at the same coordinates as that of \(g\).   (1 mark)

    ii. Using a dilation and translations, describe a different sequence of transformations of \(h\), for which its image would have both local minimums at the same coordinates as that of \(g\).   (2 marks)

Show Answers Only

a.    \(x=-1, x=a, x=2, x=2a\)

bi.  \(a=0, -2, -\dfrac{1}{2}\)

bii. \(R\ \backslash\left\{ -2, -\dfrac{1}{2}, 0, 1\right\}\)

ci.  \(g^{\prime}(x)=2(x-2)(x+1)(2x-1)\)

cii. \(\left(\dfrac{1}{2} , \dfrac{81}{16}\right)\)

ciii. \(x\in\left(-1, \dfrac{1}{2}\right)\cup (2, \infty)\)

civ. \(\left(\dfrac{1}{2}, \dfrac{27}{4}\right)\)

di.   \(\text{Translate }\dfrac{1}{2}\ \text{unit to the right and }\dfrac{81}{16}-4=\dfrac{17}{16}\ \text{units upwards.}\)

dii.  \(\text{Combination is a dilation of }h(x)\ \text{by a factor of}\ \dfrac{3}{\sqrt{10}}\ \text{followed by a }\)

\(\text{translation of }\dfrac{1}{2} \ \text{a unit to the right and an upwards translation of}\ \dfrac{9}{4} \ \text{units}\)

Show Worked Solution

a.    \(x=-1, x=a, x=2, x=2a\)

bi.  \(a=0, -2, -\dfrac{1}{2}\)

bii. \(\text{The solution must be all }R\ \text{except those that give 3 or less solutions.}\)

\(\therefore\ R\ \backslash\left\{ -2, -\dfrac{1}{2}, 0, 1\right\}\)

ci.    \(g^{\prime}(x)\) \(=2(2-x)(x+1)^2+(x-2)^22(x+1)\)
    \(=2(x-2)(x+1)(x+1+x+2)\)
    \(=2(x-2)(x+1)(2x-1)\)

  
cii.  \(\text{When  }g^{\prime}(x)=0, x=2, -1, \dfrac{1}{2}\)

\(\text{From graph local maximum occurs when }x=\dfrac{1}{2}\)

\(g\left(\dfrac{1}{2}\right)\) \(=\left(\dfrac{1}{2}+1\right)^2\left(\dfrac{1}{2}-2\right)^2\)
  \(=\dfrac{9}{4}\times \dfrac{9}{4}=\dfrac{81}{16}\)

  
\(\therefore\ \text{Local maximum at}\ \left(\dfrac{1}{2} , \dfrac{81}{16}\right)\)

ciii. \(\text{From graph}\ g^{\prime}(x)>0\ \text{when }x\in\left(-1, \dfrac{1}{2}\right)\cup (2, \infty)\)

civ.  \(\text{Use CAS to find tangent lines and solve to find intersection.}\)

\(\text{Point of intersection of tangent lines}\ \left(\dfrac{1}{2}, \dfrac{27}{4}\right)\)

di.  \(\text{Local maximum of }g(x)\ \rightarrow\left(\dfrac{1}{2}, \dfrac{81}{16}\right)\)

\(\text{From CAS local maximum of }h(x)\ \rightarrow \left(0, 4\right)\)

\(\therefore\ \text{Translate }\dfrac{1}{2}\ \text{unit to the right and }\dfrac{81}{16}-4=\dfrac{17}{16}\ \text{units upwards.}\)

dii. \(\text{Using CAS to solve }g^{\prime}(x)=0\ \text{and }h^{\prime}(x)=0\)

\(\text{Local Minimums for }g(x)\ \text{at }(-1, 0)\ \text{and }(2, 0)\ \text{which are 3 apart.}\)

\(\text{Local minimums for at }h(x)\ \text{at }\left(-\sqrt{\dfrac{5}{2}}, -\dfrac{9}{4}\right)\ \text{and }\left(\sqrt{\dfrac{5}{2}}, -\dfrac{9}{4}\right)\)

\(\therefore\ \text{Combination is a dilation of }h(x)\ \text{by a factor of}\ \dfrac{3}{\sqrt{10}}\ \text{followed by a }\)

\(\text{translation of }\dfrac{1}{2} \ \text{a unit to the right and an upwards translation of}\ \dfrac{9}{4} \ \text{units.}\)

 

Calculus, MET2 2024 VCAA 2 MC

A function  \(g: R \rightarrow R\)  has the derivative  \( { \displaystyle g^{\prime}(x)=x^3-x } \).

Given that  \(g(0)=5\), the value of \(g(2)\) is

  1. \(2\)
  2. \(3\)
  3. \(5\)
  4. \(7\)
Show Answers Only

\(D\)

Show Worked Solution
\({ \displaystyle g^{\prime}(x)}\) \(=x^3-x\)
\(g(x)\) \(=\dfrac{x^4}{4}-\dfrac{x^2}{2}+c\)

 
\(\text{Given }g(0)=5,\ c=5\) 

\(g(x)=\dfrac{x^4}{4}-\dfrac{x^2}{2}+5\)

\(\therefore\ g(2)=\dfrac{2^4}{4}-\dfrac{2^2}{2}+5=7\)

\(\Rightarrow D\)

PHYSICS, M6 2024 HSC 21

To tighten a nut, a force of 75 N is applied to a spanner at an angle, as shown.
 

  1. Calculate the magnitude of the torque produced by the applied force.   (2 marks)

  2. Explain TWO ways in which torque can be increased in a simple DC motor.   (4 marks)

Show Answers Only

a.    \(8.7\ \text{Nm  (2 sig.fig)}\)  

b.    Torque \((\tau=nIAB)\) in a simple DC motor can be increased as follows:

  • Increasing the current through the motor by increasing the voltage of the power source. This will increase the force on each arm of the motor due to the motor effect and increase the overall torque of the motor.
  • Increasing the number of coils in the DC motor. This will increase the torque as each individual coil will experience a force due to the motor effect. The forces on each coil will add together to increase the overall force on each arm of the motor increasing the torque of the motor.
  • Other answers could have included: increasing the area of the coil, increasing the strength of the external magnetic field by using electromagnets or adding a radial magnetic field as it increases the average torque applied to the motor.

Show Worked Solution

a.     \(\tau\) \(=Fr\sin\theta\)
    \(=75 \times 0.18 \times \sin 40\)
    \(=8.7\ \text{Nm  (2 sig.fig)}\)  

 

b.    Torque \((\tau=nIAB)\) in a simple DC motor can be increased as follows:

  • Increasing the current through the motor by increasing the voltage of the power source. This will increase the force on each arm of the motor due to the motor effect and increase the overall torque of the motor.
  • Increasing the number of coils in the DC motor. This will increase the torque as each individual coil will experience a force due to the motor effect. The forces on each coil will add together to increase the overall force on each arm of the motor increasing the torque of the motor.
  • Other answers could have included: increasing the area of the coil, increasing the strength of the external magnetic field by using electromagnets or adding a radial magnetic field as it increases the average torque applied to the motor.

PHYSICS, M7 2024 HSC 6 MC

The photoelectric effect is mathematically modelled by the following relationship:

\(K_{\max }=h f-\phi\)

In this model, the symbol \(\phi\) represents the amount of energy

  1. supplied by a photon to an electron.
  2. retained by an electron after being hit.
  3. required to release an electron from a material.
  4. left over after a collision of a photon with an electron.
Show Answers Only

\(C\)

Show Worked Solution
  • \(\phi\) is the symbol for the work function of the metal. 
  • The work function of a metal is defined as the minimum energy require for an electron to break free from the metal.

\(\Rightarrow C\)

PHYSICS, M8 2024 HSC 5 MC

A star cluster is a group of stars that form at the same time. Hertzsprung-Russell diagrams for three star clusters, \(X, Y\) and \(Z\) are shown.
 

Which row of the table correctly shows the three star clusters from youngest to oldest?
 

Show Answers Only

\(A\)

Show Worked Solution
  • Most stars begin on the main sequence when they begin to fuse hydrogen to helium in their core. As the stars get older and run out of hydrogen to fuse they will begin to fuse heavier elements and move off the main sequence. When stars stop fusing elements they become white dwarf stars and move to the bottom left side of the Hertzsprung-Russell diagram. 
  • Hotter stars with a higher luminosity will move off the main sequence before cooler and less luminous stars.
  • All stars in cluster \(Y\) are on the main sequence, some stars in cluster \(X\) and \(Z\) have moved off the main sequence to fuse heavier elements and some stars in cluster \(Z\) have also stopped fusing elements and turned into white dwarf stars.
  • Cluster \(Y\) is the youngest, cluster \(X\) is in the middle and cluster \(Z\) is the oldest.

\(\Rightarrow A\)

PHYSICS, M7 2024 HSC 2 MC

Which of the following provides evidence for the model of light proposed by Huygens?

  1. Emission spectra
  2. Diffraction of light
  3. Black body radiation
  4. The photoelectric effect
Show Answers Only

\(B\)

Show Worked Solution
  • Huygens’s proposed that light was a wave and light waves spread out in all directions as spherical wave fronts from a point source. 
  • Therefore the diffraction of light provided evidence for Huygens model of light as diffraction is a wave phenomena.

\(\Rightarrow B\) 

PHYSICS, M5 2024 HSC 1 MC

The diagram shows an object, \(P\), undergoing uniform circular motion.
 

Which arrow shows the direction of the net force acting on \(P\) ?

  1. \(W\)
  2. \(X\)
  3. \(Y\)
  4. \(Z\)
Show Answers Only

\(C\)

Show Worked Solution
  • During uniform circular motion, the direction of the net force acting on an object will always be towards the centre of the circle.

\(\Rightarrow C\)

CHEMISTRY, M2 EQ-Bank 3

Balance the following chemical equations:

  1. \(\ce{HCl(aq) + Zn(s) -> ZnCl2(aq) + H2(g)}\)   (1 mark)

  2. \(\ce{CuSO4(aq) + AgNO3(aq) -> Ag2SO4(s) + Cu(NO3)2(aq)}\)   (1 mark)

Show Answers Only

a.    \(\ce{2HCl(aq) + Zn(s) -> ZnCl2(aq) + H2(g)}\)

b.    \(\ce{CuSO4(aq) + 2AgNO3(aq) -> Ag2SO4(s) + Cu(NO3)2(aq)}\)

Show Worked Solution

a.    \(\ce{2HCl(aq) + Zn(s) -> ZnCl2(aq) + H2(g)}\)

b.    \(\ce{CuSO4(aq) + 2AgNO3(aq) -> Ag2SO4(s) + Cu(NO3)2(aq)}\)

BIOLOGY, M5 2024 HSC 28

Cystic fibrosis is an inherited disorder that causes damage to the lungs, digestive system and other organs in the body. A person with cystic fibrosis will have two faulty recessive alleles for the cystic fibrosis gene (CFTR) on chromosome 7.

  1. Two healthy parents, heterozygous for cystic fibrosis, have a child that does not have cystic fibrosis. They are planning to have a second child.

    Using a Punnett square, determine the probability of their second child being born with the condition. Use \(R\) for the normal CFTR allele, and \(r\) for the faulty CFTR allele.   (3 marks)

The defect that creates the faulty CFTR allele is often caused by the deletion of three nucleotides. The following diagram illustrates a small section of the CFTR gene and the corresponding amino acid sequence of the CFTR protein.
 
 
The following codon chart displays all the codons and the corresponding amino acids. The chart translates mRNA sequences into amino acids.
 
  1. Explain how the deletion of nucleotides in the CFTR gene removes only one amino acid. Include reference to the nucleotides that code for isoleucine and phenylalanine amino acids.   (4 marks)

Show Answers Only

a.    Punnett square:

\begin{array} {|c|c|c|}
\hline
\rule{0pt}{2.5ex} \text{} \rule[-1ex]{0pt}{0pt} & \boldsymbol{R} & \boldsymbol{r} \\
\hline
\rule{0pt}{2.5ex} \boldsymbol{R} \rule[-1ex]{0pt}{0pt} & \textit{RR} & \textit{Rr} \\
\hline
\rule{0pt}{2.5ex} \boldsymbol{r}\rule[-1ex]{0pt}{0pt} & \textit{Rr} & \textit{rr} \\
\hline
\end{array}

Probability of 2nd child having cystic fibrosis = 25%.
 

b.    Deletion of nucleotides in CFTR gene:

  • Three mRNA nucleotides (a codon) spell out instructions for one amino acid. The deletion here stretches across two codons that normally code for isoleucine and phenylalanine.
  • At first glance, you’d expect losing nucleotides from both codons would mess up both amino acids.
  • In isoleucine however, multiple different triplet codes can signal for its production. Its original code was AUC and after the deletion it became AUU – which still makes isoleucine.
  • Only phenylalanine gets knocked out of the protein sequence, while isoleucine stays put thanks to its flexible coding options.

Show Worked Solution

a.    Punnett square:

\begin{array} {|c|c|c|}
\hline
\rule{0pt}{2.5ex} \text{} \rule[-1ex]{0pt}{0pt} & \boldsymbol{R} & \boldsymbol{r} \\
\hline
\rule{0pt}{2.5ex} \boldsymbol{R} \rule[-1ex]{0pt}{0pt} & \textit{RR} & \textit{Rr} \\
\hline
\rule{0pt}{2.5ex} \boldsymbol{r}\rule[-1ex]{0pt}{0pt} & \textit{Rr} & \textit{rr} \\
\hline
\end{array}

Probability of 2nd child having cystic fibrosis = 25%.
 

b.    Deletion of nucleotides in CFTR gene:

  • Three mRNA nucleotides (a codon) spell out instructions for one amino acid. The deletion here stretches across two codons that normally code for isoleucine and phenylalanine.
  • At first glance, you’d expect losing nucleotides from both codons would mess up both amino acids.
  • In isoleucine however, multiple different triplet codes can signal for its production. Its original code was AUC and after the deletion it became AUU – which still makes isoleucine.
  • Only phenylalanine gets knocked out of the protein sequence, while isoleucine stays put thanks to its flexible coding options.
♦ Mean mark (b) 56%.

BIOLOGY, M6 2024 HSC 25

  1. One-Eyed Jack was a rescue dog that had been injured and lost an eye before his owner adopted him. One-Eyed Jack was cloned and the clone was born with two eyes.

  2. Explain why the cloned dog was born with two eyes.   (2 marks)

  3. Describe how animals like dogs can be cloned.   (4 marks)

Show Answers Only

a.   Reason(s) the cloned dog had two eyes:

  • The DNA used for cloning came from One-Eyed Jack’s somatic (body) cells which contained the complete genetic code for normal eye development.
  • The physical injury that caused Jack to lose his eye did not alter his genes, so it wasn’t passed on to the clone. 

b.   Animal cloning process:

  • The cloning process begins by removing the nucleus from a host egg cell.
  • This is replaced with the nucleus from a body cell of the animal to be cloned.
  • This produces a zygote.
  • After electrical stimulation causes the reconstructed cell to begin dividing, it is implanted into a surrogate mother’s uterus.
  • It then develops into a cloned offspring.

Show Worked Solution

a.   Reason(s) the cloned dog had two eyes:

  • The DNA used for cloning came from One-Eyed Jack’s somatic (body) cells which contained the complete genetic code for normal eye development.
  • The physical injury that caused Jack to lose his eye did not alter his genes, so it wasn’t passed on to the clone.  

b.   Animal cloning process:

  • The cloning process begins by removing the nucleus from a host egg cell.
  • This is replaced with the nucleus from a body cell of the animal to be cloned.
  • This produces a zygote.
  • After electrical stimulation causes the reconstructed cell to begin dividing, it is implanted into a surrogate mother’s uterus.
  • It then develops into a cloned offspring.
♦ Mean mark (b) 52%.

BIOLOGY, M8 2024 HSC 24

  1. Outline the cause of a disease due to environmental exposure.   (2 marks)

  2. Explain how an educational program or campaign can be used to decrease the incidence of a disease caused by environmental exposure.   (3 marks)

Show Answers Only

a.   Answers could include one of the following:

  • Lung cancer can be caused by exposure to inhalation of smoke from cigarettes.
  • Environmental exposure to asbestos can result in some microscopic fibres becoming lodged in the lining of a person’s lungs and cause mesothelioma (cancer).

b.   Educational program on the dangers of UV radiation:

  • An educational program in schools could teach students about the link between UV exposure and skin cancer, emphasising protection through hats and sunscreen.
  • This preventative approach helps students understand the risks and increases the chances of them modifying their behaviour to be more sun safe.
  • Overall, the program should contribute to less DNA damage in cells of participants and a reduction in their chances of developing skin cancer.
Show Worked Solution

a.   Answers could include one of the following:

  • Lung cancer can be caused by exposure to inhalation of smoke from cigarettes.
  • Environmental exposure to asbestos can result in some microscopic fibres becoming lodged in the lining of a person’s lungs and cause mesothelioma (cancer).

b.   Educational program on the dangers of UV radiation:

  • An educational program in schools could teach students about the link between UV exposure and skin cancer, emphasising protection through hats and sunscreen.
  • This preventative approach helps students understand the risks and increases the chances of them modifying their behaviour to be more sun safe.
  • Overall, the program should contribute to less DNA damage in cells of participants and a reduction in their chances of developing skin cancer.

BIOLOGY, M7 2024 HSC 22

A student designed and conducted a practical investigation to test for the presence of microbes in water and food samples.

  1. Justify a safety precaution required to prevent infection when conducting the investigation.   (2 marks)
  1. Explain how the student could ensure the reliability of the investigation.   (2 marks)

Show Answers Only

a.   Answers could include one of the following:

  • Wearing gloves when handling samples is essential to stop pathogens in the water/food entering through cuts or abrasions on bare hands, potentially causing infection.
  • Disinfecting all equipment after use is necessary because microbes can multiply rapidly and contaminated materials could spread infectious organisms to others in the laboratory. 

b.   To ensure the reliability of the investigation:

  • Student should prepare multiple food/water samples for testing to ensure consistent results across repeated trials.
  • This process allows them to verify if their findings are reproducible and reliable rather than due to chance.

Show Worked Solution

a.   Answers could include one of the following:

  • Wearing gloves when handling samples is essential to stop pathogens in the water/food entering through cuts or abrasions on bare hands, potentially causing infection.
  • Disinfecting all equipment after use is necessary because microbes can multiply rapidly and contaminated materials could spread infectious organisms to others in the laboratory. 

b.   To ensure the reliability of the investigation:

  • Student should prepare multiple food/water samples for testing to ensure consistent results across repeated trials.
  • This process allows them to verify if their findings are reproducible and reliable rather than due to chance.

BIOLOGY, M5 2024 HSC 21

A diagram of the different parts of a flower is shown. 
 

  1. Identify the structures where pollen and ovules are located.   (2 marks)

  2. Complete the table to compare features of sexual and asexual reproduction.   (3 marks)

\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \text{Feature} \rule[-1ex]{0pt}{0pt} & \quad \quad \text{Sexual}\quad \quad \rule[-1ex]{0pt}{0pt} & \quad \quad \text{Asexual}\quad \quad\\
\hline
\rule{0pt}{2.5ex} \text{Genetic variability} \\
\text{(yes/no)} \rule[-1ex]{0pt}{0pt} \\
\hline
\rule{0pt}{2.5ex} \text{Number of parents }  \\
\text{required} \rule[-1.5 ex]{0pt}{0pt}\\
\hline
\rule{0pt}{2.5ex} \text{Example of an organism }\\
\text{which uses this type of }& \text{}\\
\text{reproduction} \rule[-1ex]{0pt}{0pt}\\
\hline
\end{array}

Show Answers Only

a.   Pollen: anther

Ovule: ovary

b.   Comparison of features

\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \text{Feature} \rule[-1ex]{0pt}{0pt} & \ \ \ \ \ \ \ \ \text{Sexual}\ \ \ \ \ \ \ \  \rule[-1ex]{0pt}{0pt} & \ \ \ \ \ \ \ \text{Asexual}\ \ \ \ \ \ \  \\
\hline
\rule{0pt}{2.5ex} \text{Genetic variability} \rule[-1ex]{0pt}{0pt} & \text{Yes} \rule[-1ex]{0pt}{0pt} & \text{No} \\
\rule{0pt}{2.5ex} \text{(yes/no)} \rule[-1ex]{0pt}{0pt} & \text{} \rule[-1ex]{0pt}{0pt} & \text{} \\
\hline
\rule{0pt}{2.5ex} \text{Number of parents } \rule[-1ex]{0pt}{0pt} & \text{2} \rule[-1ex]{0pt}{0pt} & \text{1} \\
\rule{0pt}{2.5ex} \text{required} \rule[-1ex]{0pt}{0pt} & \text{} \rule[-1ex]{0pt}{0pt} & \text{} \\
\hline
\rule{0pt}{2.5ex} \text{Example of an organism } \rule[-1ex]{0pt}{0pt} & \text{} \rule[-1ex]{0pt}{0pt} & \text{} \\
\rule{0pt}{2.5ex} \text{which uses this type of } \rule[-1ex]{0pt}{0pt} & \text{Humans} \rule[-1ex]{0pt}{0pt} & \text{Bacteria} \\
\rule{0pt}{2.5ex} \text{reproduction} \rule[-1ex]{0pt}{0pt} & \text{} \rule[-1ex]{0pt}{0pt} & \text{} \\
\hline
\end{array}

Show Worked Solution

a.   Pollen: anther

Ovule: ovary 

b.   Comparison of features

\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \text{Feature} \rule[-1ex]{0pt}{0pt} & \ \ \ \ \ \ \ \ \text{Sexual}\ \ \ \ \ \ \ \  \rule[-1ex]{0pt}{0pt} & \ \ \ \ \ \ \ \text{Asexual}\ \ \ \ \ \ \  \\
\hline
\rule{0pt}{2.5ex} \text{Genetic variability} \rule[-1ex]{0pt}{0pt} & \text{Yes} \rule[-1ex]{0pt}{0pt} & \text{No} \\
\rule{0pt}{2.5ex} \text{(yes/no)} \rule[-1ex]{0pt}{0pt} & \text{} \rule[-1ex]{0pt}{0pt} & \text{} \\
\hline
\rule{0pt}{2.5ex} \text{Number of parents } \rule[-1ex]{0pt}{0pt} & \text{2} \rule[-1ex]{0pt}{0pt} & \text{1} \\
\rule{0pt}{2.5ex} \text{required} \rule[-1ex]{0pt}{0pt} & \text{} \rule[-1ex]{0pt}{0pt} & \text{} \\
\hline
\rule{0pt}{2.5ex} \text{Example of an organism } \rule[-1ex]{0pt}{0pt} & \text{} \rule[-1ex]{0pt}{0pt} & \text{} \\
\rule{0pt}{2.5ex} \text{which uses this type of } \rule[-1ex]{0pt}{0pt} & \text{Humans} \rule[-1ex]{0pt}{0pt} & \text{Bacteria} \\
\rule{0pt}{2.5ex} \text{reproduction} \rule[-1ex]{0pt}{0pt} & \text{} \rule[-1ex]{0pt}{0pt} & \text{} \\
\hline
\end{array}

CHEMISTRY, M7 2024 HSC 24

The boiling points for two series of compounds are listed.

 

  1. Plot the boiling points for each series of compounds against the number of carbon atoms per molecule.   (3 marks)

  1. With reference to hydrogen bonding and dispersion forces, explain the trends in the boiling point data of these compounds, within each series and between the series.   (4 marks)

Show Answers Only

a.     

b.     The alcohols have higher boiling points than amines of the same chain length.

  • Both alcohols and amines have polar hydrogen bonding as a result of the \(\ce{OH}\) and \(\ce{NH2}\) functional groups respectively.
  • Oxygen molecules have higher electronegativity than nitrogen molecules making the hydrogen bonding in the alcohols significantly stronger than the hydrogen bonding in amines.
  • Since the dispersion forces in amines and alcohols of the same chain length are very similar, the difference in the strength of the intermolecular bonding is dependent on the strength of the hydrogen bonding.
  • Therefore, a larger amount of thermal energy is required to separate the alcohol molecules resulting in higher boiling points than amines. 

As the chain length of the alcohols and amines increase, the boiling points also increase.

  • When the chain length increases, the number of electrons in the molecules also increase which corresponds to a larger number of dispersion forces between neighbouring molecules.
  • The stronger dispersion forces between the molecules increase the overall strength of the intermolecular forces in both the alcohols and amines therefore leading to higher boiling points as chain length increases.

Show Worked Solution

a.   

       
 

b.     The alcohols have higher boiling points than amines of the same chain length.

  • Both alcohols and amines have polar hydrogen bonding as a result of the \(\ce{OH}\) and \(\ce{NH2}\) functional groups respectively.
  • Oxygen molecules have higher electronegativity than nitrogen molecules making the hydrogen bonding in the alcohols significantly stronger than the hydrogen bonding in amines.
  • Since the dispersion forces in amines and alcohols of the same chain length are very similar, the difference in the strength of the intermolecular bonding is dependent on the strength of the hydrogen bonding.
  • Therefore, a larger amount of thermal energy is required to separate the alcohol molecules resulting in higher boiling points than amines.

As the chain length of the alcohols and amines increase, the boiling points also increase.

  • When the chain length increases, the number of electrons in the molecules also increase which corresponds to a larger number of dispersion forces between neighbouring molecules.
  • The stronger dispersion forces between the molecules increase the overall strength of the intermolecular forces in both the alcohols and amines therefore leading to higher boiling points as chain length increases.

Networks, GEN2 2024 VCAA 14

A manufacturer \((M)\) makes deliveries to the supermarket \((S)\) via a number of storage warehouses, \(L, N, O, P, Q\) and \(R\). These eight locations are represented as vertices in the network below.

The numbers on the edges represent the maximum number of deliveries that can be made between these locations each day.
 

  1. When considering the possible flow of deliveries through this network, many different cuts can be made.   
  2. Determine the capacity of Cut 1, shown above.   (1 mark)

  3. Determine the maximum number of deliveries that can be made each day from the manufacturer to the supermarket.   (1 mark)

  4. The manufacturer wants to increase the number of deliveries to the supermarket.
  5. This can be achieved by increasing the number of deliveries between one pair of locations.
  6. Complete the following sentence by writing the locations on the lines provided:
  7. To maximise this increase, the number of deliveries should be increased between
    locations ____ and  ____.       (1 mark)

    

Show Answers Only

a.    \(46\)

b.    \(37\)

c.    \(\text{R and S}\)

Show Worked Solution

a.    \(13+18+6+9=46\)

\(\text{(Reverse flow}\ Q → O\ \text{is not counted.)}\)
 

b.  

\(\text{Max deliveries (min cut)}\ =13+5+11+8=37\)

♦ Mean mark (b) 29%.

 
c.   \(\text{The number of deliveries should be increased between}\)

\(\text{locations R and S.}\)

♦ Mean mark (c) 22%.

CHEMISTRY, M6 2024 HSC 21

A solution of acetic acid reacts with magnesium metal.

Write the names of the products of this reaction in the boxes provided.   (2 marks)

Show Answers Only

  • Products: hydrogen gas \(\ce{H2(g)}\) and magnesium acetate/ethanoate \(\ce{Mg(CH3COO)2(aq)}\)

Show Worked Solution

  • Acid + active metal \(\ce{->}\) hydrogen + salt
  • Products: hydrogen gas \(\ce{H2(g)}\) and magnesium acetate/ethanoate \(\ce{Mg(CH3COO)2(aq)}\)

CHEMISTRY, M5 2024 HSC 10 MC

The following system is at equilibrium.

\(\underset{\text { propan-2-ol }}{\ce{CH_3CHOHCH_3(g)}} \rightleftharpoons \underset{\text {propan-2-one}}{\ce{CH_3COCH_3(g)}}\)\(\ce{+ H_2(g)}\)

A catalyst is added to the system.

Which row of the table correctly identifies the change in the yield of propan-2-one and the reaction rates?

\begin{align*}
\begin{array}{l}
\ & \\
\\
\textbf{A.}\\
\\
\textbf{B.}\\
\\
\textbf{C.}\\
\\
\textbf{D.}\\
\\
\end{array}
\begin{array}{|l|l|}
\hline
\quad\quad \textit{Yield of } & \quad \quad \quad \quad \textit{Reaction Rates} \\
\quad\textit{propan-2-one} & \textit{} \\
\hline
\text{Remains the same} & \text{Both forward and reverse rates} \\
\text{} & \text{are unchanged.} \\
\hline
\text{Remains the same} & \text{Both forward and reverse rates} \\
\text{} & \text{increase equally} \\
\hline
\text{Decreases} & \text{Reverse rate increases more than} \\
\text{} & \text{the forward rate increases.} \\
\hline
\text{Increases} & \text{Forward rate increases more than}\\
\text{} & \text{the reverse rate increases.}\\
\hline
\end{array}
\end{align*}

Show Answers Only

\(B\)

Show Worked Solution
  • Adding a catalyst to an equilibrium system will decrease the activation energy of both the forward and reverse reactions equally.
  • Thus, the reaction rate of the forward and reverse reactions will both increase and cause no change to the yield of the reaction.

\(\Rightarrow B\)

CHEMISTRY, M8 2024 HSC 9 MC

Which of the following is the mass spectrum of ethanamine?
 

 

Show Answers Only

\(B\)

Show Worked Solution
  • The molar mass of ethanamine, \(\ce{CH3CH2NH2}\), is 45.086 g mol\(^{-1}\)
  • The peak with the largest mass to charge ratio displays the molar mass of the substance.
  • Therefore, the parent ion peak will be at 45.

\(\Rightarrow B\)

CHEMISTRY, M8 2024 HSC 8 MC

Which pair of ions produce different colours in a flame test?

  1. \(\ce{Br^{-} and Cl^{-}}\)
  2. \(\ce{Ag^{+} and OH^{-}}\)
  3. \(\ce{Cu^{2+} and Ca^{2+}}\)
  4. \(\ce{CH_3OOO^{-} and H_2 PO_4^{-}}\)
Show Answers Only

\(C\)

Show Worked Solution
  • Only metal cations produce unique colours during a flame test due to their electron configurations.
  • As the electrons ‘fall back’ down into their shells from an excited state, they emit a specific light wave (colour).

\(\Rightarrow C\)

CHEMISTRY, M8 2024 HSC 4 MC

An infrared spectrum of an organic compound is shown.
 

     

Which of the following compounds would produce the spectrum shown?
 

Show Answers Only

\(A\)

Show Worked Solution
  • The broad absorption peak between 3500 to 3250 indicates the presence of an \(\ce{O-H}\) alcohol group.

\(\Rightarrow A\)

Networks, GEN2 2024 VCAA 13

A supermarket has five departments, with areas allocated as shown on the floorplan below.
 

The floorplan is represented by the graph below.

On this graph, vertices represent departments and edges represent boundaries between two departments.

This graph is incomplete.
 

  1. Draw the missing vertex and missing edges on the graph above. Include a label.   (1 mark)

Karla is standing in the Promotional department.

She wants to visit each department in the supermarket once only.

  1.  i.  In which department will she finish?  (1 mark)
  2. ii.  What is the mathematical name for this type of journey?  (1 mark)
  3. The supermarket adds a new Entertainment department \((E)\), and the floorplan is rearranged.
  4. The boundaries between the departments are represented in the adjacency matrix below, where a ' 1 ' indicates a boundary between the departments.

\begin{aligned}
& \ \ B \ \ \ D \ \ \  E \ \ \  F \ \ \ G \ \ \ P \\
\begin{array}{c}
B\\
D \\
E \\
F \\
G \\
P
\end{array}& \begin{bmatrix}
0 & 1 & 1 & 1 & 0 & 1 \\
1 & 0 & 0 & 1 & 1 & 0 \\
1 & 0 & 0 & 0 & 0 & 1 \\
1 & 1 & 0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 & 0 & 1 \\
1 & 0 & 1 & 1 & 1 & 0
\end{bmatrix}
\end{aligned}

  1. Use the adjacency matrix to complete the floorplan below by labelling each department. The Bakery \((B)\) is already labelled.  (1 mark)

Show Answers Only

a. 

 
b.i.   \(\text{The bakery}\)

b.ii.  \(\text{Hamiltonian Path}\)
 

c.

Show Worked Solution

a. 

b.i.  \(\text{Bakery}\)

b.ii. \(\text{The path has no repeated edges or vertices, and }\)

\(\text{incudes all the edges of the graph.}\)

\(\therefore\ \text{It is a Hamiltonian Path.}\)

c.

Matrices, GEN2 2024 VCAA 9

Vince works on a construction site.

The amount Vince gets paid depends on the type of shift he works, as shown in the table below.

\begin{array}{|l|c|c|c|}
\hline
\rule{0pt}{2.5ex} \textbf{Shift type} \rule[-1ex]{0pt}{0pt}& \textbf{Normal} & \textbf{Overtime} & \textbf {Weekend} \\
\hline
\rule{0pt}{2.5ex} \textbf{Hourly rate of pay} \rule[-1ex]{0pt}{0pt} \ \text{(\$ per hour)} & 36 & 54 & 72 \\
\hline
\end{array}

This information is shown in matrix \(R\) below.

\begin{align*}
R=\left[\begin{array}{lll}
36 & 54 & 72
\end{array}\right] \end{align*}

  1. Matrix \(R^T\) is the transpose of matrix \(R\).
  2. Determine the matrix \(R^T\).   (1 mark)

During one week, Vince works 28 hours at the normal rate of pay, 6 hours at the overtime rate of pay, and 8 hours at the weekend rate of pay.

  1. Complete the following matrix calculation showing the total amount Vince has been paid for this week.  (1 mark)

  

Vince will receive $90 per hour if he works a public holiday shift.

Matrix \(Q\), as calculated below, can be used to show Vince's hourly rate for each type of shift.

\begin{align*}
\begin{aligned}
Q & =n \times\left[\begin{array}{llll}
1 & 1.5 & 2 & p
\end{array}\right] \\
& =\left[\begin{array}{llll}
36 & 54 & 72 & 90
\end{array}\right] \end{aligned}
\end{align*}

  1. Write the values of \(n\) and \(p\).  (1 mark)

Show Answers Only

a.   \(R^T=\begin{bmatrix}
36 \\
54 \\
72
\end{bmatrix}\)

b.    \([28\quad  6\quad  8]\times R^T = [1908]\)

c.    \(n=36\ ,\ p=2.5\)

Show Worked Solution

a.   \(R^T=\begin{bmatrix}
36 \\
54 \\
72
\end{bmatrix}\)

 
b.    \(\begin{bmatrix}
28 & 6 & 8
\end{bmatrix}\times\ R^T=\begin{bmatrix}
28\times36 + 6\times54+ 8\times 72
\end{bmatrix}=[1908]\)

 
c.   \(n=\ \text{Normal hourly rate}\ =36\)

\(p=\ \text{Overtime rate}\ =\dfrac{90}{36}=2.5\)

Financial Maths, GEN2 2024 VCAA 5

Emi operates a mobile dog-grooming business.

The value of her grooming equipment will depreciate.

Based on average usage, a rule for the value, in dollars, of the equipment, \(V_n\), after \(n\) weeks is

\(V_n=15000-60 n\)

Assume that there are exactly 52 weeks in a year.

  1. By what amount, in dollars, does the value of the grooming equipment depreciate each week?   (1 mark)

  2. Emi plans to replace the grooming equipment after four years.   
  3. What will be its value, in dollars, at this time?   (1 mark)

  4. \(V_n\) is the value of the grooming equipment, in dollars, after \(n\) weeks.   
  5. Write a recurrence relation in terms of \(V_0, V_{n+1}\) and \(V_n\) that can model this value from one week to the next.   (1 mark)

  6. The value of the grooming equipment decreases from one year to the next by the same percentage of the original $15 000 value.
  7. What is this annual flat rate percentage?   (1 mark)

Show Answers Only

a.    \($60\)

b.    \($2520\)

c.    \(V_0=15\,000 , \ \ V_{n+1}=V_n-60\)

d.    \(20.8\%\)

Show Worked Solution

a.    \($60\)
 

b.    \(n=4\times 52=208\)

\(V_{208}\) \(=15\,000-60\times208\)
  \(=$2520\)

 
c.    \(V_0=15\,000 , \ \ V_{n+1}=V_n-60\)
 

d.    \(\text{Flat rate}\ =\dfrac{60}{15\,000}\times 52\times 100\%=20.8\%\)

♦ Mean mark (d) 42%.

Data Analysis, GEN2 2024 VCAA 3

The Olympic gold medal-winning height for the women's high jump, \(\textit{Wgold}\), is often lower than the best height achieved in other international women's high jump competitions in that same year.

The table below lists the Olympic year, \(\textit{year}\), the gold medal-winning height, \(\textit{Wgold}\), in metres, and the best height achieved in all international women's high jump competitions in that same year, \(\textit{Wbest}\), in metres, for each Olympic year from 1972 to 2020.

A scatterplot of \(\textit{Wbest}\) versus \(\textit{Wgold}\) for this data is also provided.

When a least squares line is fitted to the scatterplot, the equation is found to be:

\(Wbest =0.300+0.860 \times Wgold\)

The correlation coefficient is 0.9318

  1. Name the response variable in this equation.   (1 mark)

  2. Draw the least squares line on the scatterplot above.  (1 mark)

  3. Determine the value of the coefficient of determination as a percentage.  (1 mark)
  4. Round your answer to one decimal place.
  5. Describe the association between \(\textit{Wbest}\) and \(\textit{Wgold}\) in terms of strength and direction.  (1 mark)

\begin{array}{|l|l|}
\hline
\rule{0pt}{2.5ex}\text { strength } \rule[-1ex]{0pt}{0pt} & \quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\
\hline
\rule{0pt}{2.5ex}\text { direction } \rule[-1ex]{0pt}{0pt} & \\
\hline
\end{array}

  1. Referring to the equation of the least squares line, interpret the value of the slope in terms of the variables \(\textit{Wbest}\) and \(\textit{Wgold}\).  (1 mark)

  2. In 1984, the \(\textit{Wbest}\) value was 2.07 m for a \(\textit{Wgold}\) value of 2.02 m .
  3. Show that when this least squares line is fitted to the scatterplot, the residual value for this point is 0.0328.  (2 marks)

  4. The residual plot obtained when the least squares line was fitted to the data is shown below. The residual value from part f is missing from the residual plot.
     

    1. Complete the residual plot by adding the residual value from part f, drawn as a cross ( X ), to the residual plot above.   (1 mark)

    2. In part b, a least squares line was fitted to the scatterplot. Does the residual plot from part g justify this? Briefly explain your answer.  (1 mark)

  1. In 1964, the gold medal-winning height, \(\textit{Wgold}\), was 1.90m . When the least squares line is used to predict \(\textit{Wbest}\), it is found to be 1.934 m .
  2. Explain why this prediction is not likely to be reliable.  (1 mark)

Show Answers Only

a.    \(Wbest\)

b.    

c.    \(86.8\%\)

d.    \(\text{Strong, positive}\)

e.    \(Wbest\ \text{will increase, on average, by 0.86 metres for every metre of increase in}\ Wgold.\)

f.      \(Wbest\) \(=0.300 +0.86\times 2.02\)
    \(=2.0372\)

\(\therefore\ \text{Residual}\ =2.07-2.0372=0.0328\)

g.i.

g.ii.  \(\text{Yes, it is justified as there is no clear pattern, linear or otherwise.}\)

h.    \(\text{This prediction is outside the data range (1972 – 2020 → extrapolation)}\)

\(\text{and therefore cannot be relied upon.}\)

Show Worked Solution

a.    \(Wbest\)

b.    \(\text{Using points:}\ (1.90, 1.934)\ \text{and}\ (2.00, 2.02)\)
 

Mean mark (b) 51%.

c.    \(r=0.9318\ \ \Rightarrow\ \ r^2=0.9318^2=0.8682\dots\)

\(\therefore\ \text{Coefficient of determination} \approx 86.8\%\)
 

d.    \(\text{Strong, positive}\)
 

e.    \(Wbest\ \text{will increase, on average, by 0.86 metres for every metre of increase in}\ Wgold.\)
 

f.      \(Wbest\) \(=0.300 +0.86\times 2.02\)
    \(=2.0372\)

 
\(\therefore\ \text{Residual}\ =2.07-2.0372=0.0328\)

♦ Mean mark (f) 48%.

g.i.

g.ii.  \(\text{Yes, it is justified as there is no clear pattern, linear or otherwise.}\)

♦ Mean mark (g)(i) 47%.
♦ Mean mark (g)(ii) 40%.

h.    \(\text{This prediction is outside the data range (1972–2020 → extrapolation)}\)

\(\text{and therefore cannot be relied upon.}\)

♦ Mean mark (h) 50%.

Data Analysis, GEN2 2024 VCAA 2

The boxplot below displays the distribution of all gold medal-winning heights for the women's high jump, \(\textit{Wgold}\), in metres, for the 19 Olympic Games held from 1948 to 2020.

  1. Describe the shape of this data distribution.   (1 mark)

  2. For this boxplot, what is the smallest possible number of \(\textit{Wgold}\) heights lower than 1.85 m?   (1 mark)

  3.  i. Using the boxplot, show that the lower fence is 1.565 m and the upper fence is 2.325 m.  (1 mark)

  4. ii. Referring to the boxplot, the lower fence and the upper fence, explain why no outliers exist.  (1 mark)

Show Answers Only

a.    \(\text{Negatively skewed}\)

b.    \(1\)

c.i.  \(Q_1=1.85,\ Q_3=2.04,\ IQR=2.04-1.85=0.19\)

\(\text{Lower Fence}\) \(=Q_1-1.5\times IQR\)
  \(=1.85-1.5\times 0.19\)
  \(=1.565\)
\(\text{Upper Fence}\) \(=Q_1+1.5\times IQR\)
  \(=2.04+1.5\times 0.19\)
  \(=2.325\)

c.ii. \(\text{No values exist below the lower fence or above the upper fence.}\)

\(\therefore\ \text{No outliers exist.}\)

Show Worked Solution

a.    \(\text{Negatively skewed.}\)
 

b.    \(\text{Only 1 value is needed to extend the whisker below the}\)

\(\text{range of the}\ IQR.\)

♦♦♦ Mean mark (b) 3%.

c.i.  \(Q_1=1.85,\ Q_3=2.04,\ IQR=2.04-1.85=0.19\)

\(\text{Lower Fence}\) \(=Q_1-1.5\times IQR\)
  \(=1.85-1.5\times 0.19\)
  \(=1.565\)
\(\text{Upper Fence}\) \(=Q_1+1.5\times IQR\)
  \(=2.04+1.5\times 0.19\)
  \(=2.325\)

   

c.ii. \(\text{No values exist below the lower fence or above the upper fence.}\)

\(\therefore\ \text{No outliers exist.}\)