The price of a property purchased in 2006 was $200 000.
Stamp duty was paid on this purchase according to the schedule below.
The amount of stamp duty paid was
A. $2560
B. $2800
C. $5100
D. $7660
E. $9460
CORE*, FUR1 2007 VCAA 3 MC
A sum of money is invested in an account paying simple interest at a rate of 8% per annum.
The total interest earned on this investment over 6 years is $27 000.
The sum of money invested is
- `$12\ 960`
- `$45\ 000`
- `$56\ 250`
- `$202\ 500`
- `$337\ 500`
CORE*, FUR1 2007 VCAA 2 MC
A car is valued at $30 000 when new.
Its value is depreciated by 25 cents for each kilometre it travels.
The number of kilometres the car travels before its value depreciates to $8000 is
A. 32 000
B. 55 000
C. 88 000
D. 120 000
E. 550 000
CORE*, FUR1 2006 VCAA 5 MC
A photocopier is depreciated by $0.04 for each copy it makes.
Three years ago the photocopier was purchased for $48 000.
Its depreciated value now is $21 000.
The total number of copies made by the photocopier in the three years is
A. `108\ 000`
B. `192\ 000`
C. `276\ 000`
D. `525\ 000`
E. `675\ 000`
CORE*, FUR1 2006 VCAA 2 MC
A bank statement for the month of October is shown below.
Interest on this account is calculated at a rate of 0.15% per month on the minimum monthly balance.
The interest payment for the month of October will be
A. $0.19
B. $0.57
C. $0.71
D. $0.92
E. $1.28
CORE*, FUR1 2005 VCAA 9 MC
Sally planned to repay a loan fully with six equal monthly repayments of `$800`.
Interest was calculated monthly on the reducing balance.
Sally missed the third payment, but made a double payment of `$1600` in the fourth month.
Which of the following statements is true?
A. The same amount of interest is paid each month.
B. The amount owing after three months is the same as the amount owed after two months.
C. The amount owing after three months is less than the amount owed after two months.
D. To fully repay the loan, Sally will pay less than $4800.
E. To fully repay the loan, Sally will pay more than $4800.
CORE*, FUR1 2011 VCAA 4 MC
Nathan bought a $2500 bedroom suite on a contract that involves no deposit and an interest-free loan for a period of 48 months.
He has to pay an initial set-up fee of $25.
In addition, he pays an administration fee of $3.95 per month.
The total amount that Nathan will have to pay in fees for the entire 48 months, as a percentage of the original price of $2500, is closest to
A. 1.6%
B. 4.0%
C. 7.6%
D. 8.5%
E. 8.6%
CORE*, FUR1 2012 VCAA 7 MC
The following graph shows the decreasing value of an asset over eight years.
Let `P` be the value of the asset, in dollars, after `n` years.
A rule for evaluating `P` could be
A. `P = 250\ 000 xx (1 + 0.14)^n`
B. `P = 250\ 000 xx 1.14 xx n`
C. `P = 250\ 000 xx (0.14)^n`
D. `P = 250\ 000 xx (1 - 0.14)^n`
E. `P = 250\ 000 xx (1 - 0.14) xx n`
CORE*, FUR1 2012 VCAA 6 MC
CORE*, FUR1 2013 VCAA 7 MC
The graph below shows the growth in value of a $1000 investment over a period of four years.
A different amount of money is invested under the same investment conditions for eight years.
In total, the amount of interest earned on this investment is $600.
The amount of money invested is
A. `$500`
B. `$600`
C. `$1500`
D. `$2000`
E. `$2400`
CORE*, FUR1 2013 VCAA 4 MC
The purchase price of a car is $15 000.
A deposit of $3000 is paid and the balance will be repaid with 36 monthly payments of $400.
The annual flat rate of interest charged is closest to
A. 1.3%
B. 4.0%
C. 5.3%
D. 6.7%
E. 20.0%
CORE*, FUR1 2013 VCAA 2 MC
The closing price of a share on Monday was $30.
The closing price of the share on Tuesday was 5% more than its closing price on Monday.
The closing price of the share on Wednesday was 5% less than its closing price on Tuesday.
Which one of the following calculations will give the closing price of the share, in dollars, on Wednesday?
A. `30 xx 1.05 xx 0.95`
B. `30 xx 1.05 xx –0.05`
C. `30 + 1.05 xx 0.95`
D. `30 + 0.05 xx 30 - 0.05 xx 30`
E. `30 + 1.05 - 0.95`
GRAPHS, FUR1 2014 VCAA 8 MC
The constraints of a linear programming problem are given by the following set of inequalities.
| `x + y` | `<= 8` |
| `3x + 5y` | `<= 30` |
| `x` | `>= 0` |
| `y` | `>= 0` |
The coordinates of the points that define the boundaries of the feasible region for this linear programming problem are
A. `(0, 0), (0, 6), (3, 5), (8, 0)`
B. `(0, 0), (0, 6), (5, 3), (8, 0)`
C. `(0, 0), (0, 6), (5, 3), (10, 0)`
D. `(0, 0), (0, 8), (5, 3), (8, 0)`
E. `(0, 0), (0, 8), (5, 3), (10, 0)`
Show Worked Solution
`x + y = 8\ \ text{cut the axes at (0, 8), (8, 0)}`
`3x + 5y = 30\ \ text{cut the axes at (0, 6), (10, 0)}`
`text(From the diagram, 3 of the boundary points clearly)`
`text{lie at (0, 6), (0, 0), and (8, 0).}`
`:. text(Eliminate)\ C,\ D,\ text(and)\ E`
`text(Choosing between)\ A\ text(and)\ B,\ text{only (5, 3) lies}`
`text(on both lines and is therefore the intersection.)`
`:. text(Eliminate)\ A`
`=> B`
GRAPHS, FUR1 2014 VCAA 7 MC
Consider the following statements that relate to the solution of linear programming problems.
Which one of the following statements is true?
A. Only one point can be a solution.
B. No point outside the feasible region can be a solution.
C. To have a solution, the feasible region must be bounded.
D. Only the corner points of a feasible region can be a solution.
E. Only the corner points with integer coordinates can be a solution.
GRAPHS, FUR1 2014 VCAA 5 MC
The distance–time graph below shows a train’s journey between two towns.
During the journey, the train stopped for 30 minutes.
The average speed of the train, in kilometres per hour, for the journey is closest to
A. `45`
B. `50`
C. `60`
D. `65`
E. `80`
GRAPHS, FUR1 2014 VCAA 4 MC
A line passes through the points `(–1, 1)` and `(3, 5)`.
Another point that lies on this line is
A. `(0, 1)`
B. `(1, 3)`
C. `(2, 6)`
D. `(3, 4)`
E. `(4, 7)`
GRAPHS, FUR1 2014 VCAA 3 MC
The point `(2, 20)` lies on the graph of `y = k/x`, as shown below.
The value of `k` is
A. `5`
B. `10`
C. `20`
D. `40`
E. `80`
CORE*, FUR1 2014 VCAA 8 MC
Robert invested $6000 at 4.25% per annum with interest compounding quarterly.
Immediately after interest is paid at the end of each quarter, he adds $500 to his investment.
The value of Robert’s investment at the end of the third quarter, after his $500 has been added, is closest to
A. $6193
B. $7569
C. $7574
D. $7709
E. $8096
CORE*, FUR1 2014 VCAA 7 MC
New furniture was purchased for an office at a cost of $18 000.
Using flat rate depreciation, the furniture will be valued at $5000 after four years.
The expression that can be used to determine the value of the furniture, in dollars, after one year is
A. `18\ 000 - (4 xx 5000)`
B. `18\ 000 - ({18\ 000 - 5000}/4)`
C. `18\ 000 - 5000/4`
D. `(18\ 000)/4 - 5000`
E. `18\ 000 xx 0.726`
CORE*, FUR1 2014 VCAA 3 MC
Amy invests $15 000 for 150 days.
Interest is calculated at the rate of 4.60% per annum, compounding daily.
Assuming that there are 365 days in a year, the value of her investment after 150 days is closest to
A. `$15\ 279`
B. `$15\ 284`
C. `$15\ 286`
D. `$15\ 690`
E. `$16\ 776`
CORE*, FUR1 2014 VCAA 2 MC
An internet car market site charges $120 to advertise a car for sale.
The car is sold for $15 000.
The $120 charge as a percentage of the selling price of the car is
A. 0.008%
B. 0.08%
C. 0.80%
D. 1.20%
E. 1.25%
GRAPHS, FUR1 2006 VCAA 8 MC
The cost of manufacturing a number of frying pans consists of a fixed cost of $400 plus a cost of $50 per frying pan.
The manufacturer could break even by selling
A. 10 frying pans at $90 each.
B. 10 frying pans at $45 each.
C. 15 frying pans at $60 each.
D. 15 frying pans at $30 each.
E. 20 frying pans at $50 each.
GRAPHS, FUR1 2006 VCAA 7 MC
In a linear programming problem involving animal management on a farm
• `x` represents the number of cows on the farm
• `y` represents the number of sheep on the farm.
The feasible region (with boundaries included) for the problem is indicated by the shaded region on the diagram below.
One of the constraints defining the feasible region indicates that
A. there must be 20 cows and 60 sheep.
B. there must be 40 cows and 40 sheep.
C. the number of sheep cannot exceed 40.
D. the number of cows must be at least 60.
E. the total number of cows and sheep cannot exceed 80.
GRAPHS, FUR1 2006 VCAA 2 MC
The graph above represents the depth of water in a channel (in metres) as it changes over time (in hours).
During the time interval shown, the number of times the depth of the water in the channel is 10 metres is
A. `0`
B. `1`
C. `2`
D. `3`
E. `4`
Show Worked Solution
`text(From the graph above, the depth of water in the)`
`text(channel is 10m on 4 occasions.)`
`=> E`
GRAPHS, FUR1 2006 VCAA 1 MC
On the graph above the equation of the line passing through the point `(1, 2)` is
A. `x = 1`
B. `y = 1`
C. `x = 2`
D. `y = 2`
E. `y = x + 1`
Measurement, 2UG MM6 SM-Bank 01 MC
Mapupu and Minoha are two towns on the equator.
The longitude of Mapupu is `text(16°E)` and the longitude of Minoha is `text(52°W)`.
How far apart are these two towns if the radius of Earth is approximately `6400\ text(km)`?
(A) `4000\ text(km)`
(B) `7600\ text(km)`
(C) `1\ 447\ 600\ text(km)`
(D) `2\ 734\ 400\ text(km)`
GRAPHS, FUR1 2007 VCAA 9 MC
The following five constraints apply to a linear programming problem.
`x>= 0,\ \ y>= 0,\ \ x + y>=50,\ \ x + y<=100,\ \ y<=x`
In the diagram below, the shaded region (with boundaries included) represents the feasible region for this linear programming problem.
The aim is to maximise the objective function `Z = 2x + ky`.
If the maximum value of `Z` occurs only at the point `(100, 0)`, then a possible value for `k` is
A. `1`
B. `2`
C. `3`
D. `4`
E. `5`
GRAPHS, FUR1 2007 VCAA 8 MC
Which one of the following pairs of simultaneous linear equations has no solution?
| A. | `3x - y = 5` |
| `4x + y = 9` |
| B. | `2x−y = 1` |
| `4x−2y = 3` |
| C. | `x + 3y = 0` |
| `2x - y = 7` |
| D. | `x - 3y = 10` |
| `3x + 2y = 8` |
| E. | `4x + y = - 6` |
| `2x - y = 0` |
GRAPHS, FUR1 2007 VCAA 5 MC
The cost of hiring one motorbike for up to 4 hours is shown in the graph above.
Two motorbikes were hired.
The total charge for hiring the two motorbikes was $45.
The time for which each motorbike was hired could have been
A. 1 hour and 2 hours.
B. 1 hour and 3 hours.
C. 1.5 hours and 2 hours.
D. 1.5 hours and 3 hours.
E. 2 hours and 3.5 hours.
GRAPHS, FUR1 2007 VCAA 1 MC
The line above passes through the origin and the point `(2, 1)`.
The slope of this line is
A. `− 2`
B. `− 1`
C. `− 1/2`
D. `1/2`
E. `2`
GRAPHS, FUR1 2008 VCAA 6 MC
At the local bakery, the cost of four donuts and six buns is $14.70.
The cost of three donuts and five buns is $11.90.
At this bakery, the cost of one donut and two buns will be
A. `$2.80`
B. `$3.80`
C. `$3.85`
D. `$4.55`
E. `$4.85`
GRAPHS, FUR1 2008 VCAA 3 MC
The graph below shows the time `t`, in hours, taken to travel 100 km at an average speed of `s` km/h.
Which statement is false?
- As average speed increases, the time taken to travel 100 km decreases.
- It will take 2 hours to travel 100 km at an average speed of 50 km/h.
- The relationship between time and average speed is linear.
- When travelling at an average speed of 20 km/h, the 100 km journey takes 5 hours to complete.
- A formula that relates `s` and `t` is `t = 100/s, \ s > 0`
Algebra, STD2 A4 SM-Bank 27
Fiona and John are planning to hold a fund-raising event for cancer research. They can hire a function room for $650 and a band for $850. Drinks will cost them $25 per person.
- Write a formula for the cost ($C) of holding the charity event for `x` people. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- The graph below shows the planned income and costs if they charge $50 per ticket. Estimate the number of guests they need to break even. (1 mark)
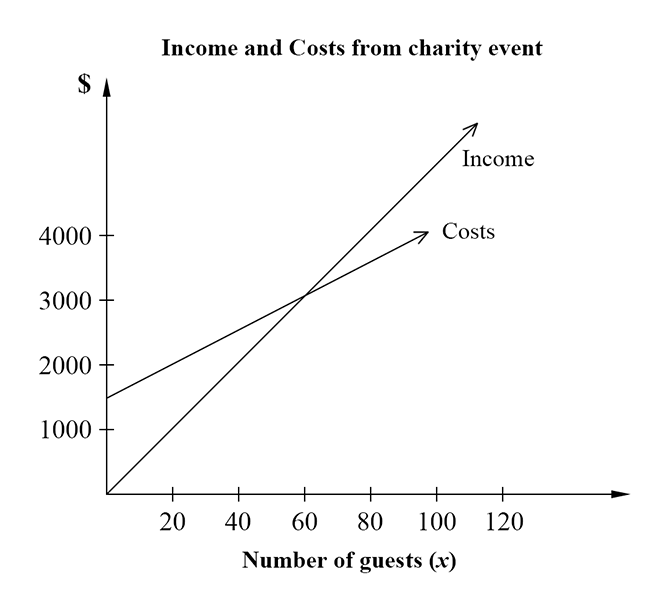
--- 1 WORK AREA LINES (style=lined) ---
- How much profit will Fiona and John make if 80 people attend their event? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Statistics, STD2 S5 SM-Bank 4 MC
The length of a type of ant is approximately normally distributed with a mean of 4.8 mm and a standard deviation of 1.2 mm.
A standardised ant length of `z\ text(= −0.5)` corresponds to an actual ant length of
A. ` text(2.4 mm)`
B. `text(3.6 mm)`
C. `text(4.2 mm)`
D. `text(5.4 mm)`
Quadratic, 2UA SM-Bank 01
Solve `9^x-10(3^x)+9=0` (2 marks)
Financial Maths, 2ADV M1 SM-Bank 11
Express the recurring decimal `0.323232...` as a fraction. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
GRAPHS, FUR1 2009 VCAA 8 MC
Brian, a landscaping contractor, charges by the hour for his company’s services.
To complete a particular job, he will have to use three workers and pay each of them $20 per hour. The fixed costs for the job are $150 and it will take four hours to complete the job.
To break even on this job, his hourly charge to the client should be
A. `$38.25`
B. `$57.50`
C. `$97.50`
D. `$127.50`
E. `$132.50`
GRAPHS, FUR1 2009 VCAA 7 MC
A school’s squash and volleyball teams plan to enter a sports competition.
A squash team requires at least 4 players.
A volleyball team requires at least 6 players.
No more than 25 students from any one school can enter the competition.
Let `x` be the number of squash players sent by the school to the competition.
Let `y` be the number of volleyball players sent by the school to the competition.
The constraints above define the feasible region shaded in the graph below.
A fee is charged for all players entering the competition. Squash players are charged $5 and volleyball players are charged $4.
Given the above constraints, the maximum cost for the school’s squash and volleyball teams to enter the competition is
A. `$44`
B. `$104`
C. `$119`
D. `$121`
E. `$144`
GRAPHS, FUR1 2009 VCAA 5-6 MC
Kathy is a tutor who offers tutorial sessions for English and History students.
Part 1
An English tutorial session takes 1.5 hours.
A History tutorial session take 30 minutes.
Kathy has no more than 15 hours available in a week for tutorial sessions.
Let `x` represent the number of English tutorial sessions Kathy has each week.
Let `y` represent the number of History tutorial sessions Kathy has each week.
An inequality representing the constraint on Kathy’s tutorial time each week (in hours) is
A. `1.5x + 30y = 15`
B. `1.5x + 30y >= 15`
C. `1.5x + 30y <= 15`
D. `1.5x + 0.5y >= 15`
E. `1.5x + 0.5y <= 15`
Part 2
Kathy prefers to have no more than 18 tutorial sessions in total each week.
She prefers to have at least 4 English tutorial sessions.
She also prefers to have at least as many History tutorial sessions as English tutorial sessions.
Let `x` represent the number of English tutorial sessions Kathy has each week.
Let `y` represent the number of History tutorial sessions Kathy has each week.
The shaded region that satisfies all of these constraints is
GRAPHS, FUR1 2009 VCAA 1-3 MC
The graph below shows the water temperature in a fish tank over a 12-hour period.
Part 1
Over the 12-hour period, the temperature of the tank is increasing most rapidly
A. during the first 2 hours.
B. from 2 to 4 hours.
C. from 4 to 6 hours.
D. from 6 to 8 hours.
E. from 8 to 10 hours.
Part 2
The fish tank is considered to be a safe environment for a type of fish if the water temperature is maintained between 24°C and 28°C.
Over the 12-hour period, the length of time (in hours) that the environment was safe for this type of fish was closest to
A. `1.5`
B. `5.0`
C. `7.0`
D. `8.5`
E. `10.5`
Part 3
The graph below can be used to determine the cost (in cents) of heating the fish tank during the first five hours of heating.
The cost of heating the tank for one hour is
A. `4\ text(cents.)`
B. `5\ text(cents.)`
C. `15\ text(cents.)`
D. `20\ text(cents.)`
E. `100\ text(cents.)`
GEOMETRY, FUR1 2006 VCAA 7 MC
In the diagram, `AD = 9\ text(cm), AC = 24\ text(cm) and DB = 27\ text(cm.)`
Line segments `AC` and `DE` are parallel.
The length of `DE` is
A. `6\ text(cm)`
B. `8\ text(cm)`
C. `12\ text(cm)`
D. `16\ text(cm)`
E. `18\ text(cm)`
Show Worked Solution
`/_CAD = /_EDB\ \ \ text{(} text(corresponding angles,)\ AC\ text(||)\ DE text{)}`
`/_DBE\ text(is common)`
`:. Delta ACB\ text(|||)\ Delta DEB\ \ text{(equiangular)}`
| `:.\ (DE)/(DB)` | `= (AC)/(AB)` | `\ \ \ text{(corresponding sides}` `\ \ \ \ text{of similar triangles)}` |
| `(DE)/27` | `= 24/36` | |
| `DE` | `= (24 xx 27)/36` | |
| `= 18\ text(cm)` |
`=> E`
GEOMETRY, FUR1 2006 VCAA 6 MC
The rectangular box shown in this diagram is closed at the top and at the bottom.
It has a volume of 6 m³.
The base dimensions are 1.5 m × 2 m.
The total surface area of this box is
A. `10\ text(m²)`
B. `13\ text(m²)`
C. `13.5\ text(m²)`
D. `20\ text(m²)`
E. `27\ text(m²)`
Measurement, 2UG 2007 HSC 28c
A piece of plaster has a uniform cross-section, which has been shaded, and has dimensions as shown.
- Use two applications of Simpson’s rule to approximate the area of the cross-section. (3 marks)
- The total surface area of the piece of plaster is `7480.8\ text(cm²)`.
- Calculate the area of the curved surface as shown on the diagram. (2 marks)
Show Worked Solution
| (i) |  |
| `A` | `= h/3 [y_0 +4y_1 + y_2]\ text(… applied twice)` |
| `= 3.6/3 (5 + 4 xx 4.6 + 3.7) + 3.6/3 (3.7 + 4 xx 2.8 + 0)` | |
| `= 32.52 + 17.88` | |
| `= 50.4\ text(cm²)` |
(ii) `text(Total Area) = 7480.8\ text(cm²)`
| `text(Area of Base)` | `= 14.4 xx 200` |
| `= 2880\ text(cm²)` |
| `text(Area of End)` | `= 5 xx 200` |
| `= 1000\ text(cm²)` |
| `text(Area of sides)` | `= 2 xx 50.4\ \ \ text{(from (i))}` |
| `= 100.8\ text(cm²)` |
`:.\ text(Area of curved surface)`
`= 7480.8 – (2880 + 1000 + 100.8)`
`= 3500\ text(cm²)`
GEOMETRY, FUR1 2006 VCAA 4 MC
The building shown in the diagram is 8 m wide and 24 m long.
The side walls are 4 m high.
The peak of the roof is 6 m vertically above the ground.
In cubic metres, the volume of this building is
A. `384`
B. `576`
C. `960`
D. `1152`
E. `4608`
Show Worked Solution
`text(Area of front of house)`
`= (4 xx 8) + 1/2 (8 xx 2)`
`= 32 + 8`
`= 40\ text(m²)`
| `V` | `= Ah` |
| `= 40 xx 24` | |
| `= 960\ text(m³)` |
`=> C`
GEOMETRY, FUR1 2007 VCAA 4 MC
A steel beam used for constructing a building has a cross-sectional area of 0.048 m2 as shown.
The beam is 12 m long.
In cubic metres, the volume of this steel beam is closest to
A. `0.576`
B. `2.5`
C. `2.63`
D. `57.6`
E. `2500`
GEOMETRY, FUR1 2007 VCAA 3 MC
A rectangle is 3.79 m wide and has a perimeter of 24.50 m.
Correct to one decimal place, the length of the diagonal of this rectangle is
A. `9.2\ text(m)`
B. `9.3\ text(m)`
C. `12.2\ text(m)`
D. `12.3\ text(m)`
E. `12.5\ text(m)`
Show Worked Solution
| `text(Perimeter)` | `= 24.50\ text(m)` |
| `24.50` | `= 2x + (2 xx 3.79)` |
| `2x` | `= 16.92` |
| `x` | `= 8.46\ text(m)` |
`text(Using Pythagoras,)`
| `d^2` | `= x^2 + 3.79^2` |
| `= 8.46^2 + 3.79^2` | |
| `= 85.9357` | |
| `:.\ d` | `= 9.27…\ text(m)` |
`=> B`
GEOMETRY, FUR1 2008 VCAA 8 MC
A regular hexagon has side length 3.0 cm and height 5.2 cm as shown in the diagram above.
The area (in cm²) of the hexagon is closest to
A. `11.7`
B. `13.5`
C. `15.6`
D. `18.0`
E. `23.4`
Show Worked Solution
| `text(Area of rectangle)` | `= 3.0 xx 5.2` |
| `= 15.6\ text(cm²)` |
`text(Using Pythagoras to find)\ h:`
| `3.0^2` | `= 2.6^2 + h^2` |
| `h^2` | `= 9 – 6.76` |
| `= 2.24` | |
| `h` | `= 1.496…` |
`text(Area of)\ \ Delta ABC`
`= 1/2 xx b xx h`
`= 1/2 xx 5.2 xx 1.496…`
`= 3.891…\ text(cm²)`
`:.\ text(Area of hexagon)`
`= 15.6 + (2 xx 3.891…)`
`= 23.38…\ text(cm²)`
`=> E`
GEOMETRY, FUR1 2008 VCAA 7 MC
Sand is poured out of a truck and forms a pile in the shape of a right circular cone. The diameter of the base of the pile of sand is 2.6 m. The height is 1.2 m.
The volume (in m³) of sand in the pile is closest to
A. `2.1`
B. `3.1`
C. `6.4`
D. `8.5`
E. `25.5`
Show Worked Solution
| `text(Radius of base)` | `= 1/2\ text(diameter)` |
| `= 1.3\ text(m)` |
| `V` | `= 1/3 pi r^2 h` |
| `= 1/3 xx pi xx 1.3^2 xx 1.2` | |
| `= 2.12 …\ text(m³)` |
`=> A`
GEOMETRY, FUR1 2008 VCAA 4 MC
The solid cylindrical rod shown above has a volume of 490.87 cm3. The length is 25.15 cm.
The radius (in cm) of the cross-section of the rod, correct to one decimal place, is
A. `2.5`
B. `5.0`
C. `6.3`
D. `12.5`
E. `19.6`
FS Comm, 2UG SM-Bank 03
Zilda needs to download an `8.3 text(MB)` file from the internet. If the download transfer rate is `5 text(kbps)`, how long will it take her to download the file (to the nearest minute)? (3 marks)
Algebra, MET1 SM-Bank 28
Consider the simultaneous linear equations below.
`4x-2y = 18`
`3x + ky = 10`
where `k` is a real constant.
- What are the values of `k` where no solutions exist? (3 marks)
--- 10 WORK AREA LINES (style=lined) ---
- What values of `k` do the simultaneous equations have a unique solution? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Algebra, 2UG AM3 SM-Bank 05
Find the value of `R_1` if
`1/R = 1/R_1 + 1/R_2`, `R = 1.12` and `R_2 = 2.24` (2 marks)
Algebra, STD2 A2 2007 HSC 27b
A clubhouse uses four long-life light globes for five hours every night of the year. The purchase price of each light globe is $6.00 and they each cost `$d` per hour to run.
- Write an equation for the total cost (`$c`) of purchasing and running these four light globes for one year in terms of `d`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Find the value of `d` (correct to three decimal places) if the total cost of running these four light globes for one year is $250. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- If the use of the light globes increases to ten hours per night every night of the year, does the total cost double? Justify your answer with appropriate calculations. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- The manufacturer’s specifications state that the expected life of the light globes is normally distributed with a standard deviation of 170 hours.
What is the mean life, in hours, of these light globes if 97.5% will last up to 5000 hours? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solution
a. `text(Purchase price) = 4 xx 6 = $24`
| `text(Running cost)` | `= text(# Hours) xx text(Cost per hour)` |
| `= 4 xx 5 xx 365 xx d` | |
| `= 7300d` | |
| `:.\ $c = 24 + 7300d` | |
b. `text(Given)\ \ $c = $250`
| `250` | `= 24 + 7300d` |
| `7300d` | `= 226` |
| `d` | `= 226/7300` |
| `= 0.03095…` | |
| `= 0.031\ $ text(/hr)\ text{(3 d.p.)}` |
c. `text(If)\ d\ text(doubles to 0.062)\ \ $text(/hr)`
| `$c` | `= 24 + 7300 xx 0.062` |
| `= $476.60` | |
| `text(S) text(ince $476.60 is less than)\ 2 xx $250\ ($500),` | |
| `text(the total cost increases to less than double)` | |
| `text(the original cost.)` | |
d. `sigma = 170`
`z\ text(-score of 5000 hours) = 2`
| `z` | `= (x – mu)/sigma` |
| `2` | `= (5000 – mu)/170` |
| `340` | `= 5000 – mu` |
| `mu` | `= 4660` |
`:.\ text(The mean life of these globes is 4660 hours.)`
Algebra, STD2 A4 2007 HSC 27a
A rectangular playing surface is to be constructed so that the length is 6 metres more than the width.
- Give an example of a length and width that would be possible for this playing surface. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Write an equation for the area (`A`) of the playing surface in terms of its length (`l`). (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
A graph comparing the area of the playing surface to its length is shown.
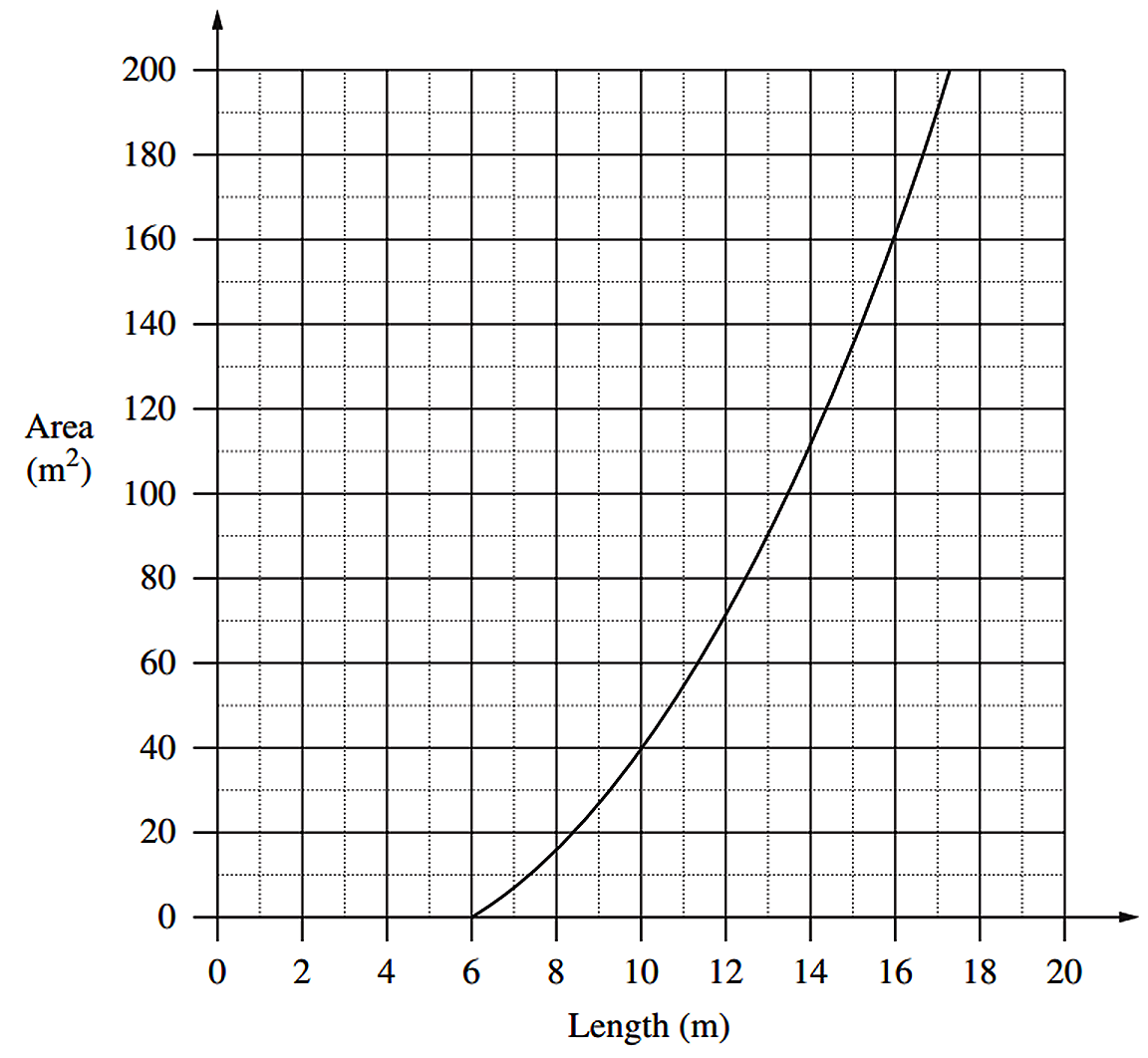
- Why are lengths of 0 metres to 6 metres impossible? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- What would be the dimensions of the playing surface if it had an area of 135 m²? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Company `A` constructs playing surfaces.
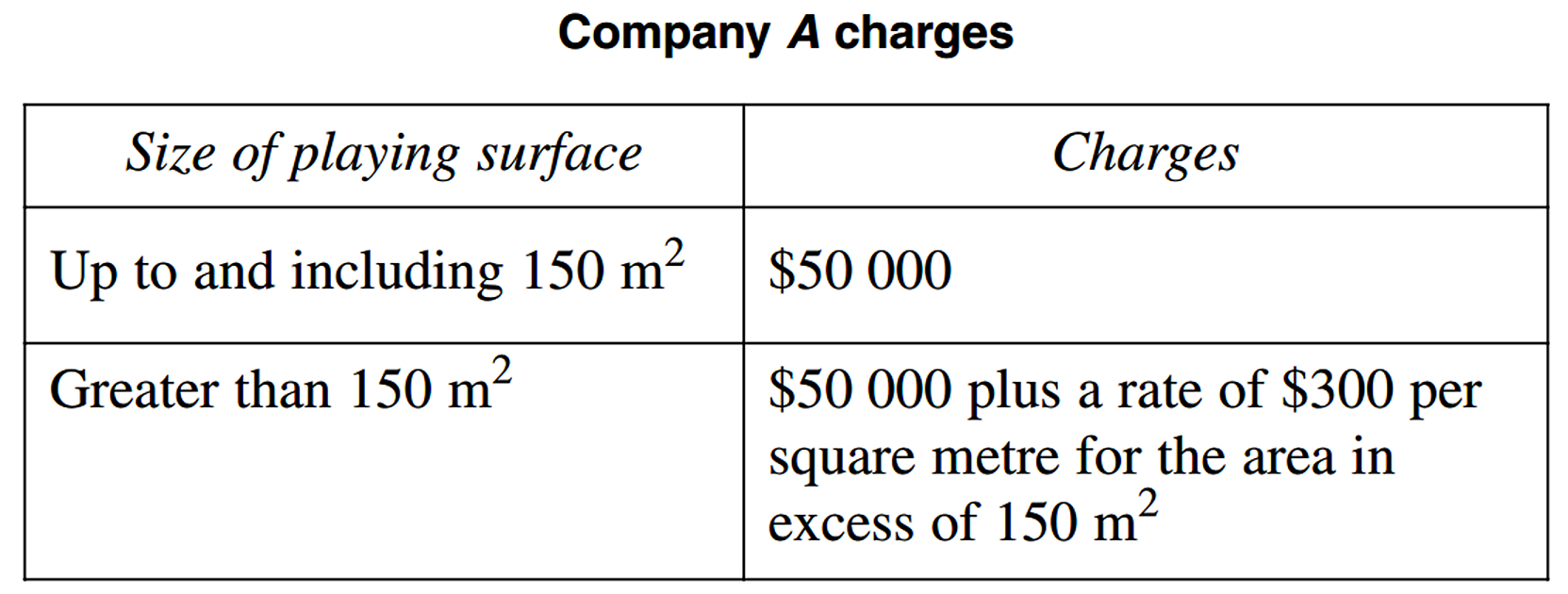
- Draw a graph to represent the cost of using Company `A` to construct all playing surface sizes up to and including 200 m².
Use the horizontal axis to represent the area and the vertical axis to represent the cost. (2 marks)
--- 8 WORK AREA LINES (style=lined) ---
- Company `B` charges a rate of $360 per square metre regardless of size.
- Which company would charge less to construct a playing surface with an area of 135 m²
Justify your answer with suitable calculations. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Answers Only
- `text(One possibility is a length of 10 m, and a width)`
`text{of 4 m (among many possibilities).}`
- `A = l (l – 6)\ \ text(m²)`
- `text(Given the length must be 6 m more than)`
`text(the width, it follows that the length)`
`text(must be greater than 6 m.)`
- `text(15 m × 9 m)`
-
- `text(Proof)\ \ text{(See worked solutions)}`
Show Worked Solution
i. `text(One possibility is a length of 10 m, and a width)`
`text{of 4 m (among many possibilities).}`
ii. `text(Length) = l\ text(m)`
`text(Width) = (l – 6)\ text(m)`
| `:.\ A` | `= l (l – 6)` |
iii. `text(Given the length must be 6m more than the width,)`
`text(it follows that the length must be greater than 6 m)`
`text(so that the width is positive.)`
iv. `text(From the graph, an area of 135 m² corresponds to)`
`text(a length of 15 m.)`
`:.\ text(The dimensions would be 15 m × 9 m.)`
| v. |  |
vi. `text(Company)\ A\ text(cost) = $50\ 000`
| `text(Company)\ B\ text(cost)` | `= 135 xx 360` |
| `= $48\ 600` |
`:.\ text(Company)\ B\ text(would charge $1400 less)`
`text(than Company)\ A.`
Financial Maths, STD2 F1 2007 HSC 26b
Myles is in his third year as an apprentice film editor.
- Myles purchased film-editing equipment for $5000.
After 3 years it has depreciated to $3635 using the straight-line method.
Calculate the rate of depreciation per year as a percentage. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Myles earns $800 per week. Calculate his taxable income for this year if the only allowable deduction is the amount of depreciation of his film-editing equipment in the third year of use. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Use this tax table to calculate Myles’s tax payable. (2 marks)
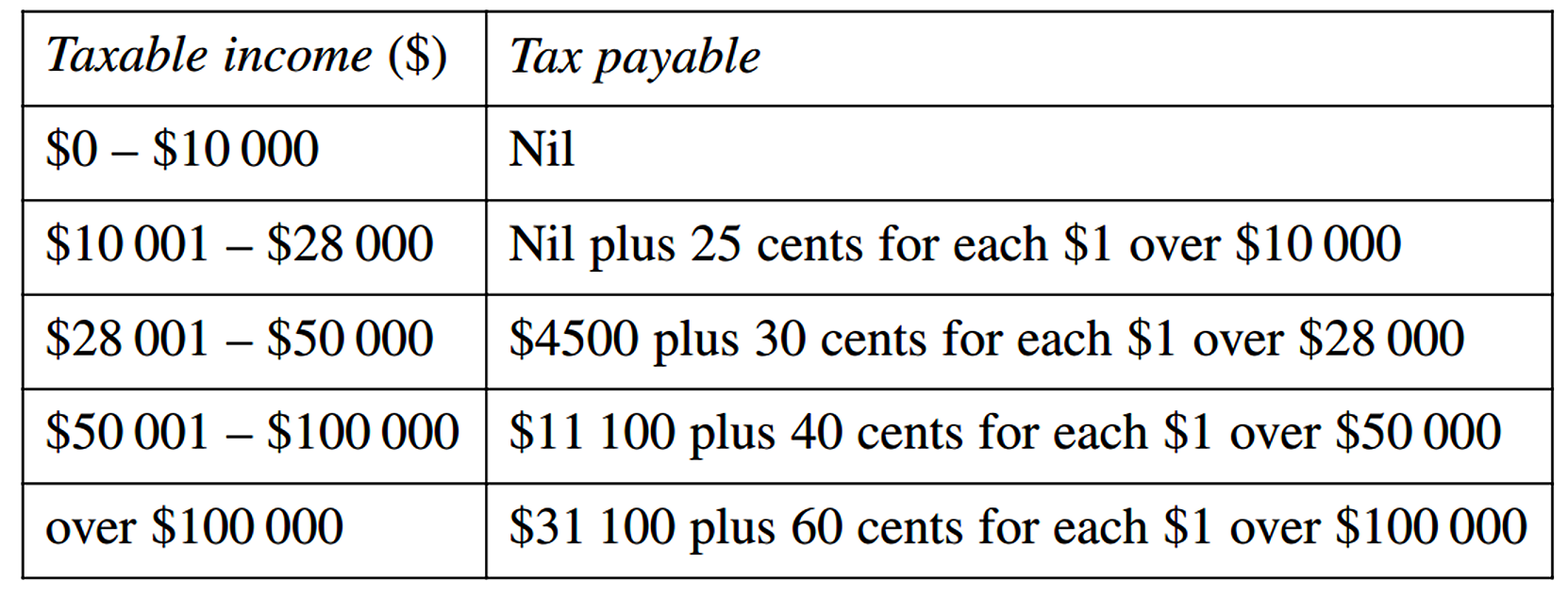
--- 4 WORK AREA LINES (style=lined) ---
Measurement, STD2 M6 2007 HSC 26a
The diagram shows information about the locations of towns `A`, `B` and `Q`.
- It takes Elina 2 hours and 48 minutes to walk directly from Town `A` to Town `Q`.
Calculate her walking speed correct to the nearest km/h. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Elina decides, instead, to walk to Town `B` from Town `A` and then to Town `Q`.
Find the distance from Town `A` to Town `B`. Give your answer to the nearest km. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Calculate the bearing of Town `Q` from Town `B`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Show Worked Solution
i. `text(2 hrs 48 mins) = 168\ text(mins)`
| `text(Speed)\ text{(} A\ text(to)\ Q text{)}` | `= 15/168` |
| `= 0.0892…\ text(km/min)` |
| `text(Speed)\ text{(in km/hr)}` | `= 0.0892… xx 60` |
| `= 5.357…\ text(km/hr)` | |
| `= 5\ text(km/hr)\ text{(nearest km/hr)}` |
| ii. |  |
`text(Using cosine rule)`
| `AB^2` | `= 15^2 + 10^2 – 2 xx 15 xx 10 xx cos 87^@` |
| `= 309.299…` | |
| `AB` | `= 17.586…` |
| `= 18\ text(km)\ text{(nearest km)}` |
`:.\ text(The distance from Town)\ A\ text(to Town)\ B\ text(is 18 km.)`
| iii |  |
| `/_CAQ` | `= 31^@\ \ \ text{(} text(straight angle at)\ A text{)}` |
| `/_AQD` | `= 31^@\ \ \ text{(} text(alternate angle)\ AC\ text(||)\ DQ text{)}` |
| `/_DQB` | `= 87 – 31 = 56^@` |
| `/_QBE` | `= 56^@\ \ \ text{(} text(alternate angle)\ DQ \ text(||)\ BE text{)}` |
`:.\ text(Bearing of)\ Q\ text(from)\ B`
`= 180 + 56`
`= 236^@`
GEOMETRY, FUR1 2011 VCAA 3 MC
The radius of a circle is 6.5 centimetres.
A square has the same area as this circle.
The length of each side of the square, in centimetres, is closest to
A. `6.4`
B. `10.2`
C. `11.5`
D. `23.0`
E. `33.2`
GEOMETRY, FUR1 2011 VCAA 2 MC
The point `Q` on building `B` is visible from the point `P` on building `A`, as shown in the diagram above.
Building `A` is 16 metres taller than building `B`.
The horizontal distance between point `P` and point `Q` is 23 metres.
The angle of depression of point `Q` from point `P` is closest to
A. `35°`
B. `41°`
C. `44°`
D. `46°`
E. `55°`
GEOMETRY, FUR1 2011 VCAA 5 MC
A right pyramid, shown below, has a rectangular base with length 4 m and width 3 m.
The height of the pyramid is 2 m.
The angle `VCO` that the sloping edge `VC` makes with the base of the pyramid, to the nearest degree, is
A. `22°`
B. `27°`
C. `34°`
D. `39°`
E. `45°`
Show Worked Solution
`text(Pyramid’s base)`
`text(Using Pythagoras,)`
| `(AC)^2` | `= 4^2 + 3^2` |
| `= 25` | |
| `AC` | `= 5` |
| `:.\ OC` | `= 2.5` |
`text(In)\ Delta VOC,`
| `tan\ theta` | `= 2/2.5` |
| `theta` | `= 38.65…^@` |
`=> D`
GEOMETRY, FUR1 2013 VCAA 7 MC
A greenhouse is built in the shape of a trapezoidal prism, as shown in the diagram above.
The cross-section of the greenhouse (shaded) is an isosceles trapezium. The parallel sides of this trapezium are 4 m and 10 m respectively. The two equal sides are each 5 m.
The length of the greenhouse is 12 m.
The five exterior surfaces of the greenhouse, not including the base, are made of glass.
The total area, in m², of the glass surfaces of the greenhouse is
A. `196`
B. `212`
C. `224`
D. `344`
E. `672`
Show Worked Solution
`text(Area of trapezoid)\ =\ 1/2\ text(h)\ (a+b)`
`text(Using Pythagoras,)`
| `h^2 + 3^2` | `= 5^2` |
| `h^2` | `= 16` |
| `h` | `= 4` |
`∴\ text{Area (trapezoid)}= 1/2 xx 4\ (10 + 4)= 28\ text(m²)`
| `text(Area of side)` | `= 12 xx 5` | `= 60\ text(m²)` |
| `text(Area of roof)` | `= 4 xx 12` | `= 48\ text(m²)` |
`∴\ text(Total area of glass surface)`
`= 2 xx (28 + 60) + 48`
`= 224\ text(m²)`
`=> C`
- « Previous Page
- 1
- …
- 104
- 105
- 106
- 107
- 108
- …
- 114
- Next Page »