SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

BIOLOGY, M1 2017 HSC 26

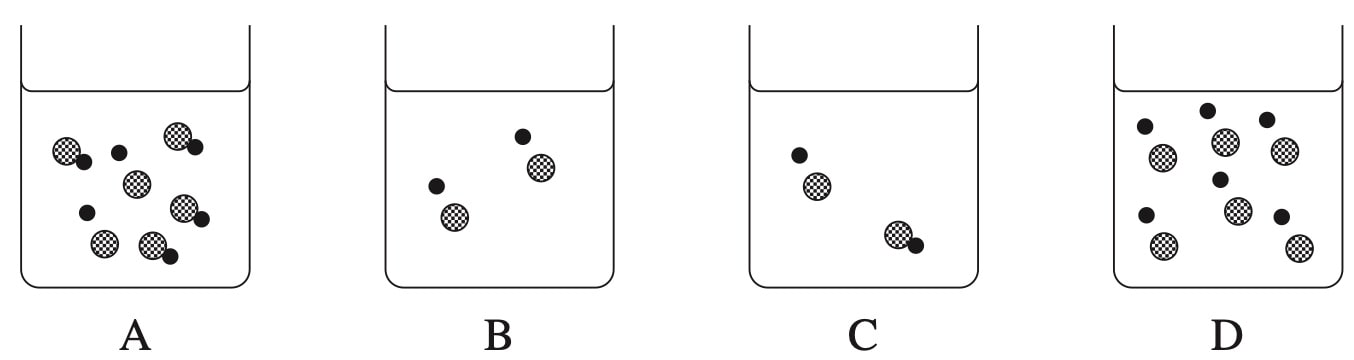
A controlled experiment was performed to investigate the effect of substrate concentration on the rate of an enzyme-catalysed reaction. Data were collected and are presented in the graph.
 

  1. What is the independent variable in this experiment?  (1 mark)

  2. Explain the trends shown in the graph.  (3 marks)

Show Answers Only

a.    Substrate concentration.

b.    Graph trends:

  • As the substrate concentration increases, the rate of reaction will increase because more substrate is available to undergo the reaction.
  • At higher substrate concentrations the rate of reaction will plateau as all enzyme active sites are utilised, so no more substrate can undergo the reaction.
Show Worked Solution

a.    Substrate concentration.

b.    Graph trends:

  • As the substrate concentration increases, the rate of reaction will increase because more substrate is available to undergo the reaction.
  • At higher substrate concentrations the rate of reaction will plateau as all enzyme active sites are utilised, so no more substrate can undergo the reaction.

BIOLOGY, M1 2017 HSC 25

Explain the difference in the urine concentration of marine fish and freshwater fish.  (4 marks)

Show Answers Only
  • Marine fish live in an environment which has a higher salt concentration than the concentration inside their cells, causing them to lose too much water through osmosis.
  • To maintain their internal environment they release very concentrated but small amounts of urine, which allows them to conserve water.
  • Freshwater fish live in an environment which has a lower salt concentration than the concentration inside their cells, causing too much water to move into their cells through osmosis.
  • To maintain their internal environment they produce large quantities of dilute urine, which allows them to expel the ‘extra’ water.
Show Worked Solution
  • Marine fish live in an environment which has a higher salt concentration than the concentration inside their cells, causing them to lose too much water through osmosis.
  • To maintain their internal environment they release very concentrated but small amounts of urine, which allows them to conserve water.
  • Freshwater fish live in an environment which has a lower salt concentration than the concentration inside their cells, causing too much water to move into their cells through osmosis.
  • To maintain their internal environment they produce large quantities of dilute urine, which allows them to expel the ‘extra’ water.

BIOLOGY, M7 SM-Bank 23

Smallpox is widely believed to be the cause of the significant population decline in Indigenous populations during early European arrival in Australia. Recent research suggests that it may have been chickenpox that caused the change in population numbers rather than smallpox. It is thought that chickenpox did not exist in Aboriginal and Torres Strait Islander communities before European arrival. Chickenpox is fairly mild in young children and is easily transmitted. It can be a fatal disease in adults who were not infected as children.

The graph below shows population numbers during the period 1780 –1850:

    • the estimated Aboriginal Australian population
    • the colonist population
    • the estimated total Australian population
       

With reference to chickenpox, explain how infection may have caused such a large impact on the Aboriginal Australian population and yet did not affect the population numbers of the colonists significantly, and why the Aboriginal population increased from 1790 to 1810.  (3 marks)

Show Answers Only
  • Childhood immunity existed in colonists due to previous exposure prior to arrival in Australia.
  • No immunity existed for the Aboriginal Australian population due to no previous exposure.
  • Aboriginal children became mildly ill when exposed in the early days of colonialism and became immune.
  • Aboriginal adults caught chickenpox in the early days of colonialism and died in disproportionately high numbers.
  • The initial exposure caused a steep decline in overall Aboriginal population. However, once Aboriginal children were immune and susceptible adults had died, there was an increase of population numbers over the next 30 years, from 1790 – 1810.
Show Worked Solution
  • Childhood immunity existed in colonists due to previous exposure prior to arrival in Australia.
  • No immunity existed for the Aboriginal Australian population due to no previous exposure.
  • Aboriginal children became mildly ill when exposed in the early days of colonialism and became immune.
  • Aboriginal adults caught chickenpox in the early days of colonialism and died in disproportionately high numbers.
  • The initial exposure caused a steep decline in overall Aboriginal population. However, once Aboriginal children were immune and susceptible adults had died, there was an increase of population numbers over the next 30 years, from 1790 – 1810.

BIOLOGY, M7 SM-Bank 22

A summary of case-control studies conducted from 1997 to 2003 showed that a single dose of varicella (chickenpox) vaccine was 97% effective in the first year after vaccination and 86% effective in the second year. From the second to eighth year after vaccination, the vaccine's effectiveness remained stable at 81% to 86%. Most vaccinated children who developed chickenpox during the eight years after vaccination had a mild case of the disease.

Why do most vaccinated individuals, if they are infected, show only a mild case of the disease?  (2 marks)

Show Answers Only

Answers should include two of the following reasons:

  • Virus enters and is detected.
  • Memory cells present.
  • Rapid antibody production where antibodies are produced in large numbers
  • Virus is neutralised
Show Worked Solution

Answers should include two of the following reasons:

  • Virus enters and is detected.
  • Memory cells present.
  • Rapid antibody production where antibodies are produced in large numbers
  • Virus is neutralised

BIOLOGY, M7 SM-Bank 27

Influenza is an infectious respiratory disease. In humans, it can be caused by the influenza A or influenza B viruses.

Antigenic drift can result in small changes to the structure of the antigens on the surface of the influenza virus, as shown in the diagram below.
 

  1. What change would have occurred within the virus to bring about the change in the structure of the antigen?  (1 mark)

  2. Vaccines against influenza are available and it is recommended that people are vaccinated each year.
  3. Explain, in terms of antigenic drift, why vaccinations are recommended yearly for influenza rather than once every few years.  (2 marks)

Show Answers Only

a.   Mutation.

b.   Correct answers could include:

  • Vaccines contain new antigens resulting in the production of new antibodies OR memory cells specific to the antigen.
  • Memory cells allow for a faster OR larger immune response.
  • Any existing memory cells specific to the previous antigens would no longer be effective.

Show Worked Solution

a.   Mutation.

b.   Correct answers could include:

  • Vaccines contain new antigens resulting in the production of new antibodies OR memory cells specific to the antigen.
  • Memory cells allow for a faster OR larger immune response.
  • Any existing memory cells specific to the previous antigens would no longer be effective.

BIOLOGY, M7 SM-Bank 7 MC

The human body does not normally produce an immune response against self cells.

Cells in the human immune system can distinguish self cells from non-self cells

  1. because non-self cells have a faster reproduction rate.
  2. due to the presence of different antigens on non-self cells.
  3. only when antibodies are attached to the surface of non-self cells.
  4. because non-self cells are always smaller in size than self cells.
Show Answers Only

`B`

Show Worked Solution
  • The human body is able to distinguish self cells from non-self cells via the presence of different surface proteins.
  • Self cells have an MHC complex while non-self cells have antigens.

`=>B`

BIOLOGY, M5 SM-Bank 25

In fruit flies, eye colour is a sex-linked trait inherited on the X chromosome. The red-eye allele R is dominant over the white-eye allele (r). A red-eyed male and white-eyed female have 50 offspring.

Use a Punnett square to predict the number of male and female offspring and their eye colour.   (3 marks)

Show Answers Only

\begin{array} {|c|c|c|}
\hline  & \text{X}^{\text{R}} & \text{Y} \\
\hline \text{X}^{\text{r}} & \text{X}^{\text{R}}\text{X}^{\text{r}} & \text{X}^{\text{R}}\text{Y} \\
\hline \text{X}^{\text{r}} & \text{X}^{\text{R}}\text{X}^{\text{r}} & \text{X}^{\text{R}}\text{Y} \\  
\hline \end{array}

  • Predicted offspring: 25 red-eyed females and 25 white-eyed males.
Show Worked Solution

\begin{array} {|c|c|c|}
\hline  & \text{X}^{\text{R}} & \text{Y} \\
\hline \text{X}^{\text{r}} & \text{X}^{\text{R}}\text{X}^{\text{r}} & \text{X}^{\text{R}}\text{Y} \\
\hline \text{X}^{\text{r}} & \text{X}^{\text{R}}\text{X}^{\text{r}} & \text{X}^{\text{R}}\text{Y} \\  
\hline \end{array}

  • Predicted offspring: 25 red-eyed females and 25 white-eyed males.

BIOLOGY, M5 SM-Bank 24

Explain how transcription factors control cell differentiation, using an example.  (3 marks)

Show Answers Only
  • Transcription factors are proteins that turn specific genes on or off by binding to nearby sections of DNA.
  • This allows different genes to be expressed in different cell types.
  • For example, the SRY gene on the Y chromosome promotes the development of testes by producing a protein that regulates the expression of genes (production of proteins) required by Sertoli cells.
Show Worked Solution
  • Transcription factors are proteins that turn specific genes on or off by binding to nearby sections of DNA.
  • This allows different genes to be expressed in different cell types.
  • For example, the SRY gene on the Y chromosome promotes the development of testes by producing a protein that regulates the expression of genes (production of proteins) required by Sertoli cells.

BIOLOGY, M5 SM-Bank 22

Describe the roles of messenger RNA and transfer RNA in protein synthesis.  (2 marks)

Show Answers Only
  • Messenger RNA (or mRNA) provides copies of the gene from the DNA template strand.
  • Transfer RNA (or tRNA) decodes mRNA sequences by matching amino acids to codons of the mRNA.
Show Worked Solution
  • Messenger RNA (or mRNA) provides copies of the gene from the DNA template strand.
  • Transfer RNA (or tRNA) decodes mRNA sequences by matching amino acids to codons of the mRNA.

BIOLOGY, M6 SM-Bank 24

In 1950 , the myxoma virus was released into Australian pest rabbit populations to reduce their numbers. The resulting disease, myxomatosis, initially wiped out 95% of the rabbit population; however, it quickly became less effective as a population control measure.

This graph shows the frequency of myxomatosis resistance in Australia's rabbit population from 1949 to 1956.
 

Use evidence from the graph and the principles of natural selection to explain how myxomatosis became ineffective as a population control measure.  (3 marks)

Show Answers Only
  • The introduction of the myxoma virus conferred a selective advantage on the myxomatosis-resistant phenotype.
  • Myxomatosis-resistant rabbits had an increased chance of surviving to reproduce and pass on the trait.
  • This led to an increase in the frequency of this phenotype in the population from approximately 9% in 1950 to approximately 96% in 1953 .
  • After 1953, most of the remaining rabbits possessed the myxomatosis-resistant phenotype, so the disease was no longer effective at reducing rabbit numbers.
Show Worked Solution
  • The introduction of the myxoma virus conferred a selective advantage on the myxomatosis-resistant phenotype.
  • Myxomatosis-resistant rabbits had an increased chance of surviving to reproduce and pass on the trait.
  • This led to an increase in the frequency of this phenotype in the population from approximately 9% in 1950 to approximately 96% in 1953 .
  • After 1953, most of the remaining rabbits possessed the myxomatosis-resistant phenotype, so the disease was no longer effective at reducing rabbit numbers.

BIOLOGY, M5 SM-Bank 23

Explain the purpose of gel electrophoresis in DNA profiling.  (2 marks)

Show Answers Only
  • Gel electrophoresis separates DNA segments based on size.
  • This process produces characteristic banding patterns.
Show Worked Solution
  • Gel electrophoresis separates DNA segments based on size.
  • This process produces characteristic banding patterns.

PHYSICS, M8 EQ-Bank 21

With reference to the earliest conditions present following the Big Bang, describe the processes that led to the transformation of radiation into matter.  (4 marks)

Show Answers Only
  • According to the Big Bang theory, the universe began as a hot, dense, and homogeneous state of pure energy.
  • As the universe expanded and cooled, this energy was converted into matter and antimatter particles, such as quarks, leptons, and their antiparticles.
  • These particles and antiparticles annihilated each other in pairs, releasing more energy in the form of radiation.
  • However, there was a slight asymmetry between matter and antimatter, which resulted in a small excess of matter over antimatter. This excess matter is what makes up the observable universe today.
  • The transformation of radiation into matter occurred in several stages (or epochs), depending on the temperature and energy of the universe.
Show Worked Solution
  • According to the Big Bang theory, the universe began as a hot, dense, and homogeneous state of pure energy.
  • As the universe expanded and cooled, this energy was converted into matter and antimatter particles, such as quarks, leptons, and their antiparticles.
  • These particles and antiparticles annihilated each other in pairs, releasing more energy in the form of radiation.
  • However, there was a slight asymmetry between matter and antimatter, which resulted in a small excess of matter over antimatter. This excess matter is what makes up the observable universe today.
  • The transformation of radiation into matter occurred in several stages (or epochs), depending on the temperature and energy of the universe.

PHYSICS, M6 EQ-Bank 29

Prior to 2019, the ampere was characterized as the unvarying current that, when sustained in two infinitely long, straight parallel conductors with negligible circular cross-section and spaced one meter apart in a vacuum, would result in a force of  `10 xx 10^{-7}` newton per metre of length between the conductors.

  1. How does Newton’s Third Law apply to this definition of the ampere?   (2 marks)
  1. Two parallel current carrying wires are 1.2 metres long each, both carrying 0.55 amperes at a distance of 25 mm apart. Calculate the force between the wires.   (2 marks)
Show Answers Only

a.   
       

  • Since the two wires in the definition carry current in the same direction, wire 1 will impart an attraction force on wire 2.
  • Similarly, wire 2 will impart an attractive force on wire 1. This force will be equal but in an opposite direction to the attractive force imparted on wire 2 (above).
  • Newton’s Third Law states that two objects interact with each other, they exert forces on each other that are equal in magnitude and opposite in direction, also known as action and reaction forces.
  • In this way, Newton’s Third Law directly describes the forces between conductors within the definition of the ampere.

b.  `2.9 xx 10^{-5}\ text{N}`

Show Worked Solution

a.   
         

  • Since the two wires in the definition carry current in the same direction, wire 1 will impart an attraction force on wire 2.
  • Similarly, wire 2 will impart an attractive force on wire 1. This force will be equal but in an opposite direction to the attractive force imparted on wire 2 (above).
  • Newton’s Third Law states that two objects interact with each other, they exert forces on each other that are equal in magnitude and opposite in direction, also known as action and reaction forces.
  • In this way, Newton’s Third Law directly describes the forces between conductors within the definition of the ampere.
b.    `F/l` `=mu_0/(2pi) xx (I_1I_2)/r`
  `F` `=(4pi xx 10^{-7})/(2pi) xx (0.55)^2/(2.5 xx 10^{-3}) xx 1.2`
    `=(2 xx 10^{-7})xx (0.55)^2/(2.5 xx 10^{-3}) xx 1.2`
    `=2.9 xx 10^{-5}\ text{N}`

CHEMISTRY, M5 EQ-Bank 29

The information in the table shows how the solubility of lead chloride is affected by temperature.  
 

Using a graph, calculate the solubility product \((K_{sp})\) of the dissolution of lead chloride at 50°C. Include a fully labelled graph and a relevant chemical equation in your answer   (6 marks)
 

Show Answers Only

\(\ce{K_{sp} = 6.4 \times 10^{-5}}\)

Show Worked Solution

 

\(\ce{PbCl2(s) \rightleftharpoons Pb^2+(aq) + 2Cl^-(aq)}\)

\(\ce{Using the graph:}\)

\(\ce{Solubility (50°) = 0.7 g/100 g water = 7 g/L}\)

\(\ce{Converting to mol L^{-1}:}\)

\[\ce{MM(PbCl2) = 207.2 + 2 \times 35.45 = 278.1}\]

\[\ce{n = \frac{m}{MM} = \frac{7}{278.1} = 0.0252 mol L^{-1}}\]

\(\ce{[Pb^2+(aq)] = 0.0252 mol L^{-1}}\)
 

\(\ce{Mole ratio \ Pb^2+ : Cl^- = 1:2}\)

\(\Rightarrow \ce{[Cl^-]  = 2 \times 0.0252 = 0.0504 mol L^{-1}}\)
 

\begin{aligned}
\ce{$K_{sp}$} & \ce{= [Pb^2+][Cl^-]^{2}} \\
 & \ce{=0.0252 \times (0.0504)^{2}}  \\
 & \ce{= 6.4 \times 10^{-5}}  \\
\end{aligned}

CHEMISTRY, M5 EQ-Bank 28

A 100 mL saturated solution of calcium hydroxide at 25°C contains 0.173 g of calcium hydroxide.

  1. Calculate the solubility product \(\ce{($K_{sp}$)}\) of this salt at 25°C.  (3 marks)

  2. Explain why the undissolved solid is not included in the expression for the solubility product constant.  (1 marks)

Show Answers Only

a.    \(\ce{$K_{sp}$ = 5.06 \times 10^{-5}}\)

b.    Undissolved solid:

  • \(\ce{[CaOH2(s)]}\) is constant throughout the reaction.
  • Since it does not change, it is not included in the equilibrium expression.
Show Worked Solution

a.   \(\ce{CaOH2(s) \rightleftharpoons Ca^2+(aq) + 2OH^-(aq)}\)

\(\ce{Solubility = 0.173 g/100 mL = 1.73 g/L}\)

\[\ce{n = \frac{m}{MM} = \frac{1.73}{74.093} = 0.00233 mol}\]

\(\ce{[Ca^{2+}] = 0.0233 mol L^{-1}}\)
 

\(\ce{Mole ratio  \ Ca^2+ : OH^- = 1:2}\)

\(\ce{$K_{sp}$   =[Ca^2+][OH^-]^{2}}\)

 

\(\ce{[OH^-]  = 2 \times 0.0233 = 0.0466 mol L^{-1}}\)
 

\begin{aligned}
\ce{$K_{sp}$} & \ce{=[Ca^2+][OH^-]^{2}}  \\
 & \ce{= 0.0233 \times (0.0466)^{2}}  \\
 & \ce{= 5.06 \times 10^{-5}}  \\
\end{aligned}

 
b.    Undissolved solid:

  • \(\ce{[CaOH2(s)]}\) is constant throughout the reaction.
  • Since it does not change, it is not included in the equilibrium expression.

CHEMISTRY, M5 EQ-Bank 26

The diagrams represent equipment used in an investigation to determine the chloride ion concentration in a water sample.
 

Describe how the chloride ion concentration in a water sample can be determined using the equipment in the diagrams. Include a relevant chemical equation.   (3 marks)

Show Answers Only
  • When the silver nitrate solution is added, chloride ions present in the water sample will precipitate with the added silver ions described by the following equation:
  •    \(\ce{Ag+(aq) +Cl^-(aq) \rightleftharpoons AgCl(s)}\)
  • Adding excess silver nitrate ensures all chloride ions precipitate out.
  • The filtering apparatus is used to filter solid silver chloride. This solid is then dried to constant mass and weighed.
  • Using the molar mass of silver chloride, the number of moles of solid silver chloride produced is calculated. Silver chloride contains silver ions and chloride ions in a 1:1 molar ratio and using this ratio, the moles of chloride present is calculated.
  • The result represents the same number of moles of chloride in the original water sample. Using the volume of the water sample, its chloride ion concentration is calculated.
Show Worked Solution
  • When the silver nitrate solution is added, chloride ions present in the water sample will precipitate with the added silver ions described by the following equation:
  •    \(\ce{Ag+(aq) +Cl^-(aq) \rightleftharpoons AgCl(s)}\)
  • Adding excess silver nitrate ensures all chloride ions precipitate out.
  • The filtering apparatus is used to filter solid silver chloride. This solid is then dried to constant mass and weighed.
  • Using the molar mass of silver chloride, the number of moles of solid silver chloride produced is calculated. Silver chloride contains silver ions and chloride ions in a 1:1 molar ratio and using this ratio, the moles of chloride present is calculated.
  • The result represents the same number of moles of chloride in the original water sample. Using the volume of the water sample, its chloride ion concentration is calculated.

CHEMISTRY, M5 EQ-Bank 24

When a sample of solid silver chloride is added to a `1.00 xx10^(-2)` mol L−1 sodium chloride solution, only some of the silver chloride dissolves.

Calculate the equilibrium concentration of silver ions in the resulting solution, given that the `K_(sp)` of silver chloride is `1.8 xx10^(-10)`.   (3 marks)

Show Answers Only

\(\ce{[Ag^+] = 1.80 \times 10^{-8} mol L^{-1}}\)

Show Worked Solution

 \(\ce{AgCl(s) \rightleftharpoons Ag^+(aq) + Cl^-(aq)}\)

\begin{array} {|l|c|c|c|}
\hline  & \ce{[AgCl(s)]} & \ce{[Ag^+(aq)]} & \ce{[Cl^-(aq)]} \\
\hline \text{Initial} &  & 0 & 1.00 \times 10^{-2} \\
\hline \text{Change} &  & +x & +x \\
\hline \text{Equilibrium} &  & x & 1.00 \times 10^{-2} +x \\
\hline \end{array}

\(\ce{Let \ $x$ = [Ag^+]}\)

\[\ce{$K_{sp}$ = [Ag^+][Cl^-]}\]

\(\ce{$K_{sp} = x$(1.00 \times 10^{-2} + $x$) = 1.80 \times 10^{-10}}\)

\(\ce{Since $x$\ is small, 1.00 \times 10^{-2} + $x$ ≈ 1.00 \times 10^{-2}}\)

\begin{aligned}
\ce{$x$(1.00 \times 10^{-2})} & \ce{= 1.80 \times 10^{-10}}  \\
\ce{$x$} & \ce{= 1.80 \times 10^{-8}}  \\
\ce{\therefore [Ag^+]} & \ce{= 1.80 \times 10^{-8} mol L^{-1}}  \\
\end{aligned}

CHEMISTRY, M5 EQ-Bank 23

Butanoic acid is a natural product and a component of human sweat.

Calculate the value of \(\ce{$K_{a}$}\) for butanoic acid if a 0.10 mol L–1 solution has a pH of 2.9 at 298 K.   (3 marks)

Show Answers Only

\(\ce{$K_{a}$ = 1.6 \times 10^{-5}}\)

Show Worked Solution

\(\ce{C3H7COOH(aq) \rightleftharpoons C3H7COO^-(aq) + H^+(aq)}\)  \[\ce{$K_{a}$ = \frac{[C3H7COO^-][H^+]}{[C3H7COOH]}}\]

\(\ce{[H^+] = 10^{-pH} = 10^{-2.9}= 1.26 \times 10^{-3} mol L^{-1}}\)

\begin{array} {|l|c|c|c|}
\hline  & \ce{[C3H7COOH]} & \ce{[C3H7COO^-]} & \ce{[H^+]} \\
\hline \text{Initial} & 0.10 & 0 & 0 \\
\hline \text{Change} & -1.26 \times 10^{-3} & +1.26 \times 10^{-3} & +1.26 \times 10^{-3} \\
\hline \text{Equilibrium} & 0.0987 & 1.26 \times 10^{-3} & 1.26 \times 10^{-3} \\
\hline \end{array}

\(K_{a}=\dfrac{(1.26 \times 10^{-3})^2}{0.0987}=1.6 \times 10^{-5} \)

CHEMISTRY, M6 EQ-Bank 13 MC

The pKa of trichloroacetic acid is 0.70 and the pKa of acetic acid is 4.8.

Which of the following identifies the acid with the higher pH and explain why?

  1. Acetic acid as it is less likely to lose a hydrogen ion
  2. Acetic acid as it is more likely to lose a hydrogen ion
  3. Trichloroacetic acid as it is less likely to lose a hydrogen ion
  4. Trichloroacetic acid as it is more likely to lose a hydrogen ion
Show Answers Only

`A`

Show Worked Solution
  • Higher pH corresponds to a weaker acid.
  • Higher pKa corresponds to a weaker acid (i.e. a higher pH).
  • Acetic acid the weaker acid (higher pKa), meaning it is less likely to dissociate in solution and lose a hydrogen ion.

`=> A`

CHEMISTRY, M6 EQ-Bank 28

The flowchart shown outlines the sequence of steps used to determine the concentration of an unknown hydrochloric acid solution.
 

Describe steps A, B and C including correct techniques, equipment and appropriate calculations. Determine the concentration of the hydrochloric acid.  (8 marks)

Show Answers Only

Step A

  • Prepare \(\ce{Na2CO3}\) by drying. Protect solid \(\ce{Na2CO3}\) from moisture in the air by storing in a desiccator.
  • Calculate mass of dried \(\ce{Na2CO3}\) required and weigh accurately.
  •    \(\ce{m(Na2CO3) = 0.1 \times 0.5 \times 105.99 = 5.30 g}\)
  • Clean and rinse a 500 mL volumetric flask with distilled water.
  • Add 5.30 grams of \(\ce{Na2CO3}\) to the volumetric flask using a funnel and wash funnel using distilled water. Add distilled water to the flask to the bottom of the meniscus.

Step B

  • Clean and rinse a 50 mL burette. Fill burette with the unknown acid and place on a retort stand.
  • Clean and rinse a 250 mL conical flask with distilled water.
  • Clean a 25 mL pipette and rinse with 0.1 M \(\ce{Na2CO3}\) solution. Fill pipette with \(\ce{Na2CO3}\) solution to bottom of meniscus.
  • Transfer all pipette solution into conical flask and add an appropriate indicator. A white background (tile) should be placed under the flask to highlight any colour changes in the solution.
  • Slowly add acid solution from the burette into the conical flask and record the volume used when the indicator changes colour.

Step C

  • The initial titration represents a test run to establish an indicative volume. Three subsequent titrations should be performed with the average titration forming the basis of \(\ce{HCl}\) concentration calculations.
  • Calculate the concentration of \(\ce{HCl}\)
  •    \(\ce{2H^+(aq) + CO3^{2-} (aq) \rightarrow H2CO3 (aq) \rightarrow H2O (l) + CO2 (g)}\)
  •    \(\ce{M(Na2CO3) = 0.1 \times 0.025 = 2.5 \times 10^{-3}}\)
  •    \(\ce{M(HCl) = 2 \times M(Na2CO3) = 5\times 10^{-3}}\)
  •    \[\ce{[HCl] = \frac{M(HCl)}{Vol HCl} = \frac{5 \times 10^{-3}}{21.4 \times 10^{-3}} = 0.234 mol L^{-1}}\]
Show Worked Solution

Step A

  • Prepare \(\ce{Na2CO3}\) by drying. Protect solid \(\ce{Na2CO3}\) from moisture in the air by storing in a desiccator.
  • Calculate mass of dried \(\ce{Na2CO3}\) required and weigh accurately.
  •    \(\ce{m(Na2CO3) = 0.1 \times 0.5 \times 105.99 = 5.30 g}\)
  • Clean and rinse a 500 mL volumetric flask with distilled water.
  • Add 5.30 grams of \(\ce{Na2CO3}\) to the volumetric flask using a funnel and wash funnel using distilled water. Add distilled water to the flask to the bottom of the meniscus.

Step B

  • Clean and rinse a 50 mL burette. Fill burette with the unknown acid and place on a retort stand.
  • Clean and rinse a 250 mL conical flask with distilled water.
  • Clean a 25 mL pipette and rinse with 0.1 M \(\ce{Na2CO3}\) solution. Fill pipette with \(\ce{Na2CO3}\) solution to bottom of meniscus.
  • Transfer all pipette solution into conical flask and add an appropriate indicator. A white background (tile) should be placed under the flask to highlight any colour changes in the solution.
  • Slowly add acid solution from the burette into the conical flask and record the volume used when the indicator changes colour.

Step C

  • The initial titration represents a test run to establish an indicative volume. Three subsequent titrations should be performed with the average titration forming the basis of \(\ce{HCl}\) concentration calculations.
  • Calculate the concentration of \(\ce{HCl}\)
  •    \(\ce{2H^+(aq) + CO3^{2-} (aq) \rightarrow H2CO3 (aq) \rightarrow H2O (l) + CO2 (g)}\)
  •    \(\ce{M(Na2CO3) = 0.1 \times 0.025 = 2.5 \times 10^{-3}}\)
  •    \(\ce{M(HCl) = 2 \times M(Na2CO3) = 5\times 10^{-3}}\)
  •    \[\ce{[HCl] = \frac{M(HCl)}{Vol HCl} = \frac{5 \times 10^{-3}}{21.4 \times 10^{-3}} = 0.234 mol L^{-1}}\]

CHEMISTRY, M7 EQ-Bank 21

With the use of a labelled diagram, describe how grease can be removed from fabric using soap.  (3 marks)

Show Answers Only

  • Soap molecules, as shown in the diagram, have a negatively charged (hydrophilic) “head” and a hydrophobic ‘tail’ consisting made up of fatty acids.
  • Hydrophobic tails are attracted to the grease particles and attach themselves. 
  • The hydrophilic heads, at the same time, are attracted to water molecules. This chain of attractions will lift grease off the fabric and suspend it in the water.
Show Worked Solution

  • Soap molecules, as shown in the diagram, have a negatively charged (hydrophilic) “head” and a hydrophobic ‘tail’ consisting made up of fatty acids.
  • Hydrophobic tails are attracted to the grease particles and attach themselves. 
  • The hydrophilic heads, at the same time, are attracted to water molecules. This chain of attractions will lift grease off the fabric and suspend it in the water.

CHEMISTRY, M6 EQ-Bank 27

What determines the pH of a buffer solution?   (2 marks)

Show Answers Only
  • The strength of the acid. The greater the pKa of (weaker) the acid, the greater the buffer pH.
  • Relative concentrations of acid and base. 
Show Worked Solution
  • The strength of the acid. The greater the pKa of (weaker) the acid, the greater the buffer pH.
  • Relative concentrations of acid and base. 

CHEMISTRY, M6 EQ-Bank 23

Propanoic acid dissociation in water can is represented in the following equation:

\(\ce{CH3CH2COOH($aq$) + H2O($l$) \rightleftharpoons CH3CH2COO^-($aq$) + H3O^{+}($aq$)}\)

Explain how the pH of the propanoic acid solution would change if it was diluted.   (3 marks)

Show Answers Only
  • Propanoic acid only partially ionises in solution and is defined as a weak acid.
  • Any dilution of the acid will result in a decrease of the concentration of all species (including the hydronium ion).
  • According to Le Chatelier, the decreasing concentrations of dissolved species will cause the equilibrium to shift to the right.
  • While this effect causes an increase in ionisation, it is not sufficient to counter the decrease in hydronium ion concentration caused by the original dilution.
  • Since the net effect causes the hydronium ion concentration to decrease, the solution will become less acidic and the pH will increase.
Show Worked Solution
  • Propanoic acid only partially ionises in solution and is defined as a weak acid.
  • Any dilution of the acid will result in a decrease of the concentration of all species (including the hydronium ion).
  • According to Le Chatelier, the decreasing concentrations of dissolved species will cause the equilibrium to shift to the right.
  • While this effect causes an increase in ionisation, it is not sufficient to counter the decrease in hydronium ion concentration caused by the original dilution.
  • Since the net effect causes the hydronium ion concentration to decrease, the solution will become less acidic and the pH will increase.

CHEMISTRY, M6 EQ-Bank 8 MC

Which of the following is NOT a Bronsted-Lowry reaction?

  1. \(\ce{NH4^+ + NH2^- \rightleftharpoons 2NH3}\)
  2. \(\ce{CO2 + OH^- \rightleftharpoons HCO3^-}\)
  3. \(\ce{HClO4 + CH3COOH \rightleftharpoons CH3COOH2^+ + ClO4^-}\)
  4. \(\ce{CH3CH2O^- + CH3NH3^+ \rightleftharpoons CH3CH2OH + CH3NH2}\)
Show Answers Only

`B`

Show Worked Solution
  • A Bronsted-Lowry reaction occurs when one species (acid) transfers a proton to another species (base).
  • Although it is an acid-base reaction, no proton transfer occurs in  \(\ce{CO2 + OH^- \rightleftharpoons HCO3^-}\)

`=> B`

CHEMISTRY, M7 EQ-Bank 27

Contrast ONE addition polymer and ONE condensation polymer in terms of their structures, properties and uses. Include structural formulae in your answers.   (7 marks)

Show Answers Only

Addition polymer – polyethylene. Condensation polymer – nylon.

Structures

  • Polyethylene is made by the addition of ethylene monomers with the following structural formula:

  • Nylon is a condensation polymer made from 1,6-diaminohexane and adipic acid, producing a by-product of water molecules. It has the following structural formula.

Properties

  • Polyethylene is inexpensive, weatherproof and relatively resistant to chemicals.
  • There are two main types of polyethylene which have different properties. Low-density polyethylene (LDPE) is semi-rigid while high density polyethylene (HDPE) is fluid.
  • Nylon is strong and relatively resistant to moisture absorptivity. It is longer lasting than polyethylene, resistant to chemicals and is used to make nylon fibre.

Applications

  • LDPE is used to produce products such as plastic soft drink bottles, flexible water pipes and cling wrap. HDPE’s fluidity make it an appropriate material for producing shopping bags, plastic crates and drums for storage.
  • Nylon is very versatile in its manufacturing uses. It is a common input for clothing, can be used for injection-moulded parts for vehicles and also as reinforcement for rubber tyres. 
  • Nylon is also used as the main material input for nylon thread which has a myriad of uses, including stitching for clothes and the production of rope.
Show Worked Solution

Addition polymer – polyethylene. Condensation polymer – nylon.

Structures

  • Polyethylene is made by the addition of ethylene monomers with the following structural formula:

  • Nylon is a condensation polymer made from 1,6-diaminohexane and adipic acid, producing a by-product of water molecules. It has the following structural formula.

Properties

  • Polyethylene is inexpensive, weatherproof and relatively resistant to chemicals.
  • There are two main types of polyethylene which have different properties. Low-density polyethylene (LDPE) is semi-rigid while high density polyethylene (HDPE) is fluid.
  • Nylon is strong and relatively resistant to moisture absorptivity. It is longer lasting than polyethylene, resistant to chemicals and is used to make nylon fibre.

Applications

  • LDPE is used to produce products such as plastic soft drink bottles, flexible water pipes and cling wrap. HDPE’s fluidity make it an appropriate material for producing shopping bags, plastic crates and drums for storage.
  • Nylon is very versatile in its manufacturing uses. It is a common input for clothing, can be used for injection-moulded parts for vehicles and also as reinforcement for rubber tyres. 
  • Nylon is also used as the main material input for nylon thread which has a myriad of uses, including stitching for clothes and the production of rope.

CHEMISTRY, M8 EQ-Bank 22

A bottle of solution is missing its label. It is either \(\ce{Pb(NO_3)_2, Ba(NO_3)_2 or Fe(NO_3)_2}\).

Using only \(\ce{HCl, NaOH}\) and \(\ce{H_2SO_4}\) solutions, outline a sequence of steps that could be followed to confirm the identity of the solution in the bottle. Include observed results and ionic equations in your answer.   (4 marks)

Show Answers Only

Step 1: Prepare samples of the original solution and \(\ce{HCl, NaOH}\)  and  \(\ce{H_2SO_4}\)  solutions and then follow the flow chart below.

Show Worked Solution

Step 1: Prepare samples of the original solution and \(\ce{HCl, NaOH}\)  and  \(\ce{H_2SO_4}\) solutions and then follow the flow chart below. 

CHEMISTRY, M5 EQ-Bank 10 MC

At a certain temperature, the \(\ce{$K_{eq}$}\) for the following reaction is 75.

\( \ce{2O3(g) \rightleftharpoons 3O2(g)}\)

0.4 mol of \(\ce{O3}\) and 1.2 mol of \(\ce{O2}\) were introduced to a 5 L reaction vessel.

Which row of the table correctly identifies the direction of the equilibrium shift and the reason for the shift?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex} \ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|c|c|}
\hline
\rule{0pt}{2.5ex}\textit{Direction favoured}\rule[-1ex]{0pt}{0pt}& \quad \quad \textit{Reason} \quad \quad \\
\hline
\rule{0pt}{2.5ex}\text{Left}\rule[-1ex]{0pt}{0pt}&Q>K_{e q}\\
\hline
\rule{0pt}{2.5ex}\text{Left}\rule[-1ex]{0pt}{0pt}& Q<K_{e q}\\
\hline
\rule{0pt}{2.5ex}\text{Right}\rule[-1ex]{0pt}{0pt}&Q>K_{e q} \\
\hline
\rule{0pt}{2.5ex}\text{Right}\rule[-1ex]{0pt}{0pt}& Q<K_{e q}\\
\hline
\end{array}
\end{align*}

Show Answers Only

\(D\)

Show Worked Solution

\[\ce{O2: c = \frac{n}{V} = \frac{1.2}{5} = 0.24 mol L^{-1}} \]

\[\ce{O3: c = \frac{n}{V} = \frac{0.4}{5} = 0.08 mol L^{-1}} \]

\[\ce{$K_{eq}$ = \frac{[O2]^{3}}{[O2]^{2}} = 75 (given)}\]

\[\ce{$Q$ = \frac{0.24^{3}}{0.08^{2}} = 2.16} \]

\(\ce{Since $Q<K_{eq}$, the reaction will shift right to favour the products until  $Q = K_{eq}$} \)

\(\Rightarrow D\)

Algebra, STD1 A1 2020 HSC 18

The distance, `d` metres, travelled by a car slowing down from `u` km/h to `v` km/h can be obtained using the formula

`v^2 = u^2-100 d`

What distance does a car travel while slowing down from 70 km/h to 40 km/h?   (2 marks)

Show Answers Only

`33 \ text{metres}`

Show Worked Solution

`u = 70 \ , \ v = 40`

`v^2` `= u^2-100d`
`40^2` `= 70^2-100d`
`100d` `= 70^2-40^2`
`:. d` `= frac{70^2-40^2}{100}`
  `= 33 \ text{metres}`

Algebra, STD1 A1 2019 HSC 34

Given the formula  `C = (A(y + 1))/24`, calculate the value of  `y`  when  `C = 120`  and  `A = 500`.   (3 marks)

Show Answers Only

`4.76`

Show Worked Solution

`text(Make)\ \ y\ \ text(the subject:)`

`C` `= (A(y + 1))/24`
`24C` `= A(y + 1)`
`y + 1` `= (24C)/A`
`y` `= (24C)/A-1`
  `= (24 xx 120)/500-1`
  `= 4.76`

Measurement, STD1 M1 2019 HSC 25

The diagram shows a sector with an angle of 120° cut from a circle with radius 10 m.

What is the perimeter of the sector? Write your answer correct to 1 decimal place.  (3 marks)

Show Answers Only

`40.9\ \ (text(1 d. p.))`

Show Worked Solution
`text(Arc length)` `= 120/360 xx 2 xx pi xx 10`
  `= 20.94`

 

`:.\ text(Perimeter)` `= 20.94 + 2 xx 10`
  `= 40.94`
  `= 40.9\ \ (text(1 d. p.))`

Measurement, STD1 M2 2020 HSC 15

The time in Melbourne is 11 hours ahead of Coordinated Universal Time (UTC). The time in Honolulu is 10 hours behind UTC. A plane departs from Melbourne at 7 pm on Tuesday and lands in Honolulu 9 hours later.

What is the time and day in Honolulu when the plane lands?   (2 marks)

Show Answers Only

`7\ text{am (Tuesday)}`

Show Worked Solution

`text{Melbourne} \ to \ text{UTC}\ + 11`

`text{Honolulu} \ to \ text{UTC}\ – 10`

`=>\ text{Honolulu is 21 hours behind Melbourne}`
 

`therefore \ text{Plane landing time}`

STRATEGY: 21 hours behind = 1 day behind + 3 hours.

`= 7\ text{pm} + 9 \ text{hours}`

`= 4\ text{am (Wednesday – Melb)}`

`= 7\ text{am (Tuesday – Honolulu)}`

Financial Maths, STD1 F3 2021 HSC 30

Blake opens a new credit card account on 1 May. He uses it, for the first time, on 4 May to buy concert tickets for $850.

He makes no further purchases or repayments during the month of May.

A statement for the credit card is issued on the last day of each month.

The statement for May shows that interest is charged at 19.75% per annum, compounding daily, from 20 May (included) until 31 May (included).

  1. What is the compound interest shown on the statement issued on 31 May?  (3 marks)

  2. The minimum payment is calculated as 3% of the closing balance on 31 May. Calculate the minimum payment.  (1 mark)

Show Answers Only
  1. `$5.54`
  2. `$25.67`
Show Worked Solution

a.   `text(Daily interest rate) = 19.75/365 = 0.05411text(%) = 0.0005411`

`text(Days incurring interest = 12)`

`text{Card balance (31 May)}` `= PV(1+r)^n`
  `= 850 (1 + 0.0005411)^12`
  `= $855.54`

 

`:.\ text(Interest)` `= 855.54-850`
  `= $5.54`

 

b.    `text(Minimum payment)` `= 855.54 xx 0.03`
    `= $25.67`

CHEMISTRY, M7 EQ-Bank 26

This flow chart shows reactions involving six different organic compounds (A to F).
 

 

Draw the structures of compounds A to F, justifying your diagrams with reference to the information provided.   (7 marks)

Show Answers Only

A:  
       

B:  
       

C:  
           

D:  
       

E:  
       

F:  
       

Show Worked Solution
  • A combines with dilute  \(\ce{H2SO4}\)  to produce two alcohols.
  • C doesn’t react with strong oxidant (i.e. it is a tertiary alcohol).

C:  
           

  • B must therefore be 2-methylbutan-1-ol or 3-methylbutan-2-ol.
  • Since B gives two products when heated with concentrated \(\ce{H2SO4}\), it must be 3-methylbutan-2-ol, as 2-methylbutan-1-ol will only produce one product.

B:  
       

  • D is a ketone, produced by B reacting with a strong oxidant.

D:  
       

  • A can be dehydrated using concentrated  \(\ce{H2SO4}\)  on either B or C.

A:  
       

  • B dehydrates to A or E. Given A‘s structure above,

E:  
       

  • C dehydrates to A or F. Again, given A’s structure above,

F:  
       

CHEMISTRY, M7 EQ-Bank 23

  1. Design a procedure that can be used to produce the ester, ethyl ethanoate, in a school laboratory.   (4 marks)

  2. Describe a safety precaution in the production of an ester in a school laboratory.   (2 marks)

Show Answers Only

a.   Methodology:

  • STEP 1: Reflux equipment using a hot plate heating source.
  • STEP 2: Pour 10 mL of ethanol into a round bottom flask. Add 20 mL of glacial (water-free) acetic acid.
  • STEP 3: Add 1 mL of concentrated \(\ce{H2SO4}\) (sulfuric acid) to the mixture. Boiling stones/chips can be added to smooth the boiling process before heating under reflux for 45 minutes.
  • STEP 4: Allow the solution to cool. The contents should then be transferred to a separating funnel.
  • STEP 5: Distilled water should be used to wash the contents which will remove excess alcohol and acetic acid. The ester layer has a density less than 1 g/mL and will therefore form a layer above the aqueous solution.
  • STEP 5: Remove the aqueous solution using the separating funnel.
  • STEP 6: By adding a solution of 1 mol L ¯1  \(\ce{Na2CO3}\) (sodium carbonate), all remaining acid will be removed. Similarly to Step 4, the ester can be isolated by removing the lower layer.

b.   Safety precaution:

  • Ethanol presents a danger due to its combustibility.
  • A safety precaution that reduces the fire threat is through the use of a hot plate for heating rather than a naked flame.
Show Worked Solution

a.   Methodology:

  • STEP 1: Reflux equipment using a hot plate heating source.
  • STEP 2: Pour 10 mL of ethanol into a round bottom flask. Add 20 mL of glacial (water-free) acetic acid.
  • STEP 3: Add 1 mL of concentrated \(\ce{H2SO4}\) (sulfuric acid) to the mixture. Boiling stones/chips can be added to smooth the boiling process before heating under reflux for 45 minutes.
  • STEP 4: Allow the solution to cool. The contents should then be transferred to a separating funnel.
  • STEP 5: Distilled water should be used to wash the contents which will remove excess alcohol and acetic acid. The ester layer has a density less than 1 g/mL and will therefore form a layer above the aqueous solution.
  • STEP 5: Remove the aqueous solution using the separating funnel.
  • STEP 6: By adding a solution of 1 mol L ¯1  \(\ce{Na2CO3}\) (sodium carbonate), all remaining acid will be removed. Similarly to Step 4, the ester can be isolated by removing the lower layer of aqueous solution using the separating funnel. 

b.   Safety precaution:

  • Ethanol presents a danger due to its combustibility.
  • A safety precaution that reduces the fire threat is through the use of a hot plate for heating rather than a naked flame.

CHEMISTRY, M7 EQ-Bank 22

Calculate the mass of methanol that must be burnt to increase the temperature of 325 g of water by 65°C, if exactly half of the heat released by this combustion is lost to the surroundings.

The heat of combustion of methanol is 726 kJ mol ¯1.  (3 marks)

Show Answers Only

7.79 g

Show Worked Solution

\(\ce{Using $q = mc\Delta T$}\):

\(\ce{$q$ = 325 \times 10^{-3} \times 4.18 \times 10^{3} \times 65 = 88 302.5 J = 88.3025 kJ}\)

\(\ce{Methanol heat combustion = 726 kJ mol^{-1} (given)}\)

\[\ce{n(CH3(OH)) = \frac{88.3025}{726} }\]

\(\ce{MM(CH3(OH)) = 12.01 + 3 \times 1.008 + 16 + 1.008 = 32.042 }\)

\[\ce{m(CH3(OH)) = \frac{88.3025}{726} \times 32.042 }\]

\(\text{Since 50% of heat is lost → twice as much methanol is needed}\)

\[\ce{m(CH3(OH)) initial = 2 \times \frac{88.3025}{726} \times 32.042 = 7.79 g} \]

CHEMISTRY, M5 EQ-Bank 5 MC

The conversion of calcium carbonate to calcium oxide and carbon dioxide is a reversible reaction and will reach equilibrium under certain conditions.

In which diagram is the system most likely to have reached equilibrium?
 

 

Show Answers Only

`D`

Show Worked Solution
  • In order to reach equilibrium, the reaction must occur in a closed system. In this system, a lid must be on the container.
  • When the reaction  \(\ce{CaCO3(s) \rightleftharpoons CaO(s) + CO2(g)} \)  has reached equilibrium, both the forwards and reverse reactions will be occurring.
  • All three species will be present.

`=>D`

CHEMISTRY, M7 EQ-Bank 24

Primary, unbranched alcohols and alkanes of the same carbon length have quite different boiling points.

Explain the difference in boiling point of these organic compounds, showing all intermolecular forces. Support your answer with diagrams.   (4 marks)

Show Answers Only
  • Alkanes are saturated hydrocarbons – i.e. they are made up of carbon and hydrogen atoms only and all atoms are joined together by single covalent bonds which are non-polar.
  • Weak intermolecular forces (Van der Waals) are therefore the only forces holding alkane molecules together and as a result, alkanes have low boiling points.

  • In contrast, alcohols have an \(\ce{OH}\) functional group. The \(\ce{OH}\) bond is polar with an oxygen “pole” that is slightly negatively charged and hydrogen “pole” that is slightly positively charged.

  • The hydrogen atom on one molecule will form an electrostatic bond with the oxygen atom on another atom creating a hydrogen bond.
  • Since hydrogen bonds are much stronger intermolecular forces than dispersion forces, the boiling points of alcohols are significantly higher than those of alkanes with the same carbon lengths.
Show Worked Solution
  • Alkanes are saturated hydrocarbons – i.e. they are made up of carbon and hydrogen atoms only and all atoms are joined together by single covalent bonds which are non-polar.
  • Weak intermolecular forces (Van der Waals) are therefore the only forces holding alkane molecules together and as a result, alkanes have low boiling points.

  • In contrast, alcohols have an \(\ce{OH}\) functional group. The \(\ce{OH}\) bond is polar with an oxygen “pole” that is slightly negatively charged and hydrogen “pole” that is slightly positively charged.

  • The hydrogen atom on one molecule will form an electrostatic bond with the oxygen atom on another atom creating a hydrogen bond.
  • Since hydrogen bonds are much stronger intermolecular forces than dispersion forces, the boiling points of alcohols are significantly higher than those of alkanes with the same carbon lengths.

CHEMISTRY, M8 EQ-Bank 22

  1. The diagram is a schematic representation of a mass spectrometer.
     

  1. Name and outline the function of the part labelled `A` in the diagram.   (2 marks)

  2. Outline the advantages of using mass spectrometry for analysis of a compound.   (3 marks)

Show Answers Only

a.   \(\ce{A}\) is a magnet.

  • It bends the charged particles that are accelerated through an electric field and directed through it.
  • The amount of bending can then be used to distinguish between and identify the particles/ions.

b.   Advantages of mass spectrometry

  • The mass spectrometer can identify the mass/charge ratio of ions that pass through it. This data can then be used to identify components of a mixture or components in a compound.
  • Different isotopes of elements in a compound can be identified by mass spectrometers. This allows the compound to be matched to a sample.
  • Mass spectrometry can provide both qualitative and quantitative data on a compound.
  • Finally, mass spectrometers only require a small quantity of a compound to perform detailed analysis, as well as being fast and sensitive.
Show Worked Solution

a.   \(\ce{A}\) is a magnet.

  • It bends the charged particles that are accelerated through an electric field and directed through it.
  • The amount of bending can then be used to distinguish between and identify the particles/ions.

b.   Advantages of mass spectrometry

  • The mass spectrometer can identify the mass/charge ratio of ions that pass through it. This data can then be used to identify components of a mixture or components in a compound.
  • Different isotopes of elements in a compound can be identified by mass spectrometers. This allows the compound to be matched to a sample.
  • Mass spectrometry can provide both qualitative and quantitative data on a compound.
  • Finally, mass spectrometers only require a small quantity of a compound to perform detailed analysis, as well as being fast and sensitive.

CHEMISTRY, M8 EQ-Bank 25

The diagram shows the infrared spectrum of a compound.

 

The molecular weight of the compound analysed is approximately 60 g mol ¯1. Suggest TWO possible compounds that could fit this spectrum and justify your selection.   (4 marks)

Show Answers Only
  • The absorbance shows an initial trough in the range 3100 – 3600 cm¯1. This absorbance maximises at around 3350 cm¯1. This data indicates the likely presence of a hydroxyl group within the compound.
  • The next trough occurs in the range 3100 – 3600 cm¯1. Its intensity trough is not broad. This data is consistent with the presence of a  \(\ce{C-H}\)  bond.
  • There is little absorbance between 2500 – 1500 cm¯1. This data indicates the absence of any  \(\ce{C=O}\)  group, discounting the possibility of the compound being carboxylic acid or a ketone.
  • An absorption peak between 1250 – 1050 cm¯1 indicates the presence of a  \(\ce{C-O}\)  bond.
  • Propanol is a compound whose structure is consistent with the data above:

       

  • The molecular weight of propanol is 60.01 g mol ¯1 which is also supported by the data.
  • Since the spectrum of isomers is similar, the two possible compounds that fit this are propan-1-ol or propan-2-ol.
Show Worked Solution
  • The absorbance shows an initial trough in the range 3100 – 3600 cm¯1. This absorbance maximises at around 3350 cm¯1. This data indicates the likely presence of a hydroxyl group within the compound.
  • The next trough occurs in the range 3100 – 3600 cm¯1. Its intensity trough is not broad. This data is consistent with the presence of a  \(\ce{C-H}\)  bond.
  • There is little absorbance between 2500 – 1500 cm¯1. This data indicates the absence of any  \(\ce{C=O}\)  group, discounting the possibility of the compound being carboxylic acid or a ketone.
  • An absorption peak between 1250 – 1050 cm¯1 indicates the presence of a  \(\ce{C-O}\)  bond.
  • Propanol is a compound whose structure is consistent with the data above:

       

  • The molecular weight of propanol is 60.01 g mol ¯1 which is also supported by the data.
  • Since the spectrum of isomers is similar, the two possible compounds that fit this are propan-1-ol or propan-2-ol.

CHEMISTRY, M8 EQ-Bank 23

\(\ce{Fe^2^+}\) and \(\ce{X} \) react to form an ionic compound according to the general equation

\(\ce{aFe^2^+ + $b$(X)\rightleftharpoons [Fe_a(X)_b]^2^a^+}\)

where \(\ce{$a$}\) and \(\ce{$b$}\) are numbers representing the ratio in which \(\ce{Fe^2^+}\) and \(\ce{X} \) combine.

Spectrophotometry was used to determine the stoichiometric ratio between \(\ce{Fe^2^+}\) and \(\ce{X} \). To do this, eight 10 mL samples were prepared by reacting solutions of \(\ce{Fe^2^+}\) with solutions of \(\ce{X} \) in varying ratios. All \(\ce{Fe^2^+}\) and \(\ce{X} \) solutions had the same concentration. The absorbance of the samples is tabulated below.
 

  1. On the grid, construct a graph of absorbance against volume of \(\ce{Fe^2^+}\) solution from 0.00 mL to 6.00 mL, and draw TWO lines of best fit.  (3 marks)
     

     

  1. The reaction proceeds according to the general equation
  2.       \(\ce{aFe^2^+ + $b$X \rightleftharpoons [Fe_a(X)_b]^2^a^+}\).
  3. Find the values of \(\ce{$a$}\) and \(\ce{$b$}\) . Justify your answer with reference to the data given and the graph in part (a).   (3 marks)

Show Answers Only

a.  
           

b.   Find values of \(\ce{$a$}\) and \(\ce{$b$}\):

  • The graph shows that as the volume of compound \(\ce{X} \) decreases between 10mL and 7.5mL, there is an increase in \(\ce{Fe^{2+}}\) ions. This indicates an excess of \(\ce{Fe^{2+}}\) ions limiting the products.
  • The absorbance reaches a maximum when the 2.5 mL of compound \(\ce{Fe^{2+}}\) is added to 7.5 mL of compound \(\ce{X}\). Since the concentrations of the initial solutions are equal (given), equal volumes contain equal moles.
  • The ratio of volumes at peak absorbance = 2.5 : 7.5 = 1 : 3 (i.e. the correct stoichiometric ratio).
  • Hence \(\ce{$a$ = 1}\) and \(\ce{$b$ = 3}\).
  • The curve then turns down sharply, indicating a reduction in \(\ce{Fe^{2+}}\).
Show Worked Solution

a.  
           

b.   Find values of \(\ce{$a$}\) and \(\ce{$b$}\):

  • The graph shows that as the volume of compound \(\ce{X} \) decreases between 10mL and 7.5mL, there is an increase in \(\ce{Fe^{2+}}\) ions. This indicates an excess of \(\ce{Fe^{2+}}\) ions limiting the products.
  • The absorbance reaches a maximum when the 2.5 mL of compound \(\ce{Fe^{2+}}\) is added to 7.5 mL of compound \(\ce{X}\). Since the concentrations of the initial solutions are equal (given), equal volumes contain equal moles.
  • The ratio of volumes at peak absorbance = 2.5 : 7.5 = 1 : 3 (i.e. the correct stoichiometric ratio).
  • Hence \(\ce{$a$ = 1}\) and \(\ce{$b$ = 3}\).
  • The curve then turns down sharply, indicating a reduction in \(\ce{Fe^{2+}}\).

CHEMISTRY, M8 EQ-Bank 12

A colorimeter was used to calculate the percentage of iron in a 0.200 gram tablet. The tablet was dissolved and oxidised, then reacted with thiosulfate according to the equation

\(\ce{Fe^3^+($aq$) + SCN^-($aq$)\rightarrow [FeSCN]^2^+($aq$)}\)

The resulting solution was made up to 200 mL with distilled water. The absorbance of the final solution was measured to be 0.6105.

The calibration curve shows the absorbance of various concentrations of \(\ce{Fe^3^+}\).
 

Calculate the percentage of iron in the tablet.   (3 marks)

Show Answers Only

0.307%

Show Worked Solution

\(\ce{Fe^{3+}($aq$) + SCN^-($aq$)\rightarrow [FeSCN]^2^+($aq$)}\)

\(\ce{\text{Using the graph:}}\)

\(\ce{Absorbance = 0.615 }\)

\(\ce{\rightarrow Initial [Fe^{3+}] in 200 mL = 55 \times 10^{-6} = 5.5 \times 10^{-5} mol L^{-1}}\)

\(\ce{n(Fe^{3+}) = c \times V = 5.5 \times 10^{-5} \times 0.2 = 1.1 \times 10^{-5} mol} \)

\(\ce{MM(Fe) = 55.85 g mol^{-1}} \)

\(\ce{m(Fe) = 1.1 \times 10^{-5} \times 55.85 = 6.14 \times 10^{-4} g} \)

\[ \ce{\therefore \text{% Fe} = \frac{6.14 \times 10^{-4}}{0.200} \times 100 = 0.307\text{%} } \]

CHEMISTRY, M8 EQ-Bank 24

A common antacid tablet contains aluminium hydroxide to neutralise stomach acid. In order for the antacid to be effective, each 500 mg tablet must contain a minimum of 200 mg of aluminium hydroxide.

Two antacid tablets were crushed and reacted with 70 mL of 0.60 mol L¯ 1 hydrochloric acid. After the antacid had reacted with the acid, the remaining hydrochloric acid was titrated against 0.60 mol L¯ 1 sodium hydroxide. The average volume of sodium hydroxide used was 35 mL.

Calculate the amount of aluminium hydroxide present in each tablet and justify whether the tablets will be effective as an antacid.   (4 marks)

Show Answers Only

\(\text{Tablets will be effective (See Worked Solutions)}\)

Show Worked Solution

\(\ce{3HCl(aq) + Al(OH)3(aq) \rightarrow AlCl3(s) + 3H2O(l)} \)

\(\ce{n(HCl^-) = c \times V = 0.6 \times 0.070 = 0.042 mol} \)

\(\ce{n(Na(OH)) = c \times V = 0.6 \times 0.035 = 0.021 mol} \)

\(\ce{Moles reacted with antacid = 0.042 – 0.021 = 0.021 mol} \)
 

\(\ce{Mole ratio = 3:1}\)

\[\ce{Moles of Al(OH)3 in 2 tablets = \frac{0.021}{3} = 0.007 mol}\]

\(\ce{Formula weight of Al(OH)3 = 27 + 3 \times (1 + 16) = 78 g}\)

\(\ce{m(Al(OH)3) in 2 tablets = 0.007 \times 78 = 0.546 g}\)

\[\ce{m(Al(OH)3) in 1 tablet = \frac{0.546}{2} = 273 g}\]

\(\text{Since 273 > 200, tablets will be effective.}\)

CHEMISTRY, M8 EQ-Bank 28

Limestone \(\ce{(CaCO_3)}\) contributes to the hardness of water by releasing \(\ce{Ca^2^+}\) ions. The following chemical equation represents this reaction.

\(\ce{CaCO3($s$) + H_2O($l$) + CO_2($g$) \rightleftharpoons Ca^2^+($aq$) + 2HCO3^-($aq$)}\)      \((\Delta H<0)\)

It has been suggested that heating water reduces its hardness.

Explain how this suggestion can be tested accurately, validly and reliably.   (9 marks)

Show Answers Only
  • Atomic absorption spectroscopy (AAS) can be used to test if heating reduces water hardness.
  • It does this by calculating the concentrations of metal ions in solutions. AAS can calculate the concentration of \(\ce{Ca^{2+}}\) in heated and non-heated samples of water and any difference in the relative concentrations of \(\ce{Ca^{2+}}\) can be used to verify the suggestion.
  • It should be noted that a reduced concentration of \(\ce{Ca^{2+}}\) indicates that the water hardness is reduced.

Methodology of testing

  • Prepare standard solutions with known concentrations of \(\ce{Ca^{2+}}\) and measure their absorbance. Plot the concentrations against the absorbance of the standard solutions and draw a calibration curve (i.e. a line of best fit).
  • Measure the absorbance of a water sample before heating and another after heating. Using the absorbance and the calibration curve, calculate the concentration of \(\ce{Ca^{2+}}\) in each sample and compare the concentrations between the heated and unheated samples.
  • The AAS should be calibrated, at which point the concentration of calcium ions can be calculated to an accuracy in the parts per million (ppm). To ensure accurate calibration of the AAS, the standard solutions need to be prepared precisely which will involve the accurate weighing of solids and the use of a pipette or a similar instrument to measure solution volumes.
  • Water used in the experiment should be de-ionised (normal drinking water has an abundance of \(\ce{Na+}\) and \(\ce{Ca^{2+}}\)).
  • The margin of experimental error decreases when sufficient calibration samples are used and the measurement of absorbance of these samples is repeated and averaged. 
  • The reliability of results increases when many samples of heated and non-heated water are used to confirm that the concentrations of \(\ce{Ca^{2+}}\) in the heated water samples are consistently lower than the concentrations of \(\ce{Ca^{2+}}\) in the unheated water samples.
  • AAS can also be used to test the validity of the results. A hollow cathode lamp for calcium can direct light through the solution. This light has a specific wavelength that will only be absorbed by calcium ions. In this way, accurate measurements are made which can then be compared against the results and provide evidence of the validity of the original suggestion.
Show Worked Solution
  • Atomic absorption spectroscopy (AAS) can be used to test if heating reduces water hardness.
  • It does this by calculating the concentrations of metal ions in solutions. AAS can calculate the concentration of \(\ce{Ca^{2+}}\) in heated and non-heated samples of water and any difference in the relative concentrations of \(\ce{Ca^{2+}}\) can be used to verify the suggestion.
  • It should be noted that a reduced concentration of \(\ce{Ca^{2+}}\) indicates that the water hardness is reduced.

Methodology of testing

  • Prepare standard solutions with known concentrations of \(\ce{Ca^{2+}}\) and measure their absorbance. Plot the concentrations against the absorbance of the standard solutions and draw a calibration curve (i.e. a line of best fit).
  • Measure the absorbance of a water sample before heating and another after heating. Using the absorbance and the calibration curve, calculate the concentration of \(\ce{Ca^{2+}}\) in each sample and compare the concentrations between the heated and unheated samples.
  • The AAS should be calibrated, at which point the concentration of calcium ions can be calculated to an accuracy in the parts per million (ppm). To ensure accurate calibration of the AAS, the standard solutions need to be prepared precisely which will involve the accurate weighing of solids and the use of a pipette or a similar instrument to measure solution volumes.
  • Water used in the experiment should be de-ionised (normal drinking water has an abundance of \(\ce{Na+}\) and \(\ce{Ca^{2+}}\)).
  • The margin of experimental error decreases when sufficient calibration samples are used and the measurement of absorbance of these samples is repeated and averaged. 
  • The reliability of results increases when many samples of heated and non-heated water are used to confirm that the concentrations of \(\ce{Ca^{2+}}\) in the heated water samples are consistently lower than the concentrations of \(\ce{Ca^{2+}}\) in the unheated water samples.
  • AAS can also be used to test the validity of the results. A hollow cathode lamp for calcium can direct light through the solution. This light has a specific wavelength that will only be absorbed by calcium ions. In this way, accurate measurements are made which can then be compared against the results and provide evidence of the validity of the original suggestion.

CHEMISTRY, M5 EQ-Bank 12

An industrial plant makes ammonia from nitrogen gas and hydrogen gas. The reaction is exothermic.  

The graph shows the adjustments made to increase the yield of ammonia.

Account for the changes in conditions that have shaped the graph during the time the system was observed. Include a relevant chemical equation in your answer.   (5 marks)

Show Answers Only

\(\ce{N2(g) + 3H2(g) \rightleftharpoons 2NH3(g) \ \ \ \ ΔH = -92 kJ mol}^{-1} \)

From \( t_0\) to \(t_1: \) the system is in equilibrium.

At \(t_1:\)

  • Nitrogen is introduced to the system and its concentration increases sharply.
  • Le Chatelier’s principle states that when a system in equilibrium is disturbed, the equilibrium will shift in the direction that minimises the change. In this case, the equilibrium will shift to the right to use up more nitrogen. A greater yield of ammonia will result until equilibrium is re-established.

At \(t_2:\)

  • The concentration of both reactants and products increases. This effect could be caused by a decrease in volume of the reaction vessel which will result in an increase in pressure on the system.
  • The above equation shows that 4 moles of gas (on the left-hand side) react to form 2 moles of gas (on the right-hand side). Le Chatelier’s principle dictates that this increase in pressure will cause the system to again shift right, to the side with fewer moles of gas, to counteract the change.
  • This right shift will further increase the yield of ammonia until equilibrium is re-established.

At \(t_3:\)

  • There is a change to the system that shifts the reaction back to the left. The gradual change in concentrations indicate that this could be due to a change in temperature.
  • Since this reaction is exothermic, the reverse reaction (left shift) absorbs heat. An increase in temperature would cause this shift, lowering the yield of ammonia until equilibrium is again restored.
Show Worked Solution

\(\ce{N2(g) + 3H2(g) \rightleftharpoons 2NH3(g) \ \ \ \ ΔH = -92 kJ mol}^{-1} \)

From \( t_0\) to \(t_1: \) the system is in equilibrium.

At \(t_1:\)

  • Nitrogen is introduced to the system and its concentration increases sharply.
  • Le Chatelier’s principle states that when a system in equilibrium is disturbed, the equilibrium will shift in the direction that minimises the change. In this case, the equilibrium will shift to the right to use up more nitrogen. A greater yield of ammonia will result until equilibrium is re-established.

At \(t_2:\)

  • The concentration of both reactants and products increases. This effect could be caused by a decrease in volume of the reaction vessel which will result in an increase in pressure on the system.
  • The above equation shows that 4 moles of gas (on the left-hand side) react to form 2 moles of gas (on the right-hand side). Le Chatelier’s principle dictates that this increase in pressure will cause the system to again shift right, to the side with fewer moles of gas, to counteract the change.
  • This right shift will further increase the yield of ammonia until equilibrium is re-established.

At \(t_3:\)

  • There is a change to the system that shifts the reaction back to the left. The gradual change in concentrations indicate that this could be due to a change in temperature.
  • Since this reaction is exothermic, the reverse reaction (left shift) absorbs heat. An increase in temperature would cause this shift, lowering the yield of ammonia until equilibrium is again restored.

PHYSICS, M5 EQ-Bank 28

A bullet is fired vertically from the surface of Mars, at the escape velocity of Mars. Another bullet is fired vertically from the surface of Earth, at the escape velocity of Earth.

Neglecting air resistance, compare the energy transformations of the two bullets.   (5 marks)

Show Answers Only
  • The total energy of the bullet fired from the surface of Mars will remain constant. Its kinetic energy will transform into potential energy as it gains altitude. 
  • As the bullet fired from Mars reaches an ‘infinite’ distance away, it escapes Mars’ gravitational attraction. Here, the kinetic energy of the bullet is zero as it has expended all of its initial kinetic energy.
  • The potential energy (`U`) of the bullet has also decreased to zero as  `U=-(GMm)/(r)`.
  • A similar process occurs for the bullet fired from the surface of Earth at its escape velocity. As the mass and radius of Earth are different to that of Mars, the actual escape velocity, `v_(esc)=sqrt((2GM)/(r))` will be different.
  • The initial values of kinetic and potential energy, `U=-(GMm)/(r)` will also be different.
Show Worked Solution
  • The total energy of the bullet fired from the surface of Mars will remain constant. Its kinetic energy will transform into potential energy as it gains altitude. 
  • As the bullet fired from Mars reaches an ‘infinite’ distance away, it escapes Mars’ gravitational attraction. Here, the kinetic energy of the bullet is zero as it has expended all of its initial kinetic energy.
  • The potential energy (`U`) of the bullet has also decreased to zero as  `U=-(GMm)/(r)`.
  • A similar process occurs for the bullet fired from the surface of Earth at its escape velocity. As the mass and radius of Earth are different to that of Mars, the actual escape velocity, `v_(esc)=sqrt((2GM)/(r))` will be different.
  • The initial values of kinetic and potential energy, `U=-(GMm)/(r)` will also be different.

PHYSICS, M5 EQ-Bank 23

A rocket carrying a satellite is launched from Earth. Once the rocket engine is switched off the satellite continues in an elliptical orbit.

Explain the satellite's changes in energy during this journey.   (3 marks)

Show Answers Only
  • During the rocket’s launch, its fuel is used up and its chemical potential energy decreases as its potential and kinetic energy both increase. In this stage the total mechanical energy of the rocket increases.
  • Once the satellite is in orbit, its total mechanical energy is constant.
  • As the satellite moves along its orbit away from Earth and gains altitude, its kinetic energy is converted into potential energy.
  • Once the satellite reaches its maximum distance from Earth within its elliptical orbit, its altitude will then begin to decrease. At this stage, its potential energy will be converted into kinetic energy with total energy remaining constant.
Show Worked Solution
  • During the rocket’s launch, its fuel is used up and its chemical potential energy decreases as its potential and kinetic energy both increase. In this stage the total mechanical energy of the rocket increases.
  • Once the satellite is in orbit, its total mechanical energy is constant.
  • As the satellite moves along its orbit away from Earth and gains altitude, its kinetic energy is converted into potential energy.
  • Once the satellite reaches its maximum distance from Earth within its elliptical orbit, its altitude will then begin to decrease. At this stage, its potential energy will be converted into kinetic energy with total energy remaining constant.

PHYSICS, M5 EQ-Bank 21

Comet Hale-Bopp is a long period comet that is believed to come from the Oort cloud which lies far beyond the outermost planets. In our solar system, Hale-Bopp travels in an elliptical orbit around the Sun and spends most of its time beyond the outermost planets.

Using a diagram, explain how the motion of Comet Hale-Bopp in its orbit supports Kepler's second law.   (3 marks)

Show Answers Only

  • Kepler’s Second Law states that a line between the comet and the sun will sweep an equal area in equal time.
  • When the comet is closer to the sun, it must travel with a greater velocity in its orbit compared to when it is far away to sweep the same area in the same time (i.e. such that `A_1=A_2`.
  • Comet Hale-Bopp supports this as it spends most of its time beyond the outermost planets. It therefore travels at a slower speed compared to when it is close to the sun. This reduced velocity allows it to sweep the same area compared to when it is closer to the sun. 
Show Worked Solution

  • Kepler’s Second Law states that a line between the comet and the sun will sweep an equal area in equal time.
  • When the comet is closer to the sun, it must travel with a greater velocity in its orbit compared to when it is far away to sweep the same area in the same time (i.e. such that `A_1=A_2`.
  • Comet Hale-Bopp supports this as it spends most of its time beyond the outermost planets. It therefore travels at a slower speed compared to when it is close to the sun. This reduced velocity allows it to sweep the same area compared to when it is closer to the sun. 

PHYSICS, M5 EQ-Bank 25

In the 1840s, French physicist, Hippolyte Fizeau performed an experiment to measure the speed of light. He shone an intense light source at a mirror 8 km away and broke up the light beam with a rotating cogwheel. He adjusted the speed of rotation of the wheel until the reflected light beam could no longer be seen returning through the gaps in the cogwheel.

The diagram shows a similar experiment. The cogwheel has 50 teeth and 50 gaps of the same width.
 

Explain why specific speeds of rotation of the cogwheel will completely block the returning light. Support your answer with calculations.   (5 marks)

Show Answers Only
  • Light travelling through a gap in the cogwheel can be completely blocked by a tooth. This occurs if a tooth moves exactly the width of a gap in the time it takes for light to travel to the mirror and back.
  • Calculating the time taken:
  •    `t=(s)/(v)=(2xx8000)/(3.00 xx10^(8))=5.33 xx10^(-5)  text{s}`
  • To completely block the light, the tooth will have moved into the path of a gap in this time. Since there are 50 teeth and 50 gaps, the wheel will have undergone one hundredth of a rotation in this time.
  •    `omega=(Delta theta)/(t)=((2pi)/(100))/(5.33 xx10^(-5))=1180  text{rad s}^(-1)`
  • Additionally, the light will also be completely blocked if the cogwheel is spun at 3, 5, 7, or any odd multiple of this speed. In these cases, the wheel turns an odd number of gap-tooth intervals in the time it takes light to return.
  • For example, at three times this speed, the wheel rotates three hundredths of a full turn during the light’s round trip, so the returning light meets the second tooth instead of a gap and is blocked.
Show Worked Solution
  • Light travelling through a gap in the cogwheel can be completely blocked by a tooth. This occurs if a tooth moves exactly the width of a gap in the time it takes for light to travel to the mirror and back.
  • Calculating the time taken:
  •    `t=(s)/(v)=(2xx8000)/(3.00 xx10^(8))=5.33 xx10^(-5)  text{s}`
  • To completely block the light, the tooth will have moved into the path of a gap in this time. Since there are 50 teeth and 50 gaps, the wheel will have undergone one hundredth of a rotation in this time.
  •    `omega=(Delta theta)/(t)=((2pi)/(100))/(5.33 xx10^(-5))=1180  text{rad s}^(-1)`
  • Additionally, the light will also be completely blocked if the cogwheel is spun at 3, 5, 7, or any odd multiple of this speed. In these cases, the wheel turns an odd number of gap-tooth intervals in the time it takes light to return.
  • For example, at three times this speed, the wheel rotates three hundredths of a full turn during the light’s round trip, so the returning light meets the second tooth instead of a gap and is blocked.

PHYSICS, M7 EQ-Bank 26

The diagram shows a light source, slits and a translucent screen arranged for an experiment on light. Light and dark bands form on the screen. The light has a wavelength of 590 nm. The diagram is not to scale.
 

  1. Explain how any one of the dark bands forms on the screen.  (3 marks)
  1. The distance between the centres of the double slit is 0.15 mm, and the distance between the double slit and the screen is 0.75 m.
  2. Calculate the distance on the screen from the centre of the central maximum to the centre of a second-order bright band.  (3 marks)
Show Answers Only

a.   Dark band formation:

  • When light arrives at the double slit, it undergoes diffraction.
  • The two slits act as sources of secondary wavefronts and light travels from both slits to the screen.
  • When light from one slit travels any odd multiple of `(lambda)/(2)` more than light from the other slit to the screen, it is out of phase and destructive interference occurs. Here waves superimpose and cancel each other out, creating dark bands.
  • For example, the dark bands either side of the central maximum form where light from one slit travels `(lambda)/(2)` further than light from the other slit.

b.   `0.0059  text{m}`

Show Worked Solution

a.  Dark band formation:

  • When light arrives at the double slit, it undergoes diffraction.
  • The two slits act as sources of secondary wavefronts and light travels from both slits to the screen.
  • When light from one slit travels any odd multiple of `(lambda)/(2)` more than light from the other slit to the screen, it is out of phase and destructive interference occurs. Here waves superimpose and cancel each other out, creating dark bands.
  • For example, the dark bands either side of the central maximum form where light from one slit travels `(lambda)/(2)` further than light from the other slit.

b.    Using  `d  sin theta=m lambda`

  `0.15 xx10^(-3)  sin theta` `=2xx590 xx10^(-9)`
  `sin theta` `=0.007867`

 

  • Using trigonometry, `tan theta=(d)/(0.75)`, where `theta` is the angular separation of the second order bright band from the central maximum and `d` is the distance between the centre of the central maximum and the centre of the second order bright band.
  • As the angle, `theta` is small, the approximation  `sin theta=tan theta`  is valid:
  •    \( \tan \theta \approx \dfrac{d}{0.75} \ \ \Rightarrow \ \ d=0.007867 \times 0.75 \approx 0.0059 \mathrm{~m} \)

PHYSICS, M7 EQ-Bank 28

In an experiment to investigate the photoelectric effect, a group of students used a piece of equipment containing a metal cathode inside a glass tube. The students were able to accurately measure both the current produced and the maximum energy of electrons in response to light hitting the cathode.

Explain how the choice of independent variable would give rise to different results. Sketch graphs to illustrate your answer.  (7 marks)

Show Answers Only

Variables: the frequency of incident light (independent), and the maximum kinetic energy of ejected electrons (dependent).

  • Students would observe that below a certain frequency, no photoelectrons would be ejected. Photons with frequency less than the threshold frequency do not have enough energy to eject an electron.
  • Above this frequency, the students would observe that as the frequency increases, the kinetic energy of ejected electrons would increase linearly. This is because a specific amount of the photon’s energy is required to eject an electron, and any photon energy remaining is transferred to the electrons as kinetic energy, consistent with  `K_(max)=hf-Phi`.
     


 

Variables: intensity of incident light (independent) and the resultant photocurrent (dependent).

  • The frequency of light would be controlled and would be above the threshold frequency.
  • They would observe as the intensity of light increases the current produced would increase linearly.
  • This is because an increasing intensity of light increases the number of photons. This increases the rate at which photons strike the metal surface which increases the rate of photoelectron emission which in turn increases the photocurrent.
     

Show Worked Solution

Variables: the frequency of incident light (independent), and the maximum kinetic energy of ejected electrons (dependent).

  • Students would observe that below a certain frequency, no photoelectrons would be ejected. Photons with frequency less than the threshold frequency do not have enough energy to eject an electron.
  • Above this frequency, the students would observe that as the frequency increases, the kinetic energy of ejected electrons would increase linearly. This is because a specific amount of the photon’s energy is required to eject an electron, and any photon energy remaining is transferred to the electrons as kinetic energy, consistent with  `K_(max)=hf-Phi`.
     


 

Variables: intensity of incident light (independent) and the resultant photocurrent (dependent).

  • The frequency of light would be controlled and would be above the threshold frequency.
  • They would observe as the intensity of light increases the current produced would increase linearly.
  • This is because an increasing intensity of light increases the number of photons. This increases the rate at which photons strike the metal surface which increases the rate of photoelectron emission which in turn increases the photocurrent.
     

PHYSICS, M8 EQ-Bank 28

Our understanding of matter is still incomplete and the Standard Model of matter is still being validated and tested. Technology plays a substantial role in this.

Explain the role of technology in developing both the Standard Model of matter and our understanding in ONE other area of physics.  (9 marks)

Show Answers Only

Technology and the development of the Standard Model

  • Technology has played a significant role in developing the standard model of matter.
  • Scientists have used the technology of linear accelerators to accelerate a beam of electrons at stationary protons. Technology was then used to analyse the scattering patterns of the electrons which was inconsistent with protons being fundamental particles.
  • It was determined that protons were comprised of both positive and negative internal charges. This led to the discovery of quarks.
  • Further, the Large Hadron Collider (LHC) is technology which accelerates protons to speeds extremely close to the speed of light, and collides them with each other.
  • When these protons collide, their dilated kinetic energy is converted to mass in the form of new particles such as the Higgs Boson. This significantly develops our understanding of the standard model of matter. 

Technology and Special Relativity

  • Another area of physics in which technology has played a vital role is special relativity.
  • Einstein’s prediction of time dilation has been validated by the Hafele-Keating experiment. Technology such as atomic clocks and high speed aeroplanes were used to demonstrate time differences recorded when atomic clocks were flown around the world.
  • In this instance, technology made it possible to validate Einstein’s predictions, improving our understanding of special relativity.
Show Worked Solution

Technology and the development of the Standard Model

  • Technology has played a significant role in developing the standard model of matter.
  • Scientists have used the technology of linear accelerators to accelerate a beam of electrons at stationary protons. Technology was then used to analyse the scattering patterns of the electrons which was inconsistent with protons being fundamental particles.
  • It was determined that protons were comprised of both positive and negative internal charges. This led to the discovery of quarks.
  • Further, the Large Hadron Collider (LHC) is technology which accelerates protons to speeds extremely close to the speed of light, and collides them with each other.
  • When these protons collide, their dilated kinetic energy is converted to mass in the form of new particles such as the Higgs Boson. This significantly develops our understanding of the standard model of matter. 

Technology and Special Relativity

  • Another area of physics in which technology has played a vital role is special relativity.
  • Einstein’s prediction of time dilation has been validated by the Hafele-Keating experiment. Technology such as atomic clocks and high speed aeroplanes were used to demonstrate time differences recorded when atomic clocks were flown around the world.
  • In this instance, technology made it possible to validate Einstein’s predictions, improving our understanding of special relativity.

PHYSICS, M7 EQ-Bank 24

Parallel light rays of intensity `I_0` pass through two polarising filters `P_1` and `P_2` to a detector. The filters are initially aligned so that they produce the maximum amount of light, then filter `P_2` is slowly rotated through 180° as shown.
 

  1. On the axes provided sketch a graph showing how the intensity of light at the detector, `I`, changes as `P_2` rotates from zero to 180°.
     

  1. `P_2` is now rotated to a position such that no light reaches the detector. Without moving `P_1` or `P_2`, a third polarising filter is inserted between `P_1` and `P_2` and rotated at an angle of 30° from `P_1`.
  2. Explain, with the aid of calculations, why the light intensity at the detector is no longer zero.
Show Answers Only

a.   

b.   Light intensity at detector:

  • `P_(2)` must be rotated 90° from `P_(1)` (no light reaches detector)
  • Calculate the light passing through the middle polariser:
  •    `I=I_(max)cos^2theta\ \ =>\ \ I_(m)=I_(1)cos^(2)30°=0.75 xxI_(1)`
  • `P_(2)` is a 60° rotation from the middle polariser:
  •    `I=I_(max)cos^2theta\ \ =>\ \ I_(2)=0.75xxI_(1)cos^(2)60°=0.1875xxI_(1)`
  • Light intensity at detector is therefore no longer zero.
Show Worked Solution

a.   

b.   Light intensity at detector:

  • `P_(2)` must be rotated 90° from `P_(1)` (no light reaches detector)
  • Calculate the light passing through the middle polariser:
  •    `I=I_(max)cos^2theta\ \ =>\ \ I_(m)=I_(1)cos^(2)30°=0.75 xxI_(1)`
  • `P_(2)` is a 60° rotation from the middle polariser:
  •    `I=I_(max)cos^2theta\ \ =>\ \ I_(2)=0.75xxI_(1)cos^(2)60°=0.1875xxI_(1)`
  • Light intensity at detector is therefore no longer zero.

PHYSICS, M7 EQ-Bank 32

Applying the law of conservation of energy, explain why  `K_max = h f-phi`.   (3 marks)

Show Answers Only
  • The law of conservation of energy states that energy cannot be created or destroyed, only transferred or transformed into different forms. 
  • The initial energy of a photon is equal to `hf`.
  • If this photon strikes a metal surface, a photoelectron may be released. Some energy is required to remove the electron from the metal surface which is equal to the work function (`phi`) of the metal.
  • The electron will also possess kinetic energy, `K_(max)`.
  • Applying the law of conservation of energy, the energy before equals the energy after, or  `hf=K_(max)+phi`.
  • Rearranging this gives  `K_(max)=hf-phi`.
Show Worked Solution
  • The law of conservation of energy states that energy cannot be created or destroyed, only transferred or transformed into different forms. 
  • The initial energy of a photon is equal to `hf`.
  • If this photon strikes a metal surface, a photoelectron may be released. Some energy is required to remove the electron from the metal surface which is equal to the work function (`phi`) of the metal.
  • The electron will also possess kinetic energy, `K_(max)`.
  • Applying the law of conservation of energy, the energy before equals the energy after, or  `hf=K_(max)+phi`.
  • Rearranging this gives  `K_(max)=hf-phi`.

PHYSICS, M8 EQ-Bank 25

An experiment was conducted to model Millikan's oil drop experiment. In the experiment, different numbers of dominoes were placed inside seven identical boxes. The boxes were then sealed and weighed. The table shows the mass of each sealed box and some preliminary analysis.
 

Analyse this experiment to assess its effectiveness in modelling Millikan's oil drop experiment.   (6 marks)

Show Answers Only

Overview Statement

  • The domino experiment models key components of Millikan’s method. It demonstrates how a fundamental unit is discovered through mass differences and the experimental assumptions involved.

Mass Measurement and Fundamental Unit

  • The smallest mass difference (4.3 g) represents the fundamental unit, like Millikan’s elementary charge.
  • All other mass differences are multiples of this base value, which is similar to Millikan’s findings where the value of the charge of an oil drop was always an integer multiple of `1.6 xx10^(-19)  text{C}`
  • This pattern reveals that objects contain whole numbers of a basic unit.
  • In this way, both experiments found indivisible units through mathematical patterns.

Experimental Method and Limitations

  • Unknown domino numbers parallel Millikan’s unknown electron counts on oil drops.
  • Multiple measurements enable statistical confidence in the fundamental value.
  • The assumption that 4.3 g equals one domino reflects Millikan’s assumption about single electrons.
  • Uncertainty about measuring single units affects both experiments’ reliability.
  • This similarity shows how both experiments require repeated trials to verify results.

Implications and Synthesis

  • The model effectively demonstrates Millikan’s analytical method for finding fundamental quantities.
  • Complementary experimental components work together: mass differences reveal patterns while multiple trials confirm values.
  • The experiment illustrates both strengths and weaknesses of Millikan’s approach.
Show Worked Solution

Overview Statement

  • The domino experiment models key components of Millikan’s method. It demonstrates how a fundamental unit is discovered through mass differences and the experimental assumptions involved.

Mass Measurement and Fundamental Unit

  • The smallest mass difference (4.3 g) represents the fundamental unit, like Millikan’s elementary charge.
  • All other mass differences are multiples of this base value, which is similar to Millikan’s findings where the value of the charge of an oil drop was always an integer multiple of `1.6 xx10^(-19)  text{C}`
  • This pattern reveals that objects contain whole numbers of a basic unit.
  • In this way, both experiments found indivisible units through mathematical patterns.

Experimental Method and Limitations

  • Unknown domino numbers parallel Millikan’s unknown electron counts on oil drops.
  • Multiple measurements enable statistical confidence in the fundamental value.
  • The assumption that 4.3 g equals one domino reflects Millikan’s assumption about single electrons.
  • Uncertainty about measuring single units affects both experiments’ reliability.
  • This similarity shows how both experiments require repeated trials to verify results.

Implications and Synthesis

  • The model effectively demonstrates Millikan’s analytical method for finding fundamental quantities.
  • Complementary experimental components work together: mass differences reveal patterns while multiple trials confirm values.
  • The experiment illustrates both strengths and weaknesses of Millikan’s approach.

PHYSICS, M7 EQ-Bank 21

  1. A student was given a smartphone with a light sensor and an angle sensor, and a computer screen which emitted polarised light. A polariser was fixed over the top of the light sensor in the smartphone.
     

  1. The student wants to use this equipment to investigate Malus's Law of polarised light. Describe a procedure that is suitable for carrying out this investigation.   (3 marks)
  1. An experiment was conducted to demonstrate Malus's Law for plane polarisation of light. The results are shown in the graph.
     

  1. Based on the graph shown, how effective was the experiment in meeting its aim?   (3 marks)
Show Answers Only

a.   Procedure steps:

  • Secure the smartphone so it can rotate at a measured and fixed distance from the computer screen.
  • Set the computer to emit a constant intensity of light.
  • Find the position of the smartphone at which light of maximum intensity is obtained. Set this position to be 0° and record the intensity.
  • Rotate the smartphone through 360° and record the intensity at regular intervals of 10°.
  • Plot obtained results on a graph. 

b.    Experiment effectiveness:

  • Malus’ Law gives the equation  `I=I_(max)cos^2theta`
  • The graph shape that is produced by the experimental data is consistent with the equation. 
  • The experiment uses a sufficient range of data to show a relationship and uses a sufficient number of data points.
  • However, the equipment used must have been incorrectly calibrated, or the measurements were not taken correctly. Measurements appear to be offset by 30° as the maximum intensity of light should occur at 0° rather than 30°. 
Show Worked Solution

a.   Procedure steps:

  • Secure the smartphone so it can rotate at a measured and fixed distance from the computer screen.
  • Set the computer to emit a constant intensity of light.
  • Find the position of the smartphone at which light of maximum intensity is obtained. Set this position to be 0° and record the intensity.
  • Rotate the smartphone through 360° and record the intensity at regular intervals of 10°.
  • Plot obtained results on a graph. 

b.    Experiment effectiveness:

  • Malus’ Law gives the equation  `I=I_(max)cos^2theta`
  • The graph shape that is produced by the experimental data is consistent with the equation. 
  • The experiment uses a sufficient range of data to show a relationship and uses a sufficient number of data points.
  • However, the equipment used must have been incorrectly calibrated, or the measurements were not taken correctly. Measurements appear to be offset by 30° as the maximum intensity of light should occur at 0° rather than 30°. 

PHYSICS, M7 EQ-Bank 23

What is the magnitude of the momentum `(\text{in kg m s}^(-1))` of an electron travelling at 0.75`c`?  (2 marks)

Show Answers Only

`3.10 xx10^(-22)  text{kg m s}^(-1)`

Show Worked Solution
`p_(v)` `=(m_(0)v)/(sqrt((1-(v^(2))/(c^(2)))))`  
  `=((9.109 xx10^(-31))(0.75 xx3 xx10^8))/(sqrt((1-((0.75c)^(2))/(c^(2)))))`  
  `=((9.109 xx10^(-31))(0.75 xx3 xx10^8))/(sqrt((1-0.75^(2)))`  
  `= 3.10 xx10^(-22)  text{kg m s}^(-1)`  

COMMENT: Note the simplification of the denominator.

PHYSICS, M7 EQ-Bank 14 MC

The graph shows the electromagnetic radiation emitted from a black body cavity.
 

What is the best estimate of the temperature of this black body?

  1. `5.9 × 10^(3) \ text{K}`
  2. `7.2 × 10^(3) \ text{K}`
  3. `1.7 × 10^(5) \ text{K}`
  4. `5.9 × 10^(6) \ text{K}`
Show Answers Only

`A`

Show Worked Solution
  • The peak wavelength of this black body is approximately 490 nm.
`lambda_(max)` `=(b)/(T)`  
`T` `=(2.898 xx10^(-3))/(490 xx10^(-9))=5.91 xx10^3  text{K}`   

 
`=>A`