SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Networks, STD2 N2 2009 FUR2 1

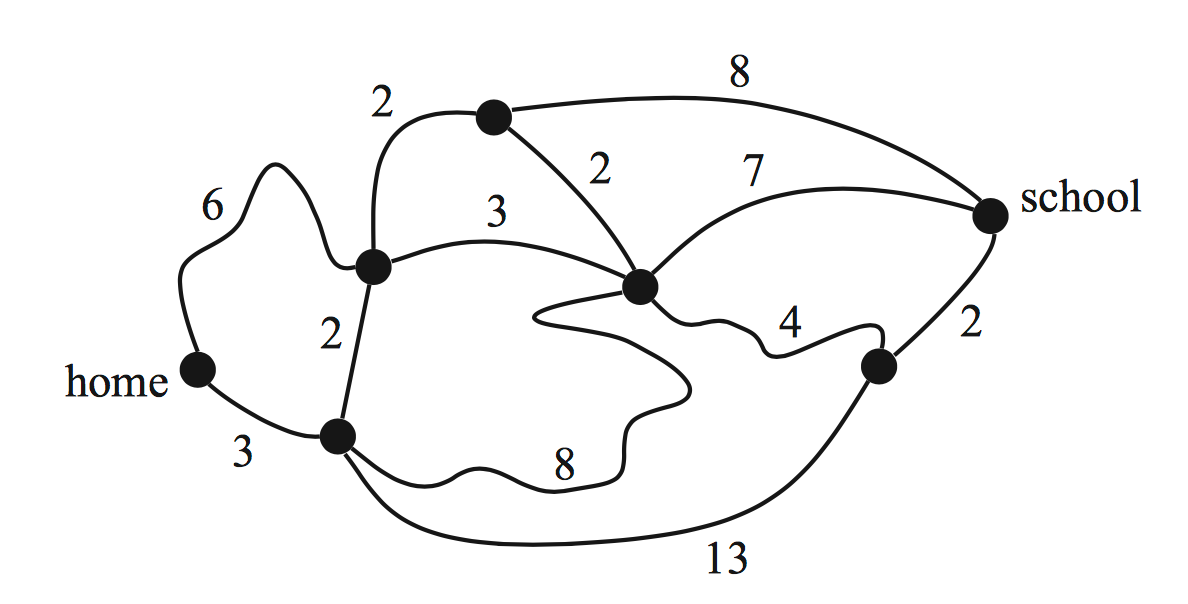
The city of Robville is divided into five suburbs labelled as `A` to `E` on the map below. 

A lake which is situated in the city is shaded on the map.

 

NETWORKS, FUR2 2009 VCAA 11

A table is constructed to represent the number of land borders between suburbs.

If there is no land border between two suburbs, the table records a '0'. If there is a single land border between two suburbs, the table records a '1', and if there are two separate land borders between the same two suburbs, the table records a '2'.
 

`{:({:\ qquadAquadBquadCquadDquadE:}),({:(A),(B),(C),(D),(E):}[(0,1,1,1,0),(1,0,1,2,0),(1,1,0,0,0),(1,2,0,0,0),(0,0,0,0,0)]):}`

 

  1. Explain why all values in the final row and final column of the table are zero.  (1 mark)

In the network diagram below, vertices represent suburbs and edges represent land borders between suburbs. 

The diagram has been started but is not finished.

 

Networks, FUR2 2009 VCAA 1_1

  1. The network diagram is missing one edge and one vertex. 

     

    On the diagram

    1. draw the missing edge  (1 mark)
    2. draw and label the missing vertex.  (1 mark)

Show Answers Only
  1. `E\ text(has no land borders with other suburbs.)`
  2. i. & ii.
    Networks, FUR2 2009 VCAA 1 Answer
Show Worked Solution

a.   `E\ text(has no land borders with other suburbs.)`

 

b.i. & ii.    Networks, FUR2 2009 VCAA 1 Answer

Networks, STD2 N2 2007 FUR2 1

A new housing estate is being developed.

There are five houses under construction in one location.

These houses are numbered as points 1 to 5 below.
  

NETWORKS, FUR2 2007 VCAA 1

 
The builders require the five houses to be connected by electrical cables to enable the workers to have a supply of power on each site.

  1. What is the minimum number of edges needed to connect the five houses?  (1 mark)

  2. On the diagram above, draw a connected graph with this number of edges.  (1 mark) 

Show Answers Only
  1. `4`
  2.  
    networks-fur2-2007-vcaa-1-answer
Show Worked Solution

a.   `text(Minimum number of edges = 4)`

 

b.   `text(One of many possibilities,)`

networks-fur2-2007-vcaa-1-answer

Networks, FUR1 2015 VCE 6 MC

The map below shows all road connections between five towns, `U`, `V`, `W`, `X` and `Y`.
 

NETWORKS, FUR1 2015 VCAA 6 MC1

 
A graph, shown below, was constructed to represent this map.


NETWORKS, FUR1 2015 VCAA 6 MC2

 
A mistake has been made in constructing this graph.

This mistake can be corrected by

A.   drawing another edge between `V` and `W`.

B.   drawing a loop at `W`.

C.   removing the loop at `V`.

D.   removing one edge between `X` and `V`.

Show Answers Only

`A`

Show Worked Solution

`text(There are two routes directly between V and W and therefore)`

`text(a second edge should connect them.)`

`=> A`

Networks, STD2 N2 2014 FUR1 3 MC

The diagram below shows the network of roads that Stephanie can use to travel between home and school.

The numbers on the roads show the time, in minutes, that it takes her to ride a bicycle along each road.

Using this network of roads, the shortest time that it will take Stephanie to ride her bicycle from home to school is 

A.  `12\ text(minutes)`

B.  `13\ text(minutes)`

C.  `14\ text(minutes)`

D.  `15\ text(minutes)`

Show Answers Only

`C`

Show Worked Solution

`text(Using Djikstra’s algorithm:)`

`text(Shortest time riding)`

`=3+2+3+4+2`

`=14\ text(minutes)`

 
`=> C`

Networks, STD2 N2 SM-Bank 37

The map of Australia shows the six states, the Northern Territory and the Australian Capital Territory (ACT).
  

In the network diagram below, each of the vertices `A` to `H` represents one of the states or territories shown on the map of Australia. The edges represent a border shared between two states or between a state and a territory.
 

  1. In the network diagram, what is the order of the vertex that represents the Australian Capital Territory (ACT)?  (1 mark)

  2. In the network diagram, Queensland is represented by which letter? Explain why.  (2 marks)

Show Answers Only

a.    `1`

b.    `text{NSW is Vertex B (it is connected to the ACT – Vertex D)}`

`=> C\ text{is Victoria as it has degree 2}`

`:.\ text(Queensland is vertex)\ A\ text(as it is connected to)\ B\ text(and has degree 3.)`

Show Worked Solution

a.     `text {ACT has 1 border (with NSW)}`

`:.\ text(Degree of ACT’s vertex = 1)`
 

b.    `text{NSW is Vertex B (it is connected to the ACT – Vertex D)}`

`=> C\ text{is Victoria as it has degree 2}`

`:.\ text(Queensland is vertex)\ A\ text(as it is connected to)\ B\ text(and has degree 3.)`

Networks, STD2 N2 2007 FUR1 4 MC

The following network shows the distances, in kilometres, along a series of roads that connect town `A` to town `B.`
 

 
The shortest distance, in kilometres, to travel from town `A` to town `B` is

A.     `9`

B.   `10`

C.   `11`

D.   `12`

Show Answers Only

`B`

Show Worked Solution

`text(Using Djikstra’s algorithm:)`

 
`text(Shortest path)`

`= 4 + 1 + 3 + 2`

`= 10`
 

`=>  B`

Networks, FUR2 2012 VCE 1

Water will be pumped from a dam to eight locations on a farm.

The pump and the eight locations (including the house) are shown as vertices in the network diagram below.

The numbers on the edges joining the vertices give the shortest distances, in metres, between locations.
 

NETWORKS, FUR2 2012 VCAA 1
 

a.i.  Determine the shortest distance between the house and the pump.  (1 mark)

a.ii. How many vertices on the network diagram have an odd degree?  (1 mark)

The total length of pipe that supplies water from the pump to the eight locations on the farm is a minimum.

This minimum length of pipe is laid along some of the edges in the network.

b.i.  On the diagram below, draw the minimum length of pipe that is needed to supply water to all locations on the farm.  (1 mark)

 

   
  NETWORKS, FUR2 2012 VCAA 1
 

b.ii. What is the mathematical term that is used to describe this minimum length of pipe in part b.i.?  (1 mark)

Show Answers Only

a.i.  `160\ text(m)`

a.ii. `2`

b.i.  `1250\ text(m)`

NETWORKS, FUR2 2012 VCAA 1 Answer

b.ii. `text(Minimal spanning tree)`

Show Worked Solution

a.i.   `text(Shortest distance)`

`=70 + 90`

`= 160\ text(m)`

MARKER’S COMMENT: Many students, surprisingly, had problems with part (a)(ii).

 

a.ii.   `2\ text{(the house and the top right vertex)}`

 

b.i.    NETWORKS, FUR2 2012 VCAA 1 Answer

 

b.ii.   `text(Minimal spanning tree)`

Networks, STD2 N2 2017 FUR2 3a

While on holiday, four friends visit a theme park where there are nine rides.

On the graph below, the positions of the rides are indicated by the vertices.

The numbers on the edges represent the distances, in metres, between rides.
 

Electrical cables are required to power the rides.

These cables will form a connected graph.

The shortest total length of cable will be used.

 

  1. Give a mathematical term to describe a graph that represents these cables.   (1 mark)

  2. Draw in the graph that represents these cables on the diagram below.   (1 mark)


 

Show Answers Only

a.   `text{Minimum spanning tree}`

b.    
       

Show Worked Solution

a.   `text{Minimum spanning tree.}`

 

b.   `text(Using Kruskal’s Algorithm)`

`text(Edge 1: 50)`

`text(Edges 2–3: 100)`

`text{Edge 4: 150 (ignore the 150 edge that creates a circuit)}`

`text{Edges 5–6: 200  (ignore the 200 edge that creates a circuit)} `

`text(Edge 7: 300)`

`text(Edge 8: 400)`
 
        

Networks, STD2 N2 2015 FUR2 1

A factory requires seven computer servers to communicate with each other through a connected network of cables.

The servers, `J`, `K`, `L`, `M`, `N`, `O` and `P`, are shown as vertices on the graph below.
 

Networks, FUR2 2015 VCAA 11

 
The edges on the graph represent the cables that could connect adjacent computer servers.

The numbers on the edges show the cost, in dollars, of installing each cable.

  1. What is the cost, in dollars, of installing the cable between server `L` and server `M`?  (1 mark)

  2. What is the cheapest cost, in dollars, of installing cables between server `K` and server `N`?  (1 mark)

  3. The computer servers will be able to communicate with all the other servers as long as each server is connected by cable to at least one other server.

    1. The cheapest installation that will join the seven computer servers by cable in a connected network follows a minimum spanning tree.

       

      Draw the minimum spanning tree on the plan below.  (1 mark) 
       

      Networks, FUR2 2015 VCAA 12
       

    2. The factory’s manager has decided that only six connected computer servers will be needed, rather than seven.

       

      How much would be saved in installation costs if the factory removed computer server `P` from its minimum spanning tree network?

       

      A copy of the graph above is provided below to assist with your working.  (1 mark)

      Networks, FUR2 2015 VCAA 12

Show Answers Only
  1. `$300`
  2. `$920`
  3. `N\ text(and)\ P\ text{(or}\ P\ text(and)\ N)`
    1.  
      Networks, FUR2 2015 VCAA 12 Answer
    2. `$120`
Show Worked Solution

a.   `$300`

 

b.   `text(Minimum cost of)\ K\ text(to)\ N`

`= 440 + 480`

`= $920`
 

MARKER’S COMMENT: Many students had difficulty finding the minimum spanning tree, often incorrectly excluding `PO` or `KL`.

c.i.  `text(Using Prim’s Algorithm:)`

`text(Starting at Vertex)\ L`

`text{1st Edge: L → M (300)}`

`text{2nd Edge: L → K (360)}`

`text{3rd Edge: K → J (250)}`

`text{4th Edge: J → P (200)  etc…}`
 

Networks, FUR2 2015 VCAA 12 Answer


c.ii.   `text(Disconnect)\ J – P\ text(and)\ O – P`

`text(Savings) = 200 + 400 = $600`

`text(Add in)\ M – N`

`text(C)text(ost) = $480`

`:.\ text(Net savings)` `= 600 – 480`
  `= $120`

Networks, STD2 N2 2011 FUR2 2

At the Farnham showgrounds, eleven locations require access to water. These locations are represented by vertices on the network diagram shown below. The dashed lines on the network diagram represent possible water pipe connections between adjacent locations. The numbers on the dashed lines show the minimum length of pipe required to connect these locations in metres.
 

NETWORKS, FUR2 2011 VCAA 2 

 
All locations are to be connected using the smallest total length of water pipe possible.

  1. On the diagram, show where these water pipes will be placed.  (1 mark)
  2. Calculate the total length, in metres, of water pipe that is required.  ( 1 mark) 
Show Answers Only
  1.  
    NETWORKS, FUR2 2011 VCAA 2 Answer
  2. `510\ text(metres)`
Show Worked Solution

a. `text(Using Prim’s Algorithm)`

`text(Starting at bottom right vertex)`

`text{1st Edge: 50}`

`text{2nd Edge: 40`

`text(3rd Edge: 50)`

`text(4th Edge: 40   etc…)`
 

NETWORKS, FUR2 2011 VCAA 2 Answer


b.   `text(Total length of water pipe)`

`= 50+40+50+40+50+60+40+60+60+60`

`= 510\ text(metres)`

Networks, STD2 N2 2008 FUR2 1

James, Dante, Tahlia and Chanel are four children playing a game.

In this children’s game, seven posts are placed in the ground.

The network below shows distances, in metres, between the seven posts.

The aim of the game is to connect the posts with ribbon using the shortest length of ribbon.

This will be a minimal spanning tree.

 

NETWORKS, FUR2 2008 VCAA 11

  1. Draw in a minimal spanning tree for this network on the diagram below.  (1 mark)


NETWORKS, FUR2 2008 VCAA 12

  1. Determine the length, in metres, of this minimal spanning tree.  (1 mark)

  2. How many different minimal spanning trees can be drawn for this network?  (1 mark)

Show Answers Only
  1.  

    `text(or)`
  2. `16\ text(metres)`
  3. `2`
Show Worked Solution

a.  `text(Using Kruskal’s Algorithm)`

`text{Edges 1-3: 2}`

`text{Edges 4-5: 3  (2 edges with weight 3 create a circuit and are ignored)`

`text(Edge 6: 4)` 
 

`text(or)`

 

b.   `text(Length of minimal spanning tree)`

`= 2+2+2+3+3+4`

`= 16\ text(metres)`
 

c.   `2`

Networks, STD2 N2 2007 FUR1 7 MC

The minimal spanning tree for the network below includes two edges with weightings `x` and `y.`
 

 
The length of the minimal spanning tree is 19.

The values of `x` and `y` could be

A.   `x = 1 and y = 7`

B.   `x = 2 and y = 5`

C.   `x = 3 and y = 5`

D.   `x = 4 and y = 5`

Show Answers Only

`C`

Show Worked Solution

`text{Using Kruskal’s Algorithm (as a guide),}`

`text(Minimum spanning tree must be:)`
 


 

`:. 19` `= y + 3 + x + 2 + 1 + 5`
`8` `= x + y`

 
`=>  C`

Networks, STD2 N2 2006 FUR1 4 MC

networks-fur1-2006-vcaa-4-mc-1

 
The minimal spanning tree for the network above will include the edge that has a weight of

A.     `3`

B.     `6`

C.     `8`

D.     `9`

Show Answers Only

`D`

Show Worked Solution

`text(Using Kruskal’s Algorithm:)`

`text{Edge 1: 1  (minimum weight)}`

`text(Edge 2: 2)`

`text{Edge 3: 4  (edge weight 3 creates a circuit and is ignored)}`

`text(Edge 4: 5   etc…)`
 

`:.\ text(Minimum spanning tree is:)`

 
`rArr D`

Networks, STD2 N2 2011 FUR1 1 MC

In the network shown, the number of vertices of even degree is

  1. `2`
  2. `3`
  3. `4`
  4. `5`
Show Answers Only

`B`

Show Worked Solution

`text{Vertices with even degrees: 2, 2, 6}`

`=>  B`

Networks, FUR1 2009 VCE 1 MC

Consider the following graph.
 

networks-fur1-2009-vcaa-1-mc

 
The smallest number of edges that need to be added to make this a connected graph is

A.   `1`

B.   `2`

C.   `3`

D.   `4`

Show Answers Only

`C`

Show Worked Solution

`text(A connected graph is one where any two vertices can be)`

`text(connected by a path.)`

`=>  C`

Networks, STD2 N2 SM-Bank 05 MC

A simple connected graph has 3 edges has 4 vertices.

This graph must be

A.   a cycle.

B.   a tree.

C.   a graph that contains a loop.

D.   a graph that contains a circuit.

Show Answers Only

`=> B`

Show Worked Solution

`text(Consider the graph below,)`

 

networks-fur1-2008-vcaa-4-mc-answer

`=> B`

Calculus, MET1 SM-Bank 35

 

The diagram shows two parallel brick walls `KJ` and `MN` joined by a fence from `J` to `M`.  The wall `KJ` is `s` metres long and  `/_KJM=alpha`.  The fence `JM` is `l` metres long.

A new fence is to be built from `K` to a point `P` somewhere on `MN`.  The new fence `KP` will cross the original fence `JM` at `O`.

Let  `OJ=x`  metres, where  `0<x<l`.

  1. Show that the total area, `A`  square metres, enclosed by `DeltaOKJ` and `DeltaOMP` is given by
  2.    `A=s(x-l+l^2/(2x))sin alpha`.   (3 marks)

  3. Find the value of `x` that makes `A` as small as possible. Justify the fact that this value of `x` gives the minimum value for `A`.   (3 marks)

  4. Hence, find the length of `MP` when `A` is as small as possible.   (1 mark)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}`
  2. `l/sqrt2`
  3. `(sqrt2-1)s\ \ text(metres)`
Show Worked Solution
i.

`A=text(Area)\  Delta OJK+text(Area)\ Delta OMP`

♦♦♦ Students found this question extremely challenging (exact results not available).

`text(Using sine rule)`

`text(Area)\ Delta OJK=1/2\ x s sin alpha` 

`text(Area)\ DeltaOMP =>text(Need to find)\ \ MP`

`/_OKJ` `=/_MPO\ \ text{(alternate angles,}\ MP\ text(||)\ KJtext{)}`
`/_PMO` `=/_OJK=alpha\ \ text{(alternate angles,}\ MP\ text(||)\ KJtext{)}`

`:.\ DeltaOJK\ text(|||)\ Delta OMP\ \ text{(equiangular)}`

`=>x/s` `=(l-x)/(MP)\ ` ` text{(corresponding sides of similar triangles)}`
`MP` `=(l-x)/x *s`  
`text(Area)\ Delta\ OMP` `=1/2 (l-x)* MP * sin alpha`
  `=1/2 (l-x)*((l-x))/x* s  sin alpha`
`:. A`  `=1/2 x*s sin alpha+1/2 (l-x)*((l-x))/x* s sin alpha`
  `=s sin alpha(1/2 x+1/2 (l-x)*((l-x))/x)`
  `=s sin alpha(1/2 x+(l-x)^2/(2x))`
  `=s sin alpha(1/2 x+l^2/(2x)-l+1/2 x)`
  `=s(x-l+l^2/(2x))sin alpha\ \ \ \ text(… as required)`

 

ii.   `text(Find)\ x\ text(such that)\ A\ text(is a minimum)`

MARKER’S COMMENT: Students who could not complete part (i) are reminded that they can still proceed to part (ii) and attempt to differentiate the result given.
Note that `l` and `alpha` are constants when differentiating. 
`A` `=s(x-l+l^2/(2x))sin alpha`
`(dA)/(dx)` `=s(1-l^2/(2x^2))sin alpha`

 
`text(MAX/MIN when)\ (dA)/(dx)=0`

`s(1-l^2/(2x^2))sin alpha` `=0`
`l^2/(2x^2)` `=1`
`2x^2` `=l^2`
`x^2` `=l^2/2`
`x` `=l/sqrt2,\ \ \ x>0`

 

`(d^2A)/(dx^2)=s((l^2)/(2x^3))sin alpha`

`text(S)text(ince)\ \ 0<alpha<90°\ \ =>\ sin alpha>0,\ \ l>0\ \ text(and)\ \  x>0`

`(d^2A)/(dx^2)>0\ \ \ =>text(MIN at)\ \ x=l/sqrt2`
 

iii.   `text(S)text(ince)\ \ MP=((l-x))/x s\ \ text(and MIN when)\ \ x=l/sqrt2`

`MP` `=((l-l/sqrt2)/(l/sqrt2))s xx sqrt2/sqrt2`
  `=((sqrt2 l-l))/l s`
  `=(sqrt2-1)s\ \ text(metres)`

 
`:.\ MP=(sqrt2-1)s\ \ text(metres when)\ A\ text(is a MIN.)`

Calculus, MET1 SM-Bank 34

2005 8a

A cylinder of radius  `x`  and height  `2h`  is to be inscribed in a sphere of radius  `R`  centred at  `O`  as shown.

  1. Show that the volume of the cylinder is given by
  2.    `V = 2pih(R^2-h^2).`   (1 mark)

  3. Hence, or otherwise, show that the cylinder has a maximum volume when
  4.    `h = R/sqrt3.`   (3 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions).}`
  2. `text{Proof (See Worked Solutions).}`
Show Worked Solution
i.    `V` `= pir^2h\ \ \ \ text{(general form)}`
    `= pix^2 xx 2h`

 

`text(Using Pythagoras:)`

`R^2` `= h^2 + x^2`
`x^2` `= R^2-h^2`
`:.V` `= 2pih(R^2-h^2)\ \ …text(as required.)` 

 

ii. `V` `= 2pih(R^2-h^2)`
    `= 2piR^2h-2pih^3`
  `(dV)/(dh)` `= 2piR^2-3 xx 2pih^2`
    `= 2piR^2-6pih^2`
  `(d^2V)/(dh^2)` `= −12pih`

 
`text(Max or min when)\ (dV)/(dh) = 0`

`2piR^2-6pih^2` `= 0`
`6pih^2` `= 2piR^2`
`h^2` `= R^2/3`
`h` `= R/sqrt3,\ \ h > 0`

 
`text(When)\ h = R/sqrt3`

`(d^2V)/(dh^2) = −12pi xx R/sqrt3 < 0`

`:.\ text(Volume is a maximum when)\ h = R/sqrt3\ text(units.)`

Calculus, MET1 SM-Bank 30

A function is given by  `f(x) = 3x^4 + 4x^3-12x^2`.

  1. Find the coordinates of the stationary points of  `f(x)`  and determine their nature.   (3 marks)

  2. Hence, sketch the graph  `y = f(x)`  showing the stationary points.   (2 marks)

  3. For what values of `x` is the function increasing?   (1 mark)

  4. For what values of `k` will  `f(x) = 3x^4 + 4x^3-12x^2 + k = 0`  have no solution?   (1 mark)

Show Answers Only
  1. `text(MAX at)\ (0,0)`
  2. `text(MIN at)\ text{(1,–5)}`
  3. `text(MIN at)\ text{(–2,–32)}`
  4. 2UA HSC 2012 14ai
     
  5. `f(x)\ text(is increasing for)\ -2 < x < 0\ text(and)\ x > 1`
  6. `text(No solution when)\ k > 32`
Show Worked Solution
i. `f(x)` `= 3x^4 + 4x^3 -12x^2`
  `f^{′}(x)` `= 12x^3 + 12x^2-24x`
  `f^{″}(x)` `= 36x^2 + 24x-24`

 

`text(Stationary points when)\ f prime (x) = 0`

`=> 12x^3 + 12x^2-24x` `=0`
`12x(x^2 + x-2)` `=0`
`12x (x+2) (x -1)` `=0`

 

`:.\ text(Stationary points at)\ x=0,\ 1\ text(or)\ –2`

`text(When)\ x=0,\ \ \ \ f(0)=0`
`f^{″}(0)` `= -24 < 0`
`:.\ text{MAX at  (0,0)}`

 

`text(When)\ x=1`

`f(1)` `= 3+4\-12 = -5`
`f^{″}(1)` `= 36 + 24\-24 = 36 > 0`
`:.\ text{MIN at  (1,–5)}`

 

`text(When)\ x=–2`

`f(–2)` `=3(–2)^4 + 4(–2)^3-12(–2)^2`
  `= 48 -32\-48`
  `= -32`
`f^{″}(–2)` `= 36(–2)^2 + 24(–2) -24`
  `=144-48-24 = 72 > 0`
`:.\ text{MIN at  (–2,–32)}`

 

ii.  2UA HSC 2012 14ai

 

♦ Mean mark (HSC) 42%
MARKER’S COMMENT: Be careful to use the correct inequality signs, and not carelessly include `>=` or `<=` by mistake.

 

iii. `f(x)\ text(is increasing for)`
  `-2 < x < 0\ text(and)\ x > 1`

 

iv.   `text(Find)\ k\ text(such that)`

♦♦♦ Mean mark (HSC) 12%.

`3x^4 + 4x^3-12x^2 + k = 0\ \ text(has no solution)`

`k\ text(is the vertical shift of)\ \ y = 3x^4 + 4x^3-12x^2`

`=>\ text(No solution if it does not cross the)\ x text(-axis.)`

`:.\ text(No solution when)\ \ k > 32`

Calculus, MET1 2014 ADV 13a

  1. Differentiate  `3 + sin 2x`.    (1 mark)

  2. Hence, or otherwise, find  `int (cos2x)/(3 + sin 2x)\ dx`.    (2 marks)

Show Answers Only
  1. `2 cos 2x`
  2. `ln (3 + sin 2x)^(1/2) + C`
Show Worked Solution
a. `y` `= 3 + sin 2x`
  `dy/dx` `= 2 cos 2x`

 

b. `int (cos 2x)/(3 + sin 2x)\ dx`
  `= 1/2 int (2 cos 2x)/(3 + sin 2x)\ dx`
  `= 1/2  ln (3 + sin 2x) + C\ \ \ \ \ text{(from part (a))}`

Calculus, MET1 2010 ADV 2e

Given that `int_0^6 ( x + k ) \ dx = 30`, and `k` is a constant, find the value of `k`.   (2 marks)

Show Answers Only

`k = 2`

Show Worked Solution
`int_0^6 ( x + k ) \ dx` `= 30`
`int_0^6 ( x + k ) \ dx` `= [ 1/2\ x^2 + kx ]_0^6`
`30` `= [(1/2xx 6^2 + 6 xx k ) – 0 ]`
`30` `= 18 + 6k`
`6k` `= 12`
`:.  k` `= 2`

Calculus, MET1 2009 ADV 2biii

Evaluate  `int_1^4 x^2 + sqrtx\ dx`.   (3 marks)

 

 

Show Answers Only

`77/3`

 

Show Worked Solution

`int_1^4 x^2 + sqrtx\ \ dx`

`= int_1^4 (x^2 + x^(1/2))\ dx`

`= [1/3 x^3 + 1/(3/2) x^(3/2)]_1^4`

`= [(x^3)/3 + 2/3x^(3/2)]_1^4`

`= [((4^3)/3 + 2/3 xx 4^(3/2))\ – (1/3 + 2/3)]`

`= [(64/3 + 16/3) – 3/3]`

`= [80/3 – 3/3]`

`= 77/3`

Calculus, MET1 2011 ADV 4d

  1. Differentiate  `y=sqrt(9-x^2)`  with respect to  `x`.   (2 marks)

Show Answers Only
  1. `- x/sqrt(9-x^2)`
  2. `-6 sqrt(9-x^2) + c`
Show Worked Solution
IMPORTANT: Some students might find calculations easier by rewriting the equation as `y=(9-x^2)^(1/2)`.
a.    `y` `= sqrt(9-x^2)`
    `= (9-x^2)^(1/2)`

 
`text{Using the function of a function rule (or “chain” rule)}`

`dy/dx` `=1/2 xx (9-x^2)^(-1/2) xx d/dx (9-x^2)`
  `= 1/2 xx (9-x^2)^(-1/2) xx -2x`
  `=-x/sqrt(9-x^2)`

 

b.    `int (6x)/sqrt(9-x^2)\ dx` `= -6 int (-x)/sqrt(9-x^2)\ dx`
    `= -6 sqrt(9-x^2) + c`

Calculus, MET1 2011 VCAA 1b

If  `g(x) = x^2 sin (2x)`,  find  `g^{prime}(pi/6).`   (2 marks)

Show Answers Only

`(sqrt 3 pi)/6 + pi^2/36`

Show Worked Solution

`g(x) = x^2 sin (2x)`

MARKER’S COMMENT: Incorrect determination of exact trig values lost many students marks here.

`text(Using Product Rule:)`

`(fh)^{prime}` `= f^{prime} h + fh^{prime}`
`g^{prime}(x)` `= 2 x sin (2x) + 2x^2 cos (2x)`
   
`:. g^{prime}(pi/6)` `= 2 (pi/6) sin (pi/3) + 2 (pi/6)^2 cos (pi/3)`
  `= pi/3 xx sqrt 3/2 + pi^2/18 xx 1/2`
  `= (sqrt 3 pi)/6 + pi^2/36`

Calculus, MET1 2015 VCAA 1b

Let  `f(x) = (log_e(x))/(x^2)`.

  1. Find  `f^{prime}(x)`.   (2 marks)

  2. Evaluate  `f^{prime}(1)`.   (1 mark)

Show Answers Only
  1. `(1 – 2log_e(x))/(x^3)`
  2. `1`
Show Worked Solution

i.   `text(Using Quotient Rule:)`

`(h/g)^{prime}` `= (h^{prime}g-hg^{prime})/(g^2)`
`f^{prime}(x)` `= ((1/x)x^2-log_e(x)*2x)/(x^4)`
  `= (1-2log_e(x))/(x^3)`

 

ii.    `f^{prime}(1)` `= (1-2log_e(1))/(1^3)`
    `= 1`

Calculus, MET1 2012 VCAA 1b

If  `f(x) = x/(sin(x))`,  find  `f^{prime}(pi/2).`   (2 marks)

Show Answers Only

`1`

Show Worked Solution

`text(Using Quotient Rule:)`

`(h/g)^{prime}` `= (h^{prime}g-h g^{prime})/g^2`
`f^{prime}(x)` `= (1 xx sin (x)-x cos (x))/(sin x)^2`
`:. f^{prime}(pi/2)` `= (sin (pi/2)-pi/2 xx cos (pi/2))/(sin(pi/2))^2`
  `= (1-0)/1^2`
  `= 1`

Calculus, MET1 2008 VCAA 1b

Let  `f(x) = xe^(3x)`.  Evaluate  `f^{prime}(0)`.   (3 marks)

Show Answers Only

`1`

Show Worked Solution

`text(Using Product Rule:)`

`(gh)^{prime} = g^{prime}h + gh^{prime}`

`f^{prime}(x)` `= x(3e^(3x)) + 1 xx e^(3x)`
`:.f^{prime}(0)` `= 0 + e^0`
  `= 1`

Calculus, 2ADV C3 SM-Bank 13

The figure shown represents a wire frame where `ABCE` is a convex quadrilateral. The point `D` is on line segment `EC` with  `AB = ED = 2\ text(cm)` and  `BC = a\ text(cm)`, where `a` is a positive constant.

`/_ BAE = /_ CEA = pi/2`

Let  `/_ CBD = theta`  where  `0 < theta < pi/2.`
 

 vcaa-2011-meth-10a
 

  1. Find `BD` and `CD` in terms of `a` and `theta`.  (2 marks)

  2. Find the length, `L` cm, of the wire in the frame, including length `BD`, in terms of `a` and `theta`.  (1 mark)

  3. Find  `(dL)/(d theta)`,  and hence show that  `(dL)/(d theta) = 0` when  `BD = 2CD`.  (2 marks)

  4. Find the maximum value of `L` if  `a = 3 sqrt 5`.  (1 mark)

Show Answers Only
  1. `BD = a cos theta,\ \ \ CD = a sin theta`
  2. `L = 4 + a + 2 a cos theta + a sin theta`
  3. `text(Proof)\ text{(See Worked Solutions)}`
  4. `L_max = 19 + 3 sqrt 5`
Show Worked Solution

i.   `text(In)\ \ Delta BCD,`

`cos theta` `= (BD)/a`
`:. BD` `= a cos theta`
`sin theta` `= (CD)/a`
`:. CD` `= a sin theta`

 

ii.   `L` `= 4 + 2 BD + CD + a`
    `= 4 + 2a cos theta + a sin theta + a`
    `= 4 + a + 2a cos theta + a sin theta`

 

iii.   `text(Noting that)\ a\ text(is a constant:)`

♦ Mean mark (Vic) 35%.

`(dL)/(d theta)= – 2 a sin theta + a cos theta`

`text(When)\ \ (dL)/(d theta) = 0`,

`- 2 a sin theta+ a cos theta` `= 0`
`a cos theta` `= 2 a sin theta`
`:.  BD` `= 2CD\ \ text{(using part (a))}`

 

iv.  `text(SP’s when)\ \ (dL)/(d theta)=0,`

♦♦♦ Mean mark (Vic) 5%.
`- 2 a sin theta+ a cos theta` `= 0`
`sin theta` `=1/2 cos theta`
`tan theta` `=1/2`

 

 vcaa-2011-meth-10ai

`text(If)\ \ tan theta=1/2,\ \ cos theta = 2/sqrt5,\ \ sin theta = 1/sqrt5`

`L_(max)` `= 4 + a + 2a cos theta + a sin theta`
  `= 4 + (3 sqrt 5) + 2 (3 sqrt 5) (2/sqrt 5) + (3 sqrt 5) (1/sqrt 5)`
  `= 4 + 3 sqrt 5 + 12 + 3`
  `= 19 + 3 sqrt 5\ text(cm)`

Calculus, 2ADV C4 SM-Bank 12

Let  `f(x) = 2e^(-x/5)\ \ \ text(for)\ \ x>=0`

A right-angled triangle `OQP` has vertex `O` at the origin, vertex `Q` on the `x`-axis and vertex `P` on the graph of  `f`, as shown. The coordinates of `P` are  `(x, f(x)).`
 

 vcaa-2013-meth-10
 

  1. Find the area, `A`, of the triangle `OPQ` in terms of `x`.  (1 mark)

  2. Find the maximum area of triangle `OQP` and the value of `x` for which the maximum occurs.  (3 marks)

  3. Let `S` be the point on the graph of  `f` on the `y`-axis and let `T` be the point on the graph of  `f` with the `y`-coordinate `1/2`.Find the area of the region bounded by the graph of  `f` and the line segment `ST`.  (2 marks)

     

 

      vcaa-2013-meth-10i

Show Answers Only
  1. `x e^(-x/5)`
  2. `5/e\ text(u²)`
     
  3. `25/4 log_e (4) – 15/2\ text(u²)`
Show Worked Solution
i.   `text(Area)` `= 1/2 xx b xx h`
    `= 1/2x(2e^(-x/5))`
  `:. A` `= xe^(-x/5)`

 

ii.   `text(Stationary point when)\ \ (dA)/(dx) = 0,`

♦ Mean mark (Vic) 35%.
`x(-1/5 e^(-x/5)) + e^(-x/5)` `= 0`
`e^(-x/5)(1 – x/5)` `= 0`
`:. x` `= 5\ \ \ \ (e^(-x/5) >0,\ \ text(for all)\ x)`

 

`text(When)\ \ x = 5,\ \ A` `= xe^(-x/5)= 5e^-1`
   

`:. A_max = 5/e\ text(u²,   when)\ \ x = 5`

 

iii.   `text(Find)\ \ S:\ F(0) = 2`

`=>S(0, 2)`

♦♦ Mean mark (Vic) 32%.

 

`text(Find)\ \ T:\ \ \ ` `2e^(-x/5)` `= 1/2`
  `e^(-x/5)` `= 1/4`
  `-x/5` `= log_e (1/4)`
  `x` `= 5 log_e (4)`

`=> T(5log_e(4), 1/2)`

 

vcaa-2013-meth-10ii

`:.\ text(Area)` `= text(Area)\ SOAT – int_0^(5 log_e(4)) (2e^(-x/5)) dx`
  `=1/2h(a+b) + 10 [e^(-x/5)]_0^(5 log_e (4))`
  `= 5/2 log_e (4) (2 + 1/2) + 10 [e^(-log_e (4)) – e^0]`
  `= 25/4 log_e (4) +10 (1/4 – 1)`
  `= 25/4 log_e (4) – 15/2\ text(u²)`

GRAPHS, FUR2 2017 VCAA 3

Lifeguards are required to ensure the safety of swimmers at the beach.

Let `x` be the number of junior lifeguards required.

Let `y` be the number of senior lifeguards required.

The inequality below represents the constraint on the relationship between the number of senior lifeguards required and the number of junior lifeguards required.

 Constraint 1  `y >= x/4`
 

  1. If eight junior lifeguards are required, what is the minimum number of senior lifeguards required?  (1 mark)

 
There are three other constraints.

 Constraint 2  `x ≥ 6`

 Constraint 3  `y ≥ 4`

 Constraint 4  `x + y ≥ 12`

  1. Interpret Constraint 4 in terms of the number of junior lifeguards and senior lifeguards required.  (1 mark)

 
The shaded region of the graph below contains the points that satisfy Constraints 1 to 4.

All lifeguards receive a meal allowance per day.

Junior lifeguards receive $15 per day and senior lifeguards receive $25 per day.

The total meal allowance cost per day, `$C`, for the lifeguards is given by

`C = 15x + 25y`

  1. Determine the minimum total meal allowance cost per day for the lifeguards.  (2 marks)
  2. On rainy days there will be no set minimum number of junior lifeguards or senior lifeguards required, therefore:

     

    • Constraint 2  `(x ≥ 6)`  and Constraint 3  `(y ≥ 4)`  are removed

     

    • Constraint 1 and Constraint 4 are to remain.
     

     

              Constraint 1  `y >= x/4`

     

              Constraint 4  `x + y >= 12`

     


    The total meal allowance cost per day,     `$C`, for the lifeguards remains as

     

    `C = 15x + 25y`

     


    How many junior lifeguards and senior lifeguards work on a rainy day if the total meal allowance cost     is to be a minimum?

     

    Write your answers in the boxes provided below.  (1 mark)


Show Answers Only

a.   `2`

b.   `text(The total combined number of junior and)`

`text(senior lifeguards must be at least 12.)`

c.   `$220`

d.   
Show Worked Solution

a.   `text(Minimum senior lifeguards) = 8/4 = 2`

 

b.   `text(The total combined number of junior and)`

`text(senior lifeguards must be at least 12.)`

 

c.   `text(Minimum cost occurs at (8, 4))`

`:. C_text(min)` `= 15 xx 8 + 25 xx 4`
  `= $220`

 

d.   `text(Consider the graph without the restrictions)`

♦♦ Mean mark 24%.
MARKER’S COMMENT: A common incorrect answer was 10 and 3.

`x >= 6quadtext(and)quady >= 4:`

`text(By inspection, intersection around (9.5, 2.4))`

`text(⇒ Minimum allowance when)`

GRAPHS, FUR2 2017 VCAA 2

A swimming race is being held in the ocean.

From the shore, competitors swim 500 m out to a buoy in the ocean and then return to the shore.

One competitor, Edgar, reaches the buoy after 12.5 minutes and completes the race in 25 minutes.

The graph below shows his distance from shore, in metres, `t` minutes after the race begins.
 

  1. What distance, in metres, has Edgar swum after 15 minutes?  (1 mark)
  2. Let `E` be Edgar’s distance from the shore, in metres, `t` minutes after the race begins.

     

    The linear relation that represents his swim out to the buoy is of the form
     

     

    `E = kt,`  where  `0 < t ≤ 12.5`

     

    The slope of the line `k` is the speed at which Edgar is swimming, in metres per minute.

     

    Show that `k = 40`.  (1 mark)

A second competitor, Zlatko, began the race at the same time as Edgar.

Below is the relation that describes Zlatko’s swim, where `Z` is his distance from the shore, in metres, `t` minutes after the race begins and `F` is the time it took Zlatko to finish the race.

`Z = {(qquadqquadqquad50t,0 < t <= 10),(−62.5t + 1125, 10 < t <= F):}`

  1. The graph below again shows the relation representing Edgar’s swim.

     

    Sketch the relation representing Zlatko’s swim on the graph below.  (2 marks)

  2. How many minutes after the start of the race were Zlatko and Edgar the same distance from the shore?

     

    Round your answer to two decimal places.  (1 mark)

Show Answers Only

a.   `600\ text(metres)`

b.   `text(See Worked Solutions)`

c.   

d.   `10.98\ text(minutes)`

Show Worked Solution
a.    `text(Distance)` `= 500 + 100`
    `= 600\ text(metres)`

 

b.   `text(When)\ t = 12.5,quadE = 500`

♦ Mean mark 49%.
MARKER’S COMMENT: Note that it was not sufficient to type in the equation and write “Solve”.

`500` `= k xx 12.5`
`:. k` `= 500/12.5`
  `= 40\ \ text(… as required)`

 

c.   `text(Zlatko reaches 500 m buoy when)`

♦ Mean mark 47%

`t = 500/50 = 10\ text(min)`

`text(Zlatko returns to shore when)`

`0` `=-62.5t + 1125`
`:. t` `= 1125/62.5= 18\ text(min)`

 

d.   `text(Same distance from shore when:)`

`40t` `= −62.5t + 1125`
`102.5t` `= 1125`
`:. t` `= 1125/102.5`
  `= 10.975…`
  `= 10.98\ text(minutes)`

GEOMETRY, FUR2 2017 VCAA 3

Some hostel buildings are arranged around a grassed area.

The grassed area is shown shaded in the diagram below.

The grassed area is made up of a square overlapping a circle.

The square has side lengths of 65 m.

The circle has a radius of 50 m.

An angle, `theta`, is also shown on the diagram.

  1. Use the cosine rule to show that the angle `theta`, correct to the nearest degree, is equal to 81°.  (1 mark)
  2. What is the perimeter, in metres, of the entire grassed area?

     

    Round your answer to the nearest metre.  (1 mark)

  3. The hostel’s management is planning to build a pathway from point A to point B, as shown on the diagram below.
     

     
    Calculate the length, in metres, of the planned pathway.

     

    Round your answer to the nearest metre.  (2 marks)

Show Answers Only

a.   `81^@`

b.   `438\ text(m (nearest metre))`

c.   `153\ text(m)`

Show Worked Solution
a.    `costheta` `= (50^2 + 50^2 – 65^2)/(2 xx 50 xx 50)`
    `= 0.155`
    `= 81.08…`
    `= 81^@\ \ text{(nearest degree)  … as required)`

 

♦♦ Mean mark part (b) 34%.

b.    `text(Perimeter)` `= (3 xx 65) + ((360-81))/360 xx 2 xx pi xx 50`
    `= 195 + 279/360 xx 2 xx pi xx 50`
    `= 438.47…`
    `= 438\ text(m (nearest metre))`

 

♦♦ Mean mark part (c) 34%.

c.   

`text(Using Pythagoras,)`

`x = sqrt(50^2 – 32.5^2) = 37.99…`

`:. text(Length)\ AB` `= 50 + 37.99… + 65`
  `= 152.99…` 
  `= 153\ text(m)` 

GEOMETRY, FUR2 2017 VCAA 2

Miki will travel from Melbourne (38° S, 145° E) to Tokyo (36° N, 140° E) on Wednesday, 20 December.

The flight will leave Melbourne at 11.20 am, and will take 10 hours and 40 minutes to reach Tokyo.

The time difference between Melbourne and Tokyo is two hours at that time of year.

  1. On what day and at what time will Miki arrive in Tokyo?  (1 mark)

Miki will travel by train from Tokyo to Nemuro and she will stay in a hostel when she arrives.

The hostel is located 186 m north and 50 m west of the Nemuro railway station.

    1. What distance will Miki have to walk if she were to walk in a straight line from the Nemuro railway station to the hostel?

       

      Round your answer to the nearest metre.  (1 mark)

    2. What is the three-figure bearing of the hostel from the Nemuro railway station?

       

      Round your answer to the nearest degree.  (1 mark)


The city of Nemuro is located 43° N, 145° E.

Assume that the radius of Earth is 6400 km.

  1. The small circle of Earth at latitude 43° N is shown in the diagram below.
     
             
     
    What is the radius of the small circle of Earth at latitude 43° N?

     

    Round your answer to the nearest kilometre.  (1 mark)

  2. Find the shortest great circle distance between Melbourne (38° S, 145° E) and Nemuro (43° N, 145° E).

     

    Round your answer to the nearest kilometre.  (1 mark)

Show Answers Only
  1. `8\ text(pm (Wed))`
  2. i. `193\ text(m  (nearest metre))`
  3. ii. `345^@`
  4. `4681\ text(km  (nearest km))`
  5. `9048\ text(km  (nearest km))`
Show Worked Solution

a.   `text{Flight arrival (in Melb time) = 11:20 + 10:40 = 22:00 (Wed)}`

♦ Mean mark 40%.
COMMENT: A surprisingly poor result for this standard question.

`text(Tokyo time)` `=\ text(Melb time less 2 hrs)`
  `= 20:00\ (text(Wed))`
  `= 8\ text(pm (Wed))`

 

b.i.  `text(Using Pythagoras:)`

`d` `= sqrt(186^2 + 50^2)`
  `= 192.603…`
  `= 193\ text(m  (nearest metre))`

 

♦♦ Mean mark part (b)(ii) 27%.
MARKER’S COMMENT: N15°W is not a 3-figure bearing and received no marks.

b.ii.    `tan theta` `= 50/186`
  `theta` `= 15.04…^@`

 

`:. text(Bearing of)\ H\ text(from)\ N`

`= 360 – 15`

`= 345^@`

 

c.   `text(Let)\ \ x = text(radius of small circle)`

♦ Mean mark part (c) 43%

`sin47^@` `= x/6400`
`:.x` `= 6400 xx sin47^@`
  `= 4680.66…`
  `= 4681\ text(km  (nearest km))`

 

d.   

`text(Shortest distance)`

♦ Mean mark part (d) 38%

`= text(Arc length)\ NM`

`= 81/360 xx 2 xx pi xx 6400`

`= 9047.78…`

`= 9048\ text(km  (nearest km))`

NETWORKS, FUR2 2017 VCAA 4

The rides at the theme park are set up at the beginning of each holiday season.

This project involves activities A to O.

The directed network below shows these activities and their completion times in days.

  1. Write down the two immediate predecessors of activity I.   (1 mark)

  2. The minimum completion time for the project is 19 days.

     

     i.  There are two critical paths. One of the critical paths is A–E–J–L–N.
    Write down the other critical path.   (1 mark)

    ii.  Determine the float time, in days, for activity F.   (1 mark)

  3. The project could finish earlier if some activities were crashed.

     

    Six activities, B, D, G, I, J and L, can all be reduced by one day.

     

    The cost of this crashing is $1000 per activity.

     

     i.  What is the minimum number of days in which the project could now be completed?   (1 mark)

    ii.  What is the minimum cost of completing the project in this time?   (1 mark)

Show Answers Only

a.     `D\ text(and)\ E`

b.i.   `A E I L N`

b.ii.   `6\ text(days)`

c.i.    `17`

c.ii.    `$4000`

Show Worked Solution

a.   `D\ text(and)\ E\ (text(note the dummy is not an activity.))`
  

b.i.   `A  E  I  L  N`

♦♦ Mean mark part (b)(i) 44% and part (b)(ii) 28%.
  

b.ii.    `text(Float time)` `= 19-(2 + 3 + 3 + 3 + 2)`
    `= 6\ text(days)`

  
c.i.   `text(Reduce activities:)\ I, J, L\ \ (text(on critical path))`

♦♦ Mean mark part (c)(i) 35%.

 `text(New critical path)\ \ A C G N\ \ text(takes 18 days.)`

`:. text(Reduce activity)\ G\ text(also.)`

`text(⇒ this critical path reduces to 17 days.)`

`text(⇒ Minimum Days = 17)`
  

c.ii.   `text(Minimum time requires crashing)\ \ I, J, L\ text(and)\ G`

♦♦♦ Mean mark part (c)(ii) 15%.

`:.\ text(Minimum Cost)` `= 4 xx 1000`
  `= $4000`

NETWORKS, FUR2 2017 VCAA 3

While on holiday, four friends visit a theme park where there are nine rides.

On the graph below, the positions of the rides are indicated by the vertices.

The numbers on the edges represent the distances, in metres, between rides.
 

  1. Electrical cables are required to power the rides.
    These cables will form a connected graph.
    The shortest total length of cable will be used.
  2. i. Give a mathematical term to describe a graph that represents these cables.   (1 mark)

  3. ii. Draw in the graph that represents these cables on the diagram below.   (1 mark)

     

Show Answers Only

a.i.   `text{Minimum spanning tree (shortest length required).}`

a.ii.   
Show Worked Solution

a.i.   `text{Minimal spanning tree (shortest length required).}`

a.ii.   

NETWORKS, FUR2 2017 VCAA 2

Bai joins his friends Agatha, Colin and Diane when he arrives for a holiday in Seatown.

Each person will plan one tour that the group will take.

Table 1 shows the time, in minutes, it would take each person to plan each of the four tours.
 

 
The aim is to minimise the total time it takes to plan the four tours.

Agatha applies the Hungarian algorithm to Table 1 to produce Table 2.

Table 2 shows the final result of all her steps of the Hungarian algorithm.
 


 

  1. In Table 2 there is a zero in the column for Colin.
    When all values in the table are considered, what conclusion about minimum total planning time can be made from this zero?   (1 mark)

  2. Determine the minimum total planning time, in minutes, for all four tours.   (1 mark)

Show Answers Only

a.   `text(Colin must plan tour 2.)`

b.   `43\ text(minutes)`

Show Worked Solution

a.   `text(Colin must plan tour 2.)`

♦ Mean mark part (a) 37%.
MARKER’S COMMENT: The answer “Colin will plan Tour 2 because he is the fastest” received no marks.

`(text(No additional information is required.))`

 

b.   `text{Allocations: Colin (T2), Diane (T3), Bai (T1), Agatha (T4)}`

`:.\ text(Minimum time)` `= 8 + 18 + 7 + 10`
  `= 43\ text(minutes)`

MATRICES, FUR2 2017 VCAA 3

Senior students at a school choose one elective activity in each of the four terms in 2018.

Their choices are communication (`C`), investigation (`I`), problem-solving (`P`) and service (`S`).

The transition matrix `T` shows the way in which senior students are expected to change their choice of elective activity from term to term.
 

`{:(qquadqquadqquadqquadquadtext(this term)),(qquadqquadqquad\ CqquadquadIqquadquadPqquad\ S),(T = [(0.4,0.2,0.3,0.1),(0.2,0.4,0.1,0.3),(0.2,0.3,0.3,0.4),(0.2,0.1,0.3,0.2)]{:(C),(I),(P),(S):}qquadtext(next term)):}`
 

Let `S_n` be the state matrix for the number of senior students expected to choose each elective activity in Term `n`.

For the given matrix `S_1`, a matrix rule that can be used to predict the number of senior students in each elective activity in Terms 2, 3 and 4 is
 

`S_1 = [(300),(200),(200),(300)],qquadS_(n + 1) = TS_n`
 

  1. How many senior students will not change their elective activity from Term 1 to Term 2?   (1 mark)

  2. Complete `S_2`, the state matrix for Term 2, below.   (1 mark)


             

  3. Of the senior students expected to choose investigation (`I`) in Term 3, what percentage chose service (`S`) in Term 2?   (2 marks)

  4. What is the maximum number of senior students expected in investigation (`I`) at any time during 2018?   (1 mark)

Show Answers Only
  1. `320`
  2.  
    `S_2 = [(250),(250),(300),(200)]`
  3. `text(25%)`
  4. `250`
Show Worked Solution

a.   `text(Students who do not change)`

♦ Mean mark 47%.

`= 0.4 xx 300 + 0.4 xx 200 + 0.3 xx 200 + 0.2 xx 300`

`= 120 + 80 + 60 + 60`

`= 320`

 

b.    `S_2 = TS_1` `= [(0.4,0.2,0.3,0.1),(0.2,0.4,0.1,0.3),(0.2,0.3,0.3,0.4),(0.2,0.1,0.3,0.2)][(300),(200),(200),(300)]`
    `= [(250),(250),(300),(200)]`

 

c.    `S_3` `= TS_2`
    `= [(260),(240),(295),(205)]`

♦♦♦ Mean mark 13%.
MARKER’S COMMENT: A poorly understood and answered question worthy of careful attention.

`text(Number)\ (I)\ text(in Term 3 = 240)`

`text(Number)\ (S)\ text(in Term 2 = 200)`

`text(S)text(ince 30% move from)\ S\ text(to)\ I\ text(each term:)`

`text(Percentage)` `= (0.3 xx 200)/240`
  `= 60/240`
  `= 25text(%)`

 

d.    `S_4` `= TS_3`
    `= [(261),(239),(294.5),(205.5)]`

♦ Mean mark 43%.

`:. text(Max number of)\ (I)\ text(students is 250.)`

`(text(During term 2))`

MATRICES, FUR2 2017 VCAA 2

Junior students at a school must choose one elective activity in each of the four terms in 2018.

Students can choose from the areas of performance (`P`), sport (`S`) and technology (`T`).

The transition diagram below shows the way in which junior students are expected to change their choice of elective activity from term to term.

 

  1. Of the junior students who choose performance (`P`) in one term, what percentage are expected to choose sport (`S`) the next term?   (1 mark)

Matrix `J_1` lists the number of junior students who will be in each elective activity in Term 1.
 

`J_1 = [(300),(240),(210)]{:(P),(S),(T):}`
 

  1. 306 junior students are expected to choose sport (`S`) in Term 2.
     
    Complete the calculation below to show this.   (1 mark)


  2. In Term 4, how many junior students in total are expected to participate in performance (`P`) or sport (`S`) or technology (`T`)?   (1 mark)

Show Answers Only
  1. `text(40%)`
  2.  `300 xx 0.4 + 240 xx 0.6 + 210 xx 0.2 = 306`
  3. `750`
Show Worked Solution

a.   `text(40%)`
 

b.  `300 xx 0.4 + 240 xx 0.6 + 210 xx 0.2 = 306`

♦♦ Mean mark part (c) 30%.

MARKER’S COMMENT: No matrix calculations were required here.


c.   `text(Each term, every student will do)\ P\ text(or)\ S\ text(or)\ T.`

`:. text(Total students (Term 4))` `=\ text(Total students (Term 1))`
  `= 300 + 240 + 210`
  `= 750`

MATRICES, FUR2 2017 VCAA 1

A school canteen sells pies (`P`), rolls (`R`) and sandwiches (`S`).

The number of each item sold over three school weeks is shown in matrix `M`.

`{:(qquadqquadqquadquadPqquadRqquadS),(M = [(35,24,60),(28,32,43),(32,30,56)]{:(text(week 1)),(text(week 2)),(text(week 3)):}):}` 

  1. In total, how many sandwiches were sold in these three weeks?   (1 mark)

  2. The element in row `i` and column `j` of matrix `M` is `m_(ij)`.
  3. What does the element `m_12` indicate?  (1 mark)

  4. Consider the matrix equation

    `[(35,24,60),(28,32,43),(32,30,56)] xx [(a),(b),(c)] = [(491.55),(428.00),(487.60)]`

    where `a` = cost of one pie, `b` = cost of one roll and `c` = cost of one sandwich.
  5.  i. What is the cost of one sandwich?   (1 mark)

The matrix equation below shows that the total value of all rolls and sandwiches sold in these three weeks is $915.60

`L xx [(491.55),(428.00),(487.60)] = [915.60]`

Matrix `L` in this equation is of order `1 × 3`.

  1. ii. Write down matrix `L`.   (1 mark)

Show Answers Only
  1. `159`
  2. `text(It represents the number of rolls sold in week 1.)`
    1. `$3.80`
    2. `text(Matrix)\ L = [0,1,1]`
Show Worked Solution
a.    `text(Total sandwiches)` `= 60 + 43 + 56`
    `= 159`

 
b.   `m_12 = 24`

`text(It represents the number of rolls sold in week 1.)`
 

c.i.    `[(a),(b),(c)]` `= [(35,24,60),(28,32,43),(32,30,56)]^(−1)[(491.55),(428.00),(487.60)]`
    `= [(4.65),(4.20),(3.80)]`

 
`:.\ text(C)text(ost of 1 sandwich = $3.80)`
 

c.ii.   `text(Matrix)\ L = [0,1,1]`

CORE, FUR2 2017 VCAA 5

Alex is a mobile mechanic.

He uses a van to travel to his customers to repair their cars.

The value of Alex’s van is depreciated using the flat rate method of depreciation.

The value of the van, in dollars, after `n` years, `V_n`, can be modelled by the recurrence relation shown below.

`V_0 = 75\ 000 qquad V_(n + 1) = V_n - 3375`

  1. Recursion can be used to calculate the value of the van after two years.

     

    Complete the calculations below by writing the appropriate numbers in the boxes provided.   (2 marks)


    1. By how many dollars is the value of the van depreciated each year?   (1 mark)
    2. Calculate the annual flat rate of depreciation in the value of the van.
    3. Write your answer as a percentage.   (1 mark)
  3. The value of Alex’s van could also be depreciated using the reducing balance method of depreciation.
  4. The value of the van, in dollars, after `n` years, `R_n`, can be modelled by the recurrence relation shown below.

     

            `R_0 = 75\ 000 qquad R_(n + 1) = 0.943R_n`

    At what annual percentage rate is the value of the van depreciated each year?   (1 mark)

Show Answers Only

a.

b.i.  `$3375`

b.ii. `4.5text(%)`

c.  `5.7text(%)`

Show Worked Solution

a.   

  
b.i.   `$3375`
  

b.ii.    `text(Annual Rate)` `= 3375/(75\ 000) xx 100`
    `= 4.5text(%)`

 

c.    `text(Annual Rate)` `= (1-0.943) xx 100text(%)`
    `= 5.7text(%)`

CORE, FUR2 2017 VCAA 6

Alex sends a bill to his customers after repairs are completed.

If a customer does not pay the bill by the due date, interest is charged.

Alex charges interest after the due date at the rate of 1.5% per month on the amount of an unpaid bill.

The interest on this amount will compound monthly.

  1. Alex sent Marcus a bill of $200 for repairs to his car.

     

    Marcus paid the full amount one month after the due date.

     

    How much did Marcus pay?   (1 mark)

Alex sent Lily a bill of $428 for repairs to her car.

Lily did not pay the bill by the due date.

Let `A_n` be the amount of this bill `n` months after the due date.

  1. Write down a recurrence relation, in terms of `A_0`, `A_(n + 1)` and `A_n`, that models the amount of the bill.   (2 marks)

  2. Lily paid the full amount of her bill four months after the due date.

     

    How much interest was Lily charged?

     

    Round your answer to the nearest cent.   (1 mark)

Show Answers Only
  1. `$203`
  2. `A_o = 428,qquadA_(n + 1) = 1.015A_n`
  3. `$26.26\ \ (text(nearest cent))`
Show Worked Solution
a.    `text(Amount paid)` `= 200 + 200 xx 1.5text(%)`
    `= 1.015 xx 200`
    `= $203`

♦ Mean mark part (b) 47%.
MARKER’S COMMENT: A recurrence relation has the initial value written first. Know why  `A_n=428 xx 1.015^n`  is incorrect.

 

b.   `A_o = 428,qquadA_(n + 1) = 1.015A_n`

 

c.    `text(Total paid)\ (A_4)` `= 1.015^4 xx 428`
    `= $454.26`

♦♦ Mean mark part (c) 29%.

`:.\ text(Total Interest)` `= 454.26-428`
  `= $26.26\ \ (text(nearest cent))`

CORE, FUR2 2017 VCAA 4

The eggs laid by the female moths hatch and become caterpillars.

The following time series plot shows the total area, in hectares, of forest eaten by the caterpillars in a rural area during the period 1900 to 1980.

The data used to generate this plot is also given.
 

The association between area of forest eaten by the caterpillars and year is non-linear.

A log10 transformation can be applied to the variable area to linearise the data.

  1. When the equation of the least squares line that can be used to predict log10 (area) from year is determined, the slope of this line is approximately 0.0085385
  2. Round this value to three significant figures.   (1 mark)
  3. Perform the log10 transformation to the variable area and determine the equation of the least squares line that can be used to predict log10 (area) from year.
  4. Write the values of the intercept and slope of this least squares line in the appropriate boxes provided below.
  5. Round your answers to three significant figures.  (2 marks)

The least squares line predicts that the log10 (area) of forest eaten by the caterpillars by the year 2020 will be approximately 2.85

  1. Using this value of 2.85, calculate the expected area of forest that will be eaten by the caterpillars by the year 2020.
  2.  i. Round your answer to the nearest hectare.   (1 mark)

  3. ii. Give a reason why this prediction may have limited reliability.   (1 mark)

Show Answers Only

a.  `0.00854\ (text(3 sig fig))`

b.  `log_10(text(area)) = −14.4 + 0.000854 xx text(year)`

c.i.  `708\ text(hectares)`

c.ii. `text(This prediction extrapolates significantly from the given)`
        `text(data range and as a result, its reliability decreases.)`

Show Worked Solution

a.   `0.0085385 = 0.00854\ (text(3 sig fig))`

♦ Mean marks of part (a) and (b) 44%.

 

b.    `log_10(text(area))` `= −14.4 + 0.000854 xx text(year)`

 

♦♦ Mean mark part (c)(i) 29%.
COMMENT: When the question specifies using the value 2.85, use it!

c.i.    `log_10(text(Area))` `= 2.85`
  `:.\ text(Area)` `= 10^2.85`
    `= 707.94…`
    `= 708\ text(hectares)`

 

c.ii.   `text(This prediction extrapolates significantly from the given)`

  `text(data range and as a result, its reliability decreases.)`

Calculus, 2ADV C3 SM-Bank 7

The graph of  `f(x) = sqrt x (1 - x)`  for  `0<=x<=1`  is shown below.
 


 

  1. Calculate the area between the graph of  `f(x)` and the `x`-axis.  (2 marks)

  2. For `x` in the interval `(0, 1)`, show that the gradient of the tangent to the graph of  `f(x)`  is  `(1 - 3x)/(2 sqrt x)`.  (1 mark)

The edges of the right-angled triangle `ABC` are the line segments `AC` and `BC`, which are tangent to the graph of  `f(x)`, and the line segment `AB`, which is part of the horizontal axis, as shown below.

Let `theta` be the angle that `AC` makes with the positive direction of the horizontal axis.
 


 

  1. Find the equation of the line through `B` and `C` in the form  `y = mx + c`, for  `theta = 45^@`.  (3 marks)

Show Answers Only
  1. `4/15\ text(units)^2`
  2. `text(Proof)\ \ text{(See Workes Solutions)}`
  3. `y = -x + 1`
Show Worked Solution
i.   `text(Area)` `= int_0^1 (sqrt x – x sqrt x)\ dx`
    `= int_0^1 (x^(1/2) – x^(3/2))\ dx`
    `= [2/3 x^(3/2) – 2/5 x^(5/2)]_0^1`
    `= (2/3 – 2/5) – (0 – 0)`
    `= 10/15 – 6/15`
    `= 4/15\ text(units)^2`

 

ii.   `f (x)` `= x^(1/2) – x^(3/2)`
  `f prime (x)` `= 1/2 x^(-1/2) – 3/2 x^(1/2)`
    `= 1/(2 sqrt x) – (3 sqrt x)/2`
    `= (1 – 3x)/(2 sqrt x)\ \ text(.. as required.)`

 

iii.  `m_(AC) = tan 45^@=1`

♦♦♦ Mean mark (Vic) part (iii) 20%.
MARKER’S COMMENT: Most successful answers introduced a pronumeral such as  `a=sqrtx`  to solve.

`=> m_(BC) = -1\ \ (m_text(BC) _|_ m_(AC))`

 
`text(At point of tangency of)\ BC,\  f prime(x) = -1`

`(1 – 3x)/(2 sqrt x)` `=-1`
`1-3x` `=-2sqrtx`
`3x-2sqrt x-1` `=0`

 
`text(Let)\ \ a=sqrtx,`

`3a^2-2a-1` `=0`
`(3a+1)(a-1)` `=0`
`a=1 or -1/3`   
`:. sqrt x` `=1` `or`   `sqrt x=- 1/3\ \ text{(no solution)}`
`x` `=1`    

 
`f(1)=sqrt1(1-1)=0\ \ =>B(1,0)`
 

`text(Equation of)\ \ BC, \ m=-1, text{through (1,0):}`

`y-0` `=-1(x-1)`
`y` `=-x+1`

Trigonometry, 2ADV T2 SM-Bank 8

Let  `(tantheta - 1) (sin theta - sqrt 3 cos theta) (sin theta + sqrt 3 costheta) = 0`.

  1. State all possible values of  `tan theta`.  (1 mark)
  2. Hence, find all possible solutions for  `(tan theta - 1) (sin^2 theta - 3 cos^2 theta) = 0`,
    where  `0 <= theta <= pi`.  (2 marks)
Show Answers Only
  1. `tan theta = 1 or tan theta = +- sqrt 3`
  2. `theta = pi/4, pi/3 or (2 pi)/3`
Show Worked Solution

i.  `(tantheta – 1) (sin theta – sqrt 3 cos theta) (sin theta + sqrt 3 costheta) = 0`

`=> tan theta = 1`

♦ Mean mark (Vic) 42%.
`=>sin theta – sqrt 3 cos theta` `=0`
`sin theta` `=sqrt3 cos theta`
`tan theta` `=sqrt3`

 

`=>sin theta + sqrt 3 cos theta` `=0`
`sin theta` `=-sqrt3 cos theta`
`tan theta` `=-sqrt3`

 

`:. tan theta = 1 or tan theta = +- sqrt 3`

 

ii.  `(tan theta – 1) (sin^2 theta – 3 cos^2 theta) = 0`

`text{Using part (i):}`

♦ Mean mark (Vic) 42%.

`(tan theta – 1) (sin theta – sqrt 3 cos theta) (sin theta + sqrt 3 cos theta) = 0`

`=> tan theta` `= 1` `qquad or qquad` `tan theta` `= +- sqrt 3`
`theta` `= pi/4`   `theta` `= pi/3, (2 pi)/3\ \ text(for)\ \ 0<=theta <= pi`

 

`:. theta = pi/4, pi/3 or (2 pi)/3`

CORE, FUR2 2017 VCAA 3

The number of male moths caught in a trap set in a forest and the egg density (eggs per square metre) in the forest are shown in the table below.
 

  1. Determine the equation of the least squares line that can be used to predict the egg density in the forest from the number of male moths caught in the trap.
  2. Write the values of the intercept and slope of this least squares line in the appropriate boxes provided below.
  3. Round your answers to one decimal place.  (2 marks)

     

         

  4. The number of female moths caught in a trap set in a forest and the egg density (eggs per square metre) in the forest can also be examined.

     

    A scatterplot of the data is shown below.
     


     
    The equation of the least squares line is

     

                  egg density = 191 + 31.3 × number of female moths

    1. Draw the graph of this least squares line on the scatterplot (provided above).   (1 mark)

    2. Interpret the slope of the regression line in terms of the variables egg density and number of female moths caught in the trap.   (1 mark)

    3. The egg density is 1500 when the number of female moths caught is 55.
    4. Determine the residual value if the least squares line is used to predict the egg density for this number of female moths.   (1 mark)
    5. The correlation coefficient is  `r = 0.862`
    6. Determine the percentage of the variation in egg density in the forest explained by the variation in the number of female moths caught in the trap.
    7. Round your answer to one decimal place.   (1 mark)
Show Answers Only

a.   `text(egg density)\ = −46.8 + 18.9 xx text(number of male moths)`

b.i.  

b.ii.  `text(Egg density per square metre increases)`

`text(by 31.3 eggs for every extra female moth)`

`text(caught in the trap.)`

b.iii.  `−412.5`

b.iv.  `text(74.3%)`

Show Worked Solution

a.   `text(By calculator)`

`text(egg density)\ = −46.8 + 18.9 xx text(number of male moths)`

 

b.i.   `text(Calculating extreme points on graph.)`

♦♦ Mean mark 26%.
MARKER’S COMMENT: Not well answered! Many students did not realise the graph started at 10 on the `x`-axis and many did not use a ruler!

`x = 10, y = 191 + 31.3 xx 10 = 504`

`x = 60, y = 191 + 31.3 xx 60 = 2069`

 

♦ Mean mark 39%.
MARKER’S COMMENT: Students must clearly refer to the increase in egg density for every one-unit increase in female moths.

b.ii.   `text(Egg density per square metre increases)`

 `text(by 31.3 eggs for every extra female moth)`

 `text(caught in the trap.)`

 

b.iii.   `text(Predicted egg density)`

♦ Mean mark 48%.

`= 191 + 31.3 xx 55`

`= 1912.5`

`:.\ text(Residual value)` `= 1500-1912.5`
  `= −412.5`

 

b.iv.   `r = 0.862`

♦ Mean mark 47%.

`r^2 = 0.862^2 = 0.7430… = 74.3text{%  (1 d.p.)}`

`:.\ text(74.3% is explained.)`

Algebra, MET2 2017 VCAA 4

Let  `f : R → R :\  f (x) = 2^(x + 1)-2`. Part of the graph of  `f` is shown below.
 

  1. The transformation  `T: R^2 -> R^2, \ T([(x),(y)]) = [(x),(y)] + [(c),(d)]`  maps the graph of  `y = 2^x`  onto the graph of  `f`.

     

    State the values of `c` and `d`.   (2 marks)

  2. Find the rule and domain for  `f^(-1)`, the inverse function of  `f`.   (2 marks)

  3. Find the area bounded by the graphs of  `f` and  `f^(-1)`.   (3 marks)

  4. Part of the graphs of  `f` and  `f^(-1)` are shown below.
     

         
     
    Find the gradient of  `f` and the gradient of  `f^(-1)`  at  `x = 0`.   (2 marks)

The functions of  `g_k`, where  `k ∈ R^+`, are defined with domain `R` such that  `g_k(x) = 2e^(kx)-2`.

  1. Find the value of `k` such that  `g_k(x) = f(x)`.  (1 mark)

  2. Find the rule for the inverse functions  `g_k^(-1)` of  `g_k`, where  `k ∈ R^+`.   (1 mark)

  3. i. Describe the transformation that maps the graph of  `g_1` onto the graph of  `g_k`.   (1 mark)

    ii. Describe the transformation that maps the graph of  `g_1^(-1)` onto the graph of  `g_k^(-1)`.   (1 mark)

  4. The lines `L_1` and `L_2` are the tangents at the origin to the graphs of  `g_k`  and  `g_k^(-1)`  respectively.
  5. Find the value(s) of `k` for which the angle between `L_1` and `L_2` is 30°.   (2 marks)

  6. Let `p` be the value of `k` for which  `g_k(x) = g_k^(−1)(x)`  has only one solution.
  7.  i. Find `p`.   (2 marks)

  8. ii. Let  `A(k)`  be the area bounded by the graphs of  `g_k`  and  `g_k^(-1)`  for all  `k > p`.
  9.     State the smallest value of `b` such that  `A(k) < b`.   (1 mark)

Show Answers Only

a.  `c =-1, \ d =-2`

b.  `f^(-1)(x) = log_2 (x + 2)-1, \ x ∈ (-2,∞)`

c.  `3-2/(log_e(2))\ text(units)²`

d. `f^{prime}(0)= 2log_e(2) and f^(-1)^{prime}(0)= 1/(2log_e(2))`

e.  `k = log_e(2)`

f.  `g_k^(-1)(x)= 1/k log_e((x + 2)/2)`

g.i.  `text(Dilation by factor of)\ 1/k\ text(from the)\ ytext(-axis)`

g.ii.  `text(Dilation by factor of)\ 1/k\ text(from the)\ xtext(-axis)`

h.  `k=sqrt3/6\ or\ sqrt3/2`

i.i.  `p = 1/2`

i.ii.  `b=4`

Show Worked Solution

a.   `text(Using the matrix transformation:)`

`x^{prime}` `=x+c\ \ => x=x^{prime}-c`
`y^{prime}` `=y+d\ \ =>y= y^{prime}-d`
   
`y^{prime}-d` `=2^((x)^{prime}-c)`
`y^{prime}` `= 2^((x)^{prime}-c)+d`

 

`:. c = -1, \ d = -2`

 

b.   `text(Let)\ \ y = f(x)`

`text(Inverse : swap)\ x\ ↔ \ y`

`x` `= 2^(y + 1)-2`
`x + 2` `= 2^(y + 1)`
`y + 1` `= log_2(x + 2)`
`y` `= log_2(x + 2)-1`

 

`text(dom)(f^(-1)) = text(ran)(f)`

`:. f^(-1)(x) = log_2 (x + 2)-1, \ x ∈ (-2,∞)`

 

c.   `text(Intersection points occur when)\ \ f(x)=f^(-1)(x)`

MARKER’S COMMENT: Specifically recommends using  `f^(-1)(x)-f(x)`  in this type of integral to avoid errors in stating the integral.

`x` `= -1, 0`

 

`text(Area)` `= int_(-1)^0 (f^(-1)(x)-f(x))\ dx`
  `= 3-2/(log_e(2))\ text(units)²`

 

d.    `f^{prime}(0)` `= 2log_e(2)`
  `f^{(-1)^prime}(0)` `= 1/(2log_e(2))`

 

e.   `g_k(x) = 2e^(kx)-2`

`text(Solve:)\ \ g_k(x) = f(x)quad text(for)\ k ∈ R^+`

`:. k = log_e(2)`

 

f.   `text(Let)\ \ y = g_k(x)`

`text(Inverse : swap)\ x\ text(and)\ y`

`x` `= 2e^(ky)-2`
`e^(ky)` `=(x+2)/2`
`ky` `=log_e((x+2)/2)`
`:. g_k^(-1)(x)` `= 1/k log_e((x + 2)/2)`

 

♦♦ Mean mark part (g)(i) 31%.

g.i.    `g_1(x)` `= 2e^x-2`
  `g_k(x)` `= 2e^(kx)-2`

 
`:. text(Dilation by factor of)\ 1/k\ text(from the)\ ytext(-axis)`

 

♦♦ Mean mark part (g)(ii) 30%.

g.ii.    `g_1^(-1)(x)` `= log_e((x + 2)/2)`
  `g_k^(-1)(x)` `= 1/klog_e((x + 2)/2)`

 
`:. text(Dilation by factor of)\ 1/k\ text(from the)\ xtext(-axis)`

 

h.   `text(When)\ \ x=0,`

♦♦♦ Mean mark part (h) 13%.

`g_k^{prime}(0)=2k\ \ => m_(L_1)=2k`

`g_k^{(-1)^prime}(0)=1/(2k)\ \ => m_(L_2)=1/(2k)`

 

`text(Using)\ \ tan 30^@=|(m_1-m_2)/(1+m_1m_2)|,`

`text(Solve:)\ \ 1/sqrt3` `=+- ((2k-1/(2k)))/2\ \ text(for)\ k`

 
`:. k=sqrt3/6\ or\ sqrt3/2`

 

i.i   `text(By inspection, graphs will touch once if at)\ \ x=0,`

♦♦♦ Mean mark part (i)(i) 4%.

`m_(L_1)` `=m_(L_2)`
`2k` `=1/(2k)`
`k` `=1/2,\ \ (k>0)`

 
`:. p = 1/2`

 

i.ii  `text(As)\ k→oo, text(the graph of)\ g_k\ text(approaches)\ \ x=0`

♦♦♦ Mean mark part (i)(ii) 2%.

`text{(vertically) and}\ \ y=-2\ \ text{(horizontally).}`

`text(Similarly,)\ \ g_k^(-1)\ \ text(approaches)\ \ x=-2`

`text{(vertically) and}\ \ y=0\ \ text{(horizontally).}`

 

`:. lim_(k→oo) A(k) = 4`

`:.b=4`

Probability, MET2 2017 VCAA 3

The time Jennifer spends on her homework each day varies, but she does some homework every day.

The continuous random variable `T`, which models the time, `t,` in minutes, that Jennifer spends each day on her homework, has a probability density function `f`, where

 

`f(t) = {{:(1/625 (t - 20)),(1/625 (70 - t)),(0):}qquad{:(20 <= t < 45),(45 <= t <= 70),(text(elsewhere)):}:}`

 

  1. Sketch the graph of `f` on the axes provided below.  (3 marks)


     

       
     

  2. Find  `text(Pr)(25 ≤ T ≤ 55)`.  (2 marks)

  3. Find  `text(Pr)(T ≤ 25 | T ≤ 55)`.  (2 marks)

  4. Find `a` such that  `text(Pr)(T ≥ a) = 0.7`, correct to four decimal places.  (2 marks)

  5. The probability that Jennifer spends more than 50 minutes on her homework on any given day is `8/25`. Assume that the amount of time spent on her homework on any day is independent of the time spent on her homework on any other day.

     

    1. Find the probability that Jennifer spends more than 50 minutes on her homework on more than three of seven randomly chosen days, correct to four decimal places.  (2 marks)

    2. Find the probability that Jennifer spends more than 50 minutes on her homework on at least two of seven randomly chosen days, given that she spends more than 50 minutes on her homework on at least one of those days, correct to four decimal places.  (2 marks)

Let `p` be the probability that on any given day Jennifer spends more than `d` minutes on her homework.

Let `q` be the probability that on two or three days out of seven randomly chosen days she spends more than `d` minutes on her homework.

  1. Express `q` as a polynomial in terms of `p`.  (2 marks)

    1. Find the maximum value of `q`, correct to four decimal places, and the value of `p` for which this maximum occurs, correct to four decimal places.  (2 marks)

    2. Find the value of `d` for which the maximum found in part g.i. occurs, correct to the nearest minute.  (2 marks)


Show Answers Only

  1.  

  2. `4/5`
  3. `1/41`
  4. `39.3649`
    1. `0.1534`
    2. `0.7626`
  6. `q =7p^2(1-p)^4(2p+3)`
    1. `p = 0.3539quadtext(and)quadq = 0.5665`
    2. `49\ text(min)`

Show Worked Solution

a.   

MARKER’S COMMENT: Many did not draw graph along `t`-axis between 0 and 20 and for  `t>70`.

 

b.   `text(Pr)(25 <= T <= 55)`

`= int_25^45 1/625 (t – 20)\ dt + int_45^55 1/625 (70 – t)\ dt`

`= 4/5`

 

c.   `text(Pr)(T ≤ 25 | T ≤ 55)`

`=(text(Pr)(T <= 25))/(text(Pr)( T <= 55))`

`= (int_20^25 1/625(t – 20)\ dt)/(1 – int_55^70 1/625(70 – t)\ dt)`

`= (1/50)/(1 – 9/50)`

`= 1/41`

 

d.   `text(Pr)(T ≥ a) = 0.7`

♦ Mean mark part (d) 36%.

`=>\ text(Pr)(T <= a) = 0.3`

`text(Solve:)`

`int_20^a 1/625(t – 20)\ dt` `= 0.3quadtext(for)quada ∈ (20, 45)`

 

`:. a == 39.3649`

 

e.i.   `text(Let)\ X =\ text(Number of days Jenn studies more than 50 min)`

`X ~\ text(Bi) (7, 8/25)`

`text(Pr)(X >= 4) = 0.1534`

 

e.ii.    `text(Pr)(X >= 2 | X >= 1)` `= (text(Pr)(X >= 2))/(text(Pr)(X >= 1))`
    `= (0.7113…)/(0.9327…)`
    `= 0.7626\ \ text{(to 4 d.p.)}`

 

f.   `text(Let)\ Y =\ text(Number of days Jenn spends more than)\ d\ text(min)`

`Y ~\ text(Bi)(7,p)`

♦ Mean mark part (f) 36%.

`q` `= text(Pr)(Y = 2) + text(Pr)(Y = 3)`
  `= ((7),(2))p^2(1 – p)^5 + ((7),(3))p^3(1 – p)^4`
  `= 21p^2(1 – p)^5 + 35p^3(1 – p)^4`
   `=7p^2(1-p)^4[3(1-p)+5p]`
  `=7p^2(1-p)^4(2p+3)`

 

g.i.   `text(Solve)\ \ q′(p) = 0,`

♦♦ Mean mark part (g)(i) 30%.

`p` `=0.35388…`
  `=0.3539\ \ text{(to 4 d.p.)}`

`:. q_text(max)= 0.5665\ \ text{(to 4 d.p.)}`

 

g.ii.   `text(Pr)(T > d) = p= 0.35388…`

♦♦♦ Mean mark part (g)(ii) 8%.

  `text(Solve:)`

`int_d^70 (1/625(70 – t))dt` `= 0.35388… quadtext(for)quadd ∈ (45,70)`

 

`:. d` `=48.967…`
  `=49\ text(mins)`

Algebra, MET2 2017 VCAA 2

Sammy visits a giant Ferris wheel. Sammy enters a capsule on the Ferris wheel from a platform above the ground. The Ferris wheel is rotating anticlockwise. The capsule is attached to the Ferris wheel at point `P`. The height of `P` above the ground, `h`, is modelled by  `h(t) = 65-55cos((pit)/15)`, where `t` is the time in minutes after Sammy enters the capsule and `h` is measured in metres.

Sammy exits the capsule after one complete rotation of the Ferris wheel.
 


 

  1. State the minimum and maximum heights of `P` above the ground.   (1 mark)

  2. For how much time is Sammy in the capsule?   (1 mark)

  3. Find the rate of change of `h` with respect to `t` and, hence, state the value of `t` at which the rate of change of `h` is at its maximum.   (2 marks)

As the Ferris wheel rotates, a stationary boat at `B`, on a nearby river, first becomes visible at point `P_1`. `B` is 500 m horizontally from the vertical axis through the centre `C` of the Ferris wheel and angle `CBO = theta`, as shown below.
 

   
 

  1. Find `theta` in degrees, correct to two decimal places.   (1 mark)

Part of the path of `P` is given by  `y = sqrt(3025-x^2) + 65, x ∈ [-55,55]`, where `x` and `y` are in metres.

  1. Find `(dy)/(dx)`.   (1 mark)

As the Ferris wheel continues to rotate, the boat at `B` is no longer visible from the point  `P_2(u, v)` onwards. The line through `B` and `P_2` is tangent to the path of `P`, where angle `OBP_2 = alpha`.
 

   
 

  1. Find the gradient of the line segment `P_2B` in terms of `u` and, hence, find the coordinates of `P_2`, correct to two decimal places.   (3 marks)

  2. Find `alpha` in degrees, correct to two decimal places.   (1 mark)

  3. Hence or otherwise, find the length of time, to the nearest minute, during which the boat at `B` is visible.   (2 marks)

Show Answers Only
  1. `h_text(min) = 10\ text(m), h_text(max) = 120\ text(m)`
  2. `30\ text(min)`
  3. `t = 7.5`
  4. `7.41^@`
  5. `(-x)/(sqrt(3025-x^2))`
  6. `P_2(13.00, 118.44)`
  7. `13.67^@`
  8. `7\ text(min)`
Show Worked Solution
a.    `h_text(min)` `= 65-55` `h_text(max)` `= 65 + 55`
    `= 10\ text(m)`   `= 120\ text(m)`

 

b.   `text(Period) = (2pi)/(pi/15) = 30\ text(min)`

 

c.   `h^{prime}(t) = (11pi)/3\ sin(pi/15 t)`

♦ Mean mark 50%.
MARKER’S COMMENT: A number of commons errors here – 2 answers given, calc not in radian mode, etc …

 

`text(Solve)\ h^{primeprime}(t) = 0, t ∈ (0,30)`

`t = 15/2\ \ text{(max)}`   `text(or)`   `t = 45/2\ \ text{(min – descending)}`

`:. t = 7.5`

 

d.   

♦ Mean mark 36%.
MARKER’S COMMENT: Choosing degrees vs radians in the correct context was critical here.

`tan(theta)` `= 65/500`
`:. theta` `=7.406…`
  `= 7.41^@`

 

e.    `(dy)/(dx)` `= (-x)/(sqrt(3025-x^2))`

 

f.   

`P_2(u,sqrt(3025-u^2) + 65),\ \ B(500,0)`

`:. m_(P_2B)` `= (sqrt(3025-u^2) + 65)/(u-500)`

 

`text{Using part (e), when}\ \ x=u,`

♦♦♦ Mean mark part (f) 18%.
MARKER’S COMMENT: Many students were unable to use the rise over run information to calculate the second gradient.

`dy/dx=(-u)/(sqrt(3025-u^2))`

 

`text{Solve (by CAS):}`

`(sqrt(3025-u^2) + 65)/(u-500)` `= (-u)/(sqrt(3025-u^2))\ \ text(for)\ u`

 

`u=12.9975…=13.00\ \ text{(2 d.p.)}`

 

`:. v` `= sqrt(3025-(12.9975…)^2) + 65`
  `= 118.4421…`
  `= 118.44\ \ text{(2 d.p.)}`

 

`:.P_2(13.00, 118.44)`

 

♦♦♦ Mean mark part (g) 7%.

g.    `tan alpha` `=v/(500-u)`
    `= (118.442…)/(500-12.9975…)`
  `:. alpha` `= 13.67^@\ \ text{(2 d.p.)}`

 

h.   

♦♦♦ Mean mark 5%.

`text(Find the rotation between)\ P_1 and P_2:`

`text(Rotation to)\ P_1 = 90-7.41=82.59^@`

`text(Rotation to)\ P_2 = 180-13.67=166.33^@`

`text(Rotation)\ \ P_1 → P_2 = 166.33-82.59 = 83.74^@`

 

`:.\ text(Time visible)` `= 83.74/360 xx 30\ text(min)`
  `=6.978…`
  `= 7\ text{min  (nearest degree)}`

Calculus, MET2 2017 VCAA 1

Let  `f : R → R,\  f (x) = x^3-5x`. Part of the graph of `f` is shown below.
 

  1. Find the coordinates of the turning points.   (2 marks)

  2. `A(−1, f (−1))`  and  `B(1, f (1))`  are two points on the graph of `f`.

     

    1. Find the equation of the straight line through `A` and `B`.   (2 marks)

    2. Find the distance `AB`.   (1 mark)

Let  `g : R → R, \ g(x) = x^3-kx, \ k ∈ R^+`.

  1. Let  `C(–1, g(−1))` and `D(1, g(1))` be two points on the graph of `g`.

     

    1. Find the distance `CD` in terms of `k`.   (2 marks)

    2. Find the values of `k` such that the distance `CD` is equal to  `k + 1`.   (1 mark)

  2. The diagram below shows part of the graphs of `g` and  `y = x`. These graphs intersect at the points with the coordinates `(0, 0)` and `(a, a)`.
  3.  
       
  4.  
    1. Find the value of `a` in terms of `k`.   (1 mark)

    2. Find the area of the shaded region in terms of `k`.   (2 marks)

Show Answers Only
  1. `(- sqrt15/3,(10sqrt15)/9)\ text(and)\ (sqrt15/3,-(10sqrt15)/9)`
    1. `y =-4x`
    2. `2sqrt17`
    1. `2sqrt(k^2-2k + 2)`
    2. `k = 1quadtext(or)quadk = 7/3`
    1. `sqrt(k + 1)`
    2. `((k + 1)^2)/4\ text(units)²`
Show Worked Solution
a.   
`text(Solve)\ \ f^{^{′}}(x)` `= 0\ \ text(for)\ x:`
`x` `= ± sqrt15/3`

 
`f(sqrt15/3) = -(10sqrt15)/9`

`f(−sqrt15/3) = (10sqrt15)/9`

`:.\ text(Turning points:)`

`(- sqrt15/3,(10sqrt15)/9)\ text(and)\ (sqrt15/3,-(10sqrt15)/9)`
 

b.i.   `A(-1,4),\ \ B(1,–4)`

`m_(AB) = (4-(−4))/(−1-(1)) = −4`

`text(Equation of)\ AB, m=-4, text(through)\ \ (-1,4):`

` y-4` `= −4(x-(−1))`
`:. y` `= −4x`

 

MARKER’S COMMENT: Students skilled in the use of technology will be much more efficient and minimise errors here.
b.ii.    `d_(text(AB))` `=sqrt((x_2-x_1)^2+(f(x_2)-f(x_1))^2)`
    `= sqrt((1- (- 1))^2 + (f(1)-f(−1))^2)`
    `= 2sqrt17`

 

c.i.    `d_(text(CD))` `=sqrt((x_2-x_1)^2+(g(x_2)-g(x_1))^2)`
    `=sqrt((1-(-1))^2+(g(1)-g(-1))^2)`
    `= 2sqrt(k^2-2k + 2)`

 

c.ii.   `text(Solve:)quad2sqrt(k^2-2k + 2) = k + 1quadtext(for)quadk > 0`

`:. k = 1quadtext(or)quadk = 7/3`
 

d.i.   `text(Solve:)quada^3-ka = a\ \ \ text(for)quad a,\ \ (a > 0)`

`:. a = sqrt(k + 1)`
 

d.ii.    `text(Area)` `= int_0^(sqrt(k + 1))(x-g(x))\ dx`
    `= ((k + 1)^2)/4\ text(units)²`

Probability, MET2 2017 VCAA 19 MC

A probability density function  `f` is given by

`f(x) = {{:(cos(x) + 1),(0):}qquad{:(k < x < (k + 1)),(text(elsewhere)):}:}`

where `0 < k < 2`.

The value of `k` is

  1. `1`
  2. `(3pi - 1)/2`
  3. `pi - 1`
  4. `(pi - 1)/2`
  5. `pi/2`
Show Answers Only

`D`

Show Worked Solution
`int_k^(k+1)(cos(x) + 1)\ dx` `=[sinx +x]_k^(k+1)`
`sin(k+1)+(k+1) -sink – k` `=1`
`sin(k+1)-sink` `=0`
`sin(k+1)-sin(pi-k)` `=0`
   
`k+1` `=pi-k`
`2k` `=pi-1`
`:.k` `=(pi-1)/2`

`=> D`

Calculus, MET2 2017 VCAA 15 MC

A rectangle `ABCD` has vertices `A(0, 0)`, `B(u, 0)`, `C(u, v)` and `D(0, v)`, where `(u, v)` lies on the graph of  `y = -x^3 + 8`, as shown below.
 

 

The maximum area of the rectangle is

  1. `root3(2)`
  2. `6 root3(2)`
  3. `16`
  4. `8`
  5. `3root3(2)`
Show Answers Only

`B`

Show Worked Solution

`A` `=u(-u^3+8)`
  `=8u-u^4`
`(dA)/(du)` `=8-4u^3`
   

`(dA)/(du)=0\ \ text(when):`

`4u^3` `=8`
`u^3` `=2`
`u` `=root3(2)`

 

`:.A_text(max)=8root3(2)-(root3(2))^4 = 6 root3(2)`

`=> B`

Probability, MET2 2017 VCAA 14 MC

The random variable `X` has the following probability distribution, where  `0 < p < 1/3`.
 

 
The variance of `X` is

  1. `2p(1 - 3p)`
  2. `1 - 4p`
  3. `(1 - 3p)^2`
  4. `6p - 16p^2`
  5. `p(5 - 9p)`
Show Answers Only

`D`

Show Worked Solution
`text(Var)(X)` `= text(E)(X^2) – [text(E)(X)]^2`
  `= [(−1)^2p + 0^2 xx 2p + 1^2(1 – 3p)] – [−p + 0 + 1 – 3p]^2`
  `= 6p – 16p^2`

`=> D`

Calculus, MET2 2017 VCAA 11 MC

The function  `f : R → R, \ f (x) = x^3 + ax^2 + bx`  has a local maximum at  `x = –1`  and a local minimum at  `x = 3`.

The values of `a` and `b` are respectively

  1. `–2\ text(and)\ \ –3`
  2. `text(2 and 1)`
  3. `text(3 and)\ \ –9`
  4. `–3\ text(and)\ \ –9`
  5. `– 6\ text(and)\ \ –15`
Show Answers Only

`D`

Show Worked Solution

`f′(x) = 3x^2 +2ax +b`

`text(Solve:)quadquadf′(−1)` `=3-2a+b= 0qquadtext(and)`
 `f′(3)` `=27+6a+b = 0qquadtext(for)\ a, b` 

 

`:. a = −3, \ b = − 9`

`=> D`

Algebra, MET2 2017 VCAA 8 MC

If  `y = a^(b - 4x) + 2`, where  `a > 0`, then `x` is equal to

  1. `1/4(b - log_a(y - 2))`
  2. `1/4(b - log_a(y + 2))`
  3. `b - log_a(1/4(y + 2))`
  4. `b/4 - log_a(y - 2)`
  5. `1/4(b + 2 - log_a(y))`
Show Answers Only

`A`

Show Worked Solution

`text(Solving for)\ x:`

`y – 2` `= a^(b – 4x)`
`b – 4x` `= log_a(y – 2)`
`4x` `= b – log_a(y – 2)`
`:. x` `= 1/4(b – log_a(y – 2))`

 
`=> A`