SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Algebra, MET2 2012 VCAA 2 MC

For the function with rule  `f(x) = x^3 - 4x`, the average rate of change of  `f(x)`  with respect to `x` on the interval `[1,3]` is

A.   `1`

B.   `3`

C.   `5`

D.   `6`

E.   `9`

Show Answers Only

`=> E`

Show Worked Solution
`text(Average ROC)` `= (f(3) – f(1))/(3 – 1)`
  `=(15-(-3))/2`
  `= 9`

`=> E`

CORE, FUR1 SM-Bank 3 MC

The decreasing value of a depreciating asset is shown in the graph below.
 

 
 

Let `A_n` be the value of the asset after `n` years, in dollars.

What recurrence relation below models the value of `A_n`?

  1. `A_0 = 120\ 000,qquadA_n = 120\ 000 xx 1.125 xx n` 
  2. `A_0 = 120\ 000,qquadA_n = 120\ 000 xx (0.125)^n` 
  3. `A_0 = 120\ 000,qquadA_n = 120\ 000 xx (1 - 0.125) xx n` 
  4. `A_0 = 120\ 000,qquadA_n = 120\ 000 xx (1 - 0.125)^n` 
  5. `A_0 = 120\ 000,qquadA_n = 120\ 000 xx (1 + 1.125)^n` 
Show Answers Only

`D`

Show Worked Solution

`text(The asset is decreasing at 12.5% per year)`

`text(on a decreasing balance basis.)`

`A_1` `= 120\ 000(1 – 0.125)^1`
`vdots`  
`A_n` `= 120\ 000(1 – 0.125)^n`

`=> D`

CORE, FUR1 SM-Bank 2 MC

Derek invests $48 000 in an investment that guarantees an annual interest rate of 4.8%, compounded monthly.

Let  `V_n`  be the value of the investment after `n` months.

Which recurrence relation below models the investment?

  1. `V_0 = 48\ 000,qquadV_(n + 1) = 1.048V_n`
  2. `V_0 = 48\ 000,qquadV_(n + 1) = 1.0048V_n`
  3. `V_0 = 48\ 000,qquadV_(n + 1) = 1.48V_n`
  4. `V_0 = 48\ 000,qquadV_(n + 1) = 1.004V_n`
  5. `V_0 = 48\ 000,qquadV_(n + 1) = 1.04V_n`
Show Answers Only

`D`

Show Worked Solution

`text(Monthly interest rate)`

`= (4.8%)/12`

`= 0.4%`

`= 0.004`
 

`:. V_(n + 1) = 1.004V_n`

`=> D`

CORE, FUR1 SM-Bank 1-2 MC

Part 1

Candy deposits $80 000 into a savings account that earns 5% interest per annum, compounded annually.

At the end of the first year, Candy withdraws $5600.

What is the balance of Candy's savings account at the start of the second year?

  1. `$74\ 400`
  2. `$77\ 600`
  3. `$78\ 400`
  4. `$85\ 600`
  5. `$89\ 600`

 

Part 2

If `B_n` is the balance of Candy's account at the start of year `n`, a recurrence equation that can be used to model the balance of the account over time is

  1. `B_(n + 1) = 1.5 B_n - 5600\ \ \ \ text(where)\ B_1 = 80\ 000`
  2. `B_(n + 1) = 0.05 B_n - 5600\ \ \ \ text(where)\ B_1 = 80\ 000`
  3. `B_(n + 1) = 1.05 (B_n - 5600)\ \ \ \ text(where)\ B_1 = 80\ 000`
  4. `B_(n + 1) = 0.05 (B_n - 5600)\ \ \ \ text(where)\ B_1 = 80\ 000`
  5. `B_(n + 1) = 1.05 B_n - 5600\ \ \ \ text(where)\ B_1 = 80\ 000`
Show Answers Only

`text(Part 1:)\ C`

`text(Part 2:)\ E`

Show Worked Solution

`text(Part 1)`

`text(Balance at start of 2nd year)`

`= 80\ 000 xx 1.05 – 5600`

`= $78\ 400`

`=> C`

 

`text(Part 2)`

`B_2` `= 80\ 000 xx 1.05 – 5600`
  `= 1.05B_1 – 5600`
`B_3` `= 1.05B_2 – 5600`
`vdots`  
`B_(n + 1)` `= 1.05B_n – 5600`

 

`=> E`

CORE, FUR2 SM-Bank 3

Luke purchased a new pizza oven for his restaurant for $23 500.

He can depreciate the pizza oven using the reducing balance method at a rate of 12.5% per year.

  1. If `V_n` represents the value of the pizza oven after `n` years, write a recurrence relation that models its value.   (1 mark)

  2. During what year will the pizza oven's value drop below $15 000?   (1 mark)

Luke has been advised that he can use flat rate depreciation at 10% of the purchase price.

  1. After 4 years, show which depreciation method gives the pizza oven the highest value?   (1 mark)

Show Answers Only
  1. `V_0 = 23\ 500,qquadV_(n + 1) = 0.875V_n`
  2. `text(year 4)`
  3. `text(See Worked Solutions)`
Show Worked Solution
a.    `V_0` `= 23\ 500`
  `V_1` `= 23\ 500-(12.5text(%) xx 23\ 500)`
    `= 0.875 V_0`
  `V_2` `= 0.875(0.875V_0)`
    `= 0.875 V_1`

  
`:.\ text(Recurrence relationship:)`

`V_0 = 23\ 500,qquadV_(n + 1) = 0.875V_n`
  

b.    `V_1` `= 0.875 xx 23\ 500 = 20\ 562.50`
  `V_2` `= 0.875 xx 20\ 562.50 = 17\ 992.1875`
  `V_3` `= 0.875 xx 17\ 992.1875 = 15\ 743.16…`
  `V_4` `= 0.875 xx 15\ 743.16… = 13\ 775.26…`

  
`:.\ text(The value drops below $15 000 in year 4.)`

  
c.   `text(Value after 4 years using reducing balance)`

`= 13\ 775.26`

`text(Depreciation each year for flat rate)`

`= 10text(%) xx 23\ 500`

`= $2350`

`text(Value of pizza oven after 4 years,)`

`= 23\ 500-(4 xx 2350)`

`= $14\ 100`
 

`:.\ text(The flat rate depreciation method)`

`text(values the pizza oven highest.)`

CORE, FUR2 SM-Bank 2

Spiro is saving for a car. He has an account with $3500 in it at the start of the year.

At the end of each month, Spiro adds another $180 to the account.

The account pays 3.6% interest per annum, compounded monthly.

    1. What is the interest rate per month?   (1 mark)
    2. Write a recurrence relation that models Spiro's investment, with `V_n` representing the balance of his account after `n` months.   (1 mark)
  2. What will be the balance of Spiro's account after 3 months?
  3. Write your answer correct to the nearest cent.   (1 mark)

Show Answers Only

    1. `0.3text(% per month)`
    2. `V_0 = 3500,qquadV_(n + 1) = V_n xx 1.003 + 180`
  2. `$4073\ \ (text(nearest $))`

Show Worked Solution

a.i.    `text(Interest rate)` `= 3.6/12`
    `= 0.3text(% per month)`

 

a.ii.    `V_0` `= 3500`
  `V_1`  `= 3500 xx 1.003 + 180`
  `V_2`  `= V_1 xx 1.003 + 180`
  `vdots`   
  `V_(n + 1)`  `= V_n xx 1.003 + 180` 

  
`:.\ text(Recurrence relationship:)`

`V_0 = 3500,qquadV_(n + 1) = V_n xx 1.003 + 180`
  

b.    `V_1` `= 3500 xx 1.003 + 180 = $3690.50`
  `V_2` `= 3690.50 xx 1.003 + 180 = $3881.5715`
`V_3` `= 3881.5715 xx 1.003 + 180` `= $4073.216…`
    `= $4073.22\ \ text{(nearest cent)}`

CORE, FUR2 SM-Bank 1

Joe buys a tractor under a buy-back scheme. This scheme gives Joe the right to sell the tractor back to the dealer through either a flat rate depreciation or unit cost depreciation.

  1. The recurrence relation below can be used to calculate the price Joe sells the tractor back to the dealer `(P_n)`, based on the flat rate depreciation, after `n` years
     
    `qquadP_0 = 56\ 000,qquadP_n = P_(n-1)-7000`
     

    1. Write the general rule to find the value of `P_n` in terms of `n`.?   (1 mark)
    2. Hence or otherwise, find the time it will take Joe's tractor to lose half of its value.   (1 mark)
  2. Joe uses the unit cost method to depreciate his tractor, he depreciates $2.75 per kilometre travelled.
    1. How many kilometres does Joe's tractor need to travel for half its value to be depreciated? Round your answer to the nearest kilometre?   (1 mark)
    2. Joe's tractor travels, on average, 2500 kilometres per year. Which method, flat rate depreciation or unit cost depreciation, will result in the greater annual depreciation? Write down the greater depreciation amount correct to the nearest dollar.   (1 mark)

Show Answers Only

  1. i.  `P_n = 56\ 000-7000n`
    ii. `4\ text(years)`
  2. i. `10\ 182\ text{km  (nearest km)}`
    ii. `text(The flat rate depreciation results in an extra)`
         `text($125 depreciation each year.)`

Show Worked Solution

a.i.    `P_1` `= P_0-7000`
  `P_2` `= P_0-7000-7000`
    `= 56\ 000-7000 xx 2`
  `vdots`  
  `P_n`  `= 56\ 000-7000n` 

 

a.ii.    `text(Depreciated value)` `= 56\ 000 ÷ 2=$28\ 000`

`text(Find)\ n,`

`28\ 000` `= 56\ 000-7000n`
`7000n` `= 28\ 000`
`:. n` `= 4\ text(years)`

 

b.i.    `text(Distance travelled)` `= ((56\ 000-28\ 000))/2.75`
    `= 10\ 181.81…`
    `= 10\ 182\ text{km  (nearest km)}`

  
b.ii.   `text(Annual depreciation of unit cost)`

`= 2500 xx $2.75`

`= $6875`

`text(Annual flat rate depreciation = $7000)`

`text(Difference)\ = 7000-6875 = $125`
 

`:.\ text(The flat rate depreciation results in an extra)`

 `text($125 depreciation each year.)`

NETWORKS, FUR2 2016 VCAA 3

A new skateboard park is to be built in Beachton.

This project involves 13 activities, `A` to `M`.

The directed network below shows these activities and their completion times in days.
 


 

  1. Determine the earliest start time for activity `M`.   (1 mark)

  2. The minimum completion time for the skateboard park is 15 days.

     

    Write down the critical path for this project.   (1 mark)

  3. Which activity has a float time of two days?   (1 mark)

  4. The completion times for activities `E, F, G, I` and `J` can each be reduced by one day.

     

    The cost of reducing the completion time by one day for these activities is shown in the table below.
     

     

       

     

    What is the minimum cost to complete the project in the shortest time possible?   (1 mark)

  5. The original skateboard park project from part (a), before the reduction of time in any activity, will be repeated at another town named Campville, but with the addition of one extra activity.

     

    The new activity, `N`, will take six days to complete and has a float time of one day.

     

    Activity `N` will finish at the same time as the project.

     

     i.  Add activity `N` to the network below.   (1 mark) 


      
    ii.  What is the latest start time for activity `N`?   (1 mark)

Show Answers Only
  1. `11\ text(days)`
  2. `AEIK`
  3. `text(Activity)\ H`
  4. `text(Minimum cost of $2000 when activity)\ I\ text(is reduced by 1 day.)`

    2. `9\ text(days from the start)`
Show Worked Solution
a.    `text(EST)` `= 1 + 4 + 6`
    `= 11\ text(days)`

  
b.   `text(Critical Path:)\ AEIK`

♦♦ Mean mark part (c) 37%, part (d) 21%.
MARKER’S COMMENT: In part (d), `ADK` cannot be crashed, therefore shortest duration is 14 days. Activity `I` is cheapest to reduce.
  

c.   `text(Activity)\ H`
  

d.   `text(Minimum days to complete is 14 days by reducing)`

`text(either)\ E\ text(or)\ I\ text(by 1 day.)`

`:. text(Minimum cost of $2000 when activity)\ I\ text(is reduced)`

`text(by 1 day.)`
  

e.i.   

♦♦ Mean mark part (e)(i) 21%, (e)(ii) 27%.
MARKER’S COMMENT: In (e)(ii), activity `N` must have an arrow on it.
  

e.ii.    `text(LST)` `=\ text(critical path time − 6 days)`
    `= 15-6`
    `= 9\ text(days from the start.)`

NETWORKS, FUR2 2016 VCAA 2

The suburb of Alooma has a skateboard park with seven ramps.

The ramps are shown as vertices `T`, `U`, `V`, `W`, `X`, `Y` and `Z` on the graph below.
 

 

The tracks between ramps `U` and `V` and between ramps `W` and `X` are rough, as shown on the graph above.

  1. Nathan begins skating at ramp `W` and follows an Eulerian trail.

     

    At which ramp does Nathan finish?   (1 mark)

  2. Zoe begins skating at ramp `X` and follows a Hamiltonian path.

     

    The path she chooses does not include the two rough tracks.

     

    Write down a path that Zoe could take from start to finish.   (1 mark)

  3. Birra can skate over any of the tracks, including the rough tracks.

     

    He begins skating at ramp `X` and will complete a Hamiltonian cycle.

     

    In how many ways could he do this?   (1 mark) 

Show Answers Only
  1. `U`
  2. `XYTUZVW`
    `XYTUZWV`
  3. `4\ text(ways)`
Show Worked Solution

a.   `text{The Eulerian trail (visits each edge exactly once):}`

“XYZWVZUYTU`

`:. text(Finishes at ramp)\ U.`
  

b.   `text{Hamiltonian Paths (touch each vertex exactly once):}`

`XYTUZVW`

`XYTUZWV`
  

c.   `text(Hamiltonian cycles:)`

♦♦ Mean mark 31%.

`XYTUZVWX`

`XYTUVZWX`

`text(These two cycles can be reversed)`

`text(to add two more possibilities.)`

`XWVZUTYX`

`XWZVUTYX`

`:. 4\ text(ways.)`

NETWORKS, FUR2 2016 VCAA 1

A map of the roads connecting five suburbs of a city, Alooma (`A`), Beachton (`B`), Campville (`C`), Dovenest (`D`) and Easyside (`E`), is shown below.
 


  

  1. Starting at Beachton, which two suburbs can be driven to using only one road?   (1 mark)

A graph that represents the map of the roads is shown below.
 


 

One of the edges that connects to vertex `E` is missing from the graph.

  1.  i. Add the missing edge to the graph above.   (1 mark)

    (Answer on the graph above)
  2. ii. Explain what the loop at `D` represents in terms of a driver who is departing from Dovenest.   (1 mark)

Show Answers Only

a.    `text(Alooma and Easyside.)`

b.i. 

b.ii. `text(The loop represents that a driver can take a route out)`

`text(of Dovenest and return home without going through another)`

`text(suburb or turning back.)`

Show Worked Solution

a.   `text(Alooma and Easyside.)`

 

b.i.   

`text(Draw a third edge between Easyside and Dovenest.)`

 

b.ii. `text(The loop represents that a driver can take a)`

♦♦ Mean mark 30%.

`text(route out of Dovenest and return home without)`

`text(going through another suburb or turning back.)`

GRAPHS, FUR2 2016 VCAA 3

A company produces two types of hockey stick, the ‘Flick’ and the ‘Jink’.

Let `x` be the number of Flick hockey sticks that are produced each month.

Let `y` be the number of Jink hockey sticks that are produced each month.

Each month, up to 500 hockey sticks in total can be produced.

The inequalities below represent constraints on the number of each hockey stick that can be produced each month.

Constraint 1 `x >= 0` Constraint 2 `y >= 0`
Constraint 3 `x + y <= 500` Constraint 4 `y <= 2x`
  1. Interpret Constraint 4 in terms of the number of Flick hockey sticks and the number of Jink hockey sticks produced each month.  (1 mark)

There is another constraint, Constraint 5, on the number of each hockey stick that can be produced each month.

Constraint 5 is bounded by Line `A`, shown on the graph below.

The shaded region of the graph contains the points that satisfy constraints 1 to 5.

  1. Write down the inequality that represents Constraint 5.  (1 mark)

The profit, `P`, that the company makes from the sale of the hockey sticks is given by

`P = 62x + 86y`

  1. Find the maximum profit that the company can make from the sale of the hockey sticks.  (1 mark)
  2. The company wants to change the selling price of the Flick and Jink hockey sticks in order to increase its maximum profit to $42 000.

    All of the constraints on the numbers of Flick and Jink hockey sticks that can be produced each month remain the same.

    The profit, `Q`, that is made from the sale of hockey sticks is now given by

    `qquadQ = mx + ny`

     

    The profit made on the Flick hockey sticks is `m` dollars per hockey stick.

    The profit made on the Jink hockey sticks is `n` dollars per hockey stick.

    The maximum profit of $42 000 is made by selling 400 Flick hockey sticks and 100 Jink hockey sticks.

    What are the values of `m` and `n`?  (2 marks)

Show Answers Only
  1. `text(Constraint 4 means the number of Jink sticks produced each)`
    `text(month is less than or equal to twice the number of flick)`
    `text(sticks produced each month.)`
  2. `y <= 300`
  3. `$38\ 200`
  4. `84`
Show Worked Solution

a.   `text(Constraint 4 means the number of Jink sticks)`

♦♦♦ Mean mark 25%.

`text(produced each month is less than or equal to)`

`text(twice the number of flick sticks produced each)`

`text(month.)`

 

b.   `y <= 300`

 

c.   `text(From the equation, 1 Jink stick produces a)`

`text(higher profit than 1 Flick stick.)`

`text(Maximum profit at)\ (200,300)`

`P` `= (62 xx 200) + (86 xx 300)`
  `= $38\ 200`

 

d.   `Q = mx + ny`

♦♦♦ Mean mark 7%.
MARKER’S COMMENT: Very few students were able to identify the need for the sliding line concept and execute it correctly in this question.

`text(Max profit at)\ (400,100)`

`(400,100)\ text(lies on)\ x + y = 500`

`=>\ text(Max profit equation has the same)`

`text(gradient as the profit line.)`

`=> m = −1, m = n`

`text(Using the maximum profit = $42 000,)`

`400m + 100n` `= 42\ 000`
`500m` `= 42\ 000`
`m` `= (42\ 000)/500`
  `= 84`

`:. m = n = 84`

GRAPHS, FUR2 2016 VCAA 2

The bonus money is provided by a company that manufactures and sells hockey balls.

The cost, in dollars, of manufacturing a certain number of balls can be found using the equation

cost = 1200 + 1.5 × number of balls

  1. How many balls would be manufactured if the cost is $1650?  (1 mark)
  2. On the grid below, sketch the graph of the relationship between the manufacturing cost and the number of balls manufactured.  (1 mark)

     

  3. The company will break even on the sale of hockey balls when it manufactures and sells 200 hockey balls.

     

    Find the selling price of one hockey ball.  (1 mark) 

Show Answers Only
  1. `300`

  3. `$7.50\ text(per ball)`
Show Worked Solution
a.    `1200 + 1.5 xx n` `= 1650`
  `:. n` `= ((1650 – 1200))/1.5`
    `= 300`

 

b.   

 

c.   `text(When)\ n = 200,`

`C` `= 1200 + 1.5 xx 200`
  `= 1500`

 

`:.\ text(Selling price if break even)`

`= 1500/200`

`= $7.50\ text(per ball)`

GRAPHS, FUR2 2016 VCAA 1

Maria is a hockey player. She is paid a bonus that depends on the number of goals that she scores in a season.

The graph below shows the value of Maria’s bonus against the number of goals that she scores in a season.

  1. What is the value of Maria’s bonus if she scores seven goals in a season?  (1 mark) 
  2. What is the least number of goals that Maria must score in a season to receive a bonus of $2500?  (1 mark)

Another player, Bianca, is paid a bonus of $125 for every goal that she scores in a season.

  1. What is the value of Bianca’s bonus if she scores eight goals in a season?  (1 mark)
  2. At the end of the season, both players have scored the same number of goals and receive the same bonus amount.

     

    How many goals did Maria and Bianca each score in the season?  (1 mark)

Show Answers Only
  1. `$1500`
  2. `15`
  3. `$1000`
  4. `text(28 goals)`
Show Worked Solution

a.   `$1500`

 

b.   `15`

 

c.    `text(Bonus)` `= 8 xx 125`
    `= $1000`

 

d.   `text(Draw the graph of Bianca’s payments on)`

`text(the same graph.)`

`text(The intersection is where both players)`

`text(receive the same bonus amount.)`

`:.\ text(Maria and Bianca each score 28 goals.)`

MATRICES, FUR2 2016 VCAA 1

A travel company arranges flight (`F`), hotel (`H`), performance (`P`) and tour (`T`) bookings.

Matrix `C` contains the number of each type of booking for a month.

`C = [(85),(38),(24),(43)]{:(F),(H),(P),(T):}`

  1. Write down the order of matrix `C`.   (1 mark)

A booking fee, per person, is collected by the travel company for each type of booking.

Matrix `G` contains the booking fees, in dollars, per booking.

`{:((qquadqquadquadF,\ H,\ P,\ T)),(G = [(40,25,15,30)]):}`

  1.  i. Calculate the matrix product  `J = G × C`.   (1 mark)

  2. ii. What does matrix `J` represent?   (1 mark) 

Show Answers Only
  1. `4 xx 1`
    1. `[6000]`
    2. `J\ text(represents the total booking fees for the travel)`
      `text(company in the given month.)`
Show Worked Solution

a.   `text(Order:)\ 4 xx 1`
 

b.i.    `J = [(40,25,15,30)][(85),(38),(24),(43)]= [6000]`

 
b.ii.  `J\ text(represents the total booking fees for the)`

♦ Mean mark 42%.

 `text(travel company in the given month.)`

GEOMETRY, FUR2 2016 VCAA 4

During a game of golf, Salena hits a ball twice, from `P` to `Q` and then from `Q` to `R`.

The path of the ball after each hit is shown in the diagram below.

After Salena’s first hit, the ball travelled 80 m on a bearing of 130° from point `P` to point `Q`.

After Salena’s second hit, the ball travelled 100 m on a bearing of 054° from point `Q` to point `R`.

  1. Another ball is hit and travels directly from `P` to `R`.

     

    Use the cosine rule to find the distance travelled by this ball.

     

    Round your answer to the nearest metre.  (2 marks)

  2. What is the bearing of `R` from `P`?

     

    Round your answer to the nearest degree.  (1 mark) 

Show Answers Only
  1. `142\ text{m  (nearest m)}`
  2. `0.87^@\ \ (text(nearest degree))`
Show Worked Solution
a.   
`PR^2` `= PQ^2 + QR^2 – 2 xx PQ xx QR xx cos104^@`
  `= 80^2 + 100^2 – 2 xx 80 xx 100 xx cos104^@`
  `= 20\ 270.75…`
  `= 142.37…`
  `= 142\ text{m  (nearest m)}`

 

b.   `text(Find)\ angle RPQ.`

`text(Using the sin rule),`

`(sin angleRPQ)/100` `= (sin104^@)/142`
`sin angle RPQ` `= (100 xx sin104^@)/142`
  `= 0.683…`
`angle RPQ` `= 43.1^@\ \ (text(1 d.p.))`

 

`:. text(Bearing of)\ R\ text(from)\ P`

`= 130 – 43.1`

`= 086.9`

`= 087^@\ \ (text(nearest degree))`

GEOMETRY, FUR2 2016 VCAA 2

Salena practises golf at a driving range by hitting golf balls from point  `T`.

The first ball that Salena hits travels directly north, landing at point  `A`.

The second ball that Salena hits travels 50 m on a bearing of 030°, landing at point  `B`.

The diagram below shows the positions of the two balls after they have landed.
  

  1. How far apart, in metres, are the two golf balls?  (1 mark)
  2. A fence is positioned at the end of the driving range.

     

    The fence is 16.8 m high and is 200 m from the point  `T`.


     
     
    What is the angle of elevation from  `T`  to the top of the fence?

     

    Round your answer to the nearest degree.  (1 mark) 

Show Answers Only
  1. `25\ text(m)`
  2. `5^@\ text{(nearest degree)}`
Show Worked Solution

a.   `text(Let)\ \ d\ text(= distance apart)`

`sin30^@` `= d/50`
`:. d` `= 50 xx sin 30^@`
  `= 25\ text(m)`

 

b.   `text(Let)\ \ x^@\ text(= angle of elevation from)\ T`

`tanx` `= 16.8/200`
  `= 0.084`
`:. x` `= 4.801…`
  `= 5^@\ text{(nearest degree)}`

CORE, FUR2 2016 VCAA 5

Ken has opened a savings account to save money to buy a new caravan.

The amount of money in the savings account after `n` years, `V_n`, can be modelled by the recurrence relation shown below.

`V_0 = 15000, qquad qquad qquad V_(n + 1) = 1.04 xx V_n`

  1. How much money did Ken initially deposit into the savings account?  (1 mark)

  2. Use recursion to write down calculations that show that the amount of money in Ken’s savings account after two years, `V_2`, will be $16 224.  (1 mark)

  3. What is the annual percentage compound interest rate for this savings account?  (1 mark)

  4. The amount of money in the account after `n` years, `Vn` , can also be determined using a rule.
    i.     Complete the rule below by writing the appropriate numbers in the boxes provided.   (1 mark)

    `V_n =` 
     
    		 `­^n xx`
     
  5. ii. How much money will be in Ken’s savings account after 10 years?   (1 mark)

Show Answers Only
  1. `$15000`
  2. `text(Proof)\ text{(See Worked Solutions)}`
  3. `4 text(%)`
  4. i. `text(See Worked Solutions)`
    ii. `$22\ 203.66` 
Show Worked Solution
a.    `text(Initial deposit)` `= V_0`
    `= $15\ 000`
b.    `V_0` `= $15\ 000`
  `V_1` `= 1.04 xx 15\ 000`
    `= $15\ 600`
  `V_2` `= 1.04 xx 15\ 600`
    `= $16\ 224\ text(… as required.)`

MARKER’S COMMENT: (b) Stating `V_2 =1.04^2 xx 15\ 600` `=16\ 224` is not using recursion as required here and did not gain a mark.
c.    `text(Annual compound interest)` `= 0.04 xx 100`
    `= 4 text(%)`

 

d.i.   `V_n` `= 1.04^n xx V_0`
d.ii.    `V_10` `= 1.04^10 xx 15\ 000`
    `= $22\ 203.664…`
    `= $22\ 203.66\ text{(nearest cent)}`

♦ Mean mark (d)(ii) 47%.
MARKER’S COMMENT: Rounding to $22 203.70 lost a mark!

CORE, FUR2 2016 VCAA 3

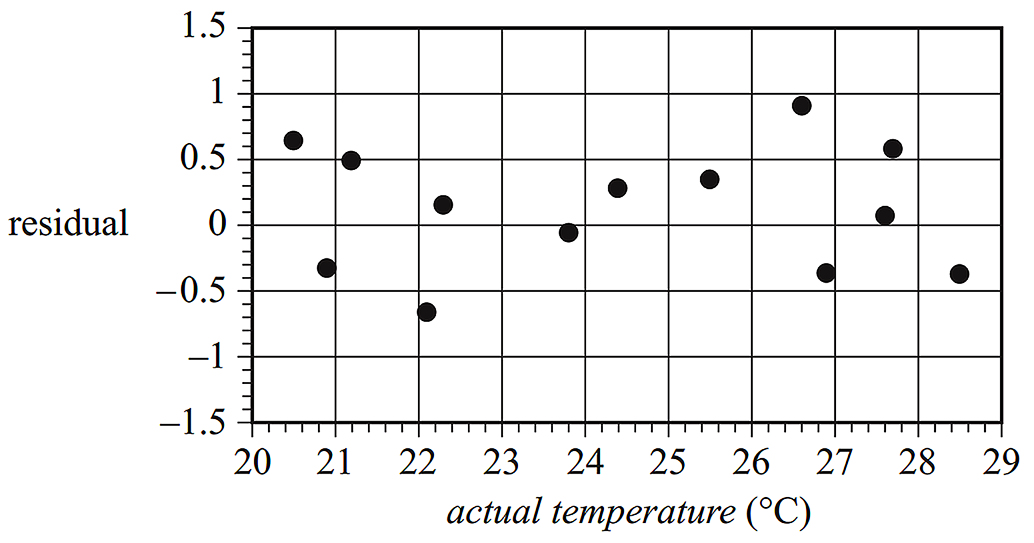
The data in the table below shows a sample of actual temperatures and apparent temperatures recorded at a weather station. A scatterplot of the data is also shown.

The data will be used to investigate the association between the variables apparent temperature and actual temperature.
 

  1. Use the scatterplot to describe the association between apparent temperature and actual temperature in terms of strength, direction and form.   (1 mark)

  2.  i. Determine the equation of the least squares line that can be used to predict the apparent temperature from the actual temperature.
  3. Write the values of the intercept and slope of this least squares line in the appropriate boxes provided below.
  4. Round your answers to two significant figures.   (3 marks)
     apparent temperature `=`    
 
 `+`  
 
 `xx`   actual temperature
  1. ii. Interpret the intercept of the least squares line in terms of the variables apparent temperature and actual temperature.   (1 mark)

  2. The coefficient of determination for the association between the variables apparent temperature and actual temperature is 0.97
  3. Interpret the coefficient of determination in terms of these variables.   (1 mark)

  4. The residual plot obtained when the least squares line was fitted to the data is shown below.
     
     
  5.  i. A residual plot can be used to test an assumption about the nature of the association between two numerical variables.
  6.     What is this assumption?   (1 mark)
  7. ii. Does the residual plot above support this assumption? Explain your answer.   (1 mark)
Show Answers Only

a.   `text(Strong, positive and linear)`

b.i.  `text(apparent temperature) = -1.7 xx 0.94 xx text(actual temperature)`

b.ii.  `text(When actual temperature is 0°C, on average,)`

`text(the apparent temperature is)\ − 1.7^@\text(C.)`

c.  `text(97% of the variation in the apparent temperature can be explained)`

`text(by the variation in the actual temperature.)`

d.i.  `text(There is a linear relationship between the two variables.)`

d.ii.  `text(The random pattern supports the assumption.)`

`text{(Students should refer to randomness or a lack of pattern}`

`text{explicitly here).}`

Show Worked Solution

a.   `text(Strong, positive and linear)`
 

b.i.   `text(By calculator:)`

`text(apparent temperature) = -1.7 xx 0.94 xx text(actual temperature)`
 

♦♦ Mean mark of part (b)(ii) – 28%.
MARKER’S COMMENT: “the predicted apparent temp is -1.7°C” also gained a mark.
b.ii.    `text(When actual temperature is 0°C, on average,)`
 

`text(the apparent temperature is)\ − 1.7^@\text(C.)`

 

♦ Mean mark 49%.
IMPORTANT: Any mention of causality loses a mark!

c.  `text(97% of the variation in the apparent temperature can be explained)`

`text(by the variation in the actual temperature.)`
  

d.i.  `text(There is a linear relationship between the two variables.)`

♦ Mean mark of both parts of (d) was 46%.

d.ii.  `text(The random pattern supports the assumption.)`

`text{(Students should refer to randomness or a lack of pattern}`

`text{explicitly here).}`

CORE, FUR2 2016 VCAA 2

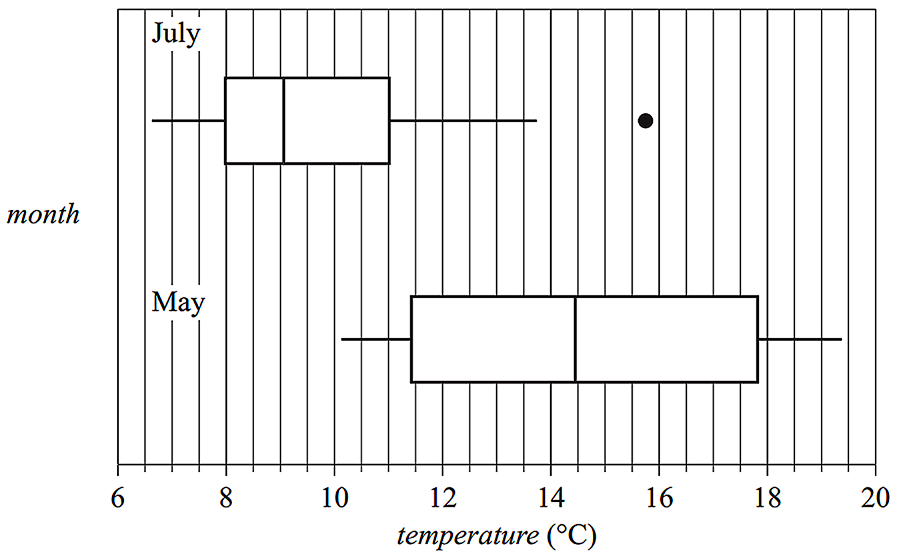
A weather station records daily maximum temperatures.

  1. The five-number summary for the distribution of maximum temperatures for the month of February is displayed in the table below.

 

  1. There are no outliers in this distribution.
  2.  i. Use the five-number summary above to construct a boxplot on the grid below.   (1 mark)

 

  1. ii. What percentage of days had a maximum temperature of 21°C, or greater, in this particular February?   (1 mark)

  2. The boxplots below display the distribution of maximum daily temperature for the months of May and July.
     

  3.   i. Describe the shapes of the distributions of daily temperature (including outliers) for July and for May.   (1 mark)

  4.  ii. Determine the value of the upper fence for the July boxplot.   (1 mark)

  5. iii. Using the information from the boxplots, explain why the maximum daily temperature is associated with the month of the year. Quote the values of appropriate statistics in your response.   (1 mark)

Show Answers Only
a.i.   

a.ii.   `text(75%)`

b.i.    `text(July – Positively skewed with an outlier.)`
  `text(May – Symmetrical with no outliers.)`

b.ii.  `15.5^@\text(C)`

b.iii. `text{The median temperature in May (14.5°C)}`

`text(differs from the median temperature in July)`

`text{(just over 9°C). This difference is why the}`

`text(maximum daily temperature is associated)`

`text(with the month.)`

Show Worked Solution
a.i.   

a.ii.   `text(75%)`

MARKER’S COMMENT: Incorrect May descriptors included “evenly or normally distributed”, “bell shaped” and “symmetrically skewed.”
b.i.    `text(July – Positively skewed with an outlier.)`
  `text(May – Symmetrical with no outliers.)`

 

b.ii.    `text(Upper fence)` `= Q_3 + 1.5 xx IQR`
    `= 11 + 1.5 xx (11 – 8)`
    `= 11 + 4.5`
    `= 15.5^@\text(C)`
♦♦ Mean mark (b)(iii) – 30%.
COMMENT: Refer to the difference in medians. Just quoting the numbers was not enough to gain a mark here.

b.iii. `text{The median temperature in May (14.5°C)}`

`text(differs from the median temperature in July)`

`text{(just over 9°C). This difference is why the}`

`text(maximum daily temperature is associated)`

`text(with the month.)`

CORE, FUR2 2016 VCAA 1

The dot plot below shows the distribution of daily rainfall, in millimetres, at a weather station for 30 days in September.
 

 

  1. Write down the
  2.  i. range   (1 mark)

  3. ii. median   (1 mark)

  1. Circle the data point on the dot plot above that corresponds to the third quartile `(Q_3).`   (1 mark)

  2. Write down the
  3.  i. the number of days on which no rainfall was recorded.   (1 mark)

  4. ii. the percentage of days on which the daily rainfall exceeded 12 mm.   (1 mark)

  1. Use the grid below to construct a histogram that displays the distribution of daily rainfall for the month of September. Use interval widths of two with the first interval starting at 0.   (2 marks) 

  

Show Answers Only
    1. `17.8\ text(mm)`
    2. `0`
  2. `text(See Worked Solutions)`

     

    1. `16\ text(days)`
    2. `10\text(%)`
  4. `text(See Worked Solutions)`
Show Worked Solution
a.i.    `text(Range)` `=\ text(High) – text(Low)`
    `= 17.8 – 0`
    `= 17.8\ text(mm)`
     

a.ii.   `text(30 data points)`

`text(Median)` `= text{15th + 16th}/2`
  `= 0`

 

b.   

 

c.i.   `16\ text(days)`

c.ii.    `text(Percentage)` `= 3/30 xx 100`
    `= 10\ text(%)`

 

d.   

NETWORKS, FUR1 2016 VCAA 6-7 MC

The directed graph below shows the sequence of activities required to complete a project.

All times are in hours.
 

 
Part 1

The number of activities that have exactly two immediate predecessors is

  1. 0
  2. 1
  3. 2
  4. 3
  5. 4

 
Part 2

There is one critical path for this project.

Three critical paths would exist if the duration of activity

  1. I were reduced by two hours.
  2. E were reduced by one hour.
  3. G were increased by six hours.
  4. K were increased by two hours.
  5. F were increased by two hours. 
Show Answers Only

`text(Part 1:)\ C`

`text(Part 1:)\ B`

Show Worked Solution

`text(Part 1)`

`I\ text(and)\ J`

`=> C`

 

`text(Part 2)`

♦ Mean mark of Part 2: 45%.

`text(The possible paths are:)`

`ADIL – 19\ text(mins)`

`BEIL – 20\ text(mins)`

`BFJL – 17\ text(mins)`

`CGJL – 13\ text(mins)`

`CHKL – 19\ text(mins)`

`text(If)\ E\ text(were reduced by 1 hour,)\ BEIL\ text(will)`

`text{take 19 minutes (i.e. 3 critical paths of 19}`

`text{minutes would exist).}`

`=> B`

NETWORKS, FUR1 2016 VCAA 2 MC

The following directed graph shows the flow of water, in litres per minute, in a system of pipes connecting the source to the sink.
 

 
The maximum flow, in litres per minute, from the source to the sink is

  1. `10`
  2. `14`
  3. `18`
  4. `20`
  5. `22`
Show Answers Only

`C`

Show Worked Solution
`text(Maximum flow)` `= 2 + 10 + 6`
  `= 18\ \ text(litres/minute)`

`=> C`

GRAPHS, FUR1 2016 VCAA 4 MC

The point  (3, –2)  satisfies the inequality

  1. `y >= 0`
  2. `y >= 2/3 x`
  3. `−2 < x < 3`
  4. `y < 5 -x`
  5. `y > x - 5` 
Show Answers Only

`D`

Show Worked Solution

`text(Consider option)\ D,`

`y` `< 5 – x`
`−2` `< 5 – 3`
`−2` `< 2\ \ \ text{(correct)}`

`=> D`

GEOMETRY, FUR1 2016 VCAA 6 MC

Marcus is on the opposite side of a large lake from a horse and its stable. The stable is 150 m directly east of the horse. Marcus is on a bearing of 170° from the horse and on a bearing of 205° from the stable.

The straight-line distance, in metres, between Marcus and the horse is closest to

  1.   `45`
  2.   `61`
  3.   `95`
  4. `192`
  5. `237`
Show Answers Only

`E`

Show Worked Solution

`text(Using the sine rule,)`

`(HM)/(sin65^@)` `= (HS)/(sin35^@)`
`HM` `= (150 xx sin 65^@)/(sin35^@)`
  `= 237.01…\ text(m)`

`=> E`

GEOMETRY, FUR1 2016 VCAA 5 MC

A water tank in the shape of a cylinder with a hemispherical top is shown below.

The volume of water that this tank can hold, in cubic metres, is closest to

  1.   `80`
  2.   `88`
  3.   `96`
  4. `105`
  5. `121`
Show Answers Only

`A`

Show Worked Solution
`V` `=\ text(cylinder + half sphere)`
  `= pir^2h + 1/2 xx 4/3 xx pir^3`
  `= pi xx 2^2 xx 5 + 1/2 xx 4/3 xx pi xx 2^3`
  `= 79.587…`
  `~~ 80\ text(m³)`

`=> A`

GEOMETRY, FUR1 2016 VCAA 3 MC

The diagram above shows the position of three cities, A, B and C.

According to the diagram

  1. A is located on a longitude of 60° N
  2. B is located on a longitude of 20° E
  3. C is located on a longitude of 40° S
  4. A and B are located on the same line of longitude
  5. A and C are located on the same line of longitude 
Show Answers Only

`E`

Show Worked Solution

`A\ text(and)\ C\ text(are on the same line)`

`text(of longitude.)`

`text(All other statements can be shown)`

`text(to be false.)`

`=> E`

MATRICES, FUR1 2016 VCAA 3 MC

The matrix equation below represents a pair of simultaneous linear equations.
 

`[(12,9),(m,3)][(x),(y)] = [(6),(6)]`
 

These simultaneous linear equations have no unique solution when `m` is equal to

  1. `−4`
  2. `−3`
  3.     `0`
  4.     `3`
  5.     `4`
Show Answers Only

`E`

Show Worked Solution
`[(x),(y)]` `= [(12,9),(m,3)]^(−1)[(6),(6)]`
  `= 1/((12 xx 3) – (9 xx m)) [(3,−9),(−m,12)][(6),(6)]`

 

`text(No unique solution occurs when)\ \ Δ=0 :`

`(12 xx 3) – (9 xx m)` `= 0`
`9m` `= 36`
`m` `= 4`

`=> E`

CORE, FUR1 2016 VCAA 20 MC

Consider the recurrence relation below.

`V_0 = 10\ 000,\ \ \ \ \ V_(n + 1) = 1.04 V_n + 500`

This recurrence relation could be used to model

  1. a reducing balance depreciation of an asset initially valued at $10 000.
  2. a reducing balance loan with periodic repayments of $500.
  3. a perpetuity with periodic payments of $500 from the annuity.
  4. an annuity investment with periodic additions of $500 made to the investment.
  5. an interest-only loan of $10 000. 
Show Answers Only

`D`

Show Worked Solution

`text(Each period, the model increases)`

♦ Mean mark 50%.

`text(the previous value by 4% and then)`

`text(adds 500 to the total.)`

`=> D`

CORE, FUR1 2016 VCAA 19 MC

The purchase price of a car was $26 000.

Using the reducing balance method, the value of the car is depreciated by 8% each year.

A recurrence relation that can be used to determine the value of the car after `n` years, `C_n` , is

  1. `C_0 = 26\ 000,\ \ \ C_(n + 1) = 0.92 C_n`
  2. `C_0 = 26\ 000,\ \ \ C_(n + 1) = 1.08 C_n`
  3. `C_0 = 26\ 000,\ \ \ C_(n + 1) = C_n + 8`
  4. `C_0 = 26\ 000,\ \ \ C_(n + 1) = C_n - 8`
  5. `C_0 = 26\ 000,\ \ \ C_(n + 1) = 0.92 C_n - 8`
Show Answers Only

`A`

Show Worked Solution

`C_0 = 26\ 000\ (text(given))`

`text(After 1 year:)`

`C_1` `= C_0 – (8text(%) xx C_0)`
  `= 0.92 C_0`

 
`text(After 2 years:)`

`C_2 = 0.92C_1`

`vdots`

`:.\ text(After)\ n\ text(years,)`

`C_(n + 1) = 0.92 C_n`

`=> A`

CORE, FUR1 2016 VCAA 14-16 MC

The table below shows the long-term average of the number of meals served each day at a restaurant. Also shown is the daily seasonal index for Monday through to Friday.

 

Part 1

The seasonal index for Wednesday is 0.84

This tells us that, on average, the number of meals served on a Wednesday is

  1. 16% less than the daily average.
  2. 84% less than the daily average.
  3. the same as the daily average.
  4. 16% more than the daily average.
  5. 84% more than the daily average.

 

Part 2

Last Tuesday, 108 meals were served in the restaurant.

The deseasonalised number of meals served last Tuesday was closest to

  1.   `93`
  2. `100`
  3. `110`
  4. `131`
  5. `152`

 

Part 3

The seasonal index for Saturday is closest to

  1. `1.22`
  2. `1.31`
  3. `1.38`
  4. `1.45`
  5. `1.49`
Show Answers Only

`text(Part 1:)\ A`

`text(Part 2:)\ E`

`text(Part 3:)\ D`

Show Worked Solution

`text(Part 1)`

`1 – 0.84 = 0.16`

`:.\ text(A seasonal index of 0.84 tell us)`

`text(16% less meals are served.)`

`=> A`

 

`text(Part 2)`

`text{Deseasonalised number (Tues)}`

`= text(actual number)/text(seasonal index)`

`= 108/0.71`

`~~ 152`

`=> E`

 

`text(Part 3)`

`text(S)text(ince the same number of deseasonalised)`

`text(meals are served each day.)`

`text{S.I. (Sat)}/190` `= 1.10/145`
`text{S.I. (Sat)}` `= (1.10 xx 190)/145`
  `= 1.44…`

`=> D`

CORE, FUR1 2016 VCAA 11-12 MC

The table below gives the Human Development Index (HDI) and the mean number of children per woman (children) for 14 countries in 2007.

A scatterplot of the data is also shown. 
 

 

Part 1

The scatterplot is non-linear.

A log transformation applied to the variable children can be used to linearise the scatterplot.

With HDI as the explanatory variable, the equation of the least squares line fitted to the linearised data is closest to

  1. log(children) = 1.1 – 0.0095 × HDI
  2. children = 1.1 – 0.0095 × log(HDI)
  3. log(children) = 8.0 – 0.77 × HDI
  4. children = 8.0 – 0.77 × log(HDI)
  5. log(children) = 21 – 10 × HDI

 

Part 2

There is a strong positive association between a country’s Human Development Index and its carbon dioxide emissions.

From this information, it can be concluded that

  1. increasing a country’s carbon dioxide emissions will increase the Human Development Index of the country.
  2. decreasing a country’s carbon dioxide emissions will increase the Human Development Index of the country.
  3. this association must be a chance occurrence and can be safely ignored.
  4. countries that have higher human development indices tend to have higher levels of carbon dioxide emissions.
  5. countries that have higher human development indices tend to have lower levels of carbon dioxide emissions.
Show Answers Only

`text(Part 1:)\ A`

`text(Part 2:)\ D`

Show Worked Solution

`text(Part 1)`

`=>A`

 

`text(Part 2)`

`text(A strong positive association does not mean)`

`text(an increase in one variable causes an increase)`

`text(in the other.)`

`=> D`

CORE, FUR1 2016 VCAA 9-10 MC

The scatterplot below shows life expectancy in years (life expectancy) plotted against the Human Development Index (HDI) for a large number of countries in 2011.

A least squares line has been fitted to the data and the resulting residual plot is also shown.
 

The equation of this least squares line is

life expectancy = 43.0 + 0.422 × HDI

The coefficient of determination is  `r^2` = 0.875
 

Part 1

Given the information above, which one of the following statements is not true?

  1. The value of the correlation coefficient is close to 0.94
  2. 12.5% of the variation in life expectancy is not explained by the variation in the Human Development Index.
  3. On average, life expectancy increases by 43.0 years for each 10-point increase in the Human Development Index.
  4. Ignoring any outliers, the association between life expectancy and the Human Development Index can be described as strong, positive and linear.
  5. Using the least squares line to predict the life expectancy in a country with a Human Development Index of 75 is an example of interpolation.

 

Part 2

In 2011, life expectancy in Australia was 81.8 years and the Human Development Index was 92.9

When the least squares line is used to predict life expectancy in Australia, the residual is closest to

  1. `–0.6`
  2. `–0.4`
  3.    `0.4`
  4.  `11.1`
  5.  `42.6`
Show Answers Only

`text(Part 1:)\ C`

`text(Part 1:)\ B`

Show Worked Solution

`text(Part 1)`

`text(Consider option)\ C,`

`text(If HDI increases by 10,)`

`text(Increase in life expectancy)`

`= 0.422 xx 10`

`= 4.22\ text(years)`

`!= 43\ text(years)`

`=> C`

 

`text(Part 2)`

`text(Predicted life expectancy)`

`= 43.0 + 0.422 xx 92.90`

`= 82.20…`

`:.\ text(Residual)` `= 81.8 – 82.20…`
  `= −0.40…`

`=> B`

CORE, FUR1 2016 VCAA 6-7 MC

Part 1

The histogram below shows the distribution of the number of billionaires per million people for 53 countries.
 

Using this histogram, the percentage of these 53 countries with less than two billionaires per million people is closest to

  1. `text(49%)`
  2. `text(53%)`
  3. `text(89%)`
  4. `text(92%)`
  5. `text(98%)`

 

Part 2

The histogram below shows the distribution of the number of billionaires per million people for the same 53 countries as in Part 1, but this time plotted on a `log_10` scale.
 

Based on this histogram, the number of countries with one or more billionaires per million people is

  1.   `text(1)`
  2.   `text(3)`
  3.   `text(8)`
  4.   `text(9)`
  5. `text(10)`
Show Answers Only

`text(Part 1:)\ D`

`text(Part 1:)\ E`

Show Worked Solution

`text(Part 1)`

`text(Percentage with less than 2)`

`= text(countries with less than 2)/text(total countries)`

`= 49/((49 + 2 + 1 + 1))`

`= 49/53`

`~~ 92.4text(%)`

`=> D`

 

`text(Part 2)`

`text(Let)\ \ x=\ text(number of billionaires per million,)`

`text(Number of countries where)\ \ x >= 1,`

♦ Mean mark 45%.
MARKER’S COMMENT: On a `log_10` scale, 1 is plotted as 0 because `log_10\ 1 = 0`, or `10^0=1`

`=> log_10 x >= 0`

`:.\ text(Number of countries)`

`= 9 + 1`

`= 10`

`=> E`

CORE, FUR1 2016 VCAA 4-5 MC

The weights of male players in a basketball competition are approximately normally distributed with a mean of 78.6 kg and a standard deviation of 9.3 kg.

Part 1

There are 456 male players in the competition.

The expected number of male players in the competition with weights above 60 kg is closest to

  1.     `3`
  2.   `11`
  3.   `23`
  4. `433`
  5. `445`

 

Part 2

Brett and Sanjeeva both play in the basketball competition.

When the weights of all players in the competition are considered, Brett has a standardised weight of  `z` = – 0.96 and Sanjeeva has a standardised weight of  `z` = – 0.26

Which one of the following statements is not true?

  1. Brett and Sanjeeva are both below the mean weight for players in the basketball competition.
  2. Sanjeeva weighs more than Brett.
  3. If Sanjeeva increases his weight by 2 kg, he would be above the mean weight for players in the basketball competition.
  4. Brett weighs more than 68 kg.
  5. More than 50% of the players in the basketball competition weigh more than Sanjeeva 
Show Answers Only

`text(Part 1:)\ E`

`text(Part 2:)\ C`

Show Worked Solution

`text(Part 1)`

`text(Find)\ ztext(-score of 60 kg)`

`ztext(-score)` `= (x – barx)/s`
  `= (60 – 78.6)/9.3`
  `= −2`

 

 

`text(Players with weight above 60 kg)`

`= 97.5text(%) xx 456`

`= 445`

`=> E`

 

`text(Part 2)`

`text(Calculate the weight of each player:)`

`text(Brett)`

`−0.96` `= (x – 78.6)/9.3`
`x` `= (9.3 xx −0.96) + 78.6`
  `~~ 69.7\ text(kg)`

 
`text(Sanjeev)`

`−0.26` `= (x – 78.6)/9.3`
`x` `= (9.3 xx −0.26) + 78.6`
  `~~ 76.2\ text(kg)`

 
`text(Consider)\ C,`

`76.182 + 2 = 78.182 < 78.6`

`:. C\ text(is not true.)`

`=> C`

Number and Algebra, NAP-C1-20

Hillary is running a cooking class.

She has 31 students in the class and needs to give them 1 egg each for a recipe.

Eggs are sold in cartons of 12.

What is the least number of egg cartons that Hillary needs to buy? 

`1` `2` `3` `4`
 
 
 
 
Show Answers Only

`text(3 cartons)`

Show Worked Solution

`text(The number of cartons needed)`

`= 31 ÷ 12`

`= 2\ \ text(remainder  7)`

`:.\ text(Hillary needs to buy 3 egg cartons.)`

Number and Algebra, NAP-C1-10

Sandy has the exact coins below in her pocket.

She buys fruit for lunch that costs $1.75.

How much money does Sandy have left?

`$0.08` `$1.00` `$1.10` `$1.20`
 
 
 
 
Show Answers Only

`$1.20`

Show Worked Solution

`$1 xx 1 = $1`

`50¢ xx 3 = $1.50`

`20¢ xx 1 = 20¢`

`10¢ xx 2 = 20¢`

`5¢ xx 1 = 5¢`

 

`text(Total worth of coins)`

`= $1 + $1.50 + 20¢ + 20¢ + 5¢`

`= $2.95`

`:.\ text(Money left)` `= $2.95 – $1.75`
  `= $1.20`

Statistics, NAP-D1-21

Benson asked his friends what their favourite ice cream flavour was.

He recorded their answers in the table below but left off same labels.

Benson remembered that

  • strawberry was the least liked flavour
  • chocolate was the most liked flavour
  • vanilla was more liked than caramel

How many of Benson's friends liked caramel the most?

 
Show Answers Only

`8`

Show Worked Solution

`text(Using the graph and the information given,)`

`=>\ text(7 preferred strawberry,)`

`=>\ text(13 preferred chocolate.)`

`:.\ text(11 preferred vanilla and 8 liked caramel the most.)`

Number and Algebra, NAP-D1-15

Tori wrote this correct number sentence.

`19 + 31 = 50`

Which of these number sentences is also correct?

 
 `50 - 19 = 31`
 
 `50 + 31 = 19`
 
 `19 - 50 = 31`
 
 `31 + 50 = 19`
Show Answers Only

`50 – 19 = 31`

Show Worked Solution

`19+31=50`

`text(Deduct 19 from both sides,)`

`19+31-19` `=50-19`
`31` `=50-19`
`50 – 19` `=31`

Measurement, NAP-E1-20

Alison buys paper clips that come in three sizes, small, medium and large.

The picture shows the lengths of the small and large clips.

What could the length of the medium paper clip be?

`text(1 centimetre)` `text(5 centimetres)` `text(7 centimetres)` `text(11 centimetres)`
 
 
 
 
Show Answers Only

`text(5 centimetres)`

Show Worked Solution

`text(Small paper clip) = 6-1.5 = 4.5\ text(cm)`

`text(Large paper clip) = 16-9=7\ text(cm)`

 

`text(Among the choices given, only 5 cm is between)`

`text(4.5 cm and 7 cm.)`

 

`:.\ text(The medium paper clip could be 5 cm.)`

Number and Algebra, NAP-E1-15

Grace used sticks to create a pattern.

 

She used 4 sticks in her first shape, 7 sticks in her second shape and 10 sticks in her third shape.

How many sticks are needed for the next shape in Grace's pattern?

`9` `10` `11` `13`
 
 
 
 
Show Answers Only

`13`

Show Worked Solution

`text(Each shape adds an extra 3 sticks.)`

`=>\ text(Sticks in the next shape)`

`=10+3`

`=13`

Number and Algebra, NAP-G1-15 SA

Jonah's soccer team got oranges at half time.

The quarters of oranges were put in a container.
 

 

 
How many whole oranges were cut into quarters and put in the container?
Show Answers Only

`4`

Show Worked Solution

`text(There are 16 orange quarters in the container.)`

`=>\ text(Each orange is cut into 4 quarters.)`

`:.\ 4\ text(full oranges are needed.)`

Number and Algebra, NAP-F1-19

Syd is 15 years old. Barney is 23 years old.

Callum is older than Syd but younger than Barney.

Which of these could be Callum's age?

`8` `21` `26` `38`
 
 
 
 
Show Answers Only

`21`

Show Worked Solution

`text(Syd’s age) < text(Callum’s age) < text(Barney’s age)`

`15 < text(Callum) < 23`

`:.\ text(Callum’s age could be 21)`

Probability, NAP-F1-18

The weather report says there is 80% chance of rain tomorrow.

Which of these describes the chance of it raining tomorrow?

`text(impossible)` `text(unlikely)` `text(likely)` `text(certain)`
 
 
 
 
Show Answers Only

`text(likely)`

Show Worked Solution

`text(Anything over 50% chance is more likely than)`

`text(not of happening. Anything that is certain of)`

`text(happening must be 100% chance.)`

`:.\ text(80% chance is “likely”.)`