Which of the following correctly expresses `T` as the subject of `B = 2pi (R + T/2)`?
- `T = B/pi-2R`
- `T = B/pi-R`
- `T = 2R-B/pi`
- `T = B/(4pi)-R/2`
Aussie Maths & Science Teachers: Save your time with SmarterEd
Which of the following correctly expresses `T` as the subject of `B = 2pi (R + T/2)`?
`A`
| `B` | `= 2pi (R + T/2)` |
| `B/(2pi)` | `= R + T/2` |
| `T/2` | `= B/(2pi)-R` |
| `T` | `= B/pi-2R` |
`=> A`
A point `P` lies between a tree, 2 metres high, and a tower, 8 metres high. `P` is 3 metres away from the base of the tree.
From `P`, the angles of elevation to the top of the tree and to the top of the tower are equal.
What is the distance, `x`, from `P` to the top of the tower?
`D`
`text(Triangles are similar)\ \ text{(equiangular)}`
`text(In smaller triangle:)`
| `h^2` | `= 2^2 + 3^2` |
| `= 13` | |
| `h` | `= sqrt 13` |
| `x/sqrt13` | `= 8/2\ \ \ text{(sides of similar Δs in same ratio)}` |
| `x` | `= (8 sqrt 13)/2` |
| `= 14.422…` |
`=> D`
`B`
`text(Smallest angle is opposite smallest side.)`
| ` cos A` | `= (b^2 + c^2-a^2)/(2bc)` |
| `= (7^2 + 8^2-6^2)/(2 xx 7 xx 8)` | |
| `= 0.6875` | |
| `A` | `=cos ^(-1)(0.6875)` |
| `:.\ A` | `= 46.567…^@` |
`=> B`
In the diagram, `XR` bisects `/_PRQ` and `XY\ text(||)\ QR`.
Prove that `Delta XYR` is an isosceles triangle. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
`text(Proof)\ text{(See Worked Solutions)}`
Let `M` be the midpoint of `(-1, 4)` and `(5, 8)`.
Find the equation of the line through `M` with gradient `-1/2`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`x + 2y-14 = 0`
`(-1,4)\ \ \ (5,8)`
| `M` | `= ( (x_1 + x_2)/2, (y_1 + y_2)/2)` |
| `= ( (-1 + 5)/2, (4 + 8)/2)` | |
| `= (2, 6)` |
`text(Equation through)\ (2,6)\ text(with)\ m = -1/2`
| `y-y_1` | `= m (x-x_1)` |
| `y-6` | `= -1/2 (x-2)` |
| `2y-12` | `= -x + 2` |
| `x + 2y-14` | `= 0` |
Expand and simplify `(sqrt3-1)(2 sqrt3 + 5)`. (2 marks)
`1 + 3 sqrt 3`
`(sqrt 3-1)(2 sqrt 3 + 5)`
`= 2 xx 3 + 5 sqrt 3-2 sqrt 3-5`
`= 1 + 3 sqrt 3`
Which equation represents the line perpendicular to `2x-3y = 8`, passing through the point `(2, 0)`?
`B`
| `2x-3y` | `= 8` |
| `3y` | `= 2x-8` |
| `y` | `= 2/3x-8/3` |
| `m` | `= 2/3` |
| `:.\ m_text(perp)` | `= -3/2\ \ \ (m_1 m_2=-1\text( for)_|_text{lines)}` |
`text(Equation of line)\ \ m = -3/2\ \ text(through)\ \ (2,0):`
| `y-y_1` | `= m (x-x_1)` |
| `y-0` | `= -3/2 (x-2)` |
| `y` | `= -3/2x + 3` |
| `2y` | `= -3x + 6` |
| `3x + 2y` | `= 6` |
`=> B`
The cost of hiring an open space for a music festival is $120 000. The cost will be shared equally by the people attending the festival, so that `C` (in dollars) is the cost per person when `n` people attend the festival.
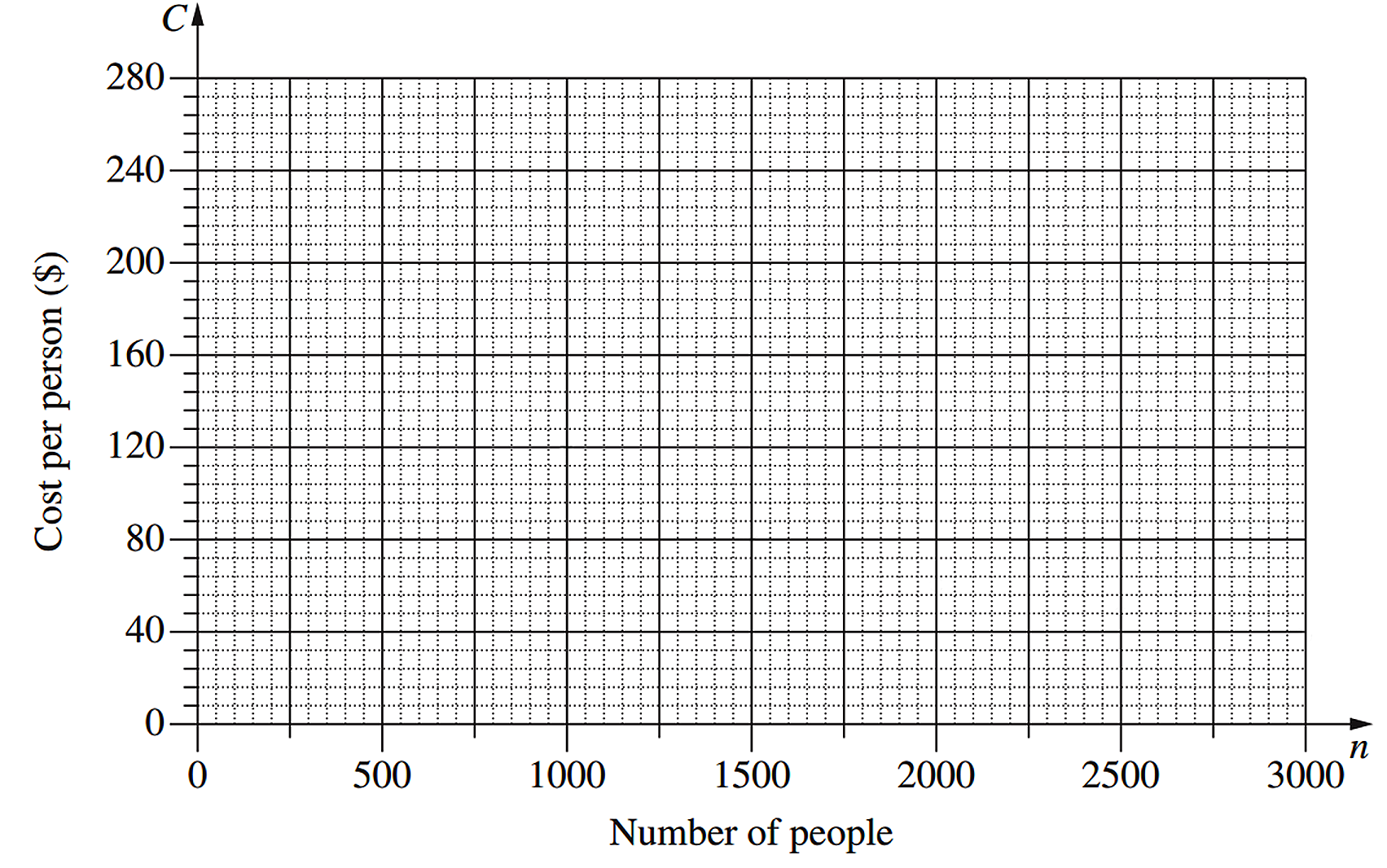
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
i.
\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\text{Number of people} (n) \rule[-1ex]{0pt}{0pt} & \ 500\ & \ 1000 \ & 1500 \ & 2000 \ & 2500\ & 3000 \ \\
\hline
\rule{0pt}{2.5ex}\text{Cost per person} (C)\rule[-1ex]{0pt}{0pt} & 240 & 120 & 80 & 60 & 48\ & 40 \ \\
\hline
\end{array}
| ii. |  |
iii. `C = (120\ 000)/n`
`n\ text(must be a whole number)`
iv. `text(Limitations can include:)`
`•\ n\ text(must be a whole number)`
`•\ C > 0`
v. `text(If)\ C = 94:`
| `94` | `= (120\ 000)/n` |
| `94n` | `= 120\ 000` |
| `n` | `= (120\ 000)/94` |
| `= 1276.595…` |
`:.\ text(C)text(ost cannot be $94 per person,)`
`text(because)\ n\ text(isn’t a whole number.)`
i.
\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\text{Number of people} (n) \rule[-1ex]{0pt}{0pt} & \ 500\ & \ 1000 \ & 1500 \ & 2000 \ & 2500\ & 3000 \ \\
\hline
\rule{0pt}{2.5ex}\text{Cost per person} (C)\rule[-1ex]{0pt}{0pt} & 240 & 120 & 80 & 60 & 48\ & 40 \ \\
\hline
\end{array}
| ii. |  |
iii. `C = (120\ 000)/n`
iv. `text(Limitations can include:)`
`•\ n\ text(must be a whole number)`
`•\ C > 0`
v. `text(If)\ C = 94`
| `=> 94` | `= (120\ 000)/n` |
| `94n` | `= 120\ 000` |
| `n` | `= (120\ 000)/94` |
| `= 1276.595…` |
`:.\ text(C)text(ost cannot be $94 per person,)`
`text(because)\ n\ text(isn’t a whole number.)`
`D`
`y = 2x-2`
`text(By elimination)`
`text(It has a)\ y\ text(intercept of)\ -2`
`=> text(Cannot be)\ B\ text(or)\ C`
`(-1, 0)text{ from}\ A\ text(doesn’t satisfy equation)`
`text(but)\ (1,0)\ text(from)\ D\ text(does)`
`=> D`
Write down the equation of the circle with centre `(-1, 2)` and radius 5. (1 mark)
`text{Circle with centre}\ (-1,2),\ r = 5`
`(x + 1)^2 + (y-2)^2 = 25`
`text{Circle with centre}\ (-1, 2),\ r = 5`
`(x + 1)^2 + (y-2)^2 = 25`
The diagram shows a regular pentagon `ABCDE`. Sides `ED` and `BC` are produced to meet at `P`.
--- 2 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
| i. |
`text(Angle sum of pentagon)=(5-2) xx 180°=540°`
| `:.\ /_CDE` | `= 540/5\ \ \ text{(regular pentagon has equal angles)}` |
| `= 108°` |
ii. `text(Show)\ Delta EPC\ text(is isosceles)`
`text(S)text(ince)\ ED=CD\ \ text{(sides of a regular pentagon)}`
`Delta ECD\ text(is isosceles)`
`/_DEC=1/2 xx (180-108)= 36^{\circ}\ \ \ text{(Angle sum of}\ Delta DEC text{)}`
`/_CDP=72^@\ \ \ (\angle PDE\ \text{is a straight angle})`
`/_DCP=72^@\ \ \ (\angle PCB\ \text{is a straight angle})`
`=> /_CPD= 180-(72 + 72)=36^{\circ}\ \ \ text{(angle sum of}\ Delta CPD text{)}`
`:.\ Delta EPC\ \text(is isosceles)\ \ \ text{(2 equal angles)}`
What are the solutions of `2x^2-5x-1 = 0`?
`D`
`2x^2-5x-1 = 0`
`text(Using)\ x = (-b +- sqrt( b^2-4ac) )/(2a)`
| `x` | `= (5 +- sqrt{\ \ (-5)^2-4 xx 2 xx(-1) })/ (2 xx 2)` |
| `= (5 +- sqrt(25 + 8) )/4` | |
| `= (5 +- sqrt(33) )/4` |
`=> D`
Sarah tried to solve this equation and made a mistake in Line 2.
| `(W+4)/3-(2W-1)/5` | `=1` | `text(... Line 1)` |
| `5W+ 20-6W-3` | `=15` | `text(... Line 2)` |
| `17-W` | `=15` | `text(... Line 3)` |
| `W` | `=2` | `text(... Line 4)` |
Copy the equation in Line 1 and continue your solution to solve this equation for `W`.
Show all lines of working. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
| `(W+4)/3-(2W-1)/5` | `=1` | `text(… Line 1)` |
| `5W+ 20-6W+ 3` | `=15` | `text(… Line 2)` |
| `23-W` | `=15` | `text(… Line 3)` |
| `W` | `=8` | `text(… Line 4)` |
| `(W+4)/3-(2W-1)/5` | `=1` | `text(… Line 1)` |
| `5W+ 20-6W+3` | `=15` | `text(… Line 2)` |
| `23-W` | `=15` | `text(… Line 2)` |
| `W` | `=8` | `text(… Line 4)` |
Triangle `PQR` is shown.
Find the size of angle `Q`, to the nearest degree. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
`110^@\ \ \ text{(nearest degree)}`
`text(Using Cosine rule)`
| `cos /_Q` | `= (a^2 + b^2-c^2)/(2ab)` |
| `= (53^2 + 66^2-98^2)/(2xx53xx66)` | |
| `=-0.3486…` |
| `:. /_Q` | `= 110.4034…` |
| `= 110^@\ \ \ text{(nearest degree)}` |
Which of the following correctly express `x` as the subject of `a=(nx)/5` ?
`B`
| `a` | `=(nx)/5` |
| `nx` | `=5a` |
| `x` | `=(5a)/n` |
`=> B`
Which of the following correctly expresses `a` as the subject of `s= ut+1/2at^2 `?
`A`
| `s` | `=ut+1/2at^2` |
| `1/2at^2` | `=s-ut` |
| `at^2` | `=2(s-ut)` |
| `a` | `=(2(s-ut))/t^2` |
`=>A`
Three towns `P`, `Q` and `R` are marked on the diagram.
The distance from `R` to `P` is 76 km. `angle RQP=26^circ` and `angle RPQ=46^@.`
What is the distance from `P` to `Q` to the nearest kilometre?
`C`
| `angle QRP` | `=180-(26+46) (180^circ\ text(in) \ Delta)` |
| `=108^circ` |
`text{Using sine rule}`
| `(PQ)/sin108^circ` | `=76/sin26^circ` |
| `PQ` | `=(76xxsin108^circ)/sin26^circ` |
| `=164.88\ text(km)` |
`=> C`
Jacques and a flagpole both cast shadows on the ground. The difference between the lengths of their shadows is 3 metres.
What is the value of `d`, the length of Jacques’ shadow? (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
`d = 1.8\ text(m)`
`text{Both triangles have right-angles with a common (ground) angle.}`
`:.\ text{Triangles are similar (equiangular)}`
` text{Since corresponding sides are in the same ratio}`
| `d/1.5` | `= (d+3)/4` |
| `4d` | `= 1.5(d + 3)` |
| `8d` | `= 3(d + 3)` |
| `= 3d + 9` | |
| `5d` | `= 9` |
| `:.d` | `= 9/5` |
| `=1.8\ text(m)` |
What is the area of this triangle, to the nearest square metre?
`C`
`text(Let unknown angle)=/_C`
| `/_C` | `= 180-(50 + 57)\ \ \ \ \ (180^@ \ text(in)\ Delta)` |
| `=73^@` |
| `:. A` | `= 1/2 ab\ sinC` |
| `= 1/2 xx 9.9 xx 8.8 xx sin73^@` | |
| `= 41.656 \ text(m²)` |
`=> C`
Which equation correctly shows `r` as the subject of `S=800(1-r)`?
`A`
| `S` | `=800(1-r)` |
| `1-r` | `=S/800` |
| `r` | `=1-S/800` |
| `=(800-S)/800` |
`=>\ A`