SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Statistics, STD1 S1 2023 HSC 13

The graph shows the frequency of scores out of 10 awarded to a museum by visitors.
 

  1. What is the mode of these data?  (1 mark)

  2. Describe TWO features of this graph.  (2 marks)

Show Answers Only

a.    \(\text{Mode = Score with the highest frequency}=9\)
 

b.    \(\text{Features could include any 2 of the following:}\)

  • \(\text{Data is negatively skewed as the mean and median are to the left of the mode}\)
  • \(\text{23 of the 24 scores, or 95.8%, are 5 or above.}\)
  • \(Q_2\text{(Median)}=8\)
  • \(Q_1=7\text{ and }Q_3=9\)
  • \(IQR=Q_1-Q_3=9-7=2\)
  • \(Q_1-1.5\times IQR=7-1.5\times 2=4\ \ \Rightarrow \ \ \text{1 is an outlier}\)
  • \(\text{Mean}=\dfrac{189}{24}=7.875\)
  • \(\text{If the outlier (1) was removed, Mean}=\dfrac{188}{23}=8.174\text{ (2 d.p.)}\)

Show Worked Solution

a.    \(\text{Mode = Score with the highest frequency}=9\)
 

b.    \(\text{Features could include any 2 of the following:}\)

  • \(\text{Data is negatively skewed as the mean and median are to the left of the mode}\)
  • \(\text{23 of the 24 scores, or 95.8%, are 5 or above.}\)
  • \(Q_2\text{(Median)}=8\)
  • \(Q_1=7\text{ and }Q_3=9\)
  • \(IQR=Q_1-Q_3=9-7=2\)
  • \(Q_1-1.5\times IQR=7-1.5\times 2=4\ \ \Rightarrow \ \ \text{1 is an outlier}\)
  • \(\text{Mean}=\dfrac{189}{24}=7.875\)
  • \(\text{If the outlier (1) was removed, Mean}=\dfrac{188}{23}=8.174\text{ (2 d.p.)}\)

♦ Mean mark (a) 47%.
♦♦♦ Mean mark (b) 18%.

Statistics, STD1 S1 2023 HSC 11

A company employs 50 people.

The annual income of the employees is shown in the grouped frequency distribution table.

\begin{array} {|c|c|c|c|}
\hline
\textit{Annual income} & \textit{Class centre} & \textit{Number of} & fx \\ \text{(\$)} & (x) & \textit{employees}\ (f) &  \\
\hline
\rule{0pt}{2.5ex} \text{40 000 – 49 999} \rule[-1ex]{0pt}{0pt} & 45\ 000 & 12 & 540\ 000 \\
\hline
\rule{0pt}{2.5ex} \text{50 000 – 59 999} \rule[-1ex]{0pt}{0pt} & 55\ 000 & 13 & 715\ 000 \\
\hline\rule{0pt}{2.5ex} \text{60 000 – 69 999} \rule[-1ex]{0pt}{0pt} & 65\ 000 & 15 & A \\
\hline\rule{0pt}{2.5ex} \text{70 000 – 79 999} \rule[-1ex]{0pt}{0pt} & 75\ 000 & 7 & 525\ 000 \\
\hline\rule{0pt}{2.5ex} \text{80 000 – 89 999} \rule[-1ex]{0pt}{0pt} & 85\ 000 & 3 & 255\ 000 \\
\hline
\hline\rule{0pt}{2.5ex}  \rule[-1ex]{0pt}{0pt} &  & \textit{Total}\ = 50 & \textit{Total = B} \\
\hline
\end{array}  

  1. What are the values of \(A\) and \(B\)?  (2 marks)

  2. Find the mean for this distribution.  (1 mark)

Show Answers Only

a.    \(A=$975\ 000\), \(B=$3\ 010\ 000\)

b.    \($60\ 200\)

Show Worked Solution

a.    \(A=65\ 000\times 15 = $975\ 000\)

\(B=540\ 000+715\ 000+975\ 000+525\ 000+255\ 000=$3\ 010\ 000\)

  

b.    \(\text{Mean}=\dfrac{\text{Total }fx}{\text{Total }f}=\dfrac{3\ 010\ 000}{50}=$60\ 200\)

♦♦♦ Mean mark (b) 12%.

Statistics, STD1 S1 2020 HSC 24

  1. The ages in years, of ten people at the local cinema last Saturday afternoon are shown.

\(38 \ \ 25 \ \ 38 \ \ 46 \ \ 55 \ \ 68 \ \ 72 \ \ 55 \ \ 36 \ \ 38\)

  1. The mean of this dataset is 47.1 years.
  2. How many of the ten people were aged between the mean age and the median age?  (2 marks)

  3. On Wednesday, ten people all aged 70 went to this same cinema.
  4. Would the standard deviation of the age dataset from Wednesday be larger than, smaller than or equal to the standard deviation of the age dataset given in part (a)? Briefly explain your answer without performing any calculations.  (2 marks)

Show Answers Only

a.     \(1\)

b.    \(\text{Standard deviation is a measure of how much the}\)

\(\text{ages of individuals differ from the mean age of the group.}\)
 

\(\Rightarrow\ \text{Standard deviation of Wednesday’s group would be}\)

\(\text{less as the mean is 70 and everyone’s age is 70.}\)

Show Worked Solution

a.     \(\text{Reorder ages in ascending order:}\)

    \(25, 36, 38, 38, 38, 46, 55 , 55, 68, 72\)

\(\text{Median} = \dfrac{\text{5th + 6th}}{2} = \dfrac{38 + 46}{2} = 42\)

\(\therefore\ \text{People with age between 42 − 47.1 = 1}\)

♦ Mean mark (a) 39%.

 
b.    \(\text{Standard deviation is a measure of how much the}\)

\(\text{ages of individuals differ from the mean age of the group.}\)
 

\(\Rightarrow\ \text{Standard deviation of Wednesday’s group would be}\)

\(\text{less as the mean is 70 and everyone’s age is 70.}\)

♦♦♦ Mean mark (b) 20%.

Statistics, STD2 S1 2017 HSC 27a

Jamal surveyed eight households in his street. He asked them how many kilolitres (kL) of water they used in the last year. Here are the results.

`220, 105, 101, 450, 37, 338, 151, 205`

  1. Calculate the mean of this set of data.  (1 mark)

  2. What is the standard deviation of this set of data, correct to one decimal place?  (1 mark)

Show Answers Only
  1. `200.875`
  2. `127.4\ \ text{(1 d.p.)}`
Show Worked Solution
i.   `text(Mean)` `= (220 + 105 + 101 + 450 + 37 + 338 + 151 + 205) ÷ 8`
    `= 200.875`
♦ Mean mark part (ii) 47%.
IMPORTANT: The population standard deviation is required here.

 

ii.   `text(Std Dev)` `= 127.357…\ \ text{(by calc)}`
    `= 127.4\ \ text{(1 d.p.)}`

Statistics, STD2 S1 2016 HSC 21 MC

A grouped data frequency table is shown.

\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex} \textit{Class Interval} \rule[-1ex]{0pt}{0pt} & \ \ \ \ \ \textit{Frequency}\ \ \ \ \  \\
\hline
\rule{0pt}{2.5ex} \text{1 – 5} \rule[-1ex]{0pt}{0pt} & 3 \\
\hline
\rule{0pt}{2.5ex} \text{6 – 10} \rule[-1ex]{0pt}{0pt} & 6 \\
\hline
\rule{0pt}{2.5ex} \text{11 – 15} \rule[-1ex]{0pt}{0pt} & 8 \\
\hline
\rule{0pt}{2.5ex} \text{16 – 20} \rule[-1ex]{0pt}{0pt} & 9 \\
\hline
\end{array}

What is the mean for this set of data?

  1.    6.5
  2.    10.5
  3.    11.9
  4.    12.4
Show Answers Only

`=> D`

Show Worked Solution

`text(Using the centre of each class interval:)`

♦ Mean mark 43%.
`text(Mean)` `= (3 xx 3 + 8 xx 6 + 13 xx 8 + 18 xx 9)/(3 + 6 + 8 + 9)`
  `= 12.42…`

`=> D`

Statistics, STD2 S1 2006 HSC 23c

Vicki wants to investigate the number of hours spent on homework by students at her high school.

  1. Briefly describe a valid method of randomly selecting 200 students for a sample.  (1 mark)

  2. Vicki chooses her sample and asks each student how many hours (to the nearest hour) they usually spend on homework during one week.

     

    The responses are shown in the frequency table.
     
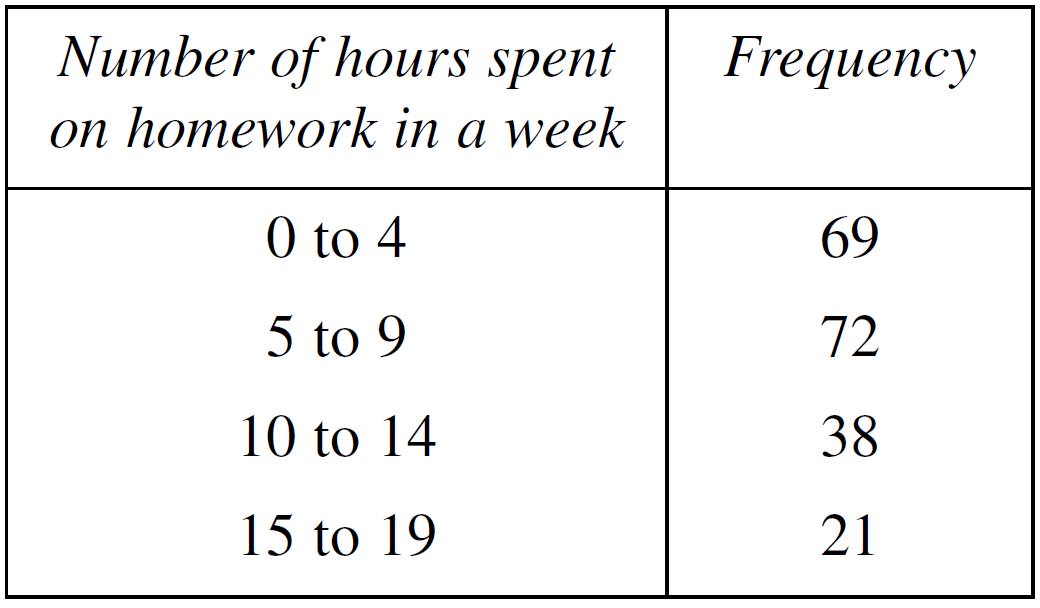
         2UG-2006-23c

    What is the mean amount of time spent on homework?  (2 marks)

Show Answers Only
  1. `text(A valid method would be using a stratified sample.)`

     

    `text(The number of students sampled in each year is)`

     

    `text(proportional to the size of each year.)`

  2. `text(7.275 hours)`
Show Worked Solution

i.   `text(A valid method would be using a stratified sample.)`

`text(The number of students sampled in each year is)`

`text(proportional to the size of each year.)`

MARKER’S COMMENT: This “routine” exercise of finding a mean from grouped data was incorrectly answered by most students! The best responses copied the table and inserted a class-centre column (see solution).

 

ii.    2UG-2006-23c Answer

 

`text(Mean)` `= text(Sum of Scores) / text(Total scores)`
  `= 1455/200`
  `= 7.275\ text(hours)`

Statistics, STD2 S1 2006 HSC 12 MC

The mean of a set of 5 scores is 62.

What is the new mean of the set of scores after a score of 14 is added?

  1.   38
  2.   54
  3.   62
  4.   76
Show Answers Only

`B`

Show Worked Solution

`text(Mean of 5 scores) = 62`

`:.\ text(Total of 5 scores) = 62 xx 5 = 310`

`text(Add a score of 14)`

`text(Total of 6 scores) = 310 + 14 = 324`

`:.\ text(New mean)` `= 324/6`
  `= 54`

`=>  B`

Statistics, STD2 S1 2005 HSC 1 MC

What is the mean of the set of scores?

`3, \ 4, \ 5, \ 6, \ 6, \ 8, \ 8, \ 8, \ 15`
 

  1. 6
  2. 7
  3. 8
  4. 9
Show Answers Only

`B`

Show Worked Solution
`text(Mean)` `= ((3 + 4 + 5 +6 + 6 + 8 + 8 + 8 + 15))/9`
  `= 63/9`
  `= 7`

 
`=> B`

Statistics, STD2 S1 2007 HSC 24a

Consider the following set of scores:

`3, \ 5, \ 5, \ 6, \ 8, \ 8, \ 9, \ 10, \ 10, \ 50.` 

  1. Calculate the mean of the set of scores.   (1 mark)

  2. What is the effect on the mean and on the median of removing the outlier?   (2 marks)

Show Answers Only
  1. `11.4`
  2. `text{If the outlier (50) is removed, the mean}`

     

    `text(would become lower.)`

  3.  

    `text(Median will NOT change.)`

Show Worked Solution

i.  `text(Total of scores)`

`= 3 + 5 + 5 + 6 + 8 + 8 + 9 + 10 + 10 +50`

`= 114`
 

`:.\ text(Mean) = 114/10 = 11.4`

 

ii.  `text(Mean)`

`text{If the outlier (50) is removed, the mean}`

`text(would become lower.)`
 

`text(Median)`

`text(The current median (10 data points))`

`= text(5th + 6th)/2 = (8 + 8)/2 = 8`

`text(The new median (9 data points))`

`=\ text(5th value)`

`= 8`
 

`:.\ text(Median will NOT change.)`

Statistics, STD2 S1 2008 HSC 23f

Christina has completed three Mathematics tests. Her mean mark is 72%.

What mark (out of 100) does she have to get in her next test to increase her mean mark to 73%?   (2 marks)

Show Answers Only

`76`

Show Worked Solution

`text(Total marks in 3 tests)`

`= 3 xx 72`

`= 216`

`text(We need 4-test mean) = 73`

`text(i.e.)\ \ \ ` `text{Total Marks (4 tests)}-:4` `= 73`
  `text(Total Marks)\ text{(4 tests)}` `= 292`

 

`:.\ text(4th test score)` `= 292 – 216`
  `= 76`

Statistics, STD2 S1 2008 HSC 13 MC

The height of each student in a class was measured and it was found that the mean height was 160 cm.

Two students were absent. When their heights were included in the data for the class, the mean height did not change.

Which of the following heights are possible for the two absent students?

  1.    155 cm and 162 cm
  2.    152 cm and 167 cm
  3.    149 cm and 171 cm
  4.    143 cm and 178 cm
Show Answers Only

`C`

Show Worked Solution

`text(S) text(ince the mean doesn’t change)`

`=>\ text(2 absent students must have a)`

`text(mean height of 160 cm.)`

`text(Considering each option given,)`

`(149 + 171) -: 2 = 160`

`=>  C`

Statistics, STD2 S1 2014 HSC 14 MC

Twenty Year 12 students were surveyed. These students were asked how many hours of sport they play per week, to the nearest hour.

The results are shown in the frequency table. 

\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex} \textit{Hours per week} \rule[-1ex]{0pt}{0pt} & \ \ \ \ \ \textit{Frequency}\ \ \ \ \  \\
\hline
\rule{0pt}{2.5ex} \text{0 – 2} \rule[-1ex]{0pt}{0pt} & 5 \\
\hline
\rule{0pt}{2.5ex} \text{3 – 5} \rule[-1ex]{0pt}{0pt} & 10 \\
\hline
\rule{0pt}{2.5ex} \text{6 – 8} \rule[-1ex]{0pt}{0pt} & 3 \\
\hline
\rule{0pt}{2.5ex} \text{9 – 11} \rule[-1ex]{0pt}{0pt} & 2 \\
\hline
\end{array}

 What is the mean number of hours of sport played by the students per week?

  1.    3.3
  2.    4.3
  3.    5.0
  4.    5.3
Show Answers Only

`B`

Show Worked Solution

`text(Using the class centres)`

`text(Total hours)` `= (1 xx 5) + (4 xx 10) + (7 xx 3) + (10 xx 2)`
  `= 5 + 40 + 21 + 20`
  `= 86`
♦ Mean mark 45%
COMMENT: The mean is calculated using “class centres” in grouped data.
`text(Mean hours)` `= 86/20 = 4.3`

`=>  B`

Statistics, STD2 S1 2011 HSC 17 MC

The heights of the players in a basketball team were recorded as 1.8 m, 1.83 m, 1.84 m, 1.86 m and 1.92 m. When a sixth player joined the team, the average height of the players increased by 1 centimetre.

What was the height of the sixth player?

  1.   1.85 m
  2.   1.86 m
  3.   1.91 m
  4.   1.93 m
Show Answers Only

`C`

Show Worked Solution
`text(Old Mean)` `=(1.8+1.83+1.84+1.86+1.92)-:5`
  `=9.25/5`
  `=1.85\ \ text(m)`

 

`text{S}text{ince the new mean = 1.86m  (given)}`

`text(New Mean)` `=text(Height of all 6 players) -: 6`
`:.1.86` `=(9.25+h)/6\ \ \ \ (h\ text{= height of new player})`
`h` `=(6xx1.86)-9.25`
  `=1.91\ \ text(m)`

`=> C`

Statistics, STD2 S1 2009 HSC 3 MC

The eye colours of a sample of children were recorded.

When analysing this data, which of the following could be found?

  1. Mean
  2. Median
  3. Mode
  4. Range
Show Answers Only

`C`

Show Worked Solution

`text(Eye colour is categorical data)`

`:.\ text(Only the mode can be found)`

`=>  C`

Statistics, STD2 S1 2009 HSC 21 MC

The mean of a set of ten scores is 14. Another two scores are included and the new mean is 16.

What is the mean of the two additional scores?

  1.    4
  2.    16
  3.    18
  4.    26
Show Answers Only

`D`

Show Worked Solution
♦♦♦ Mean mark 28%.

`text(If ) bar x\ text(of 10 scores = 14)`

  `=>text(Sum of 10 scores)= 10 xx 14 = 140`

`text(With 2 additional scores,)\ \ bar x = 16 `

  `=>text(Sum of 12 scores)= 12 xx 16 = 192`

`:.\ text(Value of 2 extra scores)` `= 192\-140`
  `= 52`

 

`:.\ text(Mean of 2 extra scores)= 52/2 = 26`

`=>  D`

Statistics, STD2 S1 2013 HSC 14 MC

The July sales prices for properties in a suburb were:

$552 000,  $595 000,  $607 000,  $607 000,  $682 000, and  $685 000.

On 1 August, another property in the same suburb was sold for over one million dollars.

If the property had been sold in July, what effect would it have had on the mean and median sale prices for July?

  1.    Both the mean and median would have changed.
  2.    Neither the mean nor the median would have changed.
  3.    The mean would have changed and the median would have stayed the same.
  4.    The mean would have stayed the same and the median would have changed.
Show Answers Only

`C`

Show Worked Solution

`text(Mean increases because new house is sold above)`

`text(the existing average.)`

`text(Initial median)= (607\ 000+607\ 000)/2=607\ 000` 

`text(New median)=607\ 000\ \ \  text{(4th value in a list of 7)}`

`=>\ C`