Solve the equation `3^(-4x) = 9^(6-x)` for `x.` (2 marks)
GEOMETRY, FUR1 SM-Bank 11 MC
Calculus, MET1 2016 VCAA 1a
Let `y = (cos(x))/(x^2 + 2)`.
Find `(dy)/(dx)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Probability, MET2 2007 VCAA 19 MC
Algebra, MET2 2007 VCAA 11 MC
The solution set of the equation `e^(4x) - 5e^(2x) + 4 = 0` over `R` is
A. `{1, 4}`
B. `{– 4, – 1})`
C. `{– 2, – 1, 1, 2})`
D. `{– log_e(2), 0, log_e(2)}`
E. `{0, log_e(2)}`
Probability, MET2 2007 VCAA 7 MC
The random variable `X` has a normal distribution with mean 11 and standard deviation 0.25.
If the random variable `Z` has the standard normal distribution, then the probability that `X` is less than 10.5 is equal to
- `text(Pr) (Z > 2)`
- `text(Pr) (Z < – 1.5)`
- `text(Pr) (Z < 1)`
- `text(Pr) (Z >= 1.5)`
- `text(Pr) (Z < – 4)`
Algebra, MET2 2007 VCAA 3 MC
If `y = log_a (7x - b) + 3`, then `x` is equal to
- `1/7 a^(y - 3) + b`
- `1/7 (a^y - 3) + b`
- `1/7 (a^(y - 3) + b)`
- `a^(y - 3) - b/7`
- `(y - 3)/(log_a(7 - b))`
Algebra, MET2 2007 VCAA 2 MC
Let `g(x) = x^2 + 2x - 3 and f(x) = e^(2x + 3).`
Then `f(g(x))` is given by
- `e^(4x + 6) + 2 e^(2x + 3) - 3`
- `2x^2 + 4x - 6`
- `e^(2x^2 + 4x + 9)`
- `e^(2x^2 + 4x - 3)`
- `e^(2x^2 + 4x - 6)`
Algebra, MET2 SM-Bank 8 MC
For the polynomial `P(x) = x^3 − ax + 4,\ \ P( – 3) = – 5.`
The value of `a` is
A. `− 12`
B. `− 5`
C. `– 3`
D. `3`
E. `6`
Algebra, MET2 SM-Bank 7 MC
If `x-2` is a factor of `2x^3 - 10x^2 + 6x + a` where `a in R text{\}{0},` then the value of `a` is
A. `-68`
B. `-20`
C. `-2`
D. `2`
E. `12`
Algebra, MET2 2008 VCAA 17 MC
The graph of the function `f(x) = e^(2x) - 2` intersects the graph of `g(x) = e^x` where
- `x = -1`
- `x = log_e(2)`
- `x = 2`
- `x = (1 + sqrt 7)/2`
- `x = log_e((1 + sqrt 7)/2)`
Graphs, MET2 2008 VCAA 8 MC
The graph of the function `f: D -> R,\ f(x) = (x - 3)/(2 - x),` where `D` is the maximal domain has asymptotes
- `x = 3,\ \ \ \ \ \ \ \ \ \ y = 2`
- `x = -2,\ \ \ \ \ y = 1`
- `x = 1,\ \ \ \ \ \ \ \ \ \ y = -1`
- `x = 2,\ \ \ \ \ \ \ \ \ \ y = -1`
- `x = 2,\ \ \ \ \ \ \ \ \ \ y = 1`
Algebra, MET2 2008 VCAA 7 MC
The inverse of the function `f: R^+ -> R,\ f(x) = 1/sqrt x - 3` is
- `{:f^-1: R^+ -> R, qquad qquad qquad qquad f^-1(x) = (x + 3)^2:}`
- `{:f^-1: R^+ -> R, qquad qquad qquad qquad f^-1(x) = 1/x^2 + 3:}`
- `{:f^-1: (3, oo) -> R, qquad qquad qquad f^-1 (x) = (-1)/(x - 3)^2:}`
- `{:f^-1: text{(−3, ∞)} -> R, qquad qquad f^-1 (x) = 1/(x + 3)^2:}`
- `{:f^-1: text{(−3, ∞)} -> R, qquad qquad f^-1 (x) = -1/x^2 - 3:}`
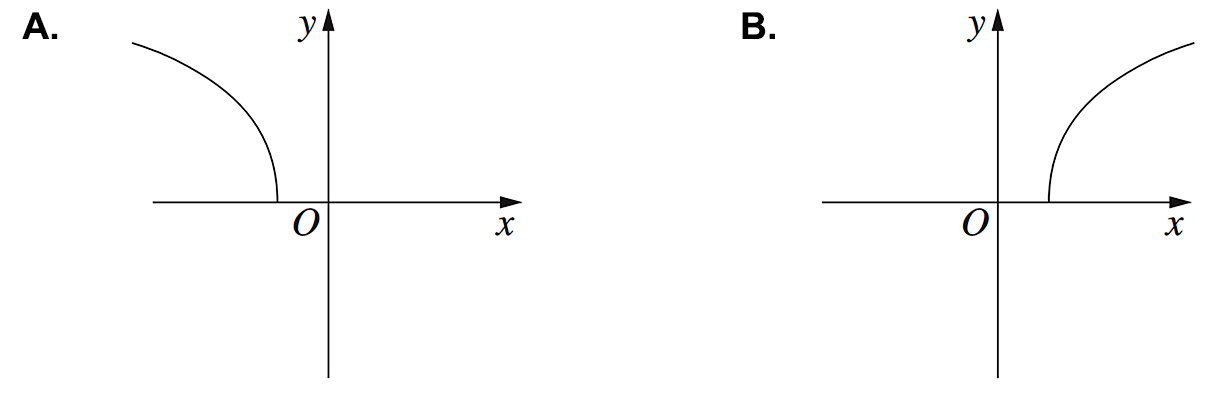
Graphs, MET2 SM-Bank 4 MC
Graphs, MET1 SM-Bank 27
The graph shown is `y = A sin bx`.
- Write down the value of `A`. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Find the value of `b`. (1 mark)
--- 6 WORK AREA LINES (style=lined) ---
- Copy or trace the graph into your writing booklet.
On the same set of axes, draw the graph `y = 3 sin x + 1` for `0 <= x <= pi`. (2 marks)
--- 10 WORK AREA LINES (style=blank) ---
Calculus, MET1 2007 ADV 2ai
Let `f(x)=(1 + tan x)^10.` Find `f^{\prime}(x)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Calculus, MET1 2007 HSC 2bi
Find an anti-derivative of `(1 + cos 3x)` with respect to `x`. (2 marks)
--- 2 WORK AREA LINES (style=lined) ---
Calculus, MET1 2006 ADV 2ai
Differentiate with respect to `x`:
Let `f(x)=x tan x`. Find `f^{prime}(x)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Graphs, MET1 SM-Bank 20
The rule for `f` is `f(x) = x-1/2 x^2` for `x <= 1`. This function has an inverse, `f^(-1) (x)`.
- Sketch the graphs of `y = f(x)` and `y = f^(-1) (x)` on the same set of axes. (Use the same scale on both axes.) (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
- Find the rule for the inverse function `f^(-1) (x)`. (2 marks)
--- 8 WORK AREA LINES (style=lined) ---
- Evaluate `f^(-1) (3/8)`. (1 mark)
--- 5 WORK AREA LINES (style=lined) ---
Calculus, MET1 2005 ADV 2ci
Find the value of `int (6x^2)/(x^3 + 1)\ dx`. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
Calculus, MET1 2006 HSC 2bi
Find an antiderivative of `int 1 + e^(7x)` with respect to `x`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Calculus, MET1 2008 ADV 3b
- Differentiate `log_e(cos x)` with respect to `x`. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
- Hence, or otherwise, evaluate `int_0^(pi/4) tan x\ dx`. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
Calculus, MET1 2016 ADV 12d
- Differentiate `y = xe^(3x)`. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- Hence find the exact value of `int_0^2 e^(3x) (3 + 9x)\ dx`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Calculus, MET1 2007 ADV 2ai
Differentiate with respect to `x`:
`(2x)/(e^x + 1).` (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
Calculus, MET1 2013 ADV 11e
Find `int e^(4x + 1) dx` (2 marks)
--- 2 WORK AREA LINES (style=lined) ---
Calculus, MET1 2012 ADV 12ai
Differentiate with respect to `x`
`(x-1)log_e x` (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
Calculus, MET1 2009 ADV 2a
Differentiate `(e^x + 1)^2` with respect to `x`. (2 marks)
--- 2 WORK AREA LINES (style=lined) ---
Calculus, MET1 2008 ADV 2aii
Differentiate with respect to `x`:
`x^2log_ex` (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
Calculus, MET1 2012 ADV 9
Let `int_1^4 1/(3x)\ dx = a log_e(b).`
Find the value of `a` and `b`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Calculus, MET1 SM-Bank 2
Let `f: (0,oo) → R,` where `f(x) = log_e (x).`
Find the equation of the tangent to `f(x)` at the point `(e, 1)`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Algebra, MET1 SM-Bank 7
Solve the equation `2^(2x + 1) = 32` for `x`. (2 marks)
Algebra, MET2 SM-Bank 4 MC
Which expression is equivalent to `4 + log_2 x?`
- `log_2 (4x)`
- `log_2 (16 + x)`
- `4 log_2 (2x)`
- `log_2 (16x)`
- `log_2 (2x)`
Calculus, MET1 2016 VCAA 3
Let `f: R text{\}{1} -> R` where `f(x) = 2 + 3/(x - 1)`.
Calculus, MET1 2016 VCAA 1b
Let `f(x) = x^2e^(5x)`.
Evaluate `f^{\prime}(1)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Probability, MET2 2009 VCAA 3
The Bouncy Ball Company (BBC) makes tennis balls whose diameters are normally distributed with mean 67 mm and standard deviation 1 mm. The tennis balls are packed and sold in cylindrical tins that each hold four balls. A tennis ball fits into such a tin if the diameter of the ball is less than 68.5 mm. --- 5 WORK AREA LINES (style=lined) --- BBC management would like each ball produced to have diameter between 65.6 and 68.4 mm. --- 5 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 4 WORK AREA LINES (style=lined) --- BBC management wants engineers to change the manufacturing process so that 99% of all balls produced have diameter between 65.6 and 68.4 mm. The mean is to stay at 67 mm but the standard deviation is to be changed. --- 6 WORK AREA LINES (style=lined) ---
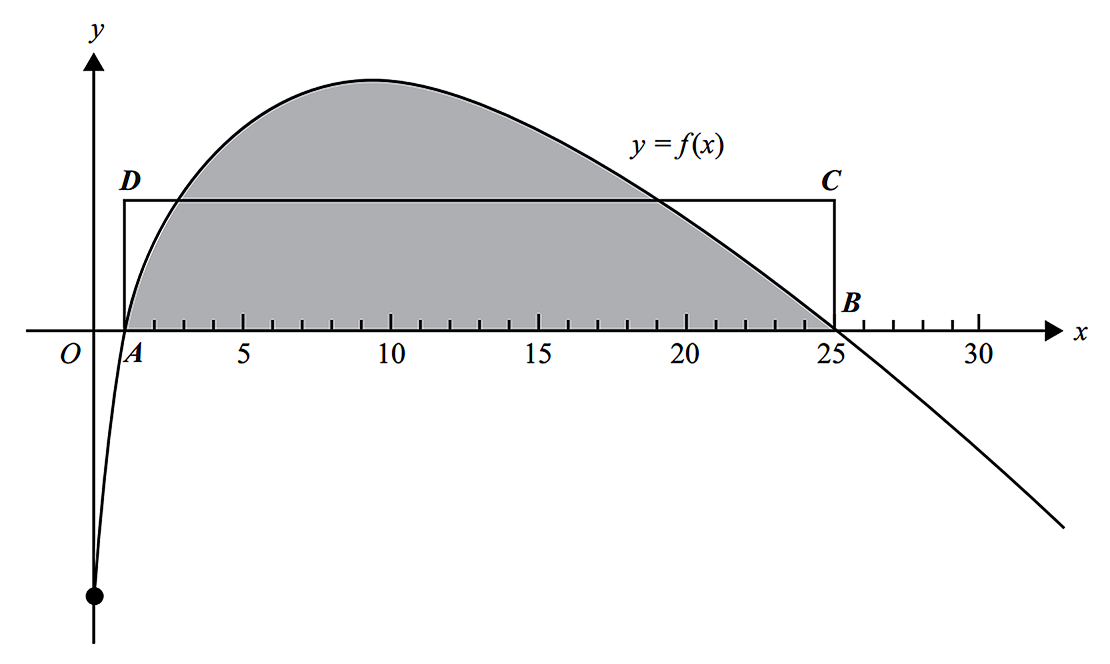
Calculus, MET2 2009 VCAA 1
Let `f: R^+ uu {0} -> R,\ f(x) = 6 sqrt x-x-5.`
The graph of `y = f (x)` is shown below.
- State the interval for which the graph of `f` is strictly decreasing. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
- Points `A` and `B` are the points of intersection of `y = f (x)` with the `x`-axis. Point `A` has coordinates `(1, 0)` and point `B` has coordinates `(25, 0)`.
Find the length of `AD` such that the area of rectangle `ABCD` is equal to the area of the shaded region. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
- The points `P (16, 3)` and `B (25, 0)` are labelled on the diagram.
- Find `m`, the gradient of the chord `PB`. (Exact value to be given.) (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Find `a in [16, 25]` such that `f prime (a) = m`. (Exact value to be given.) (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
- Find `m`, the gradient of the chord `PB`. (Exact value to be given.) (1 mark)
Calculus, MET2 2009 VCAA 8 MC
For the function `f: R -> R,\ f (x) = (x + 5)^2 (x - 1)`, the subset of `R` for which the gradient of `f` is negative is
- `(– oo, 1)`
- `(– 5, 1)`
- `(– 5, – 1)`
- `(– oo, – 5)`
- `(– 5, 0)`
Calculus, MET2 2009 VCAA 7 MC
For `y = e^(2x) cos (3x)` the rate of change of `y` with respect to `x` when `x = 0` is
- `0`
- `2`
- `3`
- `– 6`
- `– 1`
Algebra, MET2 2009 VCAA 3 MC
The maximal domain `D` of the function `f : D -> R` with rule `f (x) = log_e (2x + 1)` is
- `R\ text(\){– 1/2}`
- `(– 1/2, oo)`
- `R`
- `(0, oo)`
- `(– oo, – 1/2)`
Calculus, MET2 2011 VCAA 3
- Consider the function `f: R -> R, f(x) = 4x^3 + 5x-9`.
- Find `f^{prime}(x).` (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Explain why `f^{prime}(x) >= 5` for all `x`. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- Find `f^{prime}(x).` (1 mark)
- The cubic function `p` is defined by `p: R -> R, p(x) = ax^3 + bx^2 + cx + k`, where `a`, `b`, `c` and `k` are real numbers.
- If `p` has `m` stationary points, what possible values can `m` have? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- If `p` has an inverse function, what possible values can `m` have? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- If `p` has `m` stationary points, what possible values can `m` have? (1 mark)
- The cubic function `q` is defined by `q:R -> R, q(x) = 3-2x^3`.
- Write down a expression for `q^(-1)(x)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Determine the coordinates of the point(s) of intersection of the graphs of `y = q(x)` and `y = q^(-1)(x)`. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
- Write down a expression for `q^(-1)(x)`. (2 marks)
- The cubic function `g` is defined by `g: R -> R, g(x) = x^3 + 2x^2 + cx + k`, where `c` and `k` are real numbers.
- If `g` has exactly one stationary point, find the value of `c`. (3 marks)
--- 4 WORK AREA LINES (style=lined) ---
- If this stationary point occurs at a point of intersection of `y = g(x)` and `g^(−1)(x)`, find the value of `k`. (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
- If `g` has exactly one stationary point, find the value of `c`. (3 marks)
Measurement, STD2 M6 2005 HSC 8 MC
If `tan theta = 85`, what is the value of `theta`, correct to 2 decimal places?
- `1.37°`
- `1.56°`
- `89.33°`
- `89.20°`
Probability, MET2 2016 VCAA 3*
A school has a class set of 22 new laptops kept in a recharging trolley. Provided each laptop is correctly plugged into the trolley after use, its battery recharges. On a particular day, a class of 22 students uses the laptops. All laptop batteries are fully charged at the start of the lesson. Each student uses and returns exactly one laptop. The probability that a student does not correctly plug their laptop into the trolley at the end of the lesson is 10%. The correctness of any student’s plugging-in is independent of any other student’s correctness. --- 5 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) --- The time for which a laptop will work without recharging (the battery life) is normally distributed, with a mean of three hours and 10 minutes and standard deviation of six minutes. Suppose that the laptops remain out of the recharging trolley for three hours. --- 5 WORK AREA LINES (style=lined) --- A supplier of laptops decides to take a sample of 100 new laptops from a number of different schools. For samples of size 100 from the population of laptops with a mean battery life of three hours and 10 minutes and standard deviation of six minutes, `hat P` is the random variable of the distribution of sample proportions of laptops with a battery life of less than three hours. --- 6 WORK AREA LINES (style=lined) --- It is known that when laptops have been used regularly in a school for six months, their battery life is still normally distributed but the mean battery life drops to three hours. It is also known that only 12% of such laptops work for more than three hours and 10 minutes. --- 5 WORK AREA LINES (style=lined) --- The laptop supplier collects a sample of 100 laptops that have been used for six months from a number of different schools and tests their battery life. The laptop supplier wishes to estimate the proportion of such laptops with a battery life of less than three hours. --- 2 WORK AREA LINES (style=lined) --- The laptop supplier finds that, in a particular sample of 100 laptops, six of them have a battery life of less than three hours. --- 2 WORK AREA LINES (style=lined) --- `qquad qquad f(x) = {(((210-x)e^((x-210)/20))/400, 0 <= x <= 210), (0, text{elsewhere}):}` --- 2 WORK AREA LINES (style=lined) ---
Calculus, MET2 2016 VCAA 2
Consider the function `f(x) = -1/3 (x + 2) (x-1)^2.`
- i. Given that `g^{′}(x) = f (x) and g (0) = 1`,
- show that `g(x) = -x^4/12 + x^2/2-(2x)/3 + 1`. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- ii. Find the values of `x` for which the graph of `y = g(x)` has a stationary point. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
The diagram below shows part of the graph of `y = g(x)`, the tangent to the graph at `x = 2` and a straight line drawn perpendicular to the tangent to the graph at `x = 2`. The equation of the tangent at the point `A` with coordinates `(2, g(2))` is `y = 3-(4x)/3`.
The tangent cuts the `y`-axis at `B`. The line perpendicular to the tangent cuts the `y`-axis at `C`.
- i. Find the coordinates of `B`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- ii. Find the equation of the line that passes through `A` and `C` and, hence, find the coordinates of `C`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- iii. Find the area of triangle `ABC`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- The tangent at `D` is parallel to the tangent at `A`. It intersects the line passing through `A` and `C` at `E`.
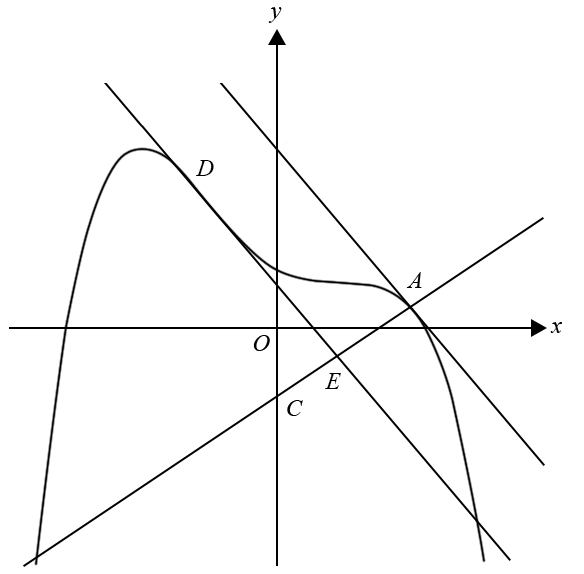
i. Find the coordinates of `D`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- ii. Find the length of `AE`. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Calculus, MET2 2016 VCAA 1
Let `f: [0, 8 pi] -> R, \ f(x) = 2 cos (x/2) + pi`.
- Find the period and range of `f`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- State the rule for the derivative function `f^{′}`. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Find the equation of the tangent to the graph of `f` at `x = pi`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Find the equations of the tangents to the graph of `f: [0, 8 pi] -> R,\ \ f(x) = 2 cos (x/2) + pi` that have a gradient of 1. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- The rule of `f^{′}` can be obtained from the rule of `f` under a transformation `T`, such that
`qquad T: R^2 -> R^2,\ T([(x), (y)]) = [(1, 0), (0, a)] [(x), (y)] + [(−pi), (b)]`
Find the value of `a` and the value of `b`. (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
- Find the values of `x, \ 0 <= x <= 8 pi`, such that `f(x) = 2 f^{′} (x) + pi`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Calculus, MET2 2010 VCAA 16 MC
The gradient of the function `f: R -> R,\ f(x) = (5x)/(x^2 + 3)` is negative for
- `-sqrt 3 < x < sqrt 3`
- `x > 3`
- `x in R`
- `x < -sqrt 3 and x > sqrt 3`
- `x < 0`
Probability, MET2 2010 VCAA 15 MC
Probability, MET2 2010 VCAA 14 MC
A bag contains four white balls and six black balls. Three balls are drawn from the bag without replacement.
The probability that they are all black is
- `1/6`
- `27/125`
- `24/29`
- `3/500`
- `8/125`
Algebra, MET2 2010 VCAA 8 MC
The function `f` has rule `f(x) = 3 log_e (2x).`
If `f(5x) = log_e (y)` then `y` is equal to
- `30x`
- `6x`
- `125x^3`
- `50x^3`
- `1000x^3`
Calculus, MET2 2010 VCAA 6 MC
A function `g` with domain `R` has the following properties.
● `g prime (x) = x^2 - 2x`
● the graph of `g(x)` passes through the point `(1, 0)`
`g (x)` is equal to
A. `2x - 2`
B. `x^3/3 - x^2`
C. `x^3/3 - x^2 + 2/3`
D. `x^2 - 2x + 2`
E. `3x^3 - x^2 - 1`
Algebra, MET2 2010 VCAA 4 MC
If `f(x) = 1/2e^(3x) and g(x) = log_e(2x) + 3` then `g (f(x))` is equal to
- `2x^3 + 3`
- `e^(3x) + 3`
- `e^(8x + 9)`
- `3(x + 1)`
- `log_e (3x) + 3`
Probability, MET2 2016 VCAA 16 MC
The random variable, `X`, has a normal distribution with mean 12 and standard deviation 0.25
If the random variable, `Z`, has the standard normal distribution, then the probability that `X` is greater than 12.5 is equal to
- `text(Pr) (Z < text{− 4)}`
- `text(Pr) (Z < text{− 1.5)}`
- `text(Pr) (Z < 1)`
- `text(Pr) (Z >= 1.5)`
- `text(Pr) (Z > 2)`
Probability, MET2 2016 VCAA 15 MC
A box contains six red marbles and four blue marbles. Two marbles are drawn from the box, without replacement.
The probability that they are the same colour is
- `1/2`
- `28/45`
- `7/15`
- `3/5`
- `1/3`
Graphs, MET2 2016 VCAA 8 MC
The UV index, `y`, for a summer day in Melbourne is illustrated in the graph below, where `t` is the number of hours after 6 am.
The graph is most likely to be the graph of
A. `y = 5 + 5 cos ((pi t)/7)`
B. `y = 5 - 5 cos ((pi t)/7)`
C. `y = 5 + 5 cos ((pi t)/14)`
D. `y = 5 - 5 cos ((pi t)/14)`
E. `y = 5 + 5 sin ((pi t)/14)`
Probability, MET2 2016 VCAA 7 MC
Algebra, MET2 2016 VCAA 5 MC
Which one of the following is the inverse function of `g: [3, oo) -> R,\ g(x) = sqrt (2x - 6)?`
- `g^(-1): [3, oo) -> R,\ g^(-1) (x) = (x^2 + 6)/2`
- `g^(-1): [0, oo) -> R,\ g^(-1) (x) = (2x - 6)^2`
- `g^(-1): [0, oo) -> R,\ g^(-1) (x) = sqrt (x/2 + 6)`
- `g^(-1): [0, oo) -> R,\ g^(-1) (x) = (x^2 + 6)/2`
- `g^(-1): R -> R,\ g^(-1) (x) = (x^2 + 6)/2`
Calculus, MET2 2016 VCAA 3 MC
Calculus, MET2 2011 VCAA 11 MC
The average value of the function with rule `f(x) = log_e(x + 2)` over the interval `[0,3]` is
- `log_e(2)`
- `1/3log_e(6)`
- `log_e(3125/4) - 3`
- `1/3log_e(3125/4) - 3`
- `(5log_e(5) - 2log_e(2) - 3)/3`
Calculus, MET2 2011 VCAA 9 MC
Algebra, MET2 2011 VCAA 5 MC
The inverse function of `g: [2,∞) -> R, g(x) = sqrt(2x - 4)` is
- `g^(−1): [2,∞) -> R, g^(−1)(x) = (x^2 + 4)/2`
- `g^(−1): [0,∞) -> R, g^(−1)(x) = (2x - 4)^2`
- `g^(−1): [0,∞) -> R, g^(−1)(x) = sqrt(x/2 + 4)`
- `g^(−1): [0,∞) -> R, g^(−1)(x) = (x^2 + 4)/2`
- `g^(−1): R -> R, g^(−1)(x) = (x^2 + 4)/2`
Graphs, MET2 2011 VCAA 1 MC
The midpoint of the line segment joining `text{(0, − 5)}` to `(d,0)` is
- `(d/2,−5/2)`
- `(0,0)`
- `((d - 5)/2,0)`
- `(0,(5 - d)/2)`
- `((5 + d)/2,0)`
- « Previous Page
- 1
- …
- 39
- 40
- 41
- 42
- 43
- …
- 57
- Next Page »