SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

CHEMISTRY, M7 2021 HSC 26

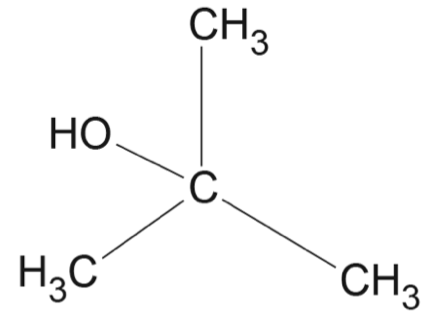
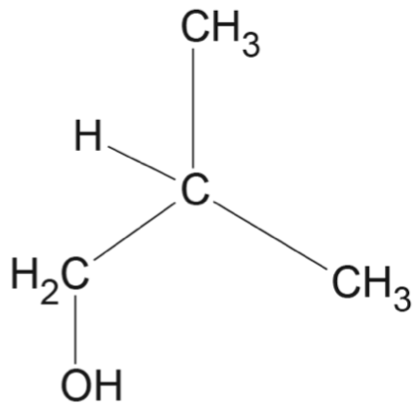
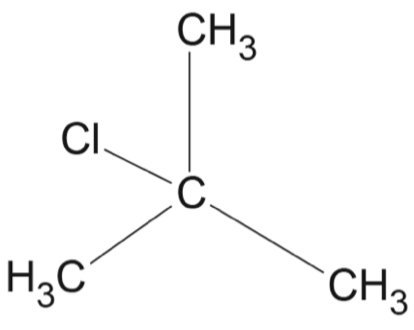
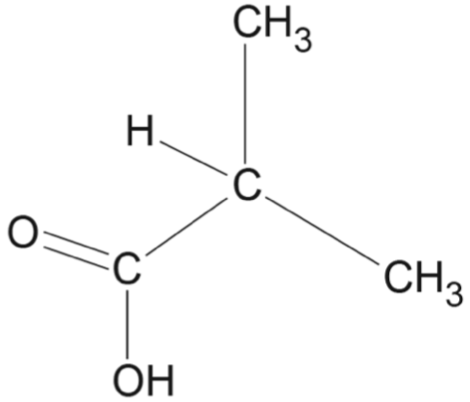
A sequence of chemical reactions, starting with 2-methylprop-1-ene, is shown in the flow chart.

  1. Complete the flow chart by drawing structural formulae for compounds `text{A}`, `text{B}`, `text{C}`, and `text{D}`.   (4 marks)
     
     

     
  2. Reflux is used in the synthesis of methyl 2-methylpropanoate.
  3. Provide TWO reasons for using this technique.   (2 marks)

Show Answers Only

a.   Compound A:

Compound B:

Compound C:

Compound D:


 

b.  Reasons for reflux technique:

  • Reflux heats the reaction mixture which increases the average kinetic energy, and thus increases the reaction rate.
  • Heating causes the volatile substances to form vapour molecules. Refluxing uses a condenser to cool the vapour molecules into liquids, and thus retains the substances.
Show Worked Solution

a.   Compound A:

Compound B:

Compound C:

Compound D:


 

b.  Reasons for reflux technique:

  • Reflux heats the reaction mixture which increases the average kinetic energy, and thus increases the reaction rate.
  • Heating causes the volatile substances to form vapour molecules. Refluxing uses a condenser to cool the vapour molecules into liquids, and thus retains the substances.

♦ Mean mark (b) 46%.

CHEMISTRY, M7 2021 HSC 24

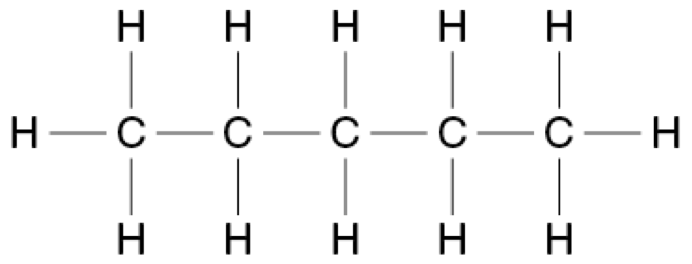
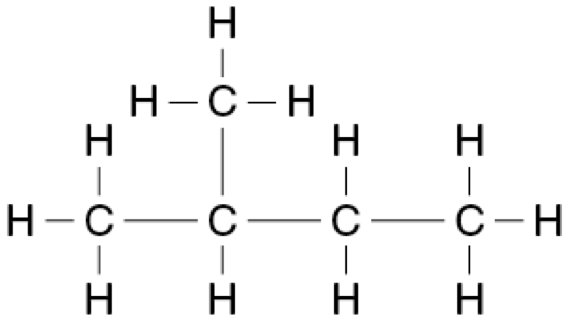
A straight-chained alkane has a molar mass of 72.146 g mol ¯1.

Provide the structural formulae for this alkane and all of its isomers.

Name these molecules using IUPAC conventions.   (4 marks)

Show Answers Only

Straight chained alkane (Pentane):

2-methylbutane:

2,2-dimethylpropane:

Show Worked Solution

Straight chained alkane (Pentane):

2-methylbutane:

2,2-dimethylpropane:

CHEMISTRY, M6 2021 HSC 23

Methanoic acid reacts with aqueous potassium hydroxide. A salt is produced in this reaction.

  1. Write a balanced chemical equation for this reaction.   (2 marks)

  2. Is the salt acidic, basic or neutral? Justify your answer.  (2 marks)

Show Answers Only

a.   `text{HCOOH}_((aq)) + text{KOH}_((aq))  -> text{KHCOO}_((aq)) + text{H}_2text{O}_((l))`, or

`text{HCOOH}_((aq)) + text{KOH}_((aq))  -> text{KHCOO}_((s)) + text{H}_2text{O}_((l))`

 

b.   Potassium methanoate is a basic salt.

This is because the `text{HCOO}^-` is a moderately strong conjugate base as it comes from a weak acid `text{HCOOH}`.

Show Worked Solution

a.   `text{HCOOH}_((aq)) + text{KOH}_((aq))  -> text{KHCOO}_((aq)) + text{H}_2text{O}_((l))`, or

`text{HCOOH}_((aq)) + text{KOH}_((aq))  -> text{KHCOO}_((s)) + text{H}_2text{O}_((l))`
 

b.   Potassium methanoate is a basic salt.

  • This is because the `text{HCOO}^-` is a moderately strong conjugate base as it comes from a weak acid `text{HCOOH}`.

CHEMISTRY, M8 2021 HSC 21

Four organic liquids are used in an experiment. The four liquids are

    • hexane
    • hex-1-ene
    • propan-1-ol
    • propanoic acid
  1. State ONE safety concern associated with organic liquids and suggest ONE way to address this safety concern.   (2 marks)

  2. The organic liquids are held separately in four flasks but the flasks are not labelled. Tests were conducted to identify these liquids. The outcomes of the tests are summarised below.   (2 marks)
     
           
    Identify the FOUR liquids.
     
           
  3. What chemical test, other than those used in part (b), could be used to confirm the identification of ONE of the liquids? Include the expected observation in your answer.   (2 marks)

Show Answers Only

a.    A safety concern is that the organic liquids are flammable.

To address this, keep substance away from open flames and keep away from ignition sources.
 

b.    Flask 1: propanoic acid  (carboxylic acids can’t be oxidised and are polar)

Flask 2: hex-1-ene (alkenes can be oxidised and are non-polar)

Flask 3: propan-1-ol (primary alcohols can be oxidised and are polar)

Flask 4: hexane (alkanes don’t react with acidified oxidants and are non-polar)
 

c.   Hex-1-ene

  • Could be identified using the bromine water test.
  • The addition of brown bromine water to an alkene causes an addition reaction where the solution changes colours from brown to colourless.

Propanoic acid

  • Could be identified through a neutralisation reaction using `text{Na}_2text{CO}_3`.
  • Effervescent reaction will result.

Propan-1-ol

  • Could be identified through an oxidation reaction using acidified dichromate.
  • The reaction would cause the solution to change from green to orange.
Show Worked Solution

a.    A safety concern is that the organic liquids are flammable.

To address this, keep substance away from open flames and keep away from ignition sources.
 

b.    Flask 1: propanoic acid  (carboxylic acids can’t be oxidised and are polar)

Flask 2: hex-1-ene (alkenes can be oxidised and are non-polar)

Flask 3: propan-1-ol (primary alcohols can be oxidised and are polar)

Flask 4: hexane (alkanes don’t react with acidified oxidants and are non-polar)
 

c.   Hex-1-ene

  • Could be identified using the bromine water test.
  • The addition of brown bromine water to an alkene causes an addition reaction where the solution changes colours from brown to colourless.

Propanoic acid

  • Could be identified through a neutralisation reaction using `text{Na}_2text{CO}_3`.
  • Effervescent reaction will result.

Propan-1-ol

  • Could be identified through an oxidation reaction using acidified dichromate.
  • The reaction would cause the solution to change from green to orange.

ENGINEERING, AE 2021 HSC 23d

Carbon fibre epoxy is an example of a composite material used in aircraft construction.

Describe the benefits of using this composite in aircraft construction in terms of both its manufacturing properties and its in-service properties.   (3 marks)

Show Answers Only
  • Carbon fibre epoxy matrices can be formed into more complex shapes and are stronger than alternative materials. This results in an improved aircraft performance.
  • Carbon fibre is often added to resin to produce a material with higher specific strength than its predecessor. This weight loss decreases fuel consumption or allows for an increased number of passengers.
  • In-service properties of composites include non-directional strength or highly directional strength behaviour depending on the composite’s nature and layup.
Show Worked Solution
  • Carbon fibre epoxy matrices can be formed into more complex shapes and are stronger than alternative materials. This results in an improved aircraft performance.
  • Carbon fibre is often added to resin to produce a material with higher specific strength than its predecessor. This weight loss decreases fuel consumption or allows for an increased number of passengers.
  • In-service properties of composites include non-directional strength or highly directional strength behaviour depending on the composite’s nature and layup.

ENGINEERING, AE 2021 HSC 23b

How has the work of aeronautical engineers helped to improve aircraft safety?   (3 marks)

Show Answers Only

Engineers are responsible for the following safety improvements:

  • Autopilot reduces risk of pilot error without removing pilot completely.
  • Changes in materials have created stronger, lighter, more durable aircraft.
  • Many built-in redundancies in case a system in the aircraft fails.
  • Safety and disaster mitigation systems in the event of an accident. 

Successful answers could also include:

  • Changes in materials have created stronger, lighter, more durable aircraft.
  • Vigilance devices ensure pilots are fully awake and concentrated.
  • Knowledge of material failure may be used to mitigate mid-air incidents.
  • Engineers use knowledge of available materials to design new aircraft.
  • Ensure maintenance work is completed to ensure safe aircraft operation.
Show Worked Solution

Engineers are responsible for the following safety improvements:

  • Autopilot reduces risk of pilot error without removing pilot completely.
  • Changes in materials have created stronger, lighter, more durable aircraft.
  • Many built-in redundancies in case a system in the aircraft fails.
  • Safety and disaster mitigation systems in the event of an accident. 

Successful answers could also include:

  • Changes in materials have created stronger, lighter, more durable aircraft.
  • Vigilance devices ensure pilots are fully awake and concentrated.
  • Knowledge of material failure may be used to mitigate mid-air incidents.
  • Engineers use knowledge of available materials to design new aircraft.
  • Ensure maintenance work is completed to ensure safe aircraft operation.

ENGINEERING, CS 2021 HSC 14 MC

The diagram shows a beam.

The beam's second moment of area is 76.96 × 106 mm4. It is subjected to a maximum bending moment of 250 kN m.

What is the maximum bending stress of the beam?

  1. 227.4 MPa
  2. 324.8 MPa
  3. 649.7 MPa
  4. 9745.3 MPa
Show Answers Only

`B`

Show Worked Solution

`M=250\ text{kNm}\ = 250 xx10^(-3)\ text{Nm}`

`y=(200)/(2)\ text{mm}\ =100 xx10^(-3)\ text{m}`

`I=76.96 xx10^(6)\ text{mm}^(4)=76.96 xx10^(-6)\ text{m}^(4)`

`S_text{bending}` `=(My)/I`  
  `=(250 xx10^(-3)xx100 xx10^(-3))/(76.96 xx10^(-6))`  
  `=324.8440…\ text{MPa}`  

 
`=>B`

ENGINEERING, TE 2021 HSC 11 MC

Which radio transmission method is most likely to have static interference?

  1. Amplitude modulation (AM)
  2. Frequency modulation (FM)
  3. Digital audio broadcast (DAB)
  4. Pulse width modulation (PWM)
Show Answers Only

`A`

Show Worked Solution

By Elimination:

  • Digital broadcasting will have very little interference (eliminate `C` and `D`)
  • The higher frequency of FM output results in less static than AM (eliminate `B`)

`=>A`

ENGINEERING, AE 2021 HSC 9 MC

A pitot tube supplies two pressure readings, total pressure and static pressure.

These pressure readings are then used to determine the

  1. sealed pressure.
  2. dynamic pressure.
  3. standard pressure.
  4. hydrostatic pressure.
Show Answers Only

`B`

Show Worked Solution
  • Dynamic Pressure = Total − Static

`=>B`

ENGINEERING, CS 2021 HSC 7 MC

The diagram shows a section of a pin jointed truss in equilibrium. The force in Member 1 is 200 kN in compression.
 

Which row of the table identifies the magnitude and nature of the forces in Member 2 and Member 3?
 

Show Answers Only

`A`

Show Worked Solution
  • The sum of horizontal forces and the sum of vertical forces must both be equal to 0.

`=>A`

ENGINEERING, PPT 2021 HSC 6 MC

A train has a total mass of 400 tonnes. It accelerates from rest to a speed of 25 m/s.

What is the kinetic energy of the train at the speed of 25 m/s?

  1. `125 × 10^(3)\ text{J}`
  2. `250 × 10^(3)\ text{J}`
  3. `125 × 10^(6)\ text{J}`
  4. `250 × 10^(6)\ text{J}`
Show Answers Only

`C`

Show Worked Solution

Using 1 tonne = 1000 kg:

`KE` `= 1/2 xx mxxv ^2`  
  `=0.5xx400\ 000 × 25^2`  
  `=125\ 000\ 000`  
  `=125 xx 10^6\ text{J}`  

 
`=>C`

BIOLOGY, M5 2020 HSC 20 MC

This chart illustrates three correlation patterns indicating the influence of genes and environment on different traits in individuals.
 

What does the data show about how genes and family environment affect the three traits?
 

Show Answers Only

`A`

Show Worked Solution
  • Trait `A` is similar in adoptive siblings that do not share much genetics.
  • Trait `B` is very similar in identical twins with identical genetics.
  • Trait `C` has little similarity between close relations or adoptive siblings.

`=>A`

BIOLOGY, M6 2020 HSC 17 MC

There are about 10 million single nucleotide polymorphisms (SNPs) found in the human genome.

Four SNPs are modelled in the diagram.
 

The SNPs modelled do not affect the phenotype of the individuals shown.

Which is the best explanation for this?

  1. Only one nucleotide is different at each SNP.
  2. The SNPs are part of DNA that is not expressed.
  3. AGA, CAA, TAT and CTC all code for the same amino acid.
  4. The SNPs are present on one strand of the DNA molecule only.
Show Answers Only

`B`

Show Worked Solution
  • Mutations that occur on non-coding DNA are not expressed as proteins.
  • Phenotype is therefore not affected.

`=>B`

BIOLOGY, M6 2020 HSC 13 MC

A type of genetic technology is shown in the diagram.
 


 

What type of cloning is modelled?

  1. Gene cloning because bacteria are used.
  2. Gene cloning because a human gene is being replicated.
  3. Whole organism cloning because identical offspring are produced.
  4. Whole organism cloning because the bacteria use asexual reproduction.
Show Answers Only

`B`

Show Worked Solution
  • A human gene is extracted and inserted into a bacterial plasmid.
  • This allows multiple copies of the gene to be produced via the process of gene cloning.

`=>B`

BIOLOGY, M8 2020 HSC 11 MC

The diagram shows a model of the human eye.
 

Which of the following correctly identifies a labelled part and its function?
 

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex} \ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|c|c|}
\hline
\rule{0pt}{2.5ex}\quad \textit{Label} \quad \rule[-1ex]{0pt}{0pt}& \quad \textit{Name} \quad & \textit{Function} \\
\hline
\rule{0pt}{2.5ex}\text{I}\rule[-1ex]{0pt}{0pt}&\text{Cornea}&\text{Refract light}\\
\hline
\rule{0pt}{2.5ex}\text{I}\rule[-1ex]{0pt}{0pt}& \text{Retina}&\quad \text{Transmit light}\quad \\
\hline
\rule{0pt}{2.5ex}\text{II}\rule[-1ex]{0pt}{0pt}& \text{Retina} &\text{Focus light}\\
\hline
\rule{0pt}{2.5ex}\text{II}\rule[-1ex]{0pt}{0pt}& \text{Cornea} &\text{Absorb light}\\
\hline
\end{array}
\end{align*}

Show Answers Only

\(A\)

Show Worked Solution
  • The cornea is the clear disc at the front of the eye, which helps protect the eye as well as refract incoming light rays.

\(\Rightarrow A\)

BIOLOGY, M8 2020 HSC 8 MC

Quarantine is ineffective as a measure to control non-infectious diseases because they

  1. cannot develop in isolation.
  2. depend on long-term exposure to a pathogen.
  3. may be inherited and affect the organism all their life.
  4. may only be treated by genetic engineering altering cells.
Show Answers Only

`C`

Show Worked Solution
  • Non-infectious diseases are often inherited (non-transmittable) diseases.
  • These affect an organism’s genome and are not transmitted or acquired by pathogens.
  • Quarantine would be an ineffective method of control.

`=>C`

BIOLOGY, M5 2020 HSC 5 MC

Which row of the table best describes DNA in both prokaryotic and eukaryotic cells?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex}\ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex} \textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex} \textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex} \textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex} \textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|c|c|}
\hline \rule{0pt}{2.5ex} \textit{Prokaryotic } \rule[-1ex]{0pt}{0pt}& \textit{Eukaryotic} \\
\hline \rule{0pt}{2.5ex} \text {Circular} \rule[-1ex]{0pt}{0pt}& \text {Circular} \\
\hline \rule{0pt}{2.5ex} \text {Circular} \rule[-1ex]{0pt}{0pt}& \text {Linear} \\
\hline \rule{0pt}{2.5ex} \text {Linear} \rule[-1ex]{0pt}{0pt}& \text {Circular} \\
\hline \rule{0pt}{2.5ex}  \text {Linear} \rule[-1ex]{0pt}{0pt}& \text {Linear} \\
\hline
\end{array}
\end{align*}

Show Answers Only

\(B\)

Show Worked Solution
  • DNA for prokaryotes is contained in a single circular chromosome, as well as in circular plasmids.
  • Eukaryotes have their main coding DNA within densely packed linear chromosomes.

\(\Rightarrow B\)

BIOLOGY, M5 2020 HSC 3 MC

The following four events occur during reproduction in a placental mammal.

  1. Fertilisation
  2. Implantation
  3. Ovulation
  4. Placental formation

In which order do these events occur?

  1. 2, 1, 3, 4
  2. 2, 4, 1, 3
  3. 3, 1, 2, 4
  4. 3, 2, 4, 1
Show Answers Only

`C`

Show Worked Solution
  • Ovulation (the production of the female gamete) must occur first, followed by fertilisation of the gamete.
  • Once it is fertilised, it implants itself in the uterine wall, followed by the formation of the placenta.

`=>C`

BIOLOGY, M5 2020 HSC 2 MC

Sexual reproduction in plants involves

  1. pollination caused by dispersal of seeds.
  2. cloning as it creates copies of the parent plant.
  3. mitosis leading to the formation of pollen grains.
  4. fertilisation as a result of fusion of male and female gametes.
Show Answers Only

`D`

Show Worked Solution
  • The key process in sexual reproduction is the fusion of male and female gametes.

`=>D`

BIOLOGY, M8 2021 HSC 32

The flow chart shows negative feedback by the hormones testosterone and inhibin in a human male.
 


 

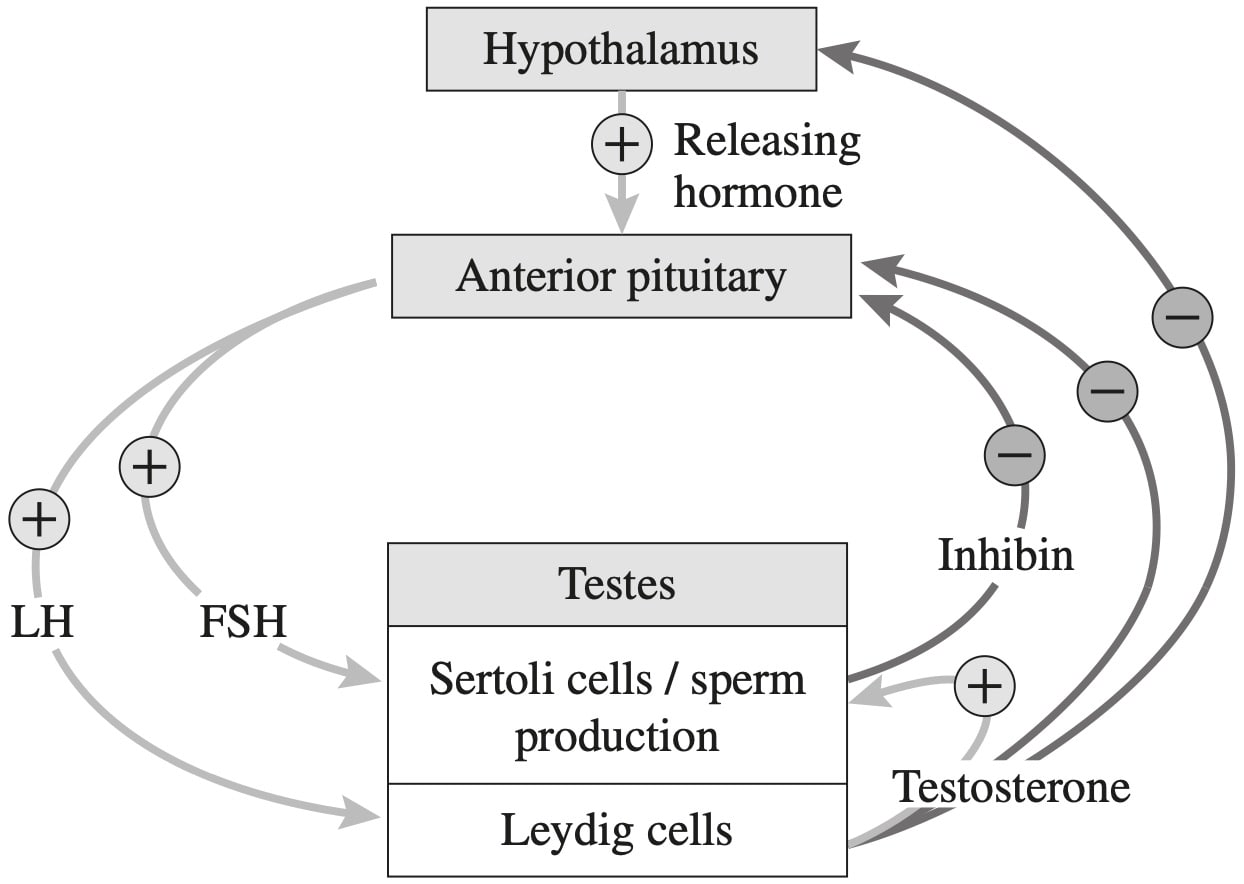
Some athletes take anabolic steroids to increase their muscle mass and strength. These steroids may be testosterone or a synthetic modification of testosterone.

Explain the changes that would occur in the testes of a male athlete continuously taking anabolic steroids. Support your answer with reference to the flow chart.   (5 marks)

Show Answers Only
  • Naturally, as shown in the diagram above, males produce Releasing Hormone via the hypothalamus, which stimulates the anterior pituitary gland to produce hormones which further stimulate the testes to produce hormones inhibin and testosterone as well as sperm (via testosterone).
  • A male taking anabolic steroids similar to testosterone will see an initial increase in sperm and inhibin.
  • However, it will also impact the negative feedback on both the hypothalamus and anterior pituitary, reducing their release of respective stimulatory hormones, reducing sperm, testosterone and inhibin.
  • Although less inhibin would mean a smaller negative feedback on the anterior pituitary caused by this hormone, the ongoing dose of testosterone would ensure a large overall negative feedback effect. 
  • Over time, with repetitive and excessive use of anabolic steroids, males will produce less sperm, testosterone and inhibin, and the testes will lose their normal function.
Show Worked Solution
  • Naturally, as shown in the diagram above, males produce Releasing Hormone via the hypothalamus, which stimulates the anterior pituitary gland to produce hormones which further stimulate the testes to produce hormones inhibin and testosterone as well as sperm (via testosterone).
  • A male taking anabolic steroids similar to testosterone will see an initial increase in sperm and inhibin.
  • However, it will also impact the negative feedback on both the hypothalamus and anterior pituitary, reducing their release of respective stimulatory hormones, reducing sperm, testosterone and inhibin.
  • Although less inhibin would mean a smaller negative feedback on the anterior pituitary caused by this hormone, the ongoing dose of testosterone would ensure a large overall negative feedback effect. 
  • Over time, with repetitive and excessive use of anabolic steroids, males will produce less sperm, testosterone and inhibin, and the testes will lose their normal function.
♦ Mean mark 50%.

Calculus, EXT2 C1 2022 HSC 5 MC

If  `int_(a)^(x)f(t)dt=g(x)`, which of the following is a primitive of  `f(x)g(x)` ?

  1. `(1)/(2)[f(x)]^(2)`
  2. `(1)/(2)[f^(')(x)]^(2)`
  3. `(1)/(2)[g(x)]^(2)`
  4. `(1)/(2)[g^(')(x)]^(2)`
Show Answers Only

`C`

Show Worked Solution
`int_a^x f(t)\ dt` `=g(x)`  
`d/dx [int_a^xf(t)\ dt]` `=g^{′}(x)`  
`f(x)` `=g^{′}(x)`  
`f(x)*g(x)` `=g^{′}(x)g(x)`  
`int f(x)*g(x)\ dx` `=int g^{′}(x)g(x)\ dx`  
  `=1/2[g(x)]^2+C`  

 
`=>C`


COMMENT: Simple examples can illustrate the logic of line 3 of the worked solution.

PHYSICS, M5 2019 HSC 35

The apparatus shown is attached horizontally to the roof inside a stationary car. The plane of the protractor is perpendicular to the sides of the car.
 

The car was then driven at a constant speed `(v)`, on a horizontal surface, causing the string to swing to the right and remain at a constant angle `(theta)` measured with respect to the vertical.

Describe how the apparatus can be used to determine features of the car's motion. In your answer, derive an expression that relates a feature of the car's motion to the angle `theta`.   (4 marks)

Show Answers Only
  • The constant deflection of the mass to the right indicates that the car has a uniform acceleration to the left.
  • Since the car’s speed is constant, it must be travelling in uniform circular motion.
  • The radius of the car’s motion can be found in terms of `theta.`

As there is no vertical acceleration of the mass, the vertical component of its tension will balance its weight:

`T_y=Tcos theta=mg\ \ …\ (1)`

The centripetal force on the mass is given by the horizontal component of its tension:

`T_x=Tsin theta=ma=(mv^2)/r\ \ …\ (2)`

Substitute `T=(mg)/costheta`  from `(1)` into `(2)`:

`T sin theta` `=(mv^2)/(r)`
`(mg xx sin theta)/(cos theta)` `=(mv^(2))/(r)`
`g xx tan theta` `=(v^(2))/(r)`
`r` `=(v^(2))/(g xx tan theta)`

 
Other expressions could include:

  • `v=sqrt(rg tan theta)`
Show Worked Solution
  • The constant deflection of the mass to the right indicates that the car has a uniform acceleration to the left.
  • Since the car’s speed is constant, it must be travelling in uniform circular motion.
  • The radius of the car’s motion can be found in terms of `theta.`

As there is no vertical acceleration of the mass, the vertical component of its tension will balance its weight:

`T_y=Tcos theta=mg\ \ …\ (1)`

The centripetal force on the mass is given by the horizontal component of its tension:

`T_x=Tsin theta=ma=(mv^2)/r\ \ …\ (2)`

Substitute `T=(mg)/costheta`  from `(1)` into `(2)`:

`T sin theta` `=(mv^2)/(r)`
`(mg xx sin theta)/(cos theta)` `=(mv^(2))/(r)`
`g xx tan theta` `=(v^(2))/(r)`
`r` `=(v^(2))/(g xx tan theta)`

 
Other expressions could include:

  • `v=sqrt(rg tan theta)`

♦ Mean mark 52%.

PHYSICS, M6 2019 HSC 33

A proton and an alpha particle are fired into a uniform magnetic field with the same speed from opposite sides as shown. Their trajectories are initially perpendicular to the field.
 


  

Explain ONE similarity and ONE difference in their trajectories as they move in the magnetic field.   (4 marks)

Show Answers Only

Similarity:

  • Both particles experience a constant force, given by  `F=qvB`, perpendicular to their velocity and the magnetic field lines and will undergo circular motion.

Difference:

  • The centripetal force acting on both particles is given by the force they experience due to the magnetic field as follows:
  •    `(mv^2)/(r)=qvB\ \ =>\ \ r=(mv)/(qB)`
  • The alpha particle has four times the mass and two times the charge of the proton
  • Therefore, the radius of its trajectory will be twice that of the protons.
Show Worked Solution

Similarity:

  • Both particles experience a constant force, given by  `F=qvB`, perpendicular to their velocity and the magnetic field lines and will undergo circular motion.

Difference:

  • The centripetal force acting on both particles is given by the force they experience due to the magnetic field as follows:
  •    `(mv^2)/(r)=qvB\ \ =>\ \ r=(mv)/(qB)`
  • The alpha particle has four times the mass and two times the charge of the proton
  • Therefore, the radius of its trajectory will be twice that of the protons.

BIOLOGY, M6 2021 HSC 15 MC

An example of the mutagenic effect of ultraviolet radiation (UV) on DNA is shown in the diagram.
 

What is the mutagenic effect that is modelled?

  1. Thymine is duplicated.
  2. Bonds are formed between adjacent bases.
  3. Nucleotides form bonds in the backbone of DNA.
  4. Thymines on the two strands of DNA form bonds.
Show Answers Only

`B`

Show Worked Solution
  • The diagram shows bonds that have formed between adjacent thymine bases on a single strand of DNA.

`=>B`

Mean mark 56%.

BIOLOGY, M6 2021 HSC 11 MC

Many transgenic crops have been genetically engineered to have traits such as herbicide resistance. In at least four different crops the transgene has been found in nearby wild plant relatives of the cultivated crops.

What is the most likely reason for this observation?

  1. Crossing over in the wild plants
  2. Gene flow from the crops to the wild plants
  3. Genetic drift from the crops to the wild plants
  4. Mutations in the wild plants that match the transgenes
Show Answers Only

`B`

Show Worked Solution
  • Gene flow is the transfer of genetic material from one population to another.
  • Therefore the genetically engineered crops have most likely pollinated the nearby wild plant relatives.

`=>B`


Mean mark 57%.

Calculus, EXT2 C1 2022 HSC 4 MC

Of the following expressions, which one need NOT contain a term involving a logarithm in its anti-derivative?

  1. `(x+2)/(x^(2)+4x+5)`
  2. `(x+2)/(x^(2)-4x-5)`
  3. `(x-1)/(x^(3)-x^(2)+x-1)`
  4. `(x+1)/(x^(3)-x^(2)+x-1)`
Show Answers Only

`C`

Show Worked Solution

`text{Consider the denominator of}\ C:`

`x^(3)-x^(2)+x-1` `=x^2(x-1)+(x-1)`  
  `=(x^2+1)(x-1)`  

 
`(x-1)/(x^(3)-x^(2)+x-1)=(x-1)/((x^2+1)(x-1))=1/(x^2+1)`

`int 1/(x^2+1)\ dx=tan^(-1)(x)+c`

`=>C`

Proof, EXT2 P1 2022 HSC 3 MC

Let `A, B, P` be three points in three-dimensional space with `A \ne B`.

Consider the following statement.

If `P` is on the line `A B`, then there exists a real number `\lambda` such that  `vec{A P}=\lambda \vec{A B}`.

Which of the following is the contrapositive of this statement?

  1. If for all real numbers `\lambda, \vec{A P}=\lambda \vec{A B}`, then `P` is on the line `A B`.
  2. If for all real numbers `\lambda, \vec{A P} \ne \lambda \vec{A B}`, then `P` is not on the line `A B`.
  3. If there exists a real number `\lambda` such that  `\vec{A P}=\lambda \vec{A B}`, then `P` is on the line `A B`.
  4. If there exists a real number `\lambda` such that  `\vec{A P} \ne \lambda \vec{A B}`, then `P` is not on the line `A B`.
Show Answers Only

`B`

Show Worked Solution

`text{Statement:}`

`text{If}\ P\ text{is on}\ AB\ \ =>\ \ EE lambda\ \ text{such that}\ \ vec{A P}=\lambda \vec{A B}`

 
`text{Contrapositive statement:}`

`text{If}\ not \ EE lambda\ \ text{such that}\ \ vec{A P}=\lambda \vec{A B}\ \ =>\ \ P\ text{is not on}\ AB`

 
`text{In other words …}`

`text{If for all real numbers}\ lambda, \vec{A P} \ne \lambda \vec{A B}, text{then}\ P\ text{is not on the line}\ A B.`

`=>B`

Proof, EXT2 P1 2022 HSC 2 MC

The following proof aims to establish that  – 4 = 0

`text{Let}` `a=-4`    
`=>` `a^2 = 16 \ text{and} ` `\ 4a + 4 = -12` `text{Line 1}`
`=>` `a^2 + 4a + 4 =` `4` `text{Line 2}`
`=>` `(a + 2)^2 =` `2^2` `text{Line 3}`
`=>` `a + 2 =` `2` `text{Line 4}`
`=>` `a =` `0`  

 
At which line is the implication incorrect?

  1. Line 1
  2. Line 2
  3. Line 3
  4. Line 4
Show Answers Only

`D`

Show Worked Solution

`text{Consider Line 4:}`

`text{Given}\ \ (a + 2)^2=2^2\ \ =>\ \ a+2=+-2`

`=>D`

PHYSICS, M6 2020 HSC 33

A strong magnet of mass 0.04 kg falls 0.78 m under the action of gravity from position `X` above a hollow copper cylinder. It then travels a distance of 0.20 m through the cylinder from `Y` to `Z` before falling freely again.
 

The magnet takes 0.5 seconds to pass through the cylinder. The displacement-time graph of the magnet is shown.
 

Analyse the motion of the magnet by applying the law of conservation of energy.

Your analysis should refer to gravity and the copper cylinder, and include both qualitative and quantitative information.   (9 marks)

Show Answers Only

During the first 0.4 seconds:

  • The magnet is accelerating downwards at 9.8 m s–2 due to gravity.
  • The magnet’s gravitational potential energy is being converted into kinetic energy consistent with the law of conservation of energy.
  • Quantitatively:
  •   `Delta E_(k)= Delta U=mg Delta h=0.04 xx9.8 xx0.78=0.30576\ \text{J}`
  • Hence 0.30576 joules of the magnet’s gravitational potential energy is converted into kinetic energy as it falls under gravity.

As magnet reaches the copper cylinder:

  • Its downwards motion causes the formation of induced currents in the cylinder which produce a magnetic field that opposes the magnet’s motion (Lenz’s law).
  • This causes the magnet to decelerate to 0.4 m s–1 and lose kinetic energy. 
  • Finding the magnets speed before entering the copper cylinder:
`E_(k)` `=(1)/(2)mv^2`  
`0.30576` `=(1)/(2)xx 0.04xx v^2`  
`v` `=3.91\ \text{m s}^{-1}`  

 

  • Quantifying the kinetic energy loss:
`Delta E_(k)` `=(1)/(2)mv^2-(1)/(2)m u^2`  
  `=(1)/(2)xx 0.04xx 3.91^2-(1)/(2)xx 0.04xx 0.4^2`  
  `=0.30256\ \text{J}`  

 

  • Applying the law of conservation of energy shows that 0.30256 J of the magnet’s kinetic energy is being converted to heat energy within the cylinder as the magnet decelerates.
  • Finally, as the magnet passes through the copper cylinder, its gravitational potential energy decreases while its velocity remains constant.
  • Quantifying the decrease in gravitational potential energy:
  •   `Delta U=mg Delta h=0.04xx 9.8xx 0.2=0.0784`
  • Hence, 0.0784 J of the magnet’s gravitational potential energy is converted into heat energy in the cylinder, consistent with the law of conservation of energy.
Show Worked Solution

During the first 0.4 seconds:

  • The magnet is accelerating downwards at 9.8 m s–2 due to gravity.
  • The magnet’s gravitational potential energy is being converted into kinetic energy consistent with the law of conservation of energy.
  • Quantitatively:
  •   `Delta E_(k)= Delta U=mg Delta h=0.04 xx9.8 xx0.78=0.30576\ \text{J}`
  • Hence 0.30576 joules of the magnet’s gravitational potential energy is converted into kinetic energy as it falls under gravity.

As magnet reaches the copper cylinder:

  • Its downwards motion causes the formation of induced currents in the cylinder which produce a magnetic field that opposes the magnet’s motion (Lenz’s law).
  • This causes the magnet to decelerate to 0.4 m s–1 and lose kinetic energy. 
  • Finding the magnets speed before entering the copper cylinder:
`E_(k)` `=(1)/(2)mv^2`  
`0.30576` `=(1)/(2)xx 0.04xx v^2`  
`v` `=3.91\ \text{m s}^{-1}`  

 

  • Quantifying the kinetic energy loss:
`Delta E_(k)` `=(1)/(2)mv^2-(1)/(2)m u^2`  
  `=(1)/(2)xx 0.04xx 3.91^2-(1)/(2)xx 0.04xx 0.4^2`  
  `=0.30256\ \text{J}`  

 

  • Applying the law of conservation of energy shows that 0.30256 J of the magnet’s kinetic energy is being converted to heat energy within the cylinder as the magnet decelerates.
  • Finally, as the magnet passes through the copper cylinder, its gravitational potential energy decreases while its velocity remains constant.
  • Quantifying the decrease in gravitational potential energy:
  •   `Delta U=mg Delta h=0.04xx 9.8xx 0.2=0.0784`
  • Hence, 0.0784 J of the magnet’s gravitational potential energy is converted into heat energy in the cylinder, consistent with the law of conservation of energy.
♦ Mean mark 51%.

PHYSICS M5 2022 HSC 35

A capsule travels around the International Space Station (ISS) in a circular path of radius 200 m as shown.
 


 

Analyse this system to test the hypothesis below.  (5 marks)

The uniform circular motion of the capsule around the ISS can be accounted for in terms of the gravitational force between the capsule and the ISS.

Show Answers Only

Find the gravitational force between the capsule and the ISS:

`F` `=(GMm)/(r^2)`  
  `=(6.67 xx10^-11 xx4.2 xx10^5 xx 1.2 xx10^4)/(200^2)`  
  `=8.4 xx10^(-6)  text{N}`  

 
Find the centripetal force required to keep the capsule in its orbit:

   `F_(c)=(mv^2)/(r)=(1.2 xx10^4 xx 0.233^2)/(200)=3.26  text{N}`

  • The gravitational force is not sufficient to provide the necessary centripetal force to keep the capsule in orbit around the ISS.
  • The hypothesis is invalid.
Show Worked Solution

Find the gravitational force between the capsule and the ISS:

`F` `=(GMm)/(r^2)`  
  `=(6.67 xx10^-11 xx4.2 xx10^5 xx 1.2 xx10^4)/(200^2)`  
  `=8.4 xx10^(-6)  text{N}`  

 
Find the centripetal force required to keep the capsule in its orbit:

`F_(c)=(mv^2)/(r)=(1.2 xx10^4 xx 0.233^2)/(200)=3.26  text{N}`

  • The gravitational force is not sufficient to provide the necessary centripetal force to keep the capsule in orbit around the ISS.
  • The hypothesis is invalid.

PHYSICS M6 2022 HSC 34

Three charged particles, `X, Y` and `Z`, travelling along straight, parallel trajectories at the same speed, enter a region in which there is a uniform magnetic field which causes them to follow the paths shown. Assume that the particles do not exert any significant force on each other.
 


 

Explain the different paths that the particles follow through the magnetic field.   (7 marks)

Show Answers Only
  • The charged particles each experience a force equal to  `F=qvB`  as they travel perpendicular to the magnetic field lines.
  • This force acts perpendicular to the direction of their velocity, so the charged particles undergo uniform circular motion with the force due to the magnetic field acting as a centripetal force.
  • The radii of their paths can be described by the equation:
`F_(c)` `=F_(b)`  
`(mv^2)/(r)` `=qvB`  
`r` `=(mv)/(qB)`  

 

  • As the strength of the magnetic field `(B)` and the speed `(v)` of the particles is the same, their trajectory is only affected by their mass to charge ratio `((m)/(q))`  which affects their radius of motion and their sign, which determines the direction which they deflect.
  • Both `X` and `Y` initially curve upwards, using the right hand palm rule, these must both be positive charges.
  • `Y` has a greater radius than `X`, so `Y`’s charge to mass ratio is greater than `X`’s.
  • `Z` initially curves downwards, using the right hand palm rule, it must have a negative charge.
  • `Z` has the same radius of motion as `X`, so the charge to mass ratios of `Z` and `X` are the same.
  • `Z` has a smaller radius than `Y`, so `Z`’s charge to mass ratio is less than that of `Y`.
Show Worked Solution
  • The charged particles each experience a force equal to  `F=qvB`  as they travel perpendicular to the magnetic field lines.
  • This force acts perpendicular to the direction of their velocity, so the charged particles undergo uniform circular motion with the force due to the magnetic field acting as a centripetal force.
  • The radii of their paths can be described by the equation:
`F_(c)` `=F_(b)`  
`(mv^2)/(r)` `=qvB`  
`r` `=(mv)/(qB)`  

 

  • As the strength of the magnetic field `(B)` and the speed `(v)` of the particles is the same, their trajectory is only affected by their mass to charge ratio `((m)/(q))`  which affects their radius of motion and their sign, which determines the direction which they deflect.
  • Both `X` and `Y` initially curve upwards, using the right hand palm rule, these must both be positive charges.
  • `Y` has a greater radius than `X`, so `Y`’s charge to mass ratio is greater than `X`’s.
  • `Z` initially curves downwards, using the right hand palm rule, it must have a negative charge.
  • `Z` has the same radius of motion as `X`, so the charge to mass ratios of `Z` and `X` are the same.
  • `Z` has a smaller radius than `Y`, so `Z`’s charge to mass ratio is less than that of `Y`.

Mean mark 60%.

PHYSICS M5 2022 HSC 33

In a hammer throw sport event, a 7.0 kg projectile rotates in a circle of radius 1.6 m, with a period of 0.50 s. It is released at point `P`, which is 1.2 m above the ground, where its velocity is at 45° to the horizontal.
 


 

  1. Show that the vertical component of the projectile's velocity at `P` is `14.2 \ text{m s}^(-1)`.   (2 marks)
  1. Calculate the horizontal range of the projectile from point `P`.    (4 marks)
Show Answers Only

a.   Proof (See Worked Solution)

b.   42.3 m

Show Worked Solution

a.   `v=(2pir)/(T)=(2 xxpi xx1.6)/(0.5)=20.106  text{ms}^(-1)`

`v_(y)=20.106 xx sin 45^@=14.2\ text{ms}^(-1)`
 

b.   `text{Time of flight}\ =>\ \text{Find}\ t\ \text{when}\ s_(y)=-1.2`

`s_(y)` `=u_(y)t+(1)/(2)a_(y)t^2`
`-1.2` `=14.2t-(1)/(2) xx9.8t^2`
`0` `=4.9t^2-14.2t-1.2`

 
`t=(14.2+-sqrt(14.2^2+4 xx4.9 xx1.2))/(2 xx4.9)=2.98  text{s}\ \ (t>0)`

 
`text{Since launch angle = 45°}\ =>\ \ u_(x)=u_(y)`

`:. s_(x)=u_(x)t=14.2 xx2.98=42.3  text{m}`

PHYSICS, M6 2022 HSC 32

One type of stationary exercise bike uses a pair of strong, movable magnets placed on opposite sides of a thick, aluminium flywheel to provide a torque to make it harder to pedal.
 


 

  1. Explain the principle by which these magnets make it harder to pedal.  (3 marks)
  1. The bike rider wants to increase the opposing torque on the flywheel. Justify an adjustment that could be made to the magnets to achieve this.  (3 marks)
Show Answers Only

a.    Magnetic breaking is a consequence of Lenz’s Law.

  • The changing magnetic flux through the wheel, as a result of its rotation, causes eddy currents to be induced (Faraday’s Law).
  • According to Lenz’s Law, these eddy currents produce a force which opposes the rotation of the wheel, making it more difficult to pedal.

b.    Adjustment to increase opposing torque:

  • Moving the magnets closer to the outer edge of the flywheel will increase the opposing torque on it. As the linear speed of the wheel is greater near the edge, the rate of change of flux passing through it will increase.
  • This increases the magnitude of induced emf as  `epsilon=-N(Delta theta)/(Delta t).`
  • Consequently, the opposing force and torque will increase.
  • Moving the magnets closer to the edge of the flywheel also increases the distance between the point of application of the opposing force and the axis of rotation of the wheel. As  `tau=rF`  this further increases opposing torque.
Show Worked Solution

a.    Magnetic breaking is a consequence of Lenz’s Law.

  • The changing magnetic flux through the wheel, as a result of its rotation, causes eddy currents to be induced (Faraday’s Law).
  • According to Lenz’s Law, these eddy currents produce a force which opposes the rotation of the wheel, making it more difficult to pedal.

b.    Adjustment to increase opposing torque:

  • Moving the magnets closer to the outer edge of the flywheel will increase the opposing torque on it. As the linear speed of the wheel is greater near the edge, the rate of change of flux passing through it will increase.
  • This increases the magnitude of induced emf as  `epsilon=-N(Delta theta)/(Delta t).`
  • Consequently, the opposing force and torque will increase.
  • Moving the magnets closer to the edge of the flywheel also increases the distance between the point of application of the opposing force and the axis of rotation of the wheel. As  `tau=rF`  this further increases opposing torque.

PHYSICS M8 2022 HSC 31

Following the Geiger-Marsden experiment, Rutherford proposed a model of the atom.
 


 

Bohr modified this model to explain the spectrum of hydrogen observed in experiments.
 


 

The Bohr-Rutherford model of the atom consists of electrons in energy levels around a positive nucleus.

How do features of this model account for all the experimental evidence above? Support your answer with a sample calculation and a diagram, and refer to energy, forces and photons.   (9 marks)

Show Answers Only

The Geiger-Marsden experiment, which involved firing alpha particles at a thin sheet of gold foil produced results which can be explained by the Bohr-Rutherford model:

  • The majority of fired alpha particles passed through the gold foil undeflected. Rutherford concluded from this that the atom had a small, central nucleus.
  • Some alpha particles were deflected and some of these were deflected at very large angles. Rutherford concluded from this that the nucleus was dense and positively charged exerting a repulsive electromagnetic force on the fired alpha particles.
  • The model accounts for Rutherford’s conclusions, placing electrons in orbits around a small positive nucleus. 

Rutherford’s model alone could not explain the emission spectra of elements such as hydrogen. Bohr’s contribution to the Bohr-Rutherford model amended this:
 

 

  • Bohr proposed that electrons orbited the atomic nucleus in quantised orbits at fixed energies. He proposed that electrons could move from a higher energy orbit (eg. n=1) to a lower energy orbit (n=3) by emitting a photon with energy  `E=hf`  equal to the energy difference between the two orbits.
  • Additionally, he proposed that electrons could move from a lower energy orbit to a higher energy orbit by absorbing a photon with energy  `E=hf`  equal to the energy difference between the two orbits. 
  • This is able to account for the given emission spectra of hydrogen, where emission lines correspond to electron transitions from higher energy orbits to the second energy orbit which produce photons within the spectrum of visible light. 

Using Rydberg’s equation it is possible to predict the emission lines of hydrogen, using an electron moving from the sixth to the second Bohr energy orbit as an example: 

`(1)/(lambda)` `=R((1)/(n_(f)^(2))-(1)/(n_(i)^(2)))`  
  `=(1.097 xx10^7)((1)/(2^(2))-(1)/(6^(2)))`  
  `=(2 xx1.097 xx10^7)/(9)`  
  `=2.438 xx10^6`  
`lambda` `=410  text{nm}`  
     
  •  This value corresponds to the leftmost line on the given spectrum, reflecting how Bohr’s model can account for the emission spectra of hydrogen.
Show Worked Solution

The Geiger-Marsden experiment, which involved firing alpha particles at a thin sheet of gold foil produced results which can be explained by the Bohr-Rutherford model:

  • The majority of fired alpha particles passed through the gold foil undeflected. Rutherford concluded from this that the atom had a small, central nucleus.
  • Some alpha particles were deflected and some of these were deflected at very large angles. Rutherford concluded from this that the nucleus was dense and positively charged exerting a repulsive electromagnetic force on the fired alpha particles.
  • The model accounts for Rutherford’s conclusions, placing electrons in orbits around a small positive nucleus. 

Rutherford’s model alone could not explain the emission spectra of elements such as hydrogen. Bohr’s contribution to the Bohr-Rutherford model amended this:
 

 

  • Bohr proposed that electrons orbited the atomic nucleus in quantised orbits at fixed energies. He proposed that electrons could move from a higher energy orbit (eg. n=1) to a lower energy orbit (n=3) by emitting a photon with energy  `E=hf`  equal to the energy difference between the two orbits.
  • Additionally, he proposed that electrons could move from a lower energy orbit to a higher energy orbit by absorbing a photon with energy  `E=hf`  equal to the energy difference between the two orbits. 
  • This is able to account for the given emission spectra of hydrogen, where emission lines correspond to electron transitions from higher energy orbits to the second energy orbit which produce photons within the spectrum of visible light. 

Using Rydberg’s equation it is possible to predict the emission lines of hydrogen, using an electron moving from the sixth to the second Bohr energy orbit as an example: 

`(1)/(lambda)` `=R((1)/(n_(f)^(2))-(1)/(n_(i)^(2)))`  
  `=(1.097 xx10^7)((1)/(2^(2))-(1)/(6^(2)))`  
  `=(2 xx1.097 xx10^7)/(9)`  
  `=2.438 xx10^6`  
`lambda` `=410  text{nm}`  
     
  •  This value corresponds to the leftmost line on the given spectrum, reflecting how Bohr’s model can account for the emission spectra of hydrogen.

♦ Mean mark 51%.

PHYSICS M7 2022 HSC 30

In a thought experiment, light travels from `X` to a mirror `Y` and back to `X` on a moving train carriage. The path of the light relative to an observer on the train is shown.
 


 

Relative to an observer outside the train, the path of the light is shown below, at three consecutive times as the train carriage moves along the track.
 

  1. Describe qualitatively how the constancy of the speed of light and the thought experiment above led Einstein to predict time dilation.  (3 marks)

  1. The train is travelling with a velocity  `v=0.96 c`. To the observer inside the train, the return journey for the light between `X` and `Y` takes 15 nanoseconds.

  2. How long would this return journey take according to the observer outside the train?  (3 marks)

Show Answers Only

a.  Consider each observer:

  • The observer on the train sees light travel a distance from `X` to `Y` and back to `X` again.
  • The observer outside the train sees light travel a longer path due to the horizontal motion of the train.
  • As the speed of light is constant for both observers, the observer outside the train must observe the light pulse to take a longer time, `t=(text{distance})/(c).`
  • This provided the basis for Einstein’s predictions of time dilation.

b.   53.6  nanoseconds

Show Worked Solution

a.  Consider each observer:

  • The observer on the train sees light travel a distance from `X` to `Y` and back to `X` again.
  • The observer outside the train sees light travel a longer path due to the horizontal motion of the train.
  • As the speed of light is constant for both observers, the observer outside the train must observe the light pulse to take a longer time, `t=(text{distance})/(c).`
  • This provided the basis for Einstein’s predictions of time dilation.

♦ Mean mark (a) 48%.

b.    \(t=\dfrac{t_0}{\sqrt{1-\dfrac{v^2}{c^2}}}=\dfrac{15}{\sqrt{1-\dfrac{(0.96 c)^2}{c^2}}} = 53.6\ \text{nanoseconds} \)

PHYSICS M7 2022 HSC 27

A laser producing red light of wavelength 655 nm is directed onto double slits separated by a distance, `d=5.0 xx 10^{-5} \ text{m}`. A screen is placed behind the double slits.
 


 

  1. Newton proposed a model of light. Use a labelled sketch to show the pattern on the screen that would be expected from Newton's proposed model.   (2 marks)
     

     
  2. When the laser light is turned on, a series of vertical bright lines are seen on the screen.
     
 
  1. Calculate the angle, `\theta`, between the centre line and the bright line at `A`.   (3 marks)
  1. The laser is replaced with one producing green light of wavelength 520 nm.
  2. Explain the difference in the pattern that would be produced.   (2 marks)
Show Answers Only

a.   
       

 
b.   `theta=1.50^@`

c.   Consider  `d sin theta = m lambda :`

  • `sin theta prop lambda`
  • Using light with a shorter wavelength decreases the angular separation of bright fringes.
  •  The bright lines will appear closer together.
Show Worked Solution
a.   
     

Mean mark part (a) 53%.

b.   Using  `d  sin  theta=mlambda:`

`5.0 xx10^(-5)  sin  theta` `=2 xx6.55xx10^(-7)`
   `sin  theta` `=(2 xx6.55xx10^(-7))/(5.0 xx10^(-5))`
   `theta` `=1.50^@`

 

c.   Consider  `d sin theta = m lambda :`

  • `sin theta prop lambda`
  • Using light with a shorter wavelength decreases the angular separation of bright fringes.
  • The bright lines will appear closer together.

PHYSICS, M7 2018 HSC 2 MC

Which graph is consistent with predictions resulting from Planck's hypothesis regarding radiation from hot objects?
 

 

Show Answers Only

`B`

Show Worked Solution
  • Planck’s hypothesis is consistent with Wein’s Law,  `lambda_(max)=(b)/(T)`, or  `lambda_(max) prop (1)/(T)`.
  • So, hotter objects have a greater peak wavelength.

`=>B`

PHYSICS, M7 2016 HSC 11 MC

What is the wavelength, in metres, of a photon with an energy of 3.5 eV?

  1. `1.2 × 10^(-6)`
  2. `3.5 × 10^(-7)`
  3. `1.18 × 10^(-15)`
  4. `5.67 × 10^(-26)`
Show Answers Only

`B`

Show Worked Solution
`E` `=3.5 xx1.602 xx10^(-19)`  
  `=5.607 xx10^(-19)  text{J}`  

 
`E=hf=(hc)/(lambda)\ \ => \ \ lambda=(hc)/(E)`

`:.lambda` `=(6.626 xx10^(-34)xx3xx10^(8))/(5.607 xx10^(-19))`  
  `=3.5 xx10^(-7)  text{m}`  

 
`=>B`

PHYSICS, M7 2016 HSC 13 MC

When light of a specific frequency strikes a metal surface, photoelectrons are emitted.

If the light intensity is increased but the frequency remains the same, which row of the table is correct?

\begin{align*}
\begin{array}{l}
\rule{0pt}{1.5ex}\text{} & \text{} \\
\text{}\rule[-0.5ex]{0pt}{0pt}& \text{} \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|l|l|}
\hline
\rule{0pt}{1.5ex}\textit{Number of photoelectrons} & \textit{Maximum kinetic energy} \\
\textit{emitted}\rule[-0.5ex]{0pt}{0pt}& \textit{of the photoelectrons} \\
\hline
\rule{0pt}{2.5ex}\text{Remains the same}\rule[-1ex]{0pt}{0pt}&\text{Remains the same}\\
\hline
\rule{0pt}{2.5ex}\text{Remains the same}\rule[-1ex]{0pt}{0pt}& \text{Increases}\\
\hline
\rule{0pt}{2.5ex}\text{Increases}\rule[-1ex]{0pt}{0pt}& \text{Remains the same} \\
\hline
\rule{0pt}{2.5ex}\text{Increases}\rule[-1ex]{0pt}{0pt}& \text{Increases} \\
\hline
\end{array}
\end{align*}

Show Answers Only

\(C\)

Show Worked Solution
  • An increase in light intensity increases the number of photons striking the metal surface.
  • This increases the number of photoelectrons emitted.
  • Since no change in frequency, the energy of photons striking metal surface remains constant.
  • Maximum kinetic energy of emitted photoelectrons remains the same.

\(\Rightarrow C\)

PHYSICS, M7 2018 HSC 17 MC

The graph shows the maximum kinetic energy of electrons ejected from different metals as a function of the frequency of the incident light.
 

What can be deduced from this graph?

  1. The maximum kinetic energy of ejected electrons is proportional to the number of photons incident on the metal surface.
  2. More photons are required to cause an electron to be ejected from zinc than from potassium.
  3. Any photon that can eject an electron from the surface of zinc must also be able to cause an electron to be ejected from potassium.
  4. For any given frequency that causes electrons to be ejected from all three metals, the number of electrons ejected is always greatest for potassium.
Show Answers Only

`C`

Show Worked Solution
  • The graph shows that zinc has a greater work function than potassium.
  • So, any photon with sufficient energy to eject a photon from the surface of zinc will also have sufficient energy to overcome the work function of potassium and eject a photon from its surface.

`=>C`

PHYSICS, M7 2014 HSC 26

  1. Calculate the energy of a photon of wavelength 415 nm.  (2 marks)
  2. An experiment was conducted using a photoelectric cell as shown in the diagram.

The graph plots the maximum kinetic energy of the emitted photoelectrons against radiation frequency for the aluminium surface.

The experiment is planned to be repeated using a voltage of 0.0 V.

Draw a line on the graph to show the predicted results of the planned experiment, and determine the radiation frequency which would produce photoelectrons with a maximum kinetic energy of 1.2 eV using a voltage of 0.0 V.  (3 marks)

Show Answers Only

`text(See Worked Solutions)`

Show Worked Solution
a.   `c` `= f lambda`
    `= hf`
    `= (hc)/lambda`
    `= (6.626 xx 10^(-34) Js xx 3 xx 10^8 ms^(-1))/(415 xx 10^(-9)m)`
    `= 4.79 xx 10^(-19) J`

 

b.  

`text(To find intercept)`

`4.1 text(V)` `= 4.1 xx 1.602 xx 10^(-19)\ text(J)` `text(of energy required to be)`
`text(supplied by the photon.)`
  `= 6.56 xx 10^(-19)\ text(J)`  
`hf` `= 6.56 xx 10^(-19)\ text(J)`  
`f` `= (6.56 xx 10^(-19))/(6.626 xx 10^(-34))`  
  `= 9.9 xx 10^14`  

`text(Gradient = same as A1)`

`text{From graph maximum KE(eV)}` `= 1.2\ text(eV)`
`text(Frequency)` `= 12.8\ text(Hz)`
  `= 12.8 xx 10^14\ text(Hz)`

PHYSICS M7 2022 HSC 26

Light of frequency  `7.5 xx10^(14) \ text{Hz}`  is incident on a calcium metal sheet which has a work function of  `2.9 \ text{eV}`. Photoelectrons are emitted.

The metal is in a uniform electric field of `5.2 \ text{NC}^{-1}`, perpendicular to the surface of the metal, as shown.
 


  

  1. Show that the maximum kinetic energy of an emitted photoelectron is  `3.2 xx10^(-20) \ text{J}`.  (3 marks)
  1. Calculate the maximum distance, `d`, an emitted photoelectron can travel from the surface of the metal.  (3 marks)
Show Answers Only
  1. Proof (See Worked Solution)
  2. `0.038  text{m.}`
Show Worked Solution
a.    `K_(max)` `=hf-Phi`
    `=6.626 xx10^(-34)xx7.5 xx10^(14)-2.9xx 1.602 xx10^(-19)`
    `=3.2 xx10^(-20)  text{J}`

 

b.   Maximum Distance:

  • The electric field will do `3.2 xx10^(-20)\ text{J}` of work to stop the electron.
`W` `=qEd`     
`3.2 xx10^(-20)` `=1.602 xx10^(-19) xx 5.2 xx d_max`  
`:.d_max` `=(3.2 xx10^(-20))/(1.602 xx10^(-19)xx 5.2)`  
  `=0.038  text{m.}`  

♦ Mean mark (b) 51%.

PHYSICS M8 2022 HSC 24

The radioactive decay curve for americium-242 is shown.
 


 

  1. Use the graph to find the half-life of Am-242 and hence show that the decay constant, `\lambda`, is `0.043` `text{h}^(-1).`   (2 marks)
  1. Calculate how long it takes until the mass of Am-242 is 8 micrograms.   (2 marks)
Show Answers Only

a.   `0.043  text{h}^(-1)`

b.  `53.55\ text{h}`

Show Worked Solution

a.   The half life of Am-242 is 16 hours.

`lambda=(ln 2)/(t_(1//2))=(ln 2)/(16)=0.043  text{h}^(-1)`
 

b.    `N` `=N_(0)e^(-lambda t)`
     `8` `=80e^(-0.043 t)`
  `e^(-0.043 t)` `=8/80`
  `-0.043t` `=ln(1/10)`
     `t` `=((-1)/(0.043))ln ((1)/(10))`
    `=53.55\ text{h}`

PHYSICS, M7 2022 HSC 23

Outline a method that could be used to determine a value for the speed of light. In your answer, identify ONE factor that would limit the accuracy of the experimental data.  (4 marks)

Show Answers Only

Foucault’s cogwheel experiment (one possible method):

  • Set up a cogwheel and a mirror 8 km apart.
  • Shine a pulse of light through one of the gaps of the cogwheel.
  • Begin to rotate the cogwheel and record the lowest speed at which the returning light is completely blocked.
  • This is the speed at which, on the light’s journey, the cogwheel has rotated through half the distance between adjacent cogs (or the distance between a cog and the adjacent gap).
  • Using the rotation speed of the wheel and the distance between a cog and a gap, calculate the time taken for light to complete its journey.
  • Calculate the speed of light using  `c=(d)/(t)`, where  `d` = 16 km.

Limitation:

  • The accuracy of this experiment is limited by errors in measurement of the distance between the cogwheel and the mirror, as well as errors measuring the speed of rotation of the cogwheel.

Other valid methods:

  • Fizeau’s rotating mirror experiment.
  • Newton’s experiment.
  • Ole Romer’s experiment observing moons of Jupiter.
  • Experiments involving resonant cavities.
Show Worked Solution

Foucault’s cogwheel experiment (one possible method):

  • Set up a cogwheel and a mirror 8 km apart.
  • Shine a pulse of light through one of the gaps of the cogwheel.
  • Begin to rotate the cogwheel and record the lowest speed at which the returning light is completely blocked.
  • This is the speed at which, on the light’s journey, the cogwheel has rotated through half the distance between adjacent cogs (or the distance between a cog and the adjacent gap).
  • Using the rotation speed of the wheel and the distance between a cog and a gap, calculate the time taken for light to complete its journey.
  • Calculate the speed of light using  `c=(d)/(t)`, where  `d` = 16 km.

Limitation:

  • The accuracy of this experiment is limited by errors in measurement of the distance between the cogwheel and the mirror, as well as errors measuring the speed of rotation of the cogwheel.

Other valid methods:

  • Fizeau’s rotating mirror experiment.
  • Newton’s experiment.
  • Ole Romer’s experiment observing moons of Jupiter.
  • Experiments involving resonant cavities.

Mean mark 56%.

PHYSICS M6 2022 HSC 22

The diagram shows features of a transformer.
 


 

For TWO features of the transformer, describe how each contributes to the transformer's efficiency.   (4 marks)

Show Answers Only

Continuous Iron Core:

  • The continuous iron core of the transformer increases the flux linkage between the primary and secondary coils. This maximises the proportion of magnetic flux produced by the primary coil that passes through the secondary coil.

Laminations:

  • The laminations in the iron core prevent the production of large eddy currents in the iron core. This reduces energy losses in the form of heat.
Show Worked Solution

Continuous Iron Core:

  • The continuous iron core of the transformer increases the flux linkage between the primary and secondary coils. This maximises the proportion of magnetic flux produced by the primary coil that passes through the secondary coil.

Laminations:

  • The laminations in the iron core prevent the production of large eddy currents in the iron core. This reduces energy losses in the form of heat.

PHYSICS M8 2022 HSC 21

The positions of two stars, `X` and `Y`, are shown in the Hertzsprung-Russell diagram.
 

  1. Compare qualitatively the surface temperature and luminosity of `X` and `Y`.   (2 marks)

  1. Identify the elements undergoing fusion in the core of each star, `X` and `Y`.   (2 marks)
Show Answers Only

a.   Surface Temperature:

  • The surface temperature of `X` is greater than the surface temperature of `Y.`

Luminosity:

  • The luminosity of `Y` is greater than the luminosity of `X.`

b.   Elements undergoing fusion:

  • `X` is a main sequence star so in its core hydrogen is being fused into helium.
  • `Y` is a red giant so in its core helium is being fused into carbon.
Show Worked Solution

a.   Surface Temperature:

  • The surface temperature of `X` is greater than the surface temperature of `Y.`

Luminosity:

  • The luminosity of `Y` is greater than the luminosity of `X.`

b.   Elements undergoing fusion:

  • `X` is a main sequence star so in its core hydrogen is being fused into helium.
  • `Y` is a red giant so in its core helium is being fused into carbon.

BIOLOGY, M7 2021 HSC 30

A study compared the incidence of disease and survival of 8134 children who had received the measles vaccine with 8134 children from a neighbouring area who remained unvaccinated against measles. Children in each group were matched for age, sex, size of dwelling, number of siblings and maternal education. The graphs show the number of measles cases among the two groups over three years.


 

The table compares the cause of death and number of deaths of the two groups over the same three years.
 

'A vaccine only protects the community against a specific disease.'

Analyse the data with reference to this statement.   (7 marks)

Show Answers Only
  • These two studies show proof that the vaccine protects against measles.
  • The graphs show the incidence of measles in vaccinated children is extremely low, occasionally zero, compared to unvaccinated children. Since these children are matched for age and other sociocultural/socioeconomic factors, it is highly likely the vaccine is responsible for this difference.
  • The table also supports this conclusion, where 40 children who were unvaccinated died due to measles compared to the 2 who died who were vaccinated.
  • The table also provides evidence that the vaccine may protect children from dying from other diseases, contradicting the statement.
  • The table also uses the same groups as the graph, again, keeping cultural/socioeconomic factors similar. It shows that children vaccinated against measles died at half the rate of unvaccinated children due to diarrhoea and dysentery, and at about a quarter of the rate for oedema.
  • However, the small differences between groups with respect to fever and the small sample size for oedema mean that further research is required.
  • In general, the vaccinated group had less than half the mortality of the unvaccinated group, supporting the conclusion that the vaccine provides a wider protection.
  • However, this statement needs qualification as the data is only with respect to the measles vaccine. 
Show Worked Solution
  • These two studies show proof that the vaccine protects against measles.
  • The graphs show the incidence of measles in vaccinated children is extremely low, occasionally zero, compared to unvaccinated children. Since these children are matched for age and other sociocultural/socioeconomic factors, it is highly likely the vaccine is responsible for this difference.
  • The table also supports this conclusion, where 40 children who were unvaccinated died due to measles compared to the 2 who died who were vaccinated.
  • The table also provides evidence that the vaccine may protect children from dying from other diseases, contradicting the statement.
  • The table also uses the same groups as the graph, again, keeping cultural/socioeconomic factors similar. It shows that children vaccinated against measles died at half the rate of unvaccinated children due to diarrhoea and dysentery, and at about a quarter of the rate for oedema.
  • However, the small differences between groups with respect to fever and the small sample size for oedema mean that further research is required.
  • In general, the vaccinated group had less than half the mortality of the unvaccinated group, supporting the conclusion that the vaccine provides a wider protection.
  • However, this statement needs qualification as the data is only with respect to the measles vaccine. 

BIOLOGY, M8 2021 HSC 29

The koala is a mammal that maintains a stable body temperature of close to 36.6°C.

A study was conducted. Koalas were observed in natural forests in south-eastern Australia. Their posture in the tree and the ambient temperature were recorded. Ambient temperatures were divided into two categories, hot and mild.

The graph shows the posture of koalas observed.
 

Explain the adaptations used by the koalas in this study to maintain a stable body temperature. Make reference to the stimulus provided.   (4 marks)

Show Answers Only
  • Posture is a behavioural adaptation that changes the surface area of skin exposed to the air or tree trunk. Posture is often seen associated with hot or mild air temperatures. 
  • In mild conditions, koalas were often seen curling up, minimising heat loss by reducing surface area exposed to air, a behaviour that was never observed during hot conditions.
  • In hotter conditions, the koalas were seen leaning against, and hugging trees much more often than during milder conditions. Since the trees were shown to have lower temperatures, this exposes their ventral surface to the cool trunk and acts as a heat sink.

Other answers could include:

  • Reference to the physiological adaptation of directing blood flow to the stomach region to increase cooling when this are is in contact with the tree.
Show Worked Solution
  • Posture is a behavioural adaptation that changes the surface area of skin exposed to the air or tree trunk. Posture is often seen associated with hot or mild air temperatures. 
  • In mild conditions, koalas were often seen curling up, minimising heat loss by reducing surface area exposed to air, a behaviour that was never observed during hot conditions.
  • In hotter conditions, the koalas were seen leaning against, and hugging trees much more often than during milder conditions. Since the trees were shown to have lower temperatures, this exposes their ventral surface to the cool trunk and acts as a heat sink.

Other answers could include:

  • Reference to the physiological adaptation of directing blood flow to the stomach region to increase cooling when this are is in contact with the tree.

BIOLOGY, M5 2021 HSC 28a

Describe the role of mRNA in human cells.   (3 marks)

Show Answers Only
  • mRNA carries a complementary copy of a gene, with uracil replacing thymine as a base, into the cytoplasm.
  • At ribosome sites this provides a template; each codon (three nucleotides) results in the addition of a specific amino acid, which forms a polypeptide chain.
Show Worked Solution
  • mRNA carries a complementary copy of a gene, with uracil replacing thymine as a base, into the cytoplasm.
  • At ribosome sites this provides a template; each codon (three nucleotides) results in the addition of a specific amino acid, which forms a polypeptide chain.

Mean mark 58%.

BIOLOGY, M6 2021 HSC 24b

The diagram shows the early stages of embryonic development from a fertilised egg. The developing ball of cells has split and monozygotic (identical) twins have formed. Mutations can occur at different times during embryonic development, for example Mutation `A` would result in both twins having the mutation in all their cells.
 


 

Explain the effects of Mutation `B` and Mutation `C` on each twin and on any offspring that they may have.   (4 marks)

Show Answers Only
  • Mutation B occurred after twin formation but prior to cell differentiation, affecting just Twin 1’s somatic and germ-line cells.
  • Through affecting germ-line cells, it will then affect the offspring.
  • Mutation C occurred after twin formation and after cell differentiation, only affecting Twin 2’s somatic cells.
  • Because it doesn’t affect germ-line cells, this mutation cannot be passed onto offspring.
Show Worked Solution
  • Mutation B occurred after twin formation but prior to cell differentiation, affecting just Twin 1’s somatic and germ-line cells.
  • Through affecting germ-line cells, it will then affect the offspring.
  • Mutation C occurred after twin formation and after cell differentiation, only affecting Twin 2’s somatic cells.
  • Because it doesn’t affect germ-line cells, this mutation cannot be passed onto offspring.

BIOLOGY, M5 2021 HSC 24a

An incidence of an autosomal dominant trait is shown in the pedigree.
 


 

Is this trait likely to be the result of a somatic or a germ-line mutation? Justify your answer.   (3 marks)

Show Answers Only
  • The mutation must be somatic as the trait is not present in the parents.
  • If the mutation were germ-line, occurring in cells that produce gametes, then the trait would most likely be seen in the parents and offspring as it is dominant.
Show Worked Solution
  • The mutation must be somatic as the trait is not present in the parents.
  • If the mutation were germ-line, occurring in cells that produce gametes, then the trait would most likely be seen in the parents and offspring as it is dominant.

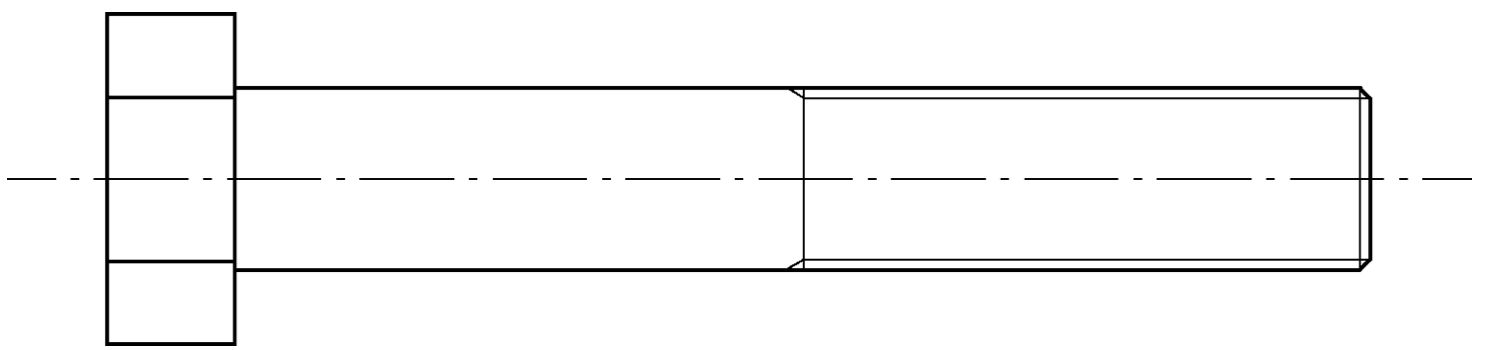
ENGINEERING, CS 2021 HSC 21b

A 100 mm long M16 × 2 bolt is used in the concrete decking of a bridge. The bolt has a thread length of 50 mm.

  1. Draw an orthogonal view, to AS 1100, to show the length of the bolt.
  2. Use the centreline provided and do NOT dimension the drawing. Use a scale of 1:1.   (3 marks)
  1. The yield stress of the bolt is 476 MPa and the diameter is 16 mm.
  2. Calculate the maximum load that the bolt can resist, assuming a Factor of Safety of 2.   (3 marks)
Show Answers Only

i. 

    

ii.   `47.9\ text{kN}`

Show Worked Solution

i. 

    

ii.   Find max load of bolt:

`text{Yield stress} = 476\ text{MPa, Bolt diameter = 16 mm}`

`text{Allowable Stress}= 476 -: 2=238\ text{MPa}`

`text{Area (bolt)}\=pir^2=pi xx 8^2=201.1\ text{mm}^2`

`text{Max Load }` `=\ text{allowable stress × area}`  
  `=238 xx 10^6 xx 201.1 xx 10^(-6)`  
  `=47\ 861.8\ text{N}`  
  `=47.9\ text{kN}`  

ENGINEERING, PPT 2021 HSC 4 MC

Which engineering drawing shows a bracket correctly dimensioned to AS 1100 drawing standards?
 

Show Answers Only

`D`

Show Worked Solution

By elimination:

  • Arrowheads are used for measurements instead of crosses (eliminate `A` and `C`).
  • In `B` the radius symbol points to the arrow marking diameter (eliminate `B`).

`=>D`

PHYSICS M8 2022 HSC 16 MC

The binding energy of helium-4 (He-4) is 28.3 MeV and the binding energy of beryllium-6 (Be-6) is 26.9 MeV.

Which of the following rows in the table is correct?
 

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex}\textbf{A.} & \\
\textbf{}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\\
\textbf{}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\\
\textbf{}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\\
\textbf{}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|l|l|}
\hline
\rule{0pt}{2.5ex}\text{He-4 requires more energy to separate}\quad & \text{He-4 is less massive than Be-6} \\
\text{into individual protons and neutrons}\rule[-1ex]{0pt}{0pt}&\text{}\\
\hline
\rule{0pt}{2.5ex}\text{He-4 requires less energy to separate}& \text{He-4 is less massive than Be-6}\\
\text{into individual protons and neutrons}\rule[-1ex]{0pt}{0pt}&\text{}\\
\hline
\rule{0pt}{2.5ex}\text{He-4 requires more energy to separate}& \text{He-4 is more massive than Be-6}\\
\text{into individual protons and neutrons}\rule[-1ex]{0pt}{0pt}&\text{}\\
\hline
\rule{0pt}{2.5ex}\text{He-4 requires less energy to separate}& \text{He-4 is more massive than Be-6} \quad \\
\text{into individual protons and neutrons}\rule[-1ex]{0pt}{0pt}&\text{}\\
\hline
\end{array}
\end{align*}

Show Answers Only

\(A\)

Show Worked Solution
  • The binding energy of a nucleus is the energy required to separate it into individual particles.
  • He-4 requires more energy to separate into individual protons and neutrons.
  • He-4 has 4 nucleons while Be-6 has 6 nucleons.
  • He-4 is less massive.

\(\Rightarrow A\)

PHYSICS M6 2022 HSC 15 MC

Two wires separated by a distance, `d`, carry equal electric currents producing a magnetic force between them.
  


  

The separation between the wires is increased to `4 d` and the current in each wire is doubled.

What happens to the magnetic force between the wires, compared to the original force?

  1. It does not change.
  2. It increases by a factor of 4 .
  3. It decreases by a factor of 4 .
  4. It decreases by a factor of 8 .
Show Answers Only

`A`

Show Worked Solution

The force per unit length between the wires:

`(F)/(l)=(mu_(0))/(2pi)(I_(1)I_(2))/(r)`
 

By increasing the distance by a factor of four, and doubling both currents, the new force per unit length is given by:

`(F)/(l)` `=(mu_(0))/(2pi)(2I_(1)2I_(2))/(4r)`  
  `=(mu_(0))/(2pi)(I_(1)I_(2))/(r)`  

 
`=>A`

PHYSICS, M7 2022 HSC 14 MC

Line `X` shows the results of an experiment carried out to investigate the photoelectric effect.
 


 

What change to this experiment would produce the results shown by line `Y` ?

  1. Increasing the frequency of the radiation
  2. Using a metal that has a greater work function
  3. Decreasing the intensity of the incident radiation
  4. Decreasing the maximum energy of photoelectrons
Show Answers Only

`B`

Show Worked Solution
  • The work function of the metals is given by the respective y-intercepts of lines `X` and `Y`. 
  • As line `Y` has a y-intercept with greater magnitude, it can be produced by using a metal with a greater work function.

`=>B`

PHYSICS M5 2022 HSC 13 MC

Two satellites share an orbit around a planet. One satellite has twice the mass of the other.
  


  

Which quantity would be different for the two satellites?

  1. Speed
  2. Momentum
  3. Orbital period
  4. Centripetal acceleration
Show Answers Only

`B`

Show Worked Solution

The orbital velocity, `v=sqrt((GM)/(r))` is independent of the mass of the orbiting body.

  • Both satellites have the same orbital velocity.
  • The momentum,  `p=mv` of the satellite with mass 2`m` is twice that of the satellite with mass `m`.
  • The two satellites have different momentum.

`=>B`

PHYSICS, M5 2022 HSC 11 MC

A projectile is launched vertically upwards. The displacement of the projectile as a function of time is shown.
 


 

Which velocity-time graph corresponds to this motion?
 

 

 

Show Answers Only

`B`

Show Worked Solution

By elimination:

  • Initially, the projectile is moving upwards (positive velocity) → Eliminate `A`
  • At  `t=2` s, the projectile reaches its maximum height and has a velocity of zero → Eliminate `D`
  • Projectile then moves downwards (negative velocity) → Eliminate `C`

`=>B`

PHYSICS M5 2022 HSC 6 MC

The elliptical orbit of a planet around a star is shown.
 


  

Which type of energy is greater at position `P` than at `Q` ?

  1. Kinetic
  2. Nuclear
  3. Potential
  4. Total
Show Answers Only

`A`

Show Worked Solution

As the planet moves from `Q`  to  `P` is converted to kinetic energy.

  • its kinetic energy must be greater at `P`.

`=>A`