SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, SPEC2 2018 VCAA 3

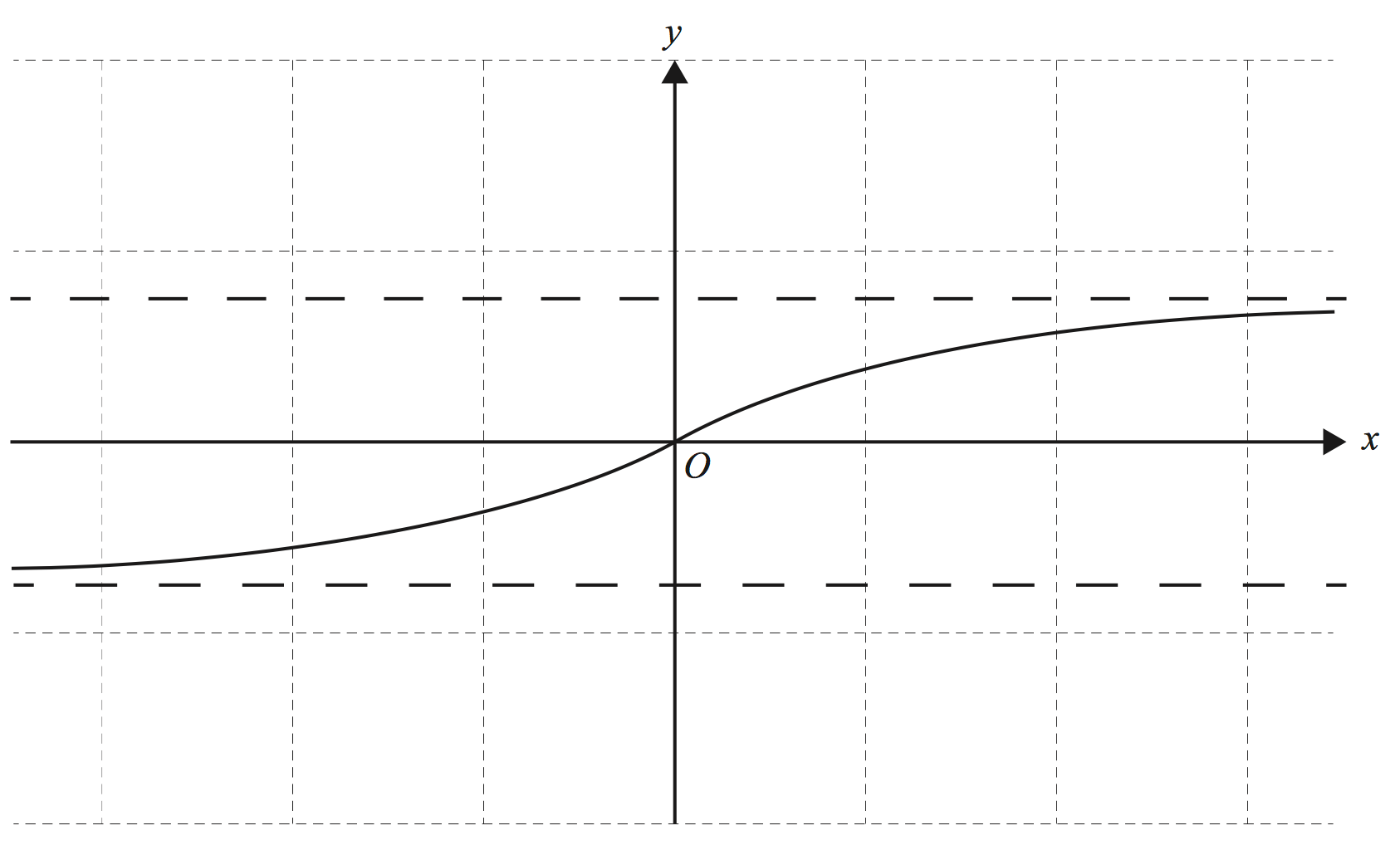
Part of the graph of  `y = 1/2 sqrt(4x^2-1)`  is shown below.
 


 

The curve shown is rotated about the `y`-axis to form a volume of revolution that is to model a fountain, where length units are in metres.

  1. Show that the volume, `V` cubic metres, of water in the fountain when it is filled to a depth of `h` metres is given by  `V = pi/4(4/3h^3 + h)`.   (2 marks)

  2. Find the depth `h` when the fountain is filled to half's its volume. Give your answer in metres, correct to two decimal places.   (2 marks)

The fountain is initially empty. A vertical jet of water in the centre fills the fountain at a rate of 0.04 cubic metres per second and, at the same time, water flows out from the bottom of the fountain at a rate of  `0.05 sqrt h`  cubic metres per second when the depth is `h` metres.

  1.  i. Show that  `(dh)/(dt) = (4-5sqrt h)/(25 pi (4h^2 + 1))`.   (2 marks)

  2. ii. Find the rate, in metres per second, correct to four decimal places, at which the depth is increasing when the depth is 0.25 m.   (1 mark)

  3. Express the time taken for the depth to reach 0.25 m as a definite integral and evaluate this integral correct to the nearest tenth of a second.   (2 marks)

  4. After 25 seconds the depth has risen to 0.4 m.
    Using Euler's method with a step size of five seconds, find an estimate of the depth 30 seconds after the fountain began to fill. Give your answer in metres, correct to two decimal places.   (2 marks)

  5. How far from the top of the fountain does the water level ultimately stabilise? Give your answer in metres, correct to two decimal places.   (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `h~~ 0.59\ text(m)`
    1. `text(Proof)\ \ text{(See Worked Solutions)}`
    2. `0.0153\ text(ms)^(-1)`
  1. `9.8\ text(seconds)`
  2. `0.43\ text(m)`
  3. `0.23\ text(m)`
Show Worked Solution

a.   `V= pi int_0^h x^2\ dy`

`y` `=1/2 sqrt(4x^2-1)`
`2y` `=sqrt(4x^2-1)`
`4y^2` `= 4x^2-1`
`4x^2` `= 4y^2 + 1`
`x^2` `= y^2 + 1/4`

 

`:. V` `= pi int_0^h y^2 + 1/4\ dy`
  `= pi[y^3/3 + y/4]_0^h`
  `= pi(h^3/3 + h/4-0)`
  `= pi(1/4((4h^3)/3 + h))`
  `= pi/4((4h^3)/3 + h)\ \ …\ text(as required)`

 

b.    `V_text(max)` `= pi/4 (4/3 xx (sqrt 3/2)^3 + sqrt 3/2)`
    `= pi/4 (sqrt 3/2 + sqrt 3/2)`
    `= (pi sqrt 3)/4`

 

`1/2 V_text(max)` `= (pi sqrt 3)/8`
`(pi sqrt 3)/8` `= pi/4 (4/3 h^3 + h)`
`sqrt 3/2` `= 4/3 h^3 + h`
`:. h` `~~0.59\ text(m)`

  

c.i.   `((dV)/(dt))_text(in)` `= 0.04`
  `((dV)/(dt))_text(out)` `= 0.05 sqrt h`
  `(dV)/(dt)` `= 0.04-0.05 sqrt h`
    `= (4-5 sqrt h)/100`
     
  `(dV)/(dh)` `= pi/4(4h^2 + 1)`
  `:. (dh)/(dt)` `= (dh)/(dV) ⋅ (dV)/(dt)`
    `= 4/(pi(4h^2 + 1)) xx (4-5 sqrt h)/100`
    `= (4-5 sqrt h)/(25 pi (4h^2 + 1))`

 

c.ii.   `(dh)/(dt)|_(h = 0.25)` `= (4-5 sqrt(0.25))/(25 pi (4(0.25)^2 + 1))`
    `~~ 0.0153\ text(ms)^(-1)`

 

d.   `(dt)/(dh) = (25 pi (4h^2 + 1))/(4-5 sqrt h)`

`:. t(0.25)` `= int_0^0.25 (25 pi (4h^2 + 1))/(4-5 sqrt h)\ dh`
  `~~9.8\ text(seconds)`

 

e.   `text(When)\ \ t=25,\ \ h=0.4\ \ text{(given)}`

♦♦ Mean mark part (e) 30%.

`:. h(30)` `~~ h(25) + 5 xx (dh)/(dt)|_(h = 0.4)`
  `~~ 0.4 + 5 xx ((4-5 sqrt 0.4)/(25 pi (4(0.4)^2 + 1)))`
  `~~ 0.43\ text(m)`

 

f.    `(dV)/(dt) = 0`

♦♦ Mean mark part (f) 32%.

`0.04-0.05 sqrt h` `= 0`
`0.04` `= 0.05 sqrt h“
`sqrt h` `= 4/5`
`h` `= 16/25`

  

`d` `= h_max-16/25`
  `= sqrt 3/2-16/25`
  `~~ 0.23\ text(m)`

Complex Numbers, SPEC2 2018 VCAA 2

  1. State the centre in the form  `(x, y)`, where  `x, y in R`, and the state the radius of the circle given by  `|z-(1 + 2i)| = 2`, where  `z in C`.   (1 mark)

  2. Graph the circle given by  `|z + 1| = sqrt 2 |z-i|`  on the Argand diagram below, labelling the intercepts with the vertical axis.   (2 marks)

     

The line given by  `|z-1| = |z-3|`  intersects the circle given by  `|z + 1| = sqrt 2 |z-i|`  in two places.

  1. Draw the line given by  `|z-1| = |z-3|`  on the Argand diagram in part c. Label the points of intersection with their coordinates.   (2 marks)

  2. Find the area of the minor segment enclosed by an arc of the circle given by  `|z + 1| = sqrt 2 |z-i|`  and part of the line given by  `|z-1| = |z-3|`.   (3 marks)
Show Answers Only
  1. `text(Centre): (1, 2), quad text(radius): 2`
  2. `text(Proof)\ text{(See Worked Solutions)}`
  3. `text(See Worked Solutions)`
  4. `text(See Worked Solutions)`
  5. `(4 pi)/3-sqrt 3`
Show Worked Solution

a.   `(x-1)^2 + (y-2)^2 = 2^2`

`:.\ text(Centre)\ (1, 2), quad text(radius) = 2`
 

b.    `y^2 + (x + 1)^2` `= (sqrt 2)^2 (x^2 + (y-1)^2)`
  `y^2 + x^2 + 2x + 1` `= 2(x^2 + y^2-2y + 1)`
  `y^2 + x^2 + 2x + 1` `= 2x^2 + 2y^2-4y + 2`
`0` `= 2x^2 + 2y^2-4y + 2-y^2-x^2-2x-1`
`0` `= x^2 + y^2-4y-2x + 1`
`0` `= (x^2-2x + 1) + (y^2-4y)`
`0` `= (x-1)^2 + (y^2-4y + 2^2)-4`
`0` `= (x-1)^2 + (y-2)^2-4`
`4` `= (x-1)^2 + (y-2)^2`

 
`:.\ text(Centre)\ (1, 2), quad text(radius) = 2`

 

c.   `ytext(-axis intercepts occur when)\ \ x=0:`

`(0-1)^2 + (y-2)^2` `= 4`
`1 + (y-2)^2` `= 4`
`(y-2)^2` `= 3`
`y-2` `= +- sqrt 3`
`y` `= 2 +- sqrt 3`

 

d.   `|z-1| = |z-3|`

`=>\ text(Graph is a line equidistant from:)\ \ 1 + 0i and 3 + 0i`

`text(Circle intercepts occur when)\ \ x=2:`

`(2- 1)^2 + (y-2)^2` `= 4`
`(y-2)^2` `= 3`
`y-2` `= +- sqrt 3`
`y` `= 2 +- sqrt 3`

 

e.   `sin theta = sqrt3/2\ \ =>\ \ theta = pi/3`

♦ Mean mark 39%.
MARKER’S COMMENT: Students who used standard formulae rather than definite integrals were more successful.

`text(Angle at centre of segment) = (2pi)/3`

`text(Height of triangle)\ (h) = 2^2-(sqrt3)^2 =1`
 

`:.\ text(Shaded Area)`

`=\ text(Area of segment – Area of triangle)`

`=((2pi)/3)/(2pi) xx pi xx 2^2-1/2 xx 2sqrt3 xx 1`

`=(4pi)/3-sqrt3`

Calculus, SPEC2 2018 VCAA 1

Consider the function  `f: D -> R`, where  `f(x) = 2 text(arcsin)(x^2-1)`.

  1. Determine the maximal domain `D` and the range of  `f`.  (2 marks)

  2. Sketch the graph of  `y = f(x)`  on the axes below, labelling any endpoints and the `y`-intercept with their coordinates.  (3 marks)


      

    `qquad` 
     

  3. Find  `f^{′}(x)`  for  `x > 0`, expressing your answer in the form  `f^{′}(x) = A/sqrt(2-x^2), \ A in R`.  (1 mark)

  4. Write down  `f^{′}(x)`  for  `x < 0`, expressing your answer in the form  `f^{′}(x) = B/sqrt(2-x^2), \ B in R`.  (1 mark)

  5. The derivative  `f^{′}(x)`  can be expressed in the form  `f^{′}(x) = {g(x)}/sqrt(2-x^2)` over its maximal domain.
  1. Find the maximal domain of  `f^{′}`.  (1 mark)

  2. Find  `g(x)`, expressing your answer as a piecewise (hybrid) function.  (1 mark)

  3. Sketch the graph of  `g` on the axes below.  (2 marks)


     

Show Answers Only

  1. `D [- sqrt 2 , sqrt 2]; qquad f(x) in [-pi, pi]`
  2. `text(See Worked Solutions)`
  3. `4/sqrt(2-x^2)`
  4. `(-4)/sqrt(2-x^2)`
    1. `x in (-sqrt2, 0) ∪ (0, sqrt 2)`
    2. `g(x) = {(-4text(,), x < 0), (\ \ \ 4text(,), x > 0):}`
    3. `text(See Worked Solutions)`

Show Worked Solution

a.   `-1 <= x^2-1 <= 1`

`=>\ 0 <= x^2<= 1`

`=>\ -sqrt2 <= x <=sqrt2`

`:.\ text(Domain:)\ [- sqrt 2 , sqrt 2]`

 

`sin^(-1)(x) in [-pi/2, pi/2]`

`=> 2 sin^(-1)(x) in [-2xx pi/2, 2 xx pi/2]`

`:.\ text(Range:)\ [-pi, pi]`

 

b.   

 

c.   `f(x) = 2 sin^(-1)(x^2-1)`

`f(x)` `=2 sin^(-1)(x^2-1)`

 
`:. f^{′}(x)= 4/sqrt(2-x^2)\ \ \ (x > 0,\ \ text(by CAS))`

 

d.    `f^{′}(x)` `= (4x)/sqrt(x^2(2-x^2))`
    `= (-4)/sqrt(2-x^2)\ \ \ (x < 0)`

 

e.i.  `f^{′}(x)\ \ text(is defined when:)`

♦♦ Mean mark part (e)(i) 21%.

`2-x^2 > 0\ \ and\ \ x!=0`

`:. x in (-sqrt2, 0) ∪ (0, sqrt 2)`

 

e.ii.  `g(x) = +- 4`

♦ Mean mark part (e)(ii) 49%, part (e)(iii) 48%.

`:.  g(x) = {(-4text(,), x < 0), (\ \ \ 4text(,), x > 0):}`

 

e.iii.   

Calculus, SPEC1-NHT 2017 VCAA 7

Let  `(dy)/(dx) = (4-y)^2`.

  1.  Express `y` in terms of `x`, where  `y(0) = 3`.  (3 marks)

  2.  Express  `(d^2y)/(dx^2)`  in terms of `y`.  (2 marks)

Show Answers Only
  1. `y = 4-1/(x + 1)`
  2. `-2(4-y)^3`
Show Worked Solution
a.    `(dy)/(dx)` `=(4-y)^2`
  `(dx)/(dy)` `= 1/(4-y)^2`
  `x` `= int 1/(4-y)^2\ dy`
    `= int (4-y)^(-2) dy`
    `= (-1)(-1)(4-y)^(-1)+ c`
    `= 1/(4-y) + c`

 
`text(When)\ \ x=0,\ \ y=3:`

`0` `= 1/(4-3) + c`
`:.c` `= -1`

 

`x` `= 1/(4-y)-1`
`x + 1` `= 1/(4-y)`
`1/(x + 1)` `= 4-y`
`:. y` `= 4-1/(x + 1)`

 

b.   `d/(dx) ((4-y)^2)`

`= 2(-1)(4-y) ⋅ (dy)/(dx)`

`= -2(4-y)(4-y)^2`

`= -2(4-y)^3`

Trigonometry, SPEC1-NHT 2017 VCAA 6

Find all real solutions of  `tan(2x) = -tan(x)`.  (3 marks)

Show Answers Only

`x = k pi, \ pi/3 + k pi, \ (2 pi)/3 + k pi, k in ZZ`

Show Worked Solution

`(2 tan (x))/(1 – tan^2(x)) = -tan(x)`

 
`text(Let)\ \ tan(x) = k,`

`(2k)/(1 – k^2)` `= -k`
`2k` `= -k(1 – k^2)`
`2k + k(1 – k^2)` `= 0`
`k(3 – k^2)` `= 0`

 
`k(3 – k^2) = 0 \ \ =>\ \  k = 0, k^2 = 3`

`=> tan(x) = 0, tan(x) = +- sqrt 3`

`:. x = k pi, \ pi/3 + k pi, \ (2 pi)/3 + k pi\ \ (k in ZZ)`

Calculus, SPEC1 2017 VCAA 10

  1.  Show that  `d/dx(x arccos(x/a)) = arccos(x/a)−x/(sqrt(a^2-x^2))`, where  `a > 0`.   (1 mark)

  2.  State the maximum domain and the range of  `f(x) = sqrt(arccos(x/2))`.   (2 marks)

  3.  Find the volume of the solid of revolution generated when the region bounded by the graph of  `y = f(x)`, and the lines  `x = −2`  and  `y = 0`, is rotated about the `x`-axis.   (4 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `x ∈ [−2, 2], \ y ∈ [0, sqrtpi]`
  3. `2pi^2`
Show Worked Solution
a.    `u` `= x,` `v` `= cos^(−1)(x/a)`
  `uprime` `= 1,`   `vprime` `= (−1)/sqrt(a^2-x^2)`
`d/(dx)(xcos^(−1)(x/a))` `= uprimev + vprimeu`
  `= cos^(−1)(x/a) + (x(−1))/sqrt(a^2-x^2)`
  `= arccos(x/a)-x/sqrt(a^2-x^2)`

 

b.   `arccos(x/2)>=0`

`text(Maximal domain:)\  x ∈ [−2, 2]`

`f(x) = (arccos(x/2))^(1/2)`

`text(Range:)\ \ y ∈ [0, sqrtpi]`

 

c.   `V` `= pi int_(−2)^2 y^2\ dx`
  `= pi int_(−2)^2 cos^(-1)(x/2)\ dx`
  `= pi int_(−2)^2 cos^(-1) (x/2)-x/sqrt(4-x^2) + x/sqrt(4-x^2)\ dx`
  `= pi [x cos^(-1)(x/2)]_(−2)^2 + pi int_(−2)^2 x/sqrt(4-x^2)\ dx`

 
`text(Let)\ \ u = 4-x^2`

♦ Mean mark part (c) 35%.

`(du)/(dx) = -2x\ \ =>\ \ -1/2 (du) = x\ dx`
 

`text(When)\ \ x=2\ \ => \ u=0`

`text(When)\ \ x=-2\ \ =>\ \ u=0`

`:. V` `= pi [2cos^(−1)(1)-(-2)cos^(−1)(−1)]-pi/2 int_0^0 1/sqrtu du`
  `= pi(2 xx 0 + 2 xx pi)`
  `= 2pi^2`

Calculus, SPEC1-NHT 2017 VCAA 2

Find  `a`  given that  `int_(-2)^a 8/(16-x^2)\ dx = log_e(6), \ a in (-2, 4)`.  (3 marks)

Show Answers Only

 `a = 4/3`

Show Worked Solution
`I` `= int_(-2)^a 8/((4-x)(4 + x))\ dx`
  `= int_(-2)^a A/(4-x) + B/(4 + x)\ dx`

 
`text(Using partial fractions:)`

`A(4 + x) + B(4-x) = 8`

`text(If)\ \ x = 4\ \ =>\ \ 8A=8\ \ =>\ \ A=1`

`text(If)\ \ x = -4\ \ =>\ \ 8B=8\ \ =>\ \ B=1`
 

`:. I` `= int_(-2)^a 1/(4-x) + 1/(4 + x)\ dx`
`ln6` `= [ln |4 + x|-ln|4-x|]_(-2)^a`
  `= ln|4 + a|-ln|4-a|-(ln|2|-ln|6|)`
  `= ln ((4 + a)/(4-a))-ln (2/6),\ \ \ (a in (-2, 4))`
  `= ln ((3(4 + a))/(4-a))`
`6` `= 3((4 + a)/(4-a))`
`2` `=(4 + a)/(4-a)`
`8-2a` `=4+a`
`:. a` `=4/3`

Complex Numbers, SPEC2 2015 VCAA 6 MC

Which one of the following relations has a graph that passes through the point  `1 + 2i`  in the complex plane?

  1. `zbarz = sqrt5`
  2. `text(Arg)(z) = pi/3`
  3. `| z - 1 | = | z - 2i |`
  4. `text(Re)(z) = 2text(Im)(z)`
  5. `z + barz = 2`
Show Answers Only

`E`

Show Worked Solution

`text(Consider each option:)`

♦ Mean mark 43%.

`A:\ \ (1 + 2i)(1 – 2i) = 1 – 4i^2 = 5`

`B:\ \ alpha = tan^(−1)(2) != pi/3`

`C:\ \ |(1 + 2i)-1 | = |2i| = 2,\ \ |1 + 2i – 2i| = |1| = 1`

`D:\ \ text(Re)(z) = 1 != 2text(Im)(z)`

`E:\ \ 1 + 2i + 1 – 2i = 2\ \ text{(correct)}`

 
`=> E`

Calculus, SPEC1 2015 VCAA 8

  1.  Show that  `int tan (2x)\ dx = 1/2 log_e |\ sec (2x)\ | + c.`  (2 marks)


  2.  The graph of  `f(x) = 1/2 arctan (x)`  is shown below
     
         
     
  3. i.  Write down the equations of the asymptotes.  (1 mark)

  4. ii. On the axes above, sketch the graph of  `f^-1`, labelling any asymptotes with their equations.  (1 mark)

  5.  Find  `f(sqrt 3).`  (1 mark)

  6.  Find the area enclosed by the graph of  `f`, the `x`-axis and the line  `x = sqrt 3.`   (2 marks)

Show Answers Only

a.   `text(Proof)\ \ text{(See Worked Solutions)}`

b. (i)   `y = -pi/4,\ \ y = pi/4`
  (ii)  

c.   `pi/6`

d.   `(sqrt 3 pi)/6-log_e sqrt 2`

Show Worked Solution

a.   `text(Let)\ \ u = cos(2x)`

`(du)/(dx) = -2 sin (2x)\ \ =>\ \ -1/2 xx du = sin (2x)\ dx`

`int tan (2x)\ dx` `= int (sin(2x))/(cos(2x))\ dx`
  `= -1/2 int 1/u\ du`
  `= -1/2 log_e |\ u\ | + c`
  `= -1/2 log_e |\ cos (2x)\ | + c`
  `= 1/2 log_e |\ sec (2x)\ | + c`

 

b.i.  `text(Range:)\ \ tan^(-1)(x) in (- pi/2,pi/2)`

`=>1/2 tan^(-1)(x) in (- pi/4, pi/4)`

`:.\ text(Asymptotes:)\ \ y = -pi/4,\ \ y = pi/4`

 

b.ii.

 

c.   `f(sqrt 3)` `= 1/2 tan^(-1) (sqrt 3)`
    `= 1/2 xx pi/3`
    `= pi/6`

 

d.    `y` `= 1/2tan^(−1)(x)`
  `2y` `= tan^(−1)(x)`
  `x` `= tan(2y)`

 

 

♦ Mean mark part (d) 49%.

`text(Area)` `=\ text(Area of rectangle – Area between graph and y-axis)`
  `= sqrt3 xx pi/6-int_0^(pi/6) tan(2y)\ dy`
  `= (sqrt3 pi)/6 -1/2[ln\ | sec(2y) |]_0^(pi/6)`
  `= (sqrt3 pi)/6-1/2[ ln(sec(pi/3))-ln(sec 0)]`
  `= (sqrt3 pi)/6-1/2 (ln2 -ln1)`
  `= (sqrt3 pi)/6-1/2 ln2`

Trigonometry, SPEC1 2015 VCAA 7

  1. Solve \(\sin (2 x)=\sin (x), x \in[0,2 \pi]\).  (3 marks)

  2. Find \(\left\{x: \operatorname{cosec}(2 x)<\operatorname{cosec}(x), x \in\left(0, \dfrac{\pi}{2}\right) \cup\left(\dfrac{\pi}{2}, \pi\right)\right\}\)   (2 marks)

Show Answers Only
  1. \(x=0, \pi, 2 \pi\) or \(x=\dfrac{\pi}{3}, \dfrac{5 \pi}{3}\)
  2. \(x \in\left(0, \dfrac{\pi}{3}\right) \cup\left(\dfrac{\pi}{2}, \pi\right)\)
Show Worked Solution

a.  \(2 \sin (x) \cos (x)=\sin (x)\)

MARKER’S COMMENT: Many students expanded sin(2x) and then cancelled sin(x) on both sides which lost a set of solutions!

\(\sin (x)(2 \cos (x)-1)=0\)

\(\sin (x)=0, \cos (x)=\dfrac{1}{2}\)

\(x=0, \dfrac{\pi}{3}, \pi, 2 \pi-\dfrac{\pi}{3}, 2 \pi\)

\(x=0, \dfrac{\pi}{3}, \pi, \dfrac{5 \pi}{3}, 2 \pi\)
 

b.  \(\text {Solving} \ \operatorname{cosec}(2 x)=\operatorname{cosec}(x), x \in(0, \pi)\left\{\dfrac{\pi}{2}\right\}:\)

♦♦ Mean mark 26%.

\(\text{Using part (a): }\)

\(\sin (2 x)=\sin (x)\) when \(x=\dfrac{\pi}{3}\)

\(\therefore \operatorname{cosec}(x)=\operatorname{cosec}(2 x)\) at \(x=\dfrac{\pi}{3}\)

\(\text {Sketch graphs:}\)
 

 

\(\text {When} \ \operatorname{cosec}(2 x)<\operatorname{cosec}(x):\)

\(x \in\left(0, \dfrac{\pi}{3}\right) \cup\left(\dfrac{\pi}{2}, \pi\right)\)

Complex Numbers, SPEC1 2015 VCAA 4

  1. Find all solutions of  `z^3 = 8i,  \ z in C` in cartesian form.   (3 marks)

  2. Find all solutions of  `(z − 2i)^3 = 8i, \ z in C`  in cartesian form.   (1 mark)

Show Answers Only
  1. `-2i, +- sqrt 3 + i`
  2. `z = 0 or z = +- sqrt 3 + 3i`
Show Worked Solution

a.   `z^3 = 8text(cis)(pi/2)`

`z_1` `= 8^(1/3)text(cis)(pi/6)`
  `= 2text(cis)(pi/6)`
  `= sqrt3 + i`
   
`z_2` `= 2text(cis)(pi/6 + (2pi)/3)`
  `= 2text(cis)((5pi)/6)`
  `= −sqrt3 + i`
   
`z_3` `= 2text(cis)(pi/6-(2pi)/3)`
  `= 2text(cis)(−pi/2)`
  `= −2i`

 
`:. z = sqrt3 + i, \ −sqrt3 + i, \ −2i`
 

♦ Mean mark part (b) 44%.

b.    `z_1-2i` `= sqrt3 + i`
  `z_1` `= sqrt3 + 3i`
     
`z_2-2i` `= −sqrt3 + i`
`z_2` `= −sqrt3 + 3i`
   
`z_3-2i` `= −2i`
`z_3` `= 0`

 
`:. z = sqrt3 + 3i, \ −sqrt3 + 3i, \ 0`

Mechanics, SPEC1 2014 VCAA 8

A body of mass 5 kg is held in equilibrium by two light inextensible strings. One string is attached to a ceiling at `A` and the other to a wall at `B`. The string attached to the ceiling is at an angle `theta` to the vertical and has tension `T_1` newtons, and the other string is horizontal and has tension `T_2` newtons. Both strings are made of the same material.

  1. i. Resolve the forces on the body vertically and horizontally, and express `T_1` in terms of  `theta`.  (2 marks)
  2. ii. Express `T_2` in terms of  `theta`.  (1 mark)
  3.  Show that  `tan (theta) < sec (theta)`  for  `0 < theta < pi/2`.  (1 mark)
  4.  The type of string used will break if it is subjected to a tension of more than 98 N.

     

     Find the maximum allowable value of  `theta`  so that neither string will break.  (3 marks)

Show Answers Only
  1.  i. `T_1 = 5g sec theta`
  2. ii. `T_2 = 5g tan theta`
  3.  `text(Proof)\ text{(See Worked Solutions)}`
  4.  `theta_max = pi/3`
Show Worked Solution
a.i.   

`text(Resolve vertically): \ 5g = T_1 cos theta`

`text(Resolve horizontally): \ T_1 sin theta = T_2`

`:. T_1 = 5g sec theta`

 

a.ii.    `T_2` `= 5g sec theta sin theta`
    `= 5g tan theta`

 

b.    `cos theta in (0, 1), \ theta in (0, pi/2)`
  `sin theta in (0, 1), \ theta in (0, pi/2)`

`:. sin theta < 1, \ theta in (0, pi/2)`

♦ Mean mark part (b) 40%.

 

`text(If)\ sin theta < 1 and cos theta > 0:`

`(sin theta)/(cos theta) < 1/(cos theta)`

`:.  tan theta < sec theta, quad 0 < theta < pi/2`

 

c.   `tan theta < sec theta \ \ =>\ \  T_2\ text(will be smaller) => \ T_1\ text(will break first)`

♦ Mean mark part (c) 46%.

`5text(g)\ sec theta_max` `= 98`
`sec theta_max` `= 98/(5 xx 9.8)`
`sec theta_max` `= 10/5`
`sec theta_max` `= 2`
`:.  theta_max` `= pi/3`

Calculus, SPEC1 2014 VCAA 5

  1. For the function with rule  `f(x) = 96 cos (3x) sin (3x)`, Find the value of `a` such that  `f(x) = a sin (6x)`.   (1 mark)

  2. Use an appropriate substitution in the form  `u = g(x)`  to find an equivalent definite integral for

     

         `int_(pi/36)^(pi/12) 96 cos (3x) sin (3x) cos^2 (6x)\ dx`  in terms of `u` only.   (3 marks)

  3. Hence evaluate  `int_(pi/36)^(pi/12) 96 cos (3x) sin (3x) cos^2 (6x)\ dx`, giving your answer in the form  `sqrt k, \ k in Z`.   (1 mark)

Show Answers Only
  1. `48`
  2. `int_(sqrt 3/2)^0-8u^2 du`
  3. `sqrt 3`
Show Worked Solution

a.   `96 cos (3x) sin(3x) = 48 (2 cos(3x) sin(3x))= 48 sin (6x)`

`:. a = 48`
 

b. `int_(pi/36)^(pi/12) 96 cos (3x) sin (3x) cos^2 (6x)\ dx`

`= int_(pi/36)^(pi/12) 48 sin (6x) cos^2 (6x)\ dx`

`u` `= cos (6x)`
`(du)/(dx)` `= -6 sin (6x)\ \ =>\ \ du = -6 sin(6x)\ dx`
   
`u(pi/12)` `= cos (pi/2) = 0`
`u(pi/36)` `= cos (pi/6) = sqrt 3/2`

 
`:. int_(pi/36)^(pi/12) 48 sin (6x) cos^2 (6x)\ dx`

`= int_(sqrt 3/2)^0-8u^2\ du`

c. `:. int_(pi/36)^(pi/12) 96 cos (3x) sin (3x) cos^2 (6x)\ dx`

`= -8 [u^3/3]_(sqrt 3/2)^0`
`= -8 (0-(sqrt 3/2)^3/3)`
`= 8/3 xx (3sqrt3)/8`
`= sqrt 3`

Statistics, SPEC2 2017 VCAA 19 MC

A confidence interval is to be used to estimate the population mean  `mu`  based on a sample mean  `barx`.

To decrease the width of a confidence interval by 75%, the sample size must be multiplied by a factor of

  1.    2
  2.    4
  3.    9
  4.  16
  5.  25
Show Answers Only

`D`

Show Worked Solution

`text(Original width) = 2m = 2 xx z σ/sqrtn`

♦ Mean mark 44%.

`text(Decreased width)\ = (2zσ)/sqrtn_2`

`text(If decreased width =)\ 1/4\ text(original width:)`

`(2zσ)/sqrtn_2` `= 1/4 ((2zσ)/sqrtn)`
`(2zσ)/sqrtn_2` `= (2zσ)/(4sqrtn)`
`1/(sqrt(n_2))` `= 1/(4sqrtn)`
`sqrt(n_2)` `= 4sqrtn`
`n_2` `= 16n`

  
`=> D`

Statistics, SPEC2 2017 VCAA 18 MC

`U` and `V` are independent normally distributed random variables, where `U` has a mean of 5 and a variance of 1, and `V` has a mean of 8 and a variance of 1. The random variable `W` is defined by  `W = 4U-3V`.

In terms of the standard normal variable  `Z, Pr(W > 5)`  is equivalent to

  1. `text(Pr)(Z > (9sqrt7)/7)`
  2. `text(Pr)(Z < 1.8)`
  3. `text(Pr)(Z < (9sqrt7)/7)`
  4. `text(Pr)(Z > 0.2)`
  5. `text(Pr)(Z > 1.8)`
Show Answers Only

`E`

Show Worked Solution

`U~N(5, 1), V~N(8, 1), Z~N (0, 1)`

♦ Mean mark 42%.

`W = 4U-3V`

`:. W~N(4 xx 5-3 xx 8, 4^2 xx 1 + (-3)^2 xx 1)`

  `~N(−4, 25)`

`text(Pr)(W > 5)` `= text(Pr)(Z > (5+4)/sqrt25)`
  `= text(Pr)(Z > 9/5)`
  `= text(Pr)(Z > 1.8)`

 
`=> E`

Mechanics, SPEC2 2017 VCAA 17 MC

Forces of 10 N and 8 N act on a body as shown below.
 


 

The resultant force acting on the body will, correct to one decimal place, have

  1. magnitude 15.6 N and act at 26.3° to the 10 N force.
  2. magnitude 9.2 N and act at 49.1° to the 10 N force.
  3. magnitude 15.6 N and act at 33.7° to the 10 N force.
  4. magnitude 9.2 N and act at 70.9° to the 10 N force.
  5. magnitude 15.6 N and act at 49.1° to the 10 N force.
Show Answers Only

`A`

Show Worked Solution

 
 

`|∑underset~F|^2` `= 10^2 + 8^2 – 2 xx 10 xx 8cos120°`
`|∑underset~F|` `= sqrt244`
  `~~ 15.6`

 

`(sin(theta))/8` `= (sin(120°))/15.62`
`sin(theta)` `= (4sqrt3)/15.62`
`:. theta` `~~ 26.3°`

 
`=> A`

Vectors, SPEC1 2017 VCAA 9

A particle of mass 2 kg with initial velocity  `3underset~i + 2underset~j`  ms−1 experiences a constant force for 10 seconds.

The particle's velocity at the end of the 10-second period  `43underset~i-18underset~j`  ms−1 .

  1. Find the magnitude of the constant force in newtons.   (2 marks)

  2. Find the displacement of the particle from its initial position after 10 seconds.   (3 marks)

Show Answers Only
  1. `4sqrt5 N`
  2. `230underset~i-80underset~j`
Show Worked Solution
a.    `u_i` `= 3` `v_i` `= 43`
  `u_j` `= 2` `v_j` `= −18`
`43` `= 3 + 10a`
`40` `= 10a`
`a_i` `= 4`

♦ Mean mark (a) 38%.

`−18` `= 2 + 10a_j`
`−20` `= 10a_j`
`a_j` `= −2`

 

`underset~a` `= 4underset~i-2underset~j`
`|underset~a|` `= sqrt(4^2 + (−2)^2)`
  `= sqrt(20)`
  `= 2sqrt5`

 

`:.|F|` `= 2 xx 2sqrt5`
  `= 4sqrt5 N`

 

b.  `underset~a = 4underset~i-2underset~j`

`underset~v` `= int4underset~i-2underset~j\ dt`
  `= (4t + C_i)underset~i + (−2t + C_j)underset~j\ \ \ (C_i, C_j ∈ R)`

 
`underset~v(0) = C_i underset~i + C_j underset~j = 3underset~i + 2underset~j`

`=> C_i = 3, C_j = 2`
 

`underset~v(t) = (4t + 3)underset~i + (2-2t)underset~j`

`underset~x(t)` `= int(4t + 3)underset~i + (2-2t)underset~j\ dt`
  `= (((4t^2)/2 +3t) + b_i)underset~i + ((2t-(2t^2)/2) + b_j)underset~j \ \ \ (b_i, b_j ∈ R)`
  `= (2t^2 + 3t + b_i)underset~i + (2t-t^2 + b_j)underset~j`

 
`underset~x(0) = b_iunderset~i + b_junderset~j`

`underset~0 => b_i = b_j = 0`

`underset~x(t) = (2t^2 + 3t)underset~i + (2t-t^2)underset~j`

`underset~x(10)` `= (2(10)^2 + 3(10))underset~i + (2(10)-10^2)underset~j`
  `= 230underset~i-80underset~j`

Calculus, SPEC1 2017 VCAA 8

A slope field representing the differential equation  `dy/dx = −x/(1 + y^2)`  is shown below.

  1. Sketch the solution curve of the differential equation corresponding to the condition  `y(−1) = 1`  on the slope field above and, hence, estimate the positive value of `x` when  `y = 0`. Give your answer correct to one decimal place.   (2 marks)

  2. Solve the differential equation  `(dy)/(dx) = (−x)/(1 + y^2)`  with the condition  `y(−1) = 1`. Express your answer in the form  `ay^3 + by + cx^2 + d = 0`, where `a`, `b`, `c` and `d` are integers.   (2 marks)

Show Answers Only
  1.  

  2. `2y^3 + 6y + 3x^2 – 11 = 0`
Show Worked Solution
a.   

♦♦ Mean mark part (a) 32%.
MARKER’S COMMENT: Solution curve should follow slope ticks and not cross them.

 

b.    `(1 + y^2)(dy)/(dx)` `= −x`
  `int 1 + y^2 dy` `= −int x\ dx`
  `y + (y^3)/3` `= −(x^2)/2 + C, C ∈ R`

 
`text(Substituting)\ (-1,1):`

`1 + (1^3)/3` `= −((−1)^2)/2 + C`
`1 + 1/3` `= −1/2 + C`
`:. C` `= 1/2 + 4/3`
  `= 11/6`

 

`y + 1/3y^3` `= −1/2x^2 + 11/6`
`6y + 2y^3` `= −3x^2 + 11`

 

`:. 2y^3 + 6y + 3x^2 – 11 = 0`

Vectors, SPEC1 2017 VCAA 7

The position vector of a particle moving along a curve at time `t` is given by  `underset~r(t) = cos^3(t)underset~i + sin^3(t)underset~j, \ 0 <= t <= pi/4`.

Find the length of the path that the particle travels along the curve from  `t = 0`  to  `t = pi/4`.  (4 marks)

Show Answers Only

`3/4`

Show Worked Solution

`x(t) = (cos(t))^3 `

♦ Mean mark 50%.

`xprime(t)= −3cos^2(t)sin(t)`

 
`y(t) = (sin(t))^3`

`yprime(t)= 3sin^2(t)cos(t)`

 

`l` `= int_0^(pi/4)sqrt((xprime(t))^2 + (yprime(t))^2)\ dt`
  `= int_0^(pi/4)sqrt(9cos^4(t)sin^2(t) + 9sin^2(t)cos^2(t))\ dt`
  `= int_0^(pi/4)3sqrt(sin^2(t)cos^2(t)(cos^2(t) + sin^2(t)))\ dt`
  `= int_0^(pi/4)3sqrt(sin^2(t)cos^2(t))\ dt`
  `= 3int_0^(pi/4)sin(t)cos(t)\ dt`
  `= 3/2 int_0^(pi/4)(2sin(t)cos(t))\ dt`
  `= 3/2int_0^(pi/4)sin(2t)\ dt`
  `= 3/2[−1/2 cos(2t)]_0^(pi/4)`
  `= −3/4(cos(pi/2) – cos(0))`
  `= 3/4`

Calculus, SPEC1 2017 VCAA 6

Let  `f(x) = 1/(arcsin(x))`.

Find  `f^{′}(x)` and state the largest set of values of `x` for which  `f^{′}(x)`  is defined.   (3 marks)

Show Answers Only

`x ∈ (−1, 1) \\ {0}`

Show Worked Solution

`u = sin^(−1)(x), \ f(u(x)) = 1/u`

♦ Mean mark 41%.

`f^{′}(u(x))` `= −u^(−2)`
`u^{′}(x)` `= 1/sqrt(1-x^2)`
`f^{′}(x)` `= (−u^(−2))/sqrt(1-x^2)`
`f^{′}(x)` `= (−1)/(arcsin^2(x)sqrt(1-x^2))`

 

`text(Domain:)\ sin^(−1)(x)\ \ x ∈[−1,1]`

`sin^(−1)(x) != 0 \ \ => \ \ x != 0`

`=> x ∈ [−1, 1] \\ {0}`
 

`f^{′}(x)\ text(doesn’t exist at end points)`

`:. x ∈ (−1, 1) \\ {0}`

Vectors, SPEC1 2017 VCAA 5

Relative to a fixed origin, the points `B`, `C` and `D` are defined respectively by the position vectors  `underset~b = underset~i - underset~j + 2underset~k, \ underset~c = 2underset~i - underset~j + underset~k`  and  `underset~d = aunderset~i - 2underset~j`  where `a` is a real constant.

Given that the magnitude of angle `BCD` is  `pi/3`, find `a`.  (4 marks)

Show Answers Only

`a = −2`

Show Worked Solution

`text(Angle between)\ overset(->)(CB)\ text(and)\ overset(->)(CD) = pi/3`

♦ Mean mark 45%.

`overset(->)(CB)` `= (1 – 2)underset~i + (−1 – −1)underset~j + (2 – 1)underset~k`
  `= −underset~i + underset~k`
`overset(->)(CD)` `= (a – 2)underset~i + (−2 – −1)underset~j + (−1 + 0)underset~k`
  `= (a – 2)underset~i – underset~j – underset~k`

 

`overset(->)(CD) · overset(->)(CB)` `= −(a – 2) + 0 – 1`
  `= 1 – a`
  `= |overset(->)(CD)||overset(->)(CB)|cos(pi/3)`

 

`1 – a` `= sqrt((a – 2)^2 + (−1)^2 + (−1)^2)sqrt((−1)^2 + (1)^2)cos(pi/3)`
`1 + a` `= sqrt(a^2 – 4a + 4 + 1 + 1) xx sqrt2 xx 1/2`
`2(1 – a)` `= sqrt(2a^2 – 8a + 12), \ \ a < 1`
`4(1 – a)^2` `= 2a^2 – 8a + 12, \ \ a < 1`
`4(1 – 2a + a^2)` `= 2a^2 – 8a + 12`
`4 – 8a + 4a^2` `= 2a^2 – 8a + 12`
`2a^2` `= 8`
`a^2` `= 4`
`:. a` `= −2\ \ \ (a<1)`

Statistics, SPEC1 2017 VCAA 4

The volume of soft drink dispensed by a machine into bottles varies normally with a mean of 298 mL and a standard deviation of 3 mL. The soft drink is sold in packs of four bottles.

Find the approximate probability that the mean volume of soft drink per bottle in a randomly selected four-bottle pack is less than 295 mL. Give your answer correct to three decimal places.   (3 marks)

Show Answers Only

`0.025`

Show Worked Solution

`X\ ~\ N(298, 3^2)`

♦ Mean mark 48%.
MARKER’S COMMENT: Many students incorrectly used the population std dev, not the sample std dev.

`barX\ ~\ N(298, (3^2)/4)`

`Z\ ~\ N(0,1)`

`text(Pr)(barX < 295)` `= text(Pr)(Z < (295 – 298)/(3/2))`
  `= text(Pr)(Z < −2)`

 


 

`text(Pr)(barX < 295)` `~~ 0.05/2`
  `= 0.025`

Calculus, SPEC1 VCAA 2017 2

Find  `int_1^(sqrt3) 1/(x(1 + x^2))\ dx`, expressing your answer in the form  `log_e(sqrt(a/b))`  (4 marks)

Show Answers Only

`ln(sqrt(3/2))`

Show Worked Solution

`text(Using partial fractions:)`

`int_1^(sqrt3) A/x + (Bx + C)/(1 + x^2)\ dx`

♦ Mean mark 48%.
MARKER’S COMMENT: A “large number” of students did not use partial fractions here.

`A(1 + x^2) + (Bx + C)x = 1`

`(A+B)x^2 + Cx+(A+C)=1`

`Cx=0\ \ =>\ C=0`

`A+C=1\ \ =>\ A=1`

`A+B=0\ \ =>\ B=-1`

 
`:. int_1^(sqrt3) 1/(x(1 + x^2))\ dx`

  `= int_1^(sqrt3) 1/x\ dx + int_1^(sqrt3) (−x)/(1 + x^2)\ dx`
  `= [ln|x|]_1^(sqrt3)-1/2 int_1^(sqrt3) (2x)/(1 + x^2)\ dx`
  `= ln(sqrt3)-ln(1)-1/2[ln(1 + x^2)]_1^(sqrt3)`
  `= ln(sqrt3)-1/2 ln(4) + 1/2 ln(2)`
  `= ln(sqrt3)-ln2 + ln(sqrt2)`
  `= ln((sqrt3 xx sqrt2)/2)`
  `= ln((sqrt6)/2)`
  `= ln(sqrt(3/2))`

Statistics, SPEC2-NHT 2018 VCAA 20 MC

A farm grows oranges and lemons. The oranges have a mean mass of 200 grams with a standard deviation of 5 grams and the lemons have a mean mass of 70 grams with a standard deviation of 3 grams.

Assuming masses for each type of fruit are normally distributed, what is the probability, correct to four decimal places, that a randomly selected orange will have at least three times the mass of a randomly selected lemon?

  1. 0.0062
  2. 0.0828
  3. 0.1657
  4. 0.8343
  5. 0.9172
Show Answers Only

`C`

Show Worked Solution

`O~N (200, 5^2) `

`L~N (70, 3^2)`

`text(Pr) text{(orange weighs at least 3 × lemon)}`

`=text(Pr) (O > 3L)`

`= text(Pr)(O-3L > 0)`
 

`text(Let)\ \ X = O-3L,`

`X~N (200-3 xx 70, 5^2 + (-3)^2 xx 3^2)`

`X~N (-10, 106)`

`text(Pr) (X > 0) ~~ 0.1657`

 
`=>  C`

Vectors, SPEC2-NHT 2018 VCAA 13 MC

Let  `underset~i`  and  `underset~j`  be unit vectors in the east and north directions respectively

At time `t, t >= 0`, the position of particle `A` is given by  `underset~r_A = (t^2 - 5t + 6) underset~i + (5t - 8) underset~j`  and the position of particle `B` is given by  `underset~r_B = (3 - t) underset~i + (t^2 - t) underset~j`.

Particle `A` will be directly east of particle `B` when `t` equals

  1. 1
  2. 2
  3. 1 and 2
  4. 2 and 4
  5. 4
Show Answers Only

`E`

Show Worked Solution

`text(Find)\ t\ text(when particles align:)`

`5t – 8` `= t^2 – t`
`0` `= t^2 – 6t – 8`
`0` `= (t – 4)(t – 2)`

 
`t = 2, quad t = 4`
 

`x_A(2)` `= 4 – 10 + 6 = 0`
`x_B(2)` `= 1 > x_A (2) \ ->\  B\ text(is East of)\ A`
`x_A(4)` `= 16 – 20 + 6 = 2`
`x_B(4)` `= -1 < x_A (2) \ ->\  A\ text(is East of)\ B`

 

`=>  E`

Calculus, SPEC1-NHT 2018 VCAA 9

  1.    i. Given that  `cot(2 theta) = a`, show that  `tan^2(theta) + 2a tan(theta)-1 = 0`.   (2 marks)

  2.  ii. Show that  `tan(theta) = -a +- sqrt(a^2 + 1)`.  (1 mark)

  3. iii. Hence, show that  `tan(pi/12) = 2-sqrt 3`, given that  `cot(2 theta) = sqrt 3`, where  `theta in (0, pi)`.   (1 mark)

  4.  Find the gradient of the tangent to the curve  `y = tan (theta)`  at  `theta = pi/12`.   (2 marks)

  5.  A solid of revolution is formed by rotating the region between the graph of  `y = tan(theta)`, the horizontal axis, and the lines  `theta = pi/12`  and  `theta = pi/3`  about the horizontal axis.
  6. Find the volume of the solid of revolution.   (3 marks)

Show Answers Only

    1. `text(Proof)\ \ text{(See Worked Solutions)}`
    2. `text(Proof)\ \ text{(See Worked Solutions)}`
    3. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `8-4 sqrt 3`
  3. `pi (2 sqrt 3-2-pi/4)`

Show Worked Solution

a.i.   `1/(tan 2 theta)` `= a`
  `1` `= a tan (2 theta)`
  `1` `= a ((2 tan (theta))/(1-tan^2(theta)))`
  `1/a (1-tan^2 (theta))` `= 2 tan (theta)`
  `1-tan^2 (theta)` `= 2a tan (theta)`
  `:. tan^2 (theta) + 2 a tan (theta)-1` `=0\ \ text(… as required)`

 

a.ii.   `[tan^2 (theta) + 2a tan (theta) + a^2]-a^2-1` `= 0`
  `(tan (theta) + a)^2` `= a^2 + 1`
  `tan (theta) + a` `= +- sqrt(a^2 + 1)`
  `:. tan (theta)` `= -a +- sqrt(a^2 + 1)`

 

a.iii.   `theta in (0, pi) \ => \ 2 theta in (0, 2 pi)`

`text(S)text(ince)\ \ cot(2theta)=sqrt3\ \ \ =>\ \ \ tan(2theta)=1/sqrt3`

  `:. 2 theta` `= pi/6, pi + pi/6`
  `theta` `= pi/12, (7 pi)/12`
  `tan (theta)` `=-sqrt 3 +- sqrt((sqrt 3)^2 + 1)`
    `=-sqrt 3 +- sqrt(3 + 1)`
    `=-sqrt 3 +- 2`

 
`:. tan (pi/12) = 2-sqrt 3,\ \ \ \ (tan (pi/12) > 0)`

 

b.   `y` `=tan(theta)`
  `y prime` `= sec^2 (theta)`
    `= 1 + tan^2 (theta)`

 

`y prime (pi/12)` `= 1 + tan^2 (pi/12)`
  `= 1 + (2-sqrt 3)^2`
  `= 1 + 4-4 sqrt 3 + 3`
  `= 8-4 sqrt 3`

 

c.   `V` `= pi int_(pi/12)^(pi/3) y^2\ d theta`
    `= pi int_(pi/12)^(pi/3) tan^2 (theta)\ d theta`
    `= pi int_(pi/12)^(pi/3) (1 + tan^2 (theta)-1)\ d theta`
    `= pi int_(pi/12)^(pi/3) (sec^2 (theta)-1)\ d theta`
    `= pi [tan (theta)-theta]_(pi/12)^(pi/3)`
    `= pi (tan (pi/3)-pi/3-(tan (pi/12)-pi/12))`
    `= pi (sqrt 3-(4 pi)/12-(2-sqrt 3) + pi/12)`
    `= pi (2 sqrt 3-2-pi/4)\ \ text(u³)`

Mechanics, SPEC2 2018 VCAA 17 MC

A tourist standing in the basket of a hot air balloon is ascending at 2 ms¯¹. The tourist drops a camera over the side when the balloon is 50 m above the ground.

Neglecting air resistance, the time in seconds, correct to the nearest tenth of a second, taken for the camera to hit the ground is

A.   2.3

B.   2.4

C.   3.0

D.   3.2

E.   3.4

Show Answers Only

`E`

Show Worked Solution

`u = 2, quad s = -50, quad a = -9.8`

`2t – 4.9t^2` `=-50`  
`4.9t^2 – 2t – 50` `= 0`  

 
`t = (2 +- sqrt((-2)^2 – 4(4.9)(-50)))/(2(4.9))`

`:. t = 3.4\ \ \ (t>0)`

 
`=>  E`

Vectors, SPEC2 2018 VCAA 12 MC

If  `|underset ~a + underset ~b| = |underset ~a| + |underset ~b|`  and  `underset ~a, underset ~b != underset ~0`, which one of the following is necessarily true?

  1. `underset ~a\ text(is parallel to)\ underset ~b`
  2. `|underset ~a| = |underset ~b|`
  3. `underset ~a = underset ~b`
  4. `underset ~a = -underset ~b`
  5. `underset ~a\ text(is perpendicular to)\ underset ~b` 
Show Answers Only

`A`

Show Worked Solution
`|underset ~a + underset ~b|^2` `= (|underset ~a| + |underset ~b|)^2\ \ \ text{(given)}`
  `= |underset ~a|^2 + 2|underset ~a||underset ~b|+|underset ~b|^2`
`underset ~a ⋅ underset ~b` `= |underset ~a||underset ~b| cos theta`

 
`=> 2|underset ~a||underset ~b| = (2 underset ~a ⋅ underset ~b)/(cos theta)`

♦♦ Mean mark 36%.

`=>|underset ~a + underset ~b|^2 = |underset ~a|^2 + (2 underset ~a ⋅ underset ~b)/(cos theta) + |b|^2`

`(underset ~a + underset ~b) * (underset ~a + underset ~b) = underset ~a ⋅ underset ~a + (2 underset ~a ⋅ underset ~b)/(cos theta) + underset ~b ⋅ underset ~b`

`underset ~a ⋅ underset ~a + 2underset ~a ⋅ underset ~b + underset ~b ⋅ underset ~b = underset ~a ⋅ underset ~a + (2 underset ~a ⋅ underset ~b)/(cos theta) + underset ~b ⋅ underset ~b`

`2 underset ~a ⋅ underset ~b = (2 underset ~a ⋅ underset ~b)/(cos theta)`

`:. cos theta = 1\ \ =>\ \  theta = 0`

`=>  A`

Complex Numbers, SPEC2 2018 VCAA 5 MC

Let  `z = a + bi`, where  `a, b in R\ text(\ {0})`

If  `z + 1/z \ in R`, which one of the following must be true?

  1. `text(Arg)(z) = pi/4`
  2. `a = -b`
  3. `a = b`
  4. `|z| = 1`
  5. `z^2 = 1` 
Show Answers Only

`D`

Show Worked Solution
`z + 1/z` `= a + bi + 1/(a + bi)`
  `= a + bi + (a – bi)/{(a + bi)(a – bi)}`
  `= a + bi + (a – bi)/(a^2 + b^2)`
  `= {(a + bi)(a^2 + b^2) + a – bi}/(a^2 + b^2)`
  `= {a(a^2 + b^2) + a}/(a^2 + b^2) + {b (a^2 + b^2) – b}/(a^2 + b^2)\ i`

 
`text(If)\ \ z + 1/z in R\ \ =>\  {b (a^2 + b^2) – b}/(a^2 + b^2) = 0`

 

`b(a^2 + b^2) – b = 0`

`b(a^2 + b^2 – 1) = 0`

`a^2 + b^2 = 1,\ \ (b !=0)`

`a^2 + b^2 = |z|^2 = 1`

`:. |z| = 1`

`=>  D`

Vectors, SPEC1 2018 VCAA 10

The position vector of a particle moving along  a curve at time `t` seconds is given by 

   `underset ~r (t) = t^3/3 underset ~i + (text{arcsin}(t) + t sqrt (1 - t^2)) underset ~j, \ 0 <= t <= 1`,

where distances are measured in metres.

The distance `d` metres that the particle travels along the curve in three-quarters of a second is given by

`d = int_0^(3/4) (at^2 + bt + c)\ dt`

Find `a, b` and `c`, where  `a, b, c in Z`.  (5 marks)

Show Answers Only

`a = -1,\ \ b = 0,\ \ c = 2`

Show Worked Solution
`x` `= t^3/3`
`x′ (t)` `=t^2`

♦♦ Mean mark 26%.

`y` `= sin^(-1)(t) + t(1 – t^2)^(1/2)`
`y′(t)` `= 1/sqrt(1 – t^2) + sqrt(1 – t^2) + t(1/2(-2t)(1 – t^2)^(-1/2))`
  `= 1/sqrt(1 – t^2) + sqrt (1 – t^2) – t^2/sqrt(1 – t^2)`
  `= (1 – t^2)/sqrt (1 – t^2) + sqrt (1 – t^2)`
  `= sqrt(1 – t^2) + sqrt(1 – t^2)`
  `= 2 sqrt (1 – t^2)`

 

`d` `= int_0^(3/4) sqrt(((dx)/(dt))^2 + ((dy)/(dt))^2)\ dt`
  `= int_0^(3/4) sqrt(t^4 + 4(1 – t^2))\ dt`
  `= int_0^(3/4) sqrt(t^4 – 4t^2 + 4)\ dt`
  `= int_0^(3/4) sqrt((t^2 – 2)^2)\ dt`

 
`text(S)text(ince distance travelled along curve is positive,)`

`text(When)\ \ 0 <= t <= 1 => sqrt((t^2 – 2)^2) = 2 – t^2 >= 0`

`d = int_0^(3/4) – t^2 + 0*t + 2\ dt`

`a = -1,\ \ b = 0,\ \ c = 2`

Calculus, SPEC1 2018 VCAA 9

A curve is specified parametrically by  `underset ~r(t) = sec(t) underset ~i + sqrt 2/2 tan(t) underset ~j, \ t in R`.

  1.  Show that the cartesian equation of the curve is  `x^2-2y^2 = 1`.   (2 marks)

  2.  Find the `x`-coordinates of the points of intersection of the curve  `x^2-2y^2 = 1`  and the line  `y = x-1`.   (1 mark)

  3.  Find the volume of the solid of revolution formed when the region bounded by the curve and the line is rotated about the `x`-axis.   (2 marks)

Show Answers Only

  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `x = 1 or x = 3`
  3. `(2 pi)/3`

Show Worked Solution

a.     `x = sec(t), qquad y = sqrt 2/2 tan(t)`

`x^2 = sec^2(t), qquad y^2 = 1/2 tan^2(t)`

`x^2 = sec^2(t), qquad 2y^2 = tan^2(t)`

`1 + tan^2(t)` `= sec^2(t)`
`1 + 2y^2` `= x^2`
`:.x^2-2y^2` `=1\ \ text(.. as required)`

 

b.    `x^2-2(x-1)^2` `= 1`
  `x^2-2(x^2-2x + 1)` `=1`
  `x^2-2x^2 + 4x-2` `=1`
  `-x^2 + 4x-2-1` `=0`
  `x^2-4x + 3` `=0`
  `(x-3) (x-1)` `=0`

 
`:. x = 1 or x = 3`

♦♦ Mean mark 30%.

 

c.   `x^2-{:2y_1:}^2` `=1`
  `{:2y_1:}^2` `=x^2-1`
  `{:y_1:}^2` `= (x^2-1)/2`
  `{:y_2:}^2` `= (x-1)^2`

 

`V` `=pi int_1^3 {:y_1:}^2-{:y_2:}^2 \ dx`
  `= pi int_1^3 (x^2-1)/2-(x-1)^2\ dx`
  `= pi [x^3/6-x/2-(x-1)^3/3]_1^3`
  `= pi [(3^3/6-3/2-2^3/3)-(1^3/6-1/2-0)]`
  `= pi (9/2-3/2-8/3-1/6 + 1/2)`
  `= pi (7/2-8/3-1/6)`
  `= pi ((21-16-1)/6)`
  `= (2 pi)/3`

Calculus, SPEC1 2018 VCAA 8

A tank initially holds 16 L of water in which 0.5 kg of salt has been dissolved. Pure water then flows into the tank at a rate of 5 L per minute. The mixture is stirred continuously and flows out of the tank at a rate of 3 L per minute.

  1.  Show that the differential equation for `Q`, the number of kilograms of salt in the tank after `t` minutes, is given by
  2. `qquad (dQ)/(dt) = -(3Q)/(16 + 2t)`  (1 mark)

  3. Solve the differential equation given in part a. to find `Q` as a function of `t`.
  4. Express your answer in the form  `Q = a/(16 + 2t)^(b/c)`, where `a, b` and `c` are positive integers.  (3 marks)

Show Answers Only
  1.  `text(Proof)\ \ text{(See Worked Solutions)}`
  2.  `Q = 32/(16 + 2t)^(3/2)`
Show Worked Solution

a. `Q_0 = 0.5, \ V_0 = 16`

♦ Net mean mark of both parts 44%.

`V(t)= 16 + (5-3) t= 16 + 2t`

`text(Concentration)\ (C)= Q/V= Q/(16 + 2t)\ text(kg/L)`

`(dQ)/(dt)= 0 xx 5-3C= -(3Q)/(16 + 2t)`
 

MARKER’S COMMENT: Many students took the common factor of 2 from  `16+2t`. This wasn’t necessary and complicated the arithmetic in part b.

b.   `-1/(3Q) * (dQ)/(dt) = 1/(16 + 2t)`

`int -1/(3Q)\ dQ` `= int 1/(16 + 2t) dt`
`-1/3 int 1/Q\ dQ` `= 1/2 int 2/(16 + 2t)\ dt`
`-1/3 ln Q` ` = [1/2 ln(16 + 2t)] + c`

 
`text(When)\ \ t=0,\ \ Q=0.5,`

`-1/3 ln (1/2)` `= 1/2 ln (16) +c`
`c` `= -1/2 ln (16) -1/3 ln (1/2)`

 

`-1/3 ln Q` `= 1/2 ln(16 + 2t) -1/2 ln(16)-1/3 ln (1/2)`
`-1/3 ln Q` `= 1/2 ln ((16 + 2t)/16)-1/3 ln (1/2)`
`-1/3 ln Q` `= ln (((16 + 2t)^(1/2))/4)-ln (2^(-1/3))`
`ln (Q^(-1/3))` `= ln (((16 + 2t)^(1/2))/(2^2 ⋅ 2^(-1/3)))`
`Q^(-1/3)` `= ((16 + 2t)^(1/2))/(2^(5/3))`
`Q` `= (((16 + 2t)^(1/2))/(2^(5/3)))^-3`
  `= (16 + 2t)^(- 3/2)/(2^(-5))`
`:. Q` `= 32/((16 + 2t)^(3/2))`

Calculus, MET1 2018 VCAA 8

Let  `f: R -> R, \ f(x) = x^2e^(kx)`, where `k` is a positive real constant.

  1.  Show that  `f^{′}(x) = xe^(kx)(kx + 2)`.   (1 mark)

  2. Find the value of `k` for which the graphs of  `y = f(x)`  and  `y = f^{′}(x)`  have exactly one point of intersection.   (3 marks)

Let  `g(x) = −(2xe^(kx))/k`. The diagram below shows sections of the graphs of `f` and `g` for  `x >= 0`.
 


 

Let `A` be the area of the region bounded by the curves  `y = f(x), \ y = g(x)` and the line  `x = 2`.

  1. Write down a definite integral that gives the value of `A`.   (1 mark)

  2. Using your result from part a., or otherwise, find the value of `k` such that  `A = 16/k`.   (3 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(One point of intersection)\ x = 0\ text(when)\ k = 1.`
  3. `int_0^2 (x^2e^(kx) + (2xe^(kx))/k)dx`
  4. `1/2 ln 4\ \ text(or)\ \ ln2`
Show Worked Solution

a.   `f(x) = x^2e^(kx)`

`f^{′}(x)` `= 2x · e^(kx) + x^2 · k · e^(kx)`
  `= xe^(kx)(kx + 2)\ \ …text(as required)`

 

b.  `text(Intersection occurs when:)`

♦♦♦ Mean mark 7%.
MARKER’S COMMENT: Most students found the correct quadratic equation but solved for `k`.

`x^2e^(kx)` `= xe^(kx)(kx + 2)`
`x^2-x(kx + 2)` `= 0,\ \ e^(kx) != 0`
`x^2-kx^2-2x` `= 0`
`x^2(1-k)-2x` `= 0`
`x[x(1-k)-2]` `= 0`

 

`:.x = 0\ \ text(or)\ \ x(1-k)-2` `= 0`
`x` `= 2/(1-k)`

 
`text(S)text(ince)\ \ x = 2/(1-k)\ \ text(is undefined when)\ \ k = 1,`

`=>\ text(One point of intersection only at)\ \ x = 0\ \ text(when)\ \ k = 1.`

 

c.    `A` `= int_0^2 f(x)\ dx-int_0^2 g(x)\ dx`
    `= int_0^2 x^2e^(kx)\ dx-int_0^2 −(2xe^(kx))/k \ dx`
    `= int_0^2 (x^2e^(kx) + (2xe^(kx))/k)dx`

♦♦ Mean mark 29%.

 

d.    `int_0^2(x^2e^(kx) + (2xe^(kx))/k)\ dx` `= 16/k`
  `1/k int_0^2(kx^2e^(kx) + 2xe^(kx))\ dx` `= 16/k`
  `1/k int_0^2(xe^(kx)(kx + 2))\ dx` `= 16/k`
  `1/k[x^2e^(kx)]_0^2` `= 16/k\ \ \ text{(using part a)}`
  `[2^2 · e^(2k)-0]` `= 16`
  `e^(2k)` `= 4`
  `2k` `= ln 4`
  `k` `= 1/2 ln 4\ \ text(or)\ \ ln2`

Calculus, MET1 2018 VCAA 7

Let `P` be a point on the straight line  `y = 2x-4`  such that the length of `OP`, the line segment from the origin `O` to `P`, is a minimum.

  1.  Find the coordinates of `P`.   (3 marks)

  2.  Find the distance `OP`. Express your answer in the form `(asqrtb)/b` , where `a` and `b` are positive integers.   (2 marks)

Show Answers Only
  1. `P(8/5, −4/5)`
  2. `(4sqrt5)/5`
Show Worked Solution

a.   `text(Solution 1)`

♦ Mean mark 42%.

`text(Let)\ \ P = (x, 2x-4)`

`L_(OP)` `= sqrt(x^2 + (2x-4)^2)`
  `= sqrt(x^2 + 4x^2-16x + 16)`
  `= sqrt(5x^2-16x + 16)`
   
`(d(L_(OP)))/(dx)` `= 1/2 · (10x-16) · (5x^2-16x + 16)^(−1/2)`

 

`text(Find)\ \ x\ \ text(when)\ \ (d(L_(OP)))/(dx) = 0,`

`10x-16` `= 0`
`x` `= 8/5`

 
`:. P(8/5, −4/5)`
 

`text(Solution 2)`

`text(Find equation of line ⊥ to)\ \ y = 2x-4`

`text(passing through the origin:)`

`m = −1/2\ \ (text(so that)\ \ m_1 m_2 = −1)`

`y` `= −1/2x\ \ …\ (1)`
`y` `= 2x-4\ \ …\ (2)`

 
`P\ text{is the intersection of (1) and (2)}`

`−1/2x` `= 2x-4`
`5/2x` `= 4`
`x` `= 8/5, y = −4/5`

 

b.  `text(Using)\ \ L_(OP)\ \ text(from part a:)`

♦ Mean mark 42%.

`L_(OP)` `= sqrt(5 · (8/4)^2-16 · 8/5 + 16)`
  `= sqrt(64/5-128/5 + 16)`
  `= sqrt(16/5)`
  `= 4/sqrt5 xx sqrt5/sqrt5`
  `= (4sqrt5)/5`

Calculus, MET2 2018 VCAA 19 MC

The graphs  `f: R -> R,\ f(x) = cos ((pi x)/2)`  and  `g: R -> R,\ g(x) = sin (pi x)` are shown in the diagram below.
 


 

An integral expression that gives the total area of the shaded regions is

A.   `int_0^3 (sin(pi x) - cos ((pi x)/2)) dx`

B.   `2 int_(5/3)^3 (sin(pi x) - cos((pi x)/2))dx`

C.   `int_0^(1/3)(cos((pi x)/2) - sin (pi x)) dx - 2 int_(1/3)^1(cos((pi x)/2) - sin (pi x)) dx`

                `- int_(5/3)^3 (cos ((pi x)/2) - sin (pi x)) dx`

D.   `2 int_1^(5/3)(cos((pi x)/2) - sin (pi x)) dx - 2 int_(5/3)^3 (cos ((pi x)/2) - sin (pi x)) dx`

E.   `int_0^(1/3) (cos((pi x)/2) - sin (pi x)) dx + 2 int_(1/3)^1(sin (pi x) - cos ((pi x)/2))dx`

                `+ int_(5/3)^3 (cos((pi x)/2) - sin (pi x)) dx`

Show Answers Only

`C`

Show Worked Solution

`text(The graph contains 2 symmetrical shaded areas:)`

♦ Mean mark 41%.
COMMENT: In each shaded area, it is critical to note which graph is “higher” and which side of the x-axis the shading is.
 

`:.\ text(Area can be represented by:)`

`int_0^(1/3)(cos((pi x)/2) – sin (pi x)) dx – 2 int_(1/3)^1(cos((pi x)/2) – sin (pi x)) dx`

         `- int_(5/3)^3 (cos ((pi x)/2) – sin (pi x)) dx`

 
`=>   C`

Calculus, MET2 2018 VCAA 17 MC

The turning point of the parabola  `y = x^2 - 2bx + 1`  is closest to the origin when

  1. `b = 0`
  2. `b = -1 or b = 1`
  3. `b = -1/sqrt 2 or b = 1/sqrt 2`
  4. `b = 1/2 or b = -1/2`
  5. `b = 1/4 or b = -1/4`
Show Answers Only

`C`

Show Worked Solution

`y = x^2 – 2bx + 1`

♦ Mean mark 45%.

`(dy)/(dx) = 2x – 2b`

`text(T.P. when)\ \ (dy)/(dx) = 0`

`2x – 2b` `= 0`
`x` `= b`

 
`text(T.P. at)\ \ P (b, 1 – b^2)`
 

`text(Find)\ \ D_p = text(distance of)\ P\ text(from origin:)`

`D_P` `= sqrt(b^2 + (1 – b^2)^2)`
  `= sqrt(b^4 – b^2 + 1)`

 
`text(When)\ \ (dD_P)/(db) = 0,\ \ b = +- 1/sqrt 2`

`=>   C`

Calculus, MET2 2018 VCAA 16 MC

Jamie approximates the area between the `x`-axis and the graph of  `y = 2 cos(2x) + 3`, over the interval  `[0, pi/2]`, using the three rectangles shown below.
 


 

Jamie’s approximation as a fraction of the exact area is

A.   `5/9`

B.   `7/9`

C.   `9/11`

D.   `11/18`

E.   `7/3`

Show Answers Only

`B`

Show Worked Solution

`text(Area of rectangles)`

♦ Mean mark 49%.

`= pi/6 xx f(pi/6) + pi/6 xx f(pi/3) + pi/6 xx f(pi/2)`

`= (7pi)/6\ text(u²)`

`text(Actual Area) = int_0^(pi/2) 2 cos (2x) + 3\ dx = (3 pi)/2`

 
`:.\ text(Fraction of exact area)`

`= (7 pi)/6 ÷ (3 pi)/2`

`= 7/9`

 
`=>   B`

Probability, MET2 2018 VCAA 15 MC

A probability density function, `f`, is given by
 

`f(x) = {(1/12 (8x -x^3)), (\ 0):} qquad {:(0 <= x <= 2), (text(elsewhere)):}`
 

The median, `m`, of this function satisfies the equation

A.   `-m^4 + 16m^2 - 6 = 0`

B.   `-m^4 + 4m^2 - 6 = 0`

C.   `m^4 - 16m^2 = 0`

D.   `m^4 - 16m^2 + 24 = 0.5`

E.   `m^4 - 16m^2 + 24 = 0`

Show Answers Only

`E`

Show Worked Solution

♦ Mean mark 49%.

`int_0^m 1/12(8x – x^3) dx` `= 0.5`
`[1/12(4x^2 – x^4/4)]_0^m` `= 0.5`
`(4m^2 – m^4/4)` `= 6`
`16m^2 – m^4` `= 24`
`m^4 – 16m^2 + 24` `= 0`

 
`=>   E`

Algebra, STD2 A2 2007 HSC 27b*

A clubhouse uses four long-life light globes for five hours every night of the year. The purchase price of each light globe is $6.00 and they each cost  `$d`  per hour to run.

  1. Write an equation for the total cost (`$c`) of purchasing and running these four light globes for one year in terms of  `d`.    (2 marks)

  2. Find the value of  `d`  (correct to three decimal places) if the total cost of running these four light globes for one year is $250.   (1 mark)

  3. If the use of the light globes increases to ten hours per night every night of the year, does the total cost double? Justify your answer with appropriate calculations.   (1 mark)

Show Answers Only
  1. `$c = 24 + 7300d`
  2. `0.031\ $ text(/hr)\ text{(3 d.p.)}`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution

a.   `text(Purchase price) = 4 xx 6 = $24`

`text(Running cost)` `= text(# Hours) xx text(Cost per hour)`
  `= 4 xx 5 xx 365 xx d`
  `= 7300d`
 
`:.\ $c = 24 + 7300d`

 

b.   `text(Given)\ $c = $250`

`=>250` `= 24 + 7300d`
`7300d` `= 226`
`d` `= 226/7300`
  `= 0.03095…`
  `= 0.031\ $ text(/hr)\ text{(3 d.p.)}`

 

c.   `text(If)\ d\ text(doubles to 0.062)\ \ $text(/hr)`

`$c` `= 24 + 7300 xx 0.062`
  `= $476.60`
   
`text(S) text(ince $476.60 is less than)\ 2 xx $250\ ($500),`
`text(the total cost increases to less than double)`
`text(the original cost.)`

 

Statistics, STD2 S1 SM-Bank 2 MC

The dot plots show the height of students in Year 9 and Year 12 in a school. They are drawn on the same scale.
 


 

Which statement about the change in heights when comparing Y9 to Y12 is correct?

  1. The mean increased and the standard deviation decreased.
  2. The mean decreased and the standard deviation decreased.
  3. The mean increased and the standard deviation increased.
  4. The mean decreased and the standard deviation increased.
Show Answers Only

`A`

Show Worked Solution

`text{Mean has increased (Y9 to Y12)}`

`text(The Year 12 data is more tightly distributed)`

`text(around the mean.)`

`:.\ text{Standard deviation has decreased (Y9 to Y12)}`

`=> A`

Financial Maths, STD2 F5 2013 23 MC

Zina opened an account to save for a new car. Six months after opening the account, she made first deposit of $1200 and continued depositing $1200 at the end of each six month period. Interest was paid at 3% per annum, compounded half-yearly.

How much was in Zina's account two years after first opening it?

  1. $4909.08
  2. $4982.72
  3. $5018.16
  4. $5094.55
Show Answers Only

`A`

Show Worked Solution

`text(Interest: 3% p.a ⇒ 1.5% per 6 months)`

♦ Mean mark 41%.

`text(After 2 years,)`

`text(Value of 1st deposit) = 1200(1.015)^3 = 1254.81`

`text(Value of 2nd deposit) = 1200(1.015)^2 = 1236.27`

`text(Value of 3rd deposit) = 1200(1.015) = 1218`

`text(Value of 4th deposit) = 1200`
 

`:.\ text(Amount in account after 2 years)`

`= 1254.81 + 1236.27 + 1218 + 1200`

`=$4909.08`

`=> A`

Statistics, STD2 S3 2017 HSC 29d*

All the students in a class of 30 did a test.

The marks, out of 10, are shown in the dot plot.
 

  1. Find the median test mark.  (1 mark)

  2. The mean test mark is 5.4. The standard deviation of the test marks is 4.22.
  3. Using the dot plot, calculate the percentage of the marks which lie within one standard deviation of the mean.  (2 marks)
Show Answers Only
  1. \(6\)
  2. \(\text{43%}\)
Show Worked Solution

i.    \(\text{30 data points}\)

\(\text{Median}\ = \dfrac{\text{15th + 16th}}{2} = \dfrac{4+8}{2} = 6\)
 

♦ Mean mark 50%.

ii.    \(\text{Lower limit}\ = 5.4-4.22 = 1.18\)

\(\text{Upper limit} = 5.4 + 4.22 = 9.62\)

\(\text{% between}\) \(= \dfrac{13}{30} \times 100\)  
  \(= 43.33… \%\)  
  \(=43\%\ \ \text{(nearest %)}\)  
♦♦ Mean mark 34%.

Financial Maths, STD2 2014 HSC 27a

Alex is buying a used car which has a sale price of  $13 380. In addition to the sale price there are the following costs:

2014 27a1

  1. Stamp Duty for this car is calculated at $3 for every $100, or part thereof, of the sale price.  
  2. Calculate the Stamp Duty payable.   (1 mark)
  3.  
  4. Alex wishes to take out comprehensive insurance for the car for 12 months. The cost of comprehensive insurance is calculated using the following: 
    1.  
    2. 2014 27a2
  5. Find the total amount that Alex will need to pay for comprehensive insurance.   (3 marks)
  6.  
  7. Alex has decided he will take out the comprehensive car insurance rather than the less expensive non-compulsory third-party car insurance.
  8. What extra cover is provided by the comprehensive car insurance?   (1 mark)

 

Show Answers Only
  1. `$402`
  2. `$985.74`
  3. `text(Comprehensive insurance covers Alex)`
  4. `text(for damage done to his own car as well.)`
  5.  
Show Worked Solution
♦♦♦ Mean mark 12%
IMPORTANT: “or part thereof ..” in the question requires students to round up to 134 to get the right multiple of $3 for their calculation.
(i)    `($13\ 380)/100 = 133.8`
`:.\ text(Stamp duty)` `= 134 xx $3`
  `= $402`

 

(ii)   `text(Base rate) = $845`

`text(FSL) =\ text(1%) xx 845 = $8.45`
 

`text(Stamp)` `=\ text(5.5%) xx(845 + 8.45)`
  `= 46.9397…`
  `= $46.94\ text{(nearest cent)}`

 

`text(GST)` `= 10 text(%) xx(845 + 8.45)`
  `= 85.345`
  `= $85.35`

 

`:.\ text(Total cost)` `= 845 + 8.45 + 46.94 + 85.35`
  `= $985.74`

 

♦ Mean mark 34%.
(iii)   `text(Comprehensive insurance covers Alex)`
  `text(for damage done to his own car as well.)`

Measurement, STD2 M1 2012 HSC 25 MC

The solid shown is made of a cylinder with a hemisphere (half a sphere) on top.
 

What is the total surface area of the solid, to the nearest square centimetre?

  1. 628 cm²
  2. 679 cm²
  3. 729 cm²
  4. 829 cm²
Show Answers Only

`B`

Show Worked Solution

`text(Total surface area)`

`= pir^2 + 2pirh + 1/2 xx 4pir^2`

`= pi xx 4^2 + 2pi xx 4 xx 21 + 1/2 xx 4pi xx 4^2`

`= 678.58…\ text(cm²)`

`=> B`

Measurement, STD2 M2 2011 HSC 27b

Pontianak has a longitude of 109°E, and Jarvis Island has a longitude of 160°W.

Both places lie on the Equator. 

  1. Calculate the shortest distance between these two places (`d`), to the nearest kilometre, using

     

      `d=theta/360 xx  2pir`  where  `theta=91°`  and  `r=6400` km   (1 mark)

  2. The position of Rabaul is 4° to the south and 48° to the west of Jarvis Island. What is the latitude and longitude of Rabaul?    (2 marks)

Show Answers Only
  1. `10\ 165\ text(km)\ \ \ text{(nearest km)}`
  2. `152^@ text(E)`
Show Worked Solution
a.  `text(Shortest distance)` `= 91/360 xx 2 pi r`
  `= 91/360 xx 2 xx pi xx 6400`
  `= 10\ 164.79…`
  `=10\ 165\ text(km)\ text{(nearest km)}`

 

♦♦ Mean mark 33%
b. `text(Latitude)`
  `4^@\ text(South of Jarvis Island)`
  `text(S)text(ince Jarvis Island is on equator)`
  `=> text(Latitude is)\ 4^@ text(S)`
   
  `text(Longitude)`
  `text(Jarvis Island is)\ 160^@ text(W)`
  `text(Rubail is)\ 48^@\ text(West of Jarvis Island, or 208° West)`
  `text(which is)\ 28^@\ text{past meridian (180°)}`
`=>\ text(Longitude)` `= (180 -28)^@ text(E)`
  `= 152^@ text(E)`

 
`:.\ text(Position is)\ (4^@text{S}, 152^@text{E})`

Measurement, STD2 M1 2008 HSC 21 MC

A sphere and a closed cylinder have the same radius.

The height of the cylinder is four times the radius.

What is the ratio of the volume of the cylinder to the volume of the sphere?

  1. `2 : 1`
  2. `3 : 1`
  3. `4 : 1`
  4. `8 : 1`
Show Answers Only

`B`

Show Worked Solution

♦♦ Mean mark 33%.

`V_text(cylinder)` `: V_text(sphere)`
`pir^2h` `: 4/3pir^3`
`underbrace(pir^2 4r)_(h = 4r)` `: 4/3pir^3`
`4pir^3` `: 4/3pir^3`
`3` `: 1`

  
`=> B`

Algebra, STD2 A2 SM-Bank 3

The average height, `C`, in centimetres, of a girl between the ages of 6 years and 11 years can be represented by a line with equation

`C = 6A + 79`

where `A` is the age in years. For this line, the gradient is 6.

  1. What does this indicate about the heights of girls aged 6 to 11?   (1 mark)

  2. Give ONE reason why this equation is not suitable for predicting heights of girls older than 12.   (1 mark)

Show Answers Only
  1. `text(It indicates that 6-11 year old girls, on average, grow 6 cm per year.)`
  2. `text(Girls eventually stop growing, and the equation doesn’t factor this in.)`
Show Worked Solution

a.  `text(It indicates that 6-11 year old girls, on average, grow)`

`text(6 cm per year.)`
 

b. `text(Girls eventually stop growing, and the equation doesn’t)`

`text(factor this in.)`

Networks, STD2 N3 2018 FUR2 1

The graph below shows the possible number of postal deliveries each day between the Central Mail Depot and the Zenith Post Office.

The unmarked vertices represent other depots in the region.

The weighting of each edge represents the maximum number of deliveries that can be made each day.
 


 

  1.  Cut A, shown on the graph, has a capacity of 10.

     

     Two other cuts are labelled as Cut B and Cut C.

    1.  Write down the capacity of Cut B.  (1 mark)

    2.  Write down the capacity of Cut C. (1 mark)

  2.  Determine the maximum number of deliveries that can be made each day from the Central Mail  Depot to the Zenith Post Office.  (1 mark)

Show Answers Only
    1. `9`
    2. `13`
  2.  `7`
Show Worked Solution
a.i.    `text{Capacity (Cut B)}` `= 3 + 2 + 4`
    `= 9`

 

a.ii.    `text{Capacity (Cut C)}` `= 3 + 6 + 4`
    `= 13`

♦ Mean mark part (b) 32%.
COMMENT: Review carefully! Most common incorrect answer was 9.

 

b.  `text(Minimum cut) = 2 + 2 + 3 = 7`

`:.\ text(Maximum deliveries) = 7`

Probability, MET1 2018 VCAA 4

Let `X` be a normally distributed random variable with a mean of 6 and a variance of 4. Let `Z` be a random variable with the standard normal distribution.

  1.  Find  `text(Pr)(X > 6)`.  (1 mark)

  2.  Find  `b`  such that  `text(Pr)(X > 7) = text(Pr)(Z < b)`.  (1 mark)

Show Answers Only

  1. `0.5`
  2. `−1/2`

Show Worked Solution

a.   `text(Mean)\ (X) = 6`

`:. text(Pr)(X > 6) = 0.5`
 

♦ Mean mark part (b) 41%.

b.    `text(Pr)(X > 7)` `= text(Pr)(X < 5)`
    `= text(Pr)(Z < (5 – 6)/2)`
    `= text(Pr)(Z < −1/2)`

 
`:. b = −1/2`

Networks, STD2 N3 2018 FUR1 5 MC

The directed network below shows the sequence of 11 activities that are needed to complete a project.

The time, in weeks, that it takes to complete each activity is also shown.
 


 

How many of these activities could be delayed without affecting the minimum completion time of the project?

  1. 3
  2. 4
  3. 5
  4. 6
Show Answers Only

`B`

Show Worked Solution

`text(Activities not on critical path can be delayed.)`

`text{Scanning forward: two critical paths exist (15 weeks)}`

♦ Mean mark 43%.

`ADHK\ text(and)\ BFJK`

`:.\ text(Activity)\ C, E, G\ text(and)\ I\ text(could be delayed)`

`=> B`

Calculus, MET2 2018 VCAA 8 MC

If  `int_1^12 g(x)\ dx = 5`  and  `int_12^5 g(x)\ dx = -6`,  then  `int_1^5 g(x)\ dx`  is equal to

A.   −11

B.     –1

C.      1

D.      3

E.     11

Show Answers Only

`B`

Show Worked Solution

♦ Mean mark 41%.

`int_1^12 g(x)\ dx` `= int_1^5 g(x)\ dx + int_5^12 g(x)\ dx`
  `= int_1^5 g(x)\ dx – int_12^5 g(x)\ dx`
`5` `= int_1^5 g(x)\ dx – (-6)`
`int_1^5 g(x)\ dx` `= -1`

 
`=>   B`

Graphs, MET2 2018 VCAA 4 MC

The point  `A (3, 2)`  lies on the graph of the function  `f`. A transformation maps the graph of  `f` to the graph of `g`,

where  `g(x) = 1/2 f(x - 1)`. The same transformation maps the point `A` to the point `P`.

The coordinates of the point `P` are

  1. `(2, 1)`
  2. `(2, 4)`
  3. `(4, 1)`
  4. `(4, 2)`
  5. `(4, 4)`
Show Answers Only

`C`

Show Worked Solution

`g(x) = 1/2 f(x – 1),\ A(3, 2)`

♦ Mean mark 48%.

`text(Dilate by a factor of)\ 1/2\ text(from)\ x text(-axis:)`

`A(3, 2) -> A′(3, 1)`
 

`text(Translate 1 unit to right:)`

`A′(3, 1) -> P(4, 1)`
 

`=>   C`

Algebra, MET2 2018 VCAA 3 MC

Consider the function  `f: [a, b) -> R,\ f(x) = 1/x`, where `a` and `b` are positive real numbers.

The range of  `f` is

  1. `[1/a, 1/b)`
  2. `(1/a, 1/b]`
  3. `[1/b, 1/a)`
  4. `(1/b, 1/a]`
  5. `[a, b)`
Show Answers Only

`D`

Show Worked Solution

`f: [a, b) -> R,\ f(x) = 1/x`

♦ Mean mark 48%.

`f(a) = 1/a,\ f(b) = 1/b`
 

`text(S) text(ince)\ a < b,`

`=>\ f(a) > f(b)`

`:.\ text(Range)\ \ f: (1/b, 1/a]`

`=>   D`

GEOMETRY, FUR2 2018 VCAA 2

Frank travelled from Melbourne (38° S, 145° E) to a tennis tournament in Ho Chi Minh City, Vietnam, (11° N, 107° E).

Frank departed Melbourne at 10.30 pm on Monday, 5 February 2018.

Frank arrived in Ho Chi Minh City at 8.00 am on Tuesday, 6 February 2019.

The time difference between Melbourne and Ho Chi Minh City is four hours.

  1.  How long did it take Frank to travel from Melbourne to Ho Chi Minh City?

     

     Give your answer in hours and minutes.   (1 mark)

Ho Chi Minh City is located at latitude 11° N and longitude 107° E.

Assume that the radius of Earth is 6400 km.

  1. i. Write a calculation that shows that the radius of the small circle of Earth at latitude 11° N is 6282 km, rounded to the nearest kilometre.  (1 mark)
  2. ii. Iloilo City, in the Philippines, is located at latitude 11° N and longitude 123° E.

     

        Find the shortest small circle distance between Ho Chi Minh City and Iloilo City.

     

        Round your answer to the nearest kilometre.  (1 mark)

Show Answers Only
    1. `text(13 hours 30 min.)`
    2. i. `text(See Worked Solutions)`
    3. ii. `1754\ text(km)`
Show Worked Solution

a.   `text{8am Ho Chi Minh (Tues) = 12 midday Melbourne (Tues)}`

♦♦ Mean mark 29%.
COMMENT: Review carefully!

`:.\ text(Travel time)` `=\ text{10:30 pm (Mon) to 12 midday (Tues)}`
  `=\ text(13 hours 30 min.)`

 

b.i.  `text(Let)\ \ x=\ text(small circle radius)`

Mean mark part (b)(i) 52%.

 


 

`cos 11^@` `= x/6400`
`:. x` `= 6400 xx cos 11^@`

 

b.ii.  `text(Iloilo City)\ ->\ text(same latitude)`

♦♦ Mean mark part (b)(ii) 33%.
MARKER’S COMMENT: Many students incorrectly used 6400 as the radius in part (b)(ii). Understand why  `6400 xx cos 11°`  is the correct radius here!

 `text(Longitudinal difference) = 123 – 107 = 16^@`
 


 

`:.\ text{Small circle distance (arc)}`

`= 16/360 xx 2 xx pi xx (6400 xx cos 11^@)`

`= 1754.38…`

`= 1754\ text{km (nearest km)}`

GRAPHS, FUR1 2018 VCAA 08 MC

A ride-share company has a fee that includes a fixed cost and a cost that depends on both the time spent travelling, in minutes, and the distance travelled, in kilometres.

The fixed cost of a ride is $2.55

Judy’s ride cost $16.75 and took eight minutes. The distance travelled was 10 km.

Pat’s ride cost $30.35 and took 20 minutes. The distance travelled was 18 km.

Roy’s ride took 10 minutes. The distance travelled was 15 km.

The cost of Roy’s ride was

  1. $17.00
  2. $19.55
  3. $20.50
  4. $23.05
  5. $25.60
Show Answers Only

`D`

Show Worked Solution

`text(Let)\ \ x\ text(= cost per minute)`

♦ Mean mark 48%.

`text(Let)\ \ y\ text(= cost per kilometres)`

`text(Judy’s ride:)`

`8x + 10y = 16.75 – 2.55 = 14.20 …\ \ (1)`

`text(Pat’s ride:)`

`20x + 18y = 30.35 – 2.55 = 27.80 …\ \ (2)`

`text(Solving simultaneously)=>\ x = 0.4, \ y = 1.1`

`:.\ text(Roy’s cost)` `= 10 xx 0.4 + 15 xx 1.1 + 2.55`
  `= $23.05`

`=> D`

GRAPHS, FUR1 2018 VCAA 07 MC

In the diagram below, the shaded region (with boundaries included) represents the feasible region for a linear programming problem.
 


 

The objective function, `Z`, has minimum values at both point `M` and point `N`.

Which one of the following could be the objective function?

  1.  ` Z = x - 2y`
  2.  `Z = x + 2y`
  3.  `Z = 2x + y`
  4.  `Z = −2x + y`
  5.  `Z = 2x + 2y`
Show Answers Only

`C`

Show Worked Solution

`text(Minimum values at)\ M\ text(and)\ N`

♦ Mean mark 40%.

`=> m_(MN) = text(gradient of objective function)`

`m_(MN) = (0 – 10)/(5 – 0) = −2`

`text(Test the gradient of each option:)`

`text(Option)\ A: \ m = (−1)/(−2) = 1/2`

`text(Option)\ B: \ m = −1/2`

`text(Option)\ C: \ m = −2`

`text(Option)\ D: \ m = 2`

`text(Option)\ E: \ m = −1`

 
`=> C`

GRAPHS, FUR1 2018 VCAA 5 MC

The graph below shows a relationship between `y` and `1/x^2`.
 


 

The graph that shows the same relationship between `y` and `x` is

A. B.
C. D.
E.    
Show Answers Only

`A`

Show Worked Solution

`y = k xx 1/x^2`

♦ Mean mark 48%.

`text(Gradient = 2)`

`:. y = 2/x^2`

`text(By trial and error, test the given point in each)`

`text(option against the equation.)`

`text(Consider option)\ A:`

`2 = 2/1^2 = 2\ \ text(correct)`

`=> A`

GRAPHS, FUR2 2018 VCAA 4

This year Robert is planning a camping trip for the members of his gold prospecting club.

The club has chosen two camp sites, Bushman’s Track and Lower Creek.

  • Let `x` be the number of members staying at Bushman’s Track.
  • Let `y` be the number of members staying at Lower Creek.
  • A maximum of 10 members can stay at Bushman’s Track.
  • A maximum of 15 members can stay at Lower Creek.
  • At least 20 members in total are attending the camping trip.

The club has decided that at least twice as many members must stay at Lower Creek than at Bushman’s Track.

These constraints can be represented by the following four inequalities.
 

`{:(text(Inequality 1)),(text(Inequality 2)),(text(Inequality 3)),(text(Inequality 4)):} qquad qquad {:(x <= 10),(y <= 15),(x + y >= 20),(y >= 2x):}`
 

The graph below shows the four lines representing Inequalities 1 to 4.

  1. On the graph above, mark with a cross (×) the five integer points that satisfy Inequalities 1 to 4.   (1 mark)

     

    `qquad qquad`(answer on the graph above.)

The cost for one member to stay at Bushman’s Track is $130. The cost for one member to stay at Lower Creek is $110.

For budgeting purposes, Robert needs to know the maximum cost of accommodation for both camp sites given Inequalities 1 to 4.

  1. Find the total maximum cost of accommodation.  (1 mark)
  2. When Robert finally made the booking, he was informed that, due to recent renovations, there were two changes to the accommodation at Lower Creek:
  • A maximum of 22 members can now stay at Lower Creek.
  • The cost for one member to stay at Lower Creek is now $140.

Twenty members will be attending the camping trip.

Find the total minimum cost of accommodation for these 20 members.  (1 mark)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `$2560`
  3. `$2740`
Show Worked Solution
a.  

♦♦ Mean mark part (a) 45%, part (b) 22%.
MARKER’S COMMENT: A poor understanding of this question type notable. Review carefully.

b.    `text{Considering the cost of each point in part (a):}`

`text(Maximum cost at)\ (7, 15)`

`:. C_max` `= 7 xx 130 + 15 xx 110`
  `= $2560`

 

c.    `x ->\ text{Bushman’s track ($130/night)}`

♦♦ Mean mark part (c) 22%.

`y ->\ text{Lower Creek (now $140/night)}`

`text(Test for minimum cost at)\ (5, 15) or (6, 14)`

`=>\ text(Minimum cost occurs at)\ (6, 14)`
 

`:. C_min` `= 6 xx 130 + 14 xx 140`
  `= $2740`

GRAPHS, FUR2 2018 VCAA 3

Robert wants to hire a geologist to help him find potential gold locations.

One geologist, Jennifer, charges a flat fee of $600 plus 25% commission on the value of gold found.

The following graph displays Jennifer’s total fee in dollars.
 


 

Another geologist, Kevin, charges a total fee of $3400 for the same task.

  1. Draw a graph of the line representing Kevin’s fee on the axes above.  (1 mark)

     

    `qquad qquad`(answer on the axes above.)

  2. For what value of gold found will Kevin and Jennifer charge the same amount for their work?  (1 mark)
  3. A third geologist, Bella, has offered to assist Robert.
  4. Below is the relation that describes Bella’s fee, in dollars, for the value of gold found.

  5. `qquad  text{fee (dollars)} = {(quad 500),(1000),(2600),(4000):}qquad qquad quad{:(qquad quad 0 <),(2000 <=),(6000 <=),(quad):}{:(text(value of gold found) < 2000),(text(value of gold found) < 6000),(text(value of gold found) < 10\ 000),(text(value of gold found) >= 10\ 000):}`


    The step graph below representing this relation is incomplete.

     

    Complete the step graph by sketching the missing information.  (2 marks)
     

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `$11\ 200`
  3. `text(See Worked Solutions)`
Show Worked Solution
a.  

 

b.    `text(Let)\ \ x = text(value of gold)`

♦ Mean mark 41%.

`text(Jennifer’s total fee) = 600 + 0.25x`

`text(Equating fees:)`

`600 + 0.25x` `= 3400`
`0.25x` `= 2800`
`:.x` `= 2800/0.25`
  `= $11\ 200`

 

c.  

GEOMETRY, FUR1 2018 VCAA 6 MC

Aaliyah is bushwalking.

She walks 5.4 km from a starting point on a bearing of 045° until she reaches a hut. From this hut, she walks 2.8 km on a bearing of 300° until she reaches a river.

From the river, she turns and walks back directly to the starting point.

The total distance that she walks, in kilometres, is closest to

  1. 8.2
  2. 13.2
  3. 13.6
  4. 14.1
  5. 14.9
Show Answers Only

`C`

Show Worked Solution

 
`text(Using cosine rule:)`

♦ Mean mark 41%.

`x` `= sqrt(2.8^2 + 5.4^2 – 2 xx 2.8 xx 5.4 xx cos75°)`
  `= 5.401…\ \ text(km)`

 

`:.\ text(Total distance)` `= 2.8 + 5.4 + 5.4`
  `= 13.6\ \ text(km)`

`=> C`