SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Trigonometry, EXT1 T3 2010 HSC 4b

  1. Express  `2 cos theta + 2 cos (theta + pi/3)`  in the form  `R cos (theta + alpha)`,
     
    where  `R > 0`  and  `0 < alpha < pi/2`.    (3 marks)

  2. Hence, or otherwise, solve  `2 cos theta + 2 cos (theta + pi/3) = 3`,   
  3. for  `0 < theta < 2pi`.    (2 marks)

Show Answers Only
  1. `2 sqrt 3 cos (theta + pi/6)`
  2. `(5pi)/3`
Show Worked Solution
i.    `2 cos theta + 2 cos (theta + pi/3)`
  `= 2 cos theta + 2 (cos theta cos (pi/3)\ – sin theta sin (pi/3))`
  `= 2 cos theta + 2 cos theta xx 1/2\ – 2 sin theta xx sqrt3/2`
  `= 2 cos theta + cos theta\ – sqrt3 sin theta`
  `= 3 cos theta\ – sqrt3 sin theta`

 
`R cos (theta + alpha) = R cos theta cos alpha – R sin theta sin alpha`

`R cos alpha` `= 3\ \ \ \ \ ` `R sin alpha` `= sqrt3`
`cos alpha` `= 3/R\ \ \ \ \ ` `sin alpha` `= sqrt3/R`

 

`tan alpha` `= sin alpha/cos alpha = sqrt3/3 = 1/sqrt3`
`tan\ pi/6` `=1/sqrt3`
`:. alpha` `=pi/6\ \ \ \ \ (0 < alpha < pi/2)`
`R^2` `= 3^2 + (sqrt3)^2`
  `= 9 + 3`
`R` `= sqrt 12 = 2 sqrt3`

 
`:.\ 2 cos theta + 2 cos (theta + pi/3) = 2 sqrt 3 cos (theta + pi/6)`

 

♦ Mean mark part (ii) 49%
MARKER’S COMMENT: Many students did not check their answers against the stated domain for `theta`.
ii.    `2 cos theta + 2 cos(theta + pi/3)` `= 3`
  `2 sqrt 3 cos (theta + pi/6)` `= 3`
  `cos (theta + pi/6)` `= 3/(2sqrt3) = sqrt3/2`
  `cos^(-1) (sqrt3/2)` `= pi/6`

 
`text(S)text(ince cos is positive in 1st and 4th quadrants,)`

`theta + pi/6` `= pi/6,\ 2pi\ – pi/6`
`:. theta` `= (5pi)/3\ \ \ \ \ (0 < theta < 2pi)`

Inverse Functions, EXT1 2010 HSC 3b

Let  `f(x) = e^(-x^2)`.  The diagram shows the graph  `y = f(x)`.
 

 Inverse Functions, EXT1 2010 HSC 3b
 

  1. The graph has two points of inflection.  
  2. Find the  `x`  coordinates of these points.   (3 marks)
  3.  
  4. Explain why the domain of  `f(x)`  must be restricted if  `f(x)`  is to have an inverse function.    (1 mark)
  5. Find a formula for  `f^(-1) (x)`  if the domain of  `f(x)`  is restricted to  `x ≥ 0`.   (2 marks)
  6. State the domain of  `f^(-1) (x)`.    (1 mark)
  7. Sketch the curve  `y = f^(-1) (x)`.    (1 mark)
  8. (1)   Show that there is a solution to the equation  `x = e^(-x^2)`  between  `x = 0.6`  and  `x = 0.7`.   (1 mark)
  9. (2)   By halving the interval, find the solution correct to one decimal place.   (1 mark)

 

Show Answers Only
  1. `x = +- 1/sqrt2` 
  2.  
  3. `text(There can only be 1 value of)\ y`
  4. `text(for each value of)\ x.`
  5.  
  6. `f^(-1)x = sqrt(ln(1/x))`
     
  7. `0 <= x <= 1`
  8.  
  9. Inverse Functions, EXT1 2010 HSC 3b Answer
  10. (1)   `text(Proof)\ \ text{(See Worked Solutions)}`
  11. (2)   `0.7\ text{(1 d.p.)}`
Show Worked Solution
(i)    `y` `= e^(-x^2)`
  `dy/dx` `= -2x * e^(-x^2)`
  `(d^2y)/(dx^2)` `= -2x (-2x * e^(-x^2)) + e ^(-x^2) (-2)`
    `= 4x^2 e^(-x^2)\ – 2e^(-x^2)`
    `= 2e^(-x^2) (2x^2\ – 1)`

 

`text(P.I. when)\ \ (d^2y)/(dx^2) = 0`

`2e^(-x^2) (2x^2\ – 1)` `= 0` 
 `2x^2\ – 1` `= 0` 
 `x^2` `= 1/2`
 `x` `= +- 1/sqrt2` 
COMMENT: It is also valid to show that `f(x)` is an even function and if a P.I. exists at `x=a`, there must be another P.I. at `x=–a`.
`text(When)\ \ ` `x < 1/sqrt2,` `\ (d^2y)/(dx^2) < 0`
  `x > 1/sqrt2,` `\ (d^2y)/(dx^2) > 0`

`=>\ text(Change of concavity)`

`:.\ text(P.I. at)\ \ x = 1/sqrt2`

`text(When)\ \ ` `x < – 1/sqrt2,` `\ (d^2y)/(dx^2) > 0`
  `x > – 1/sqrt2,` `\ (d^2y)/(dx^2) < 0`

`=>\ text(Change of concavity)`

`:.\ text(P.I. at)\ \ x = – 1/sqrt2`

 

(ii)   `text(In)\ f(x), text(there are 2 values of)\ y\ text(for)`
  `text(each value of)\ x.`
  `:.\ text(The domain of)\ f(x)\ text(must be restricted)`
  `text(for)\ \ f^(-1) (x)\ text(to exist).`

 

(iii)   `y = e^(-x^2)`

`text(Inverse function can be written)` 

`x` `= e^(-y^2),\ \ \ x >= 0`
`lnx` `= ln e^(-y^2)`
`-y^2` `= lnx`
`y^2` `= -lnx`
  `=ln(1/x)`
`y` `= +- sqrt(ln (1/x))`

 

`text(Restricting)\ \ x>=0,\ \ =>y>=0`

`:.  f^(-1) (x)=sqrt(ln (1/x))`
 

♦ Parts (iv) and (v) were poorly answered with mean marks of 39% and 49% respectively.
(iv)   `f(0) = e^0 = 1`

`:.\ text(Range of)\ \ f(x)\ \ text(is)\ \ 0 < y <= 1`

`:.\ text(Domain of)\ \ f^(-1) (x)\ \ text(is)\ \ 0 < x <= 1`

 

(v) 

Inverse Functions, EXT1 2010 HSC 3b Answer

 

(vi)(1)  `x = e^(-x^2)`

`text(Let)\ g(x) = x\ – e^(-x^2)`

`g(0.6)` `=0.6\ – e^(-0.6^2)`
  `=0.6\ – 0.6977 < 0`
`g(0.7)` `=0.7\ – e^(-0.7^2)`
  `=0.7\ – 0.6126 > 0`
`=>g(x)\ text(changes sign)`

 

`:.\ g(x)\ \ text(has a root between  0.6  and  0.7)`

`:.\ x = e^(-x^2)\ \ text(has a solution between  0.6  and  0.7)`

♦ Mean mark 37%.
MARKER’S COMMENT: Better responses showed the change in sign between `g(0.65)` and `g(0.7)` as shown in the solution.

 

(vi)(2)   `g(0.65)` `=0.65\ – e^(-0.65^2)`
    `=0.65\ – 0.655 < 0`

 

`:.\ text(A solution lies between 0.65 and 0.7)`

`:.\ x = 0.7\ \ text{(1 d.p.)}`

Combinatorics, EXT1 A1 2010 HSC 3a

At the front of a building there are five garage doors. Two of the doors are to be painted red, one is to be painted green, one blue and one orange. 

  1. How many possible arrangements are there for the colours on the doors?   (1 mark)

  2. How many possible arrangements are there for the colours on the doors if the two red doors are next to each other?    (1 mark)

Show Answers Only
  1. `60`
  2. `24`
Show Worked Solution
i.    `text(# Arrangements)` `= (5!)/(2!)`
    `= 60`

 

♦ Mean mark 50%
MARKER’S COMMENT: Drawing a diagram was a successful strategy for many students in this part.
ii.    `text(When 2 red doors are side-by-side,)`
`text(# Arrangements)` `= 4!`
  `= 24`

Calculus, EXT1 C1 2011 HSC 7a

The diagram shows two identical circular cones with a common vertical axis.  Each cone has height `h` cm and semi-vertical angle 45°.
 

2011 7a

The lower cone is completely filled with water. The upper cone is lowered vertically into the water as shown in the diagram. The rate at which it is lowered  is given by  

`(dl)/(dt) = 10`,

where `l` cm is the distance the upper cone has descended into the water after `t` seconds.

As the upper cone is lowered, water spills from the lower cone. The volume of water remaining in the lower cone at time `t` is  `V` cm³.

  1. Show that  `V = pi/3(h^3\ - l^3)`.   (1 mark)

  2. Find the rate at which `V` is changing with respect to time when  `l = 2`.     (2 marks)

  3. Find the rate at which `V` is changing with respect to time when the lower cone has lost  `1/8`  of its water. Give your answer in terms of `h`.   (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `-40 pi\ \ text(cm³)// text(sec)`
  3. `(-5pih^2)/2\ text(cm³)// text(sec)`
Show Worked Solution

i.   `text(Show that)\ V = pi/3 (h^3\ – l^3)`

 ♦ Mean mark 42% 

`text(S)text(ince)\ \ tan45° = r/h=1`

`=>r=h`

`=>\ text(Radius of lower cone) = h`

`:.\ V text{(lower cone)}` `= 1/3 pi r^2 h`
  `= 1/3 pi h^3`

 
 `text(Similarly,)`

`V text{(submerged upper cone)} = 1/3 pi l^3`

`V text{(water left)}` `= 1/3 pi h^3\ – 1/3 pi l^3`
  `= pi/3 (h^3\ – l^3)\ \ \ text(… as required)`

 

ii.  `text(Find)\ (dV)/(dt)\ text(at)\ l = 2`

`(dV)/(dt)= (dV)/(dl) xx (dl)/(dt)\ …\ text{(1)}`

`=>(dl)/(dt)` `= 10\ text{(given)}`
`text(Using)\ \ V` `= pi/3 (h^3\ – l^3)\ \ \ \ text(from part)\ text{(i)}`
`=>(dV)/(dl)` `= -3 xx pi/3 l^2`
  `= -pi l^2`

  
`text(At)\ \ l = 2,`

`text{Substitute into (1) above}`

`(dV)/(dt)` `= -pi xx 2^2 xx 10`
  `= -40 pi\ \ \ text(cm³)//text (sec)`

 

iii.  `text(Find)\ \ (dV)/(dt)\ \ text(when lower cone has lost)\ 1/8 :`

♦♦♦ Mean mark 12%
MARKER’S COMMENT: Many unsuccessful answers attempted to find an alternate version of `(dV)/(dt)`. Part (ii) directed students directly toward the correct strategy.

`text(Find)\ \ l\ \ text(when)\ \ V = 7/8 xx 1/3 pi h^3`

`pi/3 (h^3\ – l^3)` `= 7/8 xx 1/3 pi h^3`
`h^3 -l^3` `= 7/8 h^3`
`l^3` `= 1/8 h^3`
`l` `= h/2`

   
`text(When)\ \ l = h/2 ,`

`(dV)/(dt)` `= -pi (h/2)^2 xx 10\ \ …\ text{(*)}`
  `= (-5pih^2)/2\ text(cm³)// text(sec)`

 
`:. V\ text(is decreasing at the rate of)\ \  (5 pi h^2)/2\ text(cm³)//text(sec).`

Statistics, EXT1 S1 2011 HSC 6c

A game is played by throwing darts at a target. A player can choose to throw two or three darts.

Darcy plays two games. In Game 1, he chooses to throw two darts, and wins if he hits the target at least once. In Game 2, he chooses to throw three darts, and wins if he hits the target at least twice.

The probability that Darcy hits the target on any throw is  `p`, where  `0 < p < 1`.

  1. Show that the probability that Darcy wins Game 1 is  `2p- p^2`.    (1 mark)

  2. Show that the probability that Darcy wins Game 2 is  `3p^2- 2p^3`.     (1 mark)

  3. Prove that Darcy is more likely to win Game 1 than Game 2.    (2 marks)

  4. Find the value of  `p`  for which Darcy is twice as likely to win Game 1 as he is to win Game 2.    (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
  4. `p = (7 – sqrt17)/8`
Show Worked Solution

i.  `text(Show)\ P text{(wins Game 1)} = 2p\ – p^2`

♦ Mean mark 47%.

`P text{(Hits)} = P text{(H)} = p`

`P text{(Miss)} = P text{(M)} = 1 – p`
 

`P text{(Wins G1)}` `= 1 – P text{(MM)}`
  `= 1 – (1 – p)^2`
  `= 1 – 1 + 2p – p^2`
  `= 2p – p^2\ \ \ text(… as required)`

 

ii.  `text(Show)\ \ P text{(wins Game 2)} = 3p – 2p^3 :`

♦ Mean mark 40%.

`text(Darcy wins G2 if he hits 3 times, or twice.)`

`Ptext{(Hits 3 times)}=\ ^3C_3 (p)^3=p^3`

`Ptext{(Hits twice)}=\ ^3C_2 (p)^2 (1-p)=3p^2-3p^3`

 `P text{(Wins G2)}` `= p^3 + 3p^2-3p^3`
  `= 3p^2 – 2p^3\ \ \ text(… as required)`

 

♦♦♦ Mean mark 17%.
COMMENT: It is critical for students to utilise the limits of  `0<p<1`  to answer part (iii).

iii.  `text(Prove more likely to win G1 vs G2)`

`text(i.e.  Show)\ \ \ ` `2p – p^2 > 3p^2 – 2p^3`
  `2p^3 – 4p^2 + 2p` `> 0`
  `2p (p^2 – 2p + 1)` `> 0` 
  `2p (p – 1)^2` `> 0` 

 
`=> text(TRUE since)\ \ (p-1)^2>0\ \ text(and)\ \ 0 < p < 1`

`:.\ text(More likely for Darcy to win Game 1.)`
 

iv.  `text(If twice as likely to win G1 vs G2)`

♦♦ Mean mark 21%.
MARKER’S COMMENT: BE CAREFUL in formulating your equation here. Many students multiplied the wrong side by 2.
`2p\ – p^2` `= 2(3p^2 – 2p^3)`
  `= 6p^2 – 4p^3`
`4p^3 – 7p^2 + 2p` `= 0`
`p(4p^2 – 7p + 2)` `= 0`

  

`p` `= (–(–7) +- sqrt((–7)^2\ – 4 xx 4 xx 2))/(2 xx 4)`
  `= (7 +- sqrt(49\ – 32))/8`
  `= (7 +- sqrt17)/8`

 
`text(S)text(ince)\ \ 0<p<1,`

`p = (7\ – sqrt17)/8`

Trig Ratios, EXT1 2011 HSC 5a

In the diagram,  `Q(x_0, y_0)`  is a point on the unit circle  `x^2 + y^2 = 1`  at an angle  `theta`  from the positive  `x`-axis, where  `− pi/2 < theta < pi/2`. The line through  `N(0, 1)`  and  `Q`  intersects the line  `y = –1`  at  `P`. The points  `T(0, y_0)`  and  `S(0, –1)` are on the  `y`-axis.
 

 
 

  1. Use the fact that  `Delta TQN`  and  `Delta SPN`  are similar to show that
     
  2.      `SP = (2costheta)/(1\ - sin theta)`.  (2 marks)
  3.  
  4. Show that  `(costheta)/(1\ - sin theta) = sec theta + tan theta`.    (1 mark)
  5.  
  6. Show that  `/_ SNP = theta/2 + pi/4`.   (1 mark)
  7.  
  8. Hence, or otherwise, show that  `sectheta + tantheta = tan(theta/2 + pi/4)`.   (1 mark)
  9.  
  10. Hence, or otherwise, solve  `sec theta + tan theta = sqrt3`, where  `-pi/2 < theta < pi/2`.   (2 marks)

 

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
  4. `text(Proof)\ \ text{(See Worked Solutions)}`
  5. `pi/6\ text(radians)`
Show Worked Solution
(i)

 

♦ Mean mark 41%
MARKER’S COMMENT: When questions direct you to use a certain fact for a proof, use that fact!

`text(Show)\ SP = (2 cos theta)/(1\ – sin theta)`

`Delta SPN \ text(|||) \ Delta TQN\ \ \ text{(given)}`

`(SP)/(SN) = (TQ)/(TN)\ \ \ text{(corresponding sides of similar triangles)}`

`/_TQO = theta\ \ \ text{(alternate,}\ TQ\ text(||)\  x text{-axis)}`

  `sin theta` `= (OT)/1 => OT = sin theta`
`=>` `TN` `= 1\ – sin theta`
  `cos theta` `= (TQ)/1`
`=>` `TQ` `= cos theta`
`SN` `= 2\ \ \ text{(diameter of unit circle)}`
`:. (SP)/2` `= cos theta/(1\ – sin theta)`
`SP` `= (2 cos theta)/(1\ – sin theta)\ \ \ text(… as required)`

 

(ii)   `text(Show)\ \ costheta/(1\ – sin theta) = sec theta + tan theta`

♦ Mean mark 35%
`text(RHS)` `= 1/(costheta) + (sintheta)/(costheta)`
  `=(1 + sin theta)/cos theta xx cos theta/cos theta`
  `= (costheta(1 + sintheta))/(cos^2theta)`
  `= (costheta(1 + sin theta))/(1\ – sin^2 theta)`
  `= (costheta(1 + sin theta))/((1 + sin theta)(1\ – sin theta)`
  `= costheta/(1\ – sin theta)\ \ \ text(… as required)`

 

(iii)  `text(Show)\ \ /_SNP = theta/2 + pi/4`

♦♦♦ Mean mark 11%

`/_TOQ = 90\ – theta`

`text(S)text(ince)\ ON = OQ = 1\ text{(unit circle)}`

`=> Delta ONQ\ text(is isosceles)`

`:.\ /_SNP` `= 1/2 (180\ – (90\ – theta))\ \ \ \ text{(angle sum of}\ Delta ONQ text{)}`
  `= 90\ – 45 + theta/2`
  `= 45 + theta/2`
  `= pi/4 + theta/2\ \ \ text(… as required)`

 

(iv)  `text(Show)\ sec theta + tan theta = tan (theta/2 + pi/4)`

♦♦ Mean mark 28%

`text(S)text(ince)\ /_SNP = pi/4 + theta/2\ \ \ \ text{(} text(part)\ text{(iii)} text{)}`

`=> tan\  /_SNP = tan (pi/4 + theta/2)`

 

`text(Also,)\ tan\   /_SNP` `= (SP)/(SN)`
  `= ((2costheta)/(1\ – sin theta))/2`
  `= (cos theta)/(1\ – sin theta)`
  `= sec theta + tan theta\ \ \ \ text{(part (ii))}`

 

`:.\ sec theta + tan theta = tan (pi/4 + theta/2)\ \ \ text(… as required)`

 

♦ Mean mark 45%
(v)    `sec theta + tan theta` `= sqrt3,\ \ \ (-pi/2 < theta < pi/2)`
  `tan (pi/4 + theta/2)` `= sqrt3\ \ \ \ text{(part (iv))}`
  `tan (pi/3)` `= sqrt 3`

`text(S)text(ince tan is positive in)\  1^text(st) // 3^text(rd)\ text(quads)`

`theta/2 + pi/4` `= pi/3,\ (4pi)/3`
`theta/2` `= pi/12\ \ \ \ (-pi/2 < theta < pi/2)`
`:.\ theta` `= pi/6\ text(radians)`

Plane Geometry, EXT1 2011 HSC 4b

In the diagram, the vertices of  `Delta ABC`  lie on the circle with centre  `O`. The point  `D`  lies on  `BC`  such that  `Delta ABD`  is isosceles and  `/_ABC = x`.

Copy or trace the diagram into your writing booklet. 

  1. Explain why  `/_AOC = 2x`.    (1 mark)
  2. Prove that  `ACDO`  is a cyclic quadrilateral.    (2 marks)
  3. Let  `M`  be the midpoint of  `AC`  and  `P`  the centre of the circle through `A, C, D`  and  `O`. 
  4. Show that  `P, M`  and  `O`  are collinear.   (1 mark)
Show Answers Only
  1. `text(Angle at the centre of a circle is twice)`
  2. `text(angle of circumference on same arc)`
  3.  
  4. `text(Proof)\ \ text{(See Worked Solutions)}`
  5. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution
(i)

`/_AOC = 2x`

`text{(angles at circumference and}`

`text{centre on arc}\ AC text{)}`

 

♦ Mean mark 38%
STRATEGY: Proving part (ii) by showing opposite angles are supplementary also worked but was more time consuming.

(ii)  `text(Prove)\ ACDO\ text(is cyclic)`

`text(S)text(ince)\ Delta ADB\ text(is isosceles)`

`/_DAB = x\ \ \ text{(opposite equal sides in}\ Delta DBA text{)}`

`=> /_ADB` `= 180\ – 2x\ \ \ text{(angle sum of}\ Delta DAB text{)}`
`=> /_CDA` `= 2x\ \ \ text{(}CDB\ text{is a straight angle)}`

 

`text(S)text(ince chord)\ AC\ text(subtends)\ /_CDA = 2x`

`text(and)\ /_COA = 2x,`

`:.\ text(Quadrilateral)\ ACDO\ text(must be cyclic.)`

 

(iii)

 `text(Need to show)\ OM\ text(passes through)\ P,\ text(centre)`

♦♦♦ Mean mark 7%. 2nd hardest question in the 2011 paper!

`text(of circle through)\ ACDO.`

`AM` `= CM\ text{(} M\ text(is midpoint) text{)}`
`OC` `= OA\ text{(radii)}`

`OM\ text(is common)`

`:.\ Delta OAM -= Delta OCM\ \ \ text{(SSS)}`

`:. /_CMO = /_AMO\ \ \ ` `text{(corresponding angles of}`
  `\ \ text{congruent triangles)}`

 

`text(S)text(ince)\ ∠AMC\ text(is straight angle)`

`/_CMO = /_AMO = 90°`

`:.OM\ text(is perpendicular bisector)`

`text(of chord)\ AC.`

`:. OM\ text(passes through)\ P.`

`:.\ P, M,\ text(and)\ O\ text(are collinear.)`

Quadratic, EXT1 2011 HSC 3b

The diagram shows two distinct points  `P(t, t^2)`  and  `Q(1\ - t, (1\ - t)^2)`  on the parabola  `y = x^2`.  The point  `R`  is the intersection of the tangents to the parabola at  `P`  and  `Q`. 

 

  1. Show that the equation of the tangent to the parabola at  `P`  is  `y = 2tx\ – t^2`.   (2 marks)
  2. Using part  `text{(i)}`, write down the equation of the tangent to the parabola at  `Q`.     (1 mark)
  3. Show that the tangents at  `P`  and  `Q`  intersect at
    `R (1/2, t\ - t^2)`.   (2 marks)
  5. Describe the locus of  `R`  as  `t`  varies, stating any restriction on the  `y`-coordinate.   (2 marks)

 

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `y = 2 (1 -t)x\ – (1\ – t)^2`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
  4. `text(Locus of)\ R\ text(is vertical line)`
    `x = 1/2,\ y<1/4`
Show Worked Solution
(i)

`text(Show tangent at)\ P\ text(is)\ y = 2tx\ – t^2`

`y` `= x^2`
`dy/dx` `= 2x`

`x=t\ \ \ \ text(at)\ P`

`dy/dx = 2t`

`text(Find equation with)\ \ m = 2t\ \ text(through)\ \ P(t, t^2)`

`y\ – y_1` `= m(x\ – x_1)`
`y\ – t^2` `= 2t ( x\ – t)`
`y` `= 2tx\ – 2t^2 + t^2`
  `= 2tx\ – t^2\ text(… as required)`

 

(ii)  `text(T)text(angent at)\ Q\ text(has equation)`

MARKER’S COMMENT: Many students derived this equation rather than substituting the new parameter, costing them valuable time. This is a benefit of using the parametric approach.

`y = 2(1\ – t)x\ – (1\ – t)^2`

 

(iii)  `text(Need to show)\ R(1/2,\ t\ – t^2)`

`R\ text(is at intersection of tangents)`

`2tx\ – t^2` `= 2(1\ – t)x\ – (1\ – t)^2`
`2tx\ – t^2` `= 2x\ – 2tx\ – 1 + 2t\ – t^2`
`4tx\ – 2x` `= -1 + 2t\ – t^2 + t^2`
`2x(2t\ – 1)` `= 2t\ – 1`
`2x` `= 1`
`x` `= 1/2`

`text(Using)\ \ y = 2tx – t^2\ \ text(when)\ \ x = 1/2`

`y` `= 2t(1/2)\ – t^2`
  `= t\ – t^2`

`:.\ R(1/2, t\ – t^2)\ text(… as required)`

 

(iv)  `text(Locus of)\ R`

♦♦ Mean mark of 22%. 
MARKER’S COMMENT: Many students stated the locus as `y=t-t^2` rather than realising it had to be a straight line since `x=½`, and that `y=t-t^2` simply restricted the values of `y`.

`text(S)text(ince)\ x = 1/2\ text(is a constant)`

`R\ text(is a vertical line)`

`text(Now,)\ y = t\ – t^2 = t(1\ – t)`

`text(Graphically,)\ \ y\ \ text(has a maximum at)\ \ t = 1/2`

`text(Max)\ \ y = 1/2\ – (1/2)^2 = 1/4`

`=> y < 1/4\ \ text{(tangents can’t meet on parabola)}`

`:.\ text(Locus of)\ R\ text(is vertical line)\ x = 1/2,\ \ y<1/4`

Mechanics, EXT2* M1 2011 HSC 3a

The equation of motion for a particle undergoing simple harmonic motion is 

 `(d^2x)/(dt^2) = -n^2 x`,

where `x` is the displacement of the particle from the origin at time `t`, and `n` is a positive constant.

  1. Verify that  `x = A cos nt + B sin nt`, where `A` and `B` are constants, is a solution of the equation of motion.    (1 mark)

  2. The particle is initially at the origin and moving with velocity `2n`. 

     

    Find the values of `A` and `B` in the solution  `x = A cos nt + B sin nt`.    (2 marks)

  3. When is the particle first at its greatest distance from the origin?   (1 mark)

  4. What is the total distance the particle travels between  `t = 0`  and  `t = (2pi)/n`?   (1 mark)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `A = 0,\ B = 2`
  3. `t = pi/(2n)`
  4. `text(8 units)`
Show Worked Solution
i.   `x` `= A cos nt + B sin nt`
  `(dx)/(dt)` `= – An sin nt + Bn cos nt`
  `(d^2x)/(dt^2)` `= – An^2 cos nt\ – Bn^2 sin nt`
    `= -n^2 (A cos nt + B sin nt)`
    `= -n^2 x\ \ \ text(… as required)`

 

ii.   `text(At)\ \ t=0, \ x=0, \ v=2n:`

`x` `= Acosnt + Bsinnt`
`0` `= A cos 0 + B sin 0`
`:.A` `= 0`

  
`text(Using)\ \ (dx)/(dt) = Bn cos nt`

`2n` `= Bn cos 0`
`Bn` `= 2n`
`:.B` `= 2`
♦♦ Mean mark part (iii) 47%
 

iii.   `text(Max distance from origin when)\ (dx)/(dt) = 0`

`(dx)/(dt)` `= 2n cos nt`
`0` `= 2n cos nt`
`cos nt` `= 0`
`nt` `= pi/2,\ (3pi)/2,\ (5pi)/2`
`t` `= pi/(2n),\ (3pi)/(2n), …`

 

`:.\ text(Particle is first at greatest distance)`

`text(from)\ O\ text(when)\ t = pi/(2n).`

 

iv.  `text(Solution 1)`

`text(Find the distance travelled from)\ \ t=0\ \→\ \ t=(2pi)/n`

`text{(i.e. 1 full period)}`

♦♦ Mean mark 22%
MARKER’S COMMENT: Many students found the displacement at `t` rather than the distance travelled while another common error found distance as 2 x amplitude.

`text(S)text(ince)\ \ x=2 sin (nt)`

`=> text(Amplitude)=2`

`:.\ text(Distance travelled)=4 xx2=8\ text(units)`

 

`text(Solution 2)`

`text(At)\ t = 0,\ x = 0`

`text(At)\ t` `= pi/(2n)`
`x` `= 2 sin (n xx pi/(2n)) = 2`
`text(At)\ t` `= (3pi)/(2n)\ \ \ text{(i.e. the next time}\ \ (dx)/(dt) = 0 text{)}`
`x` `= 2 sin (n xx (3pi)/(2n)) = -2`
`text(At)\ t` `= (2pi)/n`
`x` `= 2 sin (n xx (2pi)/n) = 0`

 

`:.\ text(Total distance travelled)`

`= 2 + 4 + 2`
`= 8\ \ text(units)`

Calculus, EXT1 C1 2012 HSC 14c

A plane `P` takes off from a point `B`. It flies due north at a constant angle `alpha` to the horizontal. An observer is located at `A`, 1 km from `B`, at a bearing 060° from `B`.

Let `u` km be the distance from `B` to the plane and let `r` km be the distance from the observer to the plane. The point `G` is on the ground directly below the plane.
 

2012 14c
 

  1. Show that  `r = sqrt(1 + u^2 - u cos alpha)`.   (3 marks)

  2. The plane is travelling at a constant speed of 360 km/h.
  3. At what rate, in terms of  `alpha`, is the distance of the plane from the observer changing 5 minutes after take-off?    (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `(180 (60\ – cos alpha))/sqrt(901\ – 30 cos alpha)\ \ text(km/hr)`
Show Worked Solution

i.  `text(Show)\ r = sqrt(1 + u^2 – u cos alpha)`

♦ Mean mark 42%
IMPORTANT: Students should always be looking for opportunities to use the identity `sin^2 alpha“+cos^2 alpha=1` to clean up calculations with trig functions.

`text(In)\ Delta PGB:`

`cos alpha` `= (BG)/u`
`BG` `= u cos alpha`
`sin alpha` `= (PG)/(u)`
`PG` `= u sin alpha`

 
`text(In)\ Delta PGA,\ text(using Pythagoras):`

`AG^2` `= r^2\ – PG^2`
  `= r^2\ – u^2 sin^2 alpha`

 
`text(Using cosine rule in)\ Delta ABG:`

`AG^2` `= BG^2 + AB^2\ – 2 xx BG xx AB xx cos 60^@`
`r^2\ – u^2 sin^2 alpha` `= u^2 cos^2 alpha + 1\ – 2 (u cos alpha) xx 1 xx 1/2`
`r^2` `= u^2 cos^2 alpha + u^2 sin^2 alpha + 1\ – u cos alpha`
  `= u^2 (cos^2 alpha + sin^2 alpha) + 1\ – u cos alpha`
  `= u^2 + 1\ – u cos alpha`
`r` `= sqrt(u^2 + 1\ – u cos alpha)\ \ text(… as required)`

 

ii.  `text(Find)\ \ (dr)/(dt)\ text(when)\ t =5`

♦♦♦ Mean mark 14%

`(dr)/(dt) = (dr)/(du) xx (du)/(dt)`

`r` `= (u^2 + 1\ – u cos alpha)^(1/2)`
`(dr)/(du)` `= 1/2 (u^2 + 1\ – u cos alpha)^(-1/2) xx (2u\ – cos alpha)`
  `= (2u\ – cos alpha)/(2 sqrt(u^2 + 1\ – u cos alpha))`

 
`(du)/(dt)= 360\ text{km/hr   (plane’s speed)}`

 
`text(After 5 mins,)`

`u` `= 5/60 xx 360 = 30\ text(km)`
`(dr)/(dt)` `= ((2 xx 30)\ – cos alpha)/( 2 sqrt(30^2 + 1\ – 30 cos alpha)) xx 360`
  `= (180 (60\ – cos alpha))/sqrt(901\ – 30 cos alpha)\ \ text(km/hr)`

Mechanics, EXT2* M1 2012 HSC 14b

A firework is fired from `O`, on level ground, with velocity `70` metres per second at an angle of inclination  `theta`. The equations of motion of the firework are

 `x = 70t cos theta\ \ \ \ `and`\ \ \ y = 70t sin theta\ – 4.9t^2`. (Do NOT prove this.) 

The firework explodes when it reaches its maximum height.
 

2012 14b
 

  1. Show that the firework explodes at a height of  `250 sin^2 theta`  metres.   (2 marks)

  2. Show that the firework explodes at a horizontal distance of  `250 sin 2 theta`  metres from  `O`.    (1 mark)

  3. For best viewing, the firework must explode at a horizontal distance between 125 m and 180 m from `O`, and at least 150 m above the ground.

     

    For what values of  `theta`  will this occur?   (3 mark)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `66.97^@… <= theta <= 75^@\ text(for best viewing)`
Show Worked Solution

i.   `text(Show max height is)\ 250 sin^2 theta\ text(metres)`

`text(Firework explodes at max height)`

`text(Find)\ \ t\ \ text(when)\ dot y = 0`

`y = 70t sin theta\ – 4.9t^2`

`dot y = 70 sin theta\ – 9.8t`
 

`text(When)\ \ dot y = 0`

`70 sin theta\ – 9.8t` `= 0`
`9.8t` `=70 sin theta`
`t` `= 70/9.8 sin theta`

 

`:.\ y_max` `= 70 * 70/9.8 sin theta * sin theta\ – 4.9 * (70^2)/(9.8^2) sin^2 theta`
  `= 500 sin^2 theta\ – 250 sin^2 theta`
  `= 250 sin^2 theta\ text(metres)\ \ \ \ \ text(… as required)`

 

ii.  `x = 70t cos theta`

`text(At)\ \ t = 70/9.8 sin theta`

`x` `= 70 * 70/9.8 sin theta cos theta`
  `= 250 * 2 sin theta cos theta`
  `= 250 sin 2 theta\ text(metres)\ \ \ \ \ text(… as required)`

 

iii.  `text(Best viewing when)`

♦♦ Mean mark 28%
MARKER’S COMMENT: Many students ignored the findings in earlier parts and tried unsuccessfully to solve inequalities that still contained `t`.

`125 <= x <= 180\ \ text(and)\ \ y >= 150`

`text(S)text(ince)\ x = 250 sin 2 theta`

`125` `<= 250 sin 2 theta <= 180`
`1/2` `<= sin 2 theta <= 18/25`

 

`text(In the 1st quadrant)`

`30^@ <= 2 theta <= 46.054…^@`

`15^@ <= theta <= 23.0^@`

`text(In the 2nd quadrant)`

`133.94…^@` `<= 2 theta <= 150^@`
`67.0^@` `<= theta <= 75^@`

 
`text{Using part (i)}`

`text(When)\ theta = 23.0^@`

`y_(max)` `= 250 xx sin^2 23.0^@`
  `~~ 38 < 150text(m)`

 
`=> text(“Highest” max height for)\ \ 15°<=theta<=23.0\ \ text(does not satisfy.)`

 
`text(When)\ theta = 67.0…^@`

`y_text(max)` `= 250 xx sin^2 67.0^@`
  `~~ 212 > 150 text(m)`

 

`=> text(“Lowest” max height for)\ \ 67°<=theta<=75°\ \ text(satisfies.)`

`:.\ 67.0^@ <= theta <= 75^@\ text( for best viewing)`.

Plane Geometry, EXT1 2012 HSC 14a

The diagram shows a large semicircle with diameter  `AB`  and two smaller semicircles with diameters  `AC`  and  `BC`, respectively, where  `C`  is a point on the diameter  `AB`. The point  `M`  is the centre of the semicircle with diameter  `AC`.

The line perpendicular to  `AB`  through  `C`  meets the largest semicircle at the point  `D`. The points  `S`  and  `T`  are the intersections of the lines  `AD`  and  `BD`  with the smaller semicircles. The point  `X`  is the intersection of the lines  `CD`  and  `ST`.

Copy or trace the diagram into your writing booklet.  

  1. Explain why  `CTDS`  is a rectangle.   (1 mark)
  2. Show that  `Delta MXS`  and  `Delta MXC`  are congruent.     (2 marks)
  3. Show that the line  `ST`  is a tangent to the semicircle with diameter  `AC`.    (1 mark)
  4.  
Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution
(i)

`/_SDT = 90°\ text{(angle in semi-circle)}`

♦ Mean mark 49%

`/_ ASC = 90°\ \ text{(angle in semi-circle)}`

`=> /_ CSD = 90°\ \ text{(} /_ ASD\ text{is a straight angle)}`

`text(Similarly)`

`/_CTB = /_CTD=90°`

`/_SCT = 90°\ \ text{(angle sum of quadrilateral}\ CTDS text{)}`

 

`text(S)text(ince all angles are right angles,)`

`CTDS\ text(is a rectangle)` 

 

(ii)  `ST\ text(and)\ DC\ text(are diagonals of rectangle)`

`text(S)text(ince they bisect and are equal)`

`=> XS = XC`

`SM = CM\ text{(radii)}`

`MX\ text(is common)`

`:.\ Delta MXS -= Delta MXC\ text{(SSS)}`

♦ Mean mark part (iii) 41%
STRATEGY: The congruency proof in part (ii) provided the critical information to answer this efficiently. Keep previous parts of questions front and centre of your mind when working on a solution.

 

(iii)  `/_ XSM = /_ XCM = 90°`

`text{(corresponding angles of congruent triangles)}`

 

`text(S)text(ince)\ MS _|_ ST\ text(at circumference)`

`text(and)\ MS\ text(is a radius,)`

`=> ST\ text(is a tangent)`

Geometry and Calculus, EXT1 2012 HSC 13d

The concentration of a drug in the blood of a patient  `t`  hours after it was administered is given by

`C(t) = 1.4te^(–0.2t),`

where  `C(t)`  is measured in `text(mg/L)`.  

  1. Initially the concentration of the drug in the blood of the patient increases until it reaches a maximum, and then it decreases. Find the time when this maximum occurs.   (3 marks)
  3. Taking  `t = 20`  as a first approximation, use one application of Newton’s method to find approximately when the concentration of the drug in the blood of the patient reaches  `0.3\ text(mg/L)`.   (2 marks)
Show Answers Only
  1. `t = 5\ \ text(hours.)`
  2. `text(The concentration of the blood will be)`
  3. `text(approx 0.3 mg/L after 22.8 hours.)`
Show Worked Solution
(i)    `\ \ C(t)` `= 1.4 te^(-0.2t)`
  `(dC)/(dt)` `= 1.4t (-0.2)e^(-0.2t) + 1.4 e^(-0.2t)`
    `= 1.4 e^(-0.2t) (1\ – 0.2t)`

`text(Max or min when)\ (dC)/(dt) = 0`

`1.4e^(-0.2t)` `= 0 => text(has no solution)`
`(1 – 0.2t)` `= 0`
`0.2t` `= 1`
`t` `= 5\ \ text(hours)`

`text(When)\ \ t < 5,\ (dC)/(dt)>0`

`text(When)\ \ t > 5,\ (dC)/(dt)<0`

`:.\ text(Maximum when)\ \ t = 5\ text(hours.)`

 

♦ Mean mark 45% 
MARKER’S COMMENT: Only a minority of students could successfully apply Newton’s method in this instance. A must know area asked every year!
(ii)    `text(Taking)\ C = 0.3`
`0.3` `= 1.4te^(-0.2t)`
`f(t)` `= 1.4te^(-0.2t)\ – 0.3`
`f′(t)` `= 1.4t(-0.2)e^(-0.2t) + 1.4e^(-0.2t)`
  `= 1.4 e^(-0.2t) (1\ – 0.2t)`
`f(20)` `=1.4 xx 20 xx e^(-0.2 xx 20)\ – 0.3`
  `=0.21283…`
`f′(20)` `= 1.4 e^(-0.2 xx 20) (1-0.2 xx20)`
  `=-0.0769…`
`t_2`  `= 20\ – f(20)/(f prime (20))`
  `= 20\ – (0.21283…)/(-0.0769…)`
  `= 22.766…`
  `= 22.8\ text(hours)\ \ \ text{(to 1 d.p.)}`

 

`:.\ text(The concentration of the blood will be)`

`text(approx 0.3 mg/L after 22.8 hours.)`

Mechanics, EXT2* M1 2012 HSC 13c

A particle is moving in a straight line according to the equation

`x = 5 + 6 cos 2t + 8 sin 2t`, 

where `x` is the displacement in metres and `t` is the time in seconds.

  1. Prove that the particle is moving in simple harmonic motion by showing that `x`  satisfies an equation of the form  `ddot x = -n^2 (x\ - c)`.  (2 marks)

  2. When is the displacement of the particle zero for the first time?    (3 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `1.5\ text(seconds)\ text{(1 d.p.)}`
Show Worked Solution

i.  `text(Prove)\ ddot x = -n^2(x\ – c)`

`x` `= 5 + 6 cos 2t + 8 sin 2t`
`dot x` `= -12 sin 2t + 16 cos 2t`
`ddot x` `= – 24 cos 2t\ – 32 sin 2t`
  `= -4 (6 cos 2t + 8 sin 2t)`
  `= -2^2 (5 + 6 cos 2t + 8 sin 2t\ – 5)`
  `= -2^2 (x\ – 5)\ \ \ text(… as required)`

 

ii.  `text(Find)\ \ t\ \ text(when)\ \ x=0\ \ text(for 1st time:)`

♦ Mean mark 42%.
IMPORTANT: The critical insight required to solve `x=0` is to realise that the cosine of the difference between 2 angles, i.e. `cos (2t- theta)`, applies.
`5 + 6 cos 2t + 8 sin 2t` `= 0`
`6 cos 2t + 8 sin 2t` `= -5`
`6/10 cos 2t+ 8/10 sin 2t` `=-1/2`

 

 Calculus in the Physical World, EXT1 2012 HSC 13c Answer

`=>cos theta=6/10\ \ text(and)\ \ sin theta=8/10`
`cos 2t cos theta+sin 2t sin theta` `=- 1/2`
`cos(2t\ – theta)` `= – 1/2`

`text(S)text(ince)\ \ cos\ pi/3 = 1/2\ \ text(and)\ cos\ text(is negative)`

`text(in the 2nd and 3rd quadrants,)`

`=>2t\ – theta = pi\ – pi/3,\ pi + pi/3`

 

`text(We need the 1st time)\ \ x = 0`

`text(S)text(ince)\ \ cos theta` `= 6/10`
`theta` `= 0.9273…`

 

`:.\ 2t\ – 0.9273…` `= (2pi)/3`
`2t` `= (2pi)/3 + 0.9273…`
`t` `= 1/2 ((2pi)/3 + 0.9273…)`
  `= 1.5108…`
  `= 1.5\ text(seconds)\ text{(1 d.p.)}`

Quadratic, EXT1 2012 HSC 12d

Let  `A(0, –k)`  be a fixed point on the  `y`-axis with  `k > 0`. The point  `C(t, 0)`  is on the  `x`-axis. The point  `B(0, y)`  is on the  `y`-axis so that  `Delta ABC`  is right-angled with the right angle at  `C`. The point  `P`  is chosen so that  `OBPC`  is a rectangle as shown in the diagram.

2012 12d

  1. Show that  `P`  lies on the parabola given parametrically by          (2 marks)
    1. `x = t\ \ ` and`\ \ y = (t^2)/k`. 
  2. Write down the coordinates of the focus of the parabola in terms of  `k`.    (1 mark)
Show Answers Only
  1. `text(Proof)  text{(See Worked Solutions)}`
  2. `text(Focus is)\ (0, k/4)`
Show Worked Solution
♦♦ Mean mark 30%.
IMPORTANT: The highlighted right-angle in this question should flag the potential use of `m_1 xx m_2=–1`.

`A(0,–k)\ \ \ B(0,y)\ \ \ C(t,0)`

`m` `= (y_2\ – y_1)/(x_2\ – x_1)`
`m_(AC)` `= (0 + k)/(t\ – 0) = k/t`
`m_(BC)` `= (y\ – 0)/(0\ – t) = -y/t`

 

`text(S)text(ince)\ Delta ABC\ text(is right-angled)`

`m_(AC) xx m_(BC)` `= -1`
`k/t xx (-y)/t` `= -1`
`-yk` `= -t^2`
`y` `= (t^2)/k`

`text(S)text(ince)\ OBPC\ text(is a rectangle)`

`=>P\ text(has the same)\ x text(-coordinate as)\ C`
`text(and the same)\ y text(-coordinate as)\ B`

`:.P\ \ text(has coordinates)\ \ (t, (t^2)/k)`

`:.P\ text(lies on the parabola where)`
`x = t,\ \ y = (t^2)/k`

 

(ii)    `y` `= (x^2)/k`
  `x^2` `= ky`

`text(Using)\ \ x^2 = 4ay`

`4a` `=k`
`a` `=k/4`

 

`text(Parabola has vertex)\ \ (0,0)\ \ text(and)\ \ a = k/4`

`:.\ text(Focus is)\ \ (0, k/4)`

Statistics, EXT1 S1 2012 HSC 12c

Kim and Mel play a simple game using a spinner marked with the numbers  1, 2, 3, 4 and 5.
 

2012 12c
 

The game consists of each player spinning the spinner once. Each of the five numbers is equally likely to occur.

The player who obtains the higher number wins the game.

If both players obtain the same number, the result is a draw.

  1. Kim and Mel play one game. What is the probability that Kim wins the game?   (1 mark)

  2. Kim and Mel play six games. What is the probability that Kim wins exactly three games?    (2 marks)

Show Answers Only
  1. `2/5`
  2. `864/3125`
Show Worked Solution

i.  `text(Method 1)`

`P text{(Kim wins game)}`

`= P text{(K spins 5)} xx P text{(M<5)} + P text{(K spins 4)} xx P text{(M<4)} +\ …`

`= (1/5 xx 4/5) + (1/5 xx 3/5) + (1/5 xx 2/5) + (1/5 xx 1/5)`

`= 10/25`

`= 2/5`

 

♦ Mean mark 37%

`text(Method 2)`

`P text{(Draw)} = 1/5`

`:.\ P text{(Not a draw)}= 1\ – 1/5=4/5`

 
`text(S)text(ince Kim and Mel have equal chance)`

`P text{(K wins)}` `= 1/2 xx 4/5`
  `= 2/5`

 

ii.  `P text{(Kim wins)} = 2/5`

`P text{(Kim doesn’t win)} = 3/5`
 

`text(After 6 games,)`

`P text{(Kim wins exactly 3)}`

`=\ ^6C_3 (2/5)^3 (3/5)^3`

`= (6!)/(3!3!) xx 8/125 xx 27/125`

`= 864/3125`

Calculus, 2ADV C3 2009 HSC 10

`text(Let)\ \ f(x) = x - (x^2)/2 + (x^3)/3`

  1. Show that the graph of  `y = f(x)`  has no turning points.   (2 marks)

  2. Find the point of inflection of  `y = f(x)`.     (1 mark)

  3. i. Show that `1 - x + x^2 - 1/(1 + x) = (x^3)/(1 + x)`  for  `x != -1`.   (1 mark)

     

    ii. Let  `g(x) = ln (1 + x)`.

     

        Use the result in part c.i. to show that  `f prime (x) >= g prime (x)`  for all  `x >= 0`.   (2 marks)

  1. Sketch the graphs of  `y = f(x)`  and  `y = g(x)`  for  `x >= 0`.    (2 marks)

  2. Show that  `d/(dx) [(1 + x) ln (1 + x) - (1 + x)] = ln (1 + x)`.   (2 marks)

  3. Find the area enclosed by the graphs of  `y = f(x)`  and  `y = g(x)`, and the straight line  `x = 1`.   (2 marks)

Show Answers Only
  1. `text{Proof  (See Worked Solutions)}`
  2. `(1/2, 5/12)`
  3. i. `text{Proof  (See Worked Solutions)}`

     

    ii. `text{Proof  (See Worked Solutions)}` 

  4.  
        Geometry and Calculus, 2UA 2009 HSC 10 Answer
  5. `text{Proof  (See Worked Solutions)}`
  6. `1 5/12\ – 2ln2\ \ text(u²)`
Show Worked Solution
a.    `f(x) = x\ – (x^2)/2 + (x^3)/3`
♦♦ Mean mark 28% for all of Q10 (note that data for each question part is not available).
 

`text(Turning points when)\ f prime (x) = 0`

`f prime (x) = 1\ – x + x^2`

`x^2\ – x + 1 = 0`

`text(S)text(ince)\ \ Delta` `= b^2\ – 4ac`
  `= (–1)^2\ – 4 xx 1 xx 1`
  `= -3 < 0 => text(No solution)`

 
`:.\ f(x)\ text(has no turning points)`

 

b.    `text(P.I. when)\ f″(x) = 0`
`f″(x)` `= -1 + 2x = 0`
`2x` `= 1`
`x` `= 1/2`

`text(Check for change in concavity)`

`f″(1/4)` `= -1/2 < 0`
`f″(3/4)` `= 1/2 > 0`

`=>\ text(Change in concavity)`

`:.\ text(P.I. at)\ \ x = 1/2`

 

`f(1/2)` `= 1/2\ – ((1/2)^2)/2 + ((1/2)^3)/3`
  `= 1/2\ – 1/8 + 1/24`
  `= 5/12`

`:.\ text(Point of Inflection at)\ (1/2, 5/12)`

 

c.i.    `text(Show)\ 1\ – x + x^2\ – 1/(1 + x) = (x^3)/(1 + x),\ \ \ x != -1` 
`text(LHS)` `= (1+x)/(1+x)\ – (x(1+x))/(1+x) + (x^2(1+x))/((1+x))\ – 1/(1+x)`
  `= (1 + x\ – x\ – x^2 + x^2 + x^3\ – 1)/(1+x)`
  `= (x^3)/(1+x)\ \ \ text(… as required)`

 

c.ii.   `text(Let)\ g(x) = ln(1+x)`
  `g prime (x) = 1/(1 + x)`
`f prime (x)\ – g prime (x)` `= 1\ – x + x^2\ – 1/(1+x)`
  `= (x^3)/(1 + x)\ \ text{(using part (i))}`

`text(S)text(ince)\ (x^3)/(1 + x) >= 0\ text(for)\ x >= 0`

`f prime (x)\ – g prime (x) >= 0`
`f prime (x) >= g prime (x)\ text(for)\ x >= 0`
MARKER’S COMMENT: When 2 graphs are drawn on the same set of axes, you must label them. 
 

d. 

Geometry and Calculus, 2UA 2009 HSC 10 Answer
e.    `text(Show)\ d/(dx) [(1 + x) ln (1 + x)\ – (1 + x)] = ln (1 + x)`
  `text(Using)\ d/(dx) uv=uv′+vu′`
`text(LHS)` `= (1+x) xx 1/(1 + x) + ln(1+x)xx1 +  – 1`
  `= 1+ ln(1+x)\ – 1`
  `= ln(1+x)`
  `=\ text(RHS    … as required)`

 

f.    `text(Area)` `= int_0^1 f(x)\ – g(x)\ dx`
    `= int_0^1 (x\ – (x^2)/2 + (x^3)/3\ – ln(x+1))\ dx`
    `= [x^2/2\ – x^3/6 + (x^4)/12\ – (1 + x) ln (1+x) + (1+x)]_0^1`
    `text{(using part (e) above)}`
    `= [(1/2 – 1/6 + 1/12 – (2)ln2 + 2) – (ln1 + 1)]`
    `= 5/12\ – 2ln2 + 2\ – 1`
    `= 1 5/12\ – 2 ln 2\ \ text(u²)`

Calculus, 2ADV C3 2009 HSC 8a

Geometry and Calculus, 2UA 2009 HSC 8a

The diagram shows the graph of a function  `y = f(x)`. 

  1. For which values of  `x`  is the derivative,  `f^{′}(x)`, negative?    (1 mark)

  2. What happens to  `f^{′}(x)`  for large values of  `x`?    (1 mark)

  3. Sketch the graph  `y = f^{′}(x)`.     (2 marks)

Show Answers Only
  1. `f^{′}(x) < 0\ text(when)`

     

    `-1 < x < 3`

  2. `text(As)\ x -> oo`

     

    `f^{′}(x) -> 0`

  3.   
    Geometry and Calculus, 2UA 2009 HSC 8a Answer

Show Worked Solution

i.   `f^{′}(x) < 0\ text(when)`

`-1 < x < 3`

♦♦ Exact data not available.

 

ii.   `text(As)\ x -> oo,`

`f^{′}(x) -> 0`

 

♦♦ Exact data not available.
MARKER’S COMMENT: Poorly drawn graphs with axes not labelled and inaccurate scales were common.

iii.

  Geometry and Calculus, 2UA 2009 HSC 8a Answer

Trigonometry, 2ADV T3 2009 HSC 7b

Between 5 am and 5 pm on 3 March 2009, the height, `h`, of the tide in a harbour was given by

`h = 1 + 0.7 sin(pi/6 t)\ \ \ text(for)\ \ 0 <= t <= 12`

where  `h`  is in metres and  `t`  is in hours, with  `t = 0`  at 5 am. 

  1. What is the period of the function  `h`?    (1 mark)

  2. What was the value of  `h`  at low tide, and at what time did low tide occur?     (2 marks)

  3. A ship is able to enter the harbour only if the height of the tide is at least 1.35 m.

     

    Find all times between 5 am and 5 pm on 3 March 2009 during which the ship was able to enter the harbour.    (3 marks)

Show Answers Only
  1. `12\ text(hours)`
  2. `text(2pm)\ \ text{(5am + 9 hours)}`
  3. `text(6am to 10am)`
Show Worked Solution

i.   `h = 1 + 0.7 sin (pi/6 t)\ \ text(for)\ 0 <= t <= 12`

`T` `= (2pi)/n\ \ text(where)\ n = pi/6`
  `= 2 pi xx 6/pi`
  `= 12\ text(hours)`

 

`:.\ text(The period of)\ h\ text(is 12 hours.)`

 

ii.  `text(Find)\ h\ text(at low tide)`

IMPORTANT: Using `sin x=–1` for a minimum here is very effective and time efficient. This property of trig functions is often very useful in harder questions.

`=> h\ text(will be a minimum when)`

`sin(pi/6 t) = -1`

`:.\ h_text(min)` `= 1 + 0.7(-1)`
  `= 0.3\ text(metres)`

 

`text(S)text(ince)\ \ sinx = -1\ \ text(when)\ \ x = (3pi)/2`

`pi/6 t` `= (3pi)/2`
`t` `= (3pi)/2 xx 6/pi`
  `= 9\ text(hours)`

 
`:.\ text{Low tide occurs at 2pm (5 am + 9 hours)}`


iii.  `text(Find)\ \ t\ \ text(when)\ \ h >= 1.35`

`1 + 0.7 sin (pi/6 t)` `>= 1.35`
`0.7 sin (pi/6 t)` `>= 0.35`
`sin (pi/6 t)` `>= 1/2`
`sin (pi/6 t)` `= 1/2\ text(when)`
`pi/6 t` `= pi/6,\ (5pi)/6,\ (13pi)/6,\ text(etc …)`
   
`t` `= 1,\ 5\ \ \ \ \ \ (0 <= t <= 12)`

 

Trig Calculus, 2UA 2009 HSC 7b Answer

`text(From the graph,)`

`sin(pi/6 t) >= 1/2\ \ \ text(when)\ \ 1 <= t <= 5`

 
`:.\ text(Ship can enter the harbour between 6 am and 10 am.)`

Calculus, 2ADV C1 2009 HSC 6c

The diagram illustrates the design for part of a roller-coaster track. The section  `RO`  is a straight line with slope 1.2, and the section  `PQ`  is a straight line with slope  – 1.8. The section  `OP`  is a parabola  `y = ax^2 + bx`. The horizontal distance from the  `y`-axis to  `P`  is 30 m.
 

2009 6c
 

In order that the ride is smooth, the straight line sections must be tangent to the parabola at  `O`  and at  `P`.  

  1. Find the values of  `a`  and  `b`  so that the ride is smooth.   (3 marks)

  2. Find the distance  `d`, from the vertex of the parabola to the horizontal line through  `P`, as shown on the diagram.     (2 marks)

Show Answers Only
  1. `text(For a smooth ride,)\ a = -0.05\ text(and)\ b = 1.2`
  2. `16.2\ text(m)`
Show Worked Solution
i.    `y` `= ax^2 + bx`
  `dy/dx` `= 2ax + b`
  `text(At)\ \ x = 0,`
  `dy/dx` `= b`
♦♦♦ Exact data unavailable.
MARKER’S COMMENT: Successful students equated the curve gradient to the straight section as a requirement for a smooth ride.
 

`text(We need)\ m\ text(at)\ O = 1.2`

`:.\ b = 1.2`
 

`text(At)\ P,\ x = 30`

`dy/dx` `= 2 xx a xx 30 + 1.2`
  `= 60a + 1.2`

 
`text(We need)\ m\ text(at)\ P = -1.8`

`60a + 1.2` `= -1.8`
`60a` `= -3`
`a` `= -3/60`
  `= -0.05`

 
`:.\ text(For a smooth ride,)\ a = –0.05\ \ text(and)\ \ b = 1.2`

 

ii.    `y` `= -0.05x^2 + 1.2x`
  `dy/dx` `= -0.1x + 1.2`

 
`text(Find)\ x\ text(when)\ dy/dx = 0`

`-0.1x + 1.2` `= 0`
`x` `= 1.2/0.1`
  `= 12`

 
`:.\ text(MAX when)\ x = 12`

 
`text(When)\ x = 12`

`y` `= -0.05 xx 12^2 + 1.2 xx 12`
  `= -7.2 + 14.4`
  `= 7.2`

 
`text(When)\ x = 30`

`y` `= -0.05 xx 30^2 + 1.2 xx 30`
  `= -45 + 36`
  `= -9`

 

`:.\ d` `= 7.2 + |–9|`
  `= 16.2\ text(m)`

Trigonometry, 2ADV T1 2009 HSC 5c

The diagram shows a circle with centre `O` and radius 2 centimetres. The points  `A`  and  `B`  lie on the circumference of the circle and  `/_AOB = theta`.
 

2009 5c  
 

  1. There are two possible values of  `theta`  for which the area of  `Delta AOB`  is  `sqrt 3`  square centimetres. One value is  `pi/3`.

     

    Find the other value.    (2 marks)

  2. Suppose that  `theta = pi/3`.

     

    (1)  Find the area of sector  `AOB`   (1 mark)

     

    (2)  Find the exact length of the perimeter of the minor segment bounded by the chord  `AB`  and the arc  `AB`.   (2 marks)

Show Answers Only
  1. `(2pi)/3`
  2. (1)  `(2pi)/3\ \ text(cm²)`
  3. (2)  `(2 + (2pi)/3)\ text(cm)`
Show Worked Solution
i.    `text(Area)\ Delta AOB` `= 1/2 ab sin theta`
    `= 1/2 xx 2 xx 2 xx sin theta`
    `= 2 sin theta`
`2 sin theta` `= sqrt 3\ \ \ text{(given)}`
`sin theta` `= sqrt3/2`
`:. theta` `= pi/3,\ pi\ – pi/3`
  `= pi/3,\ (2pi)/3`

 

`:.\ text(The other value of)\ theta\ text(is)\ \ (2pi)/3\ \ text(radians)` 

 

ii. (1)    `text(Area of sector)\ AOB` `= pi r^2 xx theta/(2pi)`
    `= 1/2 r^2 theta`
    `= 1/2 xx 2^2 xx pi/3`
    `= (2pi)/3\ text(cm²)` 

 

ii. (2)    `text(Using the cosine rule:)`
`AB^2` `= OA^2 + OB^2\ – 2 xx OA xx OB xx cos theta`
  `= 2^2 + 2^2\ – 2 xx 2 xx 2 xx cos (pi/3)`
  `= 4 + 4\ – 4`
  `= 4`
`:.\ AB` `= 2`

 

`text(Arc)\ AB` `= 2 pi r xx theta/(2pi)`
  `= r theta`
  `= (2pi)/3\ text(cm)`

 

`:.\ text(Perimeter) = (2 + (2pi)/3)\ text(cm)`

Probability, 2ADV S1 2009 HSC 5b

On each working day James parks his car in a parking station which has three levels. He parks his car on a randomly chosen level. He always forgets where he has parked, so when he leaves work he chooses a level at random and searches for his car. If his car is not on that level, he chooses a different level and continues in this way until he finds his car.    

  1. What is the probability that his car is on the first level he searches?     (1 mark)

  2. What is the probability that he must search all three levels before he finds his car?   (1 mark)

  3. What is the probability that on every one of the five working days in a week, his car is not on the first level he searches?    (1 mark)

Show Answers Only
  1. `1/3`
  2. `1/3`
  3. `32/243`
Show Worked Solution

i.  `P text{(1st chosen)} = 1/3`
 

ii.  `P text{(search 3 levels)}`

♦♦ Mean marks of 31% and 39% for part (ii) and (iii) respectively.

`= P text{(not 1st)} xx P text{(not 2nd)}`

`= 2/3 xx 1/2`

`= 1/3`
 

iii.  `P text{(not 1st for 5 days)}`

`= 2/3 xx 2/3 xx 2/3 xx 2/3 xx 2/3`

`= 32/243`

Plane Geometry, 2UA 2009 HSC 4c

In the diagram,  `Delta ABC`  is a right-angled triangle, with the right angle at  `C`. The midpoint of  `AB`  is  `M`, and  `MP _|_ AC`.

Plane Geometry, 2UA 2009 HSC 4c_1

Copy or trace the diagram into your writing booklet. 

  1. Prove that  `Delta AMP`  is similar to  `Delta ABC`.   (2 marks)
  2. What is the ratio of  `AP`  to  `AC`?    (1 mark)
  3. Prove that  `Delta AMC`  is isosceles.   (2 marks)
  4. Show that  `Delta ABC`  can be divided into two isosceles triangles.   (1 mark)
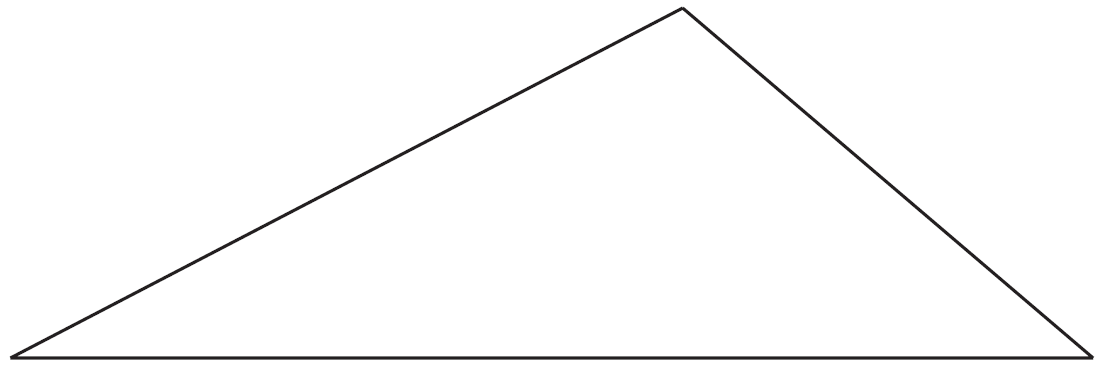
  5. Plane Geometry, 2UA 2009 HSC 4c_2
  6. Copy or trace this triangle into your writing booklet and show how to divide it into four isosceles triangles.   (1 mark)
  7.  
Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Ratio)\ AP:AC = 1:2`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
  4. `text(Proof)\ \ text{(See Worked Solutions)}`
  5. Plane Geometry, 2UA 2009 HSC 4c_2 Answer1
Show Worked Solution
(i)    `text(Need to prove)\ Delta AMP\  text(|||)\  Delta ABC`
  `/_ PAM\ text(is common)`
  `/_ MPA = /_BCA = 90°\ \ \ text{(given)}`
  `:.\ Delta AMP \ text(|||) \ Delta ABC\ \ \ text{(equiangular)}`

 

(ii)   `(AP)/(AC) = (AM)/(AB)\ \ \ ` `text{(corresponding sides of}`
    `text{similar triangles)}`

 

`text(S)text(ince)\ \ AB = 2 xx AM`
`(AP)/(AC) = 1/2`
`:.\ text(Ratio)\ AP:AC = 1:2`

 

(iii)

Plane Geometry, 2UA 2009 HSC 4c_1 Answer
`AP = PC \ \ \ text{(from part (ii))}`
`PM\ text(is common)`
`/_APM = /_CPM = 90°\ \ text{(∠}\ APC\ text{is a straight angle)}`
`:.\ Delta AMP ~= Delta CMP\ text{(SAS)}`
`=> AM = CM\ \ ` `text{(corresponding sides of}`
  `text{congruent triangles)}`

`:.\ Delta AMC\ text(is isosceles.)`

 

(iv)   `text(S)text(ince)\ \ AM` `= MC\ \ \ text{(part (iii))}`
  `AM`  `= MB\ text{(given)}`
  `:. MC`  `= MB`
`:. Delta MCB\ text(is isosceles)`
`:. Delta ABC\ text(can be divided into 2 isosceles)`
`text(triangles)\ (Delta AMC\ text(and)\ Delta MCB text{)}`

 

(v)

Plane Geometry, 2UA 2009 HSC 4c_2 Answer1
♦♦ Mean mark 25%.
MARKER’S COMMENT: Use a ruler, draw large diagrams and always pay careful attention to previous parts of the question!
`/_AFB = /_CFB = 90°`
`DF\ text(bisects)\ AB`
`EF\ text(bisects)\ BC`
`text(From part)\ text{(iv)}\ text(we get 4 isosceles)`
`text(triangles as shown.)`

Plane Geometry, 2UA 2010 HSC 10a

In the diagram  `ABC`  is an isosceles triangle with  `AC = BC = x`. The point  `D`  on the interval  `AB`  is chosen so that  `AD = CD`. Let  `AD = a`,  `DB = y`  and  `/_ADC = theta`.
 

 
 

  1. Show that  `Delta ABC`  is similar to  `Delta ACD`.    (2 marks)
  2. Show that  `x^2 = a^2 + ay`.     (1 mark)
  3. Show that  `y = a(1 − 2 cos theta )`.   (2 marks)
  4. Deduce that  `y <= 3a`.   (1 mark) 
Show Answers Only
  1. `text(Proof)  text{(See Worked Solutions)}`
  2. `text(Proof)  text{(See Worked Solutions)}`
  3. `text(Proof)  text{(See Worked Solutions)}`
  4. `text(Proof)  text{(See Worked Solutions)}`
Show Worked Solution
MARKER’S COMMENT: When dealing with multiple triangles, the best performing students label all angles clearly and unambiguously.
(i)

`/_CAD\ text(is common)`

`/_CAD = /_ACD = /_DBC`

`text{(Angles opposite equal sides in}`

`\ \ text{isosceles}\ Delta ACD\ text(and)\ Delta ABC text{)}`
 

`/_ADC = /_ACB\ \ (180^@\ text(in)\ Delta text{)}`

`:.\ Delta ABC\  text(|||) \ Delta ACD\ \ \ text{(AAA)}\ \ \ text(… as required)`

 

♦♦ Mean mark 25%.
MARKER’S COMMENT: The similarity proof in part (i) should have immediately alerted students to using similar ratios of sides to solve part (ii). Many did not follow this obvious hint.

(ii)  `text(Using similarity)`

`(AC)/(AD)` `= (AB)/(CB)` `\ \ text{(corresponding sides of}`
`\ \ \ \ text{similar triangles)}`
`x/a` `= (a + y)/x`  

 

`:.\ x^2 = a^2 + ay\ \ \ text(… as required)`

 

(iii)  `text(Show)\ \ y = a(1\ – 2 cos theta)`

`text(Using Cosine Rule:)`

`cos theta` `= (a^2 + a^2\ – x^2)/(2 xx a xx a)`
`2a^2costheta` `= 2a^2\ – x^2`
  `= 2a^2\ – (a^2 + ay)\ \ text{(from part (ii))}`
  `= a^2\ – ay`
`ay` `= a^2\ – 2a^2cos theta`
`y` `= a\ – 2a cos theta`
  `= a (1\ – 2 cos theta)\ \ \ \ text(… as required)`

 

(iv)  `text(S)text(ince)\  1 <= cos theta <= 1`

♦♦♦ Parts (iii) and (iv) mean marks – 18% and just 4% respectively.
IMPORTANT: Limits of trig functions are often extremely useful in proving inequalities (see Worked Solutions).

` -2 <= 2 cos theta <= 2`

` -1 <= 1\ – 2 cos theta <= 3`

`y` `=a(1\ – 2 cos theta)\ \ \ text{(from part (iii))}`
`:.\ y` `<= a(3)`
  `<= 3a\ \ …\ text(as required)`

Calculus, 2ADV C3 2010 HSC 9b

Let  `y=f(x)`  be a function defined for  `0 <= x <= 6`, with  `f(0)=0`. 

The diagram shows the graph of the derivative of `f`,  `y = f^{′}(x)`. 

The shaded region `A_1` has area 4 square units. The shaded region `A_2` has area 4 square units. 

  1. For which values of `x` is `f(x)` increasing?  (1 mark)

  2. What is the maximum value of `f(x)`?     (1 mark)

  3. Find the value of `f(6)`.   (1 mark)

  4. Draw a graph of  `y =f(x)`  for  `0 <= x <= 6`.   (2 marks)

Show Answers Only
  1. `f(x)\ text(is increasing when)\ 0 <= x < 2`
  2. `text(MAX value of)\ f(x) = 4`
  3. `-6`
  4.  
  5.  
Show Worked Solution
i.    `f(x)\ text(is increasing when)\ \ f^{′}(x) > 0`
  `text(From the graph)`
  `f(x)\ text(is increasing when)\ 0 <= x < 2`

 

ii.   `f^{′}(x) = 0\ \ text(when)\ \ x=2`
  `:.\ text(MAX at)\ \ x = 2`
  `int_0^2 f^{′}(x)\ dx = 4\ \ \ (text(given since)\ A_1 = 4 text{)}`
  `text(We also know)`
`int_0^2\ f^{′}(x)\ dx` `= [f(x)]_0^2`
  `= f(2)-f(0)`
  `= f(2)\ \ \ \ text{(since}\ f(0) = 0 text{)}`

`=> f(2) = 4` 

♦♦♦ Parts (ii) and (iii) proved particularly difficult for students with mean marks of 12% and 11% respectively.

 
`:.\ text(MAX value of)\ \ f(x) = 4`
 

iii.   `int_0^4 f^{′}(x)` `= A_1-A_2`
    `=0`

`text(We also know)`

`int_0^4 f^{′}(x)\ dx` `= int_2^4 f^{′}(x)\ dx + int_0^2 f^{′}(x)\ dx`
  `=[f(x)]_2^4 + 4`
  `= f(4)-f(2) + 4\ \ \ (text(note)\ f(2)=4)`
  `=f(4)`

`=> f(4) = 0`

 
`text(Gradient = – 3  from)\ \ x = 4\ \ text(to)\ \ x = 6`

`:.\ f(6)` `= -3 (6\ – 4)`
  `= -6`

  

♦♦ Mean mark 28%
EXAM TIP: Clearly identify THE EXTREMES when given a defined domain. In this case, the origin is obvious graphically, and the other extreme at `x=6`, is CLEARLY LABELLED! 
iv.  2UA HSC 2010 9bi

Calculus, 2ADV C3 2010 HSC 8d

Let  `f(x) = x^3-3x^2 + kx + 8`, where `k` is a constant.

Find the values of `k` for which `f(x)` is an increasing function.   (2 marks)

Show Answers Only

`k>3`

Show Worked Solution
`f(x)` `= x^3-3x^2 + kx + 8`
`f^{′}(x)` `= 3x^2-6x + k`

  
`f(x)\ text(is increasing when)\ \ f^{′}(x) > 0`

`=> 3x^2-6x + k > 0`

♦♦ Mean mark 28%.
MARKER’S COMMENT: The arithmetic required to solve `36-12k<0`  proved the undoing of many students.

 

`f^{′}(x)\ text(is always positive)`

`=> f^{′}(x)\ text(is a positive definite.)`

`text(i.e. when)\ \ a > 0\ text(and)\ Delta < 0`
 

`a=3>0`

`Delta = b^2-4ac`

`:. (-6)^2-(4 xx 3 xx k)` `<0`
`36-12k` `<0`
`12k` `>36`
`k` `>3`

 

`:.\ f(x)\ text(is increasing when)\ \ k > 3.`

Probability, 2ADV S1 2010 HSC 8b

Two identical biased coins are tossed together, and the outcome is recorded.

After a large number of trials it is observed that the probability that both coins land showing heads is  0.36.

What is the probability that both coins land showing tails?   (2 marks)

Show Answers Only

 `0.16`

Show Worked Solution
♦♦ Mean mark 28%.
NOTE: The most common error was `P(T_1T_2)“=1-0.36“=0.64`. Ensure you understand why this does not apply.
`P(H_1 H_2)` `=P(H_1) xx P(H_2)`
  `=0.36`

 

`text(S)text(ince coins are identical:)`

`P(H)` `= sqrt 0.36`
  `= 0.6`
`P(T)` `= 1 – P(H)`
  `=0.4`

 

`:.\ P(T_1 T_2)` `= 0.4 xx 0.4`
  `=0.16`

Calculus, 2ADV C1 2010 HSC 7b

The parabola shown in the diagram is the graph  `y = x^2`. The points  `A (–1,1)`  and  `B (2, 4)`  are on the parabola.
 

 
 

  1.  Find the equation of the tangent to the parabola at `A`.   (2 marks)

  2.  Let `M` be the midpoint of  `AB`.

     

    There is a point `C` on the parabola such that the tangent at `C` is parallel to  `AB`.

     

    Show that the line  `MC`  is vertical.   (2 marks)  

  3. The tangent at `A` meets the line `MC` at `T`.

     

    Show that the line `BT` is a tangent to the parabola.  (2 marks)

Show Answers Only
  1. `2x + y + 1 = 0`
  2. `text(Proof)  text{(See Worked Solutions)}`
  3. `text(Proof)  text{(See Worked Solutions)}`
Show Worked Solution
i.
`y` `=x^2`
`dy/dx` `= 2x` 

 
`text(At)\ \ A text{(–1,1)}\ => dy/dx = -2`
 

`text(T)text(angent has)\ \ m=text(–2),\ text(through)\ text{(–1,1):}`

`y – y_1` `= m(x\ – x_1)`
`y – 1` `= -2 (x + 1)`
`y – 1` `= -2x -2`
`2x + y + 1` `= 0`

 

 `:.\ text(T)text(angent at)\ A\ text(is)\ \ 2x + y + 1 = 0`

 

♦ Mean mark 37%.
IMPORTANT: The critical understanding required for this question is that the gradient of `AB` needs to be equated to the gradient function (i.e. `dy/dx`).

ii.   `Atext{(–1,1)}\ \ \ B(2,4)`

`M` `= ((-1+2)/2 , (1+4)/2)`
  `= (1/2, 5/2)`

 

`m_(AB)` `= (y_2 – y_1)/(x_2 – x_1)`
  `= (4 – 1)/(2 + 1)=1`

 

`text(When)\ \ dy/dx`  `= 1`
`2x` `= 1`
`x` `= 1/2`

 
`:.\ C \ (1/2, 1/4)`
 
`=>M\ text(and)\ C\ text(both have)\ x text(-value)=1/2`

`:. MC\ text(is vertical  … as required)`

 

iii.   `T\ text(is point on tangent when) \ x=1/2` 

♦♦ Mean mark 29%.

`text(T)text(angent)\ \ \ 2x + y + 1 = 0`

`text(At)\ x = 1/2`

`2 xx (1/2) + y + 1=0`

`=> y=–2`

`:.\ T (1/2, –2)`

 
`text (Given)\ \ B (2, 4)`

`m_(BT)` `= (4+2)/(2\ – 1/2)`
  `=4`

 
`text(At)\ \ B(2,4),\ text(find gradient of tangent:)`

`dy/dx = 2x=2 xx2=4`

`:.m_text(tangent) = 4=m_(BT)`

`:.BT\ text(is a tangent)`

Trigonometry, 2ADV T1 2010 HSC 6b

The diagram shows a circle with centre `O` and radius 5 cm.

The length of the arc `PQ` is 9 cm. Lines drawn perpendicular to `OP` and `OQ` at `P` and `Q` respectively meet at  `T`.
 

  1. Find  `/_POQ`  in radians.   (1 mark)

  2. Prove that  `Delta OPT`  is congruent to  `Delta OQT`.   (2 marks)

  3. Find the area of the shaded region.   (2 marks)

Show Answers Only
  1. `9/5\ text(radians)`
  2. `text(Proof)  text{(See Worked Solutions)}`
  3. `6.3\ text(cm)\ \ \ text{(to 1 d.p.)}`
  4. `9.0\ text(cm²)\ \ \ text{(to 1 d.p.)}`
Show Worked Solution
i.    `text(Length of Arc)` `= r theta`
  `9` `= 5 xx /_POQ`
  `:.\ /_ POQ` `= 9/5\ text(radians)`

 

ii.

`text(Prove)\ Delta OPT ~= Delta OQT`

`OT\ text(is common)`

 MARKER’S COMMENT: Know the difference between the congruency proof of `RHS` and `SAS`. Incorrect identification will lose a mark.

`/_OPT = /_OQT = 90°\ \ \ text{(given)}`

`OP = OQ\ \ \ text{(radii)}`

`:.\ Delta OPT ~= Delta OQT\ \ \ text{(RHS)}`
 

iii.   
`/_POT ` `= 1/2 xx /_POQ\ \ \ text{(from part (ii))}`
  `=1/2 xx 9/5`
  `= 9/10\ text(radians)`
♦♦ Mean mark below 30%.
MARKER’S COMMENT: Many students struggled to work in radians. Make sure you understand this concept.
`tan /_ POT` `= (PT)/(OP)`
`tan (9/10)` `= (PT)/5`
`PT` `= 5 xx tan(9/10)`
  `=6.3007…`
  `=6.3\ text(cm)\ \ text{(to 1 d.p.)}`

 

iv.    `text(Shaded Area = Area)\ OQTP\ – text(Area Sector)\ OQP`
♦ Mean mark 35%.
`text(Area)\ OQTP` `= 2 xx text(Area)\ Delta OPT`
  `=2 xx 1/2 xx OP xx PT`
  `= 5 xx 6.3007`
  `~~ 31.503…`
  `~~31.5\ text(cm²)`

 

`text(Area Sector)\ OQP` ` = 1/2 r^2 theta`
  `= 1/2 xx 25 xx 9/5`
  `= 22.5\ text(cm²)`

 

`:.\ text(Shaded Area)` `= 31.503\ – 22.5`
  `=9.003…`
  `=9.0\ text(cm²)\ \ \ text{(to 1 d.p.)}`

Calculus, 2ADV C3 2010 HSC 6a

Let  `f(x) = (x + 2)(x^2 + 4)`.

  1. Show that the graph  `y=f(x)`  has no stationary points.   (2 marks)

  2. Find the values of  `x`  for which the graph  `y=f(x)`  is concave down, and the values for which it is concave up.    (2 marks)

  3. Sketch the graph  `y=f(x)`,  indicating the values of the  `x`  and  `y` intercepts.   (2 marks)

Show Answers Only
  1. `text(Proof)  text{(See Worked Solutions)}`
  2.  `f(x)\ text(is concave down when)\ x < -2/3`

     

    `f(x)\ text(is concave up when)\ x > -2/3`

  3.  
Show Worked Solution

i.  `text(Need to show no  S.P.’s)`

`f(x)` `= (x+2)(x^2 + 4)`
  `=x^3 + 2x^2 + 4x + 8`
`f prime (x)` `= 3x^2 + 4x + 4`

 

`text(S.P.s  occur when)\ \ f prime (x) =0,`

`3x^2 + 4x + 4 =0`

`Delta` `= b^2\ – 4ac`
  `=4^2\ – (4 xx 3 xx 4)`
  `=16\ – 48`
  `= -32 < 0`

 

`text(S)text(ince)\ \ Delta < 0,\ \ text(No Solution)`

`:.\ text(No  S.P.’s  for)\ \ f(x)`

 

ii.  `f(x)\ text(is concave down when)\ f″(x) < 0`

MARKER’S COMMENT: The significance of the sign of the second derivative was not well understood by most students.

`f″(x) = 6x + 4`

`=> 6x + 4` `< 0`
`6x` `< -4`
`x` `< -2/3`

`:.\ f(x)\ text(is concave down when)\ x < -2/3`

`f(x)\ text(is concave up when)\ f″(x) > 0`

`f″(x) = 6x + 4`

`=> 6x + 4` `> 0`
`6x` `> -4`
`x` `> -2/3`

`:. f(x)\ text(is concave up when)\ x > -2/3`

 

♦♦ Mean mark 33%.
MARKER’S COMMENT: Students are reminded to bring a ruler to the exam and use it to draw the axes for graphing and to help with an appropriate scale.

iii.  `y text(-intercept) =2 xx4=8`

`x text(-intercept)=–2` 

 

Calculus, 2ADV C4 2010 HSC 5b

  1. Prove that  `sec^2 x + secx tanx = (1 + sinx)/(cos^2x)`.   (1 mark)

  2. Hence prove that  `sec^2 x + secx tanx = 1/(1 - sinx)`.     (1 mark)

  3. Hence, use the identity  `int sec ax tan ax\ dx=1/a sec ax`  to find the exact value of

     

          `int_0^(pi/4) 1/(1 - sinx)\ dx`.   (2 marks)

Show Answers Only
  1. `text(Proof)  text{(See Worked Solutions)}`
  2. `text(Proof)  text{(See Worked Solutions)}`
  3. `sqrt2`
Show Worked Solution

i.    `text(Need to prove)`

`sec^2x + secxtanx = (1 + sinx)/(cos^2x)`
 

`text(LHS)` `=sec^2x + secx tanx`
  `=1/(cos^2x) + 1/(cosx) xx (sinx)/cosx`
  `=1/(cos^2x) + (sinx)/(cos^2x)`
  `=(1 + sinx)/(cos^2x)`
  `= text(RHS)\ \ \ \ text(… as required)`

 

ii.   `text(Need to prove)` 

♦♦ Mean mark 31%.
`sec^2x + secx tanx` `= 1/(1\ – sinx)`
`text(i.e.)\ \ (1 + sinx)/(cos^2x)` `= 1/(1\ – sin x)\ \ \ \ \ text{(part (i))}`
`text(LHS)` `= (1 + sinx)/(cos^2x)`
  `=(1 + sin x)/(1\ – sin^2x)`
  `=(1 + sinx)/((1\ – sinx)(1 + sinx)`
  `=1/(1\ – sinx)\ \ \ \ text(… as required)`

 

iii.  `int_0^(pi/4) 1/(1\ – sinx)\ dx`

♦ Mean mark 37%.

`= int_0^(pi/4) (sec^2x + secx tanx)\ dx`

`= [tanx + secx]_0^(pi/4)`

`= [(tan(pi/4) + sec(pi/4)) – (tan0 + sec0)]`

`= [(1 + 1/(cos(pi/4)))\ – (0 + 1/(cos0))]`

`= 1 + sqrt2\ – 1`

`= sqrt2`

Calculus, 2ADV C3 2011 HSC 9c

The graph  `y = f(x)`  in the diagram has a stationary point when  `x = 1`, a point of inflection when  `x = 3`, and a horizontal asymptote  `y = –2`.
 

 Geometry and Calculus, 2UA 2011 HSC 9c
 

Sketch the graph  `y = f^{′}(x)` , clearly indicating its features at  `x = 1`  and at  `x = 3`, and the shape of the graph as  `x -> oo`.   (3 marks)

Show Answers Only

Geometry and Calculus, 2UA 2011 HSC 9c Answer

Show Worked Solution
 
♦ Mean mark 43%
IMPORTANT: Examiners regularly ask questions that require the graphing of an `f ^{′}(x)` given the `f(x)` graph and vice-versa. KNOW IT!

Geometry and Calculus, 2UA 2011 HSC 9c Answer

Plane Geometry, 2UA 2012 HSC 16a

The diagram shows a triangle  `ABC`  with sides  `BC = a`  and  `AC = b`. The points  `D`,  `E`  and  `F`  lie on the sides  `AC`,  `AB`  and  `BC`, respectively, so that  `CDEF`  is a rhombus with sides of length  `x`.

 

  1. Prove that  `Delta EBF`  is similar to  `Delta AED`.    (2 marks)
  2. Find an expression for  `x`  in terms of  `a`  and  `b`.    (2 marks)
Show Answers Only
  1. `text(Proof)\ \  text{(See Worked Solutions)}`
  2. `x = (ab)/(a + b)`
Show Worked Solution
(i)

`text(S)text(ince)\ CDEF\ text(is a rhombus)`

♦ Mean mark 47%.

  `=> BC\ |\| \ ED\ \ text(and)\ \ EF \ |\|\ CD`

`/_ FCD` `=/_ EDA\ text{(corresponding angles,}\ BC\ text(||)\ ED text{)}`
`/_FCD` `=/_BFE\ text{(corresponding angles,}\ EF\ text(||)\ CD text{)}`
`=>/_EDA` `=/_BFE`
`/_FBE` `=/_DEA\ text{(corresponding angles,}\ BC\ text(||)\ ED text{)}`

`:.\ Delta EBF\ text(|||)\ Delta AED\ \ text{(equiangular)   … as required}` 

 

(ii)  `text(In)\ Delta AED,\ DA = b\ – x\ \ \ text(and)\ \ \ ED = x`

♦ Mean mark 31%.

`text(In)\ Delta EBF,\ FE = x\ \ text(and)\ \ FB = a\ – x`

`text(Using similarity)`

`(DA)/(ED) = (EF)/(FB)`

`(b\ – x)/x` `= x/(a\ – x)`
`x^2` `= (b\ – x)(a\ – x)`
`x^2`  `= ab\ – bx\ – ax + x^2`
`0` `= ab\ – x (a + b)`
`x (a + b)` `= ab`
`x` `= (ab)/(a+b)`

Calculus, 2ADV C3 2012 HSC 14a

A function is given by  `f(x) = 3x^4 + 4x^3-12x^2`. 

  1. Find the coordinates of the stationary points of  `f(x)`  and determine their nature.   (3 marks)

  2. Hence, sketch the graph  `y = f(x)`   showing the stationary points.   (2 marks)

  3. For what values of  `x`  is the function increasing?   (1 mark)

  4. For what values of  `k`  will  `f(x) = 3x^4 + 4x^3-12x^2 + k = 0`  have no solution?   (1 mark)

Show Answers Only
  1. `text{MAX at (0,0), MINs at (1, –5) and (–2, –32)}`
  2.  
        
        2UA HSC 2012 14ai
     
  3. `f(x)\ text(is increasing for)\ -2 < x < 0\ text(and)\ x > 1`
  4. `text(No solution when)\ k > 32`
Show Worked Solution
i. `f(x)` `= 3x^4 + 4x^3-12x^2`
  `f^{′}(x)` `= 12x^3 + 12x^2-24x`
  `f^{″}(x)` `= 36x^2 + 24x-24`

 

`text(Stationary points when)\ f^{′}(x) = 0`

`12x^3 + 12x^2-24x` `=0`
`12x(x^2 + x-2)` `=0`
`12x (x+2) (x-1)` `=0`

 

 
`:.\ text(Stationary points at)\ x=0,\ 1\ text(or)\ -2`
 

`text(When)\ x=0,\ \ \ \ f(0)=0`
`f^{″}(0)` `= -24 < 0`
`:.\ text{MAX at  (0,0)}`

 

`text(When)\ x=1`

`f(1)` `= 3+4-12 = -5`
`f^{″}(1)` `= 36 + 24-24 = 36 > 0`
`:.\ text{MIN at}\  (1,-5)`

 

`text(When)\ x=–2`

`f(-2)` `=3(-2)^4 + 4(-2)^3-12(-2)^2`
  `= 48-32-48`
  `= -32`
`f^{″}(-2)` `= 36(-2)^2 + 24(-2)-24`
  `=144-48-24 = 72 > 0`
`:.\ text{MIN at  (–2, –32)}`

 

ii.  2UA HSC 2012 14ai
♦ Mean mark 42%
MARKER’S COMMENT: Be careful to use the correct inequality signs, and not carelessly include ≥ or ≤ by mistake.

 

iii. `f(x)\ text(is increasing for)`
  `-2 < x < 0\ text(and)\ x > 1`

 

iv.   `text(Find)\ k\ text(such that)`

♦♦♦ Mean mark 12%.

`3x^4 + 4x^3-12x^2 + k = 0\ text(has no solution)`

`k\ text(is the vertical shift of)\ \ y = 3x^4 + 4x^3-12x^2`

`=>\ text(No solution if it does not cross the)\ x text(-axis.)`

`:.\ text(No solution when)\ k > 32`

Calculus, 2ADV C4 2011 HSC 6c

The diagram shows the graph  `y = 2 cos x` . 
  

2011 6c 
  

  1. State the coordinates of  `P`.   (1 mark)

  2. Evaluate the integral  `int_0^(pi/2) 2 cos x\ dx`.    (2 marks)

  3. Indicate which area in the diagram,  `A`,  `B`,  `C` or  `D`, is represented by the integral
     
           `int_((3pi)/2)^(2pi) 2 cos x\ dx`.   (1 mark)

  4. Using parts (ii) and (iii), or otherwise, find the area of the region bounded by the curve  `y = 2 cos x`  and the  `x`-axis, between  `x = 0`  and  `x = 2pi` .   (1 mark)

  5. Using the parts above, write down the value of
     
         `int_(pi/2)^(2pi) 2 cos x\ dx`.   (1 mark)

Show Answers Only
  1. `P(0,2)`
  2. `2`
  3. `C`
  4. `8\ text(u²)`
  5. `-2`
Show Worked Solution

i.  `y = 2 cos x`

`text(At)\ x = 0`

`y = 2 cos 0 = 2`

`:.\ P(0,2)`

 

ii.  `int_0^(pi/2) 2 cos x\ dx`

`= [2 sin x]_0^(pi/2)`

`= [2 sin (pi/2)\ – 2 sin 0]`

`= 2\ – 0`

`= 2`
 

iii.  `C`
 

iv.    `text(S)text(ince Area)\ A` `=\ text(Area)\ C,\ \ text(and)`
  `text(Area)\ B` `= 2 xx text(Area)\ A`

 

`:.\ text(Total Area)` `= 2 + (2xx2) + 2`
  `= 8\ text(u²)`

 

MARKER’S COMMENT: “Using the parts above” in part (v) was ignored by many students. Important to know when finding an area and evaluating an integral may differ.

v.  `int_(pi/2)^(2pi) 2 cos x\ dx`

`= text(Area)\ C\ – text(Area)\ B`

`= 2\ – (2 xx 2)`

`= -2`

Real Functions, 2UA 2011 HSC 6b

A point  `P(x, y)`  moves so that the sum of the squares of its distance from each of the points  `A(–1, 0)`  and  `B(3, 0)`  is equal to 40.

Show that the locus of  `P(x, y)`  is a circle, and state its radius and centre.   (3 marks)

Show Answers Only

`text(Centre)\ (1,0),\ text(radius)\ 4\ text(units).`

Show Worked Solution
♦ Mean mark 39%.
MARKER’S COMMENT: Challenging question with many students unable to handle the algebra in expanding and completing the squares.

`text(Find locus of)\ \ P(x,y)`

`P(x,y)\ \ \ \ \ Atext{(-1,0)}\ \ \ \ \ B(3,0)`

`text(Dist)\ PA^2` `= (y_2\ – y_1)^2 + (x_2\ – x_1)^2`
  `= y^2 + (x + 1)^2`
`text(Dist)\ PB^2` `= (y\ – 0)^2 + (x\ – 3)^2`
  `= y^2 + (x\ – 3)^2`

 
`text(S)text(ince)\ \ PA^2 + PB^2 = 40`

`=> y^2 + (x + 1)^2 + y^2 + (x\ – 3)^2` `=40`
`2y^2 + x^2 + 2x + 1 + x^2\ – 6x + 9` `=40`
`2y^2 + 2x^2\ – 4x + 10` `=40`
`y^2 + x^2\ – 2x + 5` `=20`
`y^2 + (x -1)^2 + 4` `=20`
`y^2 + (x -1)^2` `=16`

 
`:.\ P(x,y)\ text(is a circle, centre)\ \ (1,0),\ text(radius 4 units.)`

Statistics, 2ADV 2011 HSC 5b

Kim has three red shirts and two yellow shirts. On each of the three days, Monday, Tuesday and Wednesday, she selects one shirt at random to wear. Kim wears each shirt that she selects only once.

  1. What is the probability that Kim wears a red shirt on Monday?    (1 mark)
  2. What is the probability that Kim wears a shirt of the same colour on all three days?     (1 mark)
  3. What is the probability that Kim does not wear a shirt of the same colour on consecutive days?   (2 marks)
Show Answers Only
  1. `3/5`
  2. `1/10`
  3. `3/10`
Show Worked Solution
i.    `P (R\ text(on Monday) text{)}` `= text(# Red)/text(# Shirts)`
    `= 3/5`

 

MARKER’S COMMENT: Students could also have drawn a probability tree setting out this problem over 3 different days (stages).
ii.    `text(S)text(ince not enough yellow shirts)`
  `P text{(same colour each day)}`

`= P (R,R,R)`

`= 3/5 xx 2/4 xx 1/3`

`= 1/10`

 

iii.   `P text{(not wearing same colour 2 days in a row)}`

`= P (Y,R,Y) + P (R,Y,R)`

♦ Mean mark 47%.
MARKER’S COMMENT: Students should clearly write what probability they are finding in words or symbols before showing calculations.

`=  (2/5 xx 3/4 xx 1/3)+(3/5 xx 2/4 xx 2/3)`

`= 6/60 + 12/60 `

`= 3/10`

Calculus, 2ADV C4 2011 HSC 4d

  1. Differentiate  `y=sqrt(9 - x^2)`  with respect to  `x`.   (2 marks)

  2. Hence, or otherwise, find  `int (6x)/sqrt(9 - x^2)\ dx`.    (2 marks)

Show Answers Only
  1. `- x/sqrt(9\ – x^2)`
  2. `-6 sqrt(9\ – x^2) + C`
Show Worked Solution
IMPORTANT: Some students might find calculations easier by rewriting the equation as `y=(9-x^2)^(1/2)`.
i.    `y` `= sqrt(9 – x^2)`
    `= (9 – x^2)^(1/2)`

 

`dy/dx` `=1/2 xx (9 – x^2)^(-1/2) xx d/dx (9 – x^2)`
  `= 1/2 xx (9 – x^2)^(-1/2) xx -2x`
  `= – x/sqrt(9 – x^2)`

 

ii.    `int (6x)/sqrt(9 – x^2)\ dx` `= -6 int (-x)/sqrt(9 – x^2)\ dx`
    `= -6 (sqrt(9 – x^2)) + C`
    `= -6 sqrt(9 – x^2) + C`

Functions, EXT1* F1 2012 HSC 8 MC

The diagram shows the region enclosed by  `y = x- 2`  and  `y^2 = 4-x`. 
  

Which of the following pairs of inequalities describes the shaded region in the diagram? 

  1. `y^2 <= 4-x\ \ and\ \ y <= x-2`  
  2. `y^2 <= 4-x\ \ and\ \ y >= x-2`  
  3. `y^2 >= 4-x\ \ and\ \ y<= x-2`  
  4. `y^2 >= 4-x\ \ and\ \ y >= x-2`
Show Answers Only

`A`

Show Worked Solution
♦  Mean mark 44%.

`text(Using information from diagram)`

`(3,0)\ text(is in the shaded region)`

`text{Substituting (3,0) into}\ \ \ y^2<=4-x,\ \ \ 0 <= 4-3 => text(true)`

`:.\ text(Cannot be)\ C\ text(or)\ D`
 

`text(Similarly)`

`(3,0)\ text(must satisfy other inequality)`

`text(i.e.)\ \ y <= x-2\ \ text(becomes)\ \ 0<= 3-2 =>\ text(true)`

`=>  A`

Functions, 2ADV F2 2013 HSC 15c

  1. Sketch the graph  `y = |\ 2x-3\ |`.   (1 mark)

  2. Using the graph from part (i), or otherwise, find all values of  `m`  for which the equation  `|\ 2x-3\ | = mx + 1`  has exactly one solution.   (2 marks)

Show Answers Only
  1.  
    2UA 2013 HSC 15c Answer
  2. `text(When)\ m = -2/3,\ m >= 2\ text(or)\ m<-2`
Show Worked Solution

i. 

♦ Mean mark 49%
MARKER’S COMMENT: Many students drew diagrams that were “too small”, didn’t use rulers or didn’t use a consistent scale on the axes!

2UA 2013 HSC 15c Answer

 

ii.

   2UA 2013 HSC 15c1 Answer

 

`text(Line of intersection)\ \ y=mx + 1\ \ text(passes through)\ \ (0,1)`

♦♦ Mean mark 25%.
COMMENT: Students need a clear graphical understanding of what they are finding to solve this very challenging, Band 6 question.

`text(If it also passes through)\ \ (1.5, 0) => text(1 solution)`

`m` `=(y_2-y_1)/(x_2-x_1)`
  `= (1 -0)/(0- 3/2)`
  `=-2/3`

  
`text(Gradients of)\ \ y=|\ 2x-3\ |\ \ text(are)\ \ 2\ text(or)\ -2`
 

`text(Considering a line through)\ \ (0,1):`

`text(If)\ \ m >= 2\ text(, only intersects once.)`
 

`text(Similarly,)`

`text(If)\ \ m<-2 text(, only intersects once.)`

`:.\ text(Only one solution when)\ \ m = -2/3,\ \ m >= 2\ \ text(or)\ \ m<-2`

Calculus, EXT1* C3 2013 HSC 15b

The region bounded by the  `x`-axis, the  `y`-axis and the parabola  `y = (x-2)^2`  is rotated about the  `y`-axis to form a solid.
 

2013 15b
 

Find the volume of the solid.   (4 marks)

Show Answers Only

 `text(Volume) = (8 pi)/3\ text(u³)`

Show Worked Solution

`text(S)text(ince rotation about the)\ y text(-axis,)`

♦ Mean mark 39%.
`(x -2)^2` `= y`
`x\-2` ` = ± y^(1/2)`
`x ` `= 2 +- y^(1/2)`

 
`text(When)\ \ x=0,\ y=4`

`:. x = 2-y^(1/2)`

`:.\ text(Volume)` `= pi int_0^4 x^2 dy`
  `= pi int_0^4 (2-y^{1/2})^2 dy`
  `= pi int_0^4 (4-4 y^{1/2} + y) dy`
  `= pi [4y-(4 xx 2/3 xx y^(3/2)) + (1/2 y^2)]_0^4`
  `= pi [4y-8/3 y^(3/2) + 1/2 y^2]_0^4`
  `= pi [(4 xx 4)-(8/3 xx 4^(3/2)) + (1/2 xx 4^2)]` 
  `= pi [16\-64/3 + 8]`
  `= (8 pi)/3\ text(u³)`

Trigonometry, 2ADV T1 2013 HSC 14c

2013 14c

 
The right-angled triangle  `ABC`  has hypotenuse  `AB = 13`. The point  `D`  is on  `AC`  such that  `DC = 4`,  `/_DBC = pi/6` and  `/_ABD = x`.

Using the sine rule, or otherwise, find the exact value of  `sin x`.   (3 marks)

Show Answers Only

 `(7sqrt3)/26 text(.)`

Show Worked Solution

`text(Find)\ \ /_ADB`

`/_ADB` `= pi/6 + pi/2 \ \ \ text{(exterior angle of}\ Delta BDC text{)}`
  `= (2pi)/3\ text(radians)`

 
`text(Find)\ \ AD`

♦ Mean mark 36%.
STRATEGY TIP: The hint to use the sine rule should flag to students that they will be dealing in non-right angled trig (i.e. `Delta ABD`) and to direct their energies at initially finding `/_ADB` and `AD`.
`tan (pi/6)` `= 4/(BC)`
`1/sqrt3` `=4/(BC)`
`BC` `=4 sqrt3`

 

`text(Using Pythagoras:)`

`AC^2 + BC^2` `= AB^2`
`AC^2 + (4sqrt3)^2` `= 13^2`
`AC^2` `= 169\-48`
  `= 121`
`=>AC` `= 11`
`:.AD` `=AC\-DC`
  `= 11 -4`
  `=7`

 

`text(Using sine rule:)`

`(AB)/(sin /_BDA)` `= (AD)/(sinx)`
`13/(sin ((2pi)/3))` `=7/(sinx)`
`13 xx sinx` `= 7 xx sin ((2pi)/3)`
`sinx` `= 7/13 xx sin((2pi)/3)`
  `= 7/13 xx sqrt3/2`
  `= (7 sqrt3)/26`

 
`:.\ text(The exact value of)\ sinx = (7sqrt3)/26 text(.)`

Trigonometry, 2ADV T3 2013 HSC 13a

The population of a herd of wild horses is given by

`P(t) = 400 + 50 cos (pi/6 t)`

where  `t`  is time in months. 

  1. Find all times during the first 12 months when the population equals 375 horses.    (2 marks)

  2. Sketch the graph of  `P(t)`  for  `0 <= t <= 12`.    (2 marks)

Show Answers Only
  1. `t=4\ text(months and 8 months)`
  2. `text(See Worked Solutions.)`
Show Worked Solution

i.  `P(t) = 400 + 50 cos (pi/6 t)`

`text(Need to find)\ t\ text(when)\ P(t) = 375`

`375` `= 400 + 50 cos (pi/6 t)`
`50 cos (pi/6 t)` `=-25`
`cos (pi/6 t)` `= – 1/2`
   
`text(S)text(ince)\ \ cos(pi/3)=1/2, text(and cos is)`
`text(negative in)\ 2^text(nd) // 3^text(rd)\ text(quadrants:)`
`=>pi/6 t` `= (pi\ – pi/3),\ (pi + pi/3),\ (3pi\ – pi/3)`
  `= (2pi)/3,\ (4pi)/3,\ (8pi)/3,\ …`
`:.t` `= 4,\ 8,\ 16,\ …`

 
`:.\ text(In the 1st 12 months,)\ P(t) = 375\ text(when)`

`t=4\ text(months and 8 months.)`

 

♦ Mean mark 39%
ii. 2UA 2013 13a ans

Calculus, 2ADV C3 2013 HSC 8 MC

The diagram shows points  `A`,  `B`,  `C`  and  `D`  on the graph  `y = f(x)`.
 

2013 8 mc

 
 At which point is  `f^{′}(x) > 0`  and  ` f^{″}(x)= 0`? 

  1. `A`  
  2. `B`  
  3. `C`  
  4. `D`  
Show Answers Only

`B`

Show Worked Solution
♦ Mean mark 48%

`text(At)\ A,\ \ \ f^{′}(x) <0`

`text(At)\ C,\ \ \ f^{′}(x) =0`

`:.\ text(It cannot be)\ A\ text(or)\ C.`

`text(At)\ D,\ \ \ f^{″}(x) >0\ \ \ text{(concave up)}`

`text(At)\ B,\ \ \ f^{″}(x) =0\ \ \ text{(concavity changes)}`

`=> B`

Trigonometry, 2ADV T3 2013 HSC 6 MC

Which diagram shows the graph  `y=sin(2x + pi/3)`?
 

2013 6 mc1

2013 6 mc2

Show Answers Only

`D`

Show Worked Solution
♦♦ Mean mark 34%

`text(At)\ x = 0 text(,)\ \ y = sin (pi/3)  = sqrt3/2`

`=>\ text(It cannot be A or C)`
 

`text(Find)\ x\ text(when)\ y = 0,`

`sin (2x + pi/3)` `= 0`
`:.\ 2x + pi/3` `= 0\ \ \ \ \ text{(sin 0 = 0)}`
`2x` `=-pi/3`
`x` `= -pi/6`

`=>  D`

Financial Maths, STD2 F4 2011 HSC 28b

Norman and Pat each bought the same type of tractor for $60 000 at the same time. The value of their tractors depreciated over time.

The salvage value `S`, in dollars, of each tractor, is its depreciated value after `n` years.

Norman drew a graph to represent the salvage value of his tractor.
 

 2011 28b

  1. Find the gradient of the line shown in the graph.   (1 mark)

  2. What does the value of the gradient represent in this situation?   (1 mark)

  3. Write down the equation of the line shown in the graph.   (1 mark)

  4. Find all the values of `n` that are not suitable for Norman to use when calculating the salvage value of his tractor. Explain why these values are not suitable.   (2 marks)

Pat used the declining balance formula for calculating the salvage value of her tractor. The depreciation rate that she used was 20% per annum.

  1. What did Pat calculate the salvage value of her tractor to be after 14 years?   (2 marks)

  2. Using Pat’s method for depreciation, describe what happens to the salvage value of her tractor for all values of `n` greater than 15.   (1 mark)

Show Answers Only
  1. `text(Gradient) =-4000`
  2. `text(The amount the tractor depreciates each year.)`
  3. `S = 60\ 000\-4000n`
  4. `text(It is unsuitable to use)`
    `n<0\ text(because time must be positive)`
    `n>15\ text(because the tractor has no more value after 15 years and)`
    `text(therefore can’t depreciate further.)`
  5. `text(After 14 years, the tractor is worth $2638.83)`
  6. `text(As)\ n\ text(increases above 15 years,)\ S\ text(decreases but remains)>0.`
  7.  
Show Worked Solution
♦♦♦ Mean mark 14%
COMMENT: The intercepts of both axes provide points where the gradient can be quickly found.
i.    `text(Gradient)` `= text(rise)/text(run)`
    `= (- 60\ 000)/15`
    `=-4000`

 

♦ Mean mark 37%

ii.   `text(The amount the tractor depreciates each year)`

 

♦♦ Mean mark 28%
COMMENT: Using the general form `y=mx+b` is quick here because you have the gradient (from part (i)) and the `y`-intercept is obviously `60\ 000`.
iii.   `text(S)text(ince)\ \ S = V_0\-Dn`
  `:.\ text(Equation of graph:)`
  `S = 60\ 000-4000n`

 

iv.   `text(It is unsuitable to use)` 

♦♦♦ Mean mark 20%
`n<0,\ text(because time must be positive:)`
`n>15,\ text(because it has no more value after 15)`
`text(years and therefore can’t depreciate further.)`

 

v.    `text(Using)\ S = V_0 (1-r)^n\ \ text(where)\ r = text(20%,)\ n = 14`
`S` `= 60\ 000 (1\-0.2)^14`
  `= 60\ 000 (0.8)^14`
  `= 2\ 638.8279…`

 

`:.\ text(After 14 years, the tractor is worth $2638.83`

 

♦ Mean mark 37%
vi.   `text(As)\ n\ text(increases above 15 years,)\ S\ text(decreases)`
  `text(but remains > 0.)`

Algebra, STD2 A4 2011 HSC 28a

The air pressure, `P`, in a bubble varies inversely with the volume, `V`, of the bubble. 

  1. Write an equation relating `P`, `V` and `a`, where `a` is a constant.    (1 mark)

  2. It is known that `P = 3` when `V = 2`.

     

    By finding the value of the constant, `a`, find the value of `P` when `V = 4`.    (2 marks)

  3. Sketch a graph to show how `P` varies for different values of `V`.

     

    Use the horizontal axis to represent volume and the vertical axis to represent air pressure.   (2 marks)


Show Answers Only
  1. `P = a/V`
  2. `P = 1 1/2`
  3.  
     
Show Worked Solution
♦ Mean mark (i) 39%
COMMENT: Expressing the proportional relationship `P prop 1/V` as the equation `P=k/V` is a core skill here.
i. `P` `prop 1/V`
    `= a/V`

 

ii. `text(When)\ P=3,\ V = 2`
`3` `= a/2`
`a` `=6`

 

`text(Need to find)\ P\ text(when)\ V = 4`  

♦ Mean mark (ii) 47%
`P` `=6/4`
  `= 1 1/2`

  

♦♦ Mean mark (iii) 26%
COMMENT: An inverse relationship is reflected by a hyperbola on the graph.
iii.

Financial Maths, STD2 F5 2011 HSC 27d

Josephine invests $50 000 for 15 years, at an interest rate of 6% per annum, compounded annually.

Emma invests $500 at the end of each month for 15 years, at an interest rate of 6% per annum, compounded monthly. 

Financial gain is defined as the difference between the final value of an investment and the total contributions.

Who will have the better financial gain after 15 years? Using the Table below* and appropriate formulas, justify your answer with suitable calculations.   (4 marks)
  2UG-2011-27d1

Show Answers Only

`text(Josephine – see Worked Solutions)`

Show Worked Solution
♦ Mean mark 42%
COMMENT: Note that compound interest vs annuity comparisons are commonly tested.

`text(Josephine)`

`text(Investment)` `= 50\ 000 (1 + 0.06)^15`
  `= 50\ 000 (1.06)^15`
  `= $119\ 827.91`

 

`text(Financial gain)` `= 119\ 827.91-50\ 000`
  `= $69\ 827.91`

 

`text(Emma)`

`text{Monthly interest rate} = text(6%)-:12=text(0.5%)`

`text{# Monthly Payments}=12 xx 15=180`

`=>\ text{Annuity Factor = 290.8187    (from Table)}`

 

`text(Investment)` `= 500 xx 290.8187`
  `= $145\ 409.35`

 

`text(Financial gain)` `= 145\ 409.35\-text(total contributions)`
  `= 145\ 409.35\-(500 xx 12 xx 15)`
  `= 145\ 409.35\-90\ 000`
  `= $55\ 409.35`

 

`:.\ text(Josephine will have the better financial gain.)`

Statistics, STD2 S5 2011 HSC 27c

Two brands of light bulbs are being compared. For each brand, the life of the light bulbs is normally distributed.

2011 27c

  1. One of the Brand B light bulbs has a life of 400 hours. 

     

    What is the  `z`-score of the life of this light bulb?  (1 mark)

  2. A light bulb is considered defective if it lasts less than 400 hours. The following claim is made:

     

    ‘Brand A light bulbs are more likely to be defective than Brand B light bulbs.’

     

    Is this claim correct? Justify your answer, with reference to  `z`-scores or standard deviations or the normal distribution.   (2 marks)

Show Answers Only
  1. `-2`
  2. `text(The claim is incorrect.)`
Show Worked Solution

i.    `z text{-score of Brand B bulb (400 hrs)}`

`= (x-mu)/sigma`
`= (400\-500)/50`
`= –2`

 

ii.   `z text{-score of Brand A bulb (400 hours)}`

♦ Mean mark 42%
MARKER’S COMMENT: A number of students found drawing normal curves in their solution advantageous.
`=(400-450)/25`
`=–2`

 
`text(S)text(ince the)\ z text(-score for both brands is –2,)`

`text(they are equally likely to be defective.)`

`:.\ text(The claim is incorrect.)`

Measurement, 2UG 2011 HSC 27b

Pontianak has a longitude of 109°E, and Jarvis Island has a longitude of 160°W`.

Both places lie on the Equator. 

  1. Find the shortest distance between these two places, to the nearest kilometre. You may assume that the radius of the Earth is 6400 km.   (2 marks)
  2.  
  3. The position of Rabaul is 4° to the south and 48° to the west of Jarvis Island. What is the latitude and longitude of Rabaul?    (2 marks)
  4.  
Show Answers Only
  1. `10\ 165\ text(km)\ \ \ text{(nearest km)}`
  2. `152^@ text(E)`
Show Worked Solution
♦♦ Mean mark 29%
(i) `text(Longitude difference)` `= 109 + 160`
    `= 269^@`
`=> text(Shortest distance)\ text{(by degree)}` `= 360\-269`
  `= 91^@`
`:.\ text(Shortest distance)` `= 91/360 xx 2 pi r`
  `= 91/360 xx 2 xx pi xx 6400`
  `= 10\ 164.79…`
  `=10\ 165\ text(km)\ text{(nearest km)}`

 

♦♦ Mean mark 33%
(ii) `text(Latitude)`
  `4^@\ text(South of Jarvis Island)`
  `text(S)text(ince Jarvis Island is on equator)`
  `=> text(Latitude is)\ 4^@ text(S)`
  `text(Longitude)`
  `text(Jarvis Island is)\ 160^@ text(W)`
  `text(Rubail is)\ 48^@\ text(West of Jarvis Island, or 208° West)`
  `text(which is)\ 28^@\ text{past meridian (180°)}`
`=>\ text(Longitude)` `= (180\ -28)^@ text(E)`
  `= 152^@ text(E)`

`:.text(Position is)\ (4^@text{S}, 152^@text{E})`

Statistics, STD2 S1 2011 HSC 27a

A company sells handbags in Paris, New York and Florence. 

Use the data in the table to complete the area chart below.   (2 marks)

 2011 27a 

2UG 2011 27a

Show Answers Only

 2011 27a

Show Worked Solution
♦♦ Mean mark 27%
COMMENT: Most common error was to not realise Area charts show cumulative data.

2011 27a

Financial Maths, 2UG 2011 HSC 26c

Furniture priced at  $20 000  is purchased. A deposit of 15% is paid. 

The balance is borrowed using a flat-rate loan at 19% per annum interest, to be repaid in equal monthly instalments over five years.

What will be the amount of each monthly instalment? Justify your answer with suitable calculations.   (4 marks) 

Show Answers Only

 `$552.50`

Show Worked Solution

`text(Purchase price) = $20\ 000`

♦ Mean mark 44%
`text(Deposit)` `=\ text(15%)\ xx 20\ 000`
  `= $3000`
`:.\ text(Loan)` `= 20\ 000\-3000`
  `= $17\ 000`
`text(Using)\ I` `= Prn`
`I` `= 17\ 000 xx\ text(19%)\ xx 5`
  `= 16\ 150`
`=>\ text(Total amount to repay)` `= 17\ 000 + 16\ 150`
  `= $33\ 150`

 

`:.\ text(Monthly instalment)` `= (33\ 150)/(12 xx 5)`
  `= (33\ 150)/60`
  `= $552.50`

Probability, 2UG 2011 HSC 26a

The two spinners shown are used in a game.

2UG 2011 26a1

Each arrow is spun once. The score is the total of the two numbers shown by the arrows.
A table is drawn up to show all scores that can be obtained in this game.

2UG 2011 26a2

  1. What is the value of `X` in the table?   (1 mark)
  2. What is the probability of obtaining a score less than 4?   (1 mark)
  3. On Spinner `B`, a 2 is obtained. What is the probability of obtaining a score of 3?   (1 mark)
  4. Elise plays a game using the spinners with the following financial outcomes.  

⇒ Win `$12` for a score of `4`

⇒ Win nothing for a score of less than `4`

⇒ Lose `$3` for a score of more than `4`

It costs `$5` to play this game. Will Elise expect a gain or a loss and how much will it be?

Justify your answer with suitable calculations.   (3 marks)

Show Answers Only
  1. `5`
  2. `1/2`
  3.  
  4. `2/3`
  5.  
  6. `text(Loss of)\ $1.50`
  7.  
Show Worked Solution

(i)   `X=3+2=5`

 

(ii)   `P(text{score}<4)=6/12=1/2`

 

(iii)   `P(3)=2/3`

 

(iv)   `P(4)=4/12=1/3`

♦ Mean mark 34%
MARKER’S COMMENT: Better responses remembered to deduct the $5 cost to play and recognised the negative result as a loss.
`P(text{score}<4)` `=6/12=1/2`
`P(text{score}>4)` `=2/12=1/6`

 

`text(Financial Expectation)`

`=(1/3xx12)+(1/2xx0)-(1/6xx3)-5`
`=4-0.5-5`
`=-1.50`

 

`:.\ text(Elise should expect a loss of $1.50) `

Financial Maths, STD2 F4 2010 HSC 25b

William wants to buy a car. He takes out a loan for  $28 000  at 7% per annum interest for four years. 

Monthly repayments for loans at different interest rates are shown in the spreadsheet.

2010 25b

How much interest does William pay over the term of this loan?   (2 marks)

Show Answers Only

`$4183.52`

Show Worked Solution
♦ Mean mark 42%
MARKER’S COMMENT: An incorrect table value used correctly in the following calculations received half-marks here. Show your working!

`text(Loan) = $28\ 000,\ \ \ \ r =\ text(7% p.a.)`

`text(Monthly repayment = $670.49`

`text(# Repayments) = 4 xx 12 = 48`

`text(Total repaid)` `= 48 xx 670.49`
  `= $32\ 183.52`

 

`:.\ text(Interest paid)` `=32\ 183.52\-28\ 000`
  `=$4183.52`

Statistics, STD2 S1 2011 HSC 25d

Data was collected from 30 students on the number of text messages they had sent in the previous 24 hours. The set of data collected is displayed.
 

2UG 2011 25d

  1. What is the outlier for this set of data? (1 mark)

  2. What is the interquartile range of the data collected from the female students? (1 mark)

Show Answers Only
  1. `71`
  2. `9`
Show Worked Solution

a.   `text(Outlier is 71)`

♦♦ Mean mark 34%
COMMENT: Ensure you can quickly and accurately find quartile values using stem and leaf graphs!

b.   `text{Lower quartile = 9   (4th female data point)}`

`text{Upper quartile = 20   (11th female data point)}`

`:.\ text{Interquartile range (female)}=20-11=9`

Statistics, STD2 S1 2011 HSC 25a

A study on the mobile phone usage of NSW high school students is to be conducted.

Data is to be gathered using a questionnaire.

The questionnaire begins with the three questions shown.

2UG 2011 25a

  1. Classify the type of data that will be collected in Q2 of the questionnaire.  (1 mark)

  2. Write a suitable question for this questionnaire that would provide discrete ordinal data.   (1 mark)

  3. An initial study is to be conducted using a stratified sample.

     

    Describe a method that could be used to obtain a representative stratified sample.  (1 mark)

  4. Who should be surveyed if it is decided to use a census for the study?  (1 mark)

Show Answers Only
  1. `text(Categorical)`
  2. `text(See Worked Solutions)`
  3. `text(See Worked Solutions)`
  4. `text(A census would involve all high school students in NSW.)`
Show Worked Solution

a.  `text(Categorical)`

 

b.  `text(How many outgoing calls do you make per day?)`

`text{(Ensure it can be answered with a numerical score.)}`

 

c.  `text(The method could be to work out how many)`

♦♦♦ Mean mark 7%. Toughest mark to get in the 2011 exam!
COMMENT: Know and be able to describe random, systematic and stratified sampling!

`text{students are in each year and ask 10% of the}`

`text{students in each year. (Note the sample of}`

`text{students in each year must be  proportional to}`

`text{their percentage in the population).}`

 

♦♦♦ Mean mark 18%.
MARKER’S COMMENT: A specific population needed (i.e. high school students).

d.  `text(A census would involve all high school)`

`text(students in NSW.)`

Financial Maths, STD2 F4 2011 HSC 23c

An amount of $5000 is invested at 10% per annum, compounded six-monthly.

2UG 2011 23c

Use the table to find the value of this investment at the end of three years.   (2 marks)

Show Answers Only

`$6700`

Show Worked Solution
♦♦ Mean mark 28%
MARKER’S COMMENT: Remember that the number of periods is the number of “compounding periods” and when asked to use the table, use the table!

`text(Interest rate)= text(10% pa)= text(5% per 6 months)`

`text(Period)= 6\ \ \ \ text{(6 x 6 months in 3 years)}`

`=> text(Table value)=1.340`

`:.\ text(Value of investment)` `=5000xx1.34`
  `=$6700`