Band 6 – Page 27

GEOMETRY, FUR1 2014 VCAA 9 MC

The middle section of a cone is shaded, as shown in the diagram below.

The surface area of the unshaded top section of the cone is 180 cm².

The surface area of the middle section of the cone, in square centimetres, is

A. `80`

B. `120`

C. `300`

D. `320`

E. `500`

Show Answers Only

`D`

Show Worked Solution

`text(Ratio of lengths of)`

♦♦ Mean mark 33%.

`text(Upper Cone : Top Section, is)`

`15:9 = 5:3`

`∴\ text(Ratio of Areas)`	`=5^2:3^2`
	`=25:9`

`text(Let Area of Upper Cone)\ = x`

`x/180`	`= 25/9`
`x`	`= 180 xx 25/9`
	`= 500\ \ text(cm²)`

`∴\ text(Area of shaded middle section)`

`= 500 – 180`

`= 320\ \ text(cm²)`

`=> D`

GEOMETRY, FUR1 2012 VCAA 9 MC

The solid `OPQR`, as shown below, is one-eighth of a sphere of radius 15 cm.

The point `O` is the centre of the sphere and the points `P, Q` and `R` are on the surface of the sphere.

`∠POQ = ∠QOR = ∠ROP = 90°`

The total surface area of the solid `OPQR`, in cm², is closest to

A. 619

B. 648

C. 706

D. 884

E. 1767

Show Answers Only

`D`

Show Worked Solution

`text (Surface Area of sphere) = 4pir^2`

♦♦ Mean mark 31%.

`:.\ text (S.A. of)\ \ PQR\ \ text{(on surface)}`

`=1/8 xx 4 pi r^2`

`= 1/8 xx 4 xx pi xx 15^2`

`= 353.43\ text(cm²)`

`text (Surface Area of sector)\ POQ`

`= 1/4pir^2`

`= 1/4pi × 15^2`

`= 176.71\ text(cm²)`

`:. text (Surface Area of solid)\ OPQR`

`= 353.43 + 3 × 176.71`

`= 883.56\ text(cm²)`

`rArr D`

Algebra, STD2 A2 2007 HSC 18 MC

Chris started to make this pattern of shapes using matchsticks.

If the pattern of shapes is continued, which shape would use exactly 486 matchsticks?

Shape 96
Shape 97
Shape 121
Shape 122

Show Answers Only

`C`

Show Worked Solution

`text(Equation rule:)`

`M = 4S + 2`

`text(Find)\ \ x\ \ text(when)\ \ M = 486:`

`486`	`= 4S+2`
`4S`	`= 484`
`S`	`=121`

`:.\ text(The 121st shape uses 486 matchsticks.)`

`=> C`

CORE, FUR1 2014 VCAA 12 MC

The seasonal index for heaters in winter is 1.25.

To correct for seasonality, the actual heater sales in winter should be

A. reduced by 20%.

B. increased by 20%.

C. reduced by 25%.

D. increased by 25%.

E. reduced by 75%.

Show Answers Only

`A`

Show Worked Solution

`text(Deseasonalised Sales)`

♦♦ Mean mark 26%.
MARKER’S COMMENT: A majority of students appeared to answer this question by inspection only which was not possible. Don’t be tricked!

`=\ text(Actual Sales)/text(Seasonal index)`

`=\ text(Actual Sales)/1.25`

`=80 text(%) xx text(Actual Sales)`

`∴\ text(Winter Sales should be reduced by 20%)`

`=> A`

CORE, FUR1 2011 VCAA 12 MC

The seasonal index for headache tablet sales in summer is 0.80.

To correct for seasonality, the headache tablet sales figures for summer should be

A. reduced by 80%

B. reduced by 25%

C. reduced by 20%

D. increased by 20%

E. increased by 25%

Show Answers Only

`E`

Show Worked Solution

`text(Deseasonalised Sales)`

♦♦♦ Mean mark 10%!
MARKERS’ COMMENT: The key to solving this problem is to rearrange the “Seasonal Index” formula in the formula sheet.

`= \ \ text(Actual Sales) / text(Seasonal index)`

`= \ \ text(Actual Sales) / 0.8`

`= \ \ 1.25 xx text(Actual Sales)`

`:.\ text(Deseasonalised Sales need Actual Sales to)`

`text(be increased by 25%)`

`=> E`

PATTERNS, FUR1 2010 VCAA 8 MC

The `n`th term in a geometric sequence is `t_n`.

The common ratio is greater than one.

A graph that could be used to display the terms of this sequence is

Show Answers Only

`A`

Show Worked Solution

`text(GP where)\ \ r>1`

♦♦♦ Mean mark 16%!

`text(General term is)\ \ \ t_n=ar^(n – 1)`

`text(Consider)\ \a>0,`

`text(the graph of)\ \t_n\ \text(will be positive and)`

`text(increase exponentially, but no graph shows this.)`

`text(Consider)\ \a<0,`

`text(the graph will be negative and increase)`

`text(exponentially in a negative direction.)`

`=> A`

CORE, FUR1 2014 VCAA 8 MC

A single back-to-back stem plot would be an appropriate graphical tool to investigate the association between a car’s speed, in kilometres per hour, and the

A. driver’s age, in years.

B. car’s colour (white, red, grey, other).

C. car’s fuel consumption, in kilometres per litre.

D. average distance travelled, in kilometres.

E. driver’s sex (female, male).

Show Answers Only

`E`

Show Worked Solution

`text(In a back-to-back stem plot, the numerical speed)`

♦♦ Mean mark 28%.

`text(data has to be plotted against categorical data)`

`text(with two options.)`

`∴\ text{Driver’s sex (M or F)}`

`=> E`

♦♦ Mean mark 29%.
MARKER’S NOTE: Postcodes here are categorical variables. Ask yourself “Does it make sense to calculate the mean of this variable?” If the answer is “No”, the variable is categorical.

`text(Categorical variables are sex, type)`

`text(of car, and post code.)`

`=>D`

`text(Part 3)`

`text(1 female driver has 3 children.)`

`=>B`

Measurement, 2UG 2008 HSC 28b

A tunnel is excavated with a cross-section as shown.

Find an expression for the area of the cross-section using TWO applications of Simpson’s rule. (2 marks)
The area of the cross-section must be 600 m². The tunnel is 80 m wide.
If the value of `a` increases by 2 metres, by how much will `b` change? (2 marks)

Show Answers Only

`(2h)/3 (4a + b)`
`b\ text(decreases by 8 m.)`

Show Worked Solution

(i)	`A`	`~~ h/3 [y_0 + 4y_1 + y_2] + h/3 [y_0 + 4y_1 + y_2]`
		`~~ h/3 [0 + 4a + b] + h/3 [b + 4a + 0]`
		`~~ (2h)/3 (4a + b)`

(ii)	`text(Given)\ \ A = 600\ text(m²)`
	`text(If 80 m wide) \ => h = 20`

`A`	`= (2h)/3 (4a + b)`
`600`	`= ((2 xx 20))/3 (4a + b)`
`4a + b`	`= (600 xx 3)/40`
`b`	`= 45 – 4a`

`:.\ text(If)\ a\ text(increases by 2 m,)\ b\ text(will)`

`text(decrease by 8 m.)`

Statistics, STD2 S5 2008 HSC 28a

The following graph indicates `z`-scores of ‘height-for-age’ for girls aged 5 – 19 years.

What is the `z`-score for a six year old girl of height 120 cm? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Rachel is 10 ½ years of age.

(1) If 2.5% of girls of the same age are taller than Rachel, how tall is she? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

(2) Rachel does not grow any taller. At age 15 ½, what percentage of girls of the same age will be taller than Rachel? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
What is the average height of an 18 year old girl? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

For adults (18 years and older), the Body Mass Index is given by

`B = m/h^2` where `m = text(mass)` in kilograms and `h = text(height)` in metres.

The medically accepted healthy range for `B` is `21 <= B <= 25`.

What is the minimum weight for an 18 year old girl of average height to be considered healthy? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The average height, `C`, in centimetres, of a girl between the ages of 6 years and 11 years can be represented by a line with equation

`C = 6A + 79` where `A` is the age in years.

(1) For this line, the gradient is 6. What does this indicate about the heights of girls aged 6 to 11? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

(2) Give ONE reason why this equation is not suitable for predicting heights of girls older than 12. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`1`
(1) `155\ text(cm)`

(2) `text(84%)`
`163\ text(cm)`
`55.8\ text(kg)`
(1) `text(It indicates that 6-11 year old girls)`

`text(grow, on average, 6cm per year)`

(2) `text(Girls eventually stop growing, and the)`

`text(equation doesn’t factor this in.)`

Show Worked Solution

i.	`z text(-score) = 1`

ii.	(1)	`text(If 2 ½ % are taller than Rachel)`
		`=> z text(-score of +2)`
		`:.\ text(She is 155 cm)`

	(2)	`text(At age)\ 15\ ½,\ 155\ text(cm has a)\ z text(-score of –1)`
		`text(68% between)\ z = 1\ text(and)\ –1`
		`=> text(34% between)\ z = 0\ text(and)\ –1`
		`text(50% have)\ z >= 0`

		`:.\ text(% Above)\ z text(-score of –1)`
		`= 50 + 34`
		`= 8text(4%)`

`:.\ text(84% of girls would be taller than Rachel at age)\ 15 ½.`

iii.	`text(Average height of 18 year old has)\ z text(-score = 0)`
	`:.\ text(Average height) = 163\ text(cm)`

iv.	`B = m/h^2`
	`h = 163\ text(cm) = 1.63\ text(m)`

`text(Given)\ \ 21 <= B <= 25,\ text(minimum healthy)`

`text(weight occurs when)\ B = 21`

`=> 21`	`= m/1.63^2`
`m`	`= 21 xx 1.63^2`
	`= 55.794…`
	`= 55.8\ text(kg)\ text{(1 d.p.)}`

v.	(1)	`text(It indicates that 6-11 year old girls, on average, grow)`
		`text(6 cm per year.)`
	(2)	`text(Girls eventually stop growing, and the equation doesn’t)`
		`text(factor this in.)`

Measurement, STD2 M6 2008 HSC 25c

Pieces of cheese are cut from cylindrical blocks with dimensions as shown.

Twelve pieces are packed in a rectangular box. There are three rows with four pieces of cheese in each row. The curved surface is face down with the pieces touching as shown.

What are the dimensions of the rectangular box? (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

To save packing space, the curved section is removed.
What is the volume of the remaining triangular prism of cheese? Answer to the nearest cubic centimetre. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. `41\ text(cm) xx 21\ text(cm) xx 15\ text(cm)`

b. `506\ text(cm)^3`

Show Worked Solution

a. `text(Box height) = 15\ text(cm)`

♦ Mean mark (a) 45%.

`text{(radius of the arc)}`

`text(Box width)`	`= 3 xx 7= 21\ text(cm)`
`text(Box length)`	`= 4x`

`text(Using cosine rule:)`

`c^2`	`= a^2 + b^2-2ab\ cos C`
`x^2`	`= 15^2 + 15^2-2 xx 15 xx 15 xx cos 40^@`
	`= 450-344.7199…= 105.2800…`
`x`	`= 10.2606…`

`text{Box length} = 4 xx 10.2606…= 41.04…`

`:.\ text(Dimensions are)\ \ 41\ text(cm) xx 21\ text(cm) xx 15\ text(cm)`

b. `text(Volume) = Ah`

♦♦♦ Mean mark (b) 22%.

`h = 7\ text(cm)`

`A= 1/2 ab\ sin C= 1/2 xx 15 xx 15 xx sin 40^@= 72.3136…`

`:. V`	`= 72.3136… xx 7= 506.195…`
	`= 506\ text(cm)^3\ \ text{(nearest whole)}`

Probability, STD2 S2 2008 HSC 24b

Three-digit numbers are formed from five cards labelled 1, 2, 3, 4 and 5.

How many different three-digit numbers can be formed? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
If one of these numbers is selected at random, what is the probability that it is odd? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
How many of these three-digit numbers are even? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
What is the probability of randomly selecting a three-digit number less than 500 with its digits arranged in descending order? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`60`
`3/5`
`24`
`1/15`

Show Worked Solution

i. `text(# Different numbers)`

♦ Mean mark 45%.

`= 5 xx 4 xx 3`

`= 60`

ii. `text(The last digit must be one of the)`

`text(5 numbers, of which 3 are odd)`

`:.\ text{P(odd)} = 3/5`

iii. `text{P(even)} = 1- text{P(odd)} = 2/5`

♦ Mean mark 48%.

`:.\ text(Number of even numbers)`

`= 2/5 xx 60`

`= 24`

iv. `text(The numbers that satisfy the criteria:)`

♦♦♦ Mean mark 10%.

`432, 431, 421, 321`

`:.\ text{P(selection)} = 4/60 = 1/15`

Algebra, 2UG 2008 HSC 19 MC

The height of a particular termite mound is directly proportional to the square root of the number of termites.

The height of this mound is 35 cm when the number of termites is 2000.

What is the height of this mound, in centimetres, when there are 10 000 termites?

(A) `16`

(B) `78`

(C) `175`

(D) `875`

Show Answers Only

`B`

Show Worked Solution

`text(Height)\ (h)`	`prop sqrt( text(Termites)\ (T)`
`=>h`	`= k sqrt T`

`text(Given)\ \ h = 35\ \ text(when)\ \ T = 2000`

`35`	`= k xx sqrt 2000`
`k`	`= 35/ sqrt 2000`
	`= 0.7826…`

`text(Find)\ \ h\ \ text(when)\ \ T = 10\ 000`

`h`	`= 0.7826… xx sqrt (10\ 000)`
	`= 78.26…\ text(cm)`

`=> B`

Calculus, 2ADV C4 2008 HSC 9c

A beam is supported at `(-b, 0)` and `(b, 0)` as shown in the diagram.

It is known that the shape formed by the beam has equation `y = f(x)`, where `f(x)` satisfies

	`f^{″}(x)`	`= k (b^2-x^2),\ \ \ \ \ `(`k` is a positive constant)
and	`f^{′}(-b)`	`= -f'(b)`.

Show that `f^{′}(x) = k (b^2x-(x^3)/3)`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
How far is the beam below the `x`-axis at `x = 0`? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ text{(See Worked Solutions)}`
`(5kb^4)/12\ text(units)`

Show Worked Solution

i.	`text(Show)\ \ f^{′}(x) = k (b^2x-x^3/3)`

`f^{″}(x)`	`= k (b^2 – x^2)`
`f^{′}(x)`	`= int k (b^2-x^2)\ dx`
	`= k int b^2-x^2\ dx`
	`= k (b^2x-x^3/3) + c`

`text(S)text(ince S.P. exists at)\ \ x = 0`

`=> f^{′}(x)`	`= 0\ \ text(when)\ \ x = 0`
`0`	`= k (b^2 * 0-0) + c`
`c`	`= 0`

`:.\ f^{′}(x) = k (b^2x-x^3/3)\ \ \ text(… as required)`

ii.	`f(x)`	`= int f^{′}(x)\ dx`
		`= k int b^2x-x^3/3\ dx`
		`= k ((b^2x^2)/2-x^4/12) + c`

`text(We know)\ \ f(x) = 0\ \ text(when)\ \ x = b`

`=> 0`	`= k ( (b^2*b^2)/2-b^4/12) + c`
`c`	`= -k ( (6b^4)/12-b^4/12)`
	`= -k ( (5b^4)/12 )`
	`= -(5kb^4)/12`

`:.\ text(When)\ \ x = 0, text(the beam is)\ \ (5kb^4)/12\ \ text(units)`

`text(below the)\ x text(-axis.)`

Combinatorics, EXT1 A1 2014 HSC 14b

Two players `A` and `B` play a game that consists of taking turns until a winner is determined. Each turn consists of spinning the arrow on a spinner once. The spinner has three sectors `P`, `Q` and `R`. The probabilities that the arrow stops in sectors `P`, `Q` and `R` are `p`, `q` and `r` respectively.

The rules of the game are as follows:

• If the arrow stops in sector `P`, then the player having the turn wins.

• If the arrow stops in sector `Q`, then the player having the turn loses and the other player wins.

• If the arrow stops in sector `R`, then the other player takes a turn.

Player `A` takes the first turn.

Show that the probability of player `A` winning on the first or the second turn of the game is `(1-r) (p + r)`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Show that the probability that player `A` eventually wins the game is `(p + r)/(1 + r)`. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

i. `text(Show)\ P text{(}A\ text(wins)\ T_1\ text(or)\ T_2 text{)} = (1-r)(p + r)`

`P (A\ text(wins on)\ T_1) = p`

`P (A\ text(wins on)\ T_2)= P text{(} A\ text(lands on)\ R,\ B\ text(lands on)\ Q text{)}= rq`

`:.\ P text{(}A\ text(wins)\ T_1\ text(or)\ T_2 text{)}= p + rq`

♦♦ Mean mark 25%.
HINT: Expand out the solution `(1-r)(p+r)=p+r-rp-r^2` to get a better idea of what you need to prove.

`text(S)text(ince)\ q = 1-(p + r),`

`P text{(} A\ text(wins)\ T_1\ text(or)\ T_2 text{)}`

`= p + r [1-(p + r)]`

`= p + r-rp-r^2`

`= (1-r)(p + r)\ \ \ text(… as required.)`

ii. `text(Show)\ P text{(}A\ text(wins eventually) text{)} = (p + r)/(1 + r)`

`P text{(} A\ text(wins)\ T_1\ text(or)\ T_2 text{)} = (1-r)(p + r)`

`P text{(} text(No result)\ T_1\ text(or)\ T_2 text{)} = r * r = r^2`

`:.\ P text{(} A\ text(wins eventually) text{)}`

`= underbrace{(1-r)(p + r) + r^2 (1-r)(p + r) + r^2*r^2 (1-r)(p + r) + …}_{text(GP where)\ \ a = (1-r)(p + r),\ \ r = r^2}`

`text(S)text(ince)\ \ 0 < r < 1 \ \ =>\ \ 0 < r^2 < 1`

♦♦♦ Mean mark 11%.
HINT: The use of ‘eventually’ in the question should flag the possibility of solving by using `S_oo` in a GP.

`:.\ S_oo`	`= a/(1-r)`
	`= ((1-r)(p + r))/(1-r^2)`
	`= ((1-r)(p + r))/((1-r)(1 + r))`
	`= (p + r)/(1 + r)\ \ \ text(… as required)`

Plane Geometry, EXT1 2009 HSC 7c

Consider the billboard below. There is a unique circle that passes through the top and bottom of the billboard (points `Q` and `R` respectively) and is tangent to the street at `T`.

Let `phi` be the angle subtended by the billboard at `S`, the point where `PQ` intersects the circle.

Copy the diagram into your writing booklet.

Show that `theta < phi` when `P` and `T` are different points, and hence show that `theta` is a maximum when `P` and `T` are the same point. (3 marks)
Using circle properties, find the distance of `T` from the building. (1 mark)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`sqrt (h (a + h))`

Show Worked Solution

(i)

♦♦ Both parts proved extremely challenging for students.
MARKER’S COMMENT: Very few students recognised that `phi` is the external angle of `Delta PSR`.

`text(Show)\ \ theta < phi\ \ text(when)\ \ P != T`

`text(Let)\ \ /_PRS = alpha`

`phi`

`= theta + alpha\ \ text{(exterior angle of}\ Delta PSR text{)}`

`:.\ theta < phi,\ alpha != 0`

`text(When)\ P\ text(and)\ T\ text(are the same point,)`

`S,\ P, and T\ \ text(are the same point.)`

`text(i.e. when)\ \ /_PRS = alpha = 0`

`:. theta\ text(will be a maximum)\ (= phi)`

`text(when)\ P = T.`

(ii) `text(Square of tangent)\ =\ text(product of)`

`text(intercepts from an external point.)`

`text(i.e.)\ \ OT^2`	`= OR xx QR`
	`= h (a + h)`
`:.\ OT`	`= sqrt (h (a + h))`

Geometry and Calculus, EXT1 2009 HSC 7b

A billboard of height `a` metres is mounted on the side of a building, with its bottom edge `h` metres above street level. The billboard subtends an angle `theta` at the point `P`, `x` metres from the building.

Use the identity `tan (A - B) = (tan A - tan B)/(1 + tanA tanB)` to show that
1. `theta = tan^(-1) [(ax)/(x^2 + h(a + h))]`. (2 marks)
The maximum value of `theta` occurs when `(d theta)/(dx) = 0` and `x` is positive.
Find the value of `x` for which `theta` is a maximum. (3 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`sqrt(h (a + h)),\ x > 0`

Show Worked Solution

(i) `text(Consider angles)\ \ A and B\ \ text(on the graph:)`

♦♦ Mean mark data not available for parts of questions although Q7 as a whole scored <30%.
MARKER’S COMMENT: Answers that included a diagram and clearly labelled angles were generally successful.

`text(Show)\ \ theta = tan^(-1) [(ax)/(x^2 + h(a + h))]`

`tan A`	`= (a + h)/x`
`tan B`	`= h/x`

`tan (A – B)`	`= ((a + h)/x – h/x)/(1 + ((a + h)/x)(h/x)) xx (x^2)/(x^2)`
	`= (x(a + h) – xh)/(x^2 + h(a + h))`
	`= (ax)/(x^2 + h(a + h)`

`text(S)text(ince)\ \ theta`	`= A – B`
`theta`	`= tan^(-1) [(ax)/(x^2 + h(a + h))]\ \ \ text(… as required.)`

(ii) `text(Max when)\ \ (d theta)/(dx) = 0\ \ text(and)\ \ x > 0`

`text(Let)\ \ u`	`= (ax)/(x^2 + h(a + h))`
`theta`	`= tan^(-1) u`
`(du)/(dx)`	`=(a[x^2 + h (a + h)] – ax * 2x)/([x^2 + h (a + h)]^2)`
	`=(-ax^2 + ah (a + h))/([x^2 + h (a + h)]^2)`

`(d theta)/(dx)`	`=(d theta)/(du) * (du)/(dx)`
	`= 1/(1 + u^2) * (du)/(dx)`
	`= 1/(1 + [(ax)/(x^2 + h(a + h))]^2) xx (-ax^2 + ah (a + h))/[x^2 + h (a + h)]^2`
	`=(-ax^2 + ah(a + h))/([x^2 + h (a + h)]^2 + a^2 x^2)`

`text(Note that)\ \ (d theta)/(dx) = 0\ \ text(when)`

`-ax^2 + ah (a + h)`	`= 0`
`ax^2`	`= ah (a + h)`
`x^2`	`= h (a + h)`
`x`	`= sqrt (h (a + h))\ \ \ \ (x > 0)`

Binomial, EXT1 2009 HSC 6b

Sum the geometric series
1. `(1 + x)^r + (1 + x)^(r + 1) + ... + (1 + x)^n`
and hence show that
1. `((r),(r)) + ((r + 1),(r)) + ... + ((n),(r)) = ((n + 1),(r + 1))`. (3 marks)
Consider a square grid with `n` rows and `n` columns of equally spaced points.
The diagram illustrates such a grid. Several intervals of gradient `1`, whose endpoints are a pair of points in the grid, are shown.
(1) Explain why the number of such intervals on the line `y = x` is equal to `((n),(2))`. (1 mark)
(2) Explain why the total number, `S_n`, of such intervals in the grid is given by
1. `S_n = ((2),(2)) + ((3),(2)) + ... + ((n - 1),(2)) + ((n),(2)) + ((n - 1),(2)) +`
  1. `... + ((3),(2)) + ((2),(2))`. (1 mark)
Using the result in part (i), show that
1. `S_n = (n(n - 1)(2n - 1))/6`. (3 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
(1) `text(Proof)\ \ text{(See Worked Solutions)}`
(2) `text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i) `(1 + x)^r + (1 + x)^(r + 1) + … + (1 + x)^n`

♦♦ Exact data unavailable although mean marks for all Q6 was < 25%.
MARKER’S COMMENT: A common mistake was to assume the number of terms in the series was `n`.

`=> text(GP where)\ \ a`	`= (1 + x)^r`
`r`	`= (1 + x)`
`#\ text(Terms)`	`= n – r + 1`

`text(Sum)`	`= (a (r^n – 1))/(r – 1)`
	`= ((1 + x)^r [(1 + x)^(n\ – r + 1) – 1])/((1 + x) – 1)`
	`= ((1 + x)^(n\ – r + 1 + r) – (1 + x)^r)/x`
	`= ((1 + x)^(n + 1) – (1 + x)^r)/x`

`text(Show)`

`((r),(r)) + ((r + 1),(r)) + … + ((n),(r)) = ((n + 1),(r + 1))`

`text(Consider series)\ (1 + x)^r + (1 + x)^(r + 1) + … + (1 + x)^n`

`text(Co-efficient of)\ \ x^r = ((r),(r)) + ((r + 1),(r)) + … + ((n),(r))`

`text(Consider sum of series)\ \ \ ((1 + x)^(n + 1)\ – (1 + x)^r)/x`

`text(Co-efficient of)\ \ x^r`	`=\ text(co-efficient of)\ \ x^(r + 1)\ \ text(in numerator)`
	`= ((n +1),(r + 1))`

`:.\ text(S)text(ince co-efficients are equal)`

`((r),(r)) + ((r + 1),(r)) + … + ((n),(r)) = ((n + 1),(r + 1))`

`text(… as required.)`

(ii)(1)	`text(All intervals start and finish at different points.)`
	`text(Any)\ n xx x\ text(grid has)\ n\ text(points on the)\ y = x\ text(diagonal.)`
	`:.\ text(Possible intervals) = ((n),(2))`

(2)	`text(The longest diagonal of)\ n xx n\ text(grid is)`
	`text(the)\ y = x\ text(diagonal with)\ ((n),(2))\ text(intervals.)`
	`text(Each side of this, there is one less point)`
	`text(on the diagonals, with)\ ((n – 1),(2))\ text(intervals.)`
	`text(This continues until there are only 2 points)`
	`text(on the diagonal with)\ ((2),(2))\ text(intervals.)`

`:.\ S_n`	`= ((2),(2)) + ((3),(2)) + … + ((n – 1),(2)) + ((n),(2))`
	`+ ((n – 1),(2)) + … + ((2),(2))`
	`text(… as required.)`

♦♦♦ Exact data unavailable although very few completed part (iii) correctly.
MARKER’S COMMENT: Note that even if part (i) wasn’t solved, the proof as stated in the question can be used to solve part (iii).

(iii)

`text(Show)\ \ S_n = (n(n – 1)(2n – 1))/6`

`S_n`	`= { ((2),(2)) + ((3),(2)) + … + ((n – 1),(2)) + ((n),(2))}`
	`+ {((n – 1),(2)) + … + ((2),(2))}`
	`= ((n + 1),(3)) + ((n),(3))\ \ \ text{(from part (i))}`
	`= ((n + 1)n(n – 1))/(3 * 2 * 1) + (n* (n – 1)(n – 2))/(3 2 * 1)`
	`= 1/6 n (n – 1) (n + 1 + n – 2)`
	`= (n(n – 1)(2n – 1))/6\ \ \ text(… as required.)`

Calculus, EXT1 C1 2009 HSC 5b

The cross-section of a 10 metre long tank is an isosceles triangle, as shown in the diagram. The top of the tank is horizontal.

When the tank is full, the depth of water is 3 m. The depth of water at time `t` days is `h` metres.

Find the volume, `V`, of water in the tank when the depth of water is `h` metres. (1 mark)

--- 6 WORK AREA LINES (style=lined) ---
Show that the area, `A`, of the top surface of the water is given by `A = 20 sqrt3 h`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
The rate of evaporation of the water is given by `(dV)/(dt) = - kA`, where `k` is a positive constant.

Find the rate at which the depth of water is changing at time `t`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
It takes 100 days for the depth to fall from 3 m to 2 m. Find the time taken for the depth to fall from 2 m to 1 m. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`10 sqrt 3 h^2\ \ text(m³)`
`text(Proof)\ \ text{(See Worked Solutions)}`
`-k\ \ \ text(metres per day)`
`100\ text(days)`

Show Worked Solution

MARKER’S COMMENT: Students who drew a diagram and included their working calculations on it were the most successful.

(i)
	`text(Let)\ A = text(area of front)`

`tan 30^@`	`= h/x`
`x`	`= h/(tan 30^@)`
	`= sqrt3 h`

`:.\ A`	`= 2 xx 1/2 xx sqrt 3 h xx h`
	`= sqrt 3 h^2\ \ text(m²)`

`V`	`= Ah`
	`= sqrt 3 h^2 xx 10`
	`= 10 sqrt3 h^2\ \ text(m³)`

(ii)	`text(Area of surface)`
	`= 10 xx 2 sqrt 3 h`
	`= 20 sqrt 3 h\ \ text(m²)`

(iii)	`(dV)/(dt)`	`= -kA`
		`= -k\ 20 sqrt3 h`

`V`	`= 10 sqrt3 h^2`
`(dV)/(dh)`	`= 20 sqrt 3 h`

`text(Find)\ (dh)/(dt)`

MARKER’S COMMENT: Half marks awarded for stating an appropriate chain rule, even if the following calculations were incorrect. Show your working!

`(dV)/(dt)`	`= (dV)/(dh) * (dh)/(dt)`
`(dh)/(dt)`	`= ((dV)/(dt))/((dV)/(dh))`
	`= (-k * 20 sqrt 3 h)/(20 sqrt 3 h)`
	`= -k`

`:.\ text(The water depth is changing at a rate)`

`text(of)\ -k\ text(metres per day.)`

♦♦♦ Exact data for part (iv) not available.
COMMENT: Interpreting a constant rate of change was very poorly understood!

(iv)	`text(S)text(ince)\ \ (dh)/(dt)\ \ text(is a constant, each metre)`
	`text(takes the same time.)`

`:.\ text(It takes 100 days to fall from 2 m to 1 m.)`

Plane Geometry, 2UA 2014 HSC 15b

In `Delta DEF`, a point `S` is chosen on the side `DE`. The length of `DS` is `x`, and the length of `ES` is `y`. The line through `S` parallel to `DF` meets `EF` at `Q`. The line through `S` parallel to `EF` meets `DF` at `R`.

The area of `Delta DEF` is `A`. The areas of `Delta DSR` and `Delta SEQ` are `A_1` and `A_2` respectively.

Show that `Delta DEF` is similar to `Delta DSR`. (2 marks)
Explain why `(DR)/(DF) = x/(x + y)`. (1 mark)
Show that
1. `sqrt ((A_1)/A) = x/(x + y)`. (2 marks)
Using the result from part (iii) and a similar expression for
1. `sqrt ((A_2)/A)`, deduce that `sqrt A = sqrt (A_1) + sqrt (A_2)`. (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Corresponding sides of similar)\ Delta text(s)`
`text(are in the same ratio.)`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i) `text(Need to show)\ Delta DEF\ text(|||) \ Delta DSR`

`/_FDE\ text(is common)`

`/_DSR = /_DEF = theta\ \ text{(corresponding angles,}\ RS\ text(||)\ FE text{)}`

`:.\ Delta DEF \ text(|||) \ Delta DSR\ \ text{(equiangular)}`

(ii) `(DR)/(DF) = (DS)/(DE) = x/(x + y)`

`text{(Corresponding sides of similar triangles)}`

♦♦ Mean mark 27%
COMMENT: The critical step in solving part (iii) is realising that you need the areas of 2 non-right angled triangles and therefore the formula `A=½\ ab sin C` is required.

(iii) `text(Show)\ sqrt((A_1)/A) = x/(x + y)`

`text(Using Area)`	`= 1/2 ab sin C`
`A_1`	`= 1/2 xx DR xx x xx sin alpha`
`A`	`= 1/2 xx DF xx (x + y) xx sin alpha`

`(A_1)/A`	`= (1/2 * DR * x * sin alpha)/(1/2 * DF * (x + y) * sin alpha)`
	`= (DR * x)/(DF * (x + y)`
	`= (x * x)/((x + y)(x + y))\ \ \ \ text{(using part(ii))}`
	`= (x^2)/((x + y)^2)`
`:.\ sqrt ((A_1)/A)`	`= x/((x + y))\ \ \ text(… as required.)`

(iv) `text(Consider)\ Delta DFE\ text(and)\ Delta SQE`

`/_FED`

`= theta\ text(is common)`

`/_FDE`

`= /_QSE = alpha\ \ `

`text{(corresponding angles,}\ DF\ text(||)\ QS text{)}`

`:.\ Delta DFE\ text(|||)\ Delta SQE\ \ text{(equiangular)}`

`(QE)/(FE) = (SE)/(DE) = y/(x +y)`

`text{(corresponding sides of similar triangles)}`

♦♦ Mean mark 26%

`A_2`	`= 1/2 xx QE xx y xx sin theta`
`A`	`= 1/2 xx FE xx (x + y) xx sin theta`
`(A_2)/A`	`= (QE * y)/(FE * (x + y))`
	`= (y^2)/((x + y)^2)`
`sqrt ((A_2)/A)`	`= y/((x + y))`

`text(Need to show)\ sqrt A = sqrt (A_1) + sqrt (A_2)`

`sqrt(A_2)/sqrtA`	`= y/((x + y))`
`sqrt (A_2)`	`= (sqrtA * y)/((x + y))`

`text(Similarly, from part)\ text{(iii)}`

`sqrt (A_1) = (sqrtA * x)/((x + y))`

`sqrt (A_1) + sqrt (A_2)`	`= (sqrt A * x)/((x + y)) + (sqrt A * y)/((x + y))`
	`= (sqrt A (x + y))/((x + y))`
	`= sqrt A\ \ \ text(… as required.)`

Trigonometry, 2ADV T2 2014 HSC 7 MC

How many solutions of the equation `(sin x-1)(tan x + 2) = 0` lie between `0` and `2 pi`?

Show Answers Only

`B`

Show Worked Solution

♦♦♦ Mean mark 25%, making it the toughest MC question in the 2014 exam.
COMMENT: Note that the “2 solutions” answer relies on the sum of an infinity of zeros not equalling zero. This concept created unintended difficulty in this question.

`text(When)\ (sin x-1)(tan x + 2) = 0`

`(sinx-1) = 0\ \ text(or)\ \ tan x + 2 = 0`

`text(If)\ \ sin x-1= 0:`

`sin x= 1\ \ =>\ \ x= pi/2,\ \ \ 0 < x < 2 pi`

`text(If)\ \ tan x + 2= 0:`

`tan x= -2`

`text{Since}\ tan\ pi/2\ text{is undefined, there are only 2 solutions when}`

`tan x = -2\ \text{(which occurs in the 1st and 4th quadrants).}`

`:.\ 2\ text(solutions)`

`=> B`

Statistics, STD2 S4 2014* HSC 30b

The scatterplot shows the relationship between expenditure per primary school student, as a percentage of a country’s Gross Domestic Product (GDP), and the life expectancy in years for 15 countries.

For the given data, the correlation coefficient, `r`, is 0.83. What does this indicate about the relationship between expenditure per primary school student and life expectancy for the 15 countries? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
For the data representing expenditure per primary school student, `Q_L` is 8.4 and `Q_U` is 22.5.

What is the interquartile range? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Another country has an expenditure per primary school student of 47.6% of its GDP.

Would this country be an outlier for this set of data? Justify your answer with calculations. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
On the scatterplot, draw the least-squares line of best fit `y = 1.29x + 49.9`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Using this line, or otherwise, estimate the life expectancy in a country which has an expenditure per primary school student of 18% of its GDP. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Why is this line NOT useful for predicting life expectancy in a country which has expenditure per primary school student of 60% of its GDP? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(It indicates there is a strong positive)`

`text(correlation between the two variables.)`
`14.1`
`text(Yes, because it’s > 43.65%)`
`73.1\ text(years)`
`text(At 60% GDP, the line predicts a life expectancy)`
`text(of 127.3. This line of best fit is only accurate)`
`text(in a lower range of GDP expediture.)`

Show Worked Solution

i.	`text(It indicates there is a strong positive)`
	`text(correlation between the two variables)`

ii.	`text(IQR)`	`= Q_U\ – Q_L`
		`= 22.5\ – 8.4`
		`= 14.1`

♦ Mean mark 35%

iii. `text(An outlier on the upper side must be more than)`

`Q_u\ +1.5xxIQR`

`=22.5+(1.5xx14.1)`

`=\ text(43.65%)`

`:.\ text(A country with an expenditure of 47.6% is an outlier).`

iv.

v. `text(Life expectancy) ~~ 73.1\ text{years (see dotted line)}`

♦♦ Mean mark 39%

`text(Alternative Solution)`

`text(When)\ x=18`

`y=1.29(18)+49.9=73.12\ \ text(years)`

♦♦♦ Mean mark 0%. The toughest question on the 2014 paper.
COMMENT: Examiners regularly ask students to identify and comment on outliers where linear relationships break down.

vi.	`text(At 60% GDP, the line predicts a life)`
	`text(expectancy of 127.3. This line of best)`
	`text(fit is only predictive in a lower range)`
	`text(of GDP expenditure.)`

Algebra, STD2 A4 2014 HSC 29a

The cost of hiring an open space for a music festival is $120 000. The cost will be shared equally by the people attending the festival, so that `C` (in dollars) is the cost per person when `n` people attend the festival.

Complete the table below by filling in the THREE missing values. (1 mark)
\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\text{Number of people} (n) \rule[-1ex]{0pt}{0pt} & \ 500\ & \ 1000 \ & 1500 \ & 2000 \ & 2500\ & 3000 \ \\
\hline
\rule{0pt}{2.5ex}\text{Cost per person} (C)\rule[-1ex]{0pt}{0pt} & & & & 60 & 48\ & 40 \ \\
\hline
\end{array}
Using the values from the table, draw the graph showing the relationship between `n` and `C`. (2 marks)
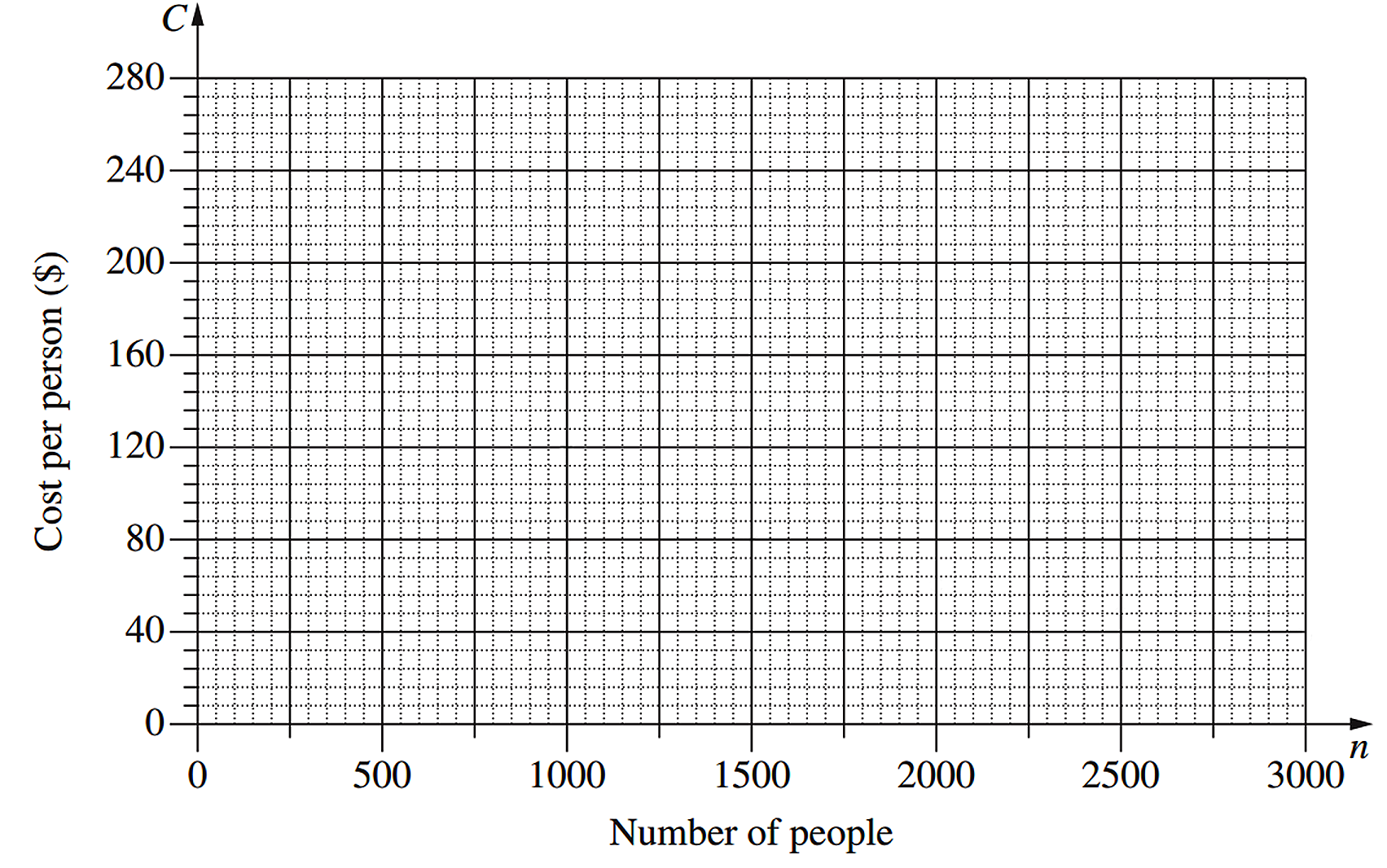
What equation represents the relationship between `n` and `C`? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Give ONE limitation of this equation in relation to this context. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Is it possible for the cost per person to be $94? Support your answer with appropriate calculations. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

\begin{array} {|l|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex}\text{Number of people} (n) \rule[-1ex]{0pt}{0pt} & \ 500\ & \ 1000 \ & 1500 \ & 2000 \ & 2500\ & 3000 \ \\
\hline
\rule{0pt}{2.5ex}\text{Cost per person} (C)\rule[-1ex]{0pt}{0pt} & 240 & 120 & 80 & 60 & 48\ & 40 \ \\
\hline
\end{array}

ii.

iii. `C = (120\ 000)/n`

`n\ text(must be a whole number)`

iv. `text(Limitations can include:)`

`•\ n\ text(must be a whole number)`

`•\ C > 0`

v. `text(If)\ C = 94:`

`94`	`= (120\ 000)/n`
`94n`	`= 120\ 000`
`n`	`= (120\ 000)/94`
	`= 1276.595…`

`:.\ text(C)text(ost cannot be $94 per person,)`

`text(because)\ n\ text(isn’t a whole number.)`

Show Worked Solution

ii.

♦ Mean mark (iii) 48%

iii. `C = (120\ 000)/n`

♦♦♦ Mean mark (iv) 7%
COMMENT: When asked for limitations of an equation, look carefully at potential restrictions with respect to both the domain and range.

iv. `text(Limitations can include:)`

`•\ n\ text(must be a whole number)`

`•\ C > 0`

v. `text(If)\ \ C = 94:`

`94`	`= (120\ 000)/n`
`94n`	`= 120\ 000`
`n`	`= (120\ 000)/94= 1276.595…`

♦ Mean mark (v) 38%

`:.\ text(C)text(ost cannot be $94 per person,)`

`text(because)\ n\ text(isn’t a whole number.)`

FS Driving, 2UG 2014 HSC 27a

Alex is buying a used car which has a sale price of $13 380. In addition to the sale price there are the following costs:

Stamp Duty for this car is calculated at $3 for every $100, or part thereof, of the sale price.
Calculate the Stamp Duty payable. (1 mark)
Alex borrows the total amount to be paid for the car including Stamp Duty and transfer of registration. Interest on the loan is charged at a flat rate of 7.5% per annum. The loan is to be repaid in equal monthly instalments over 3 years.
Calculate Alex’s monthly repayments. (4 marks)
Alex wishes to take out comprehensive insurance for the car for 12 months. The cost of comprehensive insurance is calculated using the following:
Find the total amount that Alex will need to pay for comprehensive insurance. (3 marks)
Alex has decided he will take out the comprehensive car insurance rather than the less expensive non-compulsory third-party car insurance.
What extra cover is provided by the comprehensive car insurance? (1 mark)

Show Answers Only

`$402`
`$470\ text{(nearest dollar)}`
`$985.74`
`text(Comprehensive insurance covers Alex)`
`text(for damage done to his own car as well.)`

Show Worked Solution

♦♦♦ Mean mark 12%
IMPORTANT: “or part thereof ..” in the question requires students to round up to 134 to get the right multiple of $3 for their calculation.

(i)

`($13\ 380)/100 = 133.8`

`:.\ text(Stamp duty)`	`= 134 xx $3`
	`= $402`

(ii)	`text(Total loan)`	`= $13\ 380 + 30 + 402`
		`= $13\ 812`

`text(Total interest)\ (I)`	`= Prn`
	`= 13\ 812 xx 7.5/100 xx 3`
	`= 3107.70`

`text(Total to repay)`	`= 3107.70 + 13\ 812`
	`= 16\ 919.70`

`text(# Repayments) = 3 xx 12 = 36`

`:.\ text(Monthly repayment)`	`= (16\ 919.70)/36`
	`= 469.9916…`
	`= $470\ text{(nearest dollar)}`

(iii)

`text(Base rate) = $845`

`text(FSL) =\ text(1%) xx 845 = $8.45`

`text(Stamp)`	`=\ text(5.5%) xx(845 + 8.45)`
	`= 46.9397…`
	`= $46.94\ text{(nearest cent)}`

`text(GST)`	`= 10 text(%) xx(845 + 8.45)`
	`= 85.345`
	`= $85.35`

`:.\ text(Total cost)`	`= 845 + 8.45 + 46.94 + 85.35`
	`= $985.74`

♦ Mean mark 34%.

(iv)	`text(Comprehensive insurance covers Alex)`
	`text(for damage done to his own car as well.)`

Statistics, STD2 S1 2014 HSC 26e

The times taken for 160 music downloads were recorded, grouped into classes and then displayed using the cumulative frequency histogram shown.

On the diagram, draw the lines that are needed to find the median download time. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

♦♦♦ Mean mark 17%.

Probability, STD2 S2 2014 HSC 16 MC

In Mathsville, there are on average eight rainy days in October.

Which expression could be used to find a value for the probability that it will rain on two consecutive days in October in Mathsville?

`8/31 xx 7/30`
`8/31 xx 7/31`
`8/31 xx 8/30`
`8/31 xx 8/31`

Show Answers Only

`D`

Show Worked Solution

`P text{(rains)} = 8/31\ \ \text{(independent event for each day)}`

`text{Since each day has same probability:}`

`P(R_1 R_2) = 8/31 xx 8/31`

`=> D`

♦♦♦ Mean mark 16%.
Lowest mark of any MC question in 2014!

FS Comm, 2UG 2014 HSC 5 MC

How many kilobytes are there in 2 gigabytes?

(A) `2^20`

(B) `2^21`

(C) `2^30`

(D) `2^31`

Show Answers Only

`B`

Show Worked Solution

♦♦♦ Mean mark 24%!

`2\ text(GB)`	`= 2 xx 2^20\ text(kB)`
	`= 2^21\ text(kB)`

`=> B`

Quadratic, EXT1 2014 HSC 13c

The point `P(2at, at^2)` lies on the parabola `x^2 = 4ay` with focus `S`.

The point `Q` divides the interval `PS` internally in the ratio `t^2 :1`.

Show that the coordinates of `Q` are
`x = (2at)/(1 + t^2)` and `y = (2at^2)/(1 + t^2)`. (2 marks)
Express the slope of `OQ` in terms of `t`. (1 mark)
Using the result from part (ii), or otherwise, show that `Q` lies on a fixed circle of radius `a`. (3 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`m_(OQ) = t`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i) `text(Show)\ \ Q = ((2at)/(1 + t^2), (2at^2)/(1 + t^2))`

`P (2at, at^2),\ S (0, a)`

`PS\ text(is divided internally in ratio)\ t^2: 1`

`Q`	`= ((nx_1 + mx_2)/(m + n), (ny_1 + my_2)/(m + n))`
	`= ((1(2at) + t^2(0))/(t^2 + 1), (1(at^2) + t^2 (a))/(t^2 + 1))`
	`= ((2at)/(1 + t^2), (2at^2)/(1 + t^2))\ \ text(… as required.)`

(ii)	`m_(OQ)`	`= (y_2\ – y_1)/(x_2\ – x_1)`
		`= ((2at^2)/(1 + t^2))/((2at)/(1 + t^2)) xx (1+t^2)/(1+t^2)`
		`= (2at^2)/(2at)`
		`= t`

(iii)	`text(Show)\ Q\ text(lies on a fixed circle radius)\ a`
	`text(S)text(ince)\ Q\ text(passes through)\ (0, 0)`

`=>\ text(If locus of)\ Q\ text(is a circle, it has)`

`text(diameter)\ QT\ text(where)\ T(0, 2a)`

`text(Show)\ \ QT _|_ OQ`

♦♦ Mean mark 22%

`text{(} text(angles on circum. subtended by)`

`text(a diameter are)\ 90^@ text{)}`

`m_(OQ) = t\ \ \ \ text{(see part (ii))}`

`text(Find)\ m_(QT),\ \ text(where:)`

`Q((2at)/(1 + t^2), (2at^2)/(1 + t^2)),\ \ \ \ \ T (0,2a)`

`m_(QT)`	`= (y_2\ – y_1)/(x_2\ – x_1)`
	`= ((2at^2)/(1 + t^2)\ – 2a)/((2at)/(1 + t^2)\ – 0)`
	`= (2at^2\ – 2a (1 + t^2))/(2at)`
	`= – (2a)/(2at)`
	`= – 1/t`

`m_(QT) xx m_(OT) = -1/t xx t = -1`

`=> QT _|_ OQ`

`=>O,\ T,\ Q\ text(lie on a circle.)`

`:.\ text(Locus of)\ Q\ text(is a fixed circle,)`

`text(centre)\ (0, a),\ text(radius)\ a`

Binomial, EXT1 2011 HSC 7b

The binomial theorem states that

`(1 + x)^n = sum_(r = 0)^(n) ((n),(r)) x^r` for all integers `n >= 1`.

Show that
1. `sum_(r=1)^n ((n),(r)) rx^r = nx (1 + x)^(n\ - 1)`. (2 marks)
By differentiating the result from part (i), or otherwise, show that
1. `sum_(r = 1)^n ((n),(r)) r^2 = n (n + 1) 2^(n\ - 2)`. (2 marks)
Assume now that `n` is even. Show that, for `n >= 4`,
1. `((n),(2)) 2^2 + ((n),(4)) 4^2 + ((n),(6)) 6^2 + ... + ((n),(n)) n^2 = n(n+1)2^(n\ - 3)`.
2. (3 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

♦ Mean mark 36%.
MARKER’S COMMENT: Better responses provided a narrative through the solution such as “Differentiate both sides” and “Mult. by `x`”, as seen in the solutions.

(i) `text(Show)\ sum_(r=1)^n ((n),(r)) rx^r = nx (1 + x)^(n\ – 1)`

`text(Using)\ (1 + x)^n = sum_(r=0)^n ((n),(r)) x^r :`

`(1 + x)^n = ((n),(0)) + ((n),(1)) x + ((n),(2)) x^2 + … + ((n),(n)) x^n`

`text(Differentiate both sides)`

`n(1 + x)^(n\ – 1) = ((n),(1)) + ((n),(2)) 2x + … + ((n),(n)) nx^(n\ – 1)`

`text(Multiply both sides by)\ x`

`nx (1 + x)^(n\ – 1)`	`= ((n),(1)) x + ((n),(2)) 2x^2 + … + ((n),(n)) nx^n`
	`= sum_(r=1)^n ((n),(r)) rx^r\ \ text(… as required.)`

(ii) `text(Show)\ \ sum_(r=1)^n ((n),(r)) r^2 = n (n+1) 2^(n\ – 2)`

♦♦ Mean mark 36%.

`text(Using part)\ text{(i)}`

`nx (1 + x)^(n\ – 1) = ((n),(1)) x + ((n),(2)) 2x^2 + … + ((n),(n)) nx^n`

`text(Differentiate LHS)`

`nx (n\ – 1)(1 + x)^(n\ – 2) + n(1 + x)^(n\ – 1)`

`= n (1 + x)^(n\ – 2) [x (n\ – 1) + (1 + x)]`

`= n (1 + x)^(n\ – 2) (xn\ – x + 1 + x)`

`= n (xn + 1)(1 + x)^(n\ – 2)`

`text(Differentiate RHS)`

`((n),(1)) + ((n),(2)) 2^2 x + ((n),(3)) 3^2 x^2 + … + ((n),(n)) n^2 x^(n\ – 1)\ text{… (*)}`

`text(Substitute)\ \x = 1\ text(into both sides)`

`((n),(1)) + ((n),(2)) 2^2 + … + ((n),(n)) n^2`	`= n (n + 1)(1 + 1)^(n\ – 2)`
`sum_(r=1)^n ((n),(r)) r^2`	`= n (n + 1) 2^(n\ – 2)`

(iii) `text(Show for)\ \ n >= 4`

`((n),(2)) 2^2 + ((n),(4)) 4^2 + ((n),(6)) 6^2 + … + ((n),(n)) n^2 = n (n + 1) 2^(n\ – 3)`

♦♦♦ Toughest question in the 2011 exam. Mean mark of 2%. The lowest mean of any Ext1 question since that data became available post-2009!

`text{From part(ii) … (*) we know}`

`((n),(1)) + ((n),(2)) 2^2 x + … + ((n),(n)) n^2 x^(n\ – 1) = n (xn + 1)(1 + x)^(n\ – 2)`

`text(When)\ \ x = 1`

`((n),(1)) + ((n),(2)) 2^2 + … + ((n),(n)) n^2 = n (n + 1) 2^(n\ – 2)\ \ \ \ \ …\ (1)`

`text(When)\ x = –1`

`((n),(1))\ – ((n),(2)) 2^2 + ((n),(3)) 3^2\ – …\ – ((n),(n)) n^2`

`= n (-n + 1)* 0^(n\ – 2)=0\ \ \ \ \ …\ (2)`

`text{(Note that}\ n≠2\ \ text{because}\ 0^0\ text{is undefined)}`

`(1)\ – (2)`

`2[((n),(2)) 2^2 + ((n),(4)) 4^2 + … + ((n),(n)) n^2]`	`= n (n + 1) 2^(n\ – 2) – 0`
`((n),(2)) 2^2 + ((n),(4)) 4^2 + … + ((n),(n)) n^2`	`= 1/2 n (n + 1) 2^(n\ – 2)`
	`= n (n + 1) 2^(n\ – 3)`

`:.\ text(Above statement true for integers)\ n >= 4.`

Polynomials, EXT1 2013 HSC 14c

The equation `e^t = 1/t` has an approximate solution `t_0 = 0.5`

Use one application of Newton’s method to show that `t_1 = 0.56` is another approximate solution of `e^t = 1/t`. (2 marks)
Hence, or otherwise, find an approximation to the value of `r` for which the graphs `y = e^(rx)` and `y = log_e x` have a common tangent at their point of intersection. (3 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`0.097\ text{(to 3 d.p.)}`

Show Worked Solution

MARKER’S COMMENT: Many students had difficulty expressing a valid function while too many others carelessly used `t_0=0.56` rather than 0.5.

(i)	`e^t`	`= 1/t`
	`e^t\ – 1/t`	`= 0`

`text(Let)\ \ f(t)`	`= e^t\ – 1/t`
`f prime (t)`	`= e^t + 1/(t^2)`
`f(0.5)`	`=e^0.5-1/0.5`
	`=–0.3512…`
`f′(0.5)`	`=e^0.5 +1/0.5^2`
	`=5.6487…`

`text(Applying Newton where)\ \ t_0 = 0.5`

`t_1`	`= 0.5\ – (f(0.5))/(f prime (0.5)`
	`= 0.5\ – (–0.3512…)/(5.6487…)`
	`= 0.5\ – (- 0.062)`
	`= 0.56\ text{(2 d.p.)}\ \ text(… as required.)`

(ii)	`y_1`	`= e^(rx),`	`\ \ \ \ \ (dy_1)/(dx) = re^(rx)`
	`y_2`	`= log_e x,`	`\ \ \ \ \ (dy_2)/(dx) = 1/x`

♦♦♦ 2nd toughest question on 2013 paper with mean mark 15%.
MARKER’S COMMENT: Few students used the common tangent information to equate the derivative functions.

`text(S)text(ince tangent is common),\ \ (dy_1)/(dx)=(dy_2)/(dx)`

`re^(rx)`	`= 1/x`
`e^(rx)`	`= 1/(rx)`

`text(Using part)\ text{(i)},\ rx ~~ 0.56`

`text(At intersection of curves)\ \ y_1 = y_2`

`e^(rx)`	`= log_e x`
`e^0.56`	`= log_e x`
`x`	`= e^(e^0.56)`
	`= 5.758 …`

`text(S)text(ince)\ rx`	`~~ 0.56`
`=> r`	`~~ 0.56/(5.758 … )`
	`~~ 0.0972 …`
	`~~ 0.097\ text{(to 3 d.p.)}`

Combinatorics, EXT1 A1 2013 HSC 14b

Write down the coefficient of `x^(2n)` in the binomial expansion of `(1 + x)^(4n)`. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Show that
`(1 + x^2 + 2x)^(2n) = sum_(k=0)^(2n) ((2n),(k)) x^(2n-k)(x + 2)^(2n-k)`. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
It is known that
`x^(2n-k) (x + 2)^(2n-k) = ((2n-k),(0)) 2^(2n-k) x^(2n-k) + ((2n-k),(1)) 2^(2n-k-1) x^(2n-k + 1)`
`+ ... + ((2n-k),(2n-k)) 2^0 x^(4n-2k)`. (Do NOT prove this.)
Show that
`((4n),(2n)) = sum_(k = 0)^(n) 2^(2n-2k) ((2n),(k))((2n-k),(k))`. (3 marks)
--- 12 WORK AREA LINES (style=lined) ---

Show Answers Only

i. `((4n),(2n))`

ii. `text(Proof)\ \ text{(See Worked Solutions)}`

iii. `text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

i. `text(Find co-efficient of)\ x^(2n).`

`text(Expanding)\ (1+x)^(4n):`

`((4n),(0)) + ((4n),(1))x + ((4n),(2))x^2 + … + ((4n),(2n))x^(2n) + …`

`:.\ text(Co-efficient of)\ \ x^(2n)\ text(is)\ ((4n),(2n))`

ii. `text(Show)\ (1 + x^2 + 2x)^(2n) = sum_(k=0)^(2n) ((2n),(k)) x^(2n-k) (x + 2)^(2n-k)`

♦♦ Mean mark 30%.

`text(Using)\ (1 + x^2 + 2x)^(2n) = [x(x + 2) + 1]^(2n)`

`[x (x + 2) + 1]^(2n)`

`= ((2n),(0)) (x(x + 2))^(2n) + ((2n),(1)) (x(x + 2))^(2n-1) + … + ((2n),(2n))`

`= ((2n),(0)) x^(2n)(x + 2)^(2n) + ((2n),(1)) x^(2n-1) (x + 2)^(2n-1) + … + ((2n),(2n))`

`= sum_(k=0)^(2n) ((2n),(k)) x^(2n-k) (x + 2)^(2n-k)\ text(… as required.)`

iii. `((4n),(2n))\ text(is the co-eff of)\ x^(2n)\ text(in expansion)\ (1+x)^(4x)`

`text(S)text(ince)\ (1 + x^2 + 2x)^(2n) = ((x+1)^2)^(2n) = (1 + x)^(4n)`

`=> ((4n),(2n))\ text(is co-efficient of)\ x^(2n)\ text(in expansion)\ (1 + x^2 + 2x)^(2n)`

`text(Using part)\ text{(ii):}`

`(1 + x^2 + 2x)^(2n) = sum_(k=0)^(2n) ((2n),(k))\ x^(2n-k) (x + 2)^(2n-k)`

`text(Using the given identity,)\ x^(2n)\ text(co-efficients are:)`

♦♦♦ Toughest question in the 2013 exam with Mean mark 12%!
MARKER’S COMMENT: Stating `(1+x^2+2x)^(2n)=(1+x)^(4n)` received 1 full mark. Take note.

`k = 0,`	`\ ((2n),(0))((2n-0),(0)) 2^(2n-0)`
`k = 1,`	`\ ((2n),(1))((2n-1),(1)) 2^(2n-1-1)`
`vdots`
`k = n,`	`\ ((2n),(n))((2n-n),(n)) 2^(2n-n-n)`

`:.\ ((4n),(2n))`

`= ((2n),(0))((2n),(0))2^(2n) + ((2n),(1))((2n-1),(1))2^(2n-2) + … + ((2n),(n))((n),(n)) 2^0`

` = sum_(k=0)^(n)\ ((2n),(k))((2n-k),(k)) 2^(2n-2k)\ \ \ \ text(… as required)`

Combinatorics, EXT1 A1 2010 HSC 7c

A box contains `n` identical red balls and `n` identical blue balls. A selection of `r` balls is made from the box, where `0 <= r <= n`.

Explain why the number of possible colour combinations is `r + 1`. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
Another box contains `n` white balls labelled consecutively from `1` to `n`. A selection of `n − r` balls is made from the box, where `0 <= r <= n`.

Explain why the number of different selections is `((n),(r))`. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
The `n` red balls, the `n` blue balls and the `n` white labelled balls are all placed into one box, and a selection of `n` balls is made.

Using the identity, `n2^(n-1)=sum_(k=1)^n k ((n),(k)),` or otherwise, show that the number of different selections is `(n + 2)2^(n- 1)`. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

♦♦♦ Mean mark 4%.
COMMENT: Solving this part required high level logical reasoning which proved extremely challenging for the vast majority of candidates.

i.	`text(1 Ball, # Combinations)`	`= 2\ text{(R or B)}`
	`text(2 Balls, # Combinations)`	`= 3\ text{(BB, BR, RR)}`
	`text(3 Balls, # Combinations)`	`= 4`

`text{(BBB, RBB, RRB, RRR)}`

`text(i.e. # Red balls could be 0, 1, 2, 3, …)`

`:.\ text(If)\ r\ text(balls chosen, # Combinations) = r + 1`

ii.

`text(# Selections when choosing)\ (n\ – r)\ text(from)\ n`

`= ((n),(n\ – r))`

♦♦♦ Mean mark 18%.

`((n),(n\ – r))`	`= (n!)/((n\ – r)!(n\ – (n\ – r))!)`
	`= (n!)/((n\ – r)! r!`
	`= ((n),(r))`

♦♦♦ Mean mark part (iii) 2%. Beast alert – equal lowest mean mark of any part of any question since this data has been available post-2009.

iii. `text(If)\ n\ text(balls are chosen,)`

`text(Let)\ r\ text(balls be red and blue and)`

`(n\ – r)\ text(balls be white labelled.)`

`=> text{# Combinations (Red and blue)} = r + 1`

`=> text{# Combinations (White)} = ((n),(r))`

`text(Any selection of)\ \ r\ \ text(red and blue balls would)`

`text(result in)\ \ (n-r)\ \ text(white balls, with) \ r=0,1,2,…`

`:.\ text{# Selections (for any given}\ r\ text{)}`

`= (r + 1)((n),(r))`

`= r ((n),(r)) + ((n),(r))`

`:.\ text{Total Selections}`	`= sum_(r=1)^n r ((n),(r)) + sum_(r=0)^n ((n),(r))`
	`= n2^(n\ – 1) + 2^n`
	`= n2^(n\ – 1) + 2*2^(n\ – 1)`
	`= (n + 2)2^(n\ – 1)\ text(… as required)`

Plane Geometry, EXT1 2010 HSC 5c

In the diagram, `ST` is tangent to both the circles at `A`.

The points `B` and `C` are on the larger circle, and the line `BC` is tangent to the smaller circle at `D`. The line `AB` intersects the smaller circle at `X`.

Copy or trace the diagram into your writing booklet

Explain why `/_AXD = /_ABD + /_XDB.` (1 mark)
Explain why `/_AXD = /_TAC + /_CAD.` (1 mark)
Hence show that `AD` bisects `/_BAC`. (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`/_ AXD = /_ABD + /_XDB`

`text{(exterior angle of}\ Delta BXD text{)}`

♦ Mean mark 47%

(ii)	`/_AXD`	`= /_TAD \ \ text{(angle in alternate segment)}`
		`= /_TAC + /_CAD\ \ text(… as required)`

(iii) `text(Show)\ \ /_XAD = /_CAD`

`/_ABD + /_XDB`

`=/_TAC + /_CAD\ \ text{(} text(from part)\ text{(i)} text(,)\ text{(ii)} text{)}`

`text(S)text(ince)\ /_TAC= /_ABD\ text{(angle in alternate segment)}`

♦♦ Mean mark 22%
IMPORTANT: Recognising that angles in the alternate segment are equal is an examiner favourite. LOOK FOR IT!

`=>/_XDB`	`=/_CAD`
`/_XDB`	`= /_XAD\ text{(angle in alternate segment)}`
`:. /_XAD`	`= /_CAD`

`:.\ AD\ \ text(bisects)\ /_BAC.`

Calculus, EXT1 C1 2011 HSC 7a

The diagram shows two identical circular cones with a common vertical axis. Each cone has height `h` cm and semi-vertical angle 45°.

The lower cone is completely filled with water. The upper cone is lowered vertically into the water as shown in the diagram. The rate at which it is lowered is given by

`(dl)/(dt) = 10`,

where `l` cm is the distance the upper cone has descended into the water after `t` seconds.

As the upper cone is lowered, water spills from the lower cone. The volume of water remaining in the lower cone at time `t` is `V` cm³.

Show that `V = pi/3(h^3\ - l^3)`. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
Find the rate at which `V` is changing with respect to time when `l = 2`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Find the rate at which `V` is changing with respect to time when the lower cone has lost `1/8` of its water. Give your answer in terms of `h`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`-40 pi\ \ text(cm³)// text(sec)`
`(-5pih^2)/2\ text(cm³)// text(sec)`

Show Worked Solution

i. `text(Show that)\ V = pi/3 (h^3\ – l^3)`

♦ Mean mark 42%

`text(S)text(ince)\ \ tan45° = r/h=1`

`=>r=h`

`=>\ text(Radius of lower cone) = h`

`:.\ V text{(lower cone)}`	`= 1/3 pi r^2 h`
	`= 1/3 pi h^3`

`text(Similarly,)`

`V text{(submerged upper cone)} = 1/3 pi l^3`

`V text{(water left)}`	`= 1/3 pi h^3\ – 1/3 pi l^3`
	`= pi/3 (h^3\ – l^3)\ \ \ text(… as required)`

ii. `text(Find)\ (dV)/(dt)\ text(at)\ l = 2`

`(dV)/(dt)= (dV)/(dl) xx (dl)/(dt)\ …\ text{(1)}`

`=>(dl)/(dt)`

`= 10\ text{(given)}`

`text(Using)\ \ V`	`= pi/3 (h^3\ – l^3)\ \ \ \ text(from part)\ text{(i)}`
`=>(dV)/(dl)`	`= -3 xx pi/3 l^2`
	`= -pi l^2`

`text(At)\ \ l = 2,`

`text{Substitute into (1) above}`

`(dV)/(dt)`	`= -pi xx 2^2 xx 10`
	`= -40 pi\ \ \ text(cm³)//text (sec)`

iii. `text(Find)\ \ (dV)/(dt)\ \ text(when lower cone has lost)\ 1/8 :`

♦♦♦ Mean mark 12%
MARKER’S COMMENT: Many unsuccessful answers attempted to find an alternate version of `(dV)/(dt)`. Part (ii) directed students directly toward the correct strategy.

`text(Find)\ \ l\ \ text(when)\ \ V = 7/8 xx 1/3 pi h^3`

`pi/3 (h^3\ – l^3)`	`= 7/8 xx 1/3 pi h^3`
`h^3 -l^3`	`= 7/8 h^3`
`l^3`	`= 1/8 h^3`
`l`	`= h/2`

`text(When)\ \ l = h/2 ,`

`(dV)/(dt)`	`= -pi (h/2)^2 xx 10\ \ …\ text{(*)}`
	`= (-5pih^2)/2\ text(cm³)// text(sec)`

`:. V\ text(is decreasing at the rate of)\ \ (5 pi h^2)/2\ text(cm³)//text(sec).`

Statistics, EXT1 S1 2011 HSC 6c

A game is played by throwing darts at a target. A player can choose to throw two or three darts.

Darcy plays two games. In Game 1, he chooses to throw two darts, and wins if he hits the target at least once. In Game 2, he chooses to throw three darts, and wins if he hits the target at least twice.

The probability that Darcy hits the target on any throw is `p`, where `0 < p < 1`.

Show that the probability that Darcy wins Game 1 is `2p- p^2`. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
Show that the probability that Darcy wins Game 2 is `3p^2- 2p^3`. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Prove that Darcy is more likely to win Game 1 than Game 2. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---
Find the value of `p` for which Darcy is twice as likely to win Game 1 as he is to win Game 2. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`p = (7 – sqrt17)/8`

Show Worked Solution

i. `text(Show)\ P text{(wins Game 1)} = 2p\ – p^2`

♦ Mean mark 47%.

`P text{(Hits)} = P text{(H)} = p`

`P text{(Miss)} = P text{(M)} = 1 – p`

`P text{(Wins G1)}`	`= 1 – P text{(MM)}`
	`= 1 – (1 – p)^2`
	`= 1 – 1 + 2p – p^2`
	`= 2p – p^2\ \ \ text(… as required)`

ii. `text(Show)\ \ P text{(wins Game 2)} = 3p – 2p^3 :`

♦ Mean mark 40%.

`text(Darcy wins G2 if he hits 3 times, or twice.)`

`Ptext{(Hits 3 times)}=\ ^3C_3 (p)^3=p^3`

`Ptext{(Hits twice)}=\ ^3C_2 (p)^2 (1-p)=3p^2-3p^3`

`P text{(Wins G2)}`	`= p^3 + 3p^2-3p^3`
	`= 3p^2 – 2p^3\ \ \ text(… as required)`

♦♦♦ Mean mark 17%.
COMMENT: It is critical for students to utilise the limits of `0<p<1` to answer part (iii).

iii. `text(Prove more likely to win G1 vs G2)`

`text(i.e. Show)\ \ \ `	`2p – p^2 > 3p^2 – 2p^3`
	`2p^3 – 4p^2 + 2p`	`> 0`
	`2p (p^2 – 2p + 1)`	`> 0`
	`2p (p – 1)^2`	`> 0`

`=> text(TRUE since)\ \ (p-1)^2>0\ \ text(and)\ \ 0 < p < 1`

`:.\ text(More likely for Darcy to win Game 1.)`

iv. `text(If twice as likely to win G1 vs G2)`

♦♦ Mean mark 21%.
MARKER’S COMMENT: BE CAREFUL in formulating your equation here. Many students multiplied the wrong side by 2.

`2p\ – p^2`	`= 2(3p^2 – 2p^3)`
	`= 6p^2 – 4p^3`
`4p^3 – 7p^2 + 2p`	`= 0`
`p(4p^2 – 7p + 2)`	`= 0`

`p`	`= (–(–7) +- sqrt((–7)^2\ – 4 xx 4 xx 2))/(2 xx 4)`
	`= (7 +- sqrt(49\ – 32))/8`
	`= (7 +- sqrt17)/8`

`text(S)text(ince)\ \ 0<p<1,`

`p = (7\ – sqrt17)/8`

Trig Ratios, EXT1 2011 HSC 5a

In the diagram, `Q(x_0, y_0)` is a point on the unit circle `x^2 + y^2 = 1` at an angle `theta` from the positive `x`-axis, where `− pi/2 < theta < pi/2`. The line through `N(0, 1)` and `Q` intersects the line `y = –1` at `P`. The points `T(0, y_0)` and `S(0, –1)` are on the `y`-axis.

Use the fact that `Delta TQN` and `Delta SPN` are similar to show that
`SP = (2costheta)/(1\ - sin theta)`. (2 marks)
Show that `(costheta)/(1\ - sin theta) = sec theta + tan theta`. (1 mark)
Show that `/_ SNP = theta/2 + pi/4`. (1 mark)
Hence, or otherwise, show that `sectheta + tantheta = tan(theta/2 + pi/4)`. (1 mark)
Hence, or otherwise, solve `sec theta + tan theta = sqrt3`, where `-pi/2 < theta < pi/2`. (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`pi/6\ text(radians)`

Show Worked Solution

(i)

♦ Mean mark 41%
MARKER’S COMMENT: When questions direct you to use a certain fact for a proof, use that fact!

`text(Show)\ SP = (2 cos theta)/(1\ – sin theta)`

`Delta SPN \ text(|||) \ Delta TQN\ \ \ text{(given)}`

`(SP)/(SN) = (TQ)/(TN)\ \ \ text{(corresponding sides of similar triangles)}`

`/_TQO = theta\ \ \ text{(alternate,}\ TQ\ text(||)\ x text{-axis)}`

	`sin theta`	`= (OT)/1 => OT = sin theta`
`=>`	`TN`	`= 1\ – sin theta`

	`cos theta`	`= (TQ)/1`
`=>`	`TQ`	`= cos theta`

`SN`	`= 2\ \ \ text{(diameter of unit circle)}`
`:. (SP)/2`	`= cos theta/(1\ – sin theta)`
`SP`	`= (2 cos theta)/(1\ – sin theta)\ \ \ text(… as required)`

(ii) `text(Show)\ \ costheta/(1\ – sin theta) = sec theta + tan theta`

♦ Mean mark 35%

`text(RHS)`	`= 1/(costheta) + (sintheta)/(costheta)`
	`=(1 + sin theta)/cos theta xx cos theta/cos theta`
	`= (costheta(1 + sintheta))/(cos^2theta)`
	`= (costheta(1 + sin theta))/(1\ – sin^2 theta)`
	`= (costheta(1 + sin theta))/((1 + sin theta)(1\ – sin theta)`
	`= costheta/(1\ – sin theta)\ \ \ text(… as required)`

(iii) `text(Show)\ \ /_SNP = theta/2 + pi/4`

♦♦♦ Mean mark 11%

`/_TOQ = 90\ – theta`

`text(S)text(ince)\ ON = OQ = 1\ text{(unit circle)}`

`=> Delta ONQ\ text(is isosceles)`

`:.\ /_SNP`	`= 1/2 (180\ – (90\ – theta))\ \ \ \ text{(angle sum of}\ Delta ONQ text{)}`
	`= 90\ – 45 + theta/2`
	`= 45 + theta/2`
	`= pi/4 + theta/2\ \ \ text(… as required)`

(iv) `text(Show)\ sec theta + tan theta = tan (theta/2 + pi/4)`

♦♦ Mean mark 28%

`text(S)text(ince)\ /_SNP = pi/4 + theta/2\ \ \ \ text{(} text(part)\ text{(iii)} text{)}`

`=> tan\ /_SNP = tan (pi/4 + theta/2)`

`text(Also,)\ tan\ /_SNP`	`= (SP)/(SN)`
	`= ((2costheta)/(1\ – sin theta))/2`
	`= (cos theta)/(1\ – sin theta)`
	`= sec theta + tan theta\ \ \ \ text{(part (ii))}`

`:.\ sec theta + tan theta = tan (pi/4 + theta/2)\ \ \ text(… as required)`

♦ Mean mark 45%

(v)	`sec theta + tan theta`	`= sqrt3,\ \ \ (-pi/2 < theta < pi/2)`
	`tan (pi/4 + theta/2)`	`= sqrt3\ \ \ \ text{(part (iv))}`
	`tan (pi/3)`	`= sqrt 3`

`text(S)text(ince tan is positive in)\ 1^text(st) // 3^text(rd)\ text(quads)`

`theta/2 + pi/4`	`= pi/3,\ (4pi)/3`
`theta/2`	`= pi/12\ \ \ \ (-pi/2 < theta < pi/2)`
`:.\ theta`	`= pi/6\ text(radians)`

Plane Geometry, EXT1 2011 HSC 4b

In the diagram, the vertices of `Delta ABC` lie on the circle with centre `O`. The point `D` lies on `BC` such that `Delta ABD` is isosceles and `/_ABC = x`.

Copy or trace the diagram into your writing booklet.

Explain why `/_AOC = 2x`. (1 mark)
Prove that `ACDO` is a cyclic quadrilateral. (2 marks)
Let `M` be the midpoint of `AC` and `P` the centre of the circle through `A, C, D` and `O`.
Show that `P, M` and `O` are collinear. (1 mark)

Show Answers Only

`text(Angle at the centre of a circle is twice)`
`text(angle of circumference on same arc)`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`/_AOC = 2x`

`text{(angles at circumference and}`

`text{centre on arc}\ AC text{)}`

♦ Mean mark 38%
STRATEGY: Proving part (ii) by showing opposite angles are supplementary also worked but was more time consuming.

(ii) `text(Prove)\ ACDO\ text(is cyclic)`

`text(S)text(ince)\ Delta ADB\ text(is isosceles)`

`/_DAB = x\ \ \ text{(opposite equal sides in}\ Delta DBA text{)}`

`=> /_ADB`	`= 180\ – 2x\ \ \ text{(angle sum of}\ Delta DAB text{)}`
`=> /_CDA`	`= 2x\ \ \ text{(}CDB\ text{is a straight angle)}`

`text(S)text(ince chord)\ AC\ text(subtends)\ /_CDA = 2x`

`text(and)\ /_COA = 2x,`

`:.\ text(Quadrilateral)\ ACDO\ text(must be cyclic.)`

(iii)

`text(Need to show)\ OM\ text(passes through)\ P,\ text(centre)`

♦♦♦ Mean mark 7%. 2nd hardest question in the 2011 paper!

`text(of circle through)\ ACDO.`

`AM`	`= CM\ text{(} M\ text(is midpoint) text{)}`
`OC`	`= OA\ text{(radii)}`

`OM\ text(is common)`

`:.\ Delta OAM -= Delta OCM\ \ \ text{(SSS)}`

`:. /_CMO = /_AMO\ \ \ `	`text{(corresponding angles of}`
	`\ \ text{congruent triangles)}`

`text(S)text(ince)\ ∠AMC\ text(is straight angle)`

`/_CMO = /_AMO = 90°`

`:.OM\ text(is perpendicular bisector)`

`text(of chord)\ AC.`

`:. OM\ text(passes through)\ P.`

`:.\ P, M,\ text(and)\ O\ text(are collinear.)`

Mechanics, EXT2* M1 2011 HSC 3a

The equation of motion for a particle undergoing simple harmonic motion is

`(d^2x)/(dt^2) = -n^2 x`,

where `x` is the displacement of the particle from the origin at time `t`, and `n` is a positive constant.

Verify that `x = A cos nt + B sin nt`, where `A` and `B` are constants, is a solution of the equation of motion. (1 mark)

--- 5 WORK AREA LINES (style=lined) ---
The particle is initially at the origin and moving with velocity `2n`.

Find the values of `A` and `B` in the solution `x = A cos nt + B sin nt`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
When is the particle first at its greatest distance from the origin? (1 mark)

--- 5 WORK AREA LINES (style=lined) ---
What is the total distance the particle travels between `t = 0` and `t = (2pi)/n`? (1 mark)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`A = 0,\ B = 2`
`t = pi/(2n)`
`text(8 units)`

Show Worked Solution

i.	`x`	`= A cos nt + B sin nt`
	`(dx)/(dt)`	`= – An sin nt + Bn cos nt`
	`(d^2x)/(dt^2)`	`= – An^2 cos nt\ – Bn^2 sin nt`
		`= -n^2 (A cos nt + B sin nt)`
		`= -n^2 x\ \ \ text(… as required)`

ii. `text(At)\ \ t=0, \ x=0, \ v=2n:`

`x`	`= Acosnt + Bsinnt`
`0`	`= A cos 0 + B sin 0`
`:.A`	`= 0`

`text(Using)\ \ (dx)/(dt) = Bn cos nt`

`2n`	`= Bn cos 0`
`Bn`	`= 2n`
`:.B`	`= 2`

♦♦ Mean mark part (iii) 47%

iii. `text(Max distance from origin when)\ (dx)/(dt) = 0`

`(dx)/(dt)`	`= 2n cos nt`
`0`	`= 2n cos nt`
`cos nt`	`= 0`
`nt`	`= pi/2,\ (3pi)/2,\ (5pi)/2`
`t`	`= pi/(2n),\ (3pi)/(2n), …`

`:.\ text(Particle is first at greatest distance)`

`text(from)\ O\ text(when)\ t = pi/(2n).`

iv. `text(Solution 1)`

`text(Find the distance travelled from)\ \ t=0\ \→\ \ t=(2pi)/n`

`text{(i.e. 1 full period)}`

♦♦ Mean mark 22%
MARKER’S COMMENT: Many students found the displacement at `t` rather than the distance travelled while another common error found distance as 2 x amplitude.

`text(S)text(ince)\ \ x=2 sin (nt)`

`=> text(Amplitude)=2`

`:.\ text(Distance travelled)=4 xx2=8\ text(units)`

`text(Solution 2)`

`text(At)\ t = 0,\ x = 0`

`text(At)\ t`	`= pi/(2n)`
`x`	`= 2 sin (n xx pi/(2n)) = 2`

`text(At)\ t`	`= (3pi)/(2n)\ \ \ text{(i.e. the next time}\ \ (dx)/(dt) = 0 text{)}`
`x`	`= 2 sin (n xx (3pi)/(2n)) = -2`

`text(At)\ t`	`= (2pi)/n`
`x`	`= 2 sin (n xx (2pi)/n) = 0`

`:.\ text(Total distance travelled)`

`= 2 + 4 + 2`

`= 8\ \ text(units)`

Calculus, EXT1 C1 2012 HSC 14c

A plane `P` takes off from a point `B`. It flies due north at a constant angle `alpha` to the horizontal. An observer is located at `A`, 1 km from `B`, at a bearing 060° from `B`.

Let `u` km be the distance from `B` to the plane and let `r` km be the distance from the observer to the plane. The point `G` is on the ground directly below the plane.

Show that `r = sqrt(1 + u^2 - u cos alpha)`. (3 marks)

--- 10 WORK AREA LINES (style=lined) ---
The plane is travelling at a constant speed of 360 km/h.
At what rate, in terms of `alpha`, is the distance of the plane from the observer changing 5 minutes after take-off? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`(180 (60\ – cos alpha))/sqrt(901\ – 30 cos alpha)\ \ text(km/hr)`

Show Worked Solution

i. `text(Show)\ r = sqrt(1 + u^2 – u cos alpha)`

♦ Mean mark 42%
IMPORTANT: Students should always be looking for opportunities to use the identity `sin^2 alpha“+cos^2 alpha=1` to clean up calculations with trig functions.

`text(In)\ Delta PGB:`

`cos alpha`	`= (BG)/u`
`BG`	`= u cos alpha`
`sin alpha`	`= (PG)/(u)`
`PG`	`= u sin alpha`

`text(In)\ Delta PGA,\ text(using Pythagoras):`

`AG^2`	`= r^2\ – PG^2`
	`= r^2\ – u^2 sin^2 alpha`

`text(Using cosine rule in)\ Delta ABG:`

`AG^2`	`= BG^2 + AB^2\ – 2 xx BG xx AB xx cos 60^@`
`r^2\ – u^2 sin^2 alpha`	`= u^2 cos^2 alpha + 1\ – 2 (u cos alpha) xx 1 xx 1/2`
`r^2`	`= u^2 cos^2 alpha + u^2 sin^2 alpha + 1\ – u cos alpha`
	`= u^2 (cos^2 alpha + sin^2 alpha) + 1\ – u cos alpha`
	`= u^2 + 1\ – u cos alpha`
`r`	`= sqrt(u^2 + 1\ – u cos alpha)\ \ text(… as required)`

ii. `text(Find)\ \ (dr)/(dt)\ text(when)\ t =5`

♦♦♦ Mean mark 14%

`(dr)/(dt) = (dr)/(du) xx (du)/(dt)`

`r`	`= (u^2 + 1\ – u cos alpha)^(1/2)`
`(dr)/(du)`	`= 1/2 (u^2 + 1\ – u cos alpha)^(-1/2) xx (2u\ – cos alpha)`
	`= (2u\ – cos alpha)/(2 sqrt(u^2 + 1\ – u cos alpha))`

`(du)/(dt)= 360\ text{km/hr (plane’s speed)}`

`text(After 5 mins,)`

`u`	`= 5/60 xx 360 = 30\ text(km)`
`(dr)/(dt)`	`= ((2 xx 30)\ – cos alpha)/( 2 sqrt(30^2 + 1\ – 30 cos alpha)) xx 360`
	`= (180 (60\ – cos alpha))/sqrt(901\ – 30 cos alpha)\ \ text(km/hr)`

Combinatorics, EXT1 A1 2012 HSC 11f

Use the binomial theorem to find an expression for the constant term in the expansion of
`(2x^3-1/x)^12`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
For what values of `n` does `(2x^3-1/x)^n` have a non-zero constant term? (1 mark)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

a. `-1760`

b. `n\ text(must be a multiple of 4)`

Show Worked Solution

a. `text(General term)`

`\ ^12C_k * (2x^3)^(12\-k) (-1/x)^k`

`=\ ^12C_k * (-1)^k *2^(12-k) * x^(36-3k) * x^(-k)`

`=\ ^12C_k * (-1)^k*2^(12-k) * x^(36-4k)`

`text(Constant term occurs when:)`

`36-4k=0\ \ =>\ \ k=9`

`:.\ text(Constant term)=\ ^12C_9 * (-1)^9*2^3=-(12!)/(3!9!) xx 8 = -1760`

b. `text(General term of)\ (2x^3-1/x)^n`

♦♦♦ Mean mark (ii) 16%.

`\ ^nC_k * (2x^3)^(n-k) (-1/x)^k`

`=\ ^nC_k * 2^(n-k) * x^(3n-3k) * (-1)^k * x^(-k)`

`=\ ^nC_k * (-1)^k*2^(n-k) * x^(3n-4k)`

`text(Constant term occurs when:)`

`3n-4k = 0\ \ =>\ \ k=3/4 n`

`text(S)text(ince)\ n\ text(and)\ k\ text(must be integers,)\ n\ text(must be a multiple of 4.)`

Calculus, 2ADV C3 2009 HSC 10

`text(Let)\ \ f(x) = x - (x^2)/2 + (x^3)/3`

Show that the graph of `y = f(x)` has no turning points. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Find the point of inflection of `y = f(x)`. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
i. Show that `1 - x + x^2 - 1/(1 + x) = (x^3)/(1 + x)` for `x != -1`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

ii. Let `g(x) = ln (1 + x)`.

Use the result in part c.i. to show that `f prime (x) >= g prime (x)` for all `x >= 0`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Sketch the graphs of `y = f(x)` and `y = g(x)` for `x >= 0`. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
Show that `d/(dx) [(1 + x) ln (1 + x) - (1 + x)] = ln (1 + x)`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Find the area enclosed by the graphs of `y = f(x)` and `y = g(x)`, and the straight line `x = 1`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions)}`
`(1/2, 5/12)`
i. `text{Proof (See Worked Solutions)}`

ii. `text{Proof (See Worked Solutions)}`
`text{Proof (See Worked Solutions)}`
`1 5/12\ – 2ln2\ \ text(u²)`

Show Worked Solution

a.	`f(x) = x\ – (x^2)/2 + (x^3)/3`

♦♦ Mean mark 28% for all of Q10 (note that data for each question part is not available).

`text(Turning points when)\ f prime (x) = 0`

`f prime (x) = 1\ – x + x^2`

`x^2\ – x + 1 = 0`

`text(S)text(ince)\ \ Delta`	`= b^2\ – 4ac`
	`= (–1)^2\ – 4 xx 1 xx 1`
	`= -3 < 0 => text(No solution)`

`:.\ f(x)\ text(has no turning points)`

b.	`text(P.I. when)\ f″(x) = 0`

`f″(x)`	`= -1 + 2x = 0`
`2x`	`= 1`
`x`	`= 1/2`

`text(Check for change in concavity)`

`f″(1/4)`	`= -1/2 < 0`
`f″(3/4)`	`= 1/2 > 0`

`=>\ text(Change in concavity)`

`:.\ text(P.I. at)\ \ x = 1/2`

`f(1/2)`	`= 1/2\ – ((1/2)^2)/2 + ((1/2)^3)/3`
	`= 1/2\ – 1/8 + 1/24`
	`= 5/12`

`:.\ text(Point of Inflection at)\ (1/2, 5/12)`

c.i.

`text(Show)\ 1\ – x + x^2\ – 1/(1 + x) = (x^3)/(1 + x),\ \ \ x != -1`

`text(LHS)`	`= (1+x)/(1+x)\ – (x(1+x))/(1+x) + (x^2(1+x))/((1+x))\ – 1/(1+x)`
	`= (1 + x\ – x\ – x^2 + x^2 + x^3\ – 1)/(1+x)`
	`= (x^3)/(1+x)\ \ \ text(… as required)`

c.ii.	`text(Let)\ g(x) = ln(1+x)`
	`g prime (x) = 1/(1 + x)`

`f prime (x)\ – g prime (x)`	`= 1\ – x + x^2\ – 1/(1+x)`
	`= (x^3)/(1 + x)\ \ text{(using part (i))}`

`text(S)text(ince)\ (x^3)/(1 + x) >= 0\ text(for)\ x >= 0`

`f prime (x)\ – g prime (x) >= 0`

`f prime (x) >= g prime (x)\ text(for)\ x >= 0`

MARKER’S COMMENT: When 2 graphs are drawn on the same set of axes, you must label them.

e.	`text(Show)\ d/(dx) [(1 + x) ln (1 + x)\ – (1 + x)] = ln (1 + x)`
	`text(Using)\ d/(dx) uv=uv′+vu′`

`text(LHS)`	`= (1+x) xx 1/(1 + x) + ln(1+x)xx1 + – 1`
	`= 1+ ln(1+x)\ – 1`
	`= ln(1+x)`
	`=\ text(RHS … as required)`

f.	`text(Area)`	`= int_0^1 f(x)\ – g(x)\ dx`
		`= int_0^1 (x\ – (x^2)/2 + (x^3)/3\ – ln(x+1))\ dx`
		`= [x^2/2\ – x^3/6 + (x^4)/12\ – (1 + x) ln (1+x) + (1+x)]_0^1`
		`text{(using part (e) above)}`
		`= [(1/2 – 1/6 + 1/12 – (2)ln2 + 2) – (ln1 + 1)]`
		`= 5/12\ – 2ln2 + 2\ – 1`
		`= 1 5/12\ – 2 ln 2\ \ text(u²)`

Probability, 2ADV S1 2009 HSC 9a

Each week Van and Marie take part in a raffle at their respective workplaces.
The probability that Van wins a prize in his raffle is `1/9`. The probability that Marie wins a prize in her raffle is `1/16`.

What is the probability that, during the next three weeks, at least one of them wins a prize? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`91/216`

Show Worked Solution

`P text{(Van loses)}`	`= 1-1/9 = 8/9`
`P text{(Marie loses)}`	`= 1-1/16 = 15/16`
`P text{(both lose)}`	`= 8/9 xx 15/16 = 5/6`

`text{P(At least 1 wins)}`

`= 1-P text{(both lose for 3 weeks)}`

`= 1-(5/6)(5/6)(5/6)`

`= 1-125/216`

`= 91/216`

Calculus, 2ADV C3 2009 HSC 8a

The diagram shows the graph of a function `y = f(x)`.

For which values of `x` is the derivative, `f^{′}(x)`, negative? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
What happens to `f^{′}(x)` for large values of `x`? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Sketch the graph `y = f^{′}(x)`. (2 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

`f^{′}(x) < 0\ text(when)`

`-1 < x < 3`
`text(As)\ x -> oo`

`f^{′}(x) -> 0`

Show Worked Solution

i. `f^{′}(x) < 0\ text(when)`

`-1 < x < 3`

♦♦ Exact data not available.

ii. `text(As)\ x -> oo,`

`f^{′}(x) -> 0`

♦♦ Exact data not available.
MARKER’S COMMENT: Poorly drawn graphs with axes not labelled and inaccurate scales were common.

iii.

Trigonometry, 2ADV T3 2009 HSC 7b

Between 5 am and 5 pm on 3 March 2009, the height, `h`, of the tide in a harbour was given by

`h = 1 + 0.7 sin(pi/6 t)\ \ \ text(for)\ \ 0 <= t <= 12`

where `h` is in metres and `t` is in hours, with `t = 0` at 5 am.

What is the period of the function `h`? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
What was the value of `h` at low tide, and at what time did low tide occur? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
A ship is able to enter the harbour only if the height of the tide is at least 1.35 m.

Find all times between 5 am and 5 pm on 3 March 2009 during which the ship was able to enter the harbour. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`12\ text(hours)`
`text(2pm)\ \ text{(5am + 9 hours)}`
`text(6am to 10am)`

Show Worked Solution

i. `h = 1 + 0.7 sin (pi/6 t)\ \ text(for)\ 0 <= t <= 12`

`T`	`= (2pi)/n\ \ text(where)\ n = pi/6`
	`= 2 pi xx 6/pi`
	`= 12\ text(hours)`

`:.\ text(The period of)\ h\ text(is 12 hours.)`

ii. `text(Find)\ h\ text(at low tide)`

IMPORTANT: Using `sin x=–1` for a minimum here is very effective and time efficient. This property of trig functions is often very useful in harder questions.

`=> h\ text(will be a minimum when)`

`sin(pi/6 t) = -1`

`:.\ h_text(min)`	`= 1 + 0.7(-1)`
	`= 0.3\ text(metres)`

`text(S)text(ince)\ \ sinx = -1\ \ text(when)\ \ x = (3pi)/2`

`pi/6 t`	`= (3pi)/2`
`t`	`= (3pi)/2 xx 6/pi`
	`= 9\ text(hours)`

`:.\ text{Low tide occurs at 2pm (5 am + 9 hours)}`

iii. `text(Find)\ \ t\ \ text(when)\ \ h >= 1.35`

`1 + 0.7 sin (pi/6 t)`	`>= 1.35`
`0.7 sin (pi/6 t)`	`>= 0.35`
`sin (pi/6 t)`	`>= 1/2`

`sin (pi/6 t)`	`= 1/2\ text(when)`
`pi/6 t`	`= pi/6,\ (5pi)/6,\ (13pi)/6,\ text(etc …)`

`t`	`= 1,\ 5\ \ \ \ \ \ (0 <= t <= 12)`

`text(From the graph,)`

`sin(pi/6 t) >= 1/2\ \ \ text(when)\ \ 1 <= t <= 5`

`:.\ text(Ship can enter the harbour between 6 am and 10 am.)`

Calculus, 2ADV C1 2009 HSC 6c

The diagram illustrates the design for part of a roller-coaster track. The section `RO` is a straight line with slope 1.2, and the section `PQ` is a straight line with slope – 1.8. The section `OP` is a parabola `y = ax^2 + bx`. The horizontal distance from the `y`-axis to `P` is 30 m.

In order that the ride is smooth, the straight line sections must be tangent to the parabola at `O` and at `P`.

Find the values of `a` and `b` so that the ride is smooth. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---
Find the distance `d`, from the vertex of the parabola to the horizontal line through `P`, as shown on the diagram. (2 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(For a smooth ride,)\ a = -0.05\ text(and)\ b = 1.2`
`16.2\ text(m)`

Show Worked Solution

i.	`y`	`= ax^2 + bx`
	`dy/dx`	`= 2ax + b`

`text{At}\ x=0\ \ \=>\ \ dy/dx=b`

`text(We need)\ m\ text(at)\ O = 1.2`

`:.\ b = 1.2`

`text(At)\ P,\ x = 30:`

`dy/dx= 2 xx a xx 30 + 1.2= 60a + 1.2`

`text(We need)\ m\ text(at)\ P = -1.8`

`60a + 1.2`	`= -1.8`
`60a`	`= -3`
`a`	`= -3/60= -0.05`

`:.\ text(For a smooth ride,)\ a = -0.05\ \ text(and)\ \ b = 1.2`

ii.	`y`	`= -0.05x^2 + 1.2x`
	`dy/dx`	`= -0.1x + 1.2`

`text(Find)\ x\ text(when)\ dy/dx = 0`

`-0.1x + 1.2`	`= 0`
`x`	`= 1.2/0.1= 12`

`text(MAX when)\ x = 12`

`text(When)\ x = 12:`

`y= -0.05 xx 12^2 + 1.2 xx 12= -7.2 + 14.4= 7.2`

`text(When)\ x = 30:`

`y=-0.05 xx 30^2 + 1.2 xx 30= -45 + 36= -9`

`:.\ d= 7.2 + |-9|= 16.2\ text(m)`

Plane Geometry, 2UA 2009 HSC 4c

In the diagram, `Delta ABC` is a right-angled triangle, with the right angle at `C`. The midpoint of `AB` is `M`, and `MP _|_ AC`.

Copy or trace the diagram into your writing booklet.

Prove that `Delta AMP` is similar to `Delta ABC`. (2 marks)
What is the ratio of `AP` to `AC`? (1 mark)
Prove that `Delta AMC` is isosceles. (2 marks)
Show that `Delta ABC` can be divided into two isosceles triangles. (1 mark)
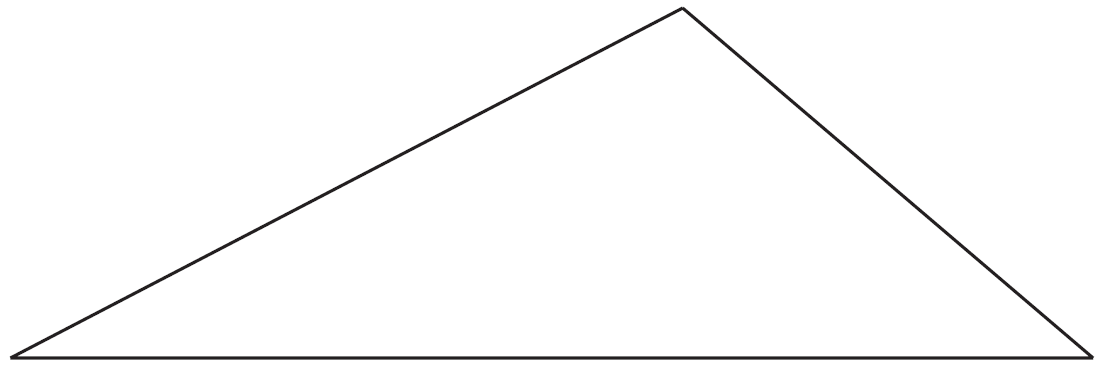
Copy or trace this triangle into your writing booklet and show how to divide it into four isosceles triangles. (1 mark)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Ratio)\ AP:AC = 1:2`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)	`text(Need to prove)\ Delta AMP\ text(\|\|\|)\ Delta ABC`
	`/_ PAM\ text(is common)`
	`/_ MPA = /_BCA = 90°\ \ \ text{(given)}`
	`:.\ Delta AMP \ text(\|\|\|) \ Delta ABC\ \ \ text{(equiangular)}`

(ii)	`(AP)/(AC) = (AM)/(AB)\ \ \ `	`text{(corresponding sides of}`
		`text{similar triangles)}`

`text(S)text(ince)\ \ AB = 2 xx AM`

`(AP)/(AC) = 1/2`

`:.\ text(Ratio)\ AP:AC = 1:2`

(iii)

`AP = PC \ \ \ text{(from part (ii))}`

`PM\ text(is common)`

`/_APM = /_CPM = 90°\ \ text{(∠}\ APC\ text{is a straight angle)}`

`:.\ Delta AMP ~= Delta CMP\ text{(SAS)}`

`=> AM = CM\ \ `	`text{(corresponding sides of}`
	`text{congruent triangles)}`

`:.\ Delta AMC\ text(is isosceles.)`

(iv)	`text(S)text(ince)\ \ AM`	`= MC\ \ \ text{(part (iii))}`
	`AM`	`= MB\ text{(given)}`
	`:. MC`	`= MB`

`:. Delta MCB\ text(is isosceles)`

`:. Delta ABC\ text(can be divided into 2 isosceles)`

`text(triangles)\ (Delta AMC\ text(and)\ Delta MCB text{)}`

(v)

♦♦ Mean mark 25%.
MARKER’S COMMENT: Use a ruler, draw large diagrams and always pay careful attention to previous parts of the question!

`/_AFB = /_CFB = 90°`

`DF\ text(bisects)\ AB`

`EF\ text(bisects)\ BC`

`text(From part)\ text{(iv)}\ text(we get 4 isosceles)`

`text(triangles as shown.)`

Calculus, EXT1* C3 2010 HSC 10b

The circle `x^2 + y^2 = r^2` has radius `r` and centre `O`. The circle meets the positive `x`-axis at `B`. The point `A` is on the interval `OB`. A vertical line through `A` meets the circle at `P`. Let `theta = /_OPA`.

The shaded region bounded by the arc `PB` and the intervals `AB` and `AP` is rotated about the `x`-axis. Show that the volume, `V`, formed is given by
`V = (pi r^3)/3 (2-3 sin theta + sin^3 theta)` (3 marks)

--- 8 WORK AREA LINES (style=lined) ---
A container is in the shape of a hemisphere of radius `r` metres. The container is initially horizontal and full of water. The container is then tilted at an angle of `theta` to the horizontal so that some water spills out.

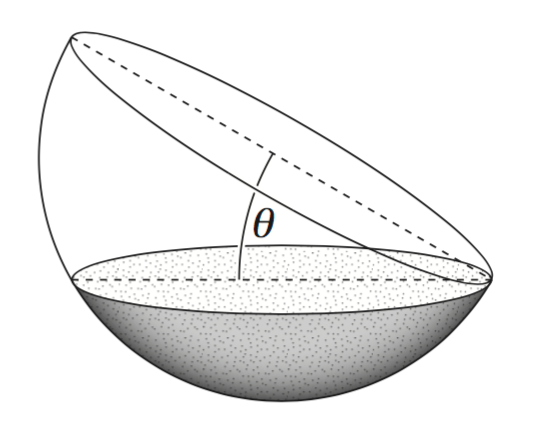
(1) Find `theta` so that the depth of water remaining is one half of the original depth. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
(2) What fraction of the original volume is left in the container? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof) text{(See Worked Solutions)}`
(1) `theta = pi/6\ text(radians)`
(2) `5/16`

Show Worked Solution

i. `text(Show that)\ V = (pir^3)/3 (2-3sin theta + sin^3 theta)`

♦♦♦ Mean mark (i) 16%.
MARKER’S COMMENT: A common error was to integrate `r^2` to `1/3 r^3` instead of `r^2 x` (note that `r` is a constant).

`sin theta`	`= (OA)/r`
`:.\ OA`	`= r sin theta`
`=> A`	`= (r sin theta, 0),\ \ \ \ B = (r,0)`

`:.V`	`= pi int_(rsintheta)^r y^2\ dx`
	`= pi int_(rsintheta)^r (r^2-x^2)\ dx\ \ \ \ text{(using}\ x^2+y^2=r^2text{)}`
	`= pi [r^2 x-(x^3)/3]_(rsintheta)^r`
	`= pi [(r^3-r^3/3)-(r^3 sin theta-(r^3 sin^3 theta)/3)]`
	`= pi ((2r^3)/3-r^3 sin theta + (r^3 sin^3 theta)/3)`
	`= (pir^3)/3 (2-3 sin theta + sin^3 theta)\ \ \ text(… as required)`

ii. (1) `text(Depth of water remaining) = 1/2 xx text(original depth:)`

♦♦♦ Part (ii) mean marks 3% and 2% for (ii)(1) and (ii)(2) respectively.

`r-r sin theta`	`=1/2 r`
`r (1-sin theta)`	`= 1/2 r`
`1-sin theta`	`= 1/2`
`sin theta`	`= 1/2`
`:.\ theta`	`= pi/6\ text(radians)`

MARKER’S COMMENT: Previous parts of a question should always be at the front and centre of a student’s mind and direct their strategy.

ii. (2)	`text(Original Volume)`	`= 1/2 xx 4/3 pi r^3`
		`= 2/3 pi r^3`

`text(New Volume)`	`= (pi r^3)/3 [2-3 sin(pi/6) + sin^3(pi/6)]`
	`= (pir^3)/3 [2-(3 xx 1/2) + (1/2)^3]`
	`= (pi r^3)/3 [2-3/2 + 1/8]`
	`= (pir^3)/3 (5/8)`
	`= (5 pi r^3)/24`

`:.\ text(Fraction of original volume left)`

`= ((5pir^3)/24)/(2/3 pi r^3)`

`= 5/24 xx 3/2`

`= 5/16`

Plane Geometry, 2UA 2010 HSC 10a

In the diagram `ABC` is an isosceles triangle with `AC = BC = x`. The point `D` on the interval `AB` is chosen so that `AD = CD`. Let `AD = a`, `DB = y` and `/_ADC = theta`.

Show that `Delta ABC` is similar to `Delta ACD`. (2 marks)
Show that `x^2 = a^2 + ay`. (1 mark)
Show that `y = a(1 − 2 cos theta )`. (2 marks)
Deduce that `y <= 3a`. (1 mark)

Show Answers Only

`text(Proof) text{(See Worked Solutions)}`
`text(Proof) text{(See Worked Solutions)}`
`text(Proof) text{(See Worked Solutions)}`
`text(Proof) text{(See Worked Solutions)}`

Show Worked Solution

MARKER’S COMMENT: When dealing with multiple triangles, the best performing students label all angles clearly and unambiguously.

(i)

`/_CAD\ text(is common)`

`/_CAD = /_ACD = /_DBC`

`text{(Angles opposite equal sides in}`

`\ \ text{isosceles}\ Delta ACD\ text(and)\ Delta ABC text{)}`

`/_ADC = /_ACB\ \ (180^@\ text(in)\ Delta text{)}`

`:.\ Delta ABC\ text(|||) \ Delta ACD\ \ \ text{(AAA)}\ \ \ text(… as required)`

♦♦ Mean mark 25%.
MARKER’S COMMENT: The similarity proof in part (i) should have immediately alerted students to using similar ratios of sides to solve part (ii). Many did not follow this obvious hint.

(ii) `text(Using similarity)`

`(AC)/(AD)`	`= (AB)/(CB)`	`\ \ text{(corresponding sides of}` `\ \ \ \ text{similar triangles)}`
`x/a`	`= (a + y)/x`

`:.\ x^2 = a^2 + ay\ \ \ text(… as required)`

(iii) `text(Show)\ \ y = a(1\ – 2 cos theta)`

`text(Using Cosine Rule:)`

`cos theta`	`= (a^2 + a^2\ – x^2)/(2 xx a xx a)`
`2a^2costheta`	`= 2a^2\ – x^2`
	`= 2a^2\ – (a^2 + ay)\ \ text{(from part (ii))}`
	`= a^2\ – ay`
`ay`	`= a^2\ – 2a^2cos theta`
`y`	`= a\ – 2a cos theta`
	`= a (1\ – 2 cos theta)\ \ \ \ text(… as required)`

(iv) `text(S)text(ince)\ 1 <= cos theta <= 1`

♦♦♦ Parts (iii) and (iv) mean marks – 18% and just 4% respectively.
IMPORTANT: Limits of trig functions are often extremely useful in proving inequalities (see Worked Solutions).

` -2 <= 2 cos theta <= 2`

` -1 <= 1\ – 2 cos theta <= 3`

`y`	`=a(1\ – 2 cos theta)\ \ \ text{(from part (iii))}`
`:.\ y`	`<= a(3)`
	`<= 3a\ \ …\ text(as required)`

Calculus, 2ADV C3 2010 HSC 9b

Let `y=f(x)` be a function defined for `0 <= x <= 6`, with `f(0)=0`.

The diagram shows the graph of the derivative of `f`, `y = f^{′}(x)`.

The shaded region `A_1` has area 4 square units. The shaded region `A_2` has area 4 square units.

For which values of `x` is `f(x)` increasing? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
What is the maximum value of `f(x)`? (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Find the value of `f(6)`. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Draw a graph of `y =f(x)` for `0 <= x <= 6`. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`f(x)\ text(is increasing when)\ 0 <= x < 2`
`text(MAX value of)\ f(x) = 4`
`-6`

Show Worked Solution

i.	`f(x)\ text(is increasing when)\ \ f^{′}(x) > 0`
	`text(From the graph)`
	`f(x)\ text(is increasing when)\ 0 <= x < 2`

ii.	`f^{′}(x) = 0\ \ text(when)\ \ x=2`
	`:.\ text(MAX at)\ \ x = 2`
	`int_0^2 f^{′}(x)\ dx = 4\ \ \ (text(given since)\ A_1 = 4 text{)}`
	`text(We also know)`

`int_0^2\ f^{′}(x)\ dx`	`= [f(x)]_0^2`
	`= f(2)-f(0)`
	`= f(2)\ \ \ \ text{(since}\ f(0) = 0 text{)}`

`=> f(2) = 4`

♦♦♦ Parts (ii) and (iii) proved particularly difficult for students with mean marks of 12% and 11% respectively.

`:.\ text(MAX value of)\ \ f(x) = 4`

iii.	`int_0^4 f^{′}(x)`	`= A_1-A_2`
		`=0`

`text(We also know)`

`int_0^4 f^{′}(x)\ dx`	`= int_2^4 f^{′}(x)\ dx + int_0^2 f^{′}(x)\ dx`
	`=[f(x)]_2^4 + 4`
	`= f(4)-f(2) + 4\ \ \ (text(note)\ f(2)=4)`
	`=f(4)`

`=> f(4) = 0`

`text(Gradient = – 3 from)\ \ x = 4\ \ text(to)\ \ x = 6`

`:.\ f(6)`	`= -3 (6\ – 4)`
	`= -6`

♦♦ Mean mark 28%
EXAM TIP: Clearly identify THE EXTREMES when given a defined domain. In this case, the origin is obvious graphically, and the other extreme at `x=6`, is CLEARLY LABELLED!

iv.

Financial Maths, 2ADV M1 2011 HSC 9d

Rationalise the denominator in the expression `1/(sqrtn + sqrt(n+1))` where `n` is an integer and `n >= 1`. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
Using your result from part (i), or otherwise, find the value of the sum

`1/(sqrt1+ sqrt2) + 1/(sqrt2 + sqrt3) + 1/(sqrt3 + sqrt4) + ... + 1/(sqrt99 + sqrt100)` (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`sqrt(n+1)\ – sqrtn`
`9`

Show Worked Solution

i. `1/(sqrtn + sqrt(n+1)) xx (sqrtn\ – sqrt(n+1))/(sqrtn\ – sqrt(n+1))`

MARKER’S COMMENT: Students connecting the information between parts (i) and (ii) were easily the most successful. AGAIN, the information from earlier parts of multi-part questions is gold plated information for directing your answer.

`= (sqrtn\ – sqrt(n+1))/((sqrtn)^2\ – (sqrt(n+1))^2)`

`= (sqrtn\ – sqrt(n+1))/(n\ – (n + 1))`

`= (sqrtn\ – sqrt(n+1))/-1`

`= sqrt(n+1)\ – sqrtn`

ii. `1/(sqrt1 + sqrt2) + 1/(sqrt2 + sqrt3) + 1/(sqrt3 + sqrt4) + … + 1/(sqrt99 + sqrt100)`

`= (sqrt2\ – sqrt1) + (sqrt3\ – sqrt2) + (sqrt4\ – sqrt3) + … + (sqrt100\ – sqrt99)`

`= – sqrt1 + sqrt 100`

♦♦♦ Mean mark 15%.

`= -1 + 10`

`= 9`

Calculus, 2ADV C4 2011 HSC 9b

A tap releases liquid `A` into a tank at the rate of `(2 + t^2/(t + 1))` litres per minute, where `t` is time in minutes. A second tap releases liquid `B` into the same tank at the rate of `(1 + 1/(t+1))` litres per minute. The taps are opened at the same time and release the liquids into an empty tank.

Show that the rate of flow of liquid `A` is greater than the rate of flow of liquid `B` by `t` litres per minute. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
The taps are closed after 4 minutes. By how many litres is the volume of liquid `A` greater than the volume of liquid `B` in the tank when the taps are closed? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof) text{(See Worked Solutions)}`
`text(There is 8 litres more of liquid)\ A\ text(than)\ B.`

Show Worked Solution

♦♦♦ Mean mark 16%
MARKER’S COMMENT: Many students incorrectly differentiated in part (i). The 1 mark allocation indicates the answer will not require an involved multi-step process.

i. `text(Show difference in flow rate)\ (D) = t`

`D`	`= (2 + t^2/(t+1))-(1+ 1/(t+1))`
	`= (2(t+1) + t^2)/(t+1)-((t+1) + 1)/(t + 1)`
	`= (2t + 2 + t^2-t-2)/(t + 1)`
	`= (t^2 + t)/(t + 1)`
	`= (t (t + 1))/(t + 1)`
	`= t\ \ \ … text(as required)`

ii. `text(Difference in Volume)`

♦♦♦ Mean mark 15%
MARKER’S COMMENT: Few students were able to answer this part. Previous parts of any question should be front and centre of your thinking when working out strategies.

`= int_0^4 (2 + t^2/(1+ t))\ dt\-int_0^4 (1 + t/(1+t))\ dt`

`= int_0^4 t\ dt\ \ \ \ \ text{(using part(i))}`

`= [t^2/2]_0^4`

`= 16/2\ – 0`

` = 8`

`:.\ text(There is 8 litres more of liquid)\ A\ text(than)\ B.`

Plane Geometry, 2UA 2011 HSC 9a

The diagram shows `Delta ADE`, where `B` is the midpoint of `AD` and `C` is the midpoint of `AE`. The intervals `BE` and `CD` meet at `F`.

Explain why `Delta ABC` is similar to `Delta ADE`. (1 marks)
Hence, or otherwise, prove that the ratio `BF : FE = 1: 2`. (2 marks)

Show Answers Only

`text(Proof) text{(See Worked Solutions)}`
`text(Proof) text{(See Worked Solutions)}`

Show Worked Solution

(i) `/_ BAC\ text(is common)`

`(AB)/(AD) = (AC)/(AE) = 1/2`

`:.\ Delta ABC\ text(is similar to)\ Delta ADE`

`text{(two sides are in the same ratio and the}`

`\ \ text{included angle is equal)}`

♦♦ Mean mark 22%.
TIP: Proving similarity via (AAA) test only requires proving 2 angles are equal because the remaining angle then must be equal – this will help save time in proofs.

(ii)

`/_ ABC = /_ ADE\ \ \ `	`text{(corresponding angles of}`
	`\ \ text{similar triangles)}`
`:. BC\ text(\|\|)\ DE\ \ text{(corresponding angles are equal)}`

`/_ FED`	`= /_ FBC\ text{(alternate,}\ BC\ text(\|\|)\ DEtext{)}`
`/_ FDE`	`= /_ FCB\ text{(alternate,}\ BC\ text(\|\|)\ DEtext{)}`
`:.\ Delta FED\ text(\|\|\|)\ Delta FBC\ \ \ text{(equiangular)}`

`=>(BF)/(FE) = (BC)/(ED)= 1/2`

`text{(corresponding sides of similar triangles)}`

`:. BF : FE = 1 : 2\ \ \ text(… as required).`

Calculus, 2ADV C3 2012 HSC 14a

A function is given by `f(x) = 3x^4 + 4x^3-12x^2`.

Find the coordinates of the stationary points of `f(x)` and determine their nature. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Hence, sketch the graph `y = f(x)` showing the stationary points. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
For what values of `x` is the function increasing? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
For what values of `k` will `f(x) = 3x^4 + 4x^3-12x^2 + k = 0` have no solution? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{MAX at (0,0), MINs at (1, –5) and (–2, –32)}`
`f(x)\ text(is increasing for)\ -2 < x < 0\ text(and)\ x > 1`
`text(No solution when)\ k > 32`

Show Worked Solution

i.	`f(x)`	`= 3x^4 + 4x^3-12x^2`
	`f^{′}(x)`	`= 12x^3 + 12x^2-24x`
	`f^{″}(x)`	`= 36x^2 + 24x-24`

`text(Stationary points when)\ f^{′}(x) = 0`

`12x^3 + 12x^2-24x`	`=0`
`12x(x^2 + x-2)`	`=0`
`12x (x+2) (x-1)`	`=0`

`:.\ text(Stationary points at)\ x=0,\ 1\ text(or)\ -2`

`text(When)\ x=0,\ \ \ \ f(0)=0`
`f^{″}(0)`	`= -24 < 0`
`:.\ text{MAX at (0,0)}`

`text(When)\ x=1`

`f(1)`	`= 3+4-12 = -5`
`f^{″}(1)`	`= 36 + 24-24 = 36 > 0`
`:.\ text{MIN at}\ (1,-5)`

`text(When)\ x=–2`

`f(-2)`	`=3(-2)^4 + 4(-2)^3-12(-2)^2`
	`= 48-32-48`
	`= -32`
`f^{″}(-2)`	`= 36(-2)^2 + 24(-2)-24`
	`=144-48-24 = 72 > 0`
`:.\ text{MIN at (–2, –32)}`

ii.

♦ Mean mark 42%
MARKER’S COMMENT: Be careful to use the correct inequality signs, and not carelessly include ≥ or ≤ by mistake.

iii.	`f(x)\ text(is increasing for)`
	`-2 < x < 0\ text(and)\ x > 1`

iv. `text(Find)\ k\ text(such that)`

♦♦♦ Mean mark 12%.

`3x^4 + 4x^3-12x^2 + k = 0\ text(has no solution)`

`k\ text(is the vertical shift of)\ \ y = 3x^4 + 4x^3-12x^2`

`=>\ text(No solution if it does not cross the)\ x text(-axis.)`

`:.\ text(No solution when)\ k > 32`

Calculus, EXT1* C3 2011 HSC 8b

The diagram shows the region enclosed by the parabola `y = x^2`, the `y`-axis and the line `y = h`, where `h > 0`. This region is rotated about the `y`-axis to form a solid called a paraboloid. The point `C` is the intersection of `y = x^2` and `y = h`.

The point `H` has coordinates `(0, h)`.

Find the exact volume of the paraboloid in terms of `h`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
A cylinder has radius `HC` and height `h`.

What is the ratio of the volume of the paraboloid to the volume of the cylinder? (1 mark)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`(pi h^2)/2\ text(u³)`
`1:2`

Show Worked Solution

IMPORTANT: Most common errors: 1-use the correct axis, and 2-check the limits!

i.	`V`	`= pi int_0^h x^2\ dy`
		`= pi int_0^h y\ dy`
		`= pi [1/2 y^2]_0^h`
		`= pi (1/2 h^2)`
		`= (pi h^2)/2 \ text(u³)`

`:.\ text(The volume of the paraboloid is)\ (pi h^2)/2\ text(u³)`

ii. `text(Radius of cylinder)\ (r) = HC`

`text(Find)\ x text(-coordinate of)\ C:`

♦♦ Mean mark of 24%.

`text(When)\ y`	`=h`
`=> x^2`	`= h`
`x`	`= sqrt h`
`:. r`	`= sqrth`

`text(Volume of cylinder)`	`= pi r^2 h`
	`= pi (sqrth)^2 h`
	`= pi h^2`

`:.\ text(Volume of paraboloid : volume of cylinder)`

`= (pi h^2)/2 : pi h^2`

`= 1:2`

Plane Geometry, 2UA 2013 HSC 16c

The diagram shows triangles `ABC` and `ABD` with `AD` parallel to `BC`. The sides `AC` and `BD` intersect at `Y`. The point `X` lies on `AB` such that `XY` is parallel to `AD` and `BC`.

Prove that `Delta ABC` is similar to `Delta AXY`. (2 marks)
Hence, or otherwise, prove that `1/(XY) = 1/(AD) + 1/(BC)`. (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`text(Prove)\ Delta ABC\ text(|||)\ Delta AXY`

COMMENT: A great example of easy marks that appear in the early stages of the final questions.

`/_YAX\ text(is common)`

`/_AYX= /_ACB\ \ \ text{(corresponding, YX || CB)}`

`:.\ Delta ABC\ text(|||)\ Delta AXY\ \ \ text{(equiangular)}`

(ii) `text(Need to prove)\ 1/(XY) = 1/(AD) + 1/(BC)`

♦♦♦ Mean mark 13%.
COMMENT: The presence of `AD` in the required proof should alert students to the strategy of finding another set of congruent triangles where this side can be utilised.

`text(Using part)\ text{(i)}`

`=>(AX)/(AB) = (XY)/(BC)`

`text(Similarly,)\ Delta ABD\ text(|||)\ Delta XBY\ \ text{(equiangular)}`

`(BX)/(AB) = (XY)/(AD)`

`text(Adding the identities)`

`(AX)/(AB) + (BX)/(AB)`	`= (XY)/(BC) + (XY)/(AD)`
`( (AX + BX) )/(AB)`	`= XY (1/(BC) + 1/(AD) )`
`(AB)/(AB)`	`= XY (1/(AD) + 1/(BC))\ \ \ \ (text(Note)\ AX + BX = AB text{)}`
`1`	`= XY (1/(AD) + 1/(BC))`
`1/(XY)`	`= 1/(AD) + 1/(BC)\ \ \ text(… as required)`

Functions, 2ADV F2 2013 HSC 15c

Sketch the graph `y = |2x-3|`. (1 mark)

--- 6 WORK AREA LINES (style=lined) ---
Using the graph from part (i), or otherwise, find all values of `m` for which the equation `|2x-3| = mx + 1` has exactly one solution. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(When)\ m = -2/3,\ m >= 2\ text(or)\ m<-2`

Show Worked Solution

♦ Mean mark 49%
MARKER’S COMMENT: Many students drew diagrams that were “too small”, didn’t use rulers or didn’t use a consistent scale on the axes!

ii.

`text(Line of intersection)\ \ y=mx + 1\ \ text(passes through)\ (0,1)`

♦♦ Mean mark 25%.
COMMENT: A clear graphical understanding of what the solution is crucial here.

`text(If it also passes through)\ (1.5, 0) => text(1 solution)`

`m=(y_2-y_1)/(x_2-x_1)= (1-0)/(0-3/2)=-2/3`

`text(Gradients of)\ \ y=|2x-3| => 2\ \text(or)\ -2`

`text(Considering a line through)\ (0,1):`

`text(If)\ \ m >= 2\ text(, only intersects once.)`

`text(Similarly,)`

`text(If)\ \ m<-2 text(, only intersects once.)`

`:.\ text(Only one solution when)\ \ m = -2/3,\ \ m >= 2\ \ text(or)\ \ m<-2`

Integration, 2UA 2013 HSC 15a

The diagram shows the front of a tent supported by three vertical poles. The poles are 1.2 m apart. The height of each outer pole is 1.5 m, and the height of the middle pole is 1.8 m. The roof hangs between the poles.

The front of the tent has area `A\ text(m²)`.

Use the trapezoidal rule to estimate `A`. (1 mark)
Use Simpson’s rule to estimate `A`. (1 mark)
Explain why the trapezoidal rule gives the better estimate of `A`. (1 mark)

Show Answers Only

`3.96\ text(m²)`
`4.08\ text(m²)`
`text(S)text(ince the tent roof is concave up, the)`
`text(trapezoidal rule uses straight lines and Simpson’s)`
`text(Rule assumes a concave down arc, the trapezoidal)`
`text(rule will be more accurate)\ text{(as per diagram)}`

Show Worked Solution

(i)	`A`	`~~ h/2 [y_0 + 2y_1 + y_2]`
		`~~ 1.2/2 [1.5 + (2 xx 1.8) + 1.5]`
		`~~ 0.6 [6.6]`
		`~~ 3.96\ text(m²)`

(ii)	`A`	`~~ h/3 [y_0 + 4y_1 + y_2]`
		`~~1.2/3 [1.5 + (4 xx 1.8) + 1.5]`
		`~~ 0.4 [10.2]`
		`~~ 4.08\ text(m²)`

♦♦♦ This proved the hardest mark to get in the whole 2013 HSC paper with a mean mark of just 3%!
MARKER’S COMMENT: Ensure you understand the different lines that result from using Simpson’s Rule vs the Trapezoidal Rule. Drawing a sketch is often the clearest way to explain (see Worked Solutions).

(iii)

`text(S)text(ince the tent roof is concave up, the)`

`text(trapezoidal rule uses straight lines and Simpson’s)`

`text(Rule assumes a concave down arc, the trapezoidal)`

`text(rule will be more accurate)\ text{(as per diagram)}`

Calculus, 2ADV C4 2013 HSC 14d

The diagram shows the graph `f(x)`.

What is the value of `a`, where `a > 0`, so that `int_-a^a f(x)\ dx = 0`? (1 mark)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

`a=4.5`

Show Worked Solution

`text(If)\ int_-a^a f(x)\ dx =0`

♦♦♦ A devilish 1-mark question mid-paper that had a mean mark of just 12%.
MARKER’S COMMENT: The fact that this question was worth only 1 mark means that it is not necessary for students to show any detailed working.

`text(We know the area below the curve)`

`text(and above the)\ x text(-axis = area above the)`

`text(curve and below the)\ x text(-axis.)`

`text(By inspection, we can see)`

`int_-3^-1 f(x)\ dx=0\ \ text(and)\ \ int_2^3 f(x)\ dx= 0`

`text(We need)\ int_3^a f(x)\ dx + int_-a^-3 f(x)\ dx`	`=-3`
`text(because)\ \ int_-1^2 f(x)\ dx=3`

`=>\ text(S)text(ince areas have height = 1, each)`

`text(must be 1.5 units wide.)`

`:. a = 4.5`

Calculus, EXT1* C1 2013 HSC 10 MC

A particle is moving along the `x`-axis. The displacement of the particle at time `t` seconds is `x` metres.

At a certain time, `dot x = -3\ text(ms)^(-1)` and `ddot x = 2\ text(ms)^(-2)`.

Which statement describes the motion of the particle at that time?

The particle is moving to the right with increasing speed.
The particle is moving to the left with increasing speed.
The particle is moving to the right with decreasing speed.
The particle is moving to the left with decreasing speed.

Show Answers Only

`D`

Show Worked Solution

♦♦ Mean mark 26%.

`text(S)text(ince)\ dot x = -3 text(ms)`^-1

`=>\ text(Particle is moving to the left)`

`text(S)text(ince)\ ddot x = 2 text(ms)`^-2

`=>\ text(Acceleration is to the right, against)`

`text(the particle’s motion)`

`:.\ text(Speed is decreasing)`

`=> D`

Financial Maths, STD2 F4 2011 HSC 28b

Norman and Pat each bought the same type of tractor for $60 000 at the same time. The value of their tractors depreciated over time.

The salvage value `S`, in dollars, of each tractor, is its depreciated value after `n` years.

Norman drew a graph to represent the salvage value of his tractor.

Find the gradient of the line shown in the graph. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
What does the value of the gradient represent in this situation? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Write down the equation of the line shown in the graph. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Find all the values of `n` that are not suitable for Norman to use when calculating the salvage value of his tractor. Explain why these values are not suitable. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Pat used the declining balance formula for calculating the salvage value of her tractor. The depreciation rate that she used was 20% per annum.

What did Pat calculate the salvage value of her tractor to be after 14 years? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Using Pat’s method for depreciation, describe what happens to the salvage value of her tractor for all values of `n` greater than 15. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Gradient) =-4000`
`text(The amount the tractor depreciates each year.)`
`S = 60\ 000\-4000n`
`text(It is unsuitable to use)`
`n<0\ text(because time must be positive)`
`n>15\ text(because the tractor has no more value after 15 years and)`
`text(therefore can’t depreciate further.)`
`text(After 14 years, the tractor is worth $2638.83)`
`text(As)\ n\ text(increases above 15 years,)\ S\ text(decreases but remains)>0.`

Show Worked Solution

♦♦♦ Mean mark 14%
COMMENT: The intercepts of both axes provide points where the gradient can be quickly found.

i.	`text(Gradient)`	`= text(rise)/text(run)`
		`= (- 60\ 000)/15`
		`=-4000`

♦ Mean mark 37%

ii. `text(The amount the tractor depreciates each year)`

♦♦ Mean mark 28%
COMMENT: Using the general form `y=mx+b` is quick here because you have the gradient (from part (i)) and the `y`-intercept is obviously `60\ 000`.

iii.	`text(S)text(ince)\ \ S = V_0\-Dn`
	`:.\ text(Equation of graph:)`
	`S = 60\ 000-4000n`

iv. `text(It is unsuitable to use)`

♦♦♦ Mean mark 20%

`n<0,\ text(because time must be positive:)`

`n>15,\ text(because it has no more value after 15)`

`text(years and therefore can’t depreciate further.)`

v.	`text(Using)\ S = V_0 (1-r)^n\ \ text(where)\ r = text(20%,)\ n = 14`

`S`	`= 60\ 000 (1\-0.2)^14`
	`= 60\ 000 (0.8)^14`
	`= 2\ 638.8279…`

`:.\ text(After 14 years, the tractor is worth $2638.83`

♦ Mean mark 37%

vi.	`text(As)\ n\ text(increases above 15 years,)\ S\ text(decreases)`
	`text(but remains > 0.)`

`text(Distance)\ \ barx`	`=2.8`
`s_x`	`≈1.822`