Solve the following simultaneous equations
\(6 x-7 y=-6\)
\(4 x+2 y=16\) (2 marks)
--- 9 WORK AREA LINES (style=lined) ---
Aussie Maths & Science Teachers: Save your time with SmarterEd
Solve the following simultaneous equations
\(6 x-7 y=-6\)
\(4 x+2 y=16\) (2 marks)
--- 9 WORK AREA LINES (style=lined) ---
\(x=\dfrac{5}{2}, \ y=3\)
\(6x-7y=-6\ \ldots\ (1)\)
\(4x+2y=16\ \ldots\ (2)\)
\(\text{Mult \((1) \times 2\ \) and \(\ (2) \times 3\):}\)
\(12 x-14 y=-12\ \ldots\ \left(1^{\prime}\right)\)
\(12 x+6 y=48\ \ldots\ \left(2^{\prime}\right)\)
\(\text{Subtract}\ \ \left(2^{\prime}\right)-\left(1^{\prime}\right):\)
\(20 y=60 \ \Rightarrow \ y=3\)
\(\text{Substitute} \ \ y=3 \ \ \text{into (2):}\)
\(4 x+6=16 \ \Rightarrow \ x=\dfrac{5}{2}\)
Solve the following simultaneous equations:
\(3 x-4 y=5\)
\(x+2 y=15\). (2 marks)
--- 8 WORK AREA LINES (style=lined) ---
\(x=7, \ y=4\)
\(3 x-4 y=5\ \ldots\ (1)\)
\( x+2 y=15\ \ldots\ (2)\)
\(\text{Multiply (2)} \times 3:\)
\(3 x+6 y=45\ \ldots\ \left(2^{\prime}\right) \)
\(\text{Subtract} \ \left(2^{\prime}\right)-(1)\) :
\(10 y=40 \ \Rightarrow \ y=4\)
\(\text{Substitute} \ \ y=4 \ \ \text{into (2):}\)
\(x+2 \times 4=15 \ \Rightarrow x=7\)
--- 8 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
a. \(\text{Proof (See Worked Solutions)}\)
b. \(\text{Proof (See Worked Solutions)}\)
a. \(A(0,4), C(4,1)\)
\(m_{AC}=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{1-4}{4-0}=-\dfrac{3}{4}\)
\(\text{Equation of line with} \ \ m=-\dfrac{3}{4} \ \ \text{through}\ (0,4):\)
| \(y-y_1\) | \(=m\left(x-x_1\right)\) |
| \(y-4\) | \(=-\dfrac{3}{4}(x-0)\) |
| \(y-4\) | \(=-\dfrac{3}{4} x\) |
| \(4 y-16\) | \(=-3 x\) |
| \(3 x+4 y-16\) | \(=0\) |
b. \(B(3,0), C(4,1)\)
\(m_{BC}=\dfrac{1-0}{4-3}=1\)
\(m_{AC} \times m_{BC}=-\dfrac{4}{3} \times 1=-\dfrac{4}{3} \neq-1\)
\(\therefore AC \ \text{is not} \ \perp \text{to} \ BC.\)
The diagram shows a line `l_1`, with equation `3x + 4y-12 = 0`, which intersects the `y`-axis at `B`.
A second line `l_2`, with equation `4x-3y = 0`, passes through the origin `O` and intersects `l_1` at `E`.
--- 3 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
a. `\text{See Worked Solution}`
b. `\text{See Worked Solution}`
a. `B\ text(is)\ y text(-intercept of)\ l_1`
`text(When)\ x = 0:`
`(3 xx 0) + 4y-12=0\ \ =>\ \ y=3`
`:.\ B\ text(is)\ (0,3)`
| b. | `l_1:\ \ 3x + 4y -12` | `= 0` |
| `4y` | `= -3x + 12` | |
| `y` | `= -3/4x + 3` |
`m(l_1)=-3/4`
| `l_2:\ \ 4x-3y` | `= 0` |
| `3y` | `= 4x` |
| `y` | `= 4/3 x` |
`m(l_2)=4/3`
`m (l_1) xx m (l_2)= -3/4 xx 4/3= -1`
`:.\ l_1\ text(and)\ l_2\ text(are perpendicular)`
--- 5 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
a. \(y=\dfrac{4-1}{-3-2}=-\dfrac{3}{5}\)
b. \(\text {Substitute}\ (7,-2) \ \text{into equation:}\)
| \(-2\) | \(=-\dfrac{3}{5} \times 7+\dfrac{11}{5}\) |
| \(-2\) | \(=-\dfrac{21}{5}+\dfrac{11}{5}\) |
| \(-2\) | \(=-2 \ \text{(correct)}\) |
\(\therefore (7,-2) \text{ lies on line.}\)
a. \((2,1),(-3,4)\)
\(\text{Gradient}=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{4-1}{-3-2}=-\dfrac{3}{5}\)
\(\text{Find equation with} \ \ m=-\dfrac{3}{5} \ \ \text{through}\ \ (2,1):\)
| \(y-1\) | \(=-\dfrac{3}{5}(x-2)\) |
| \(y\) | \(=-\dfrac{3}{5} x+\dfrac{11}{5}\) |
b. \(\text {Substitute}\ (7,-2)\ \text{into equation:}\)
| \(-2\) | \(=-\dfrac{3}{5} \times 7+\dfrac{11}{5}\) |
| \(-2\) | \(=-\dfrac{21}{5}+\dfrac{11}{5}\) |
| \(-2\) | \(=-2 \ \text{(correct)}\) |
\(\therefore (7,-2) \text{ lies on line.}\)
Consider the function shown.
Which of the following could be the equation of this function?
\(C\)
\(\text {Gradient is negative (top left } \rightarrow \text { bottom right)}\)
\(y \text{-intercept = 3 (only positive option)}\)
\(\Rightarrow C\)
Prove that the line between \((1,-1)\) and \((4,-3)\) is perpendicular to the line \(3x-2y-4=0\) (2 marks) --- 6 WORK AREA LINES (style=lined) ---
\(\text {Perpendicular lines}\ \ \Rightarrow\ m_1 \times m_2 = -1\)
\(\text {Line 1 gradient:}\)
\(P_1 (1,-1), P_2(4,-3) \)
\(m_1=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{-3+1}{4-1}=-\dfrac{2}{3}\)
\(\text {Line 2 gradient:}\)
\(3x-2y-4=0\ \ \Rightarrow \ y= \dfrac{3}{2}x-2\ \ \Rightarrow m_2=\dfrac{3}{2}\)
\(m_1 \times m_2 = -\dfrac{2}{3} \times \dfrac{3}{2} = -1\)
\(\therefore\ \text{Lines are perpendicular.}\)
\(\text {Perpendicular lines}\ \ \Rightarrow\ m_1 \times m_2 = -1\)
\(\text {Line 1 gradient:}\)
\(P_1 (1,-1), P_2(4,-3) \)
\(m_1=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{-3+1}{4-1}=-\dfrac{2}{3}\)
\(\text {Line 2 gradient:}\)
\(3x-2y-4=0\ \ \Rightarrow \ y= \dfrac{3}{2}x-2\ \ \Rightarrow m_2=\dfrac{3}{2}\)
\(m_1 \times m_2 = -\dfrac{2}{3} \times \dfrac{3}{2} = -1\)
\(\therefore\ \text{Lines are perpendicular.}\)
Which of the following could be the graph of `y= -2 x+2`?
`A`
`text{By elimination:}`
`y text{-intercept = 2 → Eliminate}\ B and C`
`text{Gradient is negative → Eliminate}\ D`
`=>A`
There are two tanks on a property, Tank `A` and Tank `B`. Initially, Tank `A` holds 1000 litres of water and Tank B is empty.
By drawing a line on the grid (above), or otherwise, find the value of `t` when the two tanks contain the same volume of water. (2 marks)
--- 2 WORK AREA LINES (style=lined) ---
a. `text{T} text{ank} \ A \ text{will pass trough (0, 1000) and (50, 0)}`
b. `text{T} text{ank} \ B \ text{will pass through (15, 0) and (45, 900)}`
`text{By inspection, the two graphs intersect at} \ \ t = 29 \ text{minutes}`
c. `text{Strategy 1}`
`text{By inspection of the graph, consider} \ \ t = 45`
`text{T} text{ank A} = 100 \ text{L} , \ text{T} text{ank B} =900 \ text{L} `
`:.\ text(Total volume = 1000 L when t = 45)`
`text{Strategy 2}`
| `text{Total Volume}` | `=text{T} text{ank A} + text{T} text{ank B}` |
| `1000` | `= 1000 – 20t + (t – 15) xx 30` |
| `1000` | `= 1000 – 20t + 30t – 450 ` |
| `10t` | `= 450` |
| `t` | `= 45 \ text{minutes}` |
The relationship between British pounds `(p)` and Australian dollars `(d)` on a particular day is shown in the graph.
--- 2 WORK AREA LINES (style=lined) ---
Convert 93 100 Japanese yen to British pounds. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
a. `m = text(rise)/text(run) = 4/7`
`p = 4/7 d`
b. `text(Yen to Australian dollars:)`
| `y` | `=76d` |
| `93\ 100` | `= 76d` |
| `d` | `= (93\ 100)/76= 1225` |
`text(Aust dollars to pounds:)`
`p= 4/7 xx 1225= 700\ text(pounds)`
`:. 93\ 100\ text(Yen = 700 pounds)`
Last Saturday, Luke had 165 followers on social media. Rhys had 537 followers. On average, Luke gains another 3 followers per day and Rhys loses 2 followers per day.
If `x` represents the number of days since last Saturday and `y` represents the number of followers, which pair of equations model this situation?
| A. | `text(Luke:)\ \ y = 165x + 3`
`text(Rhys:)\ \ y = 537x - 2` |
| B. | `text(Luke:)\ \ y = 165 + 3x`
`text(Rhys:)\ \ y = 537 - 2x` |
| C. | `text(Luke:)\ \ y = 3x + 165`
`text(Rhys:)\ \ y = 2x - 537` |
| D. | `text(Luke:)\ \ y = 3 + 165x`
`text(Rhys:)\ \ y = 2 - 537x` |
`B`
`text(Luke starts with 165 and adds 3 per day:)`
`y = 165 + 3x`
`text(Rhys starts with 537 and loses 2 per day:)`
`y = 537 – 2x`
`=> B`
Damon owns a swim school and purchased a new pool pump for $3250.
He writes down the value of the pool pump by 8% of the original price each year.
--- 1 WORK AREA LINES (style=lined) ---
--- 8 WORK AREA LINES (style=lined) ---
Ita publishes and sells calendars for $25 each. The cost of producing the calendars is $8 each plus a set up cost of $5950.
How many calendars does Ita need to sell to breakeven? (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`350`
`text(Let)\ \ x =\ text(number of calendars sold)`
`text(C)text(ost) = 5950 + 8x`
`text(Sales revenue) = 25x`
`text(Breakeven occurs when:)`
| `25x` | `= 5950 + 8x` |
| `17x` | `= 5950` |
| `:. x` | `= 350` |
Solve `1 - 3x > 10`. (2 marks)
`x < -3`
| `1 – 3x` | `> 10` |
| `-3x` | `> 9` |
| `x` | `< -3` |
What is the `x`-intercept of the line `x + 3y + 6 = 0`?
`A`
`x text(-intercept occurs when)\ y = 0:`
| `x + 0 + 6` | `= 0` |
| `x` | `= -6` |
`:. x text{-intercept is}\ (-6, 0)`
`=> A`
What is the gradient of the line `2x + 3y + 4 = 0`?
`A`
| `2x + 3y + 4` | `= 0` |
| `3y` | `= -2x-4` |
| `y` | `= -2/3 x-4/3` |
| `:.\ text(Gradient)` | `= -2/3` |
`=> A`
The diagram shows points `A(1, 0), B(2, 4)` and `C(6, 1).` The point `D` lies on `BC` such that `AD _|_ BC.`
--- 6 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
i. `text(Proof)\ \ text{(See Worked Solutions)}`
ii. `m_(AD)=4/3`
i. `B (2, 4),\ \ C (6, 1)`
`m_(BC) = (y_2-y_1)/(x_2-x_1) = (1-4)/(6-2) =-3/4`
`text(Equation of)\ \ BC,\ \ m=-3/4\ \ text(through)\ \ (2, 4):`
| `y-y_1` | `= m(x-x_1)` |
| `y-4` | `=-3/4 (x-2)` |
| `4y-16` | `= -3x + 6` |
| `3x + 4y-22` | `= 0\ text(… as required.)` |
ii. `\text{Perpendicular lines:}\ m_1 xx m_2 = -1`
`m_(BC) =-3/4\ \ =>\ \ m_(AD)=4/3\ (BC _|_ AD)`
Find the equation of the line that passes through the point `(1, 3)` and is perpendicular to `2x + y + 4 = 0`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`x-2y + 7 = 0`
| `2x + y + 4` | `= 0` |
| `y` | `= -2x-4` |
`=>\ text(Gradient) = -2`
`:. text(⊥ gradient) = 1/2\ \ \ (m_1 m_2=-1)`
`text(Equation of line)\ \ m = 1/2, \ text(through)\ (1, 3):`
| `y-y_1` | `= m (x-x_1)` |
| `y-3` | `= 1/2 (x-1)` |
| `y` | `= 1/2 x + 5/2` |
| `2y` | `= x + 5` |
| `:. x-2y + 5` | `= 0` |
Ariana’s parents have given her an interest‑free loan of $4800 to buy a car. She will pay them back by paying `$x` immediately and `$y` every month until she has repaid the loan in full.
After 18 months Ariana has paid back $1510, and after 36 months she has paid back $2770.
This information can be represented by the following equations.
`x + 18y = 1510`
`x + 36y = 2770`
i.
`:.\ text(Solution is)\ \ x = 250, \ y = 70`
ii. `text(Let)\ \ A = text(the amount paid back after)\ n\ text(months)`
`A = 250 + 70n`
`text(Find)\ n\ text(when)\ A = 4800`
| `250 + 70n` | `= 4800` |
| `70n` | `= 4550` |
| `n` | `= 65` |
`:.\ text(It will take Ariana 65 months to repay)`
`text(the loan in full.)`
What is the slope of the line with equation `2x-4y + 3 = 0`?
`C`
| `2x-4y + 3` | `= 0` |
| `4y` | `= 2x + 3` |
| `y` | `= 1/2 x + 3/4` |
`=> C`
Solve `3-5x <= 2`. (2 marks)
`x >= 1/5`
| `3-5x` | `<= 2` |
| `-5x` | `<= -1` |
| `x` | `>= 1/5` |
Sue and Mikey are planning a fund-raising dance. They can hire a hall for $400 and a band for $300. Refreshments will cost them $12 per person.
--- 2 WORK AREA LINES (style=lined) ---
The graph shows planned income and costs when the ticket price is $20
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
Sue and Mikey plan to sell 200 tickets. They want to make a profit of $1500.
--- 6 WORK AREA LINES (style=lined) ---
| i. | `$C` | `= 400 + 300 + (12 xx x)` |
| `= 700 + 12x` |
ii. `text(Using the graph intersection)`
`text(Approximately 90 people are needed)`
`text(to cover the costs.)`
iii. `text(If 150 people attend)`
| `text(Income)` | `= 150 xx $20` |
| `= $3000` |
| `text(C)text(osts)` | `= 700 + (12 xx 150)` |
| `= $2500` |
| `:.\ text(Profit)` | `= 3000 − 2500` |
| `= $500` |
iv. `text(C)text(osts when)\ x = 200:`
| `C` | `= 700 + (12 xx 200)` |
| `= $3100` |
`text(Income required to make $1500 profit)`
`= 3100 + 1500`
`= $4600`
| `:.\ text(Price per ticket)` | `= 4600/200` |
| `= $23` |
Fiona and John are planning to hold a fund-raising event for cancer research. They can hire a function room for $650 and a band for $850. Drinks will cost them $25 per person.
--- 1 WORK AREA LINES (style=lined) ---
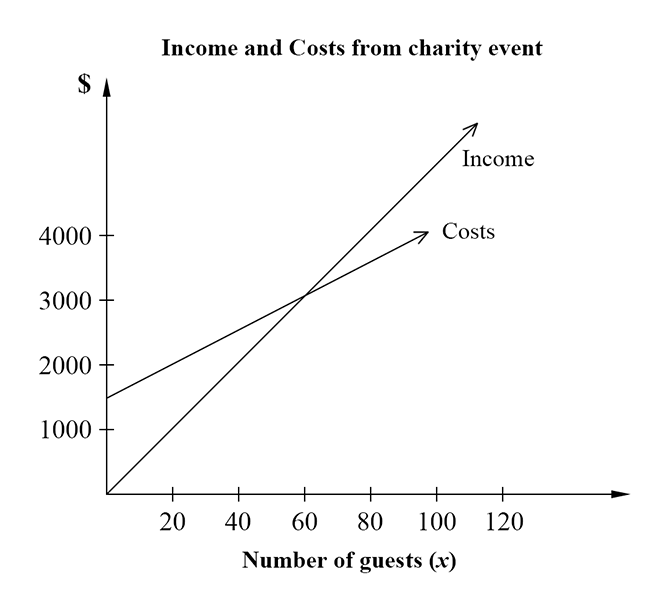
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
| i. | `text(Fixed C) text(osts)` | `= 650 + 850` |
| `= $1500` |
`text(Variable C) text(osts) = $25x`
`:.\ $C = 1500 + 25x`
| ii. | `text(From the graph)` |
| `text(C) text(osts = Income when)\ x = 60` | |
| `text{(i.e. where graphs intersect)}` |
iii. `text(When)\ \ x = 80:`
| `text(Income)` | `= 80 xx 50` | |
| `= $4000` |
| `$C` | `= 1500 + 25 xx 80` |
| `= $3500` |
| `:.\ text(Profit)` | `= 4000 – 3500` |
| `= $500` |
A clubhouse uses four long-life light globes for five hours every night of the year. The purchase price of each light globe is $6.00 and they each cost `$d` per hour to run.
--- 4 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
What is the mean life, in hours, of these light globes if 97.5% will last up to 5000 hours? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
a. `text(Purchase price) = 4 xx 6 = $24`
| `text(Running cost)` | `= text(# Hours) xx text(Cost per hour)` |
| `= 4 xx 5 xx 365 xx d= 7300d` |
`:.\ $c = 24 + 7300d`
b. `text(Given)\ \ $c = $250`
| `250` | `= 24 + 7300d` |
| `7300d` | `= 226` |
| `d` | `= 226/7300= 0.03095…` |
| `= 0.031\ $ text(/hr)\ text{(3 d.p.)}` |
c. `text(If)\ d\ text(doubles to 0.062)\ \ $text(/hr)`
`$c= 24 + 7300 xx 0.062= $476.60`
`text(S) text(ince $476.60 is less than)\ 2 xx $250\ ($500),`
`text(the total cost increases to less than double)`
`text(the original cost.)`
d. `sigma = 170`
`z\ text(-score of 5000 hours) = 2`
| `z` | `= (x – mu)/sigma` |
| `2` | `= (5000 – mu)/170` |
| `340` | `= 5000 – mu` |
| `mu` | `= 4660` |
`:.\ text(The mean life of these globes is 4660 hours.)`
Which equation represents the line perpendicular to `2x-3y = 8`, passing through the point `(2, 0)`?
`B`
| `2x-3y` | `= 8` |
| `3y` | `= 2x-8` |
| `y` | `= 2/3x-8/3` |
`m= 2/3`
`:.\ m_text(perp)= -3/2\ \ \ (m_1 m_2=-1\text( for)_|_text{lines)}`
`text(Equation of line)\ \ m = -3/2\ \ text(through)\ \ (2,0):`
| `y-y_1` | `= m (x-x_1)` |
| `y-0` | `= -3/2 (x-2)` |
| `y` | `= -3/2x + 3` |
| `2y` | `= -3x + 6` |
| `3x + 2y` | `= 6` |
`=> B`
In the diagram, the points `A` and `C` lie on the `y`-axis and the point `B` lies on the `x`-axis. The line `AB` has equation `y = sqrt3x-3`. The line `BC` is perpendicular to `AB`.
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
i. `text(Gradient of)\ \ AB = sqrt 3`
`:. m_(BC) = -1/(sqrt3)\ \ (BC _|_ AB)`
`text(Finding)\ B,`
| `0` | `= sqrt3 x-3` |
| `sqrt 3 x` | `= 3` |
| `x` | `= 3/sqrt3 xx sqrt3/sqrt3= sqrt3` |
`:. B (sqrt3, 0)`
`text(Equation of)\ \ BC\ \ text(has)\ \ m =-1/sqrt3\ \ text(through)\ \ (sqrt3, 0):`
| `y\-y_1` | `= m (x\-x_1)` |
| `y\-0` | `=-1/sqrt3 (x\-sqrt3)` |
| `y` | `=-1/sqrt3 x +1` |
ii. `AB\ \ text(cuts)\ y text(-axis when)\ \ x = 0, \ \ y=-3`
`=> A (0,–3)`
`BC\ \ text(cuts)\ y text(-axis when)\ \ x = 0, \ \ y=1`
`=> C (0,1)`
| `:. AC` | `= 4` |
| `OB` | `= sqrt 3` |
| `text(Area)\ \ Delta ABC` | `= 1/2 xx AC xx OB` |
| `= 1/2 xx 4 xx sqrt 3` | |
| `= 2 sqrt 3\ text(u²)` |
Solve `2 -3x <= 8`. (2 marks)
`x>=-2`
| `2 -3x` | `<= 8` |
| `-3x` | `<= 6` |
| `x` | `>= – 6/3` |
| `x` | `>= -2` |
The graph shows tax payable against taxable income, in thousands of dollars.

--- 1 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
| a. |  |
`text(Income on)\ $21\ 000=$3000\ \ \ text{(from graph)}`
b. `text(Using the points)\ (21,3)\ text(and)\ (39,9)`
| `text(Gradient at)\ A` | `= (y_2\-y_1)/(x_2\ -x_1)` |
| `= (9000-3000)/(39\ 000-21\ 000)` | |
| `= 6000/(18\ 000)` | |
| `= 1/3\ \ \ \ \ text(… as required)` |
c. `text(The gradient represents the tax applicable to each dollar)`
| `text(Tax)` | ` = 1/3\ text(of each dollar earned)` |
| ` = 33 1/3\ text(cents per dollar earned)` |
d. `text( Tax payable up to $21 000 = $3000)`
`text(Tax payable on income between $21 000 and $39 000)`
` = 1/3 (I\-21\ 000)`
| `:.\ text(Tax payable on)\ \ I` | `= 3000 + 1/3 (I\-21\ 000)` |
| `= 3000 + 1/3 I\-7000` | |
| `= 1/3 I\-4000` |
A function centre hosts events for up to 500 people. The cost `C`, in dollars, for the centre
to host an event, where `x` people attend, is given by:
`C = 10\ 000 + 50x`
The centre charges $100 per person. Its income `I`, in dollars, is given by:
`I = 100x`
How much greater is the income of the function centre when 500 people attend an event, than its income at the breakeven point?
`C`
`text(When)\ x=500,\ I=100xx500=$50\ 000`
`text(Breakeven when)\ \ x=200\ \ \ text{(from graph)}`
`text(When)\ \ x=200,\ I=100xx200=$20\ 000`
| `text(Difference)` | `=50\ 000-20\ 000` |
| `=$30\ 000` |
`=> C`
A factory makes boots and sandals. In any week
• the total number of pairs of boots and sandals that are made is 200
• the maximum number of pairs of boots made is 120
• the maximum number of pairs of sandals made is 150.
The factory manager has drawn a graph to show the numbers of pairs of boots (`x`) and sandals (`y`) that can be made.
--- 2 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
Compare the profits at `B` and `C`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`=> x\ text(cannot)\ >120`
`text(S)text(ince the max amount of sandals = 150`
`=> y\ text(cannot)\ >150`
`:.\ text(The line)\ AD\ text(is only possible between)\ B\ text(and)\ C.`
a. `text{We are told the number of boots}\ (x),`
`text{and shoes}\ (y),\ text(made in any week = 200)`
`=>text(Equation of)\ AD\ text(is)\ \ x + y = 200`
b. `text(S)text(ince the max amount of boots = 120)`
`=> x\ text(cannot)\ >120`
`text(S)text(ince the max amount of sandals = 150`
`=> y\ text(cannot)\ >150`
`:.\ text(The line)\ AD\ text(is only possible between)\ B\ text(and)\ C.`
c. `text(At)\ B,\ \ x = 50,\ y = 150`
| `=>$P (text(at)\ B)` | `= 24 xx 50 + 15 xx 150` |
| `= 1200 + 2250` | |
| ` = $3450` |
`text(At)\ C,\ \ x = 120 text(,)\ y = 80`
| `=> $P (text(at)\ C)` | `= 24 xx 120 + 15 xx 80` |
| `= 2880 + 1200` | |
| `= $4080` |
`:.\ text(The profits at)\ C\ text(are $630 more than at)\ B.`