SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Quadratic, 2UA 2015 HSC 12d

For what values of `k` does the quadratic equation `x^2 – 8x + k = 0` have real roots?  (2 marks)

Show Answers Only

`k <= 16`

Show Worked Solution

`x^2 – 8x + k = 0`

`text(Real roots when)\ Delta >= 0`

`b^2 – 4ac` `>= 0`
`(-8)^2 – 4 xx 1 xx k` `>= 0`
`64 – 4k` `>= 0`
`4k` `<= 64`
`k` `<= 16`

`:.\ text(Real roots exists when)\ k <= 16`

Calculus, 2ADV C4 2015 HSC 10 MC

The diagram shows the area under the curve  `y = 2/x`  from  `x = 1`  to  `x = d`.

2012 2ua 10 mc

What value of `d` makes the shaded area equal to `2`?

  1. `e`
  2. `e + 1`
  3. `2e`
  4. `e^2`
Show Answers Only

`A`

Show Worked Solution

`int_1^d 2/x\ dx = 2`

`[2 log_e x]_1^d = 2`

`2 log_e d – 2 log_e 1` `= 2`
`2 log_e d` `= 2`
`log_e d` `= 1`
`:. d` `= e`

`=> A`

L&E, 2ADV E1 2015 HSC 8 MC

The diagram shows the graph of  `y = e^x (1 + x).`
 

How many solutions are there to the equation  `e^x (1 + x) = 1-x^2`?

  1. `0`
  2. `1`
  3. `2`
  4. `3`
Show Answers Only

`C`

Show Worked Solution

`text(The graphs intersect at 2 points)`

`:. e^x(1 + x) = 1-x^2\ text(has 2 solutions)`

`=> C`

Calculus, 2ADV C4 2015 HSC 7 MC

The diagram shows the parabola  `y = 4x - x^2`  meeting the line  `y = 2x`  at  `(0, 0)`  and  `(2, 4)`.
 

2015 2ua 7 mc
 

Which expression gives the area of the shaded region bounded by the parabola and the line?

  1. `int_0^2 x^2 - 2x\ dx`
  2. `int_0^2 2x - x^2\ dx`
  3. `int_0^4 x^2 - 2x\ dx`
  4. `int_0^4 2x - x^2\ dx`
Show Answers Only

`B`

Show Worked Solution
`text(Shaded Area)` `= int_0^2 4x – x^2\ dx – int_0^2 2x\ dx`
  `= int_0^2 4x – x^2 – 2x\ dx`
  `= int_0^2 2x – x^2\ dx`

 

`=> B`

Trig Calculus, 2UA 2015 HSC 6 MC

What is the value of the derivative of  `y = 2 sin 3x - 3 tan x`  at  `x = 0`?

(A)  `-1`

(B)     `0`

(C)     `3`

(D)  `-9`

Show Answers Only

`C`

Show Worked Solution
`y` `= 2 sin 3x – 3 tan x`
`(dy)/(dx)` `= 6 cos 3x – 3 sec^2 x`

 

`text(At)\ x = 0`

`(dy)/(dx)` `= 6 cos 0 – 3 sec^2 0`
  `= 6 (1) – 3/(cos^2 0)`
  `= 6 – 3`
  `= 3`

 `=> C`

Calculus, 2ADV C4 2015 HSC 5 MC

Using the trapezoidal rule with 4 subintervals, which expression gives the approximate area under the curve  `y = xe^x`  between  `x = 1`  and  `x = 3`?

  1. `1/4(e^1 + 6e^1.5 + 4e^2 + 10e^2.5 + 3e^3)`
  2. `1/4(e^1 + 3e^1.5 + 4e^2 + 5e^2.5 + 3e^3)`
  3. `1/2(e^1 + 6e^1.5 + 4e^2 + 10e^2.5 + 3e^3)`
  4. `1/2(e^1 + 3e^1.5 + 4e^2 + 5e^2.5 + 3e^3)`
Show Answers Only

`B`

Show Worked Solution

`y = xe^x`

2UA HSC 2015 5mc

`A` `~~ h/2[y_0 + 2y_1 + 2y_2 + 2y_3 + y_4]`
  `~~ 1/4[e^1 + 3e^1.5 + 4e^2 + 5e^2.5 + 3e^3]`

 `=> B`

Plane Geometry, 2UA 2006 HSC 10b

A rectangular piece of paper `PQRS` has sides `PQ = 12` cm and `PS = 13` cm. The point `O` is the midpoint of `PQ`. The points `K` and `M` are to be chosen on `OQ` and `PS` respectively, so that when the paper is folded along `KM`, the corner that was at `P` lands on the edge `QR` at `L`. Let `OK = x` cm and `LM = y` cm.

Copy or trace the diagram into your writing booklet.

  1. Show that `QL^2 = 24x`.  (1 mark)
  2. Let `N` be the point on `QR` for which `MN` is perpendicular to `QR`.
  3. By showing that `Delta QKL\ text(|||)\ Delta NLM`, deduce that `y = {sqrt 6 (6 + x)}/sqrt x`.  (3 marks)
  4. Show that the area, `A`, of `Delta KLM` is given by
    1. `A = {sqrt 6 (6 + x)^2}/(2 sqrt x)`  (1 mark)
    2.  
  5. Use the fact that `12 <= y <= 13` to find the possible values of `x`.  (2 marks)
  6. Find the minimum possible area of `Delta KLM`.  (3 marks)
Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
  4. `2 2/3 <= x <= 6`
  5.  
  6. `53.33…\ text(cm²)`
Show Worked Solution
(i)     

 `text(Show)\ QL^2 = 24x`

`KP = KL = 6 + x`

`KQ = 6 – x`

`text(Using Pythagoras)`

`QL^2` `= KL^2 – KQ^2`
  `= (6 + x)^2 – (6 – x)^2`
  `= 36 + 12x + x^2 – 36 + 12x – x^2`
  `= 24x\ …\ text(as required)`

 

(ii)  `text(Show)\ y = {sqrt 6 (6 + x)}/sqrt x`

`text(In)\ Delta QKL`

`/_LQK=90°\ \ text{(given)}`

`text(Let)\ /_QKL = theta`

`:. /_QLK = 90 – theta\ \ text{(angle sum of}\ Delta QKL text{)}`

`text(In)\ Delta NLM`

`/_LNM=90°\ \ text{(given)}`

`/_NLM` `= 180 – (90 + 90 – theta)\ \ (/_QLN\ text(is a straight angle))`
  `= theta`

`:. Delta QKL\ text(|||)\ Delta NLM\ \ \ text{(equiangular)}`

`:. y/(MN)` `= (KL)/(QL)\ \ text{(corresponding sides of}`
  `text{similar triangles)}` 
`y/12` `= (6 + x)/sqrt(24x)`
`y` `= (12(6 + x))/(2 sqrt (6x))`
  `= (6 (6 + x))/(sqrt x xx sqrt 6) xx sqrt 6/sqrt 6`
  `= (sqrt 6 (6 + x))/sqrt x\ …\ text(as required)`

 

(iii)  `text(Area)\ DeltaKLM` `= 1/2 xx y xx KL`
  `= 1/2 xx (sqrt 6 (6 + x))/sqrt x xx (6 + x)`
  `= (sqrt 6 (6 + x)^2)/(2 sqrt x)\ …\ text(as required.)`

 

(iv)  `text(Given that)\ \ \ \ \ \ \ \ 12 <= y <= 13`

`12 <= (sqrt 6 (6 + x))/sqrt x <= 13`

`text(Consider)\ (sqrt 6 ( 6 + x))/sqrt x` `>= 12`
`(6 (6 + x)^2)/x` `>= 144`
`(6 + x)^2` `>= 24x`
`36 + 12x + x^2` `>= 24x`
`x^2 – 12x + 36` `>= 0`
`(x – 6)^2` `>= 0`
`:. x` `>= 6`

`text(However, we know)\ OP=6,\ text(and)\ x <= 6`.

`:. x = 6\ text(satisfies both conditions)`

`text(Consider)\ (sqrt 6 (6 + x))/sqrt x` `<= 13`
`(6 (6 + x)^2)/x` `<= 169`
`6 (6 + x)^2` `<= 169x`
`6 (36 + 12x + x^2)` `<= 169x`
`216 + 72x + 6x^2` `<= 169x`
`6x^2 – 97x + 216` `<= 0`

 

`text(Using the quadratic formula)`

`x` `= (-b +- sqrt (b^2 -4ac))/(2a)`
  `= (97 +- sqrt ((-97)^2 -4 xx 6 xx 216))/(2 xx 6)`
  `= (97 +- sqrt 4225)/12`
  `= (97 +- 65)/12`
  `= 13 1/2 or 2 2/3`

`:. 2 2/3 <= x <= 13 1/2`

`text(However, we know)\ x <= 6,\ text(so)`

`2 2/3 <= x <= 6\ text(satisfies both conditions)`

`:.\ text(All possible values of)\ x\ text(are)`

`2 2/3 <= x <= 6`.

 

(v)  `A = (sqrt 6 (6 + x)^2)/(2 sqrt x)`

`text(Using the quotient rule)`

`(dA)/(dx)` `= (u prime v – uv prime)/v^2`
  `= {2 sqrt 6 (6 + x) xx 2 sqrt x – sqrt 6 (6 + x)^2 xx 1/2 xx 2 xx x^(-1/2)}/(2 sqrt x)^2`
  `= {4 sqrt x sqrt 6 (6 + x) – sqrt 6 (6 + x)^2 * 1/sqrt x}/(4x)`
  `= {4 sqrt 6 x (6 + x) – sqrt 6 (6 + x)^2}/(4x sqrt x)`
  `= (sqrt 6 (6 + x) (4x – 6 – x))/(4x sqrt x)`
  `= (sqrt 6 (6 + x) (3x – 6))/(4x sqrt x)`

`text(Max or min when)\ (dA)/(dx) = 0`

`sqrt 6 (6 + x) (3x – 6) = 0`

`:. 3x = 6\ \ ,\ \ x ≠ -6`

`x = 2`

`text(However,)\ x = 2\ text(lies outside the range)`

`text(of possible values)\ \ 2 2/3 <= x <= 6`

`:.\ text(Check limits)`

`text(At)\ \ x = 2 2/3`

`A` `= (sqrt 6 (6 + 2 2/3)^2)/(2 sqrt (2 2/3))`
  `= 56.33…\ text(cm²)`

 

`text(At)\ \ x = 6`

`A` `= (sqrt 6 (6 + 6)^2)/(2 sqrt 6)`
  `= 72.0\ text(cm²)`

 

`:.\ text(Minimum area of)\ Delta KLM\ text(is 56.33… cm²)`

Integration, 2UA 2006 HSC 10a

Use Simpson’s rule with three function values to find an approximation to the value of
 
          `int_0.5^1.5 (log_e x )^3\ dx`.
 

Give your answer correct to three decimal places.  (2 marks)

Show Answers Only

`text(–0.044)\ \ \ text{(to 3 d.p.)}`

Show Worked Solution

`int_0.5^1.5 (log_e x )^3 dx`

`A` `~~ h/3 [y_0 + y_2 + 4(y_1)]`
  `~~0.5/3 [-0.3330… + 0.0666… + 0]`
  `~~ -0.04439…`
  `~~-0.044\ \ \ text{(to 3 d.p.)}`

Calculus, 2ADV C4 2006 HSC 9b

During a storm, water flows into a 7000-litre tank at a rate of `(dV)/(dt)` litres per minute, where `(dV)/(dt) = 120 + 26t-t^2` and `t` is the time in minutes since the storm began.

  1. At what times is the tank filling at twice the initial rate?  (2 marks)

  2. Find the volume of water that has flowed into the tank since the start of the storm as a function of `t`.  (1 mark)

  3. Initially, the tank contains 1500 litres of water. When the storm finishes, 30 minutes after it began, the tank is overflowing.

     

    How many litres of water have been lost?  (2 marks)

Show Answers Only
  1. `t = 6 or 20\ text(minutes)`
  2. `V = 120t + 13t^2 – 1/3t^3`
  3. `800\ text(litres)`
Show Worked Solution

i.  `(dV)/(dt) = 120 + 26t-t^2`

`text(When)\ t = 0, (dV)/(dt) = 120`

`text(Find)\ t\ text(when)\ (dV)/(dt) = 240`

`240 = 120 + 26t-t^2`

`t^2-26t + 120 = 0`

`(t-6)(t-20) = 0`

`t = 6 or 20`

`:.\ text(The tank is filling at twice the initial rate)`

`text(when)\ t = 6 and t = 20\ text(minutes)`

 

ii.  `V` `= int (dV)/(dt)\ dt`
  `= int 120 + 26t-t^2\ dt`
  `= 120t + 13t^2-1/3t^3 + c`

 
`text(When)\ t = 0, V = 0`

`=>  c = 0`

`:. V= 120t + 13t^2-1/3t^3`

 

iii.  `text(Storm water volume into the tank when)\ t = 30`

`= 120(30) + 13(30^2)-1/3 xx 30^3`

`= 3600 + 11\ 700-9000`

`= 6300\ text(litres)`
 

`text(Total volume)` `= 6300 + 1500`
  `= 7800\ text(litres)`

 

`:.\ text(Overflow)` `= 7800-7000`
  `= 800\ text(litres)`

Quadratic, 2UA 2006 HSC 9a

Find the coordinates of the focus of the parabola  `12y = x^2 - 6x - 3`.  (2 marks)

Show Answers Only

`(3, 2)`

Show Worked Solution
`12y` `= x^2 – 6x – 3`
  `= x^2 – 6x + 9 – 12`
`12y` `= (x – 3)^2 – 12`
`(x – 3)^2` `= 12y + 12`
  `= 12(y + 1)`

 

`:.\ text{Vertex is (3, –1)}`

`4a` `= 12`
`a` `= 3`

 

`:.\ text(Coordinates of focus are)\ (3, 2).`

Quadratic, 2UA 2006 HSC 7c

  1. Write down the discriminant of  `2x^2 + (k - 2)x + 8`  where  `k`  is a constant.  (1 mark)
  2. Hence, or otherwise, find the values of  `k`  for which the parabola  `y = 2x^2 + kx + 9` does not intersect the line  `y = 2x + 1`.  (2 marks)

 

Show Answers Only
  1. `k^2 – 4k – 60`
  2. `-6 < k < 10`
Show Worked Solution

(i)  `2x^2 + (k – 2)x + 8`

`Delta` `= b^2 – 4ac`
  `= (k – 2)^2 – 4 xx 2 xx 8`
  `= k^2 – 4k + 4 – 64`
  `= k^2 – 4k – 60`

 

(ii)  `y` `= 2x^2 + kx + 9` `\ \ text{…  (1)}`
`y` `= 2x + 1` `\ \ text{…  (2)}`

`text(Substitute)\ y = 2x + 1\ text{into (1)}`

`2x + 1 = 2x^2 + kx + 9`

`2x^2 + kx – 2x + 8 = 0`

`2x^2 + (k – 2)x + 8 = 0\ …\ text{(∗)}`

 

`text{The graphs will not intercept if (∗) has}`

`text(no roots, i.e.)\ \ Delta <0`

`k^2 – 4k – 60` `< 0`
`(k – 10) (k + 6)` `< 0`

HSC quadratic

`text(From the graph, no intersection when)`

`-6 < k < 10`

Quadratic, 2UA 2006 HSC 7a

Let  `alpha`  and  `beta`  be the solutions of  `x^2 - 3x + 1 = 0`.

  1. Find  `alpha beta`.  (1 mark)
  2. Hence find  `alpha + 1/alpha`.  (1 mark)  

 

Show Answers Only
  1. `1`
  2. `3`
Show Worked Solution

(i)  `x^2 – 3x + 1 = 0`

`alpha beta` `= c/a`
  `= 1`

 

(ii)  `alpha + 1/alpha` `= alpha + beta\ \ \ text{(using}\ beta = 1/alpha\ text{from part (i))}`
  `= -b/a`
  `= (-(-3))/1`
  `= 3`

Calculus, EXT1* C1 2006 HSC 6b

A rare species of bird lives only on a remote island. A mathematical model predicts that the bird population, `P`, is given by

`P = 150 + 300 e^(-0.05t)`

where `t` is the number of years after observations began.

  1. According to the model, how many birds were there when observations began?  (1 mark)

  2. According to the model, what will be the rate of change in the bird population ten years after observations began?  (2 marks)

  3. What does the model predict will be the limiting value of the bird population?  (1 mark)

  4. The species will become eligible for inclusion in the endangered species list when the population falls below `200`. When does the model predict that this will occur?  (2 marks)

Show Answers Only
  1. `450\ text(birds)`
  2. `-9.1\ text{(to 1 d.p.)}`
  3. `150\ text(birds)`
  4. `text(After 35.83… years)`
Show Worked Solution

i.  `P = 150 + 300 e^(-0.05t)`

`text(When)\ \ t = 0`

`P` `= 150 + 300 e^0`
  `= 450`

 
`:.\ text(There were 450 birds when observations began.)`
 

ii.  `(dP)/dt` `= 300 xx (-0.05) xx e^(-0.05t)`
  `= -15 e^(-0.05t)`

 
`text(When)\ \ t = 10`

`(dP)/dt` `= -15 e^(-0.05 xx 10)`
  `= -15 e^(-0.5)`
  `= -9.097…`
  `= -9.1\ text{(to 1 d.p.)}`

 

`:.\ text(After 10 years, the bird population will be)`

`text(decreasing at a rate of 9.1 birds per year.)`

 

iii.  `text(As)\ t rarr oo`

`300 e^(-0.05t) rarr 0`

`:. P = 150 + 300 e^(-0.05t) rarr 150`

`:.\ text(The model predicts a limiting population)`

`text(of 150 birds.)`

 

iv.  `text(Find)\ t\ text(when)\ P < 200`

`150 + 300 e^(-0.05t)` `< 200`
`300 e^(-0.05t)` `< 50`
`e^(-0.05t)` `< 50/300`
`ln e^(-0.05t)` `< ln­ 1/6`
`-0.05t` `< ln­ 1/6`
`t` `> (ln­ 1/6)/(-0.05t)`
`t` `> 35.83…`

 

`:.\ text(The model predicts the population)`

`text(will fall below 200 after 35.83… years.)`

Plane Geometry, 2UA 2006 HSC 6a

In the diagram, `AD` is parallel to `BC`, `AC` bisects `/_BAD` and `BD` bisects `/_ABC`. The lines `AC` and `BD` intersect at `P`.

Copy or trace the diagram into your writing booklet.

  1. Prove that `/_BAC = /_BCA`.  (1 mark)
  2. Prove that `Delta ABP ≡ Delta CBP`.  (2 marks)
  3. Prove that `ABCD` is a rhombus.  (3 marks)
Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `text(Proof)\ \ text{(See Worked Solutions)}`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution
(i)  

`text(Prove)\ /_BAC = /_BCA`

`/_BCA` `= /_CAD\ \ \ text{(alternate angles,}\ BC\ text(||)\ AD text{)}`
`/_CAD` `= /_BAC\ \ \ text{(}AC\ text(bisects)\ /_BAD text{)}`
`:. /_BAC` `= /_BCA\ …\ text(as required)`

 

(ii)  `text(Prove)\ Delta ABP ≡ Delta CBP`

`/_BAC` `= /_BCA\ \ \ text{(from part (i))}`
`/_ABP` `= /_CBP\ text{(}BD\ text(bisects)\ /_ABC text{)}`
`BP\ text(is common)`

 

`:. Delta ABP ≡ Delta CBP\ \ text{(AAS)}`

 

(iii)  `text(Using)\ Delta ABP ≡ Delta CBP`

`AP = PC\ \ text{(corresponding sides of congruent triangles)}`

`/_BPA = /_BPC\ \ text{(corresponding angles of congruent triangles)}`

`text(Also,)\ /_BPA = /_BPC = 90^@`

`text{(}/_APC\ text{is a straight angle)}`

 

`text(Considering)\ Delta APD and Delta APB`

`/_DAP` `= /_BAP\ text{(}AC\ text(bisects)\ /_BAD text{)}`
`/_DPA` `= 90^@\ text{(vertically opposite angles)}`
`:. /_DPA` `= /_BPA = 90^@`

`PA\ text(is common)`

`:. Delta APD ≡ Delta APB\ \ text{(AAS)}`

`BP = PD\ \ text{(corresponding sides of congruent triangles)}`

 

 `:. ABCD\ text(is a rhombus as its diagonals are)`

`text(perpendicular bisectors.)`

Calculus, 2ADV C4 2006 HSC 5b

  1. Show that `d/dx log_e (cos x) = -tan x.`  (1 mark)


  2.   
     
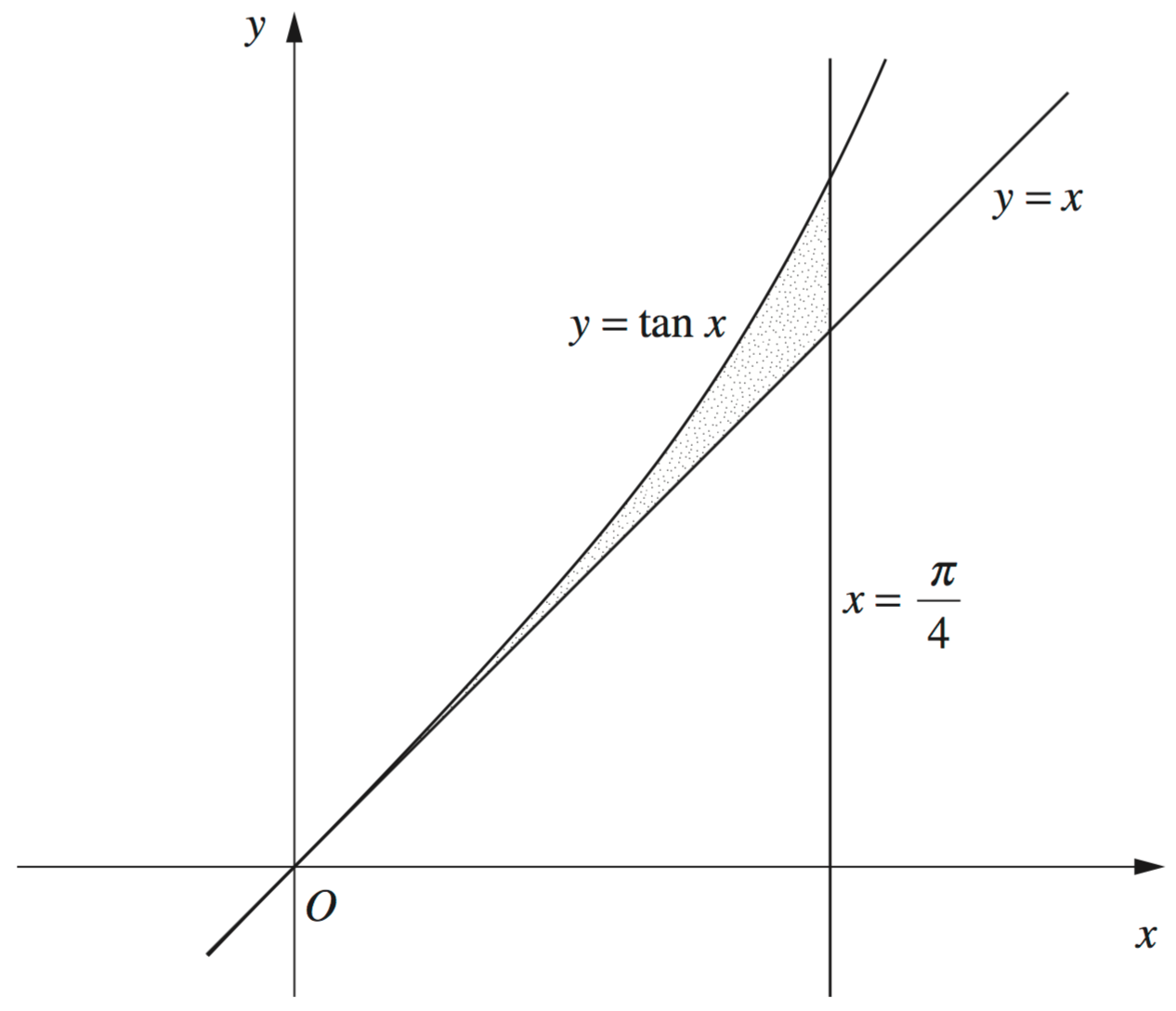
    2006 5b
     
    The shaded region in the diagram is bounded by the curve  `y =tan x`  and the lines  `y =x`  and  `x = pi/4.`

     

    Using the result of part (i), or otherwise, find the area of the shaded region.  (3 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `(1/2 log_e 2 – pi^2/32)\ text(u²)`
Show Worked Solution
i.   `d/dx log_e (cos x)` `= (-sin x)/cos x`
  `= – tan x\ …\ text(as required)`

 

ii.  `text(Shaded Area)`

`= int_0^(pi/4) tan x\ dx – int_0^(pi/4) x\ dx`

`= int_0^(pi/4) tan x – x\ dx`

`= [-log_e (cos x) – 1/2 x^2]_0^(pi/4)`

`=[(-log_e (cos­ pi/4) – 1/2 xx (pi^2)/16) – (-log_e(cos 0) – 0)]`

`= -log_e­ 1/sqrt 2 – pi^2/32 + log_e1`

`= -log_e 2^(-1/2) – pi^2/32`

`= (1/2 log_e 2 – pi^2/32)\ text(u²)`

Calculus, 2ADV C3 2004 HSC 4b

Consider the function  `f(x) = x^3 − 3x^2`.

  1. Find the coordinates of the stationary points of the curve  `y = f(x)`  and determine their nature.   (3 marks)

  2. Sketch the curve showing where it meets the axes.   (2 marks)

  3. Find the values of  `x`  for which the curve  `y = f(x)`  is concave up.   (2 marks)

Show Answers Only
  1. `text(MAX at)\ (0,0),\ \ text(MIN at)\ (2,-4)`
  2.  
    1. Geometry and Calculus, 2UA 2004 HSC 4b Answer
  3. `f(x)\ text(is concave up when)\ x>1`
Show Worked Solution
(i)    `f(x)` `= x^3 – 3x^2`
  `f'(x)` `= 3x^2 – 6x`
  `f″(x)` `= 6x – 6`

 

`text(S.P.’s  when)\ \ f'(x) = 0`

`3x^2 – 6x` `= 0`
`3x (x – 2)` `= 0`
`x` `= 0\ \ text(or)\ \ 2`

 

`text(When)\ x = 0`

`f(0)` `= 0`
`f″(0)` `= 0 – 6 = -6 < 0`
`:.\ text(MAX at)\ (0,0)`

 

`text(When)\ x = 2`

`f(2)` `= 2^3 – (3 xx 4) = -4`
`f″(2)` `= (6 xx 2) – 6 = 6 > 0`
`:.\ text(MIN at)\ (2, -4)`

 

(ii)   `f(x) = x^3 – 3x^2\ text(meets the)\ x text(-axis when)\ f(x) = 0`
`x^3 – 3x^2` `= 0`
`x^2 (x-3)` `= 0`
`x` `= 0\ \ text(or)\ \ 3`

 Geometry and Calculus, 2UA 2004 HSC 4b Answer

(iii)   `f(x)\ text(is concave up when)`
`f″(x)` `>0`
`6x – 6` `>0`
`6x` `>6`
`x` `>1`

 

`:. f(x)\ text(is concave up when)\ \ x>1`

Trigonometry, 2ADV T1 2004 HSC 4a

2004 4a
 

`AOB`  is a sector of a circle, centre  `O`  and radius 6 cm.

The length of the arc  `AB`  is  `5pi` cm.

Calculate the exact area of the sector  `AOB`.   (2 marks)

Show Answers Only

`15 pi\ text(cm²)`

Show Worked Solution
`text(Arc length)\ ` `= theta/(2 pi) xx 2 pi r = r theta`
`5 pi` `= 6 theta`
`:.\ theta` `= (5pi)/6\ text(radians)`

 

`text(Area of sector)\ AOB`

`= theta/(2pi) xx pi r^2`

`= 1/2 r^2 theta`

`= 1/2 xx 6^2 xx (5pi)/6`

`= 15pi\ text(cm²)`

Trigonometry, 2ADV T1 2004 HSC 3c

Trig Ratios, 2UA 2004 HSC 3c
 

The diagram shows a point  `P`  which is  30 km due west of the point  `Q`.

The point  `R`  is 12 km from  `P`  and has a bearing from  `P`  of  070°. 

  1. Find the distance of  `R`  from  `Q`.   (2 marks)

  2. Find the bearing of  `R`  from  `Q`.   (2 marks)

Show Answers Only
  1. `19.2\ text(km)\ \ \ text{(1 d.p.)}` 
  2. `282^@`
Show Worked Solution

i.   `text(Join)\ \ RQ\ \ text(to form)\ \ Delta RPQ`

Trig Ratios, 2UA 2004 HSC 3c Answer

`/_RPQ = 90 – 70 = 20^@`

`text(Using the cosine rule:)`

`RQ^2` `= PR^2 + PQ^2 – 2 xx PR xx PQ xx cos /_RPQ`
  `= 12^2 + 30^2 – 2 xx 12 xx 30 xx cos 20^@`
  `= 367.421…`
`:.\ RQ` `= 19.168…`
  `= 19.2\ text(km)\ \ text{(1 d.p.)}`

 

ii.   `text(Using sine rule:)`

`(sin /_RQP)/12` `= (sin 20^@)/(19.168…)`
`sin/_RQP` `= (12 xx sin 20^@)/(19.168…)`
  `= 0.214…`
`/_RQP` `= 12.36…^@`
  `= 12^@\ \ \ text{(nearest degree)}`

 

`:.\ text(Bearing of)\ R\ text(from)\ Q`

`=270+12`

`=282^@`

Probability, 2ADV S1 2006 HSC 4c

A chessboard has 32 black squares and 32 white squares. Tanya chooses three different squares at random.

  1. What is the probability that Tanya chooses three white squares?  (2 marks)

  2. What is the probability that the three squares Tanya chooses are the same colour?.  (1 mark)

  3. What is the probability that the three squares Tanya chooses are not the same colour?  (1 mark)

Show Answers Only
  1. `5/42`
  2. `5/21`
  3. `16/21`
Show Worked Solution
i.  `text(P)(WWW)` `= 32/64 xx 31/63 xx 30/62`
  `= 5/42`

 

ii.  `text{P(same colour)}`

`= P(WWW) + P(BBB)`

`= 5/42 + 32/64 xx 31/63 xx 30/62`

`= 5/42 + 5/42`

`= 5/21`

 

iii.  `text{P(not all the same colour)}`

`= 1 – text{P(same colour)}`

`= 1 – 5/21`

`= 16/21`

Calculus, EXT1* C3 2006 HSC 4b

2006 4b

In the diagram, the shaded region is bounded by the parabola  `y = x^2 + 1`, the `y`-axis and the line  `y = 5`.

Find the volume of the solid formed when the shaded region is rotated about the `y`-axis.  (3 marks)

Show Answers Only

`8 pi\ \ text(u³)`

Show Worked Solution

`y = x^2 + 1`

`x^2 = y – 1`

`V` `= pi int_1^5 x^2 \ dy`
  `= pi int_1^5 y-1 \ dy`
  `= pi [y^2/2 – y]_1^5`
  `= pi[(25/2 – 5) – (1/2 – 1)]`
  `= pi[15/2 – (-1/2)]`
  `= 8 pi\ \ text(u³)`

Trigonometry, 2ADV T1 2006 HSC 4a

In the diagram, `ABCD` represents a garden. The sector  `BCD`  has centre `B` and  `/_DBC = (5 pi)/6`

The points `A, B` and `C` lie on a straight line and  `AB = AD = 3` metres.

Copy or trace the diagram into your writing booklet.

  1. Show that  `/_DAB = (2 pi)/3.`  (1 mark)

  2. Find the length of  `BD`.  (2 marks)

  3. Find the area of the garden  `ABCD`.  (2 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `3 sqrt 3\ \ text(m)`
  3. `(9 sqrt 3 + 45 pi) / 4\ \ text(m²)`
Show Worked Solution
i.   

`text(Show)\ /_DAB = (2 pi)/3`

`/_DBA` `= pi – (5 pi)/6\ \ \ text{(π radians in straight angle}\ ABC text{)}`
  `= pi/6\ text(radians)`

 
`:. /_BDA = pi/6\ text(radians)\ \ \ text{(base angles of isosceles}\ Delta ADB text{)}`

`:. /_DAB` `= pi – (pi/6 + pi/6)\ \ \ text{(angle sum of}\ Delta ADB text{)}`
  `= (2 pi)/3\  text(radians … as required)`

 

ii.  `text(Using the cosine rule:)`

`BD^2` `= AD^2 + AB^2 – 2 xx AD xx AB xx cos {:(2 pi)/3`
  `= 9 + 9 – (2 xx 3 xx 3 xx -0.5)`
  `= 27`
`:. BD` `= sqrt 27`
  `= 3 sqrt 3\ \ text(m)`

 

iii.  `text(Area of)\ Delta ADB` `= 1/2 ab sin C`
  `= 1/2 xx 3 xx 3 xx sin{:(2 pi)/3`
  `= 9/2 xx sqrt3/2`
  `= (9 sqrt 3)/4\ \ text(m²)`

 
`text(Area of sector)\ BCD`

`= {(5 pi)/6}/(2 pi) xx pi r^2`

`= (5 pi)/12 xx (3 sqrt 3)^2`

`= (45 pi)/4\ \ text(m²)`

 

`:.\ text(Area of garden)\ ABCD`

`= (9 sqrt 3)/4 + (45 pi)/4`

`= (9 sqrt 3 + 45 pi)/4\ \ text(m²)`

Linear Functions, 2UA 2006 HSC 3a

In the diagram, `A, B and C` are the points  `(1, 4), (5, –4) and (–3, –1)`  respectively. The line  `AB`  meets the y-axis at `D`.

  1. Show that the equation of the line  `AB`  is  `2x + y - 6 = 0`.  (2 marks)
  2. Find the coordinates of the point `D`.  (1 mark)
  3. Find the perpendicular distance of the point `C` from the line  `AB`.  (1 mark)
  4. Hence, or otherwise, find the area of the triangle  `ADC`.  (2 marks)
Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `D(0, 6)`
  3. `13/sqrt 5\ text(units)`
  4.  
  5. `text(6.5 u²)`
Show Worked Solution

(i)  `text(Show)\ \ AB\ \ text(is)\ \ 2x + y – 6 = 0`

`A (1, 4)\ \ \ B (5, text(–4))`

`m_(AB)` `= (y_2 – y_1) / (x_2 – x_1)`
  `= (-4 – 4) / (5 – 1)`
  `= (-8)/4`
  `= – 2`

 
`:.\ text(Equation of)\ AB, m = -2,\ text(through)\ \ (1,4)`

`y-y_1` `=m(x-x_1)`
`y – 4` `= -2 (x – 1)`
`y – 4` `= -2x + 2`
`2x + y – 6` `= 0\ …\ text(as required)`

 

(ii)  `AB\ text(intersects y-axis at)\ D`

`0 + y – 6` `= 0`
`y` `= 6`

`:. D\ text(has coordinates)\ (0, 6)`

 

(iii)  `C\ text{(–3, –1)}`

`AB\ text(is)\ 2x + y – 6 = 0`

`_|_ text(dist)` `= |\ (ax_1 + by_1 + c)/sqrt (a^2 + b^2)\ |`
  `= |\ (2(−3) + 1(-1) – 6)/sqrt(2^2 + 1^2)\ |`
  `= |\ (-13)/sqrt 5\ |`
  `= 13/sqrt 5\ text(units)`

 

(iv)

 
`text(dist)\ AD` `= sqrt((x_2 – x_1)^2 + (y_2 – y_1)^2)`
  `= sqrt((0 – 1)^2 + (6 – 4)^2`
  `= sqrt (1 + 4)`
  `= sqrt 5`
`text(Area of)\ Delta ADC` `= 1/2 xx b xx h`
  `= 1/2 xx sqrt 5 xx 13/sqrt 5`
  `= 6.5\ text(u²)`

Trigonometry, 2ADV T1 2005 HSC 9b

Trig Ratios, 2UA 2005 HSC 9b
 

The triangle  `ABC`  has a right angle at `B, \ ∠BAC = theta` and  `AB = 6`. The line `BD` is drawn perpendicular to `AC`. The line `DE` is then drawn perpendicular to `BC`. This process continues indefinitely as shown in the diagram.

  1. Find the length of the interval `BD`, and hence show that the length of the interval  `EF`  is  `6 sin^3\ theta`.  (2 marks)

  2. Show that the limiting sum 
     
    `qquad BD + EF + GH + ···`
     
    is given by  `6 sec\ theta tan\ theta`.  (3 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(See Worked Solutions)`
Show Worked Solution
i.   Trig Ratios, 2UA 2005 HSC 9b Answer

`text(Show)\ EF = 6\ sin^3\ theta`

`text(In)\ ΔADB`

`sin\ theta` `= (DB)/6`
`DB` `= 6\ sin\ theta`
`∠ABD` `= 90 − theta\ \ \ text{(angle sum of}\ ΔADB)`
`:.∠DBE` `= theta\ \ \ (∠ABE\ text{is a right angle)}`

 

`text(In)\ ΔBDE:`

`sin\ theta` `= (DE)/(DB)`
  `= (DE)/(6\ sin\ theta)`
`DE` `= 6\ sin^2\ theta`
`∠BDE` `= 90 − theta\ \ \ text{(angle sum of}\ ΔDBE)`
`∠EDF` `= theta\ \ \ (∠FDB\ text{is a right angle)}`

 

`text(In)\ ΔDEF:`

`sin\ theta` `= (EF)/(DE)`
  `= (EF)/(6\ sin^2\ theta)`
`:.EF` `= 6\ sin^3\ theta\ \ …text(as required)`

 

ii. `text(Show)\ \ BD + EF + GH\ …`

`text(has limiting sum)\ =6 sec theta tan theta`

`underbrace{6\ sin\ theta + 6\ sin^3\ theta +\ …}_{text(GP where)\ \ a = 6 sin theta, \ \ r = sin^2 theta}`
 

`text(S)text(ince)\ \ 0 < theta < 90^@`

`−1` `< sin\ theta` `< 1`
`0` `< sin^2\ theta` `< 1`

 
`:. |\ r\ | < 1`
 

`:.S_∞` `= a/(1 − r)`
  `= (6\ sin\ theta)/(1 − sin^2\ theta)`
  `= (6\ sin\ theta)/(cos^2\ theta)`
  `= 6 xx 1/(cos\ theta) xx (sin\ theta)/(cos\ theta)`
  `= 6 sec\ theta\ tan\ theta\ \ …text(as required.)`

Calculus, EXT1* C1 2005 HSC 9a

A particle is initially at rest at the origin. Its acceleration as a function of time, `t`, is given by

`ddot x = 4sin2t`

  1. Show that the velocity of the particle is given by  `dot x = 2 − 2\ cos\ 2t`.  (2 marks)

  2. Sketch the graph of the velocity for  `0 ≤ t ≤ 2π`  AND determine the time at which the particle first comes to rest after  `t = 0`.  (3 marks)

  3. Find the distance travelled by the particle between  `t = 0`  and the time at which the particle first comes to rest after  `t = 0`.  (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(See Worked Solutions)`
  3. `2pi\ \ text(units)`
Show Worked Solution

i.   `text(Show)\ \ dot x = 2 − 2\ cos\ 2t`

`ddot x` `= 4\ sin\ 2t`
`dot x` `= int ddot x\ dt`
  `= int4\ sin\ 2t\ dt`
  `= −2\ cos\ 2t + c`

 
`text(When)\ t = 0, \ x = 0`

`0 = −2\ cos\ 0 + c`

`c = 2`

`:.dot x = 2 − 2\ cos\ 2t\ \ …text(as required)`

 

ii.  `text(Considering the range)`

`−1` `≤ \ \ \ cos\ 2t` `≤ 1`
`−2` `≤ \ \ \ 2\ cos\ 2t`  `≤ 2` 
`0` `≤ 2 − 2\ cos\ 2t` `≤ 4` 

 
`text(Period) = (2pi)/n = (2pi)/2 = pi`

Calculus in the Physical World, 2UA 2005 HSC 9a Answer

`text(After)\ t = 0,\ text(the particle next comes)`

`text(to rest at)\ t = pi.`

 

iii.  `text(Distance travelled)`

`= int_0^pi dot x\ dt`

`= int_0^pi 2 − 2\ cos\ 2t\ dt`

`= [2t − sin\ 2t]_0^pi`

`= [(2pi − sin\ 2pi) − (0 − sin\ 0)]`

`= 2pi\ \ text(units)`

Financial Maths, 2ADV M1 2005 HSC 8c

Weelabarrabak Shire Council borrowed $3 000 000 at the beginning of 2005. The annual interest rate is 12%. Each year, interest is calculated on the balance at the beginning of the year and added to the balance owing. The debt is to be repaid by equal annual repayments of $480 000, with the first repayment being made at the end of 2005.

Let  `A_n`  be the balance owing after the `n`-th repayment.

  1. Show that  `A_2 = (3 × 10^6)(1.12)^2 - (4.8 × 10^5)(1 + 1.12)`.  (1 mark)

  2. Show that  `A_n = 10^6[4 − (1.12)^n]`.  (2 marks)

  3. In which year will Weelabarrabak Shire Council make the final repayment?  (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(See Worked Solutions)`
  3. `2017`
Show Worked Solution
i.    `A_1` `= (3 xx 10^6)(1.12) − (4.8 xx 10^5)`
  `A_2` `= A_1(1.12) − (4.8 xx 10^5)`
    `= [(3 xx 10^6)(1.12) − (4.8 xx 10^5)](1.12) − (4.8 xx 10^5)`
    `= (3 xx 10^6)(1.12)^2 − (4.8 xx 10^5)(1.12) − (4.8 xx 10^5)`
    `= (3 xx 10^6)(1.12)^2 − (4.8 xx 10^5)(1 + 1.12)\ \ …text(as required)`

 

ii.  `text(Show)\ A_n = 10^6[4 − (1.12)^n]`

`A_3` `= (3 xx 10^6)(1.12)^3 − (4.8 xx 10^5)(1 + 1.12 + 1.12^2)`
`vdots`  
`A_n` `= (3 xx 10^6)(1.12)^n − (4.8 xx 10^5)(1 + 1.12 + … + 1.12^(n − 1))`
  `=> text(Noting that)\ \ (1+1.12+ … + 1.12^(n-1))\ text(is a)`
  `text(GP where)\ \ a = 1, \ \ r = 1.12`
 `A_n` `= (3 xx 10^6)(1.12)^n − (4.8 xx 10^5)((1(1.12^n − 1))/(1.12 − 1))`
  `= (3 xx 10^6)(1.12)^n − (4.8 xx 10^5)((1(1.12^n − 1))/0.12)`
  `= (3 xx 10^6)(1.12)^n − (4 xx 10^6)(1.12^n − 1)`
  `= 10^6[3(1.12)^n − 4(1.12^n − 1)]`
  `= 10^6[3(1.12)^n − 4(1.12^n) + 4]`
  `= 10^6[4 − (1.12)^n]\ \ …text(as required)`

 

iii.  `text(Find)\ n\ text(such that)\ A_n = 0`

`10^6[4 − (1.12)^n]` `= 0`
`4 − (1.12)^n` `= 0`
`1.12^n` `= 4`
`n xx ln 1.12` `= ln4`
`n` `= (ln4)/ln1.12`
  `= 12.23…\ \ text(years.)`

 

`:.\ text(The final repayment will be made)`

`text(in 2017, the thirteenth year.)`

Calculus, 2ADV C4 2005 HSC 8b

2005 8b

The shaded region in the diagram is bounded by the circle of radius 2 centred at the origin, the parabola  `y = x^2– 3x + 2`, and the `x`-axis.

By considering the difference of two areas, find the area of the shaded region.  (3 marks)

Show Answers Only

`(pi − 5/6)\ \ text(u²)`

Show Worked Solution

`text(Shaded Area = Area in the quarter circle less)`

`text(the area below the parabola between)\ x= 0 and 1.`

`text(Area of)\ 1/4\ text(circle)` `= 1/4 xx pir^2`
  `= 1/4 xx pi xx 2^2`
  `= pi\ \ \ text(u²)`

 

`text(Area below the parabola between)\ x= 0 and 1`

`=int_0^1y\ dx`

`= int_0^1x^2 − 3x + 2\ dx`

`= [x^3/3 − 3/2x^2 + 2x]_0^1`

`= [(1/3 − 3/2 + 2) − 0]`

`= 5/6`

 

`:.\ text(Shaded Area) = (pi − 5/6)\ \ \ text(u²)`

Calculus, 2ADV C3 2005 HSC 8a

2005 8a

A cylinder of radius  `x`  and height  `2h`  is to be inscribed in a sphere of radius  `R`  centred at  `O`  as shown.

  1. Show that the volume of the cylinder is given by
     
         `V = 2pih(R^2 − h^2).` (1 mark)

  2. Hence, or otherwise, show that the cylinder has a maximum volume when  `h = R/sqrt3.`  (3 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions).}`
  2. `text{Proof (See Worked Solutions).}`
Show Worked Solution
i.    `V` `= pir^2h\ \ \ \ text{(general form)}`
    `= pix^2 xx 2h`

 

`text(Using Pythagoras)`

`R^2` `= h^2 + x^2`
`x^2` `= R^2 − h^2`
`:.V` `= 2pih(R^2 − h^2)\ \ …text(as required.)` 

 

ii. `V` `= 2pih(R^2 − h^2)`
    `= 2piR^2h − 2pih^3`
  `(dV)/(dh)` `= 2piR^2 − 3 xx 2pih^2`
    `= 2piR^2 − 6pih^2`
  `(d^2V)/(dh^2)` `= −12pih`

`text(Max or min when)\ (dV)/(dh) = 0`

`2piR^2 − 6pih^2` `= 0`
`6pih^2` `= 2piR^2`
`h^2` `= R^2/3`
`h` `= R/sqrt3,\ \ h > 0`

`text(When)\ h = R/sqrt3`

`(d^2V)/(dh^2) = −12pi xx R/sqrt3 < 0`

`:.\ text(Volume is a maximum when)\ h = R/sqrt3\ text(units.)`

Calculus, EXT1* C1 2005 HSC 7b

Calculus in the Physical World, 2UA 2005 HSC 7b
 

The graph shows the velocity, `(dx)/(dt)`, of a particle as a function of time. Initially the particle is at the origin. 

  1. At what time is the displacement, `x`, from the origin a maximum?  (1 mark)

  2. At what time does the particle return to the origin? Justify your answer.  (2 marks)

  3. Draw a sketch of the acceleration,  `(d^2x)/(dt^2)`, as a function of time for  `0 ≤ t ≤ 6`.  (2 marks)

Show Answers Only
  1. `2`
  2. `4`
  3. `text(See Worked Solutions.)`
Show Worked Solution

i.   `text(Maximum displacement in graph when)`

`(dx)/(dt)` `= 0`
`:.t` `= 2`

 

ii.  `text(Particle returns to the origin when)\ t = 4.`

`text(The displacement can be calculated by the)`

`text(net area below the curve and since the)`

`text(area above the curve between)\ t = 0\ text(and)\ t = 2`

`text(is equal to the area below the curve between)`

`t = 2\ text(and)\ t = 4,\ text(the displacement returns to)`

`text{the initial displacement (i.e. the origin).}`

 

iii.   Calculus in the Physical World, 2UA 2005 HSC 7b Answer

Financial Maths, 2ADV M1 2005 HSC 7a

Anne and Kay are employed by an accounting firm.

Anne accepts employment with an initial annual salary of  $50 000. In each of the following years her annual salary is increased by $2500.

Kay accepts employment with an initial annual salary of  $50 000. In each of the following years her annual salary is increased by 4%.

  1. What is Anne’s annual salary in her thirteenth year?  (2 marks)

  2. What is Kay’s annual salary in her thirteenth year?  (2 marks)

  3. By what amount does the total amount paid to Kay in her first twenty years exceed that paid to Anne in her first twenty years?  (3 marks)

Show Answers Only
  1. `$80\ 000`
  2. `text{$80 052 (nearest dollar)}`
  3. `text{$13 904 (nearest $)}`
Show Worked Solution

i.   `text(Let)\ T_n = text(Anne’s salary in year)\ n`

`T_1 = a = $50\ 000`

`T_2 = a + d = $52\ 500`

`⇒\ text(AP where)\ a = $50\ 000,\ \ d = $2500`

`T_n = a + (n − 1)d`

`T_13` `= 50\ 000 + (13 − 1) xx 2500`
  `=80\ 000`

 

`:.\ text(Anne’s salary in her 13th year is $80 000.)`

 

ii.  `text(Let)\ K_1 =text(Kay’s salary in year)\ n`

`K_1` `= a` `= 50\ 000`
`K_2` `= ar` `= 50\ 000 xx 1.04 = 52\ 000`
`⇒\ text(GP where)\ \ a = 50\ 000, \ \ r = 1.04`
`K_n` `= ar^(n − 1)`
 `K_13` `= 50\ 000 xx (1.04)^12`
  `= $80\ 051.61…`
  `= $80\ 052\ \ \ text{(nearest dollar)}`

 

iii.  `text(Anne)`

`S_n` `= n/2[2a + (n − 1)d]`
 `S_20` `= 20/2[2 xx 50\ 000 + (20 − 1)2500]`
  `= 10[100\ 000 + 47\ 500]`
  `= $1\ 475\ 000`

 

`text(Kay)`

`S_n` `= (a(r^n − 1))/(r − 1)`
`S_20`  `= (50\ 000(1.04^20 -1))/(1.04 − 1)`
  `= $1\ 488\ 903.929…`

 

`text(Difference)`

`= 1\ 488\ 903.929… − 1\ 475\ 000`

`= $13\ 903.928…`

`= $13\ 904\ \ \  text{(nearest $)}`

 

`:.\ text(Kay’s total salary exceeds Anne’s by)\ $13\ 904`

Algebra, STD2 A4 2006 HSC 28b

A new tunnel is built. When there is no toll to use the tunnel, 6000 vehicles use it each day. For each dollar increase in the toll, 500 fewer vehicles use the tunnel.

  1. Find the lowest toll for which no vehicles will use the tunnel.  (1 mark)

  2. For a toll of $5.00, how many vehicles use the tunnel each day and what is the total daily income from tolls?  (2 marks)

  3. If `d` (dollars) represents the value of the toll, find an equation for the number of vehicles `(v)` using the tunnel each day in terms of `d`.  (2 marks)

  4. Anne says ‘A higher toll always means a higher total daily income’.

     

    Show that Anne is incorrect and find the maximum daily income from tolls. (Use a table of values, or a graph, or suitable calculations.)  (3 marks)

Show Answers Only
  1. `text($12 toll is the lowest for which)`

     

    `text(no vehicles will use the tunnel.)`

  2. `$17\ 500`
  3. `v = 6000 – 500d`
  4. `text{Proof (See Worked Solutions)}`
Show Worked Solution

i.  `text(500 less vehicles per $1 toll)`

`12 xx 500 = 6000`

`:. $12\ text(toll is the lowest for which no)`

`text(vehicles will use the tunnel.)`

 

ii.  `text(If the toll is $5)`

`5 xx 500 = 2500\ text(less vehicles)`

`:.\ text(Vehicles using the tunnel)`

`= 6000 – 2500`

`= 3500`

`:.\ text(Daily toll income)` `= 3500 xx $5`
  `= $17\ 500`

 

iii.    `d` `=\ text(toll)`
`v` `=\ text(Number of vehicles using the tunnel)`
    `:. v` `= 6000 – 500d`

 

iv.  `text(Income from tolls)`

`=\ text(Number of vehicles) xx text(toll)`

`= (6000 – 500d) xx d`

`= 6000d – 500d^2`

`= 500d (12 – d)`
 

 

`text(From the graph, the maximum income from tolls)`

`text(occurs when the toll is $6.)`

`:.\ text(Anne is incorrect.)`

 

`text(Alternate Solution)`

`text{The table of values shows that income (I) increases}`

`text(and peaks when the toll hits $6 before decreasing)`

`text(again as the toll gets more expensive.)`

`:.\ text(Anne is incorrect.)`

Financial Maths, STD2 F4 2006 HSC 27c

Kai purchased a new car for $30 000. It depreciated in value by $2000 per year for the first three years.

After the end of the third year, Kai changed the method of depreciation to the declining balance method at the rate of 25% per annum.

  1. Calculate the value of the car at the end of the third year.  (1 mark)

  2. Calculate the value of the car seven years after it was purchased.  (2 marks)

  3. Without further calculations, sketch a graph to show the value of the car over the seven years.

     

    Use the horizontal axis to represent time and the vertical axis to represent the value of the car.  (3 marks)

Show Answers Only
  1. `$24\ 000`
  2. `$7593.75`
  3. `text{See Worked Solutions}`
Show Worked Solution

i.  `text(Using)\ \ S = V_0 – Dn`

`S` `= 30\ 000 – (2000 xx 3)`
  `= $24\ 000`

 

ii.  `text(Using)\ \ S = V_0(1 – r)^n`

`text(where)\ V_0` `= 24\ 000`
`r` `= 0.25`
`n` `= 4`

 

`S` `= 24\ 000(1 – 0.25)^4`
  `= $7593.75`

 
`:.\ text(The value of the car after 7 years is $7593.75)`

 

iii.

Statistics, STD2 S4 2006 HSC 27b

Each member of a group of males had his height and foot length measured and recorded. The results were graphed and a line of fit drawn.
 

  1. Why does the value of the `y`-intercept have no meaning in this situation?  (1 mark)

  2. George is 10 cm taller than his brother Harry. Use the line of fit to estimate the difference in their foot lengths.  (1 mark)

  3. Sam calculated a correlation coefficient of  −1.2  for the data. Give TWO reasons why Sam must be incorrect.  (2 marks)

Show Answers Only
  1. `text(The y-intercept occurs when)\ x = 0.\ text(It has`
    `text(no meaning to have a height of 0 cm.)`
  2. `text(A 10 cm height difference means George should)`
    `text(have a 3 cm longer foot.)`
  3. `text(A correlation co-efficient must be between –1 and 1.)`
    `text(Foot length is positively correlated to a person’s)`
    `text(height and therefore can’t be a negative value.)`
Show Worked Solution

i.  `text(The y-intercept occurs when)\ x = 0.\ text(It has)`

`text(no meaning to have a height of 0 cm.)`

 

ii.  `text(A 20 cm height difference results in a foot length)`

`text(difference of 6 cm.)`
 

`:.\ text(A 10 cm height difference means George should)`

`text(have a 3 cm longer foot.)`

 

iii.  `text(A correlation co-efficient must be between –1 and 1.)`

`text(Foot length is positively correlated to a person’s)`

`text(height and therefore isn’t a negative value.)`

Financial Maths, STD2 F4 2006 HSC 27a

Liliana wants to borrow money to buy a house. The bank sent her an email with the following table attached.

2006 27a

  1. Liliana decides that she can afford $1000 per month on repayments.

     

    What is the maximum amount she can borrow, and how many years will she have to repay the loan?  (1 mark)

  2. Zali intends to borrow  $160 000  over 15 years from the same bank.

     

    If she chooses to borrow  $160 000  over 20 years instead, how much more interest will she pay?  (2 marks)

Show Answers Only
  1. `text{$130 000 (over 30 years)}`
  2. `$45\ 964.80`
Show Worked Solution

i.  `text(From table)`

`text{$130 000 (over 30 years)}`

 

ii.  `text(Total repayments over 15 years)`

`= $1529.04 xx 180`

`= $275\ 227.20`

`text(Total repayments over 20 years)`

`= $1338.30 xx 240`

`= $321\ 192.00`

 

`:.\ text(Extra interest over 20 years)`

`= 321\ 192.00 – 275\ 227.20`

`= $45\ 964.80`

Measurement, STD2 M2 2006 HSC 26d

Cassie flew from London to Manila. Manila is 8 hours ahead of London.

Her plane left London at 9.30 am Monday (London time), stopped for 5 hours in Singapore and arrived in Manila at 4.00 pm Tuesday (Manila time).

What was the total flying time? (Ignore time zones.)  (2 marks)

Show Answers Only

`text(17.5 hours)`

Show Worked Solution
`:.\ text(Flight time)` `=\ text{9:30 (Mon) to 4:00 pm (Tues)}`
         `- \ text{(stopover + time difference)}`
  `= 14.5 + 16-(5 + 8)`
  `= 17.5\ text(hours)`

Probability, STD2 S2 2006 HSC 26c

A new test has been developed for determining whether or not people are carriers of the Gaussian virus.

Two hundred people are tested. A two-way table is being used to record the results.
 

  1.  What is the value of  `A`?  (1 mark)

  2.  A person selected from the tested group is a carrier of the virus.

     

     What is the probability that the test results would show this?  (2 marks) 

  3.  For how many of the people tested were their test results inaccurate?  (1 mark)

Show Answers Only
  1. `98`
  2. `37/43`
  3. `28`
Show Worked Solution
i.  `A` `= 200-(74 + 12 + 16)`
  `= 98`

 

ii.  `P` `= text(# Positive carriers)/text(Total carriers)`
  `= 74/86`
  `= 37/43`

 

iii.  `text(# People with inaccurate results)`

`= 12 + 16`

`= 28`

Measurement, STD2 M6 2006 HSC 26a

Daniel conducts an offset survey to sketch a diagram, `ABCD`, of a block of land.

Daniel walks from `A` to `C`, a distance of 62 m.

When he is 15 m from `A`, he notes that point `D` is 25 m to his right.

When he is 57 m from `A`, he notes that point `B` is 20 m to his left.

This is his notebook entry.

  1. Draw a neat sketch of the block of land. Label `A, B, C` and `D` on your diagram.  (1 mark)

  2. Calculate the distance from `C` to `D`. (Give your answer to the nearest metre.)  (2 marks)

Show Answers Only
  1.  
  2. `text{53 m (nearest m)}`
Show Worked Solution
i.   

 

ii.  `text(Using Pythagoras:)`

`CD^2` `= 47^2 + 25^2`
  `= 2834`
`:. CD` `= 53.235…`
  `= 53\ text{m  (nearest m)}`

Probability, STD2 S2 2006 HSC 25c

Sonia buys three raffle tickets.

HSC 2006 25c

  1. What is the probability that Sonia wins first prize?  (1 mark)

  2. What is the probability that she wins both prizes?  (2 marks)

Show Answers Only
  1. `1/60`
  2. `1/5370`
Show Worked Solution
i.  `text{P (wins 1st prize)}` `= text(# tickets bought) / text(total tickets)`
  `= 3/180`
  `= 1/60`

 

ii.  `text{P (wins both)}` `= text{P (wins 1st)} xx text{P (wins 2nd)}`
  `= 1/60 xx 2/179`
  `= 1/5370`

Calculus, EXT1* C3 2005 HSC 6c

2005 6c
 

The graphs of the curves  `y = x^2`  and  `y = 12 - 2x^2`  are shown in the diagram.

  1. Find the points of intersection of the two curves.  (1 mark)

  2. The shaded region between the curves and the `y`-axis is rotated about the `y`-axis. By splitting the shaded region into two parts, or otherwise, find the volume of the solid formed.  (3 marks)

Show Answers Only
  1. `text{(2, 4), (–2, 4)`
  2. `24pi\ \ text(u³)`
Show Worked Solution
i.    `y` `= x^2` `\ …\ (1)`
  `y` `= 12 − 2x^2` `\ …\ (2)`

 

`text(Substitute)\ \ y = x^2\ \ text(into)\ (2)`

`x^2` `= 12 − 2x^2`
`3x^2 − 12` `= 0`
`3(x^2 − 4)` `= 0`
`x` `= ±2`
`text(When)` `\ x = 2,` `\ y = 4`
`text(When)` `\ x = text(−2),` `\ y = 4`

 
`:.\ text{Intersection at (2, 4), (−2, 4)}`
 

ii.  `text{In (1),}\ \ x^2=y`

`text{In (2),}\ \ \ y` `= 12 − 2x^2`
`2x^2` `= 12 − y`
`x^2` `= (12 − y)/2`
  `= 6 − 1/2y`

 
`:.\ text(Volume)`

`= pi int_0^4 y\ dy + pi int_4^12 6 − 1/2y\ dy`
`= pi[y^2/2]_0^4 + pi[6y − y^2/4]_4^12`
`= pi[16/2 − 0] + pi[(6 xx 12 − 12^2/4) − (6 xx 4 − 4^2/4)]`
`= 8pi + pi[36 − 20]`
`= 8pi + 16pi`
`= 24pi\ \ text(u³)`

Calculus, 2ADV C3 2005 HSC 6b

A tank initially holds 3600 litres of water. The water drains from the bottom of the tank. The tank takes 60 minutes to empty.

A mathematical model predicts that the volume, `V`  litres, of water that will remain in the tank after  `t`  minutes is given by
  

`V = 3600(1 − t/60)^2,\ \ text(where)\ \ 0 ≤ t ≤ 60`.
 

  1. What volume does the model predict will remain after ten minutes?  (1 mark)

  2. At what rate does the model predict that the water will drain from the tank after twenty minutes?  (2 marks)

  3. At what time does the model predict that the water will drain from the tank at its fastest rate?  (2 marks)

Show Answers Only
  1. `text(2500 L)`
  2. `80\ text(liters per minute)`
  3. `0`
Show Worked Solution

i.    `V = 3600(1 − t/60)^2`

`text(When)\ t = 10,`

`V` `= 3600(1 − 10/60)^2`
  `= 3600 xx (5/6)^2`
  `= 2500\ text(L)`

 

ii.   `V = 3600(1 -t/60)^2`

`text(Using chain rule:)`

`(dV)/dt` `= 3600 xx 2 xx (1 – t/60) xx d/dt(1 – t/60)`
  `= 7200(1 – t/60) xx -1/60`
  `= −120(1 – t/60)`

 

`text(When)\ \ t =20`

`(dV)/dt` `= −120(1 – 20/60)`
  `= −80`

 

`:.\ text(After 20 minutes, the water will drain)`

`text(at 80 litres per minute.)`

 

iii. `(dV)/dt` `= −120(1 − t/60)`
    `= −120 + 2t`
  `(d^2V)/dt^2` `= 2`

 
`text(S)text(ince)\ (d^2V)/dt^2\ text(is a constant, no S.P.’s)`

 

`text(Checking limits of)\ \ 0 ≤ t ≤ 60`

`text(At)\ t = 0,`

`(dV)/dt = −120(1-0) = −120\ text(L/min)`

`text(At)\ t = 60,`

`(dV)/dt = −120(1 − 60/60) = 0\ text(L/min)`

 

`:.\ text(The model predicts water will drain)`

`text(out the fastest when)\ \ t = 0.`

Integration, 2UA 2005 HSC 6a

Five values of the function `f(x)` are shown in the table.

Integration, 2UA 2005 HSC 6a

Use Simpson’s rule with the five values given in the table to estimate

`int_0^20 f(x)\ dx`.  (3 marks)

Show Answers Only

`401 2/3`

Show Worked Solution

Integration, 2UA 2005 HSC 6a Answer

`int_0^20 f(x)\ dx` `= h/3[y_0 + y_4 + 4text{(odds)} + 2text{(evens)}]`
  `= 5/3[y_0 + y_4 + 4(y_1 + y_3) + 2(y_2)]`
  `= 5/3[15 + 10 + 4(25 + 18)+ 2(22)]`
  `= 5/3[25 + 172 + 44]`
  `= 401 2/3`

Probability, 2ADV S1 2005 HSC 5d

A total of 300 tickets are sold in a raffle which has three prizes. There are 100 red, 100 green and 100 blue tickets.

At the drawing of the raffle, winning tickets are NOT replaced before the next draw.

  1. What is the probability that each of the three winning tickets is red?  (2 marks)

  2. What is the probability that at least one of the winning tickets is not red?  (1 mark)

  3. What is the probability that there is one winning ticket of each colour?  (2 marks)

Show Answers Only
  1. `1617/(44\ 551)`
  2. `(42\ 934)/(44\ 551)`
  3. `0.224\ \ text{(to 3 d.p.)}`
Show Worked Solution
i.   `P(R R R)` `= 100/300 xx 99/299 xx 98/298`
    `= 1617/(44\ 551)`

 

ii. `Ptext{(at least 1 winner NOT red)}`

`= 1 − P(R R R)`

`= 1− 1617/(44\ 551)`

`= (42\ 934)/(44\ 551)`

 

iii. `text(# Combinations of winning tickets)`

`= 3 xx 2 xx 1`

`= 6`
 

`:.P text{(one winner from each colour)}`

`= 6 xx 100/300 xx 100/299 xx 100/298`

`= 0.22446…`

`= 0.224\ \ text{(to 3 d.p.)}`

Calculus, 2ADV C3 2005 HSC 5c

Find the coordinates of the point  `P`  on the curve  `y = 2e^x + 3x`  at which the tangent to the curve is parallel to the line  `y = 5x - 3`.  (3 marks)

Show Answers Only

`(0, 2)`

Show Worked Solution

`text(Gradient of)\ \ y = 5x − 3\ text(is)\ 5.`

`y` `= 2e^x + 3x`
`(dy)/(dx)` `= 2e^x + 3`

 
`text(Find)\ \ x\ \ text(when)\ \ (dy)/(dx) = 5`

`5` `= 2e^x + 3`
`2e^x` `= 2`
`e^x` `= 1`
`x` `= 0`

 
`text(When)\ \ x = 0`

`y` `= 2e^0 + (3 xx 0)`
  `= 2`

 
`:.P\ \ text{has coordinates (0, 2)}`

Plane Geometry, 2UA 2005 HSC 5b

The diagram shows a parallelogram `ABCD` with `∠DAB = 120^@`. The side `DC` is produced to `E` so that `AD = BE`.

Prove that `ΔBCE` is equilateral.  (3 marks)

Show Answers Only

`text(See Worked Solutions)`

Show Worked Solution

`BC` `= AD\ text{(opposite sides of parallelogram}\ ABCD)`
`∠BCD` `= 120^@\ text{(opposite angles of parallelogram}\ ABCD)`
`∠BCE` `= 60^@\ (∠DCE\ text{is a straight angle)}`
`∠CEB` `= 60^@\ text{(base angles of isosceles}\ \Delta BCE)`
`∠CBE` `= 60^@\ text{(angle sum of}\ ΔBCE)`

 
`:.ΔBCE\ text(is equilateral)`

Calculus, 2ADV C3 2005 HSC 4b

A function  `f(x)`  is defined by  `f(x) = (x + 3)(x^2- 9)`.

  1. Find all solutions of  `f(x) = 0`  (2 marks)

  2. Find the coordinates of the turning points of the graph of  `y = f(x)`, and determine their nature.  (3 marks)

  3. Hence sketch the graph of  `y = f(x)`, showing the turning points and the points where the curve meets the `x`-axis.  (2 marks)

  4. For what values of `x` is the graph of  `y = f(x)`  concave down?  (1 mark)

Show Answers Only
  1. `−3 or 3`
  2. `text{53.2 cm  (to 1 d.p.)}`
  3. `text(See worked solutions)`
  4. `x < −1`
Show Worked Solutions
i.    `f(x)` `= (x + 3)(x^2 − 9)`
    `= (x + 3)(x +3)(x − 3)`
  `:. f(x)` `= 0\ text(when)\ \ x=–3\ text(or)\ 3`

 

ii.   `f (x)` `= (x +3)(x^2 − 9)`
    `= x^3 − 9x + 3x^2 − 27`
    `= x^3 + 3x^2 − 9x − 27`
  `f′(x)` `= 3x^2 + 6x − 9`
  `f″(x)` `= 6x + 6`

 

`text(S.P.’s  when)\ \ f′(x) = 0`

`3x^2 + 6x − 9` `= 0`
`3(x^2 + 2x − 3)` `= 0`
`3(x − 1)(x + 3)` `= 0`

 

`text(At)\ x =1`

`f(1)` `= (4)(−8)=−32`
 `f″(1)` `= 6 + 6=12>0`
`:.\ text(MIN at)\ (1, −32)` 

 

`text(At)\ x = −3`

`f(-3)` `= 0`
`f″(−3)` `= (6 xx −3) + 6 = −12 <0`
`:.\ text(MAX at)\ (−3, 0)`

 

iii.   Geometry and Calculus, 2UA 2005 HSC 4b Answer

 

iv.  `f(x)\ \ text(is concave down when)`

`f″(x)` `< 0`
`6x + 6` `< 0`
`6x` `< −6`
`x` `< −1`

Trigonometry, 2ADV T1 2005 HSC 4a

 Trig Calculus, 2UA 2005 HSC 4a
 

A pendulum is 90 cm long and swings through an angle of 0.6 radians. The extreme positions of the pendulum are indicated by the points `A` and `B` in the diagram.

  1. Find the length of the arc  `AB`.  (1 mark)

  2. Find the straight-line distance between the extreme positions of the pendulum.  (2 marks)

  3. Find the area of the sector swept out by the pendulum.  (1 mark)

Show Answers Only
  1. `text(54 cm)`
  2. `text{53.2 cm  (to 1 d.p.)}`
  3. `text(2430 cm²)`
Show Worked Solution
i.    `text(Arc)\ AB` `= theta/(2 pi) xx 2 pi r`
    `= rtheta`
    `= 90 xx 0.6`
    `= 54\ text(cm)`

 

ii. 

 Trig Calculus, 2UA 2005 HSC 4a Answer

`text(Using the cosine rule)`

`text(Distance)\ AB\ text(in straight line)`

`AB^2` `= 90^2 xx 90^2 − 2 xx 90 xx 90 xx cos\ 0.6`
  `= 2829.563…`
`:.AB` `= 53.193…`
  `= 53.2\ text{cm  (to 1 d.p.)}`

 

iii. `text(Area of Sector)`

`= 0.6/(2pi) xx pir^2`

`= 0.3 xx 90^2`

`= 2430\ text(cm²)`

Plane Geometry, 2UA 2005 HSC 3c

2005 3c

In the diagram, `A`, `B`  and  `C`  are the points  `(6, 0), (9, 0)`  and  `(12, 6)` respectively. The equation of the line  `OC`  is  `x - 2y = 0`. The point  `D`  on  `OC`  is chosen so that  `AD`  is parallel to  `BC`. The point  `E`  on  `BC`  is chosen so that  `DE`  is parallel to the `x`-axis.

  1.  Show that the equation of the line `AD` is `y = 2x - 12`.  (2 marks)
  2. Find the coordinates of the point `D`.  (2 marks)
  3. Find the coordinates of the point `E`.  (1 marks)
  4. Prove that  `ΔOAD\ text(|||)\ ΔDEC`.  (2 marks)
  5. Hence, or otherwise, find the ratio of the lengths `AD` and `EC`.  (1 marks)
Show Answers Only
  1. `text(See Worked Solutions)`
  2. `(8, 4)`
  3. `(11, 4)`
  4. `text(See Worked Solutions)`
  5. `2:1`
Show Worked Solution

(i)   `text(S)text(ince)\ DA\ text(||)\ CB`

`m_(DA)` `= (y_2 − y_1)/(x_2 − x_1)`
  `= (6 − 0)/(12 − 9)`
  `= 2`

 

`:.\ text(Equation of)\ AD, m = 2,\ text(through)\ A(6, 0)`

`y − y_1` `= m(x − x_1)`
 `y − 0` `= 2(x − 6)`
 `y` `= 2x − 12\ \ \ \ …\ text(as required)`

 

(ii)  `D\ text(is at the intersection of)`

`x − 2y` `= 0` `\ \ …\ (1)`
 `y` `= 2x − 12\ ` `\ \ …\ (2)` 

`text(Substitute)\ y = 2x − 12\ text{into (1)}`

`x − 2(2x − 12)` `= 0`
`x − 4x + 24` `= 0`
`text(−3)x + 24` `= 0`
`3x` `= 24`
`x` `= 8`

`text(Substitute)\ x = 8\ text{into (2)}`

`y` `= 2 xx 8 − 12 = 4`
`:.D` `= (8, 4)`

 

(iii)  `text(Distance)\ \ AB=3`

`:. E\ \ text(has coordinates)\ \ (8+3,4)-=(11,4)`

 

(iv)  `text(Prove)\ ΔOAD\ text(|||)\ ΔDEC`

`∠ODA = ∠DCE`

`text{(corresponding angles,}\ AD\ text(||)\ BC)`

`∠OAD = ∠ABE`

`text{(corresponding angles,}\ AD\ text(||)\ BC)`

`∠ABE = ∠DEC`

`text{(corresponding angles,}\ AB\ text(||)\ DE)`

`:.∠OAD = ∠DEC`

`:.ΔOAD\ text(|||)\ ΔDEC\ text{(equiangular)}`

 

(v)     `(AD)/(EC)` `= (OA)/(DE)` 
    `= 6/3` 
    `=2` 

 `text{(corresponding sides of similar triangles)}`

 

`:.\ text(Ratio of lengths)\ AD:EC = 2:1` 

Trigonometry, 2ADV T1 2005 HSC 3b

The lengths of the sides of a triangle are 7 cm, 8 cm and 13 cm.

  1. Find the size of the angle opposite the longest side.  (2 marks)

  2. Find the area of the triangle.  (1 marks)

Show Answers Only
  1. `120^@`
  2. `14sqrt3\ text(cm)`
Show Worked Solution

i.

 Trig Ratios, 2UA 2005 HSC 3b Answer1 

`∠ABC\ \ text(is opposite the longest side)`

`text(Using the cosine rule)`

`cos\ ∠ABC` `= (7^2 + 8^2 −13^2)/(2 xx 7 xx 8)`
  `= text(−)1/2`

 
`text(S)text(ince cos)\ 60^@ = 1/2\ text(and cos is negative)`

`text(in 2nd quadrant,)`

`∠ABC` `= 180− 60`
  `= 120^@`

 

ii.  `text(Using the sine rule)`

`text(Area)\ ΔABC` `= 1/2\ ab\ sin\ C`
  `= 1/2 xx 7 xx 8\ sin 120^@`
  `= 28 xx sqrt3/2`
  `= 14sqrt3\ text(cm)^2`

Financial Maths, 2ADV M1 2006 HSC 8b

Joe borrows $200 000 which is to be repaid in equal monthly instalments. The interest rate is 7.2% per annum reducible, calculated monthly.

It can be shown that the amount, `$A_n`, owing after the `n`th repayment is given by the formula:

`A_n = 200\ 000r^n - M(1 + r + r^2 + … + r^(n-1))`,

where  `r = 1.006`  and  `$M`  is the monthly repayment.  (Do NOT show this.)

  1. The minimum monthly repayment is the amount required to repay the loan in 300 instalments.

     

    Find the minimum monthly repayment.  (3 marks)

  2. Joe decides to make repayments of $2800 each month from the start of the loan.

     

    How many months will it take for Joe to repay the loan?  (2 marks)

Show Answers Only
  1. `$1439`
  2. `94\ \  text(months)`
Show Worked Solution

i.  `A_n = 200\ 000r^n – M(1 + r + r^2 + … + r^(n-1))`

`text(Find)\ M\ text(such that)\ A_n = 0\ text(when)\ n = 300`

`0 = 200\ 000(1.006^300) – M(1 + 1.006+ … + 1.006^299)`

`=>  text(Note that ) (1 + 1.006+ … + 1.006^299)\ \ text(is a)`

`text(GP)\ text(where)\ a = 1, r = 1.006, n = 300`

`0 = 200\ 000(1.006^300) – M ({1(1.006^300-1)}/(1.006 – 1))`

`M ({(1.006^300-1)}/(0.006))` `= 200\ 000(1.006^300)`
`M` `= (1\ 203\ 439.36…)/(836.199…)`
  `= 1439.177…`
  `= $1439\ \ text{(nearest dollar)}`

 
`:.\ text(The minimum monthly repayment is $1439.)`

 

ii.  `text(If)\ M = 2800,\ text(find)\ n\ text(when)\ A_n = 0`

`0 = 200\ 000(1.006^n) – 2800({(1.006^n – 1)}/0.006)`

`0 = 1200(1.006^n) – 2800(1.006^n) + 2800`

`0 = -1600(1.006^n) + 2800`

`1600(1.006^n)` `= 2800`
`1.006^n` `= 2800/1600`
`n xx ln 1.006` `= ln­ \ 1.75`
`n` `= (ln­ \ 1.75)/ln 1.006`
  `= 93.54…`
  `=94\ \ text{months  (nearest month)}`

 

`:.\ text(It will take Joe 94 months to repay the loan.)`

Calculus, 2ADV C1 2006 HSC 8a

A particle is moving in a straight line. Its displacement, `x` metres, from the origin, `O`, at time `t` seconds, where  `t ≥ 0`, is given by  `x = 1 - 7/(t + 4)`.

  1. Find the initial displacement of the particle.  (1 mark)

  2. Find the velocity of the particle as it passes through the origin.  (3 marks)

  3. Show that the acceleration of the particle is always negative.  (1 mark)

  4. Sketch the graph of the displacement of the particle as a function of time.  (2 marks)

Show Answers Only
  1. `text(–3/4 m)`
  2. `1/7\ text(ms)^-1`
  3. `text(Proof)\ \ text{(See Worked Solutions)}`
  4.  
Show Worked Solution

i.   `x = 1 – 7/(t + 4)`
 

`text(When)\ \ t = 0,`

`x` `= 1 – 7/4`
  `= -3/4 \ \ text(m)`

 
`:.\ text(Initial displacement is)\ 3/4\ text(metres to)`

`text(the left of the origin.)`

 

ii.  `x = 1 – 7/(t+4) = 1 – 7(t + 4)^-1`

`dot x` `= (-1)  -7(t + 4)^-2 xx d/(dt)(t + 4)`
  `= 7 (t + 4)^-2 xx 1`
  `= 7/(t + 4)^2`

 

`text(Find)\ t\ text(when)\ x = 0`

`0` `= 1 – 7/(t + 4)`
`7/(t + 4)` `= 1`
`7` `= (t + 4)`
`t` `= 3`

 

`text(When)\ t = 3`

`dot x` `= 7/(3 + 4)^2`
  `= 1/7\ text(ms)^-1`

 

`:.\ text(The velocity of the particle as it passes)`

`text(through the origin is)\ 1/7\ text(ms)^-1.`

 

iii.  `dot x` `= 7(t + 4)^-2`
`ddot x` `= (d dot x)/(dt) = -14 (t +4)^-3`

 
`text(Given)\ t >= 0`

`=>  (t + 4)^-3 >= 0`

`=> -14 (t + 4)^-3 <= 0`

`:. ddot x\ text(is always negative.)`
 

(iv)  2UA HSC 2006 8a

Trigonometry, 2ADV T3 2006 HSC 7b

A function  `f(x)`  is defined by  `f(x) = 1 + 2 cos x`.

  1. Show that the graph of  `y = f(x)`  cuts the `x`-axis at  `x = (2 pi)/3`.   (1 mark)

  2. Sketch the graph of  `y = f(x)`  for  `-pi <= x <= pi`  showing where the graph cuts each of the axes.   (3 marks)

  3. Find the area under the curve  `y = f(x)` between  `x = -pi/2`  and  `x = (2 pi)/3`.   (3 marks)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2.   
  3. `((7 pi)/6 + sqrt 3 + 1)\ text(u²)`
Show Worked Solution

i.   `f(x) = 1 + 2 cos x`

`f(x)\ text(cuts the)\ x text(-axis when)\ f(x) = 0`

`1 + 2 cos x` `= 0`
`2 cos x` `=-1`
 `cos x` `= -1/2`

`:.  x = (2 pi)/3\ …\ text(as required)`

 

ii.   2UA HSC 2006 7b

 

iii.  `text(Area)` `= int_(-pi/2)^((2 pi)/3) 1 + 2 cos x\ \ dx`
  `= [x + 2 sin x]_(-pi/2)^((2 pi)/3)`
  `= [((2 pi)/3 + 2 sin­ (2 pi)/3) – ((-pi)/2 + 2 sin­ (-pi)/2)]`
  `= ((2 pi)/3 + 2 xx sqrt 3/2) – ((-pi)/2 +2(- 1))`
  `= (2 pi)/3 + sqrt(3) + pi/2 + 2`
  `= ((7 pi)/6 + sqrt(3) + 2)\ text(u²)`

Calculus, 2ADV C3 2006 HSC 5a

A function  `f(x)`  is defined by  `f(x) =2x^2(3-x)`.

  1. Find the coordinates of the turning points of  `y =f(x)`  and determine their nature.  (3 marks)

  2. Find the coordinates of the point of inflection.  (1 mark)

  3. Hence sketch the graph of  `y =f(x)`, showing the turning points, the point of inflection and the points where the curve meets the `x`-axis.  (3 marks)

  4. What is the minimum value of  `f(x)`  for  `–1 ≤ x ≤4`?  (1 mark)

Show Answers Only
  1. `text(Min)\ (0, 0),\ text(Max)\ (2, 8)`
  2. `text(P.I. at)\ (1, 4)`
  3.  
  4. `-32`
Show Worked Solution
i.       `f(x)` `= 2x^2 (3-x)`
  `= 6x^2-2x^3`
`f^{prime} (x)` `= 12x-6x^2`
`f^{″}(x)` `= 12-12x`

 

`text(S.P.’s when)\ f^{′}(x) = 0`

`12x-6x^2` `= 0`
`6x(2-x)` `= 0`

`x = 0 or 2`

`text(When)\ x = 0`

`f(0)` `= 0`
`f^{″}(0)` `= 12-0 = 12 > 0`
`:.\ text(MIN at)\ (0, 0)`

 

`text(When)\ x = 2`

`f(2)` `= 2 xx 2^2 (3-2)` `= 8`
`f^{″}(2)` `= 12-(12 xx 2)` `= -12 < 0`
`:.\ text(MAX at)\ (2, 8)`

 

ii.  `text(P.I. when)\ f^{″}(x) = 0`

`12-12x` `= 0`
`12x` `= 12`
`x` `= 1`
`f^{″}(0.5)` `=6>0`
`f^{″}(1.5)` `=-6<0`

`text(S)text(ince concavity changes)\ \ =>\  text(P.I. exists)` 

`f(1)` `= 2 xx 1^2(3-1)`
  `= 4`

`:.\ text(P.I. at)\ (1, 4)`

 

iii.  `f(x)\ text(meets)\ x text(-axis when)\ f(x) = 0`

`2x^2 xx (3-x) = 0`

`x = 0 or 3`

2UA HSC 2006 5a

 

(iv)  `text(The graph clearly shows that in the given range)`

`-1<= x<=4,\ text(the minimum will occur when)\ x = 4`

`:.\ text(Minimum` `= 2 xx 4^2 (3-4)`
  `= -32`

Quadratics, 2UA 2005 HSC 1f

Find the coordinates of the focus of the parabola  `x^2 = 8(y − 1)`.  (2 marks)

Show Answers Only

`(0, 3)`

Show Worked Solution

`x^2 = 8(y − 1)`

`text(Vertex)` `= (0, 1)`
`4a` `= 8`
`a` `= 2`

Algebra, 2UA 2005 HSC 1f Answer

`:.\ text(Focus has coordinates)\ \  (0,3).`

Probability, STD2 S2 2006 HSC 28a

On a bridge, the toll of $2.50 is paid in coins collected by a machine. The machine only accepts two-dollar coins, one-dollar coins and fifty-cent coins.

  1. List the different combinations of coins that could be used to pay the $2.50 toll.  (1 mark)

  2. Jill has three two-dollar coins, six one-dollar coins and two fifty-cent coins. She selects two coins at random.

     

    What is the probability that she selects exactly $2.50?  (3 marks)

  3. At the end of a day, the machine contains `x` two-dollar coins, `y` one-dollar coins and `w` fifty-cent coins.

     

    Write an expression for the total value of coins in dollars in the machine.  (1 mark)

Show Answers Only
  1. `text(Proof)\ \ text{(See Worked Solutions)}`
  2. `6/55`
  3. `$(2x + y + 0.5w)`
Show Worked Solution

i.  `text(Combinations for $2.50)`

`$2, 50c`

`$1, $1, 50c`

`$1, 50c, 50c, 50c`

`50c, 50c, 50c, 50c, 50c`

 

ii.  `3 xx $2, 6 xx $1, 2 xx 50c`

`P($2.50)` `= (3/11 xx 2/10) + (2/11 xx 3/10)`
  `= 6/110 + 6/110`
  `= 6/55`

 

iii.  `text(Total value) = $ (2x + y + 0.5w)`

Algebra, STD2 A4 2005 HSC 28b

Sue and Mikey are planning a fund-raising dance. They can hire a hall for $400 and a band for $300. Refreshments will cost them $12 per person.

  1. Write a formula for the cost ($C) of running the dance for `x` people. (1 mark)

The graph shows planned income and costs when the ticket price is $20 

2005 28b

  1. Estimate the minimum number of people needed at the dance to cover the costs.  (1 mark)

  2. How much profit will be made if 150 people attend the dance? (1 mark)

Sue and Mikey plan to sell 200 tickets. They want to make a profit of $1500.

  1. What should be the price of a ticket, assuming all 200 tickets will be sold?  (3 marks)

Show Answers Only
  1. `700 + 12x`
  2. `text(Approximately 90)`
  3. `$500`
  4. `$23`
Show Worked Solution
i.    `$C` `= 400 + 300 + (12 xx x)`
    `= 700 + 12x`

 

ii.  `text(Using the graph intersection)`

`text(Approximately 90 people are needed)`

`text(to cover the costs.)`

 

iii.  `text(If 150 people attend)`

`text(Income)` `= 150 xx $20`
  `= $3000`
`text(C)text(osts)` `= 700 + (12 xx 150)`
  `= $2500`

 

`:.\ text(Profit)` `= 3000 − 2500`
  `= $500`

 

iv.  `text(C)text(osts when)\ x = 200:`

`C` `= 700 + (12 xx 200)`
  `= $3100`

 

`text(Income required to make $1500 profit)`

`= 3100 + 1500`

`= $4600`
 

`:.\ text(Price per ticket)` `= 4600/200`
  `= $23`

Measurement, STD2 M1 2005 HSC 28a

The Mitchell family has moved to a new house which has an empty swimming pool. The base of the pool is in the shape of a rectangle, with a semicircle on each end.

2005 28a1

  1. Explain why the expression for the area of the base of the pool is  `2xy + πy^2`.   (1 mark) 

      
            2005 28a2
      

The pool is 1.1 metres deep.

  1. The sides and base of the pool are covered in tiles. If  `x =6`  and  `y = 2.5`, find the total area covered by tiles. (Give your answer correct to the nearest square metre.)   (4 marks)

Before filling the pool, the Mitchells need to install a new shower head, which saves 6 litres of water per minute.

The shower is used 5 times every day, for 3 minutes each time.

  1. If the charge for water is $1.013 per kilolitre, how much money would be saved in one year by using this shower head? (Assume there are 365 days in a year.)   (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(80 m)^2\ text{(nearest m}^2text{)}`
  3. `$33.28\ \ text{(nearest cent)}`
Show Worked Solution
a.    `text(Area of base)` `=\ text(Area of rectangle +)`
    `\ \ \ \ \ \2 xx text(Area of semi-circle)`
    `= (x xx 2y) + 2 xx (1/2 xx pi xx y^2)`
    `= 2xy + piy^2`

 

b.    `text(Area of base)` `= (2 xx 6 xx 2.5) + (pi xx 2.5^2)`
    `= 49.634…\ text(m²)`

 

`text(Area of walls) = text(Length) xx text(Height)`

`text(Length)` `= 2x + 2 xx text(semi-circle perimeter)`
  `= (2 xx 6) + 2 xx (1/2 xx 2 xx pi xx 2.5)`
  `= 12 + 15.707…`
  `= 27.707…\ text(m)`

 

`:.\ text(Area of walls)` `= 27.707 xx 1.1`
  `= 30.478…\ text(m)^2`

 

`:.\ text(Total Area covered by tiles)`

`= 49.634… + 30.478…`

`= 80.11…`

`= 80\ text{m²  (nearest m²)}`

 

c.     `text(Water saved)` `= 5 xx 3 xx 6`
    `= 90\ text(L per day.)`

 

`text(Water saved per year)`

`= 90 xx 365`

`= 32\ 850\ text(L)`

`= 32.85\ text(kL)`

`:.\ text(Money saved)` `= 32.85 xx $1.013`
  `= $33.277…`
  `= $33.28\ text{(nearest cent)}`

Statistics, STD2 S1 2005 HSC 27d

Nine students were selected at random from a school, and their ages were recorded.

\begin{array} {|c|}
\hline
\rule{0pt}{2.5ex} \textbf{Ages} \rule[-1ex]{0pt}{0pt} \\
\hline
\rule{0pt}{2.5ex} \ \ \ \text{12     11     16} \ \ \  \rule[-1ex]{0pt}{0pt} \\ \rule{0pt}{2.5ex} \text{14     16     15} \rule[-1ex]{0pt}{0pt} \\ \rule{0pt}{2.5ex} \text{14     15     14} \rule[-1ex]{0pt}{0pt} \\
\hline
\end{array}

  1. What is the sample standard deviation, correct to two decimal places?   (2 marks)

  2. Briefly explain what is meant by the term standard deviation.   (1 mark)

Show Answers Only
  1. `text{1.69  (to 2 d.p.)}`
  2. `text(Standard deviation is a measure of how much)`

     

    `text(members of a data group differ from the mean)`

     

    `text(value of the group)`

Show Worked Solution

a.  `text(Sample standard deviation)`

`= 1.6914…\ text{(by calculator)}`

`= 1.69\ \ \ text{(to 2 d.p.)}`

 

b.  `text(Standard deviation is a measure of how much)`

`text(members of a data group differ from the mean)`

`text(value of the group.)`

Measurement, STD2 M6 2005 HSC 27c

2UG-2005-27c
 

The bearing of `C` from `A` is 250° and the distance of `C` from `A` is 36 km.

  1. Explain why  `theta`  is 110°.   (1 mark)

  2. If  `B`  is 15 km due north of  `A`, calculate the distance of  `C`  from  `B`, correct to the nearest kilometre.   (3 marks)

Show Answers Only
  1. `110^@`
  2. `text{43 km (nearest km)}`
Show Worked Solution

i.  `text(There is 360° about point)\ A`

`:.theta + 250^@` `= 360^@`
`theta` `= 110^@`

 

ii.   
`a^2` `= b^2 + c^2 − 2ab\ cos\ A`
`CB^2` `= 36^2 + 15^2 − 2 xx 36 xx 15 xx cos\ 110^@`
  `= 1296 + 225 −(text(−369.38…))`
  `= 1890.38…`
`:.CB` `= 43.47…`
  `= 43\ text{km  (nearest km)}`

Measurement, 2UG 2005 HSC 27b

This diagram represents Earth. `O` is at the centre, and `A` and `B` are points on the surface.

2UG-2005-27b

Calculate the distance from `A` to `B` along the great circle through `A` and `B`.
Give your answer in to the nearest km.   (2 marks)

Show Answers Only

`text{4803 km  (nearest km)}`

Show Worked Solution

`A : 35^@text(N)\ 20^@text(E)\ \ \ \ B:8^@text(S)\ 20^@text(E)`

HSC 2005 27b

`text(Angular difference)` `= 35^@ + 8^@`
  `= 43^@`

 

`:.text(Distance from)\ A\ text(to)\ B`

`= 43/360 xx 2 xx pi xx r`

`= 43/360 xx 2 xx pi xx 6400`

`= 4803.1…`

`= 4803\ text{km  (nearest km)}`