SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, EXT1 C3 2021 SPEC2 10 MC

The differential equation that has the diagram above as its direction field is

  1. `(dy)/(dx) = y + 2x`
  2. `(dy)/(dx) = 2x - y`
  3. `(dy)/(dx) = x+2y`
  4. `(dy)/(dx) = y - 2x`
Show Answers Only

`D`

Show Worked Solution

`text(By elimination:)`

`text(At)\ (1, 2), m = 0`

`->\ text(Eliminate)\ A, C`

`text(At)\ (0, 1),\ m\ text(is positive)`

`->\ text(Eliminate)\ B`

`=>\ D`

Functions, EXT1 F1 2021 SPEC2 7

A function is defined parametrically by

   `x(t) = 5cos(2t) + 1,\ \ y(t) = 5sin(2t)-1`

If  `A(6, –1)`  and  `B(1, 4)`  are two points that lie on the graph of the function, then find the shortest distance along the graph from `A` to `B`.   (2 marks)

Show Answers Only

`(5pi)/2`

Show Worked Solution

`x = 5cos(2t) + 1 \ => \ cos(2t) = (x-1)/5`

`y = 5sin(2t)-1 \ => \ sin(2t) = (y + 1)/5`

`(cos(2t))^2 + (sin(2t))^2` `=1`  
`(x-1)^2 + (y + 1)^2` `=25`  

 

`text(Distance)` `= 1/4 xx 2 xx pi xx r`
  `= (5pi)/2`

Complex Numbers, EXT2 N2 2021 SPEC2 5

The graph of the circle given by  `|z - 2 - sqrt3i| = 1`, where  `z ∈ C`, is shown below.
 


 

For points on this circle, find the maximum value of  `|z|`.   (2 marks)

Show Answers Only

`sqrt7+1`

Show Worked Solution

`text(Centre of circle at)\ (2, sqrt3)`

`text(Radius = 1)`

`text(By Pythagoras, line from origin to the centre of the circle)`

`d = sqrt(2^2 + sqrt(3)^2) = sqrt7`

`:. |z|_text(max) = sqrt7 + 1`

Complex Numbers, EXT2 N1 2021 SPEC2 4 MC

For  the complex number `z `, if  `text(Im)(z) > 0`, then  `text(Arg)((zbarz)/(z - barz))` is

  1. `-pi/2`
  2. `0`
  3. `pi/4`
  4. `pi`
Show Answers Only

`A`

Show Worked Solution

`text(Let)\ \ z=x+iy \ => \ barz=x-iy`

`text(Arg)((zbarz)/(z – barz))` `= text(Arg)(zbarz) – text(Arg)(z – barz)`
  `= text(Arg)(x^2 + y^2) – text(Arg)(2yi)`
  `= 0 – text(Arg)(2yi),\ \ text(where)\ y > 0`
  `= -pi/2`

`=>\ A`

Probability, MET2 2021 VCAA 17 MC

A discrete random variable `X` has a binomial distribution with a probability of success of  `p = 0.1`  for `n` trials, where  `n > 2`.

If the probability of obtaining at least two successes after `n` trials is at least 0.5, then the smallest possible value of `n` is

  1. 15
  2. 16
  3. 17
  4. 18
  5. 19
Show Answers Only

`C`

Show Worked Solution

`text(Pr) (X ≥ 2) ≥ 0.5`

`text(Pr) (X = 0)` `=\ ^n C_0 xx 0.1^0 xx 0.9^n=0.9^n`
`text(Pr) (X = 1)` `=\ ^n C_1 xx 0.1^1 xx 0.9^{n-1}=nxx0.1xx0.9^(n-1)`
`text(Pr) (X ≥ 2)` `= 1 – (text(Pr) (X=0) + text(Pr) (X=1))`

  
`text{Solve for} \ n \ text{(by CAS):}`

`1 – (0.9^n + n xx 0.1 xx 0.9^{n-1}) ≥ 0.5`

`n = 17`

`=> \ C`

Calculus, MET2 2021 VCAA 14 MC

A value of `k` for which the average value of  `y = cos (kx - pi/2)`  over the interval  `[0, pi]`  is equal to the average value of  `y = sin(x)` over the same interval is

  1. `1/6`
  2. `1/5`
  3. `1/4`
  4. `1/3`
  5. `1/2`
Show Answers Only

`E`

Show Worked Solution

`text{By CAS, solve for} \ k:`

`1/pi int_0^pi cos (kx – pi/2) dx = 1/pi int_0^pi sin (x)\ dx`

`k = 1/2`

`=> E`

Statistics, MET2 2021 VCAA 12 MC

For a certain species of bird, the proportion of birds with a crest is known to be `3/5`.

Let `overset^P` be the random variable representing the proportion of birds with a crest in samples of size `n` for this specific bird.

The smallest sample size for which the standard deviation of `overset^P` is less than 0.08 is

  1.   7
  2. 27
  3. 37
  4. 38
  5. 43
Show Answers Only

`D`

Show Worked Solution

`text{Solve by CAS:}`

`sqrt{{0.6 xx 0.4}/{n}} < 0.08`

`n > 37.5`

`=> D`

Functions, MET2 2021 VCAA 10 MC

Consider the functions  `f(x) = sqrt{x+2}`  and  `g(x) = sqrt{1-2x}`, defined over their maximal domains.

The maximal domain of the function  `h = f + g`  is.

  1. `(–2, 1/2)`
  2. `[–2,∞)`
  3. `(–∞, –2) ∪ (1/2, ∞)`
  4. `[–2, 1/2]`
  5. `[–2, 1]`
Show Answers Only

`D`

Show Worked Solution

`f(x) \ = \ sqrt{x + 2} \ => \ text{domain} \ x ≥ -2`

`g(x) \ = \ sqrt{1-2x} \ => \ text{domain} \ x ≤ 1/2`

`text{Intersection of domains = domain} \ h(x)`

`:. \ h(x) ∈ [-2, 1/2]`

`=> D`

Functions, MET2 2021 VCAA 9 MC

Let  `g(x) = x + 2`  and  `f(x) = x^2 - 4`

If `h` is the composite function given by  `h : [–5, –1) to R, h(x) = f(g(x))`, then the range of `h` is

  1. `(-3 , 5]`
  2. `[-3, 5)`
  3. `(-3, 5)`
  4. `(-4, 5]`
  5. `[-4, 5]`
Show Answers Only

`E`

Show Worked Solution
`h(x)` `= (x + 2)^2 – 4`
  `= x^2 + 4x`

 
`text{By CAS, graph} \ \ y = x^2 + 4x , \ x∈ [–5, –1)`

`text{Min at} \ (–2, –4)`

`text{Max at} \ (–5, 5)`

`:. \ text{Range of} \ h(x) ∈ [–4, 5]`

`=> E`

Calculus, MET2 2021 VCAA 7 MC

The tangent to the graph of  `y = x^3 - ax^2 + 1`  at  `x = 1` passes through the origin.

The value of `a` is

  1. `1/2`
  2. `1`
  3. `3/2`
  4. `2`
  5. `5/2`
Show Answers Only

`B`

Show Worked Solution
`y` `= x^3 – ax^2 + 1`
`dy/dx` `= 3x^2 – 2ax`

 
`text{At} \ \ x = 1 \ => \  y = 2-a, \ dy/dx = 3-2a`
 

`text{T} text{angent passes through} \ (1,2-a) \ text{and} \ (0,0)`

`m_text{tang} = 2 – a`

`text{Equating gradients:}`

`3-2a` `= 2-a`
`:. a` `= 1`

 
`=> B`

Functions, MET2 2021 VCAA 5 MC

Consider the following four functional relations.

  `f(x) = f(-x)\ \ \ \ \ -f(x) = f(-x)\ \ \ \ \ f(x) = -f(x)\ \ \ \ \ (f(x))^2 = f(x^2)`

The number of these functional relations that are satisfied by the function  `f : R -> R, \ f(x) = x`  is

  1. 0
  2. 1
  3. 2
  4. 3
  5. 4
Show Answers Only

`C`

Show Worked Solution

`text{Consider each relation}`

`f(x) = x \ ,` `f(–x) = –x \ \ ✘`
`–f(x) = –x  \ ,` ` f(-x) = –x \ \ ✓`
`f(x) = x \ ,` `–f(x) = –x \ \ ✘`
`(f(x))^2 = x^2 \ ,` `f(x^2) = x^2 \ \ ✓`

 

`=> C`

Statistics, MET2 2021 VCAA 3 MC

A box contains many coloured glass beads.

A random sample of 48 beads is selected and it is found that the proportion of blue-coloured beads in this sample is 0.125

Based on this sample, a 95% confidence interval for the proportion of blue-coloured glass beads is

  1. (0.0314, 0.2186)
  2. (0.0465, 0.2035)
  3. (0.0018, 0.2482)
  4. (0.0896, 0.1604)
  5. (0.0264, 0.2136)
Show Answers Only

`A`

Show Worked Solution

`text{Method 1}`

`overset^p = 0.125 , \ n= 48`

`text{Successes} = 0.125 xx 48 = 6`
  

`text{By CAS:}`

`text{95% C.I.} = (0.0314, 0.2186)`
 

`text{Method 2}`

`text(sd)(overset^p)` `= sqrt({0.125 (1-0.125)}/{48})`
  `= 0.04773`

 

`:.\ text{95% C.I.}` `= (0.125 – 1.96 xx 0.04773 , 0.125 + 1.96 xx 0.04773)`
  `= (0.0314 , 0.2186)`

`=> A`

Statistics, SPEC2 2021 VCAA 18 MC

A scientist investigates the distribution of the masses of fish in a particular river. A 95% confidence interval for the mean mass of a fish, in grams, calculated from a random sample of 100 fish is (70.2, 75.8).

The sample mean divided by the population standard deviation is closest to

  1.   1.3
  2.   2.6
  3.   5.1
  4. 10.2
  5. 13.0
Show Answers Only

`C`

Show Worked Solution

`barx = (70.2 + 75.8)/2 = 73`

`1.96 xx s/sqrt100` `= 73 – 70.2`
`s` `= (2.8 xx 10)/1.96`
  `= 14.29`

 
`:. barx/s = 73/14.29 ~~ 5.1`

`=>\ C`

Mechanics, SPEC2 2021 VCAA 15 MC

The diagram below shows a stationary body being acted on by four forces whose magnitudes are in newtons. The force of magnitude `F_1` newtons acts in the opposite direction to the force of magnitude 8 N.
 

The value of `F_1` is

  1. `8-2sqrt3`
  2. `2sqrt3`
  3. `8`
  4. `8 + 2sqrt3`
  5. `8-3sqrt3`
Show Answers Only

`A`

Show Worked Solution

`text(Resolve forces vertically:)`

`F_2sin60^@` `= 6sin30^@`
`F_2 sqrt3/2` `= 6 xx 1/2`
`F_2` `= 6/sqrt3`
  `= 2sqrt3`

 
`text(Resolve forces horizontally:)`

`F_1 + 6cos30^@` `= 2sqrt3 cos60^@ + 8`
`F_1 + 3sqrt3` `= sqrt3 + 8`
`F_1` `= 8 – 2sqrt3`

`=>\ A`

Mechanics, SPEC2 2021 VCAA 14 MC

A body of mass 5 kg is acted on by a net force of magnitude `F` newtons. This force causes the body to move so that its velocity,  `v\ text(ms)^(-1)`, along a straight line of motion is given by  `v = 3 + 2x`, where `x` metres is the position of the body at time `t` seconds.

When  `x = 2, F` is equal to

  1. 10
  2. 14
  3. 35
  4. 70
  5. 175
Show Answers Only

`D`

Show Worked Solution
`a` `= v · (dv)/(dx)`
  `= (3 + 2x) · 2`

 
`text(Find)\ F\ text(when)\ x = 2:`

`F` `= ma`
  `= 5 xx 2(3 + 2 xx 2)`
  `= 70\ text(N)`

 
`=>\ D`

Vectors, SPEC2 2021 VCAA 12 MC

Consider the vectors  `underset~a = x underset~i + underset~j, \ underset~b = underset~i - underset~j`  and  `underset~c = underset~i + x underset~j`.

Given that  `theta`  is the angle between  `underset~a`  and  `underset~b`,  and  `phi`  is the angle between  `underset~b`  and  `underset~c, cos(theta) cos (phi)`  is

  1. `(2(1 + x^2))/(1 - x^2)`
  2. `(sqrt2(1 - x^2))/(1 + x^2)`
  3. `-((x + 1)^2)/(2(1 + x^2))`
  4. `-((x - 1)^2)/(2(1 + x^2))`
  5. `(sqrt2(1 + x^2))/(1 - x^2)`
Show Answers Only

`D`

Show Worked Solution

`underset~a = x underset~i – underset~j, \ underset~b = underset~i – underset~j, \ underset~c = underset~i + x underset~j`

`underset~a · underset~b = |underset~a||underset~b|costheta`

`costheta = (x – 1)/(sqrt(x^2 + 1)sqrt2)`

`cos phi = (underset~b · underset~c)/(|underset~b||underset~c|) = (1 – x)/(sqrt2 sqrt(1 – x^2))`

`costheta · cos phi` `= ((x – 1)(1 – x))/(2(1 + x^2))`
  `= -((x – 1)^2)/(2(1 + x^2))`

 
`=>\ D`

Vectors, SPEC2 2021 VCAA 11 MC

Let `underset~i` be a unit vector pointing east and let `underset~j` be a unit vector pointing north.

A group of hikers travels 5 km in the direction south 30° west and then north for 10 km.

The position vector `underset~a` of the group of hikers with respect to the starting point is

  1. `underset~a = -5/2 underset~i - (5sqrt3)/2 underset~j`
  2. `underset~a = -5/2 underset~i + (10 - (5sqrt3)/2)underset~j`
  3. `underset~a = -5/2 underset~i + 10underset~j`
  4. `underset~a = -(5sqrt3)/2 underset~i + 15/2 underset~j`
  5. `underset~a = 5/2 underset~i + (10 + (5sqrt3)/2)underset~j`
Show Answers Only

`B`

Show Worked Solution

`sin30 = x/5 \ => \ x = 5/2`

`cos30 = y/5 \ => \ y = (5sqrt3)/2`

`:. P_1\ text(vector:)\  (-5/2 underset~i, -(5sqrt3)/2 underset~j)`

`:. P_2\ text(vector:)\  (-5/2 underset~i, (10 – (5sqrt3)/2)underset~j)`

`=>\ B`

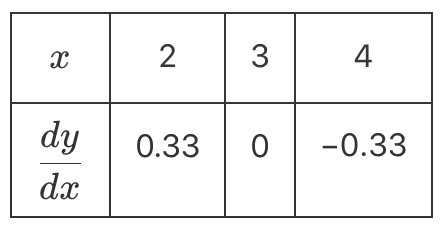
Calculus, SPEC2 2021 VCAA 10 MC

The differential equation that has the diagram above as its direction field is

  1. `(dy)/(dx) = y + 2x`
  2. `(dy)/(dx) = 2x - y`
  3. `(dy)/(dx) = 2y - x`
  4. `(dy)/(dx) = y - 2x`
  5. `(dy)/(dx) = x + 2y`
Show Answers Only

`D`

Show Worked Solution

`text(By elimination:)`

`text(At)\ (1, 2), m = 0`

`->\ text(Eliminate)\ A, C, E`

`text(At)\ (0, 1),\ m\ text(is positive)`

`->\ text(Eliminate)\ B`

`=>\ D`

Calculus, SPEC2 2021 VCAA 8 MC

Euler's method, with a step size of 0.1, is used to approximate the solution of the differential equation  `(dy)/(dx) = ysin(x)`.

Given that  `y = 2`  when  `x = 1`, the value of `y`, correct to three decimal places, when  `x = 1.2` is

  1. 2.168
  2. 2.178
  3. 2.362
  4. 2.370
  5. 2.381
Show Answers Only

`C`

Show Worked Solution

`text(Using)\ \ y_0 = 2, \ x_0 = 1, \ h = 0.1:`

`y_1` `= y_0 + h(y_0sinx_0)`
  `= 2 + 0.1(2sin1)`
  `= 2.1683`

 

`y_2` `= 2.1683 + 0.1(2.1683 xx sin 1.1)`
  `= 2.362`

 
`=>\ C`

Trigonometry, SPEC2 2021 VCAA 3 MC

The coordinates of the local maxima of the graph of  `y = 1/((cos(ax) + 1)^2 + 3)`, where  `a ∈ Rtext(\){0}`, are

  1. `((2pik)/a , 1/7), k ∈ Z`
  2. `((2pik)/a , 1/3), k ∈ Z`
  3. `(((1 + 2k)pi)/(2a) , 1/4), k ∈ Z`
  4. `((pi(1 + 2k))/a , 1/4), k ∈ Z`
  5. `((pi(1 + 2k))/a , 1/3), k ∈ Z`
Show Answers Only

`E`

Show Worked Solution

`y_text(max)\ \ text(occurs when)`

Mean mark 51%.

`(cos(ax))^2 + 3\ \ text(is a minimum)`
 

`text(Find)\ x\ text(such that:)`

`cos(ax)` `= -1`
`ax` `= pi + 2kpi, k ∈ Z`
`x` `= (pi(1 + 2k))/a`

 
`:.\ text(Local maxima at)\ ((pi(1 + 2k))/a, 1/3)`

`=>\ E`

Graphs, SPEC2 2021 VCAA 2 MC

The implied domain of the function with rule  `f(x) = cos^(-1)(log_e(bx), b > 0)`  is

  1. `(0, 1]`
  2. `[1, e]`
  3. `[1/b, e/b]`
  4. `[1/b, (e^pi)/b]`
  5. `[1/(be), e/b]`
Show Answers Only

`E`

Show Worked Solution

`f(x)\ text(is defined when)`

`-1 <= log_e(bx) <= 1`

`1/e <= bx <= e`

`1/(be) <= x <= e/b`

`=>\ E`

Vectors, SPEC1 2021 VCAA 9

Let  `underset~r(t) = (-1 + 4cos(t))underset~i + 2/sqrt3\ sin(t)underset~j`  and  `underset~s(t) = (3 sec(t)-1)underset~i + tan(t)underset~j`  be the position vectors relative to a fixed point `O` of particle `A` and particle `B` respectively for  `0 <= 1 <= c`, where `c` is a positive real constant.

    1. Show that the cartesian equation of the path of particle `A` is  `((x + 1)^2)/16 + (3y^2)/4 = 1`.   (1 mark)

    2. Show that the cartesian equation of the path of particle `A` in the first quadrant can be written as  `y = sqrt3/6 sqrt(-x^2-2x + 15)`.   (1 mark)

    1. Show that the particles `A` and `B` will collide.   (1 mark)

    2. Hence, find the coordinates of the point of collision of the two particles.   (1 mark)

    1. Show that  `d/(dx)(8arcsin ((x + 1)/4) + ((x + 1)sqrt(-x^2 -2x + 15))/2) = sqrt(-x^2-2x + 15)`.   (2 marks)


    2.    

      Hence, find the area bounded by the graph of  `y = sqrt3/6 sqrt(-x^2-2x + 15)`,  the `x`-axis and the lines  `x = 1`  and  `x = 2sqrt3-1`,  as shown in the diagram above. Give your answer in the form  `(asqrt3pi)/b`, where `a` and `b` are positive integers.   (2 marks)

Show Answers Only
    1. `text(See Worked Solutions)`
    2. `text(See Worked Solutions)`
    1. `text(See Worked Solutions)`
    2. `-1 + 2sqrt3, 1/sqrt3`
    1. `text(See Worked Solutions)`
    2. `(2sqrt3pi)/9`
Show Worked Solution

a.i.   `text(Particle A)`

`underset~r(t) = (-1 + 4cos(t))underset~i + 2/sqrt3\ sin(t)underset~j`

`x` `= -1 + 4cos(t)`
`x + 1` `= 4cos(t)`
`cos(t)` `= (x + 1)/4`
`y` `= 2/sqrt3\ sin(t)`
`sin(t)` `= (sqrt3 y)/2`

 
`text(Using)\ \ cos^2(t) + sin^2(t) = 1`

`((x + 1)^2)/16 + (3y^2)/4 = 1`

 

a.ii.  `((x + 1)^2)/16 + (3y^2)/4 = 1`

♦ Mean mark part (a)(ii) 41%.
`(x + 1)^2 + 12y^2` `= 16`
`12y^2` `= 16-x^2-2x-1`
`y^2` `= 1/12(15-x^2-2x)`
`y` `= ±sqrt(1/12 (-x^2-2x + 15))`

 
`text(In the 1st quadrant,)\ \ y > 0`

`:. y` `= 1/sqrt12 sqrt(-x^2-2x + 15)`
  `= 1/(2sqrt3) xx sqrt3/sqrt3 sqrt(-x^2-2x + 15)`
  `= sqrt3/6 sqrt(-x^2-2x + 15)`

 

b.i.   `text(If particles collide, find)\ \t\ text(that satisfies)`

`-1 + 4cos(t)` `= 3sec(t)-1\ \ text(and)`
`2/sqrt3 sin(t)` `= tan(t)`

 
`text(Equate)\ underset~j\ text(components:)`

`2/sqrt3 sin(t)` `= (sin(t))/(cos(t))`
`cos(t)` `= sqrt3/2`
`t` `= pi/6`

 
`text(Check)\ underset~i\ text(components at)\ \ t= pi/6 :`

`-1 + 4cos(pi/6)` `= 3 sec(pi/6)-1`
`-1 + 4 · sqrt3/2` `= 3· 2/sqrt3-1`
`2sqrt3` `= 2sqrt3`

 
`:.\ text(Particles collide.)`

 

b.ii.   `text(Collision occurs at)\ \ r(pi/6)`

`r(pi/6)` `= (-1 + 4cos\ pi/6, 2/sqrt3 sin\ pi/6)`
  `= (-1 + 2sqrt3, 1/sqrt3)`
♦ Mean mark part (c)(i) 37%.

 

c.i.   `d/dx (8sin^(-1) ((x + 1)/4) + ((x + 1)sqrt(-x^2 -2x + 15))/2)`

`= 8/(sqrt(1-((x + 1)/4)^2)) xx 1/4 + ((x + 1))/2 xx (-2x-2)/(2sqrt(-x^2-2x + 15)) + sqrt(-x^2-2x + 15) xx 1/2`

`= 8/(sqrt(16-(x + 1)^2))-((x + 1)^2)/(2sqrt(-x^2-2x + 15)) + sqrt(-x^2 -2x + 15)/2`

`= 16/(2sqrt(-x^2-2x + 15))-((x + 1)^2)/(2sqrt(-x^2-2x + 15))+ (-x^2-2x + 15)/(2sqrt(-x^2-2x + 15))`

`= (16-x^2-2x-1-x^2-2x + 15)/(2sqrt(-x^2-2x + 15))`

`= (2(-x^2-2x + 15))/(2sqrt(-x^2-2x + 15))`

`= sqrt(-x^2-2x + 15)`

♦ Mean mark part (c)(ii) 45%.

 

c.ii.    `text(Area)` `= int_1^(2sqrt3-1) sqrt3/6 sqrt(-x^2-2x + 15)\ dx`
    `= sqrt3/6 int_1^(2sqrt3-1) sqrt(-x^2-2x + 15)\ dx`
    `= sqrt3/6 [8sin^(-1)((x + 1)/4) + ((x + 1)sqrt(-x^2-2x + 15))/2]_1^(2sqrt3-1)`
    `= sqrt3/6 [(8sin^(-1)(sqrt3/2) + 2sqrt3 sqrt(-(2sqrt3 -1)^2-2(2sqrt3-1) + 15)/2)-(8sin^(-1)(1/2) + (2sqrt(-1-2 + 15))/2)]`
    `= sqrt3/6 [(8pi)/3 + sqrt3 sqrt(-12 + 4sqrt3-1-4sqrt3 + 2 + 15)-((8pi)/6 + sqrt12)]`
    `= sqrt3/6 ((8pi)/3 + 2sqrt3-(8pi)/6-2sqrt3)`
    `= sqrt3/6 ((8pi)/6)`
    `= (2sqrt3pi)/9`

Complex Numbers, EXT2 N2 2021 SPEC1 8

  1. Solve  `z^2 + 2z + 2 = 0`  for `z`, where  `z ∈ C`.  (1 mark)

  2. Solve  `z^2 + 2barz + 2 = 0`  for `z`, where  `z ∈ C`.  (3 marks)

Show Answers Only
  1. `z = -1 – i\ \ text(or)\ \ -1 + i`
  2. `z = 1 ± sqrt5 i`
Show Worked Solution
a.    `z^2 + 2z + 2` `= 0`
  `z^2 + 2z + 1 + 1` `= 0`
  `(z + 1)^2 + 1` `= 0`
  `(z + 1)^2 – i^2` `= 0`
  `(z + 1 + i)(z + 1 – i)` `= 0`

 
`:. z = -1 – i\ \ \ text(or)\ \ -1 + i`

 

b.   `z = x + yi \ => \ barz = x – yi`

`z^2 + 2barz + 2` `= 0`
`(x + yi)^2 + 2(x – yi) + 2` `= 0`
`x^2 + 2xyi – y^2 + 2x – 2yi + 2` `= 0`
`x^2 – y^2 + 2x + 2 + (2xy – 2y)i` `= 0`

 

`text(Find)\ \ x, y\ text(such that)`

`x^2 – y^2 + 2x + 2` `= 0\ …\ (1)`
`2xy – 2y` `= 0\ …\ (2)`

 
`text(When)\ \ 2xy – 2y = 0`

`2y(x – 1)` `= 0`
`x` `= 1`

 
`text(Substitute)\ \ x = 1\ \ text{into (1)}`

`1 – y^2 + 2 + 2` `= 0`
`y^2` `= 5`
`y` `= ±sqrt5`

 
`:. z = 1 ± sqrt5 i`

Complex Numbers, SPEC1 2021 VCAA 8

  1. Solve  `z^2 + 2z + 2 = 0`  for `z`, where  `z ∈ C`.   (1 mark)

  2. Solve  `z^2 + 2barz + 2 = 0`  for `z`, where  `z ∈ C`.   (3 marks)

Show Answers Only
  1. `z = -1-i\ \ text(or)\ \ -1 + i`
  2. `z = 1 ± sqrt5 i`
Show Worked Solution
a.    `z^2 + 2z + 2` `= 0`
  `z^2 + 2z + 1 + 1` `= 0`
  `(z + 1)^2 + 1` `= 0`
  `(z + 1)^2-i^2` `= 0`
  `(z + 1 + i)(z + 1-i)` `= 0`

 
`:. z = -1-i\ \ \ text(or)\ \ -1 + i`

 

b.   `z = x + yi \ => \ barz = x-yi`

♦♦ Mean mark part (b) 28%.
`z^2 + 2barz + 2` `= 0`
`(x + yi)^2 + 2(x-yi) + 2` `= 0`
`x^2 + 2xyi-y^2 + 2x-2yi + 2` `= 0`
`x^2-y^2 + 2x + 2 + (2xy-2y)i` `= 0`

 

`text(Find)\ \ x, y\ text(such that)`

`x^2-y^2 + 2x + 2` `= 0\ …\ (1)`
`2xy-2y` `= 0\ …\ (2)`

 
`text(When)\ \ 2xy-2y = 0`

`2y(x-1)` `= 0`
`x` `= 1`

 
`text(Substitute)\ \ x = 1\ \ text{into (1)}`

`1-y^2 + 2 + 2` `= 0`
`y^2` `= 5`
`y` `= ±sqrt5`

 
`:. z = 1 ± sqrt5 i`

Calculus, EXT1 C3 2021 SPEC1 7

The velocity of a particle satisfies the differential equation  `(dx)/(dt) = xsin(t)`,  where  `x`  centimetres is its displacement relative to a fixed point `O` at time `t` seconds.

Initially, the displacement of the particle is 1 cm.

  1. Find an expression for `x` in terms of `t`.  (3 marks)

  2. Find the maximum displacement of the particle and the times at which this occurs.  (2 marks)

Show Answers Only
  1. `x = e^(1 – cos(t))`
  2. `x_text(max) = e^2\ \ text(when)\ \ t = pi, 3pi, 5pi, …`

     

    `text(or)\ t = (2k + 1)pi\ \ text(for integral)\ \ k =0,1,2,…`

Show Worked Solution
a.    `(dx)/(dt)` `= x sin(t)`
  `int 1/x\ dx` `= int sin(t)\ dt`
  `log_e x` `= -cos(t) + c`

 

`text(When)\ \ t = 0, x = 1`

`log_e 1` `= -cos0 + c`
`c` `= 1`
`log_e x` `= -cos(t) + 1`
`:. x` `= e^(1 – cos(t))`

 

b.    `x` `= e^(1 – cos(t))`
  `(dx)/(dt)` `= sin(t) · e^(1 – cos(t))`

`text(Find)\ \ t\ \ text(when)\ \ (dx)/(dt) = 0:`

`e^(1 – cos(t)) != 0`

`sin(t) = 0\ \ text(when)\ \ t = 0, pi, 2pi, …`

`x_text(max) = e^2\ \ text(when)\ \ t = pi, 3pi, 5pi, …`

`text(or)\ \ t = (2k + 1)pi\ \ text(for integral)\ \ k =0,1,2,…`

Calculus, SPEC1 2021 VCAA 7

The velocity of a particle satisfies the differential equation  `(dx)/(dt) = xsin(t)`,  where  `x`  centimetres is its displacement relative to a fixed point `O` at time `t` seconds.

Initially, the displacement of the particle is 1 cm.

  1. Find an expression for `x` in terms of `t`.   (3 marks)

  2. Find the maximum displacement of the particle and the times at which this occurs.   (2 marks)

Show Answers Only
  1. `x = e^(1-cos(t))`
  2. `x_text(max) = e^2\ \ text(when)\ \ t = pi, 3pi, 5pi, …`

     

    `text(or)\ t = (2k + 1)pi\ \ text(for)\ \ k ∈ Z^+ ∪ {0}`

Show Worked Solution
a.    `(dx)/(dt)` `= x sin(t)`
  `int 1/x\ dx` `= int sin(t)\ dt`
  `log_e x` `= -cos(t) + c`

 

`text(When)\ \ t = 0, x = 1`

`log_e 1` `= -cos0 + c`
`c` `= 1`
`log_e x` `= -cos(t) + 1`
`:. x` `= e^(1-cos(t))`

 

b.    `x` `= e^(1-cos(t))`
  `(dx)/(dt)` `= sin(t) · e^(1-cos(t))`

`text(Find)\ \ t\ \ text(when)\ \ (dx)/(dt) = 0:`

♦♦ Mean mark part (b) 25%.

`e^(1-cos(t)) != 0`

`sin(t) = 0\ \ text(when)\ \ t = 0, pi, 2pi, …`

`x_text(max) = e^2\ \ text(when)\ \ t = pi, 3pi, 5pi, …`

`text(or)\ \ t = (2k + 1)pi\ \ text(for)\ \ k ∈ Z^+ ∪ {0}`

Vectors, SPEC1 2021 VCAA 6

Consider the three vectors  `underset~a = -underset~i + 6underset~j - 3underset~k, underset~b = 2underset~i - 8underset~j + 5underset~k`  and  `underset~c = 3underset~i + 2underset~j + |1 - p^2|underset~k`,  where  `p`  is a real constant.

Find the values of `p` for which the three vectors are linearly independent.  (4 marks)

Show Answers Only

`p ∈ R\ text(\) {±sqrt5}`

Show Worked Solution

`text(Linearly dependent when)\ \ underset~a = m underset~b + n underset~c`

`text(Equating)\ \ underset~i, underset~j\ \ text(and)\ \ underset~k\ \ text(components:)`

`-1` `= 2m + 3n\ \ …\ \ (1)`  
`6` `= -8m + 2n\ \ …\ \ (2)`  
`-3` `= 5m + |1 – p^2|n\ \ …\ \ (3)`  

 
`text(Mult)\ \ (1) xx 4`

`-4 = 8m + 12n\ \ …\ \ (1)′`

`text(Add)\ \  (2) + (1)′`

`2` `= 14n`
`n` `= 1/7`

 
`text(Substitute)\ \ n = 1/7\ \ text{into (1):}`

`-1` `= 2m + 3/7`
`2m` `= -10/7`
`m` `= -5/7`

 
`text(Substitute)\ \ m, n\ \ text{into (3):}`

`-3` `= – 25/7 + |1 – p^2| · 1/7`
`-21` `= -25 + |1 – p^2|`
`|1-p^2|` `= 4`
`1-p^2` `= ±4`
`p^2` `= 5\ \ \ (p^2 != -3)`
`p` `= ±sqrt5`

 
`:.\ text(Vectors are linearly independent for)\ \ p ∈ R\ text(\) {±sqrt5}`

Calculus, SPEC1 2021 VCAA 5

Find the gradient of the curve with equation  `e^x e^(2y) = 2e^4`  at the point  `(2, 1)`.  (3 marks)

Show Answers Only

`-1/10`

Show Worked Solution

`e^x e^(2y) + e^(4y^2) = 2e^4`

`e^x · 2e^(2y) · (dy)/(dx) + e^x · e^(2y) + e^(4y^2) · 8y · (dy)/(dx)` `= 0`
`(dy)/(dx)(e^x ·2e^(2y) + e^(4y^2) · 8y)` `= -e^x · e^(2y)`

 
`(dy)/(dx) = (-e^x · e^(2y))/(e^x · 2e^(2y) + e^(4y^2) ·8y)`

 
`text(At)\ \ (2, 1):`

`(dy)/(dx)` `= (-e^2 · e^2)/(e^2 · 2e^2 + e^4 · 8)`
  `= (-e^4)/(e^4(2 + 8))`
  `= -1/10`

Calculus, EXT1 C3 2021 SPEC1 4

The shaded region in the diagram below is bounded by the graph of  `y = sin(x)`  and the `x`-axis between the first two non-negative `x`-intercepts of the curve, that is interval  `[0, pi]`.  The shaded region is rotated about the `x`-axis to form a solid of revolution.
 
       
 
Find the volume, `V_s` of the solid formed.  (3 marks)

Show Answers Only

`(pi^2)/2\ text(u)³`

Show Worked Solution
  `V_s` `= pi int_0^pi sin^2(x)\ dx`
    `= pi int_0^pi 1/2(1 – cos(2x))\ dx`
    `= pi/2 int_0^pi 1 – cos(2x)\ dx`
    `= pi/2 [x – 1/2 sin(2x)]_0^pi`
    `= pi/2[pi – 1/2 sin(2pi) – (0 – 1/2 sin 0)]`
    `= (pi^2)/2\ text(u)³`

Calculus, SPEC1 2021 VCAA 4

  1. The shaded region in the diagram below is bounded by the graph of  `y = sin(x)`  and the `x`-axis between the first two non-negative `x`-intercepts of the curve, that is interval  `[0, pi]`.  The shaded region is rotated about the `x`-axis to form a solid of revolution.
     
           
     
    Find the volume, `V_s` of the solid formed.   (3 marks)

  2. Now consider the function  `y = sin(kx)`, where `k` is a positive real constant. The region bounded by the graph of the function and the `x`-axis between the first two non-negative `x`-intercepts of the graph is rotated about the `x`-axis to form a solid of revolution.
  3. Find the volume of this solid in term of `V_s`.   (1 mark)

Show Answers Only

  1. `(pi^2)/2\ text(u)³`
  2. `1/k V_s`

Show Worked Solution

a.    `V_s` `= pi int_0^pi sin^2(x)\ dx`
    `= pi int_0^pi 1/2(1-cos(2x))\ dx`
    `= pi/2 int_0^pi 1-cos(2x)\ dx`
    `= pi/2 [x-1/2 sin(2x)]_0^pi`
    `= pi/2[pi-1/2 sin(2pi)-(0-1/2 sin 0)]`
    `= (pi^2)/2\ text(u)³`

♦♦ Mean mark part (b) 30%.

 

b.   `y = sin(kx)\ \ text(is the dilation of)\ \ y = sin(x)\ \ text(by a factor of)`

`k\ \ text(from the)\ \ xtext(-axis)`

`:. V = 1/k V_s`

Statistics, SPEC1 2021 VCAA 3

A company produces a particular type of light globe called Shiny. The company claims that the lifetime of these globes is normally distributed with a mean of 200 weeks and it is known that the standard deviation of the lifetime of Shiny globes is 10 weeks. Customers have complained, saying Shiny globes were lasting less than the claimed 200 weeks. It was decided to investigate the complaints. A random sample of 36 Shiny globes was tested and it was found that the mean lifetime of the sample was 195 weeks.

Use  `text(Pr)(-1.96 < Z < 1.96) = 0.95`  and  `text(Pr)(-3 < Z < 3) = 0.9973`  to answer the following questions.

  1. Write down the null and alternative hypotheses for the one-tailed test that was conducted to investigate the complaints.   (1 mark)

    1. Determine the `p` value, correct to three places decimal places, for the test.   (2 marks)

    2. What should the company be told if the test was carried out at the 1% level of significance?   (1 mark)

  3. The company decided to produce a new type of light globe called Globeplus.
    Find the approximate 95% confidence interval for the mean lifetime of the new globes if a random sample of 25 Globeplus globes is tested and the sample mean is found to be 250 weeks. Assume that the standard deviation of the population is 10 weeks. Give your answer correct to two decimal places.   (1 mark)

Show Answers Only
  1. `H_0 : mu = 200`
    `H_1 : mu < 200`
    1. `0.001\ \ (text(to 3 d.p.))`
    2. `(246.08, 253.92)`
  3. `text(Reject the null hypothesis.)`
Show Worked Solution

a.   `H_0 : mu = 200`

`H_1 : mu < 200`

 

b.i.   `E(barX) = mu = 200`

♦ Mean mark part (b)(i) 48%.

`sigma(barX) = sigma/sqrtn = 10/sqrt36 = 5/3`

`p` `= text(Pr)(barX< 195 | mu = 200)`
  `= text(Pr)(z < (195-200)/(3/5))`
  `= text(Pr)(z < -3)`
  `= 1/2 (1-0.9973)`
  `= 0.00135`
  `= 0.001\ \ (text(to 3 d.p.))`

 

b.ii.   `text(1% level) => 0.01`

♦ Mean mark part (b)(ii) 49%.

  `text(S)text(ince)\ \ 0.001 < 0.01\ \ =>\ text(Strong evidence against)\ H_0`

  `:.\ text(Reject the null hypothesis.)`

 

c.   `sigma(barx) = sigma/sqrtn = 10/sqrt25 = 2`

`text(95% C.I.)` `= barx-1.96 xx 2, barx + 1.96 xx 2`
  `= (250-3.92, 250 + 3.92)`
  `= (246.08, 253.92)`

Vectors, SPEC1 2021 VCAA 1

The net force acting on a body of mass 10 kg is  `underset~F = 5underset~i + 12underset~j`  newtons.

  1. Find the acceleration of the body in `text(ms)^(-2)`.   (1 mark)

  2. The initial velocity of the body is  `-3underset~j\ \ text(ms)^(-1)`.
    Find the velocity of the body, in `text(ms)^(-1)`, at any time  `t`  seconds.   (2 marks)

  3. Find the momentum of the body, in kg `text(ms)^(-1)`, when  `t = 2`  seconds.   (1 mark)

Show Answers Only
  1. `1/2 underset~i + 6/5 underset~j`
  2. `1/2 t underset~i + (6/5 t-3) underset~j`
  3. `10 underset~i-6underset~j`
Show Worked Solution

a.   `text(Using)\ underset~F = m underset~a:`

`10underset~a` `= 5underset~i + 12underset~j`
`underset~a` `= 1/10 (5underset~i + 12underset~j)`
  `= 1/2 underset~i + 6/5 underset~j`

 

b.    `underset~v(t)` `= int underset~a\ dt`
    `= int 1/2 underset~i + 6/5 underset~j\ dt`
    `= 1/2 t underset~i + 6/5 t underset~j + c`

 
`text(When)\ t = 0, v(t) = -3underset~j`

`=> c = -3underset~j`

`underset~v(t)` `= 1/2 t underset~i + 6/5 t underset~j-3underset~j`
  `= 1/2 t underset~i + (6/5 t-3) underset~j`

 

c.    `underset~v(2) = underset~i-3/5 underset~j`

`underset~p(2)` `= m underset~v(2)`
  `= 10(underset~i-3/5 underset~j)`
  `= 10 underset~i-6underset~j`

Functions, 2ADV F2 2021 HSC 19

Without using calculus, sketch the graph of  `y = 2 + 1/(x + 4)`, showing the asymptotes and the `x` and `y` intercepts.  (3 marks)

Show Answers Only

Show Worked Solution

`text(Asymptotes:)\ x = -4`

`text(As)\ \ x -> ∞, y -> 2`

`ytext(-intercept occurs when)\ \ x = 0:`

`y = 2.25`

`xtext(-intercept occurs when)\ \ y = 0:`

`2 + 1/(x + 4) = 0 \ => \ x = -4.5`
 

GRAPHS, FUR1 2021 VCAA 5 MC

A manufacturer makes and sells heaters.

The fixed cost to manufacture the heaters is $16 000 per month.

Each heater costs $52 to produce.

The selling price of each heater is $280.

The minimum number of heaters needed to be sold per month in order to make a profit is

  1. 48
  2. 49
  3. 57
  4. 70
  5. 71
Show Answers Only

`E`

Show Worked Solution

`text{Let} \ x = \ text{number of heaters}`

`text{Revenue = 280} x`

`text{C}text{ost} = 16\ 000 + 52 x`

`text{Profit occurs when Revenue > Cost}`

`text{Find} \ x \ text{such that}`

`280 x` `> 16\ 000 + 52 x`
`228x` `> 16\ 000`
`x` `> (16\ 000)/228`
  `> 70.17`

 
`=> E`

GRAPHS, FUR1 2021 VCAA 3 MC

A line passes through the points (8, 0), (0, 6) and (5, `m`).

The value of `m` is

  1. 1.25
  2. 1.33
  3. 2.15
  4. 2.25
  5. 2.45
Show Answers Only

`D`

Show Worked Solution

`text{Equation of line through} \ (8, 0), (0,6)`

♦ Mean mark 50%.

`text(Gradient)  = {6 – 0}/{0 – 8} = – 3/4`

`y – 0` `= -3/4 (x – 8)`
`y` `= -3/4 x + 6`

 
`text{Line passes through} \ (5, m):`

`m` ` = – 3/4 (5) + 6`
  `=6-15/4`
  `= 2 1/4`

 
`=> D`

GRAPHS, FUR1 2021 VCAA 2 MC

Which one of the following represents a line with the same slope as  `y = 2x + 3`?

  1. `y - 2x = 0`
  2. `y + 2x = 0`
  3. `y = 3x + 2`
  4. `y + 2x = 3`
  5. `2y + 3 = x`
Show Answers Only

`A`

Show Worked Solution

`y = 2x + 3 => \ text{slope} = 2`

`text(Determine slope by writing each option in the form)\ \ y=mx+b`

`text{Consider option A:}`

`y – 2x` `= 0`
`y` `= 2x \ \ => text{slope} = 2`

 
`=> A`

Measurement, STD2 M1 2021 FUR1 6

A child's toy has the following design.
 

Find the area of the shaded region to the nearest square centimetre.  (2 marks)

Show Answers Only

`27\ text(cm²)`

Show Worked Solution

`text{Circle radius = 3 cm}`

`text(Consider the rectangle starting from the middle of the left circle.)`

`text{Shaded Area}` `= text{Area rectangle} –  3.5 xx text{Area circle}`
  `= (21 xx 6) – 3.5 xx pi xx 3^2`
  `= 27.03 …\ text{cm}^2`
  `=27\ text{cm²  (nearest whole)}`

GEOMETRY, FUR1 2021 VCAA 4 MC

The side length of an equilateral triangle is 4 cm, as shown in the diagram below.
 

Which one of the following is not a correct calculation for the area of this triangle?

  1. `{sqrt3 xx 4^2}/{4}`
  2. `2 xx sqrt12`
  3. `1/2 xx 4 xx 4`
  4. `4^2/2 xx sin(60^@)`
  5. `sqrt{6 (6-4)^3}`
Show Answers Only

`C`

Show Worked Solution

`text{By Pythagoras:}`

`h = sqrt{4^2 -2^2} = sqrt12 = 2 sqrt3`
 

`text{Area}` `= 2 xx (1/2 xx 2 xx 2 sqrt3)`
  `= 4 sqrt3 \ text{cm}^2`

 
`text{Option C is the only option} ≠ 4 sqrt3`
 
`=> C`

GEOMETRY, FUR1 2021 VCAA 1 MC

Which one of the following cities is closest to the Greenwich meridian?

  1. Barcelona (41° N, 2° E)
  2. Berlin (53° N, 13° E)
  3. Edinburgh (56° N, 3° W)
  4. Lomé (6° N, 1° E)
  5. Nairobi (1° N, 37° E)
Show Answers Only

`D`

Show Worked Solution

`text{Greenwich meridian has longitude} \ 0^@`

`text{Lome at} \ 1^@ \ text{is the closest.}`
 

`=> D`

MATRICES, FUR1 2021 VCAA 4 MC

Ramon and Norma are names that contain the same letters but in different order.

The permutation matrix that can change  `[(R),(A),(M),(O),(N)]` into `[(N),(O),(R),(M),(A)]`  is

A.  `[(0,0,0,0,1),(1,0,0,0,0),(0,0,1,0,0),(0,1,0,0,0),(0,0,0,1,0)]` B.  `[(0,0,0,0,1),(1,0,0,0,0),(0,0,1,0,0),(0,1,0,0,0),(0,0,0,1,0)]`  
     
C.  `[(1,0,0,0,0),(0,0,0,1,0),(0,0,0,0,1),(0,0,1,0,0),(0,1,0,0,0)]` D.  `[(0,0,0,0,1),(0,0,0,1,0),(1,0,0,0,0),(0,1,0,0,0),(0,0,1,0,0)]`  
     
E.  `[(0,0,0,0,1),(0,0,0,1,0),(1,0,0,0,0),(0,0,1,0,0),(0,1,0,0,0)]`    
Show Answers Only

`E`

Show Worked Solution

`[(0,0,0,0,1),(0,0,0,1,0),(1,0,0,0,0),(0,0,1,0,0),(0,1,0,0,0)] [(R),(A),(M),(O),(N)] = [(N),(O),(R),(M),(A)]`
 

`=> E`

MATRICES, FUR1 2021 VCAA 6 MC

A fitness centre offers four different exercise classes: aerobics `(A)`, boxfit `(B)`, cardio `(C)` and dance `(D)`.

A customer's choice of fitness class is expected to change from week to week according to the transition matrix `P`, shown below.

`qquadqquadqquadqquadqquadqquad text(this week)`

`P = {:(qquad\ A quadquadqquad \ B quadquad \ C quadqquad \ D),([(0.65,0, 0.20, 0.10),(0,0.65,0.10,0.30),(0.20,0.10,0.70,0),(0.15,0.25,0,0.60)]{:(A),(B),(C),(D):} qquad text(next week)):}`
 

An equivalent transition diagram has been constructed below, but the labeling is not complete.
 

The proportion for one of the transitions is labelled `w`.

The value of `w` is

  1. 10%
  2. 15%
  3. 20%
  4. 25%
  5. 30%
Show Answers Only

`B`

Show Worked Solution

`text{The 25% edge label must be} \ B \ text{(this week) to} \ D \ text{(next week)}`

`text{No edge exists between} \ C \ text{and} \ D`

`=> \ text{top left vertex is} \ C \ text{and top right vertex is} \ A.`

`w` `= A \ text{this week,} \ D \ text{next week}`
  `= 0.15`

 
`=> B`

MATRICES, FUR1 2021 VCAA 3 MC

`ax + 4y = 10`

`18x + by = 6`

The set of simultaneous linear equations above does not have a unique solution when

  1. `a = 2, \ b = 36`
  2. `a = 3, \ b = 22`
  3. `a = 4, \ b = 20`
  4. `a = 5, \ b = 12`
  5. `a = 6, \ b = 14`
Show Answers Only

`A`

Show Worked Solution

`text{In matrix form:}`

`[(a,4),(18,b)] [(x),(y)] = [(10),(6)]`
 

`text{No unique solution} =>\ text{det} = 0`

`ab – 4 xx 18` `= 0`
`ab` `= 72`

`=> A`

MATRICES, FUR1 2021 VCAA 2 MC

Every Friday, the same number of workers from a large office building regularly purchase their lunch from one of two locations: the deli, `D `, or the cafe, `C`.

It has been found that:

    • of the workers who purchase lunch from the deli on one Friday, 65% will return to purchase from the deli on the next Friday
    • of the workers who purchase lunch  from the cafe on one Friday, 55% will return to purchase from the cafe on the next Friday.

A transition matrix that can be used to describe this situation is

A.  `qquad text(this Friday)`
       `{:(qquad\ D quadquad \ C quad),([(0.55,0.35),(0.45,0.65)]{:(D),(C):} qquad text(next Friday)):}`		 B.  `qquad text(this Friday)`
       `{:(qquad\ D quadquad \ C quad),([(0.65,0.45),(0.45,0.55)]{:(D),(C):} qquad text(next Friday)):}`		  
     
C.  `qquad text(this Friday)`
       `{:(qquad\ D quadquad \ C quad),([(0.65,0.55),(0.45,0.55)]{:(D),(C):} qquad text(next Friday)):}`		 D.  `qquad text(this Friday)`
       `{:(qquad\ D quadquad \ C quad),([(0.65,0.45),(0.35,0.55)]{:(D),(C):} qquad text(next Friday)):}`		  
     
E.  `qquad text(this Friday)`
       `{:(qquad\ D quadquad \ C quad),([(0.65,0.55),(0.35,0.45)]{:(D),(C):} qquad text(next Friday)):}`		    
Show Answers Only

`D`

Show Worked Solution

`text{65% of workers return to deli}`

`=> e_11 = 0.65`

`text{55% of workers return to cafe}`

`=> e_22 = 0.55`
 

`text{Column elements must sum to 1}`

`=> D`

Calculus, MET1 2021 VCAA 8

The gradient of a function is given by  `(dy)/(dx) = sqrt(x + 6)-x/2-3/2`.

The graph of the function has a single stationary point at  `(3, 29/4)`.

  1. Find the rule of the function.   (3 marks)

  2. Determine the nature of the stationary point.   (2 marks)

Show Answers Only
  1. `y=2/3(x+6)^(3/2)-x^2/4-3/2x-4`
  2. `text{Maximum}`
Show Worked Solution
a.    `dy/dx` `= sqrt(x + 6)-x/2-3/2`
  `y` `=int sqrt(x + 6)-x/2-3/2\ dx`
    `=2/3(x+6)^(3/2)-x^2/4-3/2x + c`

 
`text{Graph passes through}\ (3, 29/4)`

`29/4` `=2/3*9^(3/2)-3^2/4-3/2 * 3+c`  
`29/4` `=18-9/4-9/2+c`  
`c` `=29/4-18+9/4+9/2`  
  `=-4`  

 
`:. y=2/3(x+6)^(3/2)-x^2/4-3/2x-4`

♦ Mean mark part (b) 37%.

b. 
      

`:.(3,29/4)\ text{is a maximum}.`

Graphs, MET1 2021 VCAA 4

  1. Sketch the graph of  `y = 1-2/(x-2)`  on the axes below. Label asymptotes with their equations and axis intercepts with their coordinates.   (3 marks)

     

     

  2. Find the values of  `x`  for which  `1-2/(x-2) >= 3`.   (1 mark)

Show Answers Only

a. 

b. `x in [1, 2)`

Show Worked Solution

a.   `text(Asymptotes:)`

`x=2`

`text(As)\ \ x→ +-oo, \ y→1\ \ =>\ text(Asymptote at)\ \ y=1`

`ytext(-intercept at)\ (0,2)`

`xtext(-intercept at)\ (4,0)`

♦ Mean mark part (b) 32%.

b.   `text(By inspection of the graph:)`

`1-2/(x-2) >=3\ \ text(for)\ \ x in [1, 2)`

Probability, MET1 2021 VCAA 6

An online shopping site sells boxes of doughnuts.

A box contains 20 doughnuts. There are only four types of doughnuts in the box. They are:

    • glazed, with custard
    • glazed, with no custard
    • not glazed, with custard
    • not glazed, with no custard

It is known that, in the box:

    • `1/2`  of the doughnuts are with custard
    • `7/10`  of the doughnuts are not glazed
    • `1/10`  of the doughnuts are glazed, with custard
  1. A doughnut is chosen at random from the box.
  2. Find the probability that it is not glazed, with custard.  (1 mark)

  3. The 20 doughnuts in the box are randomly allocated to two new boxes, Box A and Box B.
  4. Each new box contains 10 doughnuts.
  5. One of the two new boxes is chosen at random and then a doughnut from that box is chosen at random.
  6. Let `g` be the number of glazed doughnuts in Box A.
  7. Find the probability, in terms of `g`, that the doughnut comes from box B given that it is glazed.  (2 marks)

  8. The online shopping site has over one million visitors per day.
  9. It is know that half of these visitors are less than 25 years old.
  10. Let  `overset^P`  be the random variable representing the proportion of visitors who are less than 25 years old in a random sample of five visitors.
  11. Find  `text{Pr}(overset^P >= 0.8)`. Do not use a normal approximation.  (3 marks)

Show Answers Only

  1. `2/5`
  2. `(6-g)/6`
  3. `3/16`

Show Worked Solution

a.   `text(Create a 2-way table:)`

`text{Pr(not glazed with custard)}` `=8/20`  
  `=2/5`  

 
b.   `A_text{glazed} = g \ => \ B_text{glazed} = 6-g`

♦♦♦ Mean mark part (b) 20%.

`text{Pr(glazed)} = 6/20`

`text{Pr}(B | text{glazed})` `= (text{Pr}(B ∩ text{glazed}))/text{Pr(glazed)}`  
  `=(1/2 xx (6-g)/10)/(6/20)`  
  `=(6-g)/20 xx 20/6`  
  `=(6-g)/6`  

 
c.   `text(Let)\ \ X=\ text(number of visitors < 25 years)`

♦ Mean mark part (c) 40%.

`X\ ~\ text{Bi}(5, 0.5)`

`text{Pr}(hatP>=0.8)` `= text{Pr}(X>=4)`  
  `=\ ^5C_4 * (1/2)^4(1/2) + (1/2)^5`  
  `=5/32 + 1/32`  
  `=3/16`  

CORE, FUR1 2021 VCAA 22 MC

Joanna deposited $12 000 in an investment account earning interest at the rate of 2.8% per annum, compounding monthly.

She would like this account to reach a balance of $25 000 after five years.

To achieve this balance, she will make an extra payment into the account each month, immediately after the interest is calculated.

The minimum value of this payment is closest to

  1. $113.85
  2. $174.11
  3. $580.16
  4. $603.22
  5. $615.47
Show Answers Only

`B`

Show Worked Solution

`text{By TVM Solver:}`

`N` `= 60`
`Itext{(%)}` `= 2.8`
`PV` `= -12 000`
`PMT` `= ?`
`FV` `= 25 000`
`text(P/Y)` `= text(C/Y) = 12`

 
`:. PMT = 174.106 …`

`=> B`

CORE, FUR1 2021 VCAA 16 MC

The number of visitors to a regional animal park is seasonal.

Data is collected and deseasonalised before a least squares line is fitted.

The equation of the least squares line is

deseasonalised number of visitors = 2349 – 198.5 × month number

where month number 1 is January 2020.

The seasonal indices for the 12 months of 2020 are shown in the table below.
 

The actual number of visitors predicted for February 2020 was closest to

  1. 1562
  2. 1697
  3. 1952
  4. 2245
  5. 2440
Show Answers Only

`E`

Show Worked Solution

`text{Deseasonalised number of visitors in February}`

Mean mark 52%.

`= 2349 – 198.5 xx 2`

`= 1952`
 

`text{Actual visitors predicted in February}`

`= 1952 xx 1.25`

`= 2440`
 

`=> E`

CORE, FUR1 2021 VCAA 15 MC

The table below shows the number of visitors to an art gallery during the summer, autumn, winter and spring quarters for the years 2017 to 2019.

The quarterly average is also shown for each of these years.
 

   

The seasonal index for summer is closest to

  1. 1.077
  2. 1.081
  3. 1.088
  4. 1.092
  5. 1.096
Show Answers Only

`C`

Show Worked Solution

`text{Find summer seasonal proportion for each year:}`

`2017 \ : \ (29\ 685)/(27\ 194) = 1.09160 …`

`2018 \ : \ (25\ 420)/(23\ 183.5) = 1.09646 …`

`2019 \ : \ (31\ 496)/(29\ 243) = 1.07704 …`
 

`text{Seasonal index for summer}`

`= {1.09160 + 1.09646 + 1.07704}/{3}`

`= 1.0883`
 

`=> C`

CORE, FUR1 2021 VCAA 13 MC

The time series plot below shows the points scored by a basketball team over 40 games.
 

The nine-median smoothed points scored for game number 10 is closest to

  1. 102
  2. 108
  3. 110
  4. 112
  5. 117
Show Answers Only

`C`

Show Worked Solution

`text{Consider the 9 data points from game 6 to game 14.}`

`text{The median points scored value occurs on game} \ 9 ≈ 110.`

`=> C`

CORE, FUR1 2021 VCAA 10 MC

Oscar walked for nine consecutive days. The time, in minutes, that Oscar spent walking on each day is shown in the table below.
 

At least squares line is fitted to the data.

The equation of this line predicts that on day 10 the time Oscar spends walking will be the same as the time he spent walking on

  1. day 3
  2. day 4
  3. day 6
  4. day 8
  5. day 9
Show Answers Only

`B`

Show Worked Solution

`text{By calculator (day number = explanatory or} \ x text{-variable), the regression line is}`

`text{time}` `= 44 -\ text{day number}`
`:.\ text{time (day 10)}` `= 44 – 10`
  `= 34 \ text{minutes}`

 
`:. \ text{Day 10 time prediction is same as day 4}`
 

`=> B`

CORE, FUR1 2021 VCAA 9 MC

The heights of females living in a small country town are normally distributed:

    • 16% of the females are more than 160 cm tall.
    • 2.5% of the females are less than 115 cm tall.

The mean and the standard deviation of this female population, in centimetres, are closest to

  1. mean = 135               standard deviation = 15
  2. mean = 135               standard deviation = 25
  3. mean = 145               standard deviation = 15
  4. mean = 145               standard deviation = 20
  5. mean = 150               standard deviation = 10
Show Answers Only

`C`

Show Worked Solution

`160 -> ztext{-score} = 1`

`115 -> ztext{-score} = -2`

`1` `= {160 – mu}/sigma`
`mu + sigma` `= 160\ …\ (1)`
`-2` `= {115-mu}/sigma`
`mu-2 sigma` `= 115\ …\ (2)`

 
`(1)-(2)`

`3sigma` `=45`  
`sigma` `=15`  

 
`text{Substitute}\ \ sigma = 15\ \ text{into (1)}`

`mu = 145` 

`=> C`

CORE, FUR1 2021 VCAA 1-3 MC

The percentaged segmented bar chart below shows the age (under 55 years, 55 years and over) of visitors at a travel convention, segmented by preferred travel destination (domestic, international).
 

Part 1

The variables age (under 55 years, 55 years and over) and preferred travel destination (domestic, international) are

  1. both categorial variables.
  2. both numerical variables.
  3. a numerical variable and a categorical variable respectively.
  4. a categorical variable and a numerical variable respectively.
  5. a discrete variable and a continuous variable respectively.

 
Part 2

The data displayed in the percentaged segmented bar chart supports the contention that there is an association between preferred travel destination and age because

  1. more visitors favour international travel.
  2. 35% of visitors under 55 years favour international travel.
  3. 45% of visitors 55 years and over favour domestic travel.
  4. 65% of visitors under 55 years favour domestic travel while 45% of visitors 55 years and over favour domestic travel.
  5. the percentage of visitors who prefer domestic travel is greater than the percentage of visitors who prefer international travel.

 
Part 3

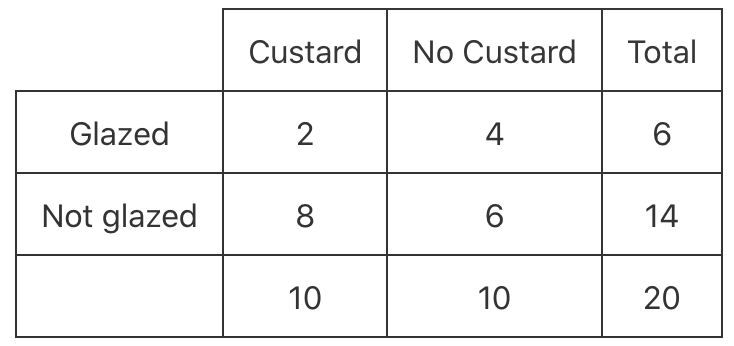
The results could also be summarised in a two-way frequency table.

Which one of the following frequency tables could match the pecentaged segmented bar chart?

 

Show Answers Only

`text(Part 1:)\ A`

`text(Part 2:)\ D `

`text(Part 3:)\ A`

Show Worked Solution

`text(Part 1)`

`text{Preferred travel destination → categorical (nominal) variable}`

`text{Age → categorical (ordinal) variable}`

`=> A`
 

`text(Part 2)`

`text(Only option)\ D\ text(highlights a change in preference for domestic travel)`

`text(between the two age categories.)`

`=>D` 

 
`text(Part 3)`

♦ Mean mark 50%.

`text(Converting the frequency table data into percentages,)`

`text(consider option)\ A:`

`91/140 xx 100 = 65text(%),\ \ 49/140 xx 100 = 35text(%)`

`90/200 xx 100 = 45text(%), \ \ 110/200 xx 100 = 55text(%)`

`=> A`

CORE, FUR1 2021 VCAA 7-8 MC

800 participants auditioned for a stage musical. Each participant was required to complete a series of ability tests for which they received an overall score.

The overall scores were approximately normally distributed with a mean score of 69.5 points and a standard deviation of 6.5 points.
 

Part 1

Only the participants who scored at least 76.0 points in the audition were considered successful,

Using the 68-95-99.7% rule, how many of the participants were considered unsuccessful?

  1. 127
  2. 128
  3. 272
  4. 672
  5. 673

 
Part 2

To be offered a leading role in the stage musical, a participant must achieve a standardised score of at least 1.80

Three participants' names and their overall scores are given in the table below.

Which one of the following statements is true?

  1. Only Amy was offered a leading role.
  2. Only Cherie was offered a leading role.
  3. Only Brian was not offered a leading role
  4. Both Brian and Cherie were offered leading roles.
  5. All three participants were offered leading roles.
Show Answers Only

`text(Part 1:)\ D`

`text(Part 2:)\ C`

Show Worked Solution

`text{Part 1}`

`mu = 69.5 \ , \ sigma= 6.5`

`ztext{-score} \ (76) = {76 – 69.5}/6.5 = 1`

`:.\  text{Unsuccessful}` `=84text(%) xx 800`
  `= 672`

`=> D`

 

`text{Part 2}`

`ztext{-score}` `= {x – mu}/sigma`
`1.8` `= {x – 69.5}/6.5`
`x` `= 1.8 xx 6.5 + 69.5`
  `= 81.2`

 
`:. \ text{Amy  and Cherie were both offered leading roles (only}`

`text{Brian wasn’t).}` 

`=> C`