Band 4 – Page 83

Algebra, STD2 A4 2018 HSC 27d

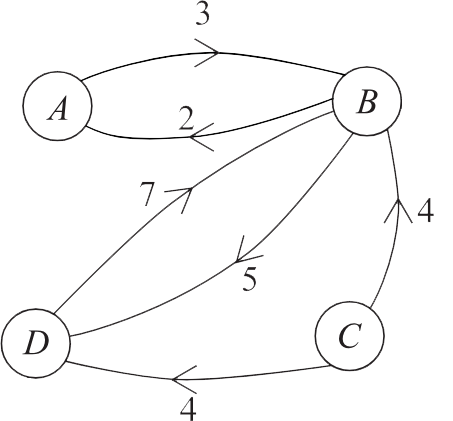
The graph displays the cost (`$c`) charged by two companies for the hire of a minibus for `x` hours.

Both companies charge $360 for the hire of a minibus for 3 hours.

What is the hourly rate charged by Company A? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Company B charges an initial booking fee of $75.

Write a formula, in the form of `c = mx + b`, for the cost of hiring a minibus from Company B for `x` hours. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
A minibus is hired for 5 hours from Company B.

Calculate how much cheaper this is than hiring from Company A. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`$120`
`c = 95x + 75`
`$50`

Show Worked Solution

i.	`text(Hourly rate)\ (A)`	`= 360 ÷ 3`
		`= $120`

ii. `m = text(hourly rate)`

`text(Find)\ m,\ text(given)\ c = 360,\ text(when)\ \ x = 3\ \ text(and)\ \ b = 75`

`360`	`= m xx 3 + 75`
`3m`	`= 285`
`m`	`= 95`

`:. c = 95x + 75`

iii.	`text(C)text(ost)\ (A)`	`= 120 xx 5 = $600`
	`text(C)text(ost)\ (B)`	`= 95 xx 5 + 75 = $550`

`:.\ text(Company)\ B’text(s hiring cost is $50 cheaper.)`

Measurement, STD2 M1 2018 HSC 27c

A shade shelter is to be constructed in the shape of half a cylinder with open ends. The diameter is 3.8 m and the length is 10 m.

The curved roof is to be made of plastic sheeting.

What area of plastic sheeting is required, to the nearest m²? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`60\ text(m² (nearest m²))`

Show Worked Solution

`text(Flatten out the half cylinder,)`

`text(Width)`	`= 1/2 xx text(circumference)`
	`= 1/2 xx pi xx 3.8`
	`= 5.969…`

`:.\ text(Sheeting required)`	`= 10 xx 5.969…`
	`= 59.69…`
	`= 60\ text(m² (nearest m²))`

Measurement, STD2 M7 2018 HSC 26g

A field diagram of a block of land has been drawn to scale. The shaded region `ABFG` is covered in grass.

The actual length of `AG` is 24 m.

If the length of `AG` on the field diagram is 8 cm, what is the scale of the diagram? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
How much fertiliser would be needed to fertilise the grassed area `ABFG` at the rate of 26.5 g /m²? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(1 : 300)`
`5008.5\ text(grams)`

Show Worked Solution

♦♦ Mean mark 32%.

i.	`text(Scale 8 cm)`	`\ :\ text(24 m)`
	`text(1 cm)`	`\ :\ text(3 m)`
	`1`	`\ :\ 300`

ii. `text(Area of rectangle)\ ABFE`

`= 6\ text(cm × 3 cm)`

`= 18\ text(m × 9 m)`

`= 162\ text(m²)`

`text(Area of)\ DeltaEFG`

`= 1/2 xx 3\ text(cm) xx 2\ text(cm)`

`= 1/2 xx 9 xx 6`

`= 27\ text(m²)`

`:.\ text(Fertiliser needed)`	`= (162 + 27) xx 26.5`
	`= 5008.5\ text(grams)`

Measurement, STD2 M1 2018 HSC 22 MC

A shape consisting of a quadrant and a right-angled triangle is shown.

What is the perimeter of this shape, correct to one decimal place?

28.6 cm
36.6 cm
66.3 cm
74.3 cm

Show Answers Only

`text(B)`

Show Worked Solution

`text(Using Pythagoras to find radius)\ (r):`

`r`	`= sqrt(10^2 – 6^2)`
	`= sqrt64`
	`= 8\ text(cm)`

`text(Arc length)`	`= 1/4 xx 2 pi r`
	`= 1/4 xx 2 xx pi xx 8`
	`= 12.56…\ text(cm)`

`:.\ text(Perimeter)`	`= 8 + 6 + 10 + 12.56…`
	`= 36.57…`

`=>\ text(B)`

Financial Maths, STD2 F1 2018 HSC 21 MC

David earns a gross income of $890 per week. Each week, 25% of this income is deducted in taxation. David budgets to save 20% of his net income.

How much does he budget to save each week?

$44.50
$133.50
$489.50
$534.00

Show Answers Only

`text(B)`

Show Worked Solution

`text(Net Income)`	`= 75text(%) xx 890`
	`= $667.50`

`text(Savings)`	`= 20text(%) xx 667.50`
	`= $133.50`

`=>\ text(B)`

Probability, STD2 S2 2018 HSC 20 MC

During a year, the maximum temperature each day was recorded. The results are shown in the table.

From the days with a maximum temperature less than 25°C, one day is selected at random.

What is the probability, to the nearest percentage, that the selected day occurred during winter?

Show Answers Only

`text(C)`

Show Worked Solution

`text{P(winter day)}`	`= (text(winter days < 25))/text(total days < 25) xx 100`
	`= 71/223 xx 100`
	`= 31.8…%`

`=>\ text(C)`

Measurement, STD2 M1 2018 HSC 18 MC

The length of a window is measured as 2.4 m.

Which calculation will give the percentage error for this measurement?

`0.05/2.4 xx 100`
`0.05/100 xx 2.4`
`0.5/2.4 xx 100`
`0.5/100 xx 2.4`

Show Answers Only

`A`

Show Worked Solution

`text{Absolute error}\ =1/2 xx text{precision}\ = 1/2 xx 0.1 = 0.05\ text{m}`

`text{% error}`	`=\ frac{text{absolute error}}{text{measurement}} xx 100%`
	`=0.05/2.4 xx 100%`

`=>A`

Measurement, STD2 M1 2018 HSC 13 MC

A rectangular pyramid has base side lengths `3x` and `4x`. The perpendicular height of the pyramid is `2x`. All measurements are in metres.

What is the volume of the pyramid in cubic metres?

`8x^3`
`9x^3`
`12x^3`
`24x^3`

Show Answers Only

`A`

Show Worked Solution

`text(Volume)`	`= 1/3Ah`
	`= 1/3(4x xx 3x xx 2x)`
	`= 8x^3`

`=>A`

Measurement, STD2 M6 2018 HSC 12 MC

The diagram shows a triangle with side lengths 8 m, 9 m and 10m.

What is the value of `theta`, marked on the diagram, to the nearest degree?

49°
51°
59°
72°

Show Answers Only

`text(D)`

Show Worked Solution

`text(Using the cosine rule:)`

`costheta`	`= (8^2 + 9^2 – 10^2)/(2 xx 8 xx 9)`
	`= 0.3125`
`:.theta`	`= cos^(−1)(0.3125)`
	`= 71.790…^@`

`=>D`

Statistics, STD2 S1 2018 HSC 11 MC

A set of data is summarised in this frequency distribution table.

Which of the following is true about the data?

Mode = 7, median = 5.5
Mode = 7, median = 6
Mode = 9, median = 5.5
Mode = 9, median = 6

Show Answers Only

`text(B)`

Show Worked Solution

`text{Mode = 7 (highest frequency of 9)}`

`text(Median = average of 15th and 16th data points.)`

`:.\ text(Median = 6)`

`=>\ text(B)`

Measurement, STD2 M6 2018 HSC 7 MC

The diagram shows the positions of towns `A`, `B` and `C`.

Town `A` is due north of town `B` and `angleCAB = 34°`

What is the bearing of town `C` from town `A`?

034°
146°
214°
326°

Show Answers Only

`C`

Show Worked Solution

`text(Bearing of Town)\ C\ text(from Town)\ A:`

`text(Bearing)`	`= 180 + 34`
	`= 214^@`

`=>C`

Statistics, STD2 S1 2018 HSC 3 MC

A survey asked the following question.

'How many brothers do you have?'

How would the responses be classified?

Categorical, ordinal
Categorical, nominal
Numerical, discrete
Numerical, continuous

Show Answers Only

`text(C)`

Show Worked Solution

`text(The number of brothers a person has is)`

`text(an exact whole number.)`

`:.\ text(Classification is numerical, discrete.)`

`=>\ text(C)`

Networks, STD2 N2 SM-Bank 23

A directed network diagram is pictured below.

The information in the network diagram is used to complete the network table below, with a "0" used to signify that no connection exists. Complete the table. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Networks, STD2 N2 SM-Bank 22

The table below represents a directed network.

Complete the network diagram below to accurately reflect the network described in the above table. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Networks, STD2 N2 SM-Bank 21

The table below represents a network.

Complete the network diagram below to accurately reflect the information in the above table. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

Mechanics, EXT2* M1 2018 HSC 13c

An object is projected from the origin with an initial velocity of `V` at an angle `theta` to the horizontal. The equations of motion of the object are

`x(t)`	`= Vt cos theta`
`y(t)`	`= Vt sin theta - (g t^2)/2.` (Do NOT prove this.)

Show that when the object is projected at an angle `theta`, the horizontal range is

`V^2/g sin 2 theta` (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Show that when the object is projected at an angle `pi/2 - theta`, the horizontal range is also

`V^2/g sin 2 theta`. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
The object is projected with initial velocity `V` to reach a horizontal distance `d`, which is less than the maximum possible horizontal range. There are two angles at which the object can be projected in order to travel that horizontal distance before landing.

Let these angles be `alpha` and `beta`, where `beta = pi/2 - alpha.`

Let `h_alpha` be the maximum height reached by the object when projected at the angle `alpha` to the horizontal.

Let `h_beta` be the maximum height reached by the object when projected at the angle `beta` to the horizontal.

Show that the average of the two heights, `(h_alpha + h_beta)/2`, depends only on `V` and `g`. (3 marks)

--- 9 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

i. `text(Horizontal range occurs when)\ \ y = 0`

`Vt sin theta – (g t^2)/2`	`= 0`
`V sin theta – (g t)/2`	`= 0`
`t`	`= (2V sin theta)/g`

`text(Find)\ \ x\ \ text(when)\ \ t=(2V sin theta)/g :`

`x`	`= Vt cos theta`
	`= V((2V sin theta)/g) cos theta`
	`= (V^2 * 2sin theta cos theta)/g`
	`= V^2/g sin 2 theta\ \ \ text(.. as required)`

ii. `text(Find)\ \ x\ \ text(when)\ \ theta = (pi/2 – theta):`

`x`	`= V^2/g sin 2 (pi/2 – theta)`
	`= V^2/g underbrace {sin (pi – 2 theta)}_{text(Using)\ \ sin (pi-theta) = sin theta}`
	`= V^2/g sin 2 theta\ \ \ text(.. as required)`

iii. `text(Highest point → half way through the flight.)`

`=> h_alpha\ \ text(occurs when)\ \ t=(V sin alpha)/g\ \ text{(by symmetry)}`

`:. h_alpha`	`= V((V sin alpha)/g) sin alpha – g/2 ((V sin alpha)/g)^2`
	`= (V^2 sin^2 alpha)/g – g/2 ((V^2 sin^2 alpha)/g^2)`
	`= (V^2 sin^2 alpha)/g – (V^2 sin^2 alpha)/(2g)`
	`= (V^2 sin^2 alpha)/(2g)`

`text(Similarly,)\ \ h_beta = (V^2 sin^2 beta)/(2g)`

♦ Mean mark 44%.

`:. (h_alpha + h_beta)/2`	`= 1/2 ((V^2 sin^2 alpha)/(2g) + (V^2 sin^2 beta)/(2g))`
	`= V^2/(4g) (sin^2 alpha + underbrace{sin^2 beta}_{text(Using)\ \ beta= pi/2 -alpha})`
	`= V^2/(4g) (sin^2 alpha + sin^2(pi/2 – alpha)) `
	`= V^2/(4g) (sin^2 alpha + cos^2 alpha)`
	`= V^2/(4g)`

`:. text(The average height depends only on)\ V\ text(or)\ g.`

The points `P(2ap, ap^2)` and `Q(2aq, aq^2)` lie on the parabola `x^2 = 4ay`. The focus of the parabola is `S(0, a)` and the tangents at `P` and `Q` intersect at `T(a(p + q), apq)`. (Do NOT prove this.)

The tangents at `P` and `Q` meet the `x`-axis at `A` and `B` respectively, as shown.

Show that `/_ PAS = 90^@`. (2 marks)
Explain why `S, B, A, T` are concyclic points. (1 mark)
Show that the diameter of the circle through `S, B, A` and `T` has length

`qquad qquad a sqrt((p^2 + 1)(q^2 + 1))`. (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(See Worked Solutions)`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i) `y=x^2/(4a)\ \ => dy/dx=x/(2a)`

`text(At)\ \ x=2ap,\ \ m_text(tang) = p`

`text(Equation of tangent)\ \ m=p, text(through)\ (2ap, ap^2):`

`y-ap^2`	`=p(x-2ap)`
`y`	`=px-ap^2`

`text(When)\ \ y=0, x=ap`

`:. A(ap,0)`

`m_(AP)`	`= (ap^2 – 0)/(2ap-ap)`
	`= p`

`m_(AS)`	`= (0 – a)/(ap – 0)`
	`= -1/p`

`m_(AP) xx m_(AS) = -1`

`:. /_PAS = 90°\ \ text(… as required)`

(ii) `text{Similarly to part (i):}`

♦ Mean mark 37%.

`=> B(aq,0)`

`=> m_(BQ) xx m_(BS) = -1`

`=> /_QBS = 90°`

`text(S)text(ince)\ \ T\ \ text(is the intersection of both tangents,)`

`/_ PAS = /_ TAS = 90^@`

`/_QBS = /_ TBS = 90^@`

`=> ST\ text(can be considered the extreme points of a circle diameter)`

`text(that is subtending 2 right angles on the circle circumference.)`

`:. SBAT\ text(are concyclic points.)`

(iii) `text(Diameter = distance)\ ST:`

♦ Mean mark 44%.

`S(0,a),\ \ T((a(p + q), apq)`

`d^2`	`= ST^2`
	`=(x_2-x_1)^2 + (y_2-y_1)^2`
	`= (a(p + q) – 0)^2 + (apq – a)^2`
	`= a^2 (p + q)^2 + a^2 (pq – 1)^2`
	`= a^2(p^2 + 2pq + q^2 + p^2q^2 – 2pq + 1)`
	`= a^2(p^2 + q^2 + p^2q^2 + 1)`
	`= a^2(p^2 + 1) (q^2 + 1)`
`:.d`	`= a sqrt((p^2 + 1)(q^2 + 1))\ \ text(… as required)`

Statistics, EXT1 S1 2018 HSC 12d

A group of 12 people sets off on a trek. The probability that a person finishes the trek within 8 hours is 0.75.

Find an expression for the probability that at least 10 people from the group complete the trek within 8 hours. (2 marks)

Show Answers Only

`text(See Worked Solutions)`

Show Worked Solution

`text{P(finishes within 8 hours)} = 0.75`

`text{P(not finish within 8 hours)} = 0.25`

`text(Let)\ \ X = text(number who finish below 8 hours)`

`:.\ text{P(at least 10 finish within 8 hours)}`

`=\ text{P(X=10) + P(X=11) + P(X=12)}`

`= ((12), (10)) (0.75)^10 (0.25)^2 + ((12), (11)) (0.75)^11 (0.25)^1 + ((12), (12)) (0.75)^12`

Calculus, EXT1 C1 2018 HSC 12b

A ferris wheel has a radius of 20 metres and is rotating at a rate of 1.5 radians per minute. The top of a carriage is `h` metres above the horizontal diameter of the ferris wheel. The angle of elevation of the top of the carriage from the centre of the ferris wheel is `theta`.

Show that `(dh)/(d theta) = 20 cos theta`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
At what speed is the top of the carriage rising when it is 15 metres higher than the horizontal diameter of the ferris wheel? Give your answer correct to one decimal place. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solution)}`
`19.8\ text{metres per minute (1 d.p)}`

Show Worked Solution

i. `text(From the diagram,)`

`sin theta`	`= h/20`
`h`	`= 20 sin theta`
`:. (dh)/(d theta)`	`= 20 cos theta`

ii. `text(Find)\ \ (dh)/(dt)\ text(when)\ h = 15:`

`(dh)/(dt)`	`= (dh)/(d theta) xx (d theta)/(dt)`
	`= (20 cos theta) xx 1.5`
	`= 30 cos theta`

`text(Find)\ cos theta\ \ text(when)\ h = 15`

`text(Using Pythagoras,)`

`cos theta`	`=sqrt(20^2 – 15^2)/20`
	`=sqrt7/4`

`:. (dh)/(dt)`	`= 30 cos theta`
	`= (15 sqrt 7)/2`
	`~~ 19.8\ text{metres per minute (1 d.p)}`

Real Functions, EXT1 2018 HSC 11e

Consider the function `f(x) = 1/(4x - 1)`.

Find the domain of `f(x)`. (1 mark)
For what values of `x` is `f(x) < 1`? (2 marks)

Show Answers Only

`{text(all real)\ x, x!=1/4}`
`x > 1/2 or x < 1/4`

Show Worked Solution

(i) `text(Domain is)\ {text(all real)\ x, x!=1/4}`

(ii)	`1/(4x – 1)`	`< 1`
	`(4x – 1)`	`< (4 x – 1)^2`
	`(4x – 1)^2 – (4x – 1)`	`> 0`
	`(4x – 1)[4x – 1- 1]`	`> 0`
	`2 (4x – 1) (2x – 1)`	`> 0`

`text(Sketching the parabola:)`

`x > 1/2 or x < 1/4.`

`text(From the graph,)`

`y > 1\ \ text(when)\ \ x < 1/4 or x > 1/2`

Plane Geometry, EXT1 2018 HSC 11d

Two secants from the point `C` intersect a circle as shown in the diagram.

What is the value of `x`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`4`

Show Worked Solution

`text(Using formula for intercepts of intersecting secants:)`

`x (x + 2)`	`= 3 (3 + 5)`
`x^2 + 2x`	`= 24`
`x^2 + 2x – 24`	`= 0`
`(x + 6) (x – 4)`	`= 0`
`:. x`	`= 4 \ \ \ (x > 0)`

Mechanics, EXT2* M1 2018 HSC 7 MC

The velocity of a particle, in metres per second, is given by `v = x^2 + 2` where `x` is its displacement in metres from the origin.

What is the acceleration of the particle at `x = 1`?

A. `2\ text(m s)^(-2)`

B. `3\ text(m s)^(-2)`

C. `6\ text(m s)^(-2)`

D. `12\ text(m s)^(-2)`

Show Answers Only

`C`

Show Worked Solution

`a`	`= d/dx (1/2 v^2)`
	`= d/dx (1/2 (x^2 + 2)^2)`
	`=1/2 xx 2 xx 2x (x^2+2)`
	`= 2x (x^2 + 2)`

`text(When)\ \ x = 1,`

`a = 6\ text(m s)^(-2)`

`⇒ C`

Polynomials, EXT1 2018 HSC 6 MC

The diagram shows the graph of `y = f(x)`. The equation `f(x) = 0` has a solution at `x = w`.

Newton’s method can be used to give an approximation close to the solution `x = w`.

Which initial approximation, `x_1`, will give the second approximation that is closest to the solution `x = w`?

A. `x_1 = a`

B. `x_1 = b`

C. `x_1 = c`

D. `x_1 = d`

Show Answers Only

`C`

Show Worked Solution

`text(Consider where the tangents at each point will cross the)`

`xtext(-axis).`

`x_1 = a\ text(will approximate the negative root.)`

`x_1 = c\ text(will cross the)\ x text(-axis closest to) \ w.`

`⇒ C`

Calculus, EXT1* C1 2018 HSC 5 MC

The diagram shows the number of penguins, `P(t)`, on an island at time `t`.

Which equation best represents this graph?

A. `P(t) = 1500 + 1500e^(-kt)`

B. `P(t) = 3000 - 1500e^(-kt)`

C. `P(t) = 3000 + 1500e^(-kt)`

D. `P(t) = 4500 - 1500e^(-kt)`

Show Answers Only

`A`

Show Worked Solution

`P(0) = 3000\ text{(from graph) → Eliminate B and C}`

`text(As),\ t -> oo,\ 1500e^(-kt) -> 0,`

`:. 1500 + 1500e^(-kt) => 1500`

`=> A`

Geometry and Calculus, EXT1 2018 HSC 4 MC

The diagram shows the graph of `y = a(x + b) (x + c) (x + d)^2`.

What are possible values of `a, b, c` and `d`?

A. `a = -6,\ \ b = -2,\ \ c = -1,\ \ d = 1`

B. `a = -6,\ \ b = 2,\ \ c = 1,\ \ d = -1`

C. `a = -3,\ \ b = -2,\ \ c = -1,\ \ d = 1`

D. `a = -3,\ \ b = 2,\ \ c = 1,\ \ d = -1`

Show Answers Only

`D`

Show Worked Solution

`text(S)text(ingle roots at:)\ \ x = -2, -1`

`text(Double root at:)\ \ x = 1`

`:. b = 2,\ \ c = 1,\ \ d = -1`

`y text(-intercept occurs when)\ x=0,`

`=> abcd^2 = -6`

`a(2)(1)(1^2) = -6`

`:.a = -3`

`⇒ D`

Trig Calculus, EXT1 2018 HSC 3 MC

What is the value of `lim_(x -> 0) (sin 3x cos 3x)/(12x)`?

A. `1/4`

B. `1/2`

C. `3/4`

D. `1`

Show Answers Only

`A`

Show Worked Solution

`lim_(x -> 0) (sin 3x cos 3x)/(12x)`	`= lim_(x -> 0) (1/2 xx 2 sin 3x cos 3x)/(12x)`
	`= lim_(x ->0) (1/2 xx sin 6x)/(12x)`
	`= 1/4 lim_(x ->0) (sin 6x)/(6x)`
	`= 1/4`

`⇒ A`

Networks, STD2 N3 2007 FUR2 4

A community centre is to be built on the new housing estate.

Nine activities have been identified for this building project.

The directed network below shows the activities and their completion times in weeks.

Determine the minimum time, in weeks, to complete this project. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Determine the float time, in weeks, for activity `D`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

The builders of the community centre are able to speed up the project.

Some of the activities can be reduced in time at an additional cost.

The activities that can be reduced in time are `A`, `C`, `E`, `F` and `G`.

Which of these activities, if reduced in time individually, would not result in an earlier completion of the project? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

The owner of the estate is prepared to pay the additional cost to achieve early completion.

The cost of reducing the time of each activity is $5000 per week.

The maximum reduction in time for each one of the five activities, `A`, `C`, `E`, `F`, `G`, is `2` weeks.

Determine the minimum time, in weeks, for the project to be completed now that certain activities can be reduced in time. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Determine the minimum additional cost of completing the project in this reduced time. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`19\ text(weeks)`
`5\ text(weeks)`
`A, E, G`
`text(15 weeks)`
`$25\ 000`

Show Worked Solution

a. `text(Scanning forwards and backwards:)`

`BCFHI\ \ text(is the critical path.)`

♦ Mean mark of all parts (combined) 40%.

`:.\ text(Minimum time)`	`= 4 + 3 + 4 + 2 + 6`
	`= 19\ text(weeks)`

b.	`text(EST of)\ D`	`= 4`
	`text(LST of)\ D`	`= 9`

`:.\ text(Float time of)\ D`	`= 9 – 4`
	`= 5\ text(weeks)`

c. `A, E,\ text(and)\ G\ text(are not currently on the critical path,)`

`text(therefore reducing their time will not result in an)`

`text(earlier completion time.)`

d. `text(Reduce)\ C\ text(and)\ F\ text(by 2 weeks each.)`

`text(However, a new critical path created:)\ BEHI\ \ text{(16 weeks)}`

`:.\ text(Also reduce)\ E\ text(by 1 week.)`

`:.\ text(Minimum completion time = 15 weeks)`

e.	`text(Additional cost)`	`= 5 xx $5000`
		`= $25\ 000`

Networks, STD2 N3 2006 FUR2 3

The five musicians are to record an album. This will involve nine activities.

The activities and their immediate predecessors are shown in the following table.

The duration of each activity is not yet known.

Use the information in the table above to complete the network below by including activities `G`, `H` and `I`. (2 marks)

There is only one critical path for this project.

How many non-critical activities are there? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

The following table gives the earliest start times (EST) and latest start times (LST) for three of the activities only. All times are in hours.

Write down the critical path for this project. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

The minimum time required for this project to be completed is 19 hours.

What is the duration of activity `I`? (1 mark)

The duration of activity `C` is 3 hours.

--- 1 WORK AREA LINES (style=lined) ---

Determine the maximum combined duration of activities `F` and `H`. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`5`
`B E G I`
`text(7 hours)`
`text(8 hours)`

Show Worked Solution

b. `text(S)text(ince no time information, possible critical paths are:)`

`ADGI, BEGI\ text(or)\ CFHI\ \ text{(all have 4 activities)}`

`:.\ text(Non-critical activities)`

`= 9 – 4 = 5`

c. `text(Critical activities have zero float time.)`

♦ Mean mark of parts (c)-(e) (combined) was 36%.

`=> A\ text(and)\ C\ text(are non-critical.)`

`:. B E G I\ text(is the critical path.)`

d.	`text(Duration of)\ \ I`	`= 19 – 12`
		`= 7\ text(hours)`

e. `text(Maximum time for)\ F\ text(and)\ H`

♦♦ MARKER’S COMMENT: Many students incorrectly answered 9 hours in part (e).

`=\ text(LST of)\ I – text(duration)\ C – text(slack time of)\ C`

`= 12 – 3 – 1`

`= 8\ text(hours)`

Networks, STD2 N3 2013 FUR2 2

A project will be undertaken in the wildlife park. This project involves the 13 activities shown in the table below. The duration, in hours, and predecessor(s) of each activity are also included in the table.

Activity `G` is missing from the network diagram for this project, which is shown below.

Complete the network diagram above by inserting activity `G`. (1 mark)
Determine the earliest starting time of activity `H`. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Given that activity `G` is not on the critical path
1. write down the activities that are on the critical path in the order that they are completed (1 mark)
  
  --- 2 WORK AREA LINES (style=lined) ---
2. find the latest starting time for activity `D`. (1 mark)
  
  --- 1 WORK AREA LINES (style=lined) ---
Consider the following statement.

‘If the time to complete just one of the activities in this project is reduced by one hour, then the minimum time to complete the entire project will be reduced by one hour.’

Explain the circumstances under which this statement will be true for this project. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Assume activity `F` is reduced by two hours.
What will be the minimum completion time for the project? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

b. `7\ text(hours)`

c.i. `AFIM`

c.ii. `14\ text(hours)`

d. `text(The statement will only be true if the crashed activity)`
`text(is on the critical path)\ \ A F I M.`

e. `text(36 hours)`

Show Worked Solution

b. `text(Scanning forwards and backwards:)`

`text(EST for Activity)\ H`

`= 4 + 3`

`= 7\ text(hours)`

c.i. `A F I M`

♦♦ Mean mark of parts (c)-(e) (combined) was 40%.

c.ii. `text(LST of)\ G = 20 – 4 = 16\ text(hours)`

`text(LST of)\ D = 16 – 2 = 14\ text(hours)`

d. `text(The statement will only be true if the time reduced activity)`

MARKER’S COMMENT: Most students struggled with part (d).

`text(is on the critical path)\ \ A F I M.`

e. `A F I M\ text(is 37 hours.)`

`text(If)\ F\ text(is reduced by 2 hours, the new critical)`

`text(path is)\ \ C E H G I M\ text{(36 hours)}`

`:.\ text(Minimum completion time = 36 hours)`

Networks, STD2 N3 2012 FUR2 2

Thirteen activities must be completed before the produce grown on a farm can be harvested.

The directed network below shows these activities and their completion times in days.

Determine the earliest starting time, in days, for activity `E`. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
An activity with zero duration starts at the end of activity `B`.

Explain why this activity is used on the network diagram. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Determine the earliest starting time, in days, for activity `H`. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
In order, list the activities on the critical path. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Determine the latest starting time, in days, for activity `J`. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`12\ text(days)`
`F\ text(has)\ B\ text(as a predecessor while)\ G\ text(and)\ H`
`text(have)\ B\ text(and)\ C\ text(as predecessors.)`
`text(S)text(ince there cannot be 2 activities called)\ B, text(a zero)`
`text{duration activity is drawn as an extension of}\ B\ text(to)`
`B\ text(show that it is also a predecessor of)\ G\ text(and)\ H.`
`15\ text(days)`
`ABHILM`
`25\ text(days)`

Show Worked Solution

a.	`text(EST of)\ E`	`= 10 + 2`
		`= 12\ text(days)`

♦ Mean mark of all parts (combined) 47%.

b. `F\ text(has)\ B\ text(as a predecessor while)\ G\ text(and)\ H`

`text(have)\ B\ text(and)\ C\ text(as predecessors.)`

`text(S)text(ince there cannot be 2 activities called)\ B, text(a zero)`

`text{duration activity is drawn as an extension of}\ B\ text(to)`

`text(show that it is also a predecessor of)\ G\ text(and)\ H.`

♦♦ “Few students” were able to correctly deal with the zero duration activity in part (c).

c. `text(Scanning forwards:)`

`text(EST for)\ H = 15\ text(days)`

d. `text(The critical path is)\ \ ABHILM`

e. `text(The shortest time to complete all the activities)`

MARKER’S COMMENT: A correct calculation based on an incorrect critical path in part (d) gained a consequential mark here. Show your working!.

`= 10 + 5 + 4 + 3 + 4 + 2`

`= 28\ text(days)`

`:.\ text(LST of)\ J`	`= 28 − 3`
	`= 25\ text(days)`

Networks, STD2 N3 2009 FUR2 4

A walkway is to be built across the lake.

Eleven activities must be completed for this building project.

The directed network below shows the activities and their completion times in weeks.

What is the earliest start time for activity E? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Write down the critical path for this project. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
The project supervisor correctly writes down the float time for each activity that can be delayed and makes a list of these times.

Determine the longest float time, in weeks, on the supervisor’s list. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

A twelfth activity, L, with duration three weeks, is to be added without altering the critical path.

Activity L has an earliest start time of four weeks and a latest start time of five weeks.

Draw in activity L on the network diagram above. (1 mark)
Activity L starts, but then takes four weeks longer than originally planned.

Determine the total overall time, in weeks, for the completion of this building project. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`7`
`BDFGIK`
`H\ text(or)\ J\ text(can be delayed for)`
`text(a maximum of 3 weeks.)`
`text(25 weeks)`

Show Worked Solution

a. `7\ text(weeks)`

♦ Mean mark of all parts (combined): 44%.

b. `text(Scanning forwards and backwards)`

`text(Critical Path is)\ BDFGIK`

c. `H\ text(or)\ J\ text(can be delayed for a maximum)`

`text(of 3 weeks.)`

e. `text(The new critical path is)\ BLEGIK.`

`=>\ text(Activity)\ L\ text(now takes 7 weeks.)`

`:.\ text(Time for completion)`

`= 4 + 7 + 1 + 5 + 2 + 6`

`= 25\ text(weeks)`

Networks, STD2 N2 SM-Bank 12

The following table shows the travelling time, in minutes, between towns which are directly connected by roads.

A dash indicates that towns are not directly connected.

Draw a network diagram showing the information in this table. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
What is the shortest travelling time between A and E? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`62\ text(minutes)`

Show Worked Solution

`text(Important to note that network diagrams)`

`text(do not need to be drawn to scale.)`

b.	`text(One strategy – using Dijkstra’s algorithm:)`

`:.\ text(Shortest travelling time is the path)\ \ A – D – B – E`

`= 10 + 32 + 20`

`= 62\ text(minutes)`

Networks, STD2 N3 SM-Bank 49

The directed graph below shows the sequence of activities required to complete a project.

The time to complete each activity, in hours, is also shown.

Find the earliest starting time, in hours, for activity `N`. (2 marks)

To complete the project in minimum time, some activities cannot be delayed.

Calculate the number of activities that cannot be delayed. (1 mark)

Show Answers Only

`12\ text(hours)`
`4`

Show Worked Solution

i. `text{Scanning forward:}`

`:.\ text(EST for)\ N`	`= CGJ`
	`= 4 +3+5`
	`= 12`

ii. `text(Critical path is:)\ CFHM`

`:. 4\ text(activities can’t be delayed.)`

Networks, STD2 N3 SM-Bank 17

The network diagram represents a system of roads connecting a shopping centre to the motorway.

Two routes from the shopping centre connect to A and one route connects D to F.

The number on the edge of each road indicates the number of vehicles that can travel on it per hour.

Draw additional road(s) on the diagram to maximise the capacity. Include the number of vehicles that can travel on each road. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Solutions could be:)`

Show Worked Solution

`text(Two possible solutions are:)`

`text(Note that the added roads above make the minimum cut/max)`

`text(flow increase to 170 vehicles per hour.)`

Networks, STD2 N3 SM-Bank 16 MC

The network diagram represents a system of roads connecting a shopping centre to the motorway.

Two routes from the shopping centre connect to A and one route connects to D to F.

The number on the edge of each road indicates the number of vehicles that can travel on it per hour.

At present, the capacity of the network from the shopping centre to the motorway is not maximised.

Which additional road(s) would increase the network capacity to its maximum?

A.	A road from A to F with a capacity of 20 vehicles per hour
B.	A road from B to E with a capacity of 30 vehicles per hour
C.	A road from C to F with a capacity of 30 vehicles per hour and a road from E to F with a capacity of 60 vehicles per hour
D.	A road from B to F with a capacity of 30 vehicles per hour and a road from D to F with a capacity of 30 vehicles per hour

Show Answers Only

`text(D)`

Show Worked Solution

`text(Consider option D:)`

`text(Adding these two roads increases the minimum cut/maximum)`

`text(flow to 170 vehicles per hour throughout the network.)`

`=>\ text(D)`

Networks, STD2 N3 SM-Bank 47

The directed graph below shows the sequence of activities required to complete a project.

All times are in hours.

Find the number of activities that have exactly two immediate predecessors. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Identify the critical path for this project. (3 marks)
If Activity E is reduced by one hour, identify the two new critical paths. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`2`
`BEIL`
`ADIL and CHKL`

Show Worked Solution

i. `I\ text(and)\ J`

`:.\ text(2 activities have exactly two immediate predecessors.)`

ii. `text(Scanning forwards:)`

`:.\ text(Initial critical path)\ BEIL`

iii. `text(If)\ E\ text(reduced by 1 hour, critical path)\ BEIL`

`text(reduces to 19 hours.)`

`:.\ text(Other critical paths of 19 hours are:)`

`ADIL = 5 + 2 + 4 + 8 = 19`

`CHKL = 2 + 6 + 3 + 8 = 19`

Networks, STD2 N3 SM-Bank 48

The network shows the activities that are needed to complete a particular project.

Find the total number of activities that need to be completed before activity L can begin. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

The duration of every activity is initially 5 hours.

If the completion times of both activity F and activity K are reduced to 3 hours each, calculate the effect on the completion time for the project. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`7`
`text(Completion time is unchanged.)`

Show Worked Solution

i. `A, B, C, D, E, H\ text(and)\ I\ text(must be completed before)\ L.`

`:.\ text(7 activities need to be completed.)`

ii. `text{Scanning forward (all activities take 5 hours):}`

`text(Activity)\ F\ text(and)\ K\ text(are not on any critical path.)`

`:.\ text(Reducing either will not change the completion time)`

`text(for the project.)`

Networks, STD2 N3 2008 FUR1 8-9 MC

The network below shows the activities that are needed to finish a particular project and their completion times (in days).

Part 1

The earliest start time for Activity K, in days, is

A. `7`

B. `15`

C. `16`

D. `19`

Part 2

This project currently has one critical path.

A second critical path, in addition to the first, would be created by

A. increasing the completion time of D by 7 days.

B. increasing the completion time of G by 1 day.

C. increasing the completion time of I by 2 days.

D. decreasing the completion time of C by 1 day.

Show Answers Only

`text(Part 1:)\ C`

`text(Part 2:)\ A`

Show Worked Solution

`text(Part 1)`

`text(Scanning forwards:)`

`text(EST for Activity)\ K`

`=\ text(Duration)\ ACFI`

`= 2 + 5 + 6 + 3`

`= 16`

`=> C`

`text(Part 2)`

♦♦ Mean mark of Part 2 was 35%.

`text(Original critical path:)\ ACFHJL\ text{(22 days)}`

`text(Consider option)\ A,`

`text(New critical path:)\ ABDJL\ text{(22 days)}`

`=> A`

Networks, STD2 N2 SM-Bank 11

A network of roads between towns shows the travelling times in minutes between towns that are directly connected.

Complete the shaded cells in the following table so that it represents the information in this network. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

`text(Note the symmetry in this table across the diagonal.)`

Networks, STD2 N2 SM-Bank 10

Consider the network pictured below.

Find the length of the shortest path from A to E. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`10`

Show Worked Solution

`text(One strategy – Using Dijkstra’s algorithm:)`

`text{The shortest path A – B – I – E has a distance (weight)}`

`text(of 10.)`

Networks, STD2 N2 SM-Bank 9

In a separate diagram or on the diagram above, show the minimum spanning tree . (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

`text(One strategy – Using Kruskal’s algorithm:)`

`text(Edges 1 – 5: AB, BC, DG, DH and EI)`

`text(Edges 6 – 8: CD, EF and HI)`

`(text(note AC cannot be chosen → creates a cycle))`

`text(NB: There is more than one minimal spanning tree in this)`

`text{circuit (having a weight of 19).}`

Networks, STD2 N3 2015 FUR1 9 MC

The table below shows, in minutes, the duration, the earliest starting time (EST) and the latest starting time (LST) of eight activities needed to complete a project.

Which one of the following directed graphs shows the sequence of these activities?

A.
B.
C.
D.

Show Answers Only

`B`

Show Worked Solution

`text(Consider option)\ B,`

`text(Scanning forwards:)`

`text(This network matches the table information.)`

`=> B`

Networks, STD2 N3 2011 FUR1 8 MC

The diagram shows the tasks that must be completed in a project.

Also shown are the completion times, in minutes, for each task.

The critical path for this project includes activities

A. `B and I.`

B. `C and H.`

C. `D and E.`

D. `F and K.`

Show Answers Only

`D`

Show Worked Solution

`text(Scanning forward:)`

`:.\ text(The critical path is)\ \ ACFIK.`

`=> D`

Networks, FUR2 2013 VCE 3

The rangers at the wildlife park restrict access to the walking tracks through areas where the animals breed.

The edges on the directed network diagram below represent one-way tracks through the breeding areas. The direction of travel on each track is shown by an arrow. The numbers on the edges indicate the maximum number of people who are permitted to walk along each track each day.

Starting at `A`, how many people, in total, are permitted to walk to `D` each day? (1 mark)

One day, all the available walking tracks will be used by students on a school excursion.

The students will start at `A` and walk in four separate groups to `D`.

Students must remain in the same groups throughout the walk.

1. Group 1 will have 17 students. This is the maximum group size that can walk together from `A` to `D`.
  Write down the path that group 1 will take. (1 mark)
2. Groups 2, 3 and 4 will each take different paths from `A` to `D`.
  Complete the six missing entries shaded in the table below. (2 marks)

Show Answers Only

`37`
1. `A B E C D`
2. `text{One possible solution is:}`

Show Worked Solution

a.	`text(Maximum flow)`	`=\ text(Minimum cut through)\ CD and ED`
		`= 24 + 13`
		`= 37`

♦ Mean mark of all parts (combined) was 41%.

`:.\ text(A maximum of 37 people can walk)`

`text(to)\ D\ text(from)\ A.`

b.i. `A B E C D`

b.ii. `text(One solution using the second possible largest)`

`text(group of 11 students and two groups from the)`

`text(remaining 9 students is:)`

Networks, STD2 N3 SM-Bank 35

The following directed graph shows the flow of water, in litres per minute, in a system of pipes connecting the source to the sink.

Calculate the maximum flow, in litres per minute, from the source to the sink. (2 marks)

Show Answers Only

`18`

Show Worked Solution

`text(Maximum Flow)`	`=\ text(Capacity of Minimum Cut)`
	`= 2 + 10 + 6`
	`= 18\ \ text(litres/minute)`

Networks, STD2 N3 SM-Bank 34

The arrows on the diagram below show the direction of the flow of waste through a series of pipelines from a factory to a waste dump.

The numbers along the edges show the number of megalitres of waste per week that can flow through each section of pipeline.

The minimum cut is shown as a dotted line.

Calculate the capacity of this cut, in megalitres of waste per week. (2 marks)

Show Answers Only

`26`

Show Worked Solution

`text(Flows from the waste dump side of the minimum cut to)`

`text(the factory side are ignored.)`

`:.\ text{Minimum Cut}`

`= 5 + 2 + 12 + 7`

`= 26\ \ text(ML/week)`

Networks, STD2 N3 2012 FUR1 6 MC

In the directed network diagram above, all vertices are reachable from every other vertex.

All vertices would still be reachable from every other vertex if we remove the edge in the direction from

A. `Q` to `U`

B. `R` to `S`

C. `S` to `T`

D. `T` to `R`

Show Answers Only

`A`

Show Worked Solution

`text(Consider option B:)`

`text(If R to S is removed, vertex S cannot be reached from other)`

`text(vertices. All vertices only remain reachable from all other vertices)`

`text(if Q to U is removed.)`

`rArr A`

Networks, STD2 N3 2006 FUR1 6 MC

In the directed graph above the weight of each edge is non-zero.

The capacity of the cut shown is

A. a + b + c + d + e

B. a + c + d + e

C. a + b + c + e

D. a + b + c – d + e

Show Answers Only

`C`

Show Worked Solution

`text(Flows in the opposite direction are not counted when)`

`text(calculating the capacity of a cut.)`

`:.\ text(Capacity of the cut) = a + b + c + e`

`rArr C`

Networks, STD2 N3 2013 FUR1 9 MC

Alana, Ben, Ebony, Daniel and Caleb are friends. Each friend has a different age.

The arrows in the graph below show the relative ages of some, but not all, of the friends. For example, the arrow in the graph from Alana to Caleb shows that Alana is older than Caleb.

Using the information in the graph, it can be deduced that the second-oldest person in this group of friends is

A. Alana

B. Ben

C. Caleb

D. Ebony

Show Answers Only

`B`

Show Worked Solution

`text(Completing the graph, we can deduce that Alana)`

`text(must be older than Daniel, etc…)`

`:.\ text(Oldest to youngest is:)`

`text(Alana, Ben, Daniel, Caleb, Ebony.)`

`=> B`

Networks, STD2 N2 SM-Bank 8

Highlight the minimal spanning tree of this network on the diagram above, or in a separate diagram. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

`text(One Strategy – Using Prim’s algorithm:)`

`text(6 vertices → 5 edges on spanning tree)`

`text(Starting at vertex A)`

`text(Edge 1: AC)`

`text(Edge 2: AD)`

`text{Edge 3: ED (reject CD which creates a cycle)}`

`text(Edge 4: EF)`

`text(Edge 5: BF)`

Networks, STD2 N2 SM-Bank 7 MC

How many spanning trees are possible for this network?

A.	`3`
B.	`8`
C.	`14`
D.	`30`

Show Answers Only

`text(C)`

Show Worked Solution

`text(S)text(ince there are 6 vertices, each spanning tree will have)`

`text{5 edges (with no cycles).}`

`text(Consider if A and B are not connected, possible spanning)`

`text(trees are:)`

`text(3 other spanning trees exist when BF is not connected, and likewise)`

`text(when EF and ED are not connected.)`

`text(Finally, 2 other spanning trees exist when AD and AC are removed, and)`

`text(when AD and CD are removed.)`

`:.\ text(Total spanning trees)`	`= 4 xx 3 + 2`
	`= 14`

Networks, STD2 N2 SM-Bank 6

Describe the shortest path between A and J in the network above and its weight. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Shortest path is:)`

`text(A – B – E – F – J)`

`text(Weight of shortest path is 15.)`

Show Worked Solution

`text(One Strategy: Using Dijkstra’s algorithm)`

`text(Shortest path is:)`

`text(A – B – E – F – J)`

`:.\ text(Weight of shortest path)`

`= 4 + 5 + 4 + 2`

`= 15`

Networks, STD2 N2 SM-Bank 5

A network of roads is pictured below, with the distances of each road represented, in kilometres, on each edge.

A driver wants to travel from A to H in the shortest distance possible.

Describe the possible paths she can take, and the total distance she must travel. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Shortest distance paths:)`

`text(A – E – H or A – F – G – H)`

`text(Shortest distance is 11 km.)`

Show Worked Solution

`text(One Strategy: Dijkstra’s algorithm)`

`text(Shortest distance paths:)`

`text(A – E – H or A – F – G – H)`

`text(Shortest distance is 11 km.)`

Networks, STD2 N2 SM-Bank 4

Complete the minimal spanning tree of the network above on the diagram below. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

`text(One Strategy: Using Prim’s algorithm)`

`text(6 vertices → need 5 edges.)`

`text{Starting at vertex A (any vertex can be chosen)}`

`text(1st Edge: AB)`

`text{2nd Edge: AC (BF also possible)}`

`text(3rd Edge: CD)`

`text(4th Edge: BF)`

`text(5th Edge: AS)`

Networks, STD2 N2 SM-Bank 3

The diagram below is a connected network.

Complete the diagram below to show the minimal spanning tree of this network. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(or)`

Show Worked Solution

`text(One Strategy – Kruskul’s algorithm)`

`text(There are 6 vertices, so we need 5 edges.)`

`text{Edge 1: BC (least weight) – could have chosen ED}`

`text{Edge 2: DE (next least weight)}`

`text{Edge 3: AF (could have been CD)}`

`text(Edge 4: CD)`

`text{Edge 5: CF or EF (reject CE as it creates a cycle)}`

`text(or)`

Networks, STD2 N2 SM-Bank 2

A school is designing a computer network between five key areas within the school.

The cost of connecting the rooms is shown in the diagram below.

Complete the spanning tree below that creates the school's network at a minimum cost. (1 mark)

--- 0 WORK AREA LINES (style=lined) ---
What is the minimum cost of the network? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`$1500`

Show Worked Solution

a. `text(One Strategy: Using Prim’s Algorithm)`

`text(Starting vertex – Staff Room)`

`text(1st edge: Staff Room – Library)`

`text(2nd edge: Library – School Office)`

`text(3rd edge: Staff Room – IT Staff)`

`text(4th edge: Library – Computer Room)`

b.	`text(Minimum Cost)`	`= 300 + 300 + 400 + 500`
		`= $1500`

Networks, STD2 N2 SM-Bank 15

Four children, James, Dante, Tahlia and Chanel each live in a different town.

The following is a map of the roads that link the four towns, `A`, `B`, `C` and `D`.

James’ father has begun to draw a network diagram that represents all the routes between the four towns on the map. This is shown below.

In this network, vertices represent towns and edges represent routes between towns that do not pass through any other town.

One more edge needs to be added to complete this network. Draw in this edge clearly on the diagram above. (1 mark)

Show Answers Only

Show Worked Solution

`text(Two routes exist that join town A directly to town B.)`

Networks, STD2 N2 SM-Bank 14

Water will be pumped from a dam to eight locations on a farm.

The pump and the eight locations (including the house) are shown as vertices in the network diagram below.

The numbers on the edges joining the vertices give the shortest distances, in metres, between locations.

How many vertices on the network diagram have an odd degree? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

The total length of all edges in the network is 1180 metres.

The total length of pipe that supplies water from the pump to the eight locations on the farm is a minimum.

This minimum length of pipe is laid along some of the edges in the network.
On the diagram below, draw the minimum length of pipe that is needed to supply water to all locations on the farm. (2 marks)
What is the mathematical term that is used to describe this minimum length of pipe? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`2`
`1250\ text(m)`
`text(Minimum spanning tree)`

Show Worked Solution

a. `2\ text{(the house and the top right vertex)}`

MARKER’S COMMENT: Many students, surprisingly, had problems with part (i).

b. `text(One Strategy – Using Prim’s algorithm:)`

`text(Starting at the house)`

`text(1st edge: 50)`

`text{2nd edge: 40 (either)}`

`text(3rd edge: 40)`

`text(4th edge: 60 etc…)`

c. `text(Minimum spanning tree)`

Networks, FUR2 2016 VCE 1

A map of the roads connecting five suburbs of a city, Alooma (`A`), Beachton (`B`), Campville (`C`), Dovenest (`D`) and Easyside (`E`), is shown below.

Starting at Beachton, which two suburbs can be driven to using only one road? (1 mark)

A graph that represents the map of the roads is shown below.

One of the edges that connects to vertex `E` is missing from the graph.

1. Add the missing edge to the graph above. (1 mark)
  
  (Answer on the graph above.)
2. Explain what the loop at `D` represents in terms of a driver who is departing from Dovenest. (1 mark)

Show Answers Only

`text(Alooma and Easyside.)`
2. `text(The loop represents that a driver can take a route out of)`
  `text(Dovenest and return home without going through another)`
  `text(suburb or turning back.)`

Show Worked Solution

a. `text(Alooma and Easyside.)`

b.i.

`text(Draw a third edge between Easyside and Dovenest.)`

b.ii. `text(The loop represents that a driver can take a)`

♦♦ Mean mark 30%.

`text(route out of Dovenest and return home without)`

`text(going through another suburb or turning back.)`

`3x^0 + 1`	`= 3(1) + 1`
	`= 4`