SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, EXT1 C1 2008 HSC 3c

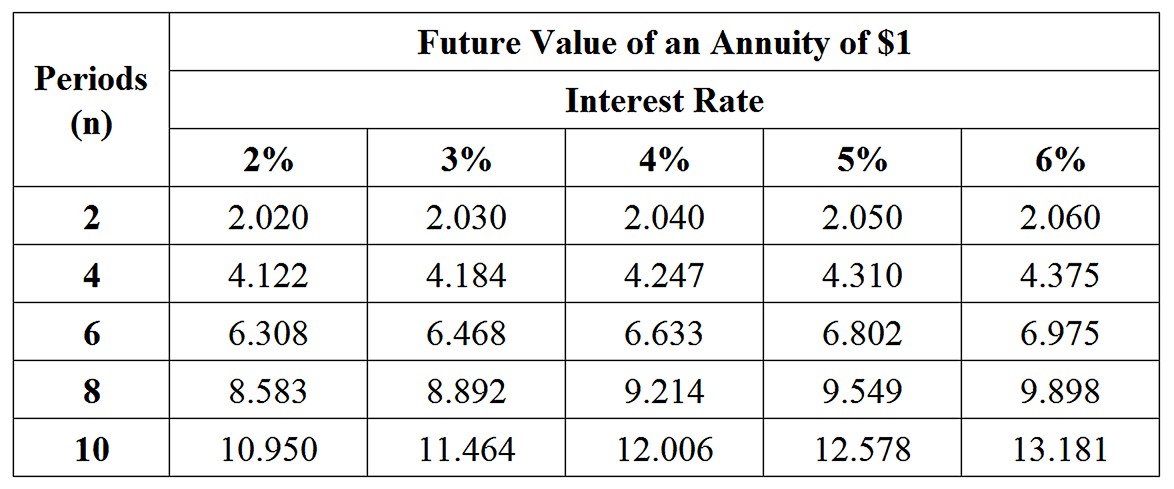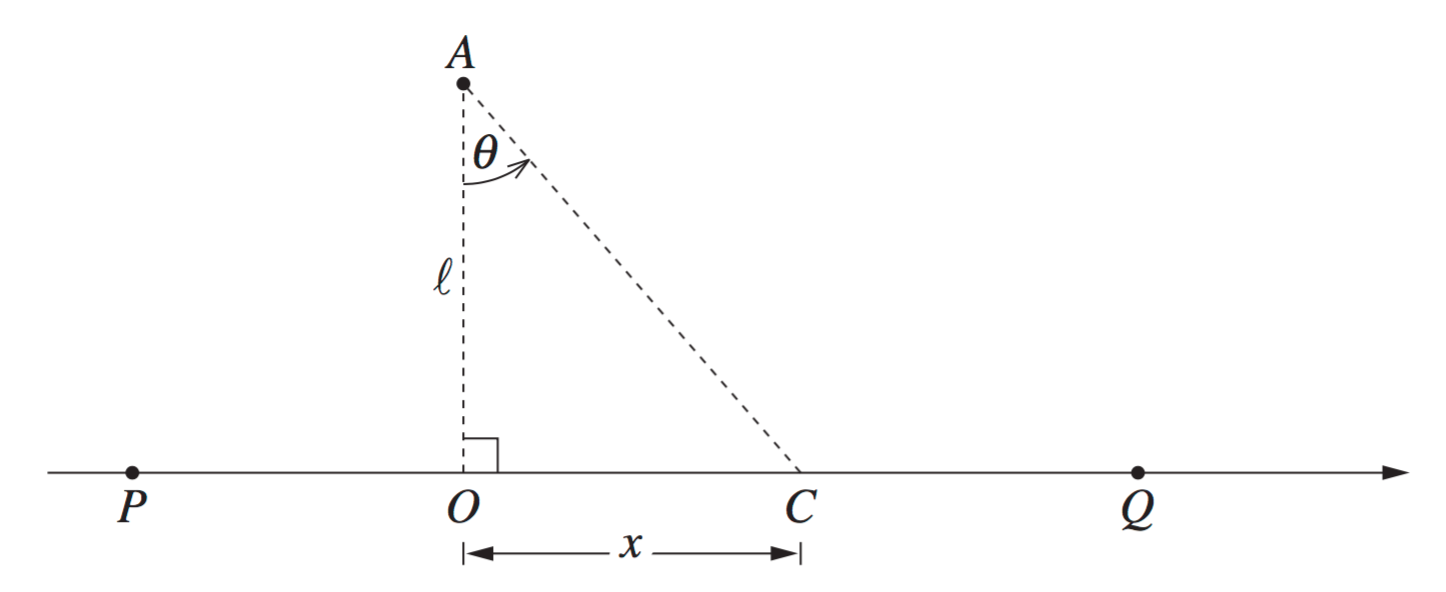
2008 3c
  
 A race car is travelling on the  -axis from    to    at a constant velocity,  .

A spectator is at    which is directly opposite  , and    metres. When the car is at  , its displacement from    is    metres and  , with  .

  1. Show that  .   (2 marks)

  2. Let    be the maximum value of  .  

     

    Find the value of    in terms of    and  .   (1 mark)

  3. There are two values of    for which  .

     

    Find these two values of  .   (2 marks)

Show Answers Only
Show Worked Solution

i. 

 

MARKER’S COMMENT: The most successful students used   and the chain rule to find .
 
 

 

ii. 

 

 

iii. 

MARKER’S COMMENT: Many students lost marks by not giving their answer in the specified range. Be careful!

 

 

Measurement, STD2 M7 SM-Bank 2

A medication is available in both tablet and liquid form.  A tablet contains 50 mg of the active ingredient while the liquid form contains 60 mg per 10 mL.  

Michael likes taking tablets and Georgia prefers liquid medicines.  If they each need 0.2 g of the active ingredient, what dosages do they take?   (3 marks) 

Show Answers Only

Show Worked Solution

 

 

 
 

 

Financial Maths, STD2 F5 SM-Bank 4

Dominique wants to save $15 000 to use as spending money when she travels overseas in 2 years' time.  

If she invests $3500 at the end of every 6 months into an account earning 4% p.a., compounded half-yearly, will she have enough?

Use the table below to justify your answer.   (2 marks)
 

 

Show Answers Only

Show Worked Solution

 

 
 

Financial Maths, STD2 F5 SM-Bank 3

Camilla buys a car for $21 000 and repays it over 4 years through equal monthly instalments.

She pays a 10% deposit and interest is charged at 9% p.a. on the reducing balance loan.

Using the Table of present value interest factors below, where represents the monthly interest and represents the number of repayments
 

2UG FM5 S-2 

  1. Calculate the monthly repayment,  , that Camilla must pay to complete the loan after 4 years  (to the nearest $).   (3 marks)

  2. Calculate the total interest paid over the life of the loan.    (1 mark)

Show Answers Only
Show Worked Solution

i. 

 

 

 
 

 

 

ii. 


 

Functions, EXT1 F2 2008 HSC 2c

The polynomial    is given by  , where    and    are constants.

The three zeros of    are  ,    and  .

Find the value of  .   (3 marks) 

Show Answers Only

Show Worked Solution

 

 

MARKER’S COMMENT: Many students displayed significant inefficiencies in solving simultaneous equations.

 

 

Measurement, 2UG 2008 HSC 28b

A tunnel is excavated with a cross-section as shown.
 

 
 

  1. Find an expression for the area of the cross-section using TWO applications of Simpson’s rule.  (2 marks)
  2. The area of the cross-section must be 600 m2. The tunnel is 80 m wide.   
  3. If the value of increases by 2 metres, by how much will change?   (2 marks)

 

Show Answers Only
  2.  
Show Worked Solution
(i)   
   
   

 

(ii)    ²
 

 

 

Statistics, STD2 S5 2008 HSC 28a

The following graph indicates  -scores of ‘height-for-age’ for girls aged  5 – 19 years.
 

 
 

  1. What is the  -score for a six year old girl of height 120 cm? (1 mark)

  2. Rachel is 10 ½  years of age. 

     

    (1)  If  2.5% of girls of the same age are taller than Rachel, how tall is she?   (1 mark)

     

    (2)  Rachel does not grow any taller. At age 15 ½, what percentage of girls of the same age will be taller than Rachel?   (2 marks)

  3. What is the average height of an 18 year old girl?   (1 mark)

For adults (18 years and older), the Body Mass Index is given by

 where    in kilograms and    in metres.

The medically accepted healthy range for    is  .

  1. What is the minimum weight for an 18 year old girl of average height to be considered healthy? (2 marks)

  2. The average height, , in centimetres, of a girl between the ages of 6 years and 11 years can be represented by a line with equation
     
               where is the age in years. 
     
    (1)  For this line, the gradient is 6. What does this indicate about the heights of girls aged 6 to 11?   (1 mark)

     

    (2)  Give ONE reason why this equation is not suitable for predicting heights of girls older than 12.   (1 mark)

Show Answers Only
  2. (1)

     

    (2)

  5. (1)

     

         

     

    (2)

     

         

Show Worked Solution
i.   

 

ii. (1)   ½
   
   
     
   (2)   ½
   
   
   
     
   
   
   

 
½

 

iii.  
 

 

iv.  
 

 

 
 

 

v. (1)  
   
  (2)
   

Financial Maths, STD2 F4 2008 HSC 27c

A plasma TV depreciated in value by 15% per annum. Two years after it was purchased it had depreciated to a value of $2023, using the declining balance method.

What was the purchase price of the plasma TV?   (2 marks)

Show Answers Only

Show Worked Solution

 

 

Measurement, 2UG 2008 HSC 27a

An aircraft travels at an average speed of  913 km/h. It departs from a town in Kenya  (0°, 38°E)  on Tuesday at 10 pm and flies east to a town in Borneo  (0°, 113°E).

  1. What is the distance, to the nearest kilometre, between the two towns? (Assume the radius of Earth is 6400 km.) (2 marks)
  2. How long will the flight take? (Answer to the nearest hour.)   (1 mark)
  3. What will be the local time in Borneo when the aircraft arrives? (Ignore time zones.)   (2 marks)

 

Show Answers Only
Show Worked Solution
(i)  


 

 
 

 

 

(ii)    
   
   
   

 

(iii)  
   
   

 


 

Statistics, STD2 S1 2008 HSC 26d

The graph shows the predicted population age distribution in Australia in 2008.
 

 

  1. How many females are in the 0–4 age group?  (1 mark)

  2. What is the modal age group?   (1 mark)

  3. How many people are in the 15–19 age group?   (2 marks)

  4. Give ONE reason why there are more people in the 80+ age group than in the 75–79 age group.   (1 mark)

Show Answers Only

  5.  

Show Worked Solution
i.   
   

 

ii.   

 

iii.  
   

 

 

 

 

 

iv.  
 

Probability, STD2 S2 2008 HSC 26b

The retirement ages of two million people are displayed in a table.
 

 
 

  1. What is the relative frequency of the 51–55 year retirement age?  (1 mark)

  2. Describe the distribution.   (1 mark)

Show Answers Only

  2.  


     

Show Worked Solution

i. 

 

ii. 

Probability, STD2 S2 2008 HSC 26a

Cecil invited 175 movie critics to preview his new movie. After seeing the movie, he conducted a survey. Cecil has almost completed the two-way table.
 

  1. Determine the value of  .   (1 mark)

  2. A movie critic is selected at random.

     

    What is the probability that the critic was less than 40 years old and did not like the movie?  (2 marks)

  3. Cecil believes that his movie will be a box office success if 65% of the critics who were surveyed liked the movie.

     

    Will this movie be considered a box office success? Justify your answer.  (1 mark)

Show Answers Only
Show Worked Solution

i.  

 
ii. 


 


 

iii.   

 

 

Probability, STD2 S2 2008 HSC 25b

In a drawer there are 30 ribbons. Twelve are blue and eighteen are red.

Two ribbons are selected at random.

  1. Copy and complete the probability tree diagram.  (1 mark)
     

     
  2. What is the probability of selecting a pair of ribbons which are the same colour?  (2 marks)

Show Answers Only
  1.  
Show Worked Solution

i. 

ii. 

 

Probability, STD2 S2 2008 HSC 24b

Three-digit numbers are formed from five cards labelled  1,  2,  3,  4  and  5.

  1. How many different three-digit numbers can be formed?  (1 mark)

  2. If one of these numbers is selected at random, what is the probability that it is odd?   (1 mark)

  3. How many of these three-digit numbers are even?   (1 mark)

  4. What is the probability of randomly selecting a three-digit number less than 500 with its digits arranged in descending order?   (2 marks)

Show Answers Only
Show Worked Solution

i. 

♦ Mean mark 45%.

 

ii. 

 

iii. 

♦ Mean mark 48%.

 

iv. 

♦♦♦ Mean mark 10%.

Financial Maths, STD2 F1 2008 HSC 24a

Bob is employed as a salesman. He is offered two methods of calculating his income.

Bob’s research determines that the average sales total per employee per month is $15 670. 

  1. Based on his research, how much could Bob expect to earn in a year if he were to choose Method 1?   (2 marks)

  2. If Bob were to choose a method of payment based on the average sales figures, state which method he should choose in order to earn the greater income. Justify your answer with appropriate calculations.   (3 marks)

Show Answers Only
Show Worked Solution

i.   

 
 

 

ii. 

 
 
 

 

Statistics, STD2 S1 2008 HSC 23e

In a survey, 450 people were asked about their favourite takeaway food. The results are displayed in the bar graph.

2008 23e
 
How many people chose pizza as their favourite takeaway food?   (2 marks)

Show Answers Only

Show Worked Solution

COMMENT: This question required measurement of the actual image on the exam. The same methodology works here.


 

Measurement, STD2 M7 2008 HSC 23c

An alcoholic drink has 5.5% alcohol by volume. The label on a 375 mL bottle says it contains 1.6 standard drinks.

  1. How many millilitres of alcohol are in a 375 mL bottle? (1 mark)

  2. It is recommended that a fully-licensed male driver should have a maximum of one standard drink every hour.

     

    Express this as a rate in millilitres per minute, correct to one decimal place.    (2 marks)

Show Answers Only
Show Worked Solution
i.   
   

 

ii.   


 

 
 

Measurement, STD2 M7 2008 HSC 20 MC

A point lies between a tree, 2 metres high, and a tower, 8 metres high. is 3 metres away from the base of the tree.

From , the angles of elevation to the top of the tree and to the top of the tower are equal.
 

What is the distance, , from to the top of the tower?

  1. 9 m
  2. 9.61 m
  3. 12.04 m
  4. 14.42 m
Show Answers Only

Show Worked Solution

 
   
 

 

Probability, STD2 S2 2008 HSC 16 MC

A bag contains some marbles. The probability of selecting a blue marble at random from this bag is  .

Which of the following could describe the marbles that are in the bag?

  1.      blue,    red
  2.      blue,    red
  3.      blue,    red,    green
  4.      blue,    red,    green 
Show Answers Only

Show Worked Solution

Statistics, STD2 S1 2008 HSC 13 MC

The height of each student in a class was measured and it was found that the mean height was 160 cm.

Two students were absent. When their heights were included in the data for the class, the mean height did not change.

Which of the following heights are possible for the two absent students?

  1.    155 cm and 162 cm
  2.    152 cm and 167 cm
  3.    149 cm and 171 cm
  4.    143 cm and 178 cm
Show Answers Only

Show Worked Solution

Statistics, STD2 S4 2008 HSC 12 MC

A scatterplot is shown.
 

Which of the following best describes the correlation between    and  ?

  1. Positive
  2. Negative 
  3. Positively skewed
  4. Negatively skewed
Show Answers Only

Show Worked Solution

Measurement, STD2 M1 2008 HSC 11 MC

The diagram shows the floor of a shower. The drain in the floor is a circle with a diameter of 10 cm.

What is the area of the shower floor, excluding the drain?
 

 
 

  1. 9686 cm²
  2. 9921 cm²
  3. 9969 cm²
  4. 10 000 cm²
Show Answers Only

Show Worked Solution
COMMENT: Students should see that answers are all in cm², and therefore use cm as the base unit for their calculations. 
 
 
  ²

 

Statistics, STD2 S1 2008 HSC 10 MC

The marks for a Science test and a Mathematics test are presented in box-and-whisker plots.
 

 Which measure must be the same for both tests?

  1. Mean
  2. Range
  3. Median
  4. Interquartile range
Show Answers Only

Show Worked Solution

Statistics, STD2 S1 2008 HSC 8 MC

What is the median of the following set of scores?
 

 
 

  1.    12
  2.    13
  3.    14
  4.    15
Show Answers Only

Show Worked Solution
 
 

 

Statistics, STD2 S1 2008 HSC 3 MC

The stem-and-leaf plot represents the daily sales of soft drink from a vending machine.

If the range of sales is 43, what is the value of  2008 3 mc  ?

 
 

  1.     
  2.    
  3.    
  4.    
Show Answers Only

Show Worked Solution

Probability, 2ADV S1 2008 HSC 9a

It is estimated that 85% of students in Australia own a mobile phone.

  1. Two students are selected at random. What is the probability that neither of them owns a mobile phone?  (2 marks)

  2. Based on a recent survey, 20% of the students who own a mobile phone have used their mobile phone during class time. A student is selected at random. What is the probability that the student owns a mobile phone and has used it during class time?   (1 mark)

Show Answers Only
Show Worked Solution

i.     

COMMENT: is syllabus notation for the complement of event .

 
 

 

ii. 

Plane Geometry, 2UA 2008 HSC 8b

In the diagram,    is a parallelogram and    and    are both squares.

Copy or trace the diagram into your writing booklet.

  1. Prove that  .  (1 mark)
  2. Prove that  .   (3 marks)
Show Answers Only
Show Worked Solution

(i) 

 

(ii)

   
 
 

 

Calculus, 2ADV C3 2008 HSC 8a

Let  .

  1. Find the coordinates of the points where the graph of    crosses the axes.  (2 marks)

  2. Show that    is an even function.   (1 mark)

  3. Find the coordinates of the stationary points of    and determine their nature.   (4 marks)

  4. Sketch the graph of  .   (1 mark)

Show Answers Only
  4.  
  5. 2UA HSC 2008 8ai
Show Worked Solution
i.   

 

 

ii.   
 
   
   

 

 

iii.  
 
 

 
   
 

 

   
 

 

iv. 

Probability, 2ADV S1 2008 HSC 7c

Xena and Gabrielle compete in a series of games. The series finishes when one player has won two games. In any game, the probability that Xena wins is    and the probability that Gabrielle wins is  .

Part of the tree diagram for this series of games is shown.
 

 
 

  1. Complete the tree diagram showing the possible outcomes.  (1 mark)
  2. What is the probability that Gabrielle wins the series?   (2 marks)

  3. What is the probability that three games are played in the series?   (2 marks)

Show Answers Only
  1.    
Show Worked Solution
i. 2UA HSC 2008 7ci

 

MARKER’S COMMENT: A tree diagram with 8 outcomes is incorrect (i.e. no third game is played if 1 player wins the first 2 games). If outcomes cannot occur, do not draw them on a tree diagram.

 

ii. 

 

iii. 

 

Trigonometry, 2ADV T1 2008 HSC 7b

2008 7b

The diagram shows a sector with radius    and angle    where  .

The arc length is  . 

  1.  Show that  .   (2 marks)

  2.  Calculate the area of the sector when  .    (2 marks)

Show Answers Only
  2. ²
Show Worked Solution
i.   

 

 

 

ii.  
   
    ²

Calculus, EXT1* C3 2008 HSC 6c

The graph of    is shown below.
 

2008 6c
 

The shaded region in the diagram is bounded by the curve  , the  -axis and the lines    and  .

Find the volume of the solid of revolution formed when the shaded region is rotated about the  -axis.  (3 marks)

Show Answers Only

³

Show Worked Solution
 
 
 
 
 
  ³

Quadratic, 2UA 2008 HSC 4c

Consider the parabola  .

  1. Write down the coordinates of the vertex.  (1 mark)
  2. Find the coordinates of the focus.   (1 mark)
  3. Sketch the parabola.   (1 mark)
  4. Calculate the area bounded by the parabola and the line  .   (3 marks)
Show Answers Only

(i)  

(ii)  

(iii)  

(iv)  ²

Show Worked Solution
(i)   

 

(ii)  
 
 

 

(iii) 2UA HSC 2008 4c 

 

(iv)  

 

 
 
 
 
 
  ²

Calculus, 2ADV C4 2008 HSC 3b

  1. Differentiate    with respect to  .  (2 marks)

  2. Hence, or otherwise, evaluate  .    (2 marks)

Show Answers Only
Show Worked Solution
i.   
 
   

 

ii.   
 
 
 
 
 
 
 

Linear Functions, 2UA 2008 HSC 3a

2008 3a

In the diagram,    is a quadrilateral. The equation of the line    is  . 

  1. Show that    is a trapezium by showing that    is parallel to  .  (2 marks)
  2. The line    is parallel to the  -axis. Find the coordinates of  .   (1 mark)
  3. Find the length of  .   (1 mark)
  4. Show that the perpendicular distance from    to    is  .   (2 marks)
  5. Hence, or otherwise, find the area of the trapezium  .   (2 marks)
Show Answers Only
  5. ²
Show Worked Solution
(i)   

 
 

 

 

(ii)   
 
 

 

(iii)  
 
 
 

 

(iv)  

 

 
 
 

 

(v)   
   

 

 

 
 
 
 
  ²

Financial Maths, STD2 F5 SM-Bank 2

The table below shows the present value of an annuity with a contribution of  $1.
 

  1. Fiona pays $3000 into an annuity at the end of each year for 4 years at 2% p.a., compounded annually.   What is the present value of her annuity?  (1 mark)

  2. If John pays $6000 into an annuity at the end of each year for 2 years at 4% p.a., compounded annually, is he better off than Fiona?  Use calculations to justify your answer.    (2 marks)

Show Answers Only
Show Worked Solution

i. 

 

 

ii. 

 

 

Mechanics, EXT2* M1 2014 HSC 14a

The take-off point on a ski jump is located at the top of a downslope. The angle between the downslope and the horizontal is  .  A skier takes off from with velocity m s−1 at an angle to the horizontal, where  .  The skier lands on the downslope at some point , a distance metres from .
 

2014 14a
 

The flight path of the skier is given by

,      (Do NOT prove this.)

where    is the time in seconds after take-off.

  1. Show that the cartesian equation of the flight path of the skier is given by
     
         .   (2 marks)

  2. Show that  
     
         .   (3 marks)

  3. Show that  
     
         .   (2 marks)

  4. Show that has a maximum value and find the value of for which this occurs.   (3 marks)

Show Answers Only
Show Worked Solution

i. 

 
 

 

ii. 

♦♦ Mean mark 28%
MARKER’S COMMENT: The key to finding and solving for is to realise you need the intersection of the Cartesian equation in (i) and the line .

 

 

 

 

iii. 

 
 

 

iv. 

♦ Mean mark 47%
IMPORTANT: Note that students can attempt every part of this question, even if they couldn’t successfully prove earlier parts.
 

 

 
 

 

Plane Geometry, EXT1 2014 HSC 13d

In the diagram,    is a diameter of a circle with centre  . The point    is chosen such that    is acute-angled. The circle intersects    and    at    and    respectively.

Copy or trace the diagram into your writing booklet.

  1. Why is   ?   (1 mark)
  2. Show that the line    is a tangent to the circle through  ,    and  .    (2 marks)
Show Answers Only
Show Worked Solution
(i)   

 

(ii)  

♦ Mean mark 37%
COMMENT: Labelling angles and etc.. can often make a proof clearer and less messy.

 

Calculus, EXT1 C1 2014 HSC 13b

One end of a rope is attached to a truck and the other end to a weight. The rope passes over a small wheel located at a vertical distance of  40 m above the point where the rope is attached to the truck.

The distance from the truck to the small wheel is , and the horizontal distance between them is  . The rope makes an angle with the horizontal at the point where it is attached to the truck.

The truck moves to the right at a constant speed of   , as shown in the diagram.
 


 

  1. Using Pythagoras’ Theorem, or otherwise, show that  .   (2 marks)

  2.  Show that  .    (1 mark)

Show Answers Only
Show Worked Solution
i.    

 
 
 

 

ii.