SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Trigonometry, EXT1 T1 2022 HSC 13c


The function `f` is defined by  `f(x)=\sin (x)`  for all real numbers `x`. Let `g` be the function defined on  `[-1,1]`  by  `g(x)=\arcsin (x)`.

Is `g` the inverse of `f`? Justify your answer.   (2 marks)

Show Answers Only

`text{The domain of}\ \ f(x) = RR`

`text{The range of}\ \ g(x) = [-pi/2,pi/2]`

`text{S}text{ince the domain}\ \ f(x) !=\ text{range of}\ \ g(x),`

`f^(-1)(x)!=g(x)`

Show Worked Solution

`text{The domain of}\ \ f(x) = RR`

`text{The range of}\ \ g(x) = [-pi/2,pi/2]`

`text{S}text{ince the domain}\ \ f(x) !=\ text{range of}\ \ g(x),`

`f^(-1)(x)!=g(x)`


♦♦ Mean mark 24%.

Statistics, EXT1 S1 2022 HSC 12e

A game consists of randomly selecting 4 balls from a bag. After each ball is selected it is replaced in the bag. The bag contains 3 red balls and 7 green balls. For each red ball selected, 10 points are earned and for each green ball selected, 5 points are deducted. For instance, if a player picks 3 red balls and 1 green ball, the score will be  `3xx10-1xx5=25`  points.

What is the expected score in the game?  (2 marks)

Show Answers Only

`-2`

Show Worked Solution

`text{Let}\ \ X=\ text{number of red balls selected}`

`X\ ~\ text{Bin}(4, 0.3)`

`text{Score}\ (X=4)=(0.3)^4xx40=0.324`

`text{Score}\ (X=3)=((4),(3))(0.3)^3(0.7)xx25=1.89`

`text{Score}\ (X=2)=((4),(2))(0.3)^2(0.7)^2xx10=2.646`

`text{Score}\ (X=1)=((4),(1))(0.3)(0.7)^3xx-5=-2.058`

`text{Score}\ (X=0)=(0.7)^4xx-20=-4.802`
 

`:.E(X)` `=0.324+1.89+2.646-2.058-4.802`  
  `=-2`  

♦♦ Mean mark 35%.

Vectors, EXT1 V1 2022 HSC 8 MC

The angle between two unit vectors `underset~a` and `underset~b` is `theta` and  `|underset~a+ underset~b| < 1`.

Which of the following best describes the possible range of values of  `theta` ?

  1. `0 <= theta < (pi)/(3)`
  2. `0 <= theta < (2pi)/(3)`
  3. `(pi)/(3) < theta <= pi`
  4. `(2pi)/(3) < theta <= pi`
Show Answers Only

`D`

Show Worked Solution

`text{By Elimination:}`

`text{Consider}\ \ underset~a=((1),(0)) and underset~b=((-1),(0))`

`|underset~a+ underset~b| =0 < 1\ \ and\ \ theta=pi`

`text{→ Eliminate A and B}`
 

`text{Consider}\ \ theta=(2pi)/3 and underset~a=((1),(0)),\ \ underset~b=((costheta),(sintheta))`

`underset~a+underset~b=((1+cos((2pi)/3)),(sin((2pi)/3)))=((1/2),(sqrt3/2))`

`|underset~a+ underset~b|^2 = (1/2)^2+(sqrt3/2)^2=1`

`:. theta !=(2pi)/3`

`text{→ Eliminate C}`

`=>D`


♦♦ Mean mark 34%.

Combinatorics, EXT1 A1 2022 HSC 7 MC

The diagram shows triangle `A B C` with points chosen on each of the sides. On side `A B`, 3 points are chosen. On side `A C`, 4 points are chosen. On side `B C`, 5 points are chosen.
 


 

How many triangles can be formed using the chosen points as vertices?

  1. 60
  2. 145
  3. 205
  4. 220
Show Answers Only

`C`

Show Worked Solution

`text{1 point taken from each side:}`

`text{Triangles} = 3 xx 4xx5=60`
 

`text{2 points taken from one side:}`

`text{Triangles}` `=((3),(2))((9),(1))+((4),(2))((8),(1))+((5),(2))((7),(1))`  
  `=145`  

 
`:.\ text{Total triangles} =60+145=205`

`=>C`


♦♦ Mean mark 37%.

Vectors, EXT1 V1 2022 HSC 6 MC

The following diagram shows the vector `underset∼u` and the vectors `underset∼i+underset∼j,-underset∼i+ underset∼j,-underset∼i- underset∼j` and `underset∼i-underset∼j`. 
 


 

Which statement regarding this diagram could be true?

  1. The projection of `underset∼u` onto  `underset∼i+ underset∼j`  is the vector  `1.1 underset∼i+ 1.8 underset∼j`.
  2. The projection of `underset∼u` onto  `-underset∼i+ underset∼j`  is the vector  `-0.4 underset∼i+0.4 underset∼j`.
  3. The projection of `underset∼u` onto  `- underset∼i- underset∼j`  is the vector  `3.2 underset∼i+3.2 underset∼j`. 
  4. The projection of `underset∼u` onto  `underset∼i- underset∼j`  is the vector  `0.5 underset∼i-0.5 underset∼j`. 
Show Answers Only

`B`

Show Worked Solution

`text{Consider each option by tracing projections on the graph:}`
 

`overset(->)(OM)= text(proj)_((-underset~i+underset~j)) underset~u`

`text{Option B’s projection is only possible correct option.}`

`=>B`


♦♦ Mean mark 38%.

 

Functions, EXT1 F2 2022 HSC 3 MC

Let `P(x)` be a polynomial of degree 5. When `P(x)` is divided by the polynomial `Q(x)`, the remainder is `2x+5`.

Which of the following is true about the degree of `Q`?

  1. The degree must be 1.
  2. The degree could be 1.
  3. The degree must be 2.
  4. The degree could be 2.
Show Answers Only

`D`

Show Worked Solution

`text{Given}\ \ P(x)\ \ text{has degree 5}`

`P(x) -: Q(x)\ \ text{has remainder}\ \ 2x+5`

`text{Consider examples to resolve possibilities:}`

`text{eg.}\ \ x^5+2x+5 -: x^3 = x^2+\ text{remainder}\ 2x+5`

`:.\ text{Degree must be 2 is incorrect}`

`Q(x)\ \ text{can have a degree of 2, 3 or 4}`

`=>D`


♦ Mean mark 51%.

Financial Maths, 2ADV M1 2022 HSC 32

In a reducing-balance loan, an amount `$P` is borrowed for a period of `n` months at an interest rate of 0.25% per month, compounded monthly. At the end of each month, a repayment of `$M` is made. After the `n`th repayment has been made, the amount owing, `$A_n`, is given by

`A_(n)=P(1.0025)^(n)-M(1+(1.0025)^(1)+(1.0025)^(2)+cdots+(1.0025)^(n-1))`

(Do NOT prove this.)

  1. Jane borrows $200 000 in a reducing-balance loan as described.

  2. The loan is to be repaid in 180 monthly repayments.

  3. Show that  `M` = 1381.16, when rounded to the nearest cent.  (2 marks)

  4. After 100 repayments of $1381.16 have been made, the interest rate changes to 0.35% per month.

  5. At this stage, the amount owing to the nearest dollar is $100 032. (Do NOT prove this.)

  6. Jane continues to make the same monthly repayments.

  7. For how many more months will Jane need to make full monthly payments of $1381.16?  (3 marks)

  8. The final payment will be less than $1381.16.
  9. How much will Jane need to pay in the final payment in order to pay off the loan?   (2 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. `83`
  3. `$931.54`
Show Worked Solution

a.   `text{Show}\ \ M=$1381.16`

`A_(n)` `=P(1.0025)^(n)-M(1+(1.0025)^(1)+(1.0025)^(2)+cdots+(1.0025)^(n-1))`  
`0` `=200\ 000(1.0025)^180-M underbrace((1+(1.0025)^(1)+(1.0025)^(2)+cdots+(1.0025)^179))_(text(GP where)\ a = 1,\ r = 1.0025,\ n = 180)`  
`0` `=200\ 000(1.0025)^180-M((1(1.0025^180- 1))/(1.0025-1))`  

`M((1.0025^180-1)/(1.0025-1))=200\ 000(1.0025)^180`

`:.M` `=200\ 000(1.0025)^180 -: (1.0025^180-1 )/(1.0025-1)`   
  `=1381.163…`  
  `=$1381.16\ \ text{… as required}`  

 

b.   `P=$100\ 032,\ \ r=1.0035  and M=$1381.16`

`text{Find}\ \ n\ \ text{when}\ \ A_n=0:`

`A_(n)` `=P(1.0035)^(n)-1381.16(1+(1.0035)^(1)+(1.0035)^(2)+cdots+(1.0035)^(n-1))`  
`0` `=100\ 032(1.0035)^n-1381.16 ((1.0035^n- 1)/(1.0035-1))`  
`0` `=100\ 032(1.0035)^n-1381.16/0.0035 (1.0035^n- 1)`  
  `=100\ 032(1.0035)^n-394\ 617(1.0035)^n- 394\ 617`  
`294\ 585(1.0035)^n` `=394\ 617`  
`1.0035^n` `=(394\ 617)/(294\ 585)`  
`n` `=ln((394\ 617)/(294\ 585))/ln1.0035`  
  `=83.674…`  
  `=83\ text{more months with full payment}`  

 


♦♦ Mean mark part (b) 38%.

c.   `text{Find}\ \ A_83:`

`A_83` `=100\ 032(1.0035)^83-1381.16 ((1.0035^83- 1)/(1.0035-1))`  
  `=928.291…`  

 
`text{Interest will be added for the last month:}`

`:.\ text{Final payment}` `=928.291… xx 1.0035`  
  `=$931.54`  

♦♦♦ Mean mark part (c) 14%.

Calculus, 2ADV C3 2022 HSC 31

A line passes through the point  `P(1,2)`  and meets the axes at  `X(x, 0)`  and  `Y(0, y)`, where `x>1`.
 

  1. Show that  `y=(2x)/(x-1)`.  (2 marks)

  2. Find the minimum value of the area of triangle `XOY`.  (4 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. `4\ text{u}^2`
Show Worked Solution

a.   `text{Show}\ \ y=(2x)/(x-1)`

`text{S}text{ince}\ \ m_(YP)=m_(PX):`

`(y-2)/(0-1)` `=(2-0)/(1-x)`  
`y-2` `=(-2)/(1-x)`  
`y` `=2-2/(1-x)`  
  `=(2(1-x)-2)/(1-x)`  
  `=(-2x)/(1-x)`  
  `=(2x)/(x-1)\ \ text{… as required}`  

 


♦♦♦ Mean mark part (a) 17%.
COMMENT: `y=(2x)/(x-1)` is the expression of a relationship between the intercepts and not the equation of the line.
b.    `A` `=1/2 xx b xxh`
    `=1/2x((2x)/(x-1))`
    `=(x^2)/(x-1)`

 

`(dA)/dx` `=((x-1)*2x-x^2(1))/((x-1)^2)`  
  `=(2x^2-2x-x^2)/((x-1)^2)`  
  `=(x(x-2))/((x-1)^2)`  

 
`text{SP’s occur when}\ \ (dA)/dx=0:`

`x=0\ \ text{or}\ \ 2`
 

`text{Use 1st derivative test to find max/min:}`

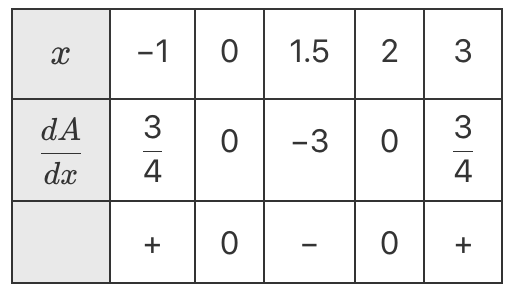
`=>\ text{MIN at}\ \ x=2`

`:.A_min` `=1/2 xx 2 xx (2xx2)/(2-1)`  
  `=4\ text{u}^2`  

♦♦ Mean mark part (b) 29%.

Statistics, 2ADV S3 2022 HSC 30

A continuous random variable \(X\) has cumulative distribution function given by

\(F(x)= \begin{cases}
1 & x>e^3 \\
\ \\
\dfrac{1}{k}\, \ln x & 1 \leq x \leq e^3 . \\
\ \\
0 & x<1\end{cases}\)

  1. Show that  \(k = 3\).  (1 mark)

  2. Given that  \(P(X < c)=2P(X > c)\), find the exact value of \(c\).  (2 marks)

Show Answers Only
  1. \(\text{Proof (See Worked Solutions)}\)
  2. \(e^2\)
Show Worked Solution

a.  \(\text{Show} \ \ k=3\)

\begin{aligned}
{\left[\dfrac{1}{k} \, \ln x\right]_1^{e^3} } & =1 \\
\dfrac{1}{k}\, \ln \left(e^3\right)-\dfrac{1}{k}\, \ln 1 & =1 \\
\dfrac{1}{k}(3)-\frac{1}{k}(0) & =1 \\
k & =3 \ldots \text{as required}
\end{aligned}


♦♦ Mean mark (a) 38%.
b.    \(P(X<c)\) \(=\left[\dfrac{1}{3}\, \ln x\right]_0^c\)
    \(=\dfrac{1}{3}\, \ln c\)

\begin{aligned}
2 P(X>c) & =2 P(1-P(X<c)) \\
& =2\left(1-\frac{1}{3} \ln c\right)
\end{aligned}

\(\text { Given } P(X<c)=2 P(X>c)\)

\begin{aligned}
\dfrac{1}{3}\, \ln c & =2-\dfrac{2}{3}\, \ln c \\
\ln c & =2 \\
\therefore c & =e^2
\end{aligned}


♦♦♦ Mean mark (b) 19%.

Calculus, 2ADV C4 2022 HSC 28

The graph of the circle  `x^2+y^2=2`  is shown.

The interval connecting the origin, `O`, and the point `(1,1)` makes an angle `theta` with the positive `x`-axis.
 

  1. By considering the value of `theta`, find the exact area of the shaded region, as shown on the diagram.  (2 marks)

Part of the hyperbola  `y=(a)/(b-x)-1`  which passes through the points `(0,0)` and `(1,1)` is drawn with the circle  `x^2+y^2=2`  as shown.
 

  1. Show that  `a=b=2`.  (2 marks)

  2. Using parts (a) and (b), find the exact area of the region bounded by the hyperbola, the positive `x`-axis and the circle as shown on the diagram.   (3 marks)

Show Answers Only
  1. `(pi-2)/4\ text{u}^2`
  2. `text{Proof (See Worked Solutions)}`
  3. `(8ln2+pi-6)/4\ text{u}^2`
Show Worked Solution

a.   `tan theta=1\ \ =>\ \ theta = pi/4`

`text{Using Pythagoras,}`

`r=sqrt(1^2+1^2)=sqrt2`

`text{Shaded Area}` `=A_text{sector}-A_Delta`  
  `=(pi/4)/(2pi) xx pi r^2-1/2 xx b xx h`  
  `=1/8xxpixx(sqrt2)^2-1/2xx1xx1`  
  `=pi/4-1/2`  
  `=(pi-2)/4\ text{u}^2`  

 


Mean mark (a) 54%.

b.   `text{Show}\ \ a=b=2`

`y=(a)/(b-x)-1\ \ text{passes through}\ \ (0,0):`

`0` `=a/(b-0)-1`  
`a/b` `=1`  
`a` `=b`  

 
`y=(a)/(b-x)-1\ \ text{passes through}\ \ (1,1):`

`1` `=a/(b-1)-1`  
`a/(b-1)` `=2`  
`a` `=2(b-1)`  
`a` `=2b-2`  
`b` `=2b-2\ \ text{(using}\ a=b)`  
`b` `=2`  

 
`:.a=b=2`
 


♦ Mean mark (b) 47%.
c.    `int_0^1 2/(2-x)-1\ dx` `=int_0^1 -2 xx (-1)/(2-x)-1\ dx`
    `=[-2ln|2-x|-x]_0^1`
    `=[(-2ln1-1)-(-2ln2-0)]`
    `=-1+2ln2`

 

`:.\ text{Total Area}` `=2ln2-1 + (pi-2)/4`  
  `=(8ln2-4+pi-2)/4`  
  `=(8ln2+pi-6)/4\ text{u}^2`  

♦♦ Mean mark (c) 36%.

Trigonometry, 2ADV T3 2022 HSC 23

The depth of water in a bay rises and falls with the tide. On a particular day the depth of the water, `d` metres, can be modelled by the equation

`d=1.3-0.6 cos((4pi)/(25)t)`,

where `t` is the time in hours since low tide.

  1. Find the depth of water at low tide and at high tide.  (2 marks)

  2. What is the time interval, in hours, between two successive low tides?  (1 mark)

  3. For how long between successive low tides will the depth of water be at least 1 metre?  (3 marks)

Show Answers Only
  1. `text{Low: 0.7 m,  High: 1.9 m}`
  2. `25/2\ text{hours}`
  3. `25/3\ text{hours}`
Show Worked Solution

a.   `text{S}text{ince}\ \ –1<=cos((4pi)/(25)t)<=1:`

`text{Low Tide}\ =1.3-0.6(1)=0.7\ text{m}`

`text{High Tide}\ =1.3-0.6(-1)=1.9\ text{m}`
 

b.   `text{Time between two low tides = Period of equation}\ (n)`

`(2pi)/n` `=(4pi)/25`  
`n/(2pi)` `=25/(4pi)`  
`n` `=25/2\ text{hours}`  

 


♦ Mean mark part (b) 47%.

c.   `text{Find}\ \ t\ \ text{when}\ \ d=1:`

`1.3-0.6 cos((4pi)/(25)t)` `=1`  
`-0.6 cos((4pi)/(25)t)` `=-0.3`  
`cos((4pi)/(25)t)` `=1/2`  

 

`(4pi)/(25)t` `=pi/3,\ \ (5pi)/3`  
`t` `=25/12,\ \ 125/12`  

 
`:.\ text{Time between low tides where water depth}\ >= 1\ text{m}`

`=125/12-25/12`

`=100/12`

`=25/3\ text{hours}`


♦ Mean mark part (c) 46%.

Functions, 2ADV F2 2022 HSC 19

The graph of the function  `f(x)=x^2`  is translated `m` units to the right, dilated vertically by a scale factor of `k` and then translated 5 units down. The equation of the transformed function is  `g(x)=3 x^2-12 x+7`.

Find the values of `m` and `k`.  (3 marks)

Show Answers Only

`m=2, \ \ k=3`

Show Worked Solution

`text{Horizontal translation}\ m\ text{units to the right:}`

`x^2\ → \ (x-m)^2`

`text{Dilated vertically by scale factor}\ k:`

`(x-m)^2\ →\ k(x-m)^2`

`text{Vertical translation 5 units down:}`

`k(x-m)^2\ →\ k(x-m)^2-5`

`y` `=k(x-m)^2-5`  
  `=k(x^2-2mx+m^2)-5`  
  `=kx^2-2kmx+(km^2-5)`  

 
`:.k=3`

`-2km` `=-12`  
`:.m` `=2`  

♦ Mean mark 51%.

Probability, 2ADV S1 2022 HSC 15

In a bag there are 3 six-sided dice. Two of the dice have faces marked  1, 2, 3, 4, 5, 6. The other is a special die with faces marked  1, 2, 3, 5, 5, 5.

One die is randomly selected and tossed.

  1. What is the probability that the die shows a 5?  (1 mark)

  2. Given that the die shows a 5, what is the probability that it is the special die?  (1 mark)

Show Answers Only
  1. `5/18`
  2. `3/5`
Show Worked Solution
a.    `P(5)` `=1/3 xx 1/6 + 1/3 xx 1/6 + 1/3 xx 1/2`
    `=1/18+1/18+1/6`
    `=5/18`

 

b.   `Ptext{(special die given a 5 is rolled)}`

`=(Ptext{(special die)} ∩  P(5))/(P(5))`

`=(1/3 xx 1/2)/(5/18)`

`=1/6 xx 18/5`

`=3/5`


Mean mark (a) 53%.
 
♦ Mean mark (b) 40%.

Functions, 2ADV F1 2022 HSC 10 MC

The graphs of `y=f(x)` and `y=g(x)` are shown.
 

Which graph best represents  `y=g(f(x))`
 

Show Answers Only

`B`

Show Worked Solution

`text{By Elimination:}`

`y=f(x)\ \ text{is an even function}`

`y=f(x)=f(-x)\ \ =>\ \ g(f(x))=g(f(-x))`

`g(f(x))\ \ text{is also an even function}`

`text{→ Eliminate A, C and D}`

`=>B`


♦ Mean mark 46%.

Functions, 2ADV F1 2022 HSC 12

A student believes that the time it takes for an ice cube to melt (`M` minutes) varies inversely with the room temperature `(T^@ text{C})`. The student observes that at a room temperature of `15^@text{C}` it takes 12 minutes for an ice cube to melt.

  1. Find the equation relating `M` and `T`.    (2 marks)

  2. By first completing this table of values, graph the relationship between temperature and time from `T=5^@C` to `T=30^@ text{C}`.   (2 marks)
     

\begin{array} {|c|c|c|c|}
\hline  \ \ T\ \  & \ \ 5\ \  & \ 15\  & \ 30\  \\
\hline M &  &  &  \\
\hline \end{array}

 
                   

Show Answers Only

a.    `M=180/T`

 b.    

\begin{array} {|c|c|c|c|}
\hline  \ \ T\ \  & \ \ 5\ \  & \ 15\  & \ 30\  \\
\hline M & 36 & 12 & 6 \\
\hline \end{array}       

 

Show Worked Solution
a.    `M` `prop 1/T`
  `M` `=k/T`
  `12` `=k/15`
  `k` `=15 xx 12`
    `=180`

 
`:.M=180/T`
 


♦ Mean mark (a) 49%.

b.   

\begin{array} {|c|c|c|c|}
\hline  \ \ T\ \  & \ \ 5\ \  & \ 15\  & \ 30\  \\
\hline M & 36 & 12 & 6 \\
\hline \end{array}

Algebra, STD2 A4 2022 HSC 24

A student believes that the time it takes for an ice cube to melt (`M` minutes) varies inversely with the room temperature `(T^@ text{C})`. The student observes that at a room temperature of `15^@text{C}` it takes 12 minutes for an ice cube to melt.

  1. Find the equation relating `M` and `T`.   (2 marks)

  2. By first completing this table of values, graph the relationship between temperature and time from `T=5^@C` to `T=30^@ text{C}.`   (2 marks)

\begin{array} {|l|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ T\ \  \rule[-1ex]{0pt}{0pt} & \ \ \ 5\ \ \  & \ \ 15\ \ \  & \ \ \ 30\ \ \  \\
\hline
\rule{0pt}{2.5ex} \ \ M\ \ \rule[-1ex]{0pt}{0pt} & & & \\
\hline
\end{array}

 
           

Show Answers Only

a.  `M prop 1/T \ \ =>\ \ M=k/T`

  `12` `=k/15`
  `k` `=15 xx 12=180`

 
`:.M=180/T`

b.   

\begin{array} {|l|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ T\ \  \rule[-1ex]{0pt}{0pt} & \ \ \ 5\ \ \  & \ \ 15\ \ \  & \ \ 30\ \  \\
\hline
\rule{0pt}{2.5ex} \ \ M\ \ \rule[-1ex]{0pt}{0pt} & 36 & 12 & 6 \\
\hline
\end{array}

 

     

Show Worked Solution
a.    `M` `prop 1/T`
  `M` `=k/T`
  `12` `=k/15`
  `k` `=15 xx 12`
    `=180`

 
`:.M=180/T`


♦♦ Mean mark part (a) 29%.

b.   

\begin{array} {|l|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ T\ \  \rule[-1ex]{0pt}{0pt} & \ \ \ 5\ \ \  & \ \ 15\ \ \  & \ \ 30\ \  \\
\hline
\rule{0pt}{2.5ex} \ \ M\ \ \rule[-1ex]{0pt}{0pt} & 36 & 12 & 6 \\
\hline
\end{array}

 

     


♦ Mean mark 44%.

Measurement, STD2 M7 2022 HSC 38

A full container has 4.8 L of a mixture of cordial and water in the ratio 1:3.

After removing 1.2 L of the mixture, more water is added to refill the container.

What is the ratio of cordial to water in the final mixture?  (3 marks)

Show Answers Only

`3:13`

Show Worked Solution

`text{Original mixture ratio}`

`text{C : W = 1.2 litres : 3.6 litres}`

`text{Removing 1.2 L of mixture, removes}`

`text{→ 300 mL cordial and 900 mL water}`
 

`text{Cordial in mixture after refill}`

`=1200-300`

`=900\ text{mL}`
 

`text{Water in mixture after refill}`

`=3600-900+1200`

`=3900\ text{mL}`
 

`:.\ text{C : W (final mixture)}`

`=900:3900`

`=3:13`


♦♦ Mean mark 33%.

Statistics, STD2 S5 2022 HSC 37

The life span of batteries from a particular factory is normally distributed with a mean of 840 hours and a standard deviation of 80 hours.

It is known from statistical tables that for this distribution approximately 60% of the batteries have a life span of less than 860 hours.

What is the approximate percentage of batteries with a life span between 820 and 920 hours?  (3 marks)

Show Answers Only

`44text{%}`

Show Worked Solution

`mu=840, \ sigma=80`

`ztext{-score (860)}\ = (x-mu)/sigma=(860-840)/80=0.25` 

`ztext{-score (820)}\ =(820-840)/80=-0.25` 

`ztext{-score (920)}\ =(920-840)/80=1`
 

`text{50% of batteries have a life span below 840 hours (by definition)}`

`=>\ text{10% lie between 840 and 860 hours}`

`=>\ text{By symmetry, 10% lie between 820 and 840 hours}`

`=> P(-0.25<=z<=0)=10text{%}`
 

`:.\ text{Percentage between 820 and 920}`

`=P(-0.25<=z<=1)`

`=P(-0.25<=z<=0) + P(0<=z<=1)`

`=10+34`

`=44text{%}`


♦♦ Mean mark 28%.

Statistics, STD2 S4 2022 HSC 35

Jo is researching the relationship between the ages of teenage characters in television series and the ages of actors playing these characters.

After collecting the data, Jo finds that the correlation coefficient is 0.4564.

A scatterplot showing the data is drawn. The line of best fit with equation  `y=-7.51+1.85 x`, is also drawn.
 


 

Describe and interpret the data and other information provided, with reference to the context given.  (4 marks)

Show Answers Only

`text{Correlation coefficient}\ (r) = 0.4564`

    • `text{Moderate and positive correlation}`

`text{Gradient of LOBF}\ = 1.85`

    • `text{On average, each extra year of a character’s age results}`
      `text{in the actor being 1.85 years older.}`

`text{Mode of data set = 15 years}`
  

`text{Limitations}`

    • `text{Data set is very restricted with just a 4 year range of}`
      `text{character ages.}`
    • `text{LOBF not useful when extrapolated to the left as it drops}`
      `text{below zero (on y-axis).}`
    • `text{Relationship describes correlation only, not causation.}`
Show Worked Solution

`text{Correlation coefficient}\ (r) = 0.4564`

    • `text{Moderate and positive correlation}`

`text{Gradient of LOBF}\ = 1.85`

    • `text{On average, each extra year of a character’s age results}`
      `text{in the actor being 1.85 years older.}`

`text{Mode of data set = 15 years}`
  

`text{Limitations}`

    • `text{Data set is very restricted with just a 4 year range of}`
      `text{character ages.}`
    • `text{LOBF not useful when extrapolated to the left as it drops}`
      `text{below zero (on y-axis).}`
    • `text{Relationship describes correlation only, not causation.}`

♦♦ Mean mark 30%.

Measurement, STD2 M1 2022 HSC 34

A composite solid is shown. The top section is a cylinder with a height of 3 cm and a diameter of 4 cm. The bottom section is a hemisphere with a diameter of 6 cm. The cylinder is centred on the flat surface of the hemisphere.
 


 

Find the total surface area of the composite solid in cm², correct to 1 decimal place.  (4 marks)

Show Answers Only

`122.5\ text{cm}^2`

Show Worked Solution
`text{S.A. of Cylinder}` `=pir^2+2pirh`  
  `=pi(2^2)+2pi(2)(3)`  
  `=16pi\ text{cm}^2`  

 

`text{S.A. of Hemisphere}` `=1/2 xx 4pir^2`  
  `=2pi(3^2)`  
  `=18pi\ text{cm}^2`  

 

`text{Area of Annulus}` `=piR^2-pir^2`  
  `=pi(3^2)-pi(2^2)`  
  `=5pi\ text{cm}^2`  

 

`text{Total S.A.}` `=16pi+18pi+5pi`  
  `=39pi`  
  `=122.522…`  
  `=122.5\ text{cm}^2\ \ text{(to 1 d.p.)}`  

♦ Mean mark 50%.

Measurement, STD2 M6 2022 HSC 33

The diagram shows an aeroplane that was flying towards an airport at  `A` on a bearing of `135^@ text{T}`. When it was at point `O`, 20 km away from the airport at  `A`, the flight course was changed. The aeroplane landed at an airport at `B` directly south of `O`. The distance from `O` to `B` is 50 km.
 


 

  1. Show that the distance between the airport at  `A` and the airport at `B` is 38.5 km, correct to 1 decimal place.  (2 marks)

  2. Use the sine rule to find the angle `O B A` to the nearest degree.  (2 marks)

  3. What is the bearing of the airport at `B` from the airport at  `A` ?  (1 mark)

Show Answers Only
  1. `text{Proof}`
  2. `22^@`
  3. `202^@text{T}`
Show Worked Solution

a.   `angle AOB=180-135=45^@`
 

`text{Using the cosine rule:}`

`AB^2` `=20^2+50^2-2xx20xx50xxcos45^@`  
  `=1485.786…`  
`:.AB` `=38.54…`  
  `=38.5\ \text{km (to 1 d.p.)}`  

♦ Mean mark part (a) 50%.

 

b.   `text{Let}\ \ theta=angleOBA`

`text{Using the sine rule:}`

`sintheta/20` `=sin45^@/38.5`  
`sintheta` `=(sin45^@xx20)/38.5`  
`:.theta` `=sin^(-1)((sin45^@xx20)/38.5)`  
  `=21.55…^@`  
  `=22^@\ \ text{(nearest degree)}`  

♦♦ Mean mark part (b) 39%.

 

c. 

`text{Bearing of}\ B\ text{from}\ \ A`

`=180 + 22`

`=202^@text{T}`


♦♦ Mean mark part (c) 25%.

Measurement, STD2 M1 2022 HSC 32

The diagram shows a park consisting of a rectangle and a semicircle. The semicircle has a radius of 100 m. The dimensions of the rectangle are 200 m and 250 m.

A lake occupies a section of the park as shown. The rest of the park is a grassed section. Some measurements from the end of the grassed section to the edge of the lake are also shown.
 

  1. Using two applications of the trapezoidal rule, calculate the approximate area of the grassed section.  (2 marks)

  2. Hence calculate the approximate area of the lake, to the nearest square metre.   (2 marks)

Show Answers Only
  1. `35\ 500\ text{m}^2`
  2. `30\ 208\ text{m}^2`
Show Worked Solution

a.   `h=100\ text{m}`

`A` `~~h/2(x_1+x_2)+h/2(x_2+x_3)`  
  `~~100/2(160+150)+100/2(150+250)`  
  `~~50xx310+50xx400`  
  `~~35\ 500\ text{m}^2`  

 

b.    `text{Total Area}` `=\ text{Area of Rectangle + Area of Semi-Circle}`
    `= (250 xx 200) + 1/2 xx pi xx 100^2`
    `=65\ 707.96\ text{m}^2`

 

`text{Area of Lake}` `=67\ 708-35\ 500`  
  `=30\ 208\ text{m}^2`  

♦ Mean mark (b) 44%.

Networks, STD2 N3 2022 HSC 31

A wildlife park has 5 main attractions `(A, B, C, D, E)` connected by directional paths. A simple network is drawn to represent the flow through the park's paths. The number of visitors who can access each path at any one time is also shown.
 

   

  1. What is the flow capacity of the cut shown?  (1 mark)

  2. By showing a suitable cut on the diagram below, explain why the network's current maximum flow capacity is less than 40 visitors.  (2 marks)
     

  3. One path is to be increased in capacity so that the overall maximum flow will be 40 visitors at any one time.
  4. Which path could be increased and by how much?  (2 marks)

Show Answers Only
  1. `40`
  2.  
     
  3. `text{Max flow = min cut = 35}`
  4. `AE\ text{or}\ DE\ text{could be increased by 5}`
Show Worked Solution

a.   `text{Flow capacity = 10 + 20 + 10 = 40}`

`text{(DE is not counted as it runs from sink → source)}`
 

b.  
       

`text{Min Cut = Max Flow}`

`text{Max Flow}` `=15+10+10`  
  `=35<40`  


♦ Mean mark part (a) 45%.
♦♦ Mean mark part (b) 33%.

 

c.   `text{Two strategies:}`

  • `AE\ text{could be increased by 5}`
  • `DE\ text{could be increased by 5}`

`text{(both strategies would increase the minimum cut to}`

  `text{40 by increasing the flow to vertex}\ E\ text{to 30)}`


Mean mark 52%.

Financial Maths, STD2 F5 2022 HSC 30

Eli is choosing between two investment options.

A table of future value interest factors for an annuity of $1 is shown.

  1. What is the value of Eli's investment after 10 years using Option 1 ?  (2 marks)

  2. What is the difference between the future values after 10 years using Option 1 and Option 2?  (2 marks)

Show Answers Only
  1. `$45\ 097.17`
  2. `$40.87`
Show Worked Solution

a.   `text{Monthly r/i}\ = 1.2/12=0.1text{%}\ \ =>\ \ r= 0.001`

`text{Compounding periods}\ (n)=12xx10=120`

`FV` `=PV(1+r)^n`  
  `=40\ 000(1+0.001)^120`  
  `=$45\ 097.17`  

 


♦ Mean mark 48%.

b.   `text{Quarterly r/i}\ = 2.4/4=0.6text{%}\ \ =>\ \ r= 0.006`

`text{Compounding periods}\ (N) =4xx10=40`

`text{Annuity factor (from table) = 45.05630}`

`FV` `=1000xx45.05630`  
  `=45\ 056.30`  

 

`text{Difference}` `=45\ 097.17-45\ 056.30`  
  `=$40.87`  

♦ Mean mark 43%.

Measurement, STD2 M1 2022 HSC 28

A dam is in the shape of a triangular prism which is 50 m long, as shown.

Both ends of the dam, `A B C` and `D E F`, are isosceles triangles with equal sides of length 25 metres. The included angles `B A C` and `E D F` are each `150^@`.

 
     

Calculate the number of litres of water the dam will hold when full.  (4 marks)

Show Answers Only

`7\ 812\ 500\ text{L}`

Show Worked Solution

`V=Ah`

`text{Use sine rule to find}\ A:`

`A` `=1/2 ab\ sinC`  
  `=1/2 xx 25 xx 25 xx sin150^@`  
  `=156.25\ text{m}^2`  

 

`:.V` `=156.25 xx 50`  
  `=7812.5\ text{m}^3`  

 

`text{S}text{ince 1 m³ = 1000 litres:}`

`text{Dam capacity}` `=7812.5 xx 1000`  
  `=7\ 812\ 500\ text{L}`  

♦♦ Mean mark 33%.

Financial Maths, STD2 F4 2022 HSC 27

A company purchases a machine for $50 000. The two methods of depreciation being considered are the declining-balance method and the straight-line method.

  1. For the declining-balance method, the salvage value of the machine after `n` years is given by the formula
  2.     `S=V_(0)xx(0.80)^(n),`
  3. where `S` is the salvage value and `V_(0)` is the initial value of the asset.
  4.  i. What is the annual rate of depreciation used in this formula?  (1 mark)
  5. ii. Calculate the salvage value of the machine after 3 years, based on the given formula.  (1 mark)
  6. For the straight-line method, the value of the machine is depreciated at a rate of 12.2% of the purchase price each year.
  7. When will the value of the machine, using this method, be equal to the salvage value found in part (a) (ii)?  (2 marks)
Show Answers Only
  1.  i. `20text{%}`
  2. ii. `$25\ 600`
  3. `text{4 years}`
Show Worked Solution

a.i.  `text{Depreciation rate}\ = 1-0.8=0.2=20text{%}`
 

a.ii.  `text{Find}\ \ S\ \ text{when}\ \ n=3:`

`S` `=V_0 xx (0.80)^n`  
  `=50\ 000 xx (0.80)^3`  
  `=$25\ 600`  

 
b.   `text{Using the SL method}`

`S_n` `= 50\ 000-(0.122 xx 50\ 000)xxn`  
  `=50\ 000-6100n`  

 

`text{Find}\ \ n\ \ text{when}\ \ S_n=$25\ 600`

`25\ 600` `=50\ 000-6100n`  
`6100n` `=24\ 400`  
`n` `=(24\ 400)/6100`  
  `=4\ text{years}`  

♦♦ Mean mark (a.i.) 24%.
COMMENT: A poor State result in part (a.i.) that warrants attention.
 
♦ Mean mark part (b) 38%.

Measurement, STD2 M6 2022 HSC 26

The diagram shows two right-angled triangles, `ABC` and `ABD`,

where `AC=35 \ text{cm},BD=93 \ text{cm}, /_ACB=41^(@)` and `/_ADB=theta`.
 
     

Calculate the size of angle `theta`, to the nearest minute.  (4 marks)

Show Answers Only

`19^@6^{′}`

Show Worked Solution

`text{In}\ Delta ABC:`

`cos 41^@` `=35/(BC)`  
`BC` `=35/(cos 41^@)`  
  `=46.375…`  

 
`angle BCD = 180-41=139^@`
 

`text{Using sine rule in}\ Delta BCD:`

`sin theta/(46.375)` `=sin139^@/93`  
`sin theta` `=(sin 139^@ xx 46.375)/93`  
`:.theta` `=sin^(-1)((sin 139^@ xx 46.375)/93)`  
  `=19.09…`  
  `=19^@6^{′}\ \ text{(nearest minute)}`  

♦ Mean mark 50%.

Financial Maths, STD2 F5 2022 HSC 25

The table shows the future value of an annuity of $1.
 
     

Zal is saving for a trip and estimates he will need $15 000. He opens an account earning 3% per annum, compounded annually.

  1. How much does Zal need to deposit every year if he wishes to have enough money for the trip in 4 years time?  (2 marks)

  2. How much interest will Zal earn on his investment over the 4 years? Give your answer to the nearest dollar.  (2 marks)

Show Answers Only
  1. `$3589.09`
  2. `$660`
Show Worked Solution

a.   `text{Using the table:}\ r=3text{%},\ \ n=4`

`text{Annuity factor}\ = 4.184`

`text{Let}\ \ A=\ text{amount invested each year}`

`FV` `=A xx 4.184`  
`15\ 000` `=A xx 4.184`  
`:.A` `=(15\ 000)/4.184`  
  `=$3585.09`  

 

b.   `text{Total payments}\ = 4 xx 3585.09=$14\ 340.36`

`text{Interest earned}` `=FV-\ text{total payments}`  
  `=15\ 000-14\ 340.36`  
  `=659.64`  
  `=$660\ \ text{(nearest $)}`  

♦♦ Mean mark 33%.

ENGINEERING, PPT 2021 HSC 22a

A baseplate used to support the wheels under a trolley is shown in pictorial view.

Construct, within the dashed-line box provided, a top view of the baseplate. Do NOT dimension.   (3 marks)
 

Show Answers Only

Top view

Show Worked Solution

Top View


♦ Mean mark 42%.

Statistics, STD2 S1 2022 HSC 19

The table shows the types of customer complaints received by an online business in a month.
 

  1. What are the values of `A` and `B`?  (2 marks)

  2. The data from the table are shown in the following Pareto chart.
     
     
  3. The manager will address 80% of the complaints.
  4. Which types of complaints will the manager address?  (1 mark)

Show Answers Only
  1. `A=160, \ B=96`
  2. `text{Stock shortages and delivery fees.}`
Show Worked Solution

a.   `A=98+62=160`

`text{% Damaged items}\ = 8/200 xx 100 = 4text{%}`

`text{Cumulative % after damaged items = 96%}`

`B = 92+4=96`
 

b.   `text{The right hand side cumulative frequency percentage}`

`text{shows that 80% of all complaints received concern}`

`text{stock shortages and delivery fees.}`

`:.\ text{The manager will address stock shortages and delivery fees.}`


♦ Mean mark part (b) 41%.

Measurement, STD2 M7 2022 HSC 4 MC

Lily wanted to estimate the number of fish in a lake.

She randomly captured 30 fish, then tagged and released them.

One week later she randomly captured 40 fish from the same lake. She found that 12 of these 40 fish were tagged.

What is the best estimate for the total number of fish in the lake?

  1. 58
  2. 70
  3. 82
  4. 100
Show Answers Only

`D`

Show Worked Solution

`text{Let}\ \ P=\ text{population of fish in lake}`

`text{Capture}\ = 30/P`

`text{Recapture}\ = 12/40`

`30/P` `=12/40`  
`12P` `=30 xx 40`  
`P` `=1200/12`  
  `=100`  

 
`=>D`


♦♦ Mean mark 37%.

Algebra, STD2 A2 2022 HSC 2 MC

Which of the following could be the graph of  `y= –2 x+2`?
 

Show Answers Only

`A`

Show Worked Solution

`text{By elimination:}`

`y text{-intercept = 2  →  Eliminate}\ B and C`

`text{Gradient is negative  → Eliminate}\ D`

`=>A`


♦ Mean mark 48%.

PHYSICS, M7 2019 HSC 25

The diagram shows a model of electromagnetic waves.
 


 

Relate this model to predictions made by Maxwell.   (4 marks)

Show Answers Only
  • The diagram shows alternating electric and magnetic fields oscillating perpendicular to each other. This relates to Maxwell’s prediction of mutual inductance; that a changing electric field induces a changing magnetic field and vice versa.
  • The diagram shows the electromagnetic wave propagating with velocity `v `. This relates to Maxwell’s prediction of a range of waves with different wavelengths, all travelling at the same speed where `c=(1)/(sqrt(mu_(0)epsilon_(0)))`.
  • The diagram also shows an electromagnetic wave emanating from an oscillating charge. This is consistent with Maxwell’s prediction that an oscillating electric charge produces a changing electric field, which in turn produces a changing magnetic field. These fields continue to mutually induce each other, producing an electromagnetic wave.
Show Worked Solution
  • The diagram shows alternating electric and magnetic fields oscillating perpendicular to each other. This relates to Maxwell’s prediction of mutual inductance; that a changing electric field induces a changing magnetic field and vice versa.
  • The diagram shows the electromagnetic wave propagating with velocity `v `. This relates to Maxwell’s prediction of a range of waves with different wavelengths, all travelling at the same speed where `c=(1)/(sqrt(mu_(0)epsilon_(0)))`.
  • The diagram also shows an electromagnetic wave emanating from an oscillating charge. This is consistent with Maxwell’s prediction that an oscillating electric charge produces a changing electric field, which in turn produces a changing magnetic field. These fields continue to mutually induce each other, producing an electromagnetic wave.

♦ Mean mark 44%.

PHYSICS, M6 2019 HSC 24

A step-up transformer is constructed using a solid iron core. The coils are made using copper wires of different thicknesses as shown.
 

The table shows electrical data for this transformer.
 

  1. Explain how the operation of this transformer remains consistent with the law of conservation of energy. Include a relevant calculation in your answer.   (3 marks)
  1. Explain how TWO modifications to this transformer would improve its efficiency.   (4 marks)
Show Answers Only

a.   The energy input into this transformer is `text{500 J s}^(-1)`

  • The energy output is given by:
  •    `P=V_(s)I_(s)=50xx 9=450\ \text{J s}^(-1)`
  •  This is consistent with the law of conservation of energy as `text{500 J s}^(-1)` of energy is converted into other energy forms such as heat.

b.    Modification 1:

  • Laminating the iron core prevents large eddy currents from being induced in it.
  • This reduces energy loss in the form of heat, increasing efficiency.

Modification 2:

  • Increasing the thickness of the wire in the primary coil.
  • This reduces its resistance, increasing the transformer’s efficiency.
Show Worked Solution

a.   The energy input into this transformer is `text{500 J s}^(-1)`

  • The energy output is given by:
  •    `P=V_(s)I_(s)=50xx 9=450\ \text{J s}^(-1)`
  •  This is consistent with the law of conservation of energy as `text{500 J s}^(-1)` of energy is converted into other energy forms such as heat.

b.    Modification 1:

  • Laminating the iron core prevents large eddy currents from being induced in it.
  • This reduces energy loss in the form of heat, increasing efficiency.

Modification 2:

  • Increasing the thickness of the wire in the primary coil.
  • This reduces its resistance, increasing the transformer’s efficiency.

♦ Mean mark part 48%.

PHYSICS, M5 2019 HSC 20 MC

In the apparatus shown, a backboard is connected by a rod to a shaft. The shaft is spun by an electric motor causing the backboard to rotate in the horizontal plane around the axis  X `–` X′.

A cube is suspended by a string so that it touches the surface of the backboard.
 

When the angular velocity of the motor is great enough, the string is cut and the position of the cube does not change relative to the backboard.

Which statement correctly describes the forces after the string is cut?

  1. The sum of the forces on the cube is zero.
  2. The horizontal force of the backboard on the cube is equal in magnitude to the horizontal force of the cube on the backboard.
  3. The horizontal force of the backboard on the cube is greater than the horizontal force of the cube on the backboard, resulting in a net centripetal force.
  4. The force of friction between the cube and the backboard is independent of the force of the backboard on the cube because these forces are perpendicular to each other.
Show Answers Only

`B`

Show Worked Solution

Using Newton’s Third Law:

  • The backboard and the cube are an action-reaction pair.
  • The force of the backboard on the cube (centripetal force) is equal in magnitude and opposite in direction to the force of the cube on the backboard.

`=>B`


♦ Mean mark 36%.

PHYSICS, M8 2019 HSC 19 MC

Consider the following nuclear reaction.

\(\text{W} + \text{X} \rightarrow \text{Y} + \text{Z}\)

Information about W, X and Y is given in the table.

\begin{array}{|c|c|}
\hline
\rule{0pt}{2.5ex}\textit{Species} & \textit{Mass defect} & \textit{Total binding energy} & \textit{Binding energy per nucleon}\\
\textit{} & \textit{(u)} \rule[-1ex]{0pt}{0pt}& \text{(MeV)} & \text{(MeV)}\\
\hline \rule{0pt}{2.5ex}\text{W} \rule[-1ex]{0pt}{0pt}& 0.00238817 & 2.224566 & 1.112283 \\
\hline \rule{0pt}{2.5ex}\text{X} \rule[-1ex]{0pt}{0pt}& 0.00910558 & 8.481798 & 2.827266 \\
\hline \rule{0pt}{2.5ex}\text{Y }\rule[-1ex]{0pt}{0pt}& 0.03037664 & 28.29566 & 7.073915 \\
\hline
\end{array}

Which of the following is a correct statement about energy in this reaction?

  1. The reaction gives out energy because the mass defect of \(\text{Y}\) is greater than that of either \(\text{W}\) or \(\text{X}\).
  2. It cannot be deduced whether the reaction releases energy because the properties of \(\text{Z}\) are not known.
  3. The reaction requires an input of energy because the mass defect of the products is greater than the sum of the mass defects of the reactants.
  4. Energy is released by the reaction because the binding energy of the products is greater than the sum of the binding energies of the reactants.
Show Answers Only

\(D\)

Show Worked Solution
  • Energy required to break \(\text{W}\) and \(\text{X}\) into their constituent nucleons:
  •    \(2.22+8.48=10.70 \ \text{MeV}\)
  • Energy released in the formation of the products is given by the sum of binding energies of \(\text{Y}\) and \(\text{Z}\):
  •    \(28.30\  \text{MeV} +\) binding energy of \(\text{Z}\)
  • As this is greater than the sum of binding energies of the reactants regardless of the binding energy of \(\text{Z}\), there is a net release of energy in the reaction.

\(\Rightarrow D\)


♦ Mean mark 31%.

PHYSICS, M6 2019 HSC 17 MC

A straight current-carrying conductor, `QR`, is connected to a battery and a variable resistor. `QR` is enclosed in an evacuated chamber with a fluorescent screen at one end.
 


 

A cathode ray enters the chamber directly above `Q`, initially travelling parallel to `QR`. It passes through the chamber and strikes the fluorescent screen causing a bright spot.

Which direction will this spot move towards if the resistance is increased?

  1. `W`
  2. `X`
  3. `Y`
  4. `Z`
Show Answers Only

`D`

Show Worked Solution

Using the right hand grip rule, the current through creates a magnetic field to the right above it. Using the right hand palm rule, this creates an upwards force on the cathode ray, which is made up of electrons.

Increasing the resistance results in:

  • decreased current through `QR`
  • decreased upwards force on the cathode ray
  • bright spot moves downwards towards `Z`.

`=>D`


♦ Mean mark 36%.

PHYSICS, M6 2019 HSC 16 MC

The diagram shows the trajectory of a particle with charge `q` and mass `m` when fired horizontally into a vacuum chamber, where it falls under the influence of gravity.
 

The horizontal distance, `d`, travelled by the particle is recorded.

The experiment is repeated with a uniform vertical electric field applied such that the particle travels the same horizontal distance, `d`, but strikes the upper surface of the chamber.
 

What is the magnitude of the electric field?

  1. `mgq`
  2. `2mgq`
  3. `(mg)/q`
  4. `(2mg)/q`
Show Answers Only

`D`

Show Worked Solution
  • As the particle travels the same distance in both scenarios the magnitude of the force it experiences is the same.
  • Initially, the only force acting on the particle is its weight, `F=mg.`
  • When the electric field is on, the particle experiences an upwards force due to the electric field, and a downwards force due to gravity,  `F=qE-mg.`
  • As these forces have the same magnitude:
`qE-mg` `=mg`  
`qE` `=2mg`  
`E` `=(2mg)/(q)`  

 
`=>D`


♦ Mean mark 42%.

PHYSICS, M5 2019 HSC 14 MC

A satellite in circular orbit at a distance `r` from the centre of Earth has an orbital velocity `v`.

If the distance was increased to `2r`, what would be the satellite's orbital velocity?

  1. `(v)/2`
  2. `0.7v`
  3. `1.4v`
  4. `2v`
Show Answers Only

`B`

Show Worked Solution

The satellites centripetal force is provided by gravity:

`F_(c)` `=F_(g)`  
`(mv^2)/(r)` `=(GMm)/(r^2)`  
`v` `=sqrt((GM)/(r))`  
`∴ v` `prop (1)/(sqrt(r))`  

 
Hence, doubling the satellites radius changes its velocity by a factor of `(1)/(sqrt(2))`

`=>B`


♦ Mean mark 42%.

PHYSICS, M7 2019 HSC 13 MC

A laser has a power output of 30 mW and emits light with a wavelength of 650 nm.

How many photons does this laser emit per second?

  1. `4.6 × 10^(14)`
  2. `9.8 × 10^(16)`
  3. `3.1 × 10^(19)`
  4. `9.3 × 10^(21)`
Show Answers Only

`B`

Show Worked Solution
`E` `=hf`  
  `=(hc)/(lambda)`  
  `=((6.626 xx10^(-34))(3 xx10^(8)))/(6.5 xx10^(-7))`  
  `=3.1 xx10^(-19)\ \text{J}`  

 
`text{Photons}=(P)/(E)=(30 xx10^(-3))/(3.1 xx10^(-19))=9.8 xx10^(16)`

`=>B`


♦ Mean mark 43%.

PHYSICS, M8 2019 HSC 12 MC

The table shows two types of quarks and their respective charges.
 

In a particular nuclear transformation, a particle having a quark composition `udd` is transformed into a particle having a quark composition `u ud`.

What is another product of this transformation? 

  1. Electron
  2. Neutron
  3. Positron
  4. Proton
Show Answers Only

`A`

Show Worked Solution
  • The particle with quark composition `udd` is a neutron.
  • It is transformed into a particle with quark composition `udd` which is a proton.
  • To conserve charge, an electron must also be a product.

`=>A`


♦ Mean mark 51%.

PHYSICS, M5 2019 HSC 9 MC

Two satellites have the same mass. One (LEO) is in low-Earth orbit and the other (GEO) is in a geostationary orbit.

The total energy of a satellite is half its gravitational potential energy.

Which row of the table correctly identifies the satellite with the greater orbital period and the satellite with the greater total energy?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex} \ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|c|c|}
\hline
\rule{0pt}{2.5ex}\textit{Greater orbital period}\rule[-1ex]{0pt}{0pt}& \textit{Greater total energy} \\
\hline
\rule{0pt}{2.5ex}\text{LEO}\rule[-1ex]{0pt}{0pt}&\text{LEO}\\
\hline
\rule{0pt}{2.5ex}\text{LEO}\rule[-1ex]{0pt}{0pt}& \text{GEO}\\
\hline
\rule{0pt}{2.5ex}\text{GEO}\rule[-1ex]{0pt}{0pt}& \text{LEO} \\
\hline
\rule{0pt}{2.5ex}\text{GEO}\rule[-1ex]{0pt}{0pt}& \text{GEO} \\
\hline
\end{array}
\end{align*}

Show Answers Only

`D`

Show Worked Solution
  • Orbital velocity decreases as the orbital radius of a satellite increases.
  • the geostationary satellite has the greater orbital period
  • Total energy increases as orbital radius increases.
  • the geostationary satellite has the greater total energy

`=>D`


♦ Mean mark 43%.

PHYSICS, M6 2019 HSC 7 MC

A bar magnet is moved away from a stationary coil.

Which diagram correctly shows the direction of the induced current in the coil and the resulting magnetic polarity of the coil?
 

 

 

Show Answers Only

`D`

Show Worked Solution
  • The current through the solenoid will produce a force that opposes the magnets motion (Lenz’s law).
  • So, there will be a north pole on the right hand side of the magnet. The right hand grip rule gives the direction of current. 

`=>D`


♦ Mean mark 47%.

PHYSICS, M6 2020 HSC 32

A rope connects a mass on a horizontal surface to a pulley attached to an electric motor as shown.
 

Explain the factors that limit the speed at which the mass can be pulled along the horizontal surface. Use mathematical models to support your answer.   (7 marks)

Show Answers Only
  • The factors limiting the speed of the mass along horizontal surface can be divided into two main parts; 1-Factors involving friction between the mass and the table and 2-Factors involving the force output of the motor and pulley.

Friction between the mass and table

  • The mass will experience a friction force of  `F_(f)=mu N`. Since the mass has no vertical acceleration,  `N=mg\ \ =>\ \ F_(f)=mu mg.`
  • The speed at which the mass can be pulled is limited by the coefficient of kinetic friction between the mass and the table `mu` and the magnitude of the mass `m`.

 Force output of the motor and pulley

  • The power of the motor depends on its torque and the pulley radius `(tau=rF sin theta).`
  • The torque produced by the motor is given by  `tau=NIAB sin theta`
  • The force of the motor and hence maximum speed at which the mass can be pulled is also limited by the number of turns of the coil in the motor, the current passing through the coils, the area of the coils and the magnetic field strength of the stator magnets.

Answers could also contain:

  • Back emf in the motor limiting its maximum speed.
  • The efficiency of the motor.
Show Worked Solution
  • The factors limiting the speed of the mass along horizontal surface can be divided into two main parts; 1-Factors involving friction between the mass and the table and 2-Factors involving the force output of the motor and pulley.

Friction between the mass and table

  • The mass will experience a friction force of  `F_(f)=mu N`. Since the mass has no vertical acceleration,  `N=mg\ \ =>\ \ F_(f)=mu mg.`
  • The speed at which the mass can be pulled is limited by the coefficient of kinetic friction between the mass and the table `mu` and the magnitude of the mass `m`.

 Force output of the motor and pulley

  • The power of the motor depends on its torque and the pulley radius `(tau=rF sin theta).`
  • The torque produced by the motor is given by  `tau=NIAB sin theta`
  • The force of the motor and hence maximum speed at which the mass can be pulled is also limited by the number of turns of the coil in the motor, the current passing through the coils, the area of the coils and the magnetic field strength of the stator magnets.

Answers could also contain:

  • Back emf in the motor limiting its maximum speed.
  • The efficiency of the motor.
Mean mark 58%.

PHYSICS, M5 2020 HSC 31

  1. The orbit of a comet is shown.
     

  1. Account for the changes in velocity of the comet as it completes one orbit from position `P`.   (3 marks)
  1. Two stars, `A` and `B`, of equal mass `m`, separated by a distance `x`, interact gravitationally such that the speed of `A` is constant.
  2. Derive an expression for the speed of `B`.   (3 marks)
Show Answers Only

a.    Changes in Velocity

  • As the comet moves from position `P` towards the sun, its gravitational potential energy (GPE) is converted into kinetic energy.
  • Increase in the comet’s kinetic energy → increase in the comet’s velocity as it moves towards the sun.
  • As the comet moves away from the sun back to` P`, its kinetic energy is converted into GPE.
  • Decrease in kinetic energy → decrease in comet’s velocity.

b.   `v_(B)=sqrt((Gm)/(2x))`

Show Worked Solution

a.    Changes in Velocity

  • As the comet moves from position `P` towards the sun, its gravitational potential energy (GPE) is converted into kinetic energy.
  • Increase in the comet’s kinetic energy → increase in the comet’s velocity as it moves towards the sun.
  • As the comet moves away from the sun back to` P`, its kinetic energy is converted into GPE.
  • Decrease in kinetic energy → decrease in comet’s velocity.

♦ Mean mark (a) 49%.

b.    As the speed of `A` is constant, it must be travelling in a circular orbit.

  • `A` and `B` are both orbiting in a circle around their centre of mass.
  • Since both comets have the same mass, the radius of their circular motion is half of the distance between them.
  • As the centripetal force keeping `B` in orbit is provided by the gravitational force acting on it due to `A`:
`F_(g)` `=F_(c)`  
`(Gm^(2))/(x^(2))` `=(m(v_(B))^(2))/((x)/(2))`  
`(Gm)/x` `=2(v_B)^2`  
`v_(B)` `=sqrt((Gm)/(2x))`  

PHYSICS, M7 2020 HSC 30b

  1. Calculate the wavelength of a proton travelling at 0.1\(c\).   (2 marks)
  1. Explain the relativistic effect on the wavelength of a proton travelling at 0.95\(c\).   (2 marks)
Show Answers Only

i.   `lambda=1xx10^(-14)` m

ii.  See Worked Solutions

Show Worked Solution
i.     `lambda` `=(h)/(mv)`
    `=(6.626 xx10^(-34))/(1.673 xx10^(-27)xx0.1 xx3xx10^(8))`
    `=1xx10^(-14)\ text{m}`

ii.    Due to momentum dilation:

  • The momentum of the proton is greater than that predicted by classical mechanics. 
  • Since  `lambda=(h)/(mv)\ \ =>\ \ lambda prop 1/(mv)`
  • The wavelength of the proton is shorter than would be predicted by classical mechanics.

♦ Mean mark (ii) 45%.

PHYSICS, M8 2020 HSC 30a

Explain, using an example, how a particle accelerator has provided evidence for the Standard Model of matter.   (3 marks)

Show Answers Only
  • A linear accelerator used electric fields to accelerate electrons to very fast speeds and collide them with protons.
  • The scattering of these electrons was analysed with technology and was inconsistent with protons being fundamental particles.
  • The obtained data showed that protons contained both positive and negative internal charges.
  • This observation contributed to the idea that protons were made up of quarks, and so provided evidence for the Standard Model of Matter.

 Answers could also mention:

  • Collision of protons accelerated to relativistic speeds at the LHC producing new, massive particles such as the Higgs-Boson hypothesised by the Standard Model of Matter. 
Show Worked Solution

  • A linear accelerator used electric fields to accelerate electrons to very fast speeds and collide them with protons.
  • The scattering of these electrons was analysed with technology and was inconsistent with protons being fundamental particles.
  • The obtained data showed that protons contained both positive and negative internal charges.
  • This observation contributed to the idea that protons were made up of quarks, and so provided evidence for the Standard Model of Matter.

 Answers could also mention:

  • Collision of protons accelerated to relativistic speeds at the LHC producing new, massive particles such as the Higgs-Boson hypothesised by the Standard Model of Matter. 


♦ Mean mark 46%.

PHYSICS, M8 2021 HSC 35

A spacecraft is powered by a radioisotope generator. Pu-238 in the generator undergoes alpha decay, releasing energy. The decay is shown with the mass of each species in atomic mass units, `u`

\begin{array} {ccccc}
\ce{^{238}Pu} & \rightarrow & \ce{^{234}U} & + & \alpha \\
238.0495\ u &  & 234.0409\ u &  & 4.0026\ u \end{array}

  1. Show that the energy released by one decay is  `9.0 × 10^(-13)` J.   (3 marks)
  1. At launch, the generator contains  `9.0 × 10^24`  atoms of Pu-238. The half-life of Pu-238 is 87.7 years.
  2. Calculate the total energy produced by the generator during the first ten years after launch.  (3 marks)
Show Answers Only
  1. `9.0xx10^(-13)\ \text{J}`
  2. `6.2xx10^(11)\ \text{J}`
Show Worked Solution

a.   `text{Find Energy released:}`

`Delta m` `=(234.0409+4.0026)-238.0495=-0.006\ u`  
`Delta m` `=0.006 xx1.661 xx10^(-27)=9.966 xx10^(-30)\ \text{kg}`  

  
`\text{Using}\ \ E=mc^2:`

`E_text{released}=9.966 xx10^(-30)xx(3xx10^(8))^(2)=9.0 xx10^(-13)\ \text{J}`

   

b.   `\text{Find total energy:}`

`lambda=(ln 2)/(t_((1)/(2)))=(ln 2)/(87.7)=0.0079\ text{year}^(-1)`

`N=N_(0)e^(-lambda t)=9xx10^(24)xxe^(-0.0079 xx10)=8.316 xx10^(24)`

`Delta N=9xx10^(24)-8.316 xx10^(24)=6.84 xx10^(23)`

`E=6.84 xx10^(23)xx9.0 xx10^(-13)=6.2 xx10^(11)\ \text{J}`


♦ Mean mark part (b) 51%.

BIOLOGY, M5 2021 HSC 12 MC

The graph shows the levels of three hormones, oestrogen, progesterone and human chorionic gonadotrophin (HCG), measured in the blood of a woman during her pregnancy.
 

Which statement can be inferred from the graph?

  1. Birth occurred about week 36.
  2. Fertilisation occurred at day 0.
  3. Implantation occurred about week 4.
  4. The placenta was formed about week 24.
Show Answers Only

`C`

Show Worked Solution
  • HCG is released once the embryo has implanted.
  • Implantation occurs approximately 5-6 days after fertilisation which can take place when ovulation occurs, approximately 2 weeks after the menstrual cycle ends.

`=>C`

♦ Mean mark 49%.

CHEMISTRY, M5 2021 HSC 19 MC

A quantity of silver nitrate is added to 250.0 mL of 0.100 mol L ¯1 potassium sulfate at 298 K in order to produce a precipitate. Silver nitrate has a molar mass of 169.9 g mol ¯1.

What mass of silver nitrate will cause precipitation to start?

  1. 0.00510 g
  2. 0.186 g
  3. 0.465 g
  4. 0.854 g
Show Answers Only

`C`

Show Worked Solution

The reaction when silver nitrate is added to potassium sulfate is:

`text{2} text{Ag} text{NO}_(3) (aq) + text{K}_(2) text{SO}_(4) (aq) →  text{Ag}_(2) text{SO}_(4) (s) + text{2} text{K} text{NO}_(3) (aq)`
 

Since each `text{K}_(2) text{SO}_(4)` molecule has 1 sulfate ion

`[text{SO}_(4) ^(2-)] = text{K}_(2) text{SO}_(4) = 0.100\ text{mol L}^(-1)`
 

`text{Ag}_(2) text{SO}_(4) (s) ⇋ 2text{Ag}^(+) (aq) + text{SO}_(4) ^(\ 2-) (aq)`

`text{K}_(sp) = [text{Ag}^(+)]^2 [text{SO}_(4) ^(2-)]`
 

From the data sheet:

`text{K}_(sp) = text{1.20 x 10}^-5`

`text{1.20 x 10}^-5 = [text{Ag}^(+)]^2  xx  [text{SO}_(4) ^(\ 2-)]`

`text{1.20 x 10}^-5 = [text{Ag}^(+)]^2  xx  [text{0.100}]`

`[text{Ag}^(+)] = 0.01095…\ text{mol L}^(-1)`

`[text{Ag}^(+)] = [text{AgNO}_(3)]`
 

`text{n(AgNO}_(3)) = text{c}  xx text{V} = 0.01095… xx 0.250 = 0.00273…\ text{mol}`

`text{m(AgNO}_(3)) = text{n} xx text{MM} = 0.00273… xx 169.9 = 0.465\ text{g}`

`=> C`


♦ Mean mark 45%.

CHEMISTRY, M8 2021 HSC 18 MC

The table lists the information from a proton NMR spectrum.
 

Which compound could have produced this spectrum?

  1. `text{1,2,2-trichlorobutane}`
  2. `text{1,3-dichloro-2-methylpropane}`
  3. `text{2-chloro-2-methylbutane}`
  4. `text{2,2-dichlorobutane}`
Show Answers Only

`D`

Show Worked Solution

By elimination:

There are 8 hydrogen atoms in total (3 + 3 + 2 = 8)

  • Eliminate A and C

Compound has a 3H singlet

  • Eliminate B

`=> D`


♦♦ Mean mark 39%.

CHEMISTRY, M8 2021 HSC 17 MC

A sample was contaminated with sodium phosphate. The sample was dissolved in water and added to an excess of acidified \(\ce{(NH_4)_2MoO_4}\) to produce a precipitate of \(\ce{(NH_4)_3PO_4.12MoO_3\ \ \ \ \ \ ($MM$ = 1877 g mol^{-1})} \).

If 24.21 g of dry \(\ce{(NH_4)_3PO_4.12MoO_3}\) was obtained, what was the mass of sodium phosphate in the original sample?

  1. 1.225 g
  2. 1.521 g
  3. 1.818 g
  4. 2.115 g
Show Answers Only

`D`

Show Worked Solution

`text{n((NH4)}_3 text{PO}_4 cdot 12text{MoO}_3\text{)}= text{m} / text{MM}= 24.21/1877= 0.01289…\ text{moles}`

Each precipitate molecule has one molecule of `text{PO}_(4) ^ (\ 3-)`

Each `text{Na}_(3) text{PO}_(4)` molecule has one molecule of `text{PO}_(4) ^ (\ 3-)`

  • `text{n(Na}_3 text{PO}_4) =\ text{n((NH_4)}_3 text{PO}_4 cdot 12text{MoO}_3)` 
  • `text{n(Na}_3 text{PO}_4)` `=\ text{m} / text{MM}`
`text{m(Na}_3 text{PO}_4)` `=\ text{n × MM}`  
  `=0.01289… xx (3 xx 22.99 + 30.97 + 4 xx 16)`  
  `= 2.115\ text{g}`  

 
`=> D`


♦♦ Mean mark 36%.

CHEMISTRY, M6 2021 HSC 16 MC

This titration curve is produced when an acid is titrated with a sodium hydroxide solution of the same concentration.

How many acidic protons does this acid possess?

  1. 1
  2. 2
  3. 3
  4. 4
Show Answers Only

`B`

Show Worked Solution
  • From the graph there are 2 equivalence points (at ~ 10 mL and 20 mL), indicating that the acid is diprotic.
  • i.e. it contains 2 acidic protons.

`=> B`


♦ Mean mark 39%.

CHEMISTRY, M6 2021 HSC 15 MC

What is the pH of the resultant solution after 20.0 mL of 0.20 mol `text{L}^{-1}\ text{HCl} (aq)` is mixed with 20.0 mL of 0.50 mol `text{L}^{-1}\ text{NaOH} (aq)`?

  1. 11.8
  2. 13.2
  3. 13.5
  4. 14.0
Show Answers Only

`B`

Show Worked Solution

The reaction when  `text{HCl} (aq)` is mixed with `text{NaOH} (aq)` is:

   `text{HCl}(aq) + text{NaOH}(aq)`  ⟶ `text{NaCl} (aq) + text{H}_2 text{O} (aq)`

   `text{n(}text{HCl})=\ text{c × V}= 0.20 xx 0.020= 0.0040\ text{mol}`

   `text{n(} text{NaOH})=\ text{c × V}=0.50 xx 0.020= 0.010\ text{mol}`

  •  `text{HCl}` is the limiting reagent and `text{NaOH}` is the excess reagent.

`text{n(} text{NaOH) leftover} = 0.010-0.0040 = 0.0060\ text{mol}`

`text{c(} text{NaOH)}= (n(text{NaOH})) / text{V}= 0.0060/0.040=0.15\ text{mol L}^(-1)`

`text{NaOH} (aq)\ ⟶\ text{Na}^(+) + text{OH}^(-)`

Therefore,

`[text{NaOH}] = [text{OH}^(-)] = 0.15\ text{mol L}^(-1)`

`text{pOH} = -text{log}_(10) [text{OH}^(-1)] = -text{log}_(10) (0.15) = 0.8239`

`text{pH}=14- text{pOH}=14-0.8239= 13.2`

`=> B`


♦ Mean mark 54%.

CHEMISTRY, M8 2021 HSC 14 MC

A sample of nickel was dissolved in nitric acid to produce a solution with a volume of 50.00 mL. 10.00 mL of this solution was then diluted to 250.0 mL. This solution was subjected to colorimetric analysis. A calibration curve for this analysis is given.
 

The solution gave an absorbance value of 0.30.

What was the mass of the sample of nickel?

  1. 0.0021 g
  2. 0.031 g
  3. 0.053 g
  4. 0.15 g
Show Answers Only

`D`

Show Worked Solution

Absorbance  = 0.30

From the calibration curve, an absorbance of 0.30 corresponds to a \(\ce{[Ni2+]}\) of \(\pu{0.0021 mol L-1}\).

\( \ce{n[(Ni^2+)]} = \pu{0.0021 mol L-1} \)

\(\ce{n(Ni^2+)}\ \text{diluted}=\text{c × V}= 0.0021 \times 0.250= 0.000525\ \text{mol} \)

This is the moles of \(\ce{Ni^2+}\) in the diluted sample, which contained only 10.0 mL of the initial 50.0 mL of the original solution.

Thus, in order to find the number of moles in the original sample, multiply the number of moles by 5.

\(\ce{n(Ni^2+)}\ \text{undiluted} = \pu{5 \times 0.000525 = 0.002625 mol}\)

\(\ce{n(Ni^2+)}\) `= text{m} / text{MM}`  
\(\ce{m(Ni^2+)}\) `=\ text{n × MM}`  
  `= 0.002625 xx 58.69`  
  `= 0.15406125… `  
  `= 0.15\ text{g (2 d.p.)}`  

  
`=> D`


♦♦ Mean mark 38%.

CHEMISTRY, M8 2021 HSC 12 MC

The mass spectrum and carbon-13 NMR for an organic compound are shown.
 

 

Which compound could produce the two spectra?
 

 

Show Answers Only

`A`

Show Worked Solution
  • The mass spectrum indicates that the m/z peak is at 98, indicating that the molecular mass of the substance is approximately 98.
  • Additionally, the C-13 NMR spectrum shows 4 signals indicating that there are 4 unique carbon environments.
  • Thus, only A has a molecular mass of 98 and fits the 4 unique carbon environments.

`=> A`


♦♦ Mean mark 35%.

PHYSICS, M6 2020 HSC 28

A metal rod sits on a pair of parallel metal rails, 20 cm apart, that are connected by a copper wire. The rails are at 30° to the horizontal.

The apparatus is in a uniform magnetic field of 1 T which is upward, perpendicular to the table.
 

A force, `F`, is applied parallel to the rails to move the rod at a constant speed along the rails. The rod is moved a distance of 30 cm in 2.5 s.

  1. Show that the change in magnetic flux through the circuit while the rod is moving is approximately `5.2 × 10^(-2)` Wb.   (2 marks)
  1. Calculate the emf induced between the ends of the rod while it is moving, and state the direction of flow of the current in the circuit.   (2 marks)
  1. The experiment is repeated without the magnetic field.
  2. Explain why the force required to move the rod is different without the magnetic field.   (3 marks)
Show Answers Only

a.   `phi=5.2 xx10^(-2)\ \text{Wb}`

b.   `epsi=2.1 xx10^(-2)  \text{V}`

The direction of the induced current is anticlockwise as viewed from above.

c.    Repeating experiment is without the magnetic field:

  • When the magnetic field is present, the induced current results in a force acting on the rod which opposes its motion (Lenz’s Law).
  • Additionally, the force required to move the rod must also overcome the downwards gravitational force.
  • Without the magnetic field, there is no opposing force due to the induced current so the force applied only needs to overcome gravity.
  • Hence, the force required to move the rod is less without the magnetic field.
Show Worked Solution
a.
`phi` `=BA cos theta`
    `=1xx(0.3 xx0.2)xx cos 30^(@)`
    `=0.05196…`
    `~~5.2 xx10^(-2)` Wb

b.
`epsi` `=-N(Delta phi)/(t)`
    `=-1xx(5.2 xx10^(-2))/(2.5)`
    `=0.208…`
    `=2.1 xx10^(-2)\ \text{V  (V>0)`

 

  • The direction of the induced current is anticlockwise as viewed from above (Lenz’s Law).


♦ Mean mark (b) 51%.

c.    Repeating experiment is without the magnetic field:

  • When the magnetic field is present, the induced current results in a force acting on the rod which opposes its motion (Lenz’s Law).
  • Additionally, the force required to move the rod must also overcome the downwards gravitational force.
  • Without the magnetic field, there is no opposing force due to the induced current so the force applied only needs to overcome gravity.
  • Hence, the force required to move the rod is less without the magnetic field.

♦ Mean mark (c) 50%.

PHYSICS, M7 2020 HSC 27

The following apparatus is used to investigate light interference using a double slit.
 

The distance, `y`, from the slits to the screen can be varied. The adjustment screws `(S)` vary the distance, `d`, between the slits. The wavelength of the laser light can be varied across the visible spectrum. The diffraction pattern shown is for a specific wavelength of light.

Explain TWO methods of keeping the distance between the maxima at `A` and `B` constant when the wavelength of the laser light is reduced.   (4 marks)

Show Answers Only

Consider  `dsin theta=m lambda`:

  • Decreasing the wavelength of light decreases the angular separation of the maxima.

To keep the distance between `A` and `B` constant:

  • Decrease the slit separation`d` causing the angular separation to increase, compensating for the effect of decreasing `lambda`. 
  • Increase the distance `y` between the slits and the screen. This increases the linear distance between `A` and `B`, mitigating the effect of the reduction in `lambda`.
Show Worked Solution

Consider  `dsin theta=m lambda`:

  • Decreasing the wavelength of light decreases the angular separation of the maxima.

To keep the distance between `A` and `B` constant:

  • Decrease the slit separation`d` causing the angular separation to increase, compensating for the effect of decreasing `lambda`. 
  • Increase the distance `y` between the slits and the screen. This increases the linear distance between `A` and `B`, mitigating the effect of the reduction in `lambda`.


♦ Mean mark 46%.

PHYSICS, M7 2020 HSC 26

  1. Describe the difference between the spectra of the light produced by a gas discharge tube and by an incandescent lamp.   (2 marks)
  1. The graph shows the curves predicted by two different models, `X` and `Y`, for the electromagnetic radiation emitted by an object at a temperature of 5000 K.
     

    Identify an assumption of EACH model which determines the shape of its curve.   (2 marks)

  1. The diagram shows the radiation curve for a black body radiator at a temperature of 5000 K.
     


     
    On the same diagram, sketch a curve for a black body radiator at a temperature of 4000 K and explain the differences between the curves.   (4 marks)

Show Answers Only

a.   The spectra of light produced by a gas discharge tube will consist of lines only at a few discrete wavelengths.

The spectra of light produced by an incandescent lamp will be a continuous spectrum.

b.   Model `X` black bodies absorb and emit energy continuously.

Model `Y` assumes that black bodies absorb and emit energy in discrete quantities.

c.

  • Using `lambda_(max)=(b)/(T)\ \ =>\ \ lambda prop (1)/(T)`
  • Therefore, the 4000 K curve will have a peak wavelength greater than the 5000 K curve.
  • The area under the curve and the intensity at all wavelengths will be less for the 4000 K curve, as the total power output of a black body decreases as its temperature decreases.
Show Worked Solution

a.    Differences:

  • The spectra of light produced by a gas discharge tube will consist of lines only at a few discrete wavelengths.
  • The spectra of light produced by an incandescent lamp will be a continuous spectrum.

♦ Mean mark (a) 39%.

b.    Assumptions of EACH model:

  • Model `X` black bodies absorb and emit energy continuously.
  • Model `Y` assumes that black bodies absorb and emit energy in discrete quantities.

♦ Mean mark (b) 44%.

c.

  • Using `lambda_(max)=(b)/(T)\ \ =>\ \ lambda prop (1)/(T)`
  • Therefore, the 4000 K curve will have a peak wavelength greater than the 5000 K curve.
  • The area under the curve and the intensity at all wavelengths will be less for the 4000 K curve, as the total power output of a black body decreases as its temperature decreases.