Band 5 – Page 46

Vectors, EXT1 V1 SM-Bank 31

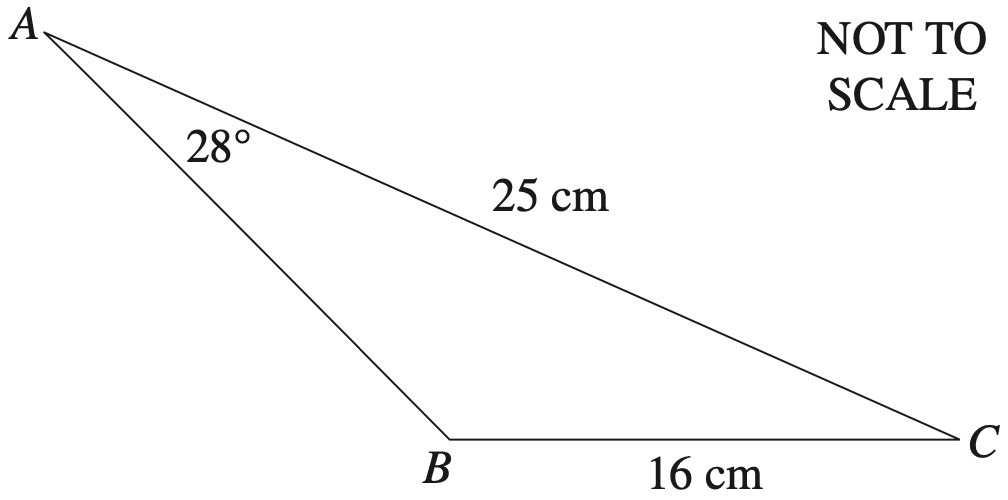
A drone is set to fly west at 38 km/h.

A cross wind diverts its path so that it travels with a speed of 45 km/h in the direction shown below.

Calculate the speed, to one decimal place, and the bearing of the cross wind, to the nearest degree. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{41.9 km/h on a bearing of 022°.}`

Show Worked Solution

`underset~u + underset~v`	`= (-45 sin 30 \ , \ 45 cos 30)`
	`= (-22.5 \ , \ {45 sqrt3}/{2})`

`underset~u = (-38 , 0) \ , \ underset~v = (x , y)`

`((-38),(0)) + ((x), (y))`	`= ((-22.5),({45 sqrt3}/{2}))`
`((x), (y))`	`= ((15.5),({45 sqrt3}/{2}))`

`\| underset~v\|`	`= sqrt{15.5^2 + {45^2 xx 3}/{4}}`
	`= 41.94…`
	`= 41.9 \ text{km/h}`

`tan theta`	`= {{45 sqrt3}/{2}}/{15.5} = 2.514`
`theta`	`= 68.3^@`

`:.\ text(The crosswind has a speed of 41.9 km/h on a bearing of 022°.)`

Mechanics, EXT2 M1 2021 HSC 16b

A particle which is projected from the origin with initial speed `u` ms^-1 at an angle of `theta` to the positive `x`-axis lands on the `x`-axis, as shown in the diagram. The particle is subject to an acceleration due to gravity of `g` ms^-1.

The position vector of the particle, `underset~r (t)`, where `t` is the time in seconds after the particle is projected, is given by

`underset~r (t) = ((ut cos theta),( - {g t^2}/{2} + u t sin theta))`. (Do NOT prove this.)

For some value(s) of `theta` there will be two times during the time of flight when the particle’s position vector is perpendicular to its velocity vector.

Find the value(s) of `theta` for which this occurs, justifying that both times occur during the time of flight. (5 marks)

Show Answers Only

`text{See Worked Solutions}`

Show Worked Solution

`underset~r (t) = ((ut cos theta),( – {g t^2}/{2} + u t sin theta)) , \ underset~v (t) = ((u cos theta),(-g t + u sin theta))`

♦♦ Mean mark 31%.

`text{If} \ \ underset~r (t) ⊥ underset~v (t) \ => \ underset~r (t) * underset~v (t) = 0`

`u t cos theta * u cos theta + (-{g t^2}/{2} + u t sin theta) (- g t + u sin theta)`	`= 0`
`u^2 t cos^2 theta + {g^2 t^3}/{2} – {g t^2}/{2} u sin theta – g t^2 u sin theta + u^2 t sin theta`	`= 0`
`u^2 t (cos^2 theta + sin^2 theta) + {g^2 t^3}/{2} – {3 u g t^2}/{2} sin theta`	`= 0`
`u^2 t + {g^2 t^3}/{2} – {3 u g t}/{2} sin theta`	`= 0`
`g^2 t^2 – 3 u g t sin theta + 2 u^2`	`= 0`

`text{If 2 roots} , \ Δ > 0 :`

`(-3 u g sin theta)^2 – 4 g^2 \ 2 u^2`	`> 0`
`9 u^2 g^2 sin^2 theta -8 g^2 u^2`	`> 0`
`u^2 g^2 (9 sin^2 theta – 8)`	`> 0`
`sin^2 theta`	`> 8/9`
`theta`	`> sin^-1 ({2 sqrt2}/{3})`

`text{S} text{ince} \ \ 0 < theta < pi/2 \ , text{only one value of} \ theta \ text{satisfies}`

`text{Checking valid times of flight}\ (t_f):`

`1/2 \ text{time of flight} \ => underset~j text{-component of} \ underset~v (t) = 0`

`1/2 g t_f`	`= u sin theta`
`t_f`	`= {2 u sin theta}/{g}`

`t`	`={3 u g sin theta ± sqrt{9 u^2 g^2 sin^2 theta – 4g^2 * 2 u ^2}}/{2 g^2}`
	`= 1/2 ({3 u sin theta}/{g} ± {u sqrt{9 sin^2 theta -8}}/{g})`
	`= {u}/{2g} (3 sin theta ± sqrt{9 sin^2 theta – 8})`

`text{S} text{ince} \ sqrt{9 sin^2 theta – 8} < sqrt{9 sin^2 theta} < 3 sin theta`

`=> \ text{in both solutions} \ \ t > 0`

`text{Consider the longer time:}`

`{u}/{2g} (3 sin theta + sqrt{9 sin^2 theta – 8})`

`< {u}/{2g} (3 sin theta + sqrt{9 sin^2 theta – 8 sin^2 theta})`

`< {u}/{2g} (3 sin theta + sin theta)`

`< {2 u sin theta}/{g}`

`:. \ text{Longer time < time of flight}`

`:. \ text{Both times occur during time of flight.}`

Vectors, EXT2 V1 2021 HSC 16a

The point `P(x, y, z)` lies on the sphere of radius 1 centred at the origin `O`.
Using the position vector of `P, overset->{OP} = x underset~i + y underset~j + z underset~k` , and the triangle inequality, or otherwise, show that `| x | + | y | + |z | ≥ 1`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Given the vectors `underset~a = ((a_1),(a_2),(a_3))` and `underset~b = ((b_1),(b_2),(b_3))` , show that
`|a_1 b_1 + a_2 b_2 + a_3 b_3 | ≤ sqrt{a_1^2 + a_2^2 + a_3^2 }\ sqrt{b_1^2 + b_2^2 + b_3^2}`. (3 marks)

--- 5 WORK AREA LINES (style=lined) ---
As in part (i), the point `P (x, y, z)` lies on the sphere of radius 1 centred at the origin `O`.
Using part (ii), or otherwise, show that `| x | + | y | + | z | ≤ sqrt3`. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{See Worked Solution}`
`text{See Worked Solution}`
`text{See Worked Solution}`

Show Worked Solution

i. `text{Triangle inequality:} \ |x| + |y| ≥ |x + y|`

♦ Mean mark (i) 50%.

`\|x\| + \|y\| + \|z\|`	` = \|x_underset~i\| + \|y_underset~j\| + \|z_underset~k\|`
	`≥ \|x_underset~i + y_underset~j\| + \|z_underset~k\|`
	`≥ \|x_underset~i + y_underset~j + z_underset~k\|`
	`≥ 1\ \ (\|overset->{OP}\| = \| x_underset~i + y_underset~j + z_underset~k \| = 1)`

ii. `text{Using the dot product:}`

♦ Mean mark (ii) 42%.

`underset~a * underset~b = a_1 b_1 + a_2 b_2 + a_3 b_3`

`underset~a * underset~b = |underset~a| |underset~b| cos theta`

`a_1 b_1 + a_2 b_2 + a_3 b_3`	`= sqrt{a_1^2 + a_2^2 + a_3^2} * sqrt{b_1^2 + b_2^2 + b_3^2} * cos theta`
`\|a_1 b_1 + a_2 b_2 + a_3 b_3\|`	`= sqrt{a_1^2 + a_2^2 + a_3^2} * sqrt{b_1^2 + b_2^2 + b_3^2} * \|cos theta\|`

`text{S} text{ince} \ -1 ≤ cos theta ≤ 1 \ => \ |cos theta| ≤ 1`

`:. \ | a_1 b_1 + a_2 b_2 + a_3 b_3 | ≤ sqrt{a_1^2 + a_2^3 + a_3^2} * sqrt{b_1^2 + b_2^2 + b_3^2}`

iii. `text{Using part (ii) with vectors:}`

♦♦♦ Mean mark (iii) 14%.

`underset~a = ((1),(1),(1)) \ , \ underset~b = (( | x| ),( |y| ),( |z| ))`

`\|\ \|x\| + \|y\| + \|z\|\ \|`	`≤ sqrt{1^2 + 1^2 + 1^2} * sqrt{ x^2 + y^2 + z^2}`
`\|x\| + \|y\| + \|z\|`	`≤ sqrt3`

Proof, EXT2 P1 2021 HSC 15d

Prove that `2^n + 3^n ≠ 5^n` for all integers `n ≥ 2`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{See Worked Solution}`

Show Worked Solution

`text(Expanding)\ \ (2 + 3)^n:`

Mean mark 51%.

`5^n`	`= (2 + 3)^n`
	`= 2^n +\ ^n C_1 2^{n-1} 3 + \ … \ + \ ^n C_{n-1} 2 3^{n-1} + 3^n`

`text{S} text{ince} \ \ ^n C_1 * 2^{n-1} *3 + \ … \ + \ ^n C_{n-1} * 2 * 3^{n-1} > 0 \ \ text{for} \ n ≥ 2`

`=> 5^n > 2^n + 3^n \ \ text{for} \ n ≥ 2`

`:. 5^n ≠ 2^n + 3^n \ \ text{for} \ n ≥ 2`

Proof, EXT2 P1 2021 HSC 15b

For integers `n ≥ 1`, the triangular numbers `t_n` are defined by `t_n = (n(n + 1))/2`, giving `t_1 = 1, t_2 = 3, t_3 = 6, t_4 = 10` and so on.

For integers `n >= 1`, the hexagonal numbers `h_n` are defined by `h_n = 2n^2-n`, giving `h_1 = 1, h_2 = 6, h_3 = 15, h_4 = 28` and so on.

Show that the triangular numbers `t_1, t_3 , t_5`, and so on, are also hexagonal numbers. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Show that the triangular numbers `t_2, t_4 , t_6`, and so on, are not hexagonal numbers. (1 mark)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solution)`
`text(See Worked Solution)`

Show Worked Solution

i. `t_n = (n(n + 1))/2`

♦ Mean mark part (i) 50%.

`text(Odd triangular numbers:)`

`→ \ text(Let)\ \ n = 2k-1\ \ text(for integers)\ \ k >= 1`

`t_(2k – 1)`	`= ((2k-1)(2k-1 + 1))/2`
	`= (2k(2k-1))/2`
	`= 2k^2-k\ \ text{(definition of hexagonal numbers)}`

`:. t_1, t_3\ …\ text(are also hexagonal numbers.)`

ii. `t_2, t_4, t_6, …`

♦ Mean mark part (ii) 1%!

`→\ text(Let)\ \ n = 2k\ \ text(for integers)\ \ k > = 1`

`t_(2k)`	`= (2k(2k + 1))/2`
	`= 2k^2 + k`

`text(Find values for)\ \ k, n\ \ text(that satisfy:)`

`2k^2 + k`	`= 2n^2 – n`
`2k^2-2n^2 + k + n`	`= 0`
`2(k-n)(k + n) + (k + n)`	`= 0`
`(k + n)(2k-2n + 1)`	`= 0`

`k = -n =>\ text(no solution)\ (k, n >= 1)`

`2k = 2n-1 =>\ text(no solution)\ \ (2k\ \ text(is even,)\ \ 2n-1\ \ text{is odd)}`

`:. t_2, t_4, t_6, …\ text(are not hexagonal numbers.)`

Proof, EXT2 P1 2021 HSC 15a

For all non-negative real numbers `x` and `y, \ sqrt(xy) <= (x + y)/2`. (Do NOT prove this.)

Using this fact, show that for all non-negative real numbers `a`, `b` and `c`,
`sqrt(abc) <= (a^2 + b^2 + 2c)/4`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Using part (i), or otherwise, show that for all non-negative real numbers `a`, `b` and `c`,
`sqrt(abc) <= (a^2 + b^2 + c^2 + a + b + c)/6`. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solution)`
`text(See Worked Solution)`

Show Worked Solution

i. `text(Show)\ \ sqrt(abc) <= (a^2 + b^2 + 2c)/4`

♦ Mean mark part (i) 50%.

`sqrt(abc) = sqrt((ab)c) <= (ab + c)/2\ …\ (1)`

`text(Let)\ \ x = a^2\ \ text(and)\ \ y = b^2:`

`sqrt(xy) = sqrt(a^2b^2) `	`<= (a^2 + b^2)/2`
`ab`	`<= (a^2 + b^2)/2\ …\ (2)`

`text{Substitute (2) into (1):}`

`sqrt(abc) <= ((a^2 + b^2)/2 + c)/2`

`sqrt(abc) <= (a^2 + b^2 + 2c)/4`

ii. `text(Show)\ sqrt(abc) <= (a^2 + b^2 + c^2 + a + b + c)/6`

♦♦♦ Mean mark part (ii) 26%.

`text{Similarly (to part a):}`

`text(If)\ \ x = b^2\ \ text(and)\ \ y = c^2`

`sqrt(abc) <= (b^2 + c^2 + 2a)/4`

`text(If)\ \ x = c^2\ \ text(and)\ \ y = a^2`

`sqrt(abc) <= (c^2 + a^2 + 2b)/4`

`:.3sqrt(abc)`	`<= (a^2 + b^2 + 2c + b^2 + c^2 + 2a + c^2 + a^2 + 2b)/4`
`3sqrt(abc)`	`<= (2(a^2 + b^2 + c^2 + a + b + c))/4`
`sqrt(abc)`	`<= (a^2 + b^2 + c^2 + a + b + c)/6`

Complex Numbers, EXT2 N2 2021 HSC 14c

Using de Moivre’s theorem and the binomial expansion of `(cos theta + i sin theta)^5`, or otherwise, show that
`cos5theta = 16cos^5theta - 20cos^3 theta + 5cos theta`. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---
By using part (i), or otherwise, show that `text(Re)(e^((ipi)/10)) = sqrt((5 + sqrt5)/8)`. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solution)`
`text(See Worked Solution)`

Show Worked Solution

i. `(cos theta + i sin theta)^5 = cos5theta + i sin 5theta\ \ text{(by De Moivre)}`

`text(Using binomial expansion:)`

`(cos theta + i sin theta)^5`

`= cos^5theta + 5cos^4theta · isin theta + 10cos^3theta · i^2sin^2theta + 10 cos^2theta · i^3sin^3theta`

`+ 5costheta · i^4sin^4theta + i^5sin^5theta`

`= cos^5theta – 10cos^3thetasin^2theta + 5costhetasin^4theta + i\ \ text{(imaginary part)}`

`text(Equating real parts:)`

`cos5theta`	`= cos^5theta – 10cos^3thetasin^2theta + 5costhetasin^4theta`
	`= cos^5theta – 10cos^3theta(1 – cos^2theta) + 5costheta(1 – cos^2theta)sin^2theta`
	`= cos^5theta – 10cos^3theta + 10cos^5theta + (5costheta – 5cos^3theta)(1 – cos^2theta)`
	`= 11cos^5theta – 10cos^3theta + 5costheta – 5cos^3theta – 5cos^3theta + 5cos^5theta`
	`= 16cos^5theta – 20cos^3theta + 5costheta`

ii. `text(Re)(e^((ipi)/10)) = cos\ pi/10`

♦♦ Mean mark 31%.

`text(Using part a:)`

`16 cos^5(pi/10) – 20cos^3(pi/10) + 5cos(pi/10) = cos((5pi)/10) = cos(pi/2) = 0`

`text(Solutions to)\ cos(5theta) = 0`

`5theta`	`= pi/2, (3pi)/2, (5pi)/2, …`
`theta`	`= pi/10, (3pi)/10, (5pi)/10, …`

`text(Let)\ cos(pi/10) = x`

`16x^5 – 20x^3 + 5x`	`= 0`
`16x^4 – 20x^2 + 5`	`= 0`

`x^2`	`= (20 ± sqrt(20^2 – 4 · 16 · 5))/(2 xx 16)`
	`= (20 ± sqrt80)/32`
	`= (5 ±sqrt5)/8`
`x`	`= ±sqrt((5 ± sqrt5)/8)`

`cos\ pi/10 > 0 \ => \ x = sqrt((5 ± sqrt5)/8)`

`1 > cos\ pi/10 > cos\ (3pi)/10 > 0`

`:.\ text(Re)\ (e^((ipi)/10)) = cos\ pi/10 = sqrt((5 + sqrt5)/8)`

Mechanics, EXT2 M1 2021 HSC 13d

An object is moving in simple harmonic motion along the `x`-axis. The acceleration of the object is given by `overset¨x = – 4 (x - 3)` where `x` is its displacement from the origin, measured in metres, after `t` seconds.

Initially, the object is 5.5 metres to the right of the origin and moving towards the origin. The object has a speed of 8 m s`\ ^(-1)` as it passes through the origin.

Between which two values of `x` is the particle oscillating? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find the first value of `t` for which `x = 0`, giving the answer correct to 2 decimal places. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`x = -2\ \ text(and)\ \ x = 8`
`0.58\ text(seconds)`

Show Worked Solution

i. `overset¨x = -4 (x – 3)`

♦ Mean mark 47%.

`d/(dx)(1/2 v^2)`	`= -4x + 12`
`1/2 v^2`	`= -2x^2 + 12x + c`

`v = 8\ \ text(when)\ \ x = 0:`

`1/2 xx 8^2 = c \ => \ c = 32`

`1/2 v^2 = -2x^2 + 12x + 32`

`text(Find)\ \ x\ \ text(when)\ \ v = 0:`

`-2x^2 + 12x + 32`	`= 0`
`x^2 – 6x – 16`	`= 0`
`(x – 8)(x + 2)`	`= 0`

`:.\ text(Particle oscillates between)\ \ x = -2\ \ text(and)\ \ x = 8`

ii. `overset¨x = -4 (x – 3) \ => \ n = 2`

♦♦ Mean mark 24%.

`text(Amplitude = 5, Centre of motion at)\ \ x = 3`

`x = 5 cos(2t + alpha) + 3`

`text(When)\ \ t = 0, x = 5.5:`

`5.5`	`= 5cos alpha + 3`
`cos alpha`	`= 1/2`
`alpha`	`= pi/3`

`:. x = 5 cos(2t + pi/3) + 3`

`text(Find)\ \ t\ \ text(when)\ \ x= 0:`

`cos(2t + pi/3)`	`= -3/5`
`2t + pi/3`	`= 2.214…`
`t`	`= 1/2(2.214… – pi/3)`
	`= 0.58\ text(seconds)\ \ text{(2 d.p.)}`

Complex Numbers, EXT2 N2 2021 HSC 13a

Indicate the locations of all of the fourth roots of the complex number `a + ib`. (2 marks)

Show Answers Only

Show Worked Solution

`4 \ text{roots:} \ z_1 , z_2 , z_3 , z_4`

♦ Mean mark 47%.

`text{arg}(z_1) = 1/4 text{arg}(a + ib)`

`|z| > 1 \ text{but less than} \ |a + ib|`

`text{Rotations between roots} = pi/2`

Vectors, EXT2 V1 2021 HSC 12e

The diagram shows the pyramid `ABCDS` where `ABCD` is a square. The diagonals of the square bisect each other at `H`.

Show that `overset->{HA} + overset->{HB} + overset->{HC} + overset->{HD} = underset~0` (1 mark)

--- 5 WORK AREA LINES (style=lined) ---

Let `G` be the point such that `overset->{GA} + overset->{GB} + overset->{GC} + overset->{GD} + overset->{GS} = underset~0`.

Using part (i), or otherwise, show that `4 overset->{GH} + overset->{GS} = underset~0`. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
Find the value of `λ` such that `overset->{HG} = λ overset->{HS}` (1 mark)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{See Worked Solution}`
`text{See Worked Solution}`
`1/5`

Show Worked Solution

i. `text{S} text{ince diagonal} \ overset->{AC} \ text{is bisected by H:}`

`overset->{HA} =- overset->{HC}`

`text{Similarly for diagonal} \ overset->{BD}`

`overset->{HB} = – overset->{HD}`

`:. \ overset->{HA} + overset->{HB} + overset->{HC} + overset->{HD}`	`= – overset->{HC} – overset->{HD} + overset->{HC} + overset->{HD}`
	`= underset~0`

ii. `overset->{GA} = overset->{GH} + overset->{HA} \ , \ overset->{GB} = overset->{GH} + overset->{HB}`

`overset->{GC} = overset->{GH} + overset->{HC} \ , \ overset->{GD} = overset->{GH} + overset->{HD}`

`overset->{GA} + overset->{GB} + overset->{GC} + overset->{GD} + overset->{GS}`

`= overset->{GH} + overset->{HA} + overset->{GH} + overset->{HB} + overset->{GH} + overset->{HC} + overset->{GH} + overset->{HD} + overset->{GS}`

`= 4 overset->{GH} + (overset->{HA} + overset->{HB} + overset->{HC} + overset->{HD} + overset->{GS})`

`= 4 overset->{GH} + overset->{GS}`

`overset->{GA} + overset->{GB} + overset->{GC} + overset->{GD} + overset->{GS} = underset~0\ \ \ text{(given)}`

`:. 4 overset->{GH} + overset->{GS} = underset~0`

iii. `overset->{HS} = overset->{HG} + overset->{GS}`

`overset->{GS} = overset->{HS} + overset->{GH}`

♦ Mean mark 48%.

`text{Using part (ii):}`

`4 overset->{GH} + overset->{HS} + overset->{GH}`	`= underset~0`
`5 overset->{GH}`	`= overset->{SH}`
`overset->{GH}`	`= 1/5 overset->{SH}`
`overset->{HG}`	`= 1/5 overset->{HS}`

`:. \ λ = 1/5`

Statistics, EXT1 S1 2021 HSC 14d

At a certain factory, the proportion of faulty items produced by a machine is `p = 3/500`, which is considered to be acceptable. To confirm that the machine is working to this standard, a sample of size `n` is taken and the sample proportion `overset^p` is calculated.

It is assumed that `overset^p` is approximately normally distributed with `mu = p` and `sigma^2 = (p(1 - p))/n`.

Production by this machine will be shut down if `overset^p >= 4/500`.

The sample size is to be chosen so that the chance of shutting down the machine unnecessarily is less than 2.5%.

Find the approximate sample size required, giving your answer to the nearest thousand. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`6000`

Show Worked Solution

`E(overset^p) = p = 3/500 = 0.006`

♦♦ Mean mark 27%.

`P(overset^p >= 4/500) < 2.5text(%)`

`=> P(overset^p >= 4/500) = P(ztext(-score) <= 2)`

`2 xx sigma`	`= 4/500 – E(overset^p)`
	`= 4/500 – 3/500`
	`= 1/500`
`sigma`	`= 1/1000`

`text(Using)\ \ sigma^2`	`= (p(1 – p))/n`
`0.001^2`	`= (0.006(0.994))/n`
`n`	`= (0.006(0.994))/(0.001^2)`
	`= 5964`
	`~~ 6000`

Calculus, EXT1 C3 2021 HSC 14b

In a certain country, the population of deer was estimated in 1980 to be 150 000.

The population growth is given by the logistic equation `(dP)/(dt) = 0.1P((C - P)/C)` where `t` is the number of years after 1980 and `C` is the carrying capacity.

In the year 2000, the population of deer was estimated to be 600 000.

Use the fact that `C/(P(C - P)) = 1/P + 1/(C - P)` to show that the carrying capacity is approximately 1 130 000. (4 marks)

Show Answers Only

`text(See Worked Solution)`

Show Worked Solution

`(dP)/(dt) = 0.1P((C – P)/C)`

♦ Mean mark 45%.

`(dt)/(dP)`	`= 10/P(C/(C – P))`
	`= 10 xx C/(P(C – P))`
	`= 10(1/P + 1/(C – P))`

`t`	`= 10 int 1/P + 1/(C – P)\ dP`
	`= 10[ln P – ln(C – P)] + c`
	`= 10 ln(P/(C – P)) + c`

`text(When)\ \ t= 0, P = 150\ 000:`

`0`	`= 10 ln((150\ 000)/(C – 150\ 000)) + c`
`c`	`= -10 ln((150\ 000)/(C – 150\ 000))`
	`= 10 ln((C – 150\ 000)/(150\ 000))`

`text(When)\ \ t = 20, P = 600\ 000:`

`20`	`= 10 ln((600\ 000)/(C – 600\ 000)) + 10 ln((C – 150\ 000)/(150\ 000))`
`2`	`= ln((600\ 000)/(C – 600\ 000) xx (C – 150\ 000)/(150\ 000))`
`2`	`= ln((4C – 600\ 000)/(C – 600\ 000))`
`e^2`	`= (4C – 600\ 000)/(C – 600\ 000)`

`e^2(C – 600\ 000)`	`= 4C – 600\ 000`
`e^2C – 4C`	`= e^2* 600\ 000 – 600\ 000`
`C(e^2 – 4)`	`= 600\ 000(e^2 – 1)`
`C`	`= (600\ 000(e^2 – 1))/(e^2 – 4)`
	`~~ 1\ 131\ 121`

`:.\ text(Carrying capacity)\ ~~1\ 130\ 000`

Proof, EXT2 P1 2021 HSC 9 MC

Four cards have either RED or BLACK on one side and either WIN or TRY AGAIN on the other side.

Sam places the four cards on the table as shown below.

A statement is made: ‘If a card is RED, then it has WIN written on the other side’.

Sam wants to check if the statement is true by turning over the minimum number of cards.

Which cards should Sam turn over?

1 and 4
3 and 4
1. 2 and 4
1, 3 and 4

Show Answers Only

`B`

Show Worked Solution

`text{L} text{ogically equivalent statements are:}`

`text{Red}`	`=> \ text{Win} \ …\ (1)`
`¬ \ text{Win}`	`=> \ ¬ \ text{Red} \ …\ (2)`

`text{To confirm statement is true}`

♦ Mean mark 48%.

`text{Card 1 – no need to turn}`

`text{Card 2 – no need to turn}`

`text{Card 3 – turn to confirm (2)}`

`text{Card 4 – turn to confirm (1)}`

`=> B`

Proof, EXT2 P1 2021 HSC 5 MC

Which of the following statements is FALSE?

`∀ a, b ∈ RR,` `a \ a^3 < b^3`
`∀ a, b ∈ RR,` `a e^{-a} > e^{-b}`
`∀ a, b ∈ (0, + ∞),` `a \ text{ln} \ a < text{ln} \ b`
`∀ a, b ∈ RR, text{with} \ a,b ≠ 0,` `a \ 1/a > 1/b`

Show Answers Only

`D`

Show Worked Solution

`text{By contradiction:}`

♦ Mean mark 50%.

`text{Consider} \ D`

`text{Let} \ \ a = -1 \ \ text{and} \ \ b = 1,`

`a \ -1 < 1 \ \ text{(TRUE)}`

`1/a > 1/b \ -> \ -1 > 1 \ \ text{(FALSE)}`

`=>\ D \ text{is false}`

Vectors, EXT1 V1 2021 HSC 14a

A plane needs to travel to a destination that is on a bearing of 063°. The engine is set to fly at a constant 175 km/h. However, there is a wind from the south with a constant speed of 42 km/h.

On what constant bearing, to the nearest degree, should the direction of the plane be set in order to reach the destination? (3 marks)

--- 9 WORK AREA LINES (style=lined) ---

Show Answers Only

$75^{\circ}$

Show Worked Solution

♦♦ Mean mark 31%.

$\text{Bearing = 063}^{\circ}\ \ \Rightarrow\ \ \angle ABC = 63^{\circ}\ \text{(alternate)}$

$\text{Using the sine rule:}$

$\dfrac{\sin \angle BAC}{42}$	$=\dfrac{\sin\,63^{\circ}}{175}$
$\sin \angle BAC$	$=\dfrac{42 \times \sin\,63^{\circ}}{175}$
	$=0.2138…$
$\angle BAC$	$=12.34…$
	$=12^{\circ}\ \text{(nearest degree)}$

$\therefore \text{Bearing to set plane on}\ = 63+12=75^{\circ}$

Trigonometry, EXT1 T2 2021 HSC 13d

The numbers `A`, `B` and `C` are related by the equations `A = B - d` and `C = B + d`, where `d` is a constant.
Show that `(sin A + sin C)/(cos A + cos C) = tan B`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Hence, or otherwise, solve `(sin\ (5theta)/7 + sin\ (6theta)/7)/(cos\ (5theta)/7 + cos\ (6theta)/7) = sqrt3` for `0 <= theta <= 2pi`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solution)`
`(14pi)/33, (56pi)/33`

Show Worked Solution

i.	`(sin A + sin C)/(cos A + cos C)`	`= (sin (B – d) + sin (B + d))/(cos (B – d) + cos (B + d))`
		`= (2sin B cos d)/(2cos B cosd)`
		`= (sin B)/(cos B)`
		`= tan B`
		`=\ text(RHS)`

ii. `text(Let)\ \ A = (5theta)/7,\ \ C = (6theta)/7`

♦ Mean mark 50%.

`B`	`= (A + C)/2`
	`= 1/2((5theta)/7 + (6theta)/7)`
	`= (11theta)/14`

`tan\ (11theta)/14`	`= sqrt3`
`(11theta)/14`	`= pi/3, (4pi)/3`
`:.theta`	`= (14pi)/33, (56pi)/33`

Calculus, EXT1 C1 2021 HSC 12b

A bottle of water, with temperature 5°C, is placed on a table in a room. The temperature of the room remains constant at 25°C. After `t` minutes, the temperature of the water, in degrees Celsius, is `T`.

The temperature of the water can be modelled using the differential equation

`(dT)/(dt) = k(T - 25)` (Do NOT prove this.)

where `k` is the growth constant

After 8 minutes, the temperature of the water is 10°C.

By solving the differential equation, find the value of `t` when the temperature of the water reaches 20°C. Give your answer to the nearest minute. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---
Sketch the graph of `T` as a function of `t`. (1 mark)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(39 minutes)`

Show Worked Solution

i.	`(dT)/(dt)`	`= k(T – 25)`
	`(dt)/(dT)`	`= 1/(k(T – 25))`
	`t`	`= 1/k int 1/(T – 25)\ dT`
	`kt`	`= ln \|T – 25\| + c`

`text(When)\ \ t = 0, T = 5 \ => \ c = -ln 20`

`kt`	`= ln \|T – 25\| – ln 20`
	`= ln \|(T – 25)/20\|`

`text(When)\ \ t = 8, T = 10`

`8k`	`= ln (15/20)`
	`= 1/8 ln(3/4)`

`text(Find)\ \ t\ \ text(when)\ \ T = 20:`

`1/8 ln (3/4)t`	`= ln \|(20 – 25)/20\|`
`t`	`= (8 ln(1/4))/(ln(3/4))`
	`= 38.55…`
	`= 39\ text{minutes (0 d.p.)}`

ii.

♦ Mean mark part (ii) 37%.

Combinatorics, EXT1 A1 2021 HSC 10 MC

The members of a club voted for a new president. There were 15 candidates for the position of president and 3543 members voted. Each member voted for one candidate only.

One candidate received more votes than anyone else and so became the new president.

What is the smallest number of votes the new president could have received?

Show Answers Only

`C`

Show Worked Solution

`text(Pigeonholes)\ (k) = 15`

♦♦ Mean mark 31%.

`text(Pigeons)\ (n) = 3543`

`n/k = 3543/15 = 236.2`

`text(By PHP, the minimum votes one candidate could receive = 237)`

`text(Smallest vote total for the candidate with the highest number)`

`text(of votes occurs when:)`

`text(- 12 candidates receive 236 votes and 3 candidates receive 237 votes)`

`:.\ text(The smallest number to elect a president is 238.)`

`=>\ C`

Functions, EXT1 F1 2021 HSC 8 MC

The diagram shows a semicircle.

Which pair of parametric equations represents the semicircle shown?

`{(x = 3 + sin t),(y = 2 + cos t):} \ \ \ \ \ text(for)\ \ -pi/2 <= t <= pi/2`
`{(x = 3 + cos t),(y = 2 + sin t):} \ \ \ \ \ text(for)\ \ -pi/2 <= t <= pi/2`
`{(x = 3 - sin t),(y = 2 - cos t):} \ \ \ \ \ text(for)\ \ -pi/2 <= t <= pi/2`
`{(x = 3 - cos t),(y = 2 - sin t):} \ \ \ \ \ text(for)\ \ -pi/2 <= t <= pi/2`

Show Answers Only

`C`

Show Worked Solution

`text(By elimination:)`

♦♦ Mean mark 31%.

`text(When)\ \ t = pi/2,`

`A(4, 2), \ B(3, 3), \ C(2, 2), \ D(3, 1)`

`->\ text(Eliminate B)`

`text(When)\ \ t = -pi/2,`

`A(2, 2), \ C(4, 2), \ D(3, 3)`

`->\ text(Eliminate D)`

`text(When)\ \ t = 0,`

`A(3, 3), \ C(3, 1)`

`->\ text(Eliminate A)`

`=>\ C`

Statistics, EXT1 S1 2021 HSC 6 MC

The random variable `X` represents the number of successes in 10 independent Bernoulli trials. The probability of success is `p = 0.9` in each trial.

Let `r = P(X ≥ 1)`.

Which of the following describes the value of `r`?

`r > 0.9`
`r = 0.9`
`0.1 < r < 0.9`
`r <= 0.1`

Show Answers Only

`A`

Show Worked Solution

`p = 0.9, \ \ barp = 0.1`

♦ Mean mark 50%.

`P(X >= 1)`	`= 1 – P(X = 0)`
	`= 1 – (0.1)^10`
	`= 0.999…`

`:. r > 0.9`

`=> A`

Measurement, STD1 M3 2021 HSC 28

A right-angled triangle `XYZ` is shown. The length of `XZ` is 16 cm and `angleYXZ = 30°`.

Find the side length, `XY`, of the triangle in centimetres, correct to two decimal places. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Hence, find the area of triangle `XYZ` in square centimetres, correct to one decimal place. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`13.86\ text(cm)`
`55.4\ text(cm)^2`

Show Worked Solution

♦♦ Mean mark part (a) 24%.

a.	`cos 30^@`	`=(XY)/16`
	`XY`	`=16 xx cos30^@`
		`=13.856…`
		`=13.86\ text(cm)\ \ text{(2 d.p.)}`

b. `text(Using the sine rule:)`

♦♦♦ Mean mark part (b) 14%.

	`text(Area)\ DeltaXYZ`	`= 1/2 ab sinC`
		`= 1/2 xx 16 xx 13.86 xx sin30^@`
		`=55.44`
		`=55.4\ text(cm)^2\ \ text{(1 d.p.)}`

Financial Maths, STD1 F3 2021 HSC 27

Tracy takes out a 30-year reducing balance loan of $680 000 to buy a house. Interest is charged at 0.25% per month. The loan is to be repaid in equal monthly instalments of $2866.91 over a term of 30 years.

Part of a spreadsheet used to model the reducing balance loan is shown.

Find the amount owing at the end of the second month. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Suppose that the interest rate reduces to 0.15% per month and the monthly instalments remain as $2866.91.
What will happen to the term of the loan? Explain your answer without using calculations. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`$677\ 663.26`
`text(Loan term will decrease.)`
`text(The repayment will pay down more of the principal each)`
`text(month, reducing the term of the loan.)`

Show Worked Solution

a. `text(In month 2:)`

♦♦ Mean mark part (a) 31%.

`text(Interest) = 678\ 833.09 xx 0.0025 = $1697.08`

`text(Repayment) = $2866.91`

`text(Balance owing)`	`= 678\ 833.09 + 1697.08 – 2866.91`
	`= $677\ 663.26`

b. `text(The term of the loan will decrease.)`

♦♦♦ Mean mark part (b) 18%.

`text(If interest rate reduces, the monthly interest amount)`

`text(payable decreases.)`

`text(The repayment will pay down more of the principal each)`

`text(month, reducing the term of the loan.)`

Measurement, STD1 M5 2021 HSC 26

The diagrams show two similar shapes. The dimensions of the small shape are enlarged by a scale factor of 1.5 to produce the large shape.

Calculate the area of the large shape. (3 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`279\ text(cm)^2`

Show Worked Solution

`text(Dimension of larger shape:)`

♦♦ Mean mark 32%.

`text(Width) = 16 xx 1.5 = 24\ text(cm)`

`text(Height) = 9 xx 1.5 = 13.5\ text(cm)`

`text(Triangle height) = 2.5 xx 1.5 = 3.75\ text(cm)`

`:.\ text(Area)`	`= 24 xx (13.5-3.75) + 1/2 xx 24 xx 3.75`
	`= 279\ text(cm)^2`

Algebra, STD1 A3 2021 HSC 25

The diagram shows a container which consists of a small cylinder on top of a larger
cylinder.

The container is filled with water at a constant rate to the top of the smaller cylinder. It takes 5 minutes to fill the larger cylinder.

Draw a possible graph of the water level in the container against time. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

♦ Mean mark 38%.

Measurement, STD1 M5 2021 HSC 24

A building plan of part of a house is shown.

What is the internal length and the internal width of the main bedroom? Give your answer in metres. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Rod wants to lay carpet in the main bedroom. The main bedroom has a wardrobe with a base area of 1.6 m². The area under the wardrobe does NOT need to be carpeted.
Carpet costs $40 per square metre. Rod buys the smallest whole number of square metres of carpet necessary. Find the cost of the carpet purchased for the bedroom. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`3.6\ text(metres)`
`$680`

Show Worked Solution

a. `text(Internal length = 5000 mm = 5 metres)`

♦ Mean mark part (a) 46%.

`text(Internal width = 3600 mm = 3.6 metres)`

♦♦ Mean mark part (b) 30%.

b.	`text(Carpet area)`	`= (5 xx 3.6) – 1.6`
		`= 16.4\ text(m²)`
		`= 17\ text{m² (round up)}`

`text(C)text(ost of carpet)`	`= 17 xx 40`
	`= $680`

Measurement, STD1 M4 2021 HSC 23

Sue walks along a trail, starting at 7 am and finishing at 10 am. The travel graph shows Sue’s journey from the start to the finish. The journey has been broken into six sections, `A`, `B`, `C`, `D`, `E` and `F`.

On two occasions Sue stopped to rest. In which sections of the journey did Sue rest? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
In which section of the journey did Sue travel fastest? Justify your answer. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Kim walked along the same trail, also starting at 7 am and finishing at 10 am. Kim walked at a constant speed for the entire journey.
By showing Kim’s journey on the grid above, determine between what times Sue was ahead of Kim. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`B\ text(and)\ E`
`text(S)text(ection)\ C.\ text(Slope is the steepest.)`
`text(8:30 am – 9:15 am)`

Show Worked Solution

a. `B\ text(and)\ E`

♦ Mean mark part (b) 44%.

b. `text(Fastest travel occurs when the slope is the steepest.)`

♦♦ Mean mark part (c) 30%.

`:. text(S)text(ection)\ C`

`text(Sue was ahead when her graph is higher than Kim’s.)`

`:.\ text(She was ahead between 8:30 am – 9:15 am)`

Measurement, STD1 M4 2021 HSC 22

A tap is leaking water. It leaks 1 drop every 4 seconds, and 15 of these drops make up 1 mL.

Find the amount of water leaked in a 24-hour period. Give the answer in litres. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
A bucket can hold 9 litres of water. How long will it take for the leaking tap to completely fill this empty bucket? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`1.44\ text(L)`
`6.25\ text(days)`

Show Worked Solution

a. `text(Drops per minute) = 60/4 = 15`

♦ Mean mark part (a) 50%.

`text(Volume per minute = 1 mL)`

`:.\ text(Volume in 24 hours)`	`= 1 xx 60 xx 24`
	`= 1440\ text(mL)`
	`= 1.44\ text(L)`

♦♦ Mean mark part (b) 32%.

b.	`text(Time to fill bucket)`	`= 9/1.44`
		`= 6.25\ text(days)`

Statistics, STD1 S3 2021 HSC 18

People are placed into groups to complete a puzzle. There are 9 different groups.

The table shows the number of people in each group and the amount of time, in minutes, for each group to complete the puzzle.

\begin{array} {|l|c|c|c|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} \textit{Number of people} \rule[-1ex]{0pt}{0pt} & 2 & 2 & 3 & 5 & 5 & 7 & 7 & 7 & 8 \\
\hline
\rule{0pt}{2.5ex} \textit{Time taken (min)} \rule[-1ex]{0pt}{0pt} & 28 & 30 & 26 & 19 & 21 & 12 & 13 & 11 & 8 \\
\hline
\end{array}

Complete the scatterplot by adding the last four points from the table. (2 marks)
Add a line of best fit by eye to the graph in part (a). (1 mark)
The graph in part (a) shows the association between the time to complete the puzzle and the number of people in the group.
Identify the form (linear or non-linear), the direction and the strength of the association. (3 marks)

--- 3 WORK AREA LINES (style=lined) ---
Calculate the mean of the time taken to complete the puzzle for the three groups of size 7 observed in the dataset. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(The association is linear, negative and strong.)`
`12\ text(minutes)`

Show Worked Solution

c. `text(Form: linear)`

♦ Mean mark (c) 50%.

`text{Direction: negative}`

`text{Strength: strong}`

d.	`text{Mean time (7 people)}`	`= (12 + 13 + 11)/3`
		`= 12\ text(minutes)`

Algebra, STD1 A1 2021 HSC 16

Make `r` the subject of the formula `P = 2r + 10`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`r = (P – 10)/2`

Show Worked Solution

♦♦ Mean mark 29%.

`P`	`= 2r + 10`
`2r`	`= P – 10`
`r`	`= (P – 10)/2`

Measurement, STD1 M2 2021 HSC 15

City A is in Sweden and is located at (58°N, 16°E). Sydney, in Australia, is located at (33°S, 151°E).

Robert lives in Sydney and needs to give an online presentation to his colleagues in City A starting at 5:00 pm Thursday, local time in Sweden.

What time and day, in Sydney, should Robert start his presentation?

It is given that 15° = 1 hour time difference. Ignore daylight saving. (3 marks)

Show Answers Only

`text(2 am Friday)`

Show Worked Solution

`text{Angular difference}\ = 151 – 16 = 135°`

♦♦ Mean mark 25%.

`=>\ text{Time difference}\ = 135/15 = 9\ text(hours)`

`text(Sydney is east of Sweden → ahead)`

`text{Presentation time (Sydney)}`	`=\ text(5 pm Thurs + 9 hours)`
	`=\ text(2 am Friday)`

Calculus, 2ADV C4 2021 HSC 28

The region bounded by the graph of the function `f(x) = 8 - 2^x` and the coordinate axes is shown

Show that the exact area of the shaded region is given by `24 - 7/ln2`. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
A new function `g(x)` is found by taking the graph of `y = -f(-x)` and translating it by 5 units to the right.
Sketch the graph of `y = g(x)` showing the `x`-intercept and the asymptote. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
Hence, find the exact value of `int_2^5 g(x)\ dx`. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solution)`
`7/(ln2) – 24`

Show Worked Solution

a. `xtext(-intercept occurs when)`

`8 – 2^x = 0 \ => \ x = 3`

`text(Area)`	`= int_0^3 8 – 2^x\ dx`
	`= [8x – (2^x)/(ln2)]_0^3`
	`= 24 – 8/(ln 2) – (0 – 1/(ln2))`
	`= 24 – 8/(ln2) + 1/(ln2)`
	`= 24 – 7/(ln2)\ \ text(u²)`

♦ Mean mark part (b) 48%.

`y = f(–x) -> text(reflect)\ \ y = f(x)\ \ text(in the)\ ytext(-axis)`

`y = -f(–x) -> text(reflect)\ \ y = f(–x)\ \ text(in the)\ xtext(-axis)`

♦♦♦ Mean mark part (c) 13%.

c. `int_2^5 g(x)\ dx\ \ text{is the same area as found in part (a)}`

`text(except it is below the)\ xtext(-axis.)`

`:. int_2^5 g(x)\ dx = 7/(ln2) – 24`

Algebra, STD1 A2 2021 HSC 5 MC

Which of the following best represents the graph of `y = -3x + 4`?

A.		B.
C.		D.

Show Answers Only

`A`

Show Worked Solution

`y = -3x + 4`

♦♦♦ Mean mark 16%.

`ytext(-intercept) = 4`

`text(Gradient is negative → slopes from)`

`text(upper left to lower right)`

`=> A`

Statistics, STD1 S1 2021 HSC 2 MC

A survey of which of the following would provide data that are both categorical and
nominal?

Hair colour
Height in centimetres
Number of people present at a concert
Size of coffee cup classified as small, medium or large

Show Answers Only

`A`

Show Worked Solution

`text(By elimination:)`

♦♦ Mean mark 25%.

`text{Qualitative (not quantitative)}`

`text{→ Eliminate B and C}`

`text(Nominal data is not ordered)`

`text{→ Eliminate D}`

`=> A`

Calculus, 2ADV C4 2021 HSC 27

Kenzo has a solar powered phone charger. Its power, `P`, can be modelled by the function

`P(t) = 400 sin(pi/12 t),\ \ 0 <= t <= 12`,

where `t` is the number of hours after sunrise.

Sketch the graph of `P` for `0 ≤ t ≤ 12`. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---

Power is the rate of change of energy. Hence the amount of energy, `E` units, generated by the solar powered phone charger from `t = a` to `t = b`, where `0 ≤ a ≤ b ≤ 12` is given by

`E = int_a^b P(t)\ dt`.

Show that `E = 4800/pi (cos\ (api)/12 - cos\ (bpi)/12)`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
To make a phone call, a phone battery needs at least 300 units of energy. Kenzo woke up 3 hours after sunrise and found that his phone battery had no units of energy. He immediately began to use his solar powered charger to charge his phone battery.
Find the least amount of time he needed to wait before he could make a phone call. Give your answer correct to the nearest minute. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
The next day, Kenzo woke up 6 hours after sunrise and again found that his phone battery had no units of energy. He immediately began to use his solar powered charger to charge his phone battery.
Would it take more time or less time or the same amount of time, compared to the answer in part (c), to charge his phone battery in order to make a phone call? Explain your answer by referring to the graph drawn in part (a). (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solution)`
`text(57 minutes)`
`text(The power produced is at its peak when)\ t = 6`
`:.\ text(It will charge in less time.)`

Show Worked Solution

b.	`E`	`= int_a^b 400 sin(pi/12 t)\ dt`
		`= [-400 · 12/pi cos(pi/12 t)]_a^b`
		`= -4800/pi cos(pi/12 b) – (-4800/pi cos(pi/12 a))`
		`= 4800/pi(cos\ (api)/12 – cos\ (bpi)/12)`

♦♦ Mean mark part (c) 29%
COMMENT: It is arguable that the nearest minute may also be 3h 58 m as the phone is not adequately charged at 3h 57 m.

c. `text(Find)\ \ b\ \ text(given)\ \ E = 300\ \ text(and)\ \ a = 3:`

`300`	`= 4800/pi (cos\ pi/4 – cos\ (bpi)/12)`
`(300pi)/4800`	`= 1/sqrt2 – cos\ (bpi)/12`
`cos\ (bpi)/12`	`= 1/sqrt2 – pi/16`
`(bpi)/12`	`= cos^(-1) (1/sqrt2 – pi/16)`
`b`	`= 12/pi cos^(-1)(1/sqrt2 – pi/16)`
	`= 3.952…`
	`= 3\ text{h 57 m (nearest minute)}`

`:.\ text(Least time before phone is charged = 57 minutes)`

♦♦ Mean mark part (d) 22%

d. `text(The power produced is at its peak when)\ \ t = 6.`

`:.\ text(It will charge in less time.)`

Functions, 2ADV F2 2021 HSC 21

Consider the graph of `y = f(x)` as shown.

Sketch the graph of `y = 4f(2x)` showing the `x`-intercepts and the coordinates of the turning points. (2 marks)

Show Answers Only

Show Worked Solution

♦ Mean mark 48%.

Statistics, 2ADV S3 2021 HSC 33

People are given a maximum of six hours to complete a puzzle. The time spent on the puzzle, in hours, can be modelled using the continuous random variable $X$ which has probability density function

$f(x)= \begin{cases}
\dfrac{A x}{x^2+4} & \text{for } 0 \leq x \leq 6,(\text { where } A>0) \\
\ \\
0 & \text {for all other values of } x
\end{cases}$

The graph of the probability density function is shown below. The graph has a local maximum.

Show that $A=\dfrac{2}{\ln 10}$. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Show that the mode of $X$ is two hours. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Show that $P(X<2)=\log _{10} 2$. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
The Intelligence Quotient (IQ) scores of people are normally distributed with a mean of 100 and standard deviation of 15.
It has been observed that the puzzle is generally completed more quickly by people with a high IQ.
It is known that 80% of people with an IQ greater than 130 can complete the puzzle in less than two hours.
A person chosen at random can complete the puzzle in less than two hours.
What is the probability that this person has an IQ greater than 130? Give your answer correct to three decimal places. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{See Worked Solution}$
$\text{See Worked Solution}$
$\text{See Worked Solution}$
$0.066$

Show Worked Solution

a. $\displaystyle\int_0^6 \dfrac{A x}{x^2+4} \, d x=1$

$\begin{aligned} \dfrac{A}{2} \int_0^6 \dfrac{2 x}{x^2+4} d x & =1 \\
\dfrac{A}{2}\left[\ln \left(x^2+4\right)\right]_0^6 & =1 \\
\dfrac{A}{2}(\ln 40-\ln 4) & =1 \\
\dfrac{A}{2} \ln \left(\dfrac{40}{4}\right) & =1 \\
\dfrac{A}{2} \ln 10 & =1 \\
A & =\dfrac{2}{\ln 10}\end{aligned}$

b. $\text{Mode \(\rightarrow f(x)$ is a MAX}\)

♦♦♦ Mean mark part (b) 24%.

$\begin{aligned}
f(x) & =\dfrac{A x}{x^2+4} \\
f^{\prime}(x) & =\dfrac{A\left(x^2+4\right)-A x(2 x)}{\left(x^2+4\right)^2} \\
& =\dfrac{A x^2+4 A-2 A x^2}{\left(x^2+4\right)^2} \\
& =\dfrac{A\left(4-x^2\right)}{\left(x^2+4\right)^2}
\end{aligned}$

$\text{\(f(x)$ max occurs when $f^{\prime}(x)=0$ :}\)

$\begin{aligned}
4-x^2 & =0 \\
x & =2 \quad(x>0)
\end{aligned}$

♦♦ Mean mark part (c) 30%.

c.	$P(X<2)$	$=\displaystyle \int_0^2 \dfrac{A x}{x^2+4} d x$
		$=\dfrac{A}{2}\left[\ln \left(x^2+4\right)\right]_0^2$
		$=\dfrac{1}{\ln 10}(\ln 8-\ln 4)$
		$=\dfrac{1}{\ln 10}\left(\ln \dfrac{8}{4}\right)$
		$=\dfrac{1}{\ln 10} \cdot \ln 2$
		$=\log _{10} 2$

d. $z \text{-score}(130)=\dfrac{x-\mu}{\sigma}=\dfrac{130-100}{15}=2$

♦♦ Mean mark part (d) 25%.

$P(z>2)=2.5 \%$

\begin{aligned}
P(\text { IQ }>130 \mid x<2) & =\dfrac{P(\text { IQ }>130 \cap X<2)}{P(X<2)} \\
& =\dfrac{0.8 \times 0.025}{\log _{10} 2} \\
& =0.0664 \ldots \\
& =0.066
\end{aligned}

Statistics, 2ADV S3 2021 HSC 32

In a particular city, the heights of adult females and the heights of adult males are each normally distributed.

Information relating to two females from that city is given in Table 1.

The means and standard deviations of adult females and males, in centimetres, are given in Table 2.

A selected male is taller than 84% of the population of adult males in this city.

By first labelling the normal distribution curve below with the heights of the two females given in Table 1, calculate the height of the selected male, in centimetres, correct to two decimal places. (4 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`178.95 \ text{cm}`

Show Worked Solution

`z text{-score (175 cm, female)} = 2`

♦ Mean mark 41%.

`z text{-score (160.6 cm, female)} = -1`

`text{Find} \ mu \ text{of female heights:}`

`mu – sigma`	`= 160.6`
`mu + 2sigma`	`= 175`
`3 sigma`	`= 175 – 160.6`
`sigma`	`= 14.4/3`
	`= 4.8 \ text{cm}`
`:. \ mu`	`= 165.4 \ text{cm}`

`text{Selected male’s height has} \ z text{-score} = 1`

`mu text{(male)} = 1.05 times 165.4 = 173.67`

`sigma \ text{(male)} = 1.1 times 4.8 = 5.28`

`:. \ text{Actual male height}`	`= 173.67 + 5.28`
	`= 178.95 \ text{cm}`

Measurement, STD2 M6 2021 HSC 39

The diagram shows a compass radial survey of the field `ABCD`.

Triangle `COB` has an area of 466 m².
Find the size of acute angle `COB`, correct to the nearest degree. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
A farmer wants to put a fence around the triangle `DOC`.
Find the length of fencing required. Give your answer in metres correct to one decimal place. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`72^@ \ text{(nearest degree)}`
`106.8 \ text{m (1 d.p.)}`

Show Worked Solution

a. `text{Using sine rule:}`

♦ Mean mark part (a) 34%.

`text{Area}`	`= 1/2 ab sinC`
`466`	`= 1/2 xx 28 xx 35 xx sin∠ COB`
`sin ∠COB`	`= 466/490`
`∠COB`	`= sin^{-1} (466/490)`
	`= 71.99`
	`= 72^@ \ text{(nearest degree)}`

♦♦ Mean mark part (b) 33%.

`∠DOC`	`= 360 – (30 + 80 + 70 + 72)`
	`= 108^@`

`text{Using the cosine rule:}`

`DC^2`	`=31^2 + 28^2 – 2 xx 31 xx 28 xx cos 108^@`
	`= 2281.4535`
`DC`	`= 47.76 … \ text{m}`

`:. \ text{Length of fence}`	`= 47.8 + 31 + 28`
	`= 106.8 \ text{m (1 d.p.)}`

Networks, STD2 N3 2021 HSC 36

A project requires completion of 11 tasks `A, B, C, . . . , K.`

A network diagram for the project giving the completion time for each task, in minutes, is shown.

Find the minimum time to complete the project. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
State the critical path for this project. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
A new task, `X`, is to be added to the project. The earliest starting time for `X` is 17 minutes, the latest starting time for `X` is 18 minutes and `X` has a completion time of 12 minutes.
Add task `X` to the given network diagram above AND state the float time for this task. (3 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`40 \ text{minutes}`
`A – C – D – E – G – J – K`
`text{Float time = 1minute}`

Show Worked Solution

a. `text{Scanning forwards:}`

♦ Mean mark part (a) 37%.

`text{Minimum completion time} = 40 \ text{minutes}`

♦ Mean mark part (b) 44%.

b. `text{Critical Path:} \ A C D E G J K`

♦♦ Mean mark part (c) 32%.

`text{Float time}\ (X)`	`= 18 – 17`
	`= 1 \ text{minute}`

Calculus, 2ADV C3 2021 HSC 31

By considering the equation of the tangent to `y = x^2 - 1` at the point `(a, a^2 - 1)`, find the equations of the two tangents to `y = x^2 - 1` which pass through `(3, –8)`. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`y = 14x – 50`

`y = -2x – 2`

Show Worked Solution

`y = x^2 – 1`

♦♦ Mean mark 36%.

`(dy)/(dx) = 2x`

`text(At)\ \ x = a, (dy)/(dx) = 2a`

`text(Find equation of line)\ \ m = 2a, text(through)\ (a, a^2 – 1):`

`y – (a^2 – 1)`	`= 2a(x – a)`
`y – a^2 + 1`	`= 2ax – 2a^2`
`y`	`= 2ax – a^2 – 1`

`text(If tangent passes through)\ (3, –8):`

`2a(3) – a^2 – 1`	`= -8`
`6a – a^2 + 7`	`= 0`
`a^2 – 6a – 7`	`= 0`
`(a – 7)(a + 1)`	`= 0`

`=> a = 7\ \ text(or)\ \ -1`

`:.\ text(Equation of tangents:)`

`y = 14x – 50`

`y = -2x – 2`

Statistics, STD2 S4 2021 HSC 33

For a sample of 17 inland towns in Australia, the height above sea level, `x` (metres), and the average maximum daily temperature, `y` (°C), were recorded.

The graph shows the data as well as a regression line.

The equation of the regression line is `y = 29.2 − 0.011x`.

The correlation coefficient is `r = –0.494`.

i. By using the equation of the regression line, predict the average maximum daily temperature, in degrees Celsius, for a town that is 540 m above sea level. Give your answer correct to one decimal place. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
ii. The gradient of the regression line is −0.011. Interpret the value of this gradient in the given context. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The graph below shows the relationship between the latitude, `x` (degrees south), and the average maximum daily temperature, `y` (°C), for the same 17 towns, as well as a regression line.

The equation of the regression line is `y = 45.6 − 0.683x`.
The correlation coefficient is `r = − 0.897`.
Another inland town in Australia is 540 m above sea level. Its latitude is 28 degrees south.
Which measurement, height above sea level or latitude, would be better to use to predict this town’s average maximum daily temperature? Give a reason for your answer. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

i. `23.3°text(C)`
ii. `text(See Worked Solutions)`
`text(Latitude. Correlation coefficient shows a stronger relationship.)`

Show Worked Solution

a.i.	`y`	`=29.2 – 0.011(540)`
		`=23.26`
		`=23.3°text{C (1 d.p.)`

♦♦ Mean mark part a.ii. 28%.

a.ii. `text(On average, the average maximum daily temperature of)`

`text(inland towns drops by 0.011 of a degree for every metre)`

`text(above sea level the town is situated.)`

♦♦♦ Mean mark part b 18%.

b. `text(The correlation co-efficient of the regression line using)`

`text(latitude is significantly stronger than the equivalent)`

`text(co-efficient for the regression line using height above sea)`

`text(level.)`

`:.\ text(The equation using latitude is preferred.)`

Statistics, 2ADV S3 2021 HSC 30

The number of hours for which light bulbs will work before failing can be modelled by the random variable `X` with cumulative distribution function

`F(x) = { {:(1 - e^(-0.01x)),(0):} {: (\ \ x >= 0), (\ \ x < 0):} :}`

Jane sells light bulbs and promises that they will work for longer than exactly 99% of all light bulbs.

Find how long, according to Jane’s promise, a light bulb bought from her should work. Give your answer in hours, rounded to two decimal places. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(460.52 hours.)`

Show Worked Solution

`text(Find)\ x\ text(when)\ \ F(x) > 0.99:`

♦♦ Mean mark 22%.

`1 – e^(-0.01x)`	`= 0.99`
`e^(-0.01x)`	`= 0.01`
`-0.01x`	`= ln(0.01)`
`x`	`= (ln(0.01))/(-0.01)`
	`= 460.517 …`
	`= 460.52\ text(hours)`

`:.\ text(Light bulbs should work at least 460.52 hours.)`

Financial Maths, 2ADV M1 2021 HSC 29

On the day that Megan was born, her grandfather deposited $5000 into an account earning 3% per annum compounded annually. On each birthday after this, her grandfather deposited $1000 into the same account, making his final deposit on Megan’s 17th birthday. That is, a total of 18 deposits were made.
Let `A_n` be the amount in the account on Megan’s `n`th birthday, after the deposit is made.
Show that `A_3 = $8554.54`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
On her 17th birthday, just after the final deposit is made, Megan has $30 025.83 in her account. You are NOT required to show this.
Megan then decides to leave all the money in the same account continuing to earn interest at 3% per annum compounded annually. On her 18th birthday, and on each birthday after this, Megan withdraws $2000 from the account.
How many withdrawals of $2000 will Megan be able to make? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solution)`
`20`

Show Worked Solution

a. `A_1 = 5000(1.03) + 1000`

`A_2`	`= [5000(1.03) + 1000](1.03) + 1000`
	`= 5000(1.03)^2 + 1000(1.03) + 1000`

`A_3`	`= 5000(1.03)^3 + 1000(1.03)^2 + 1000(1.03) + 1000`
	`= 8554.535`
	`= $8554.54`

b. `text(Megan’s 18th birthday onwards:)`

`A_1 = 30\ 025.83(1.03) – 2000`

`A_2`	`= [30\ 025.83(1.03) – 2000](1.03) – 2000`
	`= 30\ 025.83(1.03)^2 – 2000(1.03) – 2000`
	`vdots`
`A_n`	`= 30\ 025.83(1.03)^n – 2000(1 + 1.03 + 1.03^2 + … + 1.03^(n – 1))`

`text(Find)\ n\ text(when)\ \ A_n = 0:`

`30\ 025.83(1.03)^n`	`= 2000[(a(r^n – 1))/(r – 1)]`
	`= 2000((1.03^n – 1)/(1.03 – 1))`

`30\ 025.83(1.03)^n`	`= 66\ 666.67(1.03)^n – 66\ 666.67`
`36\ 640.84(1.03)^n`	`= 66\ 666.67`
`1.03^n`	`= (66\ 666.67)/(36\ 640.84)`
`n ln 1.03`	`= ln ((66\ 666.67)/(36\ 640.84))`
`n`	`= (ln ((66\ 666.67)/(36\ 640.84)))/(ln 1.03)`
	`= 20.24…`

`:.\ text(Megan can make 20 withdrawals of $2000.)`

Measurement, STD2 M6 2021 HSC 32

A right-angled triangle `XYZ` is cut out from a semicircle with centre `O`. The length of the diameter `XZ` is 16 cm and `angle YXZ` = 30°, as shown on the diagram.

Find the length of `XY` in centimetres, correct to two decimal places. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Hence, find the area of the shaded region in square centimetres, correct to one decimal place. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`13.86 \ text{cm}`
`45.1 \ text{cm}^2`

Show Worked Solution

a.	`cos 30^@`	`=(XY)/16`
	`XY`	`= 16 \ cos 30^@`
		`= 13.8564`
		`= 13.86 \ text{cm (2 d.p.)}`

b.	`text{Area of semi-circle}`	`= 1/2 times pi r^2`
		`= 1/2 pi times 8^2`
		`= 100.531 \ text{cm}^2`

♦ Mean mark part (b) 36%.

`text{Area of} \ Δ XYZ`	`= 1/2 ab\ sin C`
	`= 1/2 xx 16 xx 13.856 xx sin 30^@`
	`= 55.42 \ text{cm}^2`

`:. \ text{Shaded Area}`	`= 100.531-55.42`
	`= 45.111`
	`= 45.1 \ text{cm}^2 \ \ text{(1 d.p.)}`

Financial Maths, STD2 F5 2021 HSC 31

Present value interest factors for an annuity of $1 for various interest rates (`r`) and numbers of periods (`N`) are given in the table.

A bank lends Martina $500 000 to purchase a home, with interest charged at 1.5% per annum compounding monthly. She agrees to repay the loan by making equal monthly repayments over a 30-year period.

How much should the monthly payment be in order to pay off the loan in 30 years?

Give your answer correct to the nearest cent. (2 marks)

Show Answers Only

`$ 1725.60`

Show Worked Solution

`text{Monthly interest rate}\ (r) = 1.5/12 = 0.125text(%) = 0.00125`

♦ Mean mark 43%.

`N = 30 xx 12 = 360`

`=>\ text(PV annuity factor = 289.75411)`

`:.\ text{Monthly payment}`	`= (500\ 000)/289.75411`
	`= $1725.60`

Financial Maths, STD2 F5 2021 HSC 40

A table of future value interest factors for an annuity of $1 is shown.

Simone deposits $1000 into a savings account at the end of each year for 8 years. The interest rate for these 8 years is 0.75% per annum, compounded annually.

After the 8th deposit, Simone stops making deposits but leaves the money in the savings account. The money in her savings account then earns interest at 1.25% per annum, compounded annually, for a further two years.

Find the amount of money in Simone's savings account at the end of ten years. (3 marks)

Show Answers Only

`$8419.81`

Show Worked Solution

`text(In 1st 8 years:)`

♦ Mean mark 35%.

`text(Future value factor = 8.2132)`

`text(Value of annuity)`	`= 8.2132 xx 1000`
	`= $8213.20`

`text(After 10 years:)`

`text(Value of investment)`	`= 8213.2 xx (1.0125)^2`
	`= $8419.81`

Measurement, STD2 M6 2021 HSC 37

The diagram shows a triangle `ABC` where `AC` = 25 cm, `BC` = 16 cm, `angle BAC` = 28° and angle `ABC` is obtuse.

Find the size of the obtuse angle `ABC` correct to the nearest degree. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`133°`

Show Worked Solution

`text(Using the sine rule:)`

♦♦ Mean mark 31%.

`sin theta/25`	`= (sin 28°)/16`
`sin theta`	`= (25 xx sin 28°)/16`
`sin theta`	`= 0.73355`
`theta`	`= 47°`

`:. angleABC`	`= 180-47`
	`= 133°`

Calculus, 2ADV C3 2021 HSC 26

A particle is shot vertically upwards from a point 100 metres above ground level.

The position of the particle, `y` metres above the ground after `t` seconds, is given by

`y(t) = −5t^2 + 70t + 100`.

Find the maximum height above ground level reached by the particle. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Find the velocity of the particle, in metres per second, immediately before it hits the ground, leaving your answer in the form `asqrtb`, where `a` and `b` are integers. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`345\ text(m)`
`-20sqrt69\ text(m/s)`

Show Worked Solution

a. `y(t) = -5t^2 + 70t + 100`

`y^(′)(t) = -10t + 70`

`y^(″)(t) = -10`

`text(Max height occurs when)\ \ y^(′)(t) = 0:`

`-10t + 70`	`= 0`
`10t`	`= 70`
`t`	`= 7`

`:.\ text(Max height)\ `	`= -5(7)^2 + 70 xx 7 + 100`
	`= 345\ text(m)`

b. `text(Particle hits ground when)\ \ y = 0:`

♦ Mean mark 38%.

`0`	`= -5t^2 + 70t + 100`
`0`	`= t^2 – 14t – 20`

`text(Using quadratic formula:)`

`t`	`= (14 ± sqrt(14^2 + 4*20))/2`
	`= (14 + sqrt(276))/2\ \ \ (t > 0)`
	`= 7 + sqrt69`

`:. text(Velocity)\ (y^(′)(t))`	`= -10(7 + sqrt69) + 70`
	`= -10sqrt69\ text(m/s)`

`:.a=-10 and b=69`

Calculus, 2ADV C3 2021 HSC 23

A population, `P`, which is initially 5000, varies according to the formula

`P = 5000b^((-t)/10),`

where `b` is a positive constant and `t` is time in years, `t ≥ 0`.

The population is 1250 after 20 years.

Find the value of `t`, correct to one decimal place, for which the instantaneous rate of decrease is 30 people per year. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`35.3\ text(years)`

Show Worked Solution

`P = 1250\ \ text(when)\ \ t = 20`

♦ Mean mark 42%.

`1250`	`= 5000 · b^((-t)/10)`
`b^(-2)`	`= 1/4`
`b`	`= 2\ \ \ (b>0)`

`P`	`= 5000 · 2^((-t)/10)`
`(dP)/(dt)`	`= ln2 · -1/10 · 5000 · 2^(-(t)/10)`
	`= – 500 ln2 · 2^((-t)/10)`

`text(Find)\ t\ text(when)\ \ (dP)/(dt) = -30:`

`-30`	`= -500 ln2 · 2^((-t)/10)`
`2^((-t)/10)`	`= 3/(50 ln2)`
`ln2^((-t)/10)`	`= ln(3/(50 ln2))`
`(-t)/10`	`= (ln(3/(50 ln2)))/(ln2)`
`t`	`= (-10ln(3/(50 ln2)))/(ln2)`
	`= 35.301…`
	`= 35.3\ text(years)`

Statistics, 2ADV S3 2021 HSC 22

A random variable is normally distributed with mean 0 and standard deviation 1. The table gives the probability that this random variable lies between 0 and `z` for different values of `z`.

The probability values given in the table for different values of `z` are represented by the shaded area in the following diagram.

Using the table, find the probability that a value from a random variable that is normally distributed with a mean of 0 and standard deviation 1 lies between 0.1 and 0.5. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Birth weights are normally distributed with a mean of 3300 grams and a standard deviation of 570 grams. By first calculating a `z`-score, find how many babies, out of 1000 born, are expected to have a birth weight greater than 3528 grams. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`0.1517`
`345\ text(babies)`

Show Worked Solution

♦♦ Mean mark part (a) 29%.
COMMENT: Note the Advanced and Std2 questions varied slightly but used the same table and graph.

a.	`P(0.1 < x < 0.5)`	`= 0.1915 – 0.0398`
		`= 0.1517`

b. `mu = 330, sigma = 570`

♦ Mean mark part (b) 48%.

`ztext(-score)\ (3528)`	`= (x – mu)/sigma`
	`= (3528 – 3300)/570`
	`= 0.4`

`P(ztext(-score) > 0.4)`	`= 0.5 – 0.1554`
	`= 0.3446`

`:.\ text(Expected babies > 3528 grams)`

`= 1000 xx 0.3446`

`= 344.6`

`~~ 345\ text(babies)`

Statistics, STD2 S4 2021 HSC 28

A salesperson is interested in the relationship between the number of bottles of lemonade sold per day and the number of hours of sunshine on the day.

The diagram shows the dataset used in the investigation and the least-squares regression line.

Find the equation of the least-squares regression line relating to the dataset. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Suppose a sixth data point was collected on a day which had 10 hours of sunshine. On that day 45 bottles of lemonade were sold.
What would happen to the gradient found in part (a)? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`y=3.2x+2`
`text{Gradient would increase (steepen).}`

Show Worked Solution

a. `text(Method 1)`

♦ Mean mark part (a) 37%.

`text{Input data points (in Stats Mode “Ax + B”):}`

`(2,8), (3, 11), (5, 19), (6, 22), (9, 30)`

`=>\ y=3.2x + 2`

`text(Method 2)`

`text{Find gradient using (0, 2) and (5, 18)}:`

`m=(18-2)/(5-0) = 3.2,\ \ ytext(-intercept)\ = 2`

`:.\ text(Equation:)\ y=3.2x + 2`

Mean mark part (b) 53%.

b. `text(Method 1)`

`text{Add (10, 45) to the data set in Stats Mode above:}`

`text(Gradient increases to 4.1.)`

`text(Method 2)`

`text{Data point (10, 45) lies above the regression line.`

`:.\ text{Gradient would increase (steepen).}`

Measurement, STD2 M7 2021 HSC 25

A rectangular sportsground has been drawn to scale on a 1-cm grid as shown. The scale used is `1:3000`.

Kerry took 12 minutes to walk around the perimeter of this sportsground.

What was Kerry's average speed in kilometres per hour? (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`3.9 \ text{km/hr}`

Show Worked Solution

`text{Distance walked on map} \ = \ 2 times (8 + 5) = 26 \ text{cm}`

Mean mark 54%.

`text{Actual distance}`	` =26 times 3000`
	`= 78\ 000 \ text{cm}`
	`=780 \ text{m}`
	`= 0.78 \ text{km}`

`12 \ text{minutes}\ = 12/60 = 0.2 \ text{hours}`

`text{Speed}`	`= text{distance}/text{time}`
	`= 0.78/0.2`
	`= 3.9 \ text{km/hr}`

Algebra, STD2 A4 2021 HSC 24

A population, `P`, is to be modelled using the function `P = 2000 (1.2)^t`, where `t` is the time in years.

What is the initial population? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the population after 5 years. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
On the axes below, draw the graph of the population against time, showing the points at `t = 0` and at `t = 5`. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

`2000`
`4977`
`text{See Worked Solutions}`

Show Worked Solution

a. `text{Initial population occurs when}\ \ t = 0:`

`P= 2000 (1.2)^0= 2000`

b. `text{Find} \ P \ text{when} \ \ t = 5: `

`P`	`= 2000 (1.2)^5`
	`= 4976.64`
	`= 4977 \ text{(nearest whole)}`

♦ Mean mark (c) 48%.

Networks, STD1 N1 2021 HSC 17

The network diagram shows the travel times in minutes along roads connecting a number of different towns.

Draw a minimum spanning tree for this network and determine its length. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---
How long does it take to travel from Queentown to Underwood using the fastest route? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`\text{See Worked Solutions}`
`65 \ \text{minutes}`

Show Worked Solution

a. `text{Using Prim’s algorithm (starting at}\ W):`

♦ Mean mark part (a) 40%.

`text(1st edge:)\ \ WM`

`text(2nd edge:)\ \ WP`

`text(3rd/4th edges:)\ \ MU\ text(and)\ \ WF`

`text(5th edge:)\ \ MK`

`text(6th edge:)\ \ KQ`

`text(7th edge:)\ \ PC`

`text{Length of minimum spanning tree} \ = 160`

b.	`text{Fastest route}\ (Q\ text(to)\ U)`	`= 45 + 20`
		`= 65 \ text{minutes}`

Measurement, STD2 M6 2021 HSC 14 MC

Consider the diagram below.

What is the true bearing of `A` from `B`?

`025^@`
`065^@`
`115^@`
`295^@`

Show Answers Only

`D`

Show Worked Solution

♦♦ Mean mark 28%.

`\text{Bearing (A from B)}`	`= 270 + 25`
	`= 295^@`

`=> D`

Financial Maths, STD2 F5 2021 HSC 21

Julie invests $12 500 in a savings account. Interest is paid at a fixed monthly rate. At the end of each month, after the monthly interest is added, Julie makes a deposit of $500.

Julie has created a spreadsheet to show the activity in her savings account. The details for the first 6 months are shown.

By finding the monthly rate of interest, complete the final row above for the 7th month. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`15\ 624.20, 23.44, 16\ 147.64`

Show Worked Solution

`\text{Monthly interest rate} = \frac{18.75}{12\ 500} = 0.0015 =\ text{0.15%}`

♦ Mean mark 43%.

`\text{Row 7 calculations:}`

`\text{Beginning balance}`	`= 15\ 624.20`
`\text{Monthly interest}`	`= 15\ 624.20 \times 0.0015`
	`= 23.44`

`\text{End of month balance}`	`= 15\ 624.20 + 23.44 + 500`
	`= 16\ 147.64`

Calculus, 2ADV C3 2021 HSC 9 MC

Let `h(x) = f(g(x))` where the function `f(x)` is an odd function and the function `g(x)` is an even function.

The tangent to `y = h(x)` at `x = k`, where `k > 0`, has the equation `y = mx + c`.

What is the equation of the tangent to `y = h(x)` at `x = –k`?

`y = mx + c`
`y = -mx + c`
`y = mx - c`
`y = -mx - c`

Show Answers Only

`B`

Show Worked Solution

`h(x) = f(g(x))`

Mean mark 52%.

`h^{′}(x) = g^{′}(x) · f^{′}(g(x))`

`text(At)\ \ x = k,`

`h(k) = f(g(k))`

`h^{′}(k) = g^{′}(x) · f^{′}(g(x)) = m`

`text(At)\ \ x = –k,`

`h(–k)=f(g(–k))=f(g(k))=h(k)`

`-> c\ text(is the same)`

`h^{′}(–k)`	`= g^{′}(–k) · f^{′}(g(–k))`
	`= -g^{′}(k) · f^{′}(g(k))\ \ \ \ (g(k)\ text{is even →}\ g^{′}(–k)=–g^{′}(k))`
	`= -m`

`:.\ text(Equation of tangent is)\ \ y = -mx + c`

`=> B`

Probability, STD2 S2 2021 HSC 11 MC

There are 8 chocolates in a box. Three have peppermint centres (P) and five have caramel centres (C).

Kim randomly chooses a chocolate from the box and eats it. Sam then randomly chooses and eats one of the remaining chocolates.

A partially completed probability tree is shown.

What is the probability that Kim and Sam choose chocolates with different centres?

`\frac{15}{64}`
`\frac{15}{56}`
`\frac{15}{32}`
`\frac{15}{28}`

Show Answers Only

`D`

Show Worked Solution

♦♦ Mean mark 35%.

`Ptext{(different centres)}`	`= P text{(PC)} + P text{(CP)}`
	`=\frac{3}{8} · \frac{5}{7} + \frac{5}{8} · \frac{3}{7}`
	`= \frac{15}{56} + \frac{15}{56}`
	`= \frac{15}{28}`

`=> D`

Algebra, STD2 A4 2021 HSC 10 MC

Which of the following best represents the graph of `y = 10 (0.8)^x`?

Show Answers Only

`A`

Show Worked Solution

`\text{By elimination:}`

♦ Mean mark 41%.

`\text{When} \ x = 0 \ , \ y = 10(0.8) ^0 = 10`

`-> \ text{Eliminate B and D}`

`text(As)\ \ x→oo, \ y→0`

`-> \ text{Eliminate C}`

`=> A`

Statistics, STD2 S1 2021 HSC 7 MC

The number of downloads of a song on each of twenty consecutive days is shown in the following graph.

Which of the following graphs best shows the cumulative number of downloads up to and including each day?

Show Answers Only

`C`

Show Worked Solution

`text{The gradient of the cumulative frequency histogram}`

♦ Mean mark 50%.

`text{will increase gradually, be steepest at day 10 then}`

`text{decrease gradually.}`

`=> C`

`\|x\| + \|y\| + \|z\|`	` = \|x_underset~i\| + \|y_underset~j\| + \|z_underset~k\|`
	`≥ \|x_underset~i + y_underset~j\| + \|z_underset~k\|`
	`≥ \|x_underset~i + y_underset~j + z_underset~k\|`
	`≥ 1\ \ (\|overset->{OP}\| = \| x_underset~i + y_underset~j + z_underset~k \| = 1)`

\(\dfrac{\sin \angle BAC}{42}\)	\(=\dfrac{\sin\,63^{\circ}}{175}\)
\(\sin \angle BAC\)	\(=\dfrac{42 \times \sin\,63^{\circ}}{175}\)
	\(=0.2138…\)
\(\angle BAC\)	\(=12.34…\)
	\(=12^{\circ}\ \text{(nearest degree)}\)

c.	\(P(X<2)\)	\(=\displaystyle \int_0^2 \dfrac{A x}{x^2+4} d x\)
		\(=\dfrac{A}{2}\left[\ln \left(x^2+4\right)\right]_0^2\)
		\(=\dfrac{1}{\ln 10}(\ln 8-\ln 4)\)
		\(=\dfrac{1}{\ln 10}\left(\ln \dfrac{8}{4}\right)\)
		\(=\dfrac{1}{\ln 10} \cdot \ln 2\)
		\(=\log _{10} 2\)