7 of the world's longest rivers are listed in the table below.
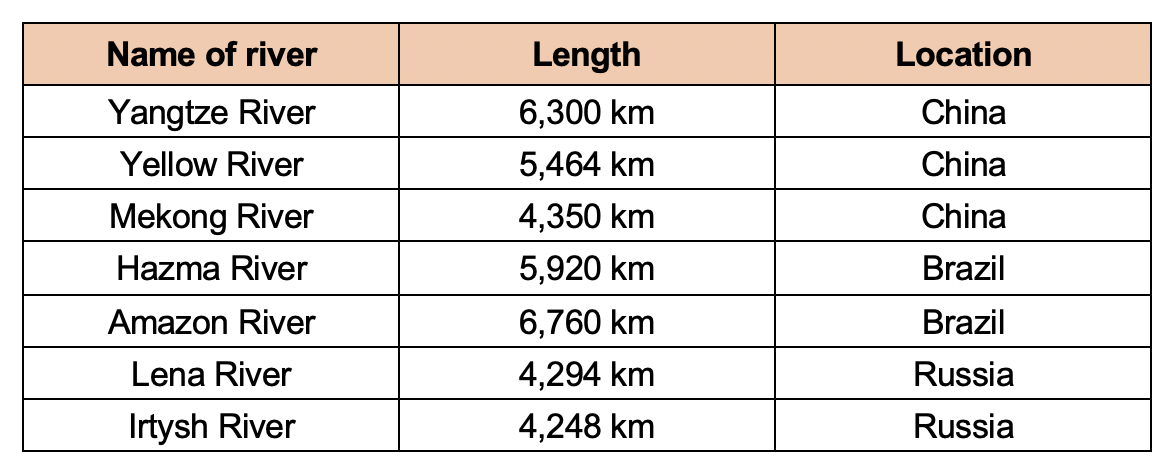
How much shorter is China's longest river compared to Brazil's longest river?
|
|
460 km |
|
|
1296 km |
|
|
2410 km |
|
|
2512 km |
Aussie Maths & Science Teachers: Save your time with SmarterEd
7 of the world's longest rivers are listed in the table below.

How much shorter is China's longest river compared to Brazil's longest river?
|
|
460 km |
|
|
1296 km |
|
|
2410 km |
|
|
2512 km |
`text{460 km}`
`text{Amazon River – Yangtze}`
`= 6760 – 6300`
`= 460 \ text{km}`
Marie flips an unbiased coin for 126 times.
Which result is most likely?
|
|
38 heads |
|
|
52 heads |
|
|
60 heads |
|
|
79 tails |
`text{60 heads}`
`text{The expected result is 63 heads or tails (half of total).}`
`therefore \ text{Most likely result is 60 heads.}`
Marie rolls a fair die 60 times.
Which result is most likely?
|
|
5 rolls of number two |
|
|
7 rolls of number two |
|
|
9 rolls of number two |
|
|
13 rolls of number two |
`text{8 rolls of number two}`
`text{The expected result is 10 rolls for each number.}`
`therefore \ text{Most likely result is 9 rolls of number two.}`
Amelia is making a pattern using nails.
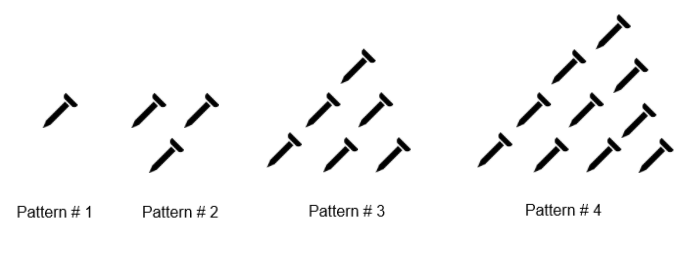
The table below shows the number of nails she needs for the pattern to be complete.
|
|
12 |
|
|
15 |
|
|
16 |
|
|
18 |
`15`
`text{Each new pattern adds the new pattern number to the previous total.}`
`text{Pattern # 5 is}`

`therefore \ text{Nails needed = 5 + 10 = 15}`
Amelia is making a pattern using flowers
The table below shows the number of flowers she needs for the pattern to be complete.
|
|
10 |
|
|
9 |
|
|
12 |
|
|
5 |
`10`
Catherine owns a walk-in wardrobe with 13 different types of bags.
There are the same number of bags of each type.
She has a total of 65 bags.
How many bags of each type does she have?
`5 \ text{bags}`
| `text{Bags of each type}` | `= frac{65}{13}` |
| `= 5 \ text{bags}` |
Richard has a bookshelf that he splits into 8 different categories.
He has a total of 152 books.
He has the same number of books in each category.
How many books in each category does he own?
`19 \ text{books}`
| `text{Books in each category}` | `= frac{152}{8}` |
| `= 19 \ text{books}` |
On a tourist map, two landmarks are measured to be 12.2 centimetres apart.
On the map, 1 centimetre represents 5 kilometres.
What is the actual distance between the landmarks?
|
|
2.44 km |
|
|
24.4 km |
|
|
6.1 km |
|
|
61.0 km |
`61.0 \ text{m}`
| `text{Actual Distance}` | `= 12.2 xx 5` |
| `= 61.0 \ text{km}` |
Two stores are 8.2 cm apart on a map.
On the map, 1 cm represents 2 km.
What is the actual distance between the stores?
|
|
4.1 km |
|
|
1.64 km |
|
|
16.4 km |
|
|
41.0 km |
`16.4 \ text{m}`
| `text{Actual Distance}` | `= 8.2 xx 2` |
| `= 16.4 \ text{km}` |
If `z= 7`, what is the value of `5z`?
|
|
35 |
|
|
55 |
|
|
57 |
|
|
75 |
`55`
| `z` | `= 5` |
| `5z` | `= 5 xx 7` |
| `=35` |
If `y= 4`, what is the value of `3y`?
|
|
7 |
|
|
10 |
|
|
12 |
|
|
34 |
`12`
| `y` | `= 4` |
| `3y` | `= 3 xx 4` |
| `=12` |
Izzie and Miranda saved $66 altogether.
Miranda saved half as much money as Izzie.
How much money did Izzie saved?
|
|
$11 |
|
|
$22 |
|
|
$30 |
|
|
$44 |
`$44`
`text(Strategy 1)`
`text{Let} \ \ 2x = text{money saved by Izzie}`
`text{Let} \ \ x = text{money saved by Miranda}`
| `2x + x` | `=66` | |
| `3x` | `=66` | |
| `x` | `=22` |
`:.\ text(Izzie saved $44)`
`text(Strategy 2)`
`text{Check each option:}`
`frac{1}{2} xx 30 + 30 = 45 \ text{(Incorrect)}`
`frac{1}{2} xx22 + 22 = 33 \ text{(Incorrect)}`
`frac{1}{2} xx 11 + 11 = 16.5 \ text{(Incorrect)}`
`frac{1}{2} xx 44 + 44 = 66 \ text{(Correct)}`
`therefore \ text{Izzie saved $44.}`
Adam and Kenneth bought a bike together that cost $150.
Adam paid twice as much money as Kenneth.
How much money did Kenneth paid?
|
|
$50 |
|
|
$75 |
|
|
$100 |
|
|
$120 |
`$50`
`text(Strategy 1)`
`text{Let} \ \ x = text{money paid by Kenneth}`
`text{Let} \ \ 2 x = text{money paid by Adam}`
| `x + 2x` | `=150` | |
| `3x` | `=150` | |
| `x` | `=50` |
`:.\ text(Kenneth paid $50).`
`text(Strategy 2)`
`text{Check each option:}`
`2(50) + 50 = 150 \ text{(Correct)}`
`2(75) + 75 = 225 \ text{(Incorrect)}`
`2(100) + 100 = 300 \ text{(Incorrect)}`
`2(120) + 120 = 360 \ text{(Incorrect)}`
Eisha won a jar of candy with 366 pieces of candy in it at her school fete.
She gave a hand full each to five of her friends.
Eisha then counted the remaining candy and found she had 232 pieces left.
How many pieces of candy did Eisha give to her friends?
`text(134)`
| `text(Pieces given to friends)` | `= 366 – 232` |
| `=134` |
Jason bought 325 eggs from the market.
When he was driving home, he had an accident and some of the eggs broke.
He counted that there were 241 eggs without any cracks.
How many eggs broke?
`text(84 eggs)`
| `text(Number of broken eggs)` | `= 325 – 241` |
| `= 84` |
Anne was driving from her house to the supermarket to buy some groceries.
She drove a total distance of 2 kilometres and 54 metres.
Which of these shows the distance, in metres, that Anne drove to get to the supermarket?
|
|
2.054 m |
|
|
254 m |
|
|
2054 m |
|
|
2540 m |
`2054\ text(m)`
`text(Conversion: 1 kilometre = 1000 metres)`
| `text{Distance}` | `= (2 × 1000) + 54` | |
| `=2000 + 54` | ||
| `=2054\ text(m)` |
John walked from his office to his home.
He walked a total of 1 kilometre and 62 metres.
Which of these shows the distance John walked in metres.
|
|
106.2 m |
|
|
162 m |
|
|
1062 m |
|
|
1620 m |
`1062\ text(m)`
`text(Conversion: 1 kilometre = 1000 metres)`
`text{Distance walked = 1000 + 62 = 1062 m}`
A standard deck of 52 cards is made up four suits - Hearts, Diamonds, Clubs and Spades - that have 13 cards each.
Lara has a standard deck of cards and draws a King without looking and returns it to the deck.
She repeats this three times and draws a King each time.
If she randomly draws a card for the 4th time, which of the following is true?
|
|
She is certain to draw a King. |
|
|
She is more likely to draw a King than a Spade. |
|
|
She is less likely to draw a King than a Queen. |
|
|
She is more likely to draw a Heart than a King. |
`text(She is more likely to draw a Heart than a King.)`
`Ptext{(Heart)} = 13/52 = 1/4`
`Ptext{(Spade)} = 13/52 = 1/4`
`Ptext{(King)} = 4/52 = 1/13`
`Ptext{(Queen)} = 4/52 = 1/13`
`:.\ text(She is more likely to draw a Heart than a King.)`
Aaron rolls a fair dice four times.
Each time he rolls the dice he gets a three.
Aaron rolls the dice for the fifth time.
Which of the following is true?
|
|
He is less likely to roll a two than a three. |
|
|
He is more likely to roll a three than a one. |
|
|
He has an equal chance of rolling a three as a six. |
|
|
He is certain to roll a three. |
`text(He has an equal chance of rolling a three as a six)`
`text(All numbers in a fair die have equal chance of appearing.)`
`:.\ text(He has an equal chance of rolling a three as a six.)`
| `320 ÷` |
|
`= 40` |
Which of the following numbers make the number sentence above correct?
|
|
8 |
|
|
16 |
|
|
20 |
|
|
80 |
`8`
`text(Check each option:)`
`text(Option 1 -)\ 320 ÷ 8 = 40\ (text(Correct))`
`text(Option 2 -)\ 320 ÷ 16 = 20`
`text(Option 3 -)\ 320 ÷ 80 = 4`
`text(Option 4 -)\ 320 ÷ 20 = 16`
`:.\ text(8 makes the number sentence correct.)`
| `7 xx` |
|
`= 161` |
What number will make the number sentence correct?
|
|
13 |
|
|
23 |
|
|
154 |
|
|
1127 |
`13`
`text(Check each option)`
`text(Option 1 -)\ 7 xx 13 = 91`
`text(Option 2 -)\ 7 xx 23 = 161\ (text(Correct))`
`text(Option 3 -)\ 7 xx 154 = 1078`
`text(Option 4 -)\ 7 xx 161 = 1127`
Sheryl has 90 cupcakes to sell to her customers.
She packed the cupcakes in boxes that fit 4 cupcakes inside.
How many full boxes of cupcakes can she sell?
|
|
21 |
|
|
23 |
|
|
22 |
|
|
20 |
`22`
`text(Number of boxes)`
`= 90 ÷ 4`
`= 22\ text(remainder 2)`
`:.\ text(Sheryl can sell 22 boxes full of cupcakes.)`
Darren bought 141 eggs from the market.
He decided to put the eggs in cartons of 12.
How many full cartons of eggs does he have?
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
`11`
`text(Number of cartons of eggs)`
`= 141 -: 12`
`= 11\ text(remainder 9)`
`:.\ text(Darren can make 11 full cartons of eggs.)`
Leo painted the patterns shown below.
All the triangles that make up the shape have the same area.
Which of the following has the largest area painted grey?
|
|
|
|
|
|
|
|
|
|
|
`text(Largest area painted → most triangles painted grey.)`
`text(Checking each option:)`
`text(Option 1 – 12 triangles painted)`
`text(Option 2 – 10 triangles painted)`
`text(Option 3 – 12 triangles painted)`
`text{Option 4 – 14 triangles painted (largest area)}`
The graph below shows the number of people in a supermarket at 15-minute intervals during a 4 hour period.
What time were the least amount of people in the supermarket?
|
|
11:15 AM |
|
|
12:00 PM |
|
|
12:30 PM |
|
|
1:45 PM |
`11:15 \ text{AM}`
`text(Each data point represents 15 minutes.)`
`:.\ text{The lowest data point in the graph is at 11:15 AM}`
The graph below shows the number of vehicles in a parking station at 30 minute intervals over a 6 hour period.
What time were the highest number of vehicles in the parking station?
|
|
5:30 PM |
|
|
4:30 PM |
|
|
3:30 PM |
|
|
5:00 PM |
`4:30 \ text(PM)`
`text{The highest data point in the graph is between 4:00 PM and 5:00 PM.}`
`therefore \ text{Highest number was at 4:30 PM.}`
The image below shows a game of noughts and crosses in progress.
What fraction of the available boxes are not filled in?
|
|
`frac{5}{9}` |
|
|
`frac{3}{8}` |
|
|
`frac{1}{2}` |
|
|
`frac{4}{9}` |
`frac{4}{9}`
| `text{Fraction}` | `= frac{ text{Squares not filled} }{ text{Total squares} }` | |
| `= frac{4}{9}` |
The image below is the plan of a farming plot.
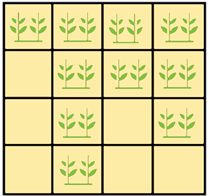
Squares containing plants represent land that is growing crops.
Which fraction shows the amount of land that is used for growing crops?
|
|
`frac{4}{5}` |
|
|
`frac{5}{8}` |
|
|
`frac{1}{2}` |
|
|
`frac{3}{8}` |
`frac{5}{8}`
| `text{Fraction}` | `= frac{ text{Squares growing crops} }{ text{Total squares} }` | |
| `= frac{10}{16}` | ||
| `= frac{5}{8}` |
Which shape has an area of exactly 12 square units?
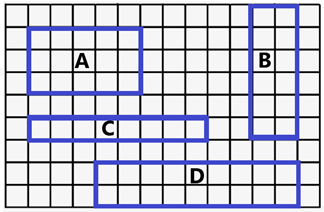
|
|
A |
|
|
B |
|
|
C |
|
|
D |
`B`
`text{Area of triangle} = text{b} xx text{h}`
`text{Check each option:}`
`text{A.} \ \ 5 xx 3 = 15 `
`text{B.} \ \ 2 xx 6 = 12 \ text{(Correct)}`
`text{C.} \ \ 8 xx 1 = 8`
`text{D.} \ \ 9 xx 2 = 18`
`therefore \ text{square B has an area of exactly 12 square units.}`
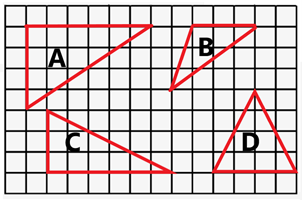
What shape has an area greater than 11 square units?
|
|
A |
|
|
B |
|
|
C |
|
|
D |
`A`
`text{Area of triangle} = frac{1}{2} xx text{b} xx text{h}`
`text{Check each option:}`
`text{A.} \ frac{1}{2} xx 6 xx 4 = 12 \ text{(Correct)}`
`text{B.} \ frac{1}{2} xx 3 xx 3 = 4.5`
`text{C} \ frac{1}{2} xx 6 xx 3 = 9`
`text{D} \ frac{1}{2} xx 4 xx 4 = 8`
`therefore \ text{triangle A has an area greater than 11 square units.}`
Barnsy owned a carp that was one quarter of a metre long.
How long was Barnsy's carp in millimetres?
|
|
4000 |
|
|
2000 |
|
|
400 |
|
|
250 |
|
|
50 |
`250`
`1 \ text{metre} = 1000 \ text{millimetres}`
| `frac{1}{4} \ text{metre}` | ` = frac{1}{4} xx 1000` |
| `= 250 \ text{millimetres}` |
Calvin bought half a kilogram of prawns from the fish market.
How many grams of prawns did Calvin buy?
|
|
5 |
|
|
25 |
|
|
50 |
|
|
500 |
|
|
750 |
`500`
`1 \ text{kilogram} = 1000 \ text{grams}`
`frac{1}{2} \ text{kilogram} = 500 \ text{grams}`
Scott expects his wine to be delivered on the 28th March.
He is told by the distributor that its delivery will be delayed by 5 days.

What day of the week will the wine now be delivered?
| Monday | Tuesday | Wednesday | Saturday |
|
|
|
|
|
`text{Tuesday}`
`text{28th March is a Thursday.}`
`therefore \ text{5 days later is a Tuesday.}`
Marty expects his gold mining drench to be delivered on the 28th of June.
Delays at customs mean it will be delivered 6 days later.

Which day of the week should the drench now be delivered?
| Saturday | Sunday | Monday | Tuesday |
|
|
|
|
|
`text{Monday}`
`text{28th June is a Tuesday.}`
`therefore \ text{6 days later is a Monday.}`
Flanno builds the shape below using identical small blocks.
| 10 | 11 | 12 | 13 |
|
|
|
|
|
`10`
`text{The smallest cube will be} \ 3 xx 3 xx 3`
`text{Bottom row = 1}`
`text{2nd row = 5}`
`text{Top row = 7}`
`therefore \ text{13 blocks needed}`
Ella builds the shape below using identical small blocks.
| 8 | 9 | 10 | 11 |
|
|
|
|
|
`10`
`text{The smallest cube will be} \ 3 xx 3 xx 3`
`text{Bottom row = 2}`
`text{2nd row = 3}`
`text{Top row = 5}`
`therefore \ text{10 blocks needed}`
Solve `3e^t = 5 + 8e^(−t)` for `t`. (3 marks)
`log_e(8/3)`
`3e^t – 5 – 8e^(−t) = 0`
`text(Multiply both sides by)\ e^t:`
`3e^(2t) – 5e^t – 8 = 0`
`text(Let)\ \ y = e^t`
| `log_2((6 – x)/(4 – x))` | `= 2` | ||
| `3y^2 – 5y – 8` | `= 0` | ||
| `(3y – 8)(y + 1)` | `= 0` | ||
| `y` | `=8/3\ quadquadquadquadquad text(or)\ \ \ \ ` | `y` | `=-1\ \ text{(No solution)}` |
| `e^t` | `= 8/3` | ||
| `:. t` | `= log_e(8/3)\ \ \ ` | ||
Two objects, each of mass `m` kilograms, are connected by a light inextensible strings that passes over a smooth pulley, as shown below. The object on the platform is initially at point A and, when it is released, it moves towards point C. The distance from point A to point C is 10 m. The platform has a rough surface and, when it moves along the platform, the object experiences a horizontal force opposing the motion of magnitude `F_1` newtons in the section AB and a horizontal force opposing the motion of magnitude `F_2` newtons when it moves in the section BC.
The force `F_1` is given by `F_1 = kmg, \ k ∈ R^+`.
Point B is midway between points A and C.
| a. |
b. i. `text(Horizontally:)`
`ma = T – F_1 = T – kmg\ …\ (1)`
`text(Vertically:)`
`ma = mg – T\ …\ (2)`
`text(Add)\ \ (1) + (2) :`
`2ma = mg – kmg`
| `:. a` | `= (g – kg)/2` |
| `= (g(1 – k))/2` |
b. ii. `text(System in motion when)\ a > 0`
`(g(1 – k))/2 > 0`
`:. k ∈ (0, 1), \ k ∈ R^+`
c. `text(AB) = 5\ (text(given)), u = 0\ (text(given))`
`text(Find)\ t\ text(when)\ s = 5:`
`s = ut + 1/2at^2`
`5 = 0 + 1/2 · (g(1 – k))/2 · t^2`
| `t^2` | `= 20/(g(1 – k))` |
| `t` | `= sqrt(20/(g(1 – k)))` |
| `= 2sqrt(5/(g(1 – k)))` |
d. `text(At B,)\ s = 5`
| `v_text(B)^2` | `= u^2 + 2as` |
| `= 0 + 2 · (g(1 – k))/2 · 5` | |
| `= 5g(1 – k)` |
`:. v_text(B) = sqrt(5g(1 – k))`
e. `text(Acceleration is against the direction of motion.)`
| `a` | `= −F/m` |
| `= −0.075g – 0.4v^2` | |
| `= −0.4(0.1875g + v^2)` |
| `d/(dx)(1/2 v^2)` | `= −0.4(0.1875g + v^2)` |
| `d/(dx)(v^2)` | `= −0.8(0.1875g + v^2)` |
| `(dx)/(d(v^2))` | `= −1.25(1/(0.1875g + v^2))` |
| `:. x` | `= −1.25 int_(2.5^2)^0 1/(0.1875 + v^2)\ dv^2` |
| `= 1.85\ text(m)` |
| `:.\ text(Distance from C)` | `= 5 – 1.85` |
| `= 3.15\ text(m)` |
Two complex numbers, `u` and `v`, are defined as `u = −2 - i` and `v = −4 - 3i`.
--- 5 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 10 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
a. `text(Let)\ \ z = x + iy`
`z – u = x + 2 + iy + i`
`z – v = x + 4 + iy + 3i`
`|z – u| = |z – v|`
| `(x + 2)^2 + (y + 1)^2` | `= (x + 4)^2 + (y + 3)^2` |
| `x^2 + 4x + 4 + y^2 + 2y + 1` | `= x^2 + 8x + 16 + y^2 + 6y + 9` |
| `-4y` | `= 4x + 20` |
| `y` | `= −x – 5` |
| b. |
|
c. `|z – u| = |z – v|\ text(is the graph of the perpendicular bisector of the)`
`text(line joining)\ u and v.`
| d.i. |
|
d.ii. `text(Arg)(z – u) = pi/4 =>\ text(gradient) = 1, ytext(-intercept at)\ (0, 1)`
`:. f: (−2, ∞) -> RR, \ f(x) = x + 1`
Two complex numbers, `u` and `v`, are defined as `u = -2-i` and `v = −4-3i`.
--- 3 WORK AREA LINES (style=lined) ---
--- 0 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 0 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
a. `text(Let)\ \ z = x + iy`
`z-u = x + 2 + iy + i`
`z-v = x + 4 + iy + 3i`
`|z-u| = |z-v|`
| `(x + 2)^2 + (y + 1)^2` | `= (x + 4)^2 + (y + 3)^2` |
| `x^2 + 4x + 4 + y^2 + 2y + 1` | `= x^2 + 8x + 16 + y^2 + 6y + 9` |
| `-4y` | `= 4x + 20` |
| `y` | `= −x-5` |
| b. |
|
c. `|z-u| = |z-v|\ text(is the graph of the perpendicular bisector of the)`
`text(line joining)\ u and v.`
| d.i. |
|
d.ii. `text(Arg)(z-u) = pi/4 =>\ text(gradient) = 1, ytext(-intercept at)\ (0, 1)`
`:. f: (−2, ∞) -> RR, \ f(x) = x + 1`
e. `|z_c-u| = |z_c-v| = |z_c-(−5i)|`
| `z_c-u` | `= (a + 2) + (b + 1)i` |
| `z_c-v` | `= (a + 4) + (b + 3)i` |
| `z_c +5i` | `= a + (b + 5)i` |
`a^2 + (b + 5)^2 = (a + 2)^2 + (b + 1)^2\ …\ (1)`
`a^2 + (b + 5)^2 = (a + 4)^2 + (b + 3)^2\ …\ (2)`
`a = −5/3, b = −10/3\ \ text{(by CAS)}`
`:.z_c = −5/3-10/3 i`
| `:.r` | `= |z_c-(−5i)|` |
| `= sqrt((−5/3)^2 + (−10/3 + 5)^2)` | |
| `= (5sqrt2)/3` |
A particle moves in the `x\ – y` plane such that its position in terms of `x` and `y` metres at `t` seconds is given by the parametric equations
`x = 2sin(2t)`
`y = 3cos(t)`
where `t >= 0`
--- 4 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
a. `text(At)\ \ t = pi/6,`
`x = 2sin\ pi/3 = sqrt3`
`y = 3cos\ pi/6 = (3sqrt3)/2`
| `:.\ text(Distance)` | `= sqrt((sqrt3)^2 + ((3sqrt3)/2)^2)` |
| `= sqrt39/2\ text(metres)` |
b.i. `(dx)/(dt) = 4cos(2t),\ \ (dy)/(dt) = −3sin(t)`
| `(dy)/(dx)` | `= (dy)/(dt) · (dt)/(dx)` |
| `= (−3sin(t))/(4cos(2t))` |
`text(When)\ t = pi :`
| `(dy)/(dx)` | `= (−3sin(pi))/(4cos(2pi))=0` |
`text(Equation of tangent where)\ \ m = 0,\ text(through)\ (0, −3):`
`y = −3`
| b.ii. | `underset~r(t)` | `= 2sin(2t)underset~i + 3cos(t)underset~j` |
| `underset~v(t)` | `= 4cos(2t)underset~i-3sin(t)underset~j` | |
| `underset~v(pi)` | `= 4cos(2pi)underset~i-3sin(pi)underset~i` | |
| `= 4underset~i` |
b.iii. `underset~a(t) = −8sin(2t)underset~i-3cos(t)underset~j`
| `underset~a(pi)` | `= −8sin(2pi)underset~i-3cos(pi)underset~j` |
| `= 3underset~j` |
| `|underset~a(pi)|` | `= sqrt(0^2 + 3^2)` |
| `= 3\ text(ms)^(−2)` |
c. `text(Find)\ t\ text(when)\ \ x = 2sin(2t) = 0\ \ text(and)\ \ y = 3cos(t) = 0:`
`t = pi/2\ \ (text(1st time))`
| d. | `text(Distance)` | `= int_0^(pi/6) sqrt(((dx)/(dt))^2 + ((dy)/(dt))^2)\ dt` |
| `= int_0^(pi/6) sqrt((4cos(2t))^2 + (−3sin(t))^2)\ dt` | ||
| `~~ 1.804\ \ (text(to 3 d.p.))` |
Pringle has 55 twenty-cent coins in his money pouch.

How much money does Pringle have?
|
|
$9.50 |
|
|
$11.00 |
|
|
$20.50 |
|
|
$55.00 |
`$11.00`
`text(5 twenty-cent coins = $1.00)`
| `:.\ text(55 twenty-cent coins)` | `=11 xx $1.00` | |
| `=$11.00` |
Sheena has 26 twenty-cent coins in her piggy bank.

How much money does Sheena have?
|
|
$26.20 |
|
|
$5.20 |
|
|
$5.00 |
|
|
$4.40 |
$5.20
`text(5 twenty-cent coins = $1.00)`
| `:.\ text(26 twenty-cent coins)` | `=5 xx $1.00 + 20\ text(cents)` | |
| `=$5.20` |
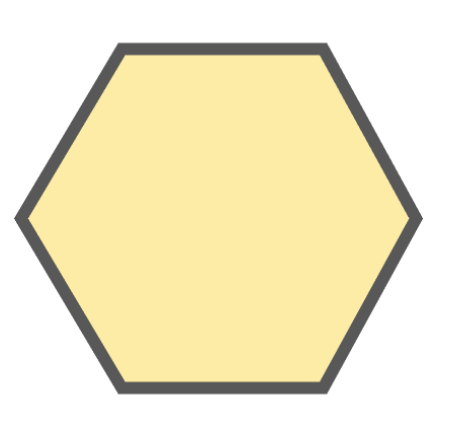
Wilde compared the weight of four different solid figures by using a balancing scale.
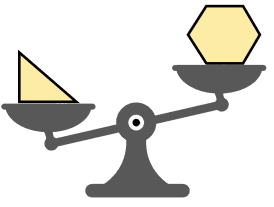
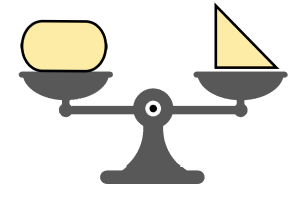
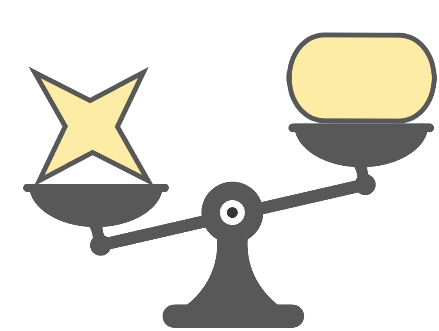
Which of the four objects is the heaviest?
 |
 |
 |
 |
|
|
|
|
|

`text{By inspection:}`
`text(Triangle → heavier than the hexagon.)`
`text(Triangle → same weight as the oval.)`
`text(Star → heavier than the oval.)`
`:.\ text(Star is the heaviest.)`

Banjo compared the weight of four different solid figures by using a balancing scale.
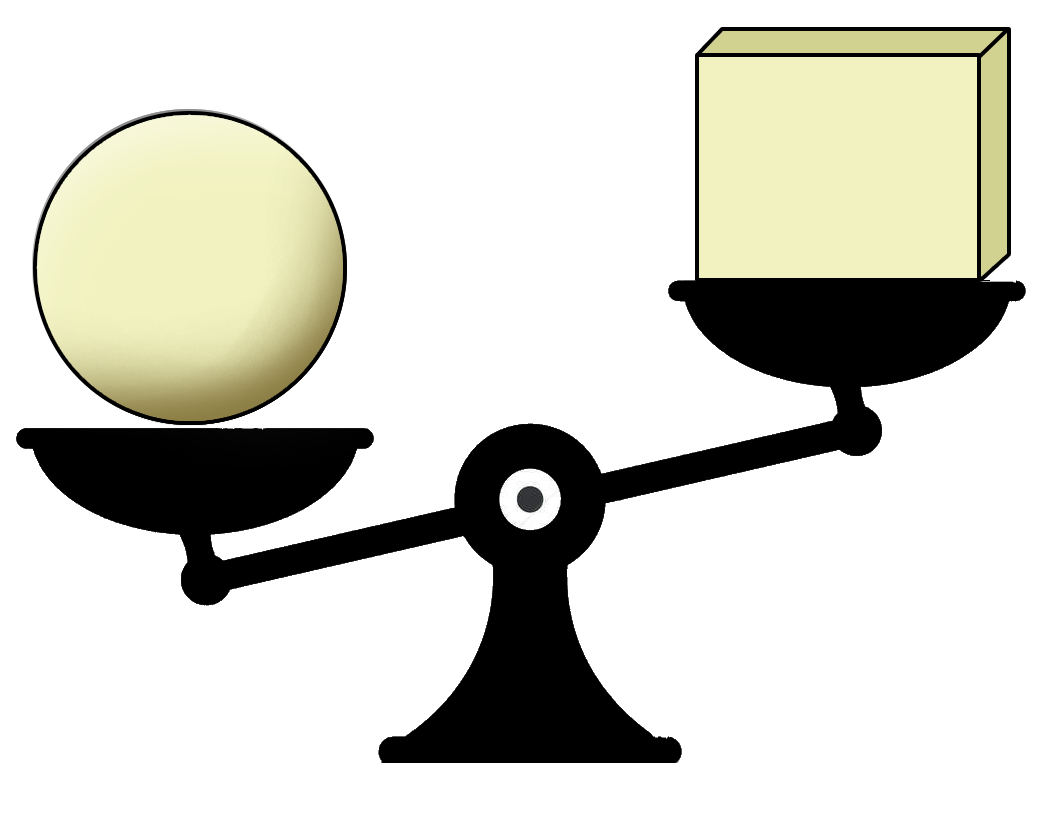
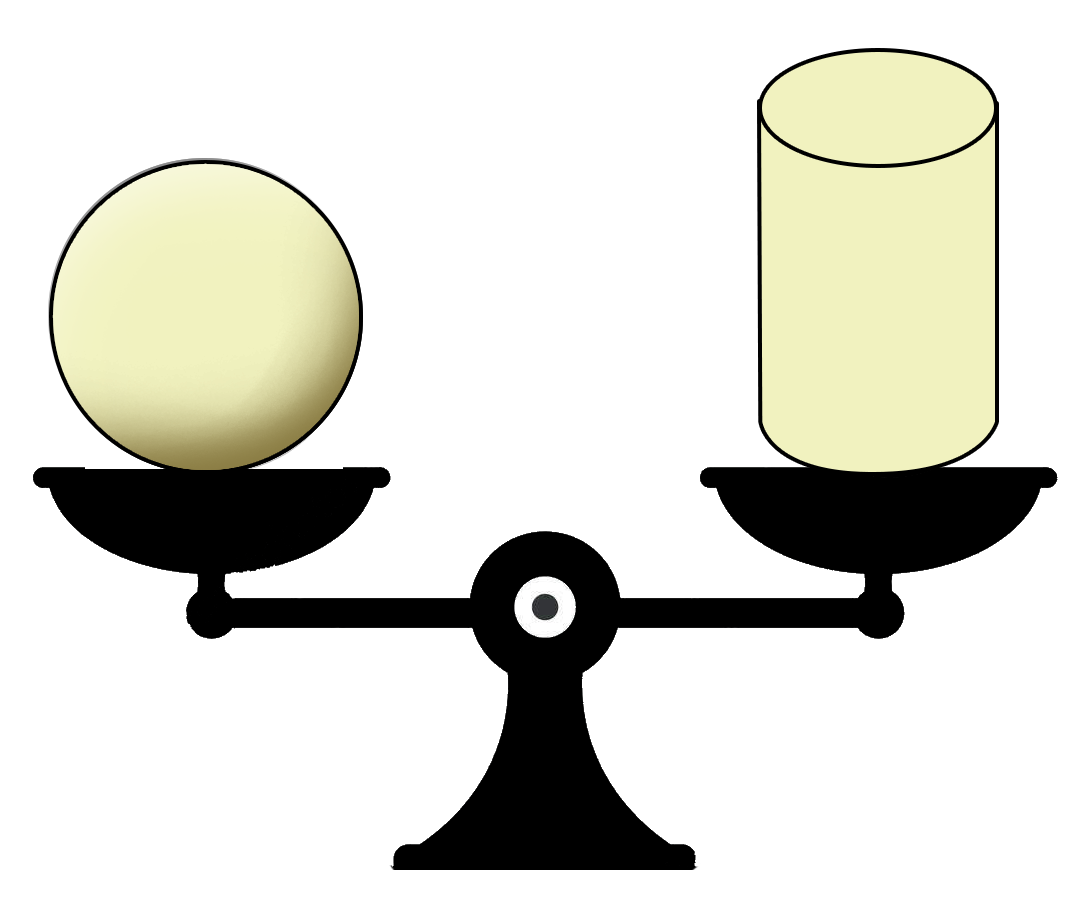
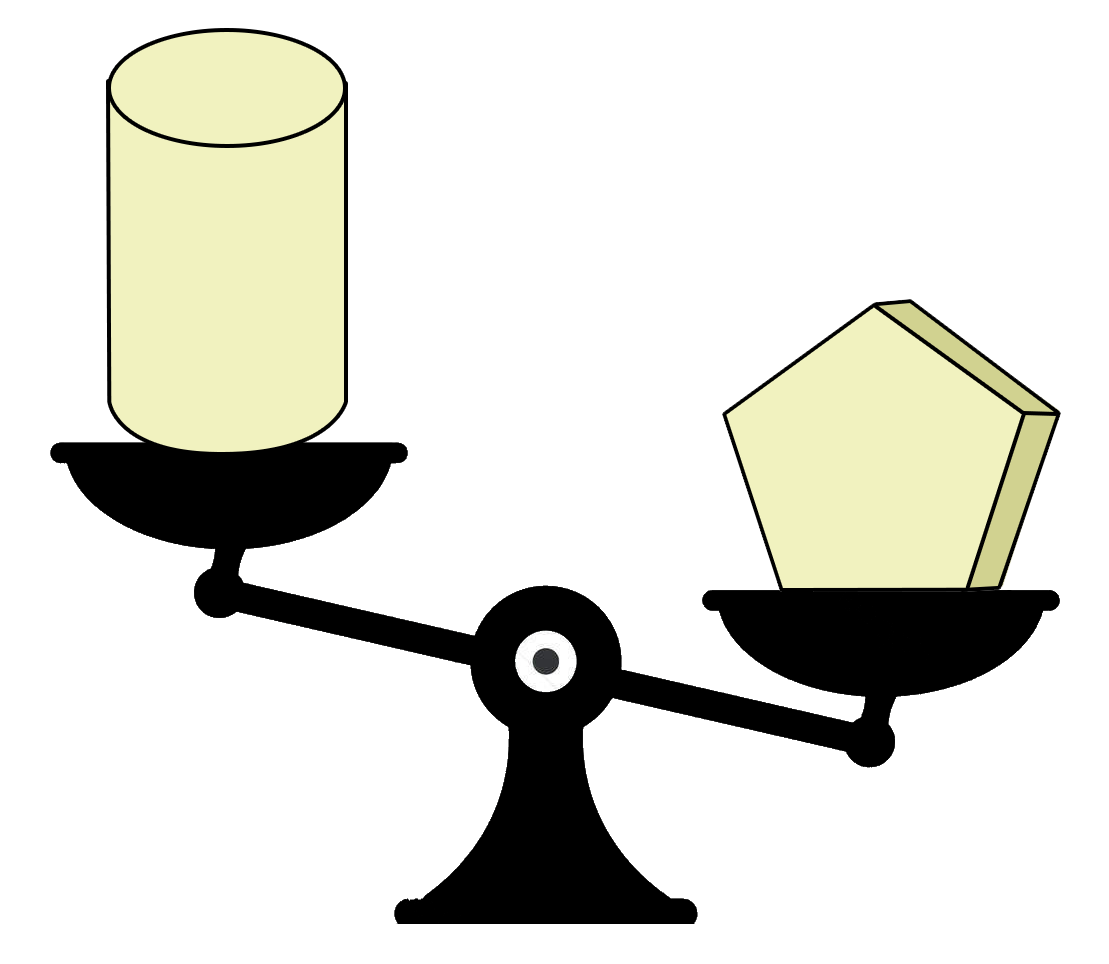
Which of the four objects is the lightest?
 |
 |
 |
 |
|
|
|
|
|

`text{By inspection:}`
`text(Sphere → lighter than the cube.)`
`text(Sphere → same weight as the cylinder.)`
`text(Cylinder → heavier than the pentagonal prism.)`
`:.\ text(Pentagonal prism is the lightest.)`

Mince decided to paint some triangles red in the four figures below.
All triangles are the same size.
Which of these figures has the smallest area that is painted red.
|
|
|
|
|
`text{Smallest area painted red = lowest number of triangles painted red.}`
`text{Check each option:}`
`text{1st Figure – 9 triangles}`
`text{2nd Figure – 9 triangles}`
`text{3rd Figure – 10 triangles}`
`text{4th Figure – 7 triangles}`
`therefore \ text{4th Figure has the smallest area painted red}`
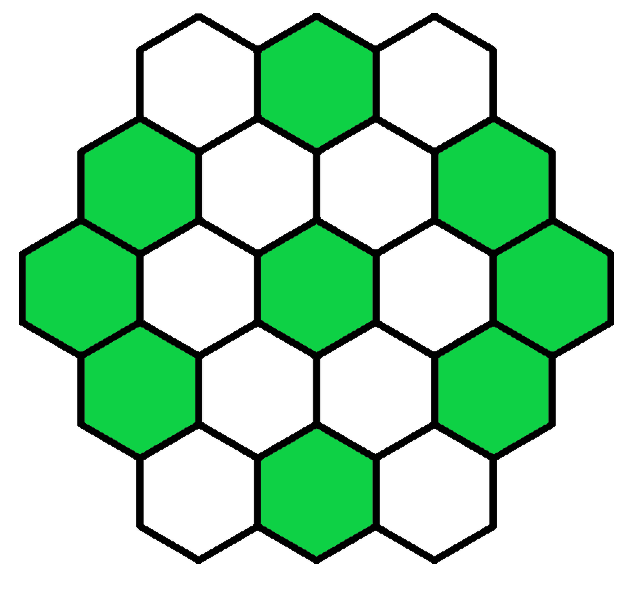
Jane painted some hexagons in the four figures pictured below.
All hexagons are the same size.
Which of these figures has the largest area that is painted green.
 |
 |
 |
 |
|
|
|
|
|

`text{Largest area painted = figure with the most hexagons painted green.}`
`text{Check each option:}`
`text{1st Figure – 11 hexagons}`
`text{2nd Figure – 9 hexagons}`
`text{3rd Figure – 13 hexagons}`
`text{4th Figure – 9 hexagons}`
`therefore \ text{3rd Figure has the largest area painted green.}`
In a bakery Michelle bought one slice of cake, one donut and a croissant.
She gave the cashier $10.00.
How much change should Michelle receive?
| $5.10 | $5.60 | $5.80 | $6.00 |
|
|
|
|
|
`$6.00`
| `text{Total cost}` | `= 1.35 + 1.20 + 1.45 ` |
| `= $4.00` |
| `text{Change}` | `= 10 – 4` |
| `= $6.00` |
Alexander went shopping and bought the following items.

He gave the cashier $50.
How much change should Alexander receive?
| $17.00 | $18.20 | $31.80 | $33.00 |
|
|
|
|
|
`$17.00`
| `text{Total cost}` | `= 9.50 + 12.10 + 11.40 ` |
| `= $33.00` |
| `text{Change}` | `= 50 – 33.00 ` |
| `= $17.00` |
Timothy started with 53 millilitres of oil in a beaker.
He saw that there was some unused oil in a test tube and returned it to the beaker.

How much of the chemical solution was poured int0 the test tube?
|
|
13 millilitres |
|
|
23 millilitres |
|
|
27 millilitres |
|
|
37 millilitres |
`27 \ text{millilitres}`
| `text{Oil in the test tube }` | `= text{New volume} – text{Original volume}` |
| `= 80 – 53` | |
| `= 27 \ text{millilitres}` |
A chemist started with 685 millilitres of a solution.
He then poured some of the solution into a test tube.

How much of the chemical solution was poured into the test tube?
|
|
90 millilitres |
|
|
135 millilitres |
|
|
145 millilitres |
|
|
185 millilitres |
`185 \ text{millilitres}`
| `text{Solution in test tube }` | `= text{New volume} – text{Original volume}` |
| `= 685 – 500` | |
| `= 185 \ text{millilitres}` |
In a neighborhood 10 villagers were asked if how many pets they own.
The results were: 3, 2, 1, 1, 1, 4, 2, 4, 5, 2
Select the dot plot that displays the data recorded
|
|
|
||
|
|
|
`text{A dot represents the number of persons that owns N pets}`
`text{From the data above:}`
`text{Owns one pet = 3}`
`text{Owns two pets = 3}`
`text{Owns three pets = 1}`
`text{Owns four pets = 2}`
`text{Owns five pets = 1}`
`therefore \ text{the correct dot plot is:}`
10 people were asked how often they went to the doctor in the last 12 months.
Their responses were: 2, 3, 3, 4, 1, 2, 5, 1, 1, 2
Choose the dot plot which correctly displays the data.
|
|
|
|
|
|
|
|
|
|
`text{From the data above:}`
`text{1 visit = 3 people}`
`text{2 visits = 3 people}`
`text{3 visits = 2 people}`
`text{4 visits = 1 person}`
`text{5 visits = 1 person}`
A bridge is drawn below.
The angle `y°` is marked from the foot of the bridge to the diagonal support.
The value of angle `y°` is
|
|
Less than 90° |
|
|
More than 180° |
|
|
Equal to 90° |
|
|
More than 90° but less than 180° |
`text{Less than} \ 90^@`
`text{The angle from the foot to the diagonal support is less than} \ 90^@`
A charity event was held for three weeks. On the first week $5000 was raised, on the second week $3500 was raised and on the last week $2000 was raised.
In the tables below, O = $500
Which table correctly shows the amount of donations raised in the 3 weeks?
|
|
|
|
|
|
|
|
|
|
`text{O represents $500 in donations.}`
`text{1st week:} \ 5000 \div 500 = 10`
`therefore \ text{Ten O symbols needed.}`
`text{2nd week:} \ 3500 \div 500 = 7`
`therefore \ text{Seven O symbols needed.}`
`text{3rd week:} \ 2000 \div 500 = 4`
`therefore \ text{Four O symbols needed.}`