common-content

v1 Financial Maths, STD2 F4 2013 HSC 26e

Lucas invests $5000.

Interest is compounded half-yearly at a rate of 3% per half-year.

Use the table to calculate the value of his investment at the end of 4 years. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`$6335`

Show Worked Solution

♦ Mean mark 44%
COMMENT: Structure your answer: 1-Find the interest rate per compounding period (same in this case). 2-Find the number of compounding periods..

`r =\ text(3% per half-year)`

`n = 8 \ \ \ \ text{(8 half-years in 4 years)}`

`⇒ \text{Table Factor} = 1.267`

`text(Investment)`	`= 5000 × 1.267`
	`= $6335`

`:.\ \text{After 4 years, investment value is } $6335`

v1 Financial Maths, STD2 F4 2014 HSC 30a

Jordan wants to accumulate $15 000 in a savings account over 10 years to buy a new car.

The account pays interest at 4% per annum compounded monthly.

Calculate how much Jordan must deposit now to achieve this goal. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`$10\ 110\ \ \text{(nearest $)}`

Show Worked Solution

♦ Mean mark 52%

`FV = 15\ 000,\ \ n = 10 \times 12 = 120,`

`r = 0.04 / 12 = 0.003333…`

`FV`	`= PV (1 + r)^n`
`15\ 000`	`= PV (1 + 0.003333…)^{120}`
`PV`	`= \frac{15\ 000}{(1.003333…)^{120}}`
	`= 10\ 109.88…`

`∴ \ \text{Jordan must deposit} \ $10\ 110\ \text{(nearest $)}`

v1 Financial Maths, STD2 F4 2015 HSC 26d

A laptop currently costs $850.

Assuming a constant annual inflation rate of 3.2%, calculate the cost of the same laptop in 4 years’ time. (2 marks)

Show Answers Only

`$962.38\ \text{(nearest cent)}`

Show Worked Solution

`FV`	`= PV(1 + r)^n`
	`= 850(1.032)^4`
	`= 850(1.132216)`
	`= 962.3836…`
	`= $962.38\ \text{(nearest cent)}`

v1 Financial Maths, STD2 F4 2018 HSC 19 MC

The table shows the compounded values of $1 at different interest rates over different periods.

Ben hopes to have $18 000 in 2 years to travel. He opens an account today which pays interest of 4% p.a., compounded quarterly.

Using the table, which expression calculates the minimum single sum that Ben needs to invest today to ensure he reaches his savings goal?

18 000 × 1.0816
18 000 ÷ 1.0816
18 000 × 1.0829
18 000 ÷ 1.0829

Show Answers Only

`text(D)`

Show Worked Solution

`text(4% annual)`

`= (4%)/4 = 1% per quarter`

`2 \ text(years) = 8 \ text(periods)`

`\text(From the table: at 8 periods and 1%, compounded value) = 1.0829`.

`:.\ text(Minimum sum) = 18\ 000 ÷ 1.0829`

`=>\ text(D)`

v1 Financial Maths, STD2 F4 2008 HSC 24c

Daniel’s funds in a retirement account are projected to have a future value of $600 000 in 15 years’ time. The interest rate is 5% per annum, with earnings calculated six-monthly.

What single amount could be invested now to produce the same result over the same period of time at the same interest rate? (3 marks)

Show Answers Only

`$288\ 629.97`

Show Worked Solution

`FV`	`= PV(1 + r)^n`
`600\ 000`	`= PV(1 + 2.5/100)^30`
`:. PV`	`= (600\ 000)/((1.025)^30)`
	`= 288\ 629.966…`
	`= $288\ 629.97`

v1 Financial Maths, STD2 F4 2022 HSC 11 MC

In eight years, the future value of an investment will be $120 000. The interest rate is 6% per annum, compounded half-yearly.

Which equation will give the present value `(PV)` of the investment?

`PV=(120\ 000)/((1+0.06)^(8))`
`PV=(120\ 000)/((1+0.03)^(8))`
`PV=(120\ 000)/((1+0.03)^(16))`
`PV=(120\ 000)/((1+0.06)^(16))`

Show Answers Only

`C`

Show Worked Solution

`text{Compounding periods} = 8 xx 2 = 16`

`text{Compounding rate} = (6text{%}) / 2 = 3text{%} = 0.03`

`PV = (120\ 000) / ((1 + 0.03) ^{16})`

`=> C`

v1 Financial Maths, STD2 F4 2016 HSC 8 MC

The table shows the future value of an investment of $1000, compounding yearly, at varying interest rates for different periods of time.

Based on the information provided, what is the future value of an investment of $3500 over 5 years at 2% pa?

$1554.80
$2835.72
$3864.28
$4312.36

Show Answers Only

`=> C`

Show Worked Solution

`text(Table factor) = 1104.08`

`:. FV`	`= 3.5 xx 1104.08`
	`= $3864.28`

`=> C`

v2 Functions, 2ADV F1 SM-Bank 54

Find the reciprocal of `1/(xy) + 1/y-z/x`. (2 marks)

Show Answers Only

`(xy)/(x+y-z)`

Show Worked Solution

`1/(xy) + 1/y-z/x`	`=1/(xy)+x/(xy)-(zy)/(xy)`
	`=(1+x-zy)/(xy)`

`text(Reciprocal of)\ \ x = x^(-1)`

`:.\ text(Reciprocal of)\ \ (1+x-zy)/(xy)=((1+x-zy)/(xy))^(-1)=(xy)/(1+x-zy)`

v1 Functions, 2ADV F1 SM-Bank 54

Find the reciprocal of `r/p-1/(pq) + 1/q`. (2 marks)

Show Answers Only

`(pq)/(p+q-r)`

Show Worked Solution

`r/p-1/(pq) + 1/q`	`=(qr)/(pq)-1/(pq)+p/(pq)`
	`=(qr-1+p)/(pq)`

`text(Reciprocal of)\ \ x = x^(-1)`

`:.\ text(Reciprocal of)\ \ (qr-1+p)/(pq)=((qr-1+p)/(pq))^(-1)=(pq)/(qr-1+p)`

v1 Functions, 2ADV F1 2004 HSC 1c

Solve `(x+4)/5-(x-2)/6 = 4`. (2 marks)

Show Answers Only

`38`

Show Worked Solution

`(x+4)/5-(x-2)/6`	`= 4`
`30((x+4)/5)-30((x-2)/6)`	`= 30 xx 4`
`6x+24-5x+10`	`= 120`
`x+34`	`= 120`
`:. x`	`= 38`

v2 Functions, 2ADV F1 2017 HSC 1 MC

What is the gradient of the line $6x+7y-1 = 0$?

$-\dfrac{6}{7}$
$\dfrac{6}{7}$
$-\dfrac{7}{6}$
$\dfrac{7}{6}$

Show Answers Only

$A$

Show Worked Solution

$6x+7y-1$	$=0$
$7y$	$=-6x+1$
$y$	$=-\dfrac{6}{7}x+\dfrac{1}{7}$

$\Rightarrow A$

Probability, STD2 S2 2024 HSC 12 MC

A survey of 370 people was conducted to investigate the association between watching Anime and the age of the person.

The two-way table shows the responses collected.

Approximately what percentage of the over 30-year-olds watch Anime?

Show Answers Only

$C$

Show Worked Solution

$\text {Total over } 30=157$

$\text {Over 30s who watch anime = 34}$

$\text {% over 30s who watch anime}\ =\dfrac{34}{157}=21.7\%$

$\Rightarrow C$

EXAMCOPY Functions, 2ADV F1 2009 HSC 1a

Sketch the graph of `y-2x = 3`, showing the intercepts on both axes. (2 marks)

--- 8 WORK AREA LINES (style=blank) ---

Show Answers Only

Show Worked Solution

`y-2x=3\ \ =>\ \ y=2x+3`

`ytext{-intercept}\ = 3`

`text{Find}\ x\ text{when}\ y=0:`

`0-2x=3\ \ =>\ \ x=-3/2`

EXAMCOPY Functions, 2ADV F1 2015 HSC 2 MC

What is the slope of the line with equation `2x - 4y + 3 = 0`?

`-2`
`-1/2`
`1/2`
`2`

Show Answers Only

`C`

Show Worked Solution

`2x – 4y + 3`	`= 0`
`4y`	`= 2x + 3`
`y`	`= 1/2 x + 3/4`

`:.\ text(Slope)\ = 1/2`

`=> C`

v1 Functions, 2ADV F1 2017 HSC 1 MC

What is the gradient of the line $4x-5y-2 = 0$?

$-\dfrac{4}{5}$
$\dfrac{4}{5}$
$\dfrac{5}{4}$
$-\dfrac{5}{4}$

Show Answers Only

$B$

Show Worked Solution

$4x-5y-2$	$=0$
$-5y$	$=-4x + 2$
$y$	$=\dfrac{4}{5}x-\dfrac{2}{5}$

$\Rightarrow B$

Trigonometry, 2ADV T1 2023 HSC 16

The diagram shows a shape `APQBCD`. The shape consists of a rectangle `ABCD` with an arc `PQ` on side `AB` and with side lengths `BC` = 3.6 m and `CD` = 8.0 m.

The arc `PQ` is an arc of a circle with centre `O` and radius 2.1 m and `∠POQ=110°`.

What is the perimeter of the shape `APQBCD`? Give your answer correct to one decimal place. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`23.8\ text{m}`

Show Worked Solution

`text{Arc}\ PQ`	`=110/360 xx pi xx 2 xx 2.1`
	`=4.03171… \ text{m}`

`text{Consider}\ ΔOPQ:`

`sin 55^@`	`=x/2.1`
`x`	`=2.1 xx sin 55^@`
	`=1.7202…`

`PQ=2x=3.440\ text{m}`

`:.\ text{Perimeter}`	`=8+(2xx3.6)+4.031+(8-3.440)`
	`=23.79…\ text{m}`
	`=23.8\ text{m (to 1 d.p.)}`

Measurement, STD2 M6 2023 HSC 33

The diagram shows a shape `APQBCD`. The shape consists of a rectangle `ABCD` with an arc `PQ` on side `AB` and with side lengths `BC` = 3.6 m and `CD` = 8.0 m.

The arc `PQ` is an arc of a circle with centre `O` and radius 2.1 m and `∠POQ=110°`.

What is the perimeter of the shape `APQBCD`? Give your answer correct to one decimal place. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`23.8\ text{m}`

Show Worked Solution

`text{Arc}\ PQ`	`=110/360 xx pi xx 2.1^2`
	`=4.03171… \ text{m}`

`text{Consider}\ ΔOPQ:`

♦ Mean mark 42%.

`sin 55^@`	`=x/2.1`
`x`	`=2.1 xx sin 55^@`
	`=1.7202…`

`PQ=2x=3.440\ text{m}`

`:.\ text{Perimeter}`	`=8+(2xx3.6)+4.031+(8-3.440)`
	`=23.79…`
	`=23.8\ text{m (to 1 d.p.)}`

Statistics, STD2 S4 2023 HSC 3 MC

The number of bees leaving a hive was observed and recorded over 14 days at different times of the day.

Which Pearson's correlation coefficient best describes the observations?

`-0.8`
`-0.2`
`0.2`
`0.8`

Show Answers Only

`D`

Show Worked Solution

`text{Correlation is positive and strong.}`

`text{Best option:}\ r=0.8`

`=>D`

NOTE: Inputting all data points into a calculator is unnecessary and time consuming here.

Functions, 2ADV F1 2022 HSC 12

A student believes that the time it takes for an ice cube to melt (`M` minutes) varies inversely with the room temperature `(T^@ text{C})`. The student observes that at a room temperature of `15^@text{C}` it takes 12 minutes for an ice cube to melt.

Find the equation relating `M` and `T`. (2 marks)

--- 2 WORK AREA LINES (style=lined) ---
By first completing this table of values, graph the relationship between temperature and time from `T=5^@C` to `T=30^@ text{C}`. (2 marks)

\begin{array} {|c|c|c|c|}
\hline \ \ T\ \ & \ \ 5\ \ & \ 15\ & \ 30\ \\
\hline M & & & \\
\hline \end{array}

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

a. `M=180/T`

\begin{array} {|c|c|c|c|}
\hline \ \ T\ \ & \ \ 5\ \ & \ 15\ & \ 30\ \\
\hline M & 36 & 12 & 6 \\
\hline \end{array}

Show Worked Solution

a.	`M`	`prop 1/T`
	`M`	`=k/T`
	`12`	`=k/15`
	`k`	`=15 xx 12`
		`=180`

`:.M=180/T`

♦ Mean mark (a) 49%.

\begin{array} {|c|c|c|c|}
\hline \ \ T\ \ & \ \ 5\ \ & \ 15\ & \ 30\ \\
\hline M & 36 & 12 & 6 \\
\hline \end{array}

Statistics, 2ADV S3 2022 HSC 26

The life span of batteries from a particular factory is normally distributed with a mean of 840 hours and a standard deviation of 80 hours.

It is known from statistical tables that for this distribution approximately 60% of the batteries have a life span of less than 860 hours.

What is the approximate percentage of batteries with a life span between 820 and 920 hours? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`44text{%}`

Show Worked Solution

`mu=840, \ sigma=80`

`ztext{-score (860)}\ = (x-mu)/sigma=(860-840)/80=0.25`

`ztext{-score (820)}\ =(820-840)/80=-0.25`

`ztext{-score (920)}\ =(920-840)/80=1`

`text{50% of batteries have a life span below 840 hours (by definintion)}`

`=>\ text{10% lie between 840 and 860 hours}`

`=>\ text{By symmetry, 10% lie between 820 and 840 hours}`

`=> P(-0.25<=z<=0)=10text{%}`

`:.\ text{Percentage between 820 and 920}`

`=P(-0.25<=z<=1)`

`=P(-0.25<=z<=0) + P(0<=z<=1)`

`=10+34`

`=44text{%}`

Statistics, 2ADV S2 2022 HSC 24

Jo is researching the relationship between the ages of teenage characters in television series and the ages of actors playing these characters.

After collecting the data, Jo finds that the correlation coefficient is 0.4564.

A scatterplot showing the data is drawn. The line of best fit with equation `y=-7.51+1.85 x`, is also drawn.

Describe and interpret the data and other information provided, with reference to the context given. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Correlation coefficient}\ (r) = 0.4564`

- `text{Moderate and positive correlation}`

`text{Gradient of LOBF}\ = 1.85`

- `text{On average, each extra year of a character’s age results}`
  `text{in the actor being 1.85 years older.}`

`text{Mode of data set = 15 years}`

`text{Limitations}`

- `text{Data set is very restricted with just a 4 year range of}`
  `text{character ages.}`
- `text{LOBF not useful when extrapolated to the left as it drops}`
  `text{below zero (on y-axis).}`
- `text{Relationship describes correlation only, not causation.}`

Show Worked Solution

`text{Correlation coefficient}\ (r) = 0.4564`

- `text{Moderate and positive correlation}`

`text{Gradient of LOBF}\ = 1.85`

- `text{On average, each extra year of a character’s age results}`
  `text{in the actor being 1.85 years older.}`

`text{Mode of data set = 15 years}`

`text{Limitations}`

- `text{Data set is very restricted with just a 4 year range of}`
  `text{character ages.}`
- `text{LOBF not useful when extrapolated to the left as it drops}`
  `text{below zero (on y-axis).}`
- `text{Relationship describes correlation only, not causation.}`

Financial Maths, 2ADV M1 2022 HSC 21

Eli is choosing between two investment options.

A table of future value interest factors for an annuity of $1 is shown.

What is the value of Eli's investment after 10 years using Option 1 ? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
What is the difference between the future values after 10 years using Option 1 and Option 2? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`$45\ 097.17`
`$40.87`

Show Worked Solution

a. `text{Monthly r/i}\ = 1.2/12=0.1text{%}\ \ =>\ \ r= 0.001`

`text{Compounding periods}\ (n)=12xx10=120`

`FV`	`=PV(1+r)^n`
	`=40\ 000(1+0.001)^120`
	`=$45\ 097.17`

b. `text{Quarterly r/i}\ = 2.4/4=0.6text{%}\ \ =>\ \ r= 0.006`

`text{Compounding periods}\ (N) =4xx10=40`

`text{Annuity factor (from table) = 45.05630}`

`FV`	`=1000xx45.05630`
	`=45\ 056.30`

`text{Difference}`	`=45\ 097.17-45\ 056.30`
	`=$40.87`

Functions, 2ADV F1 2022 HSC 1 MC

Which of the following could be the graph of `y= -2 x+2`?

Show Answers Only

`A`

Show Worked Solution

`text{By elimination:}`

`y text{-intercept = 2 → Eliminate}\ B and C`

`text{Gradient is negative → Eliminate}\ D`

`=>A`

Statistics, STD2 S5 2022 HSC 37

The life span of batteries from a particular factory is normally distributed with a mean of 840 hours and a standard deviation of 80 hours.

It is known from statistical tables that for this distribution approximately 60% of the batteries have a life span of less than 860 hours.

What is the approximate percentage of batteries with a life span between 820 and 920 hours? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`44text{%}`

Show Worked Solution

`mu=840, \ sigma=80`

`ztext{-score (860)}\ = (x-mu)/sigma=(860-840)/80=0.25`

`ztext{-score (820)}\ =(820-840)/80=-0.25`

`ztext{-score (920)}\ =(920-840)/80=1`

`text{50% of batteries have a life span below 840 hours (by definition)}`

`=>\ text{10% lie between 840 and 860 hours}`

`=>\ text{By symmetry, 10% lie between 820 and 840 hours}`

`=> P(-0.25<=z<=0)=10text{%}`

`:.\ text{Percentage between 820 and 920}`

`=P(-0.25<=z<=1)`

`=P(-0.25<=z<=0) + P(0<=z<=1)`

`=10+34`

`=44text{%}`

♦♦ Mean mark 28%.

Statistics, STD2 S4 2022 HSC 35

Jo is researching the relationship between the ages of teenage characters in television series and the ages of actors playing these characters.

After collecting the data, Jo finds that the correlation coefficient is 0.4564.

A scatterplot showing the data is drawn. The line of best fit with equation `y=-7.51+1.85 x`, is also drawn.

Describe and interpret the data and other information provided, with reference to the context given. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Correlation coefficient}\ (r) = 0.4564`

- `text{Moderate and positive correlation}`

`text{Gradient of LOBF}\ = 1.85`

- `text{On average, each extra year of a character’s age results}`
  `text{in the actor being 1.85 years older.}`

`text{Mode of data set = 15 years}`

`text{Limitations}`

- `text{Data set is very restricted with just a 4 year range of}`
  `text{character ages.}`
- `text{LOBF not useful when extrapolated to the left as it drops}`
  `text{below zero (on y-axis).}`
- `text{Relationship describes correlation only, not causation.}`

Show Worked Solution

`text{Correlation coefficient}\ (r) = 0.4564`

- `text{Moderate and positive correlation}`

`text{Gradient of LOBF}\ = 1.85`

- `text{On average, each extra year of a character’s age results}`
  `text{in the actor being 1.85 years older.}`

`text{Mode of data set = 15 years}`

`text{Limitations}`

- `text{Data set is very restricted with just a 4 year range of}`
  `text{character ages.}`
- `text{LOBF not useful when extrapolated to the left as it drops}`
  `text{below zero (on y-axis).}`
- `text{Relationship describes correlation only, not causation.}`

♦♦ Mean mark 30%.

Statistics, STD2 S4 2022 HSC 23

A teacher surveyed the students in her Year 8 class to investigate the relationship between the average number of hours of phone use per day and the average number of hours of sleep per day.

The results are shown on the scatterplot below.

The data for two new students, Alinta and Birrani, are shown in the table below. Plot their results on the scatterplot. (2 marks)
By first fitting the line of best fit by eye on the scatterplot, estimate the average number of hours of sleep per day for a student who uses the phone for an average of 2 hours per day. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{9 hours (see LOBF in diagram above)}`

Show Worked Solution

b. `text{9 hours (see LOBF in diagram above)}`

Financial Maths, STD2 F5 2022 HSC 30

Eli is choosing between two investment options.

A table of future value interest factors for an annuity of $1 is shown.

What is the value of Eli's investment after 10 years using Option 1 ? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
What is the difference between the future values after 10 years using Option 1 and Option 2? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`$45\ 097.17`
`$40.87`

Show Worked Solution

a. `text{Monthly r/i}\ = 1.2/12=0.1text{%}\ \ =>\ \ r= 0.001`

`text{Compounding periods}\ (n)=12xx10=120`

`FV`	`=PV(1+r)^n`
	`=40\ 000(1+0.001)^120`
	`=$45\ 097.17`

♦ Mean mark 48%.

b. `text{Quarterly r/i}\ = 2.4/4=0.6text{%}\ \ =>\ \ r= 0.006`

`text{Compounding periods}\ (N) =4xx10=40`

`text{Annuity factor (from table) = 45.05630}`

`FV`	`=1000xx45.05630`
	`=45\ 056.30`

`text{Difference}`	`=45\ 097.17-45\ 056.30`
	`=$40.87`

♦ Mean mark 43%.

Financial Maths, STD2 F5 2022 HSC 25

The table shows the future value of an annuity of $1.

Zal is saving for a trip and estimates he will need $15 000. He opens an account earning 3% per annum, compounded annually.

How much does Zal need to deposit every year if he wishes to have enough money for the trip in 4 years time? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
How much interest will Zal earn on his investment over the 4 years? Give your answer to the nearest dollar. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`$3589.09`
`$660`

Show Worked Solution

a. `text{Using the table:}\ r=3text{%},\ \ n=4`

`text{Annuity factor}\ = 4.184`

`text{Let}\ \ A=\ text{amount invested each year}`

`FV`	`=A xx 4.184`
`15\ 000`	`=A xx 4.184`
`:.A`	`=(15\ 000)/4.184`
	`=$3585.09`

b. `text{Total payments}\ = 4 xx 3585.09=$14\ 340.36`

`text{Interest earned}`	`=FV-\ text{total payments}`
	`=15\ 000-14\ 340.36`
	`=659.64`
	`=$660\ \ text{(nearest $)}`

♦♦ Mean mark 33%.

Statistics, STD2 S1 2022 HSC 19

The table shows the types of customer complaints received by an online business in a month.

What are the values of `A` and `B`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The data from the table are shown in the following Pareto chart.
The manager will address 80% of the complaints.
Which types of complaints will the manager address? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`A=160, \ B=96`
`text{Stock shortages and delivery fees.}`

Show Worked Solution

a. `A=98+62=160`

`text{% Damaged items}\ = 8/200 xx 100 = 4text{%}`

`text{Cumulative % after damaged items = 96%}`

`B = 92+4=96`

b. `text{The right hand side cumulative frequency percentage}`

`text{shows that 80% of all complaints received concern}`

`text{stock shortages and delivery fees.}`

`:.\ text{The manager will address stock shortages and delivery fees.}`

♦ Mean mark part (b) 41%.

Statistics, STD2 S5 2022 HSC 18

The marks in a test were normally distributed. The mean mark was 60 and the standard deviation was 15 .

What was the percentage of marks higher than 90? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`2.5text{%}`

Show Worked Solution

`ztext{-score}`	`=(x-mu)/sigma`
	`=(90-60)/15`
	`=2`

`text{% marks > 90}\ = 2.5text{%}`

Mean mark 52%.
COMMENT: A poor State result that warrants attention.

Statistics, STD2 S1 2022 HSC 15 MC

The cumulative frequency graph shows the distribution of the number of movie downloads made by 100 people in one month.

Which box-plot best represents the same data as displayed in the cumulative frequency graph?

Show Answers Only

`C`

Show Worked Solution

`text{1st quartile}\ ~~ 3`

`text{Median}\ ~~ 6`

`text{3rd quartile}\ ~~ 7`

`=>C`

♦♦♦ Mean mark 30%.

Statistics, STD2 S4 2022 HSC 12 MC

For a particular course, the recorded data show a relationship between the number of hours of study per week and the marks achieved out of 100 .

A least-squares regression line is fitted to this dataset. The equation of this line is given by

`M=20+3 H,`

where `M` is the predicted mark and `H` is the number of hours of study per week.

Based on this regression equation, which of the following is correct regarding the predicted mark of a student?

It will be 3 for zero hours of study per week.
It will be 20 for zero hours of study per week.
It will increase by 20 for every additional hour of study per week.
It will increase by 1 for every 3 additional hours of study per week.

Show Answers Only

`B`

Show Worked Solution

`text{Consider Option}\ B:`

`text{If zero hours of study are done per week}\ \ → \ \ H=0`

`:. M=20+(3 xx 0) = 20`

`=>B`

Financial Maths, STD2 F4 2022 HSC 11 MC

In ten years, the future value of an investment will be $150 000. The interest rate is 4% per annum, compounded half-yearly.

Which equation will give the present value `(PV)` of the investment?

`PV=(150\ 000)/((1+0.04)^(10))`
`PV=(150\ 000)/((1+0.04)^(20))`
`PV=(150\ 000)/((1+0.02)^(10))`
`PV=(150\ 000)/((1+0.02)^(20))`

Show Answers Only

`D`

Show Worked Solution

`text{Compounding periods}\ = 10 xx 2 = 20`

`text{Compounding rate}\ = (4text{%})/2 = 2text{%} = 0.02`

`PV=(150\ 000)/((1+0.02)^(20))`

`=>D`

Measurement, STD2 M6 2022 HSC 8 MC

Which true bearing is the same as `text{S} 48^@ text{W}`?

`132^@`
`222^@`
`228^@`
`312^@`

Show Answers Only

`C`

Show Worked Solution

`text{True bearing}`	`=180 + 48`
	`=228^@`

`=>C`

Statistics, STD2 S1 2022 HSC 5 MC

Consider the following dataset.

`{:[13,16,17,17,21,24]:}`

Which row of the table shows how the median and mean are affected when a score of 5 is added to the dataset?

Show Answers Only

`D`

Show Worked Solution

`text{Mean decreases.}`

`text{Median remains 17.}`

`=>D`

Algebra, STD2 A2 2022 HSC 2 MC

Which of the following could be the graph of `y= –2 x+2`?

Show Answers Only

`A`

Show Worked Solution

`text{By elimination:}`

`y text{-intercept = 2 → Eliminate}\ B and C`

`text{Gradient is negative → Eliminate}\ D`

`=>A`

♦ Mean mark 48%.

Statistics, STD2 S5 SM-Bank 7

800 participants auditioned for a stage musical. Each participant was required to complete a series of ability tests for which they received an overall score.

The overall scores were approximately normally distributed with a mean score of 69.5 points and a standard deviation of 6.5 points.

Only the participants who scored at least 76.0 points in the audition were considered successful.

How many of the participants were considered unsuccessful? (2 marks)

Show Answers Only

`672`

Show Worked Solution

`mu = 69.5 \ , \ sigma= 6.5`

`ztext{-score} \ (76) = {76 – 69.5}/6.5 = 1`

`:.\ text{Unsuccessful}`	`=84text(%) xx 800`
	`= 672`

Statistics, 2ADV S2 SM-Bank 5 MC

The stem plot below shows the height, in centimetres, of 20 players in a junior football team.

A player with a height of 179 cm is considered an outlier because 179 cm is greater than

162 cm
169 cm
173 cm
175.5 cm

Show Answers Only

`D`

Show Worked Solution

`Q_1 = (148 + 148)/2 = 148`

`Q_3 = (158 + 160)/2 = 159`

`IQR = 159 – 148 = 11`

`text{Upper fence}`	`= Q_3 + 1.5 xx IQR`
	`= 159 + 1.5 xx 11`
	`= 175.5`

`=> D`

Statistics, STD2 S1 SM-Bank 5 MC

The stem plot below shows the height, in centimetres, of 20 players in a junior football team.

A player with a height of 179 cm is considered an outlier because 179 cm is greater than

162 cm
169 cm
173 cm
175.5 cm

Show Answers Only

`D`

Show Worked Solution

`Q_1 = (148 + 148)/2 = 148`

`Q_3 = (158 + 160)/2 = 159`

`IQR = 159 – 148 = 11`

`text{Upper fence}`	`= Q_3 + 1.5 xx IQR`
	`= 159 + 1.5 xx 11`
	`= 175.5`

`=> D`

Statistics, STD2 S5 2021 HSC 41

In a particular city, the heights of adult females and the heights of adult males are each normally distributed.

Information relating to two females from that city is given in Table 1.

The means and standard deviations of adult females and males, in centimetres, are given in Table 2.

A selected male is taller than 84% of the population of adult males in this city.

By first labelling the normal distribution curve below with the heights of the two females given in Table 1, calculate the height of the selected male, in centimetres, correct to two decimal places. (4 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`178.95 \ text{cm}`

Show Worked Solution

`z text{-score (175 cm, female)} = 2`

♦♦♦ Mean mark 16%.

`z text{-score (160.6 cm, female)} = -1`

`text{Find} \ mu \ text{of female heights:}`

`mu – sigma`	`= 160.6`
`mu + 2sigma`	`= 175`
`3 sigma`	`= 175 – 160.6`
`sigma`	`= 14.4/3`
	`= 4.8 \ text{cm}`
`:. \ mu`	`= 165.4 \ text{cm}`

`text{Selected male’s height has} \ z text{-score} = 1`

`mu text{(male)} = 1.05 times 165.4 = 173.67`

`sigma \ text{(male)} = 1.1 times 4.8 = 5.28`

`:. \ text{Actual male height}`	`= 173.67 + 5.28`
	`= 178.95 \ text{cm}`

Statistics, 2ADV S2 2021 HSC 17

For a sample of 17 inland towns in Australia, the height above sea level, `x` (metres), and the average maximum daily temperature, `y` (°C), were recorded.

The graph shows the data as well as a regression line.

The equation of the regression line is `y = 29.2 − 0.011x`.

The correlation coefficient is `r = –0.494`.

i. By using the equation of the regression line, predict the average maximum daily temperature, in degrees Celsius, for a town that is 540 m above sea level. Give your answer correct to one decimal place. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
ii. The gradient of the regression line is −0.011. Interpret the value of this gradient in the given context. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
The graph below shows the relationship between the latitude, `x` (degrees south), and the average maximum daily temperature, `y` (°C), for the same 17 towns, as well as a regression line.

The equation of the regression line is `y = 45.6 − 0.683x`.
The correlation coefficient is `r = − 0.897`.
Another inland town in Australia is 540 m above sea level. Its latitude is 28 degrees south.
Which measurement, height above sea level or latitude, would be better to use to predict this town’s average maximum daily temperature? Give a reason for your answer. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

i. `23.3°text(C)`
ii. `text(See Worked Solutions)`
`text(Latitude. Correlation coefficient shows a stronger relationship.)`

Show Worked Solution

a.i.	`y`	`=29.2 – 0.011(540)`
		`=23.26`
		`=23.3°text{C (1 d.p.)`

a.ii. `text(On average, the average maximum daily temperature of)`

`text(inland towns drops by 0.011 of a degree for every metre)`

`text(above sea level the town is situated.)`

b. `text(The correlation co-efficient of the regression line using)`

`text(latitude is significantly stronger than the equivalent)`

`text(co-efficient for the regression line using height above sea)`

`text(level.)`

`:.\ text(The equation using latitude is preferred.)`

Statistics, STD2 S4 2021 HSC 33

For a sample of 17 inland towns in Australia, the height above sea level, `x` (metres), and the average maximum daily temperature, `y` (°C), were recorded.

The graph shows the data as well as a regression line.

The equation of the regression line is `y = 29.2 − 0.011x`.

The correlation coefficient is `r = –0.494`.

i. By using the equation of the regression line, predict the average maximum daily temperature, in degrees Celsius, for a town that is 540 m above sea level. Give your answer correct to one decimal place. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
ii. The gradient of the regression line is −0.011. Interpret the value of this gradient in the given context. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The graph below shows the relationship between the latitude, `x` (degrees south), and the average maximum daily temperature, `y` (°C), for the same 17 towns, as well as a regression line.

The equation of the regression line is `y = 45.6 − 0.683x`.
The correlation coefficient is `r = − 0.897`.
Another inland town in Australia is 540 m above sea level. Its latitude is 28 degrees south.
Which measurement, height above sea level or latitude, would be better to use to predict this town’s average maximum daily temperature? Give a reason for your answer. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

i. `23.3°text(C)`
ii. `text(See Worked Solutions)`
`text(Latitude. Correlation coefficient shows a stronger relationship.)`

Show Worked Solution

a.i.	`y`	`=29.2 – 0.011(540)`
		`=23.26`
		`=23.3°text{C (1 d.p.)`

♦♦ Mean mark part a.ii. 28%.

a.ii. `text(On average, the average maximum daily temperature of)`

`text(inland towns drops by 0.011 of a degree for every metre)`

`text(above sea level the town is situated.)`

♦♦♦ Mean mark part b 18%.

b. `text(The correlation co-efficient of the regression line using)`

`text(latitude is significantly stronger than the equivalent)`

`text(co-efficient for the regression line using height above sea)`

`text(level.)`

`:.\ text(The equation using latitude is preferred.)`

Financial Maths, STD2 F5 2021 HSC 31

Present value interest factors for an annuity of $1 for various interest rates (`r`) and numbers of periods (`N`) are given in the table.

A bank lends Martina $500 000 to purchase a home, with interest charged at 1.5% per annum compounding monthly. She agrees to repay the loan by making equal monthly repayments over a 30-year period.

How much should the monthly payment be in order to pay off the loan in 30 years?

Give your answer correct to the nearest cent. (2 marks)

Show Answers Only

`$ 1725.60`

Show Worked Solution

`text{Monthly interest rate}\ (r) = 1.5/12 = 0.125text(%) = 0.00125`

♦ Mean mark 43%.

`N = 30 xx 12 = 360`

`=>\ text(PV annuity factor = 289.75411)`

`:.\ text{Monthly payment}`	`= (500\ 000)/289.75411`
	`= $1725.60`

Trigonometry, 2ADV T1 2021 HSC 18

The diagram shows a triangle `ABC` where `AC` = 25 cm, `BC` = 16 cm, `angle BAC` = 28° and angle `ABC` is obtuse.

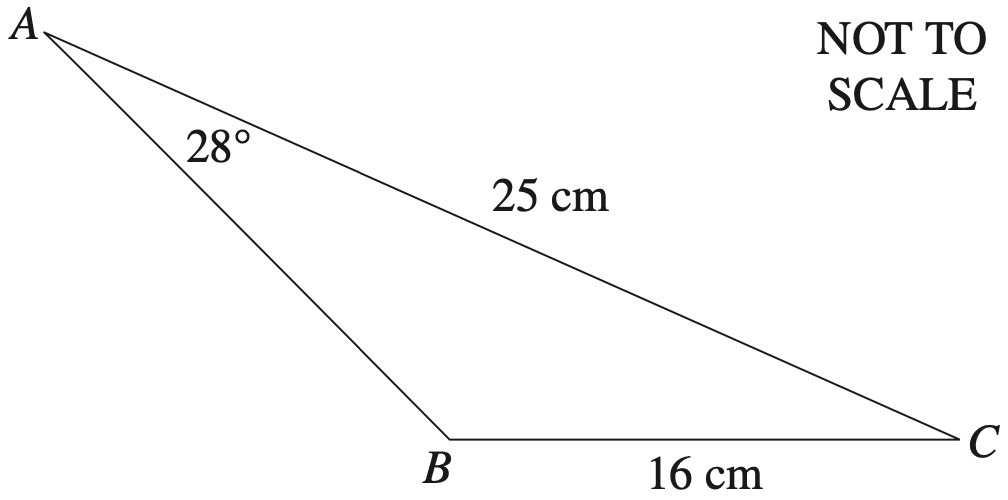
Find the size of the obtuse angle `ABC` correct to the nearest degree. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`133°`

Show Worked Solution

`text(Using the sine rule:)`

`sin theta/25`	`= (sin 28°)/16`
`sin theta`	`= (25 xx sin 28°)/16`
`sin theta`	`= 0.73355`
`theta`	`= 47°`

`:. angleABC`	`= 180-47`
	`= 133°`

Financial Maths, 2ADV M1 2021 HSC 25

A table of future value interest factors for an annuity of $1 is shown.

Simone deposits $1000 into a savings account at the end of each year for 8 years. The interest rate for these 8 years is 0.75% per annum, compounded annually.

After the 8th deposit, Simone stops making deposits but leaves the money in the savings account. The money in her savings account then earns interest at 1.25% per annum, compounded annually, for a further two years.

Find the amount of money in Simone's savings account at the end of ten years. (3 marks)

Show Answers Only

`$8419.81`

Show Worked Solution

`text(In 1st 8 years:)`

Mean mark 52%.

`text(Future value factor = 8.2132)`

`text(Value of annuity)`	`= 8.2132 xx 1000`
	`= $8213.20`

`text(After 10 years:)`

`text(Value of investment)`	`= 8213.2 xx (1.0125)^2`
	`= $$8419.81`

Financial Maths, STD2 F5 2021 HSC 40

A table of future value interest factors for an annuity of $1 is shown.

Simone deposits $1000 into a savings account at the end of each year for 8 years. The interest rate for these 8 years is 0.75% per annum, compounded annually.

Find the amount of money in Simone's savings account at the end of ten years. (3 marks)

Show Answers Only

`$8419.81`

Show Worked Solution

`text(In 1st 8 years:)`

♦ Mean mark 35%.

`text(Future value factor = 8.2132)`

`text(Value of annuity)`	`= 8.2132 xx 1000`
	`= $8213.20`

`text(After 10 years:)`

`text(Value of investment)`	`= 8213.2 xx (1.0125)^2`
	`= $8419.81`

Statistics, STD2 S5 2021 HSC 38

A random variable is normally distributed with mean 0 and standard deviation 1. The table gives the probability that this random variable lies between 0 and `z` for different values of `z`.

The probability values given in the table for different values of `z` are represented by the shaded area in the following diagram.

Using the table, show that the probability that a value from a random variable that is normally distributed with mean 0 and standard deviation 1 is greater than 0.3 is equal to 0.3821. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Birth weights are normally distributed with a mean of 3300 grams and a standard deviation of 570 grams. By first calculating a `z`-score, find how many babies, out of 1000 born, are expected to have a birth weight greater than 3471 grams. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(See Worked Solutions)`
`382`

Show Worked Solution

a. `P(z>0)=0.5`

♦♦♦ Mean mark part (a) 1%.
COMMENT: Note the Std2 and Advanced questions varied slightly but used the same table and graph.

`P(0<z<0.3)=0.1179`

`P(z>0.3) = 0.5-0.1179=0.3821`

b.	`z text{-score (3471)}`	`=(x-mu)/sigma`
		`=(3471-3300)/570`
		`=0.3`

`P(z>0.3) = 0.3821\ \ text{(see part (a))}`

`:.\ text(Number of babies > 3471 grams)`
`=1000 xx 0.3821`
`=382\ \ text{(nearest whole)}`

Measurement, STD2 M6 2021 HSC 37

The diagram shows a triangle `ABC` where `AC` = 25 cm, `BC` = 16 cm, `angle BAC` = 28° and angle `ABC` is obtuse.

Find the size of the obtuse angle `ABC` correct to the nearest degree. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`133°`

Show Worked Solution

`text(Using the sine rule:)`

♦♦ Mean mark 31%.

`sin theta/25`	`= (sin 28°)/16`
`sin theta`	`= (25 xx sin 28°)/16`
`sin theta`	`= 0.73355`
`theta`	`= 47°`

`:. angleABC`	`= 180-47`
	`= 133°`

Statistics, 2ADV S3 2021 HSC 22

A random variable is normally distributed with mean 0 and standard deviation 1. The table gives the probability that this random variable lies between 0 and `z` for different values of `z`.

The probability values given in the table for different values of `z` are represented by the shaded area in the following diagram.

Using the table, find the probability that a value from a random variable that is normally distributed with a mean of 0 and standard deviation 1 lies between 0.1 and 0.5. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Birth weights are normally distributed with a mean of 3300 grams and a standard deviation of 570 grams. By first calculating a `z`-score, find how many babies, out of 1000 born, are expected to have a birth weight greater than 3528 grams. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`0.1517`
`345\ text(babies)`

Show Worked Solution

♦♦ Mean mark part (a) 29%.
COMMENT: Note the Advanced and Std2 questions varied slightly but used the same table and graph.

a.	`P(0.1 < x < 0.5)`	`= 0.1915 – 0.0398`
		`= 0.1517`

b. `mu = 330, sigma = 570`

♦ Mean mark part (b) 48%.

`ztext(-score)\ (3528)`	`= (x – mu)/sigma`
	`= (3528 – 3300)/570`
	`= 0.4`

`P(ztext(-score) > 0.4)`	`= 0.5 – 0.1554`
	`= 0.3446`

`:.\ text(Expected babies > 3528 grams)`

`= 1000 xx 0.3446`

`= 344.6`

`~~ 345\ text(babies)`

Statistics, STD2 S4 2021 HSC 28

A salesperson is interested in the relationship between the number of bottles of lemonade sold per day and the number of hours of sunshine on the day.

The diagram shows the dataset used in the investigation and the least-squares regression line.

Find the equation of the least-squares regression line relating to the dataset. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Suppose a sixth data point was collected on a day which had 10 hours of sunshine. On that day 45 bottles of lemonade were sold.
What would happen to the gradient found in part (a)? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`y=3.2x+2`
`text{Gradient would increase (steepen).}`

Show Worked Solution

a. `text(Method 1)`

♦ Mean mark part (a) 37%.

`text{Input data points (in Stats Mode “Ax + B”):}`

`(2,8), (3, 11), (5, 19), (6, 22), (9, 30)`

`=>\ y=3.2x + 2`

`text(Method 2)`

`text{Find gradient using (0, 2) and (5, 18)}:`

`m=(18-2)/(5-0) = 3.2,\ \ ytext(-intercept)\ = 2`

`:.\ text(Equation:)\ y=3.2x + 2`

Mean mark part (b) 53%.

b. `text(Method 1)`

`text{Add (10, 45) to the data set in Stats Mode above:}`

`text(Gradient increases to 4.1.)`

`text(Method 2)`

`text{Data point (10, 45) lies above the regression line.`

`:.\ text{Gradient would increase (steepen).}`

Measurement, STD2 M6 2021 HSC 14 MC

Consider the diagram below.

What is the true bearing of `A` from `B`?

`025^@`
`065^@`
`115^@`
`295^@`

Show Answers Only

`D`

Show Worked Solution

♦♦ Mean mark 28%.

`\text{Bearing (A from B)}`	`= 270 + 25`
	`= 295^@`

`=> D`

Financial Maths, STD2 F5 2021 HSC 21

Julie invests $12 500 in a savings account. Interest is paid at a fixed monthly rate. At the end of each month, after the monthly interest is added, Julie makes a deposit of $500.

Julie has created a spreadsheet to show the activity in her savings account. The details for the first 6 months are shown.

By finding the monthly rate of interest, complete the final row above for the 7th month. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`15\ 624.20, 23.44, 16\ 147.64`

Show Worked Solution

`\text{Monthly interest rate} = \frac{18.75}{12\ 500} = 0.0015 =\ text{0.15%}`

♦ Mean mark 43%.

`\text{Row 7 calculations:}`

`\text{Beginning balance}`	`= 15\ 624.20`
`\text{Monthly interest}`	`= 15\ 624.20 \times 0.0015`
	`= 23.44`

`\text{End of month balance}`	`= 15\ 624.20 + 23.44 + 500`
	`= 16\ 147.64`

Functions, 2ADV F1 2021 HSC 11

Solve `x+(x-1)/2 = 9`. (2 marks)

Show Answers Only

`19/3`

Show Worked Solution

`x+(x-1)/2`	`=9`
`2x + x-1`	`=18`
`3x`	`=19`
`x`	`=19/3`

Probability, 2ADV S1 2021 HSC 6 MC

There are 8 chocolates in a box. Three have peppermint centres (P) and five have caramel centres (C).

Kim randomly chooses a chocolate from the box and eats it. Sam then randomly chooses and eats one of the remaining chocolates.

A partially completed probability tree is shown.

What is the probability that Kim and Sam choose chocolates with different centres?

`\frac{15}{64}`
`\frac{15}{56}`
`\frac{15}{32}`
`\frac{15}{28}`

Show Answers Only

`D`

Show Worked Solution

`Ptext{(different centres)}`	`= P text{(PC)} + P text{(CP)}`
	`=\frac{3}{8} · \frac{5}{7} + \frac{5}{8} · \frac{3}{7}`
	`= \frac{15}{56} + \frac{15}{56}`
	`= \frac{15}{28}`

`=> D`

Probability, STD2 S2 2021 HSC 11 MC

There are 8 chocolates in a box. Three have peppermint centres (P) and five have caramel centres (C).

Kim randomly chooses a chocolate from the box and eats it. Sam then randomly chooses and eats one of the remaining chocolates.

A partially completed probability tree is shown.

What is the probability that Kim and Sam choose chocolates with different centres?

`\frac{15}{64}`
`\frac{15}{56}`
`\frac{15}{32}`
`\frac{15}{28}`

Show Answers Only

`D`

Show Worked Solution

♦♦ Mean mark 35%.

`Ptext{(different centres)}`	`= P text{(PC)} + P text{(CP)}`
	`=\frac{3}{8} · \frac{5}{7} + \frac{5}{8} · \frac{3}{7}`
	`= \frac{15}{56} + \frac{15}{56}`
	`= \frac{15}{28}`

`=> D`

Functions, 2ADV F2 2021 HSC 5 MC

Which of the following best represents the graph of `y = 10 (0.8)^x`?

Show Answers Only

`A`

Show Worked Solution

`\text{By elimination:}`

`\text{When} \ x = 0 \ , \ y = 10(0.8) ^0 = 10`

`-> \ text{Eliminate B and D}`

`text(As)\ \ x→oo, \ y→0`

`-> \ text{Eliminate C}`

`=> A`

Algebra, STD2 A4 2021 HSC 10 MC

Which of the following best represents the graph of `y = 10 (0.8)^x`?

Show Answers Only

`A`

Show Worked Solution

`\text{By elimination:}`

♦ Mean mark 41%.

`\text{When} \ x = 0 \ , \ y = 10(0.8) ^0 = 10`

`-> \ text{Eliminate B and D}`

`text(As)\ \ x→oo, \ y→0`

`-> \ text{Eliminate C}`

`=> A`

Statistics, 2ADV S2 2021 HSC 4 MC

The number of downloads of a song on each of twenty consecutive days is shown in the following graph.

Which of the following graphs best shows the cumulative number of downloads up to and including each day?

Show Answers Only

`C`

Show Worked Solution

`text{The gradient of the cumulative frequency histogram}`

`text{will increase gradually, be steepest at day 10 then}`

`text{decrease gradually.}`

`=> C`

Statistics, STD2 S1 2021 HSC 7 MC

The number of downloads of a song on each of twenty consecutive days is shown in the following graph.

Which of the following graphs best shows the cumulative number of downloads up to and including each day?

Show Answers Only

`C`

Show Worked Solution

`text{The gradient of the cumulative frequency histogram}`

♦ Mean mark 50%.

`text{will increase gradually, be steepest at day 10 then}`

`text{decrease gradually.}`

`=> C`

Statistics, STD2 S1 2021 HSC 3 MC

The stem-and-leaf plot shows the number of goals scored by a team in each of ten netball games.

What is the mode of this dataset?

Show Answers Only

`C`

Show Worked Solution

`\text{Mode} -> \text{data point with highest frequency}`

`\text{Mode} = 25`

`=> C`

\(6x+7y-1\)	\(=0\)
\(7y\)	\(=-6x+1\)
\(y\)	\(=-\dfrac{6}{7}x+\dfrac{1}{7}\)

\(4x-5y-2\)	\(=0\)
\(-5y\)	\(=-4x + 2\)
\(y\)	\(=\dfrac{4}{5}x-\dfrac{2}{5}\)