SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Probability, STD2 S2 2006 HSC 6 MC

Marcella is planning to roll a standard six-sided die 60 times.

How many times would she expect to roll the number 4?

  1.   6
  2.   10
  3.   15
  4.   20
Show Answers Only

`B`

Show Worked Solution

`P(4) = 1/6`

`:.\ text(Expected times to roll 4)`

`= 1/6 xx text(number of rolls)`

`= 1/6 xx 60`

`= 10`

`=>  B`

Statistics, STD2 S1 2006 HSC 4 MC

A set of scores is displayed in a stem-and-leaf plot.
 

 2UG-2006-4MC

 
What is the median of this set of scores?

  1.   28
  2.   30
  3.   33
  4.   47
Show Answers Only

`C`

Show Worked Solution

`text(10 scores)`

`text(Median)` `= text{5th + 6th}/2`
  `= (28 + 38)/2`
  `= 33`

`=>  C`

Probability, STD2 S2 2006 HSC 1 MC

The probability of an event occurring is `9/10.`

Which statement best describes the probability of this event occurring?

  1.    The event is likely to occur.
  2.    The event is certain to occur.
  3.    The event is unlikely to occur.
  4.    The event has an even chance of occurring.
Show Answers Only

`A`

Show Worked Solution

`text(The event is highly likely to occur)`

`text(but not certain.)`

`=>  A`

Probability, STD2 S2 2005 HSC 3 MC

Four radio stations reported the probability of rain as shown in the table.
 

Which radio station reported the highest probability of rain?

  1.    `text(2AT)`
  2.    `text(2BW)`
  3.    `text(2CZ)`
  4.    `text(2DL)`
Show Answers Only

`D`

Show Worked Solution

`text(Converting all probabilities to decimals)`

`2AT` `= 0.53`
`2BW` `= 0.17`
`2CZ` `= 0.52`
`2DL` `= 0.60`

`=> D`

Statistics, STD2 S1 2005 HSC 1 MC

What is the mean of the set of scores?

`3, \ 4, \ 5, \ 6, \ 6, \ 8, \ 8, \ 8, \ 15`
 

  1. 6
  2. 7
  3. 8
  4. 9
Show Answers Only

`B`

Show Worked Solution
`text(Mean)` `= ((3 + 4 + 5 +6 + 6 + 8 + 8 + 8 + 15))/9`
  `= 63/9`
  `= 7`

 
`=> B`

Statistics, STD2 S1 2004 HSC 8 MC

This sector graph shows the distribution of 116 prizes won by three schools: X, Y and Z.
 

 
How many prizes were won by School X?

  1.   26
  2.   32
  3.   81
  4.   99
Show Answers Only

`B`

Show Worked Solution

`text(Centre angle of School X sector)`

`= 100^@\ text{(by measurement)}`
 

`:.\ text(Prizes won by school X)`

`= 100/360 xx 116`

`= 32.22\ …`

`=> B`

Statistics, STD2 S1 2004 HSC 6-7 MC

Use the set of scores  1, 3, 3, 3, 4, 5, 7, 7, 12  to answer Questions 6 and 7.
 

Question 6

What is the range of the set of scores?

  1. 6
  2. 9
  3. 11
  4. 12

 

Question 7

What are the median and the mode of the set of scores?

  1. Median 3, mode 5
  2. Median 3, mode 3
  3. Median 4, mode 5
  4. Median 4, mode 3
Show Answers Only

`text(Question 6:)\ C`

`text(Question 7:)\ D`

Show Worked Solution

`text(Question 6)`

`text(Range)` `= text(High) – text(Low)`
  `= 12 – 1`
  `= 11`

`=> C`

 

`text(Question 7)`

`text(9 scores)`

`:.\ text(Median)` `= (9 + 1) / 2`
  `=5 text(th score)`
  `= 4`

`text(Mode) = 3`

`=> D`

Probability, STD2 S2 2007 HSC 25a

Give an example of an event that has a probability of exactly  `3/4`.   (1 mark)

Show Answers Only

`text(Choosing a red ball out of a bag that)`

`text(contains 3 red balls and 1 green ball.)`

`text {(} text(An infinite amount of examples are)`

`text(possible) text{).}`

Show Worked Solution

`text(Choosing a red ball out of a bag that contains)`

`text(3 red balls and 1 green ball.)`

`text {(} text(An infinite amount of examples are)`

`text(possible) text{).}`

Statistics, STD2 S1 2007 HSC 24a

Consider the following set of scores:

`3, \ 5, \ 5, \ 6, \ 8, \ 8, \ 9, \ 10, \ 10, \ 50.` 

  1. Calculate the mean of the set of scores.   (1 mark)

  2. What is the effect on the mean and on the median of removing the outlier?   (2 marks)

Show Answers Only
  1. `11.4`
  2. `text{If the outlier (50) is removed, the mean}`

     

    `text(would become lower.)`

  3.  

    `text(Median will NOT change.)`

Show Worked Solution

i.  `text(Total of scores)`

`= 3 + 5 + 5 + 6 + 8 + 8 + 9 + 10 + 10 +50`

`= 114`
 

`:.\ text(Mean) = 114/10 = 11.4`

 

ii.  `text(Mean)`

`text{If the outlier (50) is removed, the mean}`

`text(would become lower.)`
 

`text(Median)`

`text(The current median (10 data points))`

`= text(5th + 6th)/2 = (8 + 8)/2 = 8`

`text(The new median (9 data points))`

`=\ text(5th value)`

`= 8`
 

`:.\ text(Median will NOT change.)`

Probability, STD2 S2 2007 HSC 2 MC

Each student in a class is given a packet of lollies. The teacher records the number of red lollies in each packet using a frequency table.
 

What is the relative frequency of a packet of lollies containing more than three red lollies?

  1.    `4/19`
  2.    `4/15`
  3.    `11/19`
  4.    `11/15`
Show Answers Only

`A`

Show Worked Solution

`text(# Packets with more than 3)`

`= 3 + 1 = 4`

`text(Total packets) = 19`

`:.\ text(Relative Frequency) = 4/19`

`=>  A`

Statistics, STD2 S1 2008 HSC 26d

The graph shows the predicted population age distribution in Australia in 2008.
 

 

  1. How many females are in the 0–4 age group?  (1 mark)

  2. What is the modal age group?   (1 mark)

  3. How many people are in the 15–19 age group?   (2 marks)

  4. Give ONE reason why there are more people in the 80+ age group than in the 75–79 age group.   (1 mark)

Show Answers Only
  1. `600\ 000`
  2. `35-39`
  3. `1\ 450\ 000`
  4. `text(The 80+ group includes all people over 80)`

  5.  

    `text(and is not restricted by a 5-year limit.)`

Show Worked Solution
i.    `text{# Females (0-4)}` `= 0.6 xx 1\ 000\ 000`
    `= 600\ 000`

 

ii.    `text(Modal age group)\ =` `text(35 – 39)`

 

iii.   `text{# Males (15-19)}` `= 0.75 xx 1\ 000\ 000`
    `= 750\ 000`

 

`text{# Females (15-19)}` `= 0.7 xx 1\ 000\ 000`
  `= 700\ 000`

 

`:.\ text{Total People (15-19)}` `= 750\ 000 + 700\ 000`
  `= 1\ 450\ 000`

 

iv.   `text(The 80+ group includes all people over 80)`
  `text(and is not restricted by a 5-year limit.)`

Statistics, STD2 S1 2008 HSC 23f

Christina has completed three Mathematics tests. Her mean mark is 72%.

What mark (out of 100) does she have to get in her next test to increase her mean mark to 73%?   (2 marks)

Show Answers Only

`76`

Show Worked Solution

`text(Total marks in 3 tests)`

`= 3 xx 72`

`= 216`

`text(We need 4-test mean) = 73`

`text(i.e.)\ \ \ ` `text{Total Marks (4 tests)}-:4` `= 73`
  `text(Total Marks)\ text{(4 tests)}` `= 292`

 

`:.\ text(4th test score)` `= 292 – 216`
  `= 76`

Statistics, STD2 S1 2008 HSC 23e

In a survey, 450 people were asked about their favourite takeaway food. The results are displayed in the bar graph.

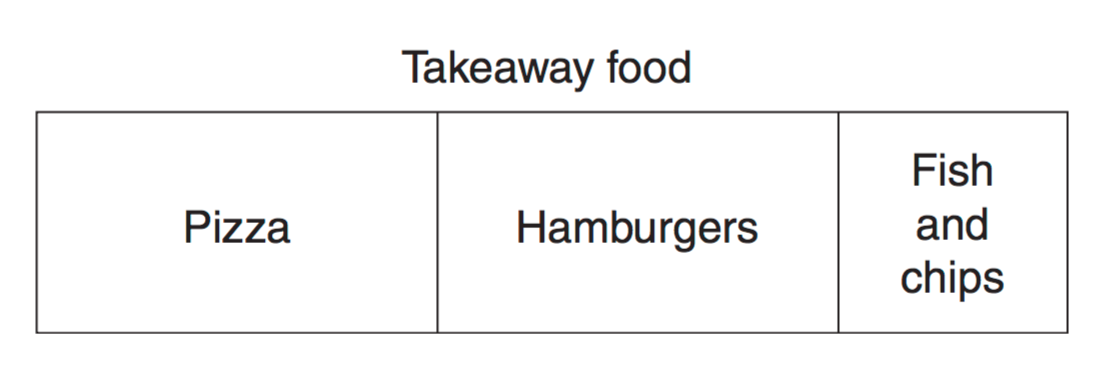
2008 23e
 
How many people chose pizza as their favourite takeaway food?   (2 marks)

Show Answers Only

`175`

Show Worked Solution

`text(Number of people who chose pizza)`

COMMENT: This question required measurement of the actual image on the exam. The same methodology works here.

`= text{Length of pizza section}/text{Total length of bar} xx 450`

`~~ 7/18 xx 450`

`~~ 175`
 

`:.\ 175\ text(people chose pizza.)`

Probability, STD2 S2 2008 HSC 16 MC

A bag contains some marbles. The probability of selecting a blue marble at random from this bag is  `3/8`.

Which of the following could describe the marbles that are in the bag?

  1.    `3`  blue,  `8`  red
  2.    `6`  blue,  `11`  red
  3.    `3`  blue,  `4`  red,  `4`  green
  4.    `6`  blue,  `5`  red,  `5`  green 
Show Answers Only

`D`

Show Worked Solution

`P(B) = 3/8`

`text(In)\ A,\ \ ` `P(B) = 3/11`
`text(In)\ B,\ \ ` `P(B) = 6/17 `
`text(In)\ C,\ \ ` `P(B) = 3/11`
`text(In)\ D,\ \ ` `P(B) = 6/16 = 3/8`

`=>  D`

Statistics, STD2 S1 2008 HSC 13 MC

The height of each student in a class was measured and it was found that the mean height was 160 cm.

Two students were absent. When their heights were included in the data for the class, the mean height did not change.

Which of the following heights are possible for the two absent students?

  1.    155 cm and 162 cm
  2.    152 cm and 167 cm
  3.    149 cm and 171 cm
  4.    143 cm and 178 cm
Show Answers Only

`C`

Show Worked Solution

`text(S) text(ince the mean doesn’t change)`

`=>\ text(2 absent students must have a)`

`text(mean height of 160 cm.)`

`text(Considering each option given,)`

`(149 + 171) -: 2 = 160`

`=>  C`

Measurement, STD2 M1 2008 HSC 11 MC

The diagram shows the floor of a shower. The drain in the floor is a circle with a diameter of 10 cm.

What is the area of the shower floor, excluding the drain?
 

 
 

  1. 9686 cm²
  2. 9921 cm²
  3. 9969 cm²
  4. 10 000 cm²
Show Answers Only

`B`

Show Worked Solution
COMMENT: Students should see that answers are all in cm², and therefore use cm as the base unit for their calculations. 
`text(Area)` `=\ text(Square – Circle)`
  `= (100 xx 100)-(pi xx 5^2)`
  `= 10\ 000-78.5398…`
  `= 9921.46…\ text(cm²)`

 
`=>  B`

Statistics, STD2 S1 2008 HSC 8 MC

What is the median of the following set of scores?
 

 
 

  1.    12
  2.    13
  3.    14
  4.    15
Show Answers Only

`C`

Show Worked Solution
`text(Median` `=(n+1)/2`
  `=(33+1)/2`
  `=\ text (17th score)`

 

`:.\ text(Median is 14)`

`=>  C`

Statistics, STD2 S1 2008 HSC 3 MC

The stem-and-leaf plot represents the daily sales of soft drink from a vending machine.

If the range of sales is 43, what is the value of  2008 3 mc  ?

 
 

  1.    `4` 
  2.    `5`
  3.    `24`
  4.    `25`
Show Answers Only

`A`

Show Worked Solution

`text(Range = High) – text(Low) = 43`

`:.\ 67 – text(Low)` `= 43`
`text(Low)` `= 24`

`:.\ N = 4`

`=>  A`

Measurement, STD2 M1 2014 HSC 12 MC

A path 1.5  metres wide surrounds a circular lawn of radius 3 metres. 

What is the approximate area of the path?

  1. 7.1 m²
  2. 21.2 m²
  3. 35.3 m²
  4. 56.5 m²
Show Answers Only

`C`

Show Worked Solution

`text(Area of annulus)`

`= pi (R^2-r^2)`

`= pi (4.5^2-3^2)`

`= pi (11.25)`

`=35.3\ text{m²  (1 d.p.)}`
 

`=>  C`

Statistics, STD2 S1 2011 HSC 25b

The graph below displays data collected at a school on the number of students
in each Year group, who own a mobile phone.
 

2UG 2011 25b
 

  1. Which Year group has the highest percentage of students with mobile phones? (1 mark)

  2. Two students are chosen at random, one from Year 9 and one from Year 10.

     

    Which student is more likely to own a mobile phone?

     

    Justify your answer with suitable calculations. (2 marks)

  3. Identify a trend in the data shown in the graph. (1 mark)

Show Answers Only
  1. `text{Year 12 (100%)}`
  2. `text(Year 10)`
  3. `text(See Worked Solutions for detail)`
Show Worked Solution

i.   `text(Year 12 (100%))`

MARKER’S COMMENT: Many students ignore the instruction to use calculations and lose marks as a result.
 

ii.     `text(% Ownership in Year 9)` `=55/70`
    `=\ text{78.6%  (1d.p.)}`
      `text(% Ownership in Year 10)` `=50/60`
    `=\ text{83.3%  (1d.p.)}`

  
`:.\ text(The Year 10 student is more likely to own a mobile phone.)`

 

iii.   `text(% Ownership increases as students)`

 `text(progress from Year 7 to Year 12.)`

Probability, STD2 S2 2011 HSC 24b

A die was rolled 72 times. The results for this experiment are shown in the table.
  

\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex} \textit{Number obtained} \rule[-1ex]{0pt}{0pt} & \textit{Frequency} \\
\hline
\rule{0pt}{2.5ex} \ 1 \rule[-1ex]{0pt}{0pt} & 16 \\
\hline
\rule{0pt}{2.5ex} \ 2 \rule[-1ex]{0pt}{0pt} & 11 \\
\hline
\rule{0pt}{2.5ex} \ 3 \rule[-1ex]{0pt}{0pt} & \textbf{A} \\
\hline
\rule{0pt}{2.5ex} \ 4 \rule[-1ex]{0pt}{0pt} & 8 \\
\hline
\rule{0pt}{2.5ex} \ 5 \rule[-1ex]{0pt}{0pt} & 12 \\
\hline
\rule{0pt}{2.5ex} \ 6 \rule[-1ex]{0pt}{0pt} & 15 \\
\hline
\end{array}

  1. Find the value of  `A`.   (1 mark)

  2. What was the relative frequency of obtaining a 4.   (1 mark)

  3. If the die was unbiased, which number was obtained the expected number of times?   (1 mark)

Show Answers Only
  1. \(10\)
  2. \(\dfrac{1}{9}\)
  3. \(5\)
Show Worked Solution
i.     \(\text{Since die rolled 72 times}\)
\(\therefore\ A\) \(=72-(16+11+8+12+15)\)
  \(=72-62\)
  \(=10\)
♦ Mean mark 38%
IMPORTANT: Many students confused ‘relative frequency’ with ‘frequency’ and incorrectly answered 8.
ii.     \(\text{Relative frequency of 4}\) \(=\dfrac{8}{72}\)
  \(=\dfrac{1}{9}\)

 

iii.  \(\text{Expected frequency of any number}\)
\(=\dfrac{1}{6}\times 72\)
\(=12\)
 
\(\therefore\ \text{5 was obtained the expected number of times.}\)

Statistics, STD2 S1 2011 HSC 17 MC

The heights of the players in a basketball team were recorded as 1.8 m, 1.83 m, 1.84 m, 1.86 m and 1.92 m. When a sixth player joined the team, the average height of the players increased by 1 centimetre.

What was the height of the sixth player?

  1.   1.85 m
  2.   1.86 m
  3.   1.91 m
  4.   1.93 m
Show Answers Only

`C`

Show Worked Solution
`text(Old Mean)` `=(1.8+1.83+1.84+1.86+1.92)-:5`
  `=9.25/5`
  `=1.85\ \ text(m)`

 

`text{S}text{ince the new mean = 1.86m  (given)}`

`text(New Mean)` `=text(Height of all 6 players) -: 6`
`:.1.86` `=(9.25+h)/6\ \ \ \ (h\ text{= height of new player})`
`h` `=(6xx1.86)-9.25`
  `=1.91\ \ text(m)`

`=> C`

Statistics, STD2 S1 2011 HSC 14 MC

A data set of nine scores has a median of 7.

The scores  6, 6, 12 and 17  are added to this data set.

What is the median of the data set now?

  1. 6
  2. 7
  3. 8
  4. 9
Show Answers Only

`B`

Show Worked Solution

`text(S)text(ince an even amount of scores are added below and)`

`text(above the existing median, it will not change.)`

`=>B`

Statistics, STD2 S1 2013 HSC 26f

Jason travels to work by car on all five days of his working week, leaving home at 7 am each day. He compares his travel times using roads without tolls and roads with tolls over a period of 12 working weeks.

He records his travel times (in minutes) in a back-to-back stem-and-leaf plot.
 

2013 26f
 

  1. What is the modal travel time when he uses roads without tolls?  (1 mark)

  2. What is the median travel time when he uses roads without tolls?   (1 mark)

  3. Describe how the two data sets differ in terms of the spread and skewness of their distributions.   (2 marks)

Show Answers Only
  1. `52\ text(minutes)`
  2. `50.5\ text(minutes)`
  3. `text(Spread)`
  4. `text{Times without tolls have a tighter spread (range = 22)}`
  5. `text{than times with tolls (range = 55).}`

  6.  

    `text(Skewness)`

  7. `text(Times without tolls shows virtually no skewness while`
  8. `text(times with tolls are positively skewed.)`
Show Worked Solution

i.  `text(Modal time) = 52\ text(minutes)`

♦ Mean mark 36%
MARKER’S COMMENT: Finding a median proved challenging for many students. Take note!

 

ii.  `text(30 times with no tolls)`

`text(Median)` `=\ text(Average of 15th and 16th)`
  `=(50 + 51)/2`
  `= 50.5\ text(minutes)`

 

♦ Mean mark 39%

 

 iii.  `text(Spread)`

`text{Times without tolls have a much tighter}`

`text{spread (range = 22) than times with tolls}`

`text{(range = 55).}`

`text(Skewness)`

`text(Times without tolls shows virtually no skewness)`

`text(while times with tolls are positively skewed.)`

Statistics, STD2 S1 2013 HSC 26b

Write down a set of six data values that has a range of 12, a mode of 12 and a minimum value of 12.   (2 marks)

Show Answers Only

 `12, 12, 12, 16, 18, 24`

Show Worked Solution

`12, 12, 12, 16, 18, 24`

`text(NB. There are many correct solutions.)`

 

Probability, STD2 S2 2010 HSC 23c

On Saturday, Jonty recorded the colour of T-shirts worn by the people at his gym. The results are shown in the graph.

 

  1. How many people were at the gym on Saturday? (Assume everyone was wearing a T-shirt).   (1 mark)

  2. What is the probability that a person selected at random at the gym on Saturday, would be wearing either a blue or green T-shirt?   (1 mark)

Show Answers Only
  1. `34`
  2. `15/34`
Show Worked Solution
i.   `text(# People)` `=5+15+10+3+1`
  `=34`

 

ii.   `P (B\ text{or}\ G)` `=P(B)+P(G)`
  `=5/34+10/34`
  `=15/34`

Statistics, STD2 S1 2010 HSC 16 MC

This back-to-back stem-and-leaf plot displays the test results for a class of 26 students.
 

2010 Q16 MC  
 

What is the median test result for the class?

  1.    `44`
  2.    `46`
  3.    `48`
  4.    `49`
Show Answers Only

`B`

Show Worked Solution
♦♦ Mean mark 35%

`text(26 results given in the data)`

  `=>text(Median is average of)\ 13^text(th)\ text(and)\ 14^text(th)`

`:.\ text(Median)` `=(45+47)/2`
  `=46`

`=>B`

Statistics, STD2 S1 2009 HSC 24a

The diagram below shows a stem-and-leaf plot for 22 scores. 
 

2UG-2009-24a
 

  1.  What is the mode for this data?   (1 mark)

  2.  What is the median for this data?     (1 mark)

Show Answers Only
  1. `78`
  2. `46`
Show Worked Solution

i.   `text(Mode) = 78`

 

ii.    `22\ text(scores)`

`=>\ text(Median is the average of 11th and 12th scores)`
 

`:.\ text(Median)` `= (45 + 47)/2`
  `= 46`

Measurement, STD2 M1 2009 HSC 11 MC

 What is the area of the shaded part of this quadrant, to the nearest square centimetre?  

  1. 34 cm²
  2. 42 cm²
  3. 50 cm²
  4. 193 cm²
Show Answers Only

`B`

Show Worked Solution
`text(Area)` `=\ text(Area of Sector – Area of triangle)`
  `= (theta/360 xx pi r^2)-(1/2 xx bh)`
  `= (90/360 xx pi xx 8^2)-(1/2 xx 4 xx 4)`
  `= 50.2654…-8`
  `= 42.265…\ text(cm²)`

`=>  B`

Probability, STD2 S2 2009 HSC 9 MC

A wheel has the numbers 1 to 20 on it, as shown in the diagram. Each time the wheel is spun, it stops with the marker on one of the numbers.
 


 

 The wheel is spun 120 times.

 How many times would you expect a number less than 6 to be obtained?

  1.   `20` 
  2.   `24` 
  3.   `30` 
  4.   `36` 
Show Answers Only

`C`

Show Worked Solution

`P(text(number < 6) ) = 5/20 = 1/4`

`:.\ text(Expected times)` `= 1/4 xx text(times spun)`
  `= 1/4 xx 120`
  `= 30`

`=>  C`

Statistics, STD2 S1 2009 HSC 3 MC

The eye colours of a sample of children were recorded.

When analysing this data, which of the following could be found?

  1. Mean
  2. Median
  3. Mode
  4. Range
Show Answers Only

`C`

Show Worked Solution

`text(Eye colour is categorical data)`

`:.\ text(Only the mode can be found)`

`=>  C`

Probability, STD2 S2 2009 HSC 1 MC

A newspaper states: ‘It will most probably rain tomorrow.’

Which of the following best represents the probability of an event that will most probably occur?   

  1.   `33 1/3 text(%)` 
  2.   `text(50%)` 
  3.   `text(80%)` 
  4.   `text(100%)` 
Show Answers Only

`C`

Show Worked Solution

`text(Probably) =>\ text(likelihood > 50%)`

`text(However 100% = certainty)`

`:.\ text(80% is the answer)`

`=> C`

Statistics, STD2 S1 2009 HSC 21 MC

The mean of a set of ten scores is 14. Another two scores are included and the new mean is 16.

What is the mean of the two additional scores?

  1.    4
  2.    16
  3.    18
  4.    26
Show Answers Only

`D`

Show Worked Solution
♦♦♦ Mean mark 28%.

`text(If ) bar x\ text(of 10 scores = 14)`

  `=>text(Sum of 10 scores)= 10 xx 14 = 140`

`text(With 2 additional scores,)\ \ bar x = 16 `

  `=>text(Sum of 12 scores)= 12 xx 16 = 192`

`:.\ text(Value of 2 extra scores)` `= 192\-140`
  `= 52`

 

`:.\ text(Mean of 2 extra scores)= 52/2 = 26`

`=>  D`

Statistics, STD2 S1 2011 HSC 11 MC

The sets of data, `X` and `Y`, are displayed in the histograms.

2UG 2011 11

Which of these statements is true?

  1.   `X` has a larger mode and `Y ` has a larger range.
  2.   `X` has a larger mode and the ranges are the same.
  3.   The modes are the same and `Y` has a larger range.
  4.   The modes are the same and the ranges are the same.
Show Answers Only

`B`

Show Worked Solution
♦ Mean mark 47%

`text(Mode of)\ X=9`

`text(Range of)\ X=9-3=6`

`text(Mode of)\ Y=8`

`text(Range of)\ Y=11-5=6`

`:. X\ text(has a larger mode and ranges are the same)`

`=>B`

Measurement, STD2 M6 2011 HSC 9 MC

Two trees on level ground, 12 metres apart, are joined by a cable. It is attached 2 metres above the ground to one tree and 11 metres above the ground to the other.

What is the length of the cable between the two trees, correct to the nearest metre? 

  1.  `9\ text(m)`
  2. `12\ text(m)`
  3. `15\ text(m)`
  4. `16\ text(m)`
Show Answers Only

`C`

Show Worked Solution

`text(Using Pythagoras)`

`c^2` `=12^2+9^2`
  `=144+81`
  `=225`
`:.c` `=15,\ \ c>0`

 
`=>C`

Probability, STD2 S2 2010 HSC 8 MC

A bag contains red, green, yellow and blue balls.

\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex} \textit{Colour} \rule[-1ex]{0pt}{0pt} & \textit{Probability} \\
\hline
\rule{0pt}{2.5ex} \text{Red} & \dfrac{1}{3} \\
\hline
\rule{0pt}{2.5ex} \text{Green}  & \dfrac{1}{4} \\
\hline
\rule{0pt}{2.5ex} \text{Yellow}  & \text{?} \\
\hline
\rule{0pt}{2.5ex} \text{Blue}  & \dfrac{1}{6} \\
\hline
\end{array}

The table shows the probability of choosing a red, green, or blue ball from the bag.

If there are 12 yellow balls in the bag, how many balls are in the bag altogether

  1.    16
  2.    36
  3.    48
  4.    60
Show Answers Only

\(C\)

Show Worked Solution
\(P(R)+P(G)+P(Y)+P(B)\) \(=1\)
\(\dfrac{1}{3}+\dfrac{1}{4}+P(Y)+\dfrac{1}{6}\) \(=1\)
\(P(Y)\) \(= 1-(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{6})\)
  \(=1-\dfrac{9}{12}\)
  \(=\dfrac{1}{4}\)
\(P(Y)\) \(=\dfrac{\text{Yellow balls}}{\text{Total balls}}\)
\(\dfrac{1}{4}\) \(=\dfrac{12}{\text{Total balls}}\)

 

\(\therefore\ \text{ Total balls}=48\)

\(\Rightarrow C\)

Probability, STD2 S2 2012 HSC 26e

The dot plot shows the number of push-ups that 13 members of a fitness class can do in one minute.

2012 26e

  1.  What is the probability that a member selected at random from the class can do more than 38 push-ups in one minute?   (1 mark)

  2.  A new member who can do 32 push-ups in one minute joins the class.

     

    Does the addition of this new member to the class change the probability calculated in part (i)? Justify your answer.    (1 mark)

Show Answers Only
  1. `7/13`
  2. `text{Yes (See Worked Solutions)}`
Show Worked Solution
i.  `P` `= text(# Members > 38 push-ups)/text(Total members)`
  `= 7/13`

 
ii.   `text(Yes.)`

`Ptext{(+ New member)}` `= text(Members > 38 push-ups)/text(Total members)`
  `= 7/14≠ 7/13`
MARKER’S COMMENT: The most successful candidates used the fraction `7/14` in their part (ii) answer rather than relying solely on words.

Probability, STD2 S2 2012 HSC 17 MC

A spinner with different coloured sectors is spun 40 times. The results are recorded in the table.

 What is the relative frequency of obtaining the colour orange? 

  1.    `3/20`  
  2.    `1/5`  
  3.    `6`  
  4.    `8` 
Show Answers Only

`A`

Show Worked Solution
♦♦ Mean mark 34%
COMMENT: Note that relative frequency is the frequency of an event divided by the total frequencies (i.e. the probability).
`text(Total frequency)` `= 40\ text(spins)`
`text(Orange freq.)` `= 40\-(2 + 4 + 6 + 10 +12)`
  `=6`
`:.\ text(Relative freq.)` `= 6/40 = 3/20`

 
`=>  A`

Statistics, STD2 S1 2010 HSC 1 MC

The results of a survey are displayed in the dot plot.

What is the range of this data?
 

2010 1 MC 
 

  1.    7
  2.    8
  3.    9
  4.    10
Show Answers Only

`C`

Show Worked Solution
`text(Range)` `=text(High)-text(Low)`
  `=9-0`
  `=9`

`=>  C`

Statistics, STD2 S1 2012 HSC 1 MC

A set of 15 scores is displayed in a stem-and-leaf plot.
 

2012 1 mc 
 

 What is the median of these scores?

  1.    7 
  2.    8
  3.   77
  4.   78
Show Answers Only

`D`

Show Worked Solution

`text(15 scores)\ \ =>\ \ text(Median is 8th)`

`:.\ \ text(Median is)\ \ 78`

`=>  D`

Measurement, STD2 M1 2013 HSC 16 MC

The shaded region shows a quadrant with a rectangle removed.
  

What is the area of the shaded region, to the nearest cm2?

  1. 38 cm²
  2. 52 cm²
  3. 61 cm²
  4. 70 cm²
Show Answers Only

`B`

Show Worked Solution
`text(Shaded area)` `=\ text(Area of segment – Area of rectangle)`
  `=1/4 pi r^2-(6xx2)`
  `=1/4 pi xx9^2-12`
  `=51.617…\ text(cm²)`

`=>\ B`

Statistics, STD2 S1 2013 HSC 15 MC

The frequency histogram shows the number of goals scored by a football team in each game in a season.
 

2013 15 mc

 
What is the mean number of goals scored per game by this team?

  1.    4
  2.    4.5
  3.    5
  4.    5.5
Show Answers Only

`C`

Show Worked Solution

`text(Total number of goals scored)`

`=(3xx3)+(4xx7)+(5xx5)+(6xx1)+(7xx0)+(8xx4)`

`=9+28+25+6+0+32`

`=100`

`text(Number of games)=3+7+5+1+4=20`

`:.\ text(Mean goals per game)=100/20=5`

`=>\ C`

Statistics, STD2 S1 2013 HSC 14 MC

The July sales prices for properties in a suburb were:

$552 000,  $595 000,  $607 000,  $607 000,  $682 000, and  $685 000.

On 1 August, another property in the same suburb was sold for over one million dollars.

If the property had been sold in July, what effect would it have had on the mean and median sale prices for July?

  1.    Both the mean and median would have changed.
  2.    Neither the mean nor the median would have changed.
  3.    The mean would have changed and the median would have stayed the same.
  4.    The mean would have stayed the same and the median would have changed.
Show Answers Only

`C`

Show Worked Solution

`text(Mean increases because new house is sold above)`

`text(the existing average.)`

`text(Initial median)= (607\ 000+607\ 000)/2=607\ 000` 

`text(New median)=607\ 000\ \ \  text{(4th value in a list of 7)}`

`=>\ C`

Statistics, STD2 S1 2013 HSC 8 MC

A high school has 100 students in each year group, Year 7 to Year 12. A survey is to be conducted to determine the average number of text messages sent per month by students at the school.

Which of the following would provide the most representative sample for this survey?

  1. All Year 7 students
  2. All physics students in Year 11 and 12
  3. 20 students chosen at random from each year group
  4. 120 students chosen at random from the school roll
Show Answers Only

`C`

Show Worked Solution

`text(The best sample would have an equal amount)`

`text(of people in each year randomly selected.)`

`=>\ C`

Probability, STD2 S2 2013 HSC 7 MC

In an experiment, a standard six-sided die was rolled 72 times. The results are shown in the table.
 

Which number on the die was obtained the expected number of times?

  1.    1
  2.    2
  3.    3
  4.    6
Show Answers Only

`B`

Show Worked Solution

`text(Probability of rolling a specific number)=1/6`

`:.\ text(After 72 rolls, a specific number is expected)`

 `1/6xx72=12\ text(times.)`

`=>\ B`

Statistics, STD2 S1 2013 HSC 6 MC

A survey was conducted where people were asked which of two brands of smartphones they preferred. The results were:

  • 48% preferred Brand X
  • 52% preferred Brand Y

A graph displaying the data is to be included in a magazine article. The editor of the magazine wishes to ensure that the graph is not misleading in any way.

Which graph should the editor choose to include in the article?
 

2013 6 mc1

2013 6 mc2

Show Answers Only

`D`

Show Worked Solution

`D\ text(is the best as it starts at zero on the)\ y text(-axis)`

`text(and has the same column widths.)`

Probability, STD2 S2 2013 HSC 1 MC

Which of the following events would be LEAST likely to occur?

  1.    Tossing a fair coin and obtaining a head
  2.    Rolling a standard six-sided die and obtaining a 3
  3.    Randomly selecting the letter 'G' from the 26 letters of the alphabet
  4.    Winning first prize in a raffle of 100 tickets in which you have 4 tickets
Show Answers Only

`C`

Show Worked Solution

`P(A)=1/2,\ \ P(B)=1/6`

`P(C)=1/26,\ \ P(D)=4/100=1/25`

 

`=>C\ text(is the least likely.)`