page-break-before-solution

v1 Algebra, STD2 A2 2010 HSC 27c

The graph shows tax payable against taxable income, in thousands of dollars.

Use the graph to find the tax payable on a taxable income of $$18\ 000$. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Use suitable points from the graph to show that the gradient of the section of the graph marked $A$ is $\dfrac{7}{15}$. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
How much of each dollar earned between $$18\ 000$ and $$33\ 000$ is payable in tax? Give your answer correct to the nearest whole number. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Write an equation that could be used to calculate the tax payable, $T$, in terms of the taxable income, $I$, for taxable incomes between $$18\ 000$ and $$33\ 000$. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

$$3000\ \ \text{(from graph)}$
$\text{See worked solution}$
$46\frac{2}{3}\approx 47\ \text{cents per dollar earned}$
$\text{Tax payable →}\ T=\dfrac{7}{15}I-5400$

Show Worked Solution

$\text{Income on}\ $18\ 000=$3000\ \ \text{(from graph)}$

ii. $\text{Using the points}\ (18, 3)\ \text{and}\ (33, 10)$

$\text{Gradient at}\ A$	$=\dfrac{y_2-y_1}{x_2-x_1}$
	$=\dfrac{10\ 000-3000}{33\ 000-18\ 000}$
	$=\dfrac{7000}{15\ 000}$
	$=\dfrac{7}{15}\ \ \ \ \text{… as required}$

♦♦ Mean mark (ii) 25%.

iii. $\text{The gradient represents the tax applicable on each dollar}$

$\text{Tax}$	$=\dfrac{7}{15}\ \text{of each dollar earned}$
	$=46\frac{2}{3}\approx 47\ \text{cents per dollar earned (nearest whole number)}$

♦♦♦ Mean mark (iii) 12%!
MARKER’S COMMENT: Interpreting gradients is an examiner favourite, so make sure you are confident in this area.

iv. $\text{Tax payable up to }$18\ 000 = $3000$

$\text{Tax payable on income between }$18\ 000\ \text{and }$33\ 000$

$=\dfrac{7}{15}(I-18\ 000)$

$\therefore\ \text{Tax payable →}\ \ T$	$=3000+\dfrac{7}{15}(I-18\ 000)$
	$=3000+\dfrac{7}{15} I-8400$
	$=\dfrac{7}{15}I-5400$

♦♦♦ Mean mark (iv) 15%.
STRATEGY: The earlier parts of this question direct students to the most efficient way to solve this question. Make sure earlier parts of a question are front and centre of your mind when devising strategy.

Functions, EXT1 F1 2010 HSC 3b*

Let `f(x) = e^(-x^2)`. The diagram shows the graph `y = f(x)`.

The graph has two points of inflection.

Find the `x` coordinates of these points. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Explain why the domain of `f(x)` must be restricted if `f(x)` is to have an inverse function. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Find a formula for `f^(-1) (x)` if the domain of `f(x)` is restricted to `x ≥ 0`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
State the domain of `f^(-1) (x)`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Sketch the curve `y = f^(-1) (x)`. (1 mark)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`x = +- 1/sqrt2`
`text(There can only be 1 value of)\ y\ text(for each value of)\ x.`
`f^(-1)x = sqrt(ln(1/x))`
`0 <= x <= 1`

Show Worked Solution

i.	`y`	`= e^(-x^2)`
	`dy/dx`	`= -2x * e^(-x^2)`
	`(d^2y)/(dx^2)`	`= -2x (-2x * e^(-x^2)) + e ^(-x^2) (-2)`
		`= 4x^2 e^(-x^2)\ – 2e^(-x^2)`
		`= 2e^(-x^2) (2x^2\ – 1)`

`text(P.I. when)\ \ (d^2y)/(dx^2) = 0`

`2e^(-x^2) (2x^2\ – 1)`	`= 0`
`2x^2\ – 1`	`= 0`
`x^2`	`= 1/2`
`x`	`= +- 1/sqrt2`

COMMENT: It is also valid to show that `f(x)` is an even function and if a P.I. exists at `x=a`, there must be another P.I. at `x=–a`.

`text(When)\ \ `	`x < 1/sqrt2,`	`\ (d^2y)/(dx^2) < 0`
	`x > 1/sqrt2,`	`\ (d^2y)/(dx^2) > 0`

`=>\ text(Change of concavity)`

`:.\ text(P.I. at)\ \ x = 1/sqrt2`

`text(When)\ \ `	`x < – 1/sqrt2,`	`\ (d^2y)/(dx^2) > 0`
	`x > – 1/sqrt2,`	`\ (d^2y)/(dx^2) < 0`

`=>\ text(Change of concavity)`

`:.\ text(P.I. at)\ \ x = – 1/sqrt2`

ii.	`text(In)\ f(x), text(there are 2 values of)\ y\ text(for)`
	`text(each value of)\ x.`
	`:.\ text(The domain of)\ f(x)\ text(must be restricted)`
	`text(for)\ \ f^(-1) (x)\ text(to exist).`

iii.

`y = e^(-x^2)`

`text(Inverse function can be written)`

`x`	`= e^(-y^2),\ \ \ x >= 0`
`lnx`	`= ln e^(-y^2)`
`-y^2`	`= lnx`
`y^2`	`= -lnx`
	`=ln(1/x)`
`y`	`= +- sqrt(ln (1/x))`

`text(Restricting)\ \ x>=0,\ \ =>y>=0`

`:. f^(-1) (x)=sqrt(ln (1/x))`

♦ Parts (iv) and (v) were poorly answered with mean marks of 39% and 49% respectively.

iv.

`f(0) = e^0 = 1`

`:.\ text(Range of)\ \ f(x)\ \ text(is)\ \ 0 < y <= 1`

`:.\ text(Domain of)\ \ f^(-1) (x)\ \ text(is)\ \ 0 < x <= 1`

Trigonometry, 2ADV’ T1 2010 HSC 5a

A boat is sailing due north from a point `A` towards a point `P` on the shore line.

The shore line runs from west to east.

In the diagram, `T` represents a tree on a cliff vertically above `P`, and `L` represents a landmark on the shore. The distance `PL` is 1 km.

From `A` the point `L` is on a bearing of 020°, and the angle of elevation to `T` is 3°.

After sailing for some time the boat reaches a point `B`, from which the angle of elevation to `T` is 30°.

Show that `BP = (sqrt3 tan 3°)/(tan20°)`. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find the distance `AB`. Give your answer to 1 decimal place. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`2.5\ text(km)\ \ text{(to 1 d.p.)}`

Show Worked Solution

i. `text(Show)\ BP = (sqrt3 tan 3°)/(tan 20°)`

`text(In)\ Delta ATP`

`tan 3°`	`= (TP)/(AP)`
`=> AP`	`= (TP)/(tan 3)`

`text(In)\ Delta APL:`

`tan 20°`	`= 1/(AP)`
`=> AP`	`= 1/tan 20`

`:. (TP)/(tan3)`	`= 1/(tan20)`
`TP`	`= (tan3°)/(tan20°)\ \ \ text(…)\ text{(} text(1)text{)}`

`text(In)\ \ Delta BTP:`

`tan 30°`	`= (TP)/(BP)`
`1/sqrt3`	`= (TP)/(BP)`
`BP`	`= sqrt3 xx TP\ \ \ \ \ text{(using (1) above)}`
	`= (sqrt3 tan3°)/(tan20°)\ \ \ text(… as required)`

ii.	`AB`	`= AP\ – BP`
	`AP`	`= 1/(tan20°)\ \ \ text{(} text(from part)\ text{(i)} text{)}`

`:.\ AB`	`= 1/(tan 20°)\ – (sqrt3 tan3°)/(tan20°)`
	`= (1\ – sqrt3 tan 3)/(tan20°)`
	`= 2.4980…`
	`= 2.5\ text(km)\ text{(to 1 d.p.)`

Plane Geometry, EXT1 2016 HSC 13c

The circle centred at `O` has a diameter `AB`. From the point `M` outside the circle the line segments `MA` and `MB` are drawn meeting the circle at `C` and `D` respectively, as shown in the diagram. The chords `AD` and `BC` meet at `E`. The line segment `ME` produced meets the diameter `AB` at `F`.

Copy or trace the diagram into your writing booklet.

Show that `CMDE` is a cyclic quadrilateral. (2 marks)
Hence, or otherwise, prove that `MF` is perpendicular to `AB`. (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

`/_ ACB`	`= /_ ADB = 90^@ qquad text{(angle in semi-circle)}`
`/_ MCE`	`= 90^@ qquad (/_ MCA\ text{is a straight angle)}`
`/_ MDA`	`= 90^@ qquad (/_ MDB\ text{is a straight angle)}`

`:. CMDE\ text(is a cyclic quad)`

`qquad text{(opposite angles are supplementary)}`

ii. `text(Consider)\ \ Delta MAB,`

♦♦♦ Mean mark 14%.

`CB\ \ text(is an altitude.)`

`AD\ \ text(is an altitude.)`

`text(S) text(ince the altitudes of a triangle are)`

`text(concurrent)\ \ text{(in}\ Delta MAB, text{at}\ Etext{),}`

`=> MF\ \ text(must be an altitude.)`

`:. MF _|_ AB`

Calculus, EXT1 C1 2016 HSC 12a

The diagram shows a conical soap dispenser of radius 5 cm and height 20 cm.

At any time `t` seconds, the top surface of the soap in the container is a circle of radius `r` cm and its height is `h` cm.

The volume of the soap is given by `v = 1/3 pir^2h`.

Explain why `r = h/4`. (1 mark)

--- 8 WORK AREA LINES (style=lined) ---
Show that `(dv)/(dh) = pi/16 h^2`. (1 mark)

--- 5 WORK AREA LINES (style=lined) ---

The dispenser has a leak which causes soap to drip from the container. The area of the circle formed by the top surface of the soap is decreasing at a constant rate of `0.04\ text(cm² s)^-1`.

Show that `(dh)/(dt) = (−0.32)/(pih)`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
What is the rate of change of the volume of the soap, with respect to time, when `h = 10`? (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`-0.2\ text(cm³ s)^-1`

Show Worked Solution

`text(Using similar triangles,)`

`r/h`	`= 5/20`
`:. r`	`= h/4\ text(… as required)`

ii.	`v`	`= 1/3 pi r^2 h`
		`= 1/3 pi · (h/4)^2 h`
		`= (pi h^3)/48`
	`:. (dv)/(dh)`	`= 3 xx (pi h^2)/48`
		`= (pi h^2)/16\ text(… as required.)`

iii.	`(dA)/(dt)`	`= -0.04\ text(cm² s)^-1`
	`A`	`= pi r^2`
		`= (pi h^2)/16`
	`:. (dA)/(dh)`	`= (pi h)/8`

`(dA)/(dt)`	`= (dA)/(dh) xx (dh)/(dt)`
`-0.04`	`= (pi h)/8 xx (dh)/(dt)`
`:. (dh)/(dt)`	`= (-0.32)/(pi h)\ text(… as required.)`

iv.	`(dv)/(dt)`	`= (dv)/(dh) · (dh)/(dt)`
		`= (pi h^2)/16 · (-0.32)/(pi h)`
		`= (-0.32 h)/16`

`text(When)\ \ h =10,`

`(dv)/(dt)`	`= (-0.32 xx 10)/16`
	`= -0.2\ text(cm³ s)^-1`

GRAPHS, FUR2 2006 VCAA 3

Harry offers dog washing and dog clipping services.

Let `x` be the number of dogs washed in one day

`y` be the number of dogs clipped in one day.

It takes 20 minutes to wash a dog and 25 minutes to clip a dog.

There are 200 minutes available each day to wash and clip dogs.

This information can be written as Inequalities 1 to 3.

Inequality 1: `x ≥ 0`

Inequality 2: `y ≥ 0`

Inequality 3: `20x + 25y ≤ 200`

Draw the line that represents `20x + 25y = 200` on the graph below. (1 mark)

In any one day the number of dogs clipped is at least twice the number of dogs washed.

Write Inequality 4 to describe this information in terms of `x` and `y`. (1 mark)
1. On the graph on page 18 draw and clearly indicate the boundaries of the region represented by Inequalities 1 to 4. (2 marks)
2. On a day when exactly five dogs are clipped, what is the maximum number of dogs that could be washed? (1 mark)

The profit from washing one dog is $40 and the profit from clipping one dog is $30.

Let `P` be the total profit obtained in one day from washing and clipping dogs.

Write an equation for the total profit, `P`, in terms of `x` and `y`. (1 mark)
1. Determine the number of dogs that should be washed and the number of dogs that should be clipped in one day in order to maximise the total profit. (1 mark)
2. What is the maximum total profit that can be obtained from washing and clipping dogs in one day? (1 mark)

Show Answers Only

`y >= 2x`
2. `2`
`P = 40x + 30y`
1. `text(2 washes and 6 clips.)`
2. `$260`

Show Worked Solution

b. `text(Inequality 4:)\ \ y >= 2x`

c.i.

c.ii. `text(When)\ y =5,\ text(the maximum value of)\ x`

♦♦ Mean mark of parts (c)-(e) (combined) was 27%.

`text{(whole number) in the feasible region is 2.)`

`:. 2\ text(dogs can be washed.)`

d. `P = 40x + 30y`

e.i. `text(Test points for maximum profit)`

`text(At)\ (0, 8),`

`text(Profit) = 40 xx 0 + 30 xx 8 = $240`

`text(At)\ (1, 7),`

`text(Profit) = 40 xx 1 + 30 xx 7 = $250`

`text(At)\ (2, 6),`

`text(Profit) = 40 xx 2 + 30 xx 6 = $260`

`:.\ text(2 washes and 6 clips produce maximum profit.)`

e.ii. `text(Maximum profit)`

`= 40 xx 2 + 30 xx 6`

`= $260`

Mechanics, EXT2 2015 HSC 14c

A car of mass `m` is driven at speed `v` around a circular track of radius `r`. The track is banked at a constant angle `theta` to the horizontal, where `0 < theta < pi/2`. At the speed `v` there is a tendency for the car to slide up the track. This is opposed by a frictional force `mu N`, where `N` is the normal reaction between the car and the track, and `mu > 0`. The acceleration due to gravity is `g`.

Show that
`v^2 = rg((tan theta + mu)/(1 - mu tan theta)).` (3 mark)
At the particular speed `V`, where `V^2 = rg`, there is still a tendency for the car to slide up the track.
Using the result from part (i), or otherwise, show that `mu < 1.` (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`text(Resolving the forces vertically)`

`N cos theta`	`= mg + mu N sin theta`
`N (cos theta – mu sin theta)`	`= mg\ \ \ …\ (1)`

`text(Resolving the forces horizontally)`

`N sin theta + mu N cos theta`	`=(m v^2)/r`
`N (sin theta + mu cos theta)`	`=(m v^2)/r\ \ \ …\ (2)`

`text(Divide)\ \ (2)÷(1)`

`((m v^2)/r)/(mg)`	`=(sin theta + mu cos theta)/(cos theta – mu sin theta)`
`v^2/(rg)`	`=(sin theta + mu cos theta)/(cos theta – mu sin theta)`
`v^2`	`=rg ((sin theta + mu cos theta)/(cos theta – mu sin theta))`
	`= rg ((tan theta + mu)/(1 – mu tan theta))`

(ii) `text(Given that)\ \ V^2=rg`

♦ Mean mark 46%.

`=> (tan theta + mu)/(1 – mu tan theta)=1`

`(tan theta + mu)`	`=(1 – mu tan theta)`
`mu(1+ tan theta)`	`=1-tan theta`
`mu`	`=(1-tan theta)/(1+ tan theta)`
	`=1- (2tan theta)/(1+ tan theta)`

`text(S)text(ince)\ \ tan theta>0\ \ text(for)\ \ 0<theta<pi/2`

`=> (2tan theta)/(1+ tan theta) >0`

`:. mu<1`

Functions, EXT1′ F1 2006 HSC 3a

The diagram shows the graph of `y =f(x)`. The graph has a horizontal asymptote at `y =2`.

Draw separate one-third page sketches of the graphs of the following:

`y = (f(x))^2` (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
`y = 1/(f(x))` (2 marks)

--- 10 WORK AREA LINES (style=lined) ---
`y = x\ f(x)` (2 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

ii.

iii.

Show Worked Solution

ii.

iii.

Polynomials, EXT2 2007 HSC 5d

In the diagram, `ABCDE` is a regular pentagon with sides of length `1`. The perpendicular to `AC` through `B` meets `AC` at `P.`

Copy or trace this diagram into your writing booklet.

Let `u = cos\ pi/5`.
Use the cosine rule in `Delta ACD` to show that `8u^3 - 8u^2 + 1 = 0.` (2 marks)
One root of `8x^3 - 8x^2 + 1 = 0` is `1/2`.
Find the other roots of `8x^3 - 8x^2 + 1 = 0` and hence find the exact value of `cos\ pi/5.` (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`(1 + sqrt 5)/4`

Show Worked Solution

(i)	`u`	`= cos\ pi/5`
	`AP`	`=u`
	`AC`	`=AD=2u`

`text(By symmetry,)\ \ /_ DAE = pi/5`

`text(Angle sum of a pentagon)=(n-2) pi=3 pi`

`:.text(Each angle of a regular pentagon)=(3 pi)/5`

`:.\ /_ CAD = pi/5`

`text(Using the cosine rule in)\ \ Delta ACD`

`1^2`	`= (2u)^2 + (2u)^2 – 2 xx 2u xx 2u cos\ pi/5`
`1`	`= 8u^2 – 8u^2 xx u`
`:.8u^3 – 8u^2 + 1 = 0`

(ii) `(2x – 1)\ \ text(is a factor)`

`8x^3 – 8x^2 + 1 = (2x – 1) (4x^2 – 2x – 1)`

`text(Other roots occur when)`

`4x^2 – 2x – 1 = 0`

`x`	`=(2 +- sqrt (4 + 16))/8`
	`=(2 +- sqrt 20)/8`
	`=(1 +- sqrt 5)/4`

`=>u\ \ text(is a root of)\ \ 8u^3 – 8u^2 + 1 = 0,\ \ \ \ (u>0)`

`:.cos\ pi/5 = (1 + sqrt 5)/4`

Functions, EXT1′ F1 2007 HSC 3a

The diagram shows the graph of `y = f(x)`. The line `y = x` is an asymptote.

Draw separate one-third page sketches of the graphs of the following:

`f(-x).` (1 mark)

--- 8 WORK AREA LINES (style=lined) ---
`f(|\ x\ |).` (2 marks)

--- 10 WORK AREA LINES (style=lined) ---
`f(x) - x.` (2 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

Show Worked Solution

MARKER’S COMMENT: In part (ii), a significant number of students graphed `y=|f(x)|`.

ii.

iii.

Harder Ext1 Topics, EXT2 2009 HSC 5a

In the diagram `AB` is the diameter of the circle. The chords `AC` and `BD` intersect at `X`. The point `Y` lies on `AB` such that `XY` is perpendicular to `AB`. The point `K` is the intersection of `AD` produced and `YX` produced.

Copy or trace the diagram into your writing booklet.

Show that `/_ AKY = /_ ABD.` (2 marks)
Show that `CKDX` is a cyclic quadrilateral. (2 marks)
Show that `B, C and K` are collinear. (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`/_ ADB = 90^@\ \ \ text{(angle in a semicircle on diameter}\ \ AB text{)}`

`text(In)\ \ Delta BDA and Delta KYA`

`/_ BAD`	`= /_ KAY\ \ text{(common angle)}`
`/_ ADB`	`= /_ KYA = 90^@`
`:./_ AKY`	`= /_ ABD\ \ text{(angle sum of triangle)}`

(ii) `text(Join)\ \ DC`

`/_ DCA`	`= /_ DBA\ \ text{(angles in the same segment on chord}\ DA text{)}`
`/_ DCA`	`= /_ XKD\ \ text{(both equal to}\ /_ DBA text{)}`

`=>text(S)text(ince)\ \ /_ DKX = /_ DCX\ \ text(are a pair of equal angles)`

`text{standing on arc}\ DX\ \ text{(in the same segment)}.`

`:.CKDX\ \ text(is a cyclic quadrilateral.)`

(iii) `/_ KDX`

`= 90^@\ \ text{(} /_ ADK\ text{is a straight angle)}`

`/_ KCX`

`= 90^@\ \ text{(opposite angles of a cyclic}`

`text{quadrilateral are supplementary)}`

`/_ ACB`

`= 90^@\ \ text{(angle in a semicircle)}`

`/_ KCX + /_ ACB = 180^@`

`:./_ BCK\ \ text(is a straight angle.)`

`:.B, C and K\ \ text(are collinear.)`

Functions, EXT1′ F1 2009 HSC 3a

The diagram shows the graph `y = f(x).`

Draw separate one-third page sketches of the graphs of the following:

`y = 1/(f(x)) .` (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
`y = f(x)\ f(x)` (2 marks)

--- 12 WORK AREA LINES (style=lined) ---
`y = f(x^2).` (2 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

ii.

iii.

Show Worked Solution

i. `text(Vertical asymptotes at)\ \ x=0 and 4`

`text(Horizontal asymptote at)\ \ y=-1/3`

ii. `y=f(x)\ f(x) = [f(x)]^2`

iii. `y=f(x^2) =>text(even function)`

`text(When)\ \ x=±2,\ \ y=f(4)=0`

Conics, EXT2 2010 HSC 5a

The diagram shows two circles, `C_1` and `C_2`, centred at the origin with radii `a` and `b`, where `a > b`.

The point `A` lies on `C_1` and has coordinates `(a cos theta, a sin theta)`.

The point `B` is the intersection of `OA` and `C_2`.

The point `P` is the intersection of the horizontal line through `B` and the vertical line through `A`.

Write down the coordinates of `B`. (1 mark)
Show that `P` lies on the ellipse
`(x^2)/(a^2) + (y^2)/(b^2) = 1`. (1 mark)
Find the equation of the tangent to the ellipse
`(x^2)/(a^2) + (y^2)/(b^2) = 1` at `P`. (2 marks)
Assume that `A` is not on the `y`-axis.
Show that the tangent to the circle `C_1` at `A`, and the tangent to the ellipse
`(x^2)/(a^2) + (y^2)/(b^2) = 1` at `P`, intersect at a point on the `x`-axis. (2 marks)

Show Answers Only

`B(b cos theta, b sin theta)`
`text{Proof (See Worked Solutions)}`
`b cos theta x + a sin theta y = ab, or`
`(x cos theta)/a + (y sin theta)/b = 1`
`text{Proof (See Worked Solutions)}`

Show Worked Solution

(i) `B(b cos theta, b sin theta)`

(ii) `text(Substitue)\ \ P(a cos theta, b sin theta)\ \ text(into)\ \ (x^2)/(a^2) + (y^2)/(b^2) = 1`

`text(LHS)`	`= (a^2 cos^2 theta)/(a^2) + (b^2 sin^2 theta)/(b^2)`
	`= cos^2 theta + sin^2 theta`
	`= 1`
	`=\ text(RHS)`

`:.P\ text(lies on the ellipse.)`

(iii) `text(Solution 1)`

`(x^2)/(a^2) + (y^2)/(b^2)`	`= 1`
`(2x)/(a^2) + (2y)/(b^2) xx (dy)/(dx)`	`= 0`
`(dy)/(dx)`	`= -(b^2x)/(a^2y)`

`text(At)\ \ P(a cos theta, b sin theta)`

`(dy)/(dx)`	`= (b^2a cos theta)/(a^2b sin theta)`
	`= -(b cos theta)/(a sin theta)`

`:.\ text(Equation of tangent at)\ P`

`y − b sin theta=`	` -(b cos theta)/(a sin theta)(x − a cos theta)`
`a sin theta y − ab sin^2 theta=`	` −b cos theta x + ab cos^2 theta`
`b cos theta x + a sin theta y=`	` ab(sin^2 theta + cos^2 theta)`
`:.b cos theta x + a sin theta y=`	`ab,\ \ \ text(or)`
`(x cos theta)/a + (y sin theta)/b=`	`1`

`text(Alternative Solution)`

`dy/dx`	`=(dy)/(d theta) xx (d theta)/(dx)`
	`=b cos theta xx 1/(-a sin theta)`
	`= -(bcos theta)/(a sin theta)`

`text{(then use the point-gradient formula as shown above)}`

(iv) `text(Finding the tangent to)\ x^2 + y^2 = 1\ text(at)\ \ A(a cos theta, a sin theta)`

`2x + 2y* (dy)/(dx)`	`=0`
`(dy)/(dx)`	`= (-x)/y`

`:.\ text(Equation of tangent)`

`y – a sin theta`	`=-(a cos theta)/(a sin theta)(x − a cos theta)`
`y sin theta – a sin^2 theta`	`=-x cos theta + a cos^2 theta`
`x cos theta + y sin theta`	`=a(sin^2 theta + cos^2 theta)`
`x cos theta + y sin theta`	`=a`
`:.y sin theta`	`=a- x cos theta`

`text(Substitute into the equation of the tangent at)\ \ P`

`b cos theta x + a sin theta y`	`=ab`
`b cos theta x+a(a- x cos theta)`	`=ab`
`bx cos theta + a^2 – ax cos theta`	`=ab`
`(b – a)x cos theta`	`=a(b – a)`
`x cos theta`	`= a`

`text(When)\ x cos theta = a,\ \ y sin theta = a − a = 0\ \ =>y=0,\ \ theta≠0`

`:.\ text(Intersection occurs on the)\ x text(-axis.)`

Graphs, EXT2 2011 HSC 6b

Let `f (x)` be a function with a continuous derivative.

Prove that `y = (f(x))^3` has a stationary point at `x = a` if `f(a) = 0` or `f prime(a) = 0.` (2 marks)
Without finding `f″(x)`, explain why `y = (f(x))^3` has a horizontal point of inflection at `x = a` if `f(a) = 0` and `f prime (a) != 0.` (1 mark)
The diagram shows the graph `y = f(x).`
Copy or trace the diagram into your writing booklet.
On the diagram in your writing booklet, sketch the graph `y = (f(x))^3`, clearly distinguishing it from the graph `y = f(x).` (3 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(See Worked Solutions)`

Show Worked Solution

(i) `text(If)\ \ f(x)\ \ text(is a function with a continuous derivative,)`

`=> f prime (x)\ \ text(exists for all)\ \ x.`

`y`	`= (f(x))^3`
`(dy)/(dx)`	`= 3 xx (f(x))^2 xx f prime(x)`

`:.\ (dy)/(dx) = 0\ \ text(when)\ \ f(x) = 0 or f prime (x) = 0`

`:.\ x = a\ \ text(is a stationary point if)\ \ f(a) = 0 or f prime(a) = 0`

♦♦♦ Mean mark part (ii) 0%!
A BEAST!

(ii) `text(If)\ \ f prime (a) != 0\ \ text(then either)\ \ f prime (a) > 0 or f prime (a) < 0,`

`and f prime (x)\ \ text(keeps that sign either side of)\ \ x = a.`

`:. text(If)\ \ f(a) = 0 and f prime(a) != 0, text(there is a stationary point at)\ \ x = a`

`text(where the slope of the curve does not change either side of)\ \ x = a.`

`text(i.e. a horizontal point of inflection occurs at)\ \ x=a`

(iii) `y = (f(x))^3`

`text(When)\ \ f(x) = 0,\ \ (f(x))^3 = 0\ \ text{(horizontal P.I. from part (ii))}`

`text(When)\ \ f(x) = 1,\ \ (f(x))^3 = 1`

`text(If)\ \ 0 < f(x) < 1,\ \ 0 < (f(x))^3 < f(x)`

`text(If)\ \ f(x) > 1,\ \ (f(x))^3 > f(x)`

`text(When)\ f prime (a) = 0,\ \ (f(x))^3\ \ text(has a maximum turning point)`

`f(x) < 0,\ \ (f(x))^3 < 0`

Volumes, EXT2 2011 HSC 3b

The base of a solid is formed by the area bounded by `y = cos x` and `y = -cos x` for `0 <= x <= pi/2.`

Vertical cross-sections of the solid taken parallel to the `y`-axis are in the shape of isosceles triangles with the equal sides of length `1` unit as shown in the diagram.

Find the volume of the solid. (3 marks)

Show Answers Only

`1/2\ \ text(u³)`

Show Worked Solution

`text(Length of base of cross-section) = 2 cos x`

`text(Using Pythagoras to find the height of cross-section)`

`h^2+cos^2 x`	`=1`
`h^2`	`=1-cos^2 x`
`h`	`=sin x\ \ \ \ \ (h>0)`

`text(Volume of vertical slice) = 1/2 xx 2 cos x xx sin x xx delta x`

`V`	`=lim_(delta x -> 0) sum_(x=0)^(pi/2) cos x sin x\ delta x`
	`=int_0^(pi/2) sin x cos x\ dx`
	`=1/2 int_0^(pi/2) sin 2 x\ dx`
	`=-1/4[cos 2x]_0^(pi/2)`
	`=-1/4[(cos pi)-(cos 0)]`
	`=-1/4 [-1 – (1)]`
	`=1/2`

`text(OR)\ \ `	`= [1/2 sin^2 x]_0^(pi/2)`
	`= 1/2`

`:. text(The volume is)\ \ 1/2\ \ text(u³)`

Functions, EXT1′ F1 2011 HSC 3a

Draw a sketch of the graph

`quad y = sin\ pi/2 x` for `0 < x < 4.` (1 mark)

--- 6 WORK AREA LINES (style=lined) ---
Find `lim_(x -> 0) x/(sin\ pi/2 x).` (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Draw a sketch of the graph

`quad y = x/(sin\ pi/2 x)` for `0 < x < 4.` (2 marks)
(Do NOT calculate the coordinates of any turning points.)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

ii. `2/pi`

iii.

Show Worked Solution

ii. `lim_(x->0) x/(sin\ pi/2 x)`	`= 2/pi lim_(x->0) (pi/2 x)/(sin\ pi/2 x)`
	`= 2/pi xx 1`
	`= 2/pi`

iii.

Conics, EXT2 2014 HSC 14b

The point `P(a cos theta , b sin theta)` lies on the ellipse `x^2/a^2 + y^2/b^2 = 1`, where `a >b`.

The acute angle between `OP` and the normal to the ellipse at `P` is `ø`.

Show that
`tan\ ø = ((a^2 − b^2)/(ab))\ sin theta cos theta.` (3 marks)
Find a value of `theta` for which `ø` is a maximum. (2 marks)

Show Answers Only

`text{Proof (See Worked Solutions)}`
`pi/4`

Show Worked Solution

♦ Mean mark 49%.

(i)	`x^2/a^2 + y^2/b^2`	`=1`
	`(2x)/(a^2) + (2y)/(b^2)*(dy)/(dx)`	`=0`
	`(2y)/(b^2)*(dy)/(dx)`	`=(2x)/(a^2)`
	`(dy)/(dx)`	`= -(b^2x)/(a^2y)`

`text(Consider)\ \ P(a cos theta , b sin theta)`

`m_text(tan)`	`= -(b^2a cos theta)/(a^2b sin theta)`
	`= -(b cos theta)/(a sin theta)`
`m_text(norm)`	`= (a sin theta)/(b cos theta)`
`m_(OP)`	`= (b\ sin\ theta)/(a\ cos\ theta)`

`text(S)text(ince)\ \ ø\ \ text(is the acute angle between two lines)`

`tan\ ø`	`=\|(m_(norm) – m_(OP))/(1+m_(norm) * m_(OP))\|`
	`=\| ((a sin theta)/(b cos theta) − (b sin theta)/(a cos theta))/(1 + (a sin theta)/(b cos theta) xx (b sin theta)/(a cos theta))\|`
	`=\| (a^2 sin theta cos theta – b^2 sin theta cos theta)/(ab cos^2 theta + ab sin^2 theta)\|`
	`= \|((a^2 − b^2) sin theta cos theta)/(ab (cos^2 theta + sin^2 theta))\|`
	`= ((a^2 − b^2)/(ab))\ sin theta cos theta\ \ \ \ text(… as required)`

(ii)	`tan\ ø`	`= ((a^2 − b^2)/(ab))\ sin theta cos theta`
		`= ((a^2 − b^2)/(2ab))\ 2 sin theta cos theta`
		`= ((a^2 − b^2)/(2ab))\ sin 2 theta`

♦♦ Mean mark 27%.
STRATEGY: The critical thought to solving this is to realise that `sin theta cos theta` can be replaced by `½\ sin 2theta`.

`=>ø\ \ text(is a maximum when)`

`((a^2 − b^2)/(2ab))\ sin 2 theta\ \ text(is a maximum)`

`:.\ text(Maximum occurs when)`

`sin 2 theta`	`=1`
`2 theta`	`= pi/2`
`theta`	`= pi/4`

Functions, EXT1 F1 2007 HSC 6b

Consider the function `f(x) = e^x − e^(-x)`.

Show that `f(x)` is increasing for all values of `x`. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Show that the inverse function is given by

`qquad qquad f^(-1)(x) = log_e((x + sqrt(x^2 + 4))/2)` (3 marks)

--- 7 WORK AREA LINES (style=lined) ---
Hence, or otherwise, solve `e^x - e^(-x) = 5`. Give your answer correct to two decimal places. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions.)}`
`text{Proof (See Worked Solutions.)}`
`1.65\ \ text{(to 2 d.p.)}`

Show Worked Solution

i.	`f(x)`	`= e^x − e^(-x)`
	`f′(x)`	`= e^x + e^(-x)`

`text(S)text(ince)\ \ `	`e^x`	`> 0\ \ text(for all)\ x`
	`e^(-x)`	`> 0\ \ text(for all)\ x`
	`f′(x)`	`> 0\ \ text(for all)\ x`

`:.f(x)\ \ text(is an increasing function for all)\ x.`

ii. `y = e^x − e^(-x)`

`text(Inverse function)`

`x`	`= e^y − 1/(e^y)`
`xe^y`	`= e^(2y) − 1`
`e^(2y) − xe^y − 1`	`= 0`

`text(Let)\ \ A = e^y`

`:.A^2 − xA − 1 = 0`

`text(Using the quadratic formula)`

`A`	`=(x ± sqrt((-x)^2 − 4 · 1 · (-1)))/(2 · 1)`
	`=(x ± sqrt(x^2 + 4))/2`

`text(S)text(ince)\ \ (x – sqrt(x^2 + 4))/2<0\ \ text(and)\ \ e^y>0,`

`:.e^y`	`= (x + sqrt(x^2 + 4))/2`
`log_e e^y`	` = log_e((x + sqrt(x^2 + 4))/2)`
`y`	`= log_e((x + sqrt(x^2 + 4))/2)`
`:.f^(-1)(x)`	`= log_e((x + sqrt(x^2 + 4))/2)\ \ …\ text(as required)`

iii.	`e^x − e^(-x)`	`= 5`
	`f(x)`	`= 5`
	`f^(-1)(5)`	`= x`

`f^(-1)(5)`	`= log_e((5 + sqrt(5^2 + 4))/2)`
	`= log_e((5 + sqrt29)/2)`
	`= 1.647…`
	`= 1.65\ \ text{(to 2 d.p.)}`

Mechanics, EXT2* M1 2006 HSC 6a

Two particles are fired simultaneously from the ground at time `t = 0.`

Particle 1 is projected from the origin at an angle `theta, \ \ 0 < theta < pi/2`, with an initial velocity `V.`

Particle 2 is projected vertically upward from the point `A`, at a distance `a` to the right of the origin, also with an initial velocity of `V.`

It can be shown that while both particles are in flight, Particle 1 has equations of motion:

`x = Vt cos theta`

`y = Vt sin theta -1/2 g t^2,`

and Particle `2` has equations of motion:

`x = a`

`y = Vt -1/2 g t^2.` Do NOT prove these equations of motion.

Let `L` be the distance between the particles at time `t.`

Show that, while both particles are in flight,

`L^2 = 2V^2t^2 (1 - sin theta) - 2aVt cos theta + a^2.` (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
An observer notices that the distance between the particles in flight first decreases, then increases.

Show that the distance between the particles in flight is smallest when

`t = (a cos theta)/(2V(1 - sin theta))` and that this smallest distance is `a sqrt ((1 - sin theta)/2).` (3 marks)

--- 12 WORK AREA LINES (style=lined) ---
Show that the smallest distance between the two particles in flight occurs while Particle 1 is ascending if

`V > sqrt((a g cos theta)/(2 sin theta \ (1 - sin theta))).` (1 mark)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

`text(Show)\ \ L^2 = 2V^2t^2 (1 – sin theta) – 2aVt cos theta + a^2`

`text(Consider)\ \ P_1`

`x_1 = Vt cos theta`

`y_1 = Vt sin theta – 1/2 g t^2`

`text(Consider)\ \ P_2`

`x_2 = a`

`y_2 = Vt -1/2 g t^2`

`text(Let)\ \ d=\ text(Vertical distance between particles)`

`d= Vt -1/2 g t^2 – (Vt sin theta – 1/2 g t^2)`

`d= Vt (1 – sin theta)`

`text(Using Pythagoras:)`

`L^2`	`= (a – x_1)^2 + d^2`
	`= (a – Vt cos theta)^2 + V^2t^2 (1 – sin theta)^2`
	`= a^2 – 2aVt cos theta + V^2t^2 cos ^2 theta + V^2t^2 (1 – 2 sin theta + sin^2 theta)`
	`= a^2 – 2aVt cos theta + V^2 t^2 (cos^2 theta + sin^2 theta + 1 – 2 sin theta)`
	`= a^2 – 2aVt cos theta + V^2 t^2 (2 – 2 sin theta)`
	`= 2 V^2 t^2 (1 – sin theta) – 2aVt cos theta + a^2\ \ text(… as required.)`

ii. `L^2 = 2V^2 t^2 (1 – sin theta) – 2a Vt cos theta + a^2`

`(d(L^2))/(dt) = 4 V^2 t\ (1 – sin theta) – 2aV cos theta`

`text(Max or min when)\ \ (d(L^2))/(dt) = 0`

`4V^2t\ (1 – sin theta)`	`= 2aV cos theta`
`t`	`= (2a V cos theta)/(4V^2 (1 – sin theta))`
	`= (a cos theta)/(2V(1 – sin theta)`

`(d^2(L^2))/(dt^2) = 4V^2(1 – sin theta) > 0\ \ text(for)\ \ V > 0,\ \ 0 < theta < pi/2`

`:.\ L^2\ \ text(is a minimum)`

`:.\ L\ \ text(is a minimum when)\ \ t = (a cos theta)/(2V (1 – sin theta)`

`text(Show minimum distance is)\ \ a sqrt {(1 – sin theta)/2}`

`text(When)\ \ t = (a cos theta)/(2V(1 – sin theta))`

`L^2`	`= 2V^2 ((a^2 cos ^2 theta)/(4V^2 (1 – sin theta)^2)) (1 – sin theta)`
	`\ \ – 2aV ((a cos theta)/(2V (1 – sin theta))) cos theta + a^2`
	`= (a^2 cos^2 theta)/(2 (1 – sin theta)) – (a^2 cos^2 theta)/((1 – sin theta)) + a^2`
	`= a^2[(cos^2 theta – 2 cos^2 theta + 2 (1 – sin theta))/(2(1 – sin theta))]`
	`= a^2[(-cos^2 theta + 2 – 2 sin theta)/(2(1 – sin theta))]`
	`= a^2[(-(1 – sin^2 theta) + 2 – 2 sin theta)/(2 (1 – sin theta))]`
	`= a^2 [(sin^2 theta – 2 sin theta + 1)/(2(1 – sin theta))]`
	`= a^2 [(1 – sin theta)^2/(2 (1 – sin theta))]`
	`= a^2 [((1 – sin theta))/2]`
`:.\ L`	`= sqrt ((a^2(1 – sin theta))/2)`
	`= a sqrt ((1 – sin theta)/2)\ \ text(… as required.)`

iii. `text(Smallest distance occurs when)`

`t = (a cos theta)/(2V (1 – sin theta)`

`text(If)\ \ P_1\ \ text(is ascending,)\ \ dot y_1 > 0`

`y_1 = Vt sin theta – 1/2 g t^2`

`dot y_1 = V sin theta – g t`

`:.\ V sin theta – g ((a cos theta)/(2V (1 – sin theta)))`	`> 0`
`2V^2 sin theta\ (1 – sin theta) – a g cos theta`	`> 0`
`2V^2 sin theta\ (1 – sin theta)`	`> ag cos theta`
`V^2`	`> (a g cos theta)/(2 sin theta\ (1 – sin theta))`
`V`	`> sqrt ((a g cos theta)/(2 sin theta\ (1 – sin theta)))\ \ text(… as required.)`

Trig Ratios, EXT1 2004 HSC 3d

The length of each edge of the cube `ABCDEFGH` is 2 metres. A circle is drawn on the face `ABCD` so that it touches all four edges of the face. The centre of the circle is `O` and the diagonal `AC` meets the circle at `X` and `Y`.

Explain why `∠FAC = 60^@`. (1 mark)
Show that `FO = sqrt6` metres. (1 mark)
Calculate the size of `∠XFY` to the nearest degree. (1 mark)

Show Answers Only

`text(See Worked Solution)`
`text(See Worked Solution)`
`44^@\ text{(nearest degree)}`

Show Worked Solution

(i)

`text(S)text(ince)\ \ FA, \ AC\ \ text(and)\ \ FC\ \ text(are all)`

`text(diagonals of sides of a cube,)`

`FA = AC = FC`

`:.ΔFAC\ \ text(is equilateral)`

`:.∠FAC = 60^@`

(ii)

`text(In)\ \ ΔAEF`

`AF^2`	`= EF^2 + EA^2`
	`= 2^2 + 2^2`
	`= 8`
`AF`	`= sqrt8`
	`= 2sqrt2`

`text(In)\ \ ΔAFO`

`sin\ 60^@`	`= (FO)/(AF)`
`sqrt3/2`	`= (FO)/(2sqrt2)`
`FO`	`= sqrt3/2 xx 2sqrt2`
	`= sqrt6\ text(metres … as required.)`

(iii)

`XY\ \ text(is the diameter of a circle AND the width)`

`text(of the cube.)`

`:.XY`	`= 2`
`:.OX`	`= OY = 1`

`tan\ ∠OFX`	`=1 /sqrt6`
`∠OFX`	`= 22.207…^@`

`:.∠XFY`	`= 2 xx 22.407…`
	`= 44.415…`
	`= 44^@\ text{(nearest degree)}`

Plane Geometry, EXT1 2006 HSC 3d

The points `P, Q` and `T` lie on a circle. The line `MN` is tangent to the circle at `T` with `M` chosen so that `QM` is perpendicular to `MN`. The point `K` on `PQ` is chosen so that `TK` is perpendicular to `PQ` as shown in the diagram.

Show that `QKTM` is a cyclic quadrilateral. (1 mark)
Show that `/_KMT = /_KQT.` (1 mark)
Hence, or otherwise, show that `MK` is parallel to `TP.` (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`/_ QMT = 90^@\ \ \ (QM _|_ MN)`

`/_ QKT = 90^@\ \ \ (PQ _|_ TK)`

`:.\ /_ QMT + /_ QKT = 180^@`

`:.\ QKTM\ \ text(is cyclic)\ \ text{(opposite angles are supplementary)}`

`text(… as required.)`

(ii) `text(Show)\ \ /_ KMT = /_ KQT`

`/_ KMQ = /_ KTQ = theta`

`text{(angles in the same segment on arc}\ \ KQ text{)}`

`/_ KQT`	`= 90 – theta\ \ text{(angle sum of}\ \ Delta KQT text{)}`
`/_ KMT`	`= /_ QMT – /_ KMQ`
	`= 90 – theta`

`:.\ /_ KMT = /_ KQT\ \ text(… as required.)`

(iii) `text(Show)\ \ MK\ text(||)\ TP`

`/_ NTP`	`= /_ KQT\ \ text{(angle in alternate segment)`
	`= 90 – theta`

`:.\ /_ NTP = /_ KMT\ \ text{(from part (ii))}`

`:.\ MK\ text(||)\ TP\ \ text{(corresponding angles are equal)}`

Mechanics, EXT2* M1 2005 6b

An experimental rocket is at a height of 5000 m, ascending with a velocity of ` 200 sqrt 2\ text(m s)^-1` at an angle of 45° to the horizontal, when its engine stops.

After this time, the equations of motion of the rocket are:

`x = 200t`

`y = -4.9t^2 + 200t + 5000,`

where `t` is measured in seconds after the engine stops. (Do NOT show this.)

What is the maximum height the rocket will reach, and when will it reach this height? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
The pilot can only operate the ejection seat when the rocket is descending at an angle between 45° and 60° to the horizontal. What are the earliest and latest times that the pilot can operate the ejection seat? (3 marks)

--- 10 WORK AREA LINES (style=lined) ---
For the parachute to open safely, the pilot must eject when the speed of the rocket is no more than `350\ text(m s)^-1`. What is the latest time at which the pilot can eject safely? (2 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`7041\ text(metres)`

`20.4\ text(seconds.)`
`40.8\ text(seconds)\ ;\ 55.8\ text(seconds)`
`49.7\ text(seconds)`

Show Worked Solution

`y = -4.9t^2 + 200t + 5000`

`dot y = -9.8t + 200`

`text(Max height occurs when)\ \ dot y = 0`

`9.8t`	`= 200`
`t`	`= 20.408…`
	`= 20.4\ text{seconds (to 1 d.p.)}`

`text(When)\ t = 20.408…`

`y`	`= -4.9 (20.408…)^2 + 200 (20.408…) + 5000`
	`= 7040.816…`
	`= 7041\ text{m (to nearest metre)}`

`:.\ text(The rocket will reach a maximum height of)`

`text(7041 metres when)\ \ t = 20.4\ text(seconds.)`

ii. `text(The rocket is descending at 45° at point)\ A\ text(on the graph.)`

`text(The symmetry of the parabolic motion means that)\ \ A`

`text(occurs when)\ \ t = 2 xx text(time to reach max height, or)`

`40.8\ text(seconds.)`

`text(Point)\ B\ text(occurs when the rocket is descending at 60°)`

`text(to the horizontal.)`

`text(At)\ \ B,`

`-tan 60° = (dot y)/(dot x)`

`text{(The gradient of the projectile becomes}`

`text{negative after reaching its max height.)}`

`dot y = -9.8t + 200`

`dot x = d/(dt) (200t) = 200`

`:.\ – sqrt 3`	`= (-9.8t + 200)/200`
`-200 sqrt 3`	`= -9.8t + 200`
`9.8t`	`= 200 + 200 sqrt 3`
`t`	`= (200 + 200 sqrt 3)/9.8`
	`= (546.410…)/9.8`
	`= 55.756…`
	`= 55.8\ text{seconds (nearest second)}`

`:.\ text(The pilot can operate the ejection seat)`

`text(between)\ \ t = 40.8 and t = 55.8\ text(seconds.)`

iii.

`v^2 = (dot x)^2 + (dot y)^2`

`text(When)\ \ v = 350`

`350^2`	`= 200^2 + (-9.8t + 200)^2`
`122\ 500`	`= 40\ 000 + (-9.8t + 200)^2`
`(-9.8t + 200)^2`	`= 82\ 500`
`-9.8t + 200`	`= +- sqrt (82\ 500)`
`9.8t`	`= 200 +- sqrt (82\ 500)`
`t`	`= (200 +- sqrt (82\ 500))/9.8`
	`= 49.717…\ \ \ (t > 0)`
	`= 49.7\ text{seconds (to 1 d.p.)}`

`:.\ text(The latest time the pilot can eject safely)`

`text(is when)\ \ t = 49.7\ text(seconds.)`

Trigonometry, 2ADV T1 2007 HSC 4c

An advertising logo is formed from two circles, which intersect as shown in the diagram.

The circles intersect at `A` and `B` and have centres at `O` and `C`.

The radius of the circle centred at `O` is 1 metre and the radius of the circle centred at `C` is `sqrt 3` metres. The length of `OC` is 2 metres.

Use Pythagoras’ theorem to show that `/_OAC = pi/2`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find `/_ ACO` and `/_ AOC`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Find the area of the quadrilateral `AOBC`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the area of the major sector `ACB`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the total area of the logo (the sum of all the shaded areas). (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`/_ ACO = pi/6\ ,\ /_ AOC = pi/3`
`sqrt 3\ \ text(m²)`
`(5 pi)/2\ text(m²)`
`((19 pi + 6 sqrt 3)/6)\ text(m²)`

Show Worked Solution

`text(In)\ Delta AOC`

`AO^2 + AC^2`	`= 1^2 + sqrt 3^2`
	`=1 + 3`
	`= 4`
	`= OC^2`

`:. Delta AOC\ \ text(is right-angled and)\ \ /_OAC = pi/2`

ii. `sin\ /_ACO`	`= 1/2`
`:. /_ACO`	`= pi/6`

`sin\ /_AOC`	`= sqrt 3/2`
`:. /_AOC`	`= pi/3`

iii. `text(Area)\ AOBC`

`= 2 xx text(Area)\ Delta AOC`

`= 2 xx 1/2 xx b xx h`

`= 2 xx 1/2 xx 1 xx sqrt 3`

`= sqrt 3\ \ text(m²)`

iv. `/_ACB = pi/6 + pi/6 = pi/3`

`:. /_ACB\ text{(reflex)}`	`= 2 pi – pi/3`
	`= (5 pi)/3`

`text(Area of major sector)\ ACB`

`= theta/(2 pi) xx pi r^2`

`= {(5 pi)/3}/(2 pi) xx pi(sqrt 3)^2`

`= (5 pi)/6 xx 3`

`= (5 pi)/2\ text(m²)`

v. `/_AOB = pi/3 + pi/3 = (2 pi)/3`

`:. /_AOB\ text{(reflex)}`	`= 2 pi – (2 pi)/3`
	`= (4 pi)/3`

`text(Area of major sector)\ AOB`

`= {(4 pi)/3}/(2 pi) xx pi xx 1^2`

`= (2 pi)/3\ text(m²)`

`:.\ text(Total area of the logo)`

`= (5 pi)/2 + (2 pi)/3 + text(Area)\ AOBC`

`= (15 pi + 4 pi)/6 + sqrt 3`

`= ((19 pi + 6 sqrt 3)/6)\ text(m²)`

Trig Ratios, EXT1 2015 HSC 12c

A person walks 2000 metres due north along a road from point `A` to point `B`. The point `A` is due east of a mountain `OM`, where `M` is the top of the mountain. The point `O` is directly below point `M` and is on the same horizontal plane as the road. The height of the mountain above point `O` is `h` metres.

From point `A`, the angle of elevation to the top of the mountain is 15°.

From point `B`, the angle of elevation to the top of the mountain is 13°.

Show that `OA = h\ cot\ 15°`. (1 mark)
Hence, find the value of `h`. (2 marks)

Show Answers Only

`text(See Worked Solutions)`
`910\ text{m (nearest metre)}`

Show Worked Solution

(i) `text(Show)\ \ OA = h\ cot\ 15^@`

`text(In)\ \ Delta MOA,`

`tan\ 15^@`	`= h/(OA)`
`OA`	`= h/(tan\ 15^@)`
	`= h\ cot\ 15^@\ \ …text(as required)`

(ii) `text(In)\ \ ΔMOB`

`tan\ 13^@`	`= h/(OB)`
`OB`	`= h/(tan\ 13^@)`
	`= h\ cot\ 13^@`

`text(In)\ \ ΔAOB`

`OA^2 + AB^2`	`= OB^2`
`OB^2 − OA^2`	`= AB^2`

`(h\ cot\ 13^@)^2 − (h\ cot\ 15^@)^2`	`= 2000^2`
`h^2[(cot^2\ 13^@ − cot^2\ 15^@)]`	`= 2000^2`

`h^2`	`= (2000^2)/(cot^2\ 13^@ − cot^2\ 15^@)`
`:. h`	`= sqrt((2000^2)/(cot^2\ 13^@ − cot^2\ 15^@))`
	`= 909.704…`
	`= 910\ text{m (nearest metre)}`

Quadratic, 2UA 2015 HSC 12e

The diagram shows the parabola `y = x^2/2` with focus `S (0, 1/2).` A tangent to the parabola is drawn at `P (1, 1/2).`

Find the equation of the tangent at the point `P`. (2 marks)
What is the equation of the directrix of the parabola? (1 mark)
The tangent and directrix intersect at `Q`.
Show that `Q` lies on the `y`-axis. (1 mark)
Show that `Delta PQS` is isosceles. (1 mark)

Show Answers Only

`y = x – 1/2`
`y = -1/2`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`y = 1/2 x^2`

`(dy)/(dx) = x`

`text(When)\ \ x = 1,\ \ (dy)/(dx) = 1`

`text(Equation of tangent,)\ m = 1,\ text(through)\ (1, 1/2):`

`y – y_1`	`= m (x – x_1)`
`y – 1/2`	`= 1 (x – 1)`
`y – 1/2`	`= x – 1`
`y`	`= x – 1/2`

(ii) `text(Directrix is)\ \ y = -1/2`

(iii) `Q\ text(is at the intersection of)`

`y = x – 1/2\ \ …\ \ text{(1)}`

`y = -1/2\ \ \ \ …\ \ text{(2)}`

`text{(1) = (2)}`

`x – 1/2`	`= -1/2`
`x`	`= 0`

`:.\ Q\ text(lies on the)\ y text(-axis)\ \ …\ \ text(as required)`

(iv) `text(Show)\ Delta PQS\ text(is isosceles.)`

`text(Distance)\ PS = 1 – 0 = 1`

`Q\ text(has coordinates)\ (0, -1/2)`

`text(Distance)\ SQ = 1/2 + 1/2 = 1`

`:. PS = SQ = 1`

`:.\ Delta PQS\ text(is isosceles)`

Plane Geometry, 2UA 2006 HSC 6a

In the diagram, `AD` is parallel to `BC`, `AC` bisects `/_BAD` and `BD` bisects `/_ABC`. The lines `AC` and `BD` intersect at `P`.

Copy or trace the diagram into your writing booklet.

Prove that `/_BAC = /_BCA`. (1 mark)
Prove that `Delta ABP ≡ Delta CBP`. (2 marks)
Prove that `ABCD` is a rhombus. (3 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`text(Prove)\ /_BAC = /_BCA`

`/_BCA`	`= /_CAD\ \ \ text{(alternate angles,}\ BC\ text(\|\|)\ AD text{)}`
`/_CAD`	`= /_BAC\ \ \ text{(}AC\ text(bisects)\ /_BAD text{)}`
`:. /_BAC`	`= /_BCA\ …\ text(as required)`

(ii) `text(Prove)\ Delta ABP ≡ Delta CBP`

`/_BAC`	`= /_BCA\ \ \ text{(from part (i))}`
`/_ABP`	`= /_CBP\ text{(}BD\ text(bisects)\ /_ABC text{)}`
`BP\ text(is common)`

`:. Delta ABP ≡ Delta CBP\ \ text{(AAS)}`

(iii) `text(Using)\ Delta ABP ≡ Delta CBP`

`AP = PC\ \ text{(corresponding sides of congruent triangles)}`

`/_BPA = /_BPC\ \ text{(corresponding angles of congruent triangles)}`

`text(Also,)\ /_BPA = /_BPC = 90^@`

`text{(}/_APC\ text{is a straight angle)}`

`text(Considering)\ Delta APD and Delta APB`

`/_DAP`	`= /_BAP\ text{(}AC\ text(bisects)\ /_BAD text{)}`
`/_DPA`	`= 90^@\ text{(vertically opposite angles)}`
`:. /_DPA`	`= /_BPA = 90^@`

`PA\ text(is common)`

`:. Delta APD ≡ Delta APB\ \ text{(AAS)}`

`BP = PD\ \ text{(corresponding sides of congruent triangles)}`

`:. ABCD\ text(is a rhombus as its diagonals are)`

`text(perpendicular bisectors.)`

Calculus, 2ADV C3 2004 HSC 4b

Consider the function `f(x) = x^3 − 3x^2`.

Find the coordinates of the stationary points of the curve `y = f(x)` and determine their nature. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Sketch the curve showing where it meets the axes. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
Find the values of `x` for which the curve `y = f(x)` is concave up. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(MAX at)\ (0,0),\ \ text(MIN at)\ (2,-4)`
`f(x)\ text(is concave up when)\ x>1`

Show Worked Solution

(i)	`f(x)`	`= x^3 – 3x^2`
	`f'(x)`	`= 3x^2 – 6x`
	`f″(x)`	`= 6x – 6`

`text(S.P.’s when)\ \ f'(x) = 0`

`3x^2 – 6x`	`= 0`
`3x (x – 2)`	`= 0`
`x`	`= 0\ \ text(or)\ \ 2`

`text(When)\ x = 0`

`f(0)`	`= 0`
`f″(0)`	`= 0 – 6 = -6 < 0`
`:.\ text(MAX at)\ (0,0)`

`text(When)\ x = 2`

`f(2)`	`= 2^3 – (3 xx 4) = -4`
`f″(2)`	`= (6 xx 2) – 6 = 6 > 0`
`:.\ text(MIN at)\ (2, -4)`

(ii)

`f(x) = x^3 – 3x^2\ text(meets the)\ x text(-axis when)\ f(x) = 0`

`x^3 – 3x^2`	`= 0`
`x^2 (x-3)`	`= 0`
`x`	`= 0\ \ text(or)\ \ 3`

(iii)

`f(x)\ text(is concave up when)`

`f″(x)`	`>0`
`6x – 6`	`>0`
`6x`	`>6`
`x`	`>1`

`:. f(x)\ text(is concave up when)\ \ x>1`

Calculus, 2ADV C4 2008 HSC 9c

A beam is supported at `(-b, 0)` and `(b, 0)` as shown in the diagram.

It is known that the shape formed by the beam has equation `y = f(x)`, where `f(x)` satisfies

	`f^{″}(x)`	`= k (b^2-x^2),\ \ \ \ \ `(`k` is a positive constant)
and	`f^{′}(-b)`	`= -f'(b)`.

Show that `f^{′}(x) = k (b^2x-(x^3)/3)`. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
How far is the beam below the `x`-axis at `x = 0`? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ text{(See Worked Solutions)}`
`(5kb^4)/12\ text(units)`

Show Worked Solution

i.	`text(Show)\ \ f^{′}(x) = k (b^2x-x^3/3)`

`f^{″}(x)`	`= k (b^2 – x^2)`
`f^{′}(x)`	`= int k (b^2-x^2)\ dx`
	`= k int b^2-x^2\ dx`
	`= k (b^2x-x^3/3) + c`

`text(S)text(ince S.P. exists at)\ \ x = 0`

`=> f^{′}(x)`	`= 0\ \ text(when)\ \ x = 0`
`0`	`= k (b^2 * 0-0) + c`
`c`	`= 0`

`:.\ f^{′}(x) = k (b^2x-x^3/3)\ \ \ text(… as required)`

ii.	`f(x)`	`= int f^{′}(x)\ dx`
		`= k int b^2x-x^3/3\ dx`
		`= k ((b^2x^2)/2-x^4/12) + c`

`text(We know)\ \ f(x) = 0\ \ text(when)\ \ x = b`

`=> 0`	`= k ( (b^2*b^2)/2-b^4/12) + c`
`c`	`= -k ( (6b^4)/12-b^4/12)`
	`= -k ( (5b^4)/12 )`
	`= -(5kb^4)/12`

`:.\ text(When)\ \ x = 0, text(the beam is)\ \ (5kb^4)/12\ \ text(units)`

`text(below the)\ x text(-axis.)`

Probability, 2ADV S1 2008 HSC 7c

Xena and Gabrielle compete in a series of games. The series finishes when one player has won two games. In any game, the probability that Xena wins is `2/3` and the probability that Gabrielle wins is `1/3`.

Part of the tree diagram for this series of games is shown.

Complete the tree diagram showing the possible outcomes. (1 mark)
What is the probability that Gabrielle wins the series? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
What is the probability that three games are played in the series? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`7/27`
`4/9`

Show Worked Solution

MARKER’S COMMENT: A tree diagram with 8 outcomes is incorrect (i.e. no third game is played if 1 player wins the first 2 games). If outcomes cannot occur, do not draw them on a tree diagram.

ii. `P text{(} G\ text(wins) text{)}`

`= P(XGG) + P (GXG) + P (GG)`

`= 2/3 * 1/3 * 1/3 + 1/3 * 2/3 * 1/3 + 1/3 * 1/3`

`= 2/27 + 2/27 + 1/9`

`= 7/27`

iii. `text(Method 1:)`

`P text{(3 games played)}`

`= P (XG) + P(GX)`

`= 2/3 * 1/3 + 1/3 * 2/3`

`= 4/9`

`text(Method 2:)`

`P text{(3 games)}`

`= 1 – [P(XX) + P(GG)]`

`= 1 – [2/3 * 2/3 + 1/3 * 1/3]`

`= 1 – 5/9`

`= 4/9`

Calculus, EXT1 C1 2009 HSC 5b

The cross-section of a 10 metre long tank is an isosceles triangle, as shown in the diagram. The top of the tank is horizontal.

When the tank is full, the depth of water is 3 m. The depth of water at time `t` days is `h` metres.

Find the volume, `V`, of water in the tank when the depth of water is `h` metres. (1 mark)

--- 6 WORK AREA LINES (style=lined) ---
Show that the area, `A`, of the top surface of the water is given by `A = 20 sqrt3 h`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
The rate of evaporation of the water is given by `(dV)/(dt) = - kA`, where `k` is a positive constant.

Find the rate at which the depth of water is changing at time `t`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
It takes 100 days for the depth to fall from 3 m to 2 m. Find the time taken for the depth to fall from 2 m to 1 m. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`10 sqrt 3 h^2\ \ text(m³)`
`text(Proof)\ \ text{(See Worked Solutions)}`
`-k\ \ \ text(metres per day)`
`100\ text(days)`

Show Worked Solution

MARKER’S COMMENT: Students who drew a diagram and included their working calculations on it were the most successful.

(i)
	`text(Let)\ A = text(area of front)`

`tan 30^@`	`= h/x`
`x`	`= h/(tan 30^@)`
	`= sqrt3 h`

`:.\ A`	`= 2 xx 1/2 xx sqrt 3 h xx h`
	`= sqrt 3 h^2\ \ text(m²)`

`V`	`= Ah`
	`= sqrt 3 h^2 xx 10`
	`= 10 sqrt3 h^2\ \ text(m³)`

(ii)	`text(Area of surface)`
	`= 10 xx 2 sqrt 3 h`
	`= 20 sqrt 3 h\ \ text(m²)`

(iii)	`(dV)/(dt)`	`= -kA`
		`= -k\ 20 sqrt3 h`

`V`	`= 10 sqrt3 h^2`
`(dV)/(dh)`	`= 20 sqrt 3 h`

`text(Find)\ (dh)/(dt)`

MARKER’S COMMENT: Half marks awarded for stating an appropriate chain rule, even if the following calculations were incorrect. Show your working!

`(dV)/(dt)`	`= (dV)/(dh) * (dh)/(dt)`
`(dh)/(dt)`	`= ((dV)/(dt))/((dV)/(dh))`
	`= (-k * 20 sqrt 3 h)/(20 sqrt 3 h)`
	`= -k`

`:.\ text(The water depth is changing at a rate)`

`text(of)\ -k\ text(metres per day.)`

♦♦♦ Exact data for part (iv) not available.
COMMENT: Interpreting a constant rate of change was very poorly understood!

(iv)	`text(S)text(ince)\ \ (dh)/(dt)\ \ text(is a constant, each metre)`
	`text(takes the same time.)`

`:.\ text(It takes 100 days to fall from 2 m to 1 m.)`

Calculus, 2ADV C3 2014 HSC 16c

The diagram shows a window consisting of two sections. The top section is a semicircle of diameter `x` m. The bottom section is a rectangle of width `x` m and height `y` m.

The entire frame of the window, including the piece that separates the two sections, is made using 10 m of thin metal.

The semicircular section is made of coloured glass and the rectangular section is made of clear glass.

Under test conditions the amount of light coming through one square metre of the coloured glass is 1 unit and the amount of light coming through one square metre of the clear glass is 3 units.

The total amount of light coming through the window under test conditions is `L` units.

Show that `y = 5 - x(1 + pi/4)`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Show that `L = 15x - x^2 (3 + (5pi)/8)`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Find the values of `x` and `y` that maximise the amount of light coming through the window under test conditions. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`x = 1.511\ text(m and)\ \ y = 2.302\ text(m)`

Show Worked Solution

`text(Frame is 10m)`

`10`	`= 2x + 2y + 1/2 pi x`
`2y`	`= 10\ – 2x\ – 1/2 pi x`
`:.y`	`= 5\ – x\ – pi/4 x`
	`= 5\ – x (1 + pi/4)\ \ \ text(… as required.)`

♦ Mean mark 35%

ii.	`text(Area)\ text{(clear)}`	`= x xx y`
	`text(Area)\ text{(colour)}`	`= 1/2 xx pi r^2`
		`= 1/2 xx pi (x/2)^2`
		`= (pi x^2)/8`

`:.\ L`	`= 3xy + ((pix^2)/8 xx 1)`
	`= 3x [5\ – x (1 + pi/4)] + (pix^2)/8\ \ \ text{(see part (i))}`
	`= 15x\ – 3x^2\ – (3x^2pi)/4 + (x^2 pi)/8`
	`= 15x\ – 3x^2\ – (5x^2 pi)/8`
	`= 15x\ – x^2 (3 + (5pi)/8)\ \ \ text(… as required)`

♦ Mean mark 38%
COMMENT: A sanity check for your answer could be to compare your answers to the perimeter restriction of 10m.

iii.	`L`	`= 15x\ – x^2 (3 + (5pi)/8)`
	`(dL)/(dx)`	`= 15\ – 2x (3 + (5pi)/8)`
	`(d^2L)/(dx^2)`	`= -2 (3 + (5pi)/8)`

`text(Max or min when)\ (dL)/(dx) = 0`

`15\ – 2x (3x + (5pi)/8)=`	`0`
`2x (3 + (5pi)/8)=`	`15`
`x=`	`15/(2 (3 + (5pi)/8)`
`=`	`1.51103…`
`=`	`1.511\ \ \ text{(3 d.p.)}`

`text(S)text(ince)\ (d^2L)/(dx^2) < 0\ \ \ => text(MAX)`

`text(When)\ \ x`	`= 1.511`
`y`	`= 5\ – 1.511 (1 + pi/4)`
	`= 2.3022…`
	`= 2.302\ text{(3 d.p.)}`

`:.\ text(MAX light when)\ x = 1.511\ text(m)`

`text(and)\ y = 2.302\ text(m.)`

Calculus, 2ADV C3 2014 HSC 15c

The line `y = mx` is a tangent to the curve `y = e^(2x)` at a point `P`.

Sketch the line and the curve on one diagram. (1 mark)

--- 8 WORK AREA LINES (style=lined) ---
Find the coordinates of `P`. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find the value of `m`. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

Show Answers Only

`P(1/2 ln (m/2), m/2)`
`2e`

Show Worked Solution

ii.	`y`	`= e^(2x)`
	`dy/dx`	`= 2e^(2x)`

`text(Gradient of)\ \ y = mx\ \ text(is)\ \ m`

♦ Mean mark 40%
COMMENT: Given `y= e^(ln(m/2))`, it follows `y=m/2`. Make sure you understand the arithmetic behind this (NB. Simply take the `ln` of both sides).

`text(Gradients equal when)`

`2e^(2x)`	`= m`
`e^(2x)`	`= m/2`
`ln e^(2x)`	`= ln (m/2)`
`2x`	`= ln (m/2)`
`x`	`= 1/2 ln (m/2)`

`text(When)\ \ x = 1/2 ln (m/2)`

`y`	`= e^(2 xx 1/2 ln (m/2))`
	`= e^(ln(m/2))`
	`= m/2`

`:.\ P (1/2 ln (m/2), m/2)`

iii. `y=mx\ \ text(passes through)\ \ (0,0)\ text(and)\ (1/2 ln (m/2), m/2)`

♦♦ Mean mark 30%.

`text(Equating gradients:)`

`(m/2 – 0)/(1/2 ln (m/2) – 0)`	`=m`
`m/2`	`=m xx 1/2 ln(m/2)`
`ln (m/2)`	`= 1`
`m/2`	`= e^1`
`m`	`= 2e`

Trigonometry, 2ADV T1 2014 HSC 13d

Chris leaves island `A` in a boat and sails 142 km on a bearing of 078° to island `B`. Chris then sails on a bearing of 191° for 220 km to island `C`, as shown in the diagram.

Show that the distance from island `C` to island `A` is approximately 210 km. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Chris wants to sail from island `C` directly to island `A`. On what bearing should Chris sail? Give your answer correct to the nearest degree. (3 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`333°`

Show Worked Solution

`text(Find)\ \ /_ABC`

`text(Let)\ D\ text(be south of)\ B`

`:.\ /_CBD = 191\ – 180 = 11°`

`/_ DBA`	`= 78°\ text{(alternate)}`
`/_ ABC`	`= 78\ – 11`
	`= 67°`

`text(Using Cosine rule:)`

`AC^2`	`= AB^2 + BC^2\ – 2 * AB * BC * cos /_ABC`
	`= 142^2 + 220^2\ – 2 xx 142 xx 220 xx cos 67°`
	`= 44\ 151.119…`

`:.\ AC`	`= 210.121…`
	`~~ 210\ text(km)\ \ \ text(… as required)`

ii. `text(Find)\ \ /_ ACB`

`text(Using Sine rule:)`

`(sin /_ ACB)/142`	`= (sin /_ABC)/210`
`sin /_ ACB`	`= (142 xx sin 67°)/210`
	`= 0.6224…`
`/_ ACB`	`= 38.494…`
	`= 38°\ text{(nearest degree)}`

`text(Let)\ E\ text(be due North of)\ C`

`/_ECB = 11°\ text{(} text(alternate to)\ /_CBD text{)}`

`:.\ /_ECA`	`= 38\ – 11`
	`= 27°`

`:.\ text(Bearing of)\ A\ text(from)\ C`

`= 360\ – 27`

`= 333°`

Trig Ratios, EXT1 2010 HSC 5a

A boat is sailing due north from a point `A` towards a point `P` on the shore line.

The shore line runs from west to east.

In the diagram, `T` represents a tree on a cliff vertically above `P`, and `L` represents a landmark on the shore. The distance `PL` is 1 km.

From `A` the point `L` is on a bearing of 020°, and the angle of elevation to `T` is 3°.

After sailing for some time the boat reaches a point `B`, from which the angle of elevation to `T` is 30°.

Show that

`qquad BP = (sqrt3 tan 3°)/(tan20°)`. (3 marks)
Find the distance `AB`. Give your answer to 1 decimal place. (1 mark)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`2.5\ text(km)\ \ text{(to 1 d.p.)}`

Show Worked Solution

(i) `text(Show)\ \ BP = (sqrt3 tan 3°)/(tan 20°)`

`text(In)\ Delta ATP`

`tan 3°`	`= (TP)/(AP)`
`=> AP`	`= (TP)/(tan 3)`

`text(In)\ Delta APL`

`tan 20°`	`= 1/(AP)`
`=> AP`	`= 1/tan 20`

`:. (TP)/(tan3)`	`= 1/(tan20)`
`TP`	`= (tan3°)/(tan20°)\ \ \ text(…)\ text{(} text(1)text{)}`

`text(In)\ \ Delta BTP`

`tan 30°`	`= (TP)/(BP)`
`1/sqrt3`	`= (TP)/(BP)`
`BP`	`= sqrt3 xx TP\ \ \ \ \ text{(using (1) above)}`
	`= (sqrt3 tan3°)/(tan20°)\ \ \ text(… as required)`

(ii)	`AB`	`= AP\ – BP`
	`AP`	`= 1/(tan20°)\ \ \ text{(} text(from part)\ text{(i)} text{)}`

`:.\ AB`	`= 1/(tan 20°)\ – (sqrt3 tan3°)/(tan20°)`
	`= (1\ – sqrt3 tan 3)/(tan20°)`
	`= 2.4980…`
	`= 2.5\ text(km)\ text{(to 1 d.p.)`

Trigonometry, EXT1 T3 2010 HSC 4b

Express `2 cos theta + 2 cos (theta + pi/3)` in the form `R cos (theta + alpha)`,

where `R > 0` and `0 < alpha < pi/2`. (3 marks)

--- 12 WORK AREA LINES (style=lined) ---
Hence, or otherwise, solve `2 cos theta + 2 cos (theta + pi/3) = 3`,
for `0 < theta < 2pi`. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`2 sqrt 3 cos (theta + pi/6)`
`(5pi)/3`

Show Worked Solution

i.	`2 cos theta + 2 cos (theta + pi/3)`
	`= 2 cos theta + 2 (cos theta cos (pi/3)\ – sin theta sin (pi/3))`
	`= 2 cos theta + 2 cos theta xx 1/2\ – 2 sin theta xx sqrt3/2`
	`= 2 cos theta + cos theta\ – sqrt3 sin theta`
	`= 3 cos theta\ – sqrt3 sin theta`

`R cos (theta + alpha) = R cos theta cos alpha – R sin theta sin alpha`

`R cos alpha`	`= 3\ \ \ \ \ `	`R sin alpha`	`= sqrt3`
`cos alpha`	`= 3/R\ \ \ \ \ `	`sin alpha`	`= sqrt3/R`

`tan alpha`	`= sin alpha/cos alpha = sqrt3/3 = 1/sqrt3`
`tan\ pi/6`	`=1/sqrt3`
`:. alpha`	`=pi/6\ \ \ \ \ (0 < alpha < pi/2)`

`R^2`	`= 3^2 + (sqrt3)^2`
	`= 9 + 3`
`R`	`= sqrt 12 = 2 sqrt3`

`:.\ 2 cos theta + 2 cos (theta + pi/3) = 2 sqrt 3 cos (theta + pi/6)`

♦ Mean mark part (ii) 49%
MARKER’S COMMENT: Many students did not check their answers against the stated domain for `theta`.

ii.	`2 cos theta + 2 cos(theta + pi/3)`	`= 3`
	`2 sqrt 3 cos (theta + pi/6)`	`= 3`
	`cos (theta + pi/6)`	`= 3/(2sqrt3) = sqrt3/2`
	`cos^(-1) (sqrt3/2)`	`= pi/6`

`text(S)text(ince cos is positive in 1st and 4th quadrants,)`

`theta + pi/6`	`= pi/6,\ 2pi\ – pi/6`
`:. theta`	`= (5pi)/3\ \ \ \ \ (0 < theta < 2pi)`

Inverse Functions, EXT1 2010 HSC 3b

Let `f(x) = e^(-x^2)`. The diagram shows the graph `y = f(x)`.

The graph has two points of inflection.
Find the `x` coordinates of these points. (3 marks)
Explain why the domain of `f(x)` must be restricted if `f(x)` is to have an inverse function. (1 mark)
Find a formula for `f^(-1) (x)` if the domain of `f(x)` is restricted to `x ≥ 0`. (2 marks)
State the domain of `f^(-1) (x)`. (1 mark)
Sketch the curve `y = f^(-1) (x)`. (1 mark)
(1) Show that there is a solution to the equation `x = e^(-x^2)` between `x = 0.6` and `x = 0.7`. (1 mark)
(2) By halving the interval, find the solution correct to one decimal place. (1 mark)

Show Answers Only

`x = +- 1/sqrt2`
`text(There can only be 1 value of)\ y`
`text(for each value of)\ x.`
`f^(-1)x = sqrt(ln(1/x))`
`0 <= x <= 1`
(1) `text(Proof)\ \ text{(See Worked Solutions)}`
(2) `0.7\ text{(1 d.p.)}`

Show Worked Solution

(i)	`y`	`= e^(-x^2)`
	`dy/dx`	`= -2x * e^(-x^2)`
	`(d^2y)/(dx^2)`	`= -2x (-2x * e^(-x^2)) + e ^(-x^2) (-2)`
		`= 4x^2 e^(-x^2)\ – 2e^(-x^2)`
		`= 2e^(-x^2) (2x^2\ – 1)`

`text(P.I. when)\ \ (d^2y)/(dx^2) = 0`

`2e^(-x^2) (2x^2\ – 1)`	`= 0`
`2x^2\ – 1`	`= 0`
`x^2`	`= 1/2`
`x`	`= +- 1/sqrt2`

COMMENT: It is also valid to show that `f(x)` is an even function and if a P.I. exists at `x=a`, there must be another P.I. at `x=–a`.

`text(When)\ \ `	`x < 1/sqrt2,`	`\ (d^2y)/(dx^2) < 0`
	`x > 1/sqrt2,`	`\ (d^2y)/(dx^2) > 0`

`=>\ text(Change of concavity)`

`:.\ text(P.I. at)\ \ x = 1/sqrt2`

`text(When)\ \ `	`x < – 1/sqrt2,`	`\ (d^2y)/(dx^2) > 0`
	`x > – 1/sqrt2,`	`\ (d^2y)/(dx^2) < 0`

`=>\ text(Change of concavity)`

`:.\ text(P.I. at)\ \ x = – 1/sqrt2`

(ii)	`text(In)\ f(x), text(there are 2 values of)\ y\ text(for)`
	`text(each value of)\ x.`
	`:.\ text(The domain of)\ f(x)\ text(must be restricted)`
	`text(for)\ \ f^(-1) (x)\ text(to exist).`

(iii)

`y = e^(-x^2)`

`text(Inverse function can be written)`

`x`	`= e^(-y^2),\ \ \ x >= 0`
`lnx`	`= ln e^(-y^2)`
`-y^2`	`= lnx`
`y^2`	`= -lnx`
	`=ln(1/x)`
`y`	`= +- sqrt(ln (1/x))`

`text(Restricting)\ \ x>=0,\ \ =>y>=0`

`:. f^(-1) (x)=sqrt(ln (1/x))`

♦ Parts (iv) and (v) were poorly answered with mean marks of 39% and 49% respectively.

(iv)

`f(0) = e^0 = 1`

`:.\ text(Range of)\ \ f(x)\ \ text(is)\ \ 0 < y <= 1`

`:.\ text(Domain of)\ \ f^(-1) (x)\ \ text(is)\ \ 0 < x <= 1`

(v)

(vi)(1) `x = e^(-x^2)`

`text(Let)\ g(x) = x\ – e^(-x^2)`

`g(0.6)`	`=0.6\ – e^(-0.6^2)`
	`=0.6\ – 0.6977 < 0`
`g(0.7)`	`=0.7\ – e^(-0.7^2)`
	`=0.7\ – 0.6126 > 0`
`=>g(x)\ text(changes sign)`

`:.\ g(x)\ \ text(has a root between 0.6 and 0.7)`

`:.\ x = e^(-x^2)\ \ text(has a solution between 0.6 and 0.7)`

♦ Mean mark 37%.
MARKER’S COMMENT: Better responses showed the change in sign between `g(0.65)` and `g(0.7)` as shown in the solution.

(vi)(2)	`g(0.65)`	`=0.65\ – e^(-0.65^2)`
		`=0.65\ – 0.655 < 0`

`:.\ text(A solution lies between 0.65 and 0.7)`

`:.\ x = 0.7\ \ text{(1 d.p.)}`

Trig Ratios, EXT1 2011 HSC 5a

In the diagram, `Q(x_0, y_0)` is a point on the unit circle `x^2 + y^2 = 1` at an angle `theta` from the positive `x`-axis, where `− pi/2 < theta < pi/2`. The line through `N(0, 1)` and `Q` intersects the line `y = –1` at `P`. The points `T(0, y_0)` and `S(0, –1)` are on the `y`-axis.

Use the fact that `Delta TQN` and `Delta SPN` are similar to show that
`SP = (2costheta)/(1\ - sin theta)`. (2 marks)
Show that `(costheta)/(1\ - sin theta) = sec theta + tan theta`. (1 mark)
Show that `/_ SNP = theta/2 + pi/4`. (1 mark)
Hence, or otherwise, show that `sectheta + tantheta = tan(theta/2 + pi/4)`. (1 mark)
Hence, or otherwise, solve `sec theta + tan theta = sqrt3`, where `-pi/2 < theta < pi/2`. (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`pi/6\ text(radians)`

Show Worked Solution

(i)

♦ Mean mark 41%
MARKER’S COMMENT: When questions direct you to use a certain fact for a proof, use that fact!

`text(Show)\ SP = (2 cos theta)/(1\ – sin theta)`

`Delta SPN \ text(|||) \ Delta TQN\ \ \ text{(given)}`

`(SP)/(SN) = (TQ)/(TN)\ \ \ text{(corresponding sides of similar triangles)}`

`/_TQO = theta\ \ \ text{(alternate,}\ TQ\ text(||)\ x text{-axis)}`

	`sin theta`	`= (OT)/1 => OT = sin theta`
`=>`	`TN`	`= 1\ – sin theta`

	`cos theta`	`= (TQ)/1`
`=>`	`TQ`	`= cos theta`

`SN`	`= 2\ \ \ text{(diameter of unit circle)}`
`:. (SP)/2`	`= cos theta/(1\ – sin theta)`
`SP`	`= (2 cos theta)/(1\ – sin theta)\ \ \ text(… as required)`

(ii) `text(Show)\ \ costheta/(1\ – sin theta) = sec theta + tan theta`

♦ Mean mark 35%

`text(RHS)`	`= 1/(costheta) + (sintheta)/(costheta)`
	`=(1 + sin theta)/cos theta xx cos theta/cos theta`
	`= (costheta(1 + sintheta))/(cos^2theta)`
	`= (costheta(1 + sin theta))/(1\ – sin^2 theta)`
	`= (costheta(1 + sin theta))/((1 + sin theta)(1\ – sin theta)`
	`= costheta/(1\ – sin theta)\ \ \ text(… as required)`

(iii) `text(Show)\ \ /_SNP = theta/2 + pi/4`

♦♦♦ Mean mark 11%

`/_TOQ = 90\ – theta`

`text(S)text(ince)\ ON = OQ = 1\ text{(unit circle)}`

`=> Delta ONQ\ text(is isosceles)`

`:.\ /_SNP`	`= 1/2 (180\ – (90\ – theta))\ \ \ \ text{(angle sum of}\ Delta ONQ text{)}`
	`= 90\ – 45 + theta/2`
	`= 45 + theta/2`
	`= pi/4 + theta/2\ \ \ text(… as required)`

(iv) `text(Show)\ sec theta + tan theta = tan (theta/2 + pi/4)`

♦♦ Mean mark 28%

`text(S)text(ince)\ /_SNP = pi/4 + theta/2\ \ \ \ text{(} text(part)\ text{(iii)} text{)}`

`=> tan\ /_SNP = tan (pi/4 + theta/2)`

`text(Also,)\ tan\ /_SNP`	`= (SP)/(SN)`
	`= ((2costheta)/(1\ – sin theta))/2`
	`= (cos theta)/(1\ – sin theta)`
	`= sec theta + tan theta\ \ \ \ text{(part (ii))}`

`:.\ sec theta + tan theta = tan (pi/4 + theta/2)\ \ \ text(… as required)`

♦ Mean mark 45%

(v)	`sec theta + tan theta`	`= sqrt3,\ \ \ (-pi/2 < theta < pi/2)`
	`tan (pi/4 + theta/2)`	`= sqrt3\ \ \ \ text{(part (iv))}`
	`tan (pi/3)`	`= sqrt 3`

`text(S)text(ince tan is positive in)\ 1^text(st) // 3^text(rd)\ text(quads)`

`theta/2 + pi/4`	`= pi/3,\ (4pi)/3`
`theta/2`	`= pi/12\ \ \ \ (-pi/2 < theta < pi/2)`
`:.\ theta`	`= pi/6\ text(radians)`

Plane Geometry, EXT1 2011 HSC 4b

In the diagram, the vertices of `Delta ABC` lie on the circle with centre `O`. The point `D` lies on `BC` such that `Delta ABD` is isosceles and `/_ABC = x`.

Copy or trace the diagram into your writing booklet.

Explain why `/_AOC = 2x`. (1 mark)
Prove that `ACDO` is a cyclic quadrilateral. (2 marks)
Let `M` be the midpoint of `AC` and `P` the centre of the circle through `A, C, D` and `O`.
Show that `P, M` and `O` are collinear. (1 mark)

Show Answers Only

`text(Angle at the centre of a circle is twice)`
`text(angle of circumference on same arc)`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`/_AOC = 2x`

`text{(angles at circumference and}`

`text{centre on arc}\ AC text{)}`

♦ Mean mark 38%
STRATEGY: Proving part (ii) by showing opposite angles are supplementary also worked but was more time consuming.

(ii) `text(Prove)\ ACDO\ text(is cyclic)`

`text(S)text(ince)\ Delta ADB\ text(is isosceles)`

`/_DAB = x\ \ \ text{(opposite equal sides in}\ Delta DBA text{)}`

`=> /_ADB`	`= 180\ – 2x\ \ \ text{(angle sum of}\ Delta DAB text{)}`
`=> /_CDA`	`= 2x\ \ \ text{(}CDB\ text{is a straight angle)}`

`text(S)text(ince chord)\ AC\ text(subtends)\ /_CDA = 2x`

`text(and)\ /_COA = 2x,`

`:.\ text(Quadrilateral)\ ACDO\ text(must be cyclic.)`

(iii)

`text(Need to show)\ OM\ text(passes through)\ P,\ text(centre)`

♦♦♦ Mean mark 7%. 2nd hardest question in the 2011 paper!

`text(of circle through)\ ACDO.`

`AM`	`= CM\ text{(} M\ text(is midpoint) text{)}`
`OC`	`= OA\ text{(radii)}`

`OM\ text(is common)`

`:.\ Delta OAM -= Delta OCM\ \ \ text{(SSS)}`

`:. /_CMO = /_AMO\ \ \ `	`text{(corresponding angles of}`
	`\ \ text{congruent triangles)}`

`text(S)text(ince)\ ∠AMC\ text(is straight angle)`

`/_CMO = /_AMO = 90°`

`:.OM\ text(is perpendicular bisector)`

`text(of chord)\ AC.`

`:. OM\ text(passes through)\ P.`

`:.\ P, M,\ text(and)\ O\ text(are collinear.)`

Quadratic, EXT1 2011 HSC 3b

The diagram shows two distinct points `P(t, t^2)` and `Q(1\ - t, (1\ - t)^2)` on the parabola `y = x^2`. The point `R` is the intersection of the tangents to the parabola at `P` and `Q`.

Show that the equation of the tangent to the parabola at `P` is `y = 2tx\ – t^2`. (2 marks)
Using part `text{(i)}`, write down the equation of the tangent to the parabola at `Q`. (1 mark)
Show that the tangents at `P` and `Q` intersect at
`R (1/2, t\ - t^2)`. (2 marks)
Describe the locus of `R` as `t` varies, stating any restriction on the `y`-coordinate. (2 marks)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`y = 2 (1 -t)x\ – (1\ – t)^2`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Locus of)\ R\ text(is vertical line)`
`x = 1/2,\ y<1/4`

Show Worked Solution

(i)

`text(Show tangent at)\ P\ text(is)\ y = 2tx\ – t^2`

`y`	`= x^2`
`dy/dx`	`= 2x`

`x=t\ \ \ \ text(at)\ P`

`dy/dx = 2t`

`text(Find equation with)\ \ m = 2t\ \ text(through)\ \ P(t, t^2)`

`y\ – y_1`	`= m(x\ – x_1)`
`y\ – t^2`	`= 2t ( x\ – t)`
`y`	`= 2tx\ – 2t^2 + t^2`
	`= 2tx\ – t^2\ text(… as required)`

(ii) `text(T)text(angent at)\ Q\ text(has equation)`

MARKER’S COMMENT: Many students derived this equation rather than substituting the new parameter, costing them valuable time. This is a benefit of using the parametric approach.

`y = 2(1\ – t)x\ – (1\ – t)^2`

(iii) `text(Need to show)\ R(1/2,\ t\ – t^2)`

`R\ text(is at intersection of tangents)`

`2tx\ – t^2`	`= 2(1\ – t)x\ – (1\ – t)^2`
`2tx\ – t^2`	`= 2x\ – 2tx\ – 1 + 2t\ – t^2`
`4tx\ – 2x`	`= -1 + 2t\ – t^2 + t^2`
`2x(2t\ – 1)`	`= 2t\ – 1`
`2x`	`= 1`
`x`	`= 1/2`

`text(Using)\ \ y = 2tx – t^2\ \ text(when)\ \ x = 1/2`

`y`	`= 2t(1/2)\ – t^2`
	`= t\ – t^2`

`:.\ R(1/2, t\ – t^2)\ text(… as required)`

(iv) `text(Locus of)\ R`

♦♦ Mean mark of 22%.
MARKER’S COMMENT: Many students stated the locus as `y=t-t^2` rather than realising it had to be a straight line since `x=½`, and that `y=t-t^2` simply restricted the values of `y`.

`text(S)text(ince)\ x = 1/2\ text(is a constant)`

`R\ text(is a vertical line)`

`text(Now,)\ y = t\ – t^2 = t(1\ – t)`

`text(Graphically,)\ \ y\ \ text(has a maximum at)\ \ t = 1/2`

`text(Max)\ \ y = 1/2\ – (1/2)^2 = 1/4`

`=> y < 1/4\ \ text{(tangents can’t meet on parabola)}`

`:.\ text(Locus of)\ R\ text(is vertical line)\ x = 1/2,\ \ y<1/4`

Plane Geometry, EXT1 2012 HSC 14a

The diagram shows a large semicircle with diameter `AB` and two smaller semicircles with diameters `AC` and `BC`, respectively, where `C` is a point on the diameter `AB`. The point `M` is the centre of the semicircle with diameter `AC`.

The line perpendicular to `AB` through `C` meets the largest semicircle at the point `D`. The points `S` and `T` are the intersections of the lines `AD` and `BD` with the smaller semicircles. The point `X` is the intersection of the lines `CD` and `ST`.

Copy or trace the diagram into your writing booklet.

Explain why `CTDS` is a rectangle. (1 mark)
Show that `Delta MXS` and `Delta MXC` are congruent. (2 marks)
Show that the line `ST` is a tangent to the semicircle with diameter `AC`. (1 mark)

Show Answers Only

`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`
`text(Proof)\ \ text{(See Worked Solutions)}`

Show Worked Solution

(i)

`/_SDT = 90°\ text{(angle in semi-circle)}`

♦ Mean mark 49%

`/_ ASC = 90°\ \ text{(angle in semi-circle)}`

`=> /_ CSD = 90°\ \ text{(} /_ ASD\ text{is a straight angle)}`

`text(Similarly)`

`/_CTB = /_CTD=90°`

`/_SCT = 90°\ \ text{(angle sum of quadrilateral}\ CTDS text{)}`

`text(S)text(ince all angles are right angles,)`

`CTDS\ text(is a rectangle)`

(ii) `ST\ text(and)\ DC\ text(are diagonals of rectangle)`

`text(S)text(ince they bisect and are equal)`

`=> XS = XC`

`SM = CM\ text{(radii)}`

`MX\ text(is common)`

`:.\ Delta MXS -= Delta MXC\ text{(SSS)}`

♦ Mean mark part (iii) 41%
STRATEGY: The congruency proof in part (ii) provided the critical information to answer this efficiently. Keep previous parts of questions front and centre of your mind when working on a solution.

(iii) `/_ XSM = /_ XCM = 90°`

`text{(corresponding angles of congruent triangles)}`

`text(S)text(ince)\ MS _|_ ST\ text(at circumference)`

`text(and)\ MS\ text(is a radius,)`

`=> ST\ text(is a tangent)`

Functions, EXT1 F1 2012 HSC 11c

Solve `x/(x - 3) < 2`. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`x<3\ \ text(or)\ \ x>6`

Show Worked Solution

`text(Solution 1)`

`x/(x – 3) < 2`

`text(When)\ \ x – 3 > 0,\ \ \ (text(i.e.)\ \ x > 3)`

`x`	`< 2 ( x – 3)`
`x`	`< 2x\ – 6`
`=>x`	`>6\ \ \ text{(satisfies both)}`

`text(When)\ \ x\ – 3 < 0,\ \ \ (text(i.e.)\ \ x<3)`

`x`	`>2 (x – 3)`
`x`	`> 2x – 6`
`x`	`<6`
`=> x`	`<3\ \ \ text{(satisfies both)}`

`:.\ text(Equation is correct for)\ x<3\ text(or)\ x>6`

`text(Solution 2)`

`x/((x\ – 3)) < 2`

`text(Multiply b.s. by)\ \ (x-3)^2`

`x(x – 3)`	`< 2(x^2 – 6x + 9)`
`x^2 – 3x`	`< 2x^2 – 12x + 18`
`x^2 – 9x + 18`	`>0`
`(x – 3)(x – 6)`	`>0`

`:.\ text(Equation correct for)\ x<3\ \ text(or)\ \ x>6`

Calculus, 2ADV C3 2010 HSC 9b

Let `y=f(x)` be a function defined for `0 <= x <= 6`, with `f(0)=0`.

The diagram shows the graph of the derivative of `f`, `y = f^{′}(x)`.

The shaded region `A_1` has area 4 square units. The shaded region `A_2` has area 4 square units.

For which values of `x` is `f(x)` increasing? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
What is the maximum value of `f(x)`? (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Find the value of `f(6)`. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
Draw a graph of `y =f(x)` for `0 <= x <= 6`. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`f(x)\ text(is increasing when)\ 0 <= x < 2`
`text(MAX value of)\ f(x) = 4`
`-6`

Show Worked Solution

i.	`f(x)\ text(is increasing when)\ \ f^{′}(x) > 0`
	`text(From the graph)`
	`f(x)\ text(is increasing when)\ 0 <= x < 2`

ii.	`f^{′}(x) = 0\ \ text(when)\ \ x=2`
	`:.\ text(MAX at)\ \ x = 2`
	`int_0^2 f^{′}(x)\ dx = 4\ \ \ (text(given since)\ A_1 = 4 text{)}`
	`text(We also know)`

`int_0^2\ f^{′}(x)\ dx`	`= [f(x)]_0^2`
	`= f(2)-f(0)`
	`= f(2)\ \ \ \ text{(since}\ f(0) = 0 text{)}`

`=> f(2) = 4`

♦♦♦ Parts (ii) and (iii) proved particularly difficult for students with mean marks of 12% and 11% respectively.

`:.\ text(MAX value of)\ \ f(x) = 4`

iii.	`int_0^4 f^{′}(x)`	`= A_1-A_2`
		`=0`

`text(We also know)`

`int_0^4 f^{′}(x)\ dx`	`= int_2^4 f^{′}(x)\ dx + int_0^2 f^{′}(x)\ dx`
	`=[f(x)]_2^4 + 4`
	`= f(4)-f(2) + 4\ \ \ (text(note)\ f(2)=4)`
	`=f(4)`

`=> f(4) = 0`

`text(Gradient = – 3 from)\ \ x = 4\ \ text(to)\ \ x = 6`

`:.\ f(6)`	`= -3 (6\ – 4)`
	`= -6`

♦♦ Mean mark 28%
EXAM TIP: Clearly identify THE EXTREMES when given a defined domain. In this case, the origin is obvious graphically, and the other extreme at `x=6`, is CLEARLY LABELLED!

iv.

Calculus, 2ADV C1 2010 HSC 7b

The parabola shown in the diagram is the graph `y = x^2`. The points `A (–1,1)` and `B (2, 4)` are on the parabola.

Find the equation of the tangent to the parabola at `A`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Let `M` be the midpoint of `AB`.

There is a point `C` on the parabola such that the tangent at `C` is parallel to `AB`.

Show that the line `MC` is vertical. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The tangent at `A` meets the line `MC` at `T`.

Show that the line `BT` is a tangent to the parabola. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`2x + y + 1 = 0`
`text(Proof) text{(See Worked Solutions)}`
`text(Proof) text{(See Worked Solutions)}`

Show Worked Solution

`y`	`=x^2`
`dy/dx`	`= 2x`

`text(At)\ \ A text{(–1,1)}\ => dy/dx = -2`

`text(T)text(angent has)\ \ m=text(–2),\ text(through)\ text{(–1,1):}`

`y – y_1`	`= m(x\ – x_1)`
`y – 1`	`= -2 (x + 1)`
`y – 1`	`= -2x -2`
`2x + y + 1`	`= 0`

`:.\ text(T)text(angent at)\ A\ text(is)\ \ 2x + y + 1 = 0`

♦ Mean mark 37%.
IMPORTANT: The critical understanding required for this question is that the gradient of `AB` needs to be equated to the gradient function (i.e. `dy/dx`).

ii. `Atext{(–1,1)}\ \ \ B(2,4)`

`M`	`= ((-1+2)/2 , (1+4)/2)`
	`= (1/2, 5/2)`

`m_(AB)`	`= (y_2 – y_1)/(x_2 – x_1)`
	`= (4 – 1)/(2 + 1)=1`

`text(When)\ \ dy/dx`	`= 1`
`2x`	`= 1`
`x`	`= 1/2`

`:.\ C \ (1/2, 1/4)`

`=>M\ text(and)\ C\ text(both have)\ x text(-value)=1/2`

`:. MC\ text(is vertical … as required)`

iii. `T\ text(is point on tangent when) \ x=1/2`

♦♦ Mean mark 29%.

`text(T)text(angent)\ \ \ 2x + y + 1 = 0`

`text(At)\ x = 1/2`

`2 xx (1/2) + y + 1=0`

`=> y=–2`

`:.\ T (1/2, –2)`

`text (Given)\ \ B (2, 4)`

`m_(BT)`	`= (4+2)/(2\ – 1/2)`
	`=4`

`text(At)\ \ B(2,4),\ text(find gradient of tangent:)`

`dy/dx = 2x=2 xx2=4`

`:.m_text(tangent) = 4=m_(BT)`

`:.BT\ text(is a tangent)`

Calculus, 2ADV C3 2012 HSC 14a

A function is given by `f(x) = 3x^4 + 4x^3-12x^2`.

Find the coordinates of the stationary points of `f(x)` and determine their nature. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Hence, sketch the graph `y = f(x)` showing the stationary points. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
For what values of `x` is the function increasing? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
For what values of `k` will `f(x) = 3x^4 + 4x^3-12x^2 + k = 0` have no solution? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{MAX at (0,0), MINs at (1, –5) and (–2, –32)}`
`f(x)\ text(is increasing for)\ -2 < x < 0\ text(and)\ x > 1`
`text(No solution when)\ k > 32`

Show Worked Solution

i.	`f(x)`	`= 3x^4 + 4x^3-12x^2`
	`f^{′}(x)`	`= 12x^3 + 12x^2-24x`
	`f^{″}(x)`	`= 36x^2 + 24x-24`

`text(Stationary points when)\ f^{′}(x) = 0`

`12x^3 + 12x^2-24x`	`=0`
`12x(x^2 + x-2)`	`=0`
`12x (x+2) (x-1)`	`=0`

`:.\ text(Stationary points at)\ x=0,\ 1\ text(or)\ -2`

`text(When)\ x=0,\ \ \ \ f(0)=0`
`f^{″}(0)`	`= -24 < 0`
`:.\ text{MAX at (0,0)}`

`text(When)\ x=1`

`f(1)`	`= 3+4-12 = -5`
`f^{″}(1)`	`= 36 + 24-24 = 36 > 0`
`:.\ text{MIN at}\ (1,-5)`

`text(When)\ x=–2`

`f(-2)`	`=3(-2)^4 + 4(-2)^3-12(-2)^2`
	`= 48-32-48`
	`= -32`
`f^{″}(-2)`	`= 36(-2)^2 + 24(-2)-24`
	`=144-48-24 = 72 > 0`
`:.\ text{MIN at (–2, –32)}`

ii.

♦ Mean mark 42%
MARKER’S COMMENT: Be careful to use the correct inequality signs, and not carelessly include ≥ or ≤ by mistake.

iii.	`f(x)\ text(is increasing for)`
	`-2 < x < 0\ text(and)\ x > 1`

iv. `text(Find)\ k\ text(such that)`

♦♦♦ Mean mark 12%.

`3x^4 + 4x^3-12x^2 + k = 0\ text(has no solution)`

`k\ text(is the vertical shift of)\ \ y = 3x^4 + 4x^3-12x^2`

`=>\ text(No solution if it does not cross the)\ x text(-axis.)`

`:.\ text(No solution when)\ k > 32`

Algebra, STD2 A2 2010 HSC 27c

The graph shows tax payable against taxable income, in thousands of dollars.

2010 27c

Use the graph to find the tax payable on a taxable income of $21 000. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Use suitable points from the graph to show that the gradient of the section of the graph marked `A` is `1/3`. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---
How much of each dollar earned between $21 000 and $39 000 is payable in tax? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Write an equation that could be used to calculate the tax payable, `T`, in terms of the taxable income, `I`, for taxable incomes between $21 000 and $39 000. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`$3000\ \ \ text{(from graph)}`
`1/3`
`33 1/3\ text(cents per dollar earned)`
`text(Tax payable on)\ I = 1/3 I\-4000`

Show Worked Solution

`text(Income on)\ $21\ 000=$3000\ \ \ text{(from graph)}`

ii. `text(Using the points)\ (21,3)\ text(and)\ (39,9)`

♦♦ Mean mark 25%

`text(Gradient at)\ A`	`= (y_2\-y_1)/(x_2\ -x_1)`
	`= (9000-3000)/(39\ 000 -21\ 000)`
	`= 6000/(18\ 000)`
	`= 1/3\ \ \ \ \ text(… as required)`

iii. `text(The gradient represents the tax applicable to each dollar)`

♦♦♦ Mean mark 12%!
MARKER’S COMMENT: Interpreting gradients is an examiner favourite, so make sure you are confident in this area.

`text(Tax)`	` = 1/3\ text(of each dollar earned)`
	` = 33 1/3\ text(cents per dollar earned)`

iv. `text( Tax payable up to $21 000 = $3000)`

`text(Tax payable on income between $21 000 and $39 000)`

♦♦♦ Mean mark 15%.
STRATEGY: The earlier parts of this question direct students to the most efficient way to solve this question. Make sure earlier parts of a question are front and centre of your mind when devising strategy.

` = 1/3 (I\-21\ 000)`

`:.\ text(Tax payable on)\ \ I`	`= 3000 + 1/3 (I\-21\ 000)`
	`= 3000 + 1/3 I\-7000`
	`= 1/3 I\-4000`

Statistics, STD2 S1 2010 HSC 26b

A new shopping centre has opened near a primary school. A survey is conducted to determine the number of motor vehicles that pass the school each afternoon between 2.30 pm and 4.00 pm.

The results for 60 days have been recorded in the table and are displayed in the cumulative frequency histogram.

Find the value of Χ in the table. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
On the cumulative frequency histogram above, draw a cumulative frequency polygon (ogive) for this data. (1 mark)
Use your graph to determine the median. Show, by drawing lines on your graph, how you arrived at your answer. (1 mark)
Prior to the opening of the new shopping centre, the median number of motor vehicles passing the school between 2.30 pm and 4.00 pm was 57 vehicles per day.

What problem could arise from the change in the median number of motor vehicles passing the school before and after the opening of the new shopping centre?

Briefly recommend a solution to this problem. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`15`
`text(Problems)`
`text(- increased traffic delays)`
`text(- increased danger to students leaving school)`
`text(Solutions)`
`text(- signpost alternative routes around school)`
`text(- decrease the speed limit in the area)`

Show Worked Solution

i.	`X`	`= 25\ -10`
		`= 15`

♦♦♦ Mean mark 18%
MARKER’S COMMENT: The ogive was poorly drawn with many students incorrectly joining the middle of each column rather than from corner to corner.

ii.

♦♦ Mean mark 25%
MARKER’S COMMENT: Many students did not “show by drawing lines on the graph” as the question asked.

iii. `text(Median)\ ~~155`

♦ Mean mark 47%
MARKER’S COMMENT: Short answers were often the best. Be concise when you can.

iv.	`text(Problems)`
	`text(- increased traffic delays)`
	`text(- increased danger to students leaving school)`

	`text(Solutions)`
	`text(- signpost alternative routes around school)`
	`text(- decrease the speed limit in the area)`

Algebra, STD2 A4 2013 HSC 30a

Wind turbines, such as those shown, are used to generate power.

In theory, the power that could be generated by a wind turbine is modelled using the equation

`T = 20\ 000w^3`

where	`T` is the theoretical power generated, in watts
	`w` is the speed of the wind, in metres per second.

Using this equation, what is the theoretical power generated by a wind turbine if the wind speed is 7.3 m/s ? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

In practice, the actual power generated by a wind turbine is only 40% of the theoretical power.

If `A` is the actual power generated, in watts, write an equation for `A` in terms of `w`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

The graph shows both the theoretical power generated and the actual power generated by a particular wind turbine.

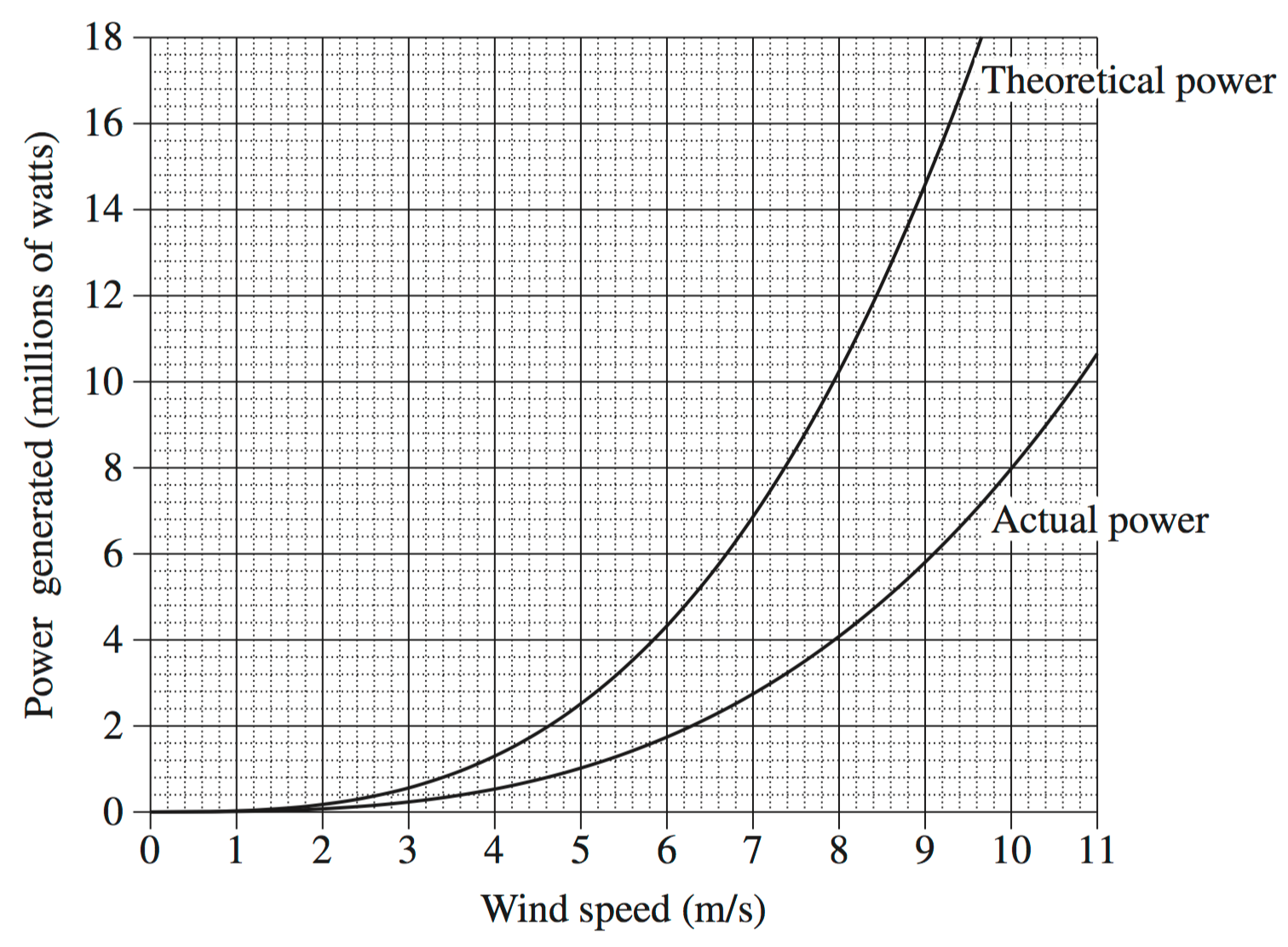
Using the graph, or otherwise, find the difference between the theoretical power and the actual power generated when the wind speed is 9 m/s. (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

A particular farm requires at least 4.4 million watts of actual power in order to be self-sufficient.

What is the minimum wind speed required for the farm to be self-sufficient? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---

A more accurate formula to calculate the power (`P`) generated by a wind turbine is

`P = 0.61 xx pi xx r^2 × w^3`

where	`r` is the length of each blade, in metres
	`w` is the speed of the wind, in metres per second.

Each blade of a particular wind turbine has a length of 43 metres.The turbine operates at a wind speed of 8 m/s.

Using the formula above, if the wind speed increased by 10%, what would be the percentage increase in the power generated by this wind turbine? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`7\ 780\ 340\ text(watts)`
`8000w^3`
`8.8\ text(million watts, or 8 748 000 watts)`
`w = 8.2\ text(m/s)\ \ \ text{(1 d.p.)}`
`text(33%)`

Show Worked Solution

i.	`T=20\ 000w^3`
	`text(If)\ \ w = 7.3`

`T`	`=20\ 000 xx (7.3)^3`
	`= 7\ 780\ 340\ text(watts)`

♦ Mean mark 34%

ii.

`text(We know)\ A = 40% xx T`

`=> A`	`=0.4 xx 20\ 000 xx w^3`
	`=8000w^3`

♦ Mean mark 38%

iii.	`text(Solution 1)`
	`text(At)\ w=9`
	`A = text(5.8 million watts)\ \ \ text{(from graph)}`
	`T = text(14.6 million watts)\ \ \ text{(from graph)}`

`text(Difference)`	`= text(14.6 million)\-text(5.8 million)`
	`= text(8.8 million watts)`

`text(Alternative Solution)`

`text(At)\ w=9`

`T`	`= 20\ 000 xx 9^3`
	`= 14\ 580\ 000\ text(watts)`

`A`	`= 8000 xx 9^3`
	`= 5\ 832\ 000\ text(watts)`

`text(Difference)`	`=14\ 580\ 000\-5\ 832\ 000`
	`=8\ 748\ 000\ \ text(watts)`

♦♦ Mean mark 25%
COMMENT: Students need to be comfortable in finding the cube roots of values – a calculation that can be required in a number of topic areas and is regularly examined.

iv.

`text(Find)\ w\ text(if)\ A=4.4\ text(million)`

`8000w^3`	`= 4\ 400\ 000`
`w^3`	`= (4\ 400\ 000)/8000`
	`= 550`

`:. w`	`= root(3)(550)`
	`=8.1932…`
	`=8.2\ text(m/s)\ \ \ text{(1 d.p.)}`

`:.\ text(The minimum wind speed required is 8.2 m/s)`

♦ Mean mark 41%
MARKER’S COMMENT: Students are reminded that a % increase requires them to find the difference in power generated at different wind speeds and divide this result by the original power output, as shown in the Worked Solution.

v.	`text(Find)\ P\ text(when)\ w=8\ text(and)\ r=43`

`P`	`= 0.61 xx pi xx r^2 xx w^3`
	`= 0.61 xx pi xx 43^2 xx 8^3`
	`= 1\ 814\ 205.92\ text(watts)`

`text(When speed of wind)\ uarr10%`

`w′ = 8 xx 110text(%) = 8.8\ text(m/s)`

`text(Find)\ P\ text(when)\ w′ = 8.8`

`P`	`=0.61 xx pi xx 43^2 xx 8.8^3`
	`= 2\ 414\ 708.08\ text(watts)`

`text(Increase in Power)`	`=2\ 414\ 708.08\-1\ 814\ 205.92`
	`= 600\ 502.16`

`:.\ text(% Power increase)`	`= (600\ 502.16)/(1\ 814\ 205.92)`
	`= 0.331`
	`= text(33%)\ \ \ text{(nearest %)}`

Measurement, STD2 M6 2009 HSC 27b

A yacht race follows the triangular course shown in the diagram. The course from `P` to `Q` is 1.8 km on a true bearing of 058°.

At `Q` the course changes direction. The course from `Q` to `R` is 2.7 km and `/_PQR = 74^@`.

What is the bearing of `R` from `Q`? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
What is the distance from `R` to `P`? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The area inside this triangular course is set as a ‘no-go’ zone for other boats while the race is on.

What is the area of this ‘no-go’ zone? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

`312^@`
`2.8\ text(km)\ \ \ text{(1 d.p.)}`
`2.3\ text(km²)\ \ \ text{(1 d.p.)}`

Show Worked Solution

`/_ PQS = 58^@ \ \ \ (text(alternate to)\ /_TPQ)`

♦♦♦ Mean mark 18%.
TIP: Draw North-South parallel lines through relevant points to help calculate angles as shown in the Worked Solutions.

`text(Bearing of)\ R\ text(from)\ Q`

`= 180^@ + 58^@ + 74^@`

`= 312^@`

ii. `text(Using Cosine rule:)`

♦ Mean mark 36%

`RP^2`	`=RQ^2` + `PQ^2` `- 2` `xx RQ` `xx PQ` `xx cos` `/_RQP`
	`= 2.7^2` + `1.8^2` `- 2` `xx 2.7` `xx 1.8` `xx cos74^@`
	`=7.29 + 3.24\ – 2.679…`
	`=7.851…`

`:.RP`	`= sqrt(7.851…)`
	`=2.8019…`
	`~~ 2.8\ text(km) (text(1 d.p.) )`

iii. `text(Using)\ \ A = 1/2 ab sinC`

♦ Mean mark 44%

`A`	`= 1/2` `xx 2.7` `xx 1.8` `xx sin74^@`
	`= 2.3358…`
	`= 2.3\ text(km²)`

`:.\ text(No-go zone is 2.3 km²)`

Quadratic, 2UA 2012 HSC 16c

The circle `x^2+(y-c)^2=r^2`, where `c>0` and `r>0`, lies inside the parabola `y=x^2`. The circle touches the parabola at exactly two points located symmetrically on opposite sides of the `y`-axis, as shown in the diagram.

Show that `4c=1+4r^2`. (2 marks)
Deduce that `c>1/2`. (1 mark)

Show Answers Only

`text{Proof (See Worked Solutions)}`
`text{Proof (See Worked Solutions)}`

Show Worked Solution

(i) `text(We need to find the intersection of)`

`x^2+(y-c)^2`	`=r^2\ \ \ text{… (1)}`
`y`	`=x^2\ \ \ text{… (2)}`

`text(Subst.)\ y=x^2\ text{into (1)}`

`y+(y-c)^2`	`=r^2`
`y+y^2-2cy+c^2`	`=r^2`
`y^2+y(1-2c)+(c^2-r^2)`	`=0`

`text(S)text(ince circle touches symmetrically)`

♦♦♦ Mean mark 18%.
MARKER’S COMMENT: Few students were successful in this part, with those that solved the simultaneous equations correctly often not realising that the `Delta=0` was a critical element in solving the problem.

`=>\ \ 1\ ytext(-value only)`

`=>Delta=b^2-4ac=0`

`(1-2c)^2-4xx1xx(c^2-r^2)`	`=0`
`1-4c+4c^2-4c^2+4r^2`	`=0`

`:.\ 4c`

`=1+4r^2\ \ \ text(… as required)`

(ii) `text(Deduce)\ c>1/2`

`text(Given)\ y^2+y(1-2c)+(c^2-r^2)`

`y=(-(1-2c)+-sqrt((1-2c)^2-4xx1xx(c^2-r^2)))/2`

`text(S)text(ince)\ y>0\ \ text(and)\ \ b^2-4ac=0`

♦♦♦ If you found this part difficult, don’t despair, it is a beast. With a mean mark of 0%, it ranks as one of the hardest questions in the history of the course.

`=>\ (-(1-2c)+-0)/2`	`>0`
`(-1+2c)/2`	`>0`
`2c`	`>1`
`c`	`>1/2\ \ text(… as required)`

Calculus, 2ADV C3 2011 HSC 10b

A farmer is fencing a paddock using `P` metres of fencing. The paddock is to be in the shape of a sector of a circle with radius `r` and sector angle `theta` in radians, as shown in the diagram.

Show that the length of fencing required to fence the perimeter of the paddock is

`P=r(theta+2)`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Show that the area of the sector is `A=1/2 Pr-r^2`. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the radius of the sector, in terms of `P`, that will maximise the area of the paddock. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Find the angle `theta` that gives the maximum area of the paddock. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Explain why it is only possible to construct a paddock in the shape of a sector if

`P/(2(pi+1)) <\ r\ <P/2` (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions)}`
`text{Proof (See Worked Solutions)}`
`r=P/4`
`2\ text(radians)`
`text{Proof (See Worked Solutions)}`

Show Worked Solution

i. `text(Need to show)\ \ P=r(theta+2)`

`P`	`=(2xxr)+theta/(2pi)xx2pir`
	`=2r+ r theta`
	`=r(theta+2)\ \ text(… as required)`

ii. `text(Need to show)\ \ A=1/2 Pr-r^2`.

`text(S)text(ince)\ \ P=r(theta+2)\ \ \ =>\ theta=(P-2r)/r`

♦ Mean mark 41%.
TIP: Area of a sector `=pi r^2 xx` the percentage of the circle that the sector angle accounts for, i.e. `theta/(2 pi)` radians. `:. A=pi r^2“ xx theta/(2 pi)=1/2 r^2 theta`.

`:. A`	`=1/2 r^2 theta`
	`=1/2 r^2*(P-2r)/r`
	`=1/2(Pr-2r^2)`
	`=1/2 Pr-r^2\ \ text(… as required)`

iii. `A=1/2 Pr-r^2`

♦♦ Mean mark 29%
MARKER’S COMMENT: The second derivative test proved much more successful and easily proven in this part. Make sure you are comfortable choosing between it and the 1st derivative test depending on the required calcs.

`(dA)/(dr)=1/2 P-2r`

`text(MAX or MIN when)\ \ (dA)/(dr)=0`

`1/2 P-2r`	`=0`
`2r`	`=1/2 P`
`r`	`=P/4`

`(d^2A)/(dr^2)=-2\ \ \ \ =>text(MAX)`

`:.\ text(Area is a MAX when)\ r=P/4\ text(units)`

iv. `text(Need to find)\ theta\ text(when area is a MAX)\ =>\ r=P/4`

♦♦♦ Mean mark 20%

`P`	`=r(theta+2)`
	`=P/4(theta+2)`
`4P`	`=P(theta+2)`
`theta+2`	`=4`
`theta`	`=2\ text(radians)`

v. `text(For a sector to exist)\ \ 0<\ theta\ <2pi, \ \ text(and)\ \ theta=(P-2r)/r`

♦♦♦ Mean mark 4%. A BEAST!
MARKER’S COMMENT: When asked to ‘explain’, students should support their answer with a mathematical argument.

`=>(P-2r)/r`	`>0`
`P-2r`	`>0`
`r`	`<P/2`

`=>(P-2r)/r`	`<2pi`
`P-2r`	`<2r pi`
`2r pi+2r`	`>P`
`2r(pi+1)`	`>P`
`r`	`>P/(2(pi+1))`

`:.P/(2(pi+1)) <\ r\ <P/2\ \ text(… as required)`

Calculus, EXT1* C1 2009 HSC 6b

Radium decays at a rate proportional to the amount of radium present. That is, if `Q(t)` is the amount of radium present at time `t`, then `Q=Ae^(-kt)`, where `k` is a positive constant and `A` is the amount present at `t=0`. It takes 1600 years for an amount of radium to reduce by half.

Find the value of `k`. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
A factory site is contaminated with radium. The amount of radium on site is currently three times the safe level.

How many years will it be before the amount of radium reaches the safe level. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`(-ln(1/2))/1600\ \ text(or 0.000433)`
`2536\ text(years)`

Show Worked Solution

i. `Q=Ae^(-kt)`

MARKER’S COMMENT: Students must be familiar with “half-life” and the algebra required. i.e. using `Q=1/2 A` within their calculations.

`text(When)\ \ t=0,\ \ Q=A`

`text(When)\ \ t=1600,\ \ Q=1/2 A`

`:.1/2 A`	`=A e^(-1600xxk)`
`e^(-1600xxk)`	`=1/2`
`lne^(-1600xxk)`	`=ln(1/2)`
`-1600k`	`=ln(1/2)`
`k`	`=(-ln(1/2))/1600`
	`=0.0004332\ \ text{(to 4 sig. figures)}`

ii. `text(Find)\ \ t\ \ text(when)\ \ Q=1/3 A :`

IMPORTANT: Know how to use the memory function on your calculator to store the exact value of `k` found in part (i) to save time.

`1/3 A`	`=A e^(-kt)`
`e^(-kt)`	`=1/3`
`lne^(-kt)`	`=ln(1/3)`
`-kt`	`=ln(1/3)`
`:.t`	`=(-ln(1/3))/k,\ \ \ text(where)\ \ \ k=(-ln(1/2))/1600`
	`=(ln(1/3) xx1600)/ln(1/2)`
	`=2535.940…`

`:.\ text(It will take 2536 years.)`

Calculus, EXT1* C1 2012 HSC 14c

Professor Smith has a colony of bacteria. Initially there are 1000 bacteria. The number of bacteria, `N(t)`, after `t` minutes is given by

`N(t)=1000e^(kt)`.

After 20 minutes there are 2000 bacteria.

Show that `k=0.0347` correct to four decimal places. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
How many bacteria are there when `t=120`? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
What is the rate of change of the number of bacteria per minute, when `t=120`? (1 mark)

--- 5 WORK AREA LINES (style=lined) ---
How long does it take for the number of bacteria to increase from 1000 to 100 000? (2 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions).}`
`64\ 328`
`2232`
`133\ text(minutes)`

Show Worked Solution

i. `N=1000e^(kt)\ text(and given)\ N=2000\ text(when)\ t=20`

`2000`	`=1000e^(20xxk)`
`e^(20k)`	`=2`
`lne^(20k)`	`=ln2`
`20k`	`=ln2`
`:.k`	`=ln2/20`
	`=0.0347\ \ text{(to 4 d.p.) … as required}`

ii. `text(Find)\ \ N\ \ text(when)\ t=120`

NOTE: Students could have used the exact value of `k=ln2/20` in parts (ii), (iii) and (iv), which would yield the answers (ii) 64,000, (iii) 2,218, and (iv) 133 minutes.

`N`	`=1000e^(120xx0.0347)`
	`=64\ 328.321..`
	`=64\ 328\ \ text{(nearest whole number)}`

`:.\ text(There are)\ 64\ 328\ text(bacteria when t = 120.)`

iii. `text(Find)\ (dN)/(dt)\ text(when)\ t=120`

MARKER’S COMMENT: This part proved challenging for many students. Differentiation is required to find the rate of change in these type of questions.

`(dN)/(dt)`	`=0.0347xx1000e^(0.0347t)`
	`=34.7e^(0.0347t)`

`text(When)\ \ t=120`

`(dN)/(dt)`	`=34.7e^(0.0347xx120)`
	`=2232.1927…`
	`=2232\ \ text{(nearest whole)}`

`:.\ (dN)/(dt)=2232\ text(bacteria per minute at)\ t=120`

iv. `text(Find)\ \ t\ \ text(such that)\ N=100,000`

`=>100\ 000`	`=1000e^(0.0347t)`
`e^(0.0347t)`	`=100`
`lne^(0.0347t)`	`=ln100`
`0.0347t`	`=ln100`
`t`	`=ln100/0.0347`
	`=132.7138…`
	`=133\ \ text{(nearest minute)}`

`:.\ N=100\ 000\ text(when)\ t=133\ text(minutes.)`

Financial Maths, 2ADV M1 2008 HSC 9b

Peter retires with a lump sum of $100 000. The money is invested in a fund which pays interest each month at a rate of 6% per annum, and Peter receives a fixed monthly payment `$M` from the fund. Thus the amount left in the fund after the first monthly payment is `$(100\ 500-M)`.

Find a formula for the amount, `$A_n`, left in the fund after `n\ ` monthly payments. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Peter chooses the value of `M` so that there will be nothing left in the fund at the end of the 12th year (after 144 payments). Find the value of `M`. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`100\ 000(1.005^n)-M((1.005^n-1)/0.005)`
`$975.85`

Show Worked Solutions

i. `r=(1+0.06/12)=1.005`

MARKER’S COMMENT: Students who developed this answer from writing the calculations of `A_1`, `A_2`, `A_3` to then generalising for `A_n` were the most successful.

`A_1`	`=(100\ 500-M)`
	`=100\ 000(1.005)^1-M`
`A_2`	`=A_1 (1.005)-M`
	`=[100\ 000(1.005^1)-M](1.005)-M`
	`=100\ 000(1.005^2)-M(1.005)-M`
	`=100\ 000(1.005^2)-M(1+1.005)`

`A_3`

`=100\ 000(1.005^3)-M(1+1.005^1+1.005^2)`

`\ \ \ \ \ vdots`

`A_n`	`=100\ 000(1.005^n)-M(1+1.005+\ …\ +1.005^(n-1))`
	`=100\ 000(1.005^n)-M((a(r^n-1))/(r-1))`
	`=100\ 000(1.005^n)-M((1(1.005^n-1))/(1.005-1))`
	`=100\ 000(1.005^n)-M((1.005^n-1)/0.005)`

ii. `text(Find)\ M\ text(such that)\ \ $A_n=0\ \ text(when)\ \ n=144`

`A_144=100\ 000(1.005)^144-M((1.005^144-1)/0.005)=0`

`M((1.005^144-1)/0.005)`	`=100\ 000(1.005^144)`
`M(1.005^144-1)`	`=500(1.005^144)`
`M`	`=(500(1.005^144))/(1.005^144-1)`
	`=975.85`

`:. M=$975.85\ \ text{(nearest cent).}`

Calculus, 2ADV C4 2010 HSC 3b

Sketch the curve `y=lnx`. (1 mark)

--- 6 WORK AREA LINES (style=lined) ---
Use the trapezoidal rule with 3 function values to find an approximation to `int_1^3 lnx\ dx` (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
State whether the approximation found in part (ii) is greater than or less than the exact value of `int_1^3 lnx\ dx`. Justify your answer. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answer Only

`text(See Worked Solutions for sketch.)`
`1.24\ \ text(u²)`
`text(See Worked Solutions)`

Show Worked Solutions

MARKER’S COMMENT: Many students failed to illustrate important features in their graph such as the concavity, `x`-axis intercept and `y`-axis asymptote (this can be explicitly stated or made graphically clear).

ii. `text(Area)`	`~~h/2[f(1)+2xxf(2)+f(3)]`
	`~~1/2[0+2ln2+ln3]`
	`~~1/2[ln(2^2 xx3)]`
	`~~1/2ln12`
	`~~1.24\ \ text(u²)` `text{(to 2 d.p.)}`

iii.

♦♦♦ Mean mark 12%.
MARKER’S COMMENT: Best responses commented on concavity and that the trapezia lay beneath the curve. Diagrams featured in the best responses.

`text(The approximation is less because the sides)`

`text{of the trapezia lie below the concave down}`

`text{curve (see diagram).}`

Financial Maths, 2ADV M1 2010 HSC 9a

When Chris started a new job, $500 was deposited into his superannuation fund at the beginning of each month. The money was invested at 0.5% per month, compounded monthly.

Let `$P` be the value of the investment after 240 months, when Chris retires.

Show that `P=232\ 175.55` (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
After retirement, Chris withdraws $2000 from the account at the end of each month, without making any further deposits. The account continues to earn interest at 0.5% per month.

Let `$A_n` be the amount left in the account `n` months after Chris's retirement.

(1) Show that `A_n=(P-400\ 000)xx1.005^n+400\ 000`. (3 marks)

--- 7 WORK AREA LINES (style=lined) ---

(2) For how many months after retirement will there be money left in the account? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions)}`
(1) `text{Proof (See Worked Solutions)}`
(2) `text(175 months)`

Show Worked Solutions

i. `P_1`	`=500(1.005)`
`P_2`	`=500(1.005^2)+500(1.005^1)`
`P_3`	`=500(1.005^3+1.005^2+1.005)`
	`vdots`
`P_240`	`=500(1.005+1.005^2+1.005^3 …+1.005^240)`

`=>\ text(GP where)\ \ a=1.005,\ text(and)\ \ r=1.005`

MARKER’S COMMENT: Common errors included using `r=1.05`, and taking the first term of the GP as 1 instead of 1.005 (note that the $500 goes in at the start of the month and earns interest before it is included in `$P_n`).

`P_240`	`=500((a(r^n-1))/(r-1))`
	`=500((1.005(1.005^240-1))/(1.005-1))`
	`=100\ 000[1.005(1.005^240-1)]`
	`=232\ 175.55`

`:.\ text(The value of Chris’ investment after 240 months)`

`text(is) \ $232\ 175.55 text( … as required)`

ii. (1) `text(After 1 month,)\ A_1=P(1.005)-2000`

IMPORTANT: At the end of the month, `$P` earns interest for the month BEFORE any withdrawal is made. Many students mistakenly had `$A_1=(P-2000)(1.005)`.

`A_2`	`=A_1(1.005)-2000`
	`=[P(1.005)-2000](1.005)-2000`
	`=P(1.005^2)-2000(1.005)-2000`
	`=P(1.005^2)-2000(1+1.005)`
	` vdots`

`A_n`

`=P(1.005^n)-2000(1+1.005+…+1.005^(n-1))`

`=>\ text(GP where)\ \ a=1\ \ text(and)\ \ r=1.005`

`A_n`	`=P(1.005^n)-2000((1(1.005^n-1))/(1.005-1))`
	`=P(1.005^n)-400\ 000(1.005^n-1)`
	`=P(1.005^n)-400\ 000(1.005^n)+400\ 000`
	`=(P-400\ 000)xx1.005^n+400\ 000\ \ text(… as required)`

ii. (2) `text(Find)\ n\ text(such that)\ A_n<=0`

♦ Mean mark 38%

`text(S)text(ince)\ P=232\ 175.55`,

`(232\ 175.55-400\ 000)(1.005^n)+400\ 000<=0`

`167\ 824.45(1.005^n)`	`>=400\ 000`
`1.005^n`	`>=(400\ 000)/(167\ 824.45)`
`n ln1.005`	`>=ln2.383443`
`n`	`>=ln2.383443/ln1.005`
`n`	`>=174.14\ \ text{(to 2 d.p.)}`

`:.\ text(There will be money left in the account for 175 months.)`

Financial Maths, 2ADV M1 2011 HSC 5a

The number of members of a new social networking site doubles every day. On Day 1 there were 27 members and on Day 2 there were 54 members.

How many members were there on Day 12? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
On which day was the number of members first greater than 10 million? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
The site earns 0.5 cents per member per day. How much money did the site earn in the first 12 days? Give your answer to the nearest dollar. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`55\ 296`
`text(20th)`
`$553`

Show Worked Solutions

MARKER’S COMMENT: Better responses stated the general term, `T_n` before any substitution was made, as shown in the worked solutions.

i. `T_1=a=27`

`T_2=27xx2^1=54`

`T_3=27xx2^2=108`

`=>\ text(GP where)\ \ a=27,\ \ r=2`

`\ \ \ vdots`

`T_n`	`=ar^(n-1)`
`T_12`	`=27 xx 2^11=55\ 296`

`:.\ text(On Day 12, there are 55 296 members.)`

ii. `text(Find)\ n\ text(such that)\ T_n>10\ 000\ 000`

MARKER’S COMMENT: Many elementary errors were made by students in dealing with logarithms. BE VIGILANT.

`T_n`	`=27(2^(n-1))`
`27xx2^(n-1)`	`>10\ 000\ 000`
`2^(n-1)`	`>(10\ 000\ 000)/27`
`ln 2^(n-1)`	`>ln((10\ 000\ 000)/27)`
`(n-1)ln2`	`>ln(370\ 370.370)`
`n-1`	`>ln(370\ 370.370)/ln 2`
`n-1`	`>18.499…`
`n`	`>19.499…`

`:.\ text(On the 20th day, the number of members >10 000 000.)`

iii. `text(If the site earns 0.5 cents per day per member,)`

`text(On Day 1, it earns)\ 27 xx 0.5 = 13.5\ text(cents)`

`text(On Day 2, it earns)\ 27 xx 2 xx 0.5 = 27\ text(cents)`

`T_1=a=13.5`

`T_2=27`

`T_3=54`

`=>\ text(GP where)\ \ a=13.5,\ \ r=2`

`S_12=text(the total amount of money earned in the first 12 Days)`

♦ Mean mark 44%.
NOTE: This question can also be easily solved by making `S_12` the total sum of members (each day) and then multiplying by 0.5 cents.

`S_12`	`=(a(r^n-1))/(r-1)`
	`=(13.5(2^12-1))/(2-1)`
	`=55\ 282.5\ \ text(cents)`
	`=552.825\ \ text(dollars)`

`:.\ text{The site earned $553 in the first 12 Days (nearest $).}`

Financial Maths, 2ADV M1 2012 HSC 12c

Jay is making a pattern using triangular tiles. The pattern has 3 tiles in the first row, 5 tiles in the second row, and each successive row has 2 more tiles than the previous row.

How many tiles would Jay use in row 20? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
How many tiles would Jay use altogether to make the first 20 rows? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Jay has only 200 tiles. How many complete rows of the pattern can Jay make? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`\ 41`
`440`
`13\ text(rows)`

Show Worked Solutions

i.	`T_1`	`=a=3`
	`T_2`	`=a+d=5`
	`T_3`	`=a+2d=7`

`=>\ text(AP where)\ \ a=3,\ \ d=2`

`\ \ \ \ \ vdots`

`T_20`	`=a+19d`
	`=3+19(2)`
	`=41`

`:.\ text(Row 20 has 41 tiles.)`

MARKER’S COMMENT: Better responses stated the formula BEFORE any calculations were performed. This enabled students to get some marks if they made an error in their working.

ii. `S_20`	`=\ text(the total number of tiles in first 20 rows)`
`S_20`	`=n/2(a+l)`
	`=20/2(3+41)`
	`=440`

`:.\ text(There are 440 tiles in the first 20 rows.)`

iii. `text(If Jay only has 200 tiles, then)\ \ S_n<=200`

NOTE: Examiners often ask questions requiring `n` to be found using the formula `S_n=n/2[2a+(n-1)d]` as this requires the solving of a quadratic, and interpretation of the answer.

`n/2(2a+(n-1)d)`	`<=200`
`n/2(6+2n-2)`	`<=200`
`n(n+2)`	`<=200`
`n^2+2n-200`	`<=0`

`n`	`=(-2+-sqrt(4+41200))/(2*1)`
	`=(-2+-sqrt804)/2`
	`=-1+-sqrt201`
	`=13.16\ \ text{(answer must be positive)}`

`:.\ text(Jay can complete 13 rows.)`

Financial Maths, 2ADV M1 2013 HSC 13d

A family borrows $500 000 to buy a house. The loan is to be repaid in equal monthly instalments. The interest, which is charged at 6% per annum, is reducible and calculated monthly. The amount owing after `n` months, `$A_n`, is given by

`qquad qquadA_n=Pr^n-M(1+r+r^2+ \ .... +r^(n-1))\ \ \ \ \ \ \ \ \ ` (DO NOT prove this)

where `$P` is the amount borrowed, `r=1.005` and `$M` is the monthly repayment.

The loan is to be repaid over 30 years. Show that the monthly repayment is $2998 to the nearest dollar. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Show that the balance owing after 20 years is $270 000 to the nearest thousand dollars. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---

After 20 years the family borrows an extra amount, so that the family then owes a total of $370 000. The monthly repayment remains $2998, and the interest rate remains the same.

How long will it take to repay the $370 000? (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions)}`
`text{Proof (See Worked Solutions)}`
`text(193 months)`

Show Worked Solutions

i. `text(Find)\ $M\ text(such that the loan is repaid over 30 years.)`

`n=30xx12=360\ text(periods)\ \ \ r=1+6/12%=1.005`

`A_360`

`=500\ 000 (1.005^360)-M(1+1.005+..+1.005^359)=0`

`=>GP\ text(where)\ a=1,\ \ r=1.005,\ \ \ n=360`

`M((1(1.005^360-1))/(1.005-1))`	`=500\ 000(1.005^360)`
`M(1004.515)`	`=3\ 011\ 287.61`
`M`	`=2997.75`

`:.$M=$2998\ \ text{(nearest dollar) … as required}`

ii. `text(Find)\ $A_n\ text(after 20 years)\ \ \ =>n=20xx12=240`

`A_240`	`=500\ 000(1.005^240)-2998(1+1.005+..+1.005^239)`
	`=1\ 655\ 102.24-2998((1(1.005^240-1))/(1.005-1))`
	`=269\ 903.63`
	`=270\ 000\ \ text{(nearest thousand) … as required}`

MARKER’S COMMENT: Within the GP formula, many students incorrectly wrote the last term as `1.005^240` rather than `1.005^239`. Note `T_n=ar^(n-1)`.

iii. `text(Loan)=$370\ 000`

`text(Find)\ n\ text(such that)\ $A_n=0,\ \ \ M=$2998`

`A_n=370\ 000(1.005^n)-2998(1+1.005+..+1.005^(n-1))=0`

♦♦ Mean mark 33%
COMMENT: Another good examination of working with logarithms. Students should understand why they must ’round up’ their answer in this question.

`370\ 000(1.005^n)`	`=2998((1(1.005^n-1))/(1.005-1))`
`370\ 000(1.005^n)`	`=599\ 600(1.005^n-1)`
`229\ 600(1.005^n)`	`=599\ 600`
`ln1.005^n`	`=ln((599\ 600)/(229\ 600))`
`n`	`=ln2.6115/ln1.005`
`n`	`=192.4`

`:.\ text(The loan will be repaid after 193 months.)`

Financial Maths, 2ADV M1 2013 HSC 12c

Kim and Alex start jobs at the beginning of the same year. Kim's annual salary in the first year is $30,000 and increases by 5% at the beginning of each subsequent year. Alex's annual salary in the first year is $33,000, and increases by $1,500 at the beginning of each subsequent year.

Show that in the 10th year, Kim's annual salary is higher than Alex's annual salary. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
In the first 10 years how much, in total, does Kim earn? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Every year, Alex saves `1/3` of her annual salary. How many years does it take her to save $87,500? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`text{Proof (See Worked Solutions)}`
`$377\ 336.78`
`text(7 years)`

Show Worked Solutions

i. `text(Let)\ \ K_n=text(Kim’s salary in Year)\ n`

`{:{:(K_1=a=30\ 000),(K_2=ar^1=30\ 000(1.05^1)):}}{:(\ =>\ GP),(\ \ \ \ \ \ a=30\ 000),(\ \ \ \ \ \ r=1.05):}`

`vdots`

`:.K_10=ar^9=30\ 000(1.05)^9=$46\ 539.85`

`text(Let)\ \ A_n=text(Alex’s salary in Year)\ n`

`{:{:(A_1=a=33\ 000),(A_2=33\ 000+1500=34\ 500):}}{:(\ =>\ AP),(\ \ \ \ \ \ a=33\ 000),(\ \ \ \ \ \ d=1500):}`

`vdots`

`A_10=a+9d=33\ 000+1500(9)=$46\ 500`

`=>K_10>A_10`

`:.\ text(Kim earns more than Alex in the 10th year)`

ii. `text(In the first 10 years, Kim earns)`

`K_1+K_2+\ ….+ K_10`

`S_10`	`=a((r^n-1)/(r-1))`
	`=30\ 000((1.05^10-1)/(1.05-1))`
	`=377\ 336.78`

`:.\ text(In the first 10 years, Kim earns $377 336.78)`

iii. `text(Let)\ T_n=text(Alex’s savings in Year)\ n`

`{:{:(T_1=a=1/3(33\ 000)=11\ 000),(T_2=a+d=1/3(34\ 500)=11\ 500),(T_3=a+2d=1/3(36\ 000)=12\ 000):}}{:(\ =>\ AP),(\ \ \ \ a=11\ 000),(\ \ \ \ d=500):}`

`text(Find)\ n\ text(such that)\ S_n=87\ 500`

♦ Mean mark 45%.
IMPORTANT: Using the AP sum formula to create and then solve a quadratic in `n` is challenging and often examined. Students need to solve and interpret the solutions.

`S_n`	`=n/2[2a+(n-1)d]`
`87\ 500`	`=n/2[22\ 000+(n-1)500]`
`87\ 500`	`=n/2[21\ 500+500n]`

`250n^2+10\ 750n-87\ 500`	`=0`
`n^2+43n-350`	`=0`
`(n-7)(n+50)`	`=0`

`:.n=7,\ \ \ \ n>0`

`:.\ text(Alex’s savings will be $87,500 after 7 years).`

\(\text{Gradient at}\ A\)	\(=\dfrac{y_2-y_1}{x_2-x_1}\)
	\(=\dfrac{10\ 000-3000}{33\ 000-18\ 000}\)
	\(=\dfrac{7000}{15\ 000}\)
	\(=\dfrac{7}{15}\ \ \ \ \text{… as required}\)

\(\therefore\ \text{Tax payable →}\ \ T\)	\(=3000+\dfrac{7}{15}(I-18\ 000)\)
	\(=3000+\dfrac{7}{15} I-8400\)
	\(=\dfrac{7}{15}I-5400\)

`tan\ ø`	`=\|(m_(norm) – m_(OP))/(1+m_(norm) * m_(OP))\|`
	`=\| ((a sin theta)/(b cos theta) − (b sin theta)/(a cos theta))/(1 + (a sin theta)/(b cos theta) xx (b sin theta)/(a cos theta))\|`
	`=\| (a^2 sin theta cos theta – b^2 sin theta cos theta)/(ab cos^2 theta + ab sin^2 theta)\|`
	`= \|((a^2 − b^2) sin theta cos theta)/(ab (cos^2 theta + sin^2 theta))\|`
	`= ((a^2 − b^2)/(ab))\ sin theta cos theta\ \ \ \ text(… as required)`