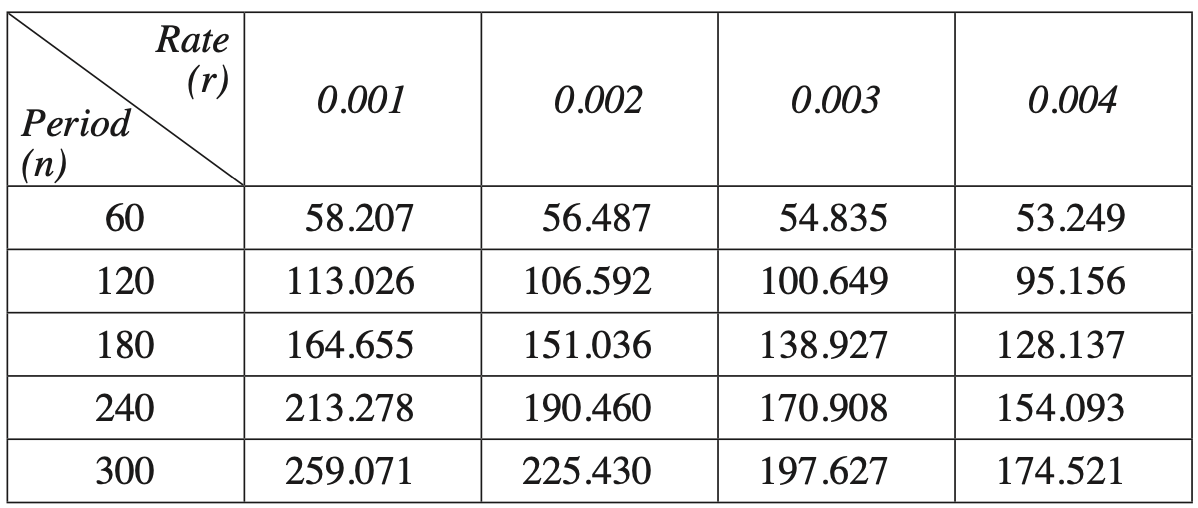
In a research study, participants were asked to record the number of minutes they spent watching television and the number of minutes they spent exercising each day over a period of 3 months. The averages for each participant were recorded and graphed.
- Describe the bivariate dataset in terms of its form and direction. (2 marks)
- Form: ..................................................................
- Direction: ............................................................
--- 0 WORK AREA LINES (style=lined) ---
The equation of the least-squares regression line for this dataset is
\(y=64.3-0.7 x\)
- Interpret the values of the slope and \(y\)-intercept of the regression line in the context of this dataset. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
- Jo spends an average of 42 minutes per day watching television.
- Use the equation of the regression line to determine how many minutes on average Jo is expected to exercise each day. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- Explain why it is NOT appropriate to extrapolate the regression line to predict the average number of minutes of exercise per day for someone who watches an average of 2 hours of television per day. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---