Use the Trapezoidal rule with three function values to find an approximation to the value of
`int_0.5^1.5 (log_e x )^3\ dx`.
Give your answer correct to three decimal places. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Aussie Maths & Science Teachers: Save your time with SmarterEd
Use the Trapezoidal rule with three function values to find an approximation to the value of
`int_0.5^1.5 (log_e x )^3\ dx`.
Give your answer correct to three decimal places. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`text(– 0.067)\ \ \ text{(to 3 d.p.)}`
The length of each edge of the cube `ABCDEFGH` is 2 metres. A circle is drawn on the face `ABCD` so that it touches all four edges of the face. The centre of the circle is `O` and the diagonal `AC` meets the circle at `X` and `Y`.
--- 2 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
| i. |
`text(S)text(ince)\ \ FA, \ AC\ \ text(and)\ \ FC\ \ text(are all)`
`text(diagonals of sides of a cube,)`
`FA = AC = FC`
`:.ΔFAC\ \ text(is equilateral)`
`:.∠FAC = 60^@`
| ii. |
`text(In)\ \ ΔAEF`
| `AF^2` | `= EF^2 + EA^2` |
| `= 2^2 + 2^2` | |
| `= 8` | |
| `AF` | `= sqrt8` |
| `= 2sqrt2` |
`text(In)\ \ ΔAFO`
| `sin\ 60^@` | `= (FO)/(AF)` |
| `sqrt3/2` | `= (FO)/(2sqrt2)` |
| `FO` | `= sqrt3/2 xx 2sqrt2` |
| `= sqrt6\ text(metres … as required.)` |
| iii. |
`XY\ \ text(is the diameter of a circle AND the width)`
`text(of the cube.)`
| `:.XY` | `= 2` |
| `:.OX` | `= OY = 1` |
| `tan\ ∠OFX` | `=1 /sqrt6` |
| `∠OFX` | `= 22.207…^@` |
| `:.∠XFY` | `= 2 xx 22.407…` |
| `= 44.415…` | |
| `= 44^@\ text{(nearest degree)}` |
A boat is sailing due north from a point `A` towards a point `P` on the shore line.
The shore line runs from west to east.
In the diagram, `T` represents a tree on a cliff vertically above `P`, and `L` represents a landmark on the shore. The distance `PL` is 1 km.
From `A` the point `L` is on a bearing of 020°, and the angle of elevation to `T` is 3°.
After sailing for some time the boat reaches a point `B`, from which the angle of elevation to `T` is 30°.
--- 6 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
i. `text(Show)\ BP = (sqrt3 tan 3°)/(tan 20°)`
| `text(In)\ Delta ATP` |
| `tan 3°` | `= (TP)/(AP)` |
| `=> AP` | `= (TP)/(tan 3)` |
`text(In)\ Delta APL:`
| `tan 20°` | `= 1/(AP)` |
| `=> AP` | `= 1/tan 20` |
| `:. (TP)/(tan3)` | `= 1/(tan20)` |
| `TP` | `= (tan3°)/(tan20°)\ \ \ text(…)\ text{(} text(1)text{)}` |
`text(In)\ \ Delta BTP:`
| `tan 30°` | `= (TP)/(BP)` |
| `1/sqrt3` | `= (TP)/(BP)` |
| `BP` | `= sqrt3 xx TP\ \ \ \ \ text{(using (1) above)}` |
| `= (sqrt3 tan3°)/(tan20°)\ \ \ text(… as required)` |
| ii. | `AB` | `= AP\ – BP` |
| `AP` | `= 1/(tan20°)\ \ \ text{(} text(from part)\ text{(i)} text{)}` |
| `:.\ AB` | `= 1/(tan 20°)\ – (sqrt3 tan3°)/(tan20°)` |
| `= (1\ – sqrt3 tan 3)/(tan20°)` | |
| `= 2.4980…` | |
| `= 2.5\ text(km)\ text{(to 1 d.p.)` |
From a point `A` due south of a tower, the angle of elevation of the top of the tower `T`, is 23°. From another point `B`, on a bearing of 120° from the tower, the angle of elevation of `T` is 32°. The distance `AB` is 200 metres.
--- 8 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
i.
ii. `text(Find)\ \ OT = h`
`text(Using the cosine rule in)\ Delta AOB :`
`200^2 = OA^2 + OB^2 – 2 * OA * OB * cos 60\ …\ text{(*)}`
`text(In)\ Delta OAT,\tan 23^@= h/(OA)`
`=> OA= h/(tan 23^@)\ …\ (1)`
`text(In)\ Delta OBT,\ tan 32^@= h/(OB)`
`=> OB= h/(tan 32^@)\ \ \ …\ (2)`
`text(Substitute)\ (1)\ text(and)\ (2)\ text(into)\ text{(*):}`
| `200^2` | `= (h^2)/(tan^2 23^@) + (h^2)/(tan^2 32^@) – 2 * h/(tan 23^@) * h/(tan 32^@) * 1/2` |
| `= h^2 (1/(tan^2 23^@) + 1/(tan^2 32^@) + 1/(tan23^@ * tan32^@) )` | |
| `= h^2 (4.340…)` | |
| `h^2` | `= (40\ 000)/(4.340…)` |
| `= 9214.55…` | |
| `:. h` | `= 95.99…` |
| `= 96\ text(m)\ \ \ text{(to nearest m)}` |
A person walks 2000 metres due north along a road from point `A` to point `B`. The point `A` is due east of a mountain `OM`, where `M` is the top of the mountain. The point `O` is directly below point `M` and is on the same horizontal plane as the road. The height of the mountain above point `O` is `h` metres.
From point `A`, the angle of elevation to the top of the mountain is 15°.
From point `B`, the angle of elevation to the top of the mountain is 13°.
--- 2 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
i. `text(Show)\ \ OA = h\ cot\ 15^@`
`text(In)\ \ Delta MOA,`
| `tan\ 15^@` | `= h/(OA)` |
| `OA` | `= h/(tan\ 15^@)` |
| `= h\ cot\ 15^@\ \ …text(as required)` |
ii. `text(In)\ \ ΔMOB`
| `tan\ 13^@` | `= h/(OB)` |
| `OB` | `= h/(tan\ 13^@)` |
| `= h\ cot\ 13^@` |
`text(In)\ \ ΔAOB:`
| `OA^2 + AB^2` | `= OB^2` |
| `OB^2 − OA^2` | `= AB^2` |
| `(h\ cot\ 13^@)^2 − (h\ cot\ 15^@)^2` | `= 2000^2` |
| `h^2[(cot^2\ 13^@ − cot^2\ 15^@)]` | `= 2000^2` |
| `h^2` | `= (2000^2)/(cot^2\ 13^@ − cot^2\ 15^@)` |
| `:. h` | `= sqrt((2000^2)/(cot^2\ 13^@ − cot^2\ 15^@))` |
| `= 909.704…` | |
| `= 910\ text{m (nearest metre)}` |
A ship sails 6 km from `A` to `B` on a bearing of 121°. It then sails 9 km to `C`. The
size of angle `ABC` is 114°.
--- 2 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
| i. |  |
`text(Let point)\ D\ text(be due North of point)\ B`
`/_ABD=180-121\ text{(cointerior with}\ \ /_A text{)}\ =59^@`
`/_DBC=114-59=55^@`
`:. text(Bearing of)\ \ C\ \ text(from)\ \ B\ \ text(is)\ 055^@`
ii. `text(Using cosine rule:)`
| `AC^2` | `=AB^2+BC^2-2xxABxxBCxxcos/_ABC` |
| `=6^2+9^2-2xx6xx9xxcos114^@` | |
| `=160.9275…` | |
| `:.AC` | `=12.685…\ \ \ text{(Noting}\ AC>0 text{)}` |
| `=13\ text(km)\ text{(nearest km)}` |
iii. `text(Need to find)\ /_ACB\ \ \ text{(see diagram)}`
| `cos/_ACB` | `=(AC^2+BC^2-AB^2)/(2xxACxxBC)` |
| `=((12.685…)^2+9^2-6^2)/(2xx(12.685..)xx9)` | |
| `=0.9018…` | |
| `/_ACB` | `=25.6^@\ text{(to 1 d.p.)}` |
`text(From diagram,)`
`/_BCE=55^@\ text{(alternate angle,}\ DB\ text(||)\ CE text{)}`
`:.\ text(Bearing of)\ A\ text(from)\ C`
| `=180+55+25.6` | |
| `=260.6` | |
| `=261^@\ text{(nearest degree)}` |
A yacht race follows the triangular course shown in the diagram. The course from `P` to `Q` is 1.8 km on a true bearing of 058°.
At `Q` the course changes direction. The course from `Q` to `R` is 2.7 km and `/_PQR = 74^@`.
--- 2 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
What is the area of this ‘no-go’ zone? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
| i. |  |
`/_ PQS = 58^@ \ \ \ (text(alternate to)\ /_TPQ)`
`text(Bearing of)\ R\ text(from)\ Q`
| `= 180^@ + 58^@ + 74^@` |
| `= 312^@` |
(ii) `text(Using Cosine rule:)`
| `RP^2` | `=RQ^2` + `PQ^2` `- 2` `xx RQ` `xx PQ` `xx cos` `/_RQP` |
| `= 2.7^2` + `1.8^2` `- 2` `xx 2.7` `xx 1.8` `xx cos74^@` | |
| `=7.29 + 3.24\ – 2.679…` | |
| `=7.851…` |
| `:.RP` | `= sqrt(7.851…)` |
| `=2.8019…` | |
| `~~ 2.8\ text(km) (text(1 d.p.) )` |
(iii) `text(Using)\ A = 1/2 ab sinC`
| `A` | `= 1/2` `xx 2.7` `xx 1.8` `xx sin74^@` |
| `= 2.3358…` | |
| `= 2.3\ text(km²)` |
`:.\ text(No-go zone is 2.3 km²)`
The diagram shows towns `A`, `B` and `C`. Town `B` is 40 km due north of town `A`. The distance from `B` to `C` is 18 km and the bearing of `C` from `A` is 025°. It is known that `∠BCA` is obtuse.
What is the bearing of `C` from `B`?
`=> D`
`text(Using the sine rule,)`
| `(sin∠BCA)/40` | `= (sin25^@)/18` |
| `sin angle BCA` | `= (40 xx sin25^@)/18` |
| `= 0.939…` | |
| `angle BCA` | `= 180 – 69.9quad(angleBCA > 90^@)` |
| `= 110.1°` |
`:. text(Bearing of)\ C\ text(from)\ B`
`= 110.1 + 25qquad(text(external angle of triangle))`
`= 135.1`
`=> D`
The following information is given about the locations of three towns `X`, `Y` and `Z`:
• `X` is due east of `Z`
• `X` is on a bearing of `145^@` from `Y`
• `Y` is on a bearing of `060^@` from `Z`.
Which diagram best represents this information?
`C`
`text(S)text(ince)\ X\ text(is due east of)\ Z`
`=> text(Cannot be)\ B\ text(or)\ D`
`text(The diagram shows we can find)`
`/_ZYX = 60 + 35^@ = 95^@`
`text(Using alternate angles)\ (60^@)\ text(and)`
`text(the)\ 145^@\ text(bearing of)\ X\ text(from)\ Y`
`=> C`
The diagram shows the position of `Q`, `R` and `T` relative to `P`.
In the diagram,
`Q` is south-west of `P`
`R` is north-west of `P`
`/_QPT` is 165°
What is the bearing of `T` from `P`?
`A`
Town `B` is 80 km due north of Town `A` and 59 km from Town `C`.
Town `A` is 31 km from Town `C`.
What is the bearing of Town `C` from Town `B`?
`C`
`text(Using the cosine rule:)`
| `cos\ /_B` | `= (a^2 + c^2 -b^2)/(2ac)` |
| `= (59^2 + 80^2 -31^2)/(2 xx 59 xx 80)` | |
| `= 0.9449…` | |
| `/_B` | `= 19^@\ text((nearest degree))` |
`:.\ text(Bearing of Town C from B) = 180-19= 161^@`
`=> C`
A piece of plaster has a uniform cross-section, which has been shaded, and has dimensions as shown.
--- 6 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
| a. |
| `A` | `~~ 3.6/2 [5 + 2(4.6 + 3.7 + 2.8) + 0]` |
| `~~ 1.8(27.2)` | |
| `~~ 48.96\ text(cm²)` |
b. `text(Total Area) = 7480.8\ text{cm² (given)}`
| `text(Area of Base)` | `= 14.4 xx 200` |
| `= 2880\ text(cm²)` |
| `text(Area of End)` | `= 5 xx 200` |
| `= 1000\ text(cm²)` |
| `text(Area of sides)` | `= 2 xx 48.96` |
| `= 97.92\ text(cm²)` |
`:.\ text(Area of curved surface)`
`= 7480.8 – (2880 + 1000 + 97.92)`
`= 3502.88`
`=3503\ text{cm² (nearest cm²)}`
A new 200-metre long dam is to be built.
The plan for the new dam shows evenly spaced cross-sectional areas.
--- 4 WORK AREA LINES (style=lined) ---
Assuming no wastage, calculate how much rainfall is needed, to the nearest mm, to fill the dam. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
| a. |
| `V` | `~~ 50/2[360 + 2(300 + 270 + 140) + 0]` |
| `~~ 25(1780)` | |
| `~~ 44\ 500\ text(m³)` |
b. `text(Convert 2 km² → m²:)`
| `text(2 km²)` | `= 2000\ text(m × 1000 m)` |
| `= 2\ 000\ 000\ text(m²)` |
`text(Using)\ \ V=Ah\ \ text(where)\ \ h= text(rainfall):`
| `44\ 500` | `= 2\ 000\ 000 xx h` |
| `:.h` | `= (44\ 500)/(2\ 000\ 000)` |
| `= 0.02225…\ text(m)` | |
| `= 22.25…\ text(mm)` | |
| `= 22\ text{mm (nearest mm)}` |
A tunnel is excavated with a cross-section as shown.
--- 4 WORK AREA LINES (style=lined) ---
If the value of `a` increases by 2 metres, by how much will `b` change? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
An aerial diagram of a swimming pool is shown.
The swimming pool is a standard length of 50 metres but is not in the shape of a rectangle.
In the diagram of the swimming pool, the five widths are measured to be:
`CD = 21.88\ text(m)`
`EF = 25.63\ text(m)`
`GH = 31.88\ text(m)`
`IJ = 36.25\ text(m)`
`KL = 21.88\ text(m)`
--- 4 WORK AREA LINES (style=lined) ---
Calculate the approximate volume of the swimming pool, in litres. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
There is a lake inside the rectangular grass picnic area `ABCD`, as shown in the diagram.
--- 6 WORK AREA LINES (style=lined) ---
The lake is 60 cm deep. Bozo the clown thinks he can empty the lake using a four-litre bucket.
--- 4 WORK AREA LINES (style=lined) ---
| a. | `text(Area of lake = Area of rectangle)\ – text(Area of grass)` |
| `text(Area of rectangle)` | `= 24 xx 55` |
| `= 1320\ text(m²)` |
`text{Area of grass (two applications)}`
| `~~ 12/2(20 + 5) + 12/2(5 + 10) + 12/2(35 + 22) + 12/2(22 + 30)` |
| `~~ 6(25 + 15 + 57 + 52)` |
| `~~ 894\ text(m²)` |
| `:.\ text(Area of lake)` | `~~ 1320\ – 894` |
| `~~ 426\ text(m²)` |
| b. | `V` | `= Ah` |
| `= 426 xx 0.6` | ||
| `= 255.6\ text(m³)` | ||
| `= 255\ 600\ text(L)\ \ \ text{(1 m³ = 1000 L)}` |
| `:.\ text(Times to fill bucket)` | `= 255\ 600 -: 4` |
| `= 63\ 900` |
Three equally spaced cross-sectional areas of a vase are shown.
Use the Trapezoidal rule to find the approximate capacity of the vase in litres. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
`3.3\ text(litres)`
Cassius is a boxer and skips to keep fit.
The table below shows the average energy used, in kilojuoles per kilogram of body mass, by a person skipping for 10 minutes at different speeds.
Cassius eats a hamburger that contains 550 kilocalories.
If Cassuis weighs 72 kilograms, how long must he skip at 150 skips per minute to burn off the energy contained in the hamburger? (1 kilocalorie = 4.184 kJ) Give your answer to 1 decimal place. (3 marks)
`13.2\ text{minutes (to 1 d.p.)}`
`text(Kilojoules in hamburger)`
`= 550 xx 4.184`
`= 2301.2`
`:.\ text(Skipping time to burn energy)`
`= 2301.2/((72 xx 24.18)) xx 10`
`= 1.321… xx 10`
`= 13.2\ text{minutes (to 1 d.p.)}`
The table shows the average energy used, in kilojoules per kilogram of body mass, by a person walking for 30 minutes at different speeds.
\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex} \text{Walking speed} \rule[-1ex]{0pt}{0pt} & \text{Energy used in 30 minutes} \\
\hline
\rule{0pt}{2.5ex} \text{3 km/h} \rule[-1ex]{0pt}{0pt} & \text{5.53 kJ/kg} \\
\hline
\rule{0pt}{2.5ex} \text{5 km/h} \rule[-1ex]{0pt}{0pt} & \text{7.37 kJ/kg} \\
\hline
\end{array}
Rob, who weighs 90 kg, drinks a large cappuccino made with full cream milk. It contains 146 kilocalories.
For approximately how long must Rob walk at 3 km/hr to burn off the energy contained in the cappuccino? (1 kilocalorie = 4.184 kilojoules)
`text(B)`
`text(Kilojoules in cappuccino)`
`= 146 xx 4.184`
`= 610.864\ text(kJ)`
`text(Energy used by Rob in 30 minutes)`
`=90 xx 5.53`
`=497.7\ text(kJ)`
`:.\ text(Time of the walk)`
`= 610.864/(497.7) xx 30`
`= 36.8…\ text(minutes)`
`=>\ text(B)`
The scale diagram shows the aerial view of a block of land bounded on one side by a road. The length of the block, `AB`, is known to be 90 metres.
Calculate the approximate area of the block of land, using three applications of the Trapezoidal rule. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
5175 m²
`text(Solution 1)`
`text(6 cm → 90 metres)`
` text(1 cm → 15 metres)`
`text(Height) = 2 xx 15 = 30\ text(metres)`
| `text(Area)` | `~~ 30/2(75 + 60) + 30/2(60 + 45) + 30/2(45 + 60)` |
| `~~ 15(135 + 105 + 105)` | |
| `~~ 5175\ text(m²)` |
`text(Solution 2)`
`text(After converting from scale:)`
| `text(Area)` | `~~ 30/2(75 + 2 xx 60 + 2 xx 45 + 60)` |
| `~~ 5175\ text(m²)` |
Let `n` be a positive integer and let `x` be a positive real number.
--- 3 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
| i. | `text(RHS)` | `= (x – 1)underbrace{(1 + x + x^2 + … + x^(n – 1) – n)}_{text(GP where)\ \ a = 1,\ r = x}` |
| `= (x – 1) ((1(x^n – 1))/(x – 1) – n)` | ||
| `= x^n – 1 – n(x – 1)` | ||
| `=\ text(LHS)` |
ii. `text(Let)\ P(x) = (x – 1)(1 + x + x^2 + … + x^(n – 1) – n)`
`text(If)\ \ x = 1, P(x) = 0`
`text(If)\ \ 0 < x < 1, \ (x – 1) < 0, \ (1 + x + x^2 + … + x^(n – 1) – n) < 0`
`=> P(x) > 0`
`text(If)\ \ x > 1, \ (x – 1) > 0, \ (1 + x + … + x^(n – 1) – n) > 0`
`=> P(x) > 0`
`x^n – 1 – n(x – 1) >= 0`
`:. x^n >= 1 + n(x – 1)`
iii. `x^n >= 1 + n(x – 1)\ \ text(for)\ \ x ∈ R^+`
`text(S)text(ince)\ a,b ∈ R^+`
| `(a/b)^n` | `>= 1 + n(a/b – 1)` |
| `(a^n)/(b^n) xx b` | `>= b + na – nb,\ \ \ \ (b > 0)` |
| `a^n b^(1 – n)` | `>= na + (1 – n)b` |
--- 7 WORK AREA LINES (style=lined) ---
--- 7 WORK AREA LINES (style=lined) ---
i. `text(By De Moivre)`
`costheta + isintheta^8 = cos8theta + isin8theta\ \ …\ (text{*})`
`text(Using Binomial Expansion)`
`(costheta + isintheta)^8`
`= cos^8theta + ((8),(1))cos^7theta * isintheta + ((8),(2)) cos^6theta *i^2sin^2theta`
`+ ((8),(3)) cos^5theta *i^3sin^3theta + ((8),(4)) cos^4theta *i^4sin^4theta + ((8),(5)) cos^3theta *i^5sin^5theta`
`+ ((8),(6)) cos^2theta *i^6sin^6theta + ((8),(7)) costheta *i^7sin^7theta + i^8sin^8theta`
`text(Equating imaginary parts of the expansion equation (*)):`
`isin8theta = ((8),(1)) cos^7theta* isintheta + ((8),(3)) icos^5theta* i^3sin^3theta`
`+ ((8),(5)) cos^3theta* i ^5sintheta + ((8),(7)) costheta *i^7sin^7theta`
`:. sin8theta = ((8),(1)) cos^7theta sintheta – ((8),(3)) cos^5theta sin^3theta`
`+ ((8),(5)) cos^3theta sin^5theta – ((8),(7)) costheta sin^7theta`
| ii. | `sin8theta` | `= 8cos^7theta sintheta – 56cos^5 sin^3theta + 56cos^3theta sin^5theta – 8costheta sin^7theta` |
| `= 2sinthetacostheta (4cos^6theta – 28cos^4theta sin^2theta + 28cos^2theta sin^4theta – 4sin^6theta)` |
`:. (sin8theta)/(sin2theta)`
`= 4cos^6theta – 28cos^4theta sin^2theta + 28cos^2theta sin^4theta – 4sin^6theta`
`= 4(1 – sin^2theta)^3 – 28(1 – sin^2theta)^2 sin^2theta + 28(1 – sin^2theta) sin^4theta – 4sin^6theta`
`= 4(1 – 3sin^2theta + 3sin^4theta + sin^6theta) – 28sin^2theta (1 – 2sin^2theta + sin^4theta)`
`+ 28sin^4theta (1 – sin^2theta) – 4sin^6theta`
`= 4 – 40sin^2theta + 96sin^4theta – 56sin^6theta`
`= 4(1 – 10sin^2theta + 24sin^4theta – 16sin^6theta)`
The point `P(acostheta, bsintheta)`, where `0 < theta < pi/2`, lies on the ellipse `(x^2)/(a^2) + (y^2)/(b^2) = 1`, where ` a > b`. The point `A(acostheta, asintheta)` lies vertically above `P` on the auxiliary circle `x^2 + y^2 = a^2`. The point `B` lies on the auxiliary circle such that `angleAOB = pi/2` and the point `Q` lies on the ellipse vertically below `B`, as shown.
The line `QO` meets the ellipse again at `Qprime(asintheta, −bcostheta)`. (Do NOT prove this.)
i. `x_Q = x_B`
`A(acostheta, asintheta)`
`text(S)text(ince)\ angleAOB = 90°,`
| `=> x_B` | `= acos(theta + pi/2)` |
| `= −asintheta` |
`text(Find)\ \ y_Q\ \ text(when)\ \ x = −asintheta`
`((−asintheta)^2)/(a^2) + (y^2)/(b^2) = 1`
| `y^2` | `= b^2(1 – sin^2theta)` |
| `= b^2cos^2theta` | |
| `=> y_Q` | `= bcostheta\ \ \ \ (y > 0)` |
`:.Q (−asintheta, bcostheta)\ \ …\ text(as required)`
ii. `m_(OP) = (b sintheta)/(acostheta) = b/a tantheta`
`m_(OQprime) = (−bcostheta)/(asintheta) = −b/a cottheta`
| `tan anglePOQprime` | `= |(m_1 – m_2)/(1 + m_1m_2)|` |
| `= |(b/atantheta + b/acottheta)/(1 – b/atantheta b/acottheta)|` | |
| `= |(ab(tantheta + cottheta))/(a^2 – b^2(tanthetacottheta))|` | |
| `= |(ab)/(a^2 – b^2)| · |(sintheta)/(costheta) + (costheta)/(sintheta)|` | |
| `= |(ab)/(a^2 – b^2)| · |(sin^2theta + cos^2theta)/(sinthetacostheta)|` | |
| `= |(ab)/(a^2 – b^2)| · |2/(sin2theta)|` | |
| `= (ab)/(a^2 – b^2) · 2/(|sin2theta|)qquadtext{(given}\ \ a > b text{)}` |
`=>\ text(Minimum angle when)\ tan anglePOQprime\ text(is a minimum.)`
`=>\ text(Minimum)\ \ (ab)/(a^2 – b^2) · 2/(|sin2theta|) = (2ab)/(a^2 – b^2) qquad (sin 2theta = 1)`
`:.\text(Minimum size of)\ anglePOQprime`
`= tan^(−1)((2ab)/(a^2 – b^2))`
Let `I_n = int_(−3)^0 x^n sqrt(x + 3)\ dx` for `n = 0, 1, 2…`
--- 8 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
i. `I_n = int_(−3)^0 x^n sqrt(x + 3)\ dx\ \ text(for)\ \ n = 0, 1, 2…`
| `u` | `= x^n` | `vprime` | `= (x + 3)^(1/2)` |
| `uprime` | `= nx^(n – 1)` | `v` | `= 2/3 (x + 3)^(3/2)` |
| `I_n` | `= [2/3 x^n(x + 3)^(3/2)]_(−3)^0 – 2/3int_(−3)^0 nx^(n – 1)(x + 3)sqrt(x + 3)\ dx` |
| `I_n` | `= 0 – (2n)/3 int_(−3)^0 x^nsqrt(x + 3) + 3x^(n – 1)sqrt(x + 3)\ dx` |
| `I_n` | `= −(2n)/3 (I_n + 3I_(n-1))` |
| `I_n + (2n)/3 I_n` | `= −2nI_(n – 1)` |
| `I_n(1 + (2n)/3)` | `= −2nI_(n – 1)` |
| `I_n((3 + 2n)/3)` | `= −2nI_(n – 1)` |
| `:. I_n` | `= (−6n)/(3 + 2n) I_(n – 1)\ \ \ text(… as required)` |
| ii. | `I_2` | `= −12/7 I_1` |
| `= −12/7 xx −6/5 I_0` | ||
| `= 72/35 int_(−3)^0 (x + 3)^(1/2)dx` | ||
| `= 72/35 xx 2/3 [(x + 3)^(3/2)]_(−3)^0` | ||
| `= 48/35 (3^(3/2))` | ||
| `= (144sqrt3)/35` |
A particle of mass `m` is attached to a light inextensible string of length `l`. The string makes an angle `theta` to the vertical.
The particle is moving in a circle of radius `r` on a smooth horizontal surface. The particle is moving with uniform angular velocity `ω`. The forces on the particle are the tension `T` in the string; the normal reaction `N` to the horizontal surface; and the gravitational force `mg`.
The particle remains in contact with the horizontal surface.
By resolving the forces on the particle in the horizontal and vertical directions, show that
`ω^2 <= g/(lcostheta)`. (3 marks)
`text(See Worked Solutions)`
`text(Resolve forces horizontally,)`
`Tsintheta = mrω^2\ \ …\ (1)`
`text(Resolve forces vertically,)`
`Tcostheta + N = mg\ \ …\ (2)`
`text(Solving simultaneously for)\ \ N:`
`text{Divide (1) by}\ sintheta`
`T = mrω^2 text(cosec)theta`
`text{Divide (2) by}\ costheta`
`T = (mg – N) sectheta`
| `(mg – N)sectheta` | `= mrω^2 text(cosec)theta` |
| `mg – N` | `= mrω^2 cottheta` |
| `N` | `= mg – mrω^2 cottheta` |
`text(Particle doesn’t leave table if)\ \ N >= 0`
| `mg – mrω^2 cottheta` | `>= 0` |
| `mrω^2 cottheta` | `<= mg` |
| `ω^2` | `<= g/(r(costheta)/(sintheta))\ \ \ \ (l = r/(sintheta))` |
| `:. ω^2` | `<= g/(lcostheta)` |
Let `z = 1 - cos2theta + isin2theta`, where `0 < theta <= pi`.
--- 6 WORK AREA LINES (style=lined) ---
--- 8 WORK AREA LINES (style=lined) ---
i. `z = 1 – cos2theta + isin2theta`
| `|\ z\ |` | `= sqrt((1 – cos2theta)^2 + sin^2 2theta)` |
| `= sqrt(1 – 2cos2theta + cos^2 2theta + sin^2 2theta)` | |
| `= sqrt(2 – 2cos2theta)` | |
| `= sqrt(2(1 – cos2theta))` | |
| `= sqrt(2(2sin^2theta))` | |
| `= 2sintheta\ \ \ text(… as required)` |
ii. `z= 1 – cos2theta + isin2theta`
| `text(arg)(z)` | `= tan^(−1)((sin2theta)/(1 – cos2theta))` |
| `= tan^(−1)((2sinthetacostheta)/(2sin^2theta))` | |
| `= tan^(−1)(cottheta)` | |
| `= tan^(−1)(tan(pi/2 – theta))` | |
| `= pi/2 – theta` |
`(text(S)text(ince)\ \ 0 < theta < pi => \ −pi/2 <= pi/2 – theta < pi/2)`
The graph `y^2 = x(1 - x)^2` is shown.
Use the method of cylindrical shells to find the volume of the solid formed when the shaded region is rotated about the line `x = 1`. (3 marks)
`(64pi)/105\ \ text(u³)`
`text(Cylindrical shell:)`
`text(Radius) = (1 – x),\ text(height) = 2y`
| `y^2` | `= x(1-x)^2` |
| `y` | `= sqrtx(1 – x)` |
| `δV` | `= 2pi(1-x)(2y)\ δx` |
| `= 2pi (1 – x) · 2sqrtx (1 – x)\ δx` | |
| `= 4pi (1 – x)^2 sqrtx\ δx` |
| `:. V` | `= int_0^1 4pi (1 – x)^2 sqrtx\ dx` |
| `= 4pi int_0^1 (1 – 2x + x^2) sqrtx\ dx` | |
| `= 4pi int_0^1 x^(1/2) – 2x^(3/2) + x^(5/2)\ dx` | |
| `= 4pi [2/3x^(3/2) – 4/5x^(5/2) + 2/7x^(7/2)]_0^1` | |
| `= 4pi[(2/3 – 4/5 + 2/7) – 0]` | |
| `= 4pi(16/105)` | |
| `= (64pi)/105\ \ text(u³)` |
The base of a solid is the region enclosed by the parabola `x = 1 - y^2` and the `y`-axis. Each cross-section perpendicular to the `y`-axis is an equilateral triangle, as shown in the diagram.
Find the volume of the solid. (3 marks)
`(4sqrt3)/15\ text(u³)`
`text(Cross section of triangle)`
| `sin60°` | `= h/(1 – y^2)` |
| `:.h` | `= sqrt3/2(1 – y^2)` |
| `δV` | `= 1/2(1 – y^2) · sqrt3/2(1 – y^2)\ δy` |
| `= sqrt3/4(1 – y^2)^2\ δy` |
| `:. V` | `= int_(−1)^1 sqrt3/4(1 – y^2)\ dy` |
| `= sqrt3/2 int_0^1 1 – 2y^2 + y^2\ dy` | |
| `= sqrt3/2 [y – 2/3y^3 + 1/5y^5]` | |
| `= sqrt3/2 [(1 – 2/3 + 1/5) – 0]` | |
| `= sqrt3/2(8/15)` | |
| `= (4sqrt3)/15\ text(u³)` |
The circle centred at `O` with radius `r` has a diameter `AB`. Points `C` and `D` are chosen on the circle as shown in the diagram. The chord `AC` has length `d`.
Show that `d = 2r sin D`. (2 marks)
`text(See Worked Solutions)`
The points `A`, `B` and `C` on the Argand diagram represent the complex numbers `u`, `v` and `w` respectively.
The points `O`, `A`, `B` and `C` form a square as shown on the diagram.
It is given that `u = 5 + 2i`.
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
| i. | `w` | `= iu` |
| `= i(5 + 2i)` | ||
| `= −2 + 5i` |
| ii. | `v` | `= u + w` |
| `= 5 + 2i + (−2 + 5i)` | ||
| `= 3 + 7i` |
| iii. | `text(arg)(w/v)` | `= text(arg)(w) – text(arg)(v)` |
| `= pi/4\ \ (text(diagonal of square bisects corner))` |
Consider the functions `f( x ) = sinx` and `g( x ) = x sinx`.
The `x`-coordinate of each stationary point of `f(x)` is very close to the `x`-coordinate of a stationary point of `g(x)`.
Suppose `f(x)` has a stationary point at `x = a` and the stationary point of `g(x)` with `x`-coordinate closest to `x = a` is at `x = b`.
Which statement is always true?
`text(C)`
`f(x) = sin x\ => fprime(x) = cos x`
`fprime(x) = 0\ \ text(when)\ \ x = pi/2, (3pi)/2, …`
`g(x) = x sin x\ => gprime(x) = sin x – x cos x`
`gprime(x) = 0\ \ text(when)\ \ −x = tan x`
`text(When)\ x > 0,\ text{intersection (where}\ gprime(x) = 0)\ text(is to)`
`text(the right of)\ \ x = pi/2.`
`text(When)\ x < 0,\ text(intersection is to the left of)\ \ x = – pi/2 .`
`:. |\ a\ | < |\ b\ |`
`=>\ text(C)`
It is given that `a`, `b` are real and `p`, `q` are purely imaginary.
Which pair of inequalities must always be true?
`B`
`a, b ->\ text(real)qquad\ p, q ->\ text(purely imaginary)`
`=> ab, pq, (ab – pq)\ text(are real)`
`=> ap, bq, (ap – bq)\ text(are purely imaginary.)`
| `(ab – pq)^2` | `>= 0` |
| `a^2b^2 + p^2q^2` | `>= 2abpq\ \ (text(Eliminate A and C))` |
| `(ap – bq)^2` | `<= 0` |
| `a^2p^2 + b^2q^2` | `<= 2abpq` |
`=>B`
Which diagram best represents the solutions to the equation `text(arg)(z) = text(arg)(z + 1 - i)`?
| A. | B. | ||
| C. | D. |
`text(D)`
| `text(arg)(z)` | `= text(arg)(z + 1 – i)` |
| `=text(arg)(z – (−1 + i))` |
`=>\ text(arg)(z – (−1 + i))\ \ text(is the argument of)\ \ z\ \ text(from)\ \ (-1+i).`
`text(Plot)\ \ (-1 + i)\ \ text(on the argand diagram and then test different)`
`text(positions of)\ \ z\ \ text(along the solutions for each option.)`
`=>\ text(D)`
Which complex number is a 6th root of `i`?
`A`
In a tennis competition a player won 7 games and lost the other games.
Altogether she played 15 games.
Finish the subtraction sentence below to show the number of games she lost.
| `\ - 7 =` |
`15 – 7 = 8`
`15 – 7 = 8`
The shaded region is enclosed by the curve `y = x^3 - 7x` and the line `y = 2x`, as shown in the diagram. The line `y = 2x` meets the curve `y = x^3 - 7x` at `O(0, 0)` and `A(3, 6)`. Do NOT prove this.
| (i) | `text(Area)` | `= int_0^3 2x – (x^3 – 7x)\ dx` |
| `= int_0^3 9x – x^3\ dx` | ||
| `= [9/2 x^2 – 1/4 x^4]_0^3` | ||
| `= [(9/2 xx 3^2 – 1/4 xx 3^4) – 0]` | ||
| `= 81/2 – 81/4` | ||
| `= 81/4\ text(units²)` |
(ii) `text(Using Simpson’s rule)`
`y = 9x – x^3`
| `text(A)` | `~~ h/3 (y_0 + 4y_1 + y_2)` |
| `= 3/6 (0 + 4 xx 81/8 + 0)` | |
| `= 1/2 (81/2)` | |
| `= 81/4\ text( … as required)` |
(iii) `y = x^3 – 7x`
`(dy)/(dx) = 3x^2 – 7`
`text(Find)\ \ x\ \ text(such that)\ \ (dy)/(dx) = 2`
| `3x^2 – 7` | `= 2` |
| `3x^2` | `= 9` |
| `x^2` | `= 3` |
| `x` | `= sqrt 3 qquad (x > 0)` |
| `y` | `= (sqrt 3)^3 – 7 sqrt 3` |
| `= 3 sqrt 3 – 7 sqrt 3` | |
| `= -4 sqrt 3` |
`:. P\ \ text(has coordinates)\ (sqrt 3, -4 sqrt 3)`
| (iv) |
| `text(dist)\ OA` | `= sqrt((3 – 0)^2 + (6 – 0)^2)` |
| `= sqrt 45` | |
| `= 3 sqrt 5` |
`text(Find)\ _|_\ text(distance of)\ \ P\ \ text(from)\ \ OA`
`P(sqrt 3, -4 sqrt 3),\ \ 2x – y=0`
| `_|_\ text(dist)` | `= |(2 sqrt 3 + 4 sqrt 3)/sqrt (3 + 2)|` |
| `= (6 sqrt 3)/sqrt 5` | |
| `:.\ text(Area)` | `= 1/2 xx 3 sqrt 5 xx (6 sqrt 3)/sqrt 5` |
| `= 9 sqrt 3\ text(units²)` |
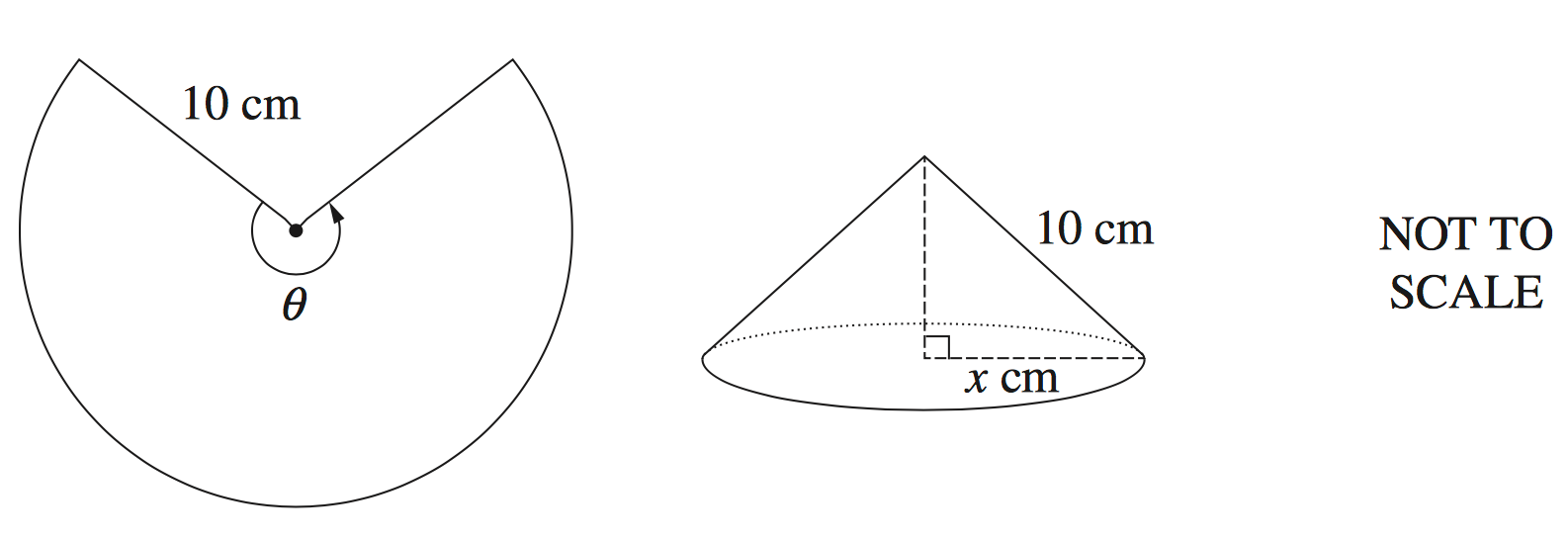
A sector with radius 10 cm and angle `theta` is used to form the curved surface of a cone with base radius `x` cm, as shown in the diagram.
The volume of a cone of radius `r` and height `h` is given by `V = 1/3 pi r^2 h`.
--- 2 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 7 WORK AREA LINES (style=lined) ---
i. `V = 1/3 pi r^2 h`
`text(Using Pythagoras,)`
`h = sqrt(100-x^2)`
`r = x`
`:.\ text(Volume) = 1/3 pi x^2 sqrt(100-x^2)`
| ii. | `V` | `= 1/3 pi x^2 sqrt(100-x^2)` |
| `(dV)/(dh)` | `= 1/3 pi [2x ⋅ sqrt(100-x^2)-2x ⋅ 1/2 (100-x^2)^(-1/2) ⋅ x^2]` | |
| `= 1/3 pi [(2x (100-x^2)-x^3)/sqrt(100-x^2)]` | ||
| `= 1/3 pi [(200 x-2x^3-x^3)/sqrt(100-x^2)]` | ||
| `= (pi x(200-3x^2))/(3 sqrt (100-x^2))\ \ text{.. as required}` |
iii. `text(Find)\ \ x\ \ text(when)\ \ (dV)/(dx) = 0`
| `200-3x^2` | `= 0` |
| `x` | `= sqrt(200/3)` |
`text(When)\ \ x < sqrt(200/3),\ (200-3x^2) > 0`
`=> (dV)/(dx) > 0`
`text(When)\ \ x > sqrt(200/3),\ (200-3x^2) < 0`
`=> (dV)/(dx) < 0`
`:.\ text(MAX when)\ \ x = sqrt(200/3)`
`text(Equating the arc length of the section)`
`text(to the circumference of the cone:)`
| `2 pi r ⋅ theta/(2 pi)` | `= 2 pi ⋅ x` |
| `10 theta` | `= 2 pi sqrt (200/3)` |
| `:. theta` | `= (2 pi ⋅ 10 sqrt 2)/(10 ⋅ sqrt 3)` |
| `= (2 sqrt 2 pi)/sqrt 3` |
The diagram shows the region bounded by the curve `y = 1/(x + 3)` and the lines `x = 0`, `x = 45` and `y = 0`. The region is divided into two parts of equal area by the line `x = k`, where `k` is a positive integer.
What is the value of the integer `k`, given that the two parts have equal areas? (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
`9`
| `text(Total Area)` | `= int_0^45 1/(x + 3)` |
| `= [ln (x + 3)]_0^45` | |
| `= ln 48 – ln 3` | |
| `= ln 16` |
| `=> int_0^k 1/(x + 3)` | `= 1/2 xx ln 16` |
| `[ln (x + 3)]_0^k` | `= ln 16^(1/2)` |
| `ln (k + 3) – ln 3` | `= ln 4` |
| `ln ((k + 3)/3)` | `= ln 4` |
| `(k + 3)/3` | `= 4` |
| `:. k` | `= 4 xx 3 – 3` |
| `= 9` |
The length of daylight, `L(t)`, is defined as the number of hours from sunrise to sunset, and can be modelled by the equation
`L(t) = 12 + 2 cos ((2 pi t)/366)`,
where `t` is the number of days after 21 December 2015, for `0 ≤ t ≤ 366`.
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
i. `L(t) = 12 + 2 cos ((2 pi t)/366)`
`text(On 21 Dec 2015) => t = 0`
| `:. L(0)` | `= 12 + 2 cos 0` |
| `= 14\ text(hours)` |
ii. `text(Shortest length of daylight occurs when)`
`cos ((2 pi t)/366) = -1`
| `:.\ text(Shortest length)` | `= 12 + 2 (-1)` |
| `= 10\ text(hours)` |
iii. `text(Find)\ \ t\ \ text(such that)\ \ L(t) = 11:`
`11 = 12 + 2 cos ((2 pi t)/366)`
`cos ((2 pi t)/366) = -1/2`
| `(2 pi t)/366` | `= (2 pi)/3` | `qquad\ \ text(or)` | `(2 pi t)/366` | `= (4 pi)/3` |
| `t` | `= 366/3` | `t` | `= (366 xx 2)/3` | |
| `= 122` | `= 244` |
`:. t = 122 or 244`
Two machines, `A` and `B`, produce pens. It is known that 10% of the pens produced by machine `A` are faulty and that 5% of the pens produced by machine `B` are faulty.
What is the probability that at least one of the pens is faulty? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
What is the probability that neither pen is faulty? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
| i. | `text{P(at least 1 faulty)}` | `= 1 – text{P(both faulty)}` |
| `= 1 – 0.9 xx 0.95` | ||
| `= 1 – 0.855` | ||
| `= 0.145` |
ii. `text{P(2 non-faulty pens})`
`= text{(choose A, NF, NF)} + P text{(choose B, NF, NF)}`
`= 1/2 xx 0.9 xx 0.9 + 1/2 xx 0.95 xx 0.95`
`= 0.405 + 0.45125`
`=0.85625`
The shaded region shown in the diagram is bounded by the curve `y = x^4 + 1`, the `y`-axis and the line `y = 10`.
Find the volume of the solid of revolution formed when the shaded region is rotated about the `y`-axis. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
`18 pi\ text(units²)`
`y = x^4 + 1`
`x^4 = y – 1`
`x^2 = +- (y – 1)^(1/2)`
`text(When)\ \ x = 0,\ \ y = 1`
`=> x^2 = (y – 1)^(1/2)`
| `:.\ text(Volume)` | `= pi int_1^10 x^2\ dy` |
| `= pi int_1^10 (y – 1)^(1/2)\ dy` | |
| `= pi xx 2/3 [(y – 1)^(3/2)]_1^10` | |
| `= (2 pi)/3 [9^(3/2) – 0]` | |
| `= (2 pi)/3 (27)` | |
| `= 18 pi\ \ text(units²)` |
In `Delta KLM, KL` has length 3, `LM` has length 6 and `/_KLM` is 60°. The point `N` is chosen on side `KM` so that `LN` bisects `/_KLM`. The length `LN` is `x`.
--- 2 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
i. `text(Using sine rule:)`
| `text(Area)\ \ Delta KLM` | `= 1/2 xx 3 xx 6 xx sin 60^@` |
| `= (9 sqrt 3)/2\ \ text(u²)` |
ii. `text(Area)\ \ Delta KLN + text(Area)\ \ Delta NLM = text(Area)\ \ Delta KLM`
`1/2 xx 3 xx x xx sin 30^@ + 1/2 xx x xx 6 xx sin 30^@ = (9 sqrt 3)/2`
| `3/4 x + 3/2 x` | `= (9 sqrt 3)/2` |
| `9/4 x` | `= (9 sqrt 3)/2` |
| `:. x` | `= (9 sqrt 3)/2 xx 4/9` |
| `= 2 sqrt 3` |
In `Delta ABC`, sides `AB` and `AC` have length 3, and `BC` has length 2. The point `D` is chosen on `AB` so that `DC` has length 2.
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
i. `text(Prove)\ \ Delta ABC\ text(|||)\ Delta CBD`
`Delta ABC\ text{is isosceles:}`
`/_ ABC = /_ ACB qquad text{(angles opposite equal sides)}`
`Delta CBD\ text{is isosceles:}`
`/_ CBD = /_ CDB qquad text{(angles opposite equal sides)}`
`text{Since}\ \ /_ ABC = /_ CBD`
`:. Delta ABC\ text(|||)\ Delta CDB qquad text{(equiangular)}`
ii. `text(Using ratios of similar triangles)`
| `(DB)/(CB)` | `= (BC)/(AC)` |
| `{(3-AD)}/2` | `= 2/3` |
| `3-AD` | `= 4/3` |
| `:. AD` | `= 5/3` |
Consider the curve `y = 6x^2 - x^3`.
--- 6 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 8 WORK AREA LINES (style=lined) ---
i. `y = 6x^2 – x^3`
`(dy)/(dx) = 12x – 3x^2`
`(d^2y)/(dx^2) = 12 – 6x`
`text(S.P.s occur when)\ \ (dy)/(dx) = 0`
`12x – 3x^2 = 0`
`3x(4 – x) = 0`
`x = 0 or 4`
`text(When)\ \ x = 0,\ (d^2y)/(dx^2) > 0`
`:.\ text(MIN at)\ (0, 0)`
`text(When)\ \ x = 4,\ (d^2y)/(dx^2) < 0`
`:.\ text(MAX at)\ (4, 32)`
ii. `text(P.I. occur when)\ \ (d^2y)/(dx^2) = 0,`
| `12 – 6x` | `= 0` |
| `x` | `= 2` |
`text(When)\ \ x = 2,\ y = 16`
`text(S)text(ince the concavity changes)`
`=>\ text(P.I. occurs at)\ \ (2, 16)`
| iii. |
The diagram shows the square `ABCD`. The point `E` is chosen on `BC` and the point `F` is chosen on `CD` so that `EC = FC`.
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
i. `AB = AD\ \ text{(sides of a square)}`
`DF = DC-CF`
`BE = BC-CE`
`text{Since}\ CE = CF\ \ text{(given), and}\ DC = BC\ \ text{(sides of a square)}`
`=> DF = BE`
`=> /_ ADF = /_ ABE = 90^@`
`:. Delta ADF \equiv Delta ABE\ \ text{(SAS)}`
| ii. | `text(Area of)\ Delta ABE` | `= 1/2 xx 14 xx 10` |
| `= 70\ text(cm)^2` |
`:.\ text(Area of)\ AECF`
`= text(Area of)\ ABCD-(2 xx 70)`
`= (14 xx 14)-140`
`= 56\ text(cm)^2`
Find the equation of the tangent to the curve `y = cos 2x` at `x = pi/6`. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
`y = -sqrt 3 x + (sqrt 3 pi + 3)/6`
| `y` | `= cos 2x` |
| `(dy)/(dx)` | `= -2 sin 2x` |
`text(When)\ \ x = pi/6:`
| `y` | `= cos pi/3 = 1/2` |
| `(dy)/(dx)` | `= -sin pi/3 = -sqrt 3` |
`text(Equation of tangent)\ \ m = -sqrt 3,\ text(through)\ (pi/6, 1/2):`
| `y – y_1` | `= m(x – x_1)` |
| `y – 1/2` | `= -sqrt 3 (x – pi/6)` |
| `y` | `= -sqrt 3 x + (sqrt 3 pi)/6 + 1/2` |
| `:. y` | `= -sqrt 3 x + (sqrt 3 pi + 3)/6` |
A game consists of two tokens being drawn at random from a barrel containing 20 tokens. There are 17 tokens labelled 10 cents and 3 tokens labelled $2. The player wins the total value of the two tokens drawn.
| i. |
ii. `text(Expectated Gain/Loss)`
COMMENT: Financial expectation included here (one example only in database) as it is possible to argue that it is an application of expectation.
`= [17/20 xx 16/19 xx 0.20 + 17/20 xx 3/19 xx 2.1`
`+ 3/20 + 17/19 xx 2.1 + 3/20 xx 2/19 xx 4] – 1`
`= 0.77 – 1`
`= −$0.23\ \ (text(or $0.23 loss))`
Last year, Luke’s taxable income was `$87\ 000` and the tax payable on this income was `$19\ 822`. This year, Luke’s taxable income has increased by `$16\ 800`.
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
a. `text(Taxable income) = 87\ 000 + 16\ 800 = $103\ 800`
| `:.\ text(Tax payable)` | `= 19\ 822 + 0.37 (103\ 800-87\ 000)` |
| `= $26\ 038` |
b. `text(Net income from last year)`
`= 87\ 000-19\ 822`
`= $67\ 178`
`text(Net income in current year)`
`= 103\ 800-26\ 038`
`= $77\ 762`
| `:.\ text(Extra money)` | `= 77\ 762-67\ 178` |
| `= $10\ 584` |
Simplify `(8x^3 - 27y^3)/(2x - 3y)`. (2 marks)
`4x^2 + 6xy + 9y^2`
| `(8x^3 – 27y^3)/(2x – 3y)` | `= ((2x)^3 – (3y)^3)/(2x – 3y)` |
| `= ((2x – 3y)(4x^2 + 6xy + 9y^2))/(2x – 3y)` | |
| `= 4x^2 + 6xy + 9y^2` |
Andrew borrowed $20 000 to be repaid in equal monthly repayments of $243 over 10 years. Having made this monthly repayment for 4 years, he increased his monthly repayment to $281. As a result, Andrew paid off the loan one year earlier.
How much less did he repay altogether by making this change? (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`$636`
| `text(Total original repayments)` | `= 10 xx 12 xx 243` |
| `= $29\ 160` |
| `text(Actual repayments)` | `= 4 xx 12 xx 243\ +\ 5 xx 12 xx 281` |
| `= $28\ 524` |
| `:.\ text(Savings)` | `= 29\ 160 – 28\ 524` |
| `= $636` |
The time in Brisbane is 4.5 hours ahead of the time in New Delhi. John flew from New Delhi to Brisbane via Singapore. His plane left New Delhi at 11.30 am (New Delhi time), stopped for 3 hours in Singapore, and arrived in Brisbane at 9.00 am the following day (Brisbane time).
What was the plane’s total flying time? (3 marks)
`14\ text(hours)`
`text(11:30 am in New Delhi = 4 pm in Brisbane)`
| `text(Total travel time)` | `= 4\ text{pm → 9 am (next day)}` |
| `= 17\ text(hours)` |
| `:.\ text(Flying time)` | `= 17-3` |
| `= 14\ text(hours)` |
Every day, a 1200-watt microwave oven is used for 45 minutes at 40% power. Electricity is charged at $0.25 per kWh.
What is the cost of running this microwave oven for 180 days? (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
`$16.20`
| `text(Daily usage)` | `= 1200 xx 45/60 xx 40text(%)` |
| `= 360\ text(watts)` |
| `text(180 day usage)` | `= 180 xx 360` |
| `= 64\ 800\ text(watts)` | |
| `= 64.8\ text(kW)` |
| `:.\ text(C)text(ost over 180 days)` | `= 64.8 xx 0.25` |
| `= $16.20` |
| `y` | `= x + 5` |
| `y + 2x` | `= 2` |
Draw these two linear graphs on the number plane below and determine their intersection. (3 marks)
--- 2 WORK AREA LINES (style=lined) ---
`(−1,4)`
The line `3x-4y + 3 = 0` is a tangent to a circle with centre (3, – 2).
What is the equation of the circle?
`D`
`text(Radius) = _|_\ text{distance of (3, −2) from}\ \ 3x-4y + 3 = 0`
| `_|_\ text(dist)` | `= |(ax_1 + by_1 + c)/sqrt(a^2 + b^2)|` |
| `= |(3(3)-4(-2) + 3)/sqrt(3^2 + (-4)^2)|` | |
| `= |(9 + 8 + 3)/sqrt 25|` | |
| `= 4` |
`text{Equation of circle, centre (3, –2) with radius 4}`
`(x-3)^2 + (y + 2)^2 = 16`
`=> D`
Joanna sits a Physics test and a Biology test.
Calculate the `z`-score for Joanna’s mark in this test. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Joanna’s `z`-score is the same in both the Physics test and the Biology test.
What is her mark in the Biology test? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
i. `x = 70, \ mu = 58, \ sigma = 8`
| `:. ztext(-score)` | `= (x – mu)/sigma` |
| `= (70 – 58)/8` | |
| `= 1.5` |
| ii. | `1.5` | `= (x – 64)/10` |
| `x – 64` | `= 15` | |
| `:. x` | `= 79` |