Band 5 – Page 32

PHYSICS, M2 2012 HSC 11 MC

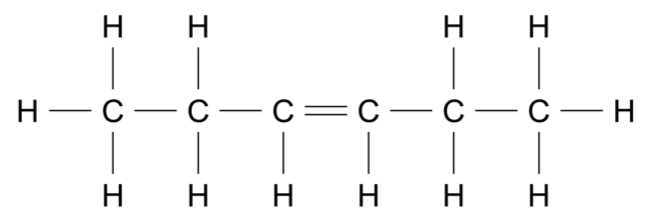
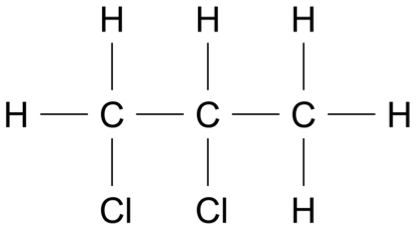
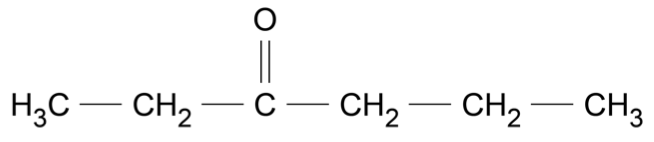Which of the following is correct about the forces acting during a rocket launch?

Equal and opposite forces act on the rocket. This enables it to continue to accelerate even in the vacuum of space.
The engines exert an upward thrust on the rocket. This thrust exceeds the downward force of the engines on the air.
The rocket engines exert a downward force on the gases being expelled. These gases exert an upward force on the engines.
The expelled gases exert a force against the launch pad. The launch pad then exerts an equal and opposite force on the rocket causing it to accelerate.

Show Only

$C$

Show Worked Solution

By Newton’s third law of motion (for every action there is an equal and opposite reaction), option $C$ is the correct answer.
Although $D$ also uses Newton’s third law, it is incorrect as it is not the launch pad exerting a force on the rocket but rather the gases expelled from the rocket.

$ \Rightarrow C$

♦ Mean mark 47%.

CHEMISTRY, M5 2023 HSC 20 MC

Nitrogen monoxide and oxygen combine to form nitrogen dioxide, according to the following equation.

$ \ce{2NO(g) + O2(g) \rightleftharpoons 2NO2(g) \quad $K$_{e q}=2.47 \times 10^{12}} $

A 2.00 L vessel is filled with 1.80 mol of $ \ce{NO2(g)} $ and the system is allowed to reach equilibrium.

What is the equilibrium concentration of $ \ce{NO(g)} $?

$ \text{0.00 mol L}^{-1}$
$ 4.34 \times 10^{-5}\ \text{mol L}^{-1} $
$6.90 \times 10^{-5}\ \text{mol L}^{-1}$
$8.69 \times10^{-5}\ \text{mol L}^{-1}$

Show Answers Only

$D$

Show Worked Solution

As 1.80 mol of $ \ce{NO2(g)} $ is added to the solution, the reverse reaction can be used to determine the equilibrium concentration of $ \ce{NO(g)} $.
$\ce{2NO2(g) \rightleftharpoons 2NO(g) + O2(g)}$
Reverse reaction $K_{eq} = \dfrac{\ce{[O_2][NO]^2}}{\ce{[NO_2]^2}}$
Forward reaction $K_{eq}$ is the inverse of $K_{eq}$ of the reverse reaction:
$K_{eq}=\dfrac{1}{2.47 \times 10^{12}}=4.0486 \times 10^{-13}$

\begin{array} {|l|c|c|c|}
\hline & \ce{2NO_2(g)} & \ce{2NO(g)} & \ce{O_2(g)} \\
\hline \text{Initial} & \ \ \ \ 0.9 & \ \ \ \ 0 & 0 \\
\hline \text{Change} & -2x & +2x & \ \ \ +x \\
\hline \text{Equilibrium} & \ \ \ \ 0.9 -2x & \ \ \ \ 2x & \ \ \ \ \ \ x \\
\hline \end{array}

$-2x$ is very small as the $K_{eq}$ for the reaction is very small, thus $0.9-2x \approx 0.9$.
By substituting the values into the $K_{eq}$ for the reverse reaction:

$4.0486 \times 10^{-13}$	$=\dfrac{(x)(2x)^2}{(0.9)^2}$
$4.0486 \times 10^{-13}$	$=\dfrac{4x^3}{(0.9)^2}$
$4x^3$	$=3.279 \times 10^{-13}$
$x$	$=4.344 \times 10^{-5}$

$\ce{[NO2] = 2 \times 4.344 \times 10^{-5} = 8.69 \times 10^{-5}\ \text{mol L}^{-1}}$

$\Rightarrow D$

♦♦ Mean mark 34%.

CHEMISTRY, M8 2023 HSC 19 MC

The diagram shows a simplified mass spectrum for butan-2-one.

Which equation best represents the process that produces the particle responsible for the peak at m/z 43 ?

$ \ce{CH3COCH2CH3^{+} \rightarrow CH3CO + ^{+}CH2CH3} $
$ \ce{CH3COCH2CH3^{+} \rightarrow CH3CO^{+} + CH2CH3} $
$ \ce{CH3COCH2CH3^{+} \rightarrow CH3CH2CH2 + ^{+}CHO} $
$ \ce{CH3COCH2CH3^{+} \rightarrow CH3CH2CH2^{+} + CHO} $

Show Answers Only

$B$

Show Worked Solution

The peaks in mass spectra represent fragments of organic molecules.
Mass Spectrometers can only detect charged particles meaning the peak at 43 m/z could only represent:
$\ce{CH3COCH2CH3^+, ^+CH2CH3, CH3CO^+, ^+CHO,}$ or $\ce{CH3CH2CH2^+}$
The m/z ratio is indicative of a fragment’s molecular weight which corresponds to $\ce{CH3CO^+}$

$\Rightarrow B$

♦ Mean mark 51%.

CHEMISTRY, M5 2023 HSC 18 MC

Carbon dioxide reacts with hydrogen gas to form carbon monoxide and water vapour in a sealed flask, according to the following equation.

$ \ce{CO2(g) + H2(g)} \rightleftharpoons \ce{CO(g) + H2O(g)} $

A temperature change was imposed on the equilibrium system at time $t$ and the rates of both the forward and reverse reactions were monitored.

Which row of the table correctly identifies the nature of both temperature change at time $ t $ and the $ \Delta H $ of the forward reaction?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex}\textit{}& \textit{} \\
\textit{}\rule[-1ex]{0pt}{0pt}& \textit{} \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|c|c|}
\hline
\rule{0pt}{2.5ex}\textit{Temperature change}& \textit{$\Delta H$ of the forward} \\
\textit{at time $t$}\rule[-1ex]{0pt}{0pt}& \textit{reaction} \\
\hline
\rule{0pt}{2.5ex}\text{Decrease}\rule[-1ex]{0pt}{0pt}&\text{+}\\
\hline
\rule{0pt}{2.5ex}\text{Decrease}\rule[-1ex]{0pt}{0pt}& \text{–}\\
\hline
\rule{0pt}{2.5ex}\text{Increase}\rule[-1ex]{0pt}{0pt}& \text{+} \\
\hline
\rule{0pt}{2.5ex}\text{Increase}\rule[-1ex]{0pt}{0pt}& \text{–} \\
\hline
\end{array}
\end{align*}

Show Answers Only

$A$

Show Worked Solution

The rate decrease is associated with a decrease in temperature (collision theory).
Since the rate slowed, the forward reaction is endothermic (requires heat to react) and thus has a positive (+) $ \Delta H $

$\Rightarrow A$

♦♦ Mean mark 39%.

CHEMISTRY, M5 2023 HSC 17 MC

What mass of lead$\text{(II)}$ iodide (MM = 461 g mol$^{-1}$) will dissolve in 375 mL of water?

0.233 g
0.293 g
0.369 g
0.621 g

Show Answers Only

$A$

Show Worked Solution

$\ce{PbI2 \rightleftharpoons Pb^2+ + 2I^-}\ \ \ \ \ \ \ K_{sp} = 9.8 \times 10^{-9}\ \text{(from data sheet)}$

$K_{sp}$	$= \ce{[Pb^2+][ 2I^-]^2}$
$9.8 \times 10^{-9}$	$= [x][ 2x]^2$
$x^3$	$=\dfrac{9.8 \times 10^{-9}}{4}$
$x$	$=0.001348\ \text{mol L}^{-1}$

$\text{Mass in 1 L}\ = 0.001348 \times 461 = 0.62147\ \text{g}$

$\text{Mass in 375 mL}\ = 0.62147 \times 0.375 = 0.233\ \text{g}$

$\Rightarrow A$

CHEMISTRY, M5 2023 HSC 16 MC

A solution contains potassium iodide and potassium chloride. It was analysed by performing a precipitation titration using silver nitrate. The titration curve for this reaction is shown, where $ \ce{pAg}=-\log _{10}\left[\ce{Ag}^{+}\right]$.

Why is this a valid and correct procedure for quantifying the amount of each anion present in the mixture?

$ \ce{AgCl} $ would precipitate out first, followed by $ \ce{AgI} $.
$ \ce{AgI}$ would precipitate out first, followed by $ \ce{AgCl} $.
Both $ \ce{AgI} $ and $ \ce{AgCl} $ precipitate out of the solution together.
Neither $ \ce{AgCl} $ nor $ \ce{AgI} $ would precipitate out of the solution.

Show Answers Only

$B$

Show Worked Solution

This procedure is only correct and valid if the ions precipitated out at different times.
Therefore $ \ce{AgI}$ would precipitate out first as it is less soluble than $ \ce{AgCl} $.

$\Rightarrow B$

♦ Mean mark 41%.

CHEMISTRY, M6 2023 HSC 14 MC

What volume of 0.540 mol L$^{-1} $ hydrochloric acid will react completely with 1.34 g of sodium carbonate?

11.7 mL
23.4 mL
29.9 mL
46.8 mL

Show Answers Only

$D$

Show Worked Solution

$\ce{2HCl + Na2CO3 \rightarrow 2NaCl +H2CO3}$

$\ce{n(Na2CO3) = \dfrac{\text{m}}{\text{MM}} = \dfrac{1.34}{105.99} = 0.0126\ \text{mol}}$

$\ce{n(HCl) = 0.0126 \times 2 = 0.0253\ \text{mol}} $

$\text{Vol (HCl)}\ = \dfrac{0.0253}{0.540} = 0.0468\ \text{L} = 46.8\ \text{mL}$

$\Rightarrow D$

♦ Mean mark 45%.

CHEMISTRY, M7 2023 HSC 8 MC

How many structural isomers have the molecular formula $ \ce{C3H6F2} $?

Show Answers Only

$C$

Show Worked Solution

Structural Isomers will have the same molecular formula but different structures.
The fluoride Ions can exists at different points on the carbon chain, changing the name and structure of the compound without altering its molecular formula.

$\Rightarrow C$

♦ Mean mark 53%.

PHYSICS, M4 2014 HSC 23

A square current-carrying wire loop is placed near a straight current-carrying conductor, as shown in the diagram.

Explain how the current in the wire loop affects the straight conductor. (3 marks)

--- 9 WORK AREA LINES (style=lined) ---

Show Answers Only

Using the right hand rule on side $BC$, the current produces a magnetic field going into the page on the bottom side of it and a magnetic field going out of the page on the top side of it.
Using the right hand rule on side $DA$, the current produces a magnetic field going into the page on the top side of it and a magnetic field going out of the page on the bottom side of it.
The straight current carrying conductor itself will produce a magnetic field going into the page on the bottom side of it and a magnetic field going out of the page on the top side of it, same as side $BC$.
Therefore, the straight conductor and side $BC$ will be attracted to each other and the straight conductor and side $DA$ will repel each other.
As $BC$ is closer to the straight conductor than $DA$, the overall net force on the straight conductor will be an attractive force towards the wire.
Note the perpendicular sides $AB$ and $CD$ have no effect on the straight conductor.

Show Worked Solution

Using the right hand rule on side $BC$, the current produces a magnetic field going into the page on the bottom side of it and a magnetic field going out of the page on the top side of it.
Using the right hand rule on side $DA$, the current produces a magnetic field going into the page on the top side of it and a magnetic field going out of the page on the bottom side of it.
The straight current carrying conductor itself will produce a magnetic field going into the page on the bottom side of it and a magnetic field going out of the page on the top side of it, same as side $BC$.
Therefore, the straight conductor and side $BC$ will be attracted to each other and the straight conductor and side $DA$ will repel each other.
As $BC$ is closer to the straight conductor than $DA$, the overall net force on the straight conductor will be an attractive force towards the wire.
Note the perpendicular sides $AB$ and $CD$ have no effect on the straight conductor.

♦ Mean mark 51%.

PHYSICS, M2 2017 HSC 29a

A spring is used to construct a device to launch a projectile. The force `(F)` required to compress the spring is measured as a function of the displacement `(x)` by which the spring is compressed.

The potential energy stored in the compressed spring can be calculated from `E_p=(1)/(2) kx^(2)`, where `k` is the gradient of the force-displacement graph shown.

A projectile of mass 0.04 kg is launched using this device with the spring compressed by 0.08 m. Calculate the launch velocity. (4 marks)

--- 12 WORK AREA LINES (style=lined) ---

Show Answers Only

$v=6.9$ ms$^{-1}$

Show Worked Solution

$k$	$=$ $\text{gradient}$
	$=\dfrac{24-6}{0.08-0.02}$
	$=300$

Finding the potential energy stored in the compressed spring:

$E_p=\dfrac{1}{2}kx^2=\dfrac{1}{2} \times 300 \times 0.08^2=0.96$ $\text{J}$

As this potential energy is converted into kinetic energy when the projectile is launched:

$E_k$	$=0.96$ $\text{J}$
$\dfrac{1}{2}mv^2$	$=0.96$
$v^2$	$=\dfrac{2 \times 0.96}{0.04}$
$v$	$=6.9$ ms$^{-1}$

Complex Numbers, EXT2 N2 2023 HSC 8 MC

A shaded region on a complex plane is shown.

Which relation best describes the region shaded on the complex plane?

$|z-i|>2|z-1|$
$|z-i|<2|z-1|$
$|z-1|>2|z-i|$
$|z-1|<2|z-i|$

Show Answers Only

$D$

Show Worked Solution

$\text{By elimination:}$

$\text{Let}\ \ z=x+iy \ \ (x,y \in \mathbb{R}) $

$\text{Since shaded area is outside the circle, coefficients of}\ x^2\ \text{and} $

$ y^2\ \text{must be positive (eliminate A and C).}$

♦♦ Mean mark 34%.

$\text{Consider option D:}$

$\|z-1\|$	$<2\|z-i\|$
$(x-1)^2+y^2$	$<4(x^2+(y-1)^2) $
$x^2-2x+1+y^2$	$<4x^2+4y^2-8y+4$
$0$	$<3x^2+2x+3y^2-8y+3$

$\text{Circle equation has centre where}\ \ x<0, y>0. $

$\Rightarrow D$

Mechanics, EXT2 M1 2023 HSC 6 MC

Which of the following functions does NOT describe simple harmonic motion?

$x=\cos ^2 t-\sin 2 t$
$x=\sin 4 t+4 \cos 2 t$
$x=2 \sin 3 t-4 \cos 3 t+5$
$x=4 \cos \left(2 t+\dfrac{\pi}{2}\right)+5 \sin \left(2 t-\dfrac{\pi}{4}\right)$

Show Answers Only

$B$

Show Worked Solution

$\text{By trial and error}$

$\text{Option}\ A:$

$x=\cos^2t-\sin\,2t=\dfrac{1}{2}\cos\,2t+\dfrac{1}{2}-\sin\,2t $

$\dot x=-\sin\,2t-2\cos\,2t $

♦♦ Mean mark 34%.

$\ddot x$	$=-2\cos\,2t+4\sin\,2t$
	$=-4\Big(\dfrac{1}{2}\cos\,2t-\sin\,2t\Big) $
	$=-4\Big(x-\dfrac{1}{2}\Big) \ \ \ \text{(SHM)}$

$\text{Similarly, options}\ C\ \text{and}\ D\ \text{can be differentiated to show} $

$\ddot x=-n^2(x-c) $

$\text{Consider option}\ B:$

$x=\sin\,4t+4\cos\,2t$

$\dot x=4\cos\,4t-8\sin\,2t$

$\ddot x$	$=-16\sin\,4t-16\cos\,2t$
	$= -16(\sin\,4t-\cos\,2t)\ \ \ \ \text{(not SHM)} $

$\Rightarrow B$

Vectors, EXT2 V1 2023 HSC 5 MC

Which of the following is a true statement about the lines $\ell_1={\displaystyle\left(\begin{array}{cc}-1 \\ 2 \\ 5\end{array}\right)+\lambda\left(\begin{array}{c}-1 \\ 3 \\ 1\end{array}\right)}$ and $\ell_2=\left(\begin{array}{c}3 \\ -10 \\ 1\end{array}\right)+\mu\left(\begin{array}{c}1 \\ -3 \\ -1\end{array}\right) ?$

$\ell_1$ and $\ell_2$ are the same line.
$\ell_1$ and $\ell_2$ are not parallel and they intersect.
$\ell_1$ and $\ell_2$ are parallel and they do not intersect.
$\ell_1$ and $\ell_2$ are not parallel and they do not intersect.

Show Answers Only

$A$

Show Worked Solution

$\text{Since}\ \ \left(\begin{array}{c}-1 \\ 3 \\ 1\end{array}\right) = -1 \left(\begin{array}{c}1 \\ -3 \\ -1\end{array}\right), \ \ell_1\ \text{is parallel to}\ \ell_2 $

$\text{Test if point}\ (3,-10,1)\ \text{lies on}\ \ell_1: $

$\text{i.e.}\ \ \exists \lambda\ \ \text{such that} $

♦ Mean mark 49%.

$ \left(\begin{array}{cc}3 \\ -10 \\ 1\end{array}\right) = \left(\begin{array}{cc}-1 \\ 2 \\ 5\end{array}\right) + \lambda \left(\begin{array}{cc}-1 \\ 3 \\ 1\end{array}\right)$

$\lambda = -4\ \ \text{satisfies equation} $

$\therefore\ \ell_1\ \text{and}\ \ell_2\ \text{are the same line.}$

$\Rightarrow A$

PHYSICS, M2 2018 HSC 23a

The diagram shows a cathode ray tube in a television.

Outline energy changes associated with the electrons passing through the gun, and when they strike the screen. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

As the electrons pass through the gun, they experience an acceleration and so have their kinetic energy increased and the electrical potential energy decreased.
When the electrons hit the screen, their kinetic energy is converted into light and heat energy by the law of conservation of energy.

Show Worked Solution

As the electrons pass through the gun, they experience an acceleration and so have their kinetic energy increased and the electrical potential energy decreased.
When the electrons hit the screen, their kinetic energy is converted into light and heat energy by the law of conservation of energy.

Mean mark 54%.

PHYSICS, M2 2018 HSC 14 MC

A pendulum can be used to determine the acceleration due to gravity using the relationship

$\displaystyle T=2 \pi \sqrt{\dfrac{l}{g}}$

where $T$ is the period and $l$ is the length of the pendulum.

The acceleration due to gravity on the surface of Mars is less than that on Earth.

Which graph relates the variables for the pendulum correctly for both planets?

Show Answers Only

$C$

Show Worked Solution

Rearranging the equation given $\Rightarrow\ \ l=\dfrac{T^2}{4\pi^2} \times g$
Thus $\ l \propto T^2$.
It will be a nonlinear graph between $l$ and $T$.
As the value of $g$ for Mars is less than that of Earth, the data line for Mars must be below that of Earth.

$\Rightarrow C$

♦ Mean mark 478%.

CHEMISTRY, M8 2023 HSC 36

An organic reaction pathway involving compounds $\text{A, B,}$ and $\text{C}$ is shown in the flow chart.

The molar mass of $\text{A}$ is 84.156 g mol$^{-1}$.

A chemist obtained some spectral data for the compounds as shown.

$ \text{Data from} \ ^{1} \text{H NMR spectrum of compound C} $
$ Chemical \ Shift \ \text{(ppm)} $	$ Relative \ peak \ area $	$ Splitting \ pattern $
$1.01$	$3$	$\text{Triplet}$
$1.05$	$3$	$\text{Triplet}$
$1.65$	$2$	$\text{Multiplet}$
$2.42$	$2$	$\text{Triplet}$
$2.46$	$2$	$\text{Quartet}$

$ ^{1} \text{H NMR chemical shift data}$
$ Type \ of \ proton $	$ \text{δ/ppm} $
$ \ce{R - C\textbf{H}3,R - C\textbf{H}2 - R}$	$0.7-1.7$
$ \left.\begin{array}{l}\ce{\textbf{H}3C - CO - \\-C\textbf{H}2 - CO -}\end{array}\right\} \begin{aligned} & \text { (aldehydes, ketones,} \\ &\text{carboxylic acids or esters) }\end{aligned}$	$2.0-2.6$
$ \ce{R - C\textbf{H}O} $	$9.4-10.00$
$ \ce{R - COO\textbf{H}} $	$9.0-13.0$

Identify the functional group present in each of compounds $\text{A}$ to $\text{C}$ and draw the structure of each compound. Justify your answer with reference to the information provided. (9 marks)

--- 28 WORK AREA LINES (style=lined) ---

Show Answers Only

Compound $\text{A}$: Alkene

Compound $\text{B}$: Secondary alcohol

Compound $\text{C}$: Ketone

Reasoning as follows:

Compound $\text{A}$ is able to undergo an addition reaction to add water across a $\ce{C=C}$ bond $\Rightarrow $ Alkene
Compound $\text{B}$ is the product of the above hydration reaction and is therefore an alcohol.
The $\ce{^{13}C\ NMR}$ spectrum of Compound $\text{A}$ confirms it is an alkene (132 ppm peak corresponding to the $\ce{C=C}$ atoms). 3 spectrum peaks indicate 3 carbon environments. The molar mass of compound $\text{A}$ is 84.156 g mol$^{-1}$ which suggests symmetry within the molecule.
The Infrared Spectrum of Compound $\text{B}$ has a broad peak at approximately 3400 cm$^{-1}$. This indicates the presence of an hydroxyl group and confirms $\text{B}$ is an alcohol.
Compound $\text{C}$ is produced by the oxidation of Compound $\text{B}$ with acidified potassium permanganate.
Compound $\text{C}$ is a carboxylic acid if $\text{B}$ is a primary alcohol or a ketone if $\text{B}$ is a secondary alcohol.
Since the $\ce{^{1}H NMR}$ spectrum of $\text{C}$ does not show any peaks between 9.0 − 13.0 ppm, it cannot be a carboxylic acid. Compound $\text{C}$ is therefore a ketone and Compound $\text{B}$ is a secondary alcohol.
The $\ce{^{1}H NMR}$ spectrum shows 5 peaks $\Rightarrow $ 5 hydrogen environments.
Chemical shift and splitting patterns information indicate:
1.01 ppm – 1.05 ppm: $\ce{CH3}$ (next to a $\ce{CH2}$)
1.65 ppm: $\ce{CH2}$ (with multiple neighbouring hydrogens)
2.42 ppm: $\ce{CH2}$ (next to the ketone $\ce{C=O}$ and a $\ce{CH2}$)
2.46 ppm: $\ce{CH2}$ (next to the ketone $\ce{C=O}$ and a $\ce{CH3}$)

Show Worked Solution

Compound $\text{A}$: Alkene

Compound $\text{B}$: Secondary alcohol

Compound $\text{C}$: Ketone

Reasoning as follows:

Compound $\text{A}$ is able to undergo an addition reaction to add water across a $\ce{C=C}$ bond $\Rightarrow $ Alkene
Compound $\text{B}$ is the product of the above hydration reaction and is therefore an alcohol.
The $\ce{^{13}C\ NMR}$ spectrum of Compound $\text{A}$ confirms it is an alkene (132 ppm peak corresponding to the $\ce{C=C}$ atoms). 3 spectrum peaks indicate 3 carbon environments. The molar mass of compound $\text{A}$ is 84.156 g mol$^{-1}$ which suggests symmetry within the molecule.
The Infrared Spectrum of Compound $\text{B}$ has a broad peak at approximately 3400 cm$^{-1}$. This indicates the presence of an hydroxyl group and confirms $\text{B}$ is an alcohol.
Compound $\text{C}$ is produced by the oxidation of Compound $\text{B}$ with acidified potassium permanganate.
Compound $\text{C}$ is a carboxylic acid if $\text{B}$ is a primary alcohol or a ketone if $\text{B}$ is a secondary alcohol.
Since the $\ce{^{1}H NMR}$ spectrum of $\text{C}$ does not show any peaks between 9.0 − 13.0 ppm, it cannot be a carboxylic acid. Compound $\text{C}$ is therefore a ketone and Compound $\text{B}$ is a secondary alcohol.
The $\ce{^{1}H NMR}$ spectrum shows 5 peaks $\Rightarrow $ 5 hydrogen environments.
Chemical shift and splitting patterns information indicate:
1.01 ppm – 1.05 ppm: $\ce{CH3}$ (next to a $\ce{CH2}$)
1.65 ppm: $\ce{CH2}$ (with multiple neighbouring hydrogens)
2.42 ppm: $\ce{CH2}$ (next to the ketone $\ce{C=O}$ and a $\ce{CH2}$)
2.46 ppm: $\ce{CH2}$ (next to the ketone $\ce{C=O}$ and a $\ce{CH3}$)

PHYSICS, M8 2023 HSC 33

Consider the following statement.

The interaction of subatomic particles with fields, as well as with other types of particles and matter, has increased our understanding of processes that occur in the physical world and of the properties of the subatomic particles themselves.

Justify this statement with reference to observations that have been made and experiments that scientists have carried out. (9 marks)

--- 22 WORK AREA LINES (style=lined) ---

Show Answers Only

Thomson’s Experiment:

Thomson’s experiment tested the interaction of cathode rays (which he discovered were negatively charged subatomic particles and named them electrons) with electric and magnetic fields to determine the charge to mass ratio ($\dfrac{q}{m}$) of the electrons.
Using both the electric and magnetic fields, Thomson balanced the forces to ensure the cathode rays travelled through undeflected. Thus:
$F_E = F_B \ \ \Rightarrow \ \ qE=qvB \ \ \Rightarrow \ \ v=\dfrac{E}{B}$
Using the magnetic field and known velocity, the cathode rays travelled in a circular path due to their negative charges interacting with the magnetic field. Thus:
$F_c=F_B\ \ \Rightarrow \ \ \dfrac{mv^2}{r}=qvB \ \ \Rightarrow \ \ \dfrac{q}{m}=\dfrac{v}{Br}$
The charge to mass ratio was determined to be 0.77 $\times$ 10$^{11}$ Ckg$^{-1}$ and was $\dfrac{1}{1800}$ times smaller than the charge to mass ratio of the proton. The number was also the same regardless of the metal cathode used, thus Thomson determined this particle was a fundamental constitute of all matter.
Therefore, the statement is true as the observations and experiment undertaken by Thomson using the interactions of particles and fields led to a greater understanding of the electrons.

Chadwick’s Experiment:

In Chadwick’s experiment, he irradiated beryllium with alpha particles which emitted a deeply penetrating radiation with neutral charge. When this particle was directed into paraffin wax, protons were emitted and detected on a screen.
Using the Laws of conservation of energy and momentum, Chadwick proposed the idea of a neutral particle and named it the neutron. He determined that the mass of this particle must be slightly greater than the mass of the proton.
Therefore, Chadwick’s observations of the neutrons led to a greater understanding of the properties of the particle, thus justifying the statement above.

Observations using particle accelerators:

Particle accelerators have led to many new scientific discoveries as a result of the interaction of particles with fields and particle-particle interactions.
Scientists have come to a greater understanding of quarks and other subatomic particles within the standard model of matter and processes of the physical world including decay trails and momentum dilation.
The Large Hadron Collider (LHC) can accelerate particles close to the speed of light using electric and magnetic fields. When particles collide, the kinetic energy is converted into mass using Einstein’s equation $E=mc^2$.
The new particles formed as a result of these collisions led to the development of the standard model and increased scientific understanding of subatomic particles including up and down quarks, W/Z bosons and the Higgs Boson.
These subatomic particles have very short lifetimes before decaying into more stable particles. Our knowledge of them is primarily from studying their decay properties which has led to a greater understanding of particle decay trails.
Observations of interactions within particles accelerators has also increased the scientific understanding of momentum dilation. As particles reach relativistic speeds, a greater force is required to accelerate them than classical physics predicts which is due to mass and momentum dilation.

PHYSICS, M5 2023 HSC 34

A 400 kg satellite is travelling in a circular orbit of radius 6.700 × 10$^6$ m around Earth. Its potential energy is –2.389 × 10$^{10}\ \text{J}$ and its total energy is –1.195 × 10$^{10}\ \text{J}$.

At point $P$, the satellite's engines are fired, increasing the satellite's velocity in the direction of travel and causing its kinetic energy to increase by 5.232 × 10$^8\ \text{J}$. Assume that this happens instantaneously and that the engine is then shut down.

The satellite follows the trajectory shown, which passes through $Q$, 6.850 × 10$^6$ m from Earth's centre.

Analyse qualitatively the energy changes as the satellite moves from $P$ to $Q$. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show that the kinetic energy of the satellite at $Q$ is 1.194 × 10$^{10}\ \text{J}$. (4 marks)

--- 5 WORK AREA LINES (style=lined) ---

Explain the motion of the satellite after it passes through $Q$. (3 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Energy changes from $P$ to $Q$:

Due to the engine shutting down immediately after increasing the kinetic energy, the total energy of the system will remain the same.
As a result of the Law of Conservation of Energy, as the distance of the satellite from the Earth increases, the gravitational potential energy of the satellite increases and the kinetic energy of the satellite decreases.

b. Using the Law of Conservation of Energy:

$E_Q$

$=U_Q+K_Q$

$=E_P+K_{\text{engine}}$

$U_Q$	$=-\dfrac{GMm}{r}$
	$=-\dfrac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 400}{6.85 \times 10^6}$
	$=-2.337 \times 10^{10}$ $\text{J}$

$K_Q$	$=E_P+K_{\text{engine}}-U_Q$
	$=-1.195 \times 10^{10} + 5.232 \times 10^8 -(-2.337 \times 10^{10})$
	$=1.194 \times 10^{10}$ $\text{J … as required}$

c. The orbital velocity at $Q$ is:

$v$	$=\sqrt{\dfrac{GM}{r}}$
	$=\sqrt{\dfrac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{6.85 \times 10^6}}$
	$=7.644 \times 10^3\ \text{ms}^{-1}$

The velocity of the satellite at $Q$ is:

$K_Q$	$=\dfrac{1}{2}mv_Q^2$
$v_Q$	$=\sqrt{\dfrac{2K_Q}{m}}$
	$=\sqrt{\dfrac{2 \times 1.194 \times 10^{10}}{400}}$
	$=7.727 \times 10^3\ \text{ms}^{-1}$

Since the velocity of the satellite at $Q$ is greater than the orbital velocity at $r$ = 6.85 × 10$^6$ m, the satellite will continue to move further away from the Earth.
Using the Law of Conservation of Energy, the kinetic energy of the satellite will decrease as the gravitational potential energy of the satellite increases. Hence the satellite will increase its distance from the Earth and slow down until the velocity of the satellite is equal to the orbital velocity at its new distance from the Earth.

Show Worked Solution

a. Energy changes from $P$ to $Q$:

Due to the engine shutting down immediately after increasing the kinetic energy, the total energy of the system will remain the same.
As a result of the Law of Conservation of Energy, as the distance of the satellite from the Earth increases, the gravitational potential energy of the satellite increases and the kinetic energy of the satellite decreases.

♦ Mean mark (a) 47%.

b. Using the Law of Conservation of Energy:

$E_Q$

$=U_Q+K_Q$

$=E_P+K_{\text{engine}}$

$U_Q$	$=-\dfrac{GMm}{r}$
	$=-\dfrac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 400}{6.85 \times 10^6}$
	$=-2.337 \times 10^{10}$ $\text{J}$

$K_Q$	$=E_P+K_{\text{engine}}-U_Q$
	$=-1.195 \times 10^{10} + 5.232 \times 10^8 -(-2.337 \times 10^{10})$
	$=1.194 \times 10^{10}$ $\text{J … as required}$

♦ Mean mark (b) 55%.

c. The orbital velocity at $Q$ is:

$v$	$=\sqrt{\dfrac{GM}{r}}$
	$=\sqrt{\dfrac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{6.85 \times 10^6}}$
	$=7.644 \times 10^3\ \text{ms}^{-1}$

The velocity of the satellite at $Q$ is:

$K_Q$	$=\dfrac{1}{2}mv_Q^2$
$v_Q$	$=\sqrt{\dfrac{2K_Q}{m}}$
	$=\sqrt{\dfrac{2 \times 1.194 \times 10^{10}}{400}}$
	$=7.727 \times 10^3\ \text{ms}^{-1}$

♦♦ Mean mark (c) 35%.

Since the velocity of the satellite at $Q$ is greater than the orbital velocity at $r$ = 6.85 × 10$^6$ m, the satellite will continue to move further away from the Earth.
Using the Law of Conservation of Energy, the kinetic energy of the satellite will decrease as the gravitational potential energy of the satellite increases. Hence the satellite will increase its distance from the Earth and slow down until the velocity of the satellite is equal to the orbital velocity at its new distance from the Earth.

CHEMISTRY, M3 2022 VCE 14 MC

The discharge reaction in a vanadium redox battery is represented by the following equation.

$\ce{VO2+(aq) + 2H+(aq) + V^2+(aq) \rightarrow V^3+(aq) + VO^2+(aq) + H2O(l)}$

When the vanadium redox battery is recharging

$\ce{H+}$ is the reducing agent.
$\ce{H2O}$ is the oxidising agent.
$\ce{VO^{2+}}$ is the reducing agent.
$\ce{VO2+}$ is the oxidising agent.

Show Answers Only

$C$

Show Worked Solution

Recharging equation:
$\ce{V^3+(aq) + VO^2+(aq) + H2O(l) \rightarrow VO2+(aq) + 2H+(aq) + V^2+(aq) }$
Only atom that changes oxidation numbers is $\ce{V}$ (eliminate A and B)
$\ce{VO2+}$ is a product of the recharging equation and cannot be the oxidising agent (eliminate D)
$\ce{VO^{2+}}$ is oxidised to $\ce{VO2+}$ with the oxidation number of $\ce{V}$ increasing from +4 to +5, making $\ce{VO^{2+}}$ the reducing agent.

$\Rightarrow C$

♦ Mean mark 53%.

CHEMISTRY, M6 2023 HSC 35

A 0.2000 mol L$^{-1} $ solution of dichloroacetic acid $ \ce{(CHCl2COOH)} $ has a pH of 1.107. Dichloroacetic acid is monoprotic.
Calculate the $ K_a $ for dichloroacetic acid. (3 marks)

--- 12 WORK AREA LINES (style=lined) ---

The following data apply to the ionisation of acetic acid $ \ce{(CH3COOH)} $ and trichloroacetic acid $ \ce{(CCl3COOH)} $.

	$ \ce{CH3 COOH }$	$ \ce{CCl3COOH} $
$ p K_a $	$4.76$	$0.51$
$ \Delta H° \text{(kJ mol}^{-1})$	$-0.1$	$+1.2$
$\Delta S° \text{(J K}^{-1} \text{ mol}^{-1})$	$-91.6$	$-5.8$
$ -T \Delta S° \text{(kJ mol}^{-1}) $	$+27.3$	$+1.7$
$ \Delta G° \text{(kJ mol}^{-1}) $	$+27.2$	$+2.9$

Explain the relative strength of these acids with reference to the data. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $K_a = 0.0501$

b. Relative strength of acids:

The $pK_a$ of trichloroacetic acid is lower than the $pK_a$ of acetic acid, so trichloroacetic acid is a stronger acid than acetic acid.
The $\Delta S°$ term for acetic acid is a significantly lower number than for the trichloroacetic acid (noting they are both negative).
In both cases, this value will contribute unfavourably to each acid’s $\Delta G°$ value, with the effect much larger for acetic acid than for trichloroacetic acid.
It follows from this result that the ionisation of acetic acid is less favourable than it is for trichloroacetic acid, making the latter the stronger acid.

Show Worked Solution

a. $\ce{CHCl2COOH(aq) \rightleftharpoons H+(aq) + CHCl2COO-(aq)} $

$\ce{[H+] = 10^{-\text{pH}} = 10^{-1.107} = 0.0782\ \text{mol L}^{-1}} $

♦ Mean mark (a) 54%.

\begin{array} {|l|c|c|c|}
\hline & \ce{CHCl2COOH(aq)} & \ce{H+(aq)} & \ce{CHCl2COO^{-}(aq)} \\
\hline \text{Initial} & \ \ \ \ 0.2000 & 0 & 0 \\
\hline \text{Change} & -0.0782 & +0.0782 & \ \ \ +0.0782 \\
\hline \text{Equilibrium} & \ \ \ \ 0.1218 & \ \ \ \ 0.0782 & \ \ \ \ \ \ 0.0782 \\
\hline \end{array}

$K_a$	$= \dfrac{\ce{[H+][CHCl2COO-]}}{\ce{[CHCl2COOH]}} $
	$= \dfrac{0.0782 \times 0.0782}{0.1218} $
	$= 0.0501$

b. Relative strength of acids:

The $pK_a$ of trichloroacetic acid is lower than the $pK_a$ of acetic acid, so trichloroacetic acid is a stronger acid than acetic acid.
The $\Delta S°$ term for acetic acid is a significantly lower number than for the trichloroacetic acid (noting they are both negative).
In both cases, this value will contribute unfavourably to each acid’s $\Delta G°$ value, with the effect much larger for acetic acid than for trichloroacetic acid.
It follows from this result that the ionisation of acetic acid is less favourable than it is for trichloroacetic acid, making the latter the stronger acid.

♦ Mean mark (b) 52%.

CHEMISTRY, M5 2023 HSC 34

When 125 mL of a magnesium nitrate solution is mixed with 175 mL of a 1.50 mol L$^{-1} $ sodium fluoride solution, 0.6231 g of magnesium fluoride (MM = 62.31 g mol$^{-1} $) precipitates. The $ K_{s p} $ of magnesium fluoride is 5.16 × 10$^{-11} $.

Calculate the equilibrium concentration of magnesium ions in this solution. (5 marks)

--- 12 WORK AREA LINES (style=lined) ---

Show Answers Only

$7.90 \times 10^{-11}\ \text{mol L}^{-1} $

Show Worked Solution

$\ce{MgF2(s) \rightleftharpoons Mg^{2+}(aq) + 2F-(aq)}$

$\ce{n(MgF2) = \dfrac{\text{m}}{\text{MM}} = \dfrac{0.6231}{62.31} = 1.000 \times 10^{-2} \text{mol}} $

$\ce{n(F^{-})_{init} = c \times V = 1.50 \times 0.175 = 0.263\ \text{mol}} $

$\ce{n(F^{-})_{after} = 0.263-2 \times 1.00 \times 10^{-2} = 0.243\ \text{mol}} $

$\ce{[F^{-}]_{after} = \dfrac{\text{n}}{\text{V}} = \dfrac{0.243}{0.300} = 0.808\ \text{mol L}^{-1}} $

♦ Mean mark 45%.

$K_{sp} = \ce{[Mg^{2+}][F^{-}]^2 }$

$\text{Since}\ K_{sp}\ \text{is small}\ \ \Rightarrow \text{assume}\ \ce{[F^{-}]_{eq} = 0.808\ \text{mol L}^{-1}} $

$\ce{[Mg^{2+}]_{eq} = \dfrac{5.16 \times 10^{-11}}{0.808^2} = 7.90 \times 10^{-11}\ \text{mol L}^{-1}} $

CHEMISTRY, M5 2023 HSC 31

Copper($\text{II}$) ions $ \ce{(Cu^{2+})} $ form a complex with lactic acid $ \ce{(C3H6O3)} $, as shown in the equation.

$ \ce{Cu^{2+}(aq)} + \ce{2C3H6O3(aq)} \rightleftharpoons \Bigl[\ce{Cu(C3H6O3)2\Bigr]^{2+}(aq)} $

This complex can be detected by measuring its absorbance at 730 nm. A series of solutions containing known concentrations of $ \Bigl[\ce{Cu(C3H6O3)_2\Big]^{2+}} $ were prepared, and their absorbances measured.

$ Concentration \ of \Bigl[\ce{Cu(C3H6O3)_2\Bigr]^{2+}} $ $ \text{(mol L}^{-1}) $	$ Absorbance $
0.000	0.00
0.010	0.13
0.020	0.28
0.030	0.43
0.040	0.57
0.050	0.72

Two solutions containing $ \ce{Cu^{2+}} \ \text{and} \ \ce{C3H6O3} $ were mixed. The initial concentrations of each in the resulting solution are shown in the table.

$ Species $	$ Initial \ Concentration$ $ (\text{mol L}^{-1}) $
$ \ce{Cu^{2+}} $	0.056
$ \ce{C3H6O3} $	0.111

When the solution reached equilibrium, its absorbance at 730 nm was 0.66.

You may assume that under the conditions of this experiment, the only species present in the solution are those present in the equation above, and that $ \Bigl[ \ce{Cu(C3H6O3)_2\Bigr]^{2+}} $ is the only species that absorbs at 730 nm.

With the support of a line graph, calculate the equilibrium constant for the reaction. (7 marks)

--- 14 WORK AREA LINES (style=lined) ---

Show Answers Only

$K_{eq}=1.3 \times 10^4$

Show Worked Solution

$\text{From graph:}$

$\text{0.66 absorbance}\ \Rightarrow\ \ \Big[\bigl[\ce{Cu(C3H6O3)2\bigr]^{2+}\Big]} = 0.046\ \text{mol L}^{-1} $

\begin{array} {|l|c|c|c|}
\hline & \ce{Cu^{2+}} & \ce{2C3H6O3(aq)} & \ce{\big[Cu(C3H6O3)2\big]^{2+}(aq)} \\
\hline \text{Initial} & \ \ \ \ 0.056 & \ \ \ \ 0.111 & 0 \\
\hline \text{Change} & -0.046 & -0.092 & \ \ \ +0.046 \\
\hline \text{Equilibrium} & \ \ \ \ 0.010 & \ \ \ \ 0.019 & \ \ \ \ \ \ 0.046 \\
\hline \end{array}

$K_{eq}=\dfrac{\ce{\Big[\big[Cu(C3H6O3)2\big]^{2+}\Big]}}{\ce{\big[Cu^{2+}\big]\big[C3H6O3\big]^2}}=\dfrac{0.046}{0.010 \times 0.019^2}=1.3 \times 10^4$

CHEMISTRY, M6 2023 HSC 32

The ammonium ion content of mixtures can be determined by boiling the mixture with a known excess of sodium hydroxide. This converts the ammonium ions into gaseous ammonia, which is removed from the system.

$ \ce{NH4^{+}(aq) + OH^{-}(aq) \rightarrow NH3(g) + H2O(l)} $

The excess sodium hydroxide can then be titrated with an acid solution of known concentration.

A fertiliser containing ammonium ions was analysed as follows.

A sample of fertiliser was treated with 50.00 mL of 1.124 mol L$^{-1} $ sodium hydroxide solution and the solution boiled.
After all of the ammonia was removed, the resulting solution was transferred to a 250.0 mL volumetric flask and made up to the mark with deionised water.
20.00 mL aliquots of this solution were titrated with 0.1102 mol L$^{-1} $ hydrochloric acid, giving the following results.

$ Titration $	$Volume \ \ce{HCl} \ \text{(mL)} $
1	22.65
2	22.05
3	22.00
4	21.95

Calculate the mass of ammonium ions in the sample of fertiliser. (5 marks)

--- 14 WORK AREA LINES (style=lined) ---

Show Answers Only

$0.4671\ \text{g} $

Show Worked Solution

$\text{Average titre (HCl)}\ =\dfrac{22.05+22.00+21.95}{3}=22.00\ \text{mL} = 0.02200\ \text{L} $

$\ce{n(HCl)} = \ce{c \times V} = 0.02200 \times 0.1102 = 2.424 \times 10^{-3}\ \text{mol} $

$\ce{n(NaOH \text{excess})} = 2.424 \times 10^{-3}\ \text{mol} $

Mean mark 56%.

$\text{In the 250 mL flask:}$

$\ce{n(NaOH \text{excess})} = \dfrac{250.0}{20.00} \times 2.424 \times 10^{-3} = 3.031 \times 10^{-2}\ \text{mol} $

$\ce{n(NaOH \text{total}) = \ce{c \times V} = 0.0500 \times 1.124 = 5.620 \times 10^{-2}\ \text{mol}} $

$\ce{n(NaOH\ \text{reacting with}\ NH4+) = 5.620 \times 10^{-2}-3.031 \times 10^{-2} = 2.589 \times 10^{-2}\ \text{mol}} $

$\ce{n(NH4+) = 2.589 \times 10^{-2}\ \text{mol}} $

$\ce{MM(NH4+) = 14.01 + 4 \times 1.008 = 18.042} $

$\ce{m(NH4+) = 2.589 \times 10^{-2} \times 18.042 = 0.4671\ \text{g}} $

CHEMISTRY, M8 2023 HSC 30

A water sample contains at least one of the following anions at concentrations of 1.0 mol L$^{-1} $.

- bromide $ \ce{(Br}^{-}) $
- carbonate $ \ce{(CO}_3{ }^{2-}) $

Outline a sequence of tests that could be performed in a school laboratory to confirm the identity of the anion or anions present. Include expected observations and TWO balanced chemical equations in your answer. (4 marks)

--- 11 WORK AREA LINES (style=lined) ---

Show Answers Only

Test 1: Add aqueous nitric acid

Bubbles indicate carbonate present. Acid removes carbonate for further testing of sample
$\ce{2H+(aq) + CO3^{2−}(aq) \rightarrow CO2(g) + H2O(l)}$

Test 2: Add silver nitrate solution

Creamy precipitate indicates bromide present
$\ce{Ag+(aq) + Br−(aq) \rightarrow AgBr(s)}$

Answer could include:

Add excess silver nitrate solution – precipitate produced
Add dilute nitric acid to the precipitate
- If bubbles are formed and a brown precipitate dissolves then carbonate was present
- If a creamy precipitate remains then bromide was present

Show Worked Solution

Test 1: Add aqueous nitric acid

Bubbles indicate carbonate present. Acid removes carbonate for further testing of sample
$\ce{2H+(aq) + CO3^{2−}(aq) \rightarrow CO2(g) + H2O(l)}$

Test 2: Add silver nitrate solution

Creamy precipitate indicates bromide present
$\ce{Ag+(aq) + Br−(aq) \rightarrow AgBr(s)}$

♦ Mean mark 53%.

Answer could include:

Add excess silver nitrate solution – precipitate produced
Add dilute nitric acid to the precipitate
- If bubbles are formed and a brown precipitate dissolves then carbonate was present
- If a creamy precipitate remains then bromide was present

CHEMISTRY, M8 2023 HSC 28

Alkene $\ce{Q}$ undergoes an addition reaction with chlorine gas to form compound $\ce{R}$.

Describe a chemical test that could be done in a school laboratory to confirm that $\ce{Q}$ is an alkene. Include expected observations in your answer. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Compound $\ce{R}$ was analysed and found to contain approximately 32% carbon by mass. The mass spectrum of compound $\ce{R}$ is shown.

Provide a structural formula for compound $\ce{R}$. Support your answer with calculations. (3 marks)

--- 9 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Chemical test for an alkene

Prepare a sample of alkene $\ce{Q}$ in a clean test tube.
Add a few drops of bromine water to the sample.
The bromine water will be decolourised if $\ce{Q}$ is an alkene.

PHYSICS, M5 2023 HSC 32

A horizontal disc rotates at 3 revolutions per second around its centre, with the top of the disc at ground level.

At 2 m from the centre of the disc, a ball is held in place at ground level on the top of the disc by a spring-loaded projectile launcher. At position $X$, the launcher fires the ball vertically upward with a velocity of 5.72 m s$^{-1}$.

Calculate the ball's position relative to the launcher's new position, at the instant the ball hits the ground. (7 marks)

--- 14 WORK AREA LINES (style=lined) ---

Show Answers Only

The position of the ball relative to the launcher’s new position is 44.19 m, 5.2$^{\circ}$ below the horizontal line of the launcher.

Show Worked Solution

Find horizontal velocity of the ball, $v_{\text{x}}$:

$T=\dfrac{1}{3} = 0.333\ \text{seconds} $

$v_{\text{x}}=\dfrac{2\pi r}{T}=\dfrac{2\pi \times 2}{0.333…}=37.699\ \text{ms}^{-1}$

♦ Mean mark 53%.

Calculating the time of flight, $t_1$:

Let $t_2$ = time to max height

$v_{\text{y}}$	$=u_{\text{y}} + at_2$
$t_2$	$=\dfrac{v_{\text{y}}-u_{\text{y}}}{a}=\dfrac{0-5.72}{-9.8}=0.58367\ \text{sec} $

Time of flight ($t_1)= 2 \times t_2= 1.167\ \text{s}$

Range of the ball from launch position:

$s_{\text{x}}=v_{\text{x}} \times t_2=37.699 \times 1.167=44.0\ \text{m}$

Position of the launcher (L) when the ball hits the ground:

Revolutions (before ball lands) = 3 × 1.167 = 3.5 revolutions
The Launcher (L) is $\frac{1}{2}$ a revolution past its starting point.
Thus, the positions of both the ball and the launcher at the time when the ball hits the ground can be demonstrated in the diagram below.

$D$	$=\sqrt{44.0^2+4^2}=44.18\ \text{m}$
$\theta$	$=\tan ^{-1}\left(\dfrac{4}{44.0}\right)=5.2^{\circ}$

The final position of the ball relative to $L$ is 44.18 m, 5.2$^{\circ}$ below the horizontal line at $L$.

CHEMISTRY, M8 2023 HSC 26

Nitric acid can be produced industrially using the process shown.

A mixture of $ \ce{NO2} $ and $ \ce{N2O4} $ enters Reactor 3 , where only $\ce{NO}_2$ is consumed by the reaction with water.
Explain, with respect to Le Chatelier's principle, what happens to the $ \ce{N2O4} $. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Explain TWO improvements that can be made to the design of the process shown. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Consider the equilibrium system in reactor 2:

$\ce{2NO2(g) \rightleftharpoons N2O4(g)}$

$\ce{NO2}$ is a reactant in Reactor 3 and is consumed by the reaction in Reactor 3, disrupting the equilibrium.
Le Chatelier’s Principle states that the position of equilibrium will shift to the left (as per the equilibrium equation above) to counter the depletion of $\ce{NO2}$.
This shift results in the further depletion of $\ce{N2O4}$. This process will eventually see all of the $\ce{N2O4}$ decomposing to form $\ce{NO2}$.

b. Design improvements:

A catalyst could be used in Reactor 1 to lower the activation energy required for the reaction to occur. This would decrease the required temperature, making the process more energy efficient.
Water is disposed of in Separator 3 and is required as a reactant in Reactor 3. A design improvement would be to recycle (rather than dispose) this water for use in Reactor 3.

PHYSICS, M6 2023 HSC 31

A roller coaster uses a braking system represented by the diagrams.

When the roller coaster car reaches the end of the ride, the two rows of permanent magnets on the car pass on either side of a thick aluminium conductor called a braking fin.

The graph shows the acceleration of the roller coaster reaching the braking fin at two different speeds.

Explain the similarities and differences between these two sets of data. (5 marks)

--- 15 WORK AREA LINES (style=lined) ---

Show Answers Only

Similarities:

Both graphs show peak negative acceleration at 0.8 seconds.
Acceleration curves converge at 3-4 seconds as both cars stop simultaneously.
The braking fin passing through permanent magnets experiences flux change, inducing EMF (Faraday’s Law).
This EMF creates eddy currents that oppose motion (Lenz’s Law), causing negative acceleration
After peak deceleration, magnetic braking effects decrease as slower speeds reduce flux change and eddy current magnitude.
Kinetic energy continuously converts to electrical resistive heating through eddy currents.

Differences:

The cart with $u = 12\ \text{ms}^{-1}$. experiences greater negative acceleration than the cart where $u = 10\ \text{ms}^{-1}$.
Higher initial velocity causes greater flux change rate in the braking fin.
This produces stronger induced EMF and larger eddy currents.
Since repulsive force is proportional to eddy current strength, the faster cart experiences greater deceleration.

Show Worked Solution

Similarities:

Both graphs show peak negative acceleration at 0.8 seconds.
Acceleration curves converge at 3-4 seconds as both cars stop simultaneously.
The braking fin passing through permanent magnets experiences flux change, inducing EMF (Faraday’s Law).
This EMF creates eddy currents that oppose motion (Lenz’s Law), causing negative acceleration
After peak deceleration, magnetic braking effects decrease as slower speeds reduce flux change and eddy current magnitude.
Kinetic energy continuously converts to electrical resistive heating through eddy currents.

Differences:

The cart with $u = 12\ \text{ms}^{-1}$. experiences greater negative acceleration than the cart where $u = 10\ \text{ms}^{-1}$.
Higher initial velocity causes greater flux change rate in the braking fin.
This produces stronger induced EMF and larger eddy currents.
Since repulsive force is proportional to eddy current strength, the faster cart experiences greater deceleration.

PHYSICS, M6 2023 HSC 30

The diagram shows apparatus that is used to investigate the interaction between the magnetic field produced by a coil and two copper rings $X$ and $Y$, when each is placed at position $P$, as shown.

Ring $X$ is a complete circular ring, and a small gap has been cut in ring $Y$. Each of the rings has a cross-sectional area of 4 × 10$^{-4}$ m².

The power supply connected to the coil produces an increasing current through the coil in the direction shown, when the switch is turned on. This produces a magnetic field at $P$ that varies as shown in the graph.

In the first part of the investigation, ring $X$ is held near the end of the electromagnet at position $P$.
Account for the force acting on the ring from 0 to 0.05 seconds after the power supply is turned on. (4 marks)

--- 7 WORK AREA LINES (style=lined) ---

i. In the second part of the investigation, ring $Y$ is placed at $P$, and the power supply is turned on.
Explain the behaviour of the ring. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

ii. Calculate the maximum induced emf in ring $Y$. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Between 0 – 0.03 seconds:

The magnetic field strength at point $P$ is increasing at a constant rate.
Thus, ring $X$ experiences a change in flux, which causes an EMF to be induced across the ring (Faraday’s Law)
This induced EMF causes a current to flow through ring $X$ that will interact in the external magnetic field to reduce the change in flux that created it (Lenz’s Law).
Thus, a clockwise current will run through the ring, creating a north pole towards the solenoid, causing the ring to have a repulsive force away from the solenoid acting on it.

Between 0.03 – 0.05 seconds:

There is no change in flux through the ring due to there being a constant magnetic field.
Therefore, there is no induced EMF or induced current.
Therefore, there is no force acting on the ring.

b.i. Ring $Y$ behaviour when placed at $P$:

Ring $Y$ will experience the same change in flux and hence the same induced EMF as ring $X$ within 0 – 0.03 seconds.
However, due to the gap in ring $Y$ (i.e. there is no closed circuit), no induced current will be able to flow through the ring.
Hence, there is no force exerted on ring $Y$.

ii. $\varepsilon = 8 \times 10^{-5}\ \text{V}$

Show Worked Solution

a. Between 0 – 0.03 seconds:

The magnetic field strength at point $P$ is increasing at a constant rate.
Thus, ring $X$ experiences a change in flux, which causes an EMF to be induced across the ring (Faraday’s Law)
This induced EMF causes a current to flow through ring $X$ that will interact in the external magnetic field to reduce the change in flux that created it (Lenz’s Law).
Thus, a clockwise current will run through the ring, creating a north pole towards the solenoid, causing the ring to have a repulsive force away from the solenoid acting on it.

Between 0.03 – 0.05 seconds:

There is no change in flux through the ring due to there being a constant magnetic field.
Therefore, there is no induced EMF or induced current.
Therefore, there is no force acting on the ring.

♦ Mean mark (a) 44%.

b.i. Ring $Y$ behaviour when placed at $P$:

Ring $Y$ will experience the same change in flux and hence the same induced EMF as ring $X$ within 0 – 0.03 seconds.
However, due to the gap in ring $Y$ (i.e. there is no closed circuit), no induced current will be able to flow through the ring.
Hence, there is no force exerted on ring $Y$.

b.ii.	$\varepsilon$	$=N\dfrac{\Delta \phi}{\Delta t}$
		$=N \dfrac{A \Delta B}{\Delta t}$
		$= 1 \times \dfrac{4 \times 10^{-4} \times (6 \times 10^{-3}-0)}{0.03-0}$
		$=8 \times 10^{-5}\ \text{V}$

♦♦ Mean mark (b)(i) 38%.
♦ Mean mark (b)(ii) 49%.

PHYSICS, M7 2023 HSC 29

When light from an incandescent lamp is passed through a plane polarising filter, the intensity of the light is reduced.

Explain this phenomenon. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

Light from an incandescent lamp is unpolarised meaning it is composed of many different planes of light waves as defined by the plane of oscillation of the electric fields of the EM waves.
The different planes of light can be resolved into components that are perpendicular and parallel to the plane of the polarising filter.
Plane polarising filters are commonly made up of long iodine molecular chains that only allow light waves with oscillating electric fields parallel to the plane of polarisation to pass through them.
The component of light with oscillating electric fields perpendicular to the plane of polarisation will be absorbed by the filter and so completely blocked from passing through the filter.
Therefore, the intensity of the light measured after passing through the polarising filter is reduced to around 50% of the original intensity of the light.

Show Worked Solution

Light from an incandescent lamp is unpolarised meaning it is composed of many different planes of light waves as defined by the plane of oscillation of the electric fields of the EM waves.
The different planes of light can be resolved into components that are perpendicular and parallel to the plane of the polarising filter.
Plane polarising filters are commonly made up of long iodine molecular chains that only allow light waves with oscillating electric fields parallel to the plane of polarisation to pass through them.
The component of light with oscillating electric fields perpendicular to the plane of polarisation will be absorbed by the filter and so completely blocked from passing through the filter.
Therefore, the intensity of the light measured after passing through the polarising filter is reduced to around 50% of the original intensity of the light.

♦ Mean mark 54%.

BIOLOGY, M6 2023 HSC 18 MC

The graph shows the increase in the global yield of wheat from 1800-2020. Genetically modified organisms (GMOs) are not currently used to grow wheat commercially.

What row in the table correctly identifies biotechnologies that have contributed to the increase in wheat yields and could be adapted to enhance commercial production in the future?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex} \ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|l|l|l|}
\hline
\rule{0pt}{2.5ex}\textit{Past}\ \text{(until 1960)}\rule[-1ex]{0pt}{0pt}& \textit{Present}\ \text{(1960-2023)}& \textit{Future}\ \text{(2023 onward)} \\
\hline
\rule{0pt}{2.5ex}\text{Selective breeding}&\text{GMO production} &\text{CRISPR}\\
\text{Embryo transfer}\rule[-1ex]{0pt}{0pt}& \text{Gene sequencing} & \text{Recombinant DNA technologies}\\
\hline
\rule{0pt}{2.5ex}\text{Selective breeding}\rule[-1ex]{0pt}{0pt}& \text{Selective breeding }& \text{CRISPR}\\
\text{Embryo transfer}\rule[-1ex]{0pt}{0pt}& \text{Gene sequencing}& \text{Stem cell engineering}\\
\hline
\rule{0pt}{2.5ex}\text{Selective breeding}\rule[-1ex]{0pt}{0pt}& \text{Artificial insemination} & \text{CRISPR} \\
\text{Hybridisation}\rule[-1ex]{0pt}{0pt}& \text{Recombinant DNA technologies} & \text{Stem cell engineering} \\
\hline
\rule{0pt}{2.5ex}\text{Selective breeding}\rule[-1ex]{0pt}{0pt}& \text{Selective breeding} & \text{CRISPR} \\
\text{Hybridisation}\rule[-1ex]{0pt}{0pt}& \text{Gene sequencing} & \text{Recombinant DNA technologies} \\
\hline
\end{array}
\end{align*}

Show Answers Only

$D$

Show Worked Solution

Wheat does not have an embryo and only animals can be artificially inseminated.

$\Rightarrow D$

♦ Mean mark 44%.

BIOLOGY, M6 2023 HSC 35

5-Bromouracil (bU) is a synthetic chemical mutagen. It bonds with adenine in place of thymine in DNA. During replication, it then binds with guanine.

This will then make a guanine-cytosine pair on one strand of DNA instead of an adenine-thymine pair.

Identify the type of mutation that is caused by bU. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Describe the possible effects on a protein if this mutation occurred within a gene. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Point mutation or substitution mutation

b. Protein effects if mutation within gene:

If this mutation occurred within coding DNA, then the RNA produced would be G–C instead of A–T (depending on the strand).
As a result, when it is read by a ribosome a different codon will be read, which may or may not code for the same amino-acid.
If the mutation codes for a different amino-acid, a different polypeptide chain will form.
This mutation process could cause the protein to fold differently which can alter it’s function or render it completely dysfunctional.
Alternatively, the new codon could also be interpreted as a stop codon, pre-emptively stopping production of the rest of the polypeptide chain.

Show Worked Solution

a. Point mutation or substitution mutation

b. Protein effects if mutation within gene:

If this mutation occurred within coding DNA, then the RNA produced would be G–C instead of A–T (depending on the strand).
As a result, when it is read by a ribosome a different codon will be read, which may or may not code for the same amino-acid.
If the mutation codes for a different amino-acid, a different polypeptide chain will form.
This mutation process could cause the protein to fold differently which can alter it’s function or render it completely dysfunctional.
Alternatively, the new codon could also be interpreted as a stop codon, pre-emptively stopping production of the rest of the polypeptide chain.

♦ Mean mark (b) 46%.

BIOLOGY, M6 2023 HSC 34

Cattle have been domesticated by humans for approximately 10 000 years. Many biotechnologies have been employed in the farming of cattle.

The table shows examples of the application of these biotechnologies.

\begin{array} {|l|l|}
\hline
\rule{0pt}{2.5ex} \textbf{Biotechnology} \rule[-1ex]{0pt}{0pt} & \textbf{Example} \\
\hline
\rule{0pt}{2.5ex} \text{Selective breeding} & \text{The offspring of highest milk producing female cows were} \\
\text{} & \text{retained and over time cows that produced more milk were bred,} \\
\text{} \rule[-1ex]{0pt}{0pt} & \text{leading to dairy breeds.} \\
\hline
\rule{0pt}{2.5ex} \text{Artificial} & \text{An American bull holds the current record for artificial} \\
\text{insemination} & \text{insemination. He produced 2.4 million units of semen and has} \\
\text{} \rule[-1ex]{0pt}{0pt} & \text{sired cattle in 50 countries.} \\
\hline
\rule{0pt}{2.5ex} \text{Whole organism} & \text{The success rate of cloning cattle is low. There are currently 30-40} \\
\text{cloning} \rule[-1ex]{0pt}{0pt} & \text{cloned cattle in Australia. They are not used commercially.} \\
\hline
\rule{0pt}{2.5ex} \text{Hybridisation } & \text{There are two species of domestic cattle, Bos taurus and Bos} \\
\text{} & \text{indicus. They can be hybridised to breed cattle with} \\
\text{} \rule[-1ex]{0pt}{0pt} & \text{characteristics of both species.} \\
\hline
\rule{0pt}{2.5ex} \text{Transgenic} & \text{The first transgenic cow produced human serum albumin in its} \\
\text{organisms} \rule[-1ex]{0pt}{0pt}& \text{milk. The use of transgenic cattle is not widespread.} \\
\hline
\end{array}

With reference to the table, evaluate the effect of biotechnologies on the biodiversity of cattle. (5 marks)

Show Answers Only

Biotechnologies can increase, decrease or maintain the size of the gene pool in populations and species, particularly in the case of cattle which have been subject to a range of biotechnologies.
Selective breeding, which decreases biodiversity, has been used for hundreds of years by farmers who oversee the reproduction of cattle with favourable characteristics, such as females who produce the most milk.
Artificial insemination, which typically reduces biodiversity, allows a single bull to sire many offspring. This process breeds out certain characteristics of cattle, reducing the diversity of the species. However, in certain circumstances, the gene pool of specific communities can be diversified through the introduction of new alleles.
Whole cattle cloning reduces biodiversity by making cloned organisms that are identical genotypes to the parent. As the success rate is low and cloned animals are infertile, this does not have the potential to have a large impact on biodiversity.
Hybridisation generally increases biodiversity by naturally mating two different cattle species and in the process, introducing genes not originally present.
Hybridisation can however also reduce biodiversity if cattle hybrids are then selectively bred in preference to the original breeds.
Transgenic organisms are produced where new alleles are artificially introduced into the species, increasing biodiversity. As this process is expensive and not widespread, it will not have a large effect on biodiversity.
In summary, the most wide spread and influential biotechnologies have the overall effect of decreasing the biodiversity of cattle.

Show Worked Solution

Biotechnologies can increase, decrease or maintain the size of the gene pool in populations and species, particularly in the case of cattle which have been subject to a range of biotechnologies.
Selective breeding, which decreases biodiversity, has been used for hundreds of years by farmers who oversee the reproduction of cattle with favourable characteristics, such as females who produce the most milk.
Artificial insemination, which typically reduces biodiversity, allows a single bull to sire many offspring. This process breeds out certain characteristics of cattle, reducing the diversity of the species. However, in certain circumstances, the gene pool of specific communities can be diversified through the introduction of new alleles.
Whole cattle cloning reduces biodiversity by making cloned organisms that are identical genotypes to the parent. As the success rate is low and cloned animals are infertile, this does not have the potential to have a large impact on biodiversity.
Hybridisation generally increases biodiversity by naturally mating two different cattle species and in the process, introducing genes not originally present.
Hybridisation can however also reduce biodiversity if cattle hybrids are then selectively bred in preference to the original breeds.
Transgenic organisms are produced where new alleles are artificially introduced into the species, increasing biodiversity. As this process is expensive and not widespread, it will not have a large effect on biodiversity.
In summary, the most wide spread and influential biotechnologies have the overall effect of decreasing the biodiversity of cattle.

BIOLOGY, M5 2023 HSC 33

Mechanisms of reproduction for both humans and generalised fungi are shown in the diagrams.

Describe the similarities and differences of reproduction in humans and generalised fungi. (4 marks)

Show Answers Only

Similarities

Both human and fungi reproduction use mitosis and meiosis.
Both human and fungi reproduction form zygotes with chromosomes from two different individuals.

Differences

Humans reproduce through sexual reproduction while fungi use asexual spores or sexual reproduction.
Humans produce egg and sperm cells which fuse to form a zygote, while fungi produce spores which germinate to produce mycelium which can be formed sexually or asexually.

Show Worked Solution

Similarities

Both human and fungi reproduction use mitosis and meiosis.
Both human and fungi reproduction form zygotes with chromosomes from two different individuals.

Differences

Humans reproduce through sexual reproduction while fungi use asexual spores or sexual reproduction.
Humans produce egg and sperm cells which fuse to form a zygote, while fungi produce spores which germinate to produce mycelium which can be formed sexually or asexually.

Mean mark 56%.

BIOLOGY, M6 2023 HSC 32

The mountain pygmy possum (Burramys parvus) is restricted to four regions in Australia's alpine zone. The species is listed as critically endangered with less than 2000 adults remaining. The range of the mountain pygmy possum has contracted due to a gradually warming climate.

Loss and degradation of these habitats have affected local populations. The graph shows changes in the Mt Buller population following recent bushfires and the introduction of male pygmy possums from Mt Bogong.

Evaluate how bushfires and the introduction of males from other locations have affected the population size and gene pool of the Mt Buller pygmy possum population. (7 marks)

--- 18 WORK AREA LINES (style=lined) ---

Show Answers Only

Environmental factors can play extremely large roles in the population and hence gene pool of the pygmy possums in Mt Buller.
This can be seen especially between 1996-2007, where three bushfires throughout those years caused the population to drop from 90 to less than 10. This is because bushfires not only kill individual possums, but also destroy their habitat, reducing shelter, food and water sources for the survivors.
This catastrophic drop in population significantly reduced the alleles present in the Mt Buller gene pool. The “new” survivor gene pool would see some alleles potentially disappear while others appear more frequently in individuals.
This may have led to genetic drift (bottleneck effect) in this population where the low diversity of alleles in the population led to a further reduction in the population between 2002–2007.
To counteract this reduction in population and gene pool size, 6 male possums were introduced from a nearby population in 2007. This was done again in 2012, and despite there being another bushfire in 2011, the population increased to 150 by 2015.
The introduction of these males in 2007 almost doubled the known population at the time, but just as importantly diversified the gene pool, an effect helped by the isolation of the two populations.
This increase in genetic diversity also improves a species’ ability to adapt to the drier and hotter climates being experienced.
It is evident that both the bushfires and the introduction of males played different but very important roles in the population size and gene pool of the Mt Buller pygmy possum population.

Show Worked Solution

Environmental factors can play extremely large roles in the population and hence gene pool of the pygmy possums in Mt Buller.
This can be seen especially between 1996-2007, where three bushfires throughout those years caused the population to drop from 90 to less than 10. This is because bushfires not only kill individual possums, but also destroy their habitat, reducing shelter, food and water sources for the survivors.
This catastrophic drop in population significantly reduced the alleles present in the Mt Buller gene pool. The “new” survivor gene pool would see some alleles potentially disappear while others appear more frequently in individuals.
This may have led to genetic drift (bottleneck effect) in this population where the low diversity of alleles in the population led to a further reduction in the population between 2002–2007.
To counteract this reduction in population and gene pool size, 6 male possums were introduced from a nearby population in 2007. This was done again in 2012, and despite there being another bushfire in 2011, the population increased to 150 by 2015.
The introduction of these males in 2007 almost doubled the known population at the time, but just as importantly diversified the gene pool, an effect helped by the isolation of the two populations.
This increase in genetic diversity also improves a species’ ability to adapt to the drier and hotter climates being experienced.
It is evident that both the bushfires and the introduction of males played different but very important roles in the population size and gene pool of the Mt Buller pygmy possum population.

population.

BIOLOGY, M6 2023 HSC 31

Describe a named genetic technology and its use in a medical application. (4 marks)

Show Answers Only

A polymerase chain reaction (PCR) is a process which allows scientists to replicate billions of copies of a specific gene.
The PCR process involves denaturing a DNA sample by heating it to around 98°C. The sample is then cooled to 60°C where DNA primers, polymerase enzymes and free nucleotides are added, making a copy of the original sample.
By repeating this process, the amount of copies acquired will increase exponentially.
This process is used in COVID-19 testing centres.
An individual’s DNA is swabbed and a PCR test is used to multiply it for COVID testing. PCR can also be used in other medical scenarios where gene cloning is required, such as in the production of mRNA vaccines.

BIOLOGY, M8 2023 HSC 27

Air pollution has been linked to a variety of non-infectious neurological (brain) disorders. Some of the symptoms include memory loss, cognitive decline and impaired movement and coordination.

500 people from each of three major cities were surveyed and were monitored and tested for a period of 12 months. Each group included males and females aged between 20 and 50 years of age.

The results after 12 months were as follows:

Evaluate the method used in this epidemiological study in determining a link between air pollution and the symptoms. (7 marks)

--- 16 WORK AREA LINES (style=lined) ---

Show Answers Only

This study is not an effective study for validating a link between air pollution and cognitive disorders due to a variety of issues with the study’s reliability, validity and accuracy.
While the study does have a reasonable sample size and uses 3 different cities, numerous important factors are not specified. These include risk factors such as age, sex, ethnicity and occupation of the participants in each city.
The 12 month timeframe of the study may not be long enough for symptoms to develop.
The study also does not signify the type and degree of symptoms that were experienced.
A non-city comparison where air pollution is low would provide good baseline data against which the data from city participants could be compared.
The study does also not take into account other important demographic factors, such as socioeconomic status and geography within a city. The proximity to industry of an individual’s workplace or residence would be a particularly important risk factor to consider.
Cities should be chosen that have different levels of air pollution in order to look for general trends in the data, such as more exposure to air pollution corresponds to a greater number of symptoms. There is no evidence that this is part of the study design.
This is not a valid nor reliable test in determining a link between air pollution and neurological disorders. Adding prior medical/family history and data relating to the testing centres/cities as well as controlling more variables will lead to a fairer test.

Show Worked Solution

This study is not an effective study for validating a link between air pollution and cognitive disorders due to a variety of issues with the study’s reliability, validity and accuracy.
While the study does have a reasonable sample size and uses 3 different cities, numerous important factors are not specified. These include risk factors such as age, sex, ethnicity and occupation of the participants in each city.
The 12 month timeframe of the study may not be long enough for symptoms to develop.
The study also does not signify the type and degree of symptoms that were experienced.
A non-city comparison where air pollution is low would provide good baseline data against which the data from city participants could be compared.
The study does also not take into account other important demographic factors, such as socioeconomic status and geography within a city. The proximity to industry of an individual’s workplace or residence would be a particularly important risk factor to consider.
Cities should be chosen that have different levels of air pollution in order to look for general trends in the data, such as more exposure to air pollution corresponds to a greater number of symptoms. There is no evidence that this is part of the study design.
This is not a valid nor reliable test in determining a link between air pollution and neurological disorders. Adding prior medical/family history and data relating to the testing centres/cities as well as controlling more variables will lead to a fairer test.

Mean mark 57%.

BIOLOGY, M7 2023 HSC 26

Malaria is a potentially fatal infectious disease that is spread to humans by infected mosquitoes. Scientists investigated the behaviour of 20 mosquitoes for an hour in each of the four containers shown.

Aim: To determine if wearing clean clothing reduces the transmission of malaria.

Assume infected mosquitoes that land on clothing transmit malaria.

Identify the dependent variable and a controlled variable in this investigation. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---
The results of the investigation showing the number of times mosquitoes landed on the clothing in an hour are provided.

\begin{array}{|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} \textit {Experiment} \rule[-1ex]{0pt}{0pt}& \textit {Container A} & \textit {Container B} & \textit {Container C} & \textit {Container D} \\
\hline
\rule{0pt}{2.5ex} 1 \rule[-1ex]{0pt}{0pt}& 15 & 7 & 12 & 5 \\
\hline
\rule{0pt}{2.5ex} 2 \rule[-1ex]{0pt}{0pt}& 19 & 5 & 9 & 3 \\
\hline
\rule{0pt}{2.5ex} 3 \rule[-1ex]{0pt}{0pt}& 12 & 4 & 14 & 6 \\
\hline
\rule{0pt}{2.5ex} 4 \rule[-1ex]{0pt}{0pt}& 18 & 6 & 13 & 4 \\
\hline
\rule{0pt}{2.5ex} 5 \rule[-1ex]{0pt}{0pt}& 19 & 6 & 10 & 3 \\
\hline
\end{array}

Justify a suitable conclusion for this investigation. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Dependant Variable: Number of mosquitos that land on the clothing.

Controlled Variable: Number of mosquitos in each container.

Alternative controlled variable: size of container

b. Data results show:

Wearing clean clothing, on average, reduces the number of mosquitos that land on clothes.
This effect occurs for both infected and uninfected mosquitos.
Conclusion: wearing clean clothing will reduce the transmission of malaria, as infected mosquitos will land on clean clothing less often than on clothing already worn for a day.

Show Worked Solution

a. Dependant Variable: Number of mosquitos that land on the clothing.

Controlled Variable: Number of mosquitos in each container.

Alternative controlled variable: size of container

♦ Mean mark 51%.

b. Data results show:

Wearing clean clothing, on average, reduces the number of mosquitos that land on clothes.
This effect occurs for both infected and uninfected mosquitos.
Conclusion: wearing clean clothing will reduce the transmission of malaria, as infected mosquitos will land on clean clothing less often than on clothing already worn for a day.

BIOLOGY, M8 2023 HSC 25c

The normal Huntingtin protein has 10–26 repeats of CAG. In Huntington's disease there are 37–80 repeats. This leads to an alteration in the structure of the protein. The graph shows the relationship between the age of onset of Huntington's disease and the number of CAG repeats.

Explain the relationship between the number of CAG repeats and the age of onset of Huntington's disease. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

The graph shows that as the number of CAG repeats is increased, the age of the onset of Huntington’s decreases.
For example, someone that has 40 repeats will experience the onset of Huntington’s at 60 years old, but someone with 120 repeats will experience symptoms and/or exhibit signs shortly after their birth.

Show Worked Solution

The graph shows that as the number of CAG repeats is increased, the age of the onset of Huntington’s decreases.
For example, someone that has 40 repeats will experience the onset of Huntington’s at 60 years old, but someone with 120 repeats will experience symptoms and/or exhibit signs shortly after their birth.

♦ Mean mark 49%.

PHYSICS, M6 2023 HSC 28

An ideal transformer is connected to a 240 V AC supply. It has 300 turns on the primary coil and 50 turns on the secondary coil.

It is connected in the circuit with two identical light globes, $X$ and $Y$, as shown.

Calculate the voltage across light globe $X$ when the switch is open. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Explain why, after the switch has been closed, the current in the primary coil is different from when the switch is open. (3 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

a. 40 V

b. When the switch is closed:

Globe $X$ and $Y$ are connected in a parallel circuit.
Once closed, the total resistance through the circuit is less than when only light globe $X$ is in the circuit.
Since $V=IR\ \ \Rightarrow\ \ R \propto \dfrac{1}{I} $. Therefore, a decrease in resistance through the circuit leads to an increase in the current.
Transformer is ideal, so Power in = Power out ( $V_{p}I_{p}=V_{s}I_{s}$ ). Hence, an increase in $I_s$ corresponds to an increase in $I_p$.
Therefore, the current in the primary coil is greater when the switch is closed.

Show Worked Solution

a.	$ \dfrac{V_p}{V_s}$	$= \dfrac{N_p}{N_s}$
	$ V_s$	$=V_p \times \dfrac{N_s}{N_p}=240 \times \dfrac{50}{300}=40\ \text{V} $

The voltage across light globe $X$ is 40 V.

b. When the switch is closed:

Globe $X$ and $Y$ are connected in a parallel circuit.
Once closed, the total resistance through the circuit is less than when only light globe $X$ is in the circuit.
Since $V=IR\ \ \Rightarrow\ \ R \propto \dfrac{1}{I} $. Therefore, a decrease in resistance through the circuit leads to an increase in the current.
Transformer is ideal, so Power in = Power out ( $V_{p}I_{p}=V_{s}I_{s}$ ). Hence, an increase in $I_s$ corresponds to an increase in $I_p$.
Therefore, the current in the primary coil is greater when the switch is closed.

♦ Mean mark (b) 39%.

PHYSICS, M6 2023 HSC 25b

Explain why the torque of a DC motor decreases as its rotational speed increases. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

Torque in a simple DC motor can be calculated using $\tau=nIAB \sin\theta$.
Initially, the current through the coil of the motor is a maximum as the motor is stationary.
As the rotational speed of the motor begins to increase, there is a change of flux experienced through the coil of the motor which will induce an EMF in the coil (Faraday’s Law).
This induced back EMF will act to oppose the original EMF that produced it (Lenz’s Law).
Thus, the voltage through the coil will decrease which will decrease the current through the coil and the torque ($\tau \propto I $).

Show Worked Solution

Torque in a simple DC motor can be calculated using $\tau=nIAB \sin\theta$.
Initially, the current through the coil of the motor is a maximum as the motor is stationary.
As the rotational speed of the motor begins to increase, there is a change of flux experienced through the coil of the motor which will induce an EMF in the coil (Faraday’s Law).
This induced back EMF will act to oppose the original EMF that produced it (Lenz’s Law).
Thus, the voltage through the coil will decrease which will decrease the current through the coil and the torque ($\tau \propto I $).

♦ Mean mark 49%.

PHYSICS, M7 2023 HSC 19 MC

The diagram represents the distribution of positive charges in identical wires when no current is flowing.

Equal currents then flow in each wire, but in opposite directions. These currents are considered conventionally as the flow of positive charge.

Which diagram represents the charge distribution in the wires, from the frame of reference of a positive charge in wire $Y$ ?

Show Answers Only

$B$

Show Worked Solution

The currents flowing through Wire $Y$ are all travelling in the same direction and at the same speed, thus they are all within the same inertial frame of reference and will not experience any relativistic effects when viewed from the frame of reference of a positive charge in $Y$.
Therefore, the separation of the charges in $Y$ from the frame of reference of $Y$ will not change.
As the positive charges in $X$ are moving in the opposite direction to the positive charges in $Y$, from the frame of reference of a positive charge in $Y$, length contraction will be observed in $X$.
Therefore, the separation of the positive charges in $X$ from the frame of reference of $Y$ will be shorter so the charges appear closer together.

$\Rightarrow B$

♦ Mean mark 44%.

PHYSICS, M5 2023 HSC 17 MC

A mass attached to a lightweight, rigid arm hanging from point $O$, oscillates freely between $X$ and $Z$.

Which statement best describes the torque acting on the arm as it oscillates?

It is constant in magnitude and direction.
It is zero at $Y$ and a maximum at $X$ and $Z$.
It is zero at $X$ and $Z$ and a maximum at $Y$.
It is constant in magnitude but its direction changes.

Show Answers Only

$B$

Show Worked Solution

In the scenario above, the only force acting the on the oscillating arm is the force due to gravity which acts vertically downwards.
The torque can be calculated by $\tau=rF\sin\theta$
The angle between the arm and force of gravity at $Y$ is $180^{\circ}$ as they are parallel, therefore $\tau=$0 $\text{Nm}$.
At $X$ and $Z$, the magnitude of the force of gravity perpendicular to the arm is a maximum, thus the magnitude of the torque at $X$ and $Z$ is a maximum.

$\Rightarrow B$

♦ Mean mark 50%.

PHYSICS, M6 2023 HSC 16 MC

In a thought experiment, two identical parallel aluminium rods, $X$ and $Y$, are carrying electric currents of equal magnitude. Rod $X$ rests on a table. Rod $Y$ remains stationary, vertically above $X$, as a result of the magnetic interaction. The masses of the connecting wires are negligible.

Which statement must be correct if rod $ Y$ is stationary?

The magnetic force acting on $X$ is upward.
The currents through $X$ and $Y$ are in the same direction.
The force the table exerts on $X$ is equal and opposite to the total weight of $X$ and $Y$.
The force the table exerts on $X$ is equal and opposite to the force of gravity acting on $Y$.

Show Answers Only

$C$

Show Worked Solution

As rod $X$ and rod $Y$ exert repulsive forces on one another, the current running through the wires must be in opposite directions and the magnetic force of $X$ is equal and opposite to the weight force of $Y$.
$F_{\text{X on Y}} = m_{\text{Y}} \times g$
The force the table exerts on $X$, is equal and opposite to the magnetic force of $Y$ on $X$ and the weight force of $X$.
$F_{\text{table on X}}=F_{\text{Y on X}} + m_{\text{X}} \times g$
$F_{\text{Y on X}} = F_{\text{X on Y}}$ as a result of Newton’s third law of motion.
$F_{\text{table on X}}= F_{\text{X on Y}} + m_{\text{X}} \times g= m_{\text{Y}} \times g + m_{\text{X}} \times g$
Therefore, the force the table exerts on $X$ is equal and opposite to the weight force of $X$ and $Y$.

$\Rightarrow C$

♦♦ Mean mark 35%.

PHYSICS, M7 2023 HSC 15 MC

What evidence resulting from investigations into the photoelectric effect is consistent with the model of light subsequently proposed by Einstein?

Photoelectrons were only ejected from a metal if the light was less than a specific wavelength.
Increasing the intensity of light on a metal increased the maximum kinetic energy of the photoelectrons.
If photons had sufficient energy to eject photoelectrons from a metal, the maximum kinetic energy was independent of the type of metal used.
The probability of photoelectrons being emitted from a metal was proportional to the duration of exposure to light for any given wavelength used.

Show Answers Only

$A$

Show Worked Solution

A photoelectron will be ejected from a metal if the energy of the photoelectron transferred from the photon is greater than the work function of the metal surface where
$K_{\text{max}}=hf-\phi\ \ \Rightarrow \ \ K_{\text{max}}=\dfrac{hc}{\lambda}-\phi$
By decreasing the wavelength of the light, the maximum kinetic energy of the photoelectron increases, thus it has enough energy to overcome the work function of the metal and be ejected from the surface of the metal.
Increasing the intensity of the light increases the number of photons but has no effect on the maximum kinetic energy of the photoelectrons.

$\Rightarrow A$

♦ Mean mark 46%.

PHYSICS, M8 2023 HSC 13 MC

Nucleus $X$ has a greater binding energy than nucleus $Y$.

What can be deduced about $X$ and $Y$ ?

$X$ is more stable than $Y$.
$Y$ is more stable than $X$.
$X$ has a greater mass defect than $Y$.
$Y$ has a greater mass defect than $X$.

Show Answers Only

$C$

Show Worked Solution

Binding energy is the energy required to split a nucleus into its nucleons.
The mass of the nucleus is less than the sum of the nucleons. The mass equivalent of the binding energy is equal to the mass defect.
As nucleus $X$ has a greater binding energy than nucleus $Y$, it can be deduced that it also has a greater mass defect.

$\Rightarrow C$

♦ Mean mark 43%.

PHYSICS, M6 2023 HSC 12 MC

Figure $\text{I}$ shows a positively charged particle accelerating freely from $X$ to $Y$, between oppositely charged plates. The change in the particle's kinetic energy is $W$.

The distance between the plates is then doubled as shown in Figure $\text{II}$ . The same charge accelerates from rest over the same distance from $X$ to $Y$.

What is the change in kinetic energy of the positively charged particle shown in Figure $\text{II}$ ?

$W$
$\dfrac{W}{2}$
$\sqrt{W}$
$2 W$

Show Answers Only

$B$

Show Worked Solution

In Figure $\text{I}$: $ W= qEd$ and $ E=\dfrac{1000V}{d} $
$W=\dfrac{1000qVd}{d}=1000qV$
In Figure $\text{II}$: $ \Delta \text{KE} =qEd$ and $ E=\dfrac{1000V}{2d} $
$\Delta \text{KE}=\dfrac{1000qVd}{2d}= \dfrac{1}{2} \times 1000qV= \dfrac{W}{2}$

$\Rightarrow B$

♦ Mean mark 55%.

PHYSICS, M7 2023 HSC 6 MC

An electron would produce an electromagnetic wave when it is

stationary.
in a stable hydrogen atom.
moving at a constant velocity.
moving at a constant speed in a circular path.

Show Answers Only

$D$

Show Worked Solution

Maxwell predicted that an accelerating charge will produce an electromagnetic wave.
As the electron moves at a constant speed in a circular path it must be experiencing an acceleration.

$\Rightarrow D$

♦ Mean mark 52%.

BIOLOGY, M4 EQ-Bank 25

The charts below show data compiled from ice core drilling sites located in Greenland and Antarctica.

How does the data provide evidence that the drastic change in gas concentration is NOT part of a natural cycle? (4 marks)

Show Answers Only

The concentrations of carbon dioxide and methane remained stable until around 1750. From 1750 to the present, methane levels increased by 200% and carbon dioxide by 40%.
This rise is mainly due to the Industrial Revolution, which began in 1760 and brought significant advances in manufacturing and agriculture.
Deforestation and the burning of fossil fuels, both of which have accelerated over time, have driven the increase in these gases.
While methane is partly linked to human activities like farming, it also originates from natural sources such as volcanic eruptions and organic matter breakdown.
The growing global population has intensified these processes, further contributing to methane emissions.

Show Worked Solution

The concentrations of carbon dioxide and methane remained stable until around 1750. From 1750 to the present, methane levels increased by 200% and carbon dioxide by 40%.
This rise is mainly due to the Industrial Revolution, which began in 1760 and brought significant advances in manufacturing and agriculture.
Deforestation and the burning of fossil fuels, both of which have accelerated over time, have driven the increase in these gases.
While methane is partly linked to human activities like farming, it also originates from natural sources such as volcanic eruptions and organic matter breakdown.
The growing global population has intensified these processes, further contributing to methane emissions.

BIOLOGY, M7 2023 HSC 22b

Explain how antibodies are produced in response to the entry of a pathogen. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

Antigens (foreign proteins) are detected by B cells as “non-self” foreign bodies.
Plasma B cells have associated antibodies with a specific shape that allows them to bind to antigens.
Once an antigen binds to the receptor of a B cell, it activates the B cell which replicates to form plasma cells.
These plasma cells produce an antibody that is specific to the antigen.
After the immune response, some B cells can remain dormant as memory cells, which can be activated upon recognition of the same antigen.

Show Worked Solution

Antigens (foreign proteins) are detected by B cells as “non-self” foreign bodies.
Plasma B cells have associated antibodies with a specific shape that allows them to bind to antigens.
Once an antigen binds to the receptor of a B cell, it activates the B cell which replicates to form plasma cells.
These plasma cells produce an antibody that is specific to the antigen.
After the immune response, some B cells can remain dormant as memory cells, which can be activated upon recognition of the same antigen.

♦ Mean mark 47%.

BIOLOGY, M7 2023 HSC 13 MC

Australian native plants can be infected by fungal and viral pathogens.

Which of the following is an active plant response to infection by pathogens?

Phagocytosis
Programmed cell death
Formation of powdery spots
Development of small stomata

Show Answers Only

$B$

Show Worked Solution

By Elimination:

Phagocytosis is a response in animals, not plants (Eliminate A).
The formation of powdery spots (commonly called powdery mildew) is a sign of fungal infection, not a response (Eliminate C).
Small stomata are an evolutionary adaptation to reduce water loss, not a response to infection (Eliminate D).

$\Rightarrow B$

♦ Mean mark 48%.

BIOLOGY, M5 2023 HSC 7 MC

The diagram shows the structure of a molecule of tRNA.

Which row of the table correctly identifies $X$ and $Y$ ?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex}\ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|l|l|}
\hline
\rule{0pt}{2.5ex} \quad \quad \quad X \quad \quad \quad \rule[-1ex]{0pt}{0pt} & \quad \quad \quad Y \quad \quad \quad \\
\hline
\rule{0pt}{2.5ex}\text{Anticodon} \rule[-1ex]{0pt}{0pt}& \text{Ribonucleotide} \\
\hline
\rule{0pt}{2.5ex}\text{Codon} \rule[-1ex]{0pt}{0pt}& \text{Ribonucleotide} \\
\hline
\rule{0pt}{2.5ex}\text{Codon} \rule[-1ex]{0pt}{0pt}& \text{Amino acid} \\
\hline
\rule{0pt}{2.5ex}\text{Anticodon} \rule[-1ex]{0pt}{0pt}& \text{Amino acid} \\
\hline
\end{array}
\end{align*}

Show Answers Only

$D$

Show Worked Solution

In a tRNA molecule, the three base sequence is called an anti-codon, and $Y$ is it’s associated amino acid.

$\Rightarrow D$

♦ Mean mark 53%.

Vectors, EXT2 V1 2023 HSC 15b

On the triangular pyramid $A B C D, L$ is the midpoint of $A B, M$ is the midpoint of $A C, N$ is the midpoint of $A D, P$ is the midpoint of $C D, Q$ is the midpoint of $B D$ and $R$ is the midpoint of $B C$.

Let $\underset{\sim}{b}=\overrightarrow{A B}, \underset{\sim}{c}=\overrightarrow{A C}$ and $\underset{\sim}{d}=\overrightarrow{A D}$.

Show that $\overrightarrow{L P}=\dfrac{1}{2}(-\underset{\sim}{b}+\underset{\sim}{c}+\underset{\sim}{d})$. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
It can be shown that

$\overrightarrow{M Q}=\dfrac{1}{2}(\underset{\sim}{b}-\underset{\sim}{c}+\underset{\sim}{d})$ and

$\overrightarrow{N R}=\dfrac{1}{2}(\underset{\sim}{b}+\underset{\sim}{c}-\underset{\sim}{d})$. (Do NOT prove these.)

Prove that

$ \Big{|}\overrightarrow{A B}\Big{|}^2+\Big{|}\overrightarrow{A C}\Big{|}^2+\Big{|}\overrightarrow{A D}\Big{|}^2+\Big{|}\overrightarrow{B C}\Big{|}^2+\Big{|}\overrightarrow{B D}\Big{|}^2+\Big{|}\overrightarrow{C D}\Big{|}^2 $

$=4\left(\Big{|}\overrightarrow{L P}\Big{|}^2+\Big{|}\overrightarrow{M Q}\Big{|}^2+\Big{|}\overrightarrow{N R}\Big{|}^2\right)$ (3 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{See Worked Solutions}$
$\text{Proof (See Worked Solutions)}$

Show Worked Solution

i.	$\overrightarrow{LP}$	$=\overrightarrow{LA}+\overrightarrow{AC}+\overrightarrow{CP} $
		$=\dfrac{1}{2} \overrightarrow{BA}+\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CD} $
		$=-\dfrac{1}{2} \underset{\sim}b +\underset{\sim}c + \dfrac{1}{2}(\underset{\sim}d-\underset{\sim}c) $
		$=-\dfrac{1}{2} \underset{\sim}b +\underset{\sim}c + \dfrac{1}{2}\underset{\sim}d-\dfrac{1}{2}\underset{\sim}c$
		$=\dfrac{1}{2} (-\underset{\sim}b+\underset{\sim}c+\underset{\sim}d) $

ii. $\overrightarrow{M Q}=\dfrac{1}{2}(\underset{\sim}{b}-\underset{\sim}{c}+\underset{\sim}{d})$

$\overrightarrow{N R}=\dfrac{1}{2}(\underset{\sim}{b}+\underset{\sim}{c}-\underset{\sim}{d})$.

$\text{RHS}$	$=4\left(\Big{\|}\overrightarrow{L P}\Big{\|}^2+\Big{\|}\overrightarrow{M Q}\Big{\|}^2+\Big{\|}\overrightarrow{N R}\Big{\|}^2\right)$
	$=4\left(\overrightarrow{L P}\cdot \overrightarrow{L P} +\overrightarrow{MQ}\cdot \overrightarrow{MQ} +\overrightarrow{NR}\cdot \overrightarrow{NR}\right)$
	$=4\Bigg{(}\dfrac{1}{4}(-\underset{\sim}b+\underset{\sim}c+\underset{\sim}d) \cdot(-\underset{\sim}b+\underset{\sim}c+\underset{\sim}d) + $
	$ \dfrac{1}{4}(\underset{\sim}{b}-\underset{\sim}{c}+\underset{\sim}{d}) \cdot(\underset{\sim}{b}-\underset{\sim}{c}+\underset{\sim}{d}) + $
	$ \dfrac{1}{4}(\underset{\sim}{b}+\underset{\sim}{c}-\underset{\sim}{d}) \cdot(\underset{\sim}{b}+\underset{\sim}{c}-\underset{\sim}{d}) \Bigg{)}$
	$=(\underset{\sim}c+(\underset{\sim}d-\underset{\sim}b)) \cdot(\underset{\sim}c+(\underset{\sim}d-\underset{\sim}b))+(\underset{\sim}d+(\underset{\sim}b-\underset{\sim}c))\cdot (\underset{\sim}d+(\underset{\sim}b-\underset{\sim}c)) + $
	$ (\underset{\sim}b+(\underset{\sim}c-\underset{\sim}d))\cdot (\underset{\sim}b+(\underset{\sim}c-\underset{\sim}d)) $
	$=\|\underset{\sim}c\|^2+2\underset{\sim}c(\underset{\sim}d-\underset{\sim}b) + \|\underset{\sim}d-\underset{\sim}b\|^2 + $
	$\|\underset{\sim}d\|^2+2\underset{\sim}d(\underset{\sim}b-\underset{\sim}c) + \|\underset{\sim}b-\underset{\sim}c\|^2 + $
	$ \|\underset{\sim}b\|^2+2\underset{\sim}b(\underset{\sim}c-\underset{\sim}d) + \|\underset{\sim}c-\underset{\sim}d\|^2 $
	$=\|\underset{\sim}b\|^2+\|\underset{\sim}c\|^2+\|\underset{\sim}d\|^2+\|\underset{\sim}b-\underset{\sim}c\|^2+\|\underset{\sim}d-\underset{\sim}b\|^2+\|\underset{\sim}c-\underset{\sim}d\|^2 + $
	$ 2(\underset{\sim}c \cdot\underset{\sim}d-\underset{\sim}c \cdot\underset{\sim}b+\underset{\sim}d \cdot\underset{\sim}b-\underset{\sim}d \cdot\underset{\sim}c+\underset{\sim}b \cdot\underset{\sim}c-\underset{\sim}b \cdot\underset{\sim}d) $
	$=\Big{\|}\overrightarrow{A B}\Big{\|}^2+\Big{\|}\overrightarrow{A C}\Big{\|}^2+\Big{\|}\overrightarrow{A D}\Big{\|}^2+\Big{\|}\overrightarrow{B C}\Big{\|}^2+\Big{\|}\overrightarrow{B D}\Big{\|}^2+\Big{\|}\overrightarrow{C D}\Big{\|}^2 + 0$
	$=\ \text{LHS} $

♦♦ Mean mark (ii) 34%.

PHYSICS, M6 2023 HSC 18 MC

The diagrams show the trajectories of two particles with the same mass and charge and which initially have the same velocity $u$, as shown. The subsequent motion of each particle is determined by its properties and by its interaction with the field in which it is moving.

$X$ and $Y$ represent the landing points in Figures $\text{I}$ and $\text{II}$.

Which row of the table shows the correct paths of the particles if the mass of each is increased by the same amount and they are given the same initial velocity $u$ ?

Show Answers Only

$A$

Show Worked Solution

The motion of a projectile within a gravitational field is independent of the mass of the projectile as all projectiles accelerate the same under gravity.
Increasing the mass of the particle within the gravitational field will have no effect on the range of the projectile, hence it will still land at $X$.
However, in an electric field the force on a charged particle is given by $F=qE$ and using Newton’s second law of motion, the equation can be rewritten as
$ma=qE\ \ \Rightarrow \ \ a=\dfrac{qE}{m}\ \ \Rightarrow\ \ a \propto \dfrac{1}{m} $
By increasing the mass of the particle, the acceleration of the particle in the electric field decreases.
It takes a greater time to reach the ground, therefore the range of the particle is increased.

$\Rightarrow A$

♦ Mean mark 45%.

BIOLOGY, M3 EQ-Bank 22

Explain how cane toads in Australia have evolved to develop longer legs and an ability to travel faster over greater distances. (3 marks)

Show Answers Only

Cane toads have rapidly multiplied to 200 million since there introduction in Australia in 1935. This is largely due to their ability to produce large amounts of offspring all year round and have no predators, as they are extremely poisonous and toxic.
As a result, they have not needed to rapidly evolve as there are no significant pressures, but they have been shown to exhibit traits which allow them to travel faster.
This trait allows those which exist on the front-line of cane toad communities to outcompete their peers as well as travel further than cane toads at the back, leading to higher reproduction rates and hence a more commonly exhibited trait.

Show Worked Solution

Cane toads have rapidly multiplied to 200 million since there introduction in Australia in 1935. This is largely due to their ability to produce large amounts of offspring all year round and have no predators, as they are extremely poisonous and toxic.
As a result, they have not needed to rapidly evolve as there are no significant pressures, but they have been shown to exhibit traits which allow them to travel faster.
This trait allows those which exist on the front-line of cane toad communities to outcompete their peers as well as travel further than cane toads at the back, leading to higher reproduction rates and hence a more commonly exhibited trait.

Calculus, EXT2 C1 2023 HSC 15a

Let $J_n= {\displaystyle \int_0^{\frac{\pi}{2}}} \sin ^n \theta \ d \theta$ where $n \geq 0$ is an integer.
Show that $J_n=\dfrac{n-1}{n} J_{n-2}$ for all integers $n \geq 2$. (3 marks)

--- 9 WORK AREA LINES (style=lined) ---
Let $I_n={\displaystyle \int_0^1 x^n(1-x)^n}\, dx $ where $ n $ is a positive integer.
By using the substitution $x=\sin ^2 \theta$, or otherwise,
show that $ I_n=\dfrac{1}{2^{2 n}} {\displaystyle \int_0^{\frac{\pi}{2}}} \sin ^{2 n+1} \theta \ d \theta $. (4 marks)

--- 12 WORK AREA LINES (style=lined) ---
Hence, or otherwise, show that $I_n=\dfrac{n}{4 n+2} I_{n-1}$, for all integers $n \geq 1$. (2 marks)
--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{See Worked Solutions}$
$\text{See Worked Solutions}$
$\text{See Worked Solutions}$

Show Worked Solution

i.	$J_n$	$= \displaystyle \int_0^{\frac{\pi}{2}} \sin^{n}\, \theta\, d\theta $
		$= \displaystyle \int_0^{\frac{\pi}{2}} \sin^{n-1}\, \theta \cdot \sin\,\theta\, d\theta $

$\text{Integrating by parts:} $

$u$	$=\sin^{n-1}\, \theta $	$u^{′}=(n-1) \cos\, \theta \cdot \sin^{n-2}\,\theta $
$v$	$=-\cos\,\theta $	$v^{′}=\sin \, \theta$

$J_n$	$= \big{[} -\cos\,\theta \cdot \sin^{n-1}\,\theta \big{]}_0^{\frac{\pi}{2}} + (n-1) \displaystyle \int_0^{\frac{\pi}{2}} \cos^{2} \theta \cdot \sin^{n-2}\theta\, d\theta$
	$=(n-1) \displaystyle \int_0^{\frac{\pi}{2}} (1-\sin^{2} \theta) \sin^{n-2}\theta\, d\theta$
	$=(n-1) \displaystyle \int_0^{\frac{\pi}{2}} \sin^{n-2}\theta-\sin^{n}\theta\, d\theta$
	$=(n-1)J_{n-2}-(n-1)J_n $

$J_n+(n-1)J_n $	$=(n-1)J_{n-2} $
$J_n(1+n-1) $	$=(n-1) J_{n-2} $
$J_n$	$= \dfrac{n-1}{n} J_{n-2} $

ii. $I_n= \displaystyle \int_0^1 x^{n}(1-x)^n\,dx $

$\text{Let}\ \ x=\sin^{2}\,\theta $

$\dfrac{dx}{d\theta}=2\sin\,\theta\, \cos\,\theta \ \Rightarrow \ dx=2\sin\,\theta \,\cos\,\theta\,d\theta $

$\text{When}\ \ x=1, \ \theta=\dfrac{\pi}{2}; \ \ x=0, \ \theta=0 $

$I_n$	$= \displaystyle \int_0^{\frac{\pi}{2}} \sin^{2n}\,\theta(1-\sin^{2}\,\theta)^{n} \cdot 2\sin\,\theta \,\cos\,\theta\,d\theta $
	$= 2 \displaystyle \int_0^{\frac{\pi}{2}} \sin^{2n+1}\,\theta \cdot \cos^{2n+1}\,\theta\,d\theta $
	$=\dfrac{2}{2^{2n+1}} \displaystyle \int_0^{\frac{\pi}{2}} (2\sin\,\theta\,\cos\,\theta)^{2n+1} d\theta $
	$=\dfrac{1}{2^{2n}} \displaystyle \int_0^{\frac{\pi}{2}} \sin^{2n+1}(2\theta)\, d\theta $

$\text{Let}\ \ u=2\theta $

$\dfrac{du}{d\theta}=2\ \ \Rightarrow\ \ \dfrac{du}{2}=d\theta$

$\text{When}\ \ \theta=\dfrac{\pi}{2}, \ u=\pi; \ \theta=0, \ u=0 $

$I_n=\dfrac{1}{2^{2n+1}} \displaystyle \int_0^{n} \sin^{2n+1} u\, du$

$\text{Since}\ \ \sin^{2n+1} u\ \ \text{is symmetrical about}\ \ u=\dfrac{\pi}{2} $

$\Rightarrow \displaystyle \int_0^{\pi} \sin^{2n+1} u\,du=2\displaystyle \int_0^{\frac{\pi}{2}} \sin^{2n+1} u\,du $

$I_n$	$= \dfrac{1}{2^{2n+1}} \cdot 2\displaystyle \int_0^{\frac{\pi}{2}} \sin^{2n+1} u\,du $
	$= \dfrac{1}{2^{2n}} \displaystyle \int_0^{\frac{\pi}{2}} \sin^{2n+1} u\,du $

$\text{Which can be expressed as:}$

$I_n= \dfrac{1}{2^{2n}} \displaystyle \int_0^{\frac{\pi}{2}} \sin^{2n+1} \theta\, d\theta $

♦♦ Mean mark (ii) 34%.

iii.	$I_n$	$=\dfrac{1}{2^{2n}} \displaystyle \int_0^{\frac{\pi}{2}} \sin^{2n+1} \theta\, d\theta $
		$=\dfrac{1}{2^{2n}} J_{2n+1} \ \ \ \text{(by definition)}$
		$=\dfrac{1}{2^{2n}} \cdot \underbrace{\dfrac{2n}{2n+1} \cdot J_{2n+1}}_{\text{using part i}} $
		$= \dfrac{n}{2(2n+1)} \cdot \dfrac{2^2}{2^{2n}}\cdot J_{2n-1} $
		$= \dfrac{n}{4n+2} \cdot \underbrace{\dfrac{1}{2^{2n-2}}\cdot J_{2n-1}}_{=I_{n-1} \ \ \text{(using part ii)}} $
		$=\dfrac{n}{4 n+2} I_{n-1}$

♦♦ Mean mark (iii) 28%.

Mechanics, EXT2 M1 2023 HSC 14c

A projectile of mass $M$ kg is launched vertically upwards from the origin with an initial speed $v_0$ m s$^{-1}$. The acceleration due to gravity is $ {g}$ ms$^{-2}$.

The projectile experiences a resistive force of magnitude $kMv^2$ newtons, where $k$ is a positive constant and $v$ is the speed of the projectile at time $t$ seconds.

The maximum height reached by the particle is $H$ metres.
Show that $H=\dfrac{1}{2 k} \ln \left(\dfrac{k v_0{ }^2+g}{g}\right)$. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---
When the projectile lands on the ground, its speed is $v_1 \text{m} \ \text{s}^{-1}$, where $v_1$ is less than the magnitude of the terminal velocity.
Show that $g\left(v_0^2-v_1^2\right)=k v_0^2 v_1^2$. (3 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{See Worked Solution}$
$\text{See Worked Solution}$

Show Worked Solution

i. $\text{Taking up as positive:}$

$M\ddot x$	$=-Mg-kMv^2$
$\ddot x$	$=-g-kv^2$
$v \cdot \dfrac{dv}{dx}$	$=-(g+kv^2) $
$\dfrac{dv}{dx}$	$=-\dfrac{g+kv^2}{v} $
$\dfrac{dx}{dv}$	$=-\dfrac{v}{g+kv^2} $
$x$	$=-\dfrac{1}{2k} \displaystyle \int \dfrac{2kv}{g+kv^2}\, dv $
	$=-\dfrac{1}{2k} \ln \|g+kv^2\|+c $

$\text{When}\ \ x=o, \ v=v_0: $

$c=\dfrac{1}{2k} \ln |g+kv_0^2| $

$x$	$=\dfrac{1}{2k} \ln \|g+kv_0^2\|-\dfrac{1}{2k} \ln \|g+kv^2\| $
	$=\dfrac{1}{2k} \ln \Bigg{\|} \dfrac{g+kv_0^2}{g+kv^2} \Bigg{\|} $

$\text{When}\ \ v=0, x=H: $

$H=\dfrac{1}{2k} \ln \Bigg{(} \dfrac{g+kv_0^2}{g} \Bigg{)},\ \ \ \ (k>0) $

ii. $\text{When projectile travels downward:} $

$M \ddot x$	$=Mg-kMv^2$
$\ddot x$	$=g-kv^2$
$v \cdot \dfrac{dv}{dx}$	$=g-kv^2$
$\dfrac{dx}{dv}$	$=\dfrac{v}{g-kv^2}$
$x$	$=-\dfrac{1}{2k} \displaystyle \int \dfrac{-2kv}{g-kv^2}\,dv $
	$=-\dfrac{1}{2k} \ln\|g-kv^2\|+c $

$\text{When}\ \ x=0, \ v=0: $

$c=\dfrac{1}{2k} \ln g $

$x=\dfrac{1}{2k} \ln \Bigg{|} \dfrac{g}{g-kv^2} \Bigg{|} $

$\text{When}\ \ x=H, \ v=v_1: $

$\dfrac{1}{2k} \ln \Bigg{(} \dfrac{g+kv_0^2}{g} \Bigg{)}$	$=\dfrac{1}{2k} \ln \Bigg{\|} \dfrac{g}{g-kv_1^2} \Bigg{\|} $
$\dfrac{g+kv_0^2}{g} $	$=\dfrac{g}{g-kv_1^2} $
$g^2$	$=(g+kv_0^2)(g-kv_1^2) $
$g^2$	$=g^2-gkv_1^2+gkv_0^2-k^2v_0^2v_1^2 $
$gkv_0^2-gkv_1^2 $	$=k^2v_0^2v_1^2 $
$gk(v_0^2-v_1^2) $	$=k^2v_0^2 v_1^2 $
$g(v_0^2-v_1^2) $	$=kv_0^2v_1^2 $

♦♦ Mean mark (ii) 31%.

BIOLOGY, M8 2023 HSC 16 MC

Mesothelioma is a non-infectious environmental disease caused by exposure to asbestos. The table shows the number of new cases, existing cases and deaths caused by Mesothelioma in Australia in 2020.

	New Cases	Existing cases - five year survival	Deaths
Males	499	801	590
Females	143	239	206
Total	642	1040	796

In 2020 the Australian population was 26 million.

What is the incidence rate for Mesothelioma in 2020 as a percentage?

0.000025%
0.000040%
0.0025%
0.0040%

Show Answers Only

$C$

Show Worked Solution

$ \text{Incidence}$	$ =\dfrac{\text{new cases} }{\text{population}} $
	$=\dfrac{642}{26\ 000\ 000} $
	$=0.000025 \times 100\text{%} $
	$= 0.0025\text{%} $

$\Rightarrow C$

♦ Mean mark 52%.

Mechanics, EXT2 M1 2023 HSC 14b

The point $P$ is 4 metres to the right of the origin $O$ on a straight line.

A particle is released from rest at $P$ and moves along the straight line in simple harmonic motion about $O$, with period $8 \pi$ seconds.

After $2 \pi$ seconds, another particle is released from rest at $P$ and also moves along this straight line in simple harmonic motion about $O$, with period $8 \pi$ seconds.

Find when and where the two particles first collide. (3 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Collision time:}\ \ t=5\pi \ \text{seconds} $

$\text{Collision position:}\ \ -2\sqrt2 \ \text{m (or}\ \ 2\sqrt2\ \text{m to left of origin}) $

Show Worked Solution

$\text{Particle is at rest at point}\ P\ \text{and moving in SHM} $

$\Rightarrow P\ \text{is at extremity of motion} $

$\text{Period}\ = 8\pi = \dfrac{2\pi}{n}\ \Rightarrow \ n=\dfrac{1}{4} $

$\text{Amplitude}\ =4 $

$\text{Particle 1:}$

$x_1=a\,\cos(nt)=4\,\cos\,\dfrac{t}{4} $

$\text{Particle 2:}$

$x_2$	$=4\,\cos\,\Big(\dfrac{t-2\pi}{4}\Big) $
	$=4\,\cos\,\Big(\dfrac{2\pi-t}{4}\Big) $
	$=4\,\cos\,\Big(\dfrac{\pi}{2}-\dfrac{t}{4}\Big) $
	$=4\,\sin\,\Big(\dfrac{t}{4}\Big) $

$\text{Collision when}\ \ x_1=x_2: $

$4\,\sin\,\Big(\dfrac{t}{4}\Big) $	$=4\,\cos\,\Big(\dfrac{t}{4}\Big) $
$\tan\,\Big(\dfrac{t}{4}\Big) $	$=1$
$\dfrac{t}{4}$	$=\dfrac{\pi}{4}, \dfrac{5\pi}{4} $
$t$	$=\pi, 5\pi, … $

$\text{1st collision occurs at}\ \ t=5\pi \ \text{seconds}\ \ (t\geq 2\pi)$

$\text{Position of collision}$

$\text{Find}\ x_1\ \text{when}\ t=5\pi : $

$x_1=4\,\cos\,\dfrac{5\pi}{4}=-\dfrac{4}{\sqrt2} = -2\sqrt2 \ \text{m}\ \ (\text{or}\ 2\sqrt2\ \text{m to left of origin}) $

♦ Mean mark 39%.

Complex Numbers, EXT2 N2 2023 14a

Let $z$ be the complex number $z=e^{\small{\dfrac{i \pi}{6}}} $ and $w$ be the complex number $w=e^{\small{\dfrac{3 i \pi}{4}}} $.

By first writing $z$ and $w$ in Cartesian form, or otherwise, show that
$|z+w|^2=\dfrac{4-\sqrt{6}+\sqrt{2}}{2}$. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
The complex numbers $z, w$ and $z+w$ are represented in the complex plane by the vectors $\overrightarrow{O A},\overrightarrow{O B}$ and $\overrightarrow{O C}$ respectively, where $O$ is the origin.
Show that $\angle A O C=\dfrac{7 \pi}{24}$. (2 marks)

--- 8 WORK AREA LINES (style=lined) ---
Deduce that $\cos \dfrac{7 \pi}{24}=\dfrac{\sqrt{8-2 \sqrt{6}+2 \sqrt{2}}}{4}$. (1 mark)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{See Worked Solutions}$
$\text{See Worked Solutions}$
$\text{See Worked Solutions}$

Show Worked Solution

i. $z=e^{\small\dfrac{i \pi}{6}} = \cos\,\dfrac{\pi}{6} + i \,\sin\,\dfrac{\pi}{6} = \dfrac{\sqrt3}{2} + \dfrac{1}{2}i $

$w=e^{\small\dfrac{3i \pi}{4}} = \cos\,\dfrac{3\pi}{4} + i \,\sin\,\dfrac{3\pi}{4} = -\dfrac{1}{\sqrt2} + \dfrac{i}{\sqrt2} $

$\|z+w\|^2$	$=\Bigg{\|} \dfrac{\sqrt3}{2}+\dfrac{1}{2}i-\dfrac{1}{\sqrt2}+\dfrac{i}{\sqrt2} \Bigg{\|}$
	$=\Bigg{\|} \Bigg{(}\dfrac{\sqrt3}{2}-\dfrac{1}{\sqrt2} \Bigg{)} +\Bigg{(}\dfrac{1}{2}+\dfrac{1}{\sqrt2}\Bigg{)}\,i \Bigg{\|}$
	$=\Bigg{\|} \dfrac{\sqrt6-2}{2\sqrt2}+\dfrac{\sqrt2+2}{2\sqrt2}\,i \Bigg{\|}$
	$= \dfrac{(\sqrt6-2)^2+(\sqrt2+2)^2}{(2\sqrt2)^2}$
	$= \dfrac{6-4\sqrt6+4+2+4\sqrt2+4}{8}$
	$=\dfrac{16-4\sqrt6+4\sqrt2}{8} $
	$=\dfrac{4-\sqrt6+\sqrt2}{2} $

ii.

$\angle AOB= \arg(w)-\arg(z)=\dfrac{3\pi}{4}-\dfrac{\pi}{6}=\dfrac{7\pi}{12} $

$ |z|=|w|=1\ \Rightarrow AOBC\ \text{is a rhombus.} $

$\overrightarrow{OC}\ \text{is a diagonal of rhombus}\ AOBC $

$\Rightarrow \overrightarrow{OC}\ \text{bisects}\ \angle AOB $

$\therefore \angle AOC= \dfrac{1}{2} \times \dfrac{7\pi}{12}=\dfrac{7\pi}{24} $

iii. $\text{In}\ \triangle AOC: $

$ \overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA} = \overrightarrow{OB} $

$\Rightarrow \overrightarrow{OB}\ \text{is represented by}\ w. $

$\text{Using the cos rule in}\ \triangle AOC: $

$\cos\,\dfrac{7\pi}{24}$	$=\dfrac{\|z\|^2+\|z+w\|^2-\|w\|^2}{2\|z\|\|z+w\|}$
	$=\dfrac{ 1+\frac{4-\sqrt6+\sqrt2}{2}-1}{2 \times 1 \sqrt{\frac{4-\sqrt6+\sqrt2}{2}}} $
	$=\dfrac{\sqrt{\frac{4-\sqrt6+\sqrt2}{2}} \times 2} {2 \times 2} $
	$=\dfrac{\sqrt{4( \frac{4-\sqrt6+\sqrt2}{2})}} {4} $
	$=\dfrac{8-2\sqrt6+2\sqrt2}{4} $

♦♦ Mean mark (iii) 26%.

\(4.0486 \times 10^{-13}\)	\(=\dfrac{(x)(2x)^2}{(0.9)^2}\)
\(4.0486 \times 10^{-13}\)	\(=\dfrac{4x^3}{(0.9)^2}\)
\(4x^3\)	\(=3.279 \times 10^{-13}\)
\(x\)	\(=4.344 \times 10^{-5}\)

\(K_{sp}\)	\(= \ce{[Pb^2+][ 2I^-]^2}\)
\(9.8 \times 10^{-9}\)	\(= [x][ 2x]^2\)
\(x^3\)	\(=\dfrac{9.8 \times 10^{-9}}{4}\)
\(x\)	\(=0.001348\ \text{mol L}^{-1}\)

\(k\)	\(=\) \(\text{gradient}\)
	\(=\dfrac{24-6}{0.08-0.02}\)
	\(=300\)

\(E_k\)	\(=0.96\) \(\text{J}\)
\(\dfrac{1}{2}mv^2\)	\(=0.96\)
\(v^2\)	\(=\dfrac{2 \times 0.96}{0.04}\)
\(v\)	\(=6.9\) ms\(^{-1}\)

\(\|z-1\|\)	\(<2\|z-i\|\)
\((x-1)^2+y^2\)	\(<4(x^2+(y-1)^2) \)
\(x^2-2x+1+y^2\)	\(<4x^2+4y^2-8y+4\)
\(0\)	\(<3x^2+2x+3y^2-8y+3\)

\(\ddot x\)	\(=-2\cos\,2t+4\sin\,2t\)
	\(=-4\Big(\dfrac{1}{2}\cos\,2t-\sin\,2t\Big) \)
	\(=-4\Big(x-\dfrac{1}{2}\Big) \ \ \ \text{(SHM)}\)

\( \text{Data from} \ ^{1} \text{H NMR spectrum of compound C} \)
\( Chemical \ Shift \ \text{(ppm)} \)	\( Relative \ peak \ area \)	\( Splitting \ pattern \)
\(1.01\)	\(3\)	\(\text{Triplet}\)
\(1.05\)	\(3\)	\(\text{Triplet}\)
\(1.65\)	\(2\)	\(\text{Multiplet}\)
\(2.42\)	\(2\)	\(\text{Triplet}\)
\(2.46\)	\(2\)	\(\text{Quartet}\)

\(K_Q\)	\(=\dfrac{1}{2}mv_Q^2\)
\(v_Q\)	\(=\sqrt{\dfrac{2K_Q}{m}}\)
	\(=\sqrt{\dfrac{2 \times 1.194 \times 10^{10}}{400}}\)
	\(=7.727 \times 10^3\ \text{ms}^{-1}\)

\(K_Q\)	\(=\dfrac{1}{2}mv_Q^2\)
\(v_Q\)	\(=\sqrt{\dfrac{2K_Q}{m}}\)
	\(=\sqrt{\dfrac{2 \times 1.194 \times 10^{10}}{400}}\)
	\(=7.727 \times 10^3\ \text{ms}^{-1}\)